Оглавление
| Введение………………………………………………………………………….. |
С.3 |
| Глава
I
. Психолого – педагогические основы формирования логического мышления младших школьников……………………………
|
с.8
|
1.1. Мышление: сущность, виды………………………………………
1.2. Приемы логического мышления младших школьников………
1.3. Особенности логического мышления младших школьников…
Выводы по 1главе………………………………………………………………..
Глава
II
. Использование логических задач при формировании логического мышления младших школьников на уроках математики..
.
2.1. Комплекс интеллектуальных игр для развития мышления учащихся …………………………………………………………………………
2.2. Использование приемов логического мышления на уроках математики в начальной школе………………..………………………………
Выводы по 2 главе………………………………………………………………..
Заключение………………………………………………………………………...
Список литературы.………………………………………………………………
Приложения……………………………………………………………………….
|
С.8
С. 16
С.22
С.27
С.28
С.28
С.35
С.50
С.51
С.53
С.56
|
ВВЕДЕНИЕ
Актуальность исследования:
вся жизнь человека постоянно ставит перед ним острые и неотложные задачи и проблемы. Возникновение таких проблем, трудностей, неожиданностей означает, что в окружающей нас действительности есть еще много неизвестного, непонятного, непредвиденного, скрытого. Следовательно, нужно все более глубокое познание мира, открытие в нем все новых и новых процессов, свойств, взаимоотношений людей и вещей. Мышление потому и необходимо, что в ходе жизни и деятельности каждый человек наталкивается на какие-то новые, неизвестные свойства предмета. Прежних знаний оказывается недостаточно. Вселенная бесконечна, и бесконечен процесс её познания. Мышление всегда устремлено в эти бескрайние глубины неизведанного, нового. Каждый человек, когда мыслит, самостоятельно делает открытие чего-то нового, неизвестного (пусть это открытие небольшое, только для себя). Например, всякий школьник, решая учебную задачу, обязательно открывает для себя нечто новое.
Мышление имеет целенаправленный характер. Необходимость в мышлении возникает прежде всего тогда, когда в ходе жизни и практики перед человеком появляется новая цель, новая проблема, новые обстоятельства и условия деятельности. По самому своему существу мышление необходимо лишь в тех ситуациях, в которых возникают эти новые цели, а старые, прежние средства и способы деятельности недостаточны (хотя и необходимы) для их достижения.
В психологии распространена следующая простейшая и несколько условная классификация видов мышления:
1) наглядно-действенное;
2) наглядно-образное;
3) абстрактное.
В ходе исторического развития люди решали встающие перед ними задачи сначала в плане практической деятельности; лишь затем из неё
выделилась деятельность теоретическая. Например, сначала наш далекий предок научился практически (шагами и т.д.) измерять земельные участки, и только потом на основе знаний, складывающихся в ходе этой практической деятельности, постепенно возникала и развивалась геометрия, как особая теоретическая наука. Практическая и теоретическая деятельности неразрывно взаимосвязаны. «Производство идей, представлений, сознания первоначально непосредственно вплетено в материальную деятельность …». Это и означает, что первичной является не чисто теоретическая, а именно практическая деятельность. Лишь по мере развития последней из неё выделяется как относительно самостоятельная теоретическая мыслительная деятельность.
Не только в историческом развитии человека, но и в процессе психического развития каждого ребенка исходной будет не чисто теоретическая, а практическая деятельность. Внутри этой последней и развивается вначале детское мышление. В преддошкольном возрасте (до трех лет включительно) мышление в основном наглядно-действенное. Ребенок анализирует и синтезирует познаваемые объекты по мере того, как он руками, практически разъединяет, расчленяет и вновь объединяет, соотносит, связывает друг с другом те или иные предметы, воспринимаемые в данный момент. Любознательные дети часто ломают свои игрушки именно с целью выяснить, «что там внутри».
В простейшей форме наглядно-образное мышление возникает преимущественно у дошкольников, т.е. в возрасте четырех — семи лет. Связь мышления с практическими действиями у них хотя и сохраняется, но не является такой тесной, прямой и непосредственной как раньше. В ходе анализа и синтеза познаваемого объекта ребенок необязательно и далеко не всегда должен потрогать руками заинтересовавший его предмет. Во многих случаях не требуется систематического практического манипулирования (действовали) с объектом, но во всех случаях необходимо отчетливо воспринимать и наглядно представлять этот объект. Иначе говоря, дошкольники мыслят лишь наглядными образцами и еще не владеют понятиями.
На основе практического и наглядно-чувственного опыта детей в школьном возрасте развивается – сначала в простейших формах – отвлеченное мышление, т. е. Мышление в форме абстрактных понятий. Мышление выступает здесь не только в виде практических действий и не только в форме наглядных образов (восприятий и представлений), а прежде всего в форме отвлеченных понятий и рассуждений.
Индивидуальные особенности мышления у различных детей проявляются прежде всего в том, что у них по-разному складывается соотношение разных и взаимодополняющих видов и форм мыслительной деятельности (наглядно-образного, наглядно-действенного и отвлеченного мышления). К индивидуальным особенностям мышления относятся также и другие качества познавательной деятельности:
- самостоятельность
- гибкость
-быстрота мысли.
Самостоятельность мышления проявляется прежде всего в умении увидеть и поставить новый вопрос, новую проблему и затем решить их своими силами. Творческий характер мышления отчетливо выражается именно в такой самостоятельности.
Гибкость мышления заключается в умении изменять намеченный путь (план) решения задач, если он не удовлетворяет тем условиям проблемы, которые постепенно вычленяются в ходе её решения и которые не удалось учесть с самого начала.
Быстрота мысли особенно нужна в тех случаях, когда от человека требуется принимать определенные решения в очень короткий срок (например, во время аварии). Но она нужна также и школьникам. Так, некоторые хорошие ученики даже в старших классах, когда их вызывают к доске решать новую для них задачу, смущаются и теряются. Эти отрицательные эмоции затормаживают их мышление; мысль начинает работать очень медленно и часто безуспешно, хотя в спокойной обстановке (дома или за партой, а не у доски) те же школьники быстро и хорошо решают подобные и даже более трудные задачи.
Эти индивидуальные особенности некоторых учеников необходимо специально учитывать, чтобы правильно оценить их умственные способности и знания.
Исходя из актуальности данной проблемы для проектирования начальной школы можно определить тему дипломной работы:
Формирование логического мышления как условие эффективности учения младших школьников.
Объект исследования
– процесс формирования логического мышления младших школьников.
Предмет исследования
– логические задачи как средства развития мышления младших школьников.
Цель исследования –
предложить и апробировать логические задачи, способствующие формированию логического мышления младших школьников.
Задачи:
· проанализировать психолого-педагогическую литературу по проблеме;
· раскрыть сущность и понятие мышления;
· подобрать логические задачи для формирования логического мышления младших школьников.
Гипотеза исследования
– в основу дипломной работы положено предположение о том, что условием эффективности учения младших школьников является формирование логического мышления.
Методы исследования
– теоретический анализ психолого- педагогической литературы, экспериментальная работа, тестирование, наблюдение, анализ результатов эксперимента.
Этапы исследования:
- теоретический: октябрь 2006 – декабрь 2006 гг. (анализ литературы, составление литературы);
- экспериментальный: январь 2007 – март 2007 гг. (накопление, обобщение, классификация, интерпретация имперического и теоретического материала, коррекция уточнения логики и результатов исследования);
- обобщающий (обработка и анализ полученных результатов, оформление дипломной работы).
Обоснованность, достоверность
положений и выводов исследования обеспечивается результатами опытной работы, адекватность методики исследования его предмету и задачам.
Апробация и внедрение результатов исследования
осуществляется по различным направлениям: выступление автора на занятиях в учебном заведении, на заседании в учебном заведении, на учебно-практических конференциях, на заседании методического совета в базовой школе; в процессе непрерывной педагогической практики студентов и др.
Практическая значимость –
рекомендована учителям для повышения уровня образованности, материал был предоставлен вниманию на методическом объединении.
База исследования –
МОУ СОШ №2 города Карасука.
Содержание дипломного исследования:
работа состоит из введения, двух глав, выводов по главам, заключения, списка литературы, приложения.
Глава 1
Психолого-педагогические основы формирования логического мышления младших школьников
1.1. Мышление: сущность, виды. Приемы логического мышления младших школьников
Жизнь человека ставит перед ним острые и неотложные задачи ипроблемы. Возникновение таких проблем, трудностей, неожиданностей означает, что в окружающей нас действительности есть еще много неизвестного, непонятного, непредвиденного, скрытого, требующего все более глубокого познания мира, открытия в нем новых и новых процессов, свойств и взаимоотношений людей и вещей. Вселенная бесконечна, и бесконечен процесс её познания. Мышление всегда устремлено в эти бескрайние глубины неизведанного, нового. Каждый человек делает множество открытий в своей жизни (неважно, что эти открытия небольшие, только для себя, а не для человечества).
Например, всякий школьник, решая учебную задачу, обязательно открывает для себя что-то новое.
Мышление
- это социально-обусловленный, неразрывно-связанный с речью психический процесс поисков и открытия существенно нового, процесс опосредствованного и обобщенного отражения действительности в ходе её анализа и синтеза. Мышление возникает на основе практической деятельности из чувственного познания и далеко выходит за его пределы.
«У здорового смысла прекрасный нюх, но зато старчески тупые зубы» -
так охарактеризовал значение мышления один из наиболее интересных исследователей К. Дункер, очевидным образом противопоставляя его здоровому смыслу [11стр. 57].С этим трудно согласиться, имея в виду, что мышление в его высших творческих человеческих формах не сводится ни к интуиции, ни к жизненному опыту, составляющим основу так называемого «здорового смысла». Что же такое мышление? Каковы его отличия от других
способов познания человеком действительности?
Прежде всего, мышление является высшим, познавательным процессом. Оно представляет собой порождение нового знания, активную форму творческого отражения и преобразования человеком действительности. Мышление порождает такой результат, какого ни в самой действительности,
ни у субъекта на данный момент времени не существует. Мышление (в элементарных формах оно имеется и у животных) также можно понимать как получение новых знаний, творческое преобразование имеющихся представлений.
Отличие мышления от других психологических процессов состоит также в том, что оно почти всегда связано с наличием проблемной ситуации, задачи, которую нужно решить, и активным изменением условий, в которых эта задача задана. Мышление в отличии от восприятия выходит за пределы чувственно данного, расширяет границы познания. В мышлении на основе сенсорной информации делаются определенные теоретические и практические выводы. Оно отражает бытие не только в виде отдельных вещей, явлений и их свойств, но и определяет связи, существующие между ними, которые чаще всего непосредственно, в самом восприятии человеку не даны. Свойства вещей и явлений, связи между ними отражаются в мышлении в обобщенной форме, в виде законов, сущностей.
На практике мышление как отдельный психический процесс не существует, оно незримо присутствует во всех других познавательных процессах: в восприятии, внимании, воображении, памяти, речи. Высшие формы этих процессов обязательно связаны с мышлением и степень его участия в этих познавательных процессах определяет их уровень развития.
Технологически исследовать мышление как процесс значит изучить внутренние, скрытые причины, приводящие к образованию тех или иных познавательных результатов. Таковыми результатами, продуктами мышления являются, например, следующие факты: решил или не решил задачу данный ученик; возник или нет у него замысел, план решения, догадка; усвоил он или нет определенные знания, способы действия; сформировалось ли у него новое понятие и т.д. За всеми этими внешне выступающими фактами психология стремления внутренний мыслительный процесс, к ним приводящий. Тем самым она исследует внутренние, специфические причины, которые позволяют объяснить, а не
только констатировать и описывать внешне выступающие психологические явления и события. Психологическая наука исходит при этом из принципа детерминизма (принципа причинной обусловленности): внешние причины действуют через внутренние условия. Иначе говоря, например, любое педагогическое воздействие влияет на человека не прямо и не непосредственно, а опосредовано-преломляясь через психическое состояние данного человека в зависимости от его чувств, мыслей и т.д.
Мышление -
это психологический процесс познания, связанный с открытием субъективного нового знания, с решением задач, с творческим преобразованием действительности.
Мышление
-
это движение идей, раскрывающее суть вещей. Его итогом является не образ, а некоторая мысль, идея.
На рис. 1 представлены основные виды мышления. Рассмотрим их подробнее.
  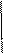  Виды мышления Виды мышления
       теоретическое теоретическое
практическое
понятийное
образное
наглядно-образное
наглядно-действенное

    Рис. 1. Основные виды мышления у человека Рис. 1. Основные виды мышления у человека
Теоретическое понятийное мышление
(абстрактное) - это такое мышление, пользуясь которым человек в процессе решения задачи обращается к понятиям, выполняет действия в уме, непосредственно не имея дела с опытом, получаемым при помощи органов чувств. Он обсуждает и ищет решение задачи с начала и до конца в уме, пользуясь готовыми знаниями, полученными другими людьми, выраженными в понятийной форме, суждениях, умозаключениях.
На основе практического и наглядно-чувственного опыта у детей в школьном возрасте развивается, сначала в простейших формах, отвлеченное мышление, т.е. мышление в форме абстрактных понятий.
Овладение понятиями в ходе усвоения школьниками основ различных наук - математики, физики, истории - имеет огромное значение в умственном развитии детей. Формирование и усвоение математических, географических, физических, биологических и многих других понятий в ходе школьного обучения составляют предмет многочисленных исследований (П.Я.Гальперин, В.В.Давыдов, Г.С.Костюк, Н.А.Менчинская,
Р.Г.Натадзе, Д.Б.Элькоиин и др.).
В этих работах детально прослеживается, какие именно признаки понятий, в какой последовательности, при каких условиях усваиваются учащимися. В конце школьного обучения у детей формируется в той или иной степени система понятий. Ученики начинают успешно оперировать не только отдельными понятиями (например, "удельный вес", "млекопитающие", "критический реализм"), но и целыми классами или системами понятий (например, система геометрических понятий).
Второй вид мышления - образно-теоретический,
в прошлые века в связи с ним называли имена поэтов, художников, архитекторов.
Теоретическое образное мышление отличается от понятийного тем, что материалом, который здесь использует человек для решения задачи, являются не понятия, суждения или умозаключения, а образы. Они или непосредственно извлекаются из памяти, или творчески воссоздаются
воображением. Таким мышлением пользуются работники литературы, искусства, вообще люди творческого труда, имеющие дело с образами. В ходе решения мыслительных задач соответствующие образы мысленно преобразуются так, чтобы человек в результате манипулирования ими смог непосредственно усмотреть решение интересующей его задачи.
Оба рассмотренных вида мышления - теоретическое понятийное и теоретическое образное - в действительности, как правило, сосуществуют. Они неплохо дополняют друг друга, раскрывают человеку разные, но взаимосвязанные стороны бытия. Теоретическое понятийное мышление дает хотя и абстрактное, но вместе с тем наиболее точное, обобщенное отражение действительности. Теоретическое образное мышление позволит получить конкретное субъективное её восприятие, которое не менее реально, чем объективно-понятийное. Без того или другого вида мышления наше восприятие действительности не было бы столь глубоким и разносторонним, точным и богатым разнообразными оттенками, каким оно является на деле.
В простейшей форме наглядно-образное мышление
возникает преимущественно у дошкольников, т.е. в возрасте четырех-семи лет. Связь мышления с практическими действиями у них хотя и сохраняется, но не является такой тесной, прямой и непосредственной, как раньше. В ходе анализа и синтеза познавательного объекта ребенок необязательно и далеко не всегда должен потрогать руками заинтересовавший его предмет. Во многих случаях не требуется систематического практического манипулирования (действования), с объектом, но во всех случаях необходимо отчетливо воспринимать и наглядно представлять этот объект. Иначе говоря, дошкольники мыслят лишь наглядными образами и ещё не владеют понятиями (в строгом смысле).
Отсутствие у дошкольников понятий наиболее отчетливо обнаруживаются в следующих экспериментах швейцарского психолога Ж. Плаже.
Детям в возрасте около семи лет показывают два совершенно
одинаковых и равных по объему шарика, сделанных из теста. Они внимательно разглядывают оба представленных предмета и говорят, что они равны. Затем на глазах у испытуемых один из шариков превращают в линейку. Дети сами видят, что к этому расплющенному шарику не прибавили ни одного кусочка теста, а просто изменили форму. Тем не менее испытуемые считают, что количество теста в линейке увеличилось.
Дело в том, что наглядно-образное мышление детей непосредственно и полностью подчинено их восприятию, и поэтому они пока не могут отвлечься, абстрагирование с помощью понятий от некоторых наиболее бросающихся в глаза свойств рассматриваемого предмета. Думая об этой лепешке, дети смотрят на неё" и видят, что на столе она занимает больше места (большое пространство), чем шарик. Их мышление, протекающее в форме наглядных образов (следуя за восприятием), приводит к выводу, что в лепешке теперь больше теста, чем в шарике.
Отличительная особенность наглядно-образного мышления состоит в том, что мыслительный процесс в нем непосредственно связан с восприятием мыслящим человеком окружающей действительности и без него совершаться не может. Мысля наглядно-образно, человек привязан к действительности, а сами необходимые для мышления образы представлены в его кратковременной и оперативной памяти (в отличии от этого образа для теоретического образного мышления извлекаются из долговременной памяти и затем преображаются).
Особенность наглядно-действенного мышления заключается в том, что сам процесс мышления представляет собой практическую преобразовательную деятельность, осуществляемую человеком с реальными предметами. Основным условием решения задачи в данном случае являются правильные действия с соответствующими предметами. Этот вид мышления представлен у людей, занятых реальным производственным трудом, результатом которого является создание какого-либо конкретного материального продукта.
Разница между теоретическим и практическим видами мышления, по
мнению Б.М.Теплова, состоит лишь в том, что «они по-разному связаны с
практикой... Работа практического мышления в основном направлена на
разрешение частных конкретных задач..., тогда как работа
теоретического мышления направлена в основном на нахождение общих
закономерностей»
И теоретическое, и практическое мышление в конечном счете связаны с практикой, но в случае практического мышления эта связь имеет более прямой, непосредственный характер. Практический ум, как правило, на каждом шагу нацелен на решение практической задачи, и его выводы непосредственно проверяются практикой здесь и теперь. Теоретический же ум выступает как опосредованный: он проверяется на практике лишь в конечных результатах его работы.
Все перечисленные виды мышления у человека сосуществуют, могут быть представлены в одной и той же деятельности.
Однако в зависимости от её характера и конечных целей доминирует тот или иной вид мышления. По этому основанию они все и различаются. По степени своей сложности, по требованиям, которые они предъявляют к интеллектуальным и другим способностям человека, все названные виды мышления не уступают друг другу.
Уточним, что мы будем понимать под мышлением. Во-первых, это процесс, благодаря которому человек мысленно проникает за пределы того, что ему дано в ощущениях и в восприятии, т.е. с помощью мышления можно получать знания, недоступные органами чувств.
Во-вторых, мышление - и это уже должно быть ясно из сказанного выше - есть процесс решения задач. Там, где нет задачи, то есть вопроса, на который необходимо найти ответ в результате специальной умственной и практической работы, там нет и мышления.
В-третьих, мышление - это не прямое, а опосредованное познание человеком действительности, то есть такое, при котором он использует
разнообразные вспомогательные приемы и средства, рассчитанные на то, чтобы получить нужные знания.
Наконец, в-четвертых, мышление - это активная действительность человека, направленная на получение новых знаний. В этой деятельности есть и внутренняя (умственная) и внешняя (практическая) сторона -действия, подчиненные определенной логике и имеющие единую цель.
Целенаправленность к логике в умственных и практических действиях -один из признаков того, что эти действия - составляющие целостный процесс мышления.
Образное - это мышление, в котором на первый план выступает действие с образами, а не с понятиями. Образное, например, мышление инженера, художника, писателя, режиссера.
Их действия, направлены на решение своих профессиональных задач, будут, конечно, содержать в себе и элементы оперирования понятиями, и практические действия, но в целом в процессе решения задач такие действия будут играть подчиненную роль.
Практическим называется мышление, в котором над действиями с понятиями и образами преобладают реальные, практические действия с материальными предметами.
Наряду с понятием «мышление», в психологии используется термин «интеллект». Что это такое? Если мышление представляет собой процесс решения задач с целью получения новых знаний и создания чего либо, то интеллект - это характеристика общих способностей, необходимых для решения таких задач.
Интеллектуально развитым называют человека, который одинаково хорошо умеет решать и умственные, и образные, и практические задачи, т.е. обладает мышлением во всех трех названных областях. Односторонне интеллектуально развитым будет такой человек, чьи мыслительные способности в основном проявляются только в одной из перечисленных областей человеческой деятельности.
преемственность всех знаний, приобретаемых в ходе человеческих историй. Эта историческая преемственность знаний возможна лишь в случае их фиксации, закрепления, сохранения и передачи от одного человека к другому, от поколения к поколению. Такая фиксация всех основных результатов познания осуществляется с помощью языка - в книгах, журналах и т.д. Во всем этом наглядно проявляется социальная природа человеческого мышления. Умственное развитие человека необходимо совершенствовать в процессе усвоения знаний, выработанных человечеством в ходе общественно-исторического развития. Процесс познания мира индивидом обусловлен, опосредствован историческим развитием научного знания, результаты которого каждый индивид осваивает в ходе обучения. Фактически это общение человека с человечеством.
Для материалистического объяснения процессов мышления, психологическая наука должна была рассматривать мышление не как «проявление духа», а как процесс, который формируется в общественной истории, протекает сначала как развернутая предметная деятельность, использует систему языка с объективно заключенной системой смысловых связей и отношений и лишь, затем принимает свернутые, сокращенные формы, приобретая характер внутренних «умственных действий».
1.2.Приемы логического мышления младших школьников
Всегда было принято считать, что без знания логики, полученного в практике мышления или путем специального изучения, нет образованного человека. Сейчас, в условиях коренного преобразования характера человеческого труда, ценность такого знания возрастает.
Растущее значение компьютерной грамотности - свидетельство важности знания логики, являющейся одной из теоретических основ электронно-вычислительной техники.
Трудно найти многогранное и сложное явление, чем человеческое мышление. Оно изучается многими науками, и логика одна из них. Всякое движение нашей мысли, постигающей истину, добро и красоту, опирается на логические законы. Мы можем не осознавать их, но вынуждены всегда следовать им.
Логика -
особая наука о мышлении. Её можно, таким образом, определить как науку о законах и операциях правильного мышления.
Логика является анализом и критикой мышления. Она начинается с
изучения фактически применяемых способов рассуждения, но не останавливается на этом. Она стремится отделить приемы, способствующие эффективному познанию действительности, от тех, которые с большей или меньшей вероятностью приводят к ошибкам и тупикам. Логика должна также систематизировать и обосновать правильные и эффективные способы рассуждения. Для этого необходимо привести в систему, выявить их взаимоотношения, показать связь теории рассуждения с практикой мышления и т.д.
История логического исследования мышления охватывает около двух с половиной тысячелетий. Из других наук раньше логики начали складываться, пожалуй, только математика и философия.
Логика возникла в IV в. до н.э. в Древней Греции. Её основателем является древнегреческий философ Аристотель (384-422 г. до н.э.).
В длинной и богатой событиями истории логика отчетливо выделяются два основных этапа. Первый -
от древнегреческой логики до возникновения в прошлом век современной логики. Второй - с этого времени до наших дней. Первый этап именуется традиционной логикой,
второй этап -современной логикой.
Традиционная логика является, таким образом, предысторией современной.
Все собственно логическое содержание традиционной логики вошло в состав современной логики и составило её незначительную и не особенно важную часть.
На первом этапе логика развивалась очень медленно. Обсуждавшиеся в ней проблемы мало отличались от проблем, поставленных еще Аристотелем. Это дало повод философу И.Канту в конце XVII в. утверждать, что логика, подобно геометрии Евклида, является завершенной наукой, не продвинувшейся ко времени Аристотеля ни на один шаг и не имеющей собственной истории.
Ошибочность такого представления была ясно показана в последние сто с небольшим лет. В логике произошла научная революция, в корне изменившая её лицо. На смену традиционной логике пришла современная.
Традиционная логика была философской наукой: она развивалась в рамках философий, пользовалась, как и философия в целом, только естественным языком, дополнительным немногими специальными символами и понятиями, законом логики давалось философское истолкование и обоснование. Современная логика как самостоятельная наука возникла на стыке столь разных наук, как философия и математика, благодаря внедрению в логические исследования математических методов.
Современную логику нередко называют математической логикой,
подчеркивая тем самым своеобразие новых её методов в сравнении с использовавшимися ранее. Эти новые методы предполагают прежде всего использование для анализа правильного мышления искусственных (формализованных) языков, позволяющих избежать двусмысленностей и логической неясности естественного языка.
Широкое использование символических средств послужило основанием для того, что новую логику стали называть также символической.
Имена «математическая логика» и «символическая логика», обычно употребляемые и сейчас, обозначают одно и то же - современную логику. Она занимается тем же чем всегда занимается логика, - исследованием правильных способов рассуждения. Однако методы, применяемые ею, принципиально отличаются от методов, характерных для старой логики.
В России всегда были люди, стоявшие на уровне достижений логики своего времени и внесшие в её развитие важный вклад.
Математик и логик П.С.Лорецкий
оказал заметное влияние на развитие алгебраических теорий логики. Он первый в России начал читать лекции по математической логике, о которой говорил, что это «по предмету своему есть логика, а по методу математика».
Физик П.Эренфест еще в 1910 г. высказал гипотезу о возможности применения современной ему логики в науке и технике. В дальнейшем его гипотеза нашла прекрасное воплощение в электронно-вычислительной технике.
Логик Н.А.Васильев
уже в начале века подверг критике считавшийся в традиционной логике одним из основных закон исключенного третьего. В дальнейшем идеи, касающиеся ограниченной применимости данного закона и близких ему способов математического доказательства, были развиты математиками А.Н.Колмогоровым, В.А.Гливенко, А.А.Марковым и др.
Знание основ логики важно для каждого человека, так как умение правильно мыслить, доказывать истинность или ложность своих либо чужих утверждений, высказываний (суждений), предположений является жизненной необходимостью. Обучаться логике приходится уже с детских лет, когда формируется абстрактное, а не только конкретное мышление. Отдельные приемы логического мышления дети начинают усваивать в детском саду: это, например, анализ и синтез, сравнение и различение, описание и характеристика. В школе с первых дней обучения учащиеся активно работают с этими логическими приемами или операциями на всех уроках, развивая, углубляя и систематизируя свои знания. Но, конечно, наиболее систематизированное изложение основных знаний по формам и законам правильного мышления дает изучение логики как философской науки, которая развивается с IV в. до н. э. начиная с трудов Аристотеля.
Законы логики действуют во все времена, для всех национальностей, всех профессий (врачей, учителей, инженеров, научных работников, юристов, космонавтов и т.д.). Знание логики способствует культурному и интеллектуальному развитию личности.
Мышление в отличие от других процессов совершается в соответствии с определенной логикой. Соответственно, в структуре мышления можно выделить следующие логические операции: сравнение, анализ, синтез, абстракция и обобщение. Сравнение вскрывает тождество и различие вещей. Результатом сравнения, кроме того, может стать классификация. Нередко она выступает как первичная форма теоретического и практического познания.
Процесс решения задач, несомненно, является моделью, с наибольшей полнотой отражающей структуру интеллектуальной деятельности, и изучение особенностей этого процесса может дать существенные материалы для понимания психологии мышления человеком. В процессе мыслительной деятельности человек познает окружающий мир с помощью особых умственных операций. Эти операции составляют различные взаимосвязанные, переходящие друг в друга стороны мышления. Основными мыслительными операциями являются анализ
, синтез
, сравнение
, абстракция
, конкретизация
и обобщение
.
Анализ
— это мысленное разложение целого на части или мысленное выделение из целого его сторон, действий, отношений. В элементарной форме анализ выражается в практическом разложении предметов на составные части. Стол, например, можно расчленить на такие части, как крышка, ножки, ящики, распорки и т.д. При знакомстве детей с каким-нибудь растением им предлагают показать ею часть (ствол, ветви, листья, корни). Анализ бывает практическим (когда мыслительный процесс не посредственно включен в речевую деятельность) и умственным (теоретическим). Если анализ оторван от других опер он становится порочным, механистичным. Элементы такого анализа наблюдаются у ребенка на первых этапах развития мышления, когда ребенок разбирает, ломает игрушки на отдельные части, никак не используя их дальше.
Синтез
— это мысленное объединение частей, свойств, действий в единое целое. Операция синтеза противоположна анализу. В его процессе устанавливается отношение отдельных предметов или явлений как элементов или частей к их сложному целому, предмету или явлению. Синтез не является механическим соединением частей и поэтому не сводится к их сумме. При соединении отдельных частей машины, при их синтезе получается не груда металла, а машина, способная передвигаться. При химическом соединении кислорода и водорода получается вода. И синтез, и анализ занимают важное место в учебном процессе. Так, при обучении чтению звуков и букв составляются слоги, из слогов — слова, из слов — предложения.
Сравнение
— это установление сходства или различия между предметами и явлениями или их отдельными признаками. Практически сравнение наблюдается при прикладывании одного предмета к другому; например, одного карандаша к другому, линейки к парте и т.п. Так происходит процесс сравнения, когда мы измеряем, пространство или взвешиваем тяжести. Сравнение бывает односторонним (неполным, по одному признаку) и многосторонним (полным, по всем признакам); поверхностным и глубоким; неопосредствованным и опосредованным. Основное требование к операции сравнения, чтобы оно проводилось в одном отношении. Для более глубокого и точного познания деятельности особенно большое значение такое качество мышления как способность находить различие в наиболее сходных предметах и сходство — в различных,
Абстракция
состоит в том, что субъект, вычленяя какие-либо свойства, признаки изучаемого объекта, отвлекается от остальных. Так мы можем говорить о зеленом цвете как о благотворно действующем на зрение человека, не указывая конкретно предметов, имеющих зеленый цвет. В этом процессе признак, отделяемый от объекта, мыслится независимо от других признаков предмета, становится самостоятельным предметом мышления. Абстрагирование обычно осуществляется в результате анализа. Именно путем абстрагирования были созданы отвлеченные, абстрактные понятия длины, широты, количества, равенства, стоимости и т.д. Абстракция — сложный процесс, зависящий от своеобразия изучаемого объекта и целей, стоящих перед исследователем. Благодаря абстракции человек может отвлечься от единичного, конкретного. В то же время абстракция не существует без чувственной опоры, иначе она становится бессодержательной, формальной. Среди видов абстракции можно выделить практическую,
непосредственно включенную в процесс деятельности; чувственную или внешнюю; высшую,
опосредованную, выраженную в понятиях [58].
Конкретизация
предполагает возвращение мысли от общего и абстрактного к конкретному с целью раскрыть содержание. К конкретизации обращаются в том случае, если высказанная мысль оказывается непонятной другим или необходимо показать проявление общего в единичном. Когда нас просят привести пример, то, по сути дела, просьба заключается в конкретизации предшествующих высказываний.
Обобщение
— мысленное объединение предметов и явлений по их общим и существенным признакам. Например, сходные признаки имеющиеся в яблоках, грушах, сливах и т.п., соединяются в одном понятии, которое мы выражаем словом «фрукты». Мыслительная деятельность всегда направлена на получение результата. Человек анализирует предметы с тем, чтобы выявить в них общие закономерности и предсказать их свойства. Психолог изучает людей, чтобы вскрыть общие закономерности их развития. Повторяемость определенной совокупности свойств в ряде предметов указывает на более или менее существенные связи между ними. При этом обобщение вовсе не предполагает отбрасывания специфических особенных свойств предметов, а заключается в раскрытии их существенных связей. Существенное, т.е. необходимо между собой связанное и именно в силу этого неизбежно повторяющееся. Простейшие обобщения заключаются в объединении объектов на основе отдельных, случайных признаков. Более сложным является комплексное обобщение, при котором объекты объединены по разным основаниям. Наиболее сложно обобщение, в котором четко выделяются видовые и родовые признаки и объект, включается в систему понятий.
1. 3. Особенности логического мышления младших школьников
К началу младшего школьного возраста психическое развитие ребёнкадостигает достаточно высокого уровня. Все психические процессы: восприятие, память, мышление, воображение, речь – уже прошли достаточно долгий путь развития. Напомним, что различные познавательные процессы, обеспечивающиемногообразные виды деятельности ребёнка, функционируют не изолированно друг от друга, а представляют сложную систему, каждый из них связан со всеми остальными. Эта связь не остаётся неизменной на протяжении детства: в разные периоды ведущее значение для общего психического развития приобретает какой-либо один из процессов. Психологические исследования показывают, что в этот период именномышление в большей степени влияет на развитие всех психических процессов. В зависимости от того, в какой степени мыслительный процесс опираетсяна восприятие, представление или понятие, различают три основных видамышления: 1. Предметно-действенное (наглядно-действенное). 2. Наглядно-образное. 3. Абстрактное (словесно-логическое). Предметно-действенное мышление – мышление, связанное с практическими, непосредственными действиями с предметом; наглядно-образное мышление – мышление, которое опирается на восприятие или представление (характерно для детей раннего возраста). Наглядно-образное мышление даёт возможность решать задачи в непосредственно данном, наглядном поле. Дальнейший путь развития мышления заключается в переходе к словесно-логическому мышлению – это мышление понятиями, лишёнными непосредственной наглядности, присущей восприятию и представлению. Переход к этой новой форме мышления связан с изменением содержания мышления: теперь это уже не конкретные представления, имеющие наглядную основу и отражающие внешние признаки предметов, а понятия, отражающие наиболее существенные свойства предметов и явлений и соотношения между ними. Это новое содержание мышления в младшем школьном возрасте задаётся содержанием ведущей деятельности учебной. Словесно-логическое, понятийное мышление формируется постепенно напротяжении младшего школьного возраста. В начале данного возрастногопериода доминирующим является наглядно-образное мышление, поэтому, если в первые два года обучения дети много работают с наглядными образцами, то в следующих классах объём такого рода занятий сокращается. По мере овладения учебной деятельностью и усвоения основ научных знаний, школьник постепенно приобщается к системе научных понятий, его умственные операции становятся менее связанными с конкретной практической деятельностью или наглядной опорой. Словесно-логическое мышление позволяет ученику решать задачи и делать выводы, ориентируясь не на наглядные признаки объектов, а на внутренние, существенные свойства и отношения. В ходе обучения дети овладевают приёмами мыслительной деятельности, приобретают способность действовать «в уме» и анализировать процесс собственных рассуждений. Уребёнка появляются логически верные рассуждения: рассуждая, он использует операции анализа, синтеза, сравнения, классификации, обобщения. Младшие школьники в результате обучения в школе, когда необходиморегулярно выполнять задания в обязательном порядке, учатся управлять своиммышлением, думать тогда, когда надо. Во многом формированию такому произвольному, управляемому мышлению способствует задания учителя на уроке, побуждающие детей к размышлению. При общении в начальных классах у детей формируется осознанное критическое мышление. Это происходит благодаря тому, что вклассе обсуждаются пути решения задач, рассматриваются различные варианты решения, учитель постоянно просит школьников обосновывать, рассказывать, доказывать правильность своего суждения. Младший школьник регулярно становится в систему, когда ему нужно рассуждать, сопоставлять разные суждения, выполнять умозаключения. В процессе решения учебных задач у детей формируются такие операциилогического мышления как анализ, синтез, сравнение, обобщение и классификация. Напомним, что анализ как мыслительное действие предполагает разложениецелого на части, выделение путём сравнения общего и частного, различения существенного и не существенного в предметах и явлениях. Овладением анализом начинается с умения ребёнка выделять в предметах иявлениях различные свойства и признаки. Как известно, любой предмет можно рассматривать с разных точек зрения. В зависимости от этого на первый план выступают та или иная черта, свойства предмета. Умения выделять свойства даётся младшим школьникам с большим трудом. И это понятно, ведь конкретное мышление ребёнка должно проделывать сложную работу абстрагирования свойства от предмета. Как правило, из бесконечного множества свойств какого-либо предмета первоклассники могут выделить всего лишь два-три. По мере развития детей, расширения их кругозора и знакомства с различными аспектами действительности такая способность, безусловно, совершенствуется. Однако это не исключает необходимости специально учить младших школьников видеть в предметах и явлениях разные их стороны, выделять множество свойств. Параллельно с овладением приёмом выделения свойств путём сравненияразличных предметов (явлений) необходимо выводить понятие общих иотличительных (частных), существенных и несущественных признаков, при этом используется такие операции мышления как анализ, синтез, сравнение и обобщение. Неумение выделять общее и существенное может серьёзно затруднить процесс обучения. В этом случае типичного материала: подведение математической задачи под уже известный класс, выделения корня в родственных словах, краткий (выделение только главного) пересказ текста, деление его на части, выбор заглавия для отрывка и т.п. Умение выделять существенное способствует формированию другого умения - отвлекаться от несущественных деталей. Это действие даётся младшим школьникам с не меньшим трудом, чем выделение существенного. В процессе обучения задания приобретают более сложный характер: в результате выделения отличительных и общих признаков уже нескольких предметов, дети пытаются разбить их на группы. Здесь необходима такая операция мышления как классификация. В начальной школе необходимость классифицировать используется на большинстве уроков, как при введении нового понятия, так и на этапе закрепления. В процессе классификации дети осуществляют анализ предложенной ситуации, выделяют в ней наиболее существенные компоненты, используяоперации анализа и синтеза, и производит обобщение по каждой группе предметов, входящих в класс. В результате этого происходит классификацияпредметов по существенному признаку. Как видно из вышеизложенных фактов все операции логического мышления тесно взаимосвязаны и их полноценное формирование возможно только в комплексе. Только взаимообусловленное их развитие способствует развитию логического мышления в целом. Приёмы логического анализа, синтеза, сравнения, обобщения и классификации необходимы учащимся уже в 1 классе, без овладения ими не происходит полноценного усвоения учебного материала. Эти данные показывают, что именно в младшем школьном возрасте необходимо проводить целенаправленную работу по обучению детей основным приёмам мыслительной деятельности. Помощь в этом могут оказать разнообразные психолого–педагогические упражнения. Выводы по 1 главе
Для материалистического объяснения процессов мышления, психологическая наука должна была рассматривать мышление не как «проявление духа», а как процесс, который формируется в общественной истории, протекает сначала как развернутая предметная деятельность, использует систему языка с объективно заключенной системой смысловых связей и отношений и лишь, затем принимает свернутые, сокращенные формы, приобретая характер внутренних «умственных действий».
Процесс решения задач, несомненно, является моделью, с наибольшей полнотой отражающей структуру интеллектуальной деятельности, и изучение особенностей этого процесса может дать существенные материалы для понимания психологии мышления человеком. В процессе мыслительной деятельности человек познает окружающий мир с помощью особых умственных операций. Эти операции составляют различные взаимосвязанные, переходящие друг в друга стороны мышления. Основными мыслительными операциями являются анализ
, синтез
, сравнение
, абстракция
, конкретизация
и обобщение
.
Одной из наиболее распространенных в психологии является классификация видов мышления в зависимости от содержания решаемой задачи. Выделяют предметно-действенное
, наглядно-образное
и словесно-логическое мышление
.
Глава 2
Использование логических задач при формировании логического мышления младших школьников
на уроках математики
2.2. Комплекс интеллектуальных игр для развития мышления учащихся
Проблема развития, коррекции и совершенствования мышления учащихся - одна из сложнейших в психолого-педагогической практике. Справедливо считается, что главный путь ее решения — рациональная организация всего учебного процесса (включая логико-содержательное построение курсов, создание проблемных ситуации и обучении, соблюдение принципа диалогичности при проведении занятий и др.). В качестве же дополнительного, вспомогательного пути может рассматриваться специально организуемый игровой тренинг мышления.
Такой тренинг полезен всем учащимся, а в особенности тем, которые испытывают заметные трудности в выполнении различных видов учебной работы: понимании и осмыслении нового материала, его запоминании и усвоении, установлении связей между различными явлениями, решении теоретических и практических задач, выражении своих мыслей в речи.
Есть основания считать, что общим базисом, или «стартовой площадкой» для полноценного протекания любого мыслительного процесса, направленного как на понимание усваиваемого материала, так и на порождение принципиально нового, является наличие как минимум трех универсальных составляющих мышления:
I) высокий уровень сформированности элементарных мыслительных операций: анализа, синтеза, сравнения, выделения существенного и др.. выступающих и качестве наиболее «дробных» элементов мышления;
2) высокий уровень активности, раскованности и плюралистичности мышления, проявляющийся в продуцировании большого количества различных гипотез, установке па множественность вариантов решения, свободе выдвижения нестандартных идеи и гибкости переходов от одной к другой;
3) высокий уровень организованности и целенаправленности мышления, проявляющийся и четкой ориентации на выделение существенного вявлениях, использовании обобщенных схем анализа явления, осознании собственных способов мышления и контроле за ними. Трудности в овладении учебным материалом у подавляющего большинства слабо успевающих учащихся но многом объясняются именно недостаточной сформированностью названных качеств мышления.
Представленный ниже комплекс интеллектуальных игр направлен прежде всего на шлифовку элементарных мыслительных операций, формирование обшей интеллектуальной раскованности и отработку средств, обеспечивающих общую организованность мыслительного процесса. Он предназначен в первую очередь для учащихся, испытывающих различные трудности в понимании, воспроизведении и практическом применении учебных знаний, а также может применяться для всех желающих усовершенствовать свое мышление. Постепенное развитие и совершенствование этих мыслительных способностей обеспечивается в ходе выполнения разнообразных задании с использованием простого, хорошо знакомого материала в непринужденной игровой обстановке при непосредственном общении со сверстниками.
Отдельные интеллектуальные игры этого комплекса расположены в основном в порядке возрастающей сложности и в ряде случаев тематически связаны друг с другом, поэтому вводить их целесообразно именно в такой последовательности
Игровые занятия проводятся с группой из 5-12 учащихся. Длительность одного занятия со школьниками — 45 мин. со студентами - около полутора часов. Частота проведения -один-два раза в неделю. Общее количество занятий но является фиксированным и зависит от исходного уровня мышления участников и темна их продвижения в выполнении игровых задании. Каждая игра «прокручивается» несколько раз на различном материале и в течение нескольких занятий. Материал для очередного варианта игры можно подбирать имеете с ее участниками, что, однако, не исключает необходимости наличия у преподавателя заранее составленных игровых «заготовок».
Преподаватель (ведущий) на первом занятии знакомит участников тренинга с проблемой совершенствования и самосовершенствования мышления, указывает на основные трудности, мешающие его эффективному протеканию. С целью повышения мотивации игроков целесообразно во вступительной беседе подчеркнуть, что: а) речь идет именно о творческом, изобретательском мышлении, а не «обычном», рутинном, б) речь идет не о формировании такого мышления, а о его пробуждении, активизации, использовании; в) такое мышление часто бывает не связанным с успеваемостью; г) пробуждение такого мышления — дело трудное, но возможное.
Вопрос об эффективности описываемого тренинга и ее критериях требует специального систематического исследования. Пока лишь укажем, что, по данным наблюдений автора и школьных учителей, работавших под его руководством, такой тренинг не проходит бесследно для учащихся и положительно сказывается на их умственном развитии. Так, у подавляющего большинства школьников обнаруживается заметное улучшение в понимании, запоминании и изложении учебного материала, повышение интереса к умственной работе. А главное, эти ребята стали активнее на уроках, у многих из них удалось снять барьер «интеллектуальной неполноценности». Немаловажен и тот факт, что часть ребят, собираясь по своей инициативе, без преподавателя, продолжали заниматься освоенными интеллектуальными играми, вовлекая при этом в свои круг новых участников и даже пытаясь самостоятельно изобретать новые аналогичные игры. В этом случае, по-видимому, можно говорить уже о возникновении процесса самосовершенствования учащимися своего мышления, исходным «трамплином» для которого послужили занятия под руководством преподавателя.
Предлагаемый комплекс включает в себя следующие интеллектуальные игры.
Составление предложений
. Берутся наугад три слова, не связанные по смыслу, например, «озеро», «карандаш» и «медведь». Надо составить как можно больше предложений, которые обязательно включали бы в себя эти три слова (можно менять их падеж и использовать другие слова). Ответы могут быть банальными («Медведь упустил в озеро карандаш»), сложными, с выходом за пределы ситуации, обозначенной тремя словами, и введением новых объектов («Мальчик взял карандаш и нарисовал медведя, купающегося в озере»), и творческими, включающими эти предметы в нестандартные связи («Мальчик, тонкий, как карандаш, стоял возле озера, которое ревело, как медведь»).
Эта игра развивает способность быстро устанавливать разнообразные, иногда совсем неожиданные связи между привычными предметами, творчески создавать новые целостные образы из отдельных разрозненных элементов.
Заметим, что в этой и описываемых ниже играх ведущему важно установить, а игрокам найти «золотую» середину между количеством и качеством ответов: необходимо, с одной стороны, стимулировать большое число любых разнообразных ответов, с другой — поощрять оригинальные, творческие ответы.
Обязательным условием эффективности этих игр является сопоставление и обсуждение игроками всех предложенных ответов и развернутое обоснование, почему именно тот или иной отпет им понравился или не понравился.
Поиск общего
. Берутся наугад дна слова, также мало связанных, например, «тарелка» и «лодка». Следует выписать как можно больше обших признаков для этих предметов. Ответы могут быть стандартными («изделия человеческих рук», «имеют глубину»), и небесполезно попытаться найти побольше таких признаков. Но особенно ценятся необычные, неожиданные ответы, позволяющие увидеть эти предметы в совершенно новом свете; их оказывается не так уж и мало. Побеждает тот, у кого список общих признаков длиннее. Можно ввести и качественные критерии: начислять дополнительные баллы за оригинальность.
В дальнейшем поступившие ответы иерархизируются по степени существенности вскрываемых в них связен между предметами (такая работа необходима, чтобы учащиеся предельно четко усвоили, что такое существенные и несущественные признаки).
При проведении этой игры не стоит опасаться, что мышление учащихся начнет в дальнейшем всюду «соскальзывать» на несущественные признаки.
Эта игра учит в разрозненном, несвязном материале находить множество общих моментов, «состыковок» и дает четкое представление о степени существенности признаков.
Исключение лишнего слова
. Берутся любые три слова, например, «собака», «помидор», «солнце». Надо оставить только те слова, которые обозначают в чем-то сходные предметы, а одно слово, «лишнее», не обладающее этим общим признаком, исключить. Следует найти как можно больше вариантов исключения лишнего слова, а главное — больше признаков, объединяющих каждую оставшуюся пару слов и не присущих исключенному, лишнему. Не пренебрегая вариантами, которые сразу же напрашиваются (исключить «собаку», а «помидор» и «солнце» оставить, потому что они круглые), желательно поискать нестандартные и в то же время очень меткие решения. Побеждает тот, у кого ответов больше.
Эта игра развивает способность не только устанавливать неожиданные связи между разрозненными явлениями, но легко переходить от одних связен к другим, не зацикливаясь на них. Игра учит также одновременно удерживать в поле мышления сразу несколько предметов и сравнивать их между собой. Немаловажно, что игра формирует и установку на то. что возможны совершенно разные способы объединения и расчленения некоторой группы предметов, и поэтому не стоит ограничиваться одним-единственным «правильным» решением, а надо искать целое их множество.
Поиск аналогов
. Называется какой-либо предмет или явление, например, «вертолет».Необходимо выписать как можно больше его аналогов, т.е. предметов, сходных с ним по существенным признакам. С также систематизировать их по группам. Побеждает тот кто назвал наибольшее число групп аналогов.
Эта игра учит выделять в группе те самые разнообразные свойства, формирует способность классифицировать явления по их признакам.
Поиск противоположных предметов
. Называется какой-либо предмет надо назвать как больше других предметов, противоположных данному.
Эта игра формирует способность «вычерпывать» из предмета различные его свойства и использовать для поиска других предметов.
Поиск соединительных звеньев
. Задаются два предмета, например, «лопата» и «автомобиль». Надо назвать предметы, являющиеся как бы «переходным мостиком» от первого ко второму. Называемые предметы должны иметь четкую логическую связь с обоими заданными предметами. Например, в нашем случае это могут быть «экскаватор» (с лопатой сходен по функции, а с автомобилем входит в одну группу - транспортные средства), «рабочий» (он копает лопатой и одновременно является владельцем автомобиля) н др. Допускается использование и двух трех соединительных звеньев (лопата - тачка -- прицеп — автомобиль). Особое внимание обращается на четкое обоснование и раскрытие содержания каждой связи между соседними элементами цепочки. Побеждает тот, кто дал наибольшее число четко аргументированных вариантов решения.
Эта игра формирует способность легко и быстро устанавливать связи между явлениями, кажущимися на первый взгляд далекими друг от друга, а также находить предметы, имеющие общие признаки одновременно с несколькими другими предметами.
Способы применения предмета
. Называется какой-либо хорошо известный предмет, например «книга». Надо назвать как можно больше различных способов его применения: книгу можно использовать как подставку для кино-проектора, можно ею прикрыть от посторонних глаз бумаги на столе и т. д. Следует ввести запрет на называние безнравственных, варварских способов применения предмета. Побеждает тот, кто укажет большее число различных функций предмета.
Эта игра развивает способность концентрировать мышление на одном предмете, умение вводить его в самые разные ситуации и взаимосвязи, открывать в обычном предмете неожиданные возможности. Эта игра может также послужить хорошей основой для дискуссии о нравственности.
Формулирование определений
. Называется знакомый всем предмет или явление, например, «дырка». Надо дать ему наиболее точное определение, которое обязательно включало бы в себя все существенные признаки этого явления и не касалось несущественных. Побеждает тот, чье определение однозначно характеризует данный предмет, т. е. любая его разновидность обязательно охватывается этим определением, но никакой другой предмет под него не подходит.
Эта игра учит четкости и стройности мышления, умению фиксировать существенные признаки, отвлекаясь от несущественных, а также способности одним «мысленным взором» охватывать массу разновидностей проявления одного и того жепредмета, порой не похожих друг на друга. Особенно полезна эта игра для тех учащихся, которые испытывают трудности при формулировании или запоминании определений.
Выражение мысли другими словами
. Берется несложная фраза, например: «Нынешнее лото будет очень теплым». Надо предложить несколько вариантов передачи этой же мысли другими словами. При этом ни одно из слов данного предложения не должно употребляться в других предложениях. Важно следить, чтобы при этом не искажался смысл высказывания. Побеждает тот. у кого больше таких вариантов.
Эта игра направлена на развитие способности легко оперировать словами, точно выражая свои мысли и передавая чужие. Известно, что критерием понимания чего-либо является свобода формы его выражения: то, что мы хорошо понимаем, мы можем легко выразить, используя разные слова. Но эта связь имеет и обратное проявление: понимание нередко достигается именно в тот момент, когда мы сумели выразить непонятную фразу другими словами, «перевести на свой язык».
Эта игра полезна и для формирования «социального мышления»: человек, легко выражающий мысль разными словами, сможет подбирать слова с учетом особенностей конкретной ситуации.
Перечень возможных причин. Описывается какая-либо необычная ситуация, например: «Вернувшись из магазина, вы обнаружили, что дверь вашей квартиры распахнута». Надо как можно быстрее назвать побольше причин этого факта, возможных его объяснений. Причины могут быть банальными («забыл закрыть дверь», «залезли воры»), но не стоит отбрасывать и маловероятные, необычные (вплоть до прилета марсиан). Побеждает тот. кто назовет больше причин, и чем они разнообразнее, тем лучше.
Эта игра развивает способность при решении любой проблемы или осмыслении любого явления сразу же искать широкий круг причин, чтобы можно было все их рассмотреть, проработать самые разные версии, не упустив из виду ни одной, и только после этого принять решение.
Сокращение рассказа.
Предъявляется отпечатанным или зачитывается короткий рассказ, аналогичный приведенному выше. Его содержание надо передать максимально сжато, используя лишь одно-два-три предложения и в них — ни одного лишнего слова. При этом основное содержание рассказа, конечно же. должно сохраниться, второстепенные же моменты и детали следует отбросить. Побеждает тот, у кого рассказ короче и при этом сохранено основное содержание. Возможна совместная доработка и «шлифовка» наиболее удачных ответов.
Эта игра особенно полезна для тех. у кого мышление не отличается четкостью и высокой организованностью, цепляется за мелочи, не доходя до главного, или постоянно смешивает главное с второстепенным. Она учит четко фиксировать только суть события, а все второстепенное отсекать.
Представляется, что разработка и широкое внедрение различных видов игрового тренинга мышления, имеющих разные задачи и адресованных разным группам учащихся, может оказаться серьезным подспорьем учебному процессу.
2.2. Использование приемов логического мышления на уроках математики в начальной школе
Развитие учащихся во многом зависит от той деятельности, которую они выполняют в процессе обучения. Продуктивная деятельность связана с активной работой мышления и находит свое выражение в таких мыслительных операциях, как анализ, синтез. Сравнение, классификация, аналогия, обобщение. Выполнение учащимися продуктивной творческой деятельности оказывает положительное влияние на развитие всех психических функций – познавательных, эмоциональных, волевых.
Сравнение.
Что такое сравнение?
Сравнение – это установление сходства и различия в двух (или более) сопоставляемых предметах. Для овладения операцией сравнения, человек должен научиться видеть сходное в разном и разное в сходном.
Огромная часть усваиваемого содержания именно в младших классах построена на сравнении.
Первое, чему необходимо научить учащегося, это умение выделять в предметах свойства. Обычно дети выделяют в предмете 3-4 свойства. Для того, чтобы дети могли увидеть в предмете множество свойств, полезно им показать прием по выделению свойств в предметах – прием сопоставления данного предмета с другими предметами, обладающими другими свойствами.
В подтверждение вышесказанного приведу фрагмент урока.
Тема: Признаки предмета.
Цель: Развитие наблюдательности.
Оборудование: набор предметов: кубики разного цвета и размера, яблоко, елочная игрушка, гирька.
Учитель: Что вы видите у меня в руках?
Ученик: Это кубик.
Учитель: Что можете сказать про этот кубик?
Ученик: Он синий.
Учитель: По цвету кубик синий. Что еще?
Ученик: Он сделан из пластмассы.
Ответы других учащихся: Он маленький.
Учитель: Все что вы сказали про кубик – это свойства кубика. Чем яблоко отличается от кубика?
Ученик: Его можно есть, оно разноцветное, круглое, а кубик одного цвета, твердый.
Учитель: Сравните гирьку и кубик.
Ученик: Кубик легкий, а гирька тяжелая.
Учитель: Сравните с елочным шариком.
Ученик: Кубик не блестящий, матовый.
Учитель: Сколько свойств кубика обнаружили?
- Свойства мы легче выделяли при сравнении одного предмета с другим.
Для формирования приема сравнения работу провожу поэтапно:
1. Выделение признаков или свойства одного объекта.
2. Установления сходства и различия между признаками двух объектов.
3. Выявление сходства между признаками трех, четырех и более объектов.
4. Выявление определенных закономерностей в изменении признаков предметов.
При выполнении этих упражнений дети пользуются соответствующей терминологией:
- Чем похожи?
- Чем отличаются?
- Что изменилось? Что не изменилось?
- Что одинаково? Что неодинаково?
- Выбери нужный рисунок.
- Найди лишний предмет.
- Измени признак.
Ориентируясь на внешние признаки, доступные для восприятия, дети могут установить сходства и различия между математическими объектами.
В чем сходства и различия:
а) выражений 6 + (7 +3) и (6 + 7) + 3;
б) чисел 304200 и 340200;
в) равенств 3 ∙ 8 = 24 и 8 ∙ 3 = 24;
г) текстов задач;
д) уравнений;
е) геометрических фигур;
ж) вычислительных приемов.
Прием сравнения можно использовать при знакомстве учеников с новыми понятиями.
Без сравнения школьник не может приобрести систематических знаний. И.М Сеченов считал сравнение самым драгоценным сокровищем человека.
Прием классификации.
Умение выделять признаки предметов и устанавливать между ними сходства и различия – основа приема классификации.
Можно выделить следующие виды заданий на классификацию:
а) подготовительные задания:
- уберите лишний предмет;
- нарисуйте фигуру такого же цвета (формы, размера);
- дайте название группе предметов;
- задания на выработку внимания и наблюдения (какой предмет убрали? что изменилось?);
- сравните похожие рисунки и найдите отличия;
б) задания, в которых на основании классификации указывает учитель;
в) задания, при выполнении которых дети сами выделяют основание для классификации.
Применение приема классификации способствует формированию положительных мотивов в учебной деятельности, т.к. подобная работа содержит элементы игры и элементы поисковой деятельности, что в свою очередь повышает активность учащихся и обеспечивает самостоятельность выполнения работы [48].
Задание № 156, с. 77, 1кл.
-По каким признакам можно разбить все фигуры слева на 2 группы, чтобы рисунку соответствовали равенства: 5+4=9, 9-7=2, 3+6=9
Разбивая на группы, ученик усваивает состав числа 9.
Приемы аналогии.
Под аналогией понимается особый вид умозаключения (рассуждения), когда от сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.
Формируя у школьников умение выполнять умозаключения по аналогии, необходимо иметь в виду следующее:
а) Аналогия основывается на сравнении.
б) Для использования аналогии необходимо иметь два объекта, один из которых известен учащимся, а второй сравнивается с ним по каким-либо признакам.
в) Для ориентации учащихся на использование аналогии необходимо в доступной для них форме разъяснить сущность последней, обратив внимание на то, что в математике нередко новый способ вычислений, преобразований можно открыть по догадке, внимательно изучив известный способ деятельности и данное новое задание.
г) Для правильного вывода по аналогии сравниваются признаки объектов, существенные в данной ситуации, на что необходимо сориентировать учащихся. А то вывод может быть неверным.
Задание: Как разделить 27: 4 = ? 89 : 10 = ?
(Нашли в делимом наибольшее число, которое делится на 10 без остатка).
- Объясни, как разделить:
148:10=14 (ост.8)
356:10=35 (ост.6)
1425:10=142 (ост.5)
24876:10=2487 (ост.6)
- Сравните частное с остатком и делимое.
Вывод делают учащиеся: при делении любого числа на 10 частное показывает, сколько всего десятков в этом числе, а цифра единиц данного числа обозначает остаток.
Вывод закрепляется:
 237 : = 23 (ост.7) 237 : = 23 (ост.7)
 4768 : = 476 (ост.8) 4768 : = 476 (ост.8)
Решение новой проблемы:
 4768 : = 47 (ост.68) требует от учащихся умозаключения по аналогии. 4768 : = 47 (ост.68) требует от учащихся умозаключения по аналогии.
Ученик: Делитель – 100, потому что частное обозначает число сотен в числе 4768, а остаток записан всеми другими числами этого числа.
Аналогия на этом уроке используется еще раз при отыскании приема деления на 1000.
В течении всей работы учащиеся вовлекаются в творческую работу, в ходе решения у учащихся формировались мыслительные операции (анализ, сравнение, обобщение) и приемы умственной деятельности (наблюдение, аналогия).
В обучении математике аналогия может быть использована при изучении свойств объектов, отношений между ними и действий с ними.
а) Аналогия свойств.
В этом случае использование аналогии позволяет вскрывать некоторые новые свойства изучаемых объектов.
Например: В классе единиц – 3 разряда, в классе тысяч – 3 разряда, а в классе миллионов - ?
Это и будет выводом по аналогии, в котором фиксируется определенное свойство вновь изучаемого объекта.
б) аналогия отношений.
Задание: 4*(3+7) и 4*3+4*6
Применяя знание смысла умножения, устанавливаем что
4*(3+7) > 4*3+4*6
Сравниваем левую и правую части. Подмечаем, что 4 умножаем не на 7, а на 6.
Теперь возьмем выражение 3*(8+9) и 3*8+3*7
По аналогии высказываем догадку, что 3*(8+9) > 3*8+3*7
Проверка высказывания может быть проведена либо путем вычислений, либо путем рассуждений.
в) Аналогия действий.
Здесь аналогия выражена в выводе о способе действия на основании изучения сравниваемого объекта.
Чтобы сделать вывод о способе умножения многозначного числа на однозначное, надо вспомнить, как умножить двузначное на однозначное:
27*3 712*2 6288*3
Аналогия в деятельности учащихся может стать приемом, который будет помогать им открывать новые знания, способы деятельности.
Аналогия – средство активизации учебно-воспитательной деятельности [64].
Анализ и синтез
Анализ связан с выделением элементов данного объекта, его признаков или свойств. Синтез – это соединение различных элементов, сторон объекта в единое целое. Выполняя задания на сравнения, классификацию, учащиеся постоянно пользуются этими приемами. Способность к аналитико- синтетической деятельности находит сое выражение не только в умении выделить элементы того или иного объекта его различные признаки или соединить элементы в единое целое, но и в умении включить его в новые связи, увидеть его новые функции.
Задания:
а) Найти отрезок BC. Что о нем можно рассказать?
  А В А В
D C E
б) Запиши все четные числа от 2 до 20 и нечетные числа от 1 до 19.
2,4,6,8,10,12 и т.д.
1,3,5,7,9,11 и т.д
Используем эти математические объекты для составления различных заданий.
Какие числа надо вычеркнуть в первом ряду, чтобы каждое последующее число было на 4 больше предыдущего.
в) Числа 234, 502 замени суммой разрядных слагаемых.
Прием обобщения.
Обобщение – это мыслительная операция, в основе которой лежит абстрагирование и группировка.
Результат обобщения фиксируется в понятиях, суждениях, правилах.
Процесс обобщения может быть по-разному организован, и в зависимости от этого говорят о двух типах обобщения: теоретическом и эмпирическом.
В курсе начальной математики наиболее часто применяется эмпирическое обобщение, при котором обобщенные знания – результат индуктивных рассуждений. Выводы, получаемые индуктивным путем, связаны с наблюдением, анализом, сравнением, с выявлением общих закономерностей и их последующим обобщением.
ФРАГМЕНТ УРОКА.
Тема: Таблица умножения и деления на 9.
Закрепление.
Задание: Разгадай закономерность в записи выражений.
76 – 67
85 – 58
94 – 49
73 – 37
Учитель: Чем они похожи?
Ученик: В записи числа использованы одинаковые числа.
Другие мнения: Записаны разности.
Учитель: Чем отличаются?
Ученик: В вычитаемом цифры поменяли местами.
Учитель: По какому правилу составлены выражения?
Ученик: В уменьшаемом число десятков больше числа единиц, в вычитаемом цифры поменяли местами.
Учитель: Вычислите значение каждой разности.
Догадайся! Чем похожи все результаты?
Мнения разных учеников. Кто-то скажет, что каждое число делится на 9.
Учитель: Проверь! Запиши выражения по тому же правилу.
Идет самостоятельная творческая работа.
65-56=9 81-18=63 82-28=54
74-47=27 93-39=54
Обсуждение. Дети называют равенства.
Учитель: Кто же сделает вывод?
Ученик: Если в уменьшаемом число десятков больше числа единиц, вычитаемое число из тех же цифр, но их поменяли местами, то результат будет делится на 9.
Индуктивное мышление характеризуется движением мысли от единичного, частного к общему.
В процессе дедуктивного умозаключения мысль движется от общего к частному, при этом отдельные частные факты подводятся под соответствующее правило, закон, понятие.
Например: В одной тетради 45 страниц, во второй – 9 страниц. Во сколько раз больше страниц в первой тетради, чем во второй? На сколько страниц меньше во второй тетради, чем в первой?
Зная правило, можно решить задачу.
Используем дедуктивный метод.
Общая посылка: Надо узнать во сколько раз 45 больше 9. На сколько 45 больше 9?
Заключение? 45:9; 45-9
Дедуктивный вывод является основным способом математических доказательств.
Чтобы развить логическое мышление младшего школьника, необходимо уделять больше времени развитию внимания.
К.Д. Ушинский говорил, что «внимание есть именно та дверь, через которую проходит все, что только входит в душу человека из внешнего мира».
1. Сколько разных ответов и каких можно получить, если поставить скобки:
10*3+7
(Ответ: 10*(3+7)=100 10*3+7=37)
2. Даны четыре цифры и знаки действий, написать как можно больше равенств:
Пример: 4:2=3-1
4 -2=3-1 и т.д.
3. Пользуясь тремя цифрами 3, 4, 5 и знаками действий, записать как можно больше различных чисел, используя каждый раз все данные цифры:
Пример: 3+4-5=2
35*4=140 и т.д.
4. В ряду чисел 9, 8, 7, 6, 5, 4, 3, 2, 1 поставьте знаки сложения так, чтобы получить 99.
(Ответ: 9+8+7+6+5+43+21=99
9+8+7+65+4+3+2+1=99)
5. Расставьте между данными числами знаки, чтобы получить верные равенства:
6 2 3 =12 6+2*3=12
1 6 4 8 = 12 16:4+8=12; 16+4-8=12
9 8 3 2 6 = 12 9+8+3-2-6 = 12
8 1 5 4 6 = 12 8-1-5+4+6=12
3 2 6 8 9 = 12 3+2+6-8+9=12
7 4 5 3 1 = 12 7-4+5+3+1=12
6. Составьте по рисункам уравнение и решите их.
15 Х

21
Х 9


21
8. На двух полках стояло 49 книг. Когда с верхней полки сняли 7 книг, то на обеих полках стало поровну. Сколько книг стояло на полках первоначально?
(Ответ: 21 и 28)
После того, как ребята познакомятся с римской нумерацией, можно предложить следующие задания:
Из палочек сложите такие неверные равенства:
XII + IX = II
X = VII – III
IV – V =I
X + X = I
VI – VI = XI
IV – I + V = II
Переложите в каждом равенстве по одной палочке так, чтобы равенства стали верными.
Также как и в первом классе нужно использовать логические задания с геометрическим содержанием.
1. Какая из этих фигур «лишняя»? Почему?

2. Сколько разных четырехугольников на чертеже?

3. Сколько на этом чертеже различных треугольников?
    В В
M

А в E K
4. Чем похожи и чем отличаются фигуры?
5. В прямоугольнике ABCD, составленном из пяти квадратов, проведена прямая АС. Сколько при этом образовалось треугольников?
      В В С В В С
A в
(Ответ: 10)
Нумерация чисел любой величины.
1. Запишите два четных, а затем два нечетных числа, следующих друг за числом 1398. Запишите по два четных и нечетных числа, предшествующих числу 1398.
2. Назовите наименьшее шестизначное число и наибольшее пятизначное число и найдите, на сколько одно число больше другого
(Ответ: на 1)
3. Запишите трехзначное число, у которого число единиц в 3 раза меньше числа десятков, а число десятков в 3 раза меньше числа сотен.
(Ответ: 931)
4. На какое число надо разделить разность наибольшего трехзначного числа и наибольшего двузначного числа, чтобы получить наибольшее однозначное число?
(Ответ: (999-99):9=100 )
5. Запишите все трехзначные числа, у которых число десятков в 2 раза больше числа единиц.
(Ответ: 105, 126, 147, 168, 189 )
6 .В записи 6 6 6 6 6 6 6 6 поставьте между некоторыми цифрами знак сложения так, чтобы получилось выражение, значение которого равно:
а) 264 б) 13332 в) 67332
7. Применяя знаки сложения, можно восемью восьмерками записать число 1000:
888+88+8+8+8
Используя знаки арифметических действий и скобки, запишите число 1000 восемью восьмерками другим способом.
7. Применяя знаки арифметических действий и скобки запишите:
а) семью семерками 700;
б) восемью семерками 700;
в) восемью двойками 200;
г) десятью четверками 500;
д) десятью шестерками 600;
е) десятью девятками 1000.
8. Как нужно расставить скобки так, чтобы получить верное равенство:
а) 3248:16-3*315-156*2=600;
б) 350-15*104-1428:14=320.
9. Из карточек сложили неверное равенство:
         1 0 1 - 1 0 2 = 1 1 0 1 - 1 0 2 = 1
Как, передвинув лишь одну карточку, сделать его верным?
10. Арифметические ребусы принадлежат к одному из типов логических задач. Учащиеся начальных классов отличаются любознательностью и для них решение логической задачи – это поиск тайны.
 Числовые ребусы – это примеры, в которых все или некоторые цифры заменены звездочками или буквами. При этом одинаковые буквы заменяют одинаковые цифры, разные буквы – разные цифры. Числовые ребусы – это примеры, в которых все или некоторые цифры заменены звездочками или буквами. При этом одинаковые буквы заменяют одинаковые цифры, разные буквы – разные цифры.
 х 9 5 _ * * 0 1 2 х 9 5 _ * * 0 1 2
 * * 8 4 * * * 8 4 *
 + * 5 _ 6 * + * 5 _ 6 *
  1 * * * * 1 * * * *
* * * * 0
Пусть дан числовой ребус:
+ У Д А Р
 У Д А Р У Д А Р
Д Р А К А
Число 8126 является решением ребуса, так как при замене буквы У на цифру 8, буквы Д на 1, буквы А на 2, буквы Р на 6 получится верный пример на сложение.
На следующем ребусе я покажу как проводить работу:
+ К И С
 К С И К С И
И С К
Сумма И + С ( в разряде десятков) оканчивается на С, но И не равно ) (см. разряд единиц). Значит, И=9 и 1 десяток в разряде единиц запомнили (решение ниже) теперь легко найти К в разряде сотен: К=4. Для С остается одна возможность: С=5.
+ К И С + К 9 С + 4 9 С + 4 9 5
       К С И К С 9 4 С 9 4 5 9 К С И К С 9 4 С 9 4 5 9
И С К 9 С К 9 С 4 9 5 4
+ ОДИН + ВАГОН + ДЕТАЛЬ
   ОДИН ВАГОН ДЕТАЛЬ ОДИН ВАГОН ДЕТАЛЬ
МНОГО СОСТАВ ИЗДЕЛИЕ
11. Есть три разных числа, таких, что их сумма равна их произведению. Что это за числа?
(Ответ: 1,2,3)
12. В числе 5 236 845 зачеркните три цифры, чтобы оставшееся число было наименьшим 7
(Ответ: 2 345)
Оставшееся число было наибольшим (6 845). Порядок расположения цифр не меняйте.
13. Цифрами 0, 1, 2, 3 запишите наибольшее и наименьшее шестизначное число. Каждую цифру использовать не менее одного раза.
14. Напишите наибольшее и наименьшее десятизначное число, все цифры которого различны.
15. Поставьте в записи числа 1234 один знак так, чтобы получилось:
а) число, большее 9, но меньшее 19;
б) число, большее 30, но меньшее 40.
16. В квадрате расставьте числа 0, 1, 2, 3, 4, 5, 6, 7, 8 так, чтобы сумма чисел в каждой строке, столбце и диагонали была одинакова.
| 44 |
99 |
22 |
| 33 |
55 |
77 |
| 88 |
11 |
66 |
Выводы по 2 главе
Развитие учащихся во многом зависит от той деятельности, которую они выполняют в процессе обучения. Продуктивная деятельность связана с активной работой мышления и находит свое выражение в таких мыслительных операциях, как анализ, синтез. Сравнение, классификация, аналогия, обобщение. Выполнение учащимися продуктивной творческой деятельности оказывает положительное влияние на развитие всех психических функций – познавательных, эмоциональных, волевых.
Чтобы развить логическое мышление младшего школьника, необходимо уделять больше времени развитию внимания.
К.Д. Ушинский говорил, что «внимание есть именно та дверь, через которую проходит все, что только входит в душу человека из внешнего мира».
Регулярное использование на уроках математики системы специальных задач и заданий, направленных на развитие логического мышления, расширяет математический кругозор младших школьников, способствует математическому развитию, повышает качество математической подготовленности, позволяет детям более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
Чтобы ребенок учился в полную силу своих способностей, стараюсь вызвать у него желание к учебе, к знаниям, помочь ребенку поверить в себя, в свои способности.
Мастерство учителя возбуждать, укреплять и развивать познавательные интересы учащихся в процессе обучения состоит в умении сделать содержание своего предмета богатым, глубоким, привлекательным, а способы познавательной деятельности учащихся разнообразными, творческими, продуктивными.
ЗАКЛЮЧЕНИЕ
В настоящее время все активнее и активнее идет поиск обновления содержания школьного образования вообще и, в частности усиления поиска новых вариантов начального курса математики с целью повышения эффективности как обучения, так и развития младших школьников. Линия на развитие познавательных процессов учащихся достаточно четко прослеживается и в действующих стандартных учебниках математики. В них есть упражнения, направленные на развитие внимания, наблюдательности, памяти учащихся, на умение проводить анализ, сравнивать предлагаемые объекты, фигуры, процессы, подмечать скрытую закономерность и т.д. Однако, как показывает практика начальной школы, предложенные в учебниках упражнения развивающего характера нуждаются в дополнительном расширении и обогащении большим числом специальных заданий, задач и упражнений содержательно-логического и нестандартного характера, заданий, требующих применения знаний в новых условиях, поданных в определенной системе.
Развитие логического мышления в значительной мере идет стихийно, поэтому большинство учащихся, даже старших классов, не овладевают начальными приемами логического мышления, а этим приемам необходимо начинать учить с начальной школы.
Прежде всего из урока в урок нужно развивать у ребенка способности к анализу и синтезу. Острота аналитического ума позволяет разобраться в сложных вопросах. Способность к синтезу помогает одновременно держать в поле зрения сложные ситуации, находить причинные связи между явлениями, овладевать длинной цепью умозаключений, открывать связи между единичными факторами и общими закономерностями.
Наша общая забота – помогать всем детям в умственном развитии, укрепляя уверенность ребенка в своих силах, повышает его интеллектуальный уровень, готовя к обучению в среднем звене.
Логическое мышление лежит в основе способностей человека, является условием обучения, приобретения знаний, формирования умений и навыков. Без мышления невозможна нормальная жизнь ни личности, ни общества. Благодаря мышлению, человек выделился из животного мира и достиг высокого уровня.
Изучив программу и методику развивающего обучения по дидактической системе Л.В. Занкова, апробировав учебник И.И. Аргинской «Математика-1», «Математика-2», «Математика-3», я пришла к выводу, что система развивающего обучения необходима для успешного умственного развития учащихся.
СПИСОК ЛИТЕРАТУРЫ
1. Аптер, М. Дж. Теория реверсивности и человеческая активность / М. Аптер // Вопр. психол. 1987. № 1. С. 162— 199.
2. Айзенк, Г. Дж. Интеллект: новый взгляд / Г. Айзенк// Вопр. психол. 1995. № 1. С. 111
3. Ананьев, Б.Г. Психология педагогической оценки // Ананьев Б.Г. Избр. психол. труды. В 2т. Т. 2. М.: Педагогика, 1980. С. 128-267.
4. Анастази, А. Психологическое тестирование. / А. Анастазин М. 1990.
5. Акентьев, В.В., Перельман, Я.И.. Смекалка для малышей. В.В. Аксентьев, Я.Н. Перельман Москва. Омега.1994 г.
6. Алексеева, Л.Г., Воронин, А.Н.. Развитие и диагностика способностей./ Л.Г. Алексеева, А.Н. Воронин Москва. Наука 1991 г.
7. Богуславская, З.М. Выделение цвета и формы детьми дошкольного возраста в зависимости от характера их деятельности / З.М. Богуславская// Доклады АПН РСФСР. № 1. М-АПН РСФСР, 1958. С. 55-58.
8. Бодалев, А.А. Межличностное восприятие и понимание // Бодалев А.А. Личность и общение: Избр. труды. М- Педагогика, 1983 С. 85-265.
9. Брушлинский, А. В. Психология мышления и кибернетика. / А.В. Брушлинский М.: АН СССР, 1970.
10. Брушлинский, А.В. Проблемы психологии субъекта. / А.В. Брушлинский М,: Изд-во РАН. 1994.
11. Бурлачук, Л.Ф., Морозов С.М. Словарь-справочник по психодиагностике. / Л.Ф. Бурлачук Изд. 2-е, перераб. и доп. СПб.: Питер, 1999.
12. В 2 кн. Кн. 1. М. Педагогика, 1982.
13. Возрастные возможности усвоения знаний / Под ред. Д.Б. Эльконина, В.В. Давыдова. М.: Просвещение, 1966.
14. Волочков, А.А. Учебная активность в структуре интегральной индивидуальности (на материале младших школьников): Автореф. канд. дис. / А.А. Волочков Пермь, 1997.
15. Вохмянина, А.Е. Изучение мышления и интеллекта. Таблица Равена./ А.Е. Вохмянина Магнитогорск. 1985 г.
16. Выготский, Л.С. Педагогическая психология. / Л.С. Выготский - М.: Педагогика, 1991.
17. Выготский, Л.С. Проблемы обучения и умственного развития / Л.С. Выготский // Избранные исследования. - М.: 1956 г.
18. Вяткин, Б.А. Интегральная индивидуальность человека и ее развитие в специфических условиях спортивной деятельности / Б.А. Вяткин // Психол. журн. 1993. Т. 14. № 2. С. 73—83.
19. Вяткин, Б.А. Стили активности как фактор развития интегральной индивидуальности / Б.А. Вяткин // Интегральное исследование индивидуальности: стиль деятельности и общения. Пермь: ПГПИ, 1992. С. 36—55.
20. Вяткин, Б.А., Щукин М.Р. Развитие учения об интегральной индивидуальности: проблемы, итоги, перспективы / Б.А. Вяткин, М.Р. Щукин // Психол. журн. Т. 18. 1997. № 3. С. 125—141.
21. Гальперин, П.Я. Основные результаты исследований по проблеме «Формирование умственных действий и понятий». / П.Я. Гальперин М.: Изд-во МГУ, 1965.
22. Гараи, Л., Кечки, М. Еще один кризис в психологии. / Л. Гараи, М. Кечки // Вопр. филос. 1997 № 4. С. 86-97.
23. Голощапова, С.В. Логические игры и задачи на уроках математики./ С.В. Голощапова Ярославль. «Академия развития». 1997 г.
24. Давыдов, В. В. Виды обобщения в обучении. / В.В. Давыдов М.: Педагогика, 1972.
25. Давыдов, В.В. Проблемы развивающего обучения. Опыт теоретического и экспериментального исследования. / В.В. Давыдов М. Педагогика, 1986.
26. Донцов, А.И., Саркисян Ш.В. Динамика межличностного восприятия в условиях совместной деятельности / А.И. Донцов, Ш.В. Саркисян // Межличностное восприятие в группе / Под ред. Г.М. Андреевой, А.И. Донцова. М.: Изд-во МГУ, 1981. С. 86-151.
27. Дружинин, В.Н. Экспериментальная психология. / В.Н. Дружинин 2-е изд., доп. СПб: Питер, 1999.
28. Зак, А.З. Развитие умственных способностей младших школьников. / А.З. Зак Москва. «Просвещение», «Владос». 1994 г.
29. Зак, А.З. Различия в мышлении детей. / А.З. Зак Москва. 1992 г.
30. Запорожец, А.В., Зинченко, В.П., Эльконин, Д.Б. Развитие мышления // Запорожец А.В., Эльконин Д.Б. Психология детей дошкольного возраста. / А.В. Запорожец, В.П. Зинченко, Б.Д. Эльконин М.: Просвещение, 1964. С. 183-246.
31. Зыкова, В.И. Оперирование понятиями при решении геометрических задач / В.И. Зыкова // Известия АПН РСФСР. 1950. Т. 28. С. 155-194.
32. Измерение интеллекта детей. Пособие для психолога-практика / Под ред Ю 3. Гильбуха Ч. 1. Киев: РОВО «Укрвузполиграф», 1992.
33. Кабардов, М.Н., Матова, М.А. Межполушарная асимметрия и вербальные и невербальные компоненты познавательных способностей / М.Н. Кабардова, М.А. Матова // Вопр. психол. 1988. № 6. С. 106-115.
34. Казанцева, Я.Э. Математика с улыбкой. Игры, ребусы, кроссворды для младших школьников. / Я.Э. Казанцева Ярославль. «Академия развития». 1998 г.
35. Климов, Е.А. Штрихи к портрету B.C. Мерлина / Е.А. Климова //Вопр. психол. 1998. № 1. С. 95—98.
36. Котик, М.А. Некоторые психологические механизмы возникновения интереса в труде / М.А. Котик //Вопр. психол. 1989. № 6. С. 81—92.
37. Кроник, А.А. Межличностное оценивание в малых группах. / А.А. Кроник Киев: Наукова думка, 1982.
38. Чилингирова, Л., Спиридонова, Б. Играя, учимся математике. / Л. Чилингирова, Б. Спиридонова Москва. «Просвещение». 1993 г.
39. Леонтьев, А.А. Педагогическое общение / А.А. Леонтьев М.: Знание, 1979.
40. Леонтьев, А.Н Деятельность. Сознание Личность / А.А. Леонтьев // Леонтьев А.Н. Избр психол. произв. В 2 т. Т 2. М.. Педагогика, 1983. С. 94-231.
41. Люблинская, А.А. Роль языка в развитии познавательной деятельности ребенка / А.А. Люблинская // Всерос. совещание. Доклады на совещании по проблемам психологии. 1954. 3-8 июля. С. 124-137.
42. Менчинская, Н.А. Мышление и процесс обучения / Н.А. Мнечинская // Исследование мышления в советской психологии / Под ред. Е.В. Шороховой. М.: Наука, 1966. С. 349-387.
43. Мерлин, В.С. Очерк интегрального исследования индивидуальности. / В.С. Мерлин М.: Педагогика, 1986.
44. Мерлин, В.С. Психология индивидуальности / В.С. Мерлин // Избр. труды / Под ред. Е.А. Климова. М.; Воронеж, 1996.
45. Модель прогнозирования персонального роста руководящих кадров // Организация управления 1990 № 9 С. 44.
46. Молл, Е. Г. Руководитель строительного производства / Е.Г. Молл М.: Стройиздат, 1991.
47. Молл, Е. Г. Управленческая карьера в России / Е.Г. Молл // Проблема теории и практики управления 1996 № 6. - С 117—120.
48. Молл, Е.Г. Консультирование по проблемам управленческой карьеры / Е.Г. Молл // Управление человеческими ресурсами стратегия и практика Алматы, 1996 С 58—61.
49. Мясоед, П.А. Методика непрямой экспресс-диагностики уровня психического развития дошкольников / П.А. Мясоед // Вопр. психол. 1996. № 2. С. 130-136.
50. Мясоед, П.А. Теория и практика в работе школьного психолога / П.А. Мясоед // Вопр. психол. 1993. № 4. С. 72-79.
51. Никитин, Б.П. Ступеньки творчества или развивающие игры. / Б.П. Никитин Москва. 1980 г.
52. Обуховский, К. Психологическая теория строения и развития личности / К. Обуховский М.: Наука, 1981
53. Обучаем по системе Занкова Л.В.1 кл., 2 кл., 3 кл. Москва. Просвещение. 1993 г.
|