Реферат: Математические модели естествознания
|
Название: Математические модели естествознания Раздел: Рефераты по математике Тип: реферат | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ББК 22.143я73 К85 Юдович В.И. К85 Математические модели естествознания. Курс лекций / В.И. Юдович. — М.: Вузовская книга, 2009. — 288 с. ISBN 5-9502-0176-0 Курс лекций по математическим моделям естествознания В.И. Юдовича состоит из трех частей: «Математические модели», «Механика», «Элементы статистической механики». Для студентов и преподавателей технических и экономических вузов, математических, механико-математических и естественно-научных факультетов и факультетов компьютерных наук и информационных технологий. ББК 22.143я73 Учебное издание ЮдовичВикторИосифович МАТЕМАТИЧЕСКИЕМОДЕЛИЕСТЕСТВОЗНАНИЯ КУРСЛЕКЦИЙ Книга издана в авторской редакции Ответственный редактор Н.Г. Карасева Технический редактор П.С. Корсунская Компьютерная верстка И.В. Островская
Подписано в печать 11.03.2009. Формат 60x84 1/16. Печать офсетная. Бумага офсетная. Усл. печ. л. 34,17. Тираж 300 экз.
ЗАО «Издательское предприятие «Вузовская книга» 125993, Москва, А-80, ГСП-3, Волоколамское шоссе, д.4, МАИ, Главный административный корпус, к. 301а. Т/ф (499) 158-02-35. E-mail: vbook@mai.ru; vbook@mail.ru c Юдович В.И., 2004 c ЗАО «Издательское предприятие ISBN 5-9502-0176-0 «Вузовская книга», 2009 ОБАВТОРЕИЭТОЙКНИГЕЭта книга — курс лекций по математическим моделям естественных наук глубокого математика и механика, создателя научной школы по математической гидродинамике, профессора Виктора Иосифовича Юдовича (4.10.1934–19.04.2006). Вся жизнь В.И. Юдовича связана с Ростовским государственным университетом (РГУ, ныне ЮФУ), куда он поступил на физмат в 1952 году и где через пять лет стал преподавать. После разделения физмата работал на механико-математическом факультете (мехмате), ведя интенсивную научную и преподавательскую работу, создавая свою научную школу и кафедру. Кандидатскую диссертацию В.И. Юдович защитил в МГУ, докторскую – в Институте проблем механики АН СССР, был членом редколлегий, ученых советов, председателем диссертационного Совета, президентом Ростовского математического общества. Энциклопедически образованный, талантливый во всем и расположенный к людям В.И. Юдович занимался гидродинамикой, для решения сложнейших проблем которой освоил все, что могло помочь ему в исследовании проблемы турбулентности. Его понимание уравнений математической физики, теории динамических систем и многих разделов математики и механики было уникальным. Более сорока лет семинару В.И. Юдовича по математической гидродинамике, куда приезжали люди из разных мест: «доклад у Юдовича» означал высокий уровень экспертизы и зачастую самому докладчику давал лучшее понимание сделанного и прояснение перспектив работы. На мехмате РГУ В.И. Юдович прочел множество курсов: от теории функций действительного переменного до механики сплошной среды. Это были оригинальные курсы, содержательные идейно и технически, сочетавшие научную точность и богатство русского языка. Остались конспекты прочитанных лекций, эти записи активно используются и помогают преподавателям. По ряду курсов В.И. Юдович подготовил печатные варианты. Это две книги «Лекции об уравнениях математической физики», с белой и синей обложками. К сожалению, не закончена третья часть, которая должна была выйти с красной обложкой, чтоб получился триколор. Двумя изданиями вышел «Практикум по решению дифференциальных уравнений», Об авторе и этой книге написанный в соавторстве с А.А. Есиповым и Л.И. Сазоновым. В.И. Юдович говорил, что интересен новый предмет – поэтому, «поставив» тот или иной курс, передавал его ученикам. Даже появлению первой в мире монографии по математической теории электрофореза (В.Г. Бабский, М.Ю. Жуков, В.И. Юдович, 1982 г.) предшествовал цикл лекций по моделированию задач массопереноса под действием электромагнитного поля. Помимо входивших в преподавательскую нагрузку лекций и заседаний еженедельного семинара, В.И. Юдович каждый год организовывал микросеминары, посвященные новым проблемам гидродинамики и математики. Прочитанные там лекции вводили учеников Юдовича и всех желающих в новые разделы и новые задачи, из этих лекций вырастали темы будущих исследований. Обзорные статьи В.И. Юдовича, написанные в начале 21 века, – попытка передать, сохранить свое понимание математической гидродинамики, которую он развивал до последних дней. В.И. Юдович был Учителем, ему было важно, чтобы начатые им исследования и работы продолжались трудами его сотрудников, он многое сделал для того, чтобы развивались механика и математика в Ростове, России и мире. Курс математических моделей естественных наук (естествознания) первый раз был прочитан им в 1991 году для студентов четвертого курса специальности «прикладная математика» мехмата. С каждым годом курс развивался, пополняясь новым материалом, в планах было включение в курс разделов по термодинамике, конвекции. Подготовкой печатного варианта лекций В.И. Юдович занимался, уже борясь с болезнью, он работал над «Математическими моделями» до последних дней. Эти лекции были размещены на кафедральном сайте, и немало читателей поделилось своими замечаниями и советами. Особая благодарность студентам мехмата 20062008 гг., активно участвовавшим в устранении опечаток, уточнении ссылок и др. В интернетовском ресурсе vkontakte.ru появилась инициированная студентами «Группа любителей литературного таланта В.И. Юдовича». В наборе и правке текстов участвовали О.А. Цывенкова, Е.В. Ширяева и И.В. Островская, взявшая на себя труд финальной редактирования и верстки. Тексты вычитывали М.Ю. Жуков, С.М. Зеньковская, Л.И. Сазонов и В.Г. Цибулин, занимавшийся подготовкой издания. ПРЕДИСЛОВИЕАВТОРАЦель этого курса — рассказать об основных моделях естествознания, научить подходам к исследованию явлений природы, её фундаментальных законов на основе математического анализа. Это — лекции. И хотя письменный курс не повторяет дословно то, что говорится на занятиях, я стараюсь сохранить стиль живого разговора с живой аудиторией. До сих пор образцом для построения математических моделей служит механика, начиная с классического труда Ньютона «Математические основы натуральной философии» [32]. Дальнейшее развитие механики вплоть до XIX века, связанное с именами, пожалуй, всех великих математиков и физиков XVII–XX в.в. — Декарт, Гюйгенс, Лейбниц, Ферма, Эйлер, Лагранж, Гамильтон, Якоби, Гаусс, Герц, Максвелл, Пуанкаре — привело к построению грандиозного здания механики систем с конечным числом степеней свободы, а также и механики сплошной среды. Вся история науки ясно показывает, что каждый серьёзный новый шаг в исследовании природы бывает неразрывно связан с развитием новых математических теорий. Нужно ли напоминать, что научные открытия непосредственно влияют на развитие технологии, а тем самым и на образ жизни людей? Время от времени возникают споры о том, какое достижение математики было самым важным и кто из математиков был самым великим. (Я не считаю такие обсуждения слишком уж серьёзными, но всё-таки...). Очень многие считают, что главным достижением было введение позиционной системы счисления, а ее автор, имя которого неизвестно (возможно, араб, а, скорее всего, индус), и был величайшим из математиков на нашей планете. С этим можно поспорить. Я склонен думать, что величайшим достижением математики является, быть может, оглавление современных книг по глобальной дифференциальной геометрии. Оно начинается с понятий топологического и метрического пространств. Затем рассматриваются многообразия, векторные поля, дифференциальные формы, тензорные поля, геодезические на многообразиях, кривизны, вариационные принципы для геодезических, группы и алгебры Ли. Это оглавление представляет собой великий план исследования, созданный и реализованный прежде всего в механике, усилиями едва ли не всех ведущих математиков трех столетий. Оказалось, что геодезические линии в геометрии в точности соответствуют движениям в механике. Далее выяснилось, что явления, с виду совершен- Предисловие автора но непохожие на механические движения тел, описываются по сути теми же законами, лишь с некоторыми изменениями, носящими мало принципиальный характер с точки зрения общих геометрических теорий. Например, в основе электродинамики лежат вариационные принципы, установленные впервые в механике. Теория относительности с ее головокружительными следствиями тоже оказывается с формальной стороны не более, чем одной из глав механики. План описания природы, созданный в механике и связанный, главным образом, с дифференциальной геометрией, является неким идеальным образцом для других наук. Однако полностью он не реализован даже в физике (за исключением, может быть, некоторых её областей, скажем, термодинамики). Время покажет, насколько этот план универсален, может ли он быть реализован, скажем, в биологии или придётся создавать иные планы. Пока что мы очень далеко от ответа на этот вопрос, хотя в различных частных областях биологии, химии, экономики применение идей и методов механики и математической физики дало уже немало интересных и глубоких результатов. Сейчас постоянно употребляются названия «математическая физика», «математическая химия», «математическая биология», «математическая экономика». Но нет никакой «физической» или «биологической» математики. Правда, в последнее время стал мелькать термин «финансовая математика», но это лингвистическое недоразумение. По-английски говорят mathematical finance, математические финансы. Это, однако, неудобопроизносимо, что и привело к появлению «финансовой математики». Некоторые недалекие люди приняли это недоразумение всерьез и предлагают учить детей складывать и вычитать не яблоки и палочки, а доллары и рубли, и дальше продолжать развивать математику в том же духе. Ну, конечно, я считаю это чушью. На самом деле, в «финансовой математике» применяются всё те же методы математического анализа, алгебры, теории вероятностей, теории меры. Решаются уравнения, по сути (а то и вовсе ничем) не отличающиеся от уравнений математической физики. Кстати, высокомерное отношение математиков к этой области не очень оправдано. Конечно, халтурщики есть во всех областях, а в новых (модных, престижных и денежных) областях их в процентном отношении бывает чуть больше, но и в финансовой математике ставятся и решаются замечательно интересные математические задачи. Имеется довольно много книг, названия которых начинаются словами «Математические модели ...» или «Математическое моделирование в ...» Дальше поминается биология, экономика, химия,... Знакомство с этими книгами сразу показывает, что речь в них идет по сути о тех или иных част- 6 В.И. Юдович. Математические модели естествознания
ных моделях математической физики. Естественнонаучная и технологическая специфика рассматриваемых проблем зачастую отражается довольно слабо. Недавно мне довелось участвовать в конференции по математическим моделям, описывающим плавающие живые организмы (biological swimmers, биологических пловцов, как образно выражается один из авторитетов в этой области Джон Кесслер (John Kessler)). На этой конференции одни докладчики рассматривали микроорганизмы в воде, другие говорили о рыбах и дельфинах. Довольно забавным образом математические модели были при этом почти одни и те же. Специфику жизни до сих пор не удается уловить и вставить в математические формулы. Обычно, математики, занимающиеся биологией, любят ссылаться на то, что их предмет много сложней, чем то, чем эанимаются физики. Так-то оно так, но в реальной жизни пока что задачи , которые решаются в математической физике и механике, как правило, куда сложнее и глубже, чем те, которые решают математические биологи. Может быть, когда-нибудь это положение изменится — когда математика по-настоящему глубоко проникнет в биологию. Один мой друг, математический биолог, отвечая на вопрос анкеты о недостатках исследований по математической биологии, написал: «Их всего два: слабое проникновение в биологическую сущность проблем и низкий математический уровень». В этом курсе я пытаюсь изложить те общие принципы и подходы к построению моделей, которые явно или неявно, правильно или не совсем правильно, применяются во всех этих областях. Возможно, главная трудность построения этого курса связана с тем, что в математическом моделировании применяется едва ли не весь математический аппарат, созданный математикой прошлого и создаваемый на наших глазах современной математикой. Между тем, в курсах, прослушанных (в обоих смыслах) студентами-математиками (и чистыми, и прикладными), многие важнейшие теории и факты даже не упоминаются. Например, наши студенты ничего не знают о дифференциальных формах, и даже когда читается курс топологии, некоторые лекторы ухитряются не упомянуть числа Бетти, когомологии, степень отображения, вращение векторного поля и т.п. В курсах алгебры зачастую даже не упоминаются унитарные, ортогональные, якобиевы трехдиагональные матрицы, не разъясняется толком понятие кратности собственного значения. Дело усугубляется тем, что книги по топологии (за редким и счастливым исключением) пишутся для топологов, книги по геометрии — соответственно, для геометров и т.д. В литературе ощущается острый дефицит учебных пособий по различным разделам математической теории, изложенным для последующего применения в прикладной науке. В итоге в ряде случаев мне приходится бегло, без детальных Предисловие автора доказательств, рассказывать об основных понятиях линейного и нелинейного функционального анализа, методах спектральной теории операторов, вариационного исчисления, дифференциальных формах и т.д. Изучение математики так или иначе начинается с освоения ее терминологии, словаря, набора определений. В современной математике вообще есть тенденция загонять все более значительную часть содержания в определения. Доказательства теорем при этом зачастую становятся короткими и тривиальными и дают не слишком много пищи для ума. В этих лекциях по ходу изложения поясняются математические термины, даются краткие определения основных понятий. Иногда они будут новыми для студента, а иногда их приходится приводить ради определенности, ввиду существующего ужасного разнобоя в употреблении слов. Один пример: некоторым лекторам кажется, что у понятия «отображение», «оператор» мало синонимов, и они добавляют еще один синоним — «функция». Лучше, по-старому, понимать функцию как отображение со значениями на вещественной оси. Синонимом служит слово «функционал», которое чаще употребляется, когда область определения — бесконечномерное пространство. МАТЕМАТИЧЕСКИЕМОДЕЛИ1. Динамические системыПод эволюцией той или иной системы будем понимать изменение ее состояния во времени. Первый вопрос, который возникает, когда мы приступаем к построению математической модели: что такое состояние данной системы? Это может быть скаляр, точка многомерного пространства, вектор, а вообще, элемент любого множества X , которое называется фазовым пространством данной системы. Правильный выбор фазового пространства, соответствующего изучаемой системе, отнюдь не тривиален и в значительной мере предопределяет наш конечный успех (или неуспех). Дело в том, что к выбору фазового пространства предъявляются достаточно суровые требования. Главное из них состоит в том, что задание начального состояния, т.е. точки x 0 ∈ X , должно однозначно определять эволюцию системы. В самом сильном варианте требуется, чтобы для каждого t ∈ R было определено состояние системы x (t ) ∈ X . Это означает, что должен быть задан эволюционный оператор Nt : X → X , отображающий фазовое пространство X в себя, и такой, что x (t ) = Nt x 0 (1.1) для всех t ∈ R и любой начальной точки x 0 ∈ X . Поскольку x (0) = x 0 для всех xo ∈ X , эволюционный оператор очевидным образом удовлетворяет условию N 0 = I, (1.2) где I — тождественный оператор: Ix = x для всех x ∈ X . Иногда его также обозначают id (от латинского слова idem — тот же). Как правило, необходимо еще наложить на эволюционный оператор Nt те или иные условия непрерывности по t , чтобы получалось, что Nt x 0 → x 0 при t → 0; понятие предельного перехода для последовательности элементов фазового пространства должно быть также определено. Иногда эволюционный оператор удаётся задать лишь для t ≥ 0. В некоторых случаях даже приходится рассматривать эволюционные операторы, Динамические системы определенные на интервале (−r 1 ,r 2 ), где r 1 , r 2 — некоторые положительные числа, а то и на полуинтервале [0,r 2 ). Фундаментальные математические модели физики обычно приводят к эволюционным операторам, обладающим дополнительным свойством, которое называется (на мой вкус, чересчур пышно) принципом причинности : N t +s = N t ◦ N s (1.3) для всех t,s ∈ R . В частности, из (1.3) следует, что для каждого t эволюционный оператор обратим, и (Nt )−1 = N −t . Ясно также, что если уже известно состояние x (s ) в момент s , то, по прошествии времени t , состояние определяется равенством x (t + s ) = Nt x (s ). Принцип причинности, выражаемый равенствами (1.2) и (1.3), означает, что семейство операторов Nt есть однопараметрическая группа с параметром t . Эта группа очевидно коммутативна: Nt ◦ Ns = Ns ◦ Nt . Во многих задачах (например, для уравнения теплопроводности) эволюционный оператор определен лишь для t ≥ 0. Тогда и принцип причинности (1.3) выполняется лишь для t,s ≥ 0. В этом случае семейство эволюционных операторов Nt образует однопараметрическую полугруппу , тоже коммутативную. Замечу, что иногда и в случае полугрупп равенство (1.3) удается доказать, но, вообще говоря, не для всех, а лишь для некоторых пар t,s таких, что, например, t > 0, а s < 0. Но во всяком случае нужно предположить, что t + s ≥ 0. Фазовые пространства, встречающиеся в приложениях, весьма разнообразны. Это может быть конечное или счетное множество, конечномерное или бесконечномерное банахово пространство, скажем, то или иное пространство функций, вектор-функций или векторных полей, конечномерное или бесконечномерное дифференцируемое многообразие . Дальше я приведу много примеров, но сразу замечу, что в целом ряде областей физики и механики сплошных сред, в гидродинамике и теории поля (уж не говоря о биологии) до сих пор неизвестно, как правильно, адекватно выбрать фазовое пространство. Кроме того, зачастую выбор фазового пространства неоднозначен — одно и то же явление может быть описано различными наборами переменных, а если даже переменные уже выбраны, то отчасти от нашего произвола зависит, какие на них налагаются дополнительные требования. Например, если фазовое пространство состоит из функций (поле температуры в области, занятой проводником тепла), то можно еще по-разному выбирать метрики или банаховы нормы. В частности, такой выбор определяет требо- В.И. Юдович. Математические модели естествознания
вания к начальному состоянию (скажем, каковы требования регулярности к начальному полю температур). Обычно под пространством понимается множество вместе с определенным на нем тем или иным способом предельным переходом для последовательностей его элементов. Наиболее общее определение (при помощи задания системы окрестностей, называемой топологией ) приводит к понятию топологического пространства . В этом курсе я не буду пользоваться столь общими пространствами. Надо сказать, что до настоящего времени общие топологические пространства мало применялись в исследовании математических моделей естественных наук (впрочем, в таких случаях всегда хочется добавить, что, быть может, потому-то и не решены некоторые из проблем, десятками, а то и сотнями лет остающихся неприступными). Как правило, достаточно рассматривать метрические пространства, и даже их специальный случай — банаховы пространства . Более того, во всех или почти во всех приложениях в физике и механике бывает достаточно считать, что фазовое пространство есть евклидово пространство, скажем, Rn со стандартным скалярным произведением или гильбертово пространство H . Впрочем, в целом ряде задач необходимо считать фазовое пространство дифференцируемым многообразием , которое является евклидовым или банаховым лишь локально. Замечу, что всякое подмножество банахова пространства является метрическим пространством (метрика сохраняется, индуцируется ). На самом деле, известно даже, что каждое метрическое пространство может быть реализовано как подмножество банахова пространства. Очевидно, каждое подмножество метрического пространства есть также метрическое пространство. С этой общностью понятия метрического пространства связана, в значительной мере, его полезность. Нередко даже в тех случаях, когда нам нужен тот или иной результат лишь для конечномерного евклидова пространства, бывает целесообразно доказывать его для произвольного банахова или метрического пространства. Дело в том, что всякий математический факт, теорема, формула становятся особенно ясными и простыми, когда они рассматриваются в естественной степени общности. Именно так — не в самой общей форме, а в естественной степени общности , которую помогает определить развитый математический вкус. Когда он изменяет, появляются тяжеловесные и мелочные рассуждения, в которых тонут главные идеи. С другой стороны, когда ведущие идеи прояснены, вполне естественно возникают и становятся довольно очевидными дальнейшие обобщения и уточнения. Определениединамическойсистемы. Под динамическойсистемой будем понимать пару (X,Nt ) — метрическое пространство X и однопара- Динамические системы метрическое семейство Nt : X → X отображений пространства X в себя такое, что выполняется принцип причинности (см.(1.3)) Каждый раз надо особо оговорить, является ли семейство Nt группой преобразований (t ∈ R ) или лишь полугруппой (t ∈ R + ). Конечно, при рассмотрении конкретной динамической системы нужно оговорить, какими свойствами регулярности по t и по x обладает однопараметрическая группа Nt (непрерывность, существование тех или иных производных, условие Липшица или Гельдера и т.д.). Интересно заметить, что групповое соотношение (1.4) само влечет определенную гладкость операторов Nt . Например, в случае, когда X — банахово пространство, а Nt для каждого t есть линейный непрерывный оператор, оказывается, что Nt зависит от t аналитически, то есть разложимо в сходящийся ряд Тейлора по степеням величины (t − t 0 ) для любого t ∈ R . Движением динамической системы (X,Nt ), определяемым начальной точкой x 0 ∈ X , назовем отображение x : t 7→ x (t ) вещественной оси R (или, соответственно, полуоси R + ) в пространство X , определяемое равенством x (t ) = Nt x 0 . (1.5) Таким образом, движение есть последовательность состояний данной динамической системы. Хотя нередко мы слышим и говорим «функция x (t )», следует различать функцию или отображение x и ее значение x (t ) при заданном t . Смешение этих понятий нередко сходит с рук, но лучше приучиться к аккуратному их употреблению, так как во многих серьезных случаях путаница между отображением и его значением может приводить к ошибкам. Траекторией (или орбитой) данного движения x : t →7 x (t ) называется множество T = [ x (t ). (1.6) t ∈R В случае полугруппы объединение следует брать по t ∈ R + , иногда употребляется термин положительная полутраектория . Когда я произношу слово «траектория», то представляю себе лыжню, на которой не видно лыжника. Мы видим пройденный им путь, но не знаем, в какой момент времени он был в той или другой точке траектории–лыжни. Траектория — множество состояний, пройденных данной системой в ходе В.И. Юдович. Математические модели естественных наук
движения. Если траектория известна, то достаточно задать закон движения по ней , чтобы движение системы было полностью определено. Нередко бывает полезным понятие графика данного движения. Это — множество точек (t,x (t )) в декартовом произведении R × X оси времени R и пространства X . Лучше уяснить связи и различия между понятиями отображения и его значения в точке, движения и мгновенного состояния динамической системы, траектории, области значений отображения и графика отображения Вам помогут упражнения к этому параграфу. 2. Автономные дифференциальные уравненияГлавным источником динамических систем можно считать автономные дифференциальные уравнения — обыкновенные и в частных производных. Рассмотрим систему дифференциальных уравнений x ˙1 = f 1 (x 1 ,x 2 ,...,xn ), x ˙2 = f 2 (x 1 ,x 2 ,...,xn ), (2.1)
Ее правые части не зависят явно от времени t , это и есть свойство автономности. Если при любых начальных данных x 01 ,x 02 ,...,x 0n задача Коши для системы (2.1) с начальными условиями x 1 (0) = x 01 , x 2 (0) = x 02 , ..., xn (0) = x 0n (2.2)имеет, и притом единственное решение x 1 (t ),x 2 (t ),...,xn (t ), определенное для всех t ∈ R (или хотя бы всех t ≥ 0), то определен эволюционный оператор Nt : Rn → Rn , который начальной точке x 0 = (x 01 ,x 02 ,...,x 0n ) ставит в соответствие значение решения x (t ) = (x 1 (t ),x 2 (t ),...,xn (t )) в момент времени t для каждого t ∈ R . Таким образом, решение x (t ) определяется равенством x (t ) = Nt x 0 . (2.3) Решение дифференциального уравнения — это и есть движение определяемой им динамической системы. Необходимо подчеркнуть, что предположение о глобальной однозначной разрешимости задачи Коши (2.1)–(2.2), которое необходимо для того, Автономные дифференциальные уравнения чтобы определить эволюционный оператор Nt , для каждой данной системы приходится проверять отдельно, и это зачастую оказывается нелегкой задачей. Все общие теоремы в теории дифференциальных уравнений говорят лишь о локальной разрешимости задачи Коши. Более того, можно утверждать, что глобальная разрешимость — существование решения, при любых начальных данных определенного для всех t , — является исключительным свойством системы дифференциальных уравнений. Подробнее об этом говорится в следующем разделе, здесь лишь замечу, что априорные оценки решений, которые необходимы для доказательства глобальной разрешимости, справедливы и могут быть получены лишь благодаря специальным свойствам системы. Таковыми являются основные законы физики — закон сохранения энергии, другие законы сохранения (момента, количества движения), второе начало термодинамики — закон возрастания энтропии и т.д. Понятие эволюционного оператора весьма полезно в теории, но нам приходится с ним работать, не имея для него, как правило, никаких аналитических формул и представлений. Заметим, что задание эволюционного оператора определяет соответствующее ему дифференциальное уравнение. Действительно, система (2.1) может быть записана как векторное дифференциальное уравнение x ˙ = F (x ). (2.4) Ее правая часть есть векторное поле на пространстве Rn , определяемое равенством F (x ) = (f 1 (x 1 ,...,xn ),f 2 (x 1 ,...,xn ),...,fn (x 1 ,...,xn )). Начальное условие (2.2) записывается в виде x (0) = x 0 . (2.5) Если Nt : Rn → Rn есть эволюционный оператор, то решение задачи Коши (2.4)–(2.5) может быть представлено в виде (2.3). Подстановка (2.3) в (2.4) дает равенство справедливое для всех x 0 ∈ Rn . Но это значит, что x 0 можно опустить и записать равенство для операторов В.И. Юдович. Математические модели естественных наук
Справа стоит композиция операторов F и Nt :
Разумеется, существование производной по времени в (2.6) предполагается. Оператор Nt обратим, и его обратный есть (Nt )−1 = N −t . «Умножая» равенство (2.7) на N −t справа, выводим Это значит, что для любого x ∈ Rn Остается еще заметить, что левая часть здесь от t не зависит, значит, не зависит от t и правая часть. Таким образом, можно положить, например, справа t = 0. Получается выражение для векторного поля F через эволюционный оператор Nt для любого x ∈ Rn . В случае линейного пространства, каковым является Rn , векторы естественным образом отождествляются с точками, а векторные поля с отображениями, поэтому можно считать, что F — оператор, действующий в Rn . Оператор (векторное поле) F , определяемый равенством (2.10), называется генератором или инфинитезимальным оператором однопараметрической группы {Nt }. Мы видим, что даже гладкое векторное поле F может и не определять эволюционный оператор (если нет глобальной разрешимости), но если уж определяет, то однозначно — теорема единственности решения задачи Коши, конечно, имеет место для гладких векторных полей. С другой стороны, задание эволюционного оператора однозначно определяет его генератор — векторное поле F . Значение дифференциальных уравнений, для которых нет единственности решения задачи Коши, в естествознании пока неясно. Иногда (как в задаче об ударных волнах в газе) неединственность просто означает, что мы пропустили некоторые условия. После того, как эти условия введены 3 О глобальной разрешимости задачи Коши и единственности решения
(в задаче об ударных волнах это условие Ренкина-Гюгонио на скачке), отбирается уже единственное решение. Встречается и такая ситуация, когда единственности решения задачи Коши нет при некоторых начальных данных, а при других она, возможно, есть. Пожалуй, в задачах естествознания мы еще не встречались с эволюционными задачами, для которых нет единственности решения. Исключительные, и до сих пор не преодоленные, трудности в доказательстве единственности решения основных начально-краевых задач гидродинамики несжимаемой жидкости привели довольно многих исследователей к гипотезе о том, что теорема единственности здесь и не справедлива. Лично я в это не верю, и много лет выдерживаю споры по этому вопросу с другими математиками. Но допустим, что в какой-нибудь задаче естествознания такая ситуация встретится. Что бы это могло означать? Необходимость перехода к вероятностному описанию? Признание за системой некоторой свободы воли? Будущее покажет. Я думаю, действительно, покажет, потому что такие системы, наверное, еще появятся в математической физике. Так уже не раз бывало, что математические абстракции и (кажущиеся) патологии реализовывались в физике. Пример тому — канторовы множества , которые Георг Кантор ввел в своих весьма абстрактных исследованиях первоначально лишь для того, чтобы глубже понять взаимоотношение между такими понятиями, как мощность и мера множества. А в настоящее время канторовы множества появляются, например, едва ли не в каждой статье журнала “Physica D”. 3. О глобальной разрешимости задачи Коши и единственности решенияСейчас я собираюсь напомнить некоторые основные результаты из теории обыкновенных дифференциальных уравнений. Мы особо сконцентрируем внимание на результатах, касающихся теорем единственности и существования решения задачи Коши, которые в общем Вам известны, но, возможно, оставались в тени. Замечу сразу, что положение с теоремами существования и единственности решения задачи Коши далеко не так благополучно, как это может показаться при чтении учебника. Речь пойдет о задаче Коши для векторного дифференциального уравнения x ˙ = F (x,t ) (3.1) в пространстве Rn с начальным условием Уравнение (3.1) можно записать в виде системы n скалярных уравнений, а начальное условие (3.2) — в виде n скалярных равенств. Когда выбран стандартный базис e 1 = (1, 0,..., 0), e 2 = (0, 1,..., 0),...,en =
где f 1 ,f 2 ,...,fn — компоненты векторного поля F , зависящего от времени. Обычно предполагается, что поле F непрерывно по совокупности переменных x,t в некоторой области пространства Rn ×R = Rn +1 , для краткости будем дальше предполагать, что поле F задано на всем пространстве Rn +1 , т.е. для всех x ∈ Rn и t ∈ R . Замечу, что определение производной x ˙ по скалярному аргументу не требует привлечения базиса. Для любого банахова пространства X производная x ˙(t ) от вектор-функции x скалярного аргумента t ∈ R по t определяется равенством: Предел в этом равенстве, вообще говоря, можно понимать по-разному — возможны различные определения производной. Если это предел по норме пространства X , получается сильная производная . В конечномерном случае все нормы эквивалентны, так что понятие сильной производной не зависит от выбора нормы, например, ее можно считать евклидовой. Если рассматривать слабую сходимость, получится понятие слабой производной ; имеется даже, вообще говоря, два типа слабой сходимости. В конечномерном случае все эти виды сходимости совпадают — имеется по существу лишь одно понятие сходимости последовательности элементов и, соответственно, лишь одно понятие производной. Замечу еще, что при выбранном базисе сходимость в конечномерном пространстве есть покоординатная сходимость (должна сходиться последовательность первых координат, последовательность вторых координат и т.д.); к тому же понятие сходимости в конечномерном пространстве не зависит и от выбора базиса. Общие теоремы существования решения задачи Коши (3.1)–(3.2) носят локальный характер. Это означает, что гарантируется лишь существование решения, определенного на некотором интервале (r 1 ,r 2 ), где r 1 < 0, r 2 > 0, содержащем начальный момент t = 0. Никак нельзя забывать (многие все-таки забывают ...), что по самому своему определению, решение дифференциального уравнения есть вектор-функция со значениями в X , определенная на интервале (именно на интервале, а не на каком-либо ином множестве!) (r 1 ,r 2 ), где −∞ ≤ r 1 < 0 и r 1 < r 2 ≤ +∞. Как раз случай, когда r 1 = −∞ и r 2 = +∞ — самый хороший, это случай глобальной разрешимости. Теорема Пеано. Пусть X — конечномерное банахово пространство, и F — непрерывная вектор-функция со значениями в X. Тогда для любого x 0 ∈ X существует, по крайней мере, одно решение задачи Коши ( 3.1)–( 3.2), определенное на некотором интервале (r 1 ,r 2 ). Разумеется, r 1 и r 2 зависят от поля F , от выбора начального момента времени (вместо t = 0 можно было бы написать t = t 0 ) и от начального значения x 0 . В условиях этой теоремы единственность решения нельзя гарантировать — даже в простейшем случае одного скалярного дифференциального уравнения нетрудно привести примеры неединственности. Классический√
пример: x ˙ = 3 x , x (0) = 0. Интересно еще поставить вопрос о том, насколько типична неединственность. Пример автономного скалярного дифференциального уравнения x ˙ = f (x ) оказывается здесь дезориентирующим. Для этого уравнения задача Коши Напомню, что множество первой категории определяется тем условием, что оно представимо в виде счетного объединения нигде не плотных множеств. Это одно из формальных определений «пренебрежимо малого» множества. Другие определения основываются на понятиях мощности, размерности, либо меры и вероятности. Подробнее о множествах первой и второй категории можно прочитать в любой книжке по теории функций вещественного переменного, например, [38], [1] или [30]. Множество называется множеством второй категории, если его дополнение в пространстве имеет первую категорию. Таким образом, множество второй категории — это массивное, большое множество, заполняющее подавляющую часть всего пространства (боюсь говорить «почти все» пространство, потому что этот термин захвачен теорией меры). Хотя результат Орлича показывает, что гладкость функции f имеет мало отношения к единственности решения задачи Коши (или поля F ), все известные теоремы единственности основываются на тех или иных условиях некоторой регулярности функции f по переменной x . Теорема единственности. Пусть, в дополнение к условиям теоремы Пеано, поле F удовлетворяет условию Липшица: |F (x 0 ,t ) − F (x 00 ,t )| ≤ L |x 0 − x 00 | с некоторой константой L > 0, хотя бы в некоторой окрестности начальной точки t = 0, x = x 0 в R × X . Тогда решение задачи Коши ( 3.1)–( 3.2) единственно. Напомню, что решения x (1) (t ) и x (2) (t ) не считаются различными, если они совпадают в пересечении их интервалов определения. Немного усилил эту теорему единственности американский математик Осгуд, который установил, что условие Липшица можно заменить условием Осгуда |F (x 0 ,t ) − F (x 00 ,t )| ≤ ω (|x 0 − x 00 |), (3.5)где ω(s ) — функция одной переменной, заданная для малых положительных s , принимающая положительные значения при s > 0 и такая, что удовлетворяет условию Верхний предел здесь несущественен. Легко заметить, что при ω(s ) = Ls , условие Осгуда превращается в условие Липшица. Если же взять ω(s ) = Ls α при 0 < α < 1, то условие Осгуда нарушается — и в самом деле, можно указать такие уравнения, для которых единственности нет. Это отнюдь не означает, что условие Осгуда необходимо для единственности — для уравнения в упражнении 5 оно нарушено, а единственность, тем не менее, имеет место. Интересно еще заметить, что если уж задача Коши для уравнения (3.1) имеет более одного решения, то на самом деле существует целое непрерывное семейство решений, образующее континуум (связное компактное множество), называемый интегральной воронкой . Это — теорема Кнезера, см. [49]. Глобальная разрешимость. Теорема об альтернативе глобальной разрешимости. Простейшие примеры показывают, что для многих дифференциальных уравнений и систем дифференциальных уравнений, по крайней мере, некоторые решения невозможно продолжить на всю вещественную ось времени или даже на полуось t ≥ 0. Более того, такую ситуацию следует считать типичной. Проведите такой эксперимент. Введите в любую стандартную программу для решения систем дифференциальных уравнений «какую попало» систему, скажем 2-го или 3-го порядка или даже скалярное дифференциальное уравнение — используйте для написания правых частей полиномы, экспоненты, тригонометрические функции и т.д. Задайте начальные данные (тоже «какие попало»). Берусь предсказать результат такого эксперимента. Решение за конечное время уйдет на бесконечность, и вычисления остановятся. Ну, может быть (это очень невероятно), решение выйдет на некоторое равновесие. Тогда измените начальные данные, и решение уйдет на бесконечность. В известной мне литературе нет строгих теорем о том, что отсутствие глобальной разрешимости, наличие взрывающихся решений является типичным. Некоторые такие теоремы, правда, довольно частного характера, мне известны, и я рассказывал о них в лекциях. Думаю, что исследование общих условий глобальной разрешимости эволюционных задач для различных классов дифференциальных уравнений в обыкновенных и частных производных (а также и интегро-дифференциальных уравнений) представляет собой актуальную и многообещающую область исследования. Особенно интересно связать глобальную разрешимость с фундаментальными законами физики. Я даже думаю, что само по себе требование глобальной разрешимости является одним из наиболее фундаментальных физических законов. Если будет развита соответствующая математическая теория, то можно ожидать, что некоторые физические законы окажутся следствием постулата глобальной разрешимости. Здесь ограничусь лишь одним примером для иллюстрации этой общей идеи. Рассмотрим скалярное дифференциальной уравнение с полиномиальной правой частью x ˙ = P (x ), P (x ) = a 1 x + a 2 x 2 + ··· + an xn , (3.7)здесь a 1 , a 2 , ...,an — вещественные постоянные. Тогда (докажите это!) для глобальной разрешимости необходимо и достаточно, чтобы этот полином был линейным, то есть, чтобы выполнялись равенства a 2 = a 3 = ··· = an = 0. Иными словами, когда это условие не выполнено, при некоторых начальных данных решение уходит на бесконечность (на самом деле, либо для всех начальных значений x (0), либо для значений на некотором луче). Можно сказать, что пространство параметров a 1 ,a 2 ,...,an есть Rn , и каждому уравнению (3.7) отвечает точка этого пространства. Так вот, глобально разрешимым уравнениям отвечает прямая в Rn — «очень тощее» множество. Его коразмерность есть n − 1. Есть еще интересный и не слишком хорошо изученный класс дифференциальных уравнений, для которого почти все начальные данные (то есть все, за исключением множества лебеговой меры ноль) отвечают решениям, определенным на всей полуоси t ≥ 0 (или даже для всех t ). Интересные результаты о таких уравнениях имеются в работе А.Я. Повзнера [36]. В этой статье приведен довольно громоздкий пример такой системы уравнений, для которой, действительно, глобально продолжимы почти все (но не все) решения. Вот простой пример. Рассмотрим комплексное дифференциальное уравнение z ˙ = z 2 . (3.8) Его решение с начальным условием z (0) = z 0 есть Очевидно, что для невещественных z
0
решение (3.9) определено для всех t
. Если же z
0
— вещественно, то при z
0
>
0 решение (3.9) можно определить лишь на интервале x ˙ = x 2 − y 2 , y ˙ = 2xy. Выходит, что глобально продолжимы все решения этой системы кроме тех, которые отвечают начальным точкам (x 0 , 0), x 0 6= 0. Очень интересно было бы исследовать общие классы систем уравнений с аналогичным поведением решений, для которых глобально продолжимы все решения, начинающиеся вне некоторого множества положительной коразмерности. О таких уравнениях, пожалуй, почти ничего сейчас неизвестно. Во всех учебниках по обыкновенным дифференциальным уравнениям после доказательства классических теорем существования и единственности решения задачи Коши следует обсуждение вопроса о возможности продолжить решение на больший интервал. Обычно, однако, это обсуждение остается как-то в тени. Я сейчас сформулирую основную теорему об альтернативе глобальной разрешимости задачи Коши. Представим себе, что мы применяем метод рассуждения от противного. Мы произносим фразу: допустим, что решение невозможно продолжить на всю полуось t ≥ 0. Что делать дальше? Следующая теорема подсказывает нам план дальнейших действий. Теорема1(обальтернативеглобальнойразрешимости). Рассмотрим задачу Коши для дифференциального уравнения в Rn x ˙ = F (x,t ), x (0) = x 0 . (3.10)Предположим, что выполнены условия классических теорем существования и единственности: F — непрерывная вектор-функция, заданная для всех (x,t ) ∈ Rn × R , и существуют непрерывные про- изводные
Тогда для решения x (t ) имеется лишь две возможности: 1) решение x (t ) можно продолжить на всю полуось t ≥ 0; 2) существует t + ∗ > 0 такое, что |x (t )| → ∞ при t → t + ∗ . Конечно, аналогичный результат справедлив и для задачи продолжения решения на отрицательную полуось: если решение x (t ) нельзя продолжить на всю полуось t ≤ 0, то найдется t − ∗ < 0 такое, что что |x (t )| → ∞ при
Областью определения решения x
(t
) может быть либо вся ось t
, либо полуось, либо интервал Явление ухода решения на бесконечность за конечное время называется коллапсом или взрывом . Согласно теореме об альтернативе, для доказательства глобальной разрешимости достаточно исключить взрыв, коллапс. А это значит, что необходимо доказать априорную оценку : предполагая, что решение существует и определено, скажем, для всех t ≥ 0, то есть нужно установить, что для него верна оценка |x (t )| ≤ M (t ), (3.11) где M (t ) — некоторая непрерывная функция. Не воспрещается даже, чтобы функция M (t ) была неограниченной на луче t ≥ 0. Важно, что априорная оценка (3.11) исключает взрыв, тогда согласно теореме, решение x (t ) определено для всех t ≥ 0. Обратите внимание на изысканную логику применяемого здесь рассуждения: мы предполагаем , что решение на [0, +∞) существует и доказываем, что тогда для него выполняется оценка (3.11). А отсюда по теореме следует, что решение и в самом деле существует. К тому же иногда функция M (t ) нам в явном виде неизвестна, но оказывается возможным доказать, что она существует. Заметим еще, что в теореме речь идет о конкретном решении x (t ), соответственно, функция M (t ) определяется для этого решения. Возможно, Вы помните из общего курса, что есть все-таки один очень важный класс систем дифференциальных уравнений (векторных дифференциальных уравнений), для которого имеет место глобальная разрешимость задачи Коши. Это линейные дифференциальные уравнения вида x ˙ = A (t )x, (3.12) в Rn или, вообще, в конечномерном банаховом пространстве X . Здесь A (t ) — непрерывная по t оператор-функция: A (t ) : X → X есть линейный оператор для каждого t ∈ R . В случае конечномерного пространства X все линейные операторы непрерывны. Результат о глобальной разрешимости сохраняется и в случае бесконечномерного пространства X , если A (t ) для каждого t есть линейные оператор, а оператор-функция A (t ) непрерывна по t в смысле нормы оператора (доказательство можно найти, например, в книге [11]). На самом деле, суть не в линейности дифференциального уравнения, а в том, что векторное поле на бесконечности растет не слишком быстро — разрешается не только линейный рост, но даже и чуть-чуть более сильный. При таких условиях удается непосредственно получить нужные априорные оценки. Об этом говорят следующие две теоремы. Сразу, однако, замечу, что уже степенной рост более быстрый, чем линейный, скажем, |x |1+ ε , ε > 0, может (хотя, конечно, не обязательно) привести к коллапсу решений. Теорема2. РассмотримзадачуКошидлядифференциальногоуравнения в Rn x ˙ = F (x,t ), x (0) = x 0 . (3.13)Пусть снова выполнены условия классических теорем существования и единственности: F — непрерывная вектор-функция, заданная для всех (x,t ) ∈ Rn × R , и существуют непрерывные производ- ные
Предположим, что выполнена следующая оценка |F(x,t)| ≤ m(t)|x|, (3.14)для всех x ∈ Rn , t ≥ 0 (достаточно потребовать, чтобы неравенство ( 3.14) выполнялось для всех x вне некоторого шара, скажем, при |x | ≥ a ). Здесь m (t ) — непрерывная функция, определенная для t ≥ 0. Тогда всякое решение задачи Коши ( 3.13) можно продолжить на всю полуось t ≥ 0. Доказательство. Предположим, что задача Коши (3.13) имеет решение x (t ). Подставим его в уравнение (3.13). Умножая полученное равенство скалярно на x (t ), получим Дальше, ради краткости, вместо x (t ) будем писать x , а вместо |x |2 — x 2 . Применяя для оценки правой части неравенство Коши-Буняковского, а затем условие теоремы (3.14), получим Это известное Вам дифференциальное неравенство. Следующее рассуждение носит довольно общий характер, повторяя в нашем конкретном случае лемму Гронуолла (см. [49]). Умножим (3.16) на Интегрируя по времени, с учетом начального условия (3.13) получим t 2R m (s )ds |x (t )|2 ≤ |x 0 |2 e 0 (3.18) или t R m (s )ds def |x (t )| ≤ |x 0 |e 0 = M (t ). (3.19)Итак, мы доказали априорную оценку (3.19). Поэтому коллапс невозможен. Осталось сослаться на теорему об альтернативе, и доказательство окончено. Теорема 3. Пусть вместо условия ( 3.14) выполняется (хотя бы при больших |x |) неравенство |F(x,t)| ≤ m(t)ϕ(|x|), (3.20)где m (t )— непрерывная на луче t ≥ 0 функция, а функция ϕ(s ) определена для s ≥ 0 и удовлетворяет условию нижний предел можно поставить какой угодно. Тогда сохраняется утверждение теоремы 2: всякое решение задачи задачи Коши ( 3.13) можно продолжить на всю полуось t ≥ 0. Это так называемая теорема Хартмана-Уинтнера (см. книгу Ф. Хартмана [49]), достаточно тривиальная. Доказывается она в основном так же, как теорема 2, думаю, Вы справитесь с этим сами. Можно сказать, что доказательства теорем 2 и 3 носят «силовой» характер, потому что они основываются на непосредственных и грубых оценках правых частей уравнений. Ограничения, принятые в этих теоремах, очень сильны, очень строги и не часто выполняются. Для большинства наиболее важных нелинейных систем правые части на бесконечности растут степенным образом (скажем, как |x |2 или |x |3 ), а то и экспоненциально. Пожалуй, в приложениях помимо линейных уравнений, теорема 2 применяется еще к уравнениям и системам с ограниченными правыми частями. Например, из нее следует глобальная разрешимость для уравнения математического маятника x ¨ + ω 2 sinx = 0. В упражнениях Вы найдете примеры систем уравнений, для которых априорные оценки решений и глобальную разрешимость задачи Коши можно вывести более тонкими приемами, с использованием их специфических свойств. Упражнения1. Докажите, что для скалярного уравнения x ˙ = a 1 x + a 2 x 2 + ...an xn (a 1 ,...,an — вещественные параметры) глобальная разрешимость на всей оси времени имеет место тогда и только тогда, когда a 2 = a 3 = ... = an = 0. Докажите также, что при n > 1 и an 6= 0 глобальная разрешимость для положительных времен t ≥ 0 имеет место в том и только в том случае, когда n — нечетно, и при этом an < 0. 2. Найдите априорную оценку решения и докажите глобальную разрешимость задачи Коши для уравнения в Rn x ˙ = F (x,t ) с ограниченной правой частью: задана оценка |F (x,t )| ≤ M (t ), где M (t ) — известная функция, определенная для всех t ∈ R , а x ∈ Rn — произвольная точка. 3. Докажите, что если потенциальная энергия V (x ) ограничена снизу (так что V (x ) ≥ h для всех x ∈ Rn при известной постоянной h ), то для обобщенного уравнения 2-го закона Ньютона x ¨ = −grad V (x ) справедлива теорема о глобальной разрешимости. Сохраняется ли этот результат после введения внешней силы F (t ) — для уравнения x ¨ = −grad V (x ) + F (t ). 4. Рассмотрите скалярное уравнение
при V (x ) = axm . При каких a и m возможен коллапс? 5. Приведите пример уравнения вида x ˙ = F (x ) на плоскости R2 такого, что поле F (x ) непрерывно, ни в одной точке не имеет производной, не удовлетворяет условию Осгуда, но тем не менее решение задачи Коши существует и единственно. 6. Найдите и нарисуйте интегральную воронку решений задачи Коши √ 7. Возможно ли, что единственность решения имеет место для отрицательных t и ее нет для положительных t (присмотритесь к предыдущему примеру). 8. Доказать, что для скалярного уравнения
с начальным условием x (0) = x 0 в случае коллапса при t = t ∗ > 0 решение x (t ) стремится к бесконечности определенного знака, то есть либо x (t ) → +∞, либо x (t ) → −∞ при t → t ∗ − 0. 4. Динамические системы с дискретным временемДинамической системой с дискретным временем называется пара (X,N ), где X — метрическое пространство, N : X → X — отображение этого пространства в себя. Движением этой системы с начальной точкой x 0 называется последовательность x 0 , x 1 = Nx 0 , x 2 = Nx 1 = N 2 x 0 , ..., xn = Nn x 0 . (4.1)Множество {xn }, n = 0, 1,... называется положительной полутраекторией, определенной начальной точкой x 0 . Выполняются следующие равенства N 0 = I, Nm +n = Nm Nn . (4.2)Первое из них — обычное определение, а второе выражает закон ассоциативности для композиции отображений. Нетрудно видеть, что это тот же закон причинности (1.4), но записанный не для произвольных t,s ∈ R , а лишь для их неотрицательных целочисленных значений t = m , s = n . Если N — обратимое отображение, то можно считать, что равенство (4.2) выполнено для всех целых m,n ∈ Z . В этом случае можно определить точки xn = (N −1 )|n | x 0 . Множество {xn }, n = 0, ±1, ±2,... называется траекторией . Очевидно, траектория определяется любой своей точкой, в частности точкой x 0 . Заметим, что множество операторов {I,N,N 2 ,... } есть полугруппа. В случае, когда оператор N обратим, ее можно расширить до группы {Nn }, n = 0, ±1, ±2,... . Каскады и потоки. Динамическую систему с дискретным временем называют также каскадом , в отличие от динамической системы с непрерывным временем, у которой есть еще название поток . Оба названия весьма выразительны, хотя термин «каскад» не всеми принят. Если рассматривается автономное дифференциальное уравнение x ˙ = F (x ) в Rn , то всегда полезно представить себе, что F есть поле скорости текущей жидкости. Это значит, что в точке x ∈ Rn задана скорость течения, хотя в этой точке появляются все время новые частицы жидкости. Если хотим проследить за движением той частицы жидкости, которая в начальный момент t = 0 находилась в точке x 0 ∈ Rn , то для этого нужно решить задачу Коши с начальным условием x (0) = x 0 . Тогда решение x (t ) = Nt x 0 дает положение этой жидкой частицы в момент t . Сейчас мы рассмотрим пути возникновения динамических систем с дискретным временем. Во-первых, динамические системы с дискретным временем (каскады) возникают при квантизации динамических систем с непрерывным временем (потоков). Во-вторых, в ряде случаев (в частности, в экологии) уже исходные математические модели оказываются динамическими системами с дискретным временем. В-третьих, рассматривая периодические дифференциальные уравнения, можно, а зачастую и полезно, перейти к рассмотрению решений лишь в точках np , кратных периоду p , что приводит к динамической системе с оператором монодромии . И, наконец, в-четвертых, динамические системы с дискретным временем возникают при исследовании автономных систем, для которых удается найти поверхность Пуанкаре и построить отображение Пуанкаре . Квантизация. Случается, что, рассматривая динамическую систему с непрерывным временем, мы желаем сократить объем информации, с которой имеем дело (храним, обрабатываем, пересылаем) и фиксировать состояние системы лишь в дискретные моменты времени, скажем, только для t = nT , где T > 0 фиксировано. Так мы поступаем, например, составляя таблицы (T — шаг таблицы) решений дифференциальных уравнений. Так поступают и руководящие организации, запрашивая отчеты лишь ежегодно (T = 1 год), а не в каждый момент времени. Вместо x (t ) = Nt x 0 мы в этом случае рассматриваем лишь последовательность xn = x (nT ) = NnT x 0 . Таким путем приходим к динамической системе с дискретным временем (X,NT ) с тем же пространством X и отображением NT . Математические модели с дискретным временем. Иногда исходная математическая модель для описания данного явления уже оказывается системой с дискретным временем. Таковы многие модели экологии и генетики. Ограничусь здесь одним примером. Рассмотрим изменение численности популяции бабочек. Будем характеризовать величину популяции в n -м поколении, скажем, ее биомассой xn ; ясно, что xn — неотрицательное число (xn ≥ 0). Когда популяция развивается беспрепятственно, действует закон Мальтуса xn +1 = bxn . (4.3) Здесь b > 0 — параметр, характеризующий популяцию. Таким образом, мы приходим к рассмотрению динамической системы (R + ,N ), где неотрицательная полуось R + есть пространство динамической системы, а N : R + → R + — отображение, определяемое равенством Nx = bx. (4.4) Если в начальный момент n = 0 (дискретного времени n ) величина популяции есть x 0 , то по рекуррентной формуле (4.3) непосредственно получаем xn = bn x 0 . (4.5) Если b > 1, то xn → ∞ при n → ∞. Если b = 1, то xn = x 0 для всех n , популяция не меняется со временем. Если b < 1, то xm → 0, популяция вымирает. Теперь понятно, почему b называется параметром жизненной силы данной популяции. Закон Мальтуса (4.3) достаточно хорошо описывает развитие не только популяции бабочек, но и вообще эволюцию всякой популяции в условиях практически неограниченного запаса питания и отсутствия сопротивления внешней среды (хищников, загрязнения среды, самоотравления популяции продуктами ее жизнедеятельности). Я говорю о бабочках, потому что для них характерно, что все особи n -го поколения погибают, рождая (n + 1)е поколение; рост может оказаться еще быстрее, чем экспоненциальный, если часть особей n -го поколения продолжает жить одновременно с (n + 1)–м, (n + 2)–м и последующими поколениями. Часто говорят, что для проверки условий применимости данной математической модели нужно рассмотреть ее как частный случай более общих моделей. Это не совсем так. Иногда модель сама громко заявляет о своей неприменимости. С одним примером мы уже встретились раньше. Если решение x (t ) дифференциального уравнения испытывает коллапс, |x (t )| → ∞ при t → t ∗ , то ясно, что при t ≥ t ∗ (а на самом деле даже раньше) модель становится неприменимой для описания дальнейшей эволюции. Закон Мальтуса при b > 1 дает другой пример. Авторы популярных книг любят приводить подсчет роста популяций бабочек, или кроликов в n -м поколении и отсюда выводить, что очень скоро такая популяция заполнит всю Землю, или что ее масса станет больше массы Солнца. Такие выводы, очевидно, решительно противоречат реальности. Это означает, что для описания дальнейшего развития популяции модель должна быть изменена. Один из простейших способов хоть как-то учесть сопротивление внешней среды развитию популяций был предложен Ферхюльстом [66] и состоял в том, что в уравнение Мальтуса добавлялось квадратичное слагаемое. После введения надлежащих масштабов измерения (максимально возможный размер популяции принимается за 1) получается динамическая система (X,N ), где X = [0, 1], а отображение N задается равенством Nx = bx (1 − x ). (4.6)Требование, чтобы для всякого x ∈ [0, 1] его образ Nx также принадлежал [0, 1], приводит к ограничению на параметр жизненной силы 0 ≤ b ≤ 4. Теперь получается, что xn +1 = bxn (1 − xn ). (4.7) С ростом n выражение для xn (через x 0 ) по этой рекуррентной формуле сильно усложняется. Чрезвычайно усложняется и поведение величин xn . Сейчас мы обсудим некоторые общие вопросы о поведении движений, а затем вернемся к нашим бабочкам. Поведение движений динамической системы на больших временах. Вообще, когда мы изучаем динамическую систему, будь то поток или каскад, наиболее интересен вопрос: что происходит при неограниченно возрастающем времени (при t → +∞ или при n → +∞)? Простейший вариант — когда последовательность xn имеет предел: xn → x ∗ . Переходя к пределу в равенстве xn +1 = Nxn (4.8) и учитывая, что xn +1 → x ∗ , заключаем, что x ∗ — неподвижная точка отображения N : Nx ∗ = x ∗ . (4.9) Когда мы строим последовательность xn по формуле (4.8), то по существу как будто бы пытаемся решить уравнение (4.9) методом итераций. Итерации могут, конечно, и не сходиться. Как ведет себя тогда последовательность xn ? Бывает, что движение xn стремится к циклу некоторого периода p . Циклом динамической системы (X,N ) или циклом отображения N : X → X называется инвариантное множество {x 1 ,x 2 ,...,xp } (заметьте, что уже по смыслу слова «множество» все точки эти различны), для точек которого верно равенство N p x j = x j , но если взять N в меньшей степени k < p , то Nk xj 6= xj ни для какого j . Например, если имеется три различные точки x 1 ,x 2 ,x 3 и выполняются равенства Nx 1 = x 3 , Nx 3 = x 2 , Nx 2 = x 1 , то это означает, что множество {x 1 ,x 2 ,x 3 } есть цикл периода 3. Заметьте, что определение периода цикла для отображений отличается от обычного определения периода функции скалярного аргумента — здесь в определение включается требование минимальности числа p , а в случае функций — нет. Например, правильно будет сказать, что функция sinx , наряду с периодом 2π, имеет периоды 4π, 6π,... , а у цикла отображения есть только один период. Вообще, подмножество Y
в X
называется инвариантным множеством динамической системы (X,N
) или отображения N
, если оно переводится отображением N
в себя, так что N
(Y
) ⊂ Y
. Это означает, что для любого x
∈ Y
и его образ Nx
∈ Y
. В этом случае можно рассмотреть сужение му Движение динамической системы может стремиться и к более сложному множеству, чем цикл. Например, даже для простого квадратичного отображения (4.6) случается, что движения стремятся к канторову множеству (это было доказано моими учениками Ю. С. Барковским и Г.М. Левиным (1980) и одновременно польским математиком Мисюревичем). Но, конечно, бывает и так, что движение xn уходит на бесконечность. Надо сказать, что достаточно удивительным образом движения каскадов могут быть сложнее, чем движения потоков. Например, как Вы знаете из теории дифференциальных уравнений, поведение решений скалярного автономного уравнения x ˙(t ) = f (x ) очень просто: всякое решение x (t ), скажем, при t > 0, либо 1) уходит на бесконечность за конечное время, либо 2) x (t ) → +∞ (−∞) при t → +∞, либо 3) стремится к некоторому равновесию x (t ) → x ∗ при t → +∞, причем f (x ∗ ) = 0. Между тем, одномерное отображение (4.6) демонстрирует весьма сложное поведение. Заметьте, что уравнения типа (4.6) получаются из дифференциального уравнения при дискретизации, когда мы решаем задачу Коши численно, например, методом Эйлера. Такое резкое различие в качественном поведении движений лишний раз напоминает нам, как осторожно нужно относиться к выводам, полученным в результате приближенных вычислений, в особенности, когда речь идет о решении уравнений на больших промежутках времени. Теорема Шарковского. В 1964 году советский математик А.Н. Шарковский доказал совершенно фантастическую теорему о циклах отображения прямой [51]. Довольно долго эта теорема была мало известной, и несколько американских математиков стали знамениты, доказав на десяток лет позже некоторые, наиболее простые частные случаи этой теоремы. А.Н. Шарковский весьма изящно изложил свою теорему, введя cпециальный порядок на множестве N натуральных чисел. Для каждой пары натуральных чисел, скажем p
и q
, вводится соотношение p
≺ q
, которое читается как “p
предшествует q
”. Будем также писать 3 ≺ 5 ≺ 7 ≺ 9 ≺ 11... ≺ 3 · 2 ≺ 5 · 2 ≺ ... ≺ 3 · 22 ≺ 5 · 22 ≺ ... ≺ ≺ 3 · 23 ≺ 5 · 23 ≺ ... 23 ≺ 22 ≺ 2 ≺ 1. (4.10) Эта упорядоченность не используется при доказательстве, но позволяет сформулировать теорему в очень изящной форме. Теорема 1 (А.Н. Шарковский, 1964). Пусть динамическая система с дискретным временем (R,T ) определяется непрерывной скалярной функцией f (x ) для x ∈ R . Отображение T : R → R определено равенством Tx = f (x ) для любого x ∈ R . Предположим, что данная система имеет цикл периода
p, тогда она также обладает циклом любого периода
Из этой теоремы, в частности, следует, что при условии существования цикла периода 3 существуют циклы всевозможных периодов, и, в частности, неподвижная точка отображения T (цикл периода 1)! Вы сами сможете извлечь из этой теоремы другие удивительные следствия. Например, если имеется цикл периода 8, то существуют также циклы периодов 4, 2 и 1. При этом можно построить отображение, у которого нет циклов других периодов. В этом смысле теорема Шарковского точна. Различные авторы приложили немало усилий в попытках перенести теорему Шарковского на многомерные отображения. Известные ныне аналогичные результаты относятся, однако, лишь к некоторым очень частным классам отображений. Усилия исследователей в этом направлении продолжаются. Периодические системы и оператор монодромии. Следующими по сложности после автономных систем идут периодические системы дифференциальных уравнений. Рассмотрим дифференциальное уравнение x ˙ = F (x,t ) (4.11) в банаховом пространстве X . Предположим, что векторное поле F зависит от времени периодически, с периодом p > 0 F (x,t + p ) ≡ F (x,t ). (4.12)Поставим для этого уравнения задачу Коши с начальным условием x (0) = a. (4.13) Предположим, что для любого a ∈ X существует единственное решение x (t ) задачи (4.11)–(4.13), определенное для t ∈ [0,p ]. Это означает, что существует оператор монодромии Mp : X → X , определяемый равенством Mp a = x (p ). (4.14) Теперь понятно, что можно, и это оказывается весьма полезным, ввести в рассмотрение динамическую систему с дискретным временем (X,Mp ). При этом фазовое пространство X
остается прежним, но вместо потока Ясно, что оператор монодромии Mp
получается из эволюционного оператора В теории периодических дифференциальных уравнений переход к дискретной динамической системе оказывается весьма полезным, например, при исследовании устойчивости периодических движений. На практике оператор монодромии остается неизвестным даже для линейного периодического уравнения (4.11) и не задается какими-либо явными формулами, но его вполне можно и нужно вычислять при помощи компьютера. Многие фундаментальные свойства оператора монодромии оказывается возможным исследовать, основываясь лишь на его определении посредством дифференциального уравнения — чем и гордится математика (точнее, раздел качественной теории дифференциальных уравнений). Отображение Пуанкаре. Рассмотрим автономное дифференциальное уравнение x ˙ = F (x ) (4.15) в Rn . Предположим, что нам известна гиперповерхность S (например, заданная скалярным уравнением Φ(x ) = 0), обладающая следующим свойством (см. Рис. 1): для любой точки x 0 ∈ S начатое от нее движение x (t ) (то есть решение задачи Коши для уравнения (4.15) с начальным условием x (0) = x 0 ) возвращается на эту поверхность. Иными словами, существует t ∗ = t ∗ (x 0 ) > 0 такое, что x (t ∗ ) ∈ S . Гиперповерхность, обладающая этим свойством, называется гиперповерхностьюПуанкаре . Чаще говорят поверхностьПуанкаре , хотя формально это правильно лишь при n = 3 (поверхность двумерна, по определению). Понятно, что движущаяся точка x (t ) вернется на поверхность S бесконечно много раз. Пусть t ∗ = t ∗ (x 0 ) > 0 — момент первого возвращения. Отображение Пуанкаре Π : S → S определяется равенством Πxo = x (t ∗ ). (4.16)
Рис. 1 Таким путем мы определим динамическую систему с дискретным временем (S, Π). При этом S — ее пространство, а Π : S → S — отображение. Исследование поведения движений системы (4.15) — во всяком случае, тех, которые пересекают поверхность S — в значительной мере сводится к исследованию итераций Πn отображения Пуанкаре. Если, например, x 0 — неподвижная точка отображения Π, так что Πx 0 = x 0 , то соответствующее движение x (t ) — периодическое. Его период есть p = t ∗ (x 0 ).
Проблема вложения каскада в поток. Давно и довольно естественно возник вопрос, можно ли данную динамическую систему (X,N ) с дискретным временем вложить в поток, то есть получить посредством квантизации из некоторой динамической системы с непрерывным временем. Оказывается, это возможно далеко не всегда, и условия, когда это возможно, в точности неизвестны. Я сейчас расскажу о двух препятствиях к такому вложению, ограничиваясь случаем, когда X = Rn . Необратимость . Предположим, что нам удалось построить такое автономное дифференциальное уравнение x ˙ = F (x ) с гладким векторным полем F (x ) и эволюционным оператором Nt так, что при некотором шаге квантизации h получается равенство Nh = N . Но оператор Nt для каждого t обратим, значит, и Nh обратим. Об этом говорят теоремы существования и единственности решения задачи Коши. Выходит, что необратимое отображение N невозможно вложить в поток. Отображение N : x 7→ bx (1 − x ) в модели популяции бабочек как раз необратимо. Потомуто так сложна определяемая им динамика на отрезке [0, 1], а для скалярных дифференциальных уравнений x ˙ = f (x ) все очень просто. Решения либо уходят на бесконечность, либо стремятся к равновесиям. Несохранение ориентации . Всякий эволюционный оператор Nt , наряду с обратимостью, имеет еще свойство сохранять ориентацию . Ориентацию пространства Rn
можно задать, фиксируя упорядоченный
базис e
1
,e
2
,...,en
этого пространства. Его мы объявляем положительным. После этого все остальные мыслимые упорядоченные базисы линейный оператор J
: Rn
→ Rn
его действием на элементы исходного базиса, полагая — отрицательным. Очевидно, что при малых деформациях положительного базиса получается также положительный базис. Действительно, при сохранении базиса J = I , detI = 1, а при его малом изменении элементы определителя меняются мало, и строгое неравенство detJ > 0 сохраняется. Отсюда нетрудно заключить, что при непрерывном изменении положительного базиса всегда будет получаться также положительный базис, при непрерывном изменении отрицательного базиса — отрицательный. Вообще, если подействовать линейным обратимым оператором A : Rn → Rn на данный базис e 1 ,e 2 ,...,en , то получается новый базис Ae 1 ,Ae 2 ,...,Aen . Он останется положительным, если detA > 0. В этом случае мы скажем, что оператор A сохраняет ориентацию пространства Rn . Если же detA < 0, то оператор меняет ориентацию: базис Ae 1 ,Ae 2 , ...,Aen будет отрицательным. Случай detA = 0, конечно, исключен, потому что оператор предполагается обратимым. Приведу пример. Пусть n = 3, e 1 = (1, 0, 0), e 2 = (0, 1, 0), e 3 = (0,
0,
1). Если теперь провести перестановку и положить
Очевидно, detJ
= −1, так что базис Типичным линейным оператором, нарушающим (говорят еще, меняющим ) ориентацию, является оператор зеркального отражения, скажем, A : (x 1 ,x 2 ,x 3 ) 7→ (x 1 ,x 2 , −x 3 ). Его определитель detA = −1. Мы доказали, в частности, что невозможно непрерывным движением в пространстве R 3 преобразовать правую перчатку — в левую. Этот факт очень волновал великого философа Э. Канта (не читали? почитайте!). Он даже считал, что основные законы арифметики, алгебры и геометрии являются врожденными, человек знает их от рождения. А вот для явлений, связанных с ориентацией пространства, делал исключение, считая, что они познаются лишь на опыте. Для нелинейного гладкого отображения ϕ : Rn → Rn понятия сохранения и несохранения ориентации определяются лишь локально. Говорят, что отображение ϕ сохраняет ориентацию в точке x ∈ Rn , если в этой точке положителен его якобиан: det ϕ 0 (x ) > 0. Замечу, что производная ϕ 0 (x ) — линейный оператор и в стандартном базисе e 1 ,...,en задается матри- цей Якоби Нетрудно доказать, что эволюционный оператор дифференциального уравнения x ˙ = F (x,t ) в Rn с гладким полем F всюду сохраняет ориентацию. Действительно, чтобы установить сохранение ориентации в точке x 0 , найдем соответствующее решение задачи Коши x (t ) = Nt x 0 . Теперь нам нужно найти производную (Nt )0 (x 0 ) и вычислить ее детерминант. Нетрудно показать, что вектор-функция u (t ) = (Nt )0 (x 0 )u 0 является решением линеаризованной на x (t ) задачи Коши u ˙ = Fx (x (t ),t )u, u (0) = u 0 . (4.18)Это означает, что операции вычисления эволюционного оператора Nt и линеаризации перестановочны (Докажите это самостоятельно). Но из курса 5 Интегралы и законы сохранения обыкновенных дифференциальных уравнений мы знаем, что для векторного линейного уравнения в Rn u ˙ = A (t )u (4.19) справедлива формула Лиувилля. Пусть Ut — эволюционый оператор уравнения (4.19), а его определитель есть detUt = W (t ). Это вронскиан, отвечающий фундаментальной системе решений u 1 (t ) = Ut e 1 , ..., un (t ) = Ut en с базисными векторами e 1 ,...,en в качестве начальных данных. Тогда t R spA (τ)d τ W (t ) = W (0)e 0 . (4.20)Из этой формулы Лиувилля следует, что W (t ) остается положительным для всех t , если он положителен при t = 0. Но W (t ) = 1 при t = 0, так что W (t ) > 0. Задача (4.18) есть, конечно, частный случай задачи (4.19) при A (t ) = Fx (x (t ),t ). При этом Ut = (Nt )0 (x 0 ). Итак, мы доказали, что det(Nt )0 (x 0 ) > 0 при всех t, а эволюционный оператор Nt сохраняет ориентацию. Отсюда следует, что невозможно вложить в поток никакое отображение, которое хотя бы в одной точке меняет ориентацию пространства. Например, нельзя вложить в поток оператор зеркального отражения (см. выше). Не удержусь от рассказа об одной проблеме, связанной с ориентацией. Вы, конечно, знаете, что современная физика еще не решила, конечна или бесконечна наша Вселенная. Ответ зависит от того, положительной или нулевой окажется средняя плотность материи во Вселенной. Между тем, точность современных измерений пока не позволяет прийти к определенному выводу. С этим связана и еще одна проблема. Если наше пространство конечно, и Вселенная представляет собой ограниченное многообразие, то встает вопрос об его ориентируемости или неориентируемости. Если оно неориентируемо, то, в принципе, это можно установить при помощи следующего эксперимента. Двигайтесь все время в одном и том же направлении, тогда рано или поздно (если Вселенная конечна) Вы вернетесь к своему начальному положению. Однако, если Вселенная неориентируема, то сердце при этом окажется у Вас справа, и нужно будет еще раз совершить тот же путь, чтобы возвратить его на положенное место. Пока такой эксперимент не проведен, вопрос об ориентируемости Вселенной остается открытым. 5. Интегралы и законы сохраненияРассмотрим дифференциальное уравнение в Rn (или вообще в банаховом пространстве X ) x ˙ = F (x,t ). (5.1)Функции, определенные на фазовом пространстве X , называются также наблюдаемыми . Если известна наблюдаемая ϕ = ϕ(x,t ), x ∈ X , t ∈ R , зависящая от времени, то можно и интересно подставить вместо x решение x (t ) уравнения (5.1) и следить за изменением величины ϕ = ϕ(x (t ),t ). Ограничиваясь пока случаем Rn , найдем производную от этой функции по t . Дифференцируя по t и учитывая, что x (t ) = (x 1 (t ),...,xn (t )) — решение уравнения (5.1), получаем Здесь Fk — есть k -я компонента поля F , так что F = (F 1 ,F 2 ,...,Fn ). Глядя на эту формулу, нетрудно понять, что целесообразно ввести новое определение: производной по времени от функции ϕ(x,t ) в силу заданного уравнения движения (5.1) называется функция ϕ ˙(x,t ), определенная для всех x ∈ Rn и t ∈ R + равенством Подчеркну, что здесь уже x не решение дифференциального уравнения, а просто произвольная точка фазового пространства Rn . Сравнивая равенства (5.2) и (5.3), приходим к важной формуле Соль в том, что в формуле (5.4) присутствует одна и та же функция ϕ˙ для всех решений x (t ). Если X — евклидово пространство, то определение (5.3) можно записать в виде где ∇ϕ — градиент функции ϕ, и аргументы x,t опущены во всех слагаемых. Теперь ограничим себя рассмотрением автономного уравнения в X x ˙ = F (x ). (5.6) Наблюдаемая ϕ(x ) называется интегралом (или первым интегралом , или константой движения ), если для любого решения x (t ) уравнения (5.6) ϕ(x (t )) = C , где C — константа, зависящая от выбранного решения (движения) x (t ). Если задано начальное условие x (t 0 ) = x 0 , то константа C определяется: C = ϕ(x (t 0 )) = ϕ(x 0 ). Конечно, всегда имеются тривиальные интегралы, это постоянные наблюдаемые: ϕ(x ) ≡ C , C = const . Найти интеграл уравнения (5.6) бывает не так уж просто. Но проверить, является ли данная гладкая функция ϕ(x ) интегралом, несложно. С учетом формулы (5.5) и определения интеграла, приходим к следующему заключению: для того, чтобы C 1 –гладкая функция была интегралом автономного уравнения (5.6), необходимо и достаточно, чтобы для всех x выполнялось уравнение
Интересно заметить, что на практике мы чаще всего находим сначала именно ∇ϕ так, чтобы выполнялось уравнение (5.7). Затем уже по данному ∇ϕ находится ϕ. Это дает повод ввести следующие определения. Косимметрия . Векторное поле L = L (x ) на евклидовом пространстве H называется косимметрией поля F на H , если для всех x ∈ H векторы F (x ) и L (x ) ортогональны: (F (x ),L (x )) = 0. (5.9)Будем также говорить, что поле L = L (x ) есть косимметрия дифференциального уравнения x ˙ = F (x ). Векторное поле L (x ) назовем голономным , если оно допускает представление в виде L (x ) = grad ϕ(x ) с некоторой функцией ϕ(x ) (приведите пример неголономного векторного поля). Теперь предыдущее утверждение об интегралах можно сформулировать иначе. Для того, чтобы функция ϕ была интегралом уравнения ( 5.6), необходимо и достаточно, чтобы векторное поле L (x ) = grad ϕ(x ) было (голономной) косимметрией поля F (x ). Эта терминология была введена в 1991 году в моей заметке [55]. Оказалось (собственно, об этом и была написана заметка), что и неголономные косимметрии имеют важные приложения в теории дифференциальных уравнений и математической физике. Голономные косимметрии, конечно, постоянно мелькали в математической литературе в связи с интегралами, но обычно оставались в тени. В действительности, однако, отыскание интеграла, как правило, начинается именно с поиска соответствующей косимметрии. Знание одного или нескольких нетривиальных интегралов уравнения (5.6) много дает для понимания динамики системы, а когда интегралов достаточно много, позволяет получить явные или почти явные формулы для решения. Долгое время усилия математиков были направлены на поиск интегралов дифференциальных уравнений и систем в надежде найти явные решения. К успеху это привело лишь в сравнительно немногих случаях. Постепенно стало ясно, что у типичного дифференциального уравнения вообще нет ни одного нетривиального интеграла. В полном объеме эта гипотеза до сих пор не доказана, но, например, Пуанкаре (в конце XIX века) установил, что многие консервативные системы не имеют других нетривиальных интегралов, кроме интеграла энергии, о котором мы подробнее будем говорить дальше. Кстати, одно из самых глупых высказываний, какие мне приходилось слышать в жизни (к сожалению, много раз), звучит примерно так: «Зачем мы будем возиться с интегралами, нам не нужны точные формулы, мы поставим систему на компьютер, да и вычислим то решение, которое нужно». На самом деле, никакой компьютер не позволяет вычислить решение на очень больших временах (за весьма редкими исключениями, к которым относятся такие решения, которые со временем асимптотически сходятся к равновесиям или к периодическим режимам). Кроме того, существование или несуществование интегралов во многом определяет качественное поведение данной системы. Вообще, применение компьютера к исследованию динамических систем требует не меньшей, а наоборот, более глубокой математической подготовки. Иначе не разобраться в том ворохе информации, который выдает машина, и даже не понять, имеет ли она какое-либо отношение к решениям заданного дифференциального уравнения. Не менее важно и то обстоятельство, что создавать адекватные и эффективные численные методы возможно лишь при достаточно глубоком понимании математической сущности уравнений и их решений. В частности, когда система уравнений обладает одним или несколькими интегралами, лучшие вычислительные схемы (скажем, сеточные или галеркинские) получаются при условии, что для приближенных решений интегралы сохраняются точно. Геометрический смысл интеграла . Пусть ϕ — интеграл уравнения (5.6). Тогда уравнение ϕ(x ) = C (5.10) для любой постоянной C
определяет множество уровня
функции ϕ. Оно может быть пустым или, наоборот (если ϕ
≡ C
), совпадать со всем пространством, но в нетривиальных случаях это — гиперповерхность
. Например, непустые множества уровня функции ϕ : R
3
→ R
, заданной равенством По определению интеграла, ϕ(x (t )) для любого решения x (t ) сохраняет постоянное значение. Если x (0) = x 0 , то это постоянное значение есть, очевидно, ϕ(x 0 ). Таким образом, движущаяся точка x (t ) все время остается на гиперповерхности ϕ(x ) = ϕ(x 0 ). (5.11) Выходит, что при исследовании динамики, определяемой уравнением (5.6), мы можем ограничиться рассмотрением движений на отдельных гиперповерхностях ϕ(x ) = C . В принципе, динамика описывается в таком случае системой дифференциальных уравнений на единицу меньшего порядка. Если имеется два интеграла ϕ1 и ϕ2 (обобщение на большее количество интегралов очевидно), то естественно ввести совместноемножествоуровня , определяемое для любых заданных констант C 1 и C 2 , равенствами ϕ1 (x ) = C 1 , ϕ2 (x ) = C 2 . (5.12)Теперь дело сведется к изучению динамики на инвариантных совместных множествах уровня. Их размерность (при условии функциональной независимости интегралов ϕ1 и ϕ2 ) уже на две единицы меньше, чем размерность фазового пространства системы. Говорят, что такие множества (подмногообразия) имеют коразмерность 2. Условие функциональной независимости интегралов, разумеется, весьма существенно. Дело в том, что если ϕ1 и ϕ2 — интегралы, то также и F (ϕ1 (x ), ϕ2 (x )) также интеграл при произвольной функции двух переменных F . Обычным достаточным условием функциональной независимости функций ϕ1 (x ) и ϕ2 (x ) служит, как вы знаете из курса анализа, требование, чтобы их матрица Якоби имела максимальный ранг. Когда количество функций совпадает с числом независимых переменных, матрица Якоби — квадратная, и это условие сводится к неравенству нулю ее определителя — якобиана. Замечу, что вполне возможно было бы по аналогии ввести интегралы ϕ(x,t ), зависящие от времени — как для автономного уравнения (5.6), так и для неавтономного уравнения (5.1). К сожалению, они редко встречаются. Приведу несколько примеров систем, допускающих интегралы. Пример 1. Гармонический осциллятор. Рассмотрим уравнение 2-го порядка x ¨ + x = 0. (5.13) Для любого решения x (t ), умножая (5.13) на x ˙, получим Таким образом, Если решить уравнение (5.13) с начальным условием x (0) = 0, x ˙(0) = 1, то получим x (t ) = sint . Таким образом, закон сохранения энергии для гармонического осциллятора выражается равенством sin2 t + cos2 t = 1. Пример2.УравненияЭйлеравращениятвердоготелавокругнеподвижной точки. Эти уравнения, возможно, самые красивые во всей механике, имеют вид Неизвестные p , q , r суть компоненты абсолютной угловой скорости ω тела в системе координат, жестко связанной с телом. Параметры A , B , C суть главные моменты инерции тела. Мы теперь хотим умножить каждое из трех уравнений на надлежащие функции, потом сложить, да так, чтобы справа получился 0. Давайте умножим их соответственно на p , q , r . В результате получим Это, очевидно, означает, что система (5.16) имеет интеграл T — кинетическая энергия тела. А нет ли еще одного интеграла? Если умножить уравнения (5.15) соответственно на Ap , Bq , Cr , то аналогично получим интеграл момента: Очевидно, он независим с интегралом T . Нельзя ли найти еще один интеграл? Нет, получился бы перебор. Система x ˙ = F (x ) в Rn (за исключением лишь не очень интересного случая уравнения x ˙ = 0) может иметь не более, чем n − 1 интеграл, наличие n независимых интегралов воспрещает всякое движение системы. Итак, мы по существу уже пришли к точному решению уравнений Эйлера! Пользуясь двумя найденными интегралами (например, исключая p и q ), мы сведем эту систему третьего порядка к одному автономному уравнению. Мы знаем, как такие уравнения решать — методом разделения переменных. Конечно, это давно проделано, и решение уравнений Эйлера выражено через эллиптические функции (см. [20]). Замечу, что фактически мы, разыскивая интегралы системы (5.15), нашли сначала две нетривиальные косимметрии этой системы: Пример 3 . На сей раз рассмотрим уравнение в частных производных — волновое уравнение utt − c 2 ∆u = 0, (5.20) для неизвестной функции u (x,t ), x ∈ D , где D — ограниченная область в Rn , ее границу ∂D будем считать гладкой. Предположим, что на границе ∂D выполняется краевое условие первого рода Возможны и условия третьего или второго рода (рассмотрите сами эти случаи). Для волнового уравнения следует ставить два начальных условия где u
0
, v
0
— известные функции, заданные в области D
. Нужно, конечно, решить вопрос о том, каким функциональным пространствам принадлежат эти функции. Например, можно считать, что v
0
∈ L
2
, а функция — пространству функций, имеющих первые производные, интегрируемые с квадратом; нолик сверху означает, что эти функции в определенном смысле удовлетворяют краевому условию (5.21). Мы, однако, в следующем рассуждении предположим, что имеется гладкое решение. Для любого такого решения u (x,t ) запишем уравнение (5.20), умножим его на ut и проинтегрируем по области D . Тогда получится равенство Интегрируя по частям, преобразуем последний интеграл: Поверхностный интеграл исчезает в силу краевого условия (5.21), из которого следует, что Из равенств (5.23) и (5.25) выводим Таким образом, функционал E (u,ut ), определенный равенством на всем фазовом пространстве 6 Неавтономные дифференциальные уравнения
волнового уравнения, которое является одним из наиболее естественных бесконечномерных аналогов уравнения второго закона Ньютона. Обратите внимание на довольно неприятное столкновение слов — «интеграл» фигурирует здесь в двух смыслах: E — интеграл волнового уравнения, и сам он выражается посредством интеграла по области D . Такая трудность характерна для прикладной математики, когда приходится применять результаты разных областей, а в каждой из них имеется своя установившаяся терминология. Что тут поделаешь? Будем хотя бы избегать выражений типа «интеграл E равен интегралу», в котором одно и то же слово имеет более одного смысла. 6. Неавтономные дифференциальные уравненияНаиболее фундаментальные законы природы инвариантны относительно сдвигов времени, а потому приводят к автономным дифференциальным уравнениям. Однако и неавтономные дифференциальные уравнения постоянно возникают в качестве математических моделей различных природных и технологических процессов. Так получается уже потому, что исключение неизвестных функций из системы автономных дифференциальных уравнений приводит к системам меньшего порядка, но неавтономным. Я покажу это на простом примере, хотя идея носит вполне общий характер. Рассмотрим автономную систему дифференциальных уравнений x ˙ = xyz, y ˙ = x + y + z, (6.1) z ˙ = z. Последнее уравнение легко решить: z (t ) = z 0 et , где z 0 — начальное значение функции z (t ). Подставляя функцию z (t ) в остальные два уравнения, приходим к неавтономной системе второго порядка x ˙ = z 0 et xy, y ˙ = x + y + z 0e t. (6.2)Мы видим, что класс всевозможных автономных дифференциальных уравнений не замкнут относительно операции исключения некоторых из неизвестных функций . А вот, например, класс систем линейных алгебраических уравнений относительно такой операции замкнут: исключение неизвестной приводит к системе линейных алгебраических уравнений на единицу меньшего порядка. Менее очевидно, что и класс полиномиальных уравнений замкнут относительно исключения неизвестных. Это устанавливается в теории результантов , в которую значительный вклад внес многолетний чемпион мира по шахматам Э. Ласкер (см. [7]). Ситуация, которую мы наблюдаем в приведенном примере, возникает всякий раз, когда рассматриваемая система разбивается на две или более подсистем, причем некоторые подсистемы эволюционируют независимо от других. Философия говорит нам, что все в мире взаимосвязано и взаимозависимо, но если это положение понимать слишком буквально, то получится, что ничего нельзя изучить, так как каждый раз мы в состоянии учитывать лишь конечное число факторов. Помогает то обстоятельство, что во многих случаях «большие системы» влияют на малые, а обратным воздействием малых систем на большие вполне допустимо пренебречь. Например, изучая динамику трамвая или космического корабля, разумно оставлять без внимания влияние их движения на движение Земли вокруг Солнца. Обобщенный закон причинности. В случае неавтономного дифференциального уравнения x ˙ = F (x,t ) (6.3) эволюционный оператор зависит от выбора начального момента. Решение задачи Коши для уравнения (6.3) с начальным условием представляется в виде Эволюционный оператор Рассмотрим три момента времени τ, s
, t
(см. Рис. 2). Наряду с выражением (6.5) для x
(t
), можно получить и другое выражение. Сначала найдем Неавтономные дифференциальные уравнения
Рис. 2
Так как это равенство верно для любых x 0 , получим равенство для операторов Это и есть обобщенный принцип причинности . Отметим очевидные равенства В случае автономного уравнения F = F (x ) нетрудно доказать (докажите!) равенство для любого h ∈ R . Полагая здесь h = −τ, получим, что Если теперь в обобщенном принципе причинности (6.7) положить τ = 0, а затем заменить t на s + τ (это уже новое τ) и воспользоваться равенством (6.10), то получится то есть принцип причинности для автономного уравнения. Посмотрим еще, какие специальные свойства имеет эволюционный оператор в случае периодического дифференциального уравнения с периодом p >
0. Если правая часть уравнения (6.3) p
-периодична, то есть F
(x,t
+ p
) = F
(x,t
), то эволюционный оператор Оператор Это равенство часто применяется в теории линейных периодических дифференциальных уравнений. Оно похоже на принцип причинности для автономных уравнений, но выполняется лишь в случае, когда один из моментов времени есть период p . Из (6.13) следует, что можно также в качестве второго момента выбрать np , где n — любое целое число: 7. Интегро-дифференциальные уравненияЭтот термин крайне неудачен. Он говорит лишь о том, что в уравнении присутствуют операции дифференцирования и интегрирования, но такие уравнения могут иметь совершенно разную природу. Объясню это на примерах. Рассмотрим уравнение для неизвестной функции f (x,t ) с областью определения x ∈ Rn , t ∈ R Здесь ∆ — оператор Лапласа, G — известное ядро интегрального оператора. Такого рода интегро-дифференциальные уравнения весьма интересны, регулярно возникают в приложениях, в частности, основные уравнения Интегро-дифференциальные уравнения
статистической механики (уравнения Больцмана, Ландау, Власова) принадлежат этому типу. Характерно, что интегрирование в (7.1) производится не по времени t
, а по пространственной переменной x
. Поэтому Производная здесь не частная, а прямая, потому что f = f (·,t ) мыслится теперь как элемент функционального пространства. Оператор A (t ) определяется правой частью уравнения (7.1), он зависит от t потому (лишь потому), что от t зависит ядро G . Уравнения, подобные (7.1), в которых присутствует интегрирование не по t , а, скажем, по пространственным переменным, собственно говоря, не требуют особой общей теории, а являются объектом теории обыкновенных дифференциальных уравнений в банаховом пространстве (см., например, [11]). Более специфичны эволюционныеинтегро-дифференциальныеуравнения , содержащие интегрирование по времени. Именно уравнения этого типа лежат, например, в основе наследственной теории упругости , описывающей поведение полимерных материалов. Находят они существенные применения и в ряде задач экологии. В этих областях уже исходные уравнения являются не дифференциальными, а интегро-дифференциальными. Я сейчас покажу, что даже если бы все исходные модели были автономными дифференциальными уравнениями, то очень скоро мы пришли бы и к интегро-дифференциальным уравнениям. Сказывается тот же недостаток класса дифференциальных уравнений — его незамкнутость относительно операции исключения части неизвестных. В благополучных случаях после операции исключения может получиться неавтономное дифференциальное уравнение (такой вариант мы с вами уже рассматривали). В более сложных ситуациях получается интегро-дифференциальное уравнение. И это я объясню на простом примере. Рассмотрим систему двух обыкновенных дифференциальных уравнений x ˙ = x + y, y ˙ = −y + x. (7.3) Потребуем, чтобы выполнялись начальные условия Исключим из этой системы неизвестную функцию y , пользуясь вторым уравнением. Если временно считать x (t ) известной функцией, то для y (t ) получается линейное неоднородное дифференциальное уравнение. С использованием начального условия находим (проще всего использовать интегрирующий множитель et ) t Z −t −(t −τ ) y (t ) = y 0 e + e x (τ)d τ. (7.5) 0 Подстановка в первое уравнение системы (7.3) дает интегро-дифференциальное уравнение для неизвестной функции x (t ) t Z −t −(t −τ ) x ˙ = x + y 0 e + e x (τ)d τ. (7.6) 0 Конечно, это чисто иллюстративный пример. Однако случается,что посредством исключения переменных удается весьма существенно упростить задачу. Бывает даже, что удается свести к скалярному интегро-дифференциальному уравнению бесконечномерную систему уравнений [13]. Весьма возможно, что интегро-дифференциальные уравнения наследственной теории упругости и экологии тоже можно получить посредством исключения некоторых скрытых переменных из более общей системы дифференциальных уравнений . Я думаю, что так оно и есть, хотя этого еще никто не проделал. Замечу еще, что бывают, конечно, сложные ситуации, в которых неизвестные исключить не удается, и не только потому, что мы не располагаем явными формулами, но и по существу, из-за того, что такое исключение, скажем, неизвестной y , возможно не для всех функций x . Такие ситуации могут быть очень интересны и до сих пор никем как следует не рассмотрены. 8 Декартово произведение динамических систем и разбиение системы на независимые подсистемы 51
И еще одно замечание. Мы говорим об исключении неизвестных в задаче Коши. Для систем дифференциальных уравнений ставятся и другие задачи, например, задача Пуанкаре о периодических решениях. Для них тоже представляет интерес проблема исключения неизвестных. Все это до сих пор мало исследовано. Очень интересно выяснить, при каких условиях такое исключение возможно, какого рода уравнения при этом получаются, а главное — что это может дать для понимания исходной системы. 8. Декартово произведение динамических систем и разбиение системы на независимые подсистемыОбычные теоретико-множественные операции — взятие объединения, пересечения, разности, симметрической разности, скажем, над двумя множествами X , Y , хотя и всегда определенные формально, пожалуй, оказываются содержательными лишь в том случае, когда эти множества состоят из элементов одной и той же природы (впрочем, объединение самых разнородных элементов может появиться в списке товаров, продаваемых некоей фирмой). Операция декартова умножения бывает интересна и без этого ограничения. Напомню, что декартово произведение X × Y есть множество всевозможных пар (x,y ), где x ∈ X , y ∈ Y . Когда множества X и Y снабжены (или, как часто говорят, оснащены ) теми или иными дополнительными структурами, бывает интересно определить соответствующие структуры и на их декартовом произведении. Так оказывается возможным определить декартово произведение групп, метрических пространств, линейных пространств, гильбертовых пространств и т. д. таким образом, что и декартово произведение оказывается, соответственно, группой, метрическим пространством, линейным пространством и т. д. Декартовым произведением
динамических систем
Говоря короче, сама идея декартова произведения состоит в том, что операции производятся отдельно в каждом пространстве X
1
и X
2
. Легко проверить, что для определенного таким образом отображения
Вполне аналогично можно определить декартово произведение трех, четырех и вообще любого набора динамических систем. Имеются и определения декартова произведения бесконечного набора динамических систем, даже не обязательно счетного. Великая операция декартова произведения множеств и отображений позволяет нам любую систему уравнений трактовать как одно уравнение. Выходит, что общая теория систем уравнений просто не нужна. Это хороший пример пользы, которую может принести концептуальный подход, удачное введение общих абстрактных понятий. Если имеются два дифференциальных уравнения, скажем, x ˙ = F (x,t ) в банаховом пространстве X и y ˙ = G (y,t ) в банаховом пространстве Y , то операция декартова произведения этих уравнений сводится к тому, что мы записываем их вяясте и ряясмяяриваем как одно уравнение. Форяяльяя эяя означает,яято мы вводим вектор z = (x,y ) ∈ X × Y и записываем полученную систему как одно уравнение z ˙ = Q (z,t ), (8.2) причем поле Q определяется равенствами Q (z,t ) = (F (x,t ),G (y,t )). (8.3)Я бы хотел, чтобы Вы почувствовали, как тривиально все то, что до сих пор здесь сказано о декартовом произведении. А выигрыш состоит в том, что, например, не нужны новые теоремы существования решения задачи Коши для систем уравнений. Проведенная операция не вывела из класса дифференциальных уравнений на банаховом пространстве. Если уравнение (8.2) можно представить в виде системы x ˙ = F (x,t ), (8.4) y ˙ = G (y,t ), то, как говорят физики, исходная система (8.2) представлена в виде объединения двух невзаимодействующих или независимых подсистем. Когда все эти уравнения автономны, получается и соответствующее разбиение динамической системы на невзаимодействующие подсистемы. 9 Производные и градиенты Задача разбиения заданной системы на невзаимодействующие подсистемы, в известном смысле обратная декартову умножению, отнюдь не тривиальна и далеко не всегда разрешима. Приведу пример, когда эта задача особенно хорошо решается. Рассмотрим линейное уравнение в пространстве Rn x ˙ = Ax (8.5) с самосопряженным оператором A (задаваемым симметричной вещественной матрицей). Известно, что у такого оператора существует ортонормальный базис векторов ϕ1 ,..., ϕn , так что A ϕk = λk ϕk для k = 1,...,n . Если разыскивать решение векторного уравнения (8.5) в виде с неизвестными коэффициентами ξk , то подстановка (8.6) в (8.5) дает для определения ξk уравнения ξ˙k = λk ξk , k = 1,...,n. (8.7)Исходная система (8.5) разбилась таким образом, на n невзаимодействующих подсистем. Нетривиальность этого разбиения проявляется хотя бы в том, что оно изменяется при изменении оператора A . Если теперь мы рассмотрим уравнение (8.5) с несимметричным оператором A
, то увидим, что разбиение не всегда возможно. Например, если n
= 2, то в случае жордановой клетки x ˙ = λx + y, (8.8) y ˙ = λy не может быть разбита на невзаимодействующие подсистемы, хотя независимое уравнение для y выделяется. Невозможно также разбиение на невзаимодействующие подсистемы для системы второго порядка, соответствующей гармоническому осциллятору x ˙ = y, y ˙ = −x. (8.9) Припомнив нормальную жорданову форму матрицы, Вы легко решите вопрос о том, когда возможно, а когда невозможно разбить заданную линейную систему (8.5) на невзаимодействующие подсистемы. 9. Производные и градиентыПроизводная по скалярному аргументу. Скорость как дифференциальный оператор . Начнем с определения производной по скалярному аргументу вектор-функции x (τ) со значениями в банаховом пространстве X . Естественно положить Здесь имеется два основных варианта: предел можно понимать в смысле сильной сходимости , то есть по норме пространства X , либо в смысле слабой сходимости . Соответственно, получаются понятия сильной и слабой производной . Когда речь будет идти о произведении, я буду в дальнейших приложениях иметь в виду, как правило, сильную производную. Вообще, когда речь идет о дифференцировании по скалярному аргументу, определения стандартны. Вполне аналогично предыдущему определяются производные от оператор-функции, матричных или тензорных функций. Важно, конечно, чтобы это были элементы линейных пространств, чтобы имело смысл выражение (9.1). Когда приходится дифференцировать вектор-функцию скалярного аргумента, принимающую значения на некотором многообразии, необходимы дополнительные ухищрения. Обойтись без этого нельзя, потому что необходимо выяснить, что такое скорость точки, движущейся по поверхности. Так как же все-таки обобщить столь привычное нам определение производной (9.1) с тем, чтобы обойтись без операции вычитания? Разумеется, когда поверхность вложена в линейное пространство, или вообще, когда рассматриваемое движение происходит на гладком подмногообразии линейного пространства, можно сохранить определение (9.1), не смущаясь тем, что разность x (τ + ε) − x (τ) не будет лежать на этой поверхности. В действительности, даже оказывается, что всякое конечномерное многообразие можно вложить в конечномерное линейное пространство достаточно высокой размерности, и притом, конечно, многими способами (это теорема Уитни). Тут, однако, получается, что определение зависит от вложения поверхности. Математику вполне понятно, что использование лишних объектов в определении может лишь усложнить рассмотрения. Если в начале такого дела, как развитие новой теории, полениться серьезно поработать над определениями, поддаться впечатлению от кажущейся простоты, то последствия будут весьма неприятными. Современная абстрактная математика очень действенна, предпочитает определения, которые кажутся, может быть, сложными на вид, но в дальнейшем обеспечивают простоту в обращении и бесперебойность работы построенного математического аппарата. Очень важно, что при этом не нужно (даже вредно) слишком глубоко задумываться на каждом шаге выкладок, а достаточно автоматически следовать формальным правилам. Подобные выкладки легко перепоручить компьютеру. К слову сказать, такую формальную систему и называют исчислением , таковы (в идеале) дифференциальное и интегральное исчисления. Я привел это лирическое вступление для того, чтобы Вы не поленились освоить следующее определение и применяли его в дальнейшем. Лишь поначалу оно может показаться вычурным. Итак, рассмотрим отображение x : R → M вещественной прямой в гладкую поверхность (и вообще, многообразие) M , то есть точку, движущуюся вдоль многообразия M по известному закону x = x (t ). Возьмем произвольную гладкую функцию f : M → R . Теперь рассмотрим f (x (t )) — это уже скалярная функция скалярного переменного t . Мы хорошо знаем, как такие функции дифференцировать. Не буду приводить здесь точных определений гладкого многообразия M и гладкой функции f на M . Скажу лишь, что отображение x : t 7→ x (t ) называется гладким, если f (x (t )) для любых гладких f имеет производную по t . Она, конечно, зависит от f , так что можно написать Если x (t 0 ) = a , и в окрестности точки a введены координаты x 1 , x 2 ,...,xn , то это равенство можно переписать в виде
Здесь vk (x (t )) есть k -я компонента скорости x ˙(t ) движущейся точки x (t ). А что такое скорость x ˙(t )? Теперь ясно, что ее следует определить как дифференциальный оператор первого порядка V в формуле (9.2). В выбранных координатах в момент времени t = t 0 мы можем написать Итак, скорость x ˙(t 0 ) оказалась линейным дифференциальным оператором! Первая практическая выгода такого определения состоит в том, что для вычисления компонент скорости в любой другой системе координат y 1 ,...,yn достаточно в равенстве (9.4) проделать замену x 1 = x 1 (y 1 ,...,yn ), ..., xn = xn (y 1 ,...,yn ). В качестве упражнения выразите компоненты вектора v в цилиндрических и сферических координатах, если он первоначально задан в декартовых координатах, так что v = (v 1 ,v 2 ,v 3 ). Я надеюсь, что чтение предыдущих абзацев побудит Вас изучить многообразия, векторы и векторные поля на многообразиях, например, по книгам [2, 3, 10]. Производные операторов и функционалов . Пусть задан оператор F : X → Y , действующий из вещественного банахова пространства X в вещественное банахово пространство Y . В частности, когда Y = R , оператор F есть функционал или функция на пространстве X . Сейчас мы рассмотрим основные определения и простейшие результаты, относящиеся к дифференцированию операторов. Производная по Гато.
Для любого h
∈ X
рассмотрим F
(x
+ sh
), где s
∈ R
. Согласно определению, производная Гато Таким образом,
линеен. Предел в (9.5) можно понимать по разному, для определенности будем считать, что речь идет о сходимости по норме пространства Y . Замечу, что обрисованная вкратце идея дифференцирования скалярных функций на многообразиях позволяет перенести определение Гато и на операторы, заданные на банаховом многообразии . Гато — талантливый французский математик, офицер французской армии, пропавший без вести во время I-й мировой войны. Производная по Фреше. Производной Фреше в точке x ∈ X от оператора F : X → Y называется линейный оператор A : X → Y , обозначаемый через F 0 (x ), такой, что для любого h ∈ X выполняется равенство F (x + h ) − F (x ) = Ah + ω(x,h ), (9.6)причем для остаточного члена ω(x,h ) справедливо предельное соотношение при h → 0, то есть при kh kX → 0. Это означает, что ω(x,h ) — слагаемое порядка выше первого относительно h . соответственно Ah есть главная линейная часть приращения оператора F . Ее называют дифференциалом Фреше. Легко видеть, что производная Фреше, когда она существует, совпадает с производной Гато. (Доказывается это непосредственно: заменим в (9.6) h на sh , разделим на s и устремим s к 0). На практике производная всегда вычисляется при помощи определения Гато, а в приложениях, как правило, нужна производная Фреше. Поэтому, найдя производную по Гато, приходится проверять условие (9.7) для остаточного члена. А вообще, производная есть производная, ее вычисление для явно заданного оператора F не вызывает серьезных трудностей, лишь бы она существовала. Пусть, например, X = Rn , Y = Rm , а оператор F задан своим координатным представлением: для любого x = (x 1 ,...,xn ) Fx = (F 1 (x 1 ,...,xn ),...,Fm (x 1 ,...,xn )). (9.8)Если функции F 1 ,...,Fm — компоненты вектора F — непрерывно дифференцируемы, то производная F 0 (x ) задается матрицей Якоби: В частности, когда m = 1, получается производная функции (функционала). Градиент. Согласно теореме Ф. Рисса, всякий линейный функционал ϕ : H → R на евклидовом или гильбертовом пространстве H может быть реализован в виде скалярного произведения. Точнее, для любого ϕ найдется элемент h ∈ H , и притом только один, такой что ϕ(x ) = (x,h ) (9.10)для всех x ∈ H . Более того, отображение J : H ∗ → H , J ϕ = h есть изометрический изоморфизм, то есть J — линейный обратимый оператор, и kh k = kJ ϕ k = kϕ k для всех ϕ ∈ H ∗ . В этом смысле иногда говорят, что сопряженное пространство H ∗ (пространство линейных функционалов) совпадает с самим пространством H . Необходимо однако помнить, что такое отождествление законно лишь до тех пор, пока фиксирован изоморфизм J . Как мы увидим дальше, это очень существенно для приложений, в частности, в механике. Пусть теперь f : H → R — функционал, заданный на H и имеющий при всех x производную f 0 (x ). Согласно теореме Рисса, существует такой элемент (вектор) g (x ) ∈ H , что линейный функционал f 0 (x ) представится в виде f 0 (x )u = (u,g (x )). (9.11)Элемент g (x ) называется градиентом функционала f в точке x и обозначается через grad f (x ). Согласно этому определению, f 0 (x )u = (u, grad f (x )). (9.12)Вектор grad f (x ) для каждого x определяет линейный функционал, который от x зависит, вообще говоря, нелинейно. Оператор grad f действует из H в H , или в символах grad f : x 7→ grad f (x ) : H → H . В отличие от производной f 0 (x ), градиент определяется заданием скалярного произведения. Он изменится, если поменять скалярное произведение. Пусть A : H → H — самосопряженный положительно определенный оператор, заданный на всем пространстве H . Это означает, что оператор A линеен, и для любых ξ, η ∈ H справедливо равенство (A ξ, η) = (ξ,A η), и (A ξ, ξ) ≥ γ2 (ξ, ξ) при некотором γ > 0. Давайте еще предположим, что оператор A ограничен и обратим, имеет ограниченный обратный A −1 . На самом деле, и то и другое можно вывести, соответственно, из предположений, что оператор A задан всюду и что он положительно определен. В математической физике чрезвычайно интересны неограниченные самосопряженные операторы, которые определены не всюду, а лишь на некоторых всюду плотных в H линейных многообразиях, см. [28]. В случае конечномерного H все эти проблемы просто не возникают. Всякий положительно определенный оператор A в H определяет новое скалярное произведение (ξ, η)A = (A ξ, η) (9.13) для любых ξ, η ∈ H . Проверьте, что все аксиомы скалярного произведения действительно выполняются. Когда оператор A имеет ограниченный обратный, это скалярное произведение эквивалентно прежнему — в том смысле, что сходимость по соответствующим нормам одна и та же. Найдем связь между градиентами, порождаемыми этими скалярным произведениями. Согласно определению (9.12), имеем равенства f 0 (x )u = (u, grad f (x )) = (u, gradA f (x ))A . (9.14)Учитывая определение (9.13), из (9.14) выводим равенства (u, grad f (x )) = (u, gradA f (x ))A = (Au, gradA f (x )) = (9.15) = (u,A gradA f (x )). Так как равенство (u, grad f (x )) = (u,A gradA f (x )) (9.16)выполнено при любых u ∈ H , заключаем, что grad и grad A связаны соотношениями grad f (x ) =A gradA f (x ), gradA f (x ) =A −1 grad f (x ). (9.17)Замечу, что подобные соотношения выполняются и в тех случаях, когда оператор A задан не на всем пространстве H , а лишь на некотором плотном в H линейном многообразии DA (это область определения оператора A ). В такой ситуации, однако, приходится проделывать еще немалую дополнительную работу. Ее первая часть — пополнение линейного многообразия DA по норме, порожденной скалярным произведением (9.13) (см. [28]). Потом еще приходится разбираться в необходимых ограничениях на функционал f и находить область определения градиентов. Сами градиенты могут и не быть непрерывными операторами — даже в случае, когда они линейны (по x ), что получается, когда f — квадратичный функционал. МЕХАНИКАОдним из главных источников фундаментальных математических моделей являются вариационные принципы механики. Современная механика началась с классической работы И.Ньютона «Математические принципы натуральной философии» (1687) [32]. Конечно, у механики была долгая и богатая предыстория (вспомним, например, Архимеда), а Галилея можно уже считать современным физиком, потому что он понял, что природу необходимо познавать при помощи экспериментов, строить теории путем обобщения полученных данных, а не искать ответы в трудах авторитетных древних авторов. До него считалось, что ответы на все вопросы можно найти у Аристотеля. Дальнейшее развитие механики привело к широким обобщениям, к определенному слиянию теоретической (аналитической) механики с дифференциальной геометрией на многообразиях. Между прочим, оказалось, что уравнения движения механической системы можно представить в очень многих различных, зачастую разительно отличающихся друг от друга, формах. Ричард Фейнман заметил, что таким свойством обладают все фундаментальные модели физики (механика, квантовая физика и квантовая теория поля). Он поставил вопрос, почему это так. Я думаю, что разные формы эволюционных уравнений простейших (они-то и являются наиболее фундаментальными) математических моделей в физике наиболее приспособлены для различных обобщений. Так, вариационные принципы Гамильтона и Мопертюи (точнее, Мопертюи-Эйлера-Лагранжа-Якоби), уравнение первого порядка в частных производных, называемое уравнением ГамильтонаЯкоби, в классической механике (почти) эквивалентны. Но принцип Гамильтона непосредственно обобщается на механику теории относительности (релятивистскую механику), за исключением механики фотонов (света, электромагнитных волн), принцип Мопертюи сохраняется и в динамике фотонов. А вот квантовая физика использует обобщение уравнения ГамильтонаЯкоби. Подходы и результаты механики находят себе применение далеко за ее пределами. Например, мы увидим дальше, что электродинамика может считаться в определённом смысле частным случаем механики. Механика Второй закон Ньютона. Несомненно, начало современной механики — это второй закон Ньютона для материальной частицы: mx ¨ = F. Здесь m — масса частицы, x (t ) = (x 1 (t ),x 2 (t ),x 3 (t )) — ее положение в момент времени t . Частица движется в пространстве R 3 , и x 1 (t ), x 2 (t ), x 3 (t ) — ее координаты, а F — действующая на частицу сила. В самом простом случае F = F (t ), то есть сила задана как функция времени. В этом случае решение уравнения легко находится двумя интегрированиями по t . Обычно сила F бывает задана как вектор-функция от аргументов x ∈ R 3 , x ˙ ∈ R 3 и времени t . Тогда уравнение второго закона Ньютона есть векторное дифференциальное уравнение второго порядка mx ¨ = F (x,x,t ˙ ). ... Случается, что F зависит от x ¨ и даже от x , а может быть, и от высших производных. Однако, такое происходит не в фундаментальных моделях, а скорее, в результате исключения переменных в более широких системах. Например, уравнение движения электронов в электромагнитном поле — третьего порядка, но это получается потому, что из общей системы исключается поле. Физики обычно говорят, что материальная точка — это тело «столь малых размеров», что ими при данных условиях можно пренебречь. Например, размеры планет столь малы по сравнению с их расстояниями до Солнца, что при изучении их движения планеты можно считать материальными точками. В астрономии так и делается, и теоретические результаты великолепно подтверждаются наблюдениями. Вместе с тем, при изучении вращения Земли или, скажем, движения самолетов и ракет необходимо учитывать размеры и форму нашей планеты. Для того, чтобы описать движение материальной точки , конечно, недостаточно задать ее положение. Правильные начальные условия включают также задание скорости: x (0) = x 0 , x ˙(0) = v 0 . Здесь x 0 = (x 01 ,x 02 ,x 03 ) ∈ R 3 — начальное положение точки, а v 0 = (v 01 ,v 02 ,v 03 ) ∈ R 3 — ее начальная скорость. Таким образом, фазовое пространство данной системы есть R 3 × R 3 , а состояние системы есть пара (x,v ), где x — положение материальной точки, а v — ее скорость. Это было грандиозным открытием Ньютона — пространство, в котором мы живем, как бы удваивается. Аристотель, конечно, не знал дифференциальных уравнений, но если прочитать внимательно его рассуждения о движении камня, то видно, что он, пожалуй, пытался описать мир, который управляется дифференциальным уравнением первого порядка. И. Ньютон на основе уравнения своего второго закона построил механику системы частиц и применил ее прежде всего к проблеме движения планет. Пожалуй, среди всех открытий Ньютона самым потрясающим было доказательство того факта, что одна и та же сила (всемирного тяготения) заставляет падать камень на Земле и удерживает планеты на их орбитах. Сначала он установил, что Луна на своей околоземной орбите действительно удерживается силой, обратно пропорциональной ее расстоянию до Земли. Забавно вспомнить, что Ньютона избрали действительным членом английской Академии наук (Royal Society) не за это открытие, и вообще не за научное открытие, а за то, что он изобрел прекрасный способ шлифовки стекла и изготовления зеркал для телескопов-рефлекторов. Сама идея телескопа-рефлектора, вместе с ее реализацией, тоже принадлежала И. Ньютону. 10. Принцип Гамильтона и уравнения Лагранжа II родаВ основу построения современной механики полагают обычно принцип Гамильтона, не вполне точно называемый также принципом наименьшего действия. Конфигурационное и фазовое пространстваПоложение механической системы есть, по определению, точка области D в пространстве Rn . Область D называется конфигурационным пространством или пространством положений данной системы. Размерность dimD конфигурационного пространства называется числом степеней свободы системы. Например, материальная точка в R 3 имеет три степени свободы, а система, состоящая из двух материальных точек, имеет шесть степеней свободы. Таким образом, число степеней свободы — это количество скалярных параметров, которые необходимо задать, чтобы однозначно определить положение системы. Сейчас мы рассматриваем системы с конечным числом степеней свободы. Однако в механике и физике сплошной среды необходимо изучать и системы с бесконечным числом степеней свободы — жидкость или газ, деформируемое упругое тело, электромагнитное поле. Соответствующие тео- рии развиваются во многом по образцу классической механики систем с конечным числом степеней свободы. Во всяком случае, формальный аппарат механики сплошной среды строится по аналогии — конечные суммы заменяются интегралами или бесконечными суммами, вместо разностей возникают производные и так далее. Конечно, переход от конечного числу степеней свободы к бесконечному — дело серьезное, и возникают многие новые проблемы. Далеко не со всеми из них в настоящее время справляется современная наука, такие проблемы сейчас составляют один из важнейших стимулов к развитию математики. Точка области D обычно обозначается через q = (q 1 ,q 2 ,...,qn ), а величины q 1 ,...,qn называются ее обобщенными или лагранжевыми координатами. Это обозначение идет от самого Лагранжа, который научился и научил механиков использовать при исследовании различных систем криволинейные координаты (и многому другому). • Надо признаться, что я с некоторым содроганием говорю, что D есть область пространства Rn . Правильно было бы сказать, что конфигурационное пространство механической системы есть дифференцируемое многообразие. Это такое пространство, для которого в окрестности каждой точки можно ввести систему координат q 1 ,q 2 , ...,qn . Такая система координат (взаимно-однозначное отображение данного подмножества на некоторый шар в Rn ) называется картой многообразия в данной координатной окрестности. Дальше мы будем работать в одной координатной окрестности, так что наши рассмотрения будут локальными. Однако, вообще говоря, нельзя ввести единой системы декартовых координат даже на таких простых многообразиях как окружность S 1 на плоскости или сфера S 2 в R 3 . Приходится разбивать многообразия на части, в каждой из которых координаты ввести можно. Эти подмножества могут (даже должны) пересекаться, в пересечениях мы имеем сразу две системы координат, и надо установить между ними соответствие. Для полного описания многообразия нужен, таким образом, целый набор локальных карт вместе с правилами их согласования в общих частях. Такой набор карт называется атласом — образец прекрасной математической терминологии (вызывает правильные и ясные аналогии). Когда все это аккуратно проделывается, то и получается теория дифференцируемого многообразия (см. [2, 3, 10, 15]). Состояние механической системы задается парой (q,v ), где q ∈ D — положение системы, а v ∈ Rn — ее обобщенная скорость. Если положение системы меняется по закону q = q (t ), то ее (обобщенная) скорость есть v = q ˙(t ), т.е. производная по времени от q (t ). Предполагается, что система, находясь в положении q , может иметь любую мгновенную скорость v . Таким образом, фазовое пространство данной механической системы есть D × Rn . • В общей ситуации конфигурационное пространство есть гладкое многообразие M, но фазовое пространство есть не просто декартово произведение, а новое многообразие, называемое касательным расслоением и обозначаемое T M. Оно лишь локально (над одной картой) является декартовым произведением. Оказывается, чтобы определить механическую систему, достаточно задать одну функцию L (q,q,t ˙ ), которая называется функцией Лагранжа или лагранжианом . Ее область определения есть расширенноефазовоепространство — декартово произведение фазового пространства и оси времени: D × Rn × R . Итак, функция L задана для любой тройки (q,q,t ˙ ), q ∈ D , q ˙ = v ∈ Rn , t ∈ R . Действие по Гамильтону . Теперь определим действие (по Гамильтону), полагая t 2 Z S = L (q (t ),q ˙(t ),t )dt. (10.1)t 1 Предполагается, что t 2 > t 1 , а в остальном моменты времени t 1 и t 2 произвольны. Заметьте еще, что здесь q ˙(t ) — на самом деле, производная по времени от вектор-функции q (t ) со значениями в Rn , а точнее, в области D . В то же время, когда мы пишем функцию Лагранжа L (q,q,t ˙ ), то q ˙ означает просто независимую переменную. Как видно, действие есть функционал, который каждой вектор-функции q (t ) со значениями в D ставит в соответствие число. Деформация и вариацияТеперь определим (гладкую) деформацию данной вектор-функции q (t ), заданной для t ∈ [t 1 ,t 2 ] (а еще лучше на всей вещественной оси). Гладкой деформацией вектор-функции q (t ) со значениями в D называется гладкая вектор-функция q ˜(t, ε) со значениями в D , определенная для t ∈ [t 1 ,t 2 ], ε ∈ (−ε0 , ε0 ) (величина ε0 > 0 не имеет значения, дальше будет видно почему), и удовлетворяющая условию q ˜(t, 0) = q (t ). (10.2)• К сожалению, во многих книгах геометры деформацию называют вариацией, отступая и от наглядности, и от прекрасной терминологии классиков (Л.Эйлера, И.Бернулли, Ж.Лагранжа). Вариацией вектор-функции q (t ), отвечающей заданной деформации q ˜(t, ε), называется • И.Бернулли и Л.Эйлер первыми стали рассматривать функционалы типа нашего действия S (правда, в связи с совсем другими задачами — о брахистохроне и т.п.). Если мы имеем дело с обычной функцией y = f (x ), то, как Вы хорошо знаете, очень полезно бывает посмотреть, какое приращение получает эта функция f (x ), когда ее аргумент x получает приращение δx . Так вот, Бернулли и Эйлер ввели вариацию сначала интуитивно, как аналог приращения аргумента ∆x . Тем, кто думает, что гениальным ученым все дается легко, я бы посоветовал почитать переписку Эйлера и Бернулли о том, как же строго определить вариацию (см. книгу [37]). Определение вариации (10.3) дал впервые Лагранж, и всем все стало ясно. Теперь даже трудно понять, что все-таки затрудняло таких людей, как Бернулли и Эйлер. В следующем определении вводится аналог приращения функции ∆y и ее дифференциала dy = f 0 (x )dx . Определим вариацию функционала S (для данного значения аргумента — вектор-функции q (t )), отвечающую данной деформации q ˜(t, ε), полагая Предполагая, что L гладко зависит от q и q ˙, и пользуясь равенством (10.2), из этого определения выводим формулу t 2 Z δS = (Lq · δq + Lq ˙ · δq˙) dt. (10.5)t 1 Мы здесь и далее применяем следующие обозначения
При этом δq ˙ определяется равенством Если теперь предположить, что q ˜(t, ε), скажем, C 2 -гладкая вектор-функция от t , ε, то дифференцирования по ε и по t коммутируют (их можно поменять местами). Тогда из (10.6) выведем
Получилась основная формула вариационного исчисления • Для вывода этой формулы достаточно предположить существование непрерывной смешанной производной ∂ 2 ∂ 2
∂t∂ ε ∂ ε∂t в учебнике Г.М.Фихтенгольца по математическому анализу, том 1, [44]). Я верю и уже говорил об этом раньше, что все математические «патологии» должны реализовываться в физике и соответствовать тем или иным природным явлениям. Неизвестно (пока!), где в физике могут возникнуть такие функции, у которых смешанные производные зависят от порядка дифференцирования. Может оказаться, что появление таких функций приведет к новым, неизвестным сейчас явлениям. Теперь мы можем заняться дальнейшим преобразованием вариации δS . Подставляя δq ˙ из (10.8) в (10.5) и проводя интегрирование по частям, придем к формуле Деформация q ˜(t, ε) данной вектор-функции q (t ) называется деформацией с закрепленными концами , если для всех ε выполнены равенства q ˜(t 1 , ε) = q (t 1 ), q ˜(t 2 , ε) = q (t 2 ). Варьируя эти равенства, то есть дифференцируя по ε при ε = 0, получим соотношения для вариации δq (t 1 ) = 0, δq (t 2 ) = 0. (10.10)Принцип ГамильтонаДля истинного движения q (t ) механической системы между любыми моментами времени t 1 и t 2 , t 1 < t 2 , действие имеет экстремальное значение по сравнению со всевозможными деформациями q ˜(t, ε) с закрепленными концами. Это означает, что выполняется равенство δS = 0, (10.11) В случае достаточно близких моментов t 1 и t 2 действие минимально. • Исторически принцип Гамильтона не был первым среди вариационных принципов механики. Таковым был принцип наименьшего действия Мопертюи (1747), который в то время был ректором Берлинского университета. Свой принцип наименьшего действия он формулировал достаточно туманно, связывая его с различными философскими и богословскими соображениями (он утверждал, что природа выбирает такие пути, которые требуют наименьшего действия и т.п.). На его счастье, однако, среди сотрудников Берлинского университета был Леонард Эйлер, который и объяснил, в чем на самом деле состоит этот принцип, и что такое действие «по Мопертюи» (оно определяется не так, как действие по Гамильтону). К дальнейшему уточнению и развитию принципа серьезно приложили руку Лагранж и Якоби. Тем не менее, В.И.Арнольд [3] цитирует Якоби, который писал, что принцип Мопертюи даже в лучших учебниках представлен так, что его нельзя понять, а потом замечает: «Не решаюсь нарушать традицию». Принцип Мопертюи вызвал насмешливую критику Вольтера. Он написал философскую повесть «Кандид», герой которой, попадая в разные мрачные и смешные передряги, каждый раз повторяет ту философскую формулировку Мопертюи, которая в пародийной форме Вольтера звучит так: «Все к лучшему в этом лучшем из миров». Вы, конечно, слыхали эту фразу. (А знаете ли Вы, что именно Вольтер сыграл решающую роль в распространении идей Ньютона на континенте?) И в принципе Мопертюи, и в принципе Гамильтона есть одна (кажущаяся) странность — условия налагаются на систему в будущие моменты времени. Это может навести на мысль, что данные принципы имеют телеологический смысл, т.е. говорят о том, что механическая система как будто стремится к некоторой высшей цели в своем движении. Конечно, это не так. Мы увидим, что из вариационного принципа Гамильтона следуют дифференциальные уравнения движения, так что на самом деле будущая эволюция механической системы определяется попросту начальными условиями. Что касается принципа Мопертюи, то, как мы увидим далее, здесь дела обстоят иначе — конечное положение системы, действительно, задается, но задаем его мы сами. Строго говоря, принцип Мопертюи относится не к задаче с начальными данными, а к краевой задаче и определяет не эволюцию, а лишь траекторию, соединяющую два положения системы. Замечу, что в литературе по этому вопросу много путаницы, некоторые авторы, обороняя этот принцип от обвинения в «телеологичности», заявляют, что и принцип Мопертюи определяет начальные данные. На самом деле, принцип Мопертюи при заданном положении системы определяет ее начальную скорость, потребную для достижения заданного конечного положения. Таким образом, цель все-таки присутствует в этом принципе, но мы сами ее выбираем. Существенное различие между двумя принципами проявляется и в том, что принцип Гамильтона определяет эволюцию (решение уравнений движения) однозначно (во всяком случае, при естественных условиях гладкости и невырожденности), тогда как принципу Мопертюи может удовлетворять много, даже бесконечно много, различных траекторий . Замечу еще, что принцип Гамильтона, являясь мощным средством вывода дифференциальных уравнений движения (а в механике сплошной среды — еще и так называемых естественных краевых условий), вместе с тем, мало пригоден для построения приближенных методов. Так получается именно потому, что условия приходится накладывать на положение системы в будущем, которое нам заранее неизвестно. Правда, в задаче о периодических движениях, когда требуется, чтобы не просто положение, а начальное состояние системы (q,q ˙) повторилось спустя период времени T , принцип Гамильтона оказывается весьма полезным и для теории (существование, единственность и неединственность периодических режимов), и для приближенного вычисления. Уравнения Лагранжа второго родаПоскольку в принципе Гамильтона допустимы лишь деформации с закрепленными концами, их вариации обращаются в ноль в начальный и конечный моменты t 1 и t 2 соответственно, см. (10.10). Формула для вариации упрощается, и принцип Гамильтона приводит к равенству Это равенство должно выполняться для произвольной вектор-функции δq = δq (t ), удовлетворяющей краевым условиям (10.10). Если бы этих краевых условий не было, то мы попросту положили или подробнее, в координатах Имеется два основных способа это доказать. Способ первый состоит в том, чтобы установить, что множество вектор-функций, удовлетворяющих краевому условию ( 10.10), всюду плотно в пространстве L 2 (точнее, L 2 ([t 1 ,t 2 ],Rn )) . Следующие рассуждения носят достаточно общий характер. Обозначим t 2 Z (f (t ) − ηk (t ))2 dt → 0. (10.15) t 1 Далее, согласно (10.12) имеем t 2 Z f(t) · ηk (t)dt = 0, k = 1,2,... (10.16)t 1 Переходя в этом равенстве к пределу, с учетом (10.15) получаем t 2 Z f 2 dt = 0. (10.17) t 1 Отсюда и вытекает, что f (t ) ≡ 0. Вышло, что мы все-таки смогли, преодолев сопротивление краевых условий, положить δq равным f в (10.12). Я опустил здесь доказательство свойства плотности, надеюсь, что оно Вам известно из функционального анализа и вариационного исчисления. • На самом деле, справедливо более сильное утверждение, которое применяется не только в случае функций и вектор-функций, заданных на отрезке, но и для функций, заданных в произвольной области (см., например, [28]). Лемма. Множествофункций C ∞ –гладкихиисчезающихвокрестности границы области D, а если область не ограничена, то также в окрестности бесконечно удаленной точки (то есть вне некоторого шара) — всюду плотно в L 2 (D ). Разумеется, окрестность, о которой идет речь в лемме, у каждой функции своя. Эта лемма распространяется и на вектор-функции со значениями в евклидовом пространстве. Замечу еще, что окончание нашего предыдущего рассуждения по сути повторяет доказательство известной — простой и важной — леммы функционального анализа. Лемма. Пусть f ∈ H — элемент гильбертова пространства H, и пусть L ⊂ H — всюду плотное в H множество. Тогда из равенства (f, η) = 0, (10.18) выполняющегося для всех η ∈ L , следует, что f = 0. Второй способ вывода уравнений Лагранжа (10.13) из равенства (10.12) связан с использованием δ–функции. Мы теперь предполагаем, что векторфункция f = Lq − dt d Lq ˙ непрерывна, и для нее выполняется равенство t 2 Z f (t ) · η(t )dt = 0 (10.19) t 1 для всех вектор-функций η, непрерывных и таких, что η(t 1 ) = η(t 2 ) = 0. Пусть t 0 ∈ (t 1 ,t 2 ) — произвольный момент времени. На сей раз построим последовательность ηk (t ) вектор-функций, которая стремится (слабо) к δ-функции δ(t − t 0 ). Тогда, полагая в (10.19) η = ηk (здесь мы должны предположить, что ηk удовлетворяет краевым условиям) и переходя к пределу, найдем, что f (t 0 ) = 0, что и требовалось (t 0 — произвольно). • Оба примененных приема являются частными случаями более общего подхода, основанного на теореме Хана-Банаха. Пусть для данного элемента f банахова пространства X выполняется равенство η(f ) = 0, где η есть произвольный линейный функционал из множества M ⊂ X ∗ , причем M плотно (или хотя бы полно) в X ∗ . Тогда f = 0. Еще раз запишем теперь уже полностью выведенные уравнения Лагранжа второго рода
Конечно, Вас не смутит присутствие здесь частных производных, они лишь участвуют в выражениях для слагаемых этого уравнения. В нормальной ситуации уравнение Лагранжа представляет собой систему обыкновенных дифференциальных уравнений второго порядка. Действительно, производя дифференцирование по t , можно придать уравнению (10.13) форму L q ˙q ˙q ¨+ L qq ˙ q ˙ + L qt ˙ − L q = 0. (10.20) Эта система не разрешена относительно вторых, старших производных. Ее можно разрешить (это и есть нормальная для задач механики ситуация), если выполнено условие Матрица в этом равенстве называется матрицей Гесса , а ее определитель — гессианом функции L (по переменным q ˙1 , q ˙2 , ... , q ˙n ). Когда условие (10.21) выполнено для всех (q,q,t ˙ ) ∈ D ×Rn ×R , уравнение (10.20) и в самом деле представляет собой систему n дифференциальных уравнений второго порядка с областью задания D × Rn × R . Вырожденные лагранжианыСлучается, что условие невырожденности (10.21) нарушается лишь в отдельных точках или на некоторых подмногообразиях фазового пространства. Мы сейчас рассмотрим вырожденные лагранжианы , для которых уравнение Лагранжа на всем фазовом пространстве «теряет порядок». Итак, назовем лагранжиан L вырожденным , если всюду (тождественно) выполнено равенство Lq ˙q ˙ (q,q,t ˙ ) = 0. (10.22) В этом случае уравнение Лагранжа (10.20) — первого порядка или вообще не является дифференциальным (становится конечным ). Из равенства (10.22) следует, что L зависит от q ˙ линейно: L = A (q,t ) · q ˙ + B (q,t ), (10.23)где A (q,t ) — вектор-функция, B (q,t ) — функция. В координатах равенство (10.23) записывается в виде L = Ai (q,t )q ˙i + B (q,t ), (10.24)Как обычно, подразумевается суммирование по i от 1 до n . Отсюда выводим Lq ˙ i = Ai , Lq ˙ = A, (10.25) Заметим, во-первых, что при выводе первого равенства (10.26) нам пришлось изменить название немого индекса i
на j
. А во-вторых, обратите внимание, что во второй формуле (10.26) появилась не сама матрица чем задуматься, а не то легко допустить ошибку. Давайте для функционала M (q,q ˙) = A (q ) · q ˙ = (A (q ),q ˙) вычислим производную Mq , не переходя к координатам. Воспользуемся определением Гато. Для любого η ∈ Rn имеем
Здесь A 0 (q ) = Aq . Таким образом, Mq = A 0∗ (q )q. ˙ (10.28) Теперь пойдем дальше. Согласно (10.25), (10.26), уравнение Лагранжа (10.20) принимает вид Это дифференциальное уравнение (формально) первого порядка в Rn
. Его можно разрешить относительно q
˙, если операторный коэффициент K
= ω(q,t ) ∧ q ˙ + At − Bq = 0, (10.30) где ω — тот самый псевдовектор, который определяется оператором K . Уравнение Лагранжа зависит от лагранжиана L линейно. Если, например, к некоторому известному лагранжиану добавить лагранжиан (10.23), то в уравнение Лагранжа добавится левая часть уравнения (10.29). Это соображение позволяет включить в гамильтонов–лагранжев формализм различные уравнения механики с гироскопическими силами. Такие системы возникают, например, когда мы рассматриваем движение во вращающейся системе координат. Примером служит сила Кориолиса, которая появляется в системе отсчета, связанной с вращающейся Землей. Дальнейшее вырождение уравнения Лагранжа (10.29) возникает, когда
Из курса анализа Вам известно (известно?), что в этом случае существует такая функция ϕ(q,t ), что A = grad ϕ = ϕq . (10.32) Вообще говоря, функцию ϕ можно определить лишь локально. Но если область D ⊂ Rn , где изменяется точка q , односвязна (например, если D = Rn ), то потенциал ϕ можно определить всюду в D . При условии (10.32) уравнение (10.29) становится конечным , недифференциальным: At − Bq = 0. (10.33) С учетом условия (10.32), это уравнение приводится к скалярному ϕt = B. (10.34) Здесь опущено слагаемое C (t ), потому что его можно убрать, включив в функцию ϕ — она ведь, согласно (10.32), определена с точностью до произвольного слагаемого, зависящего от t . Тривиальные лагранжианыМы видим, что задание лагранжиана, согласно принципу Гамильтона, однозначно определяет уравнение движения Лагранжа (10.13). Однако обратное неверно — одному и тому же уравнению (10.13) соответствует не один, а много лагранжианов. Так получается потому, что имеется целый набор тривиальных лагранжианов . Лагранжиан L 0 называется тривиальным , если отвечающее ему «уравнение Лагранжа» сводится к равенству 0 = 0. Из предыдущего следует, что тривиальный лагранжиан должен быть линеен по q ˙ (см. (10.23)), причем поле A должно быть потенциальным (см. (10.32)). Кроме того, должно выполняться равенство (10.34). В итоге приходим к выводу, что тривиальный лагранжиан должен иметь вид L
0
= Aq
˙ + B
= grad
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| f (ϕ −1 (x )) = f (x ). Можно эти равенства записать и так: |
(12.8) |
| f ◦ ϕ = f, f ◦ ϕ −1 = f. |
(12.9) |
Дальше уже существенно, что Ω — область в Rn , а отображение ϕ будем считать гладким, хотя бы класса C 1 . При этих условиях отображение ϕ определяет не только преобразование функций на Ω, но и отображение векторов, скажем, приложенных в некоторой точке a ∈ Ω. Такой вектор v можно мыслить как мгновенную скорость точки, которая в данный момент находится в положении a . Если при этом точка двигается по закону x = x (t ), и x (t 0 ) = a , то x ˙(t 0 ) = v .
Посмотрим теперь, как двигается преобразованная точка ϕ(x (t )). Ее скорость есть
![]() (12.10)
(12.10)
или в координатах
![]() .
(12.11)
.
(12.11)
Здесь ϕ 0 (x ) означает производную отображения ϕ в точке x . Эта производная в координатах задается матрицей Якоби
![]() .
(12.12)
.
(12.12)
Не совсем точно было бы написать здесь просто знак равенства, потому что матрица Якоби зависит от выбора координат, а производная ![]() — не зависит. Нетрудно дать ей инвариантное (относительно выбора координат) определение.
— не зависит. Нетрудно дать ей инвариантное (относительно выбора координат) определение.
Формулы (12.10) и (12.11) показывают, что разумно определить индуцированное преобразованием ϕ : Ω → Ω отображение векторов в произвольной точке x ∈ Ω при помощи производной отображения ϕ. Это индуцированное отображение часто обозначают ϕ∗ (x ), согласно определению ϕ∗ (x )v = ϕ 0 (x )v или в координатах
![]() .
(12.13)
.
(12.13)
Кратко то, что мы сейчас проделали, выражают словами: гладкое преобразование ϕ действует на функции посредством замены переменных, а на векторы — посредством его производной.
Инвариантные лагранжианы. Лагранжиан L (q,q ˙), не зависящий от времени, задается в декартовом произведении D × Rn , где D — область в R n .
Предположим теперь, что задана однопараметрическая группа преобразований области D g
τ
: D
→ D
. Это означает, что g
0
= id
, g
τ
+s
= g
τ
gs
для всех τ,s
∈ R
. Это отображение переводит точку q
∈ D
в точку g
τ
q
∈ D
. При этом вектор q
˙, приложенный в точке q
, подвергается индуцированному преобразованию![]() и переходит в
и переходит в![]() . Скажем, что лагранжиан L
инвариантен относительно однопараметрической группы g
τ
, если выполняется равенство
. Скажем, что лагранжиан L
инвариантен относительно однопараметрической группы g
τ
, если выполняется равенство
L(gτ q,gτ 0 (q)q˙) = L(q,q˙) (12.14)
для всех τ ∈ R , q ∈ D , q ˙ ∈ Rn .
Мы уже знаем, что однопараметрическая группа преобразований области D определяется векторным полем Q на D , так что g τ есть эволюционный оператор автономного дифференциального уравнения
![]() ,
(12.15)
,
(12.15)
при этом q (τ) = g τ q 0 есть решение задачи Коши для этого уравнения с начальным условием q (0) = q 0 .
Теорема Э.Нетер . Пусть лагранжиан L = L (q,q ˙) не зависит от времени и инвариантен относительно однопараметрической группы преобразований g τ , так что выполняется ( 12.14). Тогда соответствующая механическая система имеет интеграл
I (q,q ˙) = Lq ˙ q 0 , (12.16)
где q 0 = Q (q ).
Доказательство : Ввиду условия инвариантности (12.14) действие S инвариантно относительно преобразований g τ :
t 2 t 2
Z Z
S = L(q,q˙)dt = L(gτ q,gτ 0 (q)q˙)dt. (12.17)
t 1 t 1
Левая часть от τ не зависит. Поэтому производная от правой части по τ равна нулю.
Введем вариацию δq , соответствующую деформации g τ : q 7→ g τ q
![]() .
(12.18)
.
(12.18)
Дифференцируя это равенство по t и меняя местами производные по t и по τ, получим
![]() (12.19)
(12.19)
Теперь варьирование равенства (12.17) (то есть дифференцирование по параметру деформации τ при τ = 0) с учетом соотношений (12.18) и (12.19) дает равенство
t 2 Z
| (Lq (q,q ˙)δq + Lq ˙ (q,q ˙)δq ˙)dt = 0. t 1 |
(12.20) |
Пользуясь основной формулой вариационного исчисления δq ˙ = (δq )· и интегрируя по частям (см. формулы (10.9)), преобразуем (12.20) к виду
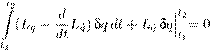 .
(12.21)
.
(12.21)
Согласно уравнению Лагранжа, интегральное слагаемое исчезает, и мы получаем
![]() .
(12.22)
.
(12.22)
Поскольку это верно для любых t 1 , t 2 , функция Lq ˙ δq = Lq ˙ q 0 есть интеграл. Теорема доказана.
Конечно, можно провести доказательство непосредственно, подставляя выражение (12.16) в уравнение Лагранжа. Но я ненавижу такие доказательства, которые скрывают путь, которым можно прийти к результату. Проведенное доказательство показывает, что условие инвариантности лагранжиана расширяет класс допустимых деформаций по сравнению с принципом Гамильтона, что и приводит к закону сохранения.
Замечу, что изложенная теорема в действительности является частным случаем значительно более общих и глубоких результатов Э. Нетер (см. книгу П. Олвера [33]).
Теперь рассмотрим приложения теоремы Нетер. Мы увидим, что основные законы сохранения имеют своей причиной свойства симметрии пространства. Замечу, что закон сохранения энергии был выведен выше в случае лагранжиана L (q,q ˙), не зависящего от времени. А это означает, что он является следствием однородности времени — инвариантности законов природы относительно сдвигов времени. Этот закон не следует непосредственно из доказанной нами теоремы, но может быть получен из более общих результатов Э. Нетер.
Трансляционная инвариантность и интеграл импульса
Рассмотрим натуральную механическую систему с лагранжианом
![]() (12.23)
(12.23)
и уравнениями движения
Mx¨ = −gradV (x). (12.24)
Здесь x — вектор-функция со значениями в H . Каждый вектор a ∈ H определяет преобразование сдвига (трансляции) Ta : H → H , Ta : x 7→ x + a . Предположим, что потенциальная энергия V (x ) инвариантна относительно сдвигов вдоль некоторого направления (заданного вектором a ). Это означает, что для любого s ∈ R и любого x ∈ H выполнено равенство V (Tsa x ) = V (x ) или V (x + sa ) = V (x ).
Преобразование Tsa действует на векторы скорости тривиально, как тождественное:
![]() .
(12.25)
.
(12.25)
Поэтому лагранжиан (12.23) инвариантен относительно преобразований Tsa . Имеем
![]() (12.26)
(12.26)
Согласно теореме Нетер, заключаем, что уравнение (12.24), при условии инвариантности потенциальной энергии V (x ) относительно сдвигов вдоль направления вектора a , имеет интеграл
I (x,x ˙) = (Mx,a ˙ ). (12.27)
Вектор Mx ˙ есть импульс (количество движения), а интеграл I лишь несущественным множителем |a | отличается от проекции импульса на направление вектора a . Важный частный случай уравнения (12.24) — система n материальных точек в R 3 . В этом случае конфигурационное пространство H = R 3n , а оператор M задается диагональной матрицей
| m 1 |
|
(12.28) |
|
| M = |
m 1 m 1 m 2 0 m 2 m 2 0 ... mn mn |
||
| mn |
|||
Здесь масса j -й частицы mj повторяется трижды на главной диагонали этой матрицы, потому что масса не зависит от направления движения (это следствие изотропности пространства).
Предположим, что потенциальная энергия не меняется при любом сдвиге всей системы частиц в направлении вектора e ∈ R 3 . Не ограничивая общности, можно считать, что e — единичный вектор: |e | = 1. Если V = V (x 1 ,...,xn ), где xj ∈ R 3 — положение j -й частицы, то это условие инвариантности запишется в виде
V (x1 + se,...,xn + se) = V (x1 ,...,xn ). (12.29)
Импульс системы частиц в R 3 имеет вид
n
IM = X mj x ˙j . (12.30)
j =1
Из предыдущего видно, что условие (12.29) влечет существование интеграла
![]() .
(12.31)
.
(12.31)
Это — закон сохранения компоненты импульса I вдоль направления e . В случае, например, потенциальной энергии
V = X wij (|xi − xj |)
1≤i<j ≤n
условие инвариантности (12.29) выполнено, очевидно, при любом векторе e . Таким образом, в этом случае имеет место закон сохранения вектора импульса .
Примечательно и практически очень важно, что форма интегралов импульса не зависит от потенциальной энергии. Поэтому законом сохранения импульса можно пользоваться, не зная явно законов взаимодействия частиц, будучи лишь уверенными в трансляционной инвариантности потенциальной энергии.
В условиях, когда сохраняется вектор импульса, центр масс системы двигается с постоянной скоростью, по инерции. Напомню, что положение центра масс, согласно определению, есть
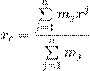 .
(12.32)
.
(12.32)
Прежде, чем перейти к выводу закона сохранения момента импульса, рассмотрим некоторые общие результаты об изометриях банаховых и гильбертовых пространств.
Изометрии и вращения банаховых и гильбертовых пространств
Оператор A : X → X , где X есть вещественное банахово пространство, называется изометрическим оператором или изометрией , если он сохраняет расстояния (Рис. 3) для любых точек x и y пространства X
kAx − Ay k = kx − y k. (12.33)
![]() x
Ax
x
Ax
![]() Ay
y
Ay
y
Рис. 3
Разумеется, это определение можно распространить и на метрические пространства.
Очевидно, оператор сдвига Ta : X → X : x 7→ x + a является изометрией для любого a ∈ X . У этого оператора при любом a 6= 0 нет неподвижных точек. Изометрическое отображение, которое обратимо и имеет неподвижную точку, называется вращением . Дальше будем считать, что эта неподвижная точка есть 0 (ноль) пространства X . Итак, оператор A будем называть вращением, если он удовлетворяет условию (12.33) и A (0) = 0.
Справедлива замечательная теорема С. Мазура и С. Улама: всякоевращениебанаховапространстваестьлинейныйоператор . Доказательство этой глубокой теоремы можно найти в книге С. Банаха [5], а также в Приложении 2 в этом курсе лекций. В случае евклидова или гильбертова пространства Вы, если постараетесь, сможете, я думаю, провести доказательство самостоятельно.
• С. Мазур и С. Улам — польские математики. Улам известен своей замечательной фантазией — среди многих его результатов вспоминается, например, идея записать ряд натуральных чисел по спирали — тогда на диагонали вдруг возникают ряды простых чисел (как он сам рассказывал, такую картинку он нарисовал на каком-то заседании, стараясь не заснуть). Ему также принадлежит идея термоядерной бомбы.
Нам дальше будут нужны лишь изометрические операторы в евклидовом или в гильбертовом вещественном пространстве H . Пусть оператор U : H → H является вращением (чаще такие операторы называются ортогональными или, особенно в случае комплексного гильбертова пространства H , унитарными ). Условие изометричности (12.33) можно записать в виде
(Ux,Ux) = (x,x). (12.34)
Мы учли, что U — линейный оператор, и заменили x −y в (12.33) на x . Это равенство можно также записать в виде
((U ∗ U − I )x,x ) = 0. (12.35)
оператор U ∗ U −I (U ∗ — сопряженный оператор) самосопряжен и порождает нулевую квадратичную форму. Поэтому
U ∗ U = I. (12.36)
В конечномерном случае отсюда следует, что ортогональный оператор обратим. Действительно det I = 1, det(U ∗ U ) = detU ∗ detU = (detU )2 .
Поэтому согласно (12.36), detU = ±1, так что U — обратимый оператор.
Мы видим также, что ортогональные операторы бывают двух типов. Те, для которых detU = 1, называются собственными вращениями , а те, для которых detU = −1, — несобственными вращениями .
Всевозможные вращения пространства Rn — собственные и несобственные — образуют ортогональную группу O (n ). Собственные вращения также образуют группу (проверьте!) SO (n ). Это подгруппа группы O (n ), хотя ее часто нужно бывает рассматривать как самостоятельный объект. Несобственные вращения, конечно, группы не образуют (почему?).
В бесконечномерном гильбертовом пространстве всевозможные вращения не образуют группы — существуют необратимые вращения. Рассмотрим, например оператор U : ` 2 → ` 2 , действующий на произвольный вектор x = (ξ1 , ξ2 ,... ) ∈ ` 2 по правилу
Ux = (0,ξ1 ,ξ2 ,...). (12.37)
такой оператор называется оператором правогосдвига . Он, очевидно, необратим: уравнение Ux = y для y = (η1 , η2 ,... ) ∈ ` 2 имеет решение только в случае, когда η1 = 0 (это условие, конечно, необходимо и достаточно). Мы видим, что существование необратимых вращений связано с существованием у гильбертова пространства изометричных ему собственных (то есть не совпадающих со всем пространством) подпространств. Разумеется, можно и очень интересно рассматривать группу вращений гильбертова пространства, которая состоит из тех и только тех вращений, которые обратимы.
Замечу, что изометрии банаховых пространств также очень интересны и соответствующие группы изометрий и группы вращений довольно разнообразны. Видимо, можно сказать, что в случае евклидовых пространств группы вращений наиболее богаты. А вот среди банаховых пространств есть такие, у которых имеется лишь конечное число вращений. Встречаются даже случаи, когда группа вращений состоит из одного тождественного оператора.
Вращение и кососимметричные операторы. Предположим, что заданное однопараметрическое семейство U (s ) : H → H вращений образует группу. Дифференцируя равенство (12.36) по s , получаем
U ∗0 (s )U (s ) + U ∗ (s )U 0 (s ) = 0, (12.38)
а затем полагая s = 0, для A = U 0 (0) выводим равенство
A ∗ + A = 0. (12.39)
Мы учли, что U (0) = I и U ∗ (0) = I . Таким образом, генератор A = U 0 (0) однопараметрической группы вращений есть кососимметрический оператор. Это означает (2.10), что группа операторов U (s ) есть эволюционный оператор уравнения
x 0 = Ax (12.40)
с кососимметрическим оператором A .
Обратное тоже верно. Рассмотрим уравнение (12.40) в H , и пусть оператор A кососимметричен: A ∗ = −A . Тогда эволюционный оператор этого уравнения U (s ) для любого s ∈ R есть вращение. Действительно, пусть x (s ) — любое решение уравнения (12.40). Умножая это уравнение на x (s ), получим
![]() .
(12.41)
.
(12.41)
Второе равенство следует из кососимметричности:
(Ax,x ) = (x,A ∗ x ) = −(x,Ax ),
так что (Ax,x ) = 0 для всех x , если A — кососимметрический оператор. Из (12.41) следует равенство
(U (s )a,U (s )a ) = (a,a ), (12.42)
где a = x (0). Поскольку a — произвольный элемент пространства H , отсюда следует, что U (s ) есть вращение. Даже в случае бесконечномерного пространства H нетрудно доказать, что U (s ) — обратимый оператор для любого s , лишь бы оператор A был ограничен.
Интересно отметить, что эволюционный оператор U (s ) неавтономного уравнения
x 0 = A (s )x (12.43)
с кососимметрическим операторным коэффициентом (A ∗ (s ) = −A (s ) для всех s ) тоже является вращением. Доказательство, данное выше для автономного случая, полностью сохраняется.
Размерность линейного пространства кососимметрических операторов
в Rn
(кососимметричных n
×n
матриц) есть, очевидно,![]() . Эта размерность совпадает с n
только при n
= 3.
. Эта размерность совпадает с n
только при n
= 3.
В пространстве R 3 кососимметрический линейный оператор действует как векторное умножение на постоянный вектор. Действительно, в этом случае для векторного произведения ω ∧ x имеем
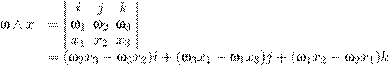 (12.44)
(12.44)
для любых x = (x 1 ,x 2 ,x 3 ) и ω = (ω1 , ω2 , ω3 ). С другой стороны, если
| то |
|
αx 2 + βx 3
Ax = −αx 1 + γx 3 .
−βx 1 − γx 2
Чтобы выражения Ax и ω ∧ x совпадали, нужно положить α = −ω3 , β = ω2 , γ = −ω1 . Таким образом, векторному произведению (12.44) соответствует кососимметрическая матрица
![]() .
(12.45)
.
(12.45)
Интеграл момента количества движения
Интегралы момента количества движения возникают, когда лагранжиан L инвариантен относительно некоторой однопараметрической подгруппы группы вращений пространства H . Такая подгруппа состоит из операторов вида esA , где ее генератор A есть кососимметрический оператор. Условие инвариантности имеет вид
L(esA x,esA x˙) = L(x,x˙). (12.46)
Согласно теореме Э. Нетер, из условия (12.46) следует, что система имеет интеграл
MA = (Lx ˙ ,Ax ) (12.47)
для всех x, x
˙ ∈ H
, s
∈ R
. Мы учли, что![]() .
.
Рассмотрим механическую систему, у которой конфигурационное пространство есть евклидово пространство H , а лагранжиан L = L (x,x ˙) не зависит от времени. Важнейшим примером служит натуральная механическая система. Ее уравнение движения дается обобщенным вторым законом Ньютона
Mx ¨ = −gradV (x ), (12.48)
а лагранжиан определяется равенством
![]() .
(12.49)
.
(12.49)
В случае натуральной системы интегралы типа момента количества движения чаще всего получаются, когда потенциальная энергия инвариантна относительно той или иной (тех или иных) подгруппы (подгрупп) группы вращений, то есть, когда выполняется условие
V (esA x ) = V (x ). (12.50)
Для инвариантности лагранжиана (12.49) нужно дополнительно потребовать, чтобы и кинетическая энергия была инвариантна, то есть, чтобы выполнялось равенство
(MesA x,e ˙ sA x ˙) = (Mx, ˙ x ˙) (12.51)
для любых x ˙ ∈ H , s ∈ R . Учитывая, что (esA )∗ = esA ∗ = e −sA , это равенство можно записать в виде
(e −sA MesA x, ˙ x ˙) = (Mx, ˙ x ˙). (12.52)
Слева и справа стоят квадратичные формы, записанные в стандартном виде, с самосопряженными операторами M и e −sA MesA , поэтому из (12.52) следует операторное равенство
e −sA MesA = M. (12.53)
Это условие зачастую довольно сложно проверить. Ему, однако, можно придать более простую форму. Дифференцируя равенство (12.53) по s , получим
− Ae−sA MesA + e−sA MesA A = 0. (12.54)
Если учесть (12.53), то это равенство принимает вид
− AM + MA = 0. (12.55)
Таким образом, из (12.53) следует, что операторы A и M коммутируют: MA = AM . Верно и обратное: если выполняется (12.55), то выполнено и условие (12.53). Действительно, вводя обозначение N (s ) = e −sA MesA , для оператор-функции N (s ) получаем дифференциальное уравнение
![]() (12.56)
(12.56)
Согласно определению N (s ) имеем также начальное условие
![]() (12.57)
(12.57)
Задача Коши (12.56), (12.57) для операторного уравнения (12.56) однозначно разрешима при любом линейном операторе M . Это доказывается точно так же, как для обычных векторных уравнений, более того, уравнение (12.56) есть частный случай векторного дифференциального уравнения. Но одно решение данной задачи Коши очевидно: N (s ) = M для всех s ∈ R . Это и означает, что равенство (12.53) является следствием равенства (12.55).
Итак, мы установили, что приинвариантностипотенциальнойэнергии ( 12.50) дополнительное условие ( 12.55) обеспечивает инвариантностьлагранжиана( 12.49)относительногруппывращений esA , где A — кососимметрический оператор.
Из теоремы Нетер теперь следует, что при выполнении условий (12.50) и (12.55) уравнение обобщенного второго закона Ньютона (12.48) допускает интеграл момента
MA = (Mx,Ax ˙ ). (12.58)
Это, конечно, частный случай интеграла (12.47).
Для механики и физики очень важен класс систем типа (12.48), возникающий при рассмотрении систем n частиц, двигающихся в R 3 (или R 2 ) при наличии парного взаимодействия между ними. Для такой системы потенциальная энергия имеет вид
V (x ) = X wij (|xi − xj |). (12.59)
1≤i<j ≤n
Оператор масс M действует в пространстве R 3n (или R 2n ) и задается, как мы уже видели, диагональной матрицей (12.28).
Как было уже отмечено раньше, в случае потенциальной энергии (12.59)
n
сохраняется вектор импульса (см. (12.30)) IM = P mj x ˙j . Теперь мы по-
j =1
кажем, что сохраняется также вектор момента импульса.
Группа U
τ
: R
3
→ R
3
вращений ![]() трехмерного пространства (конфигурационного пространства одной частицы) порождает группу вращений U
b
τ
: R
3n
→ R
3n
конфигурационного пространства системы n
частиц согласно равенству
трехмерного пространства (конфигурационного пространства одной частицы) порождает группу вращений U
b
τ
: R
3n
→ R
3n
конфигурационного пространства системы n
частиц согласно равенству
Ub τ ξ = (Uτ ξ 1 ,...,Uτ ξ n ) (12.60)
для любого ξ = (ξ
1
,...,
ξ
n
), где ![]() положение j
той частицы. Это, конечно означает, что преобразование U
τ
поворачивает всю систему частиц как целое, не меняя их взаимного расположения. Потенциальная энергия (12.59) инвариантна относительно любого вращения U
τ
:
положение j
той частицы. Это, конечно означает, что преобразование U
τ
поворачивает всю систему частиц как целое, не меняя их взаимного расположения. Потенциальная энергия (12.59) инвариантна относительно любого вращения U
τ
:
V (U b τ x ) = X wij (|U τ xi −U τ xj |) = X wij (|xi −xj |) = V (x ),
1≤i<j ≤n 1≤i<j ≤n
(12.61)
так как U τ — линейный оператор, сохраняющий расстояния. Кинетическая энергия имеет вид
![]() (12.62)
(12.62)
и также, очевидно, сохраняется при вращении U τ , более того, сохраняется каждое слагаемое в (12.62). Поскольку U τ — линейный оператор, его производная совпадает с ним самим, а значит x ˙j перейдет при вращении U τ в U τ x ˙j . При этом |U τ x ˙j | = |x ˙j | — опять-таки по свойству изометричности.
Генератор A b группы U b τ выражается через генератор A группы U τ :
![]() .
(12.63)
.
(12.63)
Заметим, что оператору A соответствует блочно-диагональная матрица, каждый блок есть матрица A . Интеграл (12.58) принимает вид
![]() .
(12.64)
.
(12.64)
Но мы уже видели, что всякий кососимметрический оператор A в R 3 реализуется как векторное умножение, так что A ξ = ω∧ξ, где ω — известный постоянный вектор (точнее, псевдовектор), ξ ∈ R 3 . Подстановка в (12.64) дает равенство
n
MA = X (mj x ˙j , ω ∧ xj ). (12.65)
j =1
Пользуясь тем, что смешанное произведение трех векторов не меняется при циклической перестановке, запишем последнее равенство в виде
![]() .
(12.66)
.
(12.66)
Поскольку ω здесь произвольный вектор, получается, что имеется целых три интеграла (положим, например, в (12.66) ω = e 1 , ω = e 2 и ω = e 3 , где e 1 , e 2 , e 3 — координатные орты в R 3 ). Иными словами, для уравнения ( 12.48) с потенциальной энергией ( 12.59) и кинетической энергией ( 12.62) выполнен закон сохранения вектора момента количества движения M , определяемого равенством
M
![]() .
(12.67)
.
(12.67)
Примечательное свойство интегралов количества движения и момента количества движения состоит в том, что они не зависят от конкретного вида потенциальной энергии и существуют всякий раз, когда потенциальная энергия обладает должными свойствами инвариантности. В определенной мере поэтому предсказания, которые мы делаем на основе законов сохранения количества движения и момента количества движения, наиболее надежны. В частности, закон сохранения момента играет значительную роль в
13 Принцип Гамильтона для систем со связями
![]()
космогонии — теории происхождения солнечной системы. Из-за большой удаленности планет от солнца момент количества движения солнечной системы огромен, и всякая космогоническая гипотеза должна этот факт объяснить. Многие космогонические гипотезы, и самая первая из них — гипотеза Лапласа, не справились с этой задачей, а потому были отвегнуты. По Лапласу, солнечная система произошла от некой быстро вращающейся жидкой массы, от экватора которой из-за центробежных сил отрывались огромные «капли», которые, застывая, превратились потом в планеты. Но ввиду закона сохранения момента, эта жидкая масса должна была бы вращаться с совершенно невероятной угловой скоростью, так что вступили бы в силу запреты теории относительности.
Другим важным свойством интегралов количества движения, момента количества движения, а также энергии, является их аддитивность . Все они получаются суммированием соответствующих величин для отдельных частиц. У механической системы нет других аддитивных интегралов. Замечу также, что в условиях общего положения, то есть для подавляющего большинства всех мыслимых механических систем вообще нет других интегралов.
13. Принцип Гамильтона для систем со связями
Во многих важных для механики случаях допустимые положения системы не могут быть произвольными точками данного многообразия, скажем, пространства Rn , а обязаны удовлетворять тем или иным соотношениям, которые называются связями .
Пусть, например, положение системы определяется как точка x ∈ Rn , удовлетворяющая уравнению
Φ(x ) = 0, (13.1)
где Φ — заданная функция. Скажем тогда, что система подчинена голономной связи (13.1). Встречаются и случаи, когда связь зависит от времени и имеет вид
Φ(x,t ) = 0. (13.2)
Связи, зависящие от времени, называются реономными (текущими). Связь вида (13.1), от времени не зависящая, называется склерономной (жесткой) или стационарной .
Уравнение (13.1) означает, что точка x (t ) пространства Rn , изображающая положение данной системы в момент t , остается все время на гиперповерхности, определяемой уравнением (13.1), в случае n = 3 — это просто поверхность. Когда связь реономна и имеет вид (13.2), движение происходит по гиперповерхности, изменяющейся по заданному закону со временем.
Нередко встречаются и более сложные связи вида
Φ(x,x,t ˙ ) = 0, (13.3)
зависящие от скорости x ˙. Такие связи называются неголономными . Впрочем, иногда уравнение вида (13.3) удается проинтегрировать по времени и привести задачу к случаю голономной связи вида (13.1) или (13.2). Дальше мы будем рассматривать лишь голономные связи, опуская иногда прилагательное «голономная».
Что может заставить частицу, движущуюся, скажем, в пространстве R 3 , оставаться все время на поверхности (13.1)? Очевидно, для этого нужно, чтобы на неё действовала некоторая сила, развиваемая связью. Эта сила, заранее неизвестная, называется реакцией связи .
Связь (13.1) называется идеальной , если её реакция направлена по нормали к гиперповерхности (13.1). В случае, когда уравнение (13.1) регулярно , то есть grad Φ(x ) 6= 0 всюду на поверхности Φ(x ) = 0, реакцию идеальной связи (13.1) можно представить в виде: −λgrad Φ, где λ — множитель Лагранжа; знак минус, конечно, не имеет серьезного значения и поставлен ради будущих удобств.
Если на частицу, движущуюся в пространстве R 3 , наложена идеальная связь вида (13.1), и кроме реакции связи, на нее не действуют иные силы, то согласно 2-му закону Ньютона, уравнение движения можно записать в виде
mx ¨ = −λgrad Φ(x ). (13.4)
Здесь m — масса частицы, x (t ) — положение частицы в момент t , λ(t ) — множитель Лагранжа, зависящий от времени t . Из-за присутствия новой неизвестной функции λ(t ) мы должны к векторному уравнению (13.4) добавить уравнение связи (13.1). В результате получается своеобразная система уравнений, в которую входят 3 скалярных дифференциальных уравнения для компонент x 1 (t ), x 2 (t ), x 3 (t ), а четвертое уравнение (13.1) не содержит производных.
Наличие в системе (13.4), (13.1) уравнения связи заметно осложняет отыскание её решений. Иногда удается избавиться от связи путем введения специальных координат на поверхности (13.1). Например, если Φ(x
) = ![]() , то целесообразно ввести полярные координаты, полагая для точек данной поверхности
, то целесообразно ввести полярные координаты, полагая для точек данной поверхности
x 1 = a cosθ, x 2 = a sinθ. (13.5)
Тогда уравнение связи (13.1) будет удовлетворено тождественно, и мы сможем составить уравнение Лагранжа 2-го рода, в котором вместо неизвестных x 1 , x 2 , будет фигурировать одна переменная θ. Обычно так и поступают, когда это возможно. Но далеко не всегда удается ввести подходящую криволинейную систему координат с тем, чтобы исключить уравнение связи. Собственно говоря, список таких удобных координат известен и не слишком длинен — наряду с полярными, это сферические, гиперболические, эллиптические, биполярные и немногие другие координаты. Более того, даже когда нужные криволинейные координаты известны, не всегда разумно их использовать. Например, уже в случае полярных координат появляются синусы и косинусы, которые являются трансцендентными функциями. Они, конечно, хороши для аналитических выкладок, но могут существенно увеличить время вычисления на компьютере. По моему заданию одна студентка на простейшем примере кругового маятника проверила, как влияет на процесс вычисления использование тригонометрических функций. Оказалось, что время вычисления может вырасти на порядок (в 3–5–10 раз) по сравнению с иным методом, требующим лишь вычисления рациональных функций.
Вывод состоит в том, что нельзя избежать исследования систем со связями. Ситуация, понятно, еще осложняется, когда на систему наложено много связей, а то и бесконечно много. Как раз такой случай возникает при исследовании несжимаемой жидкости или гибкой нерастяжимой нити.
В случае неидеальной связи на частицу в ходе её движения действует и некоторая продольная, касательная к гиперповерхности (13.1) сила, скажем, сила трения. Строго говоря, силы трения уже и не относятся к механике, они имеют немеханическое происхождение. Впрочем, в курсах механики (если они написаны не физиками-теоретиками или примкнувшими к ним математиками) обычно имеется раздел, посвященный трению. Силы трения в природе чрезвычайно разнообразны и ещё недостаточно изучены. В курсах механики рассматриваются лишь самые простые виды трения. Исключением является курс механики И.И. Воровича [8], который опубликован уже после кончины (в 2001 г.) его автора. В этом курсе дан обширный обзор современных представлений и экспериментальных результатов по силам трения соприкасающихся твердых тел. Теория внутреннего трения в жидких телах строится в гидродинамике, а для твердых тел — в теории вязкоупругости. Более общий взгляд на процессы трения в сплошных средах развивает сравнительно новая (возникшая в середине XX века) наука реология .
Дальше будем рассматривать идеальные голономные и, ради краткости, стационарные связи вида (13.1). Вполне возможно, что рассматриваемая система подчинена целому набору связей:
Φ1 (x ) = 0, ..., Φr (x ) = 0. (13.6)
Все эти связи будем считать идеальными. Каждая связь Φj (x ) = 0 развивает реакцию вида: −λj grad Φj (x ). В итоге обобщенное уравнение 2-го закона Ньютона (когда на систему не действуют никакие другие силы, кроме реакции связи) примет вид
r
Mx ¨ = −X λj grad Φj (x ), (13.7)
j =1
где M — оператор масс. Наряду с x (t ), множители Лагранжа λj также неизвестны и должны быть определены совместно с x (t ) из системы (13.6),
(13.7).
Исключение связей
Будем считать, что положение системы есть точка q ∈ Rn , удовлетворяющая r (скалярным) голономным, стационарным, идеальным связям
Φ1 (q ) = 0, ..., Φr (q ) = 0. (13.8)
Конфигурационное пространство X
данной системы есть подмногообразие в Rn
, определяемое уравнениями (13.8). Конечно, нужно наложить на заданные функции Φ1
,...,
Φr
некоторые ограничения. Будем считать их достаточно гладкими (по крайней мере, класса C
2
), и предположим, что уравнения (13.8) совместны (так что данное подмногообразие не пусто), а функции Φ1
,...,
Φr
в каждой точке q
∈ X
независимы. Последнее условие обеспечивается требованием, чтобы матрица Якоби ![]() в каж-
в каж-
дой точке q ∈ X имела максимальный ранг, равный r . Обычно это условие записывается в виде требования, чтобы один из миноров r -го порядка был отличен от нуля, например,
![]() (13.9)
(13.9)
Не нужно, однако, торопиться выписывать определители. Зачастую невырожденность, обратимость матрицы лучше устанавливать непосредственно. А в случае, когда связей бесконечно много, и вовсе определители, как правило, теряют смысл (хотя и не всегда!).
Если условие (13.9) выполнено, то мы можем применить теорему о неявной функции и установить, что в некоторой окрестности каждой точки q 0 ∈ X можно ввести новые координаты q ¯1 ,q ¯2 ,...,q ¯n , так что они взаимно однозначно выражаются через прежние:
q¯j = Q¯ j (q1 ,...,qn ), j = 1,...,n. (13.10)
Здесь Q ¯ j — гладкие функции. При этом часть многообразия X в окрестности точки q 0 определяется r уравнениями
q ¯n −r +1 = 0, q ¯n −r +2 = 0, ..., q ¯n = 0. (13.11)
Грубо говоря, можно просто положить q ¯n −r +1 = Φ1 (q 1 ,...,qn ), ..., q ¯n = Φr (q 1 ,...,qn ). (13.12)
При этом, сдвигая начало координат, можно считать, что точке q 0 соответствует точка q ¯0 = 0.
Для точек на конфигурационном пространстве X мы будем иметь выражения q 1 = Q 1 (¯q 1 ,...,q ¯n −r ), ..., qn = Qn (¯q 1 ,...,q ¯n −r ). (13.13)
Теперь ясно, что положение системы полностью определяется заданием точки q ¯= (¯q 1 ,...,q ¯n −r ) в некоторой окрестности нуля пространства Rn −r . Если лагранжиан системы L = L (q,q,t ˙ ) задан, то его можно теперь выразить через переменные q ¯1 ,...,q ¯n −r , q ¯˙1 ,...,q ¯˙n −r . Таким образом, мы избавляемся от связей и можем теперь описывать движение системы обычными уравнениями Лагранжа 2-го рода. К сожалению, это верно до тех пор, пока система не выйдет из координатной окрестности точки q 0 . Если же это произойдет, то придется вводить новую систему координат в окрестности иной точки, скажем, q 1 ∈ X . Лишь в редких случаях удается определить глобально, на всем пространстве X , такие координаты, что уравнения связей выполняются тождественно. Поэтому в общей теории мы вынуждены рассматривать локальные системы координат и переходить от одной локальной системы координат к другой, опять-таки локальной системе координат.
Конечно, такой общий метод при решении конкретных задач больше подходит для компьютера, чем для человека. Вместе с тем, должен заметить, что на сегодня соответствующие вычислительные процедуры очень слабо развиты. Создание алгоритмов и программ для решения уравнений со связями остается одной из весьма актуальных проблем вычислительной математики и математической физики.
Так или иначе, исследование и общих, и конкретных систем со связями можно и следует проводить сначала (и настолько далеко, насколько это возможно), не вводя координат и не исключая связей.
Принцип Гамильтона для систем со связями
Рассмотрим механическую систему, заданную лагранжианом L = L (q,q,t ˙ ), где q ∈ D ⊂ Rn , q ˙ ∈ Rn , и подчиненную идеальным голономным связям
Φ1 (q,t ) = 0, ..., Φr (q,t ) = 0. (13.14)
Здесь мы разрешаем функциям Φj зависеть от времени. Для произвольных моментов времени t 1 < t 2 определим, как и раньше, действие S , полагая
t 2
Z
| S = L (q,q,t ˙ )dt. t 1 Принцип Гамильтона по-прежнему записывается в виде |
(13.15) |
| δS = 0, |
(13.16) |
однако на деформации и вариации необходимо наложить дополнительные условия согласованности со связями. Объясню это подробнее.
Пусть q (t ) — истинное движение системы. Определим его деформацию q ˜ = q ˜(t, ε), сохраняя прежние условия и добавляя к ним лишь требование совместности со связями (13.14):
Φ1 (q ˜(t, ε),t ) = 0, ..., Φr (q ˜(t, ε),t ) = 0 (13.17)
для всех t и малых ε. Напомню прежние требования к деформации q ˜(t, ε). Это должна быть гладкая вектор-функция от времени t (скажем, на некотором интервале, содержащем (t 1 ,t 2 )) и от ε в некоторой окрестности точки ε = 0 в R . При ε = 0 должно получаться истинное движение: q ˜(t, 0) = q (t ). Как обычно, в принципе Гамильтона начальное и конечное положения системы должны сохраняться:
q ˜(t 1 , ε) = q (t 1 ), q ˜(t 2 , ε) = q (t 2 ) (13.18)
для всех малых ε. Варьирование, вычисление вариации по-прежнему означает применение операции
![]() (13.19)
(13.19)
Равенство (13.16), так же, как и раньше, приводит к соотношению
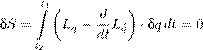 .
(13.20)
.
(13.20)
Теперь, однако, оно выполняется не для всех вариаций δq
, удовлетворяющих условиям ![]() , а лишь для вариаций δq
, удовлетворяющих дополнительным условиям, получаемым варьированием связей (13.14). Дифференцируя равенства (13.17) по ε при ε = 0, получаем эти условия в виде
, а лишь для вариаций δq
, удовлетворяющих дополнительным условиям, получаемым варьированием связей (13.14). Дифференцируя равенства (13.17) по ε при ε = 0, получаем эти условия в виде
grad Φj (q,t ) · δq = 0, j = 1,...,r. (13.21)
Поскольку t 1 и t 2 произвольны, из (13.20) следует равенство
![]() (13.22)
(13.22)
в каждый момент времени t . Равенства (13.21) говорят нам, что вариация δq ортогональна к подпространству Y , порождаемому векторами grad Φj ,
j
= 1,...,r
, а равенство (13.22) означает, что![]() ортогонально к δq
, а значит, лежит в подпространстве Y
. Поскольку векторы grad Φj
образуют базис в Y
, имеем
ортогонально к δq
, а значит, лежит в подпространстве Y
. Поскольку векторы grad Φj
образуют базис в Y
, имеем
![]() grad Φj
.
(13.23)
grad Φj
.
(13.23)
Здесь скалярные функции λj (t ), называемые множителями Лагранжа, суть коэффициенты в разложении по базису левой части уравнения (13.23). Мы получили уравнение движения в форме уравнений Лагранжа 1-го рода. Их нужно решать совместно с уравнениями связей (13.14).
Задача Коши для уравнений Лагранжа 1-го рода состоит в том, чтобы найти решение системы (13.14), (13.23) с начальными условиями
![]() .
(13.24)
.
(13.24)
Здесь следует иметь в виду, что начальная скорость q ˙0 должна быть подчинена условиям, налагаемым связями (13.14). Эти условия мы получим, подставляя q (t ) в (13.14) и дифференцируя по t при t = t 0 . Они имеют вид
![]() .
(13.25)
.
(13.25)
В частном случае натуральной системы с нулевой потенциальной энергией и кинетической энергией ![]() уравнения (13.23) совпадают с уравнениями (13.7). Уравнения 2-го рода, которые мы рассматривали раньше, получаются, когда нет связей. Сила принципа Гамильтона и вытекающих из него уравнений Лагранжа 2-го рода как раз в том и состоит, что их форма инвариантна, не зависит, по существу, от выбора координат. На практике, при переходе к новой системе координат, нужно лишь сделать соответствующую замену переменных в лагранжиане.
уравнения (13.23) совпадают с уравнениями (13.7). Уравнения 2-го рода, которые мы рассматривали раньше, получаются, когда нет связей. Сила принципа Гамильтона и вытекающих из него уравнений Лагранжа 2-го рода как раз в том и состоит, что их форма инвариантна, не зависит, по существу, от выбора координат. На практике, при переходе к новой системе координат, нужно лишь сделать соответствующую замену переменных в лагранжиане.
Замечу еще, что нередко нам удается исключить лишь часть наложенных на систему связей, так что может существовать много различных форм уравнений Лагранжа 1-го рода для движений одной и той же системы.
В заключение сформулируем принцип Гамильтона для систем со связями.
Для механической системы с лагранжианом L = L (q,q,t ˙ ), подчиненной идеальным голономным связям ( 13.14), действие по Гамильтону, определенное равенством ( 13.15), принимает экстремальное (при малых t 2 − t 1 — минимальное) значение для истинного движения, по сравнению с виртуальными движениями, подчиненными связям( 13.14)исохраняющиминачальноеиконечноеположениясистемы.
14. Принцип наименьшего действия Мопертюи
(Мопертюи–Эйлера–Лагранжа–Якоби)
Принцип Мопертюи, усовершенствованный Эйлером и Лагранжем и представленный в наиболее удобной форме Якоби, исторически был пер-
вым вариационным принципом механики. Как и принцип Гамильтона, он относится к классу интегральных вариационных принципов. Как и в случае принципа Гамильтона, речь в нем следует скорее вести об экстремуме, а минимум достигается лишь локально. Как и принцип Гамильтона, принцип Мопертюи благополучно пережил революцию в физике начала XX века. Пожалуй, он применяется реже, чем принцип Гамильтона. Вообще, скорее принцип Гамильтона, а не принцип Мопертюи, как полагал его автор, является всеобщим принципом физики. Оказалось, однако, что в теории относительности принцип Мопертюи, в отличие от принципа Гамильтона, способен описать движение фотонов — частиц нулевой массы покоя, движущихся со скоростью света. Хочется все же нарушить традицию, о которой писал Якоби (см. 10 с.), и попытаться дать ясное изложение этого принципа, который особенно тесно связывает классическую механику с дифференциальной геометрией и оптикой.
Здесь я ограничусь случаем натуральных механических систем. Будем рассматривать такую систему как материальную точку, движущуюся в евклидовом пространстве H = Rn ; фактически последующие рассмотрения, по крайней мере, на формальном уровне переносятся и на системы с бесконечным числом степеней свободы. Кинетическая энергия натуральной системы выражается в виде
![]() .
(14.1)
.
(14.1)
Здесь M — положительно определенный оператор, оператор инерции данной системы. Если в H = Rn зафиксировать естественный базис, то можно отождествлять линейные операторы с их матрицами и считать, что M = (mik )n i,k =1 . Тогда кинетическая энергия записывается в виде
![]() .
(14.2)
.
(14.2)
Вообще говоря, оператор M мог бы зависеть от x , как и матричные элементы mik . Нетрудно провести обобщение на случай M = M (x ), mik = mik (x ). Я, однако, предоставлю это читателю.
Будем также считать заданной потенциальную энергию V (x ). Тогда лагранжиан есть L = T − V , а H = T + V — полная энергия системы.
Поскольку в данном случае лагранжиан не зависит от времени, энергия H есть интеграл. Кажется естественным поэтому написать, что L = 2T −H , и ввести «укороченное действие» или действие по Мопертюи, полагая
t 2
Z
A = 2Tdt. (14.3)
t 1
Множитель 2, понятно, не существенен, но удобно его сохранить. Нужно еще уточнить выбор моментов времени t 1 и t 2 , что будет сделано ниже.
Пусть заданы точки x 1 и x 2 конфигурационного пространства H. Нас будут интересовать такие движения, то есть решения обобщенного уравнения второго закона Ньютона
Mx ¨ = −grad V (x ), (14.4)
которые начинаются в некоторый момент времени из положения x 1 (с не определенной заранее скоростью) и в некоторый момент времени (тоже заранее не определенный) приводят систему в положение x 2 . Объектом исследования являются однако, не движения сами по себе, а их траектории в конфигурационном пространстве H. Точнее говоря, это проекции фазовых траекторий в H2 на конфигурационное пространство H. Может быть, нелишне напомнить, что фазовая траектория в H2 есть “след движущейся точки” (x (t ),x ˙(t )) ∈ H2 , а соответствующая траектория в конфигурационном пространстве — след движущейся точки x (t ) ∈ H.
Будем предполагать еще, что значение интеграла энергии h фиксировано:
T + V = h (14.5)
Далее будем рассматривать гладкие кривые в конфигурационном пространстве H, соединяющие точки x 1 и x 2 . Такая кривая есть отображение x : [θ1 , θ2 ] → H : θ 7→ x (θ). Параметр θ изменяется на отрезке [θ1 , θ2 ], и при этом x (θ1 ) = x 1 и x (θ2 ) = x 2 .
Представим себе, что вдоль этой кривой происходит (виртуальное) движение, причем выполняется закон сохранения энергии (14.5). Кинетическая энергия виртуального движения принимает вид
![]() .
(14.6)
.
(14.6)
Из уравнений (14.5)–(14.6) выводим равенство
![]() .
(14.7)
.
(14.7)

Рис. 4
В знаменателе стоит x 0 = x 0 (θ(t )), штрих означает производную по θ.
Перед тем как извлекать квадратный корень, предположим, что параметр θ в виртуальном движении монотонно возрастает, так что θ ˙(t ) > 0 для всех t . Тогда из (14.7) следует скалярное дифференциальное уравнение
θ
˙ = Θ(θ),
![]() .
(14.8)
.
(14.8)
Теперь перейдем в действии по Мопертюи (14.3) от интегрирования по t к интегрированию по θ. Будем считать, что θ(t 1 ) = θ1 , а θ(t 2 ) = θ2 . Заметим, что момент t 1 можно выбирать произвольно, а момент t 2 должен быть определен из условия θ(t 2 ) = θ2 , или x (θ(t 2 )) = x 2 . В результате интеграл (14.3) принимает вид
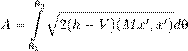 .
(14.9)
.
(14.9)
Подведем первые итоги. Равенство (14.9) определяет функционал, заданный на кривых x : θ 7→ x (θ) в конфигурационном пространстве H. Каждая такая кривая задана на сегменте [θ1 , θ2 ]. Можно было бы даже фиксировать этот отрезок и полагать, скажем, θ1 = 0, θ2 = 1. Функционал A называется действием по Мопертюи в форме Якоби . При переходе от выражения (14.3) к выражению (14.9) мы еще предполагали, что параметр θ в виртуальном движении изменяется со временем монотонно. Об этом предположении пока можно забыть, как и о самих виртуальных движениях. Мы о них еще вспомним, когда пойдет речь о восстановлении полной динамики в H2 (решения уравнения (14.4)) по найденной траектории в конфигурационном пространстве H.
Очевидно, для того чтобы выражение (14.9) имело смысл, на всей кривой θ 7→ x (θ) должно быть выполнено неравенство h − V (x (θ)) ≥ 0. Отсюда, в частности, следует, что в том случае, когда x 1 — точка строгого, хотя бы локального, минимума потенциальной энергии V (x ) (в этом случае x 1 — равновесие), должно быть выполнено условие h > V (x 1 ). Если h < V (x 1 ), то не существует кривых, на которых должен быть определен функционал A . Если же V (x 1 ) = h , то виртуальное движение не сможет выйти из точки x 1 . Аналогичное условие, конечно, должно выполняться и для точки x 2 , когда x 2 — равновесие: h > V (x 2 ). Вообще же возникает довольно тонкая проблема достижимости точки x 2 из точки x 1 при заданной энергии h . Обсуждение этой проблемы пока что отложим; замечу лишь, что она тесно связана с теорией запаса устойчивости равновесия, развитой А.Д. Мышкисом (см. книгу [4] и имеющиеся там ссылки, а также статью [59]).
Теперь мы, наконец, готовы сформулировать принцип Мопертюи.
Принцип стационарного действия Мопертюи–Эйлера–Лагранжа–Якоби
В конфигурационном пространстве H среди всех возможных (виртуальных) траекторий с фиксированной энергией h, соединяющих две точки x 1 и x 2 из H, истинная траектория доставляет действию A экстремальное значение. Когда точки x 1 и x 2 достаточно близки, этот экстремум есть минимум.
Принцип есть принцип, и его, говоря формально, не нужно доказывать. Убедимся, однако, в том, что он вполне согласуется с принципом Гамильтона и вытекающим из него уравнением Лагранжа (14.4).
Изменим обозначение вариации с δ на ∆, чтобы подчеркнуть, что на сей раз деформация и вариация неизохронны — одним и тем же значениям параметра θ отвечают различные, вообще говоря, моменты времени в виртуальных движениях. Впрочем, в данном принципе вообще нет речи о времени. Определяется вариация ∆x как обычно. Сначала вводим деформацию x e(θ, ε) истинной траектории x (θ), причем считаем выполненными условие x (θ, 0) = x (θ) для всех θ и граничные условия x e (θ1 , ε) = x 1 , e
x e(θ2 , ε) = x 2 . Тогда ∆x (θ) есть, по определению,
![]() .
(14.10)
.
(14.10)
Вычисляя вариацию A , получаем
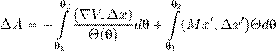 .
(14.11)
.
(14.11)
Разумеется, в принципе Мопертюи неявно предполагается существование виртуальных траекторий с заданной энергией h , соединяющих точки x 1 и x 2 . Интегрирование по частям во втором слагаемом приводит к равенству
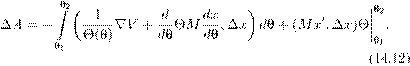
Варьирование краевых условий x e(θ1 , ε) = x 1 , x e (θ2 , ε) = x 2 дает равенства ∆x (θ1 ) = 0, ∆x (θ2 ) = 0. Поэтому внеинтегральный член в (14.12) исчезает. Согласно принципу Мопертюи, для истинной траектории ∆A = 0 и поэтому выполняется равенство
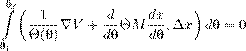 .
(14.13)
.
(14.13)
Стандартное для вариационного исчисления рассуждение, которое мы уже применяли при выводе уравнений Лагранжа из принципа Гамильтона, дает теперь уравнение истинной траектории в виде
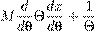 grad V
(x
) = 0.
(14.14)
grad V
(x
) = 0.
(14.14)
![]() Согласно терминологии вариационного исчисления, это уравнение называется уравнением Эйлера, отвечающим функционалу A
. Пусть теперь x
— решение уравнения движения (14.4). Предположим, что x
= x
(θ), θ1
≤ θ ≤ θ2
— отвечающая ему траектория в конфигурационном пространстве.
Согласно терминологии вариационного исчисления, это уравнение называется уравнением Эйлера, отвечающим функционалу A
. Пусть теперь x
— решение уравнения движения (14.4). Предположим, что x
= x
(θ), θ1
≤ θ ≤ θ2
— отвечающая ему траектория в конфигурационном пространстве.
![]()
![]()
![]()
![]() Чтобы по известной траектории x
(θ) восстановить движение x
(t
), достаточно знать закон движения θ = θ(t
) вдоль траектории. Тогда x
(t
) определяется равенством: x
(t
) = x
(θ(t
)). Если энергия h
, отвечающая данному движению x
(t
) задана, то θ(t
) можно определить при помощи интеграла энергии (14.5). Если предположить, что параметр θ при движении возрастает, так что θ
˙(t
) >
0, то для определения θ получается дифференциальное уравнение (14.8). Если в дифференциальном уравнении (14.4) сделать замену аргумента t
на θ, положив x
(t
) = x
(θ(t
)), то для x
(θ) получим дифференциальное уравнение
Чтобы по известной траектории x
(θ) восстановить движение x
(t
), достаточно знать закон движения θ = θ(t
) вдоль траектории. Тогда x
(t
) определяется равенством: x
(t
) = x
(θ(t
)). Если энергия h
, отвечающая данному движению x
(t
) задана, то θ(t
) можно определить при помощи интеграла энергии (14.5). Если предположить, что параметр θ при движении возрастает, так что θ
˙(t
) >
0, то для определения θ получается дифференциальное уравнение (14.8). Если в дифференциальном уравнении (14.4) сделать замену аргумента t
на θ, положив x
(t
) = x
(θ(t
)), то для x
(θ) получим дифференциальное уравнение
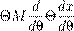 + grad V
(x
) = 0.
(14.15)
+ grad V
(x
) = 0.
(14.15)
Мы использовали здесь очевидное соотношение ![]() . Уравнение (14.15) эквивалентно уравнению (14.14) при сделанном предположении, что Θ(θ) >
0 при всех θ
∈ [θ1
,
θ1
].
. Уравнение (14.15) эквивалентно уравнению (14.14) при сделанном предположении, что Θ(θ) >
0 при всех θ
∈ [θ1
,
θ1
].
Принцип Мопертюи и геодезические на многообразии
Кинетическая энергия, а точнее, оператор масс M , как мы уже видели, определяет новую евклидову метрику на пространстве H: скалярное произведение (ξ, η)M = (M ξ, η). С точки зрения геометрии новое скалярное произведение определяет новый элемент длины ds по формуле
ds2 = (Mdx,dx) = (dx,dx)M . (14.16)
В геометрии правая часть носит название первойдифференциальнойформы . Форма (14.16) называется еще римановой метрикой , ее задание превращает H в риманово многообразие .
С использованием формулы (14.16), действие (14.9) можно записать в виде
![]() (14.17)
(14.17)
Параметр s имеет смысл длины дуги траектории x = x (s ). Конечно, эта длина связывается с определением (14.16). Снова, как мы видим, геометрия определяется распределением масс. Значения s 1 и s 2 задаются условиями x (s 1 ) = x 1 , x (s 2 ) = x 2 .
Действие в общей форме (14.17) также приобретает смысл длины траектории, если ввести еще одну риманову метрику, полагая
dS2 = 2(h − V (x))ds2 . (14.18)
Правда, эта метрика может иметь особые точки.
Самый простой случай представится, когда V (x ) = 0. Действие A принимает тогда вид
![]() (14.19)
(14.19)
√![]()
и лишьнесущественныммножителем 2h отличаетсяотдлинытраектории, соединяющей точки x 1 и x 2 и вычисленной в соответствии с M-метрикой.
Требование, чтобы эта длина была минимальна, или хотя бы экстремальна (стационарна), вытекающее из принципа Мопертюи ∆A = 0, принимает форму
∆(s 2 − s 1 ) = 0. (14.20)
В геометрии это равенство служит определением геодезической (линии). Это важный результат. Оказывается, классическая механика консервативных систем тождественна римановой дифференциальной геометрии.
Замечу, что и в общем случае действие по Мопертюи имеет смысл длины траектории, но вычисляемой согласно метрике (14.18).
Вернемся к исходному определению (14.3) действия по Мопертюи. В рассматриваемом сейчас случае, когда V = 0, кинетическая энергия T есть интеграл, так что T = h = const . Действие приобретает вид
t 2
Z
| A = 2h dt = 2h (t 2 − t 1 ). t 1 Принцип Мопертюи теперь приводит к равенству |
(14.21) |
| ∆(t 2 − t 1 ) = 0. |
(14.22) |
Это принцип Ферма: среди виртуальных траекторий, соединяющих точки x 1 и x 2 , так что x (t 1 ) = x 1 , x (t 2 ) = x 2 , истинная траектория выделяется требованием, чтобы время достижения конечной точки было минимально.
Пьер Ферма (1601–1665) сформулировал его в оптике в более общем случае неоднородной среды.
• П. Ферма — юрист и по совместительству великий математик, знал интегрирование и дифференцирование до Ньютона и Лейбница, а декартовы координаты и уравнения прямых, плоскостей и поверхностей второго порядка — до Декарта. Он научился находить максимумы и минимумы функций (помните теорему Ферма?). Весьма значительный вклад внес Ферма в физику, а также в теорию чисел. Многие открытые и доказанные им теоремы являются классическими. Знаменитая великая теорема Ферма (до сих пор неизвестно, доказал ли ее он сам) была предметом упорной и безрезультатной работы многих математиков в течение трех столетий, пока ее, наконец, завершая усилия многих ученых, не доказал английский математик Эндрью Уайлс (1995).
Преломление света. Закон Снеллиуса
Хотя еще Птолемей в II в. н. э. сделал довольно точные измерения углов падения и преломления луча света, проходящего через поверхность раздела между водой и воздухом, закон преломления света был открыт лишь в XVII веке Снеллиусом (1615) и носит его имя.
Голландский профессор Виллеброрд Снелл (1580–1626) не публиковал своих работ. Их разыскал Рене Декарт и опубликовал в 1637 году. Декарт предложил качественное и довольно туманное объяснение закона. Сейчас мы увидим, что закон Снеллиуса следует из принципа Ферма, который его впервые обосновал.
Предположим, что луч света выходит из точки A , преломляется в поверхности раздела двух сред и попадает в точку B , см. Рис. 5. Предположим, что в среде I скорость света есть v 1 , а v 2 — скорость света в среде II. Задача состоит в том, чтобы найти угол преломления β, если задан угол падения α.
Применим принцип наименьшего времени Ферма. Если путь, пройденный лучом от A до точки преломления O есть ` 1 , а его путь от точки O до B есть ` 2 , то время t , за которое луч проходит весь путь от A до B , определяется равенством
![]() .
(14.23)
.
(14.23)
Примем границу раздела за ось x , а точку преломления за начало декартовых координат. Пусть координаты точки A суть (−a, −h ), а точки B — (b,k ). Тогда справедливы соотношения:
| a = ` 1 sinα, h = ` 1 cosα, |
b = ` 2 sinβ, k = ` 2 cosβ. |
(14.24) |
![]() r B
r B
I
| r |
A
Точки A и B фиксированы, так что величины h и k заданы. Имеем равенства:
![]() .
(14.25)
.
(14.25)
С другой стороны, точка O не определена, как и величины a и b , лишь сумма a + b известна заранее. Справедливо равенство
` 1 sinα + ` 2 sinβ = a + b. (14.26)
Подстановка выражений (14.25) в это равенство дает соотношение
h tgα + k tgβ = a + b. (14.27)
Подстановка (14.25) в (14.23) дает выражение времени прохождения луча через углы α и β:
![]() .
(14.28)
.
(14.28)
Теперь нам нужно решить задачу об условном минимуме функции t = t (α, β) с условием связи (14.27). Варьирование дает соотношение:
![]() .
(14.29)
.
(14.29)
Варьирование уравнения связи (14.27) приводит к равенству
![]() .
(14.30)
.
(14.30)
Согласно принципу Ферма, δt = 0. С учетом формул (14.29), (14.30) отсюда выводим
![]() .
(14.31)
.
(14.31)
Это и есть закон Снеллиуса с конкретизацией правой части; сам Снеллиус нашел это соотношение экспериментально.
15. Применение принципа Гамильтона в механике сплошной среды
Принцип Гамильтона применим и к системам с бесконечным числом степеней свободы, каковыми являются сплошные среды — жидкости, газы, деформируемые твердые тела. Он также применим к различным физическим полям, например, к электромагнитному полю, в некотором формальном смысле это превращает электродинамику , а точнее — некоторую ее существенную часть, в раздел механики. Замечу, что уже при рассмотрении уравнения обобщенного второго закона Ньютона (11.18) размерность конфигурационного пространства не играла сколько-нибудь серьезной роли, наш вывод был по сути «безразмерным». Для физических теорий, однако, характерно, что лагранжианы, потенциальная энергия, кинетическая энергия, работа внешних сил и т.д. выражаются в виде интегралов по области, занятой сплошной средой. Введенные ранее понятия производной функционала и градиента функционала приобретают новые специфические черты, возникает интересное и важное понятие функциональной производной , которое ввел впервые Вито Вольтерра.
В этом разделе мы сначала в качестве примера выведем волновое уравнение из принципа Гамильтона. Уже в этом случае мы увидим дополнительную выгоду использования принципа Гамильтона в механике и физике сплошных сред: он не только приводит к уравнениям движения, но дает также вывод некоторых краевых условий. Такие краевые условия называются естественными. Обычно они возникают на разного рода свободных границах — свободных от внешних воздействий. Затем мы рассмотрим некоторые обобщения вместе с понятием функциональной производной. Завершается этот раздел рассмотрением конечномерных аппроксимаций бесконечномерных систем и важной роли принципа Гамильтона в построении таких аппроксимаций.
Волновое уравнение
Волновое уравнение является, пожалуй, наиболее непосредственным обобщением уравнения второго закона Ньютона на сплошную среду. С формальной стороны оно даже является частным случаем этого уравнения в гильбертовом пространстве. Самый существенный новый момент состоит в появлении неограниченных операторов. Именно по этой причине в теории нелинейных волновых уравнений остается немало белых пятен. Здесь я ограничу изложение формальным выводом.
Рассмотрим нелинейное дифференциальное уравнение в частных производных
![]() ,
(15.1)
,
(15.1)
которое должно выполняться при x ∈ D , t ∈ R. Область D ⊂ Rm будем считать ограниченной, а ее границу ∂D — гладкой. Здесь c — положительная постоянная, а γ — неотрицательная, при γ = 0 уравнение становится линейным. Функция f (x,t ) считается заданной и достаточно регулярной.
Предположим, что граница ∂D состоит из двух поверхностей S 1 и S 2 , причем на S 1 поставлено краевое условие первого рода, а на S 2 — условие второго рода:
![]() ,
,
![]() .
(15.2)
.
(15.2)
Здесь выбран довольно частный случай уравнения и краевых условий, чтобы на нем объяснить основные идеи. На самом деле, можно рассматривать гораздо более общие волновые уравнения и граничные условия, в частности, условия третьего рода, притом неоднородные.
Как известно, чтобы определить эволюцию, для уравнения второго порядка по времени нужно поставить пару начальных условий:
 .
(15.3)
.
(15.3)
Назовем u
(x,t
) перемещением, а ![]() — скоростью, хотя в приложениях
— скоростью, хотя в приложениях
∂t
u (x,t ) может иметь совсем другой физический смысл, в частности, электродинамический: например, напряженности электрического и магнитного полей удовлетворяют волновому уравнению, обычно линейному, но, возможно, и нелинейному.
Руководствуясь аналогией с уравнением второго закона Ньютона, введем следующие функционалы, которые будем называть соответственно кинетической и потенциальной энергиями:
![]() (15.4)
(15.4)
![]() (15.5)
(15.5)
Первое слагаемое в (15.5) есть внутренняя потенциальная энергия среды. Второе слагаемое описывает своего рода нелинейно-упругое взаимодействие данной сплошной среды с внешней средой, такого рода слагаемые возникают, например, когда рассматривается упругое тело на упругом основании, γ — соответствующий коэффициент жесткости. Наконец, последнее слагаемое в (15.5) есть потенциальная энергия, связанная с заданной внешней силой f .
Лагранжиан L определим равенством L = T − V , а действие по Гамильтону S — равенством (t 2 > t 1 , а в остальном t 1 и t 2 произвольны)
t 2
Z
S = Ldt. (15.6)
t 1
В более подробной записи
 (15.7)
(15.7)
Давно пора уточнить определения конфигурационного и фазового пространств данной системы. Вопрос этот не очень прост. Ясно, конечно, что конфигурационное пространство должно состоять из функций, заданных в области D с некоторыми условиями регулярности внутри области, а также и при подходе к границе ∂D . Однако выяснение правильных ограничений на дифференциальные свойства функций u (x,t ) и в данном случае, и вообще всякий раз, когда мы имеем дело с уравнениями в частных производных, — достаточно деликатное дело, и, во всяком случае, здесь нет однозначного ответа.
Для одного и того же уравнения в частных производных можно поразному выбирать конфигурационное и фазовое пространства. Первую ориентировку в этом вопросе дают нам выражения (15.4) и (15.5) для кинетической и потенциальной энергий, а также выражение (15.7) для действия S. Разумеется, нужно потребовать, чтобы все интегралы в этих выражениях сходились. Кроме того, нужно подчинить функцию u , принадлежащую конфигурационному пространству, по крайней мере, некоторым из краевых условий. На первый взгляд кажется естественным потребовать, чтобы функция u (x,t ) имела все производные, входящие в дифференциальное уравнение, то есть была C 2 -гладкой по x , t , а кроме того, удовлетворяла краевым условиям (15.2) в классическом смысле. Оказывается, однако, что такие классические решения начально-краевой задачи (15.1) – (15.3) далеко не всегда существуют, и далеко не всегда для них можно доказать единственность.
Будем пока считать, что конфигурационное пространство есть пространство![]() С.Л.Соболева, состоящее из функций, имеющих первые обобщенные производные
С.Л.Соболева, состоящее из функций, имеющих первые обобщенные производные![]() , интегрируемые с квадратом, то есть
, интегрируемые с квадратом, то есть![]() . Кроме того, предполагается, что эти функции удовлетворяют первому из краевых условий (15.2):
. Кроме того, предполагается, что эти функции удовлетворяют первому из краевых условий (15.2):
![]() .
(15.8)
.
(15.8)
Говоря точнее, пространство![]() есть замыкание множества гладких (если угодно, C
∞
-гладких) функций, определенных в области D
и удовлетворяющих условию (15.8) по норме, порождаемой скалярным произведением
есть замыкание множества гладких (если угодно, C
∞
-гладких) функций, определенных в области D
и удовлетворяющих условию (15.8) по норме, порождаемой скалярным произведением
Z
(u 1 ,u 2 ) = ∇u 1 (x ) · ∇u 2 (x )dx. (15.9)
D
◦
Если функция![]() непрерывна вплоть до границы, то она удовлетворяет условию (15.8) в обычном смысле. Вообще говоря, функции из
непрерывна вплоть до границы, то она удовлетворяет условию (15.8) в обычном смысле. Вообще говоря, функции из
![]() непрерывными не являются и краевое условие (15.8) удовлетворяется лишь в некотором обобщенном смысле [40].
непрерывными не являются и краевое условие (15.8) удовлетворяется лишь в некотором обобщенном смысле [40].
Функцию u
(x,t
) мы теперь представляем себе как вектор-функцию u
(t
)(x
) времени t
со значениями в пространстве![]() . Определение скалярного произведения (15.9) говорит нам, что
. Определение скалярного произведения (15.9) говорит нам, что![]() есть гильбертово пространство. Нужно еще потребовать, чтобы функция u
(x,t
) для каждого фиксированного t
принадлежала L
4
(D
); правда, при m
≤ 4 существование интеграла Z
есть гильбертово пространство. Нужно еще потребовать, чтобы функция u
(x,t
) для каждого фиксированного t
принадлежала L
4
(D
); правда, при m
≤ 4 существование интеграла Z
um dx (15.10)
D
следует из существования интеграла R (∇u )2 dx , согласно теореме вложе-
D
ния С.Л.Соболева.
Фазовым пространством будем считать декартово произведение![]()
L
2
(D
). Элементом этого пространства является пара функций (u
(x
),v
(x
)), причем![]() , последнее соответствует требованию, чтобы кинетическая энергия T
была конечна.
, последнее соответствует требованию, чтобы кинетическая энергия T
была конечна.
Приходится сразу признать, что дальнейший вывод волнового уравнения из принципа Гамильтона невозможно провести, строго придерживаясь сформулированных минимальных предположений о регулярности функции u . В ходе этого вывода мы будем считать ее, скажем, C ∞ -гладкой, хотя достаточно C 2 -гладкости по x и t .
Возникающий здесь логический разлад носит принципиальный характер. Дальше я постараюсь объяснить, каким образом здесь наводится порядок. Оказывается, нужно уточнить и изменить само понятие решения уравнений в частных производных.
Внимательный читатель заметил, по-видимому, что мы «забыли» о втором краевом условии (15.2). Далее будет показано, что это условие не надо вводить заранее — оно является следствием принципа Гамильтона.
Итак, принцип Гамильтона требует, чтобы действие, определенное равенством (15.7), на истинном движении было экстремально:
δS = 0. (15.11)
Как обычно, вариация δu определяется как производная от деформации
![]() ,
(15.12)
,
(15.12)
при этом деформация u ˜(x,t, ε) зависит от параметра деформации ε гладко, ε изменяется в некоторой окрестности нуля. Для всех малых ε и для любого t деформация есть достаточно гладкая функция от x, t , удовлетворяющая краевому условию первого рода
![]() .
(15.13)
.
(15.13)
Кроме того, должно выполняться равенство u ˜(x,t, 0) = u (x,t ) и, как обычно в принципе Гамильтона, должно быть выполнено «условие неподвижности концов»:
u ˜(x,t 1 , ε) = u (x,t 1 ), u ˜(x,t 2 , ε) = u (x,t 2 ) (15.14) при любом малом ε. Соответственно для вариации получаем
δu (x,t 1 ) = 0, δu (x,t 2 ) = 0. (15.15)
Замечу, что именно требование гладкости деформации как раз и вносит тот логический разлад, о котором я упоминал.
Дальше — формальные выкладки. Вычисляя вариацию, находим
t 2
Z Z
δS = (ut δut − c 2 ∇u · ∇δu − γu 3 δu + f δu )dxdt. (15.16) t 1 D
Посредством интегрирования по частям перебросим производные по t
и по xi
с δu
на соответствующие множители. Учитывая равенства (15.15) и краевое условие ![]() , следующее из (15.13), преобразуем (15.16), и, подставляя полученное выражение в (15.11), придем к равенству
, следующее из (15.13), преобразуем (15.16), и, подставляя полученное выражение в (15.11), придем к равенству
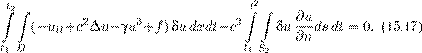
Вариация δu исчезает при t = t 1 и t = t 2 . Можно, однако, считать, что она исчезает и в полуокрестностях этих точек на [t 1 ,t 2 ]. Тогда она теряет зависимость от t 2 , и дифференцирование по t 2 дает равенство
![]() ,
(15.18)
,
(15.18)
которое должно выполняться в любой момент t (непосредственно получается в момент t 2 , но он произволен).
На поверхности S 2 вариация δu не обязана удовлетворять каким-либо краевым условиям. Если, однако, рассмотреть такие вариации, которые исчезают в окрестности границы ∂D , то мы избавимся от поверхностного интеграла в (15.18):
Z
| (−utt + c 2 ∆u − γu 3 + f )δudx = 0. D |
(15.19) |
Согласно лемме на стр. 71, из этого равенства следует, что для всех x ∈ D и t ∈ R выполняется уравнение
utt = c2 ∆u − γu3 + f(x,t). (15.20)
Теперь вернемся к равенству (15.18) для произвольных допустимых вариаций δu . В силу (15.20) объемный интеграл исчезает, и получается равенство
![]() .
(15.21)
.
(15.21)
Еще раз повторю: δu
на S
2
можно выбирать произвольно, лишь бы существовала гладкая функция η(x
) такая, что ![]() . В предположении достаточной гладкости поверхности S
2
и функции
. В предположении достаточной гладкости поверхности S
2
и функции ![]() , такую функцию η, называемую продолжением
функции δu
на границе, построить можно. Теоремы о возможности таких продолжений известны [44, 27], хотя, к сожалению, не излагаются в курсе анализа.
, такую функцию η, называемую продолжением
функции δu
на границе, построить можно. Теоремы о возможности таких продолжений известны [44, 27], хотя, к сожалению, не излагаются в курсе анализа.
Если положить в (15.21) ![]() , то получим
, то получим
![]() .
(15.22)
.
(15.22)
а значит,![]() . Мы вывели из принципа Гамильтона краевое условие на S
2
. Такие краевые условия, которые первоначально не постулируются, но получаются из условия экстремума функционала, называются в вариационном исчислении естественными
.
. Мы вывели из принципа Гамильтона краевое условие на S
2
. Такие краевые условия, которые первоначально не постулируются, но получаются из условия экстремума функционала, называются в вариационном исчислении естественными
.
Обобщенные решения
При выводе волнового уравнения из принципа Гамильтона мы были вынуждены наложить на (неизвестное!) решение дополнительные и ниоткуда не вытекающие ограничения гладкости. Когда речь идет о динамических системах с конечным числом степеней свободы, тоже приходится налагать подобные условия. Однако там это не носит принципиального характера, поскольку, получив решение, удается доказать, что оно и в самом деле обладает нужной гладкостью (это делается с помощью известной леммы Дюбуа–Реймона в вариационном исчислении). Когда же речь идет об уравнениях в частных производных, вопрос о гладкости решения всегда принципиален. Классическое решение — такое, для которого и уравнение, и краевые и начальные условия выполняются в обычном смысле, — далеко не всегда существует. Для уравнений гиперболического типа, каковым является волновое уравнение, проблема существования классического решения сложна в принципе, поскольку возможно, что в условиях очень гладких данных (коэффициентов уравнения, границы области, граничных и начальных функций) решение оказывается нерегулярным — его производные, а то и оно само, претерпевают разного рода разрывы.
В современной математической физике само понятие решения начальнокраевой задачи существенно изменено по сравнению с классическим. Рассматриваются различного рода обобщенные решения . Один из наиболее оправданных физических подходов к определению обобщенного решения основывается на принципе Гамильтона. Принцип Гамильтона не менее, а даже более фундаментален, чем уравнения Лагранжа второго рода. Вместе с тем, формулировка принципа Гамильтона не требует дополнительных предположений о гладкости решения, нужны лишь такие предположения о регулярности, которые обеспечивают существование интегралов, входящих в определение действия.
В рассматриваемом случае начально-краевой задачи (15.1)–(15.3) определение обобщенного решения основывается фактически на равенстве (15.11): δS = 0, причем δS выражается формулой (15.16) посредством интегрирования по частям.
По своему существу принцип Гамильтона не связан с конкретными начальными условиями и в регулярном случае является эквивалентом уравнения движения. Примем и здесь такую точку зрения, сделаем лишь некоторые непринципиальные упрощения. Во-первых, договоримся всегда выбирать t 1 = 0. Далее будем полагать t 2 = τ > 0 и интересоваться решением на отрезке времени [0, τ]. При этом мы ничего не теряем, так как τ — произвольно фиксировано, а если отрезок [t 1 ,t 2 ] содержится в [0, τ], мы получим прежнее определение, попросту выбирая δu так, чтобы δu (x,t ) = 0 для всех t вне [t 1 ,t 2 ]. Наконец, вместо δu (x,t ) будем для краткости писать η(x,t ).
Теперь перейдем к строгому определению обобщенного решения.
Определение. Обобщенным решением начально-краевой задачи (15.1)– (15.3) на отрезке времени [0, τ] при любом положительном τ называется функция u (x,t ) такая, что выполнены следующие условия:
1) Для любого t ∈ [0, τ] существуют и равномерно ограничены интегралы
![]() Z
Z
, (∇u (x,t ))2 dx ≤ C 2 ,
D (15.23)
где C 1 , C 2 , C 3 — положительные константы.
2)
Для любого
t
∈ [0,
τ] функция
u
(x,t
) удовлетворяет в обобщенном смысле краевому условию
![]() , а именно
, а именно
![]()
![]() 3) (принцип Гамильтона) Выполняется интегральное равенство (тождество):
3) (принцип Гамильтона) Выполняется интегральное равенство (тождество):
![]() (15.24)
(15.24)
для любой гладкой функции
η(x,t
) такой, что
η(x,
0) = 0,
η(x,
τ) = 0, и выполнено краевое условие
![]() .
.
4) Функция u (x,t ) удовлетворяет начальным условиям в обобщенном смысле (в среднем) при t → +0
![]() ,
,
(15.25)
Несколько комментариев к этому определению. При выводе волнового уравнения из принципа Гамильтона мы фактически установили, что если обобщенное решение имеет непрерывные вторые производные по x и по t , то оно удовлетворяет волновому уравнению в обычном смысле. Если к тому же сама функция и ее нормальная производная допускают определение на границе ∂D посредством предельного перехода («по непрерыввности»), то и краевые условия выполняются в обычном смысле. Выходит, что функция, удовлетворяющая условиям данного определения, оказывается классическим решением начально-краевой задачи при одном лишь дополнительном условии достаточной гладкости. Именно это и дает нам право называть ее обобщенным решением .
Мы рассматривали решение u (x,t ) для положительных времен. В случае t < 0 все аналогично. Более того, замена t → −t приводит этот случай к предыдущему.
Нетрудно проверить, что из предположения о конечности интегралов (15.23) следует, что все интегралы в интегральном тождестве (15.24) сходятся. Относительно заданной функции f достаточно предположить, что она «не чересчур разрывна», например, интегрируема с квадратом по x, t .
В определении мы предположили, что функция η гладкая. При помощи предельного перехода можно убедиться, что это тождество остается в силе и для широкого класса разрывных функций η. Например достаточно, чтобы
∂ η ∂ η
![]() производные и имели интегрируемые по x, t
квадраты.
производные и имели интегрируемые по x, t
квадраты.
∂t ∂xi
Важность применения обобщенных решений уравнений в частных производных была осознана лишь в середине прошлого века. Даже когда классическое решение существует, естественным этапом исследования оказывается доказательство существования обобщенного решения. Долгая и упорная работа математиков в этой области привела к наиболее глубоким результата в теории функций и функциональном анализе. К сожалению, здесь нет места остановиться на этом более подробно. Замечу, что одна из первых работ по обобщенным решениям волновых уравнений была выполнена И.И. Воровичем [8], который рассматривал сложные задачи о колебаниях упругих оболочек.
Функциональные производные
В том случае, когда функционалы заданы на гильбертовом пространстве функций, скажем, на пространстве L 2 (D ), понятие градиента grad ϕ может быть существенным образом конкретизировано. Соответствующее определение строится по аналогии с понятиями дифференциала и частных производных гладкой функции f (x ), x ∈ Rn . Как Вам хорошо известно, главная линейная часть приращения функции, когда ее аргумент x = (x 1 ,...,xn ) получает приращение (dx 1 ,...,dxn ), есть
![]() .
(15.26)
.
(15.26)
Это равенство может служить определением частной производной![]() .
.
Пусть теперь Φ : L 2 (D ) → R — функционал на гильбертовом пространстве L 2 (D ), где D — область в Rn . Допустимо рассматривать функционалы, заданные не на всем пространстве L 2 , а лишь на некотором всюду плотном линейном многообразии, дальше будем считать, что вводимые нами функции принадлежат области определения D(Φ) функционала Φ. Пусть теперь u ∈ D(Φ), и εδu — приращение функции u . Рассмотрим приращение Φ(u +εδu )−Φ(u ) функционала Φ. Мы рассматриваем частный случай деформации — линейной по параметру ε. Тогда производная по ε при ε = 0 дает нам вариацию функционала Φ в точке u
![]() .
(15.27)
.
(15.27)
Предположим, что эта вариация может быть представлена в виде
Z
δΦ(u ) = A (x )δu (x )dx. (15.28)
D
Разумеется, функция A (x ) вполне может довольно сложным образом зависеть от функции u — от всех ее значений, а не только от значения в точке x . В этом случае скажем, что A (x ) есть функциональная производная функционала Φ по аргументу u (x ), и введем обозначение:
![]() .
(15.29)
.
(15.29)
Обычно это обозначение сокращают и пишут
![]() .
(15.30)
.
(15.30)
Чтобы лучше пояснить аналогию между формулой (15.26) для df (x ) и формулой (15.28) для δΦ(u ), замечу, что вектор x = (x 1 ,...,xn ) можно рассматривать как функцию x (k ), определенную для k ∈ {1,...,n }, при этом попросту x (k ) = xk . С другой стороны, функцию u , заданную на D , можно трактовать как вектор, с бесконечным числом компонент, каждая из которых есть ux = u (x ), точка x ∈ D играет роль индекса. Формула (15.28) получается из формулы (15.26) в результате замен: f → Φ, x → u ,
n
f
(x
) → Φ(u
), и далее:![]() . Кроме того, ко-
. Кроме того, ко-
нечно, нужно сделать замены: df (x ) → δΦ(u ), dxk → δu (x ). Проделайте все эти замены в формуле (15.26). Получится формула (15.28).
Приведу примеры вычисления функциональной производной. Пример 1. Пусть
Z
Φ(u ) = F (u (x ),x )dx (15.31)
D
с гладкой функцией F . Тогда очевидно,
![]() .
(15.32)
.
(15.32)
Если, например F (u,x ) = ρ(x )u 2m +1 , m — натуральное число, то
![]() .
(15.33)
.
(15.33)
Пример 2. На плотном в L 2 (D ) множестве гладких функций, исчезающих на границе, определим функционал (интеграл Дирихле)
Z
Φ(u ) = (∇u )2 dx. (15.34)
D Имеем Z
δΦ(u ) = 2 (∇u ) · ∇δudx. (15.35)
D
Интегрируя по частям, с учетом краевого условия ![]() , выводим
, выводим
Z
δΦ(u ) = −2 ∆u · δudx. (15.36)
D
Следовательно,
![]() .
(15.37)
.
(15.37)
Обобщенное волновое уравнение
Не стремясь довести обобщение до крайности, рассмотрим континуальную механическую систему, определенную лагранжианом
![]() (15.38)
(15.38)
где ρ и F — известные функции своих аргументов. Будем считать, что область D ограничена, а на ее границе поставлено условие
![]() .
(15.39)
.
(15.39)
Применяя принцип Гамильтона, в предположении существования и гладкости функции u (x,t ), реализующей экстремум действия, придем к равенству
![]() .
(15.40)
.
(15.40)
Интегрируя по частям, с учетом краевого условия ![]() , получаем
, получаем
![]() .
(15.41)
.
(15.41)
Отсюда следует уравнение движения
![]() .
(15.42)
.
(15.42)
Это уравнение, применяя понятие функциональной производной, можно записать в форме, вполне аналогичной конечномерному случаю, а именно:
![]() .
(15.43)
.
(15.43)
Замечу, что подобным формальным путем можно получить уравнения типа utt + ∆u = 0, для которых задача с начальными данными некорректна. Чтобы уравнение (15.43) было действительно волновым, нужно наложить определенное условие эллиптичности на функцию F .
16 Принцип Гамильтона и конечномерные аппроксимации
бесконечномерных систем 129
![]()
Упражнения
1. Выведите из принципа Гамильтона уравнение поперечных колебанийупругой оболочки utt = −c 2 ∆2 u + f (x,t ),
где u = u (x 1 ,x 2 ,t ), а точка (x 1 ,x 2 ) ∈ S (ограниченной области R2 ). На границе ∂S = Γ должны выполняться краевые условия
![]() ,
,
![]() .
.
Эти краевые условия не являются естественными. А какие являются?
2. Докажите, что полная энергия T + V , где T и V определены формулами (15.4), (15.5), есть интеграл волнового уравнения (15.1).
16. Принцип Гамильтона и конечномерные аппроксимации бесконечномерных систем
Чтобы решить эволюционную задачу для бесконечномерной системы при помощи численных методов, ее приходится аппроксимировать конечномерными системами. Применяемые для этого методы дискретизации в основном сводятся к замене производных разностными отношениями значений функции в узлах, либо к аппроксимации решения конечными отрезками рядов Фурье по тому или иному базису. Первый подход приводит к различным сеточным методам, а второй — к методу Галеркина. Бывают полезны и различные комбинации этих двух методов. Мы рассмотрим здесь такие аппроксимации, которые сохраняют производные по времени, так что задача приводится к решению систем обыкновенных дифференциальных уравнений, иногда очень высокого порядка.
Конечно, решая численно задачу для уравнения в частных производных, нужно заботиться о хорошей аппроксимации неизвестной функции и ее производных. Однако зачастую даже более важно, чтобы аппроксимирующие системы сохраняли фундаментальные свойства исходной системы. Когда заданная система получается из принципа Гамильтона, очень важно, чтобы это свойство сохранялось и для приближенных систем. В итоге возникает очень полезная в построении численных, а также асимптотических методов идея: аппроксимировать не заданные уравнения, а лагранжиан . После этого аппроксимирующее уравнение получается из принципа Гамильтона. Я приведу здесь два простеньких примера применения этой идеи.
Разностный метод решения волновых уравнений
Рассмотрим одномерное линейное волновое уравнение
ρ(x )utt = uxx (16.1)
с краевыми условиями
![]() .
(16.2)
.
(16.2)
При этом функция ρ(x ) предполагается непрерывной и положительной: ρ(x ) > 0 для всех x . Поставим также начальные условия:
![]() .
(16.3)
.
(16.3)
Мы уже знаем, что эта задача получается из принципа Гамильтона с лагранжианом
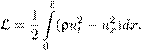 (16.4)
(16.4)
Будем решать начально-краевую задачу (16.1)–(16.3) методом прямых.
Разделим отрезок [0,`
] на n
равных частей, и пусть h
![]() , k
= 0,
1,...,n
. За новые неизвестные примем приближенные значения функции u
(x,t
) в узлах xk
, так что uk
(t
) ∼
= u
(xk
,t
). Чтобы аппроксимировать лагранжиан (16.4), примем некоторую аппроксимацию производной ux
, например, положим
, k
= 0,
1,...,n
. За новые неизвестные примем приближенные значения функции u
(x,t
) в узлах xk
, так что uk
(t
) ∼
= u
(xk
,t
). Чтобы аппроксимировать лагранжиан (16.4), примем некоторую аппроксимацию производной ux
, например, положим
![]() .
(16.5)
.
(16.5)
Краевым условиям мы удовлетворим, полагая u 0 = 0 и un = 0. Выберем некоторую квадратурную формулу для аппроксимации интеграла (16.4), например, формулу прямоугольников (или трапеций). Тогда приближенный лагранжиан будет иметь вид
![]() ,
,
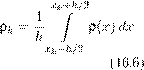
Соответствующие этому лагранжиану уравнения Лагранжа второго рода имеют вид
![]() .
(16.7)
.
(16.7)
В подробной записи имеем систему
![]() .
(16.8)
.
(16.8)
Здесь не нужно суммировать по k , хотя индексы повторяются, и нужно помнить, что u 0 = 0, un = 0. Как видим, в правой части само собой возникло стандартное разностное отношение, аппроксимирующее вторую производную uxx . Выходит, что эта наиболее популярная разностная схема получается из принципа Гамильтона.
Принцип Гамильтона и метод Галеркина
Метод Галеркина в его нестационарном варианте (иногда называемый также методом Галеркина – Фаэдо) особенно хорошо связан с принципом Гамильтона. На самом деле, стандартные галеркинские уравнения сохраняют свойство консервативности исходной системы и подчиняются принципу Гамильтона. Вместе с тем, применение принципа Гамильтона позволяет ускорить вывод галеркинских уравнений. Это я теперь и собираюсь продемонстрировать на примере начально-краевой задачи (15.1) – (15.3). Для упрощения разговоров давайте считать, что на всей границе ∂D области D выполнено краевое условие первого рода (S 1 = ∂D )
![]() .
(16.9)
.
(16.9)
Решение уравнения (15.1) разыскивается в виде обобщенного ряда Фурье:
∞ u (x,t ) = X uk (t )ϕk (x ), (16.10)
k =1
где ϕk
— гладкие функции, которые удовлетворяют краевому условию ![]() и образуют полную систему в пространстве
и образуют полную систему в пространстве![]() . В теории, а во многих случаях и на практике, удобно в качестве координатных функций
ϕk
выбирать собственные функции оператора Лапласа. Они определяются посредством решения спектральной краевой задачи
. В теории, а во многих случаях и на практике, удобно в качестве координатных функций
ϕk
выбирать собственные функции оператора Лапласа. Они определяются посредством решения спектральной краевой задачи
![]() .
(16.11)
.
(16.11)
Известно, что все собственные значения λk положительны, собственные
◦
функции ϕk образуют ортогональную систему как в L 2 (D ), так и в W
![]() , и при этом λk
→ +∞ при k
→ +∞. Для определенности нормируем собственные функции ϕk
в L
2
(D
), т.е. будем считать выполненными равенства:
, и при этом λk
→ +∞ при k
→ +∞. Для определенности нормируем собственные функции ϕk
в L
2
(D
), т.е. будем считать выполненными равенства:
Z
2
ϕk dx = 1, k = 1, 2,... (16.12)
D
Конечно, вместе с функцией ϕk , также и −ϕk удовлетворяет этому условию. Считаем, что из этих двух функций произвольно выбрана одна. Подставив выражение (16.10) в уравнение (15.1) и приравняв коэффициенты Фурье в левой и правой частях, можно получить бесконечную систему обыкновенных дифференциальных уравнений для неизвестных функций uk (t ). Идея метода Галеркина состоит в том, что эта бесконечная система урезается: оставляются лишь уравнения для u 1 (t ),...,um (t ), причем в этих уравнениях все высшие коэффициенты um +1 ,um +2 ,... полагаются равными нулю. Выходит, что приближенное решение имеет вид
m
um (x,t ) = X uk (t )ϕk (x ). (16.13)
k =1
Следуя высказанной выше идее, мы должны вычислить приближенные кинетическую энергию Tm и потенциальную энергию Vm , подставляя um (x,t ) вместо u (x,t ) в (15.4) и (15.5). Затем определяется приближенный лагранжиан Lm как функция от обобщенных координат u 1 ,...,um — и пишется уравнение Лагранжа второго рода, вытекающее из принципа Гамильтона в случае лагранжиана Lm .
Дальше мы применяем свойства ортогональности системы {ϕk } в L 2 и
◦ (1)
W 2 :
Z Z
ϕk ϕl dx = δkl , ∇ϕk · ∇ϕl dx = λk δkl , (16.14)
D D
где δkl — символ Кронекера. Имеем
![]() .
(16.15)
.
(16.15)
Далее получаем
![]() (16.16)
(16.16)
.
Здесь известные коэффициенты ck 1 k 2 k 3 k 4 и fk определяются равенствами
Z
| c k 1 k 2 k 3 k 4 = ϕk 1 ϕk 2 ϕk 3 ϕk 4 dx, D |
(16.17) |
| Z fk (t ) = f ϕk dx. |
(16.18) |
D ∞
При этом очевидно, что f (x,t ) = P fk (t )ϕk (x ), так что fk — коэффи-
k =1
циент Фурье функции f .
Поясню вычисление слагаемого четвертой степени в (16.16). Здесь применяется простой технический прием — представление четвертой степени суммы в виде четырехкратной суммы:
![]() .
.
(16.19) Интегрируя это равенство по x , приходим к выражению для коэффициента, данному в (16.17).
Уравнения Лагранжа, отвечающие лагранжиану Lm = Tm −Vm , имеют вид
![]() (16.20)
(16.20)
Учитывая выражения (16.15) и (16.16) для Tm и Vm , получаем систему обыкновенных дифференциальных уравнений:
![]() ,
(16.21) k
= 1,
2,...,m.
,
(16.21) k
= 1,
2,...,m.
Если здесь взять m = ∞, то получится бесконечная система, эквивалентная исходной краевой задаче. Я предоставляю вам самостоятельно проверить, что метод Галеркина в стандартной форме приводит к той же системе (16.21).
В принципе, метод Галеркина является весьма общим, он применим и в случае неконсервативных систем — когда сила не может быть определена посредством ее потенциальной энергии (потенциальную энергию вообще невозможно определить). Впрочем, известны и соответствующие неголономные обобщения принципа Гамильтона, в которых уже нет функционала действия, но постулируются соотношения для вариаций, из которых вытекают уравнения движения.
По-видимому, использование приближенных методов типа метода Галеркина и метода сеток является самым мощным средством доказательства теорем существования и единственности решения для начально-краевых задач механики и физики сплошных сред. В частности, галеркинские уравнения типа уравнений (16.21) содержат лишь полиномиальные нелинейности, так что их правые части оказываются гладкими. Теорема единственности решения и теорема о локальной разрешимости задачи Коши для таких уравнений непосредственно следуют из классических результатов. Вместе с тем, сохраняя консервативную природу исходной задачи, эти уравнения обладают интегралом энергии, а иногда и другими интегралами. Это дает возможность во многих случаях, и в частности для системы (16.21) (см. упражнение 5), получить априорную оценку решения, а вместе с тем, и глобальную теорему существования решения задачи Коши.
Обоснование приближенного метода, скажем, метода Галеркина состоит в доказательстве сходимости последовательности приближенных решений при m → ∞. Это действительно удается сделать с использованием современных средств функционального анализа и теории функций вещественных переменных. Замечу, что во многих случаях, особенно в стационарных задачах, удается установить лишь компактность множества приближенных решений. Случается, что различные последовательности приближенных решений сходятся к различным решениям краевой задачи для уравнений в частных производных. Здесь нет ничего удивительного — многие нелинейные стационарные краевые задачи действительно допускают несколько решений. К сожалению, здесь нет места остановиться на этих увлекательных вопросах подробнее (см. [22]).
Упражнения
1. Доказать, что уравнение движения, отвечающее кинетической энергии T и потенциальной энергии V вида
![]()
имеет вид
![]() ,
,
где
Убедитесь в том, что в случае
![]()
это уравнение превращается в уравнение (15.1). 2. Рассмотрим волновое уравнение
u tt = c 2∆u
в ограниченной области D ⊂ Rn с краевым условием третьего рода
![]() .
.
Докажите, что это уравнение имеет интеграл
![]()
3. Докажите, что уравнение малых поперечных колебаний упругой пластины
utt = −k ∆2 u,
например, с краевыми условиями
![]() ,
,
![]()
может быть получено из принципа Гамильтона, если определить потенциальную энергию равенством
![]()
4. Докажите, что в случае Φ(u ) = R ρ(x )|u (x )|α dx при α > 1 и регуD
лярной функции ρ(x ) функциональная производная имеет вид
![]()
5. Докажите, что галеркинская система (16.21) обладает интеграломэнергии
Em = Tm + Vm .
Пользуясь этим, докажите, что задача Коши для данной системы глобально разрешима для положительных t .
17. Динамика гибкой нерастяжимой нити
Специфические, очень интересные, широко применяемые на практике и во многом таинственные в теории динамические системы со связями возникают в механике сплошной среды. Среди них наиболее важные — несжимаемая жидкость и гибкая нерастяжимая нить . Сейчас мы применим принцип Гамильтона для систем со связями, обобщив его на системы с бесконечным числом степеней свободы, каковой является нить, и выведем уравнение движения нити. Сразу скажу, что наш вывод будет во многом формальным (хотя и гораздо более строгим, чем в обычных книгах по механике). Мы увидим, какие нужно ставить краевые условия. В частности, будет найдено естественное краевое условие, которое «возникает само собой» из принципа Гамильтона.
Начинать следует с определения положения системы, а затем определить конфигурационное и фазовое пространства. Физики говорят, что
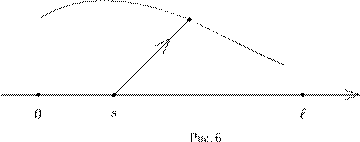 x
(s,t
)
x
(s,t
)
нить — это деформируемое твердое тело, у которого один из размеров много больше двух других. Конечно, это скорее относится к области применимости той математической модели, которую мы собираемся построить. Ясно, что необходимо иметь хотя бы интуитивное представление о том объекте, который мы стремимся описать при помощи математики.
Нить есть одномерная сплошная среда , другие одномерные сплошные среды — стержни, балки (в простейшем варианте, когда не учитывается их толщина), струйки пыли (одномерные пылевые среды ).
Представим себе, что фиксировано стандартное состояние нити — отрезок [0,` ] на вещественной оси, ` — длина нити. С точки зрения механики, мы рассматриваем недеформированное состояние нити. Но лучше понимать его абстрактно — не интересоваться поначалу, как эта недеформированная нить вложена в пространство, в котором происходит движение реальной нити.
Положение нити в данный момент t есть отображение x : [0,` ] → R 3 (см. Рис. 6). Технически удобно считать, что точка на отрезке [0,` ] задается своей декартовой координатой s . Мы сейчас имеем дело с нитью в пространстве R 3 , иногда интересно рассматривать нить в Rn или на некотором подмногообразии в Rn , а то и на произвольном многообразии.
Условие нерастяжимости нити означает, что не только ее полная длина ` не меняется в ходе движения, но и длина каждой ее дуги между s 1 и s 2 также не может меняться. Это можно записать в дифференциальной форме, для квадратов элементов длины: dx 2 = ds 2 . Замечая, что dx 2 = x 02 ds 2 , запишем условие нерастяжимости нити в виде
x 02 = 1. (17.1)
Здесь x 0 = x 0 (s,t ) — производная по s от x . Заметим, что x = (x 1 ,x 2 ,x 3 ) ∈ R 3 . Соотношение (17.1) далее трактуется как уравнение идеальной стационарной связи.
Итак, положение нерастяжимой нити есть отображение x : [0,` ] → R 3 , удовлетворяющее уравнению ( 17.1). Если ничего больше не добавлять, получится, что мы рассматриваем нить со свободными концами. В случае, когда конец нити (скажем, левый s = 0) закреплен или совершает движение по заданному закону, нужно еще поставить дополнительное условие
![]() ,
(17.2)
,
(17.2)
где x 0 (t ) — заданный закон движения этого конца. В случае, когда x 0 (t ) = a , т.е. положение не зависит от времени, выходит, что конец нити зафиксирован в точке a . Условие (17.2) также можно трактовать как идеальную связь. Это, конечно, означает, что мы пренебрегаем трением в точке закрепления нити.
Для определенности дальше будем рассматривать нить, у которой левый конец двигается по заданному закону, а правый — свободен. В этом случае условие (17.2) следует включить в определение конфигурационного пространства.
Нить — натуральная механическая система, её лагранжиан есть разность между кинетической энергией T и потенциальной энергией V :
L = T − V. (17.3)
Чтобы определить кинетическую энергию, нужно задать линейную плотность ρ(s ). Тогда
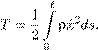 (17.4)
(17.4)
В более общей ситуации имеется функция распределения µ = µ(s ) массы вдоль нити. Функция µ(s ) есть масса отрезка нити [0,s ). Тогда кинетическая энергия задается интегралом Стилтьеса
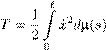 .
(17.5)
.
(17.5)
В том случае, когда функция µ(s ) непрерывно дифференцируема (или хотя бы абсолютно непрерывна), выражение (17.5) переходит в (17.4), причем ρ(s ) = µ 0 (s ). Дальше будем считать что кинетическая энергия выражается формулой (17.4).
Потенциальную энергию одномерной сплошной среды, которая двигается в R 3 , вообще говоря, можно подразделить на внутреннюю и внешнюю. Модель абсолютно гибкой нити строится на предположении, что внутренняя потенциальная энергия Vi = 0. В общей ситуации приходится учитывать как потенциальную энергию сжатия (её сейчас нет, потому что нить несжимаема), так и потенциальную энергию изгиба — тогда получаются различные модели упругого стержня или балки .
Внешняя потенциальная энергия создается внешними силами, действующими на нить. Если, например, нить находится в поле силы тяжести, то гравитационная потенциальная энергия задается формулой
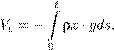 (17.6)
(17.6)
где g — вектор ускорения силы тяжести. Предполагая, что кроме силы тяжести, нет иных внешних сил, мы можем записать лагранжиан абсолютно гибкой нити в виде (17.3), где T дается формулой (17.4), а V = Ve — формулой (17.6). Действие тогда записывается в форме
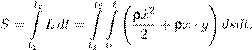 (17.7)
(17.7)
Теперь перейдем к применению принципа Гамильтона (δS = 0), с учетом связи (17.1) (точнее, бесконечного множества связей (17.1)).
Итак, пусть x = x (s,t ) — истинное движение. Рассмотрим его деформацию x ˜ = x ˜(s,t, ε), определенную для ε ∈ (−ε0 , ε0 ), ε0 > 0; величина ε0 далее нигде не фигурирует, так что достаточно сказать, что ε изменяется в некоторой окрестности нуля. При этом мы предполагаем, что отображение x ˜ : (s,t, ε) →7 x ˜(s,t, ε) обладает некоторой гладкостью, достаточной для следующих преобразований. Если угодно, можно считать сначала, что x ˜ ∈ C ∞ , а затем уточнить, сколько производных на самом деле нужно. По определению деформации для всех s и t имеет место равенство x ˜(s,t, 0) = x (s,t ). Кроме того, деформация x ˜(s,t, ε) для всех малых ε должна удовлетворять уравнениям связей. В нашем случае это условие нерастяжимости нити (17.1), а также и условие закрепления (17.2):
x ˜02 (s,t, ε) = 1, (17.8) x ˜(0,t, ε) = x 0 (t ). (17.9)
В принципе Гамильтона требуется, чтобы при заданных начальном и конечном моментах времени t 1 и t 2 деформация удовлетворяла условиям «закрепления концов»
x ˜(s,t 1 , ε) = x (s,t 1 ), x ˜(s,t 2 , ε) = x (s,t 2 ). (17.10)
Варьируя эти равенства, получаем условия для вариации
![]() .
(17.11)
.
(17.11)
Напомню еще, что операция варьирования δ есть дифференцирование по параметру деформации ε при ε = 0, так что
![]() .
(17.12)
.
(17.12)
Применение варьирования дает вариацию. Например, вариация δx определяется равенством
![]() .
(17.13)
.
(17.13)
Варьирование связей (17.8) и (17.9) дает равенства
![]() ,
(17.14)
,
(17.14)
(17.15)
Ради краткости, в формуле (17.14) опущены аргументы s и t , а в (17.15) — t .
Варьируя действие (17.7), получаем
t 2 `
Z Z
δS = (ρx ˙ · δx ˙ + ρg · δx )dsdt. (17.16)
t 1 0
Преобразуя первое слагаемое посредством интегрирования по частям по t с учетом (17.11) и применяя принцип Гамильтона, приходим к соотношению
t 2 ` Z Z
(−ρx ¨ + ρg ) · δxdsdt = 0, (17.17)
t 1 0
которое должно выполняться для всех вектор-функций δx (s,t ), удовлетворяющих условиям (17.11), (17.14), (17.15) и, конечно, достаточно гладких.
Чтобы избавиться от мешающих двигаться дальше ограничений на вариацию δx , применим метод Лагранжа. Умножая уравнение (17.14) на новую неизвестную (пока произвольную) функцию λ = λ(s,t ) (множитель Лагранжа) и интегрируя по s , t , получим
t 2 ` Z Z
| λx 0 · δx 0 dsdt = 0. t 1 0 Вычитая (17.18) из (17.17), получим |
(17.18) |
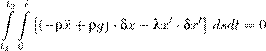 .
(17.19)
.
(17.19)
Условие связи (17.15) пока оставляем без внимания, дальше оно будет использовано. Мы можем теперь считать, как обычно в вариационных задачах со связями, что функция λ выбрана таким образом, что равенство (17.19) выполняется для вариаций δx , которые уже не обязаны удовлетворять условию (17.14).
Учитывая, что равенство (17.19) имеет место для любых t 1 и t 2 , можно убрать интеграл по t (формально дифференцируем по t 2 и учитываем, что t 2 произвольно). Таким образом, имеем
![]() .
(17.20)
.
(17.20)
Это соотношение выполняется в каждый момент времени t . Перебросим производную по s с δx 0 на второй множитель λx 0 в последнем слагаемом посредством интегрирования по частям. Учитывая краевое условие на левом конце (17.15), получаем
![]() .
(17.21)
.
(17.21)
Теперь мы еще раз применим идею вывода естественного краевого условия, которая была уже использована раньше в случае волнового уравнения. Сначала мы рассматриваем равенство (17.21) в том частном случае, когда δx = 0 при s = ` , и показываем, что из полученного интегрального равенства уже следует уравнение движения
ρx ¨ = (λx 0 )0 + ρg, (17.22)
которое должно выполняться для всех t и s ∈ (0,` ).
Но после того, как уравнение (17.22) выведено, мы видим, что интеграл в (17.21) исчезает для любых δx . В результате имеем равенство
![]() .
(17.23)
.
(17.23)
Поскольку ![]() можно выбирать произвольно, имеем право положить в
можно выбирать произвольно, имеем право положить в
![]() . В результате находим естественное краевое усло-
. В результате находим естественное краевое усло-
вие на свободном конце нити s = ` :
![]() .
(17.24)
.
(17.24)
Еще раз мы убеждаемся в двойной пользе принципа Гамильтона в механике сплошной среды — он дает не только уравнения движения, но и естественные краевые условия. Последние получаются на тех частях границы области, занятой сплошной средой, где первоначально не ставятся никакие краевые условия или задан неполный набор краевых условий. Примерами могут служить свободные границы (никаких краевых условий для деформаций) или подвижные твердые границы.
Таким образом, для описания динамики нити при поставленных выше условиях мы получили уравнение (17.22) с краевыми условиями (17.24) и (17.2)). В начальный момент времени должны быть заданы положение нити и соответствующее поле скоростей:
![]() ,
(17.25)
,
(17.25)
(17.26)
Заметим, что вектор-функции x 0 и v не вполне произвольны. Они должны удовлетворять условиям, вытекающим из уравнения связи
![]() .
(17.27)
.
(17.27)
Второе равенство получается дифференцированием по t при t = 0 уравнения (17.1).
Физический смысл множителя Лагранжа λ. Когда мы применяем принцип Гамильтона, физический смысл множителя Лагранжа остается в тени.
![]()
( ((((((XX(
![]()
![]() s
r
s
r
![]()
Рис. 7
Рассмотрим элемент нити между точками s и s + ds (см. Рис. 7). Так как нить не сопротивляется изгибу, силы, действующие на выбранный элемент со стороны остальных частей в точках s и s + ds , касательны к нити (поперечных сил нет). Поэтому такую силу можно записать в виде λx 0 , где λ = λ(s,t ) — некоторая функция. Внутренняя сила λx 0 (s + ds,t ) действует на элемент нити «справа» — со стороны больших значений s . Она возникает в результате взаимодействия выбранного элемента нити с остальной частью нити. По третьему закону Ньютона слева действует сила −λx 0 , отличающаяся лишь знаком. Мы видим, что равнодействующая двух сил, растягивающих элемент нити (s,s + ds ), есть (λx 0 )0 ds — с точностью до малых высшего порядка относительно ds . Сравнивая это выражение с правой частью уравнения (17.22), заключаем, что λ есть величина растягивающего усилия в точке нити. При этом положительным λ соответствует растяжение, а отрицательным — сжатие нити. Дальше мы покажем, что λ(s,t ) > 0 для всех s , t , так что нить всегда находится в растянутом состоянии в каждой своей точке.
Нить всегда растянута. Интуиция говорит нам, что нить, не сопротивляющаяся изгибу, не может выдержать сжатия. Если её всё-таки сжать, то при малейшем отклонении от строго прямолинейной формы она начнёт сильно морщиться, по ней пойдут очень короткие волны. Так как нет никаких ограничений на длину таких волн и их амплитуды, окажется, что возникнут волны сколь угодно малой длины с большими амплитудами. Это означает, что гладкость решения сильно портится — настолько, что решение вообще может быть разрушено. Все это типично для некорректных задач типа задачи теплопроводности для отрицательных времен или задачи Коши для уравнения Лапласа. Дальше мы увидим, что именно эта последняя задача, действительно, возникнет, если мы вздумаем рассматривать задачу о сжатой нити. Понятно, что описанные патологии связаны с чрезмерной идеализацией модели. Они исчезают, если учесть изгибную жесткость и/или внутреннее вязкое трение. Замечу, что в подобных ситуациях большой интерес представляет исследование асимптотического поведения решений соответствующих краевых задач (для равновесий одномерной сплошной среды), а также и начально-краевых задач для движений нити при стремлении к нулю изгибной жесткости и коэффициента трения. Те же вопросы возникают, конечно, и для многомерных сплошных сред. В настоящее время проблемы такого рода почти не изучены.
Сейчас мы в простейшем случае докажем, что нить всюду растянута. Результат, который будет получен, допускает довольно сильное расширение. Но всё-таки в самой общей ситуации, когда на нить действуют внешние силы, а концы её совершают произвольное движение, может оказаться, что она кое-где и сжата. В таких случаях приходится заключить, что модель абсолютно гибкой нити недостаточна для описания реального движения реальной нити. Следует всегда помнить, что в науке мы умеем работать лишь с моделями реальных объектов, а не с самими объектами.
Предположим, что нить двигается в невесомости (g = 0), а её левый конец фиксирован. При этих условиях уравнение движения (17.22) принимает вид
| а краевые условия суть |
ρx ¨ = (λx 0 )0 , |
(17.28) |
![]() ,
(17.29)
,
(17.29)
![]() (17.30)
(17.30)
По-прежнему должно выполняться условие нерастяжимости нити (17.1) x 02 = 1. Мы докажем теперь, что λ(s,t ) > 0 при всех t и s ∈ [0,` ), правый конец исключен ввиду краевого условия (17.30).
Разделим уравнение (17.28) на ρ и продифференцируем его по s . В результате получится уравнение
![]() .
(17.31)
.
(17.31)
Мы намереваемся умножить это уравнение скалярно на x 0 . При этом будут полезны соотношения, получаемые из уравнения связи (17.1) двумя последовательными дифференцированиями по s :
x 0 · x 00 = 0, x 0 · x 000 = −x 002 . (17.32)
Нужна ещё и формула, получаемая из уравнения связи (17.1) двумя дифференцированиями по t :
x 0 · x ¨0 = −x ˙02 . (17.33)
Теперь всё готово. Умножим (17.31) скалярно на x 0 , с использованием уравнения связи (17.1) и выведенных из него соотношений (17.32) и (17.33) получаем уравнение
![]() .
(17.34)
.
(17.34)
Это уравнение Штурма–Лиувилля относительно λ с коэффициентами, которые выражаются через производные по s от x (s,t ). Заметим, что в каждый момент времени, зная x (s,t ), можно определить λ(s,t ) — не нужно решать задачу с начальными данными. Это общая ситуация для задач со связями.
Однако я немножко поторопился сказать, что можно определить растягивающее усилие для λ — нужны еще краевые условия. На правом конце (s = ` ) имеется условие (17.30). Условие на левом конце (s = 0) мы выведем из уравнения движения (17.28). Если предположить, что решение является достаточно гладким, можно использовать это уравнение и на конце s = 0. Тогда получается, что при s = 0
0 = λx 00 + λ 0 x 0 , (17.35)
так как![]() в силу краевого условия (17.29) (оно выполняется для всех t
, а потому его можно по t
дифференцировать). Умножая (17.35) скалярно на x
0
и применяя (17.1) и (17.32), видим, что
в силу краевого условия (17.29) (оно выполняется для всех t
, а потому его можно по t
дифференцировать). Умножая (17.35) скалярно на x
0
и применяя (17.1) и (17.32), видим, что ![]() .
.
Итак, уравнение Штурма–Лиувилля (17.34) следует решать при краевых условиях
![]() ,
,
![]() .
(17.36)
.
(17.36)
Из теории краевых задач Штурма–Лиувилля следует, что решение λ(s,t ) краевой задачи (17.34), (17.36) положительно при 0 ≤ s < ` . Здесь существенно, что в (17.34) коэффициент при λ неположителен, равно как и свободный член. Доказательство Вы можете провести самостоятельно, усвоив идеи доказательства принципов максимума-минимума, например, по книгам [56, 57].
Жесткость систем со связями. Сейчас я собираюсь, отправляясь от примера нерастяжимой нити, обсудить явление жесткости , которое специфично для систем со связями. Я поколебался в выборе эпитета, но так и не решил, «приятное» или «неприятное» это явление, и ни на одном из них не остановился. С явлением жесткости или частичной жесткости связаны интересные следствия — как позитивные, так и негативные.
Рассмотрим нерастяжимую нить с закреплёнными концами. Соответствующие краевые условия имеют вид
![]() (17.37)
(17.37)
где a и b — известные точки пространства R 3 . Очевидно, что при этом должно быть выполнено условие
|a − b | ≤ `, (17.38)
где ` — длина нити. Если |a − b | > ` , то не существует ни одной векторфункции x (s,t ), удовлетворяющей условию связи x 02 = 1 и краевым условиям (17.37). Если же расстояние между точками a и b в точности равно ` , то, очевидно, существует лишь одна такая вектор-функция, соответствующая прямолинейному положению нити между точками a и b . Нить не сможет двигаться! Это и есть явление жесткости. Более общее условие |a − b | ≤ ` назовем условием совместности связей (17.37) и x 02 = 1 (нерастяжимость).
Понятно, что всякий раз, когда назначаются условия связей, нужно позаботиться об их совместности (непротиворечивости), не то получится, что движение невозможно, и мы ставим задачу с пустым содержанием. Если связи совместны, то всё равно может случиться, что им удовлетворяет лишь одно положение системы или некоторый дискретный набор положений, а движение все-таки невозможно.
Более интересно явление частичной жесткости . Если система имеет конечное число степеней свободы, скажем, объемлющее пространство есть Rn , и наложено конечное число r связей, то в условиях невырожденности размерность k конфигурационного пространства системы есть n −r . Если же оказалось, что k < n − r , то скажем, что система частично жесткая, а величина n − r − k есть мера этой жесткости.
 HH
HH
Особенно интересен тот случай, когда и размерность объемлющего пространства, и количество связей бесконечны. В результате может получиться, что система имеет конечное число степеней свободы. Именно эта ситуация возникает в задаче о движении абсолютно твёрдого тела (например, в R 3 ). Связи в этом случае требуют, чтобы расстояния между любыми двумя точками тела оставались неизменными в ходе движения. В результате оказывается, что конфигурационное пространство конечномерно, именно шестимерно, число степеней свободы твердого тела равно 6. Если же одна точка тела закреплена, то получается система с тремя степенями свободы. А когда закреплены две точки, то остается одна степень свободы — тело может лишь вращаться вокруг оси, проходящей через эти две (ну, конечно, различные) точки.
Кстати, именно по этой, довольно формальной причине, динамика абсолютно твердого тела попадает в курсы классической механики, а не в курсы механики сплошной среды. Дальше я собираюсь рассмотреть задачу о движении твердого тела подробнее.
Динамика нити с одним закрепленным концом. Рассмотрим абсолютно гибкую нерастяжимую нить с закрепленным левым концом, и пусть к её правому концу приложено растягивающее усилие T = T i , см. Рис. 8. Правый конец подвижен, но ему разрешается перемещаться лишь вдоль оси x 1 . Нетрудно представить себе, каким образом можно практически обеспечить изображенный на Рис. 8 способ приложения нагрузки: достаточно прикрепить к жесткому шарниру на правом конце нити еще одну нить, перебросить её через ворот и к её свободному концу подвесить груз, см. Рис. 9. Мы предположим, что все виды трения пренебрежимо малы (честнее говорить: отсутствуют, равны нулю), и что эта дополнительная нить (а может, стержень или трубка, через которую пропущена нить) остается всё время параллельной оси x 1 .
| 5 кг |
![]() Уравнение движения можно вывести из принципа Гамильтона. Система эта натуральна, её лагранжиан L
есть разность между кинетической энерeH
e
H
e '
j $ &%
Уравнение движения можно вывести из принципа Гамильтона. Система эта натуральна, её лагранжиан L
есть разность между кинетической энерeH
e
H
e '
j $ &%
Рис. 9
гией Ek и потенциальной энергией V :
L = Ek − V. (17.39)
В определении лагранжиана пришлось изменить обозначение, так как буква T занята — общепринято через T обозначать растягивающее усилие. В предположении, что нить однородна, и погонная масса нити ρ (она же — линейная плотность) равна единице, кинетическая энергия задается равенством
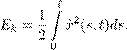 (17.40)
(17.40)
При этом x = x (s,t ), s ∈ [0,` ], t ∈ R — параметрическое уравнение положения нити в момент t , ` — её длина. Потенциальная энергия V , связанная с заданным растягивающим усилием T , имеет вид
| V = −Tx 1 (`,t ). Действие по Гамильтону определяется теперь равенством |
(17.41) |
| t 2 t 2 Z Z S = Ldt = (Ek − V )dt. t 1 t 1 Наряду с условием нерастяжимости |
(17.42) |
| x 02 (s,t ) = 1, |
(17.43) |
к числу связей относятся также краевые условия на левом конце и два условия на правом конце нити:
![]() .
(17.44)
.
(17.44)
Еще одно условие на правом конце получится далее из самого принципа Гамильтона как естественное.
Согласно принципу Гамильтона для систем со связями δS = 0. Для деформаций уравнения связей (17.43), (17.44) должны быть выполнены, а вариация δx должна удовлетворять условиям, получающимся при варьировании равенств (17.43), (17.44)
![]() (17.45)
(17.45)
![]() .
(17.46)
.
(17.46)
Равенство δS = 0, согласно (17.42), имеет вид
t 2 ` t 2
Z Z Z
x ˙ · δxdsdt ˙ + T δx 1 (`,t )dt = 0. (17.47)
t 1 0 t 1
Как и ранее, проводим в первом слагаемом (17.47) интегрирование по частям, а затем дифференцированием по t 2 избавляемся от интеграла по времени. В результате получим соотношение
`
Z
−x ¨ · δxds + T δx 1 (`,t ) = 0, (17.48)
0
которое должно выполняться в каждый момент t (мы заменили t 2 на t ).
Из уравнения (17.45), умножая его на множитель Лагранжа λ = λ(s,t ), после интегрирования по частям получаем
![]() .
(17.49)
.
(17.49)
С учетом условий (17.46) имеем
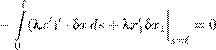 .
(17.50)
.
(17.50)
Вычитая это равенство из (17.48), получаем
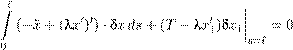 .
(17.51)
.
(17.51)
Применяя стандартное рассуждение, связанное с переходом к вариациям δx , исчезающим на границе, снова получаем уравнение движения нити
x ¨ = (λx 0 )0 , (17.52)
а затем, возвращаясь к произвольным вариациям, удовлетворяющим условиям (17.45) и (17.46), и учитывая, что ![]() может быть произвольным, получаем естественное краевое условие на правом конце
может быть произвольным, получаем естественное краевое условие на правом конце
![]() (17.53)
(17.53)
Таким образом, уравнение движения (17.52) остается прежним. Вообще, уравнения движения, как легко понять, не меняются при переходе к новым краевым условиям. Также должно выполняться условие нерастяжимости нити (17.43), а краевые условия задаются равенствами (17.44) и (17.53).
Конечно, краевое условие (17.53) можно вывести и непосредственно, заодно лучше поняв его механический смысл. Для этого нужно разложить заданное растягивающее усилие T
, см. Рис. 8, на сумму двух компонент, одна из которых ортогональна линии действия усилия — оси x
1
, а другая — касательна к нити и равна ![]() в точке s
= `
. Ортогональная к оси x
1
компонента уравновешивается реакцией связи (x
2
= 0, x
3
= 0 при s
= `
) и в дальнейшем не участвует. Касательная же к нити компонента дает растягивающее усилие λx
0
на конце нити. Таким образом, должно быть выполнено равенство
в точке s
= `
. Ортогональная к оси x
1
компонента уравновешивается реакцией связи (x
2
= 0, x
3
= 0 при s
= `
) и в дальнейшем не участвует. Касательная же к нити компонента дает растягивающее усилие λx
0
на конце нити. Таким образом, должно быть выполнено равенство
λx 0 = (T · x 0 )x 0 , (17.54)
что совпадает с (17.53).
Присмотримся к краевому условию (17.53). Из него следует не слишком приятный вывод: продольное усилие λ при s
= `
оказывается бесконечно большим, если![]() в некоторый момент t
. Равенство
в некоторый момент t
. Равенство ![]() означает, что нить в точке s
= `
ортогональна к оси x
1
. Реакция связи (17.44) (x
2
= 0, x
3
= 0), если она идеальна, тоже ортогональна оси x
1
. Выходит, что растягивающее усилие T
, действующее вдоль оси x
1
, ничем не уравновешено. Мы пришли к парадоксальному выводу. Что же происходит на самом деле? Во-первых, ясно, что наша модель уже не может описать поведение реальной системы при t > t
0
, если в момент t
= t
0
оказалось, что
означает, что нить в точке s
= `
ортогональна к оси x
1
. Реакция связи (17.44) (x
2
= 0, x
3
= 0), если она идеальна, тоже ортогональна оси x
1
. Выходит, что растягивающее усилие T
, действующее вдоль оси x
1
, ничем не уравновешено. Мы пришли к парадоксальному выводу. Что же происходит на самом деле? Во-первых, ясно, что наша модель уже не может описать поведение реальной системы при t > t
0
, если в момент t
= t
0
оказалось, что![]() . Как бы ни была мала масса той конструкции на Рис. 9 («держалки») и самой нити, именно она определяет движение нити в момент времени сразу после t
= t
0
. Построенная нами модель сама заявляет о своей несостоятельности и требует включить дополнительную информацию. Нетрудно показать (попытайтесь!), что с учетом массы «держалки» краевое условие (17.53) при s
= `
должно быть заменено более общим:
. Как бы ни была мала масса той конструкции на Рис. 9 («держалки») и самой нити, именно она определяет движение нити в момент времени сразу после t
= t
0
. Построенная нами модель сама заявляет о своей несостоятельности и требует включить дополнительную информацию. Нетрудно показать (попытайтесь!), что с учетом массы «держалки» краевое условие (17.53) при s
= `
должно быть заменено более общим:
![]() .
(17.55)
.
(17.55)
Здесь m — масса «держалки», а уравнение (17.55) получается применением II-го закона Ньютона; массой нити мы по-прежнему пренебрегаем, считая, что она «много меньше» (так обычно говорят, хотя точнее было бы сказать «во много раз меньше»). Подробнее о задачах с краевыми условиями типа (17.55) рассказано в работе [54].
Было бы «математической глупостью», применяя нашу модель на практике, совсем забыть о той компоненте усилия T , которая уравновешивается реакцией связи. Если она оказывается слишком большой, то связь может разорваться, и условия применимости нашей модели будут наруше-
ны. А потому докажите, что эта реакция равна вектору ![]() .
.
![]() Его абсолютная величина есть
Его абсолютная величина есть![]() . Она обращается в ноль, когда
. Она обращается в ноль, когда ![]() при s
= `
(нить касается оси x
1
в точке s
= `
), и стремится к
при s
= `
(нить касается оси x
1
в точке s
= `
), и стремится к
бесконечности при![]() (нить ортогональна к оси x
1
при s
= `
).
(нить ортогональна к оси x
1
при s
= `
).
Подведем итог. В условиях, соответствующих Рис. 8, уравнение движения нити и условие её нерастяжимости имеют вид
| x ¨ = (λx 0 )0 , |
(17.56) |
| x 02 = 1. |
(17.57) |
Соответствующие краевые условия суть
![]() (17.58)
(17.58)
(17.59)
Напомню, что третье краевое условие (17.59) выполняется лишь в предположении, что ![]() для всего интервала времени t
, на котором рассматривается движение нити. Если же оно нарушается, придется перейти к более общему краевому условию типа (17.55).
для всего интервала времени t
, на котором рассматривается движение нити. Если же оно нарушается, придется перейти к более общему краевому условию типа (17.55).
Начальные условия состоят в задании положения нити и поля скоростей составляющих её точек при t = 0:
![]() .
(17.60)
.
(17.60)
Как всегда при наличии связей, начальные данные должны быть с ними согласованы. Начальное положение x 0 должно удовлетворять условию нерастяжимости нити (17.57) и краевым условиям (17.58) вместе с первыми двумя условиями (17.59):
![]() (17.61)
(17.61)
. (17.62)
Начальное поле скоростей должно быть подчинено условиям, получаемым дифференцированием уравнений связи по t при t = 0:
![]() (17.63)
(17.63)
. (17.64)
18. Уравнение колебаний струны
Удивительное дело — едва ли не во всех распространенных учебниках по математической физике уравнение поперечных колебаний струны выводится некорректно — и с физической, и с математической точки зрения. Некоторым исключением является лишь классическая книга Р. Куранта и Д. Гильберта [18].
Линейное уравнение струны описывает малые, а точнее говоря, бесконечно малые колебания около её прямолинейной формы равновесия. Обычно вне обсуждения остается вопрос о законности перехода от более точных нелинейных уравнений к линеаризованным. Для уравнений гиперболического типа, описывающих волновые процессы, эта проблема все ещё составляет немалую трудность. К тому же, в механике и в математической физике нередко случается, что истинные нелинейные уравнения вообще выпадают из поля зрения, не выписываются явно, и остается неясным, какую,
собственно говоря, задачу мы решаем приближенно, переходя к линейным уравнениям. Сама проблема исследования взаимосвязи между решениями нелинейных и соответствующих им линеаризованных уравнений «заметается под ковер». Случается, что к линейному уравнению струны дописываются довольно произвольно нелинейные слагаемые, и такие уравнения называются уравнениями нелинейной струны (пример: utt − uxx + u 3 = 0). Разумеется, подобные уравнения бывают очень интересными, описывают разнообразные волновые процессы, служат хорошими моделями, помогающими понять роль нелинейности в проблеме распространения волн. И всё-таки можно довольно уверенно предположить, что не искусственно составляемые уравнения, а фундаментальные модели, выводимые из «первых принципов» (таких, как закон сохранения энергии, закон возрастания энтропии в замкнутой системе, принцип Гамильтона), лучше описывают явления реального мира и оказываются проще для исследования. В истории науки не раз бывало, что модели, составленные по принципу их (кажущейся на первый взгляд!) простоты, на деле оказываются как раз наиболее сложными, вырожденными и трудно поддающимися анализу. Я говорю это как некоторое оправдание рассмотренной дальше, внешне довольно сложной системы уравнений абсолютно гибкой нити, которая при линеаризации и порождает уравнение струны. Проблема обоснования законности линеаризации здесь отнюдь не проста и на сегодняшний день остается открытой.
Дальше мы увидим, что уравнение струны получается как уравнение малых колебаний нити, растягиваемой продольной силой, около её прямолинейного положения равновесия. Определенная тонкость постановки этой задачи связана с необходимостью как-то обойти эффект жесткости связи. Имеются разные способы снятия жесткости. Можно было бы рассмотреть растяжимую нить, отказавшись вовсе от условия связи (довольно интересно проделать это подробно). Оставаясь в рамках механики систем со связями, интересно (и идейно) рассмотреть минимальное ослабление связей, допустив подвижность одного из концов нити и сохранив условие её нерастяжимости. По этому пути мы теперь и пойдем. Еще один вариант вывода уравнения струны возникает, когда рассматривается нить переменной длины — скажем, длинная нитка, у которой один конец закреплен, пропущена через игольное ушко и растягивается заданной силой, а мы следим за событиями лишь по одну сторону от игольного ушка. К этой задаче я надеюсь вернуться позднее.
Прямолинейное равновесие нити и его возмущения. Довольно очевидно, что система уравнений и краевых условий (17.56)–(17.59) допускает решение, не зависящее от времени и отвечающее прямолинейной форме равновесия нити:
x ¯1 = s, x ¯2 = 0, x ¯3 = 0, λ ¯ = T. (18.1)
Первые три соотношения говорят, что нить располагается вдоль оси x 1 — линии действия силы T . Величина λ ¯ после этого определяется из уравнения
(17.56).
Для произвольного решения (x, λ) положим
x = ¯x + u, λ = λ ¯ + µ, (18.2)
где x ¯ = (s, 0, 0) = s i (i — координатный орт оси x 1 ), λ ¯ = T . Векторфункция u (s,t ) называется возмущением формы равновесия x ¯, а функция µ(s,t ) — возмущением продольного усилия λ ¯ = T .
Подставляя выражения (18.2) в уравнения и краевые условия (17.56)–
(17.59), получим нелинейную систему для возмущений u , µ
u ¨ = (Tu 0 + µi + µu 0 )0 , (18.3)
![]() (18.4)
(18.4)
![]() (18.5)
(18.5)
![]() ,
µ
,
µ![]()
Характерной чертой уравнений возмущений является наличие тривиального решения, в данном случае это u = 0, µ = 0. Действительно, когда возмущения исчезают, мы возвращаемся к известному решению — равновесию
(18.1).
Вывод уравнения колебаний струны. Линеаризуем систему (18.3)–
(18.6). Это значит — в каждом из этих уравнений оставим лишь линейные
0 , u 0 2 и т.п. члены, а чисто нелинейные относительно µ и u , например, µu отбросим. В результате придём к линеаризованной системе
![]() (18.7)
(18.7)
(18.8)
(18.9)
,
µ![]() .
(18.10)
.
(18.10)
Разумеется, уравнения, которые были линейными и однородными, остались без изменения.
Как видим, переход от нелинейнных уравнений к линеаризованным — довольно грубая операция. При использовании линеаризованных уравнений можно надеяться лишь на описание движений, достаточно близких к основному режиму. Когда речь идет об уравнениях в частных производных, неизбежно встает вопрос и о том, в каком смысле понимается близость решений полной системы и линеаризованной. Например, отбрасывая в (18.4) слагаемое u 02 и переходя к (18.8), приходится предполагать, что не просто возмущение u , но и его производная достаточно малы. Нелегко определить, что значит «достаточно». Когда математики произносят такие слова, то это означает лишь, что существует или должна существовать такая положительная константа η > 0, что при условии |u 0 | < η известна некоторая хорошая оценка разности между решениями двух систем. Даже когда теория установила, что такая константа η существует, обычно бывает непросто получить для неё хорошие оценки. В конце концов, как правило, приходится прибегать к численному или натурному эксперименту.
Замечу еще, что во многих случаях никак нельзя ожидать, что решения полной нелинейной задачи остаются близкими неограниченно долго. Мы можем потребовать, чтобы возмущения были малы в начальный момент. Если окажется, что соответствующее решение линеаризованной системы неограниченно возрастает со временем, то очевидно, что исходное предположение о малости отброшенных слагаемых нарушается. При этом, во многих случаях удается строго доказать — для обыкновенных дифференциальных уравнений это сделал А.М. Ляпунов, — что подобное поведение решений линеаризованной системы означает неустойчивость основного решения полной системы.
Результаты Ляпунова о законности линеаризации в проблеме устойчивости перенесены и на некоторые классы бесконечномерных задач, см. [11], [58]. Однако в рассматриваемой нами сейчас проблеме, как и во многих других аналогичных проблемах о нелинейных колебаниях, вопрос о законности линеаризации до сих пор не рассмотрен. Тем более замечательно, что многие выводы, вытекающие из анализа уравнения колебаний струны, прекрасно подтверждаются опытом. Тут даже хочется чуть-чуть пофилософствовать и спросить, не относится ли это вообще ко всем математическим проблемам естествознания. Ведь каждый раз при построении математической модели приходится пренебрегать столь многими факторами, что совпадение теоретических выводов с экспериментом выглядит просто как чудо. Быть может, самое сильное переживание исследователя — видеть, как экспериментальные точки ложатся на теоретический график (или точки, рассчитанные по теории, ложатся на экспериментальный график).
Вернемся, однако, к системе (18.7)–(18.10). Из (18.8) следует, что u 1 не зависит от s , а тогда, согласно краевому условию (18.9), u 1 ≡ 0. С учетом этого факта векторное уравнение движения (18.7) в координатной форме примет вид
|
|
(18.11) |
| u ¨2 = Tu 002, u ¨3 = Tu 003. |
(18.12) (18.13) |
Из (18.11) и краевого условия (18.10) следует, что µ = 0, так что в принятом приближении сила натяжения нити остается равной T . Уравнения (18.12) и (18.13) имеют одну и ту же форму — это уравнение поперечных колебаний струны . Мы его запишем в виде
u ¨ = c 2 u 00 , (18.14)
где c 2 — квадрат скорости распространения поперечных волн
![]() .
(18.15)
.
(18.15)
Раньше мы принимали погонную массу нити ρ (она еще называется линейной плотностью) равной единице. Вообще, она появляется как множитель в левой части уравнений (18.12), (18.13), откуда и получается выражение (18.15). Глядя на эту формулу, особенно ясно, что упругость нити тут не при чем, странно, что этого не заметили авторы многих учебников.
Предыдущий вывод дал также краевые условия для уравнения струны (18.14), см. (18.9), (18.10): u 2 и u 3 должны исчезать на концах. Опуская индексы, запишем эти условия первого рода для уравнения (18.14):
![]() .
(18.16)
.
(18.16)
Другие краевые условия. Помимо условий первого рода (18.16), для уравнений струны часто используются также краевые условия второго и третьего рода. Они соответствуют иным способам закрепления подвижного правого конца нити.
Пусть на правый конец нити действует внешняя сила с известной потенциальной энергией ϕ(x (` )). Например, можно себе представить, что нить прикреплена к подвижному шарниру на твердой подставке, а последняя приделана к подвижной платформе, но не жестко, а при помощи упругих пружин, см. Рис. 10.
![]() HH
HH
Рис. 10
В этом случае краевое условие при s = ` примет вид
![]() grad
grad ![]() .
(18.17)
.
(18.17)
Предположим, что потенциальная энергия ϕ такова, что нелинейная система уравнений движения нити допускает равновесие (18.1): x ¯1 = s , x ¯2 = 0, x ¯3 = 0, λ ¯ = T . Это налагает на функцию ϕ ограничения ϕx 1 (`, 0, 0) = −T, ϕx 2 (`, 0, 0) = 0, ϕx 3 (`, 0, 0) = 0. (18.18)
Поворотом осей x 2 , x 3 можно добиться исчезновения слагаемого с x 2 x 3 в выражении потенциальной энергии (привести квадратичную форму от x 2 , x 3 к главным осям). При таком выборе осей x 2 , x 3 разложение Тейлора функции ϕ в точке (`, 0, 0) принимает вид
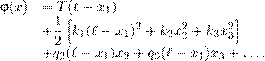 (18.19)
(18.19)
Здесь опущены члены степени 3 и выше.
Переходя к возмущениям равновесия (18.1), т.е. полагая x (s,t ) = ¯x + u (s,t ), λ(s,t ) = T +µ(s,t ), запишем краевое условие (18.17) при s = ` в виде
(T + µ)(i + u 0 ) = −grad ϕ(` + u 1 ,u 2 ,u 3 ). (18.20)
Здесь через uk обозначено uk (`,t ), k = 1, 2, 3. В координатах имеем соотношения
(T + µ)(1 + u 0 1 ) = −ϕx 1 (` + u 1 ,u 2 ,u 3 ),
(T + µ)u 0 2 = −ϕx 2 (` + u 1 ,u 2 ,u 3 ), (18.21) (T + µ)u 0 3 = −ϕx 3 (` + u 1 ,u 2 ,u 3 ).
Правые части вычисляем при помощи равенства (18.19). Имеем
ϕx 1 (` + u 1 ,u 2 ,u 3 ) = −T + k 1 u 1 − q 2 u 2 − q 3 u 3 ,
ϕx 2 (` + u 1 ,u 2 ,u 3 ) = k 2 u 2 − q 2 u 1 , (18.22) ϕx 3(` + u 1,u 2,u 3) = k 3u 3 − q 3u 1.
Линеаризация соотношений (18.21) дает краевые условия для струны
Tu 01 + µ = −k 1u 1 + q 2u 2 + q 3u 3,
Tu 0 2 = −k 2 u 2 + q 2 u 1 , (18.23)
Tu 03 = −k 3u 3 + q 3u 1.
Линеаризация условия нерастяжимости на равновесии (18.1) дает по-прежнему равенство![]() , что вместе с краевым условием (18.16) приводит к u
1
(s,t
) = 0. Уравнения (18.23) поэтому записываются в виде
, что вместе с краевым условием (18.16) приводит к u
1
(s,t
) = 0. Уравнения (18.23) поэтому записываются в виде
µ = q 2 u 2 + q 3 u 3 ,
Tu 0 2 = −k 2 u 2 , (18.24)
Tu 03 = −k 3u 3.
Как и раньше, первое условие служит для определения величины µ, а остальные два дают краевые условия при s = ` для уравнений струны. При k 2 6= 0 и k 3 6= 0 — это условия 3-го рода, которые, опуская индексы, можно записать в виде
u0
(`,t) = −βu(`,t), 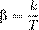 . (18.25)
. (18.25)
Нетрудно понять, что величины k 2 и k 3 суть не что иное как жесткости упругих элементов (пружин), удерживающих точку опоры правого конца нити s = ` вблизи оси x 1 . Таким образом, условия 3-го рода соответствуют упругому закреплению конца нити около линии действия растяжения. Когда нить очень сильно натянута (в пределе T → ∞), или когда жесткость пружины очень мала (k → 0), то есть при β = 0 условие (18.25) — второго рода.
Неоднородная нить и неоднородная струна. Если линейная плотность нити ρ = ρ(s ) не постоянна, то ее кинетическая энергия принимает вид
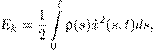 (18.26)
(18.26)
| и уравнение движения есть |
|
| ρ(s )x ¨ = (λx 0 )0 . |
(18.27) |
Некорректность задачи о сжатой нити. Выше мы предполагали, что нить растягивается внешней нагрузкой и T > 0. Однако ничто не мешает, как-будто, проделать все предыдущие выводы и при T < 0 — когда внешняя сила сжимает нить. В результате, однако, вместо гиперболического уравнения струны получается (пусть линейная плотность ρ = const ) уравнение эллиптического типа
![]() ,
(18.28)
,
(18.28)
которое несущественно отличается от уравнения Лапласа (а при k = 1) совпадает. Хорошо известно (см., например, [28]), что задача Коши для уравнения (18.28) некорректна . Решение при начальных условиях
![]() (18.29)
(18.29)
даже для C ∞ -гладких функций u 0 (s ), v 0 (s ), как правило, не существует, а если и существует, то малейшее начальное возмущение чрезвычайно быстро возрастает по времени и за конечное время уходит на бесконечность. Это показывает, что сжатая нить ужасающе неустойчива.
Снова модель заявляет нам о своей неадекватности. На сей раз к корректной задаче можно прийти, если учесть сопротивление реальной нити изгибу. Это соответствует добавлению потенциальной энергии, зависящей от кривизны κ = x 00 , точнее, от ее квадрата:
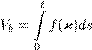 (18.30)
(18.30)
с заданной функцией f
. В простейшем варианте полагают![]() , D >
0. В итоге получается модель несжимаемого стержня (балки)
.
, D >
0. В итоге получается модель несжимаемого стержня (балки)
.
Было бы очень интересно рассмотреть динамику балки при очень малой изгибной жесткости D и понять, возможно ли, и в каком смысле, осуществить предельный переход при D → 0. Я ожидаю, что лишь привлечение методов теории вероятности поможет описать эту весьма сложную динамику, не поддающуюся детерминированному анализу.
О необходимом числе краевых условий и практическом значении теоремединственности. Постановка краевых условий на подвижном конце нити — непростое дело, в особенности, если мы хотим не только получить корректную математическую модель, а намереваемся описать реальную ситуацию — скажем, колебания струн гитары и скрипки или электрического провода между двумя столбами. Разумеется, те схемы закрепления подвижного конца нити, которые изображены на Рис. 8–10, не следует понимать слишком буквально, они приведены лишь для иллюстрации. Например, пружинки просто означают, что в точке опоры действует упругая сила, которая стремится возвратить конец нити в его равновесное положение. Эта сила зависит только от величины отклонения — линейно (по Гуку) или нелинейно.
Дальше я еще собираюсь обсудить иной вариант закрепления и рассмотреть «нить, продетую сквозь игольное ушко» или тонкую трубку. Принципиальное отличие этого способа закрепления от всех предыдущих состоит в том, что на сей раз длину нити нельзя считать фиксированной, потому что мы держим под наблюдением лишь её часть. В итоге задача попадает в тот разряд моделей, которые описывают системы с переменным составом частиц . Аналогичные проблемы возникают в гидродинамике, когда изучается движение жидкости в некоторой известной области, граница которой или, по крайней мере, её часть проницаема для жидкости. В результате частицы жидкости могут входить в область извне и уходить из неё. Принцип Гамильтона неприменим к системам с переменным составом материальных частиц.
Обсудим парадоксальное различие между краевым условием (17.24) на свободном конце нити (![]() ) и краевым условием (17.59) в случае, когда нить растягивается (
) и краевым условием (17.59) в случае, когда нить растягивается (![]() при s
= `
).
при s
= `
).
Почему в случае растяжения (T > 0) необходимо три краевых условия, а если его нет (T = 0), то достаточно одного? А может быть, и на свободном конце нужны дополнительные условия?
Такого рода сомнения разрешает лишь теорема единственности решения начально-краевой задачи. Если при поставленных условиях её удается доказать, то это, безусловно, означает, что никаких иных условий ставить не нужно. Замечу, что теорема существования, напротив показывает, что поставленные условия непротиворечивы, нет лишних условий, которые следовало бы отбросить.
Доказательства теорем единственности и теорем существования решения различных начально-краевых задач для нити технически довольно сложны, а глобальные теоремы существования вообще неизвестны.
Здесь я ограничусь простейшим случаем, когда в начальный момент нить неподвижна, а её форма может быть произвольной. Итак, рассмотрим случай начальных условий
![]() ,
,
![]() (18.31)
(18.31)
для всех s ∈ [0,` ]. Краевые условия соответствуют закреплённому левому концу и свободному правому
![]() ,
,
![]() .
(18.32)
.
(18.32)
Докажем, что уравнениедвижениянити x ¨ = (λx 0 )0 ,подчинённойтребованию нерастяжимости x 02 = 1 и условиям (18.31), (18.32), имеет единственное решение x (s,t ) = x 0 (s ), λ(s,t ) = 0.
Доказательство. Умножив уравнение движения (17.52) на x ˙ и интегрируя по s , выводим
![]() (18.33)
(18.33)
Внеинтегральные члены обращаются в ноль в силу краевых условий (18.32);
так как![]() , также и
, также и![]() . Дифференцируя по t
уравнение связи x
02
= 1, получаем равенство
. Дифференцируя по t
уравнение связи x
02
= 1, получаем равенство
x 0 · x ˙0 = 0, (18.34)
из которого следует, что интеграл в правой части (18.33) также равен нулю. Таким образом,
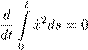 .
(18.35)
.
(18.35)
Из этого равенства и начального условия (18.32), следует, что x ˙ ≡ 0. Выходит, что x (s,t ) = x (s ), а от t не зависит. Поэтому x (s,t ) = x (s, 0) = x 0 (s ) для всех t и s , ввиду начального условия (18.31). Наше утверждение, таким образом, доказано.
Разумеется, «физически очевидно», что нить, на которую не действуют никакие силы, вечно остается в покое при любой её начальной форме (начальное поле скоростей — нулевое). Математик, однако, обязан подобные утверждения проверять, исходя из построенной модели, что хотя бы в какой-то мере подтверждает ее правильность. Физики, часто выступая против «теорем существования» (я поставил кавычки, потому что они обычно имеют в виду вообще чрезмерно педантичные обоснования, и нередко в этом бывают правы), обычно признают полезность теорем единственности. Когда некоторое решение удается получить, приятно знать, что нет других решений. Тут все согласны. Впрочем, фон Карман утверждал, что физики обычно пишут правильные дифференциальные уравнения движения, но никогда не пишут правильно краевые условия.
19. Специальная теория относительности Эйнштейна
Теория относительности хорошо изложена во многих книгах — см. «Теория поля» Л.Д. Ландау и Е.М. Лифшица [21], «Теория относительности» Вольфганга Паули [34]. Последний труд был написан 20-летним студентом, был очень высоко оценен, попал в физическую энциклопедию и до сих пор является одним из лучших обзоров раннего периода развития этой теории. А всё-таки я рекомендую начать с чтения работы самого А. Эйнштейна «К электродинамике движущихся сред», она сейчас легко доступна [52].
В основе теории Эйнштейна лежат два постулата.
1. Постулат относительности. Постулируется существование трехпараметрического семейства систем отчета, называемых инерциальными , в которых все законы природы «выглядят одинаково». Все эти системы движутся друг относительно друга поступательно с постоянной скоростью (3 параметра — три компоненты этой скорости).
Этот постулат далее конкретизируется посредством указания преобразований перехода от одной системы отсчета к другой. Таковыми оказываются преобразования Лоренца. Эйнштейн понял, что электромагнитное поле столь тесно связано с пространством и временем, что его свойства инвариантности суть не что иное, как свойства инвариантности пространства и времени.
2. Постулат постоянства скорости света. Во всех инерциальных системах отсчета скорость света c в вакууме одна и та же и равна (с хорошей
точностью) 3 · 1010 см/сек. Более точное значение: c = 2. 99792 · 1010 см/сек.
Этот постулат кажется особенно поразительным, поскольку мы уж очень привыкли к галилееву правилу сложения скоростей. Его «экспериментальное обоснование» парадоксально и состоит, по Эйнштейну, в том, что никто не наблюдал стоячих электромагнитных волн. А если бы выполнялись обычные правила Галилея, то, как кажется, электромагнитные волны в надлежащей движущейся системе координат остановились бы.
Сейчас уже почти забыт замечательный популяризатор науки, особенно астрономии, Камилл Фламмарион. Возможно, он вообще был первым популяризатором, автором–изобретателем жанра. Иногда он немного отклонялся от популяризации в сторону фантастики. В одной его книге космический путешественник летит в космическом корабле со скоростью, большей скорости света и наблюдает события на Земле в обратном порядке. Убитый Цезарь поднимается, Брут и Кассий разбегаются от него, прячут ножи, и т. д. Скоро мы увидим, что движение со сверхсветовой скоростью невозможно. Интересно заметить, что и другое экспериментальное обоснование специальной теории относительности столь же парадоксально и состоит в том, что попытки обнаружить так называемый эфирный ветер, «обдувающий» Землю, привели к отрицательному результату. Эфир — гипотетическая среда, заполняющая все пространство, колебания которой и представляют собой электромагнитные волны. Примечательно, что целью Майкельсона, который в течение десятилетий проводил все более точные эксперименты, было как раз обнаружение эфира. Эксперименты, однако, привели к выводу, что эфир не существует. Казалось бы, логика развития науки такова, что, основываясь на результатах опытов Майкельсона (а также Майкельсона-Морли и ряда других, аналогичных), Эйнштейн и вывел свой постулат. Нередко так логично и излагают эту историю в книгах. Однако сам Эйнштейн утверждал, что до публикации его знаменитой статьи он ничего не слышал об опытах Майкельсона. Мне лично кажется, что соображение об отсутствии стоячих электромагнитных волн — посильнее любых конкретных экспериментальных результатов. Поражает также положенное в основу работы Эйнштейна убеждение физика, что электромагнитное поле столь интимно связано с пространством и временем, что его свойства, собственно говоря, и есть свойства пространства и времени.
Возвращаясь от общей философии к делу, посмотрим, какие следствия вытекают из 2-го постулата. Представим себе, что зафиксирована некоторая инерциальная система отсчета (декартова система координат x 1 , x 2 , x 3 и время t ). Замечу, что возможность пользоваться единой для всего пространства декартовой системой координат характерна (постулируется) для специальной теории относительности . В общей теории относительности, называемой также теорией гравитации , приходится рассматривать неевклидово пространство, обладающее кривизной.
Теперь введем подвижную систему координат![]() и соответствующее ей время t
0
. Предположим, что в начальный момент времени t
= 0 обе системы координат совпадают. Будем предполагать, что "штрихованная" система координат движется с постоянной скоростью v
в направлении оси x
3
. (Поостережемся, однако, использовать формулу
и соответствующее ей время t
0
. Предположим, что в начальный момент времени t
= 0 обе системы координат совпадают. Будем предполагать, что "штрихованная" система координат движется с постоянной скоростью v
в направлении оси x
3
. (Поостережемся, однако, использовать формулу![]() — в теории относительности она неверна!).
— в теории относительности она неверна!).
Теперь представим себе, что в начальный момент времени t = 0 (при этом и t 0 = 0) в общем начале координат двух систем вспыхнула лампочка, возник источник электромагнитной волны. В исходной системе координат её фронт (множество точек, до которых в момент времени t дошла волна) задаётся уравнением
![]() .
(19.1)
.
(19.1)
Это сфера радиуса ct , где c — скорость света.
Но в подвижной системе координат уравнение этой поверхности, согласно двум постулатам, можно записать в аналогичной форме
![]() .
(19.2)
.
(19.2)
Замечу, что с точки зрения подвижной системы координат свет достигает границы сферы (19.1) неодновременно. Изменяется наш взгляд на природу времени. События, которые происходят одновременно в некоторой системе отсчета оказываются не одновременными в другой, движущейся относительно первой системе отсчета. одновременность событий относительна.
Эйнштейн предположил, что между старыми и новыми координатами имеется линейная зависимость (это можно доказать при помощи теоремы Мазура-Улама, см. Приложение 2). После линейной замены квадратичная форма (19.2) перейдет в квадратичную форму от x 1 , x 2 , x 3 , t . Чтобы при этом сфера (19.2) перешла в сферу (19.1), необходимо и достаточно выполнение соотношения
![]() .
(19.3)
.
(19.3)
Фронт волны есть физическая реальность, а системы координат мы вводим сами. В (19.3) κ = κ(v
) может зависеть лишь от v
. Но "неподвижная" система координат x
1
, x
2
, x
3
двигается относительно подвижной системы координат![]() со скоростью −v
, поэтому должно выполняться также
со скоростью −v
, поэтому должно выполняться также
равенство
![]() .
(19.4)
.
(19.4)
Сравнение этих двух равенств дает соотношение
κ(v )κ(−v ) = 1. (19.5)
В специальной теории относительности сохраняются постулаты об однородности и изотропности пространства. Изотропность, независимость свойств пространства от направления движения, влечет равенство κ(v ) = κ(−v ). Тогда из (19.5) следует, что κ2 (v ) = 1. Отсюда κ(v ) = ±1. Знак минус следует отбросить, потому что при v = 0 мы должны, очевидно, иметь κ(0) = 1. Если еще предположить, что κ(v ) непрерывно зависит от v (физики обычно считают ниже своего достоинства упоминать о таких математических «мелочах» — до тех пор, пока не произойдут большие неприятности из-за разрывов), получается, что κ(v ) = 1 для всех v . Выходит, что координаты и время в двух рассматриваемых системах отсчета должны быть связаны соотношением
![]() .
(19.6)
.
(19.6)
Связь между координатами и временем в двух системах отсчета разыскиваем теперь в виде x 01 = x 1 x 02 = x 2
x 03 = α x 3 + β t (19.7) t 0 = γx 3 + δt.
Константы α, β, γ, δ (зависящие от v ) находятся из условия (19.6). Искомое преобразование представляет собой известное преобразование Лоренца :
![]() (19.8)
(19.8)
,
где ε = v/c . К этим же формулам можно придти, разыскивая преобразования, относительно которых инвариантно волновое уравнение. Когда скорость движения v мала по отношению к скорости света, то есть в пределе ε → 0, преобразования Лоренца переходят в преобразования Галилея
![]() (19.9)
(19.9)
Как видим, с математической точки зрения вывод соотношений (19.8) весьма прост. Однако физические выводы поразительны. Оказывается, время не абсолютно, в чем был уверен Ньютон, а зависит от движения выбранной системы отсчета.
Раньше мы уже установили, что замена преобразований Галилея на преобразования Лоренца приводит к изменению закона сложения скоростей. Например, рассмотрим еще одну систему координат, которая движется также в направлении оси x 3 с постоянной скоростью u по отношению к подвижной системе координат. Тогда её скорость w по отношению к неподвижной системе координат оказывается равной не v + u (как получилось бы согласно преобразованиям Галилея), а определяется равенством
![]() .
(19.10)
.
(19.10)
Сокращение длин и отрезков времени. Еще до развития теории относительности Х. Лоренц и Дж. Фицджеральд для объяснения результатов некоторых экспериментов ввели предположение о сокращении длины тел в направлении их движения. Сначала казалось, что эффект Лоренца– Фицджеральда является динамическим , и сокращение длин происходит под действием некоторых неизвестных нам сил, скажем, сопротивления эфира движению тел. Возникала несколько смутная аналогия с движением тел в воздухе или воде. Быть может, главное достижение А. Эйнштейна (так считают многие физики) состоит в том, что он понял кинематический характер всех основных релятивистских эффектов — просто (просто!) так устроены пространство и время.
Теперь посмотрим, как непринужденно теория относительности объясняет эффект Лоренца–Фицджеральда, а заодно предсказывает еще более поразительный эффект сокращения отрезков времени. Ход времени зависит от движения тел! Время течет по-разному в движущемся поступательно с постоянной скоростью корабле и на «неподвижном» берегу. Это нелегко было усвоить современникам.
![]() Итак, представим себе, что в фиксированной («неподвижной») системе координат имеется стержень, длины `
, расположенный вдоль оси x
3
между r r r PP
Итак, представим себе, что в фиксированной («неподвижной») системе координат имеется стержень, длины `
, расположенный вдоль оси x
3
между r r r PP
z 1 z 2 z 3
Рис. 11
точками z 1 и z 2 , так что z 2 − z 1 = ` . Если теперь измерить длину этого стержня в подвижной (штрихованной) системе координат в момент t 0 , то получим
![]() ,
,
![]() .
(19.11)
.
(19.11)
Обозначим через![]() длину стержня в подвижной системе координат. Вычитая формулы (19.11) одну из другой, придем к равенству
длину стержня в подвижной системе координат. Вычитая формулы (19.11) одну из другой, придем к равенству
![]() .
(19.12)
.
(19.12)
Получается, что длина `
в неподвижной системе координат больше, чем длина стержня в движущейся системе. Аналогично воспользуемся связью между моментами времени![]() . Имеем
. Имеем
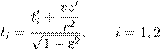 .
(19.13)
.
(19.13)
Далее получаем соотношения между отрезком времени t
2
− t
1
и соответствующим отрезком времени![]() в движущейся системе координат
в движущейся системе координат
![]() .
(19.14)
.
(19.14)
Эта простая формула влечет следствия, которые с большим трудом укладываются в сознание. Вы, наверное, слышали о так называемом парадоксе близнецов.
Представим себе, что один из двух близнецов садится в космический корабль и путешествует на нем со скоростью, достаточно близкой к скорости света. Потом он возвращается на Землю. Формула (19.14) говорит, что на Земле, к моменту его возвращения, прошло времени в ![]() больше, чем то время
больше, чем то время![]() , которое близнец-путешественник провел в своем космическом корабле. Таким образом, если ε достаточно близко к 1, то есть v
близко к c
, на Земле могло пройти сколь угодно большое время. Писателифантасты не раз эксплуатировали эту идею.
, которое близнец-путешественник провел в своем космическом корабле. Таким образом, если ε достаточно близко к 1, то есть v
близко к c
, на Земле могло пройти сколь угодно большое время. Писателифантасты не раз эксплуатировали эту идею.
Высказывались и различные возражения против парадокса близнецов. Главное из них состоит в том, что космический корабль, чтобы набрать скорость v , должен двигаться ускоренно, а специальная теория относительности не может описать, что происходит в движущейся ускоренно системе. Ответ другой спорящей стороны состоит в том, что корабль может набрать скорость с очень малым ускорением, а затем находиться в свободном полете со скоростью v значительно более долгое время. Разумеется, и тормозить при посадке на Землю он должен с малым ускорением. Тогда условия будут близки к тем, которые хорошо описываются теорией относительности. Другое возражение основывается на том, что при разгоне тела до скорости, близкой к скорости света, нужно затратить невообразимо огромную энергию. Ну, это уж не кажется таким принципиальным. Кстати, движение в ускоренных системах координат прекрасно описывается общей теорией относительности, и парадокс близнецов при этом сохраняется. Так что дело лишь за экспериментальной проверкой на людях. На элементарных частицах «парадокс» полностью подтвержден.
Механика теории относительности. Я уже говорил раньше, что Эйнштейн развил кинематику теории относительности, обнаружив при этом новые удивительные свойства пространства и времени. Но он пошел и дальше, создав релятивистскую динамику . Ее специфика связана с относительностью времени, отсутствием абсолютного ньютоновского времени, зависимостью времени от движения системы отсчета, естественно связанной с движущимся телом или материальной частицей.
Нетрудно убедиться, что в теории относительности инвариантна следующая величина
(¯x 1 − x 1 )2 + (¯x 2 − x 2 )2 + (¯x 3 − x 3 )2 − c 2 (t ¯− t )2 , (19.15)
которой присвоено несколько странное название «интервал». Здесь (x 1 ,x 2 ,x 3 ,t ), (¯x 1 ,x ¯2 ,x ¯3 ,t ¯) — две точки в одной и той же системе отсчета. Каждая такая точка четырехмерного пространства называется (может, чересчур пышно) событием . Разумеется, инвариантность в теории относительности, или релятивистская инвариантность , означает инвариантность относительно преобразования Лоренца. Лишь величины, не зависящие от нашего субъективного выбора системы отсчета, могут иметь физический смысл.
В случае, когда все приращения в (19.15) бесконечно малы, это выражение принимает вид
![]() .
(19.16)
.
(19.16)
Оказывается естественным ввести собственное время τ движущейся по произвольному закону xj = xj (t ) точки, полагая
![]() .
(19.17)
.
(19.17)
Отсюда для определения функции τ = τ(t ) получаем дифференциальное уравнение
![]() .
(19.18)
.
(19.18)
![]() Здесь ε = v/c
, причем скорость
Здесь ε = v/c
, причем скорость![]() определяется по заданному закону движения точки. Добавив начальное условие τ(0) = 0, мы определим собственное время частицы однозначно.
определяется по заданному закону движения точки. Добавив начальное условие τ(0) = 0, мы определим собственное время частицы однозначно.
Георг Минковский существенно упростил теорию, заметив, что после введения комплексной (чисто мнимой) переменной x 4 = ict , интервал (19.15) преобразуется к сумме квадратов. После этого становится ясно, что преобразование Лоренца получается попросту из преобразования вращения четырехмерного пространства переменных x 1 , x 2 , x 3 , x 4 . При этом, проводя многие аналитические выкладки, можно надолго забыть, что переменная x 4 играет особую роль (алгебра — сильная наука!), и вспомнить об этом лишь тогда, когда нужно осмыслить окончательный ответ. Такое четырехмерное пространство, с выделенной особо переменной x 4 , носит название четырехмерный мир Минковского . (К слову сказать, когда идут дискуссии о том, является ли наше пространство трехмерным или четырехмерным, а может, имеет большую размерность, то речь идет именно о пространстве. Существование еще одной переменной t подразумевается. В современной квантовой теории поля рассматриваются и варианты очень больших размерностей: быть может, наше пространство 9-мерно или даже 20-мерно. Главным аппаратом в этой науке служит теория групп Ли.)
В механике (точнее, в динамике) теории относительности, как и в классической механике, работает принцип Гамильтона. Изменение, однако, состоит в том, что вместо абсолютного времени, которого не существует, нужно использовать собственное время движущейся материальной частицы. Я ограничусь здесь случаем материальной частицы. Случай твердого тела вызвал известные трудности в связи с невозможностью передачи «сигнала» с произвольно большой скоростью. Ведь твердое тело целиком и мгновенно реагирует на движение любой его части. Трудности здесь разрешил
П. Эренфест. Впрочем, Ландау считал, что твердые тела просто невозможны в теории относительности.
В четырехмерном пространстве Минковского определяется релятивистский лагранжиан L = L (x,u, τ), где x = (x 1 ,x 2 ,x 3 ,x 4 ), u = (u 1 ,u 2 ,u 3 ,u 4 ), τ — собственное время движения частицы, а величины uj (j = 1,..., 4) суть компоненты релятивистской 4-скорости, определяемой дифференцированием по τ (а не по t ):
![]() .
(19.19)
.
(19.19)
Здесь t — время в некоторой фиксированной системе отсчета, которую мы можем считать неподвижной. Четвертая координата — особая:
![]() .
(19.20)
.
(19.20)
Целесообразно ввести еще компоненты скорости ![]() в неподвижной системе координат.
в неподвижной системе координат.
Далее, для любых двух моментов τ1 и τ2 (пусть τ1 < τ2 ) собственного времени τ мы определяем релятивистское (инвариантное относительно преобразования Лоренца) действие
![]() .
(19.21)
.
(19.21)
| Теперь постулируется вариационный принцип Гамильтона |
|
| δI = 0. |
(19.22) |
По-прежнему предполагается, что деформации не меняют начального и конечного положений частицы. Замечу, что вариационный принцип (19.22) имеет двойственную природу — он похож и на классический принцип Гамильтона, и на принцип Мопертюи–Якоби, описывающий движение на изоэнергетических поверхностях.
Чтобы найти лагранжиан свободной материальной частицы, можно действовать по аналогии с классической механикой. Пространство по-прежнему предполагается изотропным и однородным, но вместо принципа относительности Галилея, принимается принцип относительности Эйнштейна — инвариантность относительно преобразований Лоренца. Если воспользоваться представлением Минковского для четырехмерного пространства– времени, то нетрудно прийти к лагранжиану
![]() .
(19.23)
.
(19.23)
Сравните это выражение с классическим:
![]() .
(19.24)
.
(19.24)
Величина m 0 в (19.23) называется массой покоя частицы. Дальше мы увидим, что в отличие от классической механики, масса частицы зависит от её скорости (!).
Зная лагранжиан (19.23), мы можем определить релятивистские импульсы :
![]() .
(19.25)
.
(19.25)
Уравнения движения, вытекающие из вариационного принципа (19.22), имеют вид
![]() .
(19.26)
.
(19.26)
Для свободной материальной частицы (лагранжиан (19.23)) эти уравнения принимают вид
![]() .
(19.27)
.
(19.27)
Когда на частицу действуют внешние силы с компонентами Kj , в уравнениях появляется правая часть
![]() .
(19.28)
.
(19.28)
Величины Kj суть компоненты вектора, называемого силой Минковского.
Если перейти в уравнениях (19.27) и (19.28) к дифференцированию по t , получим
![]() .
(19.29)
.
(19.29)
Мы использовали формулы (19.19), (19.20) и тот факт, что![]() .
.
Если теперь ввести обозначение
![]() ,
(19.30)
,
(19.30)
то можно увидеть, что релятивистское уравнение движения (19.29) есть попросту уравнение движения частицы с переменной массой m :
![]() .
(19.31)
.
(19.31)
Итак, выяснилось, что масса — понятие относительное, она зависит от скорости движения. При этом масса m движущейся частицы всегда больше массы покоя m 0 .
В развитии физики играет существенную роль принципсоответствия . Мы уверены, что классическая механика, подтвержденная невообразимо огромным экспериментальным материалом, не будет опровергнута никакими новыми открытиями — в своей области применимости . Всякая новая теория должна содержать новый параметр, в теории относительности это — скорость света c или ε = v/c , такой, что в пределе, в данном случае при c = ∞ или ε = 0, новая механика переходит в классическую. То же самое относится и к другим обобщениям фундаментальных теорий классической физики, и в первую очередь, к квантовой механике. Конечно, принцип соответствия работает и при дальнейших обобщениях новых физических теорий.
Итак, мы ожидаем, что при ε → 0 релятивистские уравнения движения должны переходить в классические. Подсчитаем лагранжиан (19.23). Имеем
![]() .
(19.32)
.
(19.32)
Теперь перепишем выражение для релятивистского действия (19.21) в случае лагранжиана (19.23), переходя к интегрированию по времени t . Имеем
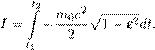 (19.33)
(19.33)
При малых ε подынтегральное выражение в (19.33) можно представить в виде
![]()
Итак, в классическом пределе, при ε → 0 лагранжиан в (19.33) принимает вид
![]() .
(19.35)
.
(19.35)
Постоянный множитель ![]() , конечно, несущественен. Дополнительное слагаемое −m
0
c
2
заставляет нас насторожиться. Если представить себе, что лагранжиан есть разность между кинетической и потенциальной энергиями, то выходит, что появилась дополнительная потенциальная энергия
, конечно, несущественен. Дополнительное слагаемое −m
0
c
2
заставляет нас насторожиться. Если представить себе, что лагранжиан есть разность между кинетической и потенциальной энергиями, то выходит, что появилась дополнительная потенциальная энергия
E = m 0 c 2 , (19.36)
которой обладает неподвижная материальная частица. Пока что трудно утверждать, что эта формула имеет серьезный физический смысл, потому что постоянный лагранжиан тривиален. Такое слагаемое в (19.35) можно просто отбросить, это не повлияет на уравнение движения. Итак, мы установили, что при ε → 0 релятивистские уравнения движения частицы переходят в классические.
Энергия в теории относительности. Мы будем пользоваться общим определением энергии в механике Гамильтона-Лагранжа:
E = vLv − L. (19.37)
Подправим выражение (19.33), внося в него такой постоянный множитель, чтобы в пределе ε → 0 получались в точности классическое действие и классический лагранжиан. Согласно (19.35), для этого нужно умножить (19.33) на 2. В результате получаем релятивистское действие в виде
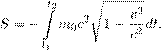 (19.38)
(19.38)
Лагранжиан дается формулой
![]() .
(19.39)
.
(19.39)
Теперь вычислим энергию E . Из (19.39) имеем
![]() .
(19.40)
.
(19.40)
По формуле (19.37) получаем
![]() .
(19.41)
.
(19.41)
Вот теперь нет сомнений, что при v = 0 частица действительно обладает энергией покоя , определяемой по формуле (19.36). Вообще, формула (19.41) описывает глубокую связь между массой и энергией и, в некотором смысле, их эквивалентность. Множитель c 2 выглядит как коэффициент перехода от одних единиц измерения к другим, вроде механического эквивалента теплоты. При желании энергию можно было бы измерять в граммах или других единицах массы.
Когда элементарные частицы — протоны, нейтроны и электроны — объединяются в один атом, масса атома оказывается меньше суммарной массы этих частиц. Теряется свойство аддитивности массы. Причина состоит в том, что при таком соединении испускается свет, электромагнитная волна. Частицы света имеют нулевую массу покоя (для них m 0 = 0). Двигаются они, понятно, со скоростью c . Если при этом излучается энергия ∆E , то возникает дефект массы
![]() .
(19.42)
.
(19.42)
Так теория относительности непринужденно объяснила, почему атомные массы (чаще говорят о весах) элементов меньше, чем суммарные массы составляющих атомы частиц.
20. Каноническая гамильтонова форма уравнений механики
При определенных условиях общего положения (невырожденности системы) уравнения Лагранжа могут быть приведены к канонической форме
Гамильтона. В случае n степеней свободы уравнения Лагранжа представляют собой систему n уравнений второго порядка, а соответствующая гамильтонова система содержит 2n уравнений первого порядка. Канонические (ныне чаще называемые гамильтоновыми ) уравнения не только отличаются особым изяществом, но обладают рядом специфических алгебраических и геометрических свойств, делающих их наиболее удобным инструментом исследования в механике и ее приложениях. В дальнейшем я продемонстрирую применение гамильтоновых уравнений в статистической механике .
ПреобразованиеЛежандра. Рассмотрим функцию двух скалярных переменных f (x,y ). Ее дифференциал запишем в виде
![]() .
(20.1)
.
(20.1)
Замечая, что udx = d (ux ) − xdu , можно переписать равенство (20.1) в виде
d (xu − f ) = xdu − vdy. (20.2)
Теперь сделаем одновременную замену функции и ее аргументов, полагая
g (u,y ) = xu − f. (20.3)
Здесь, вместо x , y , введены аргументы u и y .
Это и есть преобразование Лежандра по переменной x . Заметим, что такое преобразование можно провести не всегда, а лишь в том случае, когда замена переменных (x,y ) → (u (x,y ),y ) взаимно однозначна в области определения функции f . Для того, чтобы эта взаимная однозначность имела место, хотя бы локально, достаточно (согласно теореме о неявной функции), чтобы был отличен от нуля якобиан:
![]() .
(20.4)
.
(20.4)
Гамильтоновы уравнения. Канонические уравнения Гамильтона получаются из уравнений Лагранжа второго рода посредством преобразования Лежандра по всем обобщенным скоростям q ˙i . Можно применить формулу (20.3), но, как и во многих других случаях, целесообразно воспользоваться лишь идеей, а выкладки провести непосредственно.
Запишем дифференциал функции Лагранжа L (q,q,t ˙ ) при фиксированном t в виде
![]() .
(20.5)
.
(20.5)
Введем обозначения
![]() (20.6)
(20.6)
и назовем p вектором импульса , pi — его i -ая компонента; i = 1,...,n , если n — число степеней свободы.
Далее используем равенства
![]() .
(20.7)
.
(20.7)
| В компактной форме они записываются как |
|
| Lq ˙ · dq ˙ = d (p · q ˙) − q ˙ · dp. Введем функцию Гамильтона H = H (p,q,t ), полагая |
(20.8) |
| H = p · q ˙ − L = pi q ˙i − L. |
(20.9) |
Теперь, подставляя выражение (20.8) в (20.5), приходим к формуле
dH = q ˙ · dp − Lq · dq. (20.10)
Отсюда следуют равенства
Hp = q, ˙ Hq = −Lq . (20.11)
До этого момента мы не вспоминали об уравнении Лагранжа
![]() ,
(20.12)
,
(20.12)
которое теперь запишем в виде p ˙ = Lq .
В результате из соотношений (20.11) и (20.12) выводим канонические уравнения Гамильтона
p ˙ = −Hq , q ˙ = Hp , (20.13)
или, в координатах,
![]() ,
,
![]() (20.14)
(20.14)
Гамильтониан H = H (p,q,t ), как видно из его определения (20.9), есть не что иное как полная механическая энергия системы, выраженная через координаты и импульсы . В случае, когда он не зависит от времени, выполняется закон сохранения энергии: H (p,q ) есть интеграл гамильтоновой системы (20.14) (проверьте!).
Подчеркну, что преобразование Лежандра, которое привело нас к гамильтоновым уравнениям (20.14), применимо не всегда. Может оказаться, что в фазовом пространстве имеются поверхности, линии или отдельные точки, в которых отсутствует взаимно однозначная связь между обобщенными скоростями q ˙i и импульсами pj . Это происходит, когда нарушаются условия теоремы о неявной функции для уравнения p = Lq ˙ (q,q ˙):
![]() .
(20.15)
.
(20.15)
Гамильтонова система (20.14) допускает красивую и полезную трактовку как одно векторное уравнение в R2n
. Определим вектор x
∈
R2n
, полагая x
= (q,p
) = (q
1
,...,qn
,p
1
,...,pn
). Вместо H
(p,q
) будем теперь писать H
= H
(x
). Тогда grad H
можно записать в виде grad![]()
Введем оператор J : R2n → R2n , задав его операторной матрицей
![]() ,
(20.17)
,
(20.17)
где In : Rn → Rn — тождественный оператор в Rn . Заметим, что J 2 = −I 2n (I 2n — тождественный оператор в R2n ). Система (20.14) записывается теперь в виде
x ˙ = J grad H (x ). (20.18)
Гамильтонова форма уравнения второго закона Ньютона. Обобщенное уравнение второго закона Ньютона определяется лагранжианом
![]() ,
(20.19)
,
(20.19)
где x — точка евклидова пространства H. В случае конечномерного евклидового пространства H, dimH = n , его можно отождествить с Rn . Замечу, однако, что развиваемый формализм не зависит от размерности и применим, например, к волновому уравнению. Иное дело, что в случае бесконечномерного гильбертова пространства H нужны, конечно, дополнительные обоснования производимых нами операций. Аналогично (20.7) вводим импульс p , полагая
p = Lx ˙ = Mx ˙ . (20.20)
Гамильтониан, соответствующий лагранжиану (20.19), получаем с использованием формулы (20.9), выражая скорость через импульс посредством равенства x ˙ = M −1 p . Он имеет вид
![]()
Соответственно, гамильтонова форма обобщенного уравнения второго закона Ньютона имеет вид
| p ˙ = −grad V (x ), x ˙ = M −1 p. Мы воспользовались здесь простой общей формулой |
(20.22) |
grad ![]() (20.23)
(20.23)
справедливой для любого линейного самосопряженного
оператора A
(для произвольного линейного оператора справа следует написать ![]()
Хотя здесь нет места для строгого изложения, не могу удержаться от того, чтобы не привести следующий пример из математической физики. Волновое уравнение. Рассмотрим волновое уравнение в области в ⊂
Rn
ρ(x )utt = c 2 ∆u (20.24)
с краевым условием
![]() .
(20.25)
.
(20.25)
Здесь ρ(x ) — непрерывная неотрицательная функция, удовлетворяющая условию ρ(x ) ≥ ρ0 > 0, c > 0 — положительная константа, как и ρ0 . Мы уже видели, см. формулы (5.20) – (5.27), что это уравнение допускает интеграл энергии. Кинетическая энергия T и потенциальная энергия V задаются формулами
![]() (20.26)
(20.26)
(20.27)
Вы помните, что градиент функционала V , заданного на гильбертовом пространстве H , в точке u ∈ H определяется равенством
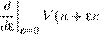 ) = (grad V
(u
),v
),
(20.28)
) = (grad V
(u
),v
),
(20.28)
которое должно выполняться для любого v ∈ H . Левая часть этого равенства есть дифференциал Гато в точке u , и предполагается, что он является также и дифференциалом Фреше.
В нашем случае H = L
2
(D), и grad V
(u
) определен не для всех u
, а лишь для достаточно гладких функций, скажем, для u
∈ C
2
(D) (а более того, для![]() ). Для такой функции u
имеем
). Для такой функции u
имеем
![]()
В промежуточном равенстве использована C
1
-гладкость функции v
, но последнее равенство имеет смысл уже для любой функции![]() . Его можно обосновать непосредственно, приближая
. Его можно обосновать непосредственно, приближая![]() гладкими функциями. Таким образом, для достаточно гладких функций u
получаем
гладкими функциями. Таким образом, для достаточно гладких функций u
получаем
grad ![]() (20.30)
(20.30)
Подчеркну, что градиент в (20.30) берется в пространстве H = L 2 (D ). Вы, конечно, помните, что градиент зависит от выбора скалярного произведения.
Поскольку рассматриваемая система натуральна, так что L = T − V , имеем
![]()
Lu = −grad V = c 2 ∆u
Таким образом, гамильтонова форма волнового уравнения имеет вид
![]() (20.31)
(20.31)
(20.32)
Вырожденныелагранжианы. Для вырожденных лагранжианов — линейных по скорости и имеющих вид L (q,q ˙) = A (q,t )q ˙ + B (q,t ), см. (10.23), очевидно, Lq ˙q ˙ = 0 тождественно. Поэтому преобразование Лежандра неприменимо ни в какой точке. В этом случае гамильтониан H не зависит от q ˙ и даже тождественно равен нулю при B ≡ 0. Действительно, согласно общему определению, p = Lq ˙ = A (q,t ), и
H = p · q ˙ − L = A (q,t ) · q ˙ − A (q,t ) · q ˙ − B (q,t ) = −B (q,t ). (20.33)
Действуя формально, мы можем написать соответствующие гамильтоновы уравнения в виде p ˙ = Bq , q ˙ = 0. Однако эти уравнения не имеют никакого отношения к исходной системе уравнений Лагранжа (объясните, почему?). Это лишний раз напоминает нам о необходимости контролировать законность проводимых формальных выкладок.
Интересно заметить, что в математической физике встречаются такие системы, которые имеют гамильтонову форму по своей исходной постановке. Замечательный пример тому — уравнения Кирхгофа , описывающие динамику системы вихревых нитей (или точечных вихрей на плоскости, либо на иной поверхности) в жидкости. По всей видимости, их нельзя получить ни из каких лагранжевых уравнений. Эта система последние десятилетия вызывает повышенный интерес исследователей и как своеобразный пример, на котором испытываются и развиваются новые методы качественной теории дифференциальных уравнений, и как подходящая модель для описания вихрей в атмосфере, а также электронных колонн при электрическом газовом разряде. О системе уравнений Кирхгофа можно прочитать практически в любом учебнике по гидродинамике. С новейшим развитием теории можно познакомиться по книге [45].
Интересный вопрос о возможности построения системы уравнений Лагранжа, которой бы отвечала заданная гамильтонова система, по-моему, совсем не разобран. Дело сводится к решению нелинейного дифференциального уравнения в частных производных первого порядка, которое получает-
∂L
ся подстановкой выражения импульса p
= ![]() через обобщенные коорди-
через обобщенные коорди-
∂q ˙
наты q и обобщенные скорости q ˙ в равенство (20.9), выражающее гамильтониан через лагранжиан. Это дифференциальное уравнение относительно неизвестной функции L = L (q,q,t ˙ ) записывается в виде
![]() (20.34)
(20.34)
Далеко не всегда у него есть решение, определенное на всем расширенном фазовом пространстве переменных (q,q,t ˙ ). Подобные результаты можно получить, лишь налагая на гамильтониан специальные ограничения. Вместе с тем, механика не содержит никаких ограничений такого рода. Выходит, что нужно искать дополнительные свойства гамильтонианов, которые вытекают из законов термодинамики.
Замечу, что подобные проблемы постоянно возникают в механике и в математической физике. И уравнения механики, и уравнение диффузии, и волновые уравнения зачастую содержат функции от переменных состояния и параметры, которые предлагается определять из экспериментов. Любые знания об этих функциях, скажем, о зависимости коэффициента теплопроводности от температуры или о зависимости скорости распространения волны в данной среде от параметров ее состояния, могут существенно сократить необходимую экспериментальную работу. В идеале, дело должно сводиться к экспериментальному определению небольшого числа констант. Иногда к такому приятному результату нас приводят те или иные асимптотические методы.
Скобка Пуассона. Для любой гладкой функции F (p,q ), заданной на фазовом пространстве гамильтоновой системы (20.13), можно найти ее производную F ˙ (p,q ) в силу уравнения движения (20.13) в векторной форме
| F ˙ = F q H p − F p H q , или в координатах |
(20.35) |
![]() .
(20.36)
.
(20.36)
Правая часть этого уравнения называется скобкой Пуассона функций F и H и обозначается как {F,H }. Очевидно, функция F является интегралом гамильтоновой системы с гамильтонианом H в том и только в том случае, когда
{F,H } = 0. (20.37)
Оказывается полезным определить скобку Пуассона {F,G } для произвольных гладких функций F (p,q ) и G (p,q ), полагая
{F,G} = Fq Gp − Fp Gq . (20.38)
Введенная таким образом билинейная операция над функциями кососимметрична:
{F,G } = −{G,F }. (20.39)
Скобка Пуассона определяет своего рода умножение пары функций. Эта операция, согласно (20.39), кососимметрична и неассоциативна. Некоторой заменой ассоциативности служит тождество Якоби для тройки произвольных гладких функций f , g , h :
{f,{g,h}} + {g,{h,f}} + {h,{f,g}} = 0. (20.40)
Билинейная операция, обладающая свойствами (20.39) и (20.40) для произвольных пар и, соответственно, троек из некоторого линейного пространства, определяет важную алгебраическую структуру — алгебру Ли.
Тождество Якоби допускает красивую алгебраическую трактовку. Оператор A , действующий в алгебре Ли, называется дифференцированием этой алгебры, если для него справедливо равенство, которое можно назвать равенством Лейбница
A{g,h} = {Ag,h} + {g,Ah}. (20.41)
Каждый элемент f определяет линейный оператор Af по формуле
Af g = {f,g }. (20.42)
Тождество Якоби говорит, что оператор Af есть дифференцирование алгебры Ли . Действительно, учитывая кососимметричность скобки Пуассона, равенство (20.40) можно переписать в виде
{f,{g,h}} = {{f,g},h} + {g,{f,h}}, (20.43)
что совпадает с (20.41) при A = Af .
Как доказал Пуассон, если F и G — два интеграла гамильтоновой системы (20.13), их скобка Пуассона {F,G } также есть интеграл. Это означает, что множество всевозможных C ∞ -гладких интегралов гамильтонова уравнения образует алгебру Ли.
Результат Пуассона может вызвать неоправданный оптимизм по поводу проблемы интегрируемости уравнений Гамильтона. Может показаться, что последовательно вычисляя скобки Пуассона известных нам интегралов, можно найти достаточное их число для полного решения гамильтоновой системы. Увы, скобка двух интегралов может оказаться тривиальным интегралом (константой) или функцией от уже известных интегралов. Так оно обычно и получается. Например, знание интегралов энергии, импульса и момента импульса не позволяет найти новые интегралы гамильтоновой системы.
21 Силы трения. Диссипация энергии
Интересная и очень важная для механики, геометрии и вариационного исчисления теория канонических гамильтоновых систем рассмотрена во многих книгах, см. классическое изложение в [14, 46]. Современное изложение в рамках геометрии многообразий дано в книге В.И.Арнольда [3].
Упражнения
1. Докажите, что гамильтонову систему (20.14) можно записать в виде
p ˙i = {pi ,H }, q ˙i = {qi ,H },
или, вводя очевидные векторные обозначения,
p ˙ = {p,H }, q ˙ = {q,H }.
2. Докажите, что если бы скобка Пуассона обладала свойством ассоциативности, то отсюда следовало бы тождество Якоби.
3. Докажите (а если не получится, найдите доказательство в рекомендованных книгах [14, 46, 3]) тождество Якоби (20.40).
4. Из тождества Якоби (20.40) выведите утверждение Пуассона: вместес двумя интегралами F и G , также их скобка Пуассона {F,G } есть интеграл.
5. Докажите, что для любых трех гладких функций F , G , K от p и p в случае, когда K обращается в ноль вне некоторого шара, справедливо равенство
Z Z
{G,F }K dpdq = F {K,G }dpdq.
R2n R2n
Отсюда следует, что в случае недифференцируемой функции F скобке Пуассона {F,G } можно придать смысл обобщенной функции — распределения.
6. Докажите, что преобразование Лежандра переводит выпуклые функции в выпуклые. Более того, справедливо равенство guu (u,y ) = fxx (x,y ) в обозначениях (20.2), (20.3).
7. Запишите интегралы импульса и момента импульса для гамильтоновой формы второго закона Ньютона (20.22) в условиях, когда все они существуют. Найдите их скобки Пуассона. Докажите, что эти 6 интегралов порождают алгебру Ли, так что новых интегралов этим способом получить не удается.
21. Силы трения. Диссипация энергии
В природе все реальные механические системы находятся под действием тех или иных сил трения. Брошенный на Земле камень не сохраняет постоянную поступательную скорость движения, как то предписывается законом Галилея (он же — первый закон Ньютона), а довольно скоро останавливается из-за сопротивления воздуха и сухого трения о поверхность, когда он катится по земле. Силы трения — немеханического происхождения. Поэтому, как правило, в курсах механики, написанных физиками (Ландау и Лифшиц, Голдстейн, Синг), силы трения не рассматриваются. Вместе с тем, механики, рассчитывающие на инженерные приложения своей науки, уделяют значительное внимание силам трения (Лойцянский и Лурье, Аппель, Леви – Чивита и др.). Пожалуй, наиболее полное представление о большой сложности законов трения и о современном состоянии их изучения можно получить по книге И.И. Воровича [8]. Вообще, надо признать, что силы трения, возникающие из-за взаимодействия системы с окружающей средой, пожалуй, наиболее сложные из известных нам сил природы.
Простейшее, и не вполне точное, определение сил трения состоит в том, что они ведут к уменьшению, к рассеянию энергии . Часто употребляемый синоним слова рассеяние — диссипация . Неточность этого определения связана с тем обстоятельством, что зачастую силы трения имеют двойственную природу и могут иногда приводить и к увеличению энергии. Вообще, силы трения очень разнообразны, и трудно, если не сказать невозможно, сформулировать единообразно общие законы трения. Здесь мы рассмотрим лишь простейшие виды трения.
Само понятие о диссипации энергии возникает, когда рассматриваются незамкнутые системы и не все виды энергии принимаются во внимание. Скажем, диссипация механической энергии означает, что часть энергии превращается в другие виды, обычно — в тепловую энергию.
Начнем с обобщенного уравнения второго закона Ньютона в евклидовом пространстве H :
Mx ¨ = −grad V (x ). (21.1)
Как мы знаем, для этого уравнения справедлив закон сохранения механической энергии: полная механическая энергия
![]() (21.2)
(21.2)
является интегралом уравнения (21.1). Когда система двигается во внешней среде, действует дополнительная сила, возникающая из-за взаимодействия со средой (сила сопротивления внешней среды), которая в обычных условиях (скажем, в спокойной и безветренной атмосфере) приводит к затуханию движения. Когда тело находится в покое, сила сопротивления равна нулю. Если допустить, что она гладко зависит от скорости x ˙, то можно утверждать, что хорошим приближением при малых скоростях будет закон трения
F = −B (x )x, ˙ (21.3)
где B (x ) для каждого x ∈ H есть линейный оператор. Тогда уравнение (21.1) придется заменить уравнением
Mx ¨ = −grad V (x ) − B (x )x. ˙ (21.4)
Вычисляя производную по времени от энергии E , получаем уравнение изменения энергии :
![]() .
(21.5)
.
(21.5)
Поскольку согласно определению, действие силы трения приводит к уменьшению энергии, нужно считать, что B (x ) для каждого x является положительно определенным, или хотя бы положительным оператором, так что для любого ξ ∈ H и любого x выполняется неравенство
(B (x )ξ, ξ) ≥ 0. (21.6)
Если это неравенство может превратиться в равенство лишь для ξ = 0, так что оператор B (x ) является строго положительным , то говорят, что сила трения −B (x )x ˙ обладает свойством полной диссипации . В этом случае, согласно уравнению (21.5), энергия E уменьшается, диссипирует при любых движениях. Замечу, что в конечномерном случае из строгой положительности следует положительная определенность оператора, в бесконечномерных задачах это уже не так.
Естественно ввести диссипативную функцию Рэлея W , полагая
![]() .
(21.7)
.
(21.7)
Тогда сила трения F = −B (x )x ˙ выражается в виде
F = −grad x ˙ W. (21.8)
Силу трения, определяемую диссипативной функцией, называют рэлеевской . Чаще всего встречается рэлеевская сила трения F = −Bx ˙ с оператором B , не зависящим от x .
В определении Рэлея весьма существенно требование симметричности оператора B . Именно это свойство однозначно определяет оператор B при заданной диссипативной функции W , которая является квадратичной формой от x ˙. Произвольный линейный оператор A : H → H можно представить в виде суммы
A = Ar + Ac , (21.9)
где Ar — симметричный оператор, а Ac — кососимметричный. Они выражаются формулами
![]() .
(21.10)
.
(21.10)
Ясно, что кососимметрическое слагаемое не дает вклада в квадратичную форму (A ξ, ξ), поскольку (Ac ξ, ξ) = 0 для всех ξ ∈ H . Силы вида Ac x ˙ тоже, конечно, встречаются в механике, но имеют совсем иную физическую природу: это гироскопическиесилы . Такая сила не совершает работы при реальных движениях, не вносит вклада в уравнение изменения энергии (21.5). Рэлей, вводя требование симметричности для оператора B , со вкусом разделил эти два вида сил. Интересно, что еще Ньютон, выводя закон сохранения живой силы (так тогда называли кинетическую энергию), заметил, что сила, в каждый момент времени ортогональная к скорости, не препятствует сохранению живой силы. Курьезно, что это замечание Ньютона несколько сот лет оставалось почти неизвестным из-за того, что при переводе главного труда Ньютона с латыни на английский как раз в этом месте допустили ошибку.
Приведу здесь общее определение. Оператор Γ : H → H , действующий в евклидовом (в частности, гильбертовом) пространстве H , называется гироскопическим , если для всех ξ ∈ H выполняется равенство
(Γξ, ξ) = 0. (21.11)
В частности, кососимметрический оператор есть линейный гироскопический. Можно еще сказать, что гироскопическим называется оператор, который является косимметрией тождественного оператора Ix = x .
Одним из классических примеров гироскопической силы служит сила Кориолиса Fc = 2ω ∧ v , возникающая в уравнениях относительного движения, записываемых в подвижной системе координат, вращающейся с угловой скоростью ω. Гироскопическую силу, например, приходится учитывать при расчете движения тел относительно Земли.
Диссипация энергии при движении вязкой жидкости, функционал Рэлея
Уравнения Навье–Стокса в случае несжимаемой жидкости имеют вид
![]() (21.12)
(21.12)
div v = 0, (21.13)
где v = v (x,t ) — поле скорости, p = p (x,t ) — давление, x — точка
пространства R
3
(или R
2
), t
— время, а материальная производная
![]() дается равенством:
дается равенством:![]() . Будем считать, что жидкость заключена в области D
⊂ R
3
, граница которой ∂D
неподвижна и непроницаема для жидкости, так что выполняется краевое условие
. Будем считать, что жидкость заключена в области D
⊂ R
3
, граница которой ∂D
неподвижна и непроницаема для жидкости, так что выполняется краевое условие
![]() .
(21.14)
.
(21.14)
Предполагается, что на жидкость не действуют никакие внешние силы, впрочем, если сила потенциальна, какова, например, сила тяжести, то её удельную потенциальную энергию можно просто добавить к давлению, а на скорость она не влияет.
Наша цель сейчас — во-первых, показать, что сила ньютоновского трения ν∆v (ν > 0 — кинематический коэффициент вязкости) является рэлеевской — при естественном обобщении данного понятия. Для этого мы введем соответствующий функционал Рэлея. Затем мы покажем, что при сформулированных условиях кинетическая энергия жидкости экспоненциально затухает при t → +∞. Замечу, что в следующих рассмотрениях существование и единственность решения задачи (21.12)–(21.14) с начальным условием
![]() (21.15)
(21.15)
предполагается. В (21.15) начальное поле скорости v 0 — достаточно гладкое и соленоидальное (div v 0 = 0). На самом деле, существование и единственность доказаны лишь в двумерном случае, а в трехмерном — это одна из самых трудных проблем математической гидродинамики, решенная лишь для малых начальных скоростей v 0 . Недавно частный институт Клэя в США объявил премию в 1 млн долларов за её решение. О современном состоянии проблемы Вы можете прочитать в моей статье [53].
На пространстве гладких соленоидальных полей, удовлетворяющих краевому условию (21.14), определим квадратичный функционал W , полагая
![]() (21.16)
(21.16)
Интегрируя по частям, можно и полезно привести функционал W к виду, содержащему лишь первые производные. Учитывая, что граничные интегралы пропадают ввиду краевого условия (21.14), получаем
![]() (21.17)
(21.17)
Варьируя W , находим
![]() (21.18)
(21.18)
Таким образом, градиент функционала W в пространстве L 2 (D ) имеет вид
grad W = −ν∆v. (21.19)
Итак, W, действительно, есть диссипативный функционал Рэлея, ньютоновское трение является рэлеевским. Вспоминая определение функциональной производной и функционального градиента, можно также написать
− ν∆v = Grad W [v ], (21.20)
или в координатах
![]() .
(21.21)
.
(21.21)
Теперь докажем, что нелинейный член в уравнении Навье – Стокса обладает гироскопическим свойством. Мы установим более общее равенство
Z
(u,∇)v · v dx = 0, (21.22)
D
если векторное поле u
соленоидально и касательно к границе ![]() 0. Имеем
0. Имеем
![]() (21.23) Интегрируя по частям, получаем
(21.23) Интегрируя по частям, получаем
![]() div
div ![]() (21.24)
(21.24)
Оба слагаемых справа исчезают, ввиду предположенных свойств поля u , что и приводит к равенству (21.22).
Заметим, что от поля v
не пришлось ничего требовать, кроме достаточной регулярности. Кроме того, краевое условие (21.14) использовано здесь не в полной мере — требуется лишь, чтобы на границе исчезла нормальная компонента скорости. Поэтому равенство (21.22) справедливо и в том случае, когда u
— поле скоростей идеальной жидкости при условии непроницаемости границы (![]()
Теперь умножим уравнение движения вязкой жидкости (21.12) скалярно на v и проинтегрируем по области D . Примем в расчет равенство (21.22) при u = v , а также равенство
Z
| v · ∇pdx = 0. D В результате получим уравнение диссипации энергии |
(21.25) |
![]() (21.26)
(21.26)
которое в терминах кинетической энергии T и функционала Рэлея W записывается в виде
![]() (21.27)
(21.27)
Замечу, что равенство (21.27) весьма желательно, по существу даже необходимо, сохранять при любых способах аппроксимации уравнения Навье – Стокса. Можно даже рекомендовать при построении сеточной или спектральной аппроксимации начинать с аппроксимации функций T и W . Опыт говорит, что нарушение фундаментального уравнения (21.27) приводит к непригодности приближенной схемы решения, которая в таком случае может давать даже качественные неправильные результаты. Например, кинетическая энергия T может оказаться бесконечно большой, хотя, согласно точному уравнению (21.26), она монотонно убывает со временем.
Экспоненциальное затухание энергии
В случае сил трения с полной диссипацией, в предположении, что система конечномерна, можно доказать, что возмущения устойчивого равновесия затухают экспоненциально. Решения линейной задачи суть линейные комбинации элементарных решений вида e λ t ϕ, причем все собственные значения λ лежат в левой полуплоскости: Reλ < 0; в отсутствие гироскопических сил все они вещественны. В достаточно общих условиях теорема Ляпунова о законности линеаризации устанавливает, что экспоненциальное затухание сохраняется и для нелинейной задачи. В бесконечномерных задачах, скажем, в механике сплошной среды, ситуация осложняется. Линеаризованная задача может обладать непрерывным спектром, так что для ее решений уже нет такого простого представления. Даже когда подобное представление решений линеаризованной задачи, на сей раз в виде бесконечного ряда, имеет место, может статься, что вообще невозможно дать никакой квалифицированной оценки скорости затухания — возмущения могут затухать сколь угодно медленно, см. упражнения 1,2.
Сейчас мы покажем, что в случае ограниченной области D , при условии неподвижности границы, возмущения все-таки затухают экспоненциально. Решающую роль далее играет неравенство Фридрихса
Z Z
u 2 dx ≤ γ −1 (∇u )2 dx, (21.28)
D D
которое справедливо для любых функций u , исчезающих на границе области D , константа γ = γD зависит лишь от области D , которая сейчас предполагается ограниченной.
Если векторное поле v исчезает на границе ∂D , то записываем неравенство (21.28) для каждой его декартовой компоненты vi , i = 1, 2, 3 и, суммируя полученные неравенства, приходим к неравенству Фридрихса для векторного поля
Z Z
v 2 dx ≤ γ −1 (∇v )2 dx, (21.29)
D D
Замечу, что неравенство Фридрихса заведомо несправедливо для неограниченных областей D , содержащих окрестность бесконечно удаленной точки, например, для областей, внешних по отношению к шару или другой ограниченной области. Вместе с тем, оно остается справедливым например для слоя между двумя плоскостями, если предполагать, что функция u исчезает на бесконечности. На самом деле, неравенство (21.28) остается верным, если расстояние ρ(x,∂D ) точки x ∈ D от границы ∂D ограничено сверху. Слой этим свойством обладает, а угол на плоскости или клин в R3 — не обладает, и для них неравенство (21.28) уже неверно; (см., однако, упражнение 3).
Понятно, что неравенство (21.28) остается верным, если константу γ уменьшить. Наилучшее, то есть наибольшее, значение константы γ в этом неравенстве есть наименьшее собственное значение оператора Лапласа при краевом условии первого рода. Известен вариационный принцип (см. [28]): наименьшее собственное значение λ1 спектральной краевой задачи
![]() (21.30)
(21.30)
можно определить как минимум функционала
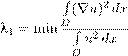 ,
(21.31)
,
(21.31)
Минимум здесь берется по всевозможным функциям, исчезающим на границе области D .
Вообще для оператора Лапласа с краевым условием первого рода существует бесконечная последовательность собственных значений λ1 ≤ λ2 ≤ ... ≤ λn ≤ ... , причем λn → ∞, когда n → ∞. Все они положительны и полупросты. В случае скалярных функций можно доказать, что λ1 — простое собственное значение, которому отвечает единственная (с точностью до ненулевого скалярного множителя) собственная функция ϕ1 ; известно, что она не меняет знака в области D . Можно считать, что ϕ1 (x ) > 0 для всех x ∈ D , см.[28]; [18].
Обратимся к уравнению изменения энергии (21.26) ((21.27)). Оценивая правую часть при помощи неравенства Фридрихса (21.29)
![]() (21.32)
(21.32)
| Из (21.32) стандартно выводим оценку |
|
| T (t ) ≤ T (0)e −2 γν t . |
(21.33) |
Таким образом, кинетическая энергия жидкости экспоненциально убывает. В качестве γ можно взять определенное выше собственное значение λ1 .
Однако наилучшее (то есть наибольшее) значение этой постоянной находится посредством решения спектральной задачи Стокса
| −∆v = µ v − ∇q, |
(21.34) |
| div v = 0, |
(21.35) |
![]() .
(21.36)
.
(21.36)
Можно доказать, что и эта спектральная задача имеет последовательность положительных собственных значений µ1 ≤ µ2 ≤ ... ≤ µn ≤ ... , µn → +∞ при n → ∞, см.[58]. В качестве γ в (21.33) можно взять µ1 , и этот результат уже не улучшаем: существуют решения линеаризованной на равновесии v 0 = 0 системы Навье – Стокса, которые затухают в точности по закону e −2 νµ 1 t . Более того, решения с таким же поведением имеются и у нелинейной системы Навье – Стокса.
Остается повторить, что наш вывод основывается на предположении, что существует гладкое решение, определенное для всех t > 0. В настоящее время это предположение доказано для произвольных гладких начальных полей лишь в двумерном случае, а для трехмерного случая представляет собой одну из самых жгучих нерешенных проблем современной математики.
Нужно еще подчеркнуть, что проблема поведения решения при t → +∞ резко усложняется, когда на границе области D задана ненулевая скорость, и когда имеются непотенциальные массовые силы. Один из классиков математической гидродинамики Э.Хопф меланхолически заметил, что в такой общей ситуации течение жидкости при t → +∞ по-прежнему стремится к чему-то, “но это что-то далеко от того, чтобы быть единственным стационарным течением” (“...but this something is far from to be a single stationary point”). Здесь мы встречаемся с новым, до сих пор таинственным явлением — турбулентностью. Возникают сложные режимы течения жидкости, в которых скорость и давление претерпевают сложные хаотические колебания в пространстве и во времени.
Упражнения
1. Рассмотрим дифференциальное уравнение x ˙ = −Ax в гильбертовом пространстве H . Предположим, что A самосопряженный оператор, и его спектр состоит из положительных собственных значений λ1 ,..., λk ,... , причем λk → 0 при k → ∞, а также предельной точки 0. Докажите, что все решения этого уравнения стремятся к нулю при t → ∞, но могут стремиться к нулю сколь угодно медленно: какова бы ни была положительная функция ρ(t ), определенная при t > 0, найдется такое решение данного уравнения, для которого выполнено предельное равенство
![]() .
.
Указание. Докажите, что эволюционный оператор U (t ) этого уравнения при t → +∞ стремится к нулю поточечно, но неравномерно. Примените теорему Банаха–Штейнгауза.
2. Докажите, что всякое решение уравнения теплопроводности ![]()
∆u
во всем пространстве Rn
с условием![]() и с начальным условием u
(x,
0) = ϕ(x
), причем ϕ
∈ L
2
(Rn
), стремится к нулю при t
→ +∞ по норме L
2
: R
u
2
(x,t
)dx
→ 0, причем эта сходимость может быть сколь
и с начальным условием u
(x,
0) = ϕ(x
), причем ϕ
∈ L
2
(Rn
), стремится к нулю при t
→ +∞ по норме L
2
: R
u
2
(x,t
)dx
→ 0, причем эта сходимость может быть сколь
R n угодно медленной (см. упражнение 1).
3. Пусть D есть угол на плоскости, определяемый в полярных координатах (r, θ) неравенством 0 < θ < α, где 0 < α < 2π. Докажите, что неравенство Фридрихса в этом случае уже несправедливо, но для любой функции u , исчезающей на границе, справедливо неравенство
![]()
причем µ — положительная постоянная, зависящая только от α, но не от функции u . Сформулируйте и докажите аналогичный результат для случая, когда D — конус в Rn .
4. Докажите, что всякая функция, определенная на пространстве R 3 , непрерывно дифференцируемая и затухающая на бесконечности, удовлетворяет неравенству Лерэ
![]()
если интеграл в правой части сходится; x ∈ R 3 — произвольная точка.
Указание. Рассмотрите интеграл
![]()
Примените интегрирование по частям и неравенство Коши–Буняковского.
ЭЛЕМЕНТЫСТАТИСТИЧЕСКОЙМЕХАНИКИ
В статистической механике наиболее удобной формой уравнений оказалась гамильтонова. Механическая система определяется заданием ее гамильтониана H (q,p ). Предполагается, что он не зависит от времени, так что выполняется закон сохранения энергии и H есть интеграл системы
q ˙ = Hp , p ˙ = −Hq .
Число степеней свободы n в приложениях статистической механики очень велико. Вы помните число Авогадро 6. 023 · 1023 — число молекул в одной грамм-молекуле вещества. Нет надежды не только на то, чтобы решить столь большие системы уравнений, но даже их записать. Другая трудность состоит в том, что нет никакой возможности найти или измерить начальные данные для такой системы.
С другой стороны, нам и не нужны столь детальные знания, скажем, о движении молекул воздуха. Что бы мы с ними стали делать? Здесь возникает довольно обычная для физики проблема сокращения информации . Цель, конечно, состоит в том, чтобы уменьшить объем информации о процессе до уровня, допускающего ее хранение и обработку, а вместе с тем, достаточного для предсказания и управления. Выходом оказывается применение идей и подходов теории вероятностией.
Главный постулат статистической механики гласит, что измеряемые в опытах макроскопические величины — температура, плотность, концентрации компонент (например, соли в рассоле), напряженности электрического и магнитного полей и т.д. суть средние (математические ожидания), вычисленные в соответствии с надлежащей инвариантной плотностью. В принципе, здесь могла бы фигурировать инвариантная мера общего вида, не обязательно абсолютно непрерывная относительно меры Лебега. Однако в известных мне работах по статистической физике применяются исключительно инвариантные меры, определяемые инвариантными плотностями. Могу предположить, что использование более общих инвариантных мер — дело будущего.
Из приведенного выше постулата следует вывод, что все макроскопические уравнения физики суть уравнения для средних, для математических ожиданий соответствующих величин. Это относится и к уравнению тепло-
22 О законах термодинамики
проводности (диффузии), и к уравнениям механики сплошной среды. Такая трактовка, например, уравнения теплопроводности позволяет объяснить его парадоксальное свойство — тот факт, что изменение температуры (или концентрации) в некоторый момент времени мгновенно влияет на поле температуры (концентрации) во всей области, занятой проводником тепла. Выходит, как будто, что тепло распространяется с бесконечно большой скоростью. На самом деле, с бесконечной скоростью распространяется плотность вероятности.
Другое важное следствие основного постулата состоит в том, что макроскопические уравнения, в принципе, должны быть дополнены уравнениями для случайных отклонений от средних. Эти отклонения называются флуктуациями соответствующих величин, и обычно они бывают малыми. Несмотря на это, именно флуктуации вызывают некоторые макроскопически наблюдаемые явления. Например, голубой цвет неба объясняется рассеиванием солнечного света на флуктуациях плотности воздуха в высоких слоях атмосферы. О другом замечательном явлении того же рода — о броуновском движении — дальше мы поговорим подробнее.
Как и многие другие общие положения естествознания, приведенный выше принцип не содержит ясных условий его применимости. Вам, наверное, бросилось в глаза, что он ничего не говорит о том, какая именно инвариантная плотность (если их много) является «надлежащей». Мы теперь рассмотрим то распределение вероятности в фазовом пространстве системы, которое, если не всегда, то, во всяком случае, для весьма широкого круга явлений оказывается адекватным и блестяще подтверждается экспериментом.
22. О законах термодинамики
В настоящее время термодинамика, по крайней мере, некоторое ее ядро, вполне формализовано и может считаться с формальной точки зрения одним из разделов математической физики. Она основывается на небольшом числе аксиом, обычно называемых законами или началами. Перед тем как напомнить Вам начала термодинамики, замечу, что название «термодинамика» неточно. На самом деле, эта наука изучает равновесные, статические состояния, а не эволюцию. Более правильным было бы название «термостатика», хотя в термодинамике рассматриваются также квазистатические процессы — столь медленные, что в каждый момент времени к ним применимы начала термодинамики. Поскольку термин термодинамика был уже занят, истинную термодинамику стали называть неравновесной термодинамикой.
Нулевоеначалотермодинамики. Оно состоит в том, что в число параметров, описывающих состояние изучаемой системы, входит температура T . Другими параметрами могут быть объем, плотность, концентрации различных компонент вещества, а также и параметры, характеризующие электромагнитное поле, скажем, напряженности электрического и магнитного полей. Возможно и появление иных параметров, характеризующих различные поля и виды вещества.
Термодинамика, особенно неравновесная термодинамика — наука с большой претензией, полагающая, что она должна описывать любую физическую систему. Если даже температура не входит в число параметров состояния некоторой системы, то физик скажет, что в ней процессы изотермичны (происходят при постоянной температуре).
Первое начало термодинамики. Первым началом термодинамики называют закон сохранения и превращения энергии применительно к термодинамическим системам. Этот закон в дифференциальной форме может быть выражен равенством
dE = δQ + δA. (22.1)
Здесь E — внутренняя энергия системы. Постулируется , что E — функция состояния системы. Далее δQ — элементарное количество тепла, переданное системе в результате данного процесса. Подчеркннем, что, вообще говоря, не существует функции состояния Q , так что обозначение δQ следует понимать как единый символ, δQ — функция процесса, а не состояния. Наконец, δA — элементарная работа, произведенная над системой внешними силами, это также функция процесса, и не существует такой функции состояния A . Однако во многих важных случаях внешние силы оказываются потенциальными, и тогда можно записать, что δA = dW , где W — потенциальная энергия внешних сил, которая уже является функцией состояния.
С математической точки зрения, dE , δQ и δA суть дифференциальные 1–формы, называемые также пфаффовыми формами. Если x 1 ,...,xn — параметры состояния, то каждую из 1–форм, например δA , можно представить в виде
![]() .
(22.2)
.
(22.2)
Не всякая такая форма может быть представлена как дифференциал некоторой функции, если это возможно, то форму называют точной . Напри-
О законах термодинамики
мер, для энергии E = E (x 1 ,...,xn ) имеем
![]() .
(22.3)
.
(22.3)
Второе начало (второй закон) термодинамики. Этот закон по существу состоит из двух частей. Первая из них (мало известная широкой публике) состоит в том, что существует функция состояния S, называемая энтропией, такая, что дифференциальная форма δQ может быть представлена в виде
δQ = TdS. (22.4)
Таким образом, форма δQ , не будучи точной, является голономной — превращается в точную пфаффову форму после умножения на интегрирующий множитель 1/T . При обратимых процессах энтропия остается постоянной.
Вторая часть закона состоит в том, что при необратимых процессах в замкнутой термодинамической системе энтропия всегда возрастает. Система называется замкнутой , если она не взаимодействует с другими системами, в частности, на нее не действуют извне механические или, скажем, электрические силы, а также исключена теплопередача — поступление теплоты от других систем или отвод тепла.
Второе начало термодинамики широко известно и зачастую поминается в различных вульгаризованных формах. Стоит подчеркнуть, что энтропия возрастает лишь в замкнутых системах, а в столь сложных системах как живые организмы, росту энтропии противостоит взаимодействие с внешним миром (питание, дыхание), дающее постоянный приток энергии. В форме замкнутой системы живые организмы не могут существовать. В конечном счете, условием жизни на Земле является приток энергии от солнца. Гораздо меньше приток энергии от радиоактивного распада веществ, входящих в состав вещества Земли.
Замечу еще, что у второго начала термодинамики имеются и другие, более приземленные формулировки. Например, можно его выразить так: теплота не может передаваться от холодного тела к горячему (с более высокой температурой) . Теплота не может передаваться от холодного тела к горячему ни в каком процессе, если в нем не участвуют другие тела.
Второе начало термодинамики занимает особое место среди всех физических законов. Это единственный закон, который, как говорят, определяет «стрелу времени», направление эволюции.
Основные законы термодинамики были установлены в середине XIX века в трудах Джоуля, Майера, Карно (первое начало термодинамики) и Карно, Клаузиуса, Кельвина (второе начало). Имеется еще третье начало термодинамики (постулат Нернста), которое гласит, что абсолютный нуль температуры недостижим. Первой задачей статистической механики, которую стал развивать Людвиг Больцман, было объяснение законов термодинамики на основе представления о веществе как о совокупности атомов и молекул.
23. Теоремы Пуанкаре о возвращении
Прелесть математической физики для исследователя состоит и в том, что никогда не знаешь, чем нужно будет заниматься завтра. Математическая физика изумительно разнообразна и по постановке проблем, и по привлекаемому математическому аппарату. Признаюсь, мне иногда трудно понять, как это у многих чистых математиков хватает терпения десятки лет заниматься одним и тем же, оставаясь в узких рамках одного предмета.
Мы сейчас начинаем постепенно переходить от классической механики к статистической физике (механике). Первой основной целью этой науки является объяснение и углубленное понимание основных законов термодинамики. Например, мы с вами увидим, как из классической механики с применением идей теории вероятностей можно вывести закон Клапейрона– Менделеева для газов. В основе этого исследования лежит представление о веществе, скажем, о газе, как о совокупности взаимодействующих материальных частиц. Из всех мыслимых форм уравнений движения в механике наиболее подходящими для развития статистической механики оказались гамильтоновы уравнения. Мы уже сделали первый шаг к развитию статистической механики, когда вывели уравнение Лиувилля и нашли инвариантную меру на изоэнергетической поверхности. И вот оказывается, что для второго шага нужно теперь заняться работой на значительно более высоком уровне абстракции.
Вообще, математические идеи и теории становятся наиболее понятными и обозримыми, когда они излагаются в надлежащей степени общности. Тут, конечно, нужно чувство меры, бывает и так, что чрезмерная общность рассмотрения затемняет главные идеи.
Анри Пуанкаре в конце XIX-го века первым понял, сколь безнадежно пытаться найти полный набор интегралов для достаточно сложных и общих механических систем. Он построил примеры таких систем, у которых нет
иных интегралов, кроме интеграла энергии. Более того, именно такая ситуация является типичной. Пуанкаре рассматривал системы, получаемые малым возмущением некоторой вполне интегрируемой системы. Оказалось, что таким путем в условиях общего положения получаются неинтегрируемые системы.
Как вообще доказать, что некоторая система не имеет интеграла? Это может случиться, если движения системы весьма сложны, например, имеется движение — решение x (t ) соответствующей системы дифференциальных уравнений в Rn , траектория T которого всюду плотна в некоторой области в в Rn . Если теперь предположить, что имеется интеграл ϕ(x ), так что ϕ(x (t )) = c (c — постоянная) для всех t , то в итоге получится, что функция ϕ(x ) постоянна всюду на плотном множестве в в — на траектории T . Но если ϕ — непрерывная функция, постоянная на плотном множестве, то она постоянна и на его замыкании, так что ϕ(x ) = c всюду в области D. Выходит, ϕ — тривиальный интеграл, по крайней мере, в области D.
Если допустить, что ϕ — аналитическая функция, то по теореме единственности для аналитических функций выйдет, что ϕ(x ) = c всюду в Rn .
Для аналитических функций ϕ при определенных дополнительных условиях бывает даже достаточно предположить, что траектория T плотна не во всей области D, а лишь, на некоторой гиперповерхности. И отсюда уже удается вывести, что эта функция есть константа.
Оказывается, траектории со столь сложным поведением действительно существуют в механических системах, что и препятствует существованию нетривиальных интегралов.
Пространство с мерой. Пусть X — множество, его элементы могут иметь любую природу. Предположим, что выделен некоторый класс Σ его подмножеств, который является σ-алгеброй. Это означает, что теоретикомножественные операции — взятие объединения, пересечения, разности, дополнения, примененные даже счетное число раз, не выводят за пределы класса Σ. Например, если множества E 1 , E 2 ,... принадлежат классу Σ (в символах En ∈ Σ, n = 1, 2,... ), то их объединение и пересечение также принадлежат классу Σ, или в символах,
![]() ,
,
(23.1)
Если E ∈ Σ, и E 0 = X \ E — его дополнение, то и E 0 ∈ Σ.
Мера. Согласно определению, мера µ есть неотрицательная σ-аддитивная функция множеств, заданная на некоторой σ-алгебре Σ. Это означает, что класс Σ содержит пустое множество ∅ и все множество X , и для любого счетного набора непересекающихся множеств E 1 ,E 2 ,... ∈ Σ справедливо равенство
µ![]() .
(23.2)
.
(23.2)
Подчеркну, что это равенство постулируется лишь для случая, когда Ek ∩ En = ∅ при k 6= n . На самом деле, оно справедливо и при несколько более широких условиях (см. ниже).
Множества, принадлежащие классу Σ, называются измеримыми, а точнее, µ-измеримыми. Это уточнение нужно, конечно, лишь в случае, когда мы имеем дело с несколькими мерами.
Замечу, что в современной математике в ходу и различные обобщения понятия меры — рассматриваются конечно-аддитивные меры, знакопеременные меры (почему-то не привился выразительный термин заряд ), векторнозначные меры. Знакомясь с литературой, посмотрите, что означает в каждом случае термин мера .
Зачастую разрешается, чтобы мера µ принимала и бесконечное значение. Если µ(X ) < ∞, то и мера любого измеримого множества конечна. В этом случае мера µ называется конечной.
Согласно принятой идеологии, множествами меры ноль мы пренебрегаем — не считаем, что два измеримых множества E и F различны, если они отличаются на множество меры ноль. В символах это означает, что µ(E ∆F ) = 0; напомню, что симметрическая разность E ∆F определяется как E ∆F = (E \ F ) ∩ (F \ E ).
Точно также не различаются отображения пространств с мерой, если их значения различны лишь для множества значений аргумента, которое имеет нулевую меру.
Очень часто то или иное свойство устанавливается не для всех точек пространства с мерой, а лишь для всех точек за исключением множества точек, имеющих меру ноль. В этом случае говорят, что данное свойство имеет место для почти всех точек или почти всюду , или для почти любой точки. Заметим, что понятие «почти всюду» зависит от выбора меры, поэтому, когда нужно быть более точными, говорят «µ-почти всюду» и т. д.
Говоря более строго, в теории пространств с мерой и их отображений, мы имеем дело не с множествами и не с отображениями, а с классами эквивалентных множеств и классами эквивалентных отображений. При этом всякое множество меры ноль рассматривается по сути, как пустое множество, потому что оно эквивалентно пустому. Соответственно, если µ(E 1 ∩ E 2 ) = 0, то измеримые множества E 1 и E 2 трактуются, как непересекающиеся. В частности, равенство (23.2) верно и в том случае, когда µ(Ek ∩ E` ) = 0 при всех k и ` , лишь бы k 6= ` . (Проверьте это).
Отображения, сохраняющие меру. Отображение T : X → X называется измеримым, если (полный) прообраз T −1 (E ) всякого измеримого множества E есть измеримое множество. Если отображение T взаимно однозначно, то можно сформулировать это определение в эквивалентной и чуть более наглядной форме. Именно, потребуем, чтобы отображение T переводило всякое измеримое множество в измеримое: E ∈ Σ → TE ≡ T (E ) ∈ Σ.
Скажем, что измеримое и взаимно однозначное отображение T : X → X сохраняет меру µ, если для всякого E ∈ Σ
µ(TE ) = µ(E ). (23.3)
Для взаимно однозначных отображений равенство (23.3) можно записать в эквивалентной форме
µ(T −1 E ) = µ(E ) (23.4)
для всех E ∈ Σ. На самом деле, определение (23.4) имеет преимущества по сравнению с (23.3). Первое преимущество носит технический характер и состоит в том, что в дальнейших рассмотрениях гораздо чаще придется пользоваться именно равенством (23.4). Второе преимущество — более принципиально: определение (23.4) распространяется и на не взаимно однозначные отображения. При этом T −1 E означает полный прообраз — множество всех тех x ∈ X , которые под действием отображения T переходят в E , то есть, по определению,
T −1 E = {x : Tx ∈ E }.
Теорема 1 (теорема Пуанкаре о возвращении множеств). Пусть E — измеримое множество в пространстве с конечной мерой (X, Σ, µ), причем µ(E ) > 0. Пусть T : X → X — отображение, сохраняющее меру µ. Тогда найдется такое натуральное n, что (см. рис. 12)
µ(Tn E ∩ E ) > 0. (23.5)
Доказательство. Рассуждая от противного, предположим, что для всех n = 1, 2,...
µ(Tn E ∩ E ) = 0. (23.6)
Рис. 12
Тогда из (23.6) последует, что множества Tk E и Tn E тоже имеют пересечение меры ноль: µ(Tk E ∩ Tn E ) = 0 для всех натуральных k и n при k 6= n . Для определенности будем считать, что k < n . Тогда
µ(Tk E ∩ Tn E ) = µ(Tk (E ∩ Tn −k E )) = µ(E ∩ Tn −k E ) = 0. (23.7)
Мы учли, что Tk сохраняет меру µ, как и отображение T , а затем воспользовались равенством (23.6).
Таким образом, мы построили последовательность измеримых, попарно непересекающихся множеств E , TE , T 2 E,... . Все они имеют одну и ту же меру: µ(Tk E ) = µ(E ) = m > 0. Но отсюда следует равенство
µ![]() (23.8)
(23.8)
для любого n = 1, 2,... (мы считаем, что T 0 = id ). Так как мера любого подмножества в X не превосходит µ(X ), получаем
nm < µ(X ). (23.9)
Ввиду конечности меры µ, это неравенство не может выполняться для всех натуральных n . Полученное противоречие показывает, что равенство (23.6) при некотором n нарушается. Теорема доказана.
• Замечу, что на последнем шаге доказательства мы воспользовались аксиомой Архимеда. Это он в своей работе «Псаммит, или исчисление песчинок» установил, что выбрав любую единицу измерения, скажем, веса или длины (у нас это m ), можно для любого сколь угодно большого числа (у нас это µ(X )) найти столь большое n , что неравенство (23.9) будет нарушено. В этой работе Архимед очень близко подошел к открытию позиционной системы счисления (многие, самые крупные математики, считают, что это было величайшим открытием за всю историю науки). Конечно, сейчас все это очевидно, но кто-то должен был первым это понять. Это сделал Архимед.
Английский историк Арнольд Тойнби написал работу, в которой попытался предугадать, как развивалось бы человечество, если бы Архимед действительно сделал это открытие. Получилось, что развитие техники пошло бы несравненно быстрее, возможно, она развилась бы в других странах, и мир сейчас был бы совсем иным.
Из теоремы Пуанкаре вытекает важное следствие, которое применяется, пожалуй, чаще, чем сама теорема.
Следствие 1. В условиях теоремы 1 существует последовательность натуральных чисел n 1 , n 2 ,..., стремящаяся к бесконечности ( nk → +∞), такая что
µ(Tn k E ∩ E ) > 0. (23.10)
Доказательство. Пусть N — натуральное число. Применим теорему 1 к отображению TN : X → X , которое, конечно, тоже сохраняет меру µ. Получится, что для некоторой его степени TNk
µ(TNk E ∩ E ) > 0. (23.11)
Положим n 1 = Nk . Повторим это рассуждение с заменой N на n 1 . Тогда получится, что пересечение множества Tn 1 k 1 E = TNkk 1 E с E имеет положительную меру. Положим n 2 = Nkk 1 . Продолжая аналогично, мы построим последовательность n 1 < n 2 < ... < nk < ... такую, что выполняется (23.10).
Согласно этому следствию, «возвращение» (частичное) множества E будет происходить бесконечно много раз, при сколь угодно больших значениях дискретного времени n .
Теорема 2 (теорема Пуанкаре о возвращении точек). Пусть E — измеримое множество в пространстве с мерой (X, Σ, µ), и преобразование T : X → X сохраняет меру µ. Предположим, что мера µ конечна: µ(X ) < +∞. Тогда для почти любой точки x ∈ E найдется натуральное число n = n (x ) такое, что Tn x ∈ E .
Доказательство. Напомню, что выражение «почти любая» означает, что множество исключительных точек имеет меру ноль. Более точное выражение: µ-почти любая. Хотя формально мы не обязаны вводить в условия теоремы требование, чтобы мера множества E была положительна, ясно, что случай µ(E ) = 0 бессодержателен — все множество E может тогда быть исключительным. Таким образом, дальше можно считать, что µ(E ) > 0.
Построим подмножество F ⊂ E , состоящее из исключительных точек. Обозначим дополнение X \E через E 0 . Тогда T −1 E 0 есть множество точек, которые не попадают в E после однократного применения преобразования T (после одного шага итераций), T −2 E 0 — множество точек, не попадающих в E после двух шагов, ..., T −n E 0 — после n шагов, и т. д. Ясно, что множество
F = E ∩ T −1 E 0 ∩ ... ∩ T −n E 0 ∩ ...
есть множество точек множества E , не возвращающихся в E никогда.
Множества F и T −n F не пересекаются при любом натуральном n . Действительно, если x ∈ F ∩ T −n F , то Tn x ∈ F ⊂ E , то есть точка x возвращалась бы, в противоречии с определением множества F .
Теперь мы можем установить, что множества F , T −1 F , ..., T −n F,... попарно не пересекаются. Действительно, T −k F ∩ T −n F = T −k (F ∩ T −(n −k ) F ), когда, например, n > k . Понятно, что образ пустого множества (при отображении T −k ) пуст.
Построена последовательность непересекающихся множеств F , T −1 F ... , T −n F,... , имеющих одну и ту же меру: µ(T −n F ) = µ(F ). Как мы уже видели, ввиду конечности меры µ, это возможно лишь в случае µ(F ) = 0. Теорема доказана.
Следствие 2. Для почти любого x ∈ E существует бесконечная последовательность натуральных чисел n 1 , n 2 ,... такая, что nk → ∞ и Tn k x ∈ E .
Доказательство. Доказательство проводится, по сути, так же, как и в случае теоремы о возвращении множеств. Проведите его сами. Заметьте лишь, что когда мы говорим «почти для всех точек», то каждый раз приходится иметь в виду различные множества меры ноль. Но счетное объединение множеств меры ноль (вот она — σ-аддитивность!) есть множество меры ноль.
24 Гидродинамическая интерпретация систем дифференциальных
уравнений и теорема Лиувилля 205
![]()
В приложениях к механике мы можем выбрать в качестве множества E сколь угодно малую окрестность (любого!) заданного состояния в фазовом пространстве. Получится, что в будущем система много раз будет возвращаться в эту — сколь угодно малую окрестность. Представим себе, например, что рассматриваемая механическая система есть совокупность молекул воздуха в этой аудитории. Выберем состояние, в котором весь воздух сосредоточился вблизи одного угла, а остальная часть аудитории — вакуум. Выходит, время от времени весь воздух в этой комнате будет собираться вблизи угла (если бы однажды было создано такое состояние). Всем, кто находится далеко от этого угла, придется плохо.
Сейчас это уже трудно себе представить, но в конце XIX века многие выдающиеся ученые сильно сомневались в существовании атомов. Примеры вроде нашего примера с воздухом считались сильными возражениями против статистической теории газов. Конечно, никто еще не видел, чтобы весь воздух собрался в одной части комнаты. Людвиг Больцман, внесший огромный вклад в развитие этой теории, на подобные возражения ответил очень коротко: «Долго же вам придется ждать!» И в самом деле, современные оценки показывают, что подобное явление очень мало вероятно, вероятное время его ожидания составляет много миллиардов лет, что превосходит время существования Вселенной. Философы спорят, считать ли такие явления возможными, но мало вероятными, или попросту объявить их невозможными. На практике мы конечно, считаем их невозможными, во всяком случае, действуем, не принимая такие «возможности» во внимание.
24. Гидродинамическая интерпретация систем дифференциальных уравнений и теорема Лиувилля
Рассмотрим дифференциальное уравнение в Rn
x ˙ = v (x,t ). (24.1)
Предположим, чтобы не отвлекаться от главного, что задача Коши для уравнения (24.1) с начальным условием
x (0) = a (24.2)
глобально однозначно разрешима: для любого a ∈ Rn задача Коши (24.1)– (24.2) имеет, и притом единственное, решение x = x (a,t ), определенное для всех t ∈ R. Кроме того, будем предполагать, что поле v гладко зависит от x и от t .
В этих условиях эволюционный оператор Nt : Rn → Rn определен для всех t ∈ R, a ∈ Rn , так что
x (a,t ) = Nt a. (24.3)
Для неавтономного уравнения (24.1) оператор Nt зависит, конечно, от выбора начального момента, но здесь мы не собираемся его менять.
Представим себе, что пространство Rn заполнено некоторой жидкостью. Решение x (a,t ) будем трактовать как движение жидкой частицы, которая в момент времени t = 0 находилась в точке a . Векторное поле v (x,t ) приобретает смысл скорости той жидкой частицы, которая в момент t находится в точке x ∈ Rn .
В гидродинамике применяются два подхода к описанию движений жидкости. В первом из них, который называется эйлеровым , изучается эволюция поля скорости v (x,t ) течения жидкости. Второй подход называется лагранжевым и состоит в описании движения жидкой частицы x (a,t ). Названия эти условны — Эйлер знал оба подхода. Эйлерово и лагранжево описания течения жидкости связаны между собой посредством задачи Коши (24.1)–(24.2). Если известно поле скорости v (x,t ), то чтобы найти движение частиц x (a,t ), нужно решить задачу Коши (24.1)–(24.2) для всех a . Если известно движение x (a,t ) любой частицы, то поле скорости v (x,t ) определяется как x ˙(a,t ), где a выражено через x , так что
v (X,t ) = x ˙(a (X,t ),t ), (24.4)
где a = a (X,t ) находится из уравнения x (a,t ) = X для любого X ∈ Rn .
Уравнение неразрывности — уравнение Лиувилля
Изложенная гидродинамическая интерпретация задачи Коши (24.1)– (24.2) вызывает к жизни новые вопросы. Теперь начальное значение a не будет фиксированным, мы будем заниматься всей совокупностью задач Коши, рассматривая a как новую векторную переменную. Как Вам известно из курса обыкновенных дифференциальных уравнений, в случае гладкого поля v (x,t ) вектор-функция x (a,t ) гладко зависит от a ∈ Rn и от t ∈ R.
Зная, как двигаются жидкие частицы, мы можем проследить и за эволюцией областей, состоящих из одних и тех же частиц. Если D — некоторая область в Rn , то составляющие ее при t = 0 жидкие частицы в момент t занимают объем Dt = Nt (D ). Представим себе, что при t = 0 задана плотность ρ0 (a ) рассматриваемой жидкости. Поставим вопрос о том, как найти плотность жидкости ρ(x,t ) в момент t в предположении, что выполняется
Рис. 13
закон сохранения массы. К решению этого вопроса можно применить как эйлеров подход, так и лагранжев.
Лагранжев подход. В лагранжевой форме закон сохранения масс записывается в виде
ρ(x,t )dx = ρ0 (a )da. (24.5)
Это дифференциальная форма закона. Если вспомнить формулу преобразования объемных интегралов при замене переменных, придем к формуле
![]() (24.6)
(24.6)
в которой появляются матрица Якоби
![]()
и абсолютная величина ее определителя — якобиана. В результате приходим к уравнению неразрывности в лагранжевой форме
![]() ,
(24.7)
,
(24.7)
где a
= (Nt
)−1
x
; в автономном случае, когда v
= v
(x
) и не зависит от t
, можно записать![]() .
.
Якобиан![]() , на самом деле, положителен, поэтому и опущен знак модуля в (24.7). Действительно, J
≡ 1 при t
= 0 и не может обращаться в ноль (см. упражнение 2).
, на самом деле, положителен, поэтому и опущен знак модуля в (24.7). Действительно, J
≡ 1 при t
= 0 и не может обращаться в ноль (см. упражнение 2).
Заметим, что положительность функции ρ никак не использована, так что предыдущий вывод годится и для знакопеременной функции ρ. Например, он применим, когда ρ — плотность электрических зарядов, да и вообще, к произвольной функции ρ.
Эйлеров подход. Закон сохранения массы дает соотношение
Z Z
ρ(x,t )dx = ρ0 (a )da (24.8)
Dt D
для любой области D ⊂ Rn и ее образа Dt = Nt (D ) под действием эволюционного оператора Nt . Действительно, справа стоит масса жидкости, заключенной в области D , а слева — масса той же жидкости, занимающей в момент t область Dt .
Воспользуемся известной формулой дифференцирования по параметру интеграла по области, зависящей от этого параметра,
![]() (24.9)
(24.9)
Предполагается, что функция ρ достаточно регулярна, скажем, непрерывно дифференцируема по параметру t , а граница ∂Dt — гладкая и гладко зависит от t . Через vn = vn (x,t ), x ∈ ∂Dt , обозначена нормальная компонента скорости точки границы (иногда говорят «кажущаяся» скорость). Знак плюс у второго слагаемого соответствует выбору внешней нормали. Если граница области Dt (или ее часть) задана уравнением Φ(x,t ) = 0, причем
Φ(x,t ) < 0 при x ∈ Dt , то орт внешней нормали n можно представить в
![]() ∇
∇
виде n— в предположении, что нигде на границе знаменатель не
обращается в ноль. При этом vn дается формулой
![]() .
(24.10)
.
(24.10)
В случае области Dt можем написать: vn = v · n. Вообще же, формула (24.9) не требует знания движения частиц внутри области и поля их скоростей v . По-видимому, формула (24.9) Вам известна из курса механики сплошной среды, см. также книгу С.Л.Соболева [40].
Формула (24.9) имеет весьма наглядный смысл, она говорит, что масса жидкости изменяется лишь вследствие двух причин: изменения плотности внутри области со временем и наличия потока плотности внутрь области через границу.
Поскольку поле скорости v (x,t ) известно, поверхностный интеграл в
(24.9) можно преобразовать в объемный интеграл при помощи формулы Гаусса–Остроградского, в результате получим
![]() + div(
+ div(![]() .
(24.11)
.
(24.11)
Последнее равенство выполняется в силу (24.8). Напомню, что в декартовых координатах дивергенция поля v
= (v
1
,...,vn
) выражается в виде div![]() .
.
Очевидно, в качестве Dt можно выбрать произвольную область в Rn . Ее прообраз есть D = (Nt )−1 (Dt ). Но если интеграл от некоторой непрерывной функции по произвольной области равен нулю, то сама эта функция тождественно равна нулю. Если о функции известно лишь, что она интегрируема по Лебегу, то она при таком условии равна нулю почти всюду. Таким образом, из (24.11) следует уравнение неразрывности в эйлеровой форме , называемое также уравнением Лиувилля
![]() + div ρv
= 0.
(24.12)
+ div ρv
= 0.
(24.12)
Наш вывод представляет собой вполне очевидное обобщение вывода уравнения неразрывности в механике сплошной среды. Разумеется, для этого вывода физический смысл функции ρ, а также ее положительность, не имеют значения.
Можно также получить уравнение неразрывности (24.12) из лагранжева уравнения неразрывности (24.7). Для этого достаточно продифференцировать уравнение (24.7) по t (при фиксированном a ) и применить результат упражнения 2. Уравнение неразрывности получится в виде
![]() div v
= 0.
(24.13)
div v
= 0.
(24.13)
Здесь через![]() обозначена производная по t
при фиксированном a
, то есть при фиксированной жидкой частице. Она называется материальной производной
(а также субстанциональной
или индивидуальной
). В эйлеровых переменных материальная производная выражается формулой
обозначена производная по t
при фиксированном a
, то есть при фиксированной жидкой частице. Она называется материальной производной
(а также субстанциональной
или индивидуальной
). В эйлеровых переменных материальная производная выражается формулой
![]() .
(24.14)
.
(24.14)
Разумеется, уравнения (24.12) и (24.13) совпадают.
В общей теории дифференциальных уравнений в частных производных первого порядка (см., например, несколько старомодное, но весьма наглядное изложение в книге В.В. Степанова [41]) переход к лагранжеву описанию называется методом характеристик . Характеристики уравнения неразрывности (24.12) суть движение жидких частиц. Полученное выше лагранжево уравнение неразрывности (24.7) дает возможность свести решение задачи Коши для уравнения (24.12) с начальным условием ρ(x, 0) = ρ0 (x ) к решению задачи Коши (24.1), (24.2) для уравнения характеристик.
Ответ записывается в виде
![]() ,
(24.15)
,
(24.15)
где
Инвариантная мера и инвариантная плотность
В случае, когда v = v (x ), т.е. не зависит от t , особый интерес представляют решения уравнений Лиувилля, не зависящие от времени. Если такое решение ρ(x ) всюду неотрицательно: ρ(x ) ≥ 0 для всех x ∈ Rn , то его называют инвариантной плотностью . Если еще выполняется равенство
Z
ρ(x )dx = 1, (24.16)
Rn
то такую плотность называют нормированной или вероятностной , а также плотностью вероятности . Знание плотности вероятности ρ позволяет для любой наблюдаемой ϕ, то есть функции ϕ : Rn → R на фазовом пространстве системы, определить ее среднее значение равенством
![]() (24.17)
(24.17)
В теории вероятностей наблюдаемое ϕ носит название случайной величины
, а ее среднее ϕ![]() называется математическим ожиданием
данной случайной величины.
называется математическим ожиданием
данной случайной величины.
Инвариантная плотность определяет инвариантную меру µ(Ω) всякого измеримого по Лебегу множества Ω. Достаточно положить
µ![]() (24.18)
(24.18)
Свойства инвариантности выражается равенством
µ(Nt Ω) = µ(Ω). (24.19)
Замечу, что, во-первых, не всякая мера обладает плотностью, а лишь меры, абсолютно непрерывные по отношению к мере Лебега. Во-вторых, определение инвариантной меры естественно распространяется и на необратимое отображение N произвольного пространства с мерой (X, µ). В таком случае, однако, определение следует видоизменить: вместо (24.19), потребовать, чтобы выполнялось равенство
µ(N −1 Ω) = µ(Ω). (24.20)
При этом N −1 Ω означает полный праобраз измеримого относительно µ отображения N . Для обратимых отображений оба определения, конечно, эквивалентны.
Проблемам, связанным с инвариантными мерами динамических систем — потоков и каскадов, посвящена эргодическая теория динамических систем — одна из самых красивых и увлекательных областей математики; читайте книги [48, 31]. Подробнее об инвариантных мерах мы поговорим дальше.
Наиболее простой и весьма важный случай инвариантной плотности представится, если уравнение Лиувилля (24.12) допускает постоянное решение ρ = 1. Для этого, очевидно, нужно, чтобы выполнялось условие
div v = 0. (24.21)
Лагранжево уравнение неразрывности (24.7) в этом случае принимает вид
![]() .
(24.22)
.
(24.22)
В частности, это означает, что имеет место сохранение объемов
Vol Dt = Vol D (24.23)
для любой области D ⊂ Rn , причем Dt = Nt D . Жидкость, таким образом, в этом случае несжимаема (конечно, и нерастяжима). Сформулируем полученные результаты подробнее.
Предложение. Для того чтобы фазовая жидкость уравнения (24.1) была несжимаемой, и жидкие объемы не менялись со временем, необходимо и достаточно, чтобы поле скоростей v (x,t ) было соленоидально, то есть удовлетворяло уравнению (24.21). При этом уравнение Лиувилля принимает вид
![]() .
(24.24)
.
(24.24)
Функция ρ,такимобразом,являетсявэтомслучаеинтеграломуравнения (24.1).
Отсюда вытекает важное для статистической механики следствие: если векторное поле v = v (x ) соленоидально, а ρ(x ) — некоторый интеграл уравнения (24.1), то Φ(ρ) является решением уравнения Лиувилля (а также, конечно, и интегралом) при любой гладкой функции одного переменного Φ.
Стоит подчеркнуть, что, существование инвариантной плотности, как и существование нетривиального интеграла, есть весьма специальное свойство дифференциального уравнения — вообще говоря, дифференциальное уравнение в Rn инвариантных плотностей не имеет (см. упражнения 4 и 5).
Несжимаемость фазовой жидкости для гамильтоновой системы
В случае гамильтоновой системы (см. (20.14))
![]() (24.25)
(24.25)
уравнение Лиувилля (24.12) принимает вид
![]() .
(24.26)
.
(24.26)
Надеюсь, Вас не затруднит, что первые n переменных 2n -мерной системы (24.25) обозначаются через q 1 ,...,qn , а остальные — через p 1 ,...,pn .
Припомнив определение скобки Пуассона (20.38), можем записать уравнение (24.26) в компактной форме
![]() .
(24.27)
.
(24.27)
Физики обычно называют уравнением Лиувилля именно формулу (24.27) или (24.26). Это уравнение даже в общем случае гамильтониана H (q,p,t ) всегда имеет постоянное стационарное решение. Таким образом, плотность ρ = 1 инвариантна. Фазоваяжидкостьгамильтоновойсистемынесжимаема . Этот вывод полагается в основу статистической механики , которой мы скоро станем заниматься.
Вероятностная трактовка уравнения Лиувилля и инвариантной плотности
Рассмотрим снова задачу Коши (24.1)–(24.2). Предположим теперь, что a — случайная точка в Rn , и ее случайное распределение задается
25 Распределение Гиббса
плотностью вероятности ρ0 (a ). При этом считаем, что дальнейшее движение точки уже не является случайным, а происходит в соответствии с дифференциальным уравнением (24.1). Это означает, что плотность вероятности ρ(x,t ) в момент времени t удовлетворяет уравнению (24.7). Но из уравнения (24.7) следует, как мы уже установили, уравнение Лиувилля (24.12). Таким образом, мы приходим к важному выводу.
Если случайное распределение начальных точек a определяется плотностью вероятности ρ0 (a ), причем дальнейшее движение, когда точка a уже зафиксирована, определяется дифференциальным уравнением (24.1), то в момент времени t соответствующая плотность вероятности ρ(x,t ) есть решение уравнения Лиувилля (24.12) с начальным условием ρ(x, 0) = ρ0 (x ).
Упражнения
1. Пусть D — ограниченная область с гладкой границей S . Предполо-
![]()
жим, что гладкое в замкнутой области D поле v (x,t ) для любого t касается поверхности S (имеет на S нулевую нормальную компоненту). Докажите, что в этом случае задача Коши (24.1)–(24.2) глобально однозначно разрешима. Докажите также, что в случае неограниченной области D это утверждение становится уже неверным, но будет все-таки верным, если на бесконечности поле v растет не быстрее, чем линейно.
2. Применяя формулу дифференцирования определителя по параметру, докажите, что якобиан![]() , где x
= x
(a,t
) — решение задачи
, где x
= x
(a,t
) — решение задачи
Коши (24.1)–(24.2), удовлетворяет уравнению
![]()
3. Докажите формулу
div ρv = ρdiv v + v · ∇ρ
и установите совпадение уравнений (24.12) и (24.13). 4. Докажите, что скалярное уравнение
x ˙ = −x
не имеет инвариантной плотности.
5. Какими свойствами должен обладать спектр n × n матрицы A , чтобы линейное дифференциальное уравнение x ˙ = Ax в Rn допускало инвариантную плотность. (Ответ покажет Вам, сколь редким свойством является наличие инвариантной плотности.)
25. Распределение Гиббса
Поскольку гамильтониан H есть интеграл гамильтоновой системы (?? ), а фазовая жидкость гамильтоновой системы несжимаема, то H = H (q,p ) является решением уравнений Лиувилля. Тогда и функция ρ = ρ(H ) = ρ(H (q,p )) также удовлетворяет уравнению Лиувилля. Потребуем, чтобы инвариантная плотность ρ была вероятностной, то есть, чтобы выполнялось равенство Z
ρdx = 1. (25.1)
R2n
Здесь dx = dq dp — элемент объема фазового пространства. Возможно, что конфигурационным пространством системы оказывается не все Rn , а область D ⊂ Rn . Тогда фазовое пространство есть D ×Rn , и вместо (25.1) должно быть выполнено
Z
ρdx = 1. (25.2)
D ×Rn
При столь слабом ограничении существует обычно бесконечно много инвариантных плотностей вида ρ = ρ(H ). Сейчас мы опишем принцип выбора единственной инвариантной плотности посредством предположения о максимальном хаосе в системе. Следующий ниже вывод появился лишь в середине XX-го века, сам Гиббс рассуждал иначе [9].
Дальше для определенности считаем, что фазовое пространств есть R2n .
Энтропия вероятностной системы. Рассмотрим систему, которая может принимать n состояний, причем вероятность j -го состояния есть pj . Энтропия S этой системы по определению дается равенством
![]() .
(25.3)
.
(25.3)
Если pj = 0 для некоторого j , то будем считать, что pj lnpj = 0, и это слагаемое в (25.3) можно пропустить.
Энтропия является мерой беспорядка (хаоса, неопределенности в системе), лишь постоянным множителем log 2 e она отличается от информации по Клоду Шеннону , поскольку в теории информации приняты двоичные логарифмы.
Естественным обобщением (25.3) на случай непрерывного распределения с плотностью ρ служит равенство
![]() (25.4)
(25.4)
В случае условия (25.2) следует интегрировать по D × Rn .
Выберем среди всех инвариантных плотностей ρ(H ) ту, которая доставляет максимум энтропии S при дополнительном условии постоянства средней энергии системы
![]() (25.5)
(25.5)
![]()
Здесь E — заданная средняя энергия.
Мы пришли к задаче на условный экстремум. Решаем ее хорошо известным Вам методом Лагранжа. Вводим гладкую деформацию ρ ˜(x, ε) искомой функции ρ и определяем соответствующую этой деформации вариацию
![]() .
.
Варьируя функционал S и полагая δS = 0, получаем равенство
Z
(lnρ + 1)δρdx = 0. (25.6)
R2n
Это равенство выполняется, однако, не для произвольных вариаций δρ, а лишь для таких, которые удовлетворяют дополнительным условиям, выводимым посредством варьирования условий связи (25.1) и (25.5)
Z
δρdx = 0, (25.7)
R2n
Z
H δρdx = 0. (25.8)
R2n
Умножая (25.7) на постоянную λ, а равенство (25.8) — на µ, и складывая с
(25.6), придем к равенству
Z
(lnρ + 1 + λ + µH )δρdx = 0. (25.9)
R2n
При этом множители Лагранжа λ и µ можно считать выбранными таким образом, что условия связи (25.1) и (25.5) выполнены, так что равенство (25.9) выполняется уже для произвольной функции δρ. Отсюда следует равенство
lnρ + 1 + λ + µH = 0. (25.10)
В итоге приходим к распределению Гиббса
![]() .
(25.11)
.
(25.11)
Мы всего лишь изменили обозначения констант, положив A = e −1− λ ,
1
B
= ![]() . Постоянные A
и B
должны быть найдены из условий связи (25.1)
. Постоянные A
и B
должны быть найдены из условий связи (25.1)
µ и (25.5). В частности, из условия нормировки (25.1) выводим
![]() (25.12)
(25.12)
Равенство (25.5) перепишется теперь в виде
![]() (25.13)
(25.13)
Сделаем теперь обычные для статистической механики предположения о гамильтониане H . Разумеется, в каждом конкретном случае их следует проверять перед тем, как применять дальнейшие выводы статистической механики.
1◦ . Функция H ограничена снизу. Поскольку гамильтониан определен с точностью до произвольной аддитивной постоянной, мы можем и будем считать, что H (p,q ) ≥ 0 всюду.
2◦ . Интеграл (25.12) сходится при любом B > 0.
3◦ . Функция E (B ) на луче B > 0 строго монотонно возрастает, изменяясь от нуля (при B → 0) до +∞ (Рис. 14)
![]()
Из предположения 3◦ следует, что при любом заданном E > 0 из уравнения (25.13) однозначно находятся значения B . Тогда P (B ) определяется однозначно равенством (25.12). Замечу, что в проблемах, связанных с фазовыми переходами , встречаются гамильтонианы, для которых такой однозначности нет.
Энтропия S , определенная равенством (25.4), также может быть выражена как функция от B . Подставляя в это равенство выражение (25.11) для
Рис. 14
ρ, получаем
![]() .
(25.14)
.
(25.14)
Теперь заметим, что E (B ) можно выразить через P (B ). Действительно, дифференцируя по B интеграл P (B ) в (25.12), получаем
![]() .
(25.15)
.
(25.15)
Отсюда находим искомое выражение E (B )
![]() .
(25.16)
.
(25.16)
Мы пришли к важному выводу: основные в данной теории функции энергия E (B ) и энтропия S (B ) выражаются через единственную функцию P (B ):
![]() (25.17)
(25.17)
Это выражение называется статистическим интегралом .
В приложениях статистической механики к конкретным системам главная часть работы как раз и состоит в вычислении и исследовании статистического интеграла. Это может даже показаться курьезным, так как P (B ) в теории играет чисто служебную роль, определяя нормирующий множитель. В порядке нравоучения прикладным математикам замечу, что теоретики вообще очень легко в своих рассуждениях переходят, например, к нормированному базису. Это «всего лишь» операция умножения заданных функций на константы. Реализуя соответствующие алгоритмы в программах для ЭВМ, не следует обычно воспроизводить такие операции буквально — вычисление этих нормирующих множителей может оказаться весьма трудоемким и во многих случаях существенно увеличить время вычислений.
Физический смысл параметра B . Его невозможно понять, рассматривая лишь одну систему. Пусть заданы две системы с гамильтонианами H 1 = H 1 (q 1 ,p 1 ) и H 2 = H 2 (q 2 ,p 2 ). Предположим, что они независимы и составляют вместе одну систему с гамильтонианом H = H 1 + H 2 . При этом H = H (q 1 ,p 1 ,q 2 ,p 2 ) — функция, определенная на декартовом произведении фазовых пространств двух подсистем. Первой системе соответствует параметр B 1 , а второй — параметр B 2 . Ввиду предположенной независимости двух подсистем, распределение Гиббса для объединенной системы должно иметь вид
(25.18)
![]() .
.
С другой стороны, поскольку постулируется универсальность распределения Гиббса, должно иметь место равенство
![]() .
(25.19)
.
(25.19)
Поскольку выражения (25.18) и (25.19) должны совпадать, получается равенство
![]() ,
(25.20)
,
(25.20)
которое очевидно выполняется при B 1 = B 2 = B , причем A определяется по формуле
A = 1/P (B ), P (B ) = P 1 (B )P 2 (B ). (25.21)
Нетрудно доказать, что верно и обратное, см. ниже упражнение 2.
Таким образом, выяснилось, что при объединении двух систем в одну соответствующие параметры B 1 и B 2 уравниваются. Но точно так же ведет себя температура при вступлении двух тел в тепловой контакт. Если их
Рис. 15
температуры различны, то начинается процесс теплообмена, и в результате температура выравнивается. Это наводит на мысль отождествить параметр B
с температурой. Параметр B
имеет размерность энергии, поскольку аргумент![]() у экспоненты в распределении Гиббса должен быть безразмерным. Становится понятным, что температура T
есть по своей природе некоторая энергия, а для параметра B
справедливо выражение
у экспоненты в распределении Гиббса должен быть безразмерным. Становится понятным, что температура T
есть по своей природе некоторая энергия, а для параметра B
справедливо выражение
B = kT, (25.22)
где k — постоянный коэффициент, зависящий лишь от выбора единиц измерения энергии и температуры. В частности, измерения дали для постоянной Больцмана k значение
k
= 1.
38 · 10−16
![]() эрг
.
(25.23) град
эрг
.
(25.23) град
Мы можем теперь окончательно записать распределение Больцмана в виде
![]() .
(25.24)
.
(25.24)
Постоянная Больцмана k , как видим, очень мала. Поэтому распределение Гиббса (25.24) оказывается весьма острым, δ-образным (при k → 0 оно стремится к δ-распределению в смысле сходимости обобщенных функций), см. Рис. 15
Плотность ρ максимальна около точки минимума гамильтониана H и очень быстро спадает при отклонении от этой точки (куда быстрее, чем на рисунке!). Поэтому средние, вычисленные относительно этой плотности, оказываются очень близкими к значениям соответствующих функций в точке минимума гамильтониана, а флуктуации в обычных условиях весьма малы. Точнее говоря, большие флуктуации весьма маловероятны.
Далее мы применим изложенные здесь общие результаты к статистической теории идеального газа и твердого тела.
26. Статистическая механика идеального газа
Рассмотрим систему n частиц, двигающихся в пространстве R3 и не взаимодействующих между собой. Обозначим массу i -частицы через mi . Пусть xi — ее положение в R3 , x ˙i — ее скорость. Тогда импульс есть pi = mi x ˙i , а гамильтониан Hi — ее кинетическая энергия, выраженная через импульс
![]() .
(26.1)
.
(26.1)
Поскольку частицы не взаимодействуют, гамильтониан системы H есть сумма частных гамильтонианов
![]() .
(26.2)
.
(26.2)
Далее будем считать, что рассматриваемые частицы двигаются в области D ⊂ R3 , имеющей конечный объем V . Таким образом, конфигурационное пространство данной системы есть Dn = D × ... × D , а фазовое пространство есть (D × R3 )n = Dn × R3n . Мы уже знаем, что для дальнейшего исследования достаточно вычислить статистический интеграл P (B ), где B = kT .
Вычислениестатистическогоинтеграла. В случае гамильтониана (26.2) имеем
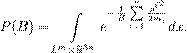 (26.3)
(26.3)
где dx = dq 1 ...dqn dp 1 ...dpn — элемент объема в фазовом пространстве.
Заметим, что подынтегральное выражение не зависит от qi , i = 1,...,n , и представляется в виде произведения множителей, каждый из которых зависит лишь от одного из импульсов pi . Отсюда следует, что интеграл (26.3) можно представить в виде
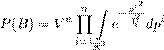 ,
γi
2
= 2mi
B.
(26.4)
,
γi
2
= 2mi
B.
(26.4)
| Общая идея этой выкладки заключается в применении формулы |
|
| Z Z Z f (x )g (y )d µ(x )d ν(y ) = f (x )d µ(x ) · g (y )d ν(y ), |
(26.5) |
X ×Y X Y
которая справедлива для любой пары пространств с мерой (X, µ) и (Y, ν) и обобщается на любое количество таких пространств. Формула (26.4) выражает P (B ) через произведение однотипных интегралов вида
![]() (26.6)
(26.6)
где dp = dp 1 dp 2 dp 3 — элемент объема в R3 . Еще раз применяя ту же идею, получаем
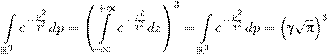 .
(26.7)
.
(26.7)
Здесь использовано хорошо известное значение гауссова интеграла вероятности при γ > 0:
![]() .
(26.8)
.
(26.8)
Применяя формулу (26.7), находим интеграл (26.4) в виде
![]() .
(26.9)
.
(26.9)
Запишем этот результат в виде
![]() ,
(26.10)
,
(26.10)
где не очень существенная константа C определяется равенством
![]() .
(26.11)
.
(26.11)
Применяя формулу (25.16), находим зависимость энергии от параметра B
(по сути, от температуры) в виде
![]() (26.12)
(26.12)
Мы пришли к довольно удивительному выводу, что энергия E зависит лишь от температуры и не зависит от объема V
![]() (26.13)
(26.13)
Еще удивительнее, однако, тот факт, что формула (26.13) великолепно подтверждается экспериментом.
Итак, средняя внутренняя энергия идеального газа — системы n невзаимодействующих частиц — линейно зависит от температуры T и от числа частиц, а от объема не зависит.
Примечательно, что энергия E не зависит и от масс частиц, то есть идеальный газ может быть смесью любого числа различных компонент. Допускается даже, что каждая компонента может быть представлена лишь одной молекулой.
Формула (26.13) позволяет найти теплоемкость
идеального газа. Вообще, теплоемкость c
определяется как производная ![]() . Чтобы избежать недоразумений, сразу скажу, что в общей ситуации теплоемкость не является функцией состояния
, а является, скорее, функцией процесса. Например, приходится различать теплоемкости при постоянном давлении (cp
) и при постоянном объеме (cV
). В данном случае все проще. Дифференцируя равенство (26.13), получаем
. Чтобы избежать недоразумений, сразу скажу, что в общей ситуации теплоемкость не является функцией состояния
, а является, скорее, функцией процесса. Например, приходится различать теплоемкости при постоянном давлении (cp
) и при постоянном объеме (cV
). В данном случае все проще. Дифференцируя равенство (26.13), получаем
![]() (26.14)
(26.14)
Мы пришли к выводу, что теплоемкость идеального газа зависит лишь от числа частиц и не зависит ни от объема, ни от температуры.
Средняя кинетическая энергия частицы.
Вычислим среднюю кинетическую энергию j
-ой частицы. Это означает, что нужно найти математическое ожидание наблюдаемой![]() . Напомню, что для любой наблюдаемой ϕ = ϕ(q,p
) ее среднее определяется равенством
. Напомню, что для любой наблюдаемой ϕ = ϕ(q,p
) ее среднее определяется равенством
![]() (26.15) Соответственно получаем
(26.15) Соответственно получаем
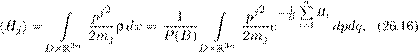
Это выражение, как и интеграл, определяющий P (B ), можно представить в виде произведения интегралов двух типов. Интегралы по области D от 1 дают множитель V n . Остальные интегралы вычисляются по R3 , причем подынтегральное выражение в i -ом множителе зависит лишь от pi . Теперь заметим, что, за исключением j -го множителя в интеграле (26.16), все остальные множители — такие же, как и в интеграле (26.3). Чуть поразмыслив, мы можем написать формулу
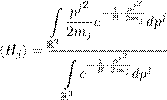 .
(26.17)
.
(26.17)
Знаменатель мы уже вычисляли. Он представляется в виде произведения трех гауссовых интегралов, что дает равенство
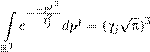 ,
γj
2
= 2mj
B
= 2mj
kT.
(26.18)
,
γj
2
= 2mj
B
= 2mj
kT.
(26.18)
Числитель в (26.17) сначала разбиваем на сумму трех интегралов в соответствии с равенством![]() . Эти слагаемые получаются друг из друга циклической перестановкой индексов компонент
. Эти слагаемые получаются друг из друга циклической перестановкой индексов компонент![]() , а потому одинаковы. Таким образом, имеем
, а потому одинаковы. Таким образом, имеем
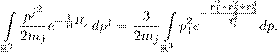 (26.19)
(26.19)
Мы еще заменили pj
на p
— переменную интегрирования можно обозначить как угодно. вещественной оси. Из них два гауссовы, и их произведение естьИнтеграл (26.19) представим в виде произведения трех интегралов по(γj
√
π![]() )2
.
)2
.
Третий множитель имеет вид (p 1 заменяем на z )
![]() .
(26.20)
.
(26.20)
Подставляя полученные значения интегралов в (26.17), имеем
![]() .
(26.21)
.
(26.21)
Окончательно получаем
![]() (26.22)
(26.22)
Мы пришли к важному выводу: средняя кинетическая энергия движения частицы (молекулы) есть температура идеального газа — с точностью до множителя
![]() , отвечающего переходу от механических единиц измерения к тепловым.
, отвечающего переходу от механических единиц измерения к тепловым.
Существенно также, что правая часть в (26.22) не зависит от массы частицы .
И еще один интересный вывод можно сделать, сопоставляя формулы (26.22) и (26.13). Мы видим, что энергия равномерно распределяется по частицам независимо от их масс
. Более того, коэффициент 3 в (26.22) отнюдь не случаен — это размерность пространства R3
, число степеней свободы одной частицы. Фактически мы уже использовали то обстоятельство, что каждая из компонент![]() вносит один и тот же вклад в среднюю кинетическую энергию. (См. также упражнение 3).
вносит один и тот же вклад в среднюю кинетическую энергию. (См. также упражнение 3).
Это частный случай довольно общего закона статистической механики о равнораспределении (equipartition) энергии по степеням свободы. Хотя этот принцип и не всегда выполняется, он имеет немалое эвристическое значение. В том случае, когда гамильтониан представляет собой сумму квадратов параметров, определяющих состояние системы, он превращается в строгую теорему, один частный случай ее мы фактически доказали.
Дальше мы рассмотрим и другие случаи, когда этот принцип работает.
Формула (26.22) является основой (ни более, ни менее!) механической теории теплоты, объясняя механический смысл главной термодинамической величины — температуры.
Флуктуация энергии.
Статистическая механика ставит и решает также принципиально новые задачи, позволяя, в частности, исследовать флуктуации. После того как вычислено математическое ожидание, естественно заняться дисперсией
случайной величины![]() . Согласно определению, дисперсия D(Hj
) дается формулой
. Согласно определению, дисперсия D(Hj
) дается формулой
![]()
D(Hj ) = D(Hj − Hj )2 E . (26.23)
Отсюда непосредственно следует формула
![]() D(Hj
) = DHj
2
E
− H
2
j
.
(26.24)
D(Hj
) = DHj
2
E
− H
2
j
.
(26.24)
Первое слагаемое вычисляем при помощи приема, который был применен
![]()
при вычислении среднего Hj . Имеем (сравните с формулой (26.17))
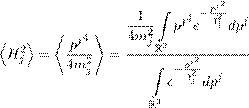 .
(26.25)
.
(26.25)
![]()
Мы уже знаем, что знаменатель в этой формуле есть (γj √ π)3 . Для вычисления числителя вводим сферические координаты (r, ϕ, θ) с центром в нуле и замечаем, что подынтегральное выражение не зависит от ϕ и θ. Поэтому числитель выражается формулой
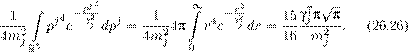
Множитель 4π — площадь единичной сферы (появился после интегрирования по ϕ и θ). Последний интеграл посредством интегрирования по частям сводится к гауссову и легко вычисляется, что и сделано (проверьте!). Подстановка в (26.25) дает равенство
![]() .
(26.27)
.
(26.27)
Теперь из (26.24) получаем
![]() .
(26.28)
.
(26.28)
Средняя квадратичная флуктуация определяется как корень квадрат-
![]()
ный из дисперсии, в данном случае это p D(Hi ). Ее отношение к математическому ожиданию назовем относительной (среднеквадратичной) флуктуацией . Вычисляя ее, получаем
![]() .
(26.29)
.
(26.29)
Как видим, это довольно большая величина: ![]() . Выходит,
. Выходит,
вполне можно ожидать изменения кинетической энергии частицы-молекулы на 80%. Не противоречит ли это нашему заявлению, что флуктуации макроскопических величин весьма малы? Нет, не противоречит, потому что энергия одной молекулы не является макроскопической величиной. Если мы рассмотрим энергию Em выбранного произвольного набора m частиц, то согласно принципу равнораспределения найдем, что
![]() (26.30)
(26.30)
Этот результат не зависит, конечно, от того, какие именно m частиц выбраны. Далее заметим, что для независимых случайных величин, каковыми являются H 1 ,...,Hm , дисперсия суммы равняется сумме дисперсий
![]() .
(26.31)
.
(26.31)
На самом деле, для справедливости этой формулы достаточно несколько более слабого свойства случайных величин, чем независимость, см. упражнение 4.
Применяя формулу (26.28), из (26.31) выводим
![]() (26.32)
(26.32)
Соответственно для среднеквадратичной флуктуации получаем
![]() (26.33)
(26.33)
27 Метод Лапласа асимптотической оценки интегралов
![]()
а для относительной среднеквадратичной флуктуации
![]() .
(26.34)
.
(26.34)
Из этой формулы видим, что для макроскопических количеств газа, скажем, при m ∼ 1020 относительная флуктуация очень мала, вряд ли даже может быть непосредственно измерена в опыте.
27. Метод Лапласа асимптотической оценки интегралов
Малость постоянной Больцмана наводит на мысль применить для вычисления средних (по формуле (26.15)) асимптотический метод Лапласа [42]. Сейчас я, не вдаваясь в доказательства, приведу вывод основных формул метода. Затем мы их применим к задачам статистической механики. Рассмотрим интеграл
![]() (27.1)
(27.1)
Здесь δ — малый положительный параметр, и нас интересует асимптотическое поведение этого интеграла при δ → 0. Будем предполагать, что функция H (x ) — достаточно гладкая, ограничена снизу и растет на бесконечности, например, при больших x имеется оценка снизу
H (x ) ≥ C |x |α , (27.2)
где C и α — известные положительные константы.
Относительно функции ϕ(x ) также предположим, что она гладкая и растет на бесконечности не быстрее, чем степенным образом, так что
|ϕ(x )| ≤ C 1 |x |β , (27.3)
где C 1 и β — известные положительные константы. В принятых условиях интеграл (27.1) существует при любом δ > 0 (возможны, конечно, и иные условия).
Предположим, что x 0 — точка строгого абсолютного минимума функции H . Более того, допустим, что разложение Тейлора функции H в окрестности точки x 0 имеет вид
![]() (27.4)
(27.4)
причем опущены члены порядка 3 и выше, а второй дифференциал положительно определен . В координатах формула (27.4) запишется в виде
![]()
Дальше нам понадобится разложение функции ϕ
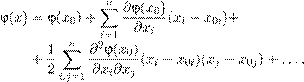 (27.6)
(27.6)
Для вывода асимптотической формулы Лапласа сначала устанавливается, что главный член асимптотики не изменится, если в (27.1) перейти от интегрирования по всему пространству Rn к интегрированию по любой окрестности точки x 0 фиксированного, не зависящего от δ размера.
Это значит, что мы собираемся выбросить из интеграла (27.1) величину
![]() (27.7)
(27.7)
где η — произвольно фиксированное положительное число. Применяя неравенства (27.2) и (27.3), получим оценку
![]() (27.8)
(27.8)
Положим |x − x 0 | = r . Заметим, что dx = rn −1 drdS , где dS — элемент площади единичной сферы Sn −1 с центром в точке x 0 . Поскольку подынтегральное выражение в (27.8) зависит только от r , из (27.8) следует неравенство
![]() (27.9)
(27.9)
где σn −1 есть площадь сферы Sn −1 . Сделаем в последнем интеграле замену r = δ 1/ α ρ. В результате получим
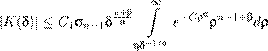 .
(27.10)
.
(27.10)
Интеграл в этом неравенстве при δ → 0 затухает быстрее δ q при любом q > 0. Вы легко убедитесь в этом, применив правило Лапиталя для вычисления предела отношения нитеграла и величины δ q при δ → 0. Получается, что для любого p > 0 имеет место предельное соотношение
![]() .
(27.11)
.
(27.11)
Этот результат справедлив при любом η > 0, лишь бы число η было фиксировано и не зависело от δ.
Положим J(δ) = J1 (δ) + K (δ), где
![]() (27.12)
(27.12)
Дальше мы увидим, что интеграл J 1 (δ) допускает степенную асимптотику при δ → 0, которая к тому же от величины η не зависит. Ввиду (27.11), интеграл J(δ) имеет ту же самую асимптотику, что и J1 (δ).
Пользуясь произволом в выборе η, полагаем его столь малым, чтобы можно было воспользоваться для приближения функций H и ϕ их разложениями Тейлора (27.5) и (27.6). Ограничиваясь первыми членами, в результате получим
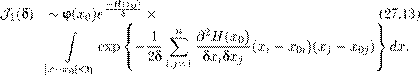
Несложное обоснование того факта, что отбрасывание остаточного члена не влияет на главные члены асимптотики, опущу.
Обозначим через A оператор Гесса функции H в точке x 0 :
![]() .
(27.14)
.
(27.14)
Применяя это обозначение и вновь переходя в (27.13) к интегрированию по Rn , приходим к асимптотике
![]() (27.15)
(27.15)
Мы еще сделали замену x − x 0 → x в последнем интеграле. Неизменность степенной асимптотики при переходе от интегрирования по шару к интегрированию по всему Rn доказывается точно также, как и выше при выводе оценки интеграла K (δ).
Следующий шаг состоит в том, что в последней формуле мы возвращаемся к интегрированию по Rn . Конечно, нужно доказать, что добавление интеграла по внешнему шару не меняет главного члена асимптотики. Предполагая, что это сделано, придем к асимптотике
![]() (27.16)
(27.16)
Здесь для вычисления последнего интеграла применяется следующий стандартный прием. Квадратичную форму можно ортогональным преобразованием привести к сумме квадратов: сделать замену x = Uy , так что в новых переменных
![]() .
(27.17)
.
(27.17)
Здесь λ1 ,..., λn — собственные числа оператора Гесса A (27.14), которые, по предположению, положительны. Ортогональный оператор U сохраняет объемы, так что |detU | = 1. Поэтому dx = dy , и мы приходим к равенству
![]() (27.18)
(27.18)
Последний интеграл представляется в виде произведения гауссовых интегралов
![]() .
(27.19)
.
(27.19)
В результате получаем
![]() .
(27.20)
.
(27.20)
Мы использовали тот факт, что detA = λ1 · ... · λn .
Теперь окончательно приходим к асимптотике при δ → 0:
![]() .
(27.21)
.
(27.21)
В случае, когда ϕ(x 0 ) 6= 0, это асимптотическое равенство означает, что при δ → 0 отношение левой и правой частей выражения (27.21) стремится к единице.
Случай ϕ(x 0 ) = 0. Если же ϕ(x 0 ), то формула (27.19) говорит лишь, что J(δ) → 0 при δ → 0. Мы можем уточнить асимптотическое поведение интеграла J(δ), прибавляя следующие члены разложения функции ϕ(x ). Нетрудно видеть, что члены первой степени на дают вклада в главный член асимптотики. Если привлечь члены второй степени и провести выкладки, аналогичные предыдущим, то получим
![]() (27.22)
(27.22)
где B — матрица Гесса функции ϕ
![]() (27.23)
(27.23)
и через нее выражается второй дифференциал функции ϕ: d 2 ϕ(x 0 )ξ 2 = (B ξ, ξ), где ξ ∈ Rn .
Вычислим интеграл
![]() (27.24)
(27.24)
Снова сделаем замену переменной x = Uy , приводящую форму (Ax,x ) к сумме квадратов, см. (27.17). Интеграл S (δ) запишется тогда в виде
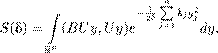 (27.25) Пусть ϕ1
,...,
ϕn
— ортонормальная система собственных векторов оператора A
, так что A
ϕj
= λj
ϕj
, причем собственные значения λj
все положительны. Введем векторы ψj
, полагая ψj
= U
−1
ϕj
. Произвольный вектор x
∈ Rn
допускает разложение
(27.25) Пусть ϕ1
,...,
ϕn
— ортонормальная система собственных векторов оператора A
, так что A
ϕj
= λj
ϕj
, причем собственные значения λj
все положительны. Введем векторы ψj
, полагая ψj
= U
−1
ϕj
. Произвольный вектор x
∈ Rn
допускает разложение
![]() .
(27.26)
.
(27.26)
| Соответственно |
n y = U −1 x = X yj ψj , |
(27.27) |
j =1
и интеграл (27.25) запишется в виде
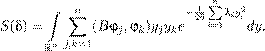 (27.28)
(27.28)
Теперь заметим, что интегралы от слагаемых, отвечающих индексам j 6= k , исчезают. Это происходит потому, что соответствующий интеграл по Rn выражается в виде произведения одномерных интегралов, и при этом целых два множителя — интегралы по yj и yk — нулевые. Это интегралы от нечетных функций. Выражение для S (δ) упрощается и принимает вид
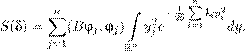 (27.29)
(27.29)
С такими интегралами мы уже умеем обращаться. Действуя так же как при вычислении интеграла (26.16), получаем
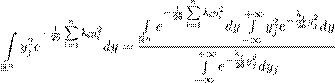 .
(27.30)
.
(27.30)
Для вычисления первого множителя в числителе воспользуемся формулой (27.20). В результате получаем
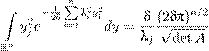 .
(27.31)
.
(27.31)
Окончательно приходим к формуле
![]() .
(27.32)
.
(27.32)
Замечу, что для квадратичных гамильтонианов, с которыми мы до сих пор и имели дело, занимаясь идеальным газом и твердым телом, полученные здесь асимптотические равенства (27.21) и (27.32) превращаются в точные.
Имеется и другой, идейно даже лучший способ вычисления интеграла (27.24). Ради краткости опустим коэффициент ![]() в следующих выкладках
в следующих выкладках
(в окончательном результате заменим потом![]() ). Воспользуемся очевидным равенством
). Воспользуемся очевидным равенством
![]() (27.33)
(27.33)
Для вычисления последнего интеграла воспользуемся формулой (27.20) при 2δ = 1. Имеем
![]() .
(27.34)
.
(27.34)
Заметим, что при малых t оператор A − tB остается положительно определенным, так что наши действия законны. Отметим формулу (см. ниже упражнения 5 и 6)
![]() .
(27.35)
.
(27.35)
При помощи (27.34) и (27.35) получаем
![]() .
(27.36)
.
(27.36)
Возвращаясь к (27.22), с применением (27.36), получаем асимптотическую формулу для интеграла J(δ), определенного равенством (27.1) в случае
ϕ(x
0
) (не забывая заменить![]()
![]() sp(A
−1
B
).
(27.37)
sp(A
−1
B
).
(27.37)
Упражнения
1. Докажите, что максимум энтропии вероятностной системы с n
состояниями достигается при![]() . При этом S
= lnn
.
. При этом S
= lnn
.
2. Докажите, что равенство (25.21) при постоянных B 1 , B 2 , B , A может выполняться для всех p 1 , q 1 , p 2 , q 2 , лишь в случае B 1 = B 2 = B , если оба гамильтониана нетривиальны (не сводятся к постоянным).
3. Докажите, что для идеального газа выполняется равенство
![]() (27.38)
(27.38)
4. Пусть ξ1 ,..., ξm — случайные величины (т.е. функции на пространстве (X, µ) с вероятностной мерой µ). Если условие hξi ξj i = 0 выполнено всякий раз, когда i 6= j , то справедлива формула для дисперсий
![]() .
.
5. Докажите, что для любого линейного оператора B : Rn → Rn справедлива формула
![]()
Для этого припомните, как выводится формула Лиувилля для вронкскиана, и примените правило дифференцирования определителей.
6. Докажите, что если A и B — линейные операторы в Rn , причем, оператор A обратим, то справедлива формула
![]() .
.
Здесь нужно воспользоваться результатом предыдущего упражнения и тем фактом, что определитель произведения операторов равен произведению определителей операторов.
7. Вычислите интеграл
Z
(Bx,x )2e −(Ax,x )dx,
Rn
где A — положительно определенный оператор.
28 Градиентные системы
8. Докажите равенство
Z
(Bx,x )(Cx,x )e −(Ax,x ) dx
Rn
= detA hsp(A −1 B )sp(A −1 C ) − sp(A −1 BA −1 C )i
9. Докажите непосредственно, что выражения (27.28) и (27.36) совпадают.
28. Градиентные системы
Градиентное уравнение в конечномерном евклидовом, или гильбертовом пространстве H имеет вид
x ˙ = grad S (x ) (28.1)
с известной, достаточно гладкой функцией S , называемой потенциалом градиентного уравнения. Поле G (x ) называется потенциальным , если его можно представить в виде G (x ) = grad S (x ) с некоторой функцией S (x ). Основное свойство такого уравнения состоит в том, что для всякого решения x (t ) функция S (x (t )) монотонно возрастает. Для доказательства достаточно вычислить производную S ˙ в силу заданного уравнения движения (28.1). В результате получаем равенство
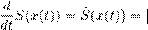 grad S
(x
(t
))|2
≥ 0.
(28.2)
grad S
(x
(t
))|2
≥ 0.
(28.2)
Таким образом, S есть возрастающая функция Ляпунова уравнения (28.1).
Второе начало термодинамики состоит в том, что энтропия замкнутой термодинамической системы со временем возрастает. Поэтому можно сказать, что градиентные уравнения описывают поведение систем типа замкнутых термодинамических, причем потенциал S играет роль энтропии. К этому можно добавить, что формула (28.2) вместе с ее интерпретацией, сохраняется и для более общей системы вида
| x ˙ = grad S (x ) + F (x ), если для всех x ∈ H выполнено соотношение |
(28.3) |
| (grad S (x ),F (x )) = 0. |
(28.4) |
Равенство (28.4) означает, что векторные поля grad S и F образуют косимметрическую пару. Интересный класс уравнений вида (28.3) представляют дифференциальные уравнения
x ˙ = grad S (x ) + A (x )grad S (x ), (28.5)
где линейный оператор A (x ) может зависеть от x нелинейно, однако для каждого x ∈ H является кососимметричным. Напомню, что оператор A : H → H называется кососимметричным, если для всех x ∈ H выполнено равенство (Ax,x ) = 0. В этом случае A ∗ = −A .
Хороший пример уравнения (28.5) дает уравнение в R 3 вида
x ˙ = grad S (x ) + ω(x ) ∧ grad S (x ). (28.6)
Обобщением уравнения (28.5) может служить уравнение
x ˙ = grad S (x ) + Γ(x )grad S (x ), (28.7)
где Γ(x ) есть гироскопический оператор, равенство (Γ(x )ξ, ξ) = 0 выполняется для всех x ∈ H , ξ ∈ H .
Дальше мы рассмотрим некоторые эффекты, производимые дополнительным слагаемым F в уравнении (28.3).
Восстановление потенциала по заданному полю
Если задано автономное дифференциальное уравнение
x ˙ = G (x ) (28.8)
в H , то несложно проверить является ли оно градиентным. Наиболее прямой путь состоит в следующем (см. также упражнения 2–4). Допустим, что G (x ) = grad S (x ). Фиксируем точку x 0 ∈ H , и пусть x — произвольная точка пространства H . Рассмотрим отрезок, соединяющий точки x 0 и x , т.е. множество точек x 0 + ε(x − x 0 ), где ε ∈ [0, 1]. Далее положим x − x 0 = u . Имеем
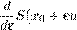 ) = (grad S
(x
0
+ εu
),u
).
(28.9)
) = (grad S
(x
0
+ εu
),u
).
(28.9) 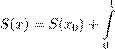 (grad S
(x
0
+ εu
),u
)d
ε (28.10)
(grad S
(x
0
+ εu
),u
)d
ε (28.10)
Интегрируя по ε выводим равенство
Если известно, что поле G потенциально, то потенциал дается формулой
![]() (28.11)
(28.11)
Остается проверить, является ли в действительности построенная функция S (x ) потенциалом данного поля G (x ). Дифференцируя равенство (28.11), получаем
![]() (28.12)
(28.12)
для любого вектора v ∈ H . Это равенство можно также записать в виде
![]() .
(28.13)
.
(28.13)
Мы использовали здесь тот факт, что линейный функционал (в частности, операцию скалярного умножения на вектор v ) можно вносить под знак интеграла.
Отсюда видно, что отвечающее потенциалу S поле имеет вид
grad![]() .
(28.14)
.
(28.14)
Напомню, что градиент grad S (x ) определяется требованием, чтобы для всех v ∈ H выполнялось равенство
(grad S (x ),v ) = S 0 (x )v. (28.15)
В итоге, получается, что поле G (x ) потенциально, и построенная функция S (x ) является потенциалом, в том и только в том случае, когда для любых x 0 и x , принадлежащих H , выполняется равенство:
![]() .
(28.16)
.
(28.16)
В конкретных задачах обычно бывает проще, не используя эту формулу, непосредственно проверить, выполняется ли равенство grad S (x ) = G (x ).
Примеры градиентных систем
Следующий пример показывает, как естественно возникают градиентные системы в механике. Рассмотрим общее уравнение механики Ньютона с рэлеевской силой трения
Mx ¨ = −grad V (x ) − grad v W (v ), v = x, ˙ (28.17)
где W — диссипативная функция Рэлея, а V — потенциальная энергия. Если на систему не действуют потенциальные внешние силы, так что V = const , а grad V (x ) = 0, то для скорости v получится уравнение
Mv ˙ = −grad v W (v ). (28.18)
При M = I уравнение (28.18) является градиентным и совпадает с (28.1), если положить S = −W . Однако и в общем случае положительно определенного оператора M уравнение (28.18) принимает градиентную форму, если ввести в пространстве H новую метрику со скалярным произведением (ξ, η)M = (M ξ, η), см. (11.20):
v ˙ = −grad M W (v ). (28.19)
Уравнение (28.18) обладает двумя функциями Ляпунова: диссипативной функцией W
и кинетической энергией![]() . Справедливы
. Справедливы
соотношения
![]() ,
(28.20)
,
(28.20)
![]() dW
−(grad W
)2
.
(28.21)
dW
−(grad W
)2
.
(28.21)
= dt
Замечу, что выведенное нами ранее уравнение диссипации энергии для системы Навье–Стокса является, по сути, частным случаем уравнения (28.20). Для линеаризованного уравнения (с выброшенным слагаемым (v, ∇)v ) справедливо и уравнение, аналогичное (28.21). Проверить это будет для Вас хорошим упражнением.
Еще один важный пример градиентного уравнения дает уравнение теплопроводности в ограниченной области D ⊂ Rn
![]() (28.22)
(28.22)
где κ > 0 — коэффициент температуропроводности. Пусть на границе выполнено краевое условие первого рода
![]() .
(28.23)
.
(28.23)
Действительно, нетрудно проверить (обязательно проверьте!), что
κ∆u
= Grad ![]() .
(28.24)
.
(28.24)
Здесь Grad означает функциональный градиент.
Равновесия градиентной системы и их устойчивость
Равновесия градиентного уравнения (28.1) определяются уравнением
grad S (x ) = 0. (28.25)
Таким образом, равновесия уравнения (28.1) являются критическими точками потенциала S . Это по сути — вариационный принцип, полезный при исследовании и вычислении равновесий.
![]() Если x
— некоторое равновесие уравнения (28.1), то соответствующее линеаризованное уравнение имеет вид
Если x
— некоторое равновесие уравнения (28.1), то соответствующее линеаризованное уравнение имеет вид
 u
˙ = (grad S
)0
(x
)u.
(28.26)
u
˙ = (grad S
)0
(x
)u.
(28.26)
В случае H = Rn векторное уравнение (28.1) можно записать в координатной форме
![]() (28.27)
(28.27)
Соответственно уравнение (28.26) записывается в виде
![]() (28.28)
(28.28)
Здесь подразумевается суммирование по j = 1,...,n . Матрица этой системы
![]() (28.29)
(28.29)
в случае C 2 –гладкой функции S симметрична. Поэтому все ее собственные значения вещественны и полупросты (являются простыми полюсами резольвенты (λI − A )−1 ), так что присоединенные векторы отсутствуют, и жорданова нормальная форма оператора A диагональна. Общее решение системы (28.28) записывается в виде
![]() ,
(28.30)
,
(28.30)
где ck — произвольные постоянные, λk — вещественные собственные значения, а ϕk — отвечающие им собственные векторы: A ϕk = λk ϕk .
![]()
![]()
![]() Если все λk
<
0, то равновесие x
асимптотически устойчиво по линейному приближению. Теорема Ляпунова о законности линеаризации позволяет в этом случае установить асимптотическую устойчивость равновесия x
и для полной системы (28.27). Нормальные моды — частные решения uk
(t
) = e
λ
k
t
ϕk
— в этом случае монотонно затухают со временем. Говорят, что равновесие x монотонно
асимптотически устойчиво.
Если все λk
<
0, то равновесие x
асимптотически устойчиво по линейному приближению. Теорема Ляпунова о законности линеаризации позволяет в этом случае установить асимптотическую устойчивость равновесия x
и для полной системы (28.27). Нормальные моды — частные решения uk
(t
) = e
λ
k
t
ϕk
— в этом случае монотонно затухают со временем. Говорят, что равновесие x монотонно
асимптотически устойчиво.
![]() Симметричность линейного оператора A
= (grad S
)0
(x
) можно установить и не пользуясь координатами: приводимое ниже доказательство сохраняет силу и для непрерывных операторов grad S
(x
) с C
2
–гладким потенциалом S
, в случае неограниченных операторов потребуются еще рассуждения об области определения оператора A
.
Симметричность линейного оператора A
= (grad S
)0
(x
) можно установить и не пользуясь координатами: приводимое ниже доказательство сохраняет силу и для непрерывных операторов grad S
(x
) с C
2
–гладким потенциалом S
, в случае неограниченных операторов потребуются еще рассуждения об области определения оператора A
.
Пусть x
, u
, v
— произвольные элементы пространства H
, а ε и µ — вещественные параметры. Рассмотрим вторую производную![]()
εu + µv ). Как и в случае функций, заданных на пространстве Rn , эта производная при условии, что S ∈ C 2 (даже при несколько меньших ограничениях), не зависит от порядка дифференцирования по переменным ε, µ.
Вспоминая определение градиента (28.15), выводим
![]() (grad S
(x
+ εu
),v
) =
(grad S
(x
+ εu
),v
) =
(28.31) = ((grad S )0 (x )u,v ) = (u, (grad S )0 (x )v ).
Последнее равенство получается, если сначала продифференцировать по ε, а затем по µ. Оно и означает, что A ∗ = A .
Заметим, что всякое равновесие градиентного уравнения (28.1) является также и равновесием уравнения (28.3) при условии (28.4). Действительно, умножая уравнение равновесий
grad S (x ) + F (x ) = 0 (28.32)
для уравнения (28.3) скалярно на grad S (x ), с учетом условия (28.4) получаем, что |grad S (x )|2 = 0. Таким образом, из уравнения (28.32) следует, что grad S (x ) = 0. Обратное, вообще говоря, неверно (см. упражнение 1). Более того, может случиться, что у уравнения (28.32) вообще нет решений, тогда как уравнение grad S (x ) = 0 имеет много решений.
Колебательная устойчивость и колебательная неустойчивость
![]()
![]()
![]()
![]() Уже в самых простых случаях присутствие дополнительного слагаемого F
в уравнении (28.3) может привести к появлению комплексных собственных значений в спектре линеаризованного на равновесии x
оператора. Рассмотрим например уравнение (28.5), и пусть x
— его равновесие, так что grad S
(x
) = 0. Линеаризованное на x
уравнение имеет вид
Уже в самых простых случаях присутствие дополнительного слагаемого F
в уравнении (28.3) может привести к появлению комплексных собственных значений в спектре линеаризованного на равновесии x
оператора. Рассмотрим например уравнение (28.5), и пусть x
— его равновесие, так что grad S
(x
) = 0. Линеаризованное на x
уравнение имеет вид
 u
˙ = (I
+ A
(x
))(grad S
)0
(x
)u.
(28.33)
u
˙ = (I
+ A
(x
))(grad S
)0
(x
)u.
(28.33)
Для определения показателя σ нормальной моды u (t ) = e σ t ϕ имеем задачу на собственные значения
![]() σϕ = (I
+ A
(x
))B
ϕ,
(28.34)
σϕ = (I
+ A
(x
))B
ϕ,
(28.34)
![]() где B
= (grad S
)0
(x
) — симметричный оператор B
= B
∗
. Если, напри-
где B
= (grad S
)0
(x
) — симметричный оператор B
= B
∗
. Если, напри-
![]() мер,
мер,![]() , то grad S
(x
) = βx
, и x
= 0 — равновесие, которое единственно при β
6= 0. Далее получаем (grad S
)0
(0) = βI
, и уравнение (28.34) принимает вид
, то grad S
(x
) = βx
, и x
= 0 — равновесие, которое единственно при β
6= 0. Далее получаем (grad S
)0
(0) = βI
, и уравнение (28.34) принимает вид
![]() σϕ = β(I
+ A
(x
))ϕ.
(28.35)
σϕ = β(I
+ A
(x
))ϕ.
(28.35)
![]()
![]()
![]() Предположим, что A
(x
) 6= 0. Как известно, спектр всякого ненулевого кососимметрического оператора в Rn
, скажем оператора A
(x
), состоит из некоторого количества пар чисто мнимых собственных значений ∓i
ωk
, ωk
>
0, k
= 1,...,s
и, быть может, собственного значения 0 кратности r
(очевидно, 2s
+ r
= n
). Соответственно, спектр оператора β(I
+ A
(x
)) состоит из собственных значений
Предположим, что A
(x
) 6= 0. Как известно, спектр всякого ненулевого кососимметрического оператора в Rn
, скажем оператора A
(x
), состоит из некоторого количества пар чисто мнимых собственных значений ∓i
ωk
, ωk
>
0, k
= 1,...,s
и, быть может, собственного значения 0 кратности r
(очевидно, 2s
+ r
= n
). Соответственно, спектр оператора β(I
+ A
(x
)) состоит из собственных значений ![]() , а также, возможно, точки β. Собственным значениям σ
∓
k
отвечают нормальные моды e
β
(1∓
ω
k
)t
ϕ
∓
k
. Так как Reσ
∓
k
= β, все они затухают, если β <
0. Это случай колебательной устойчивости.
, а также, возможно, точки β. Собственным значениям σ
∓
k
отвечают нормальные моды e
β
(1∓
ω
k
)t
ϕ
∓
k
. Так как Reσ
∓
k
= β, все они затухают, если β <
0. Это случай колебательной устойчивости.
Многие физики без особых обоснований рассматривают чисто градиентные системы как типичные замкнутые термодинамические системы. Видимо поэтому укрепился предрассудок, что в замкнутой термодинамической системе, если уж равновесие устойчиво, то непременно имеет место монотонная устойчивость. Поэтому, когда Б.П. Белоусов в 1951 году обнаружил, что если слить в пробирку раствор солей церия, малоновой кислоты и серной кислоты, то возникает химическая реакция, при которой достигаемое в конце концов равновесие устойчиво колебательно , ему не поверили. Реакция Б.П. Белоусова, которую сейчас время от времени демонстрируют по телевидению, очень красива — раствор становится, то красным, то голубым.
Неприятно, хотя и поучительно, вспомнить, что рецензенты статьи Белоусова действовали так же, как церковники, которые отказывались взглянуть в зрительную трубу Галилея, чтобы лично убедиться, что на Солнце есть пятна. Зачем глядеть, когда и так было ясно, что никаких пятен нет и быть не может? Рецензенты статьи Белоусова тоже заранее знали, что колебательных реакций не бывает. Они нарушали основной принцип науки: факты — впереди теорий. Ведь только и нужно было подойти к своим полкам с реактивами и, глядя в текст Белоусова, смешать указанные им реагенты в нужных пропорциях. Церковь уже покаялась и оправдала Галилея, что же касается рецензентов Белоусова, то о них ничего неизвестно.
Статья Белоусова так и не была опубликована в серьезных физических и химических журналах. К счастью, С.Э. Шноль в Пущине понял важность этой работы, помог опубликовать реферат статьи в «Рефератах по радиационной медицине», издаваемых Институтом биофизики Министерства здравоохранения СССР, и поручил своему аспиранту А.М. Жаботинскому продолжить работу. За исследование колебательных химических реакций в 1980 году Белоусову и Жаботинскому была присуждена Ленинская премия (Белоусову — посмертно).
Упражнения
1. Пусть H
= R
3
, потенциал![]() , а поле
, а поле![]()
![]() . Проверьте, что уравнение grad S
(x
) = 0 в этом случае имеет решения, которые не являются решениями уравнения grad S
(x
)+F
(x
) = 0. Более того, последнее уравнение, вообще, не имеет решений. Попытайтесь обобщить этот пример.
. Проверьте, что уравнение grad S
(x
) = 0 в этом случае имеет решения, которые не являются решениями уравнения grad S
(x
)+F
(x
) = 0. Более того, последнее уравнение, вообще, не имеет решений. Попытайтесь обобщить этот пример.
2. Докажите, что для потенциальности гладкого поля G (x ) в H необходимо и достаточно, чтобы для любого x производная G 0 (x ) была симметричным оператором, т.е. выполнялось равенство
(G 0 (x )ξ, η) = (ξ,G 0 (x )η), ξ, η ∈ H.
3. Докажите, что для потенциальности гладкого поля G (x ) необходимо и достаточно, чтобы интеграл по любой замкнутой кривой γ в H равнялся нулю:
![]() .
.
Продумайте определение интеграла по кривой в H , заданной параметрическим уравнением x = c (t ), 0 ≤ t ≤ 1. Докажите, что критерием потенциальности может также служить независимость интеграла по кривой, соединяющей две произвольные точки x 0 и x 1 , от вида кривой (он должен зависеть лишь от x 0 , x 1 ).
Замечание. Этот критерий сохраняет силу также для произвольной области в H , тогда как критерий упражнения 2 в части достаточности обобщается лишь на односвязные области в H . Подробности по поводу результатов упражнений смотрите в книге М.М. Вайнберга [6].
4. Пусть H = Rn , и уравнение x ˙ = G (x ) в координатах имеет вид
x ˙i = Gi (x ), i = 1,...,n.
Докажите, что поле G (x ) потенциально в том и только в том случае, когда выполняется равенство
![]()
Приведите пример поля на плоскости R 2 в кольце r 1 < |x | < r 2 , для которого эти условия выполнены, хотя поле не является потенциальным.
5. Выведите градиентное уравнение в частных производных, отвечающее потенциалу
![]()
где K — гладкая функция, D — область в Rn .
6. Докажите, что в случае H = R 3 оператор F (x ) = ω ∧ x (ω — постоянный вектор) — кососимметричен. Докажите, что его собственные значения суть 0 и ∓i |ω |. Исследуйте устойчивость нулевого решения уравнения
u ˙ = βu + ω ∧ u.
7. Каковы будут последствия добавления к правой части уравнения (28.1) слагаемого εF (x ) с малым параметром ε и функцией F , удовлетворяющей условию (28.4)?
8. Напишите общий вид уравнения в H , для которого заданная функция S (x ) является функцией Ляпунова. Найдите также общий вид дифференциального уравнения, для которого функция S (x ) является интегралом.
9. Найдите в Интернете описание истории открытия Белоусова и полюбуйтесь на анимацию реакции Белоусова–Жаботинского.
29. Малые колебания механической системы около
положения равновесия
Уравнения «малых колебаний» системы около положения равновесия получаются посредством линеаризации системы на заданном равновесии. Кавычки я поставил потому, что далеко не всегда, а лишь в случае устойчивого равновесия эти уравнения, действительно, описывают колебания. Вообще, если известно равновесие x 0 ∈ Rn автономной системы
x ˙ = f (x ) (29.1)
в Rn , то линеаризация уравнения (29.1) на равновесии x 0 — это довольно грубая операция. Она состоит в том, что мы полагаем x (t ) = x 0 + u (t ), а затем, подставляем это выражение в уравнение (29.1), и как говорили классики: «разлагаем правую часть уравнения в ряд Тейлора по степеням u , после чего отбрасываем все члены ряда, кроме линейных». Конечно, в этой классической формулировке предполагалась аналитичность векторного поля f (x ), тогда как на самом деле достаточно C 1 –гладкости. Линеаризованное уравнение , называемое также иногда линеаризацией уравнения (29.1), записывается в виде
u ˙ = Au, (29.2)
где A
= f
0
(x
0
) — линейный оператор, не зависящий от времени. В координатах он определяется матрицей![]() . Его правая часть отличается от правой части точного уравнения возмущений
. Его правая часть отличается от правой части точного уравнения возмущений
u ˙ = f (x 0 + u ) (29.3)
на малую величину o (u ) при u → 0, а если f ∈ C 2 , то, точнее, на величину O (u 2 ) при u → 0.
Заметим, что как точное уравнение возмущения (29.3), так и линеаризованное уравнение (29.2) имеют тривиальное решение u (t ) ≡ 0, соответствующее равновесию x 0 уравнения (29.1).
В координатах уравнение (29.2) записывается в виде системы
![]() (29.4)
(29.4)
где fi — компонента поля f (x ) = (f 1 (x ),...,fn (x )).
Вполне аналогично строится уравнение, линеаризованное на произвольном решении x 0 (t ) более общего уравнения
x ˙ = f (x,t ). (29.5)
Предположим, что решение x 0 (t ) определено для всех t ≥ 0. Представим решение x (t ) в виде x (t ) = x 0 (t ) + u (t ), слагаемое u (t ) называется возмущением основного решения x 0 (t ). Подстановка в уравнение (29.5) дает уравнение возмущений в виде
u ˙ = f (x 0 (t ) + u (t ),t ) − f (x 0 (t ),t ). (29.6)
Заранее ясно, что уравнение возмущений имеет тривиальное решение u (t ) ≡ 0. Линеаризация уравнения возмущений дает линейное уравнение, обобщающее (29.4)
u˙ = f0 (x0 (t),t)u. (29.7)
Дальше мы будем, однако, заниматься в основном равновесиями.
Устойчивость по Ляпунову
Если задаться конкретным промежутком времени [0,T ], то из общих результатов теории дифференциальных уравнений о непрерывной зависимости решения задачи Коши от начальных данных можно заключить, что решение задачи Коши для уравнения (29.1), а также и для уравнения (29.2) с начальным условием u (0) = u 0 , будет отличаться не более, чем на ε (ε > 0 и произвольно) от нулевого решения u = 0, если u 0 достаточно мало, точнее, если ku 0 k < δ, где δ = δ(ε).
На самом деле, однако, как это впервые ясно осознал Ляпунов, важно, чтобы малость возмущения u сохранялась на бесконечном промежутке времени [0, ∞).
Определение. Равновесие x 0 уравнения (29.1) называется устойчивым по Ляпунову, если выполнены следующие два условия:
1◦ ) существует окрестность нуля в Rn , скажем, шар B (0, ρ) радиуса ρ > 0 с центром в нуле, что задача Коши для уравнения (29.3) с начальным условием u (0) = u 0 имеет единственное решение u (t ), определенное для всех t ≥ 0 при любом u 0 ∈ B (0, ρ);
2◦ ) для любого ε > 0 существует такое δ > 0, что для любого начального поля u 0 , имеющего столь малую норму, что ku 0 k < δ, решение u (t ) задачи Коши для уравнения (29.3) с начальным условием u (0) = u 0 удовлетворяет неравенству ku (t )k < ε для всех t ≥ 0.
Таким образом, устойчивость по Ляпунову есть непрерывная зависимость решения задачи Коши для уравнения (29.1) от начальных данных (из окрестности точки x 0 ), равномерная по времени t на бесконечном промежутке времени [0, ∞].
Если равновесие x 0 устойчиво по Ляпунову и, кроме того, возмущения затухают при t → +∞, так что ku (t )k → 0 при t → +∞, то скажем, что оно асимптотически устойчиво .
На первый взгляд может показаться, что из свойства притяжения (затухания возмущений) равновесия x 0 следует и его устойчивость. А.М. Ляпунов проявил здесь глубокую проницательность, включив требование устойчивости в определение, хотя примеры решений, обладающих свойством притяжения, но неустойчивых, появились лет через пятьдесят. Возмущения таких решений (по крайней мере, некоторые) при t → +∞ затухают, но сначала их нормы вырастают до фиксированной, немалой величины. При этом можно подобрать решения с таким поведением, отвечающие сколь угодно малым начальным возмущениям.
До Ляпунова многие авторы занимались устойчивостью равновесий и движений. Существовало и несколько определений устойчивости — устойчивость по Лагранжу, устойчивость по Пуассону и т.д. Эти определения применяются иногда до сих пор, но имеют довольно частное значение. Когда говорят, что решение устойчиво, то подразумевается, что оно устойчиво по Ляпунову .
В приложениях теории устойчивости по сути используется, хотя обычно явно и не формулируется, принцип Ляпунова : данный режим движения системы можно наблюдать экспериментально в течение достаточно долгого (неограниченно долгого) времени в том и только в том случае, когда этот режим устойчив по Ляпунову.
Разумеется, устойчивость по Ляпунову есть качественное понятие, как и понятие непрерывности. На практике зачастую оно должно дополняться некоторыми количественными характеристиками. Скажем, интересно бывает уточнить, сколь малым должно быть δ (возмущение в начальный момент), чтобы обеспечить ε-малость возмущения для всех t ≥ 0. Когда некоторое равновесие или движение неустойчиво, возникает ряд новых вопросов. Насколько быстро рост возмущения разрушит основной режим?
Даже и неустойчивый режим (скажем, равновесие карандаша, стоящего на острие) можно наблюдать в течение некоторого времени, и интересно это время оценить. Это время может даже оказаться столь большим, что на практике мы сочтем основной режим устойчивым. Следующий вопрос — каково дальнейшее поведение возмущенных движений, когда они уже достаточно далеко отошли от основного? Думаю, что у Вас возникнет немало подобных вопросов. Замечательно, однако, что на практике принцип Ляпунова работает даже и без всяких количественных уточнений.
Теории устойчивости посвящены многие трактаты [24, 50, 25, 12, 26, 39, 11], начиная со знаменитой диссертации Александра Михайловича Ляпунова (1892). Вначале рассматривались конечномерные системы (обыкновенные дифференциальные уравнения) [24, 50, 25, 12, 26, 39], а затем и бесконечномерные [11].
Если нулевое решение линейного уравнения (29.2) устойчиво (в этом случае, очевидно, все его решения устойчивы, а потому допустимо называть устойчивым уравнение), то говорят, что равновесие x 0 уравнения (29.1) устойчиво по линейному приближению , или что оно устойчиво относительно бесконечно малых возмущений .
А.М. Ляпунов развил методы исследования устойчивости решений, и, в частности, равновесий нелинейных систем дифференциальных уравнений — это знаменитые первый и второй (он же прямой ) методы Ляпунова .
Первый метод Ляпунова основывается на линеаризации дифференциального уравнения на основном решении. А.М. Ляпунов указал условия, при которых исследование устойчивости по линейному приближению оказывается достаточным для решения вопроса об устойчивости основного решения. Он также развил методы исследования устойчивости в критических случаях — когда линейного приближения недостаточно и приходится привлекать следующие (после линейных) члены разложения ряда Тейлора данного дифференциального уравнения в окрестности основного режима. Наиболее полные результаты получаются в проблеме устойчивости равновесия автономной системы или периодического движения периодической системы. Приведу здесь результаты Ляпунова о законности линеаризации в задаче устойчивости (неустойчивости) равновесия автономной системы. Векторное поле f в уравнении (29.1) должно удовлетворять определенным условиям регулярности, достаточно, чтобы оно было C 2 –гладким.
Напомню, что в конечномерном случае спектр σ(A ) линейного оператора A есть набор его собственных значений σ(A ) = {λ1 ,..., λk }. Здесь k — число различных собственных значений, так что k ≤ n .
Теорема 1. Пусть спектр линейного оператора A = f 0 (x 0 ) — коэффициента в линеаризованном уравнении (29.2) — расположен в левой полуплоскости: все его собственные значения λ1 , λ2 ,..., λk имеют отрицательные действительные части. Тогда равновесие x 0 нелинейного уравнения (29.1) асимптотически устойчиво.
Если же хотя бы одно собственное значение, скажем, λj имеет положительную действительную часть ( Reλj > 0), то равновесие неустойчиво.
Эта теорема не охватывает лишь те случаи, когда оператор A не имеет собственных значений в правой полуплоскости, но имеется хотя бы одно собственное число на мнимой оси. Такие случаи и называются критическими , это означает, что выполнено нестрогое неравенство Reλi ≤ 0 при i = 1,...,k , причем хотя бы для одного собственного значения λj имеет место равенство Reλj = 0. В любой книге по теории устойчивости (см., например, [50, 25, 12, 47]) Вы найдете результаты по устойчивости в различных критических случаях, а также формулировки многочисленных нерешенных проблем этой интересной области теории дифференциальных уравнений.
Здесь остается заметить, что в задаче устойчивости равновесия консервативной механической системы, когда не учитываются силы трения и другие факторы диссипации энергии, асимптотическая устойчивость равновесия невозможна (см. упражнение 1). Вместе с тем, результат о законности линеаризации в задаче о неустойчивости из теоремы 29 применим и к таким задачам.
Второй (прямой) метод Ляпунова возник как широкое и содержательное обобщение теоремы Лагранжа об устойчивости равновесия натуральной механической системы в случае, когда оно дает потенциальной энергии строгий минимум . Подробное изложение прямого метода Ляпунова Вы найдете в уже цитированных руководствах по теории устойчивости. Этот метод позволяет получать результаты и об устойчивости, и о неустойчивости, и об асимптотической устойчивости как для автономных, так и для неавтономных дифференциальных уравнений. Здесь я ограничусь лишь теоремой об устойчивости равновесия автономного уравнения. Пусть x 0 — равновесие автономного уравнения в Rn
x ˙ = f (x ). (29.8)
Полагая x (t ) = x 0 + u (t ), где u (t ) — возмущения, запишем соответствующее уравнение возмущений
u ˙ = f (x 0 + u ). (29.9)
Мы помним, что устойчивость равновесия x 0 — то же самое, что и устойчивость тривиального решения u (t ) = 0 уравнения возмущений.
Предположим, что известна функция V (u ), определенная в некоторой окрестности нуля в Rn и такая, что V (0) = 0 и V (u ) > 0 при u 6= 0. Такая функция называется определенно положительной (или положительно определенной ). Будем предполагать, что функция V непрерывно дифференцируема, и вычислим ее производную по времени V ˙ в силу уравнения возмущений (29.9). Имеем
V ˙ = −W ; W = −(grad V (u ),f (x 0 + u )) (29.10)
(см. (5.3)). Знак минус в этой формуле поставлен ради будущих удобств.
Скажем, что функция U неположительна (Ляпунов и некоторые его последователи употребляют термин отрицательная ), если выполняется условие U (0) = 0 и U (u ) ≤ 0 всюду.
Аналогично, функция U называется неотрицательной, если U (0) = 0 и U (u ) ≥ 0 всюду (по терминологии Ляпунова, положительная функция).
Обратите внимание, что во всех этих определениях предполагается выполненным условие U (0) = 0. Замечу, что аргумент 0 появился потому, что речь идет о нулевом решении.
Приведу здесь теорему Ляпунова об устойчивости для рассматриваемого частного случая.
Теорема 2. Пусть функция V определенно положительна, а ее производная неположительна. Тогда равновесие x 0 уравнения (29.8) (или,чтотоже,нулевоерешениеуравнениявозмущений (29.9))устойчиво по Ляпунову.
Сделаем несколько замечаний по поводу этой теоремы. Я не привожу здесь доказательства, но суть теоремы нетрудно усмотреть из рисунка 16, где показано расположение поверхностей уровня функции V в окрестности точки u = 0. Рисунок показывает, что в условиях теоремы, когда значение V не возрастает, движение не может уйти далеко от точки 0.
Далее замечу, что эта теорема не исключает случая, когда функция V является интегралом уравнения (29.8), а производная V ˙ ≡ 0. Чаще всего именно этот случай и возникает в приложениях, в этой ситуации данная теорема незаменима, а метод линеаризации не работает.
Очевидно, в теореме Ляпунова можно взять функцию V определенно отрицательной, если потребовать, чтобы производная V ˙ была неотрицательной. Этот случай сводится к предыдущему заменой V на −V .
Хотя в теории переход к уравнению возмущений удобен и практически всегда проводится, он не является необходимым. Условие определенной
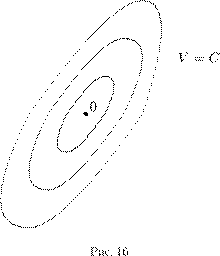
положительности функции V (u ) означает, что она в точке u = 0 достигает строгого минимума . Можно рассматривать функцию V (x ), определенную в окрестности точки x 0 и достигающую в ней строгого минимума. Тогда, та функция, которая фигурирует в теореме, естественно записывается в виде
V (u ) = V (x 0 + u ) − V (x 0 ). (29.11)
Приведу общее определение функции Ляпунова дифференциального уравнения. Это такая функция V (x,t ), что монотонно возрастает (либо убывает) для любого решения x (t ). Функция V , удовлетворяющая условиям теоремы 2, обычно называется функцией Ляпунова первого рода. Пожалуй, вообще, единственный способ узнать что-то о качественном поведении решения дифференциального уравнения, не решая его, состоит в том, чтобы найти его функцию Ляпунова. Сама по себе теорема 2 не содержит указаний о том, каким образом мы можем такую функцию построить. Практически полезных общих методов здесь не существует. Однако для ряда важных классов уравнений надлежащие функции Ляпунова известны. В механике зачастую бывает достаточно в качестве функции Ляпунова использовать полную механическую энергию, быть может, в комбинации с другими интегралами (импульса, момента импульса и т.д.), если они нам известны.
Устойчивость равновесия механической системы
Ограничимся натуральными системами, для которых лагранжиан имеет вид
L = T − V, (29.12)
где V = V (q ) — потенциальная энергия, а кинетическая энергия T есть квадратичная форма относительно скоростей с коэффициентами, зависящими, вообще говоря, от координат:
![]() .
(29.13)
.
(29.13)
Здесь q = (q 1 ,...,qn ) — точка n -мерного конфигурационного пространства. Специфика состоит в том, что мы теперь имеем дело с уравнениями второго порядка — уравнениями Лагранжа второго рода. Пусть q 0 — равновесие, так что q ˙0 = 0. Введем возмущения u , полагая q (t ) = q 0 + u , q ˙ = u ˙ для любого решения q (t ). Линеаризацию уравнений Лагранжа на решении q 0 можно провести, работая с лагранжианом L . Для этого достаточно подставить выражение q = q 0 + u в формулу (29.12) и выделить главную квадратичную часть лагранжиана. Для кинетической энергии имеем
![]() ,
(29.14)
,
(29.14)
где многоточие обозначает слагаемые степени выше второй относительно u , u ˙. Для потенциальной энергии V разложение можем написать в виде
![]() (29.15)
(29.15)
где опущенный остаточный член имеет степень выше второй относительно q ; в случае, когда V ∈ C 3 , он имеет порядок не ниже третьего. Выражение u 2 можно трактовать как тензорный квадрат , для нас сейчас это просто обозначение.
Первое слагаемое в (29.15) есть несущественная константа, и можно положить V (q 0 ) = 0. Второе слагаемое исчезает, потому что q 0 — равновесие и, следовательно, является критической точкой потенциальной энергии.
В результате можем написать
L = T 2 − V 2 + ..., (29.16)
где T 2 дается формулой (29.14), а квадратичная форма V 2 имеет вид
![]() .
(29.17)
.
(29.17)
В (29.16) опущены члены порядка малости выше второго при u → 0. Мы видим, что квадратичная форма (29.17) задается симметричной матрицей Гесса функции V
![]() .
(29.18)
.
(29.18)
Линеаризованные на равновесии q 0 уравнения Лагранжа (полные уравнения нет нужды здесь выписывать) определяются лагранжианом
![]() ,
(29.19)
,
(29.19)
где A — оператор Гесса (29.18), а оператор M задается матрицей с коэффициентами mik (q 0 ). В итоге линеаризованное уравнение, которое является уравнением Лагранжа второго рода с лагранжианом (29.19), принимает вид
Mu ¨ = −Au. (29.20)
Это — общий вид уравнения малых колебаний натуральной механической системы около равновесия q 0 . Мы видим, что уравнение малых колебаний сохраняет форму обобщенного уравнения 2-го закона Ньютона.
Кинетическая энергия есть положительно определенная квадратичная форма относительно скоростей. Поэтому оператор M
положительно определен:![]() . Оператор A
= grad V
2
самосопряжен. Он может быть как знакоопределенным, так и знакопеременным.
. Оператор A
= grad V
2
самосопряжен. Он может быть как знакоопределенным, так и знакопеременным.
Из теоремы 29 непосредственно следует теорема Лагранжа об устойчивости равновесия. Как я уже говорил раньше, исторически теоремы прямого метода Ляпунова возникли как обобщение этой теоремы. Вместе с тем, сама теорема Лагранжа явилась замечательным обобщением принципа Торричелли (1642 г.): механическая система находится в устойчивом равновесии, когда ее центр тяжести занимает наинизшее возможное положение. Разумеется, во времена Торричелли (гениального ученика гениального Галилея), даже во времена Лагранжа понятие устойчивости не было строго оформлено. Поэтому, быть может, правильно было бы говорить о теореме Торричелли–Лагранжа–Ляпунова.
Теорема 3. (Теорема Лагранжа). Равновесие q 0 механической системы (29.20) устойчиво если потенциальная энергия V достигает в точке q 0 (хотя бы локального) строгого минимума.
Доказательство. Нетрудно видеть, что в условиях теоремы Лагранжа полная механическая энергия E = T + V есть функция Ляпунова первого рода. Действительно, для любого q из окрестности q 0 и произвольного q ˙ имеем
E(q,q˙) ≥ V (q) > V (q0 ) = E(q0 ,0). (29.21)
Первое неравенство выполнено потому, что T — положительно определенная квадратичная форма, второе неравенство — в силу условия теоремы. Последнее равенство верно потому, что q ˙0 = 0. Мы доказали, что E достигает строгого минимума в положении равновесия q 0 . Так как E ˙ = 0, условия теоремы (29) выполнены, и теорема Лагранжа доказана
Как известно, достаточным условием строгого минимума служит положительная определенность второго дифференциала V 2 потенциальной энергии V в критической точке q 0 .
Таким образом, из положительной определенности оператора A следует устойчивость равновесия q 0 по Ляпунову . Выходит, что в этой ситуации линеаризация все-таки законна, хотя мы имеем дело с критическим случаем.
Естественно возникает вопрос об условиях неустойчивости равновесия. Это — проблема обращения теоремы Ляпунова, которая до сих пор не решена и остается объектом исследований. Ляпунов доказал, что равновесие q 0 неустойчиво в том случае, когда второй дифференциал d 2 V (q 0 )(ξ, ξ) может для некоторых векторов ξ принимать отрицательные значения . В частности, q 0 — неустойчивое равновесие, когда второй дифференциал отрицательно определен, и функция V в точке q 0 достигает максимума (самая сильная неустойчивость). Случай, когда форма d 2 V (q 0 )(ξ, ξ) неотрицательна, но не положительно определена, является критическим и требует дальнейшего исследования с учетом высших членов разложения Тейлора функции V . Повторюсь, хотя многие авторы продолжали исследования Ляпунова (см. [50, 39, 17]), проблема неустойчивости равновесия полностью не решена.
Если разыскивать частные решения уравнения (29.20) в виде
u ω (t ) = ei ω t ϕ, (29.22)
где ϕ — постоянный вектор, придем к спектральной задаче: найти числа ω (вообще говоря, комплексные) такие, что уравнение
A ϕ = ω2 M ϕ (29.23)
имеет ненулевое решение ϕ. При M = I это обычная задача на собственные значения для оператора A . Имеются различные способы свести общую задачу (29.23) к обыкновенной задаче на собственные значения для самосопряженного оператора. Видимо, лучший из них — попросту обратить в (29.23) оператор M и перейти от стандартной метрики в Rn к новой, порождаемой скалярным произведением
| (ϕ, ψ)M = (M ϕ, ψ). Тогда уравнение (29.23) примет вид |
(29.24) |
| M −1A ϕ = ω2ϕ, |
(29.25) |
и при этом оператор M −1 A оказывается самосопряженным относительно метрики (29.24). Действительно, для любых ϕ и ψ имеется равенство
(M −1 A ϕ, ψ)M = (A ϕ, ψ) = (ψ,A ϕ) = (ϕ,M −1 A ψ)M . (29.26)
Мы уже раньше видели (см. формулу (11.19) и последующий текст), что переход от стандартного скалярного произведения к скалярному произведению (29.24), порождаемому оператором масс M , приводит общее уравнение второго закона Ньютона к его частному случаю с оператором M = I . Как вы знаете, все собственные значения самосопряженного оператора вещественны. Поэтому вещественны все собственные числа оператора M −1 A , и соответственно, частота ω вещественна, если ω 2 > 0, и является чисто мнимой при ω 2 < 0. Это, впрочем, можно установить и непосредственно. Умножим уравнение (29.23) скалярно на ϕ (напомню, что в комплексном случае (ϕ, ψ) = P ϕk ψk ∗ , если ϕ = (ϕ1 ,..., ϕn ) и ψ =
k
(ψ1 ,..., ψn )). В результате получаем
![]() .
(29.27)
.
(29.27)
Поскольку M и A — симметричные операторы, числитель и знаменатель этой дроби вещественны (см. упражнение 3), причем знаменатель положителен.
Как известно из линейной алгебры, симметричный оператор M −1 A всегда имеет ортонормальный собственный базис, состоящий из собственных векторов ϕ1 ,..., ϕn , которым отвечают вещественные собственные значе-
ния ![]() . Выполняются равенства
. Выполняются равенства
Aϕj = ω 2 j Mϕj , j = 1,...,n. (29.28)
Поскольку операторы A и M вещественны, собственные векторы ϕj можно также считать вещественными. Согласно формуле (29.22), каждому собственному значению ω 2 отвечает пара решений e ±i ω t ϕ, называемых нормальными колебаниями , или нормальными модами .
Общее решение уравнения (29.20) можно представить в виде линейной комбинации нормальных колебаний:
n
u (t ) = X cj ei ω j t ϕ j . (29.29)
j =−n
При этом мы полагаем ω−j
= −ωj
, ϕ−j
= ϕj
. Для вещественных решений ![]() . Здесь мы считаем, что c
0
= 0, а ω0
и ϕ0
не определены.
. Здесь мы считаем, что c
0
= 0, а ω0
и ϕ0
не определены.
Решение (29.29) описывает колебания, когда все частоты ωj вещественны, то есть, когда собственные числа ω 2 j положительны. Это соответствует тому случаю, когда оператор A положительно определен. Тогда и квадратичная форма d 2 V (q 0 )(u,u ) = (Au,u ) положительно определена. По теореме Лагранжа–Ляпунова, равновесие q 0 в этом случае устойчиво. Заметим, что и интеграл энергии
![]() (29.30)
(29.30)
есть положительно определенная форма от u и u ˙.
Если разыскивать решение уравнения (29.20) в виде
![]() ,
(29.31)
,
(29.31)
то для координаты xj в собственном базисе получим уравнение гармонического осциллятора
x ¨j + ω 2 j xj = 0. (29.32)
Мы приходим к важному выводу: в случае устойчивого равновесия q 0 , когда второй дифференциал d 2 V (q 0 )(u,u ) = (Au,u ) есть положительно определенная форма, уравнение малых колебаний может быть представлено как набор n независимых гармонических осцилляторов, где n — число степеней свободы системы.
Я уже упоминал раньше, см. 8, о такого рода нетривиальных разбиениях динамической системы на независимые подсистемы. Замечу, что и в неустойчивом случае уравнение «малых колебаний» (29.20) представляется как декартово произведение независимых подсистем, по-прежнему определяемых уравнениями (29.32). В этом случае, однако, те из уравнений (29.32), для которых ω 2 j < 0, описывают не колебания, а экспоненциально растущие или экспоненциально затухающие движения, чему и соответствуют поставленные выше кавычки. В случае ω 2 j = 0 большинство решений уравнения (29.32) линейно растет со временем, лишь решения, отвечающие начальному условию вида x (0) = a , x ˙(0) = 0, — постоянны.
Возможность разбиения динамической системы на невзаимодействующие подсистемы оказывается особенно важной, когда применяются вероятностные методы. Зачастую наличие тех или иных свойств статистической независимости оказывается решающим для успеха исследования. Дальше мы рассмотрим применение статистической механики к теории твердого тела — замечательный пример плодотворности изложенных здесь идей.
Упражнения.
1. Пользуясь теоремой Лиувилля о сохранении фазовых объемов, докажите, что равновесие гамильтоновой системы не может быть асимптотически устойчивым.
2. Докажите, что нулевое равновесие уравнения
x ¨ = −x 3
устойчиво по Ляпунову, хотя условия теоремы Лагранжа нарушены.
3. Пусть линейный оператор A действует в комплексном (унитарном) пространстве Cn . Докажите, что он самосопряжен в том и только в том случае, когда его квадратичная форма (A ϕ, ϕ) при всех ϕ ∈ Cn принимает вещественные значения.
4. При каких условиях решение (29.29) периодично по t ? Вообще говоря, оно лишь квазипериодично .
5. Докажите, что если уравнение
Mu ¨ = Au,
где M
и A
— самосопряженные операторы, причем![]() , имеет экспоненциально растущее решение, то оно имеет также экспоненциально затухающее решение с тем же показателем экспоненты.
, имеет экспоненциально растущее решение, то оно имеет также экспоненциально затухающее решение с тем же показателем экспоненты.
30 Статистическая механика твердого тела
![]()
30. Статистическая механика твердого тела
Теперь речь пойдет о простейшей модели твердого тела в статистической механике. Представим себе кристаллическую решетку, в узлах которой q 1 ,...,qn располагаются частицы — ионы или атомы. Обычно эти частицы несут некоторый электрический заряд — например, в узлах кубической кристаллической решетки поваренной соли находятся ионы натрия и хлора. Более редкий случай — когда в узлах решетки расположены электрически нейтральные атомы — представляет алмаз. Частицы взаимодействуют между между собой, и это взаимодействие описывается потенциальной энергией V (q ). Здесь q = (q 1 ,...,qn ), где qi ∈ R3 — положение i -й частицы. Таким образом, q ∈ R3n . Предположим, что частицы совершают малые колебания около своих равновесных положений q 01 ,q 02 ,...,q 0n . Предполагается, что система натуральна, и ее гамильтониан имеет вид
![]() .
(30.1)
.
(30.1)
Импульс p выражается через оператор масс M (q ) формулой
p = M (q )q. ˙ (30.2)
Здесь q ˙ = (q ˙1 ,...,q ˙n ) — скорость, q ˙ ∈ R3n .
Положим q = q 0 + u , где u — возмущение положения системы. Так как в случае равновесия q 0 = 0, p 0 = 0, можно считать, что q и p суть возмущения.
Простейшая модель получается, когда мы предполагаем колебания частиц около их положений равновесия столь малыми, что можно применить уравнения малых колебаний (см. (29.20))
Mu ¨ = −Au, (30.3)
где M = M (q 0 ), а оператор A (см. (29.18)) определяется матрицей Гесса потенциальной энергии V . Гамильтониан этой системы есть квадратичная относительно возмущений u, u ˙ часть гамильтониана (30.1). Далее будем предполагать, что оператор A положительно определен, так что равновесие q 0 есть точка строгого минимума потенциальной энергии V :
![]() .
(30.4)
.
(30.4)
Как мы уже видели, система (30.3) может быть представлена как декартово произведение 3n экземпляров гармонических осцилляторов. Каждый из них описывается уравнением вида (см. (29.32))
x ¨j + ω 2 j xj = 0, (30.5)
где частоты ωj
отличны от нуля и вещественны в силу предположения ![]() 0 (оператор масс мы всегда считаем положительно определенным). При этом возмущение положения равновесия u
(t
) определяется разложением по нормальным модам (см. (29.31))
0 (оператор масс мы всегда считаем положительно определенным). При этом возмущение положения равновесия u
(t
) определяется разложением по нормальным модам (см. (29.31))
![]() ,
(30.6)
,
(30.6)
где ϕj — собственный вектор оператора M −1 A , отвечающий собственному значению ω 2 j . В переменных xj гамильтониан (30.4) принимает вид
![]() .
(30.7)
.
(30.7)
Пора остановиться и перевести дух. Все предыдущее есть не более, чем некоторые наводящие соображения. Мы можем теперь сказать, что простейшая модель твердого тела есть линейная динамическая система, состоящая из (представляющая собой декартово произведение) 3n невзаимодействующих гармонических осцилляторов. Более того, даже и конкретные значения частот ωj не играют серьезной роли в дальнейшем.
Перейдем к вычислению статистического интеграла
![]() (30.8)
(30.8)
В случае гамильтониана (30.4) интеграл P (B ) представляется в виде произведения 6n гауссовых интегралов:
![]() .
(30.9)
.
(30.9)
Статистическая механика твердого тела
Далее получаем
![]() .
(30.10)
.
(30.10)
Здесь мы считаем (имеем право!), что ωj > 0. Окончательно имеем
![]() .
(30.11)
.
(30.11)
Теперь находим энергию E (B ) по формуле (25.16). Заметим, что P (B ) = CB 3n , где C — константа, зависящая от частот ωj . Поэтому lnP (B ) = 3n lnB + const , и вспоминая, что B = kT , получаем
E = 3nkT. (30.12)
Как и в случае идеального газа, энергия зависит лишь от температуры и числа частиц. Мы можем вычислить также теплоемкость c (точнее, cV — теплоемкость при постоянном объеме):
![]() (30.13)
(30.13)
Таким образом, теплоемкость зависит лишь от числа частиц и не зависит от их природы, а также и от температуры. Это — известный закон Дюлонга и Пти (1819 г.), которые экспериментально обнаружили, что у всех элементов в твердом состоянии атомная удельная теплоемкость (то есть удельная теплоемкость с поправкой на различный атомный вес) одна и та же. В экспериментах нередко наблюдаются большие отклонения от этого закона, но при достаточно высоких температурах. Пока сохраняется твердое состояние, закон, как правило, выполняется. Нужно сразу признать, что статистическая механика оказалась не в состоянии объяснить отклонения от данного закона при низких температурах. Это расхождение между теорией и экспериментом было одним из важнейших стимулов к развитию квантовой механики , точнее, квантовой статистики .
Приложение 1. Типичность единственности и
нетипичность неединственности решения задачи Коши
Здесь мы рассмотрим дифференциальное уравнение
x ˙ = f (x,t ) (A.1)
с непрерывной скалярной функцией f : R 2 → R , заданной на всей плоскости R 2 . На самом деле, следующие рассмотрения можно провести вполне аналогично и для уравнений в Rn . Имеются и дальнейшие обобщения — на уравнения в банаховом пространстве X , на уравнения с многозначными функциями и т. д.
Наша цель — изложить доказательство удивительной теоремы Владислава Орлича (1932, [65]) (исследования Орлича были продолжены в работах [62, 63, 64]). Эта теорема показывает, что в определенном смысле (разъясненном ниже), типичной является ситуация, когда для уравнения
(A.1) с начальным условием вида
![]() (A.2)
(A.2)
решение для всех точек (x 0 ,t 0 ) ∈ R 2 единственно! И это несмотря на то, что одного лишь свойства непрерывности функции√ f , как показывают про-
![]()
стые примеры (вспомните задачу Коши x ˙ = 3 x , x (0) = 0), для единственности недостаточно. Удивительное дело, этот фундаментальный результат польского математика совсем мало известен, не упоминается в трактатах по дифференциальным уравнениям и в учебниках. Более того, весьма распространен предрассудок, что типична как раз неединственность. По-видимому, так получается потому, что многие верят в "принцип хрупкости хорошего". Этот принцип, говорящий, что все хорошее встречается редко и легко портится, применим, к сожалению, ко многим проблемам математики и жизни. Но он, выходит, отказывает применительно к задаче Коши (A.1), (A.2). Не считать же "хорошим" случаем неединственность решения.
В шутку я проводил голосование среди математиков, сначала в России, а затем в нескольких американских университетах, по вопросу о том, что типично — единственность или неединственность. Этот демократический способ решения проблемы дал правильный результат лишь на семинаре в Институте Куранта в Нью-Йорке, причем соотношение голосов за правильный ответ (единственность!) и против него было, кажется, 14:12, многие воздержались. Выдающиеся специалисты по дифференциальным урав-
нениям оказались в разных партиях. Получив, наконец, правильный ответ, я прекратил такие эксперименты.
Дальше нам понадобится ряд понятий из функционального анализа. Вероятно, они вам большей частью известны, а здесь я их лишь кратко напомню.
Категория множества по Бэру. Пусть X — метрическое пространство. Множество M ⊂ X называется всюду плотным в X , если его за-
![]()
мыкание M совпадает с X . Эквивалентное требование таково: в каждом шаре пространства X найдется хотя бы одна точка множества M . Либо так: для любой точки x ∈ X найдется последовательность точек x 1 , x 2 ,... множества M такая, что xn → x , то есть ρ(xn ,x ) → 0. Здесь ρ — метрика, и ρ(x,y ) — расстояние между точками x и y в X .
Множество M ⊂ X называется нигде не плотным в X , если для каждого шара в X найдется расположенный внутри него шар, не содержащий ни одной точки множества M .
Типичные примеры: множество Q всех рациональных чисел всюду плотно в метрическом пространстве R . Множество Qn всевозможных векторов пространства Rn , имеющих рациональные координаты, всюду плотно в Rn . Множество Z всех целых числе нигде не плотно в R . Прямая в R 2 нигде не плотна.
Нетривиальный пример нигде не плотного множества построил Г. Кантор. Рассмотрим сегмент [0,
1]. Выбросим из него интервал![]() . С двумя оставшимися отрезками проделаем такую же процедуру: разделим каждый из них на 3 равных отрезка и выбросим среднюю часть. С оставшимися четырьмя отрезками проделаем то же самое. Продолжим эти действия до бесконечности. Оставшееся канторово множество
K
нигде не плотно на [0,
1]. В этом случае X
= [0,
1], ρ(x,y
) = |x
− y
|. Заметьте, что построенное таким образом канторово множество состоит из всевозможных чисел на отрезке [0,
1], имеющих разложение в троичную дробь, в котором отсутствует цифра 2.
. С двумя оставшимися отрезками проделаем такую же процедуру: разделим каждый из них на 3 равных отрезка и выбросим среднюю часть. С оставшимися четырьмя отрезками проделаем то же самое. Продолжим эти действия до бесконечности. Оставшееся канторово множество
K
нигде не плотно на [0,
1]. В этом случае X
= [0,
1], ρ(x,y
) = |x
− y
|. Заметьте, что построенное таким образом канторово множество состоит из всевозможных чисел на отрезке [0,
1], имеющих разложение в троичную дробь, в котором отсутствует цифра 2.
Канторовы множества долгое время казались математикам абстрактной и вычурной выдумкой. Однако в середине XX века они стали появляться в теории динамических систем и, по сути, во всех областях нелинейной математической физики (конечно, не обязательно в процедуре Кантора делить отрезки на равные части).
Множество M называется множеством 1-ой категории по Бэру, если его можно представить как счетное объединение нигде не плотных множеств. Например, множество Q рациональных чисел в R , а также и Qn в Rn , суть множества 1-й категории, хотя бы по тому, что они сами счетны.
Множества, не являющиеся множествами 1-й категории, называются множествами 2-й категории. Среди них особенный интерес представляют вычеты . Множество M ⊂ X называется вычетом , если оно — 2-й категории, а его дополнение X \ M есть множество 1-й категории. Замечу, что всякое полное метрическое пространство X есть множество второй категории — в себе. В этом случае и всякое непустое открытое множество в X — тоже второй категории, и дополнение всякого множества первой категории имеет вторую категорию, а значит, является вычетом.
Понятно, что множества 1-й категории — это в некотором роде "малые множества зачастую пренебрежимо малые. Напротив, явления, которые происходят для всех точек множества 2-й категории, в аналогичном смысле можно рассматривать как типичные (конечно, типичность явления не означает, что оно происходит всегда, может быть несколько, даже бесконечно много, различных типичных ситуаций, см. упражнение 4).
Конечно, имеются и другие подходы к определению "пренебрежимо малых" и типичных множеств. Напомню два других варианта. Первый из них связан с размерностями. Например, гладкая кривая или гладкая поверхность в R 3 может считаться "пренебрежимым" множеством (замечу, что гладкость здесь очень существенна — как показал Пеано, непрерывная кривая может проходить через все точки куба). Второй подход связан с мерой. Пренебрежимыми считаются множества меры 0, иногда их даже называют нулевыми . Обычно также "пренебрежимо малыми" считаются конечные подмножества бесконечных множеств, или вообще подмножества меньшей мощности . Когда-то математики были поражены результатом Кантора: квадрат и отрезок прямой — множества равномощные (докажите!)
Надо еще подчеркнуть, что понятия плотного, нигде не плотного множества, а также множеств 1-ой и 2-ой категории зависят от выбора метрики. Эти понятия определяются и для более общих топологических пространств, и тоже зависят от выбора топологии . Вполне может случиться, что множество 1-ой категории X станет множеством 2-ой категории, если мы на том же множестве X введем другую метрику или топологию. Точно так же множество, имеющее нулевую меру µ, может оказаться множеством положительной меры µ1 .
Пространство функций C (R 2 ). Каждая функция f : R 2 → R :
(x,t ) 7→ f (x,t ) определяет на всей плоскости R 2 дифференциальное уравнение вида (A.1). Будем рассматривать пространство всевозможных непрерывных функций на плоскости. Чтобы иметь право произносить слово "пространство необходимо определить, что мы понимаем под сходимостью последовательности функций f 1 (x,t ), f 2 (x,t ),... .
Скажем, что fn → f , если для любого компакта в R 2 (а можно сказать проще, для любого круга) имеет место равномерная сходимость fn (x,t ) → f (x,t ), здесь f — предельная функция. Это пространство мы и обозначим через C (R 2 ).
Оказывается, невозможно так определить банахову норму, чтобы сходимость по этой норме совпадала с введенной только что равномерной сходимостью на компактах. Можно однако ввести метрику, определяющую такой тип сходимости. Для этого достаточно положить
![]() .
(A.3)
.
(A.3)
Здесь Bk — круг радиуса k с центром в точке (0, 0), так что Bk = {(x,t ) : x 2 + t 2 ≤ k 2 }. Для любой непрерывной функции f норма в C (Bk ) определяется равенством
![]() .
(A.4)
.
(A.4)
Вам станет понятно, откуда взялся ряд (A.3), если Вы припомните определение метрики в пространстве всевозможных последовательностей S (см.
[23]).
Нетрудно установить (установите!), что введенная равенством (A.3) метрика превращает пространство C (R 2 ) в полное метрическое пространство.
Замечу, что дальнейшее использование пространства C (R 2 ) относится скорее к красивому оформлению, нежели к сути идеи Орлича.
Множество уравнений с точками неединственности. Рассмотрим множество M ⊂ C (R 2 ), состоящее из таких функций f , что задача Коши (A.1), (A.2) хотя бы для одной точки (x 0 ,t 0 ) ∈ R 2 имеет более одного решения. Такую точку (x 0 ,t 0 ) назовем точкой неединственности . Понятно, что дополнение C (R 2 ) \ M состоит из таких функций f , что задача (A.1), (A.2) для всех точек (x 0 ,t 0 ) имеет единственное решение.
Для любой точки (x 0 ,t 0 ) ∈ R 2 и пары положительных чисел τ и a определим множество M (x 0 ,t 0 , τ,a ) ⊂ C (R 2 ), состоящее из таких функций f (x,t ), что в круге B 1 (x 0 ,t 0 ) радиуса 1 с центром (x 0 ,t 0 ) уравнение (A.1) имеет хотя бы одну точку неединственности, скажем, (x ˜0 ,t ˜0 ), и при этом выполняются следующие условия:
1) Существуют два решения x (t ) и x ∗ (t ) уравнения x ˙ = f (x,t ), удовлетворяющие одному и тому же начальному условию x (t ˜0 ) = x ˜0 , x ∗ (t ˜0 ) = x ˜0 ; при этом оба решения определены (по крайней мере) на интервале (t ˜0 − τ,t ˜0 + τ), см. Рис. 17.
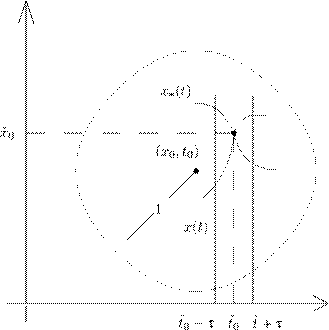
Рис. 17
2) Решения x (t ) и x ∗ (t ) подчинены неравенствам
| |x (t ) − x 0 | ≤ 1, |x ∗ (t ) − x 0 | < 1 для всех t ∈ (t ˜0 − τ,t ˜0 + τ). 3) Выполнена оценка снизу |
(A.5) |
| sup |x (t ) − x ∗ (t )| ≥ a. |
(A.6) |
t ˜0 −τ<t<t ˜0 +τ
Доказательство теоремы Орлича основывается на следующих двух леммах.
Лемма 1. Множество M (x 0 ,t 0 , τ,a ) при любом выборе точки (x 0 ,t 0 ) в R 2 и положительных чисел τ и a замкнуто в C (R 2 ). Доказательство. Суть дела, конечно в том, что все условия, определяющие множество M (x 0 ,t 0 , τ,a ), выдерживают предельный переход в пространстве C (R 2 ). Главным является условие (A.6), которое обеспечивает сохранение неединственности при этом предельном переходе. Небольшая техническая трудность связана с тем, что сама точка неединственности предельного уравнения заранее не определена.
Итак, пусть дана последовательность функций fn ∈ M (x 0 ,t 0 , τ,a ), которая сходится к некоторой функции f ∈ C (R 2 ) в смысле метрики (A.3). Мы должны доказать, что f ∈ M (x 0 ,t 0 , τ,a ).
Согласно определению множества M
(x
0
,t
0
,
τ,a
), для любого n
= 1,
2,...
определена пара решений![]() задачи Коши с начальной точкой
задачи Коши с начальной точкой ![]()
![]() .
(A.7)
.
(A.7)
Здесь ![]() — та самая точка неединственности, которая в общем определении обозначена через x
˜0
,t
˜0
. При этом оба решения определены на интервале
— та самая точка неединственности, которая в общем определении обозначена через x
˜0
,t
˜0
. При этом оба решения определены на интервале ![]() , и, согласно (A.6), выполняются неравенства
, и, согласно (A.6), выполняются неравенства
![]() ,
(A.8)
,
(A.8)
![]() (A.9)
(A.9)
Поскольку все точки неединственности расположены в единичном круге B
1
(x
0
,t
0
), а этот (замкнутый) круг компактен, можно выбрать такую подпоследовательность индексов nk
, что соответствующие точки неединственности ![]() сходятся к некоторой предельной точке
сходятся к некоторой предельной точке ![]() .
.
Ради краткости будем считать, что этот переход к подпоследовательности уже проделан, так что![]() .
.
Теперь наша цель — доказать, что возможно так выбрать подпоследовательность значений индекса n
, что соответствующие подпоследовательности решений xn
(t
) и xn
∗
(t
) будут сходиться соответственно к некоторым решениям ![]() равномерно на любом сегменте, содержащемся в интервале
равномерно на любом сегменте, содержащемся в интервале
![]() . Определим подпоследовательность сегментов
. Определим подпоследовательность сегментов ![]() , где
, где ![]() , m
= 1,
2,...
. Очевидно, что достаточно доказать равномерную сходимость на каждом из сегментов Im
, так как любой сегмент, содержащийся в интервале
, m
= 1,
2,...
. Очевидно, что достаточно доказать равномерную сходимость на каждом из сегментов Im
, так как любой сегмент, содержащийся в интервале ![]() , содержится в каждом сегменте Im
, начиная с некоторого значения m
.
, содержится в каждом сегменте Im
, начиная с некоторого значения m
.
Рассмотрим, например, последовательность функций xn
(t
) (с решениями![]() все аналогично) и докажем, что эта последовательность компактна в
C
(Im
) — в пространстве функций непрерывных на сегменте Im
. Точнее было бы сказать, что речь идет о сужении каждой из функций на сегмент Im
. Для этого, конечно, надо потребовать, чтобы сегмент Im
содержался в интервале задания
все аналогично) и докажем, что эта последовательность компактна в
C
(Im
) — в пространстве функций непрерывных на сегменте Im
. Точнее было бы сказать, что речь идет о сужении каждой из функций на сегмент Im
. Для этого, конечно, надо потребовать, чтобы сегмент Im
содержался в интервале задания ![]() решения xn
(t
). Это верно, возможно, не для всех n
, но для всех n
, начиная с некоторого, такие значения n
и будем рассматривать.
решения xn
(t
). Это верно, возможно, не для всех n
, но для всех n
, начиная с некоторого, такие значения n
и будем рассматривать.
Согласно критерию Арцела (см. [23]), достаточно установить, что последовательность функций xn (t ) на Im равномерно ограничена и равностепенно непрерывна. Равномерная ограниченность непосредственно следует из определения множества M (x 0 ,t 0 , τ,a ): из (A.8) вытекает, что |xn (t )| ≤ |x 0 |+1 для всех n и для всех t . Для доказательства равностепенной непрерывности, как известно, достаточно установить равномерную ограниченность последовательности производных x ˙n (t ) на сегменте Im . Но из уравнения (A.7), которому удовлетворяет xn (t ), следует оценка
![]() ,
(A.10)
,
(A.10)
где Πm — прямоугольник на плоскости R 2 : Πm = J 0 × Im , причем J 0 = [x 0 − 1,x 0 + 1].
Действительно, движущаяся точка xn (t ) при t ∈ Im не выходит из прямоугольника Πm , согласно неравенству (A.8). Поскольку fn сходится к f равномерно на Πm (как и на любом компакте), правая часть в (A.10) ограничена (m — фиксировано) величиной max|f (x,t )| + δ, где δ > 0 — Πm
произвольно фиксировано, равномерно по n для n ≥ N δ . Здесь число N δ определяется по заданному δ.
Таким образом, мы проверили условия критерия Арцела и можем утверждать, что последовательность xn (t ) компактна в C (Im ).
Теперь выберем из последовательности xn
(t
) подпоследовательность, равномерно сходящуюся на сегменте I
1
. Из этой подпоследовательности выберем подпоследовательность, сходящуюся на сегменте I
2
. Продолжая этот процесс неограниченно и применяя диагональную процедуру Георга Кантора, мы получим подпоследовательность последовательности функций xn
(t
), которая равномерно сходится на каждом сегменте Im
(m
= 1,
2,...
), а значит, вообще на любом сегменте, содержащемся в интервале ![]() . Итак, существует предельная функция x
∞
(t
), заданная и непрерывная на всем интервале
. Итак, существует предельная функция x
∞
(t
), заданная и непрерывная на всем интервале ![]() . Аналогично последовательность
. Аналогично последовательность![]() сходится к непрерывной функции
сходится к непрерывной функции ![]() на том же интервале.
на том же интервале.
Докажем теперь, что![]() суть решения предельной задачи Коши
суть решения предельной задачи Коши
![]() .
(A.11)
.
(A.11)
Для этого достаточно заметить, что задача Коши (A.7) (дифференциальное уравнение вместе с начальным условием) эквивалентна интегральному уравнению, которому удовлетворяет xn (t )
t
Z
n n n
x (t ) = x 0 + fn (x (s ),s )ds. (A.12)
t n 0
Перейдем в этом уравнении к пределу, когда n
пробегает выделенную нами подпоследовательность значений. Тогда![]()
равномерно на любом сегменте Im . Поскольку fn → f равномерно на любом компакте, выполнены условия известной Вам теоремы о предельном переходе под знаком интеграла. Таким путем мы приходим к интегральному уравнению
t
Z
x ∞ (t ) = x ∞ 0 + f (x ∞ (s ),s )ds, (A.13)
t ∞0
из которого следует, что x ∞ (t ) является решением задачи Коши
![]() .
(A.14)
.
(A.14)
Аналогично устанавливается, что и функция![]() — решение этой же задачи Коши.
— решение этой же задачи Коши.
Мы уже видели, что ![]() . Переходя к пределу в (A.8) и (A.9), приходим к неравенствам (проделайте подробные доказательства)
. Переходя к пределу в (A.8) и (A.9), приходим к неравенствам (проделайте подробные доказательства)
![]() ,
(A.15)
,
(A.15)
| sup |x ∞ (t ) − x ∞ ∗ (t )| ≥ a. t ∞ 0 −τ<t<t ∞ 0 +τ |
(A.16) |
Мы доказали, что предельная функция принадлежит множеству f ∈ M (x 0 ,t 0 , τ,a ), а вместе с тем и лемму 1.
Лемма 2. Множество M (x 0 ,t 0 , τ,a ) нигде не плотно для любой точки (x 0 ,t 0 ) и любых чисел τ > 0, a > 0.
Доказательство. Рассуждая от противного, допустим, что множество M (x 0 ,t 0 , τ,a ) плотно в некотором шаре пространства C (R 2 ). Ввиду замкнутости, оно целиком содержит этот шар. В каждом шаре пространства C (R 2 ), как известно, плотно также и множество гладких функций C ∞ (нам сейчас достаточно рассматривать сужения функций из C (R 2 ) на круг B 1 (x 0 ,t 0 )). Но для гладкой функции f (x,t ) мы знаем теорему единственности задачи Коши для уравнения x ˙ = f (x,t ). Значит такая функция не может принадлежать множеству M (x 0 ,t 0 , τ,a ) (красиво?). Лемма 2 доказана.
Теорема Орлича. Множество M функций f ∈ C (R 2 ) таких, что уравнение x ˙ = f (x,t )обладаетхотябыоднойточкойнеединственности на плоскости R 2 , является множеством первой категории в C (R 2 ).
Доказательство. Очевидно, что всякая функция f такая, что существует хотя бы одна точка неединственности уравнения x ˙ = f (x,t ), принадлежит некоторому множеству M (x 0 ,t 0 , τ,a ). Более того, ясно, что при этом можно считать числа x 0 , t 0 , τ, a рациональными. Множество Q всех рациональных чисел счетно, множество всех четверок рациональных чисел x 0 , t 0 , τ, a тоже счетно (докажите!). Мы установили, что множество M является счетным объединением
M = [ M(x0 ,t0 ,τ,a) (A.17)
по всем x 0 , t 0 , τ, a ∈ Q . Согласно лемме 2, каждое из множеств M (x 0 ,t 0 , τ,a ) нигде не плотно. Теорема доказана.
В свете этой теоремы ситуация с проблемой единственности решения задачи Коши выглядит драматической. На самом деле, единственность — при любой начальной точке! — имеет место для подавляющего большинства уравнений x ˙ = f (x,t ), f ∈ C (R 2 ). В то же время классическая теорема единственности относится к функциям f , удовлетворяющих условию Липшица, которые в совокупности образуют множество 1-й категории в C (R 2 ). Ситуация с теоремой единственности Осгуда чуть менее ясна. Если зафиксировать в этой теореме функцию g (s ), оценивающую модуль непрерывности функции f , и рассматривать лишь такие f , для которых локально, вблизи каждой точки (x 0 ,t 0 ) ∈ R 2 , выполнено неравенство
|f (x 0 ,t ) − f (x 00 ,t )| ≤ Kg (|x 0 − x 00 |), K > 0, (A.18)
то нетрудно доказать, что соответствующее множество Cg имеет 1-ю категорию.
Вопрос: какова категория множества всех f, удовлетворяющих условиям теоремы Осгуда?
Напомню, что функция g должна лишь подчиняться требованию
![]() .
(A.19)
.
(A.19)
При этом, конечно, предполагается, что g (0) = 0, но g (s ) > 0 для всех s > 0 (или для s достаточно малых). Имеются небольшие обобщения теоремы Осгуда, скажем, в неравенстве (A.18) можно еще допустить множитель ϕ(t ) при достаточной регулярности функции ϕ (см. [35, 49]).
Все это говорит о том, что нужно и интересно искать новые подходы к доказательству теоремы единственности задачи Коши. "Силовые подходы основанные на оценках типа (A.18) абсолютной величины разности f (x 0 ,t ) и f (x 00 ,t ) для пары решений x 0 и x 00 , по-видимому, не приводят к результату для очень многих дифференциальных уравнений, обладающих, на самом деле, свойством единственности.
Надо признаться, что предыдущее утверждение может оказаться "ложной тревогой". В математике не так уж редко случается, что то или иное явление происходит в "подавляющем большинстве" случаев, но установить, что оно происходит в данном конкретном случае, очень трудно, а то и практически невозможно. Например, известно, что в ситуации общего положения линейный оператор A : Rn → Rn имеет ненулевой определитель и обратим, но доказать, что данный определитель отличен от нуля, — непростое дело. Оказалось, что в общей проблеме обратимости оператора A целесообразно изменить постановку вопроса: вместо индивидуального оператора A , рассматривать однопараметрическое семейство операторов A − λI . Тогда можно установить, что обратимость имеет место для всех значений λ, кроме конечного набора собственных значений (в случае банахова пространства и вполне непрерывного оператора A — кроме не более чем счетного множества значений). Это всё, что может дать общая теория. Выяснение того, для каких λ оператор A − λI обратим, и для каких он необратим, распадается на необозримое множество различных частных теорий, которые в совокупности образуют спектральную теорию линейных операторов, и еще, пожалуй, не оформившуюся в самосостоятельную дисциплину бесконечномерную линейную алгебру.
Другой пример — свойства эргодичности и перемешивания динамической системы [48]. Для конкретных систем доказательство эргодичности и перемешивания, как правило, чрезвычайно трудно, хотя доказано, что эргодические системы образуют множество 2-ой категории при определенном выборе топологии. Кстати, это как раз хороший пример зависимости категории по Бэру от выбора топологии.
Если проводить аналогию между проблемой единственности и перечисленными выше проблемами, то с некоторой вероятностью (по-моему, не очень большой) можно опасаться, что для уравнения x ˙ = f (x,t ), где f — всего лишь непрерывная функция, не получится вполне общей теоремы единственности. Интересно, однако, найти пусть частные, условия, обеспечивающие единственность для множества таких уравнений 2-й категории.
О других подходах к проблеме неединственности. Наряду с классификацией множеств по Бэру, имеются и другие подходы к проблеме сравнения множеств по их "массивности". Например, если на рассматриваемом множестве (нас сейчас интересует C (R 2 )) задана некоторая мера, принято и естественно считать "пренебрежимо малыми" множества меры 0. Существенно заметить, что в случае, когда на данном множестве определены и метрика, и мера, эти два подхода могут существенно разойтись. В частности, множество 1-й категории может иметь положительную меру.
В.И. Арнольд не раз обращал внимание на подобное расхождение в ряде важных вопросов теории динамических систем. Поэтому, рассказывая ему о теореме Орлича, я предвидел, что он спросит и о подходе к данной проблеме с точки зрения меры. Это трудный вопрос. Неясно даже, как его корректно сформулировать, поскольку для бесконечномерных метрических пространств не существует естественного аналога меры Лебега в Rn . Какую же меру выбрать? От этого выбора тоже зависит результат. В такой ситуации интересно для начала рассмотреть семейства дифференциальных уравнений, зависящие от конечного числа параметра, например, выбрать в качестве их правых частей конечные линейные комбинации функций из
n
C (R 2 ), скажем, P ck fk (x,t ). Теперь каждому уравнению с такой правой
k =1
частью соответствует точка (c
1
,...,cn
) ∈ Rn
. И резонно спросить, какова мера Лебега множества точек, отвечающих уравнениям, обладающим точками неединственности. При этом можно считать, что коэффициенты ck
ограничены, например, неравенством![]() . Нетрудно привести примеры таких семейств уравнений
. Нетрудно привести примеры таких семейств уравнений
![]() ,
(A.20)
,
(A.20)
для которых точки неединственности присутствуют при любом выборе коэффициентов (например, положим fk (x,t ) = |x |1/ 2k ); тогда (0,t 0 ) — точка неединственности при любом t 0 . Предположим однако, что данное семейство содержит хотя бы одно уравнение, для которого верна теорема единственности решения задачи Коши при любом выборе начальной точки. Что можно тогда сказать о мере множества тех уравнений семейства (я уже отождествил уравнение и определяющую его точку (c 1 ,c 2 ,...,cn )), которые обладают хотя бы одной точкой неединственности?
Поставим вопрос о мере множества тех точек (c 1 ,c 2 ,...,cn ) ∈
n
Rn и удовлетворяющих условию P c 2 k ≤ a 2 (при заданном a > 0),
k =1
для которых уравнение ( A.20) имеет хотя бы одну точку неединственности. При этом предполагается, что для некоторого набора c 0 1 ,...,c 0 n единственность имеет место для всех начальных точек в R 2.
У меня нет полной уверенности, что это уже окончательная постановка задачи. В конце концов, лишь красивый ответ может подтвердить разумность вопроса. Есть однако надежда, что двигаясь в намеченном направлении, возможно прийти к интересным постановкам задач, допускающих содержательные решения.
О глобальной разрешимости. Наряду с единственностью, представляет значительный интерес глобальная разрешимость задачи Коши для дифференциального уравнения x ˙ = f (x,t ). Глобальная разрешимость означает, что для любой начальной точки решение задачи Коши (все решения, если их много) можно продолжить на всю временную ось (или хотя бы на положительную полуось — это другой вариант вопроса).
Типична ли глобальная разрешимость? Какова категория множества глобально разрешимых уравнений? Мне кажется, что в отличие от единственности, глобальная разрешимость нетипична. Может быть, кто-нибудь возьмется подтвердить или опровергнуть эту гипотезу.
Упражнения к Приложению A
1. Доказать, что множество вещественных чисел, в разложении которых в k -ричную дробь какая либо цифра, начиная с некоторого места, отсутствует, есть множество 1-й категории в R .
2. Из результата предыдущего упражнения вывести, что существуют такие числа, что в их разложениях в k -ричную дробь для любого k , каждая значащая цифра присутствует бесконечно много раз. Более того, множество таких чисел является вычетом.
3. Доказать, что множество ограниченных
непрерывных функций есть множество первой категории в C
(R
2
). Доказать, что и множество непрерывных функций f
, таких что ![]() (при фиксированном α) — ограниченная функция на R
2
, — тоже множество 1-й категории в C
(R
2
).
(при фиксированном α) — ограниченная функция на R
2
, — тоже множество 1-й категории в C
(R
2
).
4. Докажите, что как существование у вещественного полинома x 2 + px + q пары вещественных простых корней, так и существование у него пары комплексно сопряженных корней — типичные ситуации, а существование кратного корня — нетипично (в смысле категорий соответствующих множеств точек (p,q ) на плоскости R 2 ). Как обобщить этот вывод на полиномы n -й степени?
5. Рассмотрим пространство функций C (a,b ), непрерывных на интервале (a,b ). Определим сходимость в этом пространстве, считая, что fn → f , если и только если fn (x ) → f (x ) равномерно по x на любом сегменте [α, β] ⊂ (a,b ). По аналогии с метрикой (A.3), определите метрику, отвечающую этому типу сходимости.
6. Докажите, что множество функций из C (R 2 ), удовлетворяющих условию Липшица, есть множество 1-й категории.
7. Останется ли верной теорема Орлича, если в ней заменить пространство C (R 2 ) на банахово пространство MC (R 2 ) непрерывных и ограниченных на R 2 функций? Норма в этом пространстве определяется равенством:
![]() .
.
8. Вспомните доказательство и докажите, что задача Коши x ˙ = f (x ), x (0) = x 0 для одного скалярного дифференциального уравнения имеет, и притом единственное, решение для любой непрерывной функции f (x ) при одном лишь условии, что f (x 0 ) 6= 0.
√![]()
9. Рассмотрите задачу Коши x ˙ = 3 x + εt , x (0) = 0. При ε = 0 решение неединственно. А при ε 6= 0?
10. Рассмотрите уравнение x ˙ = |x +ε |t |β |α , при 0 < α < 1, и 0 < β < 1. При ε = 0 у него есть точка неединственности. Имеются ли точки неединственности при ε 6= 0? (Конечно модули уродуют это уравнение, но их можно опустить, если выбрать в качестве α и β правильные дроби с нечетными знаменателями). Ответ мне в данный момент неизвестен. Теорема Орлича подсказывает гипотезу: при ε 6= 0 — всегда единственность. Любопытно также посмотреть, что дадут стандартные программы решения задачи Коши применительно к уравнениям такого типа.
11. Если физик-экспериментатор покажет Вам матрицу, например, размеров 10×10, элементы которой получены путем измерений, и спросит какова ее жорданова форма, Вы можете уверенно отвечать, что диагональная. Почему?
12. А теперь представьте себе, что Ваш друг, физик-экспериментатор из предыдущего упражнения, попросил Вас привести к диагональному виду два-три десятка матриц 10×10. Еще он Вам сообщил, что каждая из этих матриц многократно проверена независимыми экспериментами. Анализируя диагональные формы этих матриц, он рассчитывает получить важные физические выводы (допустим, об озоновой дыре, либо о строении кристаллов). У Вас имеется несколько стандартных программ диагонализации матриц, все они Вами хорошо проверены и много раз применены для различных матриц 20-го и 30-го порядка. И вот выяснилось, что все Ваши программы отказываются работать для этих матриц. Скорей всего, Вы должны поздравить своего друга-физика с большим успехом. Почему? Что Вы предлагаете делать дальше?
Приложение 2. Изометрии и вращения банахова
пространства. Теорема Мазура и Улама
Здесь изложена замечательная теорема Мазура и Улама о линейности изометрического отображения U : X → Y одного банахова пространства в другое, при условии, что 0 ∈ X переходит в 0 ∈ Y , так что U (0) = 0. Сохраняя основную идею доказательства [5], я попытался прояснить его ход при помощи введения понятия центра множества в метрическом пространстве.
Центрограниченногомножества. Пусть X — метрическое пространство, и M ⊂ X — ограниченное множество в нем. Это означает, что M содержится в некотором шаре пространства X . Определим диаметр d (M ) множества M , полагая
d (M ) = sup ρ(x,y ). (A.1)
x,y ∈M
Очевидно, для ограниченных множеств, и только для них, диаметр конечен. Теперь определим 1-центр C 1 (M ) множества M , полагая
![]() .
(A.2)
.
(A.2)
Таким образом, множество C 1 (M ) состоит из всевозможных точек пространства X , удаленных от произвольной точки множества M не более, чем на половину диаметра множества M .
Например, 1-центр шара в евклидовом пространстве есть попросту множество, состоящее из одной точки — его центра. Бывает, что 1-центр множества пуст: выбросим центр некоторого шара из X , тогда 1-центр шара полученного пространства не будет содержать ни одной точки.
Теперь по индукции определим n -центр Cn (M ) для любого натурального n = 2, 3... , полагая
C 2 (M ) = C 1 (C 1 (M )) ∩ C 1 (M ), ..., Cn (M ) (A.3) = C 1 (Cn −1 (M )) ∩ Cn −1 (M ),...
Заметим, что 1-центр C 1 (M ) конструируется из точек пространства X , в то время как n -центр Cn (M ) при n = 2, 3,... обязан быть подмножеством (n − 1)-центра.
Определим, наконец, центр ограниченного множества M ⊂ X как пересечение всех n -центров
![]() (A.4)
(A.4)
Лемма 1. Центр всякого ограниченного множества M метрического пространства X содержит не более одной точки
Доказательство. Докажем, что диаметр n -центра, по крайней мере, в 2n −1 раз меньше чем d (M ):
![]() .
(A.5)
.
(A.5)
Если x, y ∈ C 1 (M ), то ввиду определения 1-центра (A.2), выполняется неравенство
ρ(x,y) ≤ d(M). (A.6)
Если x, y ∈ Cn (M ), n ≥ 2, то x, y ∈ Cn −1 (M ), поэтому
![]() .
.
Отсюда сразу следует неравенство (A.5) при n = 2, а затем по индукции и для любых n .
Неравенство (A.5) показывает, что диаметр центра C (M ) равен нулю. Это доказывает лемму 1.
Дальше будем считать, что X — банахово пространство, так что ρ(x 1 ,x 2 ) = kx 1 − x 2 kX , где k · kX — норма в пространстве X .
Скажем, что множество M ⊂ X центрально-симметрично , и ξ ∈ X его центр симметрии , если точки x = ξ ± u принадлежат M . Заметим, что преобразование S : M → M , определенное равенством Sx = ¯x = 2ξ − x есть инверсия : S 2 x = x ¯¯ = x , S 2 = I .
Лемма 2. Если множество M в X — центрально-симметрично, то и его n-центры также центрально-симметричны (с тем же центром симметрии ξ), а центр C (M ) либо пуст, либо состоит из одной точки ξ.
Доказательство. Докажем, что 1-центр C 1 (M ) центрально-симметричен относительно точки ξ. Пусть x = ξ + u ∈ C 1 (M ). Это означает, что неравенство
![]() (A.7)
(A.7)
выполнено для любых z ∈ M . Неравенство (A.7) остается верным и при замене z на z ¯, так как z ¯ ∈ M . Поэтому имеем
![]() (A.8)
(A.8)
Таким образом, 1-центр C 1 (M ) центрально-симметричен. Очевидная индукция дает тот же результат и для n -центра Cn (M ). Тогда и центр C (M ) центрально-симметричен, будучи пересечением центрально симметричных множеств. Если теперь допустить, что центр C (M ) содержит точку x = ξ + u , то также и точка x ¯ = ξ − u ему принадлежит. Но, по лемме 1, эти точки должны совпадать. Поэтому u = 0, и лемма 2 доказана.
Следствие.
Пусть множество
M
= {x
1
,x
2
}, где
x
1
и
x
2
произвольные точки в
X. Тогда для множества
M, состоящего из двух точек
x
1
и
x
2
, центр
C
(M
) есть множество, состоящее из одной точки
![]() .
.
Изометрии и вращения. Напомню, что отображение U : X → Y
метрического пространства X в метрическое пространство Y называется изометрическим или изометрией , если для любых x 1 , x 2 ∈ X выполнено равенство
ρY (Ux1 ,Ux2 ) = ρX (x1 ,x2 ). (A.9)
В случае банаховых пространств X и Y равенство (A.9) записывается в виде
kUx1 − Ux2 kY = kx1 − x2 kX . (A.10)
Очевидно, всякое изометрическое отображение непрерывно. Столь же очевидно, что изометрия отображает пространство X на свой образ U (X ) взаимно однозначно.
В любом банаховом пространстве X каждому элементу h можно поставить в соответствие изометрическое отображение Lh : x 7→ x +h , называемое переносом или трансляцией на вектор h . Если U : X → X — изометрия банахова пространства X , то отображение U 0 , определяемое равенством U 0 x = Ux − U (0) — также изометрия. При этом точка 0 ∈ X есть неподвижная точка отображения U 0 , так что U 0 (0) = 0.
Взаимно однозначное отображение U : X → X называется вращением (банахова пространства X ), если оно изометрично и оставляет неподвижной точку ноль.
Подчеркну, что в следующей теореме не требуется, чтобы образ U (X ) пространства X при отображении U совпадал со всем пространством Y .
Теорема Мазура и Улама. Всякое изометрическое отображение U : X → Y банахова пространства X в банахово пространство Y , переводящее 0 пространства X в 0 пространства Y (так что U (0) = 0) — линейно.
Доказательство.
Пусть x
1
и x
2
— произвольные точки в X
. Согласно следствию, центр множества {x
1
,x
2
} есть ![]() .
.
Определения n
-центров и центра множества связаны лишь с метрикой, а изометрия U
ее сохраняет. Поэтому ясно, что отображение U
переводит центр любого множества M
⊂ X
в центр его образа U
(M
) ⊂ Y
. Поскольку центр множества {Ux
1
,Ux
2
} есть ![]() , приходим к равенству
, приходим к равенству
![]() .
(A.11)
.
(A.11)
Полагая здесь x 1 = x и x 2 = 0 и учитывая, что U (0) = 0, для любого x ∈ X получим равенство
![]() (A.12)
(A.12)
Теперь для произвольных x 1 , x 2 ∈ X , полагая в (A.12) x = x 1 + x 2 и применяя (A.11), выводим
![]() (A.13)
(A.13)
.
Это означает, что оператор U аддитивен . Хорошо известно (см. ниже лемму 3), что, вместе с непрерывностью в нуле (а изометрический оператор непрерывен всюду), это свойство влечет линейность оператора U . Теорема доказана.
Лемма 3. Пусть оператор U : X → Y ( X и Y — банаховы) аддитивен и непрерывен в точке 0 ∈ X . Тогда он непрерывен всюду и однороден, то есть U — линейный оператор.
Доказательство. По условию, для любых x 1 , x 2 ∈ X выполняется равенство
U (x 1 + x 2 ) = Ux 1 + Ux 2 . (A.14)
Из него по индукции получается более общее равенство
U(x1 + x2 + ... + xm ) = Ux1 + Ux2 + ... + Uxm . (A.15)
Полагая x 1 = x 2 = ... = xm = x , выводим равенство
U (mx ) = mUx (A.16)
для любого натурального m
и любого x
∈ X
. Заменяя здесь![]() , получим
, получим
![]() (A.17)
(A.17)
Поскольку m ∈ N в (A.16) и (A.17) произвольно, для любого рациональ-
ного числа![]() , выводим равенство
, выводим равенство
![]() (A.18)
(A.18)
Итак, всякое положительное рациональное число можно выносить за знак оператора U . Покажем, что можно выносить и −1. Действительно, если положить в (A.14) x 1 = x 2 = 0, то получится, что U (0) = 2U (0), так что U (0) = 0. Далее, если положить в (A.14) x 1 = x и x 2 = −x , то получим
U (0) = Ux + U (−x ).
Так как U
(0) = 0, выходит, что U
(−x
) = −U
(x
). Теперь ясно, что равенство (A.18) справедлива для любых рациональных![]() .
.
Докажем, что из непрерывности аддитивного оператора в точке 0 следует его непрерывность в произвольной точке x . Действительно, если xn →
x , то ξn = xn − x → 0 и
Uxn −Ux = U (x +ξn )−Ux = Ux +U ξn −Ux = U ξn → 0, (A.19)
ввиду непрерывности оператора U в нуле. Итак, оператор U непрерывен в любой точке x ∈ X .
Если теперь λ
∈ R
— любое вещественное число, то мы возьмем последовательность рациональных чисел вида![]() , сходящуюся к λ, и, переходя к пределу в (A.18), найдем
, сходящуюся к λ, и, переходя к пределу в (A.18), найдем
U (λx ) = λUx. (A.20)
Итак, оператор U непрерывен всюду, аддитивен и однороден, то есть линеен. Лемма 3 доказана.
Как доказал З. Хажинский [61], всякий изометрический оператор, действующий в конечномерном линейном метрическом пространстве также линеен. Для доказательства он построил по данной метрике преднорму (отличается от нормы только тем, что она может обращаться в ноль и на ненулевых векторах) с тем же нулем, инвариантную относительно всех изометрий. Далее, в [61] использована теорема Мазура–Улама и индукция по размерности пространства.
Упражнения к Приложению B
1. Метрическое пространство X состоит из 5-и точек: x 1 , x 2 , x 3 , x 4 ,x 5 . Метрику зададим, полагая ρ(x 1 ,x 2 ) = 1, ρ(x 1 ,x 3 ) = 1, ρ(x 1 ,x 4 ) = 1; ρ(x 1 ,x 5 ) = 2; ρ(x 2 ,x 3 ) = 1/ 2; ρ(x 2 ,x 4 ) = 1/ 2; ρ(x 2 ,x 5 ) = 1; ρ(x 3 ,x 4 ) = 1/ 2; ρ(x 3 ,x 5 ) = 1; ρ(x 4 ,x 5 ) = 1. Проверьте выполнение аксиом метрики. Найдите 1-центр этого пространства, а также его центр.
s x 4
x 1 s s x 3 s x 5
s x 2
2. Докажите, что для всякого шара B в банаховом пространстве X центр C (B ) есть его центр в обычном смысле слова.
3. Пусть U : X → Y — изометрическое отображение метрического пространства X в метрическое пространство Y . Докажите, что для любого множества M ⊂ X с непустым центром C (M ) = {ξ } его образ U (M ) ⊂ Y также имеет центр η ∈ Y и U ξ = η. Докажите также, что U (Cn (M )) = Cn (U (M )).
4. Пусть D
— множество в Rn
, содержащее не менее, чем n
+ 1 точку, среди которых имеется точка 0 ∈ Rn
, а остальные n
точек линейно независимы. Индуцированная на нем метрика пространства Rn
превращает D
в метрическое пространство. Пусть U
: D
→ Rn
— изометрическое отображение, оставляющее точку 0 неподвижной. Докажите, что его можно считать линейным. Точнее, существует линейное изометрическое отображение U
ˆ
: Rn
→ Rn
, однозначно определяемое отображением U
, и такое, что его сужение на D
есть U
, или, в символах:![]() .
.
5. Докажите, что, если в теореме Мазура и Улама отбросить условие сохранения нуля, то можно утверждать, что изометрическое отображение аффинно , то есть U = U 0 +Lh , где Lh — трансляция на постоянный вектор h , а U 0 — линейное изометрическое отображение.
ЛИТЕРАТУРА
[1] Александров П.С., Колмогоров А.И. Введение в теорию функций действительного переменного. М.–Л.: ГТТИ, 1938. 268 с.
[2] Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: Наука, 1984. 271 с.
[3] Арнольд В.И. Математические методы классической механики. М.: Наука, 1989. 472 с.
[4] Бабский В.Г., Копачевский Н.Д., Мышкис А.Д., Слобожанин Л.А., Тюпцов А.Д. Гидромеханика невесомости. М.: Наука, 1976. 504 с.
[5] Банах С. Теория линейных операций. Москва–Ижевск, РХД. 2001. 272 с.
[6] Вайнберг М.М. Вариационные методы исследования нелинейных операторов. — М.: Гостехиздат, 1956. — 344 с.
[7] Ван дер Варден Б.Л. Алгебра. М. Наука, 1976. 648 с.
[8] Ворович И.И. Лекции по динамике Ньютона. Современный взгляд на механику Ньютона и ее развитие — Москва–Ижевск: Инст. комп. исследов., 2004. — 680 с.
[9] Гиббс Дж.В. Термодинамика. Статистическая механика. М.: Наука, 1982. 323 с.
[10] Громол Д., Клингенберг В., Мейер В. Риманова геометрия в целом. М.: Мир, 1971. 343 с.
[11] Далецкий Ю.Л., Крейн М.Г. Устойчивость решений дифференциальных уравнений в банаховом пространстве. М.: Наука, 1970. 534 с.
[12] Демидович Б.П. Лекции по математической теории устойчивости. M.: Наука. 1967. 472 с.
[13] Зеньковская С.М., Юдович В.И. Метод интегро-дифференциальных уравнений и цепных дробей в задаче параметрического возбуждения волн // ЖВМ и МФ. 2004. № 4. С. 370–384.
[14] Зоммерфельд А. Механика. М.: ИЛ, 1947. 391 с.
[15] Зорич В.А. Математический анализ. Т. I, II. М.:Наука, 1984. 642 с.
[16] Козлов В.В. Асимптотические движения и проблема обращения теоремы Лагранжа – Дирихле // ПММ. 1986. Т. 50. Вып. 6. С. 928–937.
[17] Козлов В.В., Паламодов В.П. Об асимптотических решениях уравнений классической механики // ДАН СССР. 1982. Т. 263, № 2. С. 285–
289.
[18] Курант Р., Гильберт Д. Методы математической физики. Т. 1. М.–Л.: Гостехиздат, 1951. 476 с.
[19] Ламб Г. Гидродинамика. М.: Гостехиздат, 1947. 928 с.
[20] Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 1988. 216 с.
[21] Ландау Л.Д., Лифшиц Е.М. Теория поля. М.: Наука, 1988. 508 с.
[22] Лионс Ж.-Л. Некоторые методы решения нелинейных краевых задач. М.: Мир, 1972. 588 c.
[23] Люстерник Л.А., Соболев В.И. Элементы функционального анализа. М.: Наука, 1965. 518 с.
[24] Ляпунов А.М. Общая задача об устойчивости движения. М.–Л.: Гостехиздат, 1950. 471 с.
[25] Малкин И.Г. Теория устойчивости движения. М.: Наука. 1966. 532 c.
[26] Меркин Д.Р. Введение в теорию устойчивости движения. М.: Наука. 1987. 304 с.
[27] Миранда К. Уравнения с частными производными эллиптического типа. М.: Изд-во ИЛ, 1957. 256 с.
[28] Михлин С.Г. Вариационные методы в математической физике. М.: ГИТТЛ, 1957. 476 с.
[29] Михлин С.Г. Уравнения математической физики. M.: Наука, 1968. 576 с.
[30] Натансон И.П. Теория функций вещественной переменной. М.: Наука, 1974. 480 с.
[31] Немыцкий В.В., Степанов В.В. Качественная теория дифференциальных уравнений. М.-Л.: ГИТТЛ, 1949. 550 с.
[32] Ньютон И. Математические начала натуральной философии. — М.: Наука, 1989. — 688 с.
Newton I. Philosophiae Naturalis Principia Mathematica, London, 1687;
[33] Олвер П. Приложение групп Ли к дифференциальным уравнениям. М.: Мир, 1989. 640 с.
[34] Паули В. Теория относительности. М.: Наука, 1991. 328 с.
[35] Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: Наука, 1970. 280 с.
[36] Повзнер А.Я. Теорема существования в целом для нелинейной системы и индекс дефекта линейного оператора // Сибирский математический журнал. 1964. Т. 5, № 2. С. 377–386.
[37] Полак Л.С. Вариационные принципы механики. М.: Физ.-мат. лит. 1960. 932 с.
[38] Рудин У. Основы математического анализа. М.: Мир, 1976. 320 с.
[39] Руш Н., Абетс П., Лалуа М. Прямой метод Ляпунова в теории устойчивости. М.: Мир, 1980. 300 с.
[40] Соболев С.Л. Уравнения математической физики. М.: ГИТТЛ, 1954. 444 с.
[41] Степанов В.В. Курс дифференциальных уравнений. — М.: Физматгиз, 1959. 468 c.
[42] Федорюк М.В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений. Наука. 1983. 352 с.
[43] Фейнман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Т.12. — M.: Мир, 1976. 439 с.
[44] Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. I, II, III. М.: Наука, 1964.
[45] Фундаментальные и прикладные проблемы теории вихрей. Под ред. Борисова А.В., Мамаева И.С., Соколовского М.А. Москва-Ижевск:
Инcт. комп. исследов. 2003. 704 с.
[46] Хаар Д. Основы гамильтоновой механики. М.: Наука, 1974. 225 c.
[47] Хазин Л.Г., Шноль Э.Э. Устойчивость критических положений равновесия. Пущино: ОНТИ НЦБИ АН СССР, 1985.
[48] Халмош П.Р. Лекции по эргодической теории. Ижевск: Изд. дом "Удмуртский университет 1999. 136 с.
[49] Хартман Ф. Обыкновенные дифференциальные уравнения. — М.: Мир, 1970. 720 с.
[50] Четаев Н.Г. Устойчивость движения. Гостехиздат. 1955. 176 c.
[51] Шарковский А.Н. Сосуществование циклов непрерывного преобразования прямой в себя // Украинский матем. журнал. 1964. Т. XVI, № 1. С. 61–70.
[52] Эйнтштейн А. Собрание научных трудов. Т. 1. М.: Наука, 1965. С. 7–
35.
[53] Юдович В.И. Глобальная разрешимость против коллапса в динамике несжимаемой жидкости // В сб. «математические проблемы XX века». М.: Фазис, 2003. С. 519–548.
[54] Юдович В.И. Динамика нити // Деп. в ВИНИТИ 10.10.95, №2725В95.
[55] Юдович В.И. Косимметрия, вырождение решений операторных уравнений, возникновение фильтрационной конвекции // Мат. заметки. 1991. Т. 49. N. 5. C. 142–148.
[56] Юдович В.И. Лекции об уравнениях математической физики. Изд-во Ростовского ун-та, 1998. 240 с.
[57] Юдович В.И. Лекции об уравнениях математической физики. Часть вторая. Изд-во Ростовского ун-та, 1999. — 255 с.
[58] Юдович В.И. Метод линеаризации в гидродинамической теории устойчивости. Ростов-на-Дону, изд-во РГУ, 1984. 192 с. (Англ. перевод: Yudovich V. I. “The Linearization Method in Hydrodynamical Stability Theory”, Translation of mathematical monographs, 74 ,
American Mathematical Society, Providence, Rhodeisland, 177 p., (1989))
[59] Юдович В.И., Срубщик Л.С. Динамическое прощелкивание и запас устойчивости нелинейной упругой системы // ПММ. Т. 50. 1986. С. 426–435.
[60] Broer L.J.F. On the Dynamics of Strings // J. Engineering Mathematics. 1970. Vol. 4. No. 3. P. 195–202.
[61] Charzinski Z. Sur les transformations isometrique dans les espace du type´ (F), Studia Math., 13, 1953, pp. 94–121.
[62] Janda J. Uber die Kategorie der Menge stetiger Funktionen, welche¨ Differentialgleihungen ohne Eindeutigkeit bestimmen // Czechoslovak Mathematical Journal, 23 (98), no. 1, 1973, 30–33.
[63] Kisielewicz M. Description of a class of differential equations with setvalued solutions // Atti Ac. Naz. Lincei. Rend. Cl. Sci. fis.mat. e natur. 58, no. 2, 1975, 158–162.
[64] Kisielewicz M. Description of a class of differential equations with setvalued solutions // Atti Ac. Naz. Lincei. Rend. Cl. Sci. fis.mat. e natur. 58, no. 3, 1975, 338–341.
[65] Orlicz W. Zur Theorie der Differentialgleichung y 0 = f (t,y ) // Bull. de Acad. Pol. des Sciences, Ser. A, 1932, 221–228.
[66] Verhulst, P. F. Notice sur la loi que la population pursuit dans son accroissement // Correspondance mathe’matique et physique. 1838.
10:113–121.
ОГЛАВЛЕНИЕ
Об авторе и этой книге 2
Предисловие автора 4
Математические модели 8
1 Динамические системы . . . . . . . . . . . . . . . . . . . . 8
2 Автономные дифференциальные уравнения . . . . . . . . . 12
3 О глобальной разрешимости задачи Коши и единственности
решения . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
4 Динамические системы с дискретным временем . . . . . . . 26
5 Интегралы и законы сохранения . . . . . . . . . . . . . . . 38
6 Неавтономные дифференциальные уравнения . . . . . . . . 45
7 Интегро-дифференциальные уравнения . . . . . . . . . . . 48
8 Декартово произведение динамических систем и разбиение
системы на независимые подсистемы . . . . . . . . . . . . . 51
9 Производные и градиенты . . . . . . . . . . . . . . . . . . . 54
Механика 60
10 Принцип Гамильтона и уравнения Лагранжа II рода . . . . . 62
11 Лагранжианы материальных частиц . . . . . . . . . . . . . 75
12 Законы сохранения в механике . . . . . . . . . . . . . . . . 82
13 Принцип Гамильтона для систем со связями . . . . . . . . . 99 14 Принцип наименьшего действия Мопертюи
(Мопертюи–Эйлера–Лагранжа–Якоби) . . . . . . . . . . . 106 15 Применение принципа Гамильтона в механике сплошной среды116
16 Принцип Гамильтона и конечномерные аппроксимации бесконечномерных систем . . . . . . . . . . . . . . . . . . . . . 129 17 Динамика гибкой нерастяжимой нити . . . . . . . . . . . . . 136
18 Уравнение колебаний струны . . . . . . . . . . . . . . . . . 152
19 Специальная теория относительности Эйнштейна . . . . . . 162
20 Каноническая гамильтонова форма уравнений механики . . . 174
21 Силы трения. Диссипация энергии . . . . . . . . . . . . . . 184
Содержание
![]()
Элементы статистической механики 194
22 О законах термодинамики . . . . . . . . . . . . . . . . . . . 195
23 Теоремы Пуанкаре о возвращении . . . . . . . . . . . . . . 198
24 Гидродинамическая интерпретация систем дифференциальных уравнений и теорема Лиувилля . . . . . . . . . . . . . . 205 25 Распределение Гиббса . . . . . . . . . . . . . . . . . . . . . 214
26 Статистическая механика идеального газа . . . . . . . . . . 220
27 Метод Лапласа асимптотической оценки интегралов . . . . . 227
28 Градиентные системы . . . . . . . . . . . . . . . . . . . . . 235
29 Малые колебания механической системы около положения равновесия . . . . . . . . . . . . . . . . . . . . . . . . . . . 244
30 Статистическая механика твердого тела . . . . . . . . . . . 257
Приложение 1. Типичность единственности и нетипичность
неединственности решения задачи Коши 260
Приложение 2. Изометрии и вращения банахова пространства.
Теорема Мазура и Улама 274
ЛИТЕРАТУРА 281
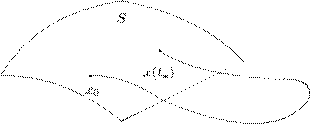
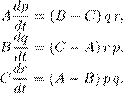 (5.15)
(5.15)
 (10.4)
(10.4)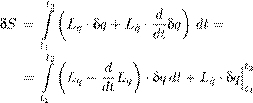 .
(10.9)
.
(10.9)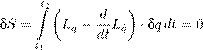 .
(10.12)
.
(10.12)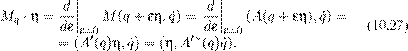
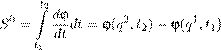 ,
(10.36)
,
(10.36)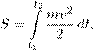 (11.11)
(11.11)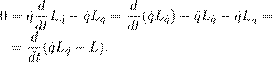 (12.1)
(12.1)