Реферат: Некоторые дополнительные вычислительные методы
|
Название: Некоторые дополнительные вычислительные методы Раздел: Рефераты по математике Тип: реферат | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Министерство образования и науки РФ ГОУ ВПО “УГТУ-УПИ” Курсовая работа по “Вычислительной математике” на тему: “Некоторые дополнительные вычислительные методы” Семестр № 3 Преподаватель Кочнев В.П. Студент гр. № р-23021д Логиновских М.А. Номер зачетной книжки 17309013 Екатеринбург 2004 _____________________________________________________________________________ Домашнее задание по ________________________________ № ________________ № записи в книге регистрации __________________ дата регистрации ___________200_г. Преподаватель _________________________________________ Студент _________________________________________ группа № ________________ Деканат ФДО _______________ СОДЕРЖАНИЕ 1. Решение систем линейных уравнений …………………………………………………… 3 а) Схема Халецкого ……………………………………………………………………....... 3 б) Метод Зейделя и условия сходимости ………………………………………………… 5 2. Методы решения нелинейных уравнений ……………………………………………….. 6 а) Метод хорд ………………………………………………………………………………. 7 б) Метод Ньютона (метод касательных) …………………………………………………. 8 в) Метод итерации ………………………………………………………………………… 9 3. Интерполирование и экстраполирование ……………………………………………….. 11 а) Интерполирование с помощью многочленов ………………………………………… 11 б) Интерполяционный многочлен Лагранжа ……………………………………………. 12 в) Интерполяционные многочлены Стирлинга и Бесселя ……………………………… 13 г) Тригонометрическое интерполирование …………………………………….………... 15 4. Численное дифференцирование и интегрирование ……………………………….…….. 16 а) Постановка задачи численного интегрирования ……………………………………... 16 б) Составные квадратурные формулы ………………………………………………….… 17 5. Приближенное вычисление обыкновенных дифференциальных уравнений ………….. 18 а) Метод Рунге-Кутта ……………………………………………………………………… 18 б) Экстраполяционные методы Адамса ………………………………………………….. 20 в) Метод Милна ……………………………………………………………………………. 20 г) Краевые задачи для обыкновенных дифференциальных уравнений ………………... 21 6. Приближенные методы решения дифференциальных уравнений с частными производными ………………………………………………………………………………… 21 а) Классификация дифференциальных уравнений второго порядка …………………… 22 б) Постановка краевых задач ……………………………………………………………… 23 в) Метод конечных разностей (метод сеток) …………………………………………….. 24 г) Разностные схемы для решения уравнения теплопроводности ……………………… 25 д) Разностные схемы для решения уравнения колебания струны ……………………… 26 7. Список литературы ………………………………………………………………………… 27 1. Решение систем линейных уравнений Системы линейных уравнений (СЛУ) имеют в вычислениях очень большое значение, так как к ним может быть приведено приближенное решение широкого круга задач. Так, основными источниками возникновения СЛУ являются теория электрических цепей, уравнения балансов и сохранения в механике, гидравлике и т.д. Существует несколько способов решения таких систем, которые в основном делятся на два типа: 1) точные методы , представляющие собой конечные алгоритмы для вычисления корней системы, 2) итерационные методы , позволяющие получать корни системы с заданной точностью путем сходящихся бесконечных процессов. Заметим, что даже результаты точных методов являются приближенными из-за неизбежных округлений. Для итерационных процессов также добавляется погрешность метода. Пример системы линейных уравнений: Или в матричном виде: где
Схема Халецкого Запишем систему линейных уравнений в матричном виде: где A=[aij ] – квадратная матрица порядка nи
Представим матрицу Aв виде произведения нижней треугольной матрицы B=[bij
] и верхней треугольной матрицы C=[cij
] с единичной диагональю
Тогда элементы bij и cij определяются по формулам
Отсюда искомый вектор xможет быть вычислен из уравнений Так как матрицы Bи C – треугольные, то системы легко решаются:
Из этих двух формул видно, что числа yi
выгодно вычислять вместе с коэффициентами cij
. Этот метод получил название схемы Халецкого
. В схеме применяется обычный контроль с помощью сумм. Если матрица A – симметрическая aij
=aji
, то Пример. Решить систему Решение. В первый раздел таблицы впишем матрицу коэффициентов системы, ее свободные члены и контрольные суммы. Далее так как Имеем: Переходим к заполнению второго столбца раздела II, начиная со второй строки. Пользуясь формулами, определяем Далее определяя по формулам, заполняем вторую сетку для раздела II:
Затем переходим к третьему столбцу, вычисляя его элементы В разделе Ш, пользуясь формулами, определяем Текущий контроль осуществляется с помощью столбца ∑, над которым производятся те же действия, что и над столбцом свободных членов.
Метод Зейделя и условия сходимости Этот метод представляет собой модификацию метода простой итерации. Его смысл заключается в том, что при вычислении (k+1)-го приближения неизвестной xi
учитываются уже вычисленные ранее (k+1)-е приближения x1,
x2
, ..., xi-1
. Пусть дана приведенная линейная система Обычно процесс Зейделя сходится быстрее, чем метод простой итерации. Бывает, что процесс Зейделя сходится, когда простая итерация расходится и т.п. Правда, бывает и наоборот. Во всяком случае, достаточные условия сходимости для метода простой итерации достаточны и для сходимости метода Зейделя. То есть процесс итерации сходится, если выполнено одно из условий 1) Пример. Методом Зейделя решить систему уравнений Решение. Приведем эту систему к виду, удобному для итерации, В качестве нулевых приближений корней возьмем: Применяя процесс Зейделя, последовательно получим:
Результаты вычислений с точностью до четырех знаков помещены в таблице:
Точные значения корней: 2. Методы решения нелинейных уравнений Как известно, далеко не всякое уравнение f(x)=0 можно решить точно, т.е. не всегда можно найти число Метод хорд Пусть дано уравнение f(x)=0, где функция f(x) определена и непрерывна на интервале [a, b] и f(a)f(b)<0. Пусть для определенности f(a)<0 и f(b)>0. Разделим отрезок [a, b] в отношении - f(a):f(b). Это даст нам приближенное значение корня x1 = a + h1 , где
Далее этот прием применяем к одному из отрезков [a, x1 ] или [x1 , b], на концах которого функция f(x) имеет противоположные знаки. Аналогично находим второе приближение x2 и т.д. Геометрически этот способ эквивалентен замене кривой y = f(x) хордой, проходящей через точки А[a, f(a)] и B[b, f(b)].
f(b)
f(b)
Действительно, уравнение хорды АВ имеет вид При х = х1
и y = 0, получим Полагая, что на отрезке [a, b] вторая производная f''(x) сохраняет постоянный знак, метод хорд сводится к двум различным вариантам. Из рис. 1 видно, что конец а неподвижен и последовательные приближения: x0 =b;
образуют ограниченную монотонно убывающую последовательность, причем a<ξ<…<xn +1 <xn <…<x1 <x0 . Из рис. 2 видно, что неподвижен конец b и последовательные приближения: x0 =a;
образуют ограниченную монотонно возрастающую последовательность, причем x0 <x1 <x2 <…<xn <xn+1 <…<ξ<b. Таким образом, для вычисления корня уравнения имеем две различные вычислительные формулы. За неподвижный конец выбираем тот конец, для которого знак функции f(x) совпадает со знаком второй производной f''(x). Пример. Найти положительный корень уравнения Решение. Прежде всего отделяем корень. Так как
Так как Таким образом, Метод Ньютона (метод касательных) Пусть корень ξ уравнения f(x)=0, отделен на отрезке [a, b], причем первая и вторая производные f'(x) и f''(x) непрерывны и сохраняют определенные знаки при
Если в качестве начального приближения выбрать точку х0
=В0
, то процесс быстро сходится. Если же выбрать точку х0
=А, то х1
Пример. Вычислить методом Ньютона отрицательный корень уравнения
Решение. Полагая в левой части уравнение
Останавливаясь на Метод итерации Заменим уравнение f(x)=0 эквивалентным x=φ(x). Выберем некоторое начальное приближение x0 и вычислим дальнейшие приближения по формулам x1 = φ(x0 ), x2 = φ(x1 ), …, xn = φ(xn -1 ). Если последовательность xn имеет предел, то итерационный процесс xn = φ(xn -1 ) (n=1, 2, …) называется сходящимся. Пусть функция φ(x) непрерывна. Переходя к пределу в равенстве xn = φ(xn -1 ), получим
Теорема 1. Пусть корень
Следствие 1. Если требуется найти корень с точностью ε, то кончаем итерационный процесс тогда, когда Следствие 2. Так как Теорема 2. Если Привести уравнение f(x)=0 к виду x=φ(x) таким образом, чтобы получить сходящийся итерационный процесс, можно различными способами. Рассмотрим два из них: 1) уравнение f(x)=0 равносильно при λ≠0 уравнению λf(x)=0 и уравнению x= λf(x)+x. Обозначим λf(x)+x через φ(x), получим x= φ(x). Параметр λ подберем так, чтобы функция φ'(x)= λf'(x)+1 на [a, b] была по модулю меньше единицы. 2) если Пример. Методом итерации найти корень уравнения 5x-8lnx=8 с точностью 0,01. Решение. Запишем уравнение в виде
Уравнение имеет два корня:
Так как φ’(z0
)≈3>1, то итерационный процесс расходится. Найдем функцию
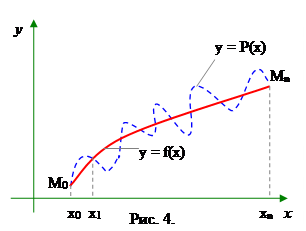
3. Интерполирование и экстраполирование Задача интерполирования состоит в том, чтобы по значениям функции f(x) в нескольких точках отрезка восстановить ее значения в остальных точках данного отрезка. Разумеется, такая постановка задачи допускает сколь угодно много решений. Задача интерполирования возникает, например, в том случае, когда известны результаты измерений yk = f(xk ) некоторой физической величины f(x) в точках xk , k = 0, 1,…, n и требуется определить ее значение в других точках. Интерполирование используется также при необходимости сгущения таблиц, когда вычисление значений f(x) по точным формулам трудоемко. Иногда возникает необходимость приближенной замены (аппроксимации) данной функции (обычно заданной таблицей) другими функциями, которые легче вычислить. При обработке эмпирических (экспериментальных) зависимостей, результаты обычно представлены в табличном или графическом виде. Задача заключается в аналитическом представлении искомой функциональной зависимости, то есть в подборе формулы, корректно описывающей экспериментальные данные. Интерполирование с помощью многочленов Пусть функциональная зависимость задана таблицей y0 =
f(x0
); …, y1
= f(x1
); …, yn
=
f(xn
). Обычно задача интерполирования формулируется так: найти многочлен P(x) = Pn
(x) степени не выше n, значения которого в точках xi
(i = 0, 1 2,…, n) совпадают со значениями данной функции, то есть P(xi
) = yi
. Геометрически это означает, что нужно найти алгебраическую кривую вида
Для любой непрерывной функции f(x) сформулированная задача имеет единственное решение. Действительно, для отыскания коэффициентов а0
, а1
, а2
,…, аn
получаем систему линейных уравнений Инт ерполяционный многочлен Лагранжа Пусть на отрезке [a,b
] некоторая функция f(x
) задана лишь в некоторых точках
Кроме того, пусть задана некоторая точка Этот многочлен называется многочленом Лагранжа . Его основные свойства: 1) это - многочлен степени 2) 3) если фиксировать любое число где Сказанное означает, что если функция Пример. Построить интерполяционный многочлен Лагранжа для функции заданной таблицей
И найти значение функции при x=4. Решение. Используя формулу Лагранжа найдем: После некоторых преобразований получим Интерполяционные многочлены Стирлинга и Бесселя Взяв среднее арифметическое первой и второй интерполяционных формул Гаусса
где Легко видеть, что Кроме формулы Стирлинга, часто употребляется формула Бесселя. Для вывода этой формулы воспользуемся второй интерполяционной формулой Гаусса
Возьмем Если выбрать за начальные значения
Примем теперь за начальные значения
Взяв среднее арифметическое формул, после несложных преобразований получим интерполяционную формулу Бесселя
где Интерполяционная формула Бесселя, как следует из способа получения ее, представляет собой полином, совпадающий с данной функцией Тригонометрическое интерполирование Пусть функция f (х ) представлена на некотором отрезке [0, 2p]таблицей значений f (хi ) в равноотстоящих узлах хi = 2p(i- 1)/ (2N+ 1), i = 1, 2, ...,2N+ 1. Тогда тригонометрическим интерполирующим многочленом назовем многочлен степени m вида:
Задача тригонометрической интерполяции состоит в построении тригонометрического полинома, который бы наиболее полно удовлетворял условиям Рm (хi )= f (хi ) для любого i= 1, 2, ..., 2 N+ 1. Можно показать, что решением этой задачи является полином именно того вида, коэффициенты которого вычисляют по следующим формулам:
Интерполяция сплайнами Пусть отрезок [a, b] разбит на n равных частей [xi , xi+1 ], где xi =a+ih, i=0, ..., n, xn =b, h=(b-a)/n. Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a, b], а на каждом частичном отрезке [xi , xi+1 ] в отдельности является некоторым алгебраическим многочленом. Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на [a,b] производной - дефектом сплайна. На практике широкое распространение получили сплайны третьей степени, имеющие на [a, b] непрерывную, по крайней мере, первую производную. Эти сплайны называются кубическими и обозначаются S3 (x). Пусть на отрезке [a, b] в узлах сетки в заданы значения некоторой функции fi =f(xi ), i=0, ..., n. Интерполяционным кубическим сплайном S3 (x) называется сплайн S3 (x)=аi0 +аi1 (x - xi )+аi2 (x - xi )2 +аi3 (x - xi )3 , xÎ[xi , xi +1 ], удовлетворяющий условиям S3 (xi )=f(xi ), i=0, ..., n. Данный сплайн на каждом из отрезков [xi , xi+1 ], i=0, ..., n-1 определяется четырьмя коэффициентами, и поэтому для его построения на всем промежутке [a, b] необходимо определить 4n коэффициентов. Для их однозначного определения необходимо задать 4n уравнений. Условие S3 (xi )=f(xi ), i=0, ..., n дает 2n уравнений, при этом функция S3 (xi ), удовлетворяющая этим условиям, будет непрерывна во всех внутренних узлах. Условие непрерывности производных сплайна Вместе получается 4N-2 уравнений. Два дополнительных условия обычно задаются в виде ограничений на значение производных сплайна на концах промежутка [a, b] и называются краевыми условиями. Наиболее употребительны следующие типы краевых условий: а) S' 3 (а)=f'(а), S'(b)=f'(b) ; б) S" 3 (а)= f"(а), S"( b)= f"( b) ; в) г) S''' 3 (x p +0 )=S''' 3 (x p -0 ), р =1, n-1 . 4. Численное дифференцирование и интегрирование Если функция f(x) заданна аналитически ее первообразная F(x) является элементарной функцией, то Постановка задачи численного интегрирования Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой
. Обычный прием механической квадратуры состоит в том, что данную функцию f(x) на рассматриваемом отрезке [a, b] заменяют интерполирующей или аппроксимирующей функцией φ(x) простого вида, а затем приближенно полагают: Пn+1
(x)=(x-x0
)(x-x1
)…(x-xn
), причем Ln
(xi
)=yi
(i=0, 1, 2, …, n). Заменяя функцию f(x) полиномом Ln
(x), получим равенство
1) коэффициенты Ai при данном расположении узлов не зависят от выбора функции f(x); 2) для полинома степени nполученная формула – точная, так как тогда Ln
(x)=f(x); следовательно, формула Составные квадратурные формулы Приведем ряд простейших квадратурных формул, используемых в практике численного интегрирования функции f(x) на некотором интервале [a, b], разбитого на nравных отрезков точками a0
=a, a1
=a+h, a2
=a+2h, …, an
=a+nh+b, где n=0,1, …, kи Формула прямоугольников: Погрешность формулы определяется выражением
Формула трапеций: Погрешность формулы определяется выражением
Формула Симпсона: Погрешность формулы определяется выражением
Если длина интервала [a, b] велика для применения простейших квадратурных формул, то поступают следующим образом: 1) интервал [a, b] разбивают точками xi
, 2) на каждом частичном интервале [xi
, xi
+1
] применяют простейшую квадратурную формулу, находят приближенное значение интеграла 3) из полученных выражений Qi составляют (отсюда и название составная формула ) квадратурную формулу для всего интервала [a, b]; 4) абсолютную погрешность Rсоставной формулы находят суммированием погрешностей Ri на каждом частичном интервале. 5. Приближенное вычисление обыкновенных дифференциальных уравнений Обыкновенным дифференциальным уравнением
называется равенство
Метод Рунге-Кутта Изложим идею метода на примере: Интегрируя это уравнение в пределах от x до x + h (0 < h <1), получим равенство
Постараемся составить линейную комбинацию величин ji
, i = 0, 1, ..., q, которая будет являться аналогом квадратурной суммы и позволит вычислить приближенное значение приращения Dy:
Метод четвертого порядка для q =
3, имеет вид
Особо широко известно другое вычислительное правило Рунге-Кутта четвертого порядка точности:
Метод Рунге-Кутта имеет погрешность четвертого порядка (~ h4 ). Правило Рунге. Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно оценить по формуле В формуле O(xi
) – главный член погрешности, Экстраполяционные методы Адамса Широко распространенным семейством многошаговых методов являются методы Адамса. Простейший из них, получающийся при Пусть найдены значения Тогда разностная схема четвертого порядка метода Адамса запишется в виде Сравнивая метод Адамса с методом Рунге — Кутта той же точности, отмечаем его экономичность, поскольку он требует вычисления лишь одного значения правой части на каждом шаге. Но метод Адамса неудобен тем, что невозможно начать счет по одному лишь известному значению Метод Милна Пусть на отрезке [a, b] требуется найти численное решение дифференциального уравнения
Абсолютная погрешность значения Пример. Дано дифференциальное уравнение y’=y-x, удовлетворяющие начальному условию x0 =0, y(x0 )=1,5. Вычислить с точность до 0,01 значение решения этого уравнения при x=1,5. Решение. Выберем начальный шаг вычисления. Из условия h4 <0,01 получим h=0,25 Составим таблицу
Получаем ответ y=(1,5)=4,74. Краевые задачи для обыкновенных дифференциальных уравнений На практике приходится часто решать задачи, когда условия задаются при двух значениях независимой переменной (на концах рассматриваемого отрезка). Такие задачи, называемые краевыми, получаются при решении уравнений высших порядков или систем уравнений. Стандартная постановка краевой задачи для обыкновенных дифференциальных уравнений выглядит следующим образом
Общая классификация методов решения краевых задач: существуют точные, приближенные и численные методы. 6. Приближенные методы решения дифференциальных уравнений с частными производными Кроме обычных дифференциальных уравнений существуют так называемые дифференциальные уравнения с частными производными. Далее они будут рассмотрены более подробно. Классификация дифференциальных уравнений второго порядка Рассмотрим уравнение второго порядка Уравнение Уравнение Уравнение Дифференциальное уравнение Если последнее уравнение гиперболического типа, то уравнение характеристик имеет два интеграла: С помощью замены переменных В этом случае осуществляем замену переменных Полагая Постановка краевых задач Классическим решением краевой задачи называются всяка функция, удовлетворяющая дифференциальному уравнению в каждой точке внутри области задания этого уравнения и непрерывная в рассматриваемой области, включая границу. Соответствующую постановку краевой задачи называют классической. Существует несколько таких задач:
уравнения колебания струны и уравнения теплопроводности. Рассмотрим процесс колебания тонкой бесконечной струны под действием непрерывно распределенной внешней силы с плотностью f. Предположим, что сила действует в одной плоскости – плоскости колебания струны (x, u), а струна является гибкой упругой нитью. Пусть величина натяжения, возникающая в струне вследствие ее изгиба, подчиняется закону Гука, а сами колебания достаточно малы. Тогда величина смещения u (x, t) удовлетворяет уравнению колебания струны: Исследуем теперь процесс распределения температуры в тонком бесконечном стержне. Предполагается, что тепловой поток подчиняется закону Фурье, а изменение температуры тела пропорционально количеству теплоты, сообщаемой телу. Предположим, что внутри стержня может выделяться и поглощаться теплота, характеризуемая плотностью тепловых источников f. Тогда распределение температуры в стержне описывается уравнением теплопроводности:
режим распределения температуры в ограниченной тонкой пластине произвольной формы с гладкой границей. Пусть функция u(x, y) выражает температуру каждой точки пластины. При обычных законах распространения тепла функция u(x, y) удовлетворяет уравнению Пуассона: В зависимости от теплового режима на границе получаются три граничных условия для функции u(x, y). Пусть Г – граница рассматриваемой области в – определения уравнения Лапласа. Математическая формулировка граничных условий может быть задана в следующем виде: граничное условие Iрода: граничное условие IIрода: граничное условие IIIрода: Производная берется по внешней нормали к кривой Г; λ>0 – коэффициент теплопроводности; φ0 , φ1 , φ2 – заданные на Г функции, причем φ2 есть произведение коэффициента теплопроводности на температуру внешней среды, соприкасающейся с телом. Таким образом, краевая задача заключается в том, чтобы найти классическое решение уравнения Пуассона или Лапласа, удовлетворяющее одному из граничных условий.
стержне единичной длины. Поместим один из концов в точку x=0, а другой – в точку x=1. Распределение температуры в таком стержне в течение некоторого интервала времени 0<t<Tописывается уравнением Граничное условие Iрода (на конце стержня x=0 заданна температура): Граничное условие IIрода (на конце стержня x=0 задан тепловой поток): Граничное условие IIIрода: Для другого конца стержня x=1 правые части граничных условий заменяются соответственно на ψ0 (t), ψ1 (t), ψ2 (t). Заметим, что начальное и граничное условия должны удовлетворять так называемым условиям сопряжения, т.е. при условии Iрода u0 (0)=φ0 (0), при условии IIрода u0 x (0)=φ1 (0), при условии IIIрода -u0 x (0)+λu0 (0)=φ2 (0). Аналогичные условия сопряжения должны выполнятся и на другом конце стержня x=1. Сформулируем одну из возможных краевых задач. Найти классическое решение уравнения Метод конечных разностей (метод сеток) Численные методы, основанные на разностной аппроксимации производных называется разностным методом, методом конечных разностей или методом сеток. Пусть заданно линейное дифференциальное уравнение, записанное в символическом виде: Для единственного решения данного уравнения к нему необходимо присоединить краевые условия: Разностный метод решения этих двух задач можно представить в виде двух этапов:
Для построения разностной схемы первым шагом является замена области Второй шаг в построении разностной схемы состоит в аппроксимации дифференциального выражения Luнекоторым разностным выражением, а функцию непрерывного аргумента f – сеточной функцией, т.е. в построение некоторого разностного аналога для данного уравнения, при данных краевых условиях. Такая аппроксимация приводит к системе алгебраических уравнений относительно значений некоторой сеточной функции
Где Lh и φh – разностные операторы, аппроксимирующие соответственно Lи l; υh – искомая сеточная функция, аппроксимирующая решение u; fh , φh – заданные сеточные функции, аппроксимирующие fи φ. Совокупность разносных уравнений, аппроксимирующих исходную задачу – есть разностная схема. Рассмотрим их подробнее на примерах уравнения теплопроводности и колебания струны. Разностные схемы для решения уравнения теплопроводности (параболический тип) Рассмотрим первую краевую задачу для уравнения теплопроводности в прямоугольнике
В области
Производные левой части уравнения В соответствии с данной аппроксимацией построим два разностных аналога уравнения Здесь Начальное и граничное условия для первой краевой задачи аппроксимируются точно: Для второй и третьей краевых задач граничные условия аппроксимируются на основе разностных выражений. Полагая r=τ/h2
получим Анализ показывает, что погрешность аппроксимации схем есть Разностные схемы для решения уравнения колебания струны (гиперболический тип) Рассмотрим первую краевую задачу для уравнения колебания струны в прямоугольнике
Применение метода конечных разностей к решению задачи по существу мало чем отличается от его применения к уравнению теплопроводности. Область
Разностная аппроксимация принимает вид
Начальные условия аппроксимируются следующим образом: Граничные условия аппроксимируются точно так же, как и для уравнения теплопроводности: Значение Анализ показывает, что погрешность аппроксимации схем есть Список литературы
|
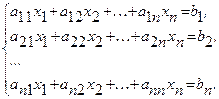
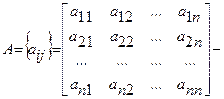 матрица коэффициентов системы;
матрица коэффициентов системы; - вектор неизвестных;
- вектор неизвестных; 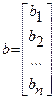 - вектор свободных членов.
- вектор свободных членов.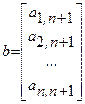 - векторы-столбцы.
- векторы-столбцы.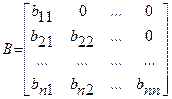 и
и 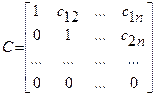 .
.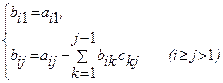 и
и 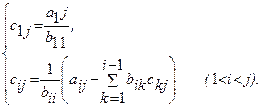
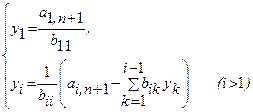 и
и 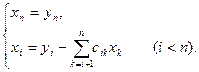
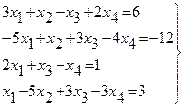
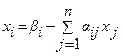 (i = 1, 2, …n). Выберем произвольно начальные приближения корней
(i = 1, 2, …n). Выберем произвольно начальные приближения корней 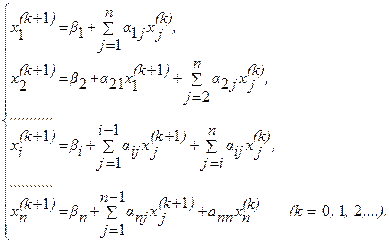
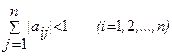 или 2)
или 2) 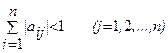 .
.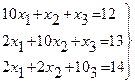
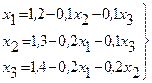
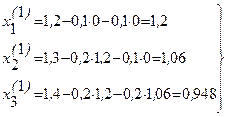
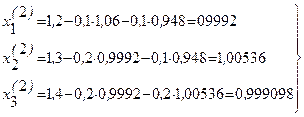 и т.д.
и т.д.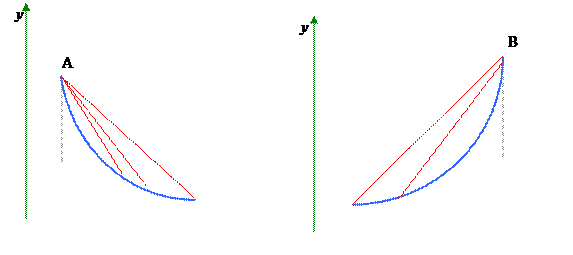

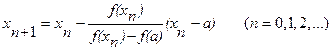
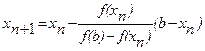
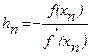 . Подставив полученное выражение в формулу ξ=xn
+hn
, найдем следующее значение корня:
. Подставив полученное выражение в формулу ξ=xn
+hn
, найдем следующее значение корня: 
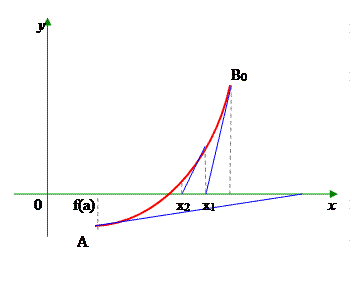 Графическое нахождение корня методом Ньютона (рис. 3).
Графическое нахождение корня методом Ньютона (рис. 3).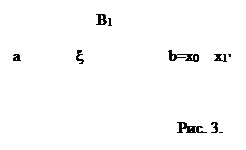
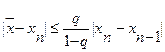 .
.
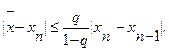
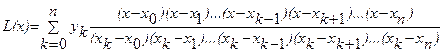 .
.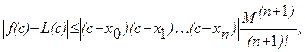
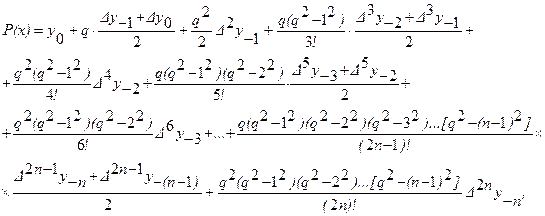
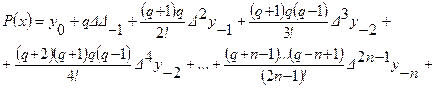
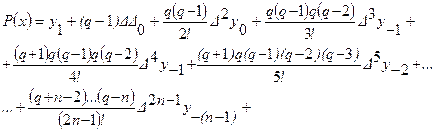
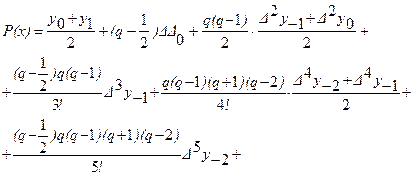

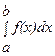 вычисляется по формуле Ньютона-Лейбница:
вычисляется по формуле Ньютона-Лейбница: 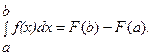 В тех случаях, когда функция f(x) задана аналитически, но ее первообразная не является элементарной функцией или отыскать ее сложно, а также в случае, когда функция f(x) задана графически или таблично, для вычисления
В тех случаях, когда функция f(x) задана аналитически, но ее первообразная не является элементарной функцией или отыскать ее сложно, а также в случае, когда функция f(x) задана графически или таблично, для вычисления 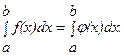 Функция φ(x) должна быть такова, чтобы интеграл
Функция φ(x) должна быть такова, чтобы интеграл 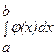 вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности. Пусть для функции y=f(x) известны в n+1 точках x0
, x1
, x2
, …, xn
отрезка [a, b] соответствующие значения f(xi
)=yi
(i=0, 1, 2, …, n). Требуется приближенно найти
вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности. Пусть для функции y=f(x) известны в n+1 точках x0
, x1
, x2
, …, xn
отрезка [a, b] соответствующие значения f(xi
)=yi
(i=0, 1, 2, …, n). Требуется приближенно найти 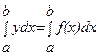 По заданным значениям yi
построим полином Лагранжа
По заданным значениям yi
построим полином Лагранжа 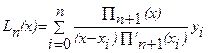 , где
, где 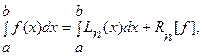 где Rn
[f] – ошибка квадратурной формулы. Отсюда получаем приближенную квадратурную формулу
где Rn
[f] – ошибка квадратурной формулы. Отсюда получаем приближенную квадратурную формулу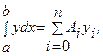 где
где 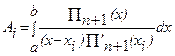 (i=0, 1, 2, …, n). Для вычисления Ai
заметим, что
(i=0, 1, 2, …, n). Для вычисления Ai
заметим, что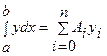 - точная при y=xk
(k=0, 1, 2, …, n), т.е. Rn
[xk
]=0 при k=0, 1, …, n. Полагая y=xk
(k=0, 1, 2, …, n), получим линейную систему из n+1 уравнений
- точная при y=xk
(k=0, 1, 2, …, n), т.е. Rn
[xk
]=0 при k=0, 1, …, n. Полагая y=xk
(k=0, 1, 2, …, n), получим линейную систему из n+1 уравнений 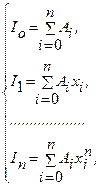 - где
- где 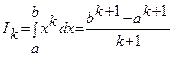 (k=0, 1, …, n), из которой можно определить коэффициенты A0
, A1
, …, An
.
(k=0, 1, …, n), из которой можно определить коэффициенты A0
, A1
, …, An
.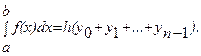
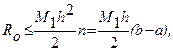 где
где 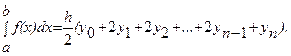
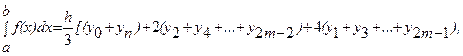 где
где 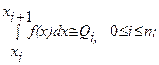
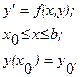
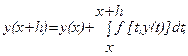 которое посредством последнего интеграла связывает значения решения рассматриваемого уравнения в двух точках, удаленных друг от друга на расстояние шага h. Для удобства записи данного выражения используем обозначение
которое посредством последнего интеграла связывает значения решения рассматриваемого уравнения в двух точках, удаленных друг от друга на расстояние шага h. Для удобства записи данного выражения используем обозначение 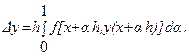 Указав эффективный метод приближенного вычисления интеграла в выражении
Указав эффективный метод приближенного вычисления интеграла в выражении 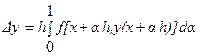 , мы получим при этом одно из правил численного интегрирования уравнения
, мы получим при этом одно из правил численного интегрирования уравнения 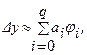 где
где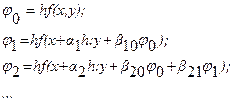
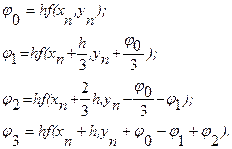
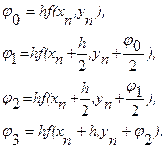
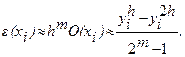
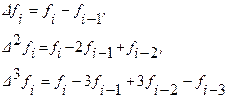 .
.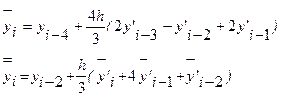 – где
– где 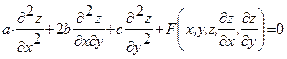 , где
, где 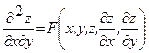 называется каноническим уравнением гиперболического типа.
называется каноническим уравнением гиперболического типа.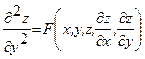 называется каноническим уравнением параболического типа.
называется каноническим уравнением параболического типа.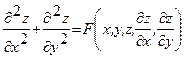 называется каноническим уравнением эллиптического типа.
называется каноническим уравнением эллиптического типа.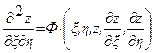 . Для уравнения параболического типа оба семейства характеристик совпадают, т.е. уравнение характеристик дает лишь один интеграл
. Для уравнения параболического типа оба семейства характеристик совпадают, т.е. уравнение характеристик дает лишь один интеграл  . Для уравнения эллиптического типа интегралы уравнения характеристик имеют вид
. Для уравнения эллиптического типа интегралы уравнения характеристик имеют вид 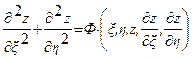 .
.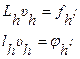
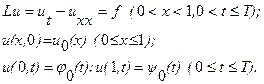
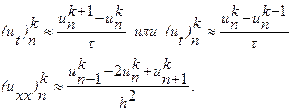
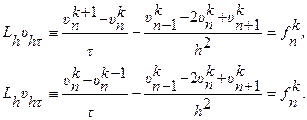
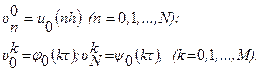
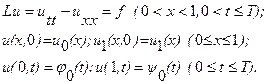
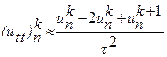 .
. 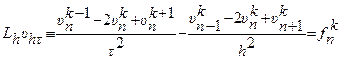 .
.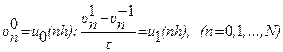 .
.