Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального
образования
Алтайский государственный технический университет им. И. И. Ползунова
Кафедра высшей математики
Расчетное задание по эконометрики
Барнаул 2011
Вариант №35
Имеются данные:
Таблица 1
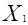
|

|
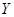
|
| 28 |
30 |
28 |
| 26 |
34 |
24 |
| 19 |
33 |
31 |
| 30 |
37 |
30 |
| 29 |
40 |
34 |
| 36 |
44 |
31 |
| 39 |
46 |
25 |
| 38 |
42 |
34 |
| 43 |
47 |
36 |
| 49 |
50 |
37 |
В Excelсоставим вспомогательную таблицу:
Таблица 2
х1
|
х2
|
у
|
ух1
|
ух2
|
y^
|
y-y^
|
|y-y^|*100/y
|
x1x2
|
| 28 |
30 |
28 |
784 |
840 |
27,89 |
0,11 |
0,38 |
840,00 |
| 26 |
34 |
24 |
806 |
816 |
28,78 |
-4,78 |
19,93 |
884,00 |
| 19 |
33 |
31 |
570 |
1023 |
27,99 |
3,01 |
9,70 |
627,00 |
| 30 |
37 |
30 |
900 |
1110 |
29,86 |
0,14 |
0,45 |
1110,00 |
| 29 |
40 |
34 |
986 |
1360 |
30,57 |
3,43 |
10,10 |
1160,00 |
| 36 |
44 |
31 |
1116 |
1364 |
32,13 |
-1,13 |
3,66 |
1584,00 |
| 39 |
46 |
25 |
975 |
1150 |
32,88 |
-7,88 |
31,52 |
1794,00 |
| 38 |
42 |
34 |
1292 |
1428 |
31,77 |
2,23 |
6,57 |
1596,00 |
| 43 |
47 |
36 |
1548 |
1692 |
33,44 |
2,56 |
7,10 |
2021,00 |
| 49 |
50 |
37 |
1813 |
1850 |
34,67 |
2,33 |
6,29 |
2450,00 |
| Ср.знач |
33,7 |
40,3 |
31 |
1079 |
1263,3 |
31,00 |
0,00 |
9,57 |
1406,60 |
С Помощью вычисленных данных, вычислим дисперсию, коэффициент корреляции, среднее квадратичное отклонение и определим наиболее значимый фактор.
Таблица 3
| Дисперсия |
71,61 |
39,81 |
17,40 |
| Коэф.корреляции |
0,51 |
0,53 |
0,91 |
| Среднее квадратичное отклонение |
8,46 |
6,31 |
4,17 |
| β1 |
0,15 |
| β2 |
0,39 |
| a |
17,99 |
| b1 |
0,08 |
| b2 |
0,26 |
| Rух1х2 |
0,54 |
| Fфакт |
1,409 |
| FфактХ1 |
0,04 |
| FфактХ2 |
0,27 |
Для характерной относительной силы влияния х1 и х2 рассчитаем средний коэффициент эластичности Э̅ухi:
| Э̅ух1 |
0,171215 |
| Э̅ух2 |
0,485234 |
Расчитав FфактХ1 и FфактХ2 выбрали из них более значимый фактор х2=0,27 по отношению к х1=0,04
2. Линейная регрессия. Уравнение в общем виде имеет вид: у=а+
b
*х. расчеты приведены в таблице 4.
Таблица 4
| х1
|
у
|
yx |
y^ |
y-y^ |
|y-y^|*100/y
|
| 30 |
28 |
840 |
27,498 |
0,502 |
1,79 |
| 34 |
24 |
816 |
28,858 |
-4,858 |
20,24 |
| 33 |
31 |
1023 |
28,518 |
2,482 |
8,01 |
| 37 |
30 |
1110 |
29,878 |
0,122 |
0,41 |
| 40 |
34 |
1360 |
30,898 |
3,102 |
9,12 |
| 44 |
31 |
1364 |
32,258 |
-1,258 |
4,06 |
| 46 |
25 |
1150 |
32,94 |
-7,938 |
31,75 |
| 42 |
34 |
1428 |
31,578 |
2,422 |
7,12 |
| 47 |
36 |
1692 |
33,278 |
2,722 |
7,56 |
| 50 |
37 |
1850 |
34,298 |
2,702 |
7,30 |
| 40,30 |
31,00 |
1263,30 |
31,00 |
0,00 |
9,74 |
Дисперсия 39,81 17,40 79,83
а 17,30
b 0,34
Ср.квад.отк. 6,31 4,17
F-табл 4,46
Уравнение линейной регрессии выглядит так:
Ŷ=17,30 – 0,34x
График линейной регрессии

3. Степенная регрессия. Уравнение в общем виде имеет вид: у=а*х
b
.
Таблица 5
| У |
Х1 |
Y |
X |
XY |
Y^2 |
X^2 |
Ŷ=10^C*x^b |
y-ŷ |
(y-ŷ)^2 |
Ai=I(y-ŷ)/yI*100 |
y-yср |
(y-yср)^2 |
| 1 |
28 |
30 |
1,45 |
1,48 |
2,14 |
2,09 |
2,18 |
27,21 |
0,79 |
0,63 |
2,84 |
-3,00 |
9,00 |
| 2 |
24 |
34 |
1,38 |
1,53 |
2,11 |
1,90 |
2,35 |
28,71 |
-4,71 |
22,14 |
19,61 |
-7,00 |
49,00 |
| 3 |
31 |
33 |
1,49 |
1,52 |
2,26 |
2,22 |
2,31 |
28,34 |
2,66 |
7,07 |
8,58 |
0,00 |
0,00 |
| 4 |
30 |
37 |
1,48 |
1,57 |
2,32 |
2,18 |
2,46 |
29,77 |
0,23 |
0,05 |
0,78 |
-1,00 |
1,00 |
| 5 |
34 |
40 |
1,53 |
1,60 |
2,45 |
2,35 |
2,57 |
30,78 |
3,22 |
10,38 |
9,48 |
3,00 |
9,00 |
| 6 |
31 |
44 |
1,49 |
1,64 |
2,45 |
2,22 |
2,70 |
32,06 |
-1,06 |
1,13 |
3,42 |
0,00 |
0,00 |
| 7 |
25 |
46 |
1,40 |
1,66 |
2,32 |
1,95 |
2,76 |
32,68 |
-7,68 |
58,96 |
30,71 |
-6,00 |
36,00 |
| 8 |
34 |
42 |
1,53 |
1,62 |
2,49 |
2,35 |
2,63 |
31,43 |
2,57 |
6,61 |
7,56 |
3,00 |
9,00 |
| 9 |
36 |
47 |
1,56 |
1,67 |
2,60 |
2,42 |
2,80 |
32,98 |
3,02 |
9,11 |
8,38 |
5,00 |
25,00 |
| 10 |
37 |
50 |
1,57 |
1,70 |
2,66 |
2,46 |
2,89 |
33,87 |
3,13 |
9,81 |
8,46 |
6,00 |
36,00 |
| Итого |
310,00 |
403,00 |
14,87 |
16,00 |
23,81 |
22,16 |
25,64 |
307,81 |
2,19 |
125,91 |
99,83 |
0,00 |
174,00 |
| Ср.знач |
31,00 |
40,30 |
1,49 |
1,60 |
2,38 |
2,22 |
2,56 |
12,59 |
9,98 |
| Дисперс |
17,40 |
39,81 |
0,004 |
0,005 |
13,47 |
| Ср.кв.отк |
4,17 |
6,31 |
| b=(СРЗНАЧ(xy)-СРЗНАЧ(y)*СРЗНАЧ(x))/Dx |
0,43 |
а=6,33 |
| C=lg(a) |
0,80 |
| n |
10,00 |
| rxy=КОРЕНЬ(1-(Σ(y-ŷ)^2/Σ(y-yср)^2) |
0,53 |
умеренная линейная зависимость |
| Rxy=rxy^2 |
0,28 |
| Fфакт=(Rxy/(1-Rxy))*(n-2) |
3,06 |
| Fтабл |
4,46 |
График степенной регрессии

У = 6,33*х0,43
4. Показательная регрессия. Уравнение в общем виде имеет вид: у=а*
bx
.
Расчеты приведены в таблице 6.
Таблица 6
| y |
x1 |
Y |
Yx |
Y^2 |
X^2 |
ŷ=a*b^x |
y-ŷ |
(y-ŷ)^2 |
Ai=I(y-ŷ)/yI*100 |
y-yср |
(y-yср)^2 |
(y-yср)^2 |
| 1 |
28 |
30 |
1,45 |
43,41 |
2,09 |
900,00 |
27,41 |
0,59 |
0,35 |
2,10 |
-3,00 |
9,00 |
28 |
| 2 |
24 |
34 |
1,38 |
46,93 |
1,90 |
1156,00 |
28,65 |
-4,65 |
21,60 |
19,37 |
-7,00 |
49,00 |
24 |
| 3 |
31 |
33 |
1,49 |
49,21 |
2,22 |
1089,00 |
28,33 |
2,67 |
7,11 |
8,60 |
0,00 |
0,00 |
31 |
| 4 |
30 |
37 |
1,48 |
54,65 |
2,18 |
1369,00 |
29,61 |
0,39 |
0,15 |
1,30 |
-1,00 |
1,00 |
30 |
| 5 |
34 |
40 |
1,53 |
61,26 |
2,35 |
1600,00 |
30,61 |
3,39 |
11,51 |
9,98 |
3,00 |
9,00 |
34 |
| 6 |
31 |
44 |
1,49 |
65,62 |
2,22 |
1936,00 |
31,99 |
-0,99 |
0,98 |
3,19 |
0,00 |
0,00 |
31 |
| 7 |
25 |
46 |
1,40 |
64,31 |
1,95 |
2116,00 |
32,70 |
-7,70 |
59,31 |
30,80 |
-6,00 |
36,00 |
25 |
| 8 |
34 |
42 |
1,53 |
64,32 |
2,35 |
1764,00 |
31,29 |
2,71 |
7,34 |
7,97 |
3,00 |
9,00 |
34 |
| 9 |
36 |
47 |
1,56 |
73,15 |
2,42 |
2209,00 |
33,06 |
2,94 |
8,62 |
8,16 |
5,00 |
25,00 |
36 |
| 10 |
37 |
50 |
1,57 |
78,41 |
2,46 |
2500,00 |
34,18 |
2,82 |
7,98 |
7,63 |
6,00 |
36,00 |
37 |
| Итого |
310,00 |
403,00 |
14,87 |
601,27 |
22,16 |
16639,00 |
307,83 |
2,17 |
124,94 |
99,09 |
0,00 |
174,00 |
310,00 |
| Ср.знач |
31,00 |
40,30 |
1,49 |
60,13 |
2,22 |
1663,90 |
12,49 |
9,91 |
31,00 |
| Дисперс |
17,40 |
39,81 |
0,00 |
17,40 |
| Ср.кв.отк |
4,17 |
6,31 |
0,06 |
4,17 |
| B=(СРЗНАЧ(xy)-СРЗНАЧ(y)*СРЗНАЧ(x))/Dx |
0,00 |
| A=СРЗНАЧ(Y)-B*СРЗНАЧ(X) |
1,29 |
| b=10^B |
1,01 |
| a=10^C |
19,69 |
| n |
10,00 |
| rxy=КОРЕНЬ(1-(Σ(y-ŷ)^2/Σ(y-yср)^2) |
0,53 |
| Rxy=rxy^2 |
0,28 |
умеренная линейная зависимость |
| Fфакт=(Rxy/(1-Rxy))*(n-2) |
3,14 |
| Fтабл |
4,46 |
График показательной регрессии
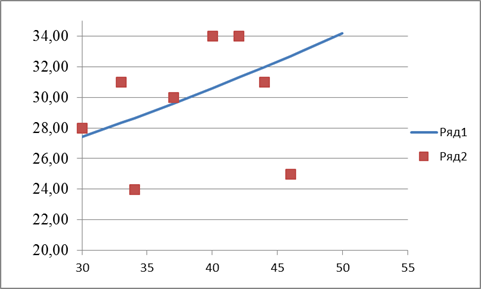
У= 1969*1,01
5. Модель регрессии равносторонней гиперболы. Уравнение в общем виде имеет вид: у=а +
b
*(1/х).
Таблица 7
| y |
z=1/x |
yz |
z^2 |
y^2 |
ŷ=a+b*z |
y-ŷ |
(y-ŷ)^2 |
Ai=I(y-ŷ)/yI*100 |
x2 |
y-yср |
(y-yср):2 |
y |
| 1 |
28 |
0,01562500 |
0,44 |
0,00024414 |
784,00 |
28,09 |
-0,09 |
0,01 |
0,33 |
64 |
-3,00 |
9,00 |
28 |
| 2 |
24 |
0,01666667 |
0,40 |
0,00027778 |
576,00 |
29,94 |
-5,94 |
35,26 |
24,74 |
60 |
-7,00 |
49,00 |
24 |
| 3 |
31 |
0,01538462 |
0,48 |
0,00023669 |
961,00 |
27,67 |
3,33 |
11,12 |
10,76 |
65 |
0,00 |
0,00 |
31 |
| 4 |
30 |
0,01612903 |
0,48 |
0,00026015 |
900,00 |
28,99 |
1,01 |
1,03 |
3,38 |
62 |
-1,00 |
1,00 |
30 |
| 5 |
34 |
0,01724138 |
0,59 |
0,00029727 |
1156,00 |
30,96 |
3,04 |
9,26 |
8,95 |
58 |
3,00 |
9,00 |
34 |
| 6 |
31 |
0,01818182 |
0,56 |
0,00033058 |
961,00 |
32,62 |
-1,62 |
2,64 |
5,24 |
55 |
0,00 |
0,00 |
31 |
| 7 |
25 |
0,01785714 |
0,45 |
0,00031888 |
625,00 |
32,05 |
-7,05 |
49,69 |
28,20 |
56 |
-6,00 |
36,00 |
25 |
| 8 |
34 |
0,01818182 |
0,62 |
0,00033058 |
1156,00 |
32,62 |
1,38 |
1,89 |
4,04 |
55 |
3,00 |
9,00 |
34 |
| 9 |
36 |
0,01886792 |
0,68 |
0,00035600 |
1296,00 |
33,84 |
2,16 |
4,66 |
6,00 |
53 |
5,00 |
25,00 |
36 |
| 10 |
37 |
0,01851852 |
0,69 |
0,00034294 |
1369,00 |
33,22 |
3,78 |
14,27 |
10,21 |
54 |
6,00 |
36,00 |
37 |
| Итого |
310,00 |
0,17265392 |
5,38 |
0,00299498 |
9784,00 |
310,00 |
0,00 |
129,84 |
101,85 |
582,00 |
174,00 |
310,00 |
| Ср.знач |
31,00 |
0,01726539 |
0,54 |
0,00029950 |
978,40 |
12,98 |
10,18 |
58,20 |
31,00 |
| Дисперс |
17,4000 |
0,00000140 |
17,4000 |
| Ср.кв.отк |
4,17 |
0,00118519 |
4,17 |
| b=(СРЗНАЧ(zy)-СРЗНАЧ(y)*СРЗНАЧ(z))/Dz |
1773,12 |
| a=СРЗНАЧ(y)-b*СРЗНАЧ(z) |
0,39 |
| n |
10,00 |
| rxy=КОРЕНЬ(1-(Σ(y-ŷ)^2/Σ(y-yср)^2) |
0,50 |
| Rxy=rxy^2 |
0,25 |
| Fфакт=(Rxy/(1-Rxy))*(n-2) |
2,72 |
| Fтабл |
4,46 |
| Σ(y-yср)^2 |
174,00 |
У = 0,39 + (1773,12)* 1/х
График регрессии равносторонней гиперболы

На следующем графике приведены зависимости ŷ(х), у(х).

Выводы
:
| a
|
b
|
уравнение
|
| Линейная модель
|
17,30 |
0,34 |
У=17,30-0,34х |
| Степенная модель
|
6,33 |
0,43 |
У=6,33* |
| Показательная модель
|
19,69 |
1,01 |
У=1969*1,01 |
| Модель равносоронней гиперболы
|
0,39 |
1773,12 |
У=0,39+1773,12* |
|




