|
Задача №1
Дано:
На предприятии выпускающем неоднородную продукцию четырех видов, при производстве изделий используются ресурсы: трудовые, материальные, мощности. Затраты ресурсов на обработку каждого изделия указаны в таблице №1. В ней же указаны потенциальные возможности предприятия по каждому из видов ресурсов, а также доход от реализации единицы изделия каждого вида.
| Затраты ресурсов и производственные
|
показатели
|
| Вид ресурсов
|
Затраты ресурсов на производство 1 изделия
|
Производственные возможности предприятия по каждому
|
| |
Вид 1
|
Вид 2
|
ВидЗ
|
Вид 4
|
виду ресурсов
|
| Трудовые (чел/нед) Материальные (кг) Мощности (час)
|
1
7
3
|
1
5
5
|
1
3
10
|
1
2
15
|
15
120
100
|
| Доход от продажи единицы продукции
|
4
|
5
|
9
|
11
|
Максимизировать
|
| Прибыль от продажи единицы продукции
|
2
|
10
|
6
|
20
|
Максимизировать
|
| Объем выпускаемой продукции
|
x1
|
x2
|
x3
|
x4
|
Определить
|
Требуется составить:
производственный план предприятия, который включает показатели по номенклатуре (по видам изделий) и по объему, т.е. сколько изделий соответствующего вида изделия следует изготовить предприятию, чтобы доход и прибыль при их реализации были максимальными. Составить математическую модель задачи и решить ее.
Решение
:
В качестве неизвестного примем x1
- количество единиц изделий первого вида, изготовленного на предприятии, аналогично x2
, x3
, x4
- количество единиц второго, третьего и четвертого вида. Тогда для производства такого количества изделий потребуется затратить 1х1
+1х2
+1х3
+1х4
- человеко/недель трудовых ресурсов. Так как общий фонд рабочего времени не может превышать 15 человеко/недель, то должно выполняться неравенство:
1x1
+lx2
+lx3
+lx4
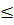 15 15
Аналогичные рассуждения относительно возможного использования материальных
ресурсов и мощностей приведут к следующим неравенствам:
7х1
+5х2
+Зх3
+2х4
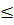 120 120
3х1
+5x2
+10х3
+15х4
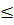 100 100
1х1
+1х2
+1х3
+1х4
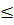 15 15
7х1
+5x2
+3x3
+2x4
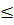 120 120
3х1
+5х2
+10х3
+15х4
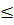 100 100
При этом, так как количество изготовляемых изделий не может быть отрицательным, то
x1
 0, х2 0, х2
 0, х3 0, х3
 0, х4 0, х4
 0. 0.
Если будет изготовлено x
1
…
...
x
4
единиц изделий соответствующего вида, то доход от их реализации может быть представлен в виде следующей функции
Fl(x)=4x1
+5x2
+9x3
+11x4
 max max
x={x1
,x2
,x3
,x4
}
x={xj, j=1-4}
Цель производителя получить доход от продажи изделий, как можно выше. Эта
целенаправленность может быть выражена в виде задачи линейного программирования:
F1(х)=mах(4х1
+5х2
+9х3
+11x4
),
При ограничениях
1x1
+lx2
+lx3
+lx4
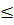 15, 15,
7х1
+5х2
+Зх3
+2х4
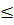 120, 120,
3х1
+5x2
+10х3
+15х4
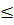 100, 100,
x1
 0, х2 0, х2
 0, х3 0, х3
 0, х4 0, х4
 0. 0.
Аналогично можно сформулировать задачу для определения максимальной прибыли:
F2(x)=max(2x1
+10x2
+6x3
+20x4
),
При ограничениях
1x1
+lx2
+lx3
+lx4
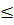 15, 15,
7х1
+5х2
+Зх3
+2х4
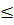 120, 120,
3х1
+5x2
+10х3
+15х4
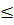 100, 100,
x1
 0, х2 0, х2
 0, х3 0, х3
 0, х4 0, х4
 0. 0.
Как правило, руководитель фирмы принимает решение с учетом обоих критериев дохода и прибыли, то есть Fl(x) и F2(x):
Opt F(x)={maxF1(x)=( 4х1
+5х2
+9х3
+11x4
),
maxF2(x)=( 2x1
+10x2
+6x3
+20x4
)},
при ограничениях:
1x1
+lx2
+lx3
+lx4
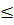 15, 15,
7х1
+5х2
+Зх3
+2х4
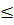 120, 120,
3х1
+5x2
+10х3
+15х4
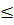 100, 100,
x1
 0, х2 0, х2
 0, х3 0, х3
 0, х4 0, х4
 0. 0.
В этой задаче формулируется следующее: требуется найти неотрицательное решение x
1
…
...
x
4
, в системе неравенств (А) такое, при котором функции F1, F2 принимают максимальные значения.
Линейная функция F, максимум которой требуется определить, вместе с системой неравенств (А) и условием не отрицательности переменных образует математическую модель исходной задачи.
Так как функции F1, F2 линейные, а система (А) содержит только линейные неравенства, то получившаяся задача является задачей линейного программирования. Для ее решения используем метод, основанный на нормализации критериев и принципе гарантированности результатов.
Решение задачи линейного программирования в системе
MATLAB
cvec=[-4. -5. -9. -11.;
-2. -10. -6. -20.]
a=[1. 1. 1. 1.;
7. 5. 3. 2.;
3. 5. 10. 15.]
b=[15. 120. 100.]
Aeq=[]; beq=[];
x0=[0. 0. 0. 0.];
[x1, f1]=linprog(cvec(1,:),a, b, Aeq, beq, x0)
[x2, f2]=linprog(cvec(2,:),a, b, Aeq, beq, x0)
Fx=[cvec(1,:)*x1 cvec(2,:)*x1;
cvec(1,:)*x2 cvec(2,:)*x2]
Lx=[Fx(1,1)/f1, Fx(1,2)/f2
Fx(2,1)/f1 Fx(2,2)/f2]
krl=[-1. 0. 0. 0. 0]
f1=-f1; f2=-f2;
a0=[1. -4/f1 -5/f1 -9/f1 -11/f1;
1. -2/f2 -10/f2 -6/f2 -20/f2;
0. 1. 1. 1. 1.;
0. 7. 5. 3. 2.;
0. 3. 5. 10. 15.]
b0=[0. 0. 15. 120. 100.]
Aeq=[]; beq=[]
x0=[0. 0. 0. 0. 0.]
[x0,l0]=linprog(krl,a0,b0,Aeq,beq,x0)
cvec0=[0. -4. -5. -9. -11.;
0. -2. -10. -6. -20.]
Fx0=[cvec0(1,:)*x0 cvec0(2,:)*x0]
Lx0=[Fx0(1)/f1 Fx0(2)/f2]
Результаты решения в системе
MATLAB
:
cvec =
-4 -5 -9 -11
-2 -10 -6 -20
a =
1 1 1 1
7 5 3 2
3 5 10 15
b =
15 120 100
Optimization terminated successfully.
x1 =
7.1429
0.0000
7.8571
0.0000
f1 =
-99.2857
Optimization terminated successfully.
x2 =
0.0000
12.5000
0.0000
2.5000
f2 =
-175.0000
Fx =
-99.2857 -61.4286
-90.0000 -175.0000
Lx =
1.0000 0.3510
0.9065 1.0000
krl =
-1 0 0 0 0
a0 =
1.0000 -0.0403 -0.0504 -0.0906 -0.1108
1.0000 -0.0114 -0.0571 -0.0343 -0.1143
0 1.0000 1.0000 1.0000 1.0000
0 7.0000 5.0000 3.0000 2.0000
0 3.0000 5.0000 10.0000 15.0000
b0 =
0 0 15 120 100
beq =
[]
x0 =
0 0 0 0 0
Optimization terminated successfully.
x0 =
0.9218
0.0000
11.7396
1.5207
1.7396
l0 =
-0.9218
cvec0 =
0 -4 -5 -9 -11
0 -2 -10 -6 -20
Fx0 =
-91.5207 -161.3135
Lx0 =
-0.9218 -0.9218
|