. .

(dimstein@list.ru)

, .

, 2007 .

.

- ,

- . -

! !

! ! . "

! ! ,

# $$#

!. %

& ,

! , ! & .

1.

!

" # # . $ # -

, – # .

% , # # & & –

’ . ( ( # &# & & ) # . )

# , ’ # .

& # #

, ’ # &. * ’

’ # # ,

- ,

. *

& #&# # # & & –

& & – # !" # "

(# ) . +# # #

& #, #

’ # # # .

( #

(’ # - , # ). ( & # & #

# & & – ’ . ,# , & , ’ # #. ) # , #

’ ,

# #.

* # #

( ! ( ’ # ), #

’ . $ ’

# & #

.

2.

# &#

( ! , & ’ . )

– - -%

"& - [14]. * ’

&# # # & & & & , # &:

# #, # # ( , #).

, - -%

, 24 .

# , - -% . ( #" ,

# ’ . * . # # ,

# .

. 0 - ,

’ , , & , # # #

(Ωα⋅µν=Ωα⋅[µν]):

(1) Ω^α _⋅ µν=∆^α _µ ν−∆^α _ν µ

# ∆^α _µ ν – . * ’ . .

∆^α _µ ν # :

(2)

# K – , # #

(K _α µν= K _[ αµ_] ν), Γ_µ ^α _ν – % ( , . 1-3).

$ # #

" $. # & ( ) ’ ( ’ # ) #:

(3) dds 2x 2µ µ dxds α dxds β= 0

+∆(αβ)

d 2x µ

(4) ds 2 +Γαµβ dxds α dxds β= 0

(3) #, (4) ’ .

. $ (3) (4) # #, #,

# :

(5) ∆µ(αβ) =Γαµβ

$ (2) ’ # !:

(6) ∆^µ _[ αβ] = K ^µ _⋅ αβ

, # #

#. , # (K _α µν= K _[ αµν_] ). . (1) (6) ’

!

(7)

* ’ .

3. !" " !"# !- " $ % ! && #

, & -

- -% , #, ( ),

’ #, ,

# .

1) . ( # -

# :

(8) ds ² = g _µν dx ^µ dx ^ν

g _µ ν # ∇_α g _µ ν= 0,

# ∇_α – # # x ^α ( ,

. 4-5).

2) . . 0 ,

, ",

# & . ,

A , # # (2)

#:

(9) ∆^α _µ ν=Γ_µ ^α _ν + iA ^α _⋅ µν

# A _α µν=−A _µ αν=−A _α νµ=−A _ν µα= A _[ αµν_] . . % #

:

(10)

$ # A

# #:

(11) A αµν=−εαµνσA σ

# A ^µ – # , ε_α βµν – 2 3 .

A ^µ # # :

(12) A µ=−εµαβγA αβγ

( # ’ , # # ’ a ^µ :

(13) a ^µ = q ˆA ^µ

# q ˆ – ’ #. . ! (13)

’ . % q ˆ #

# ! # , , &

( A ~ A ^µ ~ 1/q ˆ ).

1 " (9) # :

(14) Ω^α _⋅ µν= 2∆^α _[ µν_] = 2iA ^α _⋅ µν

$ # "

. * # ,

#

∆^α _µ ν #

# , # Γ_µ ^α _ν ( , . 6).

1 - &# " - R :

1 F _µ ν , #

F _µν :

(25) F _µ ν= ¹ ε_µ ναβF ^αβ

2

* (24) (11), & &#, # - (25) :

(26) F _µν =∂_µ A _ν −∂_ν A _µ

, # " ’ .

. (13) (26) " ’ f _µ ν

# # #

- :

(27) f _µν =∂_µ a _ν −∂_ν a _µ = q ˆF _µν

. - (21)

# :

(28) R = g µνR (µν) = R ~ − 6 A αA α

# R ~ = R ^{~ µ} _⋅µ – .

1 , # ’ , # #

& ’ . * ’ ’

( ), "

’ – - .

A ^µ # -

F _µ ν & ’ a ^µ

" f _µ ν, & & ’ .

4. ’ $ !"( %’ #$"# #

4 , # -

, ,

:

(29) δ L_G − g в ⁴ x = 0

# L_G – # . 2 , - , # ,

(29). 2 L_G , ( ! ,

- .

* & ’- ( , . 9-10)

- :

(30.1) Rc

(30.2) Rc R ^µν R _αβ

(30.3) Rc

(30.4) Rc (4) ≡δα⋅β⋅γ⋅λ⋅µνστR µνR αβR στR γλ

* " & - #

#, , " & #

. & "& & - (30) # # . * Rc ⁽¹⁾ (30.1) # R . (28) (13)

:

(31) Rc (1) = R = R ~ −6A αA α= R ~ − q ˆ62 a αa α

$ Rc ⁽²⁾ (30.2) δ^α _⋅ ^β _⋅ µν &

# - ,

(32) Rc ⁽²⁾ f ^αβ f _α β q ˆ

# & # & & - Rc ⁽¹⁾ Rc ⁽²⁾ , " !

# .

3 L_G

. (§ 2). . ’ #

# L ² (R ) , # :

(33) L ^{2 =} (R − R ₀ )² = R ² − 2R ₀ R + R ₀ ²

# R ₀ – . 2 L_G L ²

&

- :

(34) L G = L 2 (R n →Rc (n ) )=Rc (2) −2R 0Rc (1) + R 02

$ (34) # # & " #

(33). * R ₀ , &# L_G ,

# ,

. . " (31) (32) #

#:

(35) L G =− R ₀ 1q ˆ2 f αβf αβ+ R ~ − q ˆ62 a αa α− R 20

. ’ ,

&#:

(36) q ˆ = ^{8 π}

κR ₀

(37) Λ= ^{R 0}

4

# Λ – (Λ ~ 10^{−56 −2} ), κ – ( ! . .

" ! (36) # L_G ! #:

(38) L_G =−(f ^αβ f _αβ + 6R ₀ a ^α a _α )+ R ^~ − ¹ R ₀

2

( # #

(39) δ −(f αβf αβ + 6R 0 a αa α)+ R ~ − 1 R 0 − g в 4 x = 0

2

~ = g

# R

(40)

(41)

#

(42)

(43)

G _µ ν –

.

’

1

’

’

# ^µν R ^~ µν. $ g ^µν , Γ_µ ^α _ν a ^α ( ) ( (10)):

G µ

∇~σf µσ+3R 0a µ= 0

# :

≡ R ~_µ ν − 1 g _µ ν^R ~

G _µ ν

2

T ˆµν ≡ 41π f a µa a αa α

( ! , T ^ˆ _µ ν – " ’ - ’ . (40) (41), & , # #

’ # .

#

’ # (41)

- ’ (43), (40) # ( ! , #

. ’ (41) - ,

& .

(44) _µ a ^µ

1 ^{T ˆ} _µ ν # # ’ #

&, ’ - :

(45) ∇_µ T ˆ^µν = ∇^~ _µ T ˆ^µν = 0

$ & (45) (40) #

" # 5 , & .

#

R ₀ . . (40) :

(46) − R ~ + R 0 = − 3κ4πR 0 a αa α = −6A αA α

, # " (28) &#,

(47) R ₀ = R ^~ −6A ^α A _α = R

1 , R ₀ . *

(40) ! (47) !.

(40) (41) # ,

, & ( ),

& #. 3 ,

, . $ :

(48) G _µ

(49) ∇^~ _σ f ^µσ +3R ₀ a ^µ =ξj ^µ

# T _µ ν = T ^ˆ _µ ν +T ^~ µν, T ^~ µν – ’ - , T _µ ν – ’ - , j ^µ – , ξ – (ξ= 4π/ ).

& & #

, & # :

(50) ∇_µ π^µ = ∇^~ _µ π^µ = 0

(51) ∇_µ j ^µ = ∇^~ _µ j ^µ = 0

# π^µ = µu ^µ ( ), j ^µ = ρu ^µ ( #), µ –

, ρ – # , u ^µ –

# (dx ^µ d ^τ ). $ µ ρ # ,

" . $ & µ, ρ u ^µ , # .

- #

. * # (49) #

& # (51) 2 #

’ :

(52) ∇_µ a ^µ = ∇^~ _µ a ^µ = 0

(

. ( ’ (49), # a ^µ #.

* # # (48)

& # ’ - :

(53) ∇_µ T ^µν = ∇^~ _µ T ^µν = 0

. ’ ’ -

:

(54) ∇~µT ~µν = −∇~µT ˆµν

. " (44) (49) (52) T ^{~ µν} (54)

! #:

(55) j ^µ

(55) #

& .

1 # , #

# . 1 ’ - # ! #,

~ = µu _µ u _ν =π_µ u _ν ,

# & # & , T _µ ν

# µ – #, u _µ – #

# #. # (55) # ’ #

" & (50) #:

(56) j ^µ

+ # # # , # #

# ’- . $ ’ π^µ =µu ^µ = m δ(x − x ₀ )u ^µ j ^µ =ρu ^µ = q δ(x − x ₀ )u ^µ , # m q – # . $

(56) " , u ^β ∇^~ _β u ^ν = du ^ν d τ+ Γ_α ^ν _β u ^α u ^β , :

du ^ν

(57) +Γ_α ν_β u αu β₌ q f u β

d τ mc

# # .

(58) # !, & # & . $

# & # & ’ ! # #:

(59) a ^µ = a ₀ ^µ sin(kx −ωt )

# x – # # # & . *

’ ω k !:

(60) ω² = ² (k ² +3R ₀ )

# c – # # &

#. . ! (60) ’ & ! # #,

, # ’ ’ ,

# # :

(61) 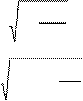v =^ω k = c 1+ ³ k ^R ₂ ⁰ > c

(62) v = ^d dk ^ω = c 1− 3R ₀ ω^{c 2} ₂ < c

1 , ’ # , & (58), ’ # # ! # c (62). % # (61) (62)

( # ). &

# c . , c

# & , ’ ! # .

$ - ! (58)

#. . (58) ’

’ & # & # :

(64) ϕ = ^q e ^−αr

r

# ϕ= a ⁰ (’ ), q – ’ #, α= 3R ₀ = m _γ c / , r – # # #. - α

(64) « » ’ .

. , &

’ (58) , ,

! ’ & , m _γ :

3R ⁰

(63) m _γ =

c

* ’ # # (62). .

(63)

. (63) ’ .

* ! (37) , &

’ :

(64) 3R ₀ ~10^{−55 −2}

(65) m _γ ~ 10⁻⁶⁵

* # # #

’ . . ’

# # # # :

(66) m _γ < 3⋅10⁻⁶⁰

1 (65) # ’ . ( ,

# ’ , # " # # ’ , # ’ .

7. ,#%-(

. &

’ , ’ ’ & # . *

#&#,

# ’ . $ - -% ( ). * ’ -

.

. # #

, ’ – ( ),

# & -

. / # ’ # & & ’

. ( #

, " ’ –

# - . * ’ #

# &

’ .

$ & & & (

) # & & # # &

# #, # #.

, # ’

, #"

. 3 ’ &

# , ( ’ - ). ) &

’ # , "

’ # ’ - ’ . $ & &

. * , # " & &

’ , # !

2 . $ &, # , , ( ! ( ).

. ’ , " ’ ,

. * ’

, . * # &#

’ .

$ , #

, # & &

& ! .

_____________________

"

1. 0 - -% :

∆αµν = Γµαν + K α⋅µν

K αµν = −K µαν

2. ." % :

^σ =∂^{µ g} , # g = det g _µ ν

Γµσ

2g

3. $ # :

Ωαµν = ∆αµν − ∆ανµ = K αµν − K ανµ

K αµν = 1 (Ωαµν − Ωµαν − Ωναµ)

2

4. :

δu µ = −∆µαβu αdx β, δu µ = ∆αµβu αdx β

5. % # :

∇µu ν = ∂µu ν + ∆νσµu σ, ∇~µu ν = ∂µu ν + Γσνµu σ

∇µu ν = ∂µu ν − ∆σνµu σ, ∇~µu ν = ∂µu ν − Γνσµu σ

6. % # # ∆^α _µ ν = Γ_µ ^α _ν + iA ^α _⋅ µν:

A α⋅µα = A α⋅(µν) = 0, ∆αµα = Γµαα , ∆α(µν) = Γµαν

∇µu µ = ∂µu µ+ ∆µσµu σ = ∂µu µ+ Γσµµu σ

∇_µ T (µν⁾ = ∂_µ T (µν⁾ +∆µ_σµ T (σν⁾ + ∆ν_{( σµ )} T (µσ⁾ = ∂_µ T µν + Γ_σ µ_µ T (σν⁾ + Γ_σ ν_µ T (µσ⁾

7. 1 - :

(∇µ∇ν −∇ν∇µ)u λ = R λ⋅σµνu σ + Ωσ⋅µν∇σu λ

R α⋅βµν = ∂µ∆αβν − ∂ν∆αβµ+ ∆ατµ∆τβν − ∆ατν∆τβµ

Ω^α _⋅ µν = ∆^α _µ ν − ∆^α _ν µ

8. - - :

R

+∇~ α −∇~νK α⋅βµ+ K α⋅τµK τ⋅βν− K α⋅τνK τ⋅βµ

µK ⋅βν

9. 1 2 3 :

ε_αβγλ = _g [αβγλ], ε^αβγλ =− ¹ [αβγλ]

+1, αβγλ - " 0123

[αβγ^λ ]= −1, αβγλ - " 0123

0, αβγλ #

10. * ’- :

δα⋅β⋅γ⋅ λ⋅µνστ ≡ −εαβγλεµνστ δα⋅β⋅γ⋅µνσ ≡ −εαβγτεµνστ

!"#!&"#

1. Einstein A., The Meaning of Relativity, Princeton Univ. Press, Princeton, N.Y, 1950

(* #: (!& ! )., . , 2, ., 1955).

2. ). (!& ! , . & #, 1. 1-2, #- «) », ., 1966.

3. E. Schrodinger, Space-Time Structure, Cambridge University Press, 1960 (* #:

(. 6#, * - , , )7 ,

2000).

4. * *. "., * & +. ,., 1 , #- «) », ., 1973.

5. C. W. Misner, K. S. Thorne, and J. A. Wheeler, Gravitation, Freeman, San Francisco,

1973 (* #: -. , , . . , " . / , / , #- « », .,

1977).

6. 0. ). " $ , . 1. % , ). .. 2 , . : #

, #- «) », ., 1986.

7. E. Cartan, Lecons sur la Geometrie des Espaces de Riemann, Gauthier-Villars, Paris, 1928 and 1946 (* #: % (., -

, #- /, ., 1960).

8. +. Cartan, On Manifolds with an Affine Connection and the Theory of General Relativity, translated by A. Magnon and A. Ashtekar (Bibliopolis, Naples, 1986).

9. %. %. 1 , ) # -

, #- «+# -..», 2002 .

10. 3. . - $ , 0 & # , 7),

1 119. . 3, 1976.

11. Alberto Saa, Einstein-Cartan theory of gravity revisited, gr-qc/9309027 (1993).

12. Hong-jun Xie and Takeshi Shirafuji, Dynamical torsion and torsion potential, gr-qc/9603006 (1996).

13. V.C. de Andrade and J.G. Pereira, Torsion and the Electromagnetic Field, gr-qc/9708051 (1999).

14. Yuyiu Lam , Totally Asymmetric Torsion on Riemann-Cartan Manifold, gr-qc/0211009 (2002).