Российский Государственный Аграрный Университет-
МСХА им. К.А.Тимирязева
Калужский филиал
Кафедра экономики и статистики
Курсовая работа
По дисциплине: «Статистика»
На тему: Статистико-экономический анализ эффективности производства молока по совокупности районов Калужской области (на примере Думиничского района)
Калуга, 2008
Оглавление
Введение
Глава 1. Использование метода группировок в исследовании эффективности производства молока
1.1 Построение ранжированного и интервального рядов распределения по одному факторному признаку
1.2 Анализ типических групп по показателям
Глава 2. Статистико-экономический анализ основных показателей выборочной совокупности
2.1 Комбинированная группировка по двум факторным признакам
2.2 Индексный анализ
2.3 Корреляционно – регрессионный анализ зависимости результативного показателя от факторных показателей
Глава 3. Статистический анализ динамических рядов (на примере Думиничского района)
3.1 Анализ рядов динамики
3.2 Выравнивание рядов динамики
3.3 Корреляционно-регрессионный анализ
3.4 Индексный анализ
Выводы
Список использованной литературы
Фишки
Ключ к фишкам
Приложение
ВВЕДЕНИЕ
Тема курсовой работы актуальна, потому что в настоящее время необходимо проводить анализы эффективности производства молока и другой сельскохозяйственной продукции, тем самым выявлять тенденции развития.
Целью курсовой работы является проведение статистико-экономического анализа эффективности производства молока по районам.
Предметом исследования данной курсовой работы является производство молока, а объектами исследования являются районы Калужской области.
Задачами являются:
- Построение ранжированного и интервального ряда распределения по одному признаку;
- Анализ типических группы;
- Проведение индексный анализ;
- Создание факторной группировки по двум признакам;
- Проведение корреляционно-регрессионный анализ;
- Оценка параметры полученного корреляционного уравнения;
- Проведение аналитических методов выравнивания рядов динамики;
В курсовой работе применяются такие методы как дедуктивный индуктивный, диалектический (развитие), статистический, анализа и синтеза, а также абстрактный, расчетно-конструктивные методы, эмпирический, монографический, метод индексов, метод группировок, средних величин, корреляционно-регрессионный анализ, дисперсионный анализ и ряды динамики.
В качестве источников литературы были использованы:
-учебники;
- учебные пособия;
- научная и методическая литература.
ГЛАВА 1. ИСПОЛЬЗОВАНИЕ МЕТОДА ГРУППИРОВОК В ИССЛЕДОВАНИИ ЭФФЕКТИВНОСТИ ПРОИЗВОДСТВА МОЛОКА
1.1 Построение ранжированного и интервального рядов распределения по одному факторному признаку
Имеются данные статистического наблюдения средней цене реализации молока, рублей за центнер по районам Калужской области в 2006 году. Нужно выделить, используя метод статистических группировок, типические группы районов с различным соотношением этих показателей и установить основные причины этих различий.
Составим ранжированный ряд по этому признаку (табл.1.1).
Таблица 1.1 - Ранжированный ряд распределения цены реализации молока, руб./ц
| № |
Районы |
Показатель |
№ |
Районы |
Показатель |
| 1 |
Барятинский |
531 |
13 |
Износковский |
650 |
| 2 |
Ульяновский |
538 |
14 |
Дзержинский |
654 |
| 3 |
Мосальский |
546 |
15 |
Сухинический |
682 |
| 4 |
Бабынинский |
555 |
16 |
Тарусский |
691 |
| 5 |
Спас-Деминский |
557 |
17 |
Боровский |
703 |
| 6 |
Мещовский |
586 |
18 |
Думиничский |
717 |
| 7 |
Жиздринский |
596 |
19 |
Малоярославский |
771 |
| 8 |
Хвастовический |
607 |
20 |
Ферзиковский |
776 |
| 9 |
Юхновский |
614 |
21 |
Перемышельский |
777 |
| 10 |
Козельский |
634 |
22 |
Жуковский |
800 |
| 11 |
Людиновский |
645 |
23 |
Медынский |
804 |
| 12 |
Куйбышевский |
647 |
Для большей наглядности изобразим ранжированный ряд графически, для этого построим график, в котором на оси абсцисс укажем районы в ранжированном ряду, а на оси ординат - величину группировочного признака (рис.1.1)
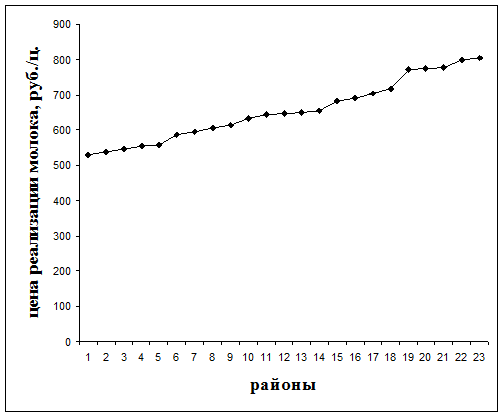
Рисунок 1.1 Огива Гальтона распределения цены реализации молока, руб./ц.
Проанализируем полученные данные. Как видно из графика, существуют явные различия между предприятиями по цене реализации молока, руб./ц., что, прежде всего можно объяснить тем, что направления производства данных предприятий часто различаются, соответственно, уровень производства и реализации также различен, также данный факт можно обосновать различием рынков сбыта продукции и удалённостью от центра. Размах колебаний составляет от первого до последнего района 273 руб./ц. Возрастание этого соотношения от района к району, происходит скачкообразно от 1 до 2 на 7 руб/ц., от 3 до 13 на 104 руб/ц., от 14 до 17 на 49 руб/ц., от 18 до 23 на 87 руб/ц.
Поскольку между районами различия небольшие, выделить их в типические группы на основании анализа ранжированного ряда в нашем случае невозможно. Поэтому далее необходимо построить интервальный ряд распределения районов с достаточно большим числом групп, оценить качественное состояние каждой группы путем построения промежуточно-аналитической группировки и перейти от нее к типическим группам.
Построим интервальный вариационный ряд распределения районов по цене реализации молока, руб./ц. Количество групп необходимое для построения группировки, вычислим по формуле Стержесса.
N=1+3,32*lgn (1.1)
где, N- Число групп;
n- Количество элементов в совокупности
N=1+3,32*lg 23= 1+3,32*1,36=5,512=5
Разделим всю совокупность районов на 6 групп, и найдем величину интервала по формуле:
H=(Xmax
-Xmin
)/n (1.2)
где, Xmax
=804-максимальное значение признака в изучаемом ранжированном ряду (район №23);
Xmin
=531 - минимальное значение (район №1).
Величина интервала составит:
H=(804-531)/5=54,6
Построим ряд распределения районов, при этой величине интервала, значение Xmin
=531, тогда верхняя граница первой группы составит:
531+54,6=585,6; 585,6+54,6=640,2-верхняя граница второй группы и т.п.
Распределим организации по установленным группам и подсчитаем их число в каждой группе (табл.1.2).
Таблица 1.2 - Ряд распределения предприятий при величине интервала 54,6
| № группы |
Группы по средней цене реализации молока, ц. |
Число предприятий |
| I |
До 585,6 |
5 |
| II |
585,6 – 640,2 |
5 |
| III |
640,2 – 694,8 |
6 |
| IV |
694,8 – 749,4 |
2 |
| V |
Выше 749, 4 |
5 |
Для наглядности изобразим интервальный ряд в виде гистограммы (рис.1.2).
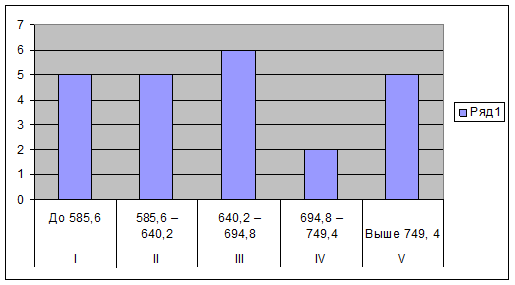
Рисунок 1.2 Интервальный ряд распределения
Как видно из таблицы 1.2 и рисунка 1.2, распределение предприятий по группам не равномерно. Преобладают хозяйства с ценой реализацией молока руб./ц., лежащие в интервале I,II,III и V. т.е. в интервалах до 585,6;от 585,5 до 694,8 и 749,4 и выше руб./ц. В группы с более низкой ценой реализации молока входит меньше хозяйств.
Теперь покажем, какие районы входят в каждую группу (табл.1.3).
Таблица 1.3 - Распределение районов Калужской области по группам цены реализации молока, руб./ц.
| № |
Районы |
группы |
№ |
Районы |
группы |
| 1 |
Барятинский |
I
|
13 |
Износковский |
III
|
| 2 |
Ульяновский |
14 |
Дзержинский |
| 3 |
Мосальский |
15 |
Сухиничский |
| 4 |
Бабынинский |
16 |
Тарусский |
| 5 |
Спас-Деменский |
17 |
Боровский |
IV
|
| 6 |
Мещовский |
II
|
18 |
Думиничский |
| 7 |
Жиздринский |
19 |
Малоярославецкий |
V
|
| 8 |
Хвастовичский |
20 |
Ферзиковский |
| 9 |
Юхновский |
21 |
Перемышльский |
| 10 |
Козельский |
22 |
Жуковский |
| 11 |
Людиновский |
III |
23 |
Медынский |
| 12 |
Куйбышевский |
1.2. Анализ типических групп
Аналитическая группировка проводится для изучения взаимосвязи между признаками, положенными в основание группировки, и признаками, используемыми для характеристики групп. Она позволяет оценить качественные особенности каждой группы интервального ряда, объединить однородные и малочисленные группы. Следует рассчитать средние абсолютные показатели: среднегодовое поголовье коров молочного стада, голов; валовый надой от коров молочного стада, ц.; количество работников в животноводстве, чел.; площадь с/х угодий, га.; количество реализованного молока, ц.; выручено всего от реализации молока, тыс.руб. Все данные запишем в табл.1.4.
Таблица 1.4 - Сводные данные по аналитическим группам
| № группы |
Группы по цене реализации молока, руб./ц. |
Число районов |
Среднегодовое поголовье коров молочного стада, голов |
Валовый надой от коров молочного стада, ц |
Количество работников, занятых в с/х производстве, чел. |
Площадь с/х угодий, га. |
Количество реализованного молока, ц |
Выручено всего от реализованного молока, тыс.руб. |
| I |
До 585,6 |
5 |
2016 |
41004 |
509 |
273300 |
30523 |
16705 |
| II |
585,6-640,2 |
5 |
7610 |
244859 |
1823 |
309400 |
211533 |
129786 |
| III |
640,2-694,8 |
6 |
6210 |
204590 |
2184 |
291800 |
173682 |
115513 |
| IV |
694,8-749,4 |
2 |
3362 |
145230 |
754 |
70400 |
70297 |
49446 |
| V |
Выше 749,4 |
5 |
13513 |
596758 |
3378 |
265600 |
531229 |
417844 |
| итого |
23 |
32711 |
1232441 |
8648 |
1210500 |
1017264 |
729294 |
Определим далее относительные показатели, которые необходимо рассчитать для выявления типических групп, результаты запишем в табл.1.5.( см. Приложение 1)
Проанализируем показатели, сопоставив их между собой и по группам, и решим вопрос об укрупнении групп. Судя по приведенным в таблице показателям видно, что I группа имеют низкие показатели, и поэтому мы можем обозначить ее как низшую типическую группу. II, III и IV группы имеют показатели выше предыдущих, но они ниже показателей V группы. Поэтому мы их объединим и назовем средней типической группой.V группа имеет высокие показатели, поэтому ее мы назовем высшей типической группой.
Таким образом, в данной совокупности на основании анализа промежуточной аналитической группировки следует выделить три типические группы: низшую, в которую входят 5 районов; среднюю – 13 районов; высшую – 5 районов.
Отразим эти данные в таблице 1.6.
Таблица 1.6 - Показатели интенсификации
| Название показателей |
Типические группы |
В среднем по совокупности |
| низшая |
средняя |
высшая |
| 1. количество районов |
5 |
13 |
5 |
| 2. валовый надой на 1 корову, ц. |
20,3 |
34,2 |
44,2 |
33,3 |
| 3. Валовый надой на 1 работника, занятого в с/х производстве, ц |
80,6 |
124,5 |
176,7 |
126,3 |
| 4. Валовый надой на площадь с/х угодий, ц |
0,2 |
1,0 |
2,2 |
1,1 |
| 5. Выручено на 100 га с/х угодий, тыс.руб. |
6,1 |
45,2 |
157,3 |
61,1 |
| 6. Выручено на 1 корову, тыс.руб. |
8,3 |
17,4 |
30,9 |
18,4 |
| 7.Выручено на 1 работника, занятого в с/х производстве, тыс.руб. |
32,8 |
61,9 |
123,7 |
69,0 |
| 8. Количество коров на 1 работника, занятого в с/х производстве, гол |
4,0 |
3,6 |
4,0 |
3,8 |
| 9. Количество коров на 100 га с/х угодий, гол |
0,7 |
2,7 |
5,1 |
2,8 |
| 10. Количество реализованного молока на 1 работника, занятого в с/х производстве, ц |
60,0 |
95,6 |
157,3 |
101,3 |
| 11. Количество реализованного молока на 1 корову, ц |
15,1 |
26,8 |
39,3 |
27,0 |
Проанализируем показатели таблицы 1.6. Оценим распределение районов по типическим группам. Сопоставим одноименные показатели между группами. Сравним крайние группы. Валовый надой на 1 корову, ц. в III группе больше, чем в I 44,2-20,3=23,9 ц, или в 2,2 раза; валовый надой на 1 работника, ц на 176,7-80,6=96,1 ц, или в 2,2 раза; валовый надой на площадь с/х угодий, ц. на 2,2-0,2=2 ц или в 11 раз; выручка на 100 га с/х угодий, тыс.руб. на 157,3-6,1=151,2 тыс.руб. или в 25,8 раз; выручка на 1 корову, тыс. руб. на 30,9 – 8,3=22,6 тыс.руб. или в 3,7 раза.; выручка на 1 работника, тыс.руб. на 123,7- 32,8=90,9 или в 3,8 раза; количество коров на 1 работника, гол на 4,0-4,0=0 гол. или в 1 раз (т.е. не изменилось); количество коров на 100 га с/х угодий, гол. на 5,1-0,7=4,4 гол. или в 7,3 раза; количество реализованного молока на 1 работника, ц на 157,3-60,0=97,3 ц. или в 1,7 раза; количество реализованного молока на 1 корову, ц. на 39,3-15,1=24,2 ц. или в 2,6 раза.
Теперь сравним II и I типические группы.
Валовый надой на 1 корову, ц. во II группе больше, чем в I на 34,2-20,3=13,9 ц, или в 1,7 раза; валовый надой на 1 работника животноводства, ц на 124,5-80,6=43,9 ц, или в 1,5 раза; валовый надой на площадь с/х угодий, ц. на 1,0-0,2=0,8 ц или в 5 раз; выручка на 100 га с/х угодий, тыс.руб. на 45,2-6,1= 39,1 тыс.руб. или в 7,4 раза; выручка на 1 корову, тыс. руб. на 17,4-8,3=9,1 тыс.руб. или в 2,1 раза.; выручка на 1 работника животноводства, тыс.руб. на 61,9-32,8=29,1 тыс.руб. или в 1,9 раза; количество коров на 1 работника животноводства, гол на 3,6-4,0=-0,4 гол. или в 0,9 раз (т.е. уменьшилась); количество коров на 100 га с/х угодий, гол. на 2,7-0,7=2 гол. или в 3,9 раза; количество реализованного молока на 1 работника, ц на 95,6-60,0=35,6 ц. или в 1,6 раза; количество реализованного молока на 1 корову, ц. на 26,8-15,1=11,7 ц. или в 1,8 раза.
Глава 2. СТАТИСТИКО-ЭКОНОМИЧЕСКИЙ АНАЛИЗ ПРОИЗВОДСТВА МОЛОКА ПО СОВОКУПНОСТИ РАЙОНОВ КАЛУЖСКОЙ ОБласти
2.1 Комбинационная группировка
Если в основу группировки положено несколько признаков, то такую группировку называют сложной. При использовании комбинационной группировки группы, выделенные по одному из признаков, затем подразделяются на подгруппы по другому признаку, в свою очередь подгруппы могут быть разделены по следующему признаку и т.д. Общее число выделенных групп будет равно произведению числа группировочных признаков на число выделенных групп в каждой из них.
Требуется определить влияние цены реализации молока, руб./ц. на выручку на 100 га площади с/х угодий, руб. Выделим типические группы по намеченным признакам. Для этого построим и проанализируем ранжированный и интервальный ряд по первому группировочному признаку, определим величину интервала и число групп в нем. Затем внутри каждой группы по цене реализации молока, руб./ц. – построим ранжированный и интервальный ряды и по второму признаку –выручено на 10 га с/х угодий, руб , а также установим число групп и интервал.
Выделим две типические группы по цене реализации молока, руб./ц.
H=(Xmax
- Xmin
)/n;
H=(804-531)/2=136,5
В результате получим интервальный ряд:
I –до 667,5
II-более 667,5
Таблица 2.1 – Ранжированный ряд по цене реализации молока, руб./ц.
| № |
Районы |
Цена реализации молока,руб./ц. |
№ |
Районы |
Цена реализации молока,руб./ц. |
| 1 |
Барятинский |
531 |
13 |
Износковский |
650 |
| 2 |
Ульяновский |
538 |
14 |
Дзержинский |
654 |
| 3 |
Мосальский |
546 |
15 |
Сухиничский |
682 |
| 4 |
Бабынинский |
555 |
16 |
Тарусский |
691 |
| 5 |
Спас-Деменский |
557 |
17 |
Боровский |
703 |
| 6 |
Мещовский |
586 |
18 |
Думиничский |
717 |
| 7 |
Жиздринский |
596 |
19 |
Малоярославецкий |
771 |
| 8 |
Хвастовичский |
607 |
20 |
Ферзиковский |
776 |
| 9 |
Юхновский |
614 |
21 |
Перемышльский |
777 |
| 10 |
Козельский |
634 |
22 |
Жуковский |
800 |
| 11 |
Людиновский |
645 |
23 |
Медынский |
804 |
| 12 |
Куйбышевский |
647 |
Следующим этапом будет построение ранжированного ряда по второму показателю – выручено на 100 га с/х угодий, руб.
Таблица 2.2 – Ранжированный ряд по выручки на 100 га с/х угодий, руб.
| № |
Районы |
Выручено на 100 га с/х угодий, руб. |
№ |
Районы |
Выручено на 100 га с/х угодий, руб. |
| 1 |
Хвастовический |
0,63 |
13 |
Малоярославский |
43,30 |
| 2 |
Ферзиковский |
2,40 |
14 |
Бабынинский |
48,91 |
| 3 |
Боровский |
5,17 |
15 |
Думинический |
50,63 |
| 4 |
Спас-Деминский |
5,62 |
16 |
Юхновский |
60,73 |
| 5 |
Ульяновский |
5,93 |
17 |
Жуковский |
72,90 |
| 6 |
Барятинский |
8,39 |
18 |
Износковский |
96,26 |
| 7 |
Сухинический |
8,91 |
19 |
Куйбышевский |
102,71 |
| 8 |
Мещовский |
16,20 |
20 |
Тарусский |
128,55 |
| 9 |
Дзержинский |
20,98 |
21 |
Мосальский |
150,49 |
| 10 |
Медынский |
36,76 |
22 |
Перемышельский |
151,28 |
| 11 |
Людиновский |
39,47 |
23 |
Жиздринский |
359,17 |
| 12 |
Козельский |
42,06 |
Выделим в этом ранжированном ряду три типические группы. Величина интервала составит: H=(359,17-0,63)/3=119,51
Получаем второй интервальный ряд:
I-до 120,14
II- 120,14-239,65
III-более 239,65
Каждая группа по второму показателю будет подразделяться на две группы по первому признаку.
Составим макет комбинационной таблицы, в которой предусмотрим подразделение совокупности на группы и подгруппы, а также графы для записи числа районов, валового надоя от коров молочного стада, ц. и количества коров молочного стада, гол.
Таблица 2.3 – Влияние цены реализации молока, руб./ц. выручки на 100 га с/х угодий, тыс.руб. на валовый надой на 1 корову молочного стада, ц.
№ группы
|
Группа по выручке на 100 га с/х угодий, тыс.руб
|
Подгруппа по цене реализации молока, руб/ц
|
Количество районов
|
Валовый надой от коров молочного стада, ц
|
Количество коров молочного стада, гол
|
Валовый надой на 1 корову молочного стада, ц
|
1
|
До 120,14
|
До 667,5 |
12 |
378934 |
12201 |
31,06 |
| Более 667,5 |
7 |
698636 |
16409 |
42,58 |
| 2 |
120,14-239,65 |
До 667,5 |
1 |
9974 |
428 |
23,30 |
| Более 667,5 |
2 |
130625 |
3121 |
41,85 |
| 3 |
Более 239,65 |
До 667,5 |
1 |
16242 |
552 |
29,42 |
| Более 667,5 |
- |
- |
- |
- |
Проанализируем полученные данные зависимости между выручкой на 100 га с/х угодий, тыс.руб. и ценой реализации молока, руб/ц.
Построим комбинационную таблицу следующей формы (табл.2.4.)
Таблица 2.4 - Зависимость затрат на 1 корову, тыс.руб. и себестоимости 1 ц. молока, руб.
| Подгруппа по цене реализации молока, руб/ц |
Группа по выручке на 100 га с/х угодий, тыс.руб |
до 120,14
I
|
120,14-239,65
II
|
более 239,65
III
|
В среднем |
| До 667,5 |
31,06 |
23,30 |
29,42 |
27,93 |
| Более 667,5 |
42,58 |
41,85 |
- |
28,14 |
| В среднем |
36,82 |
32,58 |
14,71 |
Комбинированная группировка позволяет оценить степень влияния на валовый надой на 1 корову молочного стада, ц. каждого фактора в отдельности и их взаимосвязи.
Сравним группыпо валовому надою на 1 корову, ц . Проанализируем валовый надой на 1 корову, ц. При цене реализации молока, ц. до 667,5 руб./ц. изменяется валовый надой на 1 корову, ц. изменялся по мере увеличения выручки на 100 га с/ угодий с 31,06 в I группе до 23,30 во II и 29,42 в III группе. При цене реализации молока, руб/ц, более 667,5 руб./ц. валовый надой на 1 корову уменьшается, в III группе нет, т.к. при выручке со 100 га с/х угодий более 239,65 руб/ц цена реализации в данной группе ниже 667,5,в I группе больше, чем в II на 42,85-41,85=1 ц.
2.2 Индексный анализ
С помощью индексного метода необходимо проанализировать изменение производство молока во II низшей группе по сравнению с I. По группам районов с разным производством молока имеются данные о поголовье коров и надое на 1 корову. Рассчитаем объем производства молока по каждой типической группе и данные занесем в таблицу 2.5
I = = 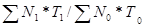  (2.1), (2.1),
Где N , N , N - поголовье коров в низшей и высшей группах соответственно; - поголовье коров в низшей и высшей группах соответственно;
T , T , T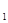 - надой на 1 корову в низшей и высшей группах; - надой на 1 корову в низшей и высшей группах;
N T T - производство молока в низшей группе; - производство молока в низшей группе;
N T T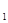 - производство молока в высшей группе. - производство молока в высшей группе.
Рассчитаем индекс поголовья коров и индекс надоя на 1 корову по следующим формулам:
I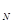 = =   (2.2.) (2.2.)
I = =   (2.3.) (2.3.)
Где N T T - условное производство молока при поголовье коров в высшей группе и надое молока на 1 корову в низшей группе, ц.; - условное производство молока при поголовье коров в высшей группе и надое молока на 1 корову в низшей группе, ц.;
N T T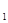 - условное производство молока при поголовье коров в низшей группе и надое молока на 1 корову в высшей группе, ц. - условное производство молока при поголовье коров в низшей группе и надое молока на 1 корову в высшей группе, ц.
I = 597274,6/ 40924,8= 14,6 = 597274,6/ 40924,8= 14,6
I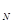 = 274313,9/40924,8=6,7 = 274313,9/40924,8=6,7
I =89107,2/40924,8= 2,2 =89107,2/40924,8= 2,2
Как видно, производство молока увеличилось в высшей группе по сравнению с низшей на 1360 % или на 597274,6-40924,8=556349,8 ц. Это следует из того, что условное поголовье увеличилось на 570% или на 274313,9-40924,8=233389,1 гол. и условный надой на 1 корову на 120 % или на 89107,2-40924,8= 48182,4 ц.
2.3
Корреляционно – регрессионный анализ зависимости результативного показателя от факторных показателей
Статистические распределения характеризуются наличием более или менее значительной вариации в величине признака у отдельных единиц совокупности.
Естественно, возникает вопрос о том, какие же причины формируют уровень признака в данной совокупности и каков конкретный вклад каждой из них. Изучение зависимости вариации признака от окружающих условий и составляет содержание теории корреляции.
Изучение действительности показывает, что вариация каждого изучаемого признака находится в тесной связи и взаимодействии с вариацией других признаков, характеризующих исследуемую совокупность единиц. В корреляционных связях между изменением факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных.
Корреляционно-регрессионный анализ проводится для определения степени связи между результатом и факторами, влияющими на результат.
Анализ влияния факторов на валовый надой на 1 корову, ц проводится по следующим данным: цена реализации молока, руб./ц– x1
, и выручка на 100 га с/х угодий, тыс. руб - x2
. Для начала необходимо определить характер связи между признаками и установить форму связи между ними.
Средние значения и изменение результативного и факторных признаков в совокупности в приложении № 2, приложении №3 .
В результате решений уравнения на ЭВМ были получены следующие его параметры:
Y=4,79+0,03 *X1
+0,08*X2
Интеграция полученных параметров следует:
A0
=4,79 условное начало содержательной интерпретации не подлежит;
A1
=0,03– коэффициент чистой регрессии при первом факторе свидетельствует о том, что при изменении цены реализации молока, руб./ц., валовый надой на 1 корову, ц. в среднем изменится на 0,03 ц. при условии, что другие факторы остаются постоянными;
A2
=0,08- коэффициент чистой регрессии при втором факторе показывает, что при изменении выручки на 100 га с/х угодий, руб. вызывает изменение валового надоя на 1 корову, ц. при условии, что другие факторы остается постоянными.
Коэффициенты парной корреляции 0,70 свидетельствуют, что между валовым надоем на 1 корову, ц. и средней ценой реализации, руб/ц. существует связь средней силы и прямая зависимость, а 0,79- показывает, что связь сильная и прямая зависимость с выручкой на 100 га с/х угодий, тыс.руб.
Для сравнения коэффициентов регрессии выразим их в виде β - коэффициентах и коэффициентов эластичности.
β – коэффициенты показывают, что если величина фактора изменяется на одно среднеквадратическое отклонение, результативный признак увеличится (уменьшится) на величину β – коэффициента своего квадратического отклонения, при постоянстве остальных факторов.
Коэффициенты эластичности показывают, что если величина факторного признака увеличится на 1%, результативный признак увеличится (уменьшится) соответственно на коэффициент эластичности, выраженный в % при постоянстве других факторов.
Рассчитаем среднее значение признака и определим среднеквадратическое отклонение.
ỹ=∑y/n (2.4)
где, ỹ- среднее значение результативного признака;
∑y- сумма результативного признака по всем районам;
n- число районов (23).
ỹ=31,47
1
=∑ X1
/n (2.5)
где, X1
- среднее значение первого факторного признака;
∑ X1
- сумма первого факторного признака по всем районам;
n- число районов (23).
X1
=655,70
X2
=∑ X2
/n, где
X2
- среднее значение второго факторного признака;
∑ X2
- сумма второго факторного признака по всем районам;
n- число районов (23).
X2
=63,37
бy
=(∑(yi
-y)2
/n)1/2
; бy
=2428,75 (2.5)
бх1
=(∑(xi
1
-x1
)2
/n)1/2
;бх1
=167776,87 (2.6)
бх2
=(∑(xi
2
-x1
)2
/n)1/2
;бх2
=139984,85 (2.7)
Теперь можно определить β - коэффициенты и коэффициенты эластичности.
β1
=0,03*бх1
/бy
;β1
=0,03*167776,87/2428,75=2,07 (2.8)
β2
=0,08*бх2
/бy
;β2
=0,08*139984,85/2428,75=4,61 (2.9)
Сопоставление β – коэффициентов показывает, что наиболее сильное влияние на варьирование результативного фактора оказывает выручка на 100 га с/х угодий, тыс.руб., менее сильное воздействии – цена реализации молока, руб./ц.
Э1
=а1
* X1
/ ỹ; Э1
=0,03*655,70/31,47=0,63% (2.10)
Э2
=а2
* X2
/ ỹ; Э2
=0,08*63,37/31,47=0,16 % (2.11)
Первый коэффициент эластичности показывает, что при изменении цены реализации молока, руб./ц. на 1% валовый надой на 1 корову, ц. изменится на 0,63%. Второй коэффициент эластичности показывает, что при изменении выручки на 100 га с/х угодий, тыс.руб. на 1% валовый надой на 1 корову, ц. изменится на 0,16%.
Таким образом, из анализа видно, что на валовый надой на 1 корову, ц влияет и цена реализации молока, руб/ц, и выручка на 100 га с/х угодий, тыс.руб. примерно одинаково.
Коэффициент множественной корреляции равен 0,81, он говорит о том, что связь сильная (приложение №3). Также был рассчитан коэффициент детерминации, который является квадратом коэффициент корреляции. Он показывает, насколько тесной является связь между выбранными показателями. В нашем случае он равен 0,65, т.е. связь между признаками средняя.
Проверка значимости коэффициента множественной корреляции показала, что F = 18,98, при значимости Fтабл.
=3,42 при пятипроцентном уровне. Таким образом, F = 18,98, при значимости Fтабл.
=3,42 при пятипроцентном уровне. Таким образом, F > Fтабл
, что позволяет с вероятностью 95 % утверждать существенность различий в величине дисперсий и соответственно сделать вывод об адекватности модели. > Fтабл
, что позволяет с вероятностью 95 % утверждать существенность различий в величине дисперсий и соответственно сделать вывод об адекватности модели.
В качестве критериев проверки гипотез относительно двух средних используется критерий t- Стьюдента. Фактическое значение t равно 0,35;
1,48;3,15, а табличное t=2,07, необходимо признать справедливость альтернативной гипотезы.
ГЛАВА 3. СТАТИСТИЧЕСКИЙ АНАЛИЗ ДИНАМИЧЕСКИХ РЯДОВ (НА ПРИМЕРЕ ДУМИНИЧСКОГО РАЙОНА)
3.1
Анализ рядов динамики
Важной задачей статистики является изучение явления во времени. Для решения этой задачи необходимо иметь данные по определенному кругу показателей на ряд моментов времени, следующих друг за другом.
Ряд расположенных в хронологической последовательности статистических показателей динамический ряд. Статистические показатели, характеризующие изучаемое явление называют уровнями ряда. Динамический ряд представляет собой последовательность уровней, сопоставляя которые между собой можно характеристику скорости и интенсивности развития явления. В результате сравнения уровней получается система относительных и абсолютных показателей динамики: абсолютный прирост, коэффициент роста, темп прироста, абсолютное значение одного процента прироста.
Выделяют базисные и цепные показатели динамики.
Показатели динамики с постоянной базой сравнения характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень, до данного (i- го) периода. Показатели динамики с переменной базой сравнения характеризуют интенсивность изменения уровня от периода к периоду в пределах изучаемого явления.
Проанализируем изменения состояния эффективности производства молока в Думиничском районе в динамике за последние 10 лет.
Возьмем показатели валового надоя на 1 корову, ц; количество коров на 1 работника, гол.; окупаемость затрат, руб.
Рассмотрим расчет показателей по ряду динамики валового надоя на 1 корову (табл.3.1)
Таблица 3.1 – Показатели динамики валового надоя на 1 корову, кг.
| Годы |
Значение |
Абсолютный прирост |
Темп роста, % |
Темп прироста, % |
Абсолютное значение 1% прироста |
| цепной |
базисный |
цепной |
базисный |
| цепной |
базисный |
| 1997 |
1536 |
- |
- |
- |
100 |
- |
- |
- |
| 1998 |
1488 |
-48 |
-48 |
97 |
97 |
-3,12 |
-3,12 |
15,38 |
| 1999 |
1651 |
163 |
115 |
111 |
107 |
10,95 |
7,49 |
14,89 |
| 2000 |
1850 |
199 |
314 |
112 |
120 |
12,05 |
20,44 |
16,51 |
| 2001 |
2016 |
166 |
480 |
109 |
131 |
8,97 |
31,25 |
18,51 |
| 2002 |
1758 |
-258 |
222 |
087 |
114 |
-12,8 |
14,45 |
20,16 |
| 2003 |
1832 |
74 |
296 |
104 |
119 |
4,21 |
19,27 |
17,58 |
| 2004 |
1786 |
-46 |
250 |
097 |
116 |
-2,51 |
16,28 |
18,33 |
| 2005 |
1677 |
-109 |
141 |
094 |
109 |
-6,1 |
9,18 |
17,87 |
| 2006 |
1784 |
107 |
248 |
106 |
116 |
6,38 |
16,15 |
16,77 |
Рассчитаем для данного динамического ряда средний уровень за период, который рассчитывается по формуле:
Ỹ=∑уi
/n (3.1)
где, Ỹ- средний уровень за период;
∑уi
-сумма значений;
n - число лет исследуемых в динамике.
Средний темп роста:
  =(Yn
/Y0
)1/10
(3.2) =(Yn
/Y0
)1/10
(3.2)
где, n - порядковый номер последнего уровня.
0 - первый порядковый номер.
Средний темп прироста:
  = =   *100- 100% (3.3) *100- 100% (3.3)
где   - средний темп роста. - средний темп роста.
Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах.
Подставим необходимые значение в формулы, получаем, что средний уровень за период равен 24,8, средний темп роста – 1,01, средний темп прироста - 1%.Темп прироста показывает, что валовый надой на 1 корову, кг. в среднем по району за 1997-2006 года увеличился в среднем за год на 1 %.
Максимальное значение было достигнуто в 2001 году, и оно составило 2016 кг. Минимальное значение наблюдалось в 1998 году и равнялось 1488 кг.
Теперь рассмотрим расчет показателей по ряду динамики количества коров на 1 работника, гол.(табл. 3.2)
Таблица 3.2 – Показатели динамики количества коров на 1 работника, гол.
| Годы |
Значение |
Абсолютный прирост |
Темп роста, % |
Темп прироста, % |
Абсолютное значение 1% прироста |
| цепной |
базисный |
цепной |
базисный |
| цепной |
базисный |
| 1997 |
3 |
- |
- |
- |
100 |
- |
- |
- |
| 1998 |
3 |
- |
- |
100 |
100 |
- |
- |
- |
| 1999 |
3 |
- |
- |
100 |
100 |
- |
- |
- |
| 2000 |
3 |
- |
- |
100 |
100 |
- |
- |
- |
| 2001 |
3 |
- |
- |
100 |
100 |
- |
- |
- |
| 2002 |
4 |
1 |
1 |
133,3 |
133,3 |
33,3 |
33,3 |
0,03 |
| 2003 |
5 |
1 |
2 |
125,0 |
33,3 |
25,0 |
-66,7 |
0,04 |
| 2004 |
6 |
1 |
3 |
120,0 |
200,0 |
20,0 |
100,0 |
0,05 |
| 2005 |
4 |
-2 |
1 |
66,7 |
133,3 |
-33,3 |
33,3 |
0,06 |
| 2006 |
6 |
2 |
3 |
150,0 |
200,0 |
50,0 |
50,0 |
0,04 |
Аналогично рассчитаем средний уровень за период, средний темп роста и средний темп прироста для количества коров на 1 работника, гол.
Подставив необходимые значение в формулы, получаем, что средний уровень за период равен 0,3, средний темп роста – 1,07, средний темп прироста - 7%.Темп прироста показывает, что количество коров на 1 работника, гол. в среднем по району за 1997-2006 года в среднем за год увеличилось на 7 %.
Максимальное значение было достигнуто в 2004 и 2006 годах, и оно составило 6 гол. Минимальное значение наблюдалось с 1997 по 2001 годы и равнялось 3 гол.
Аналогично рассмотрим расчет показателей по ряду динамики окупаемости затрат, руб.(табл. 3.3)
Таблица 3.3 – Показатели динамики окупаемости затрат, руб
| Годы |
Значение |
Абсолютный прирост |
Темп роста, % |
Темп прироста, % |
Абсолютное значение 1% прироста |
| цепной |
базисный |
цепной |
базисный |
| цепной |
базисный |
| 1997 |
2,84 |
- |
- |
- |
100 |
- |
- |
- |
| 1998 |
1,52 |
-1,32 |
-1,32 |
53,52 |
53,52 |
-46,48 |
-46,48 |
0,028 |
| 1999 |
3,34 |
1,82 |
0,50 |
219,74 |
117,61 |
119,74 |
17,61 |
0,015 |
| 2000 |
2,60 |
-0,74 |
-0,24 |
77,84 |
91,55 |
-22,16 |
-8,45 |
0,033 |
| 2001 |
4,58 |
1,98 |
1,98 |
176,15 |
161,27 |
76,15 |
61,27 |
0,026 |
| 2002 |
5,85 |
1,27 |
3,01 |
127,73 |
205,99 |
27,73 |
105,99 |
0,046 |
| 2003 |
5,59 |
-0,26 |
2,75 |
95,56 |
196,83 |
-4,44 |
96,83 |
0,059 |
| 2004 |
2,60 |
-2,99 |
-0,24 |
46,51 |
91,55 |
-53,49 |
-8,45 |
0,056 |
| 2005 |
2,78 |
0,18 |
-0,06 |
106,92 |
97,89 |
6,92 |
-2,11 |
0,026 |
| 2006 |
1,43 |
-1,35 |
-1,41 |
51,44 |
50,35 |
-48,56 |
-49,65 |
0,028 |
Подставив необходимые значение в формулы, получаем, что средний уровень за период равен – 0,14, средний темп роста –0,93 , средний темп прироста - -7%.Темп прироста показывает, что окупаемость затрат, руб. в среднем по району за 1997-2006 года уменьшился в среднем за год на 7 %.
Максимальное значение было достигнуто в 2002 году, и оно составило 5,85 руб. Минимальное значение наблюдалось в 2006 году и равнялось 1,43 руб.
Рассмотрев данные ряды динамики, приходим к выводу о том, что в них уровни ряда претерпевают самые различные изменения, то возрастают, то убывают.
3.2 Выравнивание рядов динамики
Выравнивание ряда динамики способом наименьших квадратов заключается в отыскивание уровней кривой, которая наиболее точно отражала бы основную тенденцию изменения уровней в зависимости от времени. Параметры уравнения находят способом наименьших квадратов.
Уравнения, выражающие уровни динамического ряда в виде некоторой функции времени t называют трендом.
Этот прием выравнивания, как и другие приемы, следует применять в сочетании с методом укрупнения периодов. Если в ряду имеются качественно специфические периоды, то выявление тенденций при помощи метода наименьших квадратов целесообразно в пределе каждого из них.
Проведем выравнивание динамического ряда по способу наименьших квадратов для первого признака – валовый надой на 1 корову, ц. Проведем выбор уравнения, поскольку эффективность выравнивания в значительной мере зависит от правильности выбора уравнения, которое более точно может проявить присущую ряду тенденцию. Для этого проанализируем данные приложения.
По данным таблицы (приложение №4) видно, что, несмотря на колебания валового надоя на 1 корову, ц. прослеживается тенденция их поведения. Поэтому логично предположить, что для проявления тенденции можно использовать уравнение прямой:
yi
=a0
+ a1
*t (3.4)
или уравнение второго порядка
yi
=a0
+ a1
*t+ a2
*t2
(3.5)
где, a0
, a1,
a2
-неизвестные параметры уравнения;
t - значение дат (порядковый номер).
Для определения параметров уравнения параболы используют программу на ПК «Динамика». Все рассчитанные данные предложены в приложении № 4.
В нашем случае уравнение прямой будет иметь следующий вид:
y = 17,38 + 0,19t, а уравнение параболы: y = 18,57 + 0,19t - 0,11t^2. Коэффициент
a1
=0,19, характеризует среднее увеличение данного признака в год,
a0
=17,38 - значение выровненного уравнения признака для центрального года в динамическом ряду принятого за начало отсчета, при t=0. Остаточное среднее квадратического отклонения оценивает степень приближения линейного тренда с фактическим уровнем динамического ряда. Колебание фактического уровня рассматриваемого признака около прямой составляет 1,33 или 7,7% (1,33/17,38*100) по отношению к среднему уровню ряда.
Полученные коэффициенты из уравнения параболы: a0
=18,57-выравненный уровень признака для центрального ряда динамики (2001 год), при t=0, a1
=0,19 -это среднее значение признака за год, a2
=-0,11 - ускорение уменьшения признака.
Остаточное среднее значение по параболе 0,95, ниже остаточного среднего значения, полученного при выравнивании по уравнению прямой. Случайное колебание около выравненного уравнения составляет 7,7% (по прямой) против 5,1% (по параболе). Следовательно, парабола точнее воспроизводит характер изменения признака за исследуемый период времени. Однако, различия малы, значит, для выравнивания данного ряда можно использовать также и уравнение прямой.
Аналогично проведем анализ по количеству коров на 1 работника занятого в сельскохозяйственном производстве, гол. и по окупаемости затрат, руб.
Проведем анализ по количеству коров на 1 работника занятого в сельскохозяйственном производстве, гол. Уравнение прямой будет иметь вид: y = 3,98 + 0,29t, а параболы y = 3,81 + 0,29t + 0,02t^2 .
Коэффициент a1
=0,29-характеризует среднее увеличение количества коров на 1 работника занятого в с/х производстве, a0
=3,98- значение выровненного признака для центрального года динамики (2001) при t=0. Полученные коэффициенты из уравнения параболы: a0
=3,81-выравненный уровень признака для центрального ряда динамики (2001 год), при t=0, a1
=0,29 -это среднее значение признака за год, a2
=0,02 - ускорение увеличения признака (приложение №5).
Колебание фактического значения признака около прямой составляет 0,52 или 0,52*100/3,98=13,1% по отношению к среднему уровню ряда. Остаточное среднеквадратическое отклонение, полученное при выравнивании параболы несколько ниже (0,51%), чем по прямой. Случайная колебаемость около выровненного уравнения составляет 0,51*100/3,81=13,4%.
Для выявления изменений окупаемости затрат, руб. имеем уравнение прямой y = 3,31 + 0,03t и уравнение параболы y = 4,67 + 0,03t - 0,12t^2 (приложение №6). Колебание фактического признака около прямой составляет 1,46 или 1,46*100/3,31=44,1% по отношению к среднему уровню ряда. Остаточное отклонение по параболе 1,00. Случайная колебаемость около выровненного ряда составляет: 1,00*100/4,67=21,4%. Следовательно, парабола точнее воспроизводит характер изменения изучаемого признака за исследуемый период.
Проанализировав показатели динамического ряда можно сделать вывод, что за период с 1997 по 2006 год валовый надой на 1 корову ц., количество коров на 1 работника, гол. и окупаемость затрат, руб. то возрастают, то убывают.
Сглаживание ряда динамики при помощи скользящей средней предполагает последовательный расчет средних за период сдвигаемых на одну дату. При этом, достигается взаимное погашение случайных колебаний отдельных уравнений динамического ряда. Полученный ряд средних, характеризующий закономерное изменение уровня от одной даты к другой, проявляя, тем самым тенденцию развития явления.
При использовании метода скользящих средних необходимо, прежде всего, правильно выбрать величину интервального скольжения, интервал должен быть достаточно большим и обеспечить взаимное погашение случайных отклонений уровней. Если в развитии явления замечается определенная цикличность (периодичность), то интервал скользящей следует брать равным продолжительности цикла. Чем длиннее интервал скольжения, тем в большей мере выражается ряд в результате осреднения и исходных уравнений.
Для расчета скользящих суммируем валовый надой на 1 корову, ц. за первый период (1997-1999 годы), затем, опуская данные валового надоя на 1 корову, ц. за следующее трехлетие (1998-2000 годы) и так далее.
Сумму делим на число лет в периоде скольжения и полученную среднюю относительно к середине периода скольжения.
Выровненный ряд валового надоя на 1 корову, ц. при помощи скользящей средней в приложении № 4.Средние скользящее показывают, что валовый надой на 1 корову, ц увеличился на 17,49-15,58=1,91 ц.
Аналогично проведем анализ по количеству коров на 1 работника занятого в с/х производстве, гол. Выровненный ряд по этому признаку в приложении № 5. Средние скользящие наглядно показывают, что количество коров на 1 работника занятого в с/х производстве увеличилось на 5,20 – 2,95=2,25 гол.
Данные для анализа окупаемости затрат, руб. в приложении № 6. Средние скользящие наглядно показывают уменьшение окупаемости затрат, руб. на 2,27-2,57=-0,3.
На основании анализа динамического ряда можно сделать вывод, что в Думиничском районе валовый надой на 1 корову, ц., количество коров на 1 работника занятого в с/х производстве, гол. увеличились, а окупаемость затрат, руб. уменьшилась.
Далее с помощью программы «Динамика» составляем прогноз на 2007 и 2008 гг для валового надоя на 1 корову, ц., для количества коров на 1 работника, занятого в с/х производстве, гол. и для окупаемости затрат, руб.
Проанализируем тренды для данных показателей.
Валовый надой на 1 корову, ц. по прямой в 2008 году увеличился по сравнению с 2007 годом на 18,72-18,53=0,19 ц. А по параболе этот показатель уменьшился в 2008 году по сравнению с 2007 на 14,61-15,83=-1,22 ц.
Количество коров на 1 работника, гол. по прямой в 2008 году увеличилось по сравнению с 2007 годом на 6,01-5,72=0,29 гол., и по параболе количество коров на 1 работника, гол в 2008 году увеличилось по сравнению с 2007 годом на 6,61-6,12=0,49 гол.
Окупаемость затрат, руб. по прямой в 2008 году увеличилась по сравнению с 2007 годом на 3,51-3,48=0,03 руб., а по параболе наблюдается уменьшение окупаемости затрат, руб. в 2008 году по сравнению с 2007 годом на -1,58-0,40=-1,98 руб.
3.3 Корреляционно – регрессионный анализ
Корреляционная связь – это неполная связь между признаками, которая проявляется при большом числе наблюдений. Используя метод корреляции, можно определить среднее измерение результативного признака под влиянием одного или нескольких факторов. Так как между факторными показателями может также существовать положительная корреляционная связь, то для оценки степени их влияния на результативный признак целесообразно использовать множественную корреляцию.
В данной модели в качестве результативного признака возьмём показатель – валовый надой на 1 корову, ц, в качестве факторных признаков количество коров на 1 работника, гол. и окупаемость затрат, руб.В результате решений уравнения на ЭВМ были получены следующие его параметры (приложение №7).
Y=14,33+0,40*X1
+0,44*X2
Интеграция полученных параметров следует:
A0
=14,33- условное начало содержательной интерпретации не подлежит;
A1
=0,40-коэффициент чистой регрессии при первом факторе свидетельствует о том, что при изменении количества коров на 1 работника, гол., валовый надой на 1 корову, ц. в среднем изменится на 0,40 при условии, что другие факторы остаются постоянными;
A2
=0,44- коэффициент чистой регрессии при втором факторе показывает, что при изменении окупаемости затрат, руб. вызывает изменение валового надоя на 1 корову, ц. на 0,44 при условии, что другие факторы остается постоянными.
Коэффициент множественной корреляции 0,54 показывает, что связь между признаками средняя.
Коэффициент множественной детерминации показывает, насколько тесной является связь между выбранными показателями. В нашем случае он равен 0,29 т.е. связь между признаками средняя.
Коэффициенты парной корреляции 0,32 свидетельствуют, что между валовым надоем на 1 корову, ц. и количеством коров на 1 работника, гол. существует слабая связь и прямая зависимость, а 0,46- показывает, что связь более сильная и прямая зависимость, с окупаемостью затрат, руб.
Рассчитаем теперь β-коэффициенты и коэффициенты эластичности по приведенным во второй главе формулам:
σу
=21,81 ; σх1
= 11,97 ; σх2
= 21,51.
β1
= 0,22 ; β2
= 0,43
Каждый из бета коэффициентов показывает, на сколько средних квадратических отклонений изменится валовый надой на 1 корову ,ц., если соответствующий фактор изменится на своё среднее квадратическое отклонение. Коэффициенты эластичности в данном случае будут равны:
Э1
= 0,09 ; Э2
= 0,08, то есть, если количество коров на 1 работника, гол. увеличится на 1 %, то валовый надой на 1 корову, ц. увеличится на 0,09% и если окупаемость затрат, руб. увеличится на 1%, то валовый надой на 1 корову, ц. увеличится на 0,08 %
Проверка значимости коэффициента множественной корреляции показала, что Fрасч
= 4,46, при значимости Fтабл.
=4,10 при пятипроцентном уровне. Таким образом, Fрасч
> Fтабл
, что позволяет с вероятностью 95 % утверждать существенность различий в величине дисперсий и соответственно сделать вывод об адекватности модели.
В качестве критериев проверки гипотез относительно двух средних используется критерий t- Стьюдента. Фактическое значение t равно 7,11, 0,92, 1,39 а табличное t=2,23, необходимо признать справедливость альтернативной гипотезы.
3.4
Индексный метод анализа
Установим производство молока в 2005г. по сравнению 2006г. Установим, в какой мере это изменение произошло за счет поголовья коров, гол. и за счет валового надоя на 1 корову, ц. В качестве базисного примем значение 2005г., значения 2006 группы возьмем как отчетные величины.
Вычислим индекс производства молока.
Таблица 3.4 – Расчет индекса производства молока
| продукция |
Исходные данные |
Расчетные данные |
| Поголовье коров, гол. |
Надой на 1 корову, ц |
Производство молока |
| I |
II |
I |
II |
I |
II |
Условный |
N |
N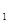 |
T |
T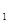 |
N T T |
N T T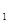 |
N T T |
N T T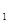 |
| Молоко |
852 |
191 |
16,77 |
17,84 |
14288,04 |
3407,44 |
3203,07 |
15199,68 |
I = =   (3.6), (3.6),
Где N , N , N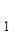 - поголовье коров в 2005 и 2006 годах соответственно; - поголовье коров в 2005 и 2006 годах соответственно;
T , T , T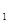 - надой на 1 корову в 2005 и 2006 годах; - надой на 1 корову в 2005 и 2006 годах;
N T T - производство молока в 2005 году; - производство молока в 2005 году;
N T T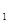 - производство молока в 2006 году. - производство молока в 2006 году.
Рассчитаем индекс поголовья коров и индекс надоя на 1 корову по следующим формулам:
I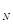 = = 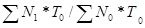  (3.7) (3.7)
I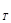 = = 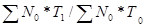  (3.8) (3.8)
Где N T T - условное производство молока при поголовье коров в 2006 году, гол. и надое молока на 1 корову в 2005 году, ц.; - условное производство молока при поголовье коров в 2006 году, гол. и надое молока на 1 корову в 2005 году, ц.;
N T T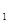 - условное производство молока при поголовье коров в 2005 году, гол. и надое молока на 1 корову в 2006 году, ц. - условное производство молока при поголовье коров в 2005 году, гол. и надое молока на 1 корову в 2006 году, ц.
I = 3407,44/ 14288,04= 0,24 = 3407,44/ 14288,04= 0,24
I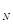 = 3203,07/14288,04=0,22 = 3203,07/14288,04=0,22
I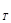 =15199,68/14288,04= 1,06 =15199,68/14288,04= 1,06
Как видно, производство молока уменьшилось в 2006 году по сравнению с 2005 годом на 76% или на 3407,44-14288,04=-10880,6 ц. Это следует из того, что условное поголовье уменьшилось на 78% или на 3203,07-14288,04=-11084,97 гол. и условный надой на 1 корову увеличился на 6% или на 15199,68-14288,04=911,64 ц.
ВЫВОДЫ
По итогам анализа данной курсовой работы сделаем следующие выводы:
1. В результате построения ранжированного и интервального рядов распределения по группировочному признаку (цена реализации молока, руб/ц) были выделены 5 групп. Наиболее часто встречаются районы по величине этого признака в интервале от 640,2 до 694,8 руб/ц., менее до 585,6; от 585,6до 640,2 и выше 749,4 руб./ц. а наиболее редко от 694,8 до 749,4 руб/ц. Затем эти группы были объединены в три типические группы.
2. Самой многочисленной типической группой является средняя (13 районов), а высшая и низшая по количеству входящих районов равны (5 районов). Показатели в типической группе возрастают от низшей группы к высшей.
3. В результате проведения комбинированной группировки были выделены 2 группы по выручке на 100 га с/х угодий, тыс.руб. и 3 подгруппы по цене реализации молока, руб./ц.
4. При проведении индексного анализа по низшей и высшей типическим группам было получено: производства молока в высшей группе больше, чем в низшей на 1360%.
5. По данным корреляционно-регрессионного анализа было выявлено, что связь между валовым надоем на 1 корову, ц. и ценой реализации молока, руб/ц и выручкой на 100 га с/х угодий, тыс. руб.примерно одинакова.
6. На основании анализа динамического ряда можно сделать вывод, что в Думиничском районе валовый надой на 1 корову, ц., количество коров на 1 работника, гол. и окупаемость затрат, руб. ведут себя скачкообразно, т.е, то увеличиваются, то уменьшаются.
7. Также было проведено сглаживание динамических рядов по прямой и параболе.
8. При проведении корреляционно-регрессионного анализа по Думиничскому району было выявлено, что между валовым надоем на 1 корову, ц. и окупаемостью затрат, руб./ц. существует близкая связь, а связь менее сильная с количеством коров на 1 работника занятого в с/х производстве.
9. При проведении индексного анализа получили, что производство молока в Думиничском районе уменьшилось в 2006 году по сравнению с 2005 годом на 76%.
Список использованной литературы
1.
Брылев А.А., Гореева Н.М., Демидова Л.Н., Родионова Е.А. Методические указания по выполнению курсовой работы по дисциплине «статистика». Калуга 2004.
2.
Зинченко А.Н., Шайкина Е.В., Шибалкин А.Е., Тарасов О.Б., «Практикум по статистике»: Учебник , 2001г. – 392 с.: ил.
3.
Практикум по статистике: Учебник пособие для ВУЗов под ред. В.М. Симчеры / ВЗФЭИ – М.: Финстатинформ, 1992г.
4.
«Калужская обл. в 2004 году», стат. сборник. Калуга 2005;
5.
Российский статистический ежегодник. Официальное издание. Госкомстат РФ, 1994 – 1996.
6.
Районы и города Калужской области в 1999 году. Части 1,2. Госкомстат РФ. Калуга 2003.
ФИШКИ
| Районы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 1 |
Бабынинский |
555 |
61500 |
785 |
12660 |
173 |
9304 |
5160 |
16,13 |
73,18 |
0,21 |
8,39 |
6,57 |
29,83 |
4,54 |
128 |
53,78 |
11,85 |
| 2 |
Барятинский |
531 |
48100 |
278 |
7811 |
68 |
5365 |
2851 |
28,10 |
114,87 |
0,16 |
5,93 |
10,26 |
41,93 |
4,09 |
58 |
78,90 |
19,30 |
| 3 |
Боровский |
703 |
31400 |
3171 |
141822 |
720 |
67243 |
47255 |
44,72 |
196,98 |
4,52 |
150,49 |
14,90 |
65,63 |
4,4 |
1010 |
93,39 |
21,21 |
| 4 |
Дзержинский |
654 |
60900 |
1545 |
54967 |
1062 |
45534 |
29784 |
35,58 |
51,76 |
0,90 |
48,91 |
19,28 |
28,05 |
1,45 |
254 |
42,88 |
29,47 |
| 5 |
Думиничский |
717 |
39000 |
191 |
3408 |
34 |
3054 |
2191 |
17,84 |
100,24 |
0,09 |
5,62 |
11,47 |
64,44 |
5,6 |
49 |
89,82 |
15,99 |
| 6 |
Жиздринский |
596 |
49100 |
552 |
16242 |
102 |
13349 |
7953 |
29,42 |
159,24 |
0,33 |
16,20 |
14,41 |
77,97 |
5,4 |
112 |
130,87 |
24,18 |
| 7 |
Жуковский |
800 |
40800 |
3814 |
197115 |
930 |
183206 |
146542 |
51,68 |
211,95 |
4,83 |
359,17 |
38,42 |
157,57 |
4,1 |
935 |
197,00 |
48,04 |
| 8 |
Износковский |
650 |
42500 |
47 |
499 |
20 |
412 |
268 |
10,62 |
24,95 |
0,01 |
0,63 |
5,7 |
13,40 |
2,35 |
11 |
20,60 |
8,77 |
| 9 |
Козельский |
634 |
75000 |
2591 |
83979 |
633 |
71843 |
45544 |
32,41 |
132,67 |
1,12 |
60,73 |
17,58 |
71,95 |
4,09 |
345 |
113,50 |
27,73 |
| 10 |
Куйбышевский |
647 |
53200 |
1245 |
40966 |
297 |
34592 |
22374 |
32,90 |
137,93 |
0,77 |
42,06 |
17,97 |
75,33 |
4,19 |
403 |
116,47 |
27,78 |
| 11 |
Людиновский |
645 |
28100 |
718 |
22885 |
200 |
17184 |
11090 |
31,87 |
114,43 |
0,81 |
39,47 |
15,45 |
55,45 |
3,59 |
256 |
85,92 |
23,93 |
| 12 |
Малоярославецкий |
771 |
61900 |
2287 |
96852 |
642 |
82495 |
63579 |
42,35 |
150,86 |
1,56 |
102,71 |
27,80 |
99,03 |
3,56 |
369 |
128,50 |
36,07 |
| 13 |
Медынский |
804 |
46400 |
1551 |
74437 |
456 |
55574 |
44664 |
46,70 |
155,78 |
1,60 |
96,26 |
28,80 |
96,05 |
3,34 |
334 |
119,51 |
35,83 |
| 14 |
Мещовский |
586 |
77400 |
1340 |
32522 |
296 |
27707 |
16239 |
24,29 |
109,97 |
0,42 |
20,98 |
12,12 |
54,86 |
4,53 |
173 |
93,60 |
20,68 |
| 15 |
Мосальский |
546 |
49800 |
428 |
9974 |
125 |
8119 |
4436 |
23,30 |
79,79 |
0,20 |
8,91 |
10,36 |
35,49 |
3,42 |
86 |
64,95 |
18,97 |
| 16 |
Перемышльский |
777 |
58000 |
2495 |
108994 |
563 |
95982 |
74561 |
43,69 |
193,60 |
1,88 |
128,55 |
29,88 |
132,44 |
4,43 |
430 |
170,48 |
38,47 |
| 17 |
Спас-Деменский |
557 |
55000 |
390 |
7845 |
85 |
5112 |
2846 |
20,12 |
92,29 |
0,14 |
5,17 |
7,30 |
33,48 |
4,59 |
71 |
60,14 |
13,11 |
| 18 |
Сухиничский |
682 |
76700 |
2029 |
63642 |
494 |
56903 |
38835 |
31,37 |
128,83 |
0,83 |
50,63 |
19,14 |
78,61 |
4,11 |
265 |
115,19 |
28,04 |
| 19 |
Тарусский |
691 |
30400 |
626 |
21631 |
111 |
19057 |
13162 |
34,55 |
194,87 |
0,71 |
43,30 |
21,03 |
118,58 |
5,64 |
206 |
171,68 |
30,44 |
| 20 |
Ульяновский |
538 |
58900 |
135 |
2714 |
58 |
2623 |
1412 |
20,10 |
46,79 |
0,05 |
2,40 |
10,46 |
24,34 |
2,33 |
23 |
45,22 |
19,43 |
| 21 |
Ферзиковский |
776 |
58500 |
3366 |
121360 |
778 |
113972 |
88498 |
36,05 |
155,99 |
2,07 |
151,28 |
26,29 |
113,75 |
4,33 |
575 |
146,49 |
33,86 |
| 22 |
Хвастовичский |
607 |
56400 |
1955 |
74889 |
510 |
67795 |
41118 |
38,31 |
146,84 |
1,33 |
72,90 |
21,03 |
80,62 |
3,83 |
347 |
132,93 |
34,68 |
| 23 |
Юхновский |
614 |
51500 |
1172 |
37197 |
282 |
30839 |
18932 |
31,74 |
131,90 |
0,72 |
36,76 |
16,15 |
67,13 |
4,16 |
228 |
109,36 |
26,31 |
КЛЮЧ К ФИШКАМ
1 – цена реализации молока, руб/ц.
2 – площадь с/х угодий, га
3 – среднегодовое поголовье коров молочного стада, гол.
4 – валовый надой от коров молочного стада, ц.
5 – количество работников, занятых в с/х производстве, чел.
6 – количество реализованного молока, ц.
7 – выручено всего от реализованного молока, тыс.руб
8 – валовый надой на 1 корову молочного стада, ц.
9 – валовый надой на 1 работника, занятого в с/х производстве, ц.
10 – валовый надой на площадь с/х угодий, ц.
11 – выручено на 100 га с/х угодий, тыс.руб.
12 – выручено на 1 корову молочного стада, тыс. руб
13 – выручено на 1 работника, занятого в с/х производстве, тыс.руб
14 – количество коров молочного стада на 1 работника, занятого в с/х производстве, гол.
15 – количество коров молочного стада на 100 га с/х угодий, гол.
16 – количество реализованного молока на 1 работника, занятого в с/х производстве, ц.
17 –количество реализованного молока на 1 корову молочного стада, ц.
|