Ł Łæ æ Æ Ł — ææŁØæŒ Ø ŁŁ

Œ -ˇ Æ ªæŒŁØ ª æ æ ßØ ºŁ ı Ł æŒŁØ Ł æŁ

— æ … -ª Ł æŒ Æ

˛ º Œ ŁŒ Ł Œ ß ŁÆ ß¿

: ˚ ŁŒ ˚ æ Ł ˚ æ Ł Ł

ˆ : 3093/2 Œ º : — Ł Ł Ł æŒŁØ

ˇ º :

˚ Ł ŁØ ¨ª Ł

Œ -ˇ Æ ª

2010

˛ªº º Ł

1 ı Ł æŒ 1

2 ºŁ 1

3 — æ 4

4 ¸Ł 12

1 ı Ł æŒ

• ˝ Ø Ł ªŁŁ Ł º ß Œ ŁŁ ª Ł ª æ Ł ßı æ æ ŁØ º Œ Ł º Ø æº ø ª 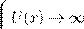Ł :

, Ł

, Ł

, Ł

˙ æ .

• ˇ æ Ł ª ŁŒŁ º ßı Œ ŁØ Łı æ æ ŁØ. ´ß ŁæºŁ æ Ł Æ Ł º Œ Œ Ł æ Œ ß º Œ ßı æ æ -

ŁØ.

—Łæ. 1: ˇ Ł º º

2 ºŁ

(1)

ˆ Łº Ł ß æ æ Ø ŒŁ Ł æŒ Ø Ł Ł º Ø

ªŁØ º Œ Ł º º [3]:

H ˆ = T ˆ + U ˆ

— ºŁ ß , æ º łŁæ :

(2)

… ª , Ł º º (

(3)

(4)

´ Œ Ø ı ŁŒ º Œ Ł Ł Ł Ł æŒŁı æ Æ ŁØ -

Œº ß º Ł º ß æº Ł [4]:

• æº Ł Ł ŒŁ

(5)

˝ æ æ ß Ł ª Ł Ł ºŁ Ł Œ ŁŁ ϕ (t ):

ˇ æ Ł ª Ł Ł ßÆ ŒŁ Æ , Æß Œ Ł

Ψ (x,t ) Æߺ Ł .

(6)

3 — æ …

• ˇ ºŁ Ł Ł Œ ŁŁ f (x ) Œ ı æŁ ª º æ Ł:

— ł Ł Ł y = e^kx : k ² e^kx − æ² 2e^kx = 0 ⇒ k ² − æ² = 0 ⇒ k = ±æ

y = C 1e æx + C 2e −æx

¨ æº Ł ª º æ Ł y : C ₁ → 0 ⇒ y = C ₂ e ^−æx

.Œ. U (x ) → ∞ ⇒ æ → ∞ ⇒ y → 0

(7)

• — ææ Ł ł Ł Ł Ł :

(8)

• — ææ Ł ł Ł Ł Ł :

y ⁰⁰ − α ² y = 0 (9)

— ł Ł Ł y = e^kx : k ² e^kx − α ² 2e^kx = 0 ⇒ k ² − α ² = 0 ⇒ k = ±α

y = C 1e αx + C 2e −αx

• Ł (4) º æ Œ :

ˇ º Ł Ł (9), Æø ł Ł : y ₁ = A sh(κx ) + B ch(κx )

¯æºŁ f (x ) … : (0) = 0;æºŁ f (x ) … : y ₁ (0) = 0

f (x ) … :

y ₁ ⁰ = Aκ ch(κx ) + Bκ sh(κx ) y ₁ ⁰ (0) = Aκ = 0

.Œ. κ 6= 0 → A = 0

y ₁ = B ch(κx ) (10)

f (x ) … :

(11)

• Ł (4) º æ Œ :

ˇ º Ł Ł (8), Æø ł Ł : y ₂ = D sin(γx + ϕ_D ) ¨ Œ ßı æº ŁØ:

(12)

, Ł



y _{1 +} = B ch(κx ), Ł



, Ł

, Ł

, Ł

, Ł

• ¨ æº ŁØ ª º æ Ł f (x ) ß Œ æº øŁ æ ł Ł :

+ f (x ) … :

˜º Ææ ł Ł ª æ ª Ł … ß :

(13)

− f (x ) … :

˜º Ææ ł Ł ª æ ª Ł … ß :

(14)

• ˜º ł Ł (13) Ł (14) ææ Ł ø… Ł :

(15)

( … ß ł Ł )

( … ß ł Ł )

(16)

• ´ … Ł Œ Ł

ŁØ f (z ):

Ł ºŁ Ł æ Ææ ßı Œ-

, Ł

y ₁ + = B ch(p(2π )2 − η 2z ), Ł

, Ł

, Ł

^ y _{1 −} = A sh(^{p 2} − η ² z ), Ł

(2π )



, Ł

• ¨ æº Ł Ł ŒŁ ºŁ Œ æ ß A , B Ł D , º Ææ æŁæ æ n = 0:

¨æ º Ł ß æ Ł, º æŁæ º … ßı ł ŁØ:

¨ º … ßı ł ŁØ:

Łæº ł Ł

1. … ł Ł : η ₃ = 5. 261

2. ˝ … ł Ł : η ₄ = 5. 308

3. ªŁŁ ª Ł ª æ Ł ßı æ æ ŁØ º Œ Łº Ø :

, Ł



y _{1 +} = 0. 270ch(3. 435z ), Ł

, Ł

4 :

, Ł

, Ł , Ł

3 :

4 :

6. ˆ ŁŒŁ º ßı Œ ŁØ:

—Łæ. 3: 3 æ Ł æ æ Ł

—Łæ. 4: 4 æ Ł æ æ Ł

4 ¸Ł