|
Метод вращений решения линейных систем
Как и в методе Гаусса, цель прямого хода преобразований в этом методе–приведение системы к треугольному виду последовательным обнулением поддиагональных элементов сначала первого столбца, затем второго и т.д.
Умножим первое уравнение исходной системы (1) на с1
,
второе на s1
и сложим их ; полученным уравнением заменим первое уравнение системы. Затем первое уравнение исходной системы умножаем на –s1
, второе на c
1
и результатом их сложения заменим второе уравнение . Таким образом, первые два уравнения (1) заменяются уравнениями
 
Отсюда  . Эти числа можно интерпретировать как косинус и синус некоторого угла  (отсюда название метод вращения
, каждый шаг такого преобразования можно рассматривать как вращение расширенной матрицы системы в плоскости обнуляемого индекса).
В результате преобразований получим систему
где
Далее первое уравнение системы заменяется новым, полученным сложением результатов умножения первого и третьего уравнений соответственно на
а третье–уравнением, полученное при сложении результатов умножения тех же 
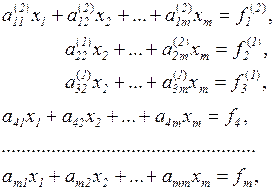
где
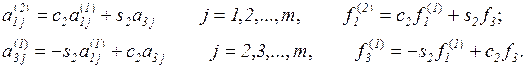
Выполнив преобразование m-1
раз, придем к системе
Вид полученной системы такой же, как после первого этапа преобразований методом Гаусса. Эта система обладает следующим свойством: длина любого вектора-столбца (эвклидова норма) расширенной матрицы остается такой же, как у исходной матрицы. Следовательно, при выполнении преобразований не наблюдается рост элементов.
Далее по этому же алгоритму преобразуется матрица
и т.д.
В результате m
-1 этапов прямого хода система будет приведена к треугольному виду.
Нахождение неизвестных не отличается от обратного хода метода Гаусса.
Всего метод вращения требует примерно  операций умножения и деления.
Пример:
Дана СЛУ:
х1
+2х2
+3х3
=8
3х1
+х2
+х3
=3
2х1
+3х2
+х3
=5
Умножим первое уравнение на с1, второе на s1, сложим их, а потом умножим первое на ( –s1), а второе на с1 и сложим. Результат : система (1) из 2 измененных уравнений и 1 оставшегося:
x1(c1+3s1)+x2(2c1+s1)+x3(3c1+s1)=8c1+3s1
x1(3c1-s1)+x2(c1-2s1)+x3(c1-3s1)=3c1-8s1
2x1+3x2+x3=5
Найти c1 и s1
-s1+3c1=0
c1=1/10^1/2
s1=3/10^1/2
Подставим эти значения в первые два уравнения системы (1), получим новую систему (2):
10x1+5x2+6x3=17
-5x2-8x3=-21
2x1+3x2=5
Умножим уравнение 1 из системы(2) на с2, третье на s2, сложим их, а потом умножим первое на ( –s2), а второе на с2 и сложим. Результат : система (3):
2x1(5c2+s2)+x2(5c2+3s2)+x3(6c2+s2)=17c2+5s2
2x1(c2-5s2)+x2(3c2-5s2)+x3(c2-5s2)=5c2-17s2
Найти c2 и s2:
-10s2+2c2=0
c2=5/26^1/2
s2=1/26^1/2
Подставим эти значения в уравнения 1 и 3 системы (3), получим систему (4):
52x1+28x2+31x3=90
-5x2-8x3=-21
-10x2-x3=-8
Теперь, оставляя 1 уравнение без изменений, умножим второе на с3, третье на s3, сложим их., умножим второе на (-s3), третье на с3, сложим и их. Результат : система (5):
52x1+28x2+31x3=90
5x2(-c3-2s3)+x3(-8c3-s3)=-21c3-8s3
5x2(-2c3+s3)+x3(-c3+8s3)=-8c3+21s3
Найдем c3 и s3:
10s3-5c3=0
c3=-1/5^1/2
s3=-2/5^1/2
Подставим найденные значения во 2 и 3 уравнения системы (5) и найдем результирующую систему (6):
52x1+28x2+31x3=90
35x2-10x3=15
-15x3=-30
Ответы:
х1=0
х2=1
х3=2
|