| УРАВНЕНИЕ ЛАПЛАСА И ГАРМОНИЧЕСКИЕ ФУНКЦИИ
Основные понятия
Мы начнем с самого простого и важного из эллиптических уравнений, а именно с уравнения Лапласа.
Это уравнение имеет вид
- ∆
u
=
f
(
x
)
Здесь f
(
x
)
— заданная функция. Если f
(
x
)≠0
, то уравнение (1) называется неоднородным уравнением Лапласа.
При f
(
x
) = 0
имеем однородное уравнение Лапласа
∆
u
=
0
Неоднородное уравнение Лапласа часто называют уравнением Пуассона.
В более подробной записи уравнения Лапласа — неоднородное и однородное — выглядят так:

и соответственно

Рассмотрим некоторую замкнутую поверхность Г, не обязательно связную» и пусть Г ограничивает область Ω, конечную (рис. 1) или бесконечную (рис.2) В обоих случаях предполагается» что сама поверхность Г конечна. Будемизучать поведение решений однородного уравнения Лапласа в подобных областях.
Функция и (х)
называется гармонической в конечной области
Ω, если она в этой области дважды непрерывно дифференцируема и удовлетворяет однородному уравнению Лапласа.

Будем говорить, что функция и(х) гармоническая в бесконечной области
Ω, если в каждой точке этой области, находящейся на конечном расстоянии or начала, u
(
x
)
дважды непрерывно дифференцируема, удовлетворяйi однородному уравнению Лапласа и па бесконечности имеет порядок
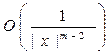 ,так что для достаточно больших |х|
имеет место неравенство ,так что для достаточно больших |х|
имеет место неравенство

где т
— размерность пространства, а С — некоторая постоянная. В случае двумерной области (т = 2)
условие (3) означает, что гармоническая в бесконечной области функция ограничена на бесконечности.
Подчеркнем, что определение гармонической функции относится только к случаю открытой области
(т. е. открытого связного множества); если говорят о функции, гармонической в замкнутой области, то под этим понимают, что данная функция гармонична в более широкой открытой области.
Заметим еще, что определение гармонической функции не накладывает никаких ограничений на поведение функции на границе области.
Пример 1: Если Ω — бесконечная область, то функция и (х) =
1 гармоническая только при т = 2.
Если m
>
2
, то в бесконечной области эта функции негармонична. Однако она гармонична в любой конечной области при любом т.
Пример 2. В двумерной плоскости функция

где z
= х+
i
у
, гармонична в любой области, которая не содержит начала координат.
Пример 3. Функция 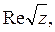 z
=
x
+
iy
, гармонична в круге |
z
| < R
(
R
— любое положительное число), разрезанном вдоль какого-либо из его радиусов. z
=
x
+
iy
, гармонична в круге |
z
| < R
(
R
— любое положительное число), разрезанном вдоль какого-либо из его радиусов.
Пример 4. Функция двух переменных и
= х2
+ у2
не является гармонической ни в какой области, так как она не удовлетворяет однородному уравнению Лапласа
∆(
x
2
+
y
2
) = 4 ≠ 0.
Пример 5. Функция u
=
x
2
-
y
2
гармонична в любой конечной области.
На двумерной плоскости конформное преобразование не меняет однородного уравнения Лапласа. В случае любого т
это не так, но все же существует преобразование, которое переводит любую гармоническую функцию в гармоническую же. Это пре образование Кельвина,
которое переводит точку
х (хи
х2
, ... , хт
)
в точку х’ (х’и
х’2
, ... , х’т
)
, симметричную с точкой х
относительно сферы данного радиуса R
с центром в начале координат, а дан ную функцию и (х)
переводит в функцию
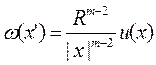
Напомним, что точки х
и х'
называются симметричными относительно названной выше сферы, если они лежат на одном луче, исходящем из начала, и если | х | • | х'| =
R
2
. Декартовы координаты симметричных точек связаны соотношением
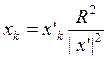
Простой, хотя и довольно громоздкий подсчет приводит к соотношению
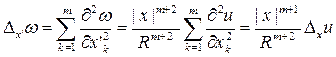
поэтому если  то то 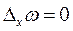 . .
|