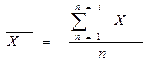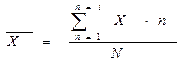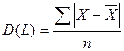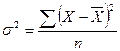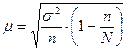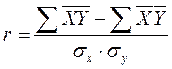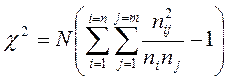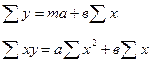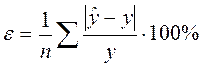Реферат: Анализ рынка трехкомнатных квартир в микрорайонах Гидростроителей, Пашковский, Славянский

Федеральное агентство по образованию

Кубанский государственный технологический университет

Кафедра технологии организации, экономики строительства

и управления недвижимостью

Семестровая работа

по дисциплине «Количественные методы оценки недвижимости»

тема: «Анализ рынка трехкомнатных квартир в микрорайонах: Гидростроителей, Пашковский, Славянский»

Специальность : 270115

Содержание:

1.Введение……………………………………………………………………..…3

2.Описание работы……………...…………………………………………….….5

3. Цели и задачи работы……………………………………………………….....8

4.Расчет характеристик………………………………………………………..…9

5.Выбраковка данных…………………………………………………………....14

6.Корреляционно-регрессионный анализ данных.........……………………….15

7. Сравнительный анализ недвижимости в городе Краснодаре………………18

8.Качественный анализ сгруппированных признаков…………………….…...22

9. Составление уравнения регрессии……………………………………….…..24

10.Проверка точности и адекватности полученной модели…………………..27

11. Заключение……………………………………………………………….......28

12.Приложение…………………………………………………………………..29

Введение.

Краснодар – это столица Краснодарского края, региона, инвестиционный потенциал которого оценивается как один из наиболее высоких в России. В рейтинге журнала Forbes, опубликованном в 2009 году, Краснодар является самым привлекательным городом для ведения бизнеса после двух столиц – Москвы и Санкт-Петербурга.
По официальным данным, население Краснодара вместе с пригородами составляет 791 тыс. жителей. Однако фактически, эта цифра значительно больше. По заявлениям местных властей, наличное население Краснодара превышает 1,2 млн. человек, а официальное достижение статуса города-миллионера планируется к 2012-2013 году.
Одним из самых стремительно развивающихся секторов экономики города является строительная отрасль. Темпы ввода жилой, коммерческой и индустриальной недвижимости находятся на очень высоком уровне и непрерывно ускоряются на протяжении последних лет.

В 2010 году в Краснодаре было введено 1 100 тыс. кв. м. жилой недвижимости – треть от общего объема введенного жилья в Краснодарском крае. С 2010 года объемы ввода увеличились на 87%. Более 62% от общей площади жилого фонда города приходится на кирпичную и панельную технологии строительства.
По состоянию на конец декабря 2010 года, в процессе строительства находится 150 домов, общая площадь которых составляет 2 834 тыс. кв. м. По данным аналитиков рынка недвижимости, наибольшая активность застройщиков наблюдалась в Центральном (18%), Юбилейном (16%) и Фестивальном микрорайонах (15%).
Средняя стоимость квадратного метра на первичном рынке жилой недвижимости по всем типам, классам и районам города в 2010 году составила 46 000 руб. По сравнению с 209 году снижение цен составило 4,7%, что объясняется негативным влиянием мирового экономического кризиса.
На вторичном рынке жилой средняя стоимость квадратного метра составила 58 400 руб., что на 18% больше, чем в 2010 году. Это связано с тем, что вторичный рынок Краснодара менее подвержен влиянию кризисных явлений и объем продаж на нем сократился не столь значительно, как на первичном.
Отличительной особенностью рынка жилой недвижимости Краснодара является то, что объемы строящихся и планируемых проектов слишком велики по сравнению с другими крупными городами ЮФО. При сохранении существующих объемов ввода рынок жилой недвижимости Краснодара станет насыщенным уже к 2012-2013 гг.
Однако, экономический кризис, наблюдаемый в России в конце 2009 года, позволяет говорить о том, что сдача большинства строящихся проектов будут перенесена на более поздние периоды, а работы по планируемым проектам приостановятся. Это замедлит насыщение рынка в ближайшей перспективе. При этом население, численность которого постоянно растет, будет создавать дополнительный спрос на жилье, повышая тем самым инвестиционную привлекательность данного рынка.

Описание работы

Данная работа представляет собой подбор и обработку данных методом регрессионного анализа. Он представляет собой способ подбора для описания материальных функций (одной или нескольких независимых переменных). Основная задача метода сводится к нахождению коэффициентов исследуемой функции (параметров модели), которая представляет собой значимость (вес) каждого фактора при расчете конечного результата.

Подбор данных для сравнительного анализа осуществляется выборочным методом по ряду причин:

1) Невозможность полного охвата всех данных по рынку недвижимости;

2) Не все данные о продаваемых объектах недвижимости попадают в объявления;

3) Данные по продаваемым объектам недвижимости часто не представлены полностью.

В нашей работе используется случайный выборочный подход, т.е. отбор квартир для изучения осуществлялся рандомизированным методом.

При изучении стоимости объектов аналогов при сравнительном методе можно увидеть, что цена изменяется в зависимости от ряда факторов: площади, этажности, комнатности, состояния ремонта и т.д. При этом некоторые факторы оказывают гораздо большее влияние на цену объекта, чем другие, а некоторые достоверно не влияют на объект. Выявить достоверно влияющие факторы позволяет расчет коэффициента корреляции. Он показывает направление и тесноту связи между влияющими признаками и результативным фактором (ценой).

Процентная доля влияния изучаемого признака на результативный описывается коэффициентом детерминации. Он равен квадрату коэффициента корреляции, умноженного на 100 процентов.

После установления степени влияния каждого факторного признака по результатам выброса не влияющих достоверно факторов приступаем к разработке функциональной зависимости между ценой и влияющими показателями в виде уравнения регрессии:

y = a₁ *x₁ +a₂ *x₂ +….+a_n *x_n +b

На основе базы данных по квартирам г.Краснодара была составлена таблица(в приложении таблица №1). Всем качественным характеристикам, которые необходимо учитывать в дальнейших расчетах, присвоены коэффициенты. Коэффициенты района присвоены следующим образом: ГМР - 1, ПМР - 2, СМР - 3. Коэффициент этажа рассчитывается на основании дельты этажа от 1 до 3, дельта этажа рассчитывается как "средний этаж” “-” “исходный этаж", взятая по модулю представляет собой число в диапазоне от 0 до 9. Коэффициент ремонта рассчитан на основе состояния ремонта. Евроремонту присвоен коэффициент - 1, а стяжке – 3, если существует косметический ремонт, или судя по всему не требуется, то - 2. После присвоения коэффициентов приступаем к расчету доверительного интервала, чтобы затем исключить из выборки квартиры, не подлежащие рассмотрению из-за ничтожной вероятности совершения сделки по ним. Чтобы рассчитать доверительный интервал, необходимо посчитать: среднее значение признака, генеральную дисперсию и ошибку выборки.

Ошибка выборки рассчитывается по формуле, применяющейся при случайном бесповторном отборе. Полученное значение используется для расчета значения которое рассчитывается по формуле: "ошибка выборки * критерий Фишера". Критерий Фишера берется из справочных таблиц в соответствии с числом N - это общее количество квартир рассматриваемого диапазона. После вышеописанных вычислений рассчитывается доверительный интервал и исключаются не входящие в него. После выполнения всех вышеописанных операций, в таблице остаются квартиры, подлежащие рассмотрению. Общее количество составляет 120 квартир.

Цели и задачи.

Цель работы: провести анализ рынка трех комнатных квартир для микрорайонов: Гидростроителей, Пашковский и Славянский, для оценки состояния изучаемого сегмента рынка недвижимости на данный момент времени.

Задачи работы:

1.Произвести первичную выборку объектов. Составить журнал первичной документации.

2.Расчитать основные характеристики выборки.

3.Произвести выбраковку данных.

4.Выполнить корреляционно-регрессионный анализ данных.

5.Провести качественный анализ сгруппированных признаков.

6.Проерить точность и адекватность полученной модели.

Расчет характеристик.

Рассчитываем межгрупповые и внутригрупповые обобщающие характеристики, такие как:

1.Среднее арифметическое значение:

2. Среднее гармоническое значение:

3. Размах данных:

R = X_max – X_mi

4. Среднее линейное отклонение:

5. Дисперсия.

5. Среднее квадратичное отклонение:

6.Вариацию признаков:

7.Ошибку выборки:

8.Количество степеней свободы:

М = (n-1)(l-1)

Первичные расчетные значения

Трехкомнатные квартиры в мкр.Гидростроителей:

Группа однородная по площади, но неоднородная по цене.

Однокомнатные квартиры в мкр.Пашковский:

Группа однородная по площади и цене.

Трехкомнатные квартиры в мкр.Славянский:

Группа однородная по площади и цене.

Выводы:

1. Наибольшая средняя площадь 3-х комнатных квартир составляет 79,01 м² в ПМР

2. Наименьшая средняя площадь 3-х комнатных квартир составляет 67,71 м² в ГМР

3. Наибольшая средняя цена по продаже 3-х комнатных квартир составляет 2,99 млн.р. в ПМР

4. Наименьшая средняя цена по продаже 3-х квартир составляет 2,52млн.р. в СМР

5. Максимальная площадь среди 3-х комнатных квартир составляет 134 м² в ГМР

6. Максимальная цена по продаже 3-х комнатных квартир составляет 9,8млн.р. в ГМР

7. Минимальная площадь среди 3-х комнатных квартир составляет 40 м² в ГМР

8. Минимальная цена по продаже 1-х комнатных квартир составляет 1,3 млн.р. в ГМР

9. Наибольший размах выборки по цене составил 7,9 млн.р. в ГМР

10. Наибольший размах выборки по площади составил 86 м² в ГМР

11. Наименьший размах выборки по цене составил 2,1 млн.р. в ПМР

12. Наименьший размах выборки по площади составил 59 м² в ПМР

13. Наибольшее варьирование по цене составило 35,8% в ГМР

14. Наибольшее варьирование по площади составило 24,8 % СМР

15. Наименьшее варьирование по цене составило 16,7% в ПМР

16. Наименьшее варьирование по площади составило 20,3 % в ПМР

Выбраковка данных.

Для того чтобы произвести выбраковку данных необходимо рассчитать границы доверительного интервала по формуле:

Т.к. группа квартир в ГМР неоднородна, разделили на 2 группы: до средней цены и после. По 1 группе доверительный интервал составил от 2,21 до 2,43 млн.р.., т.о. выбраковалось 26 объектов из 41; это №: 35( 1,9 млн.р.),66(1,65 млн.р.),67(1,4млн.р.),68(1,3млн.р.),82(2 млн.р.),88(2 млн.р.),90(2 млн.р.),29(2,5 млн.р.),34(2,6 млн.р.),37(2,5 млн.р.),39(2,5 млн.р.),42(2,6 млн.р.),74(2,65 млн.р.),75(2,6 млн.р.),76(2,55 млн.р.),77(2,65 млн.р.),78(2,6 млн.р.),79(2,5 млн.р.),80(2,6 млн.р.),91(2,45 млн.р.),97(2,5 млн.р.),98(2,5 млн.р.),100(2,5 млн.р.),105(2,5 млн.р.),106(2,5 млн.р.),107(2,6 млн.р.). По 2 группе доверительный интервал составил от 2,58 до 3,8 млн.р.., т.о. выбраковалось 1 объект из 28; это №: 24(9,8 млн.р.)

По ПМР составил от 2,627 до 3,348 млн.р., т.о. выбраковалось 8 объектов из 24 ; это №: 12(2,15 млн.р. ),15(2,4 млн.р.),55(1,6 млн.р.),56(2,15 млн.р.),57(2,6 млн.р.),63(3,7 млн.р.),64(3,557 млн.р.),65(3,55 млн.р.).

По СМР составил от 1,96 до 3,05 млн.р., т.о. выбраковалось 8 объектов из 27; это №: 43(1,4 млн.р.),44(1,8 млн.р.),45(1,85 млн.р.),46(1,9 млн.р.),47(1,95 млн.р.),48(1,95 млн.р.),112(1,9 млн.р.),115(1,95 млн.р.).

Корреляционно-регрессионный анализ данных.

Важной задачей любого исследования, связанного со статическим изучением материалов является выявление и изучение силы и направленности связей между признаками.

Например, как влияет район расположения на цену объектов недвижимости. Может ли влиять расположение на различных этажах на цену квартиры.

Силу связи и ее направленность можно установить различными методами.

Более точным и информативным является метод корреляционного анализа.

При данном методе производится расчет коэффициента корреляции (парной или множественной), отражающей зависимость результативного признака Y от факторного признака соответственно X.

Коэффициент корреляции рассчитывается по следующей формуле:

Абсолютное значение коэффициента корреляции изменяется в пределах

По абсолютному значению коэффициента корреляции можно судить:

О силе связи

О направленности связи

Если коэффициент корреляции находится в пределах:

- связь сильная (жесткая)

- связь средняя

- связь слабая

- связь линейная, зависимость прямая.

- связь отсутствует

, то связь прямая (при увеличении Х, увеличивается Y)

, то связь обратная (при увеличении X, уменьшается Y)

Таким образом, коэффициент корреляции (парный) дает возможность установить:

Силу связи между признаками

направленность связи

Коэффициент корреляции дает представление о силе и направленности связи, но не дает представления о доли влияния изменения факторного признака на изменение соответствующего результативного признака.

Для учета доли влияния рассчитывают коэффициент детерминации:

d = r²

Более наглядно представление о доли влияния факторного признака на результативный можно судить по процентному соотношению влияния:

d = r² × 100%

Выводы:

Коэффициенты корреляции (r) и детерминации (d):

1.По району ГМР:

1.1 По площади: r = 0,52; в = 26,59

«Связь между факторным признаком прямая и средняя, т.о. изменение района расположения квартиры в ГМР определяет ее стоимость на 26,59 %».

1.2. По ∆ этажа: r = 0,37; в = 13,79

«Связь между факторным признаком средняя и прямая, т.о. изменение этажа расположения квартиры в ГМР определяет ее стоимость на 13,79%».

1.3 По состоянию квартиры: r =- 0,26; в = 7,05

«Связь между факторным признаком слабая и обратная, т.о. изменение состояния квартиры в ГМР определяет ее стоимость на 7,05%».

2. По ПМР:

2.1. По площади: r = 0,38; в = 14,07

«Связь между факторным признаком средняя и прямая, т.о. изменение площади квартиры в ПМР определяет ее стоимость на 14,07%».

2.2. По ∆ этажа: r = -0,33; в =10,9

«Связь между факторным признаком средняя и обратная, т.о. изменение этажа расположения квартиры в ПМР определяет ее стоимость на 10,9%».

2.3 По состоянию квартиры: r = 0,3; в = 8,9

«Связь между факторным признаком слабая и прямая, т.о. изменение состояния квартиры в ГМР определяет ее стоимость на 8,9%».

3. По СМР:

3.1. По площади: r = 0,7; в = 49,5

«Связь между факторным признаком сильная и прямая, т.о. изменение площади квартиры в ЧМР определяет ее стоимость на 49,5%».

3.2. По ∆ этажа: r = 0,79; в = 61,89

«Связь между факторным признаком сильная и прямая, т.о. изменение этажа расположения квартиры в ЧМР определяет ее стоимость на 61,89%».

3.3 По состоянию квартиры: r =- 0,28; в = 8,08

«Связь между факторным признаком слабая и обратная, т.о. изменение состояния квартиры в ГМР определяет ее стоимость на 8,08%».

Сравнительный анализ недвижимости по корреляции в городе Краснодаре

По площади:

Связь по трехкомнатным квартирам в ГМР между общей площадью и ценой квартиры средняя прямая, значение 0,52, что похоже на аналогичную ситуацию в КМР,ЧМР, ПМР.

Связь по трехкомнатным квартирам в ПМР между общей площадью и ценой квартиры средняя прямая, значение 0,38, что похоже на аналогичную ситуацию в КМР,ЧМР,ГМР.

Связь по трехкомнатным квартирам в СМР между общей площадью и ценой квартиры средняя прямая, значение 0,7, что похоже на аналогичную ситуацию в ЧМР, ГМР.

По ∆ этажа:

Связь по трехкомнатным квартирам в ГМР между Δ и ценой квартиры средняя прямая, значение 0,4, что похоже на аналогичную ситуацию в ФМР,ПМР.

Связь по трехкомнатным квартирам в ПМР между Δ и ценой квартиры средняя обратная, значение -0,33, что похоже на аналогичную ситуацию в ФМР,ГМР.

Связь по трехкомнатным квартирам в СМР между Δ и ценой квартиры средняя обратная, значение 0,8, что НЕ похоже на аналогичную ситуацию в районах

По состоянию:

Связь по трехкомнатным квартирам в ГМР между общим состоянием и ценой квартиры слабая обратная, значение -0,27, что похоже на аналогичную ситуацию в СМР,ЧМР,ПМР.

Связь по трехкомнатным квартирам в ПМР между общим состоянием и ценой квартиры слабая прямая, значение 0,3, что похоже на аналогичную ситуацию в СМР,ГМР,ЧМР.

Связь по трехкомнатным квартирам в СМР между общим состоянием и ценой квартиры слабая прямая, значение -0,3, что похоже на аналогичную ситуацию в ПМР,ГМР,ЧМР.

Качественный анализ сгруппированных признаков

Ранговые признаки имеют, как правило, несколько градаций, поэтому изучение их при помощи коэффициента ассоциации и контингенции может быть затруднено.

Для изучения связи таких признаков используется методика расчета коэффициента Пирсона.

После расчета полученное значение сравнивают со справочным.

Если , то делается вывод о достоверном влиянии группы признаков А на Б.

Если , то влияние отсутствует.

Коэффициент Пирсона () мы рассчитывали исходя из общей средней площади всех исследуемых объектов, разделив квартиры каждого сегмента условно на две группы, т.е. меньше или больше общей средней площади.

Коэффициент ассоциации ;

Q=0,03139

Коэффициент контингенции

;

Ф=0,0149

Размер квартиры слабо влияет на её состояние, коэффициент ассоциации 0,03139.

Взаимовлияние размера квартиры и её состояния очень слабое, коэффициент контингенции=0,0149.

Коэффициент ассоциации больше коэффициента контингенции, следовательно, размер квартиры вероятно определяет её состояние.

Изучение связи качественных ранговых признаков

Значит, связь между районом и классом квартиры отсутствует.

Изучение взаимовлияния качественных признаков района расположения квартиры и её состояния с помощью коэффициента Чупрова показало, что связь между этими показателями слабая.

Составление уравнения регрессии

Уравнение регрессии позволяет установить количественную связь между факторными и результативными признаками, то есть найти количественное соотношение изменения признака Y на одну единицу признака X.

Простейшее уравнение регрессии:

y = a+bx

a – обеспечение смещения кривой по вертикали, относительно оси X, то есть по прямой Y.

B – Обуславливает наклон прямой.

Параметры уравнения регрессии находятся методом наименьших квадратов путем решения системы уравнений.

Уравнение регрессии может представлять из себя различную функцию, которая подбирается исходя из формы построенной графически.

Уравнение может иметь формы:

линейная

гиперболическая

степенная

логарифмическая

полиноминальная. В уравнении факторные признаки возводятся в различные друг от друга признаки.

Для вычисления коэффициентов уравнения регрессии воспользуемся программой Matrixer, и составим уравнения для нашего исследования:

Расчет с без учетом выбраковки, количество объектов = 120:

Обычный метод наименьших квадратов

(линейная регрессия)

Зависимая переменная: р[#цена]

Количество наблюдений: 120

(Регрессия без константы!)

Переменная Коэффициент Станд. ошибка t-статистика Знач.

1 р[#состо_ние_] -0.1984106267 0.0620385908 -3.1981807468 [0.0018]

2 р[#дельта] 0.0734815664 0.0361660169 2.0317848835 [0.0445]

3 р[#площадь] 0.0414718842 0.0020534895 20.195810194 [0.0000]

4 р[район] -0.0440588145 0.0624974596 -0.7049696871 [0.4822]

R^2adj. = 52.865142743% DW = 1.8859

R^2 = 54.053416456% S.E. = 0.5986933182

Сумма квадратов остатков: 41.5783079544793

Максимум логарифмической функции правдоподобия: -106.677834689621

AIC = 1.8612972448 BIC = 1.9774427341

F(3,116) = 45.48903 [0.0000]

Нормальность: Chi^2(2) = 2242.898 [0.0000]

Гетероскедастичность: Chi^2(1) = 29.44408 [0.0000]

Функциональная форма: Chi^2(1) = 3.200829 [0.0736]

AR(1) в ошибке: Chi^2(1) = 0.33828 [0.5608]

ARCH(1) в ошибке: Chi^2(1) = 0.063824 [0.8006]

Расчет с учетом выбраковки, количество объектов = 77:

Обычный метод наименьших квадратов

(линейная регрессия)

Зависимая переменная: р2[цена_млн]

Количество наблюдений: 77

(Регрессия без константы!)

Переменная Коэффициент Станд. ошибка t-статистика Знач.

1 р2[сост] -0.0606650934 0.0488994195 -1.2406096847 [0.2187]

2 р2[дельта] 0.1070148051 0.0324382214 3.299034302 [0.0015]

3 2р[район] 0.0300604966 0.0537958531 0.5587883614 [0.5780]

4 р2 [площадь] 0.0358621999 0.0018103588 19.80944326 [0.0000]

R^2adj. = 40.692983262% DW = 1.9979

R^2 = 43.003646252% S.E. = 0.4021602065

Сумма квадратов остатков: 11.9682295437227

Максимум логарифмической функции правдоподобия: -37.5735297817469

AIC = 1.0916289688 BIC = 1.2427000474

F(3,74) = 18.61096 [0.0000]

Нормальность: Chi^2(2) = 2.090194 [0.3517]

Гетероскедастичность: Chi^2(1) = 2.396194 [0.1216]

Функциональная форма: Chi^2(1) = 13.5042 [0.0002]

AR(1) в ошибке: Chi^2(1) = 5.62E-04 [0.9811]

ARCH(1) в ошибке: Chi^2(1) = 0.001647 [0.9676]

Проверка точности и адекватности модели.

Точность и адекватность модели можно проверить следующими способами:

Проверка точности модели

n – количество элементов в исследуемой группе

y – фактическое значение

- расчетное значение (теоретическое)

Проверка адекватности модели производится путем расчета коэффициента . Впоследствии для перевода в процентное соотношение.

В результате расчета получаем:

По первичным данным:

Точность модели: ,

значит точность исследования:

Адекватность модели:

С учетом выбраковки данных:

Точность модели: ,

значит точность исследования:

Адекватность модели:

Заключение.

В работе был проведен анализ рынка трёх- и четырехкомнатных квартир для микрорайонов: СМР, ГМР и ПМР. Была произведена первичная выборка данных, расчет основных характеристик выборки и выбраковка данных.

В ходе работы был проведен корреляционно-регрессионный анализ данных. С помощью программы Matrixer были вычислены коэффициенты уравнений регрессии и составлены уравнения регрессии по первичным данным и с учетом выбраковки.

По коэффициентам уравнений регрессии была проведена проверка точности и адекватности полученной модели:

— по первичным данным точность полученной модели 85,19%, адекватность полученной модели 61,59%.

— с учетом выбраковки точность полученной модели 89,07%, адекватность полученной модели 61,05%.