| ЗАДАНИЕ
на курсовой проект
по курсу «Переходные процессы в системах электроснабжения»
Тема проекта
«Расчет переходного процесса в системе электроснабжения»
Исходные данные:
| №
|
Генераторы
|
Трансформаторы
|
Реакторы
|
Линии
|
Синхронные
Компенсаторы
|
Нагрузка
|
| |
Sн
|
Uн
|
X''d
|
cosφн
|
Sн
|
Uв
|
Uс
|
Uн
|
Uкв-с
|
Uкс-н
|
Uкв-н
|
X
|
км
тип провода
|
Sн
|
Uн
|
x''d
|
Sн
|
| |
МВА
|
КВ
|
о.е.
|
о.е.
|
МВА
|
кВ
|
кВ
|
кВ
|
%
|
%
|
%
|
Ом
|
|
МВА
|
кВ
|
о.е.
|
МВА
|
| 1
|
37,5
|
10,5
|
0,143
|
0,8
|
125
|
242
|
121
|
10,5
|
11
|
45
|
28
|
0,4
|
70
АС-120
|
15
|
11
|
0,165
|
20
|
| 2
|
37,5
|
10,5
|
0,143
|
0,8
|
125
|
242
|
121
|
10,5
|
11
|
45
|
28
|
30
|
40
АС-120
|
|
|
|
12
|
| 3
|
68,8
|
10,5
|
0,16
|
0,8
|
80
|
2423
|
|
10,5
|
|
|
11
|
|
52
АС-120
|
|
|
|
7
|
| 4
|
68,8
|
10,5
|
0,16
|
0,8
|
80
|
242
|
|
10,5
|
|
|
11
|
|
80
АС-240
|
|
|
|
8
|
| 5
|
|
|
|
|
125
|
121
|
|
10,5
|
|
|
10,5
|
|
70
АС-240
|
|
|
|
|
| 6
|
|
|
|
|
32
|
115
|
|
10,5
|
|
|
10,5
|
|
200
АС-240
|
|
|
|
|
| 7
|
|
|
|
|
80
|
230
|
|
11
|
|
|
11
|
|
61
АС-240
|
|
|
|
|
| 8
|
|
|
|
|
25
|
115
|
|
10,5
|
|
|
28
|
|
70
АС-120
|
|
|
|
|
РЕФЕРАТ
Объём курсового проекта с., рис., 4 табл., 2 источника.
СЭС, КЗ, ОЗЗ, МЕТОД ЭКВИВАЛЕНТНЫХ ЭДС, МЕТОД ТИПОВЫХ КРИВЫХ, МЕТОД НЕСИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
Объектом исследования является аварийный режим работы системы электроснабжения.
Цель работы – расчет токов трехфазного и несимметричного короткого замыкания.
В процессе расчетов использовались метод эквивалентных ЭДС, метод типовых кривых и метод несимметричных составляющих.
Полученные результаты позволили выбрать необходимое оборудование, а именно выключатель, а также настроить уставки релейной защиты и автоматики.
Содержание
Введение
1 .Задание на курсовую работу
2 Расчет методом эквивалентных ЭДС
2.1 Составление схемы замещения исходной электрической схемы
2.2 Определение параметров элементов схемы замещения
2.3 Преобразование схемы замещения к простейшему виду
2.4 Определение расчетных величин
3 Расчет методом типовых кривых
3.1 Составление схемы замещения исходной электрической схемы
3.2 Преобразование схемы замещения к простейшему виду
3.3 Определение изменения периодической составляющей тока КЗ во времени
3.4 Расчёт мощности К.З.
4 Расчет несимметричного КЗ методом симметричных составляющих
4.1 Составление схем замещения отдельных последовательностей
4.2 Преобразование схемы замещения к простейшему виду
4.3 Определение расчетных величин
5 Сравнение полученных результатов
Заключение
Приложение
Список использованных источников
Развитие электроэнергетики неразрывно связано с формированием и совершенствованием Единой Электроэнергетической системы. Вообще под энергетической системой понимается совокупность электростанций, электрических и тепловых сетей, соединенных между собой и связанных общностью режима в непрерывном процессе производства, преобразования и распределения электрической энергии и теплоты при общем управлении этим режимом.
Курсовая работа является составной частью дисциплины “Переходные процессы в системах электроснабжения”. Основной её целью является: приобретение навыков определения токов нормального и аварийного режимов, а также остаточных напряжений при симметричном и несимметричных видах коротких замыканий (КЗ) в месте повреждения и произвольном месте схемы.
Переходные процессы для схем являются самыми тяжёлыми режимами. Номинальные параметры оборудования в этих режимах могут быть превышены в несколько раз.
Указанные величины используются в энергетических расчётах для выбора и проверки электрических проводников и оборудования, устройств релейной защиты и противоаварийной автоматики (РЗА).
Ток трёхфазного КЗ используется для выбора электрических аппаратов, проводников и установок РЗА, поэтому расчётными в данном случае являются условия, при которых ток КЗ максимален. Следовательно, в схеме замещения необходимо учитывать все возможные источники, включая двигательную и обобщённую нагрузку напряжением выше 1кВ, имеющую небольшую электрическую удалённость от точки КЗ, а также трансформаторы, автотрансформаторы, реакторы, линии, связывающие источники с местом повреждения.
1. Для начального момента трехфазного КЗ методом эквивалентных ЭДС найти:
-действующее значение периодической составляющей тока КЗ в месте
повреждения и в ветви с выключателем;
-ударный ток в точке КЗ и в ветви с выключателем;
-наибольшее действующее значение полного тока КЗ в ветви с
выключателем;
2. При симметричном КЗ в той же точке схемы методом типовых кривых определить:
-изменение периодической составляющей тока КЗ во времени для точки КЗ (0-0.5сек)
-мощность КЗ (в нулевой момент времени).
З. Методом симметричных составляющих для заданного вида несимметричного КЗ:
-построить векторные диаграммы токов и напряжений для места повреждения и выключателя, рассчитав необходимые для этого величины;
-найти модуль периодической составляющей тока КЗ для точки несимметрии упрощенным способом.
4. Провести сопоставление и анализ полученных в п.п.3-5 величин.
Исходные данные
| №
|
Генераторы
|
Трансформаторы
|
Реакторы
|
Линии
|
Синхронные
Компенсаторы
|
Нагрузка
|
| |
Sн
|
Uн
|
X''d
|
cosφн
|
Sн
|
Uв
|
Uс
|
Uн
|
uкв-с
|
uкс-н
|
uкв-н
|
X
|
км/тип провода
|
Sн
|
Uн
|
x''d
|
Sн
|
| |
МВА
|
КВ
|
о.е.
|
о.е.
|
МВА
|
кВ
|
кВ
|
кВ
|
%
|
%
|
%
|
Ом
|
|
МВА
|
кВ
|
о.е.
|
МВА
|
| 1
|
37,5
|
10,5
|
0,143
|
0,8
|
125
|
242
|
121
|
10,5
|
11
|
45
|
28
|
0,4
|
70/АС-120
|
15
|
11
|
0,165
|
20
|
| 2
|
37,5
|
10,5
|
0,143
|
0,8
|
125
|
242
|
121
|
10,5
|
11
|
45
|
28
|
30
|
40/АС-120
|
|
|
|
12
|
| 3
|
68,8
|
10,5
|
0,16
|
0,8
|
80
|
242
|
|
10,5
|
|
|
11
|
|
52/АС-120
|
|
|
|
7
|
| 4
|
68,8
|
10,5
|
0,16
|
0,8
|
80
|
242
|
|
10,5
|
|
|
11
|
|
80/АС-240
|
|
|
|
8
|
| 5
|
|
|
|
|
125
|
121
|
|
10,5
|
|
|
10,5
|
|
70/АС-240
|
|
|
|
|
| 6
|
|
|
|
|
32
|
115
|
|
10,5
|
|
|
10,5
|
|
200/АС-240
|
|
|
|
|
| 7
|
|
|
|
|
80
|
230
|
|
11
|
|
|
11
|
|
61/АС-240
|
|
|
|
|
| 8
|
|
|
|
|
25
|
115
|
|
10,5
|
|
|
28
|
|
70/АС-120
|
|
|
|
|
Номинальная мощность соседней энергосистемы Sн
=250МВА

Рис 1.1. Расчётная схема
2.1 Составление схемы замещения исходной электрической схемы
Для определения параметров схемы замещения используем точное приведение в именованных единицах (ТПИЕ). Параметры всех элементов схемы замещения приведём к той ступени, где произошло короткое замыкание (точка К12
).Uб
=242кВ.
Схема замещения сети представлена на рисунке 2.1.
2.2 Определение параметров элементов схемы замещения
Найдём параметры схемы замещения
Генераторы:
G1, G2:
XG1
=XG2
=X’’
d
∙Uн
2
/Sн
∙KT1H
2
=0,143∙10,52
/37,5∙(242/10,5)2
=223,324(Ом);
EG1
=EG2
=(1+ X’’
d
∙sinφн) ∙ Uн
∙KT1H
==(1+ 0,143∙0,6) ∙ 10,5∙(242/10,5)= 262,7636(кB);
G3, G4:
XG3
=XG4
=X’’
d
∙Uн
2
/Sн
∙KT3
2
=0,16∙10,52
/68,8∙(242/10,5)2
=136,195(Ом);
EG1
=EG2
=(1+ X’’
d
∙sinφн) ∙ Uн
∙KT3H
==(1+ 0,16∙0,6) ∙ 10,5∙(242/10,5)= 265,232(кB);
Трансформаторы:
Т1, Т2:
Найдём напряжения короткого замыкания для каждой обмотки:
uкв
=0,5∙(uкв-с
+uкв-н
-uкс-н
)=0,5∙(11+28-45)<0;
uк
c
=0,5∙(uкв-с
+uкс-н
-uкв-н
)=0,5∙(11+45-28)=14%;
uкн
=0,5∙(uкс-н
+uкв-н
-uкв-с
)=0,5∙(45+28-11)=31%;
Т.к. uкв
<0, то Хв
=0;
Хс
=(uкс
/100)∙Uв2
/Sн= (14/100)∙2422
/125=65,592(Ом);
Хн
=(uкн
/100)∙Uв2
/Sн= (31/100)∙2422
/125=145,239(Ом);
Эти сопротивления одинаковы для трансформаторов Т1 и Т2.
Т3, Т4:
ХТ3
=ХТ4
=(uк
/100)∙Uв2
/Sн=(11/100)∙2422
/80=80,526(Ом);
Т5:
ХТ5
=(uк
/100)∙Uв2
/Sн∙(КТ1
)2
= (10,5/100)∙1212
/125∙(242/121)2
=49,194(Ом);
Т5:
ХТ5
=(uк
/100)∙Uв2
/Sн∙(КТ1
)2
= (10,5/100)∙1212
/125∙(242/121)2
=49,194(Ом);
Т6:
ХТ6
=(uк
/100)∙Uв2
/Sн∙(КТ1
)2
= (10,5/100)∙1152
/32∙(242/121)2
=173,578(Ом);
Т7:
ХТ7
=(uк
/100)∙ Uв2
/Sн= (11/100)∙2302
/80=72,738(Ом);
Т8:
Трансформатор двухобмоточный с расщеплённой обмоткой НН
Кр=4∙(Uквн1
/ Uквн
-1)=4∙(20/28-1)=-1,143; где Uквн1
принято равным 20% согласно «Методическим указаниям».
Хн1
=Хн2
= (Uквн
/100) ∙Uн
2
/Sн
∙Кр
/2∙KT
1
2
=(28/100) ∙1152
/25∙(-1,143/2)∙(242/121)2
=-338,56(Ом);
ХВ
=(Uквн
/100) ∙Uн
2
/Sн
∙(1-Кр
/4)∙KT
1
2
==(28/100) ∙1152
/25∙(1+1,143/4)∙(242/121)2
=761,76(Ом);
Реакторы:
L1:
XL
1
=Х∙(KT
4
)2
=0.4∙(242/10,5)2
=212,477(Ом);
L2
XL
2
=Х∙(KT
2
)2
=30∙(242/121)2
=120(Ом);
Линии:
Xw1
=0.427∙70∙(KT2
)2
=0.427∙70∙(242/121)2
=119,56(Ом);
Xw2
=0.427∙40∙(KT2
)2
=0.427∙40∙(242/121)2
=68,32(Ом);
Xw3
=0.427∙52∙(KT2
)2
=0.427∙52∙(242/121)2
=88,816(Ом);
Xw4
=0.405∙80∙(KT2
)2
=0.405∙80∙(242/121)2
=129,6(Ом);
Xw
5
=0.435∙70=30,45(Ом);
Xw6
=0.435∙200=87(Ом);
Xw7
=0.435∙61=0.435∙61=26,535(Ом);
Xw
8
=0.427∙70∙(KT
2
)2
=0.435∙70∙(242/121)2
=119,56(Ом);
Синхронный компенсатор:
GS: XGS
=x’’
d
∙Uн
2
/Sн
∙(КТ6
)2
∙(КТ1
)2
=0,165∙(112
/15) ∙(115/10,5)2
∙(242/121)2
=638,6385(Ом);3
EGS
=(1+ x’’
d
)∙Uн
∙КТ6
∙КТ5
=(1+0,165)∙11∙(115/10,5) ∙(242/121)=280,7095(кВ);
Обобщённая нагрузка:
Н1:
Xн1
=Х’’
н*(н)
∙Uн
2
/Sн
∙(КТ6
)2
∙(КТ2
)2
=0,35∙(10,52
/20)∙(115/10,5)2
∙(242/121)2
=925,75(Ом);
Ен1
=Е’’
н*(н)
∙ Uн
∙(КТ6
)∙(КТ2
)=0,85∙10,5∙(115/10,5)∙(242/121)=195,5(кВ);
Н2:
Xн2
=Х’’
н*(н)
∙Uн
2
/Sн
∙(КТ7
)2
=0,35∙(10,52
/12)∙(230/11)2
=1405,839(Ом);
Ен1
=Е’’
н*(н)
∙ Uн
∙(КТ7
) =0,85∙10,5∙(230/11) =186,6(кВ);
Н3:
Xн3
=Х’’
н*(н)
∙Uн
2
/Sн
∙(КТ8
)2
∙(КТ2
)2
=0,35∙(10,52
/7)∙(115/10,5)2
∙(242/121)2
=2645(Ом);
Ен3
=Е’’
н*(н)
∙Uн
∙(КТ8
)∙(КТ2
)=0,85∙10,5∙(115/10,5)∙(242/121)=195,5(кВ);
Н4:
Xн4
=Х’’
н*(н)
∙Uн
2
/Sн
∙(КТ8
)2
∙(КТ2
)2
=0,35∙(10,52
/8)∙(115/10,5)2
∙(242/121)2
=2314,375(Ом);
Ен4
=Е’’
н*(н)
∙Uн
∙(КТ8
)∙(КТ2
)=0,85∙10,5∙(115/10,5)∙(242/121)=195,5(кВ);
Соседняя энергосистема:
E=242B;
XC
=Uн
2
/Sk
∙(KT
5
)2
∙(KT
2
)2
=10,52
/250∙(121/10,5)2
∙(242/121)2
=234,256(Ом);
 Рис. 2.1. Схема замещения сети Рис. 2.1. Схема замещения сети
Для нахождения тока трехфазного короткого замыкания необходимо эквивалентировать схему относительно точки КЗ при помощи известных методов (последовательное и параллельное включение элементов, преобразования из звезды в треугольник и обратно).
Сначала сложим все последовательно включенные сопротивления (рис2.1.), в результате получим схему рис. 2.2.
XT
3
W
7
=XT
3
+XW
7
=80,526+26,535=136.195(Ом);
XT
4
W
5
=XT
4
+XW
5
=80,526+30,45=110.976(Ом);
ХН2Т7
=ХН2
+ХТ7
=1405,839+72,738=1478,577(Ом);
XG
1
T
1
H
=XG
1
+XT
1
H
=223,324+145,239=368,563(Ом);
XG
2
T
2
H
=XG
2
+XT
2
H
=223,324+145,239=368,563(Ом);
ХT
8
HH
1
H
3
=XT
8
H
1
+XH
3
=-338,56+2645=2306,44(Ом);
ХT
8
HH
2
H
4
=XT
8
H
2
+XH
4
=-338,56+2314,375=1975,815(Ом);
ХСТ5
=XС
+XТ5
=234,256+49,194=283,45(Ом);
Так как потенциалы точек 6 и 7 равны, то их можно объединить и треугольник XG
4
XG
3
XL
1
преобразовать в звезду:
Х1
=XG
3
XG
4
/(XG
4
+XG
3
+XL
1
)=38,256(Ом); Х2
= =XL
1
XG
3
/(XG
4
+XG
3
+XL
1
)=59,683(Ом);
Х3
= XL
1
XG
4
/(XG
4
+XG
3
+XL
1
)=59,683(Ом);
Складываем параллельно ветви с ЭДС EG
1
, EG
2
:
E2
=(EG1
XG2T2H
+EG2
XG1T1H
)/(XG2T2H
+XG1T1H
)=262,764(кВ);
XGT
12
=XG
1
T
1
H
/2=368,563/2=184,281(Ом)
Преобразуем параллельное соединение сопротивлений ХТ2С
иХТ1С
:
ХТ12С
=ХТ2С
/2=65,592/2=32,796(Ом);
Преобразуем параллельное соединение ветвей с ЕН3
и ЕН4
:
ЕН34
=(EН3
XТ8НН2Н4
+EН4
XТ8НН1Н3
)/(X Т8НН2Н4
+X Т8НН1Н3
)=195,5(кВ);
ХН34
= XТ8НН2Н4
∙ XТ8НН1Н3
/(XТ8НН2Н4
+XТ8НН1Н3
)=
=1975,815∙2306,444/(1975,815+2306,444)=1064,182(Ом);
Преобразуем параллельное соединение ветвей с ЕGS
и ЕН1
:
ЕGSH
=(EGS
XН1
+EН1
XGS
)/(X GS
+X Н1
)=(280.71∙925,75+195,5∙ 638,639)/(638,639+925,75)=245,924(кВ);
ХGS
Н
=XGS
∙ XН1
/(XН1
+XGS
)= 925.75∙638.639/(638.639+925.75)
=377,924(Ом);
Получившаяся схема – на рис. 2.3.
Сложим последовательные сопротивления (рис. 2.4)
ХGST
6
=XGSH
+XT
6
=377.924+173.578=551.502(Ом);
XH
34
T
8
=XH
34
+XT
8
B
=1064,182+761,781=1825,942(Ом);
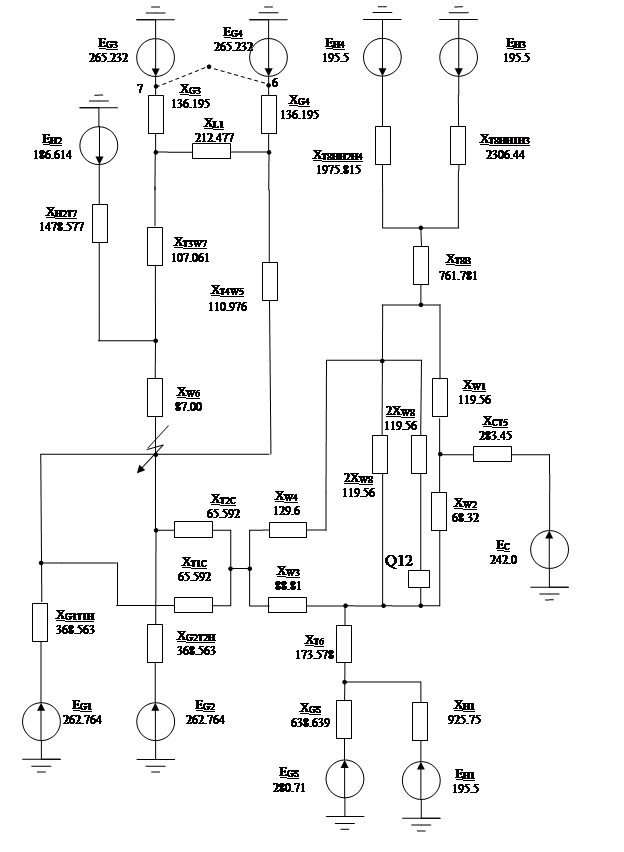
Рис. 2.2.
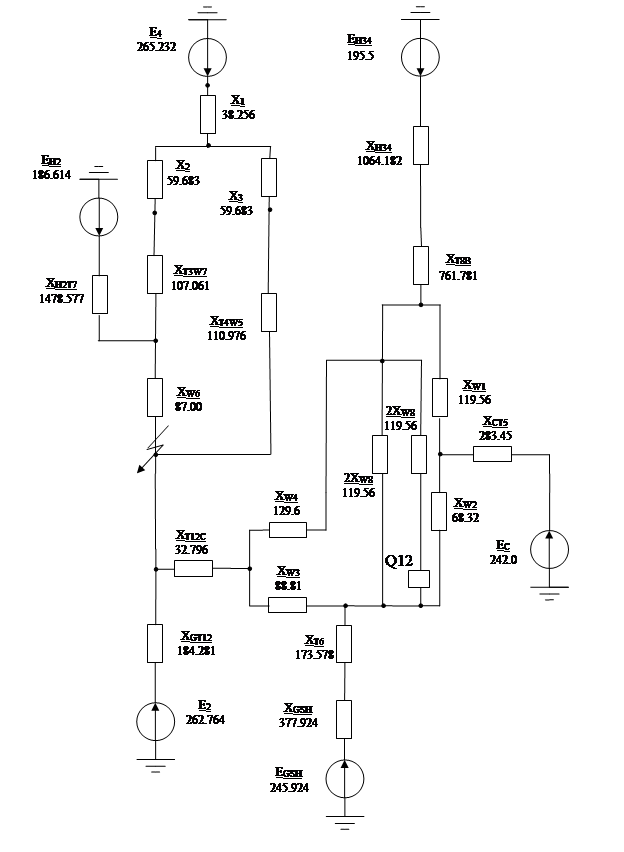
Рис 2.3.

Рис. 2.4
Далее преобразуем звезду 4-5-6 в треугольник:
Х45
=Х4
+Х5
+Х4
Х5
/Х6
=166,744+87+166,744∙87/1478,577=263,555(Ом);
Х46
=Х4
+Х6
+Х4
Х6
/Х5
=166,744+1478,577+166,744∙1478,577/87=4479,15(Ом);
Х56
=Х5
+Х6
+Х5
Х6
/Х4
=87,00+1478,577+87∙1478,577/166,744=2337,038(Ом);
Также преобразуем звезду XW
1
– XW
2
– XCT
5
в треугольник 7-8-9:
Х78
=ХW
1
+ХW
2
+ХW
1
ХW
2
/ХCT
5
=119,56+68,32+119,56∙68,32/283,45=216,698(Ом);
Х89
=ХW
2
+ХCT
5
+ХW
2
ХCT
5
/ХW
1
=68,32+283,45+68,32∙283,45/119,56=513,741(Ом);
Х79
=ХW
1
+ХCT
5
+ХW
1
ХCT
5
/ХW
2
=119,56+283,45+119,56∙283,45/68,32=899,047(Ом)
(Схема на рис. 2.5.)

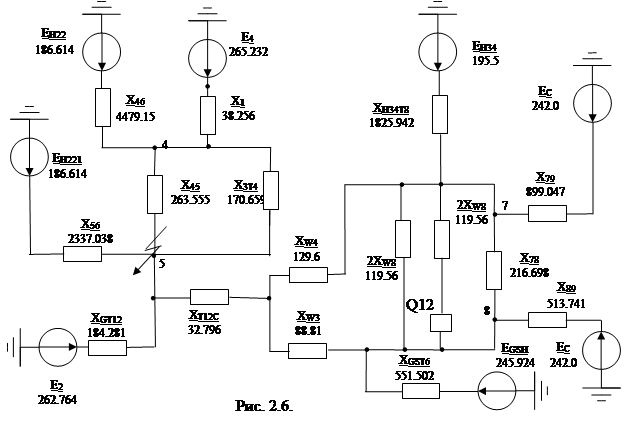
Рис. 2.5.
Перенесём ЭДС ЕН2
через узел 6, и ЕС
через узел 9 (рис. 2.6.)
Преобразуем параллельно соединённые ветви EН34
– ХН34Т8
и ЕС
– Х79
Е11
=(ЕС
∙ХН34Т8
+ЕН34
∙Х79
)/(ХН34Т8
+Х79
)= =(242,0∙1825,942+195,5∙899,047)/(1825,942+899,047)=226,658(кВ);
Х11
=ХН34Т8
∙Х79/(ХН34Т8
+Х79
)=1825,942∙899,047/(1825,942+899,047)= =602,427(Ом);
Преобразуем параллельно соединённые ветви EGSH
– ХGST
6
и ЕС
– Х89
Е33
=(ЕС
∙ХGS
Т6
+ЕGSH
∙Х89
)/(ХGST
6
+Х89
)= =(242,0∙551,502+245,924∙513,741)/(551,502+513,741)=243,892(кВ);
Х3
=ХGST
6
∙Х89
/(ХGST
6
+Х89
)=551,502∙513,741/(551,502+513,741)=265,976(Ом);
Преобразуем параллельно соединённые ветви EH
22
– Х46
и Е4
– Х1
Е44
=(ЕH
22
∙Х1
+Е4
∙Х46
)/(Х1
+Х46
)= =(186,614∙38,256+265,232∙4479,15)/(38,256+4479,15)=264,566(кВ);
Х44
=Х1
∙Х46
/(Х1
+Х46
)=38,256∙4479,15/(38,256+4479,15)=37,932(Ом);
Преобразуем параллельно соединённые сопротивления Х45
и Х3Т4
Х345
=Х3Т4
∙Х45
/(Х3Т4
+Х45
)=170,659∙263,555/(170,659+263,555)=103,585(Ом);
Преобразуем параллельно соединённые сопротивления Х45
и Х3Т4
Х345
=Х3Т4
∙Х45
/(Х3Т4
+Х45
)=170,659∙263,555/(170,659+263,555)=103,585(Ом);
Преобразуем параллельно соединённые ветви EH
221
– Х56
и Е2
– ХGT
12
Е22
=(ЕH
221
∙ХGT
12
+Е2
∙Х56
)/(ХGT
12
+Х56
)=
=(186,614∙184,281+262,764∙2337,038)/(184,281+2337,038)=257,198(кВ);
Х22
=ХGT
12
∙Х56
/(ХGT
12
+Х56
)=184,281∙2337,038/(184,281+2337,038)=170,812(Ом);
Преобразуем параллельно соединённые сопротивления 2ХW
8
и Х78
ХW
87
=(2ХW
8
)∙Х78
/(2ХW
8
+Х78
)=119,56∙216,698/(119,56+216,698)=77,049(Ом); Схема после данных преобразований на рис. 2.7.

Преобразуем последовательно соединённые сопротивления Х44
и Х345
:
Х445
=Х44
+Х345
=37,932+103,585=141,517(Ом);
Преобразуем параллельно соединённые сопротивления 2ХW
8
и ХW87
ХW
878
=(2ХW
8
)∙ХW
87
/(2ХW
8
+ХW
87
)=119,56∙77,049/(119,56+77,049)=46,854(Ом);
(рис 2.8.)

Преобразуем треугольник XW
4
XW
878
XW
3
в звезду:
ХY
1
=XW
878
∙XW
3
/(XW
878
+XW
3
+XW
4
)=46,845∙88,81/(46,845+88,81+129,6)= =15,687(Ом);
ХY
2
=XW
4
∙XW
878
/(XW
878
+XW
3
+XW
4
)=129,6∙46,845∙/(46,845+88,81+129,6)= =22,891(Ом);
ХY
3
= XW
4
∙XW
3
/(XW
878
+XW
3
+XW
4
)= =129,6∙88,81/(46,845+88,81+129,6)=43,392(Ом);
Преобразуем параллельно соединённые ветви E22
– Х22
и Е44
– Х445
Е24
=(Е22
∙Х445
+Е44
∙Х22
)/(Х445
+Х22
)= =(257,198∙141,517+264,566∙170,812)/(141,517+170,812)=261,228(кВ);
Х24
=Х22
∙Х445
/(Х22
+Х445
)=170,812∙141,517/(170,812+141,517)=77,395(Ом);
(рис. 2.9.)

Преобразуем последовательно соединённые сопротивления ХТ12С
и ХY
3
:
ХT
2
Y
3
=ХT
12
C
+ХY
3
=32,796+43,392=76,188(Ом);
Преобразуем последовательно соединённые сопротивления X11
и XY
2
:
Х1
Y
2
=Х11
+ХY
2
=602,427+22,891=625,318(Ом);
Преобразуем последовательно соединённые сопротивления X3
и XY
1
:
Х3
Y
1
=Х3
+ХY
1
=265,976+15,687=281,663(Ом);
(Рис 2.10.)

Преобразуем параллельно соединённые ветви E11
– Х1
Y
2
и Е33
– Х3
Y
1
Е31
=(Е11
∙Х3
Y
1
+Е33
∙Х1
Y
2
)/(Х3
Y
1
+Х1
Y
2
)= =(226,658∙281,664+243,892∙625,318)/(281,664+625,318)=238,54(кВ);
ХY
32
=Х1
Y
2
∙Х3
Y
1
/(Х1
Y
2
+Х3
Y
1
)=625,318∙281,664/(625,318+281,664) =194,193(Ом);
(Рис 2.11.)

Преобразуем последовательно соединённые сопротивления XT
2
Y
3
и XY
32
:
ХTY
=ХT
2
Y
3
+ХY
32
=76,188+194,193=270,381(Ом);
ETY
=E31
; (Рис. 2.12.)
 
Определим действующее значение сверхпереходной периодической составляющей тока трехфазного КЗ:
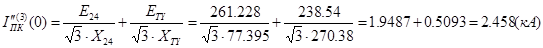 ; ;
Ударный коэффициент принимаем равным 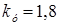 . .
Ударный ток в точке КЗ:
 . .
Для определения тока в ветви с выключателем развернем обратно схему замещения. Токи в ветвях будем находить при помощи метода узловых потенциалов. (см. рис. 2.8, 2.9, 2.10).
φМ
=(ETY
∙XT
2
Y
3
)/XTY
=67.216(кВ);
φ7
= E11
- (E11
- φМ
)∙X11
/X1
Y
2
=226,658 - (226,658-67,216)∙602,427/625,318= =73,0525(кВ);
φ8
=Е33
- (E33
- φМ
)∙X3
/X3
Y
1
=243,892-(243,892-67,216)∙265,976/281,664= =77,056(кВ);
I(3)
Q
12
=(φ8
- φ7
)/(2XW
8
∙√3)∙(KT
2
)=(77.056-73.0525)/(119.56∙√3)∙2=0.038665(кА)= =38,665(А) – ток через выключатель с учётом коэффициента трансформации.
Ударный ток в ветви с выключателем:
iyQ
12
=√2∙I(3)
Q
12
∙kуд
=√2∙38,665∙1,8=98,425(А)
Наибольшее действующее значение полного тока КЗ через выключатель:

Схема замещения для данного метода приведена на рис. 3.1. Она получена на основе схем рис. 2.4-2.5. с учётом отбрасывания ветвей с нагрузками до места их присоединения.
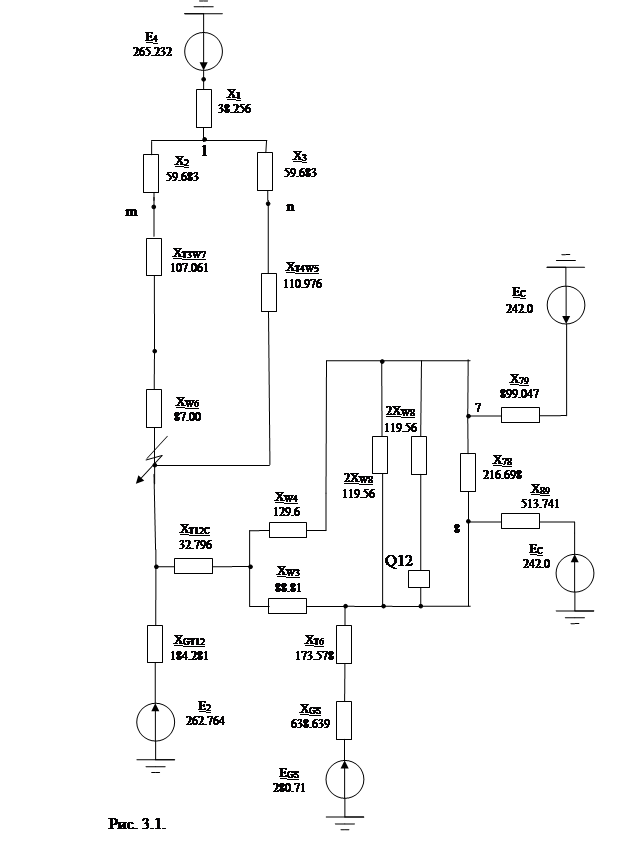
Х4
=Х2
+ХТ3
W
7
+XW
6
=59.683+107.061+87.00=253.744(Ом);
Х5
=Х3
+ХТ4
W
5
=59.683+110.976=170.659(Ом);
ХGST
6
=XT
6
+XGS
=173.578+638.639=812.217(Ом);
Три параллельно соединённых сопротивления: 2ХW
8
, 2XW
8
, X78
.
X7
=X78
∙ХW
8
/(X78
+ХW
8
)=216.698∙59.78/(216.698+59.78)=46.854(Ом);
Где ХW
8
=2XW
8
/2=119.56/2=59.78(Ом);
Рис. 3.2.

Преобразуем параллельно соединённые ветви EС
– Х89
и ЕGS
– ХGST
6
Е5
=(ЕC
∙ХGST
6
+ЕGS
∙Х89
)/(Х6
+Х89
)= =(242,0∙812,217+280,71∙513,741)/(812,217+513,741)=256,998(кВ);
ХE5
= ХGST
6
∙Х89
/( Х6
+Х89
)=812,217∙513,741/(812,217+513,741)=314,693(Ом);
Полученная схема – на рис.3.3.

Преобразуем параллельно соединённые сопротивления Х4
и Х5
Х6
=Х4
∙Х5
/(Х4
+Х5
)=253,744∙170,659/(253,744+170,659)=102,034(Ом);

Преобразуем треугольник XW
4
, XW
3
, X7
в звезду:
X7’
=XW
3
∙XW
4
/(XW
3
+XW
4
+X7
)=88.81∙129.6/(88.81+129.6+46.845)=43.392(Ом)
XР
7
=X7
∙XW4
/(XW3
+XW4
+X7
)=46.845∙129.6/(88.81+129.6+46.845)=22.891(Ом)
XР8
=XW
3
∙X7
/(XW
3
+XW
4
+X7
)=88.81∙46.845/(88.81+129.6+646.845)=15.687(Ом)
Полученная схема на рис. 3.5.

Преобразуем последовательно соединённые сопротивления XР7
и X79
:
ХР79
=ХР7
+Х79
=22,891+899,047=921,938(Ом);
Преобразуем последовательно соединённые сопротивления XР8
и XЕ5
:
ХРЕ5
=ХР8
+ХЕ5
=15,687+314,693=330,38(Ом);
Преобразуем последовательно соединённые сопротивления X6
и X1
:
Х8
=Х6
+Х1
=102,034+38,256=140,29(Ом);
Схема после данных преобразований – на рис. 3.6.

Преобразуем параллельно соединённые ветви EС
– ХР79
и Е5
– ХРЕ5
ЕС5
=(ЕC
∙ХРЕ5
+Е5
∙ХР79
)/(ХР79
+ХРЕ5
)= =(242,0∙330,38+256,998∙921,938)/(921,938+330,38)=253,041(кВ);
Х9
= ХРЕ5
∙ХР79
/(ХРЕ5
+ХР79
)= 330,38∙921,938/(330,38+921,938)=243,221(Ом);
Полученная схема – на рис.3.7.

Преобразуем последовательно соединённые сопротивления X7’
, X9
и ХТ12С
:
Х10
=Х7’
+Х9
+ХТ12С
=43,392+243,221+32,796=319,409(Ом); (рис. 3.8.)
 
3.3 Определение изменения периодической составляющей тока КЗ во времени
Определим действующее значение сверхпереходной периодической составляющей тока КЗ (см. рис. 3.8):

Определим токи в ветвях с генераторами:
φl
=(E4
/X8
)∙X1
=265.232/140.29∙102.034=192.905(кВ); см. рис 3.1., 3.8.
φm
=φl
-φl
/(X2
+XT
3
W
7
+XW
6
)∙XW
6
=192.905+192.905/(59.683+107.061+87.00)∙59.683= =147.532(кВ); см. рис 3.8., 3.9.

φn
=φl
-φl
/(X3
+XT
4
W
5
)∙X3
=192.905--192.905/(59.683+110.976)∙59.683==125.442(кВ);
см. рис 3.8., 3.9.
IG3
(0)=(EG3
-φm
)/(√3∙XG3
)=(265.232--147.532)/(√3∙136.195)=0.4989(кА);
IG4
(0)=(EG4
-φn
)/(√3∙XG4
)=(265.232--125.445)/(√3∙136.195)=0.593(кА);
IG1
(0)=IG2
(0)=EG2
/(XG1T1H
∙√3)=262.764/(368.563∙√3)=0.4116(кА); (см. рис 2.2)
Найдём токи в ветви с системой и синхронным компенсатором
φР
=ЕС5
-ЕС5
∙X9
/X10
=253.041-253.041/(319.409)∙243.221=60.357(кВ);
(рис. 3.6, 3.7)
φ7
=ЕС
-(ЕС
-φР
)∙X79
/XP
79
=242.0-(242.0-60.357)/(921.938)∙899.047=64.867(кВ); (рис. 3.5, 3.6)
φ8
=Е5
-(Е5
-φР
)∙XЕ5
/XP
Е5
=256.998-(256.998-60.357)/(330.38)∙314.693=69.694(кВ); (рис. 3.5, 3.6)
IGS
(0)=(EGS
-φ8
)/(ХGS
Т6
∙√3)=(280.71-69.694)/(812.217∙√3)=0.15(кА);
(см. рис. 3.2.)
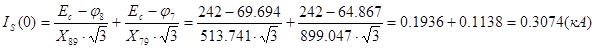 ; (см. рис. 3.2.) ; (см. рис. 3.2.)
Определим номинальный ток синхронного компенсатора , приведённый к 9базисному напряжению по формуле:
Iн
GS
=S/(√3∙Uн
∙KT
1
∙KT
6
)=15/(√3∙10.5∙(115/10.5)∙(242/121))=0.0377(кА).
Для G1: Iн
=37.5/(√3∙242)=0.0895(кА).
Далее находим номер типовой кривой. nGS
=IGS
(0)/Iн
GS
=0.15/0.0377=3.984≈4;
Определим номинальные токи генераторов , приведённые к базисному напряжению по формуле:
Iн
=S/(√3∙Uн
∙KTi
)= S/(√3∙242).
Для G1: Iн
=37.5/(√3∙242)=0.0895(кА).
Номер типовой кривой определяется аналогично синхронному компенсатору.
Для остальных генераторов данные сведены в таблицу:
Таблица 2.
| |
G1
|
G2
|
G3
|
G4
|
GS
|
S
|
| Iп
(0)
|
0,412
|
0,412
|
0,499
|
0,593
|
0,150
|
0,307
|
| Iном
|
0,089
|
0,089
|
0,164
|
0,164
|
0,038
|
1
|
| n(расч.)
|
4,601
|
4,601
|
3,040
|
3,610
|
3,984
|
-
|
| n
|
5
|
5
|
3
|
4
|
5
|
-
|
Примечание: ток величину периодической составляющей тока энергосистемы считаем постоянной на всём протяжении к.з.
По типовым кривым для нужных моментов времени находим γ=Iп
(t)/Iном
;
Определяем для каждого элемента Iп
(t) и находим изменение периодической составляющей тока к.з. в месте замыкания по формуле: I(t)(3)
=IG
1
(t)+IG
2
(t)+IG
3
(t)+IG
4
(t)+IGS
(t)+IS
;
Таблица 3. Расчёт методом типовых кривых
| t,c
|
IG
1
(t),
кА
|
IG
2
(t),
кА
|
IG
3
(t), кА
|
IG
4
(t), кА
|
IGS
(t), кА
|
IS
,
кА
|
I(t)(3)
, кА
|
| 0
|
0,412
|
0,412
|
0,499
|
0,593
|
0,150
|
0,307
|
2,372
|
| 0.05
|
0,391
|
0,391
|
0,479
|
0,557
|
0,141
|
0,307
|
2,266
|
| 0.1
|
0,340
|
0,340
|
0,444
|
0,516
|
0,130
|
0,307
|
2,077
|
| 0.15
|
0,313
|
0,313
|
0,424
|
0,492
|
0,124
|
0,307
|
1,973
|
| 0.2
|
0,303
|
0,303
|
0,419
|
0,471
|
0,119
|
0,307
|
1,922
|
| 0.25
|
0,296
|
0,296
|
0,409
|
0,462
|
0,117
|
0,307
|
1,888
|
| 0.3
|
0,288
|
0,288
|
0,404
|
0,456
|
0,115
|
0,307
|
1,860
|
| 0.35
|
0,284
|
0,284
|
0,403
|
0,450
|
0,114
|
0,307
|
1,842
|
| 0.4
|
0,282
|
0,282
|
0,402
|
0,444
|
0,112
|
0,307
|
1,830
|
| 0.45
|
0,280
|
0,280
|
0,401
|
0,441
|
0,112
|
0,307
|
1,821
|
| 0.5
|
0,280
|
0,280
|
0,400
|
0,439
|
0,111
|
0,307
|
1,817
|
| 0.6
|
0,276
|
0,276
|
0,400
|
0,439
|
0,111
|
0,307
|
1,808
|
| 0.7
|
0,276
|
0,276
|
0,399
|
0,439
|
0,111
|
0,307
|
1,808
|
| 0.8
|
0,276
|
0,276
|
0,399
|
0,436
|
0,110
|
0,307
|
1,804
|
| 0.9
|
0,275
|
0,275
|
0,400
|
0,439
|
0,111
|
0,307
|
1,806
|
| 1.0
|
0,274
|
0,274
|
0,400
|
0,439
|
0,111
|
0,307
|
1,805
|
| 1.1
|
0,272
|
0,272
|
0,400
|
0,436
|
0,110
|
0,307
|
1,797
|
| 1.2
|
0,270
|
0,270
|
0,400
|
0,433
|
0,109
|
0,307
|
1,789
|
| 1.3
|
0,269
|
0,269
|
0,400
|
0,433
|
0,109
|
0,307
|
1,787
|
| 1.4
|
0,268
|
0,268
|
0,400
|
0,430
|
0,109
|
0,307
|
1,781
|
| 1.5
|
0,263
|
0,263
|
0,400
|
0,427
|
0,108
|
0,307
|
1,769
|
| 1.6
|
0,261
|
0,261
|
0,401
|
0,427
|
0,108
|
0,307
|
1,765
|
| 1.7
|
0,259
|
0,259
|
0,401
|
0,424
|
0,107
|
0,307
|
1,758
|
| 1.8
|
0,257
|
0,257
|
0,401
|
0,421
|
0,106
|
0,307
|
1,750
|
| 1.9
|
0,255
|
0,255
|
0,401
|
0,418
|
0,106
|
0,307
|
1,742
|
| 2.0
|
0,255
|
0,255
|
0,401
|
0,415
|
0,105
|
0,307
|
1,740
|
| 2.1
|
0,255
|
0,255
|
0,401
|
0,415
|
0,105
|
0,307
|
1,740
|
| 2.2
|
0,255
|
0,255
|
0,401
|
0,415
|
0,105
|
0,307
|
1,740
|
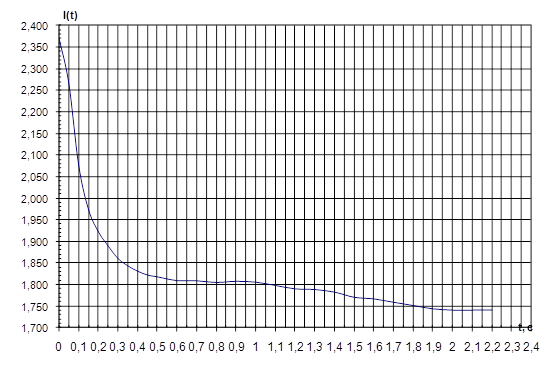
Рис. 3.10 Изменение тока в месте замыкания во времени
3.4 Расчёт мощности К.З.
S=√3∙Uб
∙I(0)(3)
=√3∙242∙2,372=994,239(МВА);
4
Расчет несимметричного КЗ методом симметричных составляющих
Несимметричные короткие замыкания могут служить расчетными видами КЗ для выбора и проверки аппаратов и проводников(сети 110 кВ и выше), а также при расчетах уставок и проверке на чувствительность цепей РЗА. В сетях 110-220 кВ обычно используется  , , 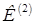 и и 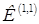 . В нашем случае примем для расчета . В нашем случае примем для расчета  . .
При расчете используем метод симметричных составляющих и правило эквивалентности прямой последовательности. Определим ток прямой последовательности особой фазы А в месте КЗ, а далее найдем все остальные симметричные составляющие токов и напряжений.
4.1
Составление схем замещения отдельных последовательностей
Схема замещения прямой последовательности аналогична схеме рассмотренной при расчете трехфазного КЗ. (см. рис. 2.12).
Е1Σ
=(Е24
∙XTY
+ETY
∙X24
)/(X24
+XTY
)=
=(261.228∙270.38+238.54∙77.395)/(77.395+270.38)=256.179(кВ); (4.1)
Х1
Σ
=XTY
∙X24
/(X24
+XTY
)=270,38∙77,395/(270,38+77,395)=60,171(Ом); (4.2)
Схема замещения обратной последовательности аналогична схеме прямой, но без ЭДС генерирующих ветвей, следовательно:
Х2Σ
=60,171.(4.3)
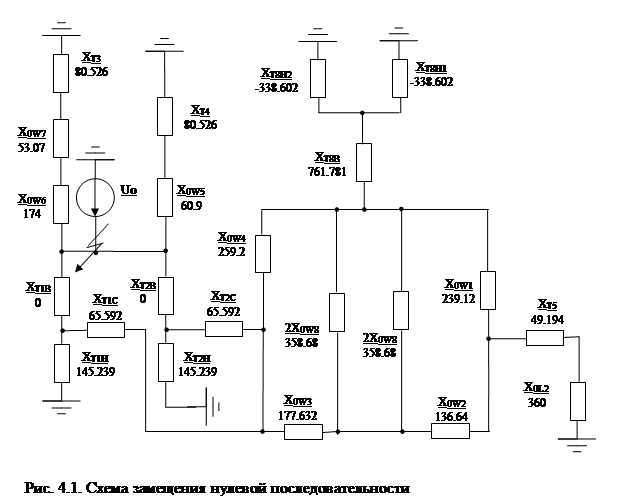
Схема замещения нулевой последовательности (см. рис. 4.1) будет зависеть от режима работы нейтралей трансформаторов. Сопротивления нулевой последовательности трансформаторов будут равны сопротивлениям прямой последовательности. Сопротивления линий будут отличаться на коэффициент k, зависящий от наличия или отсутствия грозозащитного троса линии. В нашем случае примем, что все одноцепные и двухцепные линии имеют грозозащитный трос, коэффициенты равны 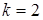 и и  соответственно. соответственно.
Определим сопротивления линий с учетом вышесказанного:
X0
W
1
=2∙119.56=239.12(Ом);
X0
W
2
=2∙68.32=136.64(Ом);
X0
W
3
=2∙88.816=177.632(Ом);
X0
W
4
=2∙129.6=259.2(Ом);
X0
W
5
=2∙30.45=60.9(Ом);
X0
W
6
=2∙87=174(Ом);
X0
W
7
=2∙26.535=53.07(Ом);
X02
W
8
=3∙119.56=358.68(Ом);
Сопротивление реактора L2 учитываем утроенной величиной: Х0
L
2
=3∙120=360(Ом). (рис 4.1.)
4.2
Преобразование схемы замещения к простейшему виду
Преобразуем последовательно соединённые сопротивления XT
5
и X0
L
2
:
Х0Т5
L
2
=XT
5
+X0
L
2
=49.194+360=409.194(Ом);
Преобразуем последовательно соединённые сопротивления XT
3
, X0
W
7
и X0
W
6
:
X0T3W7
=XT3
+X0W7
+X0W6
=80.526+53.07+174=307.596(Ом);
Преобразуем последовательно соединённые сопротивления XT
4
и X0
W
5
:
X0
T
4
W
5
=XT
4
+X0
W
5
=80.526+60.9=141.426(Ом);
Преобразуем параллельно соединённые сопротивления XT
1Н
и XТ2Н
:
Х0АТН
=ХТ1Н
/2=145,239/2=72,619(Ом);
Параллельно соединённые сопротивления XT
1С
и XТ2С
уже преобразовывались в главе 2 курсового проекта:
Х0АТС
=ХТ12С
=32,796(Ом);
Х0Т8
=ХТ8В
+ХТ8Н1
/2=761,781-169,301=592,48(Ом); (рис. 4.2.)

Х0
W8
=179.34(Ом); (см. рис. 4.3.)

Преобразуем звезду 7-8-9 в треугольник:
Х078
=Х0
W
1
+Х0
W
2
+Х0
W
1
Х0
W
2
/Х0
T
5
L
2
=239,12+136,64+239,12∙136,64/409,194=455,608(Ом);
Х079
=Х0
W
1
+Х0
T
5
L
2
+Х0
W
1
Х0
T
5
L
2
/Х0
W
2
=239,12+409,194+239,12∙409,194/136,64= =1364,403(Ом);
Х089
=Х0
W
2
+Х0
T
5
L
2
+Х0
W
2
Х0
T
5
L
2
/Х0
W
1
=136,64+409,194+136,64∙409,194/239,12= =779,659(Ом); (рис. 4.4.)

Преобразуем параллельно соединённые X0
W
8
и X078
:
Х088
=Х0
W
8
∙X078
/(Х0
W
8
+X078
)=179.34∙455.608/(179.34+455.608)=128.686(Ом);
Сопротивления Х079
и Х089
можно «разрезать» по узлу 9. (рис 4.5.)

Преобразуем треугольник X0
W
4
– X0
W
3
– X088
в звезду:
X01
=X0
W
3
∙X0
W
4
/(X0
W
3
+X0
W
4
+Х088
)=177,632∙259,2/(177,632+259,2+128,686)=81,416(Ом);
X07’
=X088
∙X0
W
4
/(X0
W
3
+X0
W
4
+Х088
)=128,686∙259,2/(177,632+259,2+128,686)=58,982(Ом);
X08’
=X088
∙X0
W
3
/(X0
W
3
+X0
W
4
+Х088
)=128,686∙177,632/(177,632+259,2+128,686)=40,421(Ом);
Рис. 4.6.

Преобразуем последовательно соединённые сопротивления Х0АТС
и Х01
:
Х0А1
=Х0АТС
+Х01
=32,796+81,416=114,212(Ом);
Преобразуем последовательно соединённые сопротивления X0789
и X07’
:
Х0789’
=X0789
+X07’
=413,096+58,982=472,078(Ом);
Преобразуем последовательно соединённые сопротивления X089
и X08’
:
Х089’
=X089
+X08’
=779,659+40,421=820,08(Ом); (рис. 4.7.)

Х01А1
=Х0А1
+Х0789’
∙X089’
/(X089’
+X0789’
)=114,212+472,078∙820,08/(820,08+472,078)=413,821(Ом); (рис 4.8.).
 
Х0Σ
=Х01А1
∙Х0Р
/(Х01А1
+Х0Р
)=413,821∙41,507/(413,821+41,507)=37,723(Ом).
4.3 Определение расчетных величин
Ток прямой последовательности фазы А:
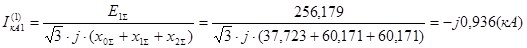
Iк
A2
=Iк
0
=IкА
1
=-j0,936(кА);
Для места к.з.:
IкА
=3∙IкА1
=3∙(-j0,936)=-j2,808(кА);
IкВ
=IкС
=0;
UкА1
=j(x2
Σ
+x0
Σ
)∙IкА1
=j(60,171+37,723)∙(-j0,936)=91,629(кВ);
Uка2
=-j∙x2
Σ
∙IкА1
=-j∙60,171∙(-j0,936)=-56,32(кВ);
U0
=-j∙37,723∙(-j0,936)=-35,309(кВ);
Напряжения фаз в месте К3:
UкА
=0;
UкВ
=UкА1
∙а2
+ UкА2
∙а+ U0
=91,629∙(-1/2-j√3/2)-56,32∙(-1/2+j√3/2)-35,309=-52.963-128.128j=138.643e-
j
112.459
(кВ);
UкС
= UкА1
∙а+ UкА2
∙а2
+ U0
=91,629∙(-1/2+j√3/2)-56,32∙(-1/2-j√3/2)-35,309==-52.963+128.128j=138.643ej
112.459
(кВ);
Векторные диаграммы токов и напряжений в месте КЗ представлены на рисунке в Приложении.
Определим ток в ветви с выключателем и напряжение в узле, наиболее близком к выключателю в режиме однофазного к.з. При расчёте потенциал узла, в котором произошло замыкание, принимаем равным напряжению той последовательности, для которой составляется схема замещения.
Для нулевой последовательности (см. рис. 4.8.):
Ток через сопротивление ХА101
: IA
101
=U0
/jXA
101
=-35,309/(j413,821)=
=j85,32(A); Направление тока: к месту замыкания.
φ010
=U0
-IA
101
∙jX0
A
1
=-35.309-j85.32∙j114.212/1000=-25.564(кВ) (см. рис. 4.7)
φ07
=φ010
∙jX07’
/j(X07’
+X0789
)+φ010
=25.564∙58.982/(58.982+413.096)-25.564=
=-22.37(кВ);
φ08
=|φ010
|∙jX08’
/j(X08’
+X089
)+φ010
=25.564∙40.421/(40.421+779.659)-25.564=
=-24.304(кВ);
I0
Q
12
=(φ07
-φ08
)/j2X0
W
8
=(-22.37-(-24.304))/j358.68=-j5.392(A); направление тока: от узла 7 к узлу 8.
Для прямой последовательности:
 
Ток через сопротивление ТY:
ITY
=(ETY
/√3-Uк
A
1
)j/XTY
=(238.54/√3-91.629)/j270.38=-j0.1705(кА); (рис. 4.9.)

φМ1
=Uк
A
1
+ITY
∙jXT
2
Y
3
=91,629-j0,1705∙j76,188=104,619(кВ); (рис. 4.10)

φ71
=φМ1
+(Е11
/√3-φМ1
)∙jXY
2
/j( XY
2
+ X11
)=104,619+(226,658/√3-104,619)∙22, 891/625,318=105,58(кВ);
φ81
=φМ1
+(Е33
/√3-φМ1
)∙jXY
1
/j( XY
1
+ X3
)=104,619+(243,892/√3-104,619)∙15,687/281,663=106,635(кВ);
(рис. 4.11.)
I1
Q
12
=(φ81
-φ71
)/j2XW
8
=(106,635-105,58)/119,56=-j8,82(А); Направление тока от узла 8 к узлу 7. (рис. 2.8.)
Обратная последовательность:
 
Ток через сопротивление ТY:
ITY
2
=Uк
A
2
/jXTY
=-56.32/j270.38=j0.208(кА); (рис. 4.12.)

φМ2
=Uк
A
2
-ITY
2
∙XT
2
Y
3
=-56,32-j0,208∙j76,188=-40,473(кВ); (рис. 4.13)
 
φ72
=φМ2
-φМ2
∙jXY
2
/j( XY
2
+ X11
)=-40.473+40.473∙22, 891/625,318=-38,991(кВ);
φ82
=φМ2
-φМ2
∙jXY
1
/j( XY
1
+ X3
)=-40.473+40.473∙15,687/281,663=-38,218(кВ);
(Рис 4.14.)
I2
Q
12
=(φ82
-φ72
)/j2XW
8
=(-38,218-(-38,991))/j119,56=-j6,46(А); Направление тока от узла 8 к узлу 7. (рис. 2.8.)
Токи в фазах в месте установки выключателя:
IQ
12
A
=I1
Q
12
+ I2
Q
12
+ I0
Q
12
=-j8,82-j6,46+j5.392=-9,888 (A);
IQ12
В
= I1Q12
∙а2
+ I2Q12
∙а+ I0Q12
=-j8.82∙(-1/2-j√3/2)-j6.46∙(-1/2+j√3/2)+j5,392=-2.044+13.032i=13.191ej98.963
(A);
IQ12C
= I1Q12
∙а+ I2Q12
∙а2
+ I0Q12
=-j8.82∙(-1/2+j√3/2)-j6.46∙(-1/2-j√3/2)+j5,392=2.044+13.032i=13.191ej81.128
(A);
UQ12
А
=φ81
+ φ82
+ φ80
=106.635-38.218-24.304=44.113(кВ);
UQ12
В
= φ81
∙а2
+ φ82
∙а+ φ80
=106,635∙(-1/2-j√3/2)-38, 218∙(-1/2+j√3/2)-24,304=-58.513+125.446i=138.421ej115.064
(кВ);
UQ12
С
= φ81
∙а+ φ82
∙а2
+ φ80
=106,635∙(-1/2+j√3/2)-38, 218∙(-1/2-j√3/2)-24,304=-58.513-125.446i=138.421e-j115.064
(кВ);
Векторные диаграммы см. в Приложении.
Найдем модуль периодической составляющей тока КЗ для точки несимметрии упрощенным способом:
I(1)
=m(1)
∙I(1)
A
1
=3∙-j0,936=-j2.808(кА).
Результаты расчетов сведем в таблицу 4.
| №
п/п
|
Величина
|
Метод эквивалентных ЭДС
|
Метод типовых кривых
|
Метод симметричных составляющих
|
| 1
|
Периодическая составляющая тока КЗ в месте повреждения, кА
|
2,458
|
2,372
|
2,808
|
| 2
|
Ударный ток в точке КЗ, кА
|
6,257
|
-
|
-
|
| 3
|
Ударный ток в ветви с выключателем, А
|
98,425
|
-
|
-
|
Расчет периодической составляющей тока КЗ методом типовых кривых даёт погрешность 3,5 % для нулевого момента времени, что является допустимым, вследствие того, что сам метод типовых кривых дает погрешность 10-20%.
Ударный ток в ветви с выключателем получился меньше вероятно возможного, так как выключатель достаточно удалён от места КЗ. Токи разных последовательностей имеют в ветви с выключателем разное направление. Ток трёхфазного КЗ получился несколько меньшим тока однофазного КЗ. Поэтому выбор оборудования и уставок РЗА должен производиться по току однофазного КЗ.
В данном курсовом проекте был произведён расчёт аварийных режимов в заданной схеме электроснабжения, а именно трёхфазного короткого замыкания и замыкания фазы на землю.
При нахождении параметров схемы замещения был использован метод точного приведения в именованных единицах. Там, где это необходимо, в качестве Uбаз
было принято напряжение ступени, на которой произошло к.з., а именно 242кВ.
Для расчёта тока трёхфазного замыкания был использован метод эквивалентных ЭДС.
Для нахождения изменения периодической составляющей тока к.з. во времени был использован метод типовых кривых. Мощность к.з. превышает суммарную номинальную мощность всех источников, что свидетельствует о большой нагрузке на оборудование в этом режиме, даже, несмотря на то, что точка к.з. относительно удалена от каждого конкретного источника.
При нахождении тока несимметричного замыкания был использован метод симметричных составляющих, в удобстве которого для расчёта токов и напряжений в любом месте схемы, мне и удалось убедиться при выполнении данного курсового проекта.
Для несимметричного короткого замыкания были построены векторные диаграммы токов и напряжений.
|