| Содержание
Иррациональные уравнения
Числовая функция. Способы задания функции
Основные свойства функции
Графики функций. Простейшие преобразования графиков функцией
Обратная функция
Степенная функции, её свойства и графики
Показательная функция, её свойства и графики
Показательные неравенства
Логарифмы и их свойства
Логарифмические уравнения
Тригонометрические функции числового аргумента
Функция y sinx ее свойства и график
Обратные тригонометрические функции, их свойства и графики
Частные случаи тригонометрических уравнений
Тригонометрические уравнения
Аксиомы стереометрии и следствия из них
Взаимное расположение двух прямых в пространстве
Скрещивающиеся прямые. Признак скрещивающихся прямых
Теорема о трех перпендикулярах
Алгебра
Действительные числа. Приближение действительных чисел конечными десятичными дробями.
Веще́ственное, или действи́тельное число - математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений [2]
. Если натуральные числа возникли в процессе счета, рациональные - из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами
.
Абсолютная погрешность и её граница.
Пусть имеется некоторая числовая величина, и числовое значение, которое ей присвоено 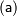 , считается точным, тогда под погрешностью приближенного значения числовой величины
(ошибкой
) , считается точным, тогда под погрешностью приближенного значения числовой величины
(ошибкой
) 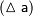 понимают разность между точным и приближенным значением числовой величины: понимают разность между точным и приближенным значением числовой величины: 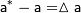 . Погрешность может принимать как положительное так и отрицательное значение. Величина . Погрешность может принимать как положительное так и отрицательное значение. Величина 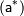 называется известным приближением
к точному значению числовой величины - любое число, которое используется вместо точного значения. Простейшей количественной мерой ошибки является абсолютная погрешность. Абсолютной погрешностью
приближенного значения называется известным приближением
к точному значению числовой величины - любое число, которое используется вместо точного значения. Простейшей количественной мерой ошибки является абсолютная погрешность. Абсолютной погрешностью
приближенного значения 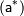 называют величину называют величину 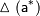 , про которую известно, что: , про которую известно, что: 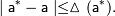 Относительная погрешность и её граница. Относительная погрешность и её граница.
Качество приближения существенным образом зависит от принятых единиц измерения и масштабов величин, поэтому целесообразно соотнести погрешность величины и ее значение, для чего вводится понятие относительной погрешности. Относительной погрешностью
приближенного значения называют величину 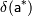 , про которую известно, что: , про которую известно, что: 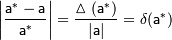 . Относительную погрешность часто выражают в процентах. Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерения. . Относительную погрешность часто выражают в процентах. Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерения.
Уравнение, в которых под знаком корня содержится переменная, называют иррациональными. При решении иррациональных уравнений полученные решения требуют проверки, потому, например, что неверное равенство при возведении в квадрат может дать верное равенство. В самом деле, неверное равенство при возведении в квадрат даёт верное равенство 12
= (-1) 2
, 1=1. Иногда удобнее решать иррациональные уравнения, используя равносильные переходы.
Возведём обе части этого уравнения в квадрат; После преобразований приходим к квадратному уравнению; и подставим.
Комплексные числа. Действия над комплексными числами.
Ко́мпле́ксные чи́сла - расширение множества вещественных чисел, обычно обозначается 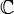 . Любое комплексное число может быть представлено как формальная сумма x
+ iy
, где x
и y
- вещественные числа, i
- мнимая единица Комплексные числа образуют алгебраически замкнутое поле - это означает, что многочлен степени n
с комплексными коэффициентами имеет ровно n
комплексных корней, то есть верна основная теорема алгебры. Это одна из основных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках - электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других. . Любое комплексное число может быть представлено как формальная сумма x
+ iy
, где x
и y
- вещественные числа, i
- мнимая единица Комплексные числа образуют алгебраически замкнутое поле - это означает, что многочлен степени n
с комплексными коэффициентами имеет ровно n
комплексных корней, то есть верна основная теорема алгебры. Это одна из основных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках - электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.
Сравнение a
+ bi
= c
+ di
означает, что a
= c
и b
= d
(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение (a
+ bi
) + (c
+ di
) = (a
+ c
) + (b
+ d
) i
.
Вычитание (a
+ bi
) − (c
+ di
) = (a
− c
) + (b
− d
) i
.
Умножение
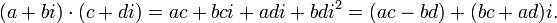
Деление 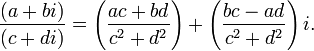
В математике числовая функция - это функция, области определения и значений которой являются подмножествами числовых множеств - как правило, множества действительных чисел 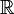 или множества комплексных чисел или множества комплексных чисел 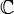 . .
Словесный: С помощью естественного языка Игрек равно целая часть от икс. Аналитический: С помощью аналитической формулы f
(x
) = x
!
Графический С помощью графика  Фрагмент графика функции Фрагмент графика функции 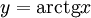 . .
Табличный: С помощью таблицы значений
| x
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| y
|
1
|
1
|
2
|
3
|
5
|
8
|
13
|
21
|
34
|
55
|
| |
|
|
|
|
|
|
|
|
|
|
1) Область определения функции и область значений функции
. Область определения функции
- это множество всех допустимых действительных значений аргумента x
(переменной x
), при которых функция y = f (x)
определена.
Область значений функции
- это множество всех действительных значений y
, которые принимает функция. В элементарной математике изучаются функции только на множестве действительных чисел.2) Нуль функции
- такое значение аргумента, при котором значение функции равно нулю.3) Промежутки знакопостоянства функции
- такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.4) Монотонность функции
. Возрастающая функция
(в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции. Убывающая функция
(в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.5) Четность (нечетность) функции
. Четная функция
- функция, у которой область определения симметрична относительно начала координат и для любого х
из области определения выполняется равенство f (-x) = f (x).
График четной функции симметричен относительно оси ординат. Нечетная функция
- функция, у которой область определения симметрична относительно начала координат и для любого х
из области определения справедливо равенство f (-x) = - f (x
). График нечетной функции симметричен относительно начала координат.6) Ограниченная и неограниченная функции
. Функция называется ограниченной
, если существует такое положительное число M, что |f (x) | ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная
.7) Периодическость функции
. Функция f (x) - периодическая
, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f (x+T) = f (x). Такое наименьшее число называется периодом функции
. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
График функции
- множество точек, у которых абcциссы являются допустимыми значениями аргумента x
, а ординаты - соответствующими значениями функции y
.
 Прямая линия
- график линейной функции y = ax + b
. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т.0 (y = ax - прямая пропорциональность) Прямая линия
- график линейной функции y = ax + b
. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т.0 (y = ax - прямая пропорциональность)
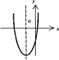 Парабола
- график функции квадратного трёхчлена у = ах2
+ bх + с
. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2
+ bx +с =0 Парабола
- график функции квадратного трёхчлена у = ах2
+ bх + с
. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2
+ bx +с =0
 Гипербола
- график функции Гипербола
- график функции 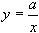 . При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х (а > 0) или у - х (а < 0). . При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х (а > 0) или у - х (а < 0).
 Логарифмическая функция y = loga
x
(a > 0) Логарифмическая функция y = loga
x
(a > 0)
Тригонометрические функции.
При построении тригонометрических функций мы используем радианную
меру измерения углов. Тогда функция y
= sin x
представляется графиком (рис. 19). Эта кривая называется синусоидой
.
 График функции y
= cos x
представлен на рис. 20; это также синусоида, полученная в результате перемещения графика y
= sin x
вдоль оси Х
влево на График функции y
= cos x
представлен на рис. 20; это также синусоида, полученная в результате перемещения графика y
= sin x
вдоль оси Х
влево на  /2. /2.
 
Основные свойства функций. Монотонность, четность, нечетность, периодичность функций.
Область определения функции и область значений функции
. Область определения функции
- это множество всех допустимых действительных значений аргумента x
(переменной x
), при которых функция y = f (x)
определена.
Область значений функции
- это множество всех действительных значений y
, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.2) Нуль функции
- такое значение аргумента, при котором значение функции равно нулю.3) Промежутки знакопостоянства функции
- такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.4) Монотонность функции
.
Возрастающая функция
(в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция
(в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.5) Четность (нечетность) функции
. Четная функция
- функция, у которой область определения симметрична относительно начала координат и для любого х
из области определения выполняется равенство f (-x) = f (x).
График четной функции симметричен относительно оси ординат. Нечетная функция
- функция, у которой область определения симметрична относительно начала координат и для любого х
из области определения справедливо равенство f (-x) = - f (x
). График нечетной функции симметричен относительно начала координат.6) Ограниченная и неограниченная функции
. Функция называется ограниченной
, если существует такое положительное число M, что |f (x) | ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная
.7) Периодическость функции
. Функция f (x) - периодическая
, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f (x+T) = f (x). Такое наименьшее число называется периодом функции
. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Периодические функции. Правила нахождения основного периода функции.
Периоди́ческая фу́нкция
― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода). Все тригонометрические функции являются периодическими. Являются неверными
утверждения относительно суммы периодических функций: Сумма 2 функций с соизмеримыми (даже основными) периодами T
1
и T
2
является функция с периодом НОК (T
1
,T
2
). Сумма 2 непрерывных функций с несоизмеримыми (даже основными) периодами является непериодической функцией. Не существует периодических функций, не равных константе, у которой периодами являются несоизмеримые числа.
Построение графиков степенных функций.
Степенная функция.
Это функция: y = axn
, где a, n
- постоянные. При n
= 1 получаем прямую пропорциональность
: y
= ax
; при n
= 2 - квадратную параболу
; при n
= 1 - обратную пропорциональность
или гиперболу
. Таким образом, эти функции - частные случаи степенной функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно, при n
= 0 степенная функция превращается в постоянную величину: y
= a
, т. e. её график - прямая линия, параллельная оси Х
, исключая начало координат (поясните, пожалуйста, почему?). Все эти случаи (при a
= 1) показаны на рис.13 (n
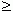 0) и рис.14 (n
< 0). Отрицательные значения x
здесь не рассматриваются, так как тогда некоторые функции: 0) и рис.14 (n
< 0). Отрицательные значения x
здесь не рассматриваются, так как тогда некоторые функции:
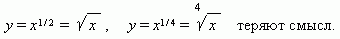  . .
Обра́тная фу́нкция
- функция, обращающая зависимость, выражаемую данной функцией. Функция 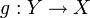 является обратной к функции является обратной к функции 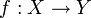 , если выполнены следующие тождества: , если выполнены следующие тождества: 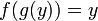 для всех для всех 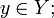 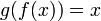 для всех для всех 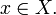
Предел функции в точке. Основные свойства предела.
Корень n-ой степени и его свойства.
Корнем n-ой степени из числа a называется такое число, n-ая степень которого равна a.
Определение: Арифметическим корнем n-ой степени из числа a называют неотрицательное число, n-ая степень которого равна a.
Основные свойства корней:

Степень с произвольным действительным показателем и его свойства.
Пусть дано положительное число 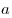 и произвольное действительное число и произвольное действительное число 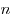 . Число . Число 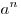 называется степенью, число называется степенью, число 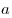 - основанием степени, число - основанием степени, число 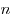 - показателем степени. - показателем степени.
По определению полагают:
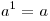 . .
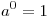 . .
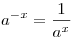 , , 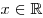 . .
Если 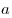 и и 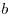 - положительные числа, - положительные числа, 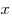 и и 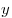 - любые действительные числа, то справедливы следующие свойства: - любые действительные числа, то справедливы следующие свойства:
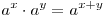 . .
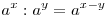 . .
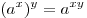 . .
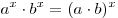 . .
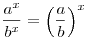 . .
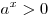 . .
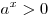
Степенная функция
комплексного переменного f
(z
) = zn
с целочисленным показателем определяется с помощью аналитического продолжения аналогичной функции вещественного аргумента. Для этого применяется показательная форма записи комплексных чисел. степенная функция с целочисленным показателем является аналитической во всей комплексной плоскости, как произведение конечного числа экземпляров тождественного отображения f
(z
) = z
. Согласно теореме единственности эти два признака достаточны для единственности полученного аналитического продолжения. Пользуясь таким определением, можно сразу сделать вывод о том, что степенная функция комплексного переменного обладает значительными отличиями от своего вещественного аналога.
Это функция вида 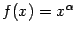 , , 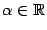 . Рассматриваются такие случаи: . Рассматриваются такие случаи:
а). Если 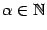 , то , то 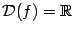 . Тогда . Тогда 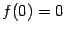 , , 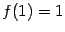 ; если число ; если число 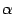 - чётное, то и функция - чётное, то и функция 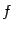 - чётная (то есть - чётная (то есть 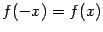 при всех при всех 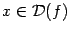 ); если число ); если число 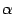 - нечётное, то и функция - нечётное, то и функция 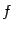 - нечётная (то есть - нечётная (то есть 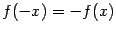 при всех при всех 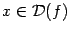 ). ).
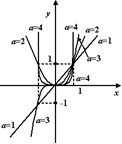
Показательная функция
- математическая функция 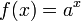 . .
В вещественном случае основание степени 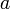 - некоторое неотрицательное вещественное число, а аргументом функции является вещественный показатель степени. - некоторое неотрицательное вещественное число, а аргументом функции является вещественный показатель степени.
В теории комплексных функций рассматривается более общий случай, когда аргументом и показателем степени может быть произвольное комплексное число.
В самом общем виде - uv
, введена Лейбницем в 1695 г.
Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной).
Свойства 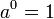 ; ; 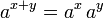 ; ; 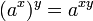 . .
Показательные уравнения.
Перейдем непосредственно к показательным уравнениям. Для того чтобы решить показательное уравнение необходимо воспользоваться следующей теоремой: Если степени равны и основания равны, положительны и отличны от единицы, то равны и их показатели степеней. Докажем эту теорему: Пусть a>1 и aх
=ay
.
Докажем, что в этом случае х=y. Допустим противное тому, что требуется доказать, т.е. допустим, что x>у или что x<у. Тогда получим по свойству показательной функции, что либо aх
<ay
либо aх
>ay
. Оба эти результата противоречат условию теоремы. Следовательно, x=у, что и требовалось доказать.
Также доказывается теорема и для случая, когда 0<a<1. Замечание. Из равенства aх
=ay
не обязательно следует что x=у. Из равенства 1х
=1y
также не обязательно вытекает равенство x=у. Самым простым показательным уравнением является уравнения вида aх
=ay
, где a>0 и a≠1.
Неравенства вида (или меньше) при а (х) >0
и решаются на основании свойств показательной функции: для 0 < а (х) < 1
при сравнении f (x)
и g (x)
знак неравенства меняется, а при а (х) > 1
- сохраняется. Самый сложный случай при а (х) < 0
. Здесь можно дать только общее указание: определить, при каких значениях х
показатели f (x)
и g (x)
будут целыми числами, и выбрать из них те, которые удовлетворяют условию. Наконец, если исходное неравенство будет выполняться при а (х) = 0
или а (х) = 1
(например, когда неравенства нестрогие), то нужно рассмотреть и эти случаи.
Логарифм числа b
по основанию a
(от греч. λόγος - "слово", "отношение" и ἀριθμός - "число" [1]
) определяется как показатель степени, в которую надо возвести основание a
, чтобы получить число b
. Обозначение: 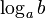 . Из определения следует, что записи . Из определения следует, что записи 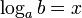 и и 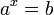 равносильны. Пример: равносильны. Пример: 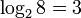 , потому что , потому что 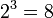 . Свойства . Свойства
Основное логарифмическое тождество: 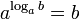
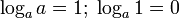
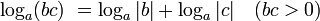
Логарифмическая функция, её свойства и графики.
Логарифмической функцией называется функция вида f
(x
) = loga
x
, определённая при 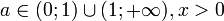
Область определения: 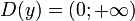
Область значения: 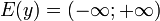
График любой логарифмической функции проходит через точку (1; 0)
Производная логарифмической функции равна:
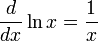
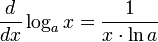 
Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим примером логарифмического уравнения служит уравнение loga
х = b (где а > 0, а
 1).
Его решение x = ab
. 1).
Его решение x = ab
.
Решение уравнений на основании определения логарифма, например, уравнение loga
х = b (а > 0, а  1)
имеет решение х = аb
. 1)
имеет решение х = аb
.
Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их:
если loga
f (х) = loga
g (х),
то f (х) = g (х),
f (х) >0
, g (х) >0
, а > 0
, а  1
. 1
.
Метод приведения логарифмического уравнения к квадратному.
Метод логарифмирования обеих частей уравнения.
Метод приведения логарифмов к одному и тому же основанию.
Логарифмические неравенства.
Неравенство, содержащее переменную только под знаком логарифма, называется логарифмическим: loga
f (х) > loga
g (х).
При решении логарифмических неравенств следует учитывать общие свойства неравенств, свойство монотонности логарифмической функции и область ее определения. Неравенство loga
f (х) > loga
g (х)
равносильно системе f (x) > g (x) > 0 при a > 1
и системе 0 < f (x) < g (x) при 0 < а < 1
.
Радианное измерение углов и дуг. Синус, косинус, тангенс, котангенс.
Градусная мера.
Здесь единицей измерения является градус (
обозначение ) -
это поворот луча на 1/360 часть одного полного оборота. Таким образом, полный оборот луча равен 360. Один градус состоит из 60 минут (
их обозначение ‘); одна минута - соответственно из 60 секунд (
обозначаются “).
Радианная мера.
Как мы знаем из планиметрии (см. параграф "Длина дуги" в разделе "Геометрическое место точек. Круг и окружность"), длина дуги l,
радиус r
и соответствующий центральный угол 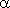 связаны соотношением: связаны соотношением: 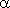 = l / r. = l / r.
Эта формула лежит в основе определения радианной меры измерения углов. Так, если l
= r,
то 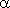 = 1, и мы говорим, что угол = 1, и мы говорим, что угол 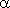 равен 1 радиану, что обозначается: равен 1 радиану, что обозначается: 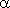 = 1 рад
. Таким образом, мы имеем следующее определение радианной меры измерения: = 1 рад
. Таким образом, мы имеем следующее определение радианной меры измерения:
Радиан есть центральный угол,
у которого длина дуги и радиус равны
(Am
B = AO, рис.1). Итак, радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги.

Тригонометрические функции острых углов можно определить как отношение длин сторон прямоугольного треугольника.
Синус:

Косинус:

Тангенс:

Котангенс:

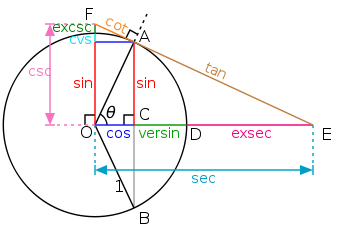
Определение
.
Синусом числа х называется число, равное синусу угла в х радианов. Косинусом числа х называется число, равное косинусу угла в х радианов
.
Аналогично определяются и другие тригонометрические функции числового аргумента х
.
Формулы привидения.

Формулы сложения. Формулы двойного и половинного аргумента.
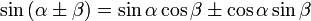
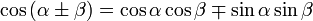
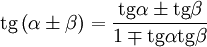
Двойного.
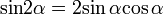 ; ;
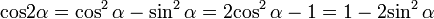
(
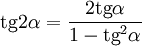 ; ; 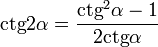 . .
Тригонометрические функции и их графики. Основные свойства тригонометрических функций.
Тригонометрические функции
- вид элементарных функций. Обычно к ним относят синус
(sin x
), косинус
(cos x
), тангенс
(tg x
), котангенс
(ctg x
), Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.
Свойства:
1. в (y) =R.
2. Е (у) = [-1; 1].
3. Функция у = sinx - нечетная, так как по определению синуса тригонометрического угла sin (-
x)
= - y/R = - sinx
, где R - радиус окружности, у - ордината точки (рис).
4. Т = 2л - наименьший положительный период. Действительно,
sin (x+p) = sinx.

5. Точки пересечения с осями координат:
с осью Ох: sinx
= 0; х = pn, nÎZ;
с осью Oy: если х = 0, то у = 0,6. Промежутки знакопостоянства:
sinx > 0
, если xÎ (2pn; p + 2pn), nÎZ;
sinx < 0
, если хÎ (p + 2pn; 2p+pn), nÎZ.
Знаки синуса в четвертях
у > 0 для углов а первой и второй четвертей.
у < 0 для углов ее третьей и четвертой четвертей.
7. Промежутки монотонноти:
y =
sinx
возрастает на каждом из промежутков [-p/2 + 2pn; p/2 + 2pn],
nÎz и убывает на каждом из промежутков [p/2 + 2pn; 3p/2 + 2pn], nÎz.
8. Точки экстремума и экстремумы функции:
xmax
= p/2 + 2pn, nÎz; y
max
= 1;
ymax
= - p/2 + 2pn, nÎz; ymin
= - 1.
Свойства функции у =
cosx
и ее график:
Свойства:
1. в (y) = R.
2. Е (у) = [-1; 1].
3. Функция у =
cosx
- четная, так как по определению косинуса тригонометрического угла cos (-a) = x/R = cosa на тригонометрическом круге (рис)

4. Т = 2p - наименьший положительный период. Действительно,
cos (x+2pn) = cosx.
5. Точки пересечения с осями координат:
с осью Ох: cosx = 0;
х = p/2 + pn, nÎZ;
с осью Оу: если х = 0,то у = 1.
6. Промежутки знакопостоянства:
cosx > 0
, если хÎ (-p/2+2pn; p/2 + 2pn), nÎZ;
cosx < 0
, если хÎ (p/2 + 2pn; 3p/2 + 2pn), nÎZ.
Доказывается это на тригонометрическом круге (рис). Знаки косинуса в четвертях:
x > 0 для углов a первой и четвертой четвертей.
x < 0 для углов a второй и третей четвертей.
7. Промежутки монотонноти:
y =
cosx
возрастает на каждом из промежутков [-p + 2pn; 2pn],
nÎz и убывает на каждом из промежутков [2pn; p + 2pn], nÎz.
Свойства функции у =
tgx
и ее график: свойства -
1. в (y) = (xÎR, x ¹ p/2 + pn, nÎZ).
2. E (y) =R.
3. Функция y = tgx - нечетная
4. Т = p - наименьший положительный период.
5. Промежутки знакопостоянства:
tgx > 0
при хÎ (pn; p/2 + pn;), nÎZ;
tgx < 0
при xÎ (-p/2 + pn; pn), nÎZ.
Знаки тангенса по четвертям смотри на рисунке.

6. Промежутки монотонности:
y =
tgx
возрастает на каждом из промежутков
(-p/2 + pn; p/2 + pn),
nÎz.
7. Точки экстремума и экстремумы функции:
нет.
8. x = p/2 + pn, nÎz - вертикальные асимптоты
Свойства функции у =
ctgx
и ее график:
Свойства:
1. в (y) = (xÎR, x ¹ pn, nÎZ). 2. E (y) =R.
3. Функция y =
ctgx
- нечетная.
4. Т = p - наименьший положительный период.
5. Промежутки знакопостоянства:
ctgx > 0
при хÎ (pn; p/2 + pn;), nÎZ;
ctgx < 0
при хÎ (-p/2 + pn; pn), nÎZ.
Знаки котангенса по четвертям смотри на рисунке.
6. Функция у
= ctgx
возрастает на каждом из промежутков (pn; p + pn), nÎZ.
7. Точек экстремума и экстремумов у функции у =
ctgx
нет.
8. Графиком функции у =
ctgx
является тангенсоида
, полученная сдвигом графика y= tgx
вдоль оси Ох влево на p/2 и умножением на (-1) (рис)

Обра́тные тригонометри́ческие фу́нкции
(круговые функции
, аркфункции
) - математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций: аркси́нус
, аркко́синус
, аркта́нгенс
, арккотангес.
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки "арк-" (от лат. arc
- дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1
для арксинуса и т.п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1. Основное соотношение
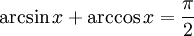 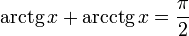
Функция y=arcsinX, её свойства и графики.
Арксинусом
числа m
называется такой угол x
, для которого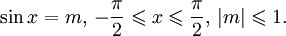 Функция y
= sinx
непрерывна и ограничена на всей своей числовой прямой. Функция y
= arcsinx
является строго возрастающей. Функция y
= sinx
непрерывна и ограничена на всей своей числовой прямой. Функция y
= arcsinx
является строго возрастающей. 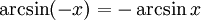 (функция является нечётной). (функция является нечётной).

Функция y=arccosX, её свойства и графики.
Арккосинусом
числа m
называется такой угол x
, для которого 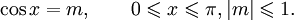
Функция y
= cosx
непрерывна и ограничена на всей своей числовой прямой. Функция y
= arccosx
является строго убывающей. cos (arccosx
) = x
при 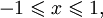 arccos (cosy
) = y
при arccos (cosy
) = y
при 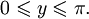 D
(arccosx
) = [− 1; 1], (область определения), E
(arccosx
) = [0; π]. (область значений). Свойства функции arccos D
(arccosx
) = [− 1; 1], (область определения), E
(arccosx
) = [0; π]. (область значений). Свойства функции arccos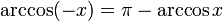 (функция центрально-симметрична относительно точки (функция центрально-симметрична относительно точки 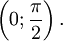

Функция y=arctgX, её свойства и графики.
Арктангенсом
числа m
называется такой угол α, для которого 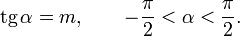 Функция Функция 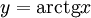 непрерывна и ограничена на всей своей числовой прямой. Функция непрерывна и ограничена на всей своей числовой прямой. Функция 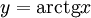 является строго возрастающей. является строго возрастающей.
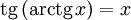 при при
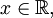 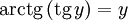 при при 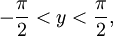 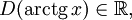 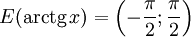
Свойства функции arctg
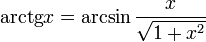 , ,
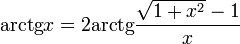 . .

Функция y=arcctg, её свойства и графики.
Арккотангенсом
числа m
называется такой угол x
, для которого 
Функция 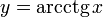 непрерывна и ограничена на всей своей числовой прямой. непрерывна и ограничена на всей своей числовой прямой.
Функция 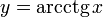 является строго убывающей. является строго убывающей. 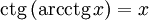 при при 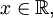 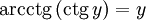 при 0 < y
< π при 0 < y
< π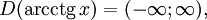 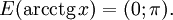 Свойства функции arcctg Свойства функции arcctg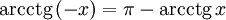 (график функции центрально-симметричен относительно точки (график функции центрально-симметричен относительно точки 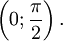 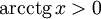 при любых x
. при любых x
.
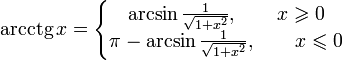 . .

Простейшие тригонометрические уравнения.
Определение.
Уравнения вада sin x = a
; cos x = a
; tg x = a
; ctg x = a
, где x
- переменная, a R, называются простейшими тригонометрическими уравнениями. R, называются простейшими тригонометрическими уравнениями.



Определение.
Уравнения вада sin x = a
; cos x = a
; tg x = a
; ctg x = a
, где x
- переменная, a R, называются простейшими тригонометрическими уравнениями. R, называются простейшими тригонометрическими уравнениями.
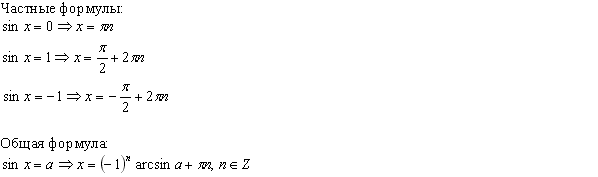
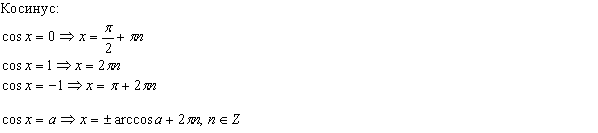




Основные фигуры в пространстве: точки, прямые и плоскости. Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.
А1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. А2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
| 
|
АB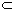  Прямая АВ лежит в плоскости Прямая АВ лежит в плоскости 
|
| рис.5
|
|
Замечание.
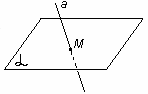
Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
| 
|
а   = М Прямая а и плоскость = М Прямая а и плоскость  пересекаются в точке М. пересекаются в точке М.
|
| Рис.6
|
|
А3.
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Следствие 1.
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Следствие 2.
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Две прямые, заданные уравнениями
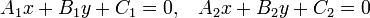 или или
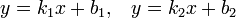 пересекаются в точке. пересекаются в точке.
Параллельность прямой и плоскости.
Определение 2.3
Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая a параллельна плоскости α, то пишут a || α. Теорема 2.4 Признак параллельности прямой и плоскости.
Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости. Доказательство Пусть b 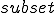 α, a || b и a α, a || b и a 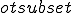 α (чертеж 2.2.1). Доказательство проведем от противного. Пусть a не параллельна α, тогда прямая a пересекает плоскость α в некоторой точке A. Причем A α (чертеж 2.2.1). Доказательство проведем от противного. Пусть a не параллельна α, тогда прямая a пересекает плоскость α в некоторой точке A. Причем A 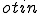 b, так как a || b. Согласно признаку скрещивающихся прямых прямые a и b скрещивающиеся. Мы пришли к противоречию. Теорема 2.5
Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a. Доказательство Действительно, прямые a и b не являются скрещивающимися, так как они лежат в плоскости β. Кроме того, эти прямые не имеют общих точек, так как a || α. Определение 2.4
Прямую b иногда называют следом плоскости β на плоскости α. b, так как a || b. Согласно признаку скрещивающихся прямых прямые a и b скрещивающиеся. Мы пришли к противоречию. Теорема 2.5
Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a. Доказательство Действительно, прямые a и b не являются скрещивающимися, так как они лежат в плоскости β. Кроме того, эти прямые не имеют общих точек, так как a || α. Определение 2.4
Прямую b иногда называют следом плоскости β на плоскости α.
Прямые называются скрещивающимися при выполнении следующего условия: Если представить, что одна из прямых принадлежит произвольной плоскости, то другая прямая будет пересекать эту плоскость в точке, не принадлежащей первой прямой. Иными словами, две прямые в трёхмерном евклидовом пространстве скрещиваются, если не существует плоскости, их содержащей. Проще говоря, две прямые в пространстве, не имеющие общих точек, но не являющиеся параллельными.
Теорема (1): Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Теорема (2): Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Теорема (3): Если стороны двух углов соответственно сонаправлены, то такие углы равны.
Параллельность прямых. Свойства параллельных плоскостей.
Параллельными (иногда - равнобежными) прямыми
называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается. Свойства Параллельность - бинарное отношение эквивалентности, поэтому разбивает всё множество прямых на классы параллельных между собой прямых. Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две) 2 параллельные прямые в пространстве лежат в одной плоскости. б При пересечении 2 параллельных прямых третьей, называемой секущей
: Секущая обязательно пересекает обе прямые. При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства: Накрест лежащие
углы равны. Соответственные
углы равны. Односторонние
углы в сумме составляют 180°.
Перпендикулярность прямой и плоскости.
Прямая, пересекающая плоскость, называется перпендикулярной
этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ
.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
2-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ
.
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
| Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной.
|

Пусть AB
- перпендикуляр к плоскости α, AC
- наклонная и c
- прямая в плоскости α, проходящая через точку C
и перпендикулярная проекции BC
. Проведем прямую CK
параллельно прямой AB
. Прямая CK
перпендикулярна плоскости α (так как она параллельна AB
), а значит, и любой прямой этой плоскости, следовательно, CK
перпендикулярна прямой c
. Проведем через параллельные прямые AB
и CK
плоскость β (параллельные прямые определяют плоскость, причем только одну). Прямая c
перпендикулярна двум пересекающимся прямым, лежащим в плоскости β, это BC
по условию и CK
по построению, значит, она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит, перпендикулярна и прямой AC
.
Обратная теореме о трех перпендикулярах
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.
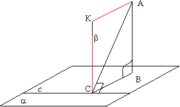
Пусть АВ
- перпендикуляр к плоскости a
, АС
- наклонная и с
- прямая в плоскости a
, проходящая через основание наклонной С
. Проведем прямую СК
, параллельно прямой АВ
. Прямая СК
перпендикулярна плоскости a
(по этой теореме, так как она параллельна АВ
), а значит и любой прямой этой плоскости, следовательно, СК
перпендикулярна прямой с
. Проведем через параллельные прямые АВ
и СК
плоскость b
(параллельные прямые определяют плоскость, причем только одну). Прямая с
перпендикулярна двум прямым лежащим в плоскости b
, это АС
по условию и СК
по построению, значит она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит перпендикулярна и прямой ВС
. Другими словами проекция ВС
перпендикулярна прямой с
, лежащей в плоскости a
.
Перпендикуляр и наклонная.
Перпендикуляром
, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра
.
Наклонной
, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной
. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной
.
Определение 1
. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения. Конец отрезка, лежащий на данной прямой, называется основанием перпендикуляра.
Определение 2
. Наклонной, проведенной из данной точки к данной прямой, называется отрезок, соединяющий данную точку с любой точкой прямой, неявляющейся основанием перпендикуляра, опущенного из этой же точки на данную прямую.  AB - перпендикуляр к плоскости α. AB - перпендикуляр к плоскости α.
AC - наклонная, CB - проекция.
С - основание наклонной, B - основание перпендикуляра.
Угол между прямой и плоскостью.
Углом между прямой и плоскостью
называется любой угол между прямой и ее проекцией на эту плоскость.
Двугранный угол.
Двугранный угол
- пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями. Полуплоскости называются гранями
двугранного угла, а их общая прямая - ребром
. Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре.
Перпендикулярность двух плоскостей.
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ.
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
|