| 1.Матрицы и линейные операции над ними. Умножение матриц.
Матрицей называется прямоугольная таблица чисел, числа из которых состоит матрица называют её элементами.
Количество строк и столбцов определяют размерность матрицы. Например(m´n). Если количество строк совпадает с количеством столбцов, то матрица – квадратная, в этом случае кол-во строк (столбцов) определяют порядок матрицы.
Матрица у которой диагональные элементы равны еденице, а все остальные нулю - называют единичной матрицей.(E,J)
Матрицу С (m´n) называют суммой матриц А и B, если Сij
определяются следующим образом Сij
=aij
+bij
Матрицу С (m´n) называют разностью матриц А и B, если Сij
определяются следующим образом Сij
=aij
-bij
Матрицу С (m´n) называют произведением матрицы А на вещественное число l если Сij
определяются следующим образом Сij
=laij
Матрицу С (m´n) называют произведением матрицы А на матрицу В если:
1) Матрица С имеет размерность (m´n)
2) Элементы матрицы С определяются следующим образом:
Сij
=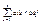 , Cij
=ai
1
´b1
j
+ai
2
´b2
j
+ai
3
´b3
j
+…+aik
´bkj , Cij
=ai
1
´b1
j
+ai
2
´b2
j
+ai
3
´b3
j
+…+aik
´bkj
Из определения произведения матриц следует, что кол-во столбцов матрицы А должно совпадать с кол-вом строк матрицы В. Произведение матриц вычисляется по правилу “строка на столбец”. Для того чтобы вычислить элемент Сij
необходимо все элементы i строки матрицы А умножить на соответствующие элементы j столбца матрицы В и сложить. А´В¹В´А.
А*
=(а*
ij
) называется транспонированной по отношению к матрице А если выполняется равенство а*
ij
=аji
, А=(аij
) таким образом если матрица А имеет размерность (m´n) то А*
имеет размерность (n ´m).
2.Определители квадратных матриц и их свойства. Миноры и алгебраические дополнения.
Определитель состоит из слагаемых, каждый из которых содержит сомножители стоящие в разных строках и столбцах.
Определителем второго порядка называется число (det(A)), которое равно а11
´а22
-а12
´а21
, таким образом определителем второго порядка называют следующее выражение
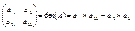
Определителем третьего порядка называется число (det(A)), которое вычисляется при помощи равенства det(A)=a11
a22
a33
+a12
a23
a31
+a31
a21
a32
-a13
a22
a31
-a12
a21
a33
-a11
a23
a32
Свойства определителей
а) Определитель транспонированной матрицы равен определителю исходной матрицы.
б) Если все элементы строки умножить на некоторое число, то и величина определителя умножится на это же число.
в) Если определитель содержит строку (столбец) все элементы которой равны нулю, то такой определитель равен нулю.
г) Если определитель содержит две одинаковые строки (столбца), то этот определитель равен нулю.
д) Если в определителе поменять местами строки (столбцы), то знак определителя изменится на противоположный.
е) Величина определителя не изменится если ко всем элементам одной строки прибавить все элементы другой, умноженные на некоторое число. (Аналогично для столбцов).
ё) Если какую-либо строку определителя можно представить в виде суммы двух строк a1
и a2
, то тогда определитель можно представить в виде суммы двух определителей в одном из которых рассматриваемая строка заменена на строку a1
, а в другом на a2
.
ж) (Теорема Лопласа) Определитель произведения двух матриц равен произведению определителей этих матриц. det(A´B)=det(A)´det(B).
Алгебраические дополнения и миноры.
Минором k-го порядка называют определитель размерностью (k´k), выбранный из матрицы размерностью (m´n).
Если в матрице А вычёркивается строка Ni
, а столбец Nj
, то минор, получающийся при удалении строки и столбца называется алгебраическим дополнением.
3. Определитель
n
-го порядка. Теорема о разложении определителя.
Определителем n-го порядка называется алгебраическая сумма n! слагаемых, каждое из которых представляет произведение n элементов матрицы стоящих в разных строках и разных столбцах, знак с которым каждое слагаемое входит в алгебраическую сумму определяется чётностью подстановки составленной из индексов элементов входящих в данное произведение.
Теорема.
Пусть дана матрица А порядка n, тогда определитель матрицы А можно представить в виде суммы произведений элементов какой-либо строки на их алгебраическое дополнение. Сумма произведений элементов какой-либо строки на соответствующее алгебраическое дополнение элементов другой строки равна нулю. Аналогичное утверждение имеет место для столбцов.
det(A)=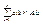 , , 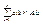 , если i¹j. , если i¹j. 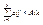 , если j¹k. , если j¹k.
Данная теорема позволяет сводить вычисления порядка n к порядку n-1. Если определитель матрицы А равен нулю, то такая матрица называется вырожденной. Если какой-нибудь минор равен нулю, то он называется вырожденным минором.
Наивысший порядок не вырожденных миноров называют – рангом (rang(A))
4. Обратная матрица. Построение обратной матрицы.
Пусть дана квадратная матрица А=(aij
), матрица В называется обратной по отношению к матрице А, если выполняется равенство: А´В=В´А=Е. Если такая матрица В существует, то её обозначают А-1
.
Метод Гаусса нахождения обратной матрицы:
1) Строится матрица Ã=(А/Е), которая получается из матрицы А приписыванием справа единичной матрицы.
2) При помощи элементарных преобразований матрицу Ã приводят к виду (Е/В), если это удаётся сделать, то матрица В будет обратной. Если невозможно, то обратной матрицы не существует, как правило это происходит тогда, когда в результате элементарных преобразований получается матрица, у которой в некоторой строке первые n элементов равны нулю.
5. Системы линейных уравнений. Основные понятия и определения.
Системой линейных уравнений называют систему равенств:

aij
, bj
–
заданные. xj
–
неизвестная.
Решением этой системы называется такой набор чисел x1
, x2
,…xn
. для которых уравнения превращаются в верные равенства.
A= , Х= , Х=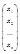 , В= , В=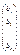
Х и В – называются вектор столбцами. В матричном виде система выглядит А´Х=В.
Система называется совместной, если она имеет хотя бы одно решение, в противном случае система не совместна.
Система называется определённой, если она имеет единственное решение, если система имеет более одного решения то система неопределённая.
Решение системы линейных уравнений с помощью метода Крамера.
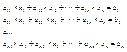
Где Аij
– алгебраические дополнения. Умножим первое у-е на А11
, а второе на А21
и тд. Сложим получившиеся равенства:
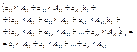 
По теореме о разложении определителя по элементам столбца сумма слагаемых стоящих перед x1
будет равна определителю матрицы А. Сумма слагаемых перед x2
и x1
будет равна нулю. В правой части равенства стоит величина равная определителю, который получается из определителя матрицы А с заменой первого столбца на вектор столбец В. Обозначим этот определитель через 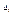 , тогда равенство можно записать в виде , тогда равенство можно записать в виде 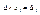 , если первую строку системы умножить на А21
и тд., и сложим получившиеся равенства, то получим , если первую строку системы умножить на А21
и тд., и сложим получившиеся равенства, то получим 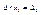 , где , где 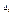 - определитель полученный из определителя матрицы А заменой второго столбца на вектор столбец В. Продолжая этот процесс получим систему линейных уравнений: - определитель полученный из определителя матрицы А заменой второго столбца на вектор столбец В. Продолжая этот процесс получим систему линейных уравнений:
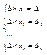 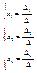
Числа x1,
x2
, …xn
являются решениями системы.
6. Решение системы линейных уравнений с помощью обратной матрицы. Метод Гаусса решения систем линейных уравнений.
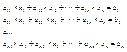
Для данной системы построим расширенную матрицу, Ã которая равна:
Ã=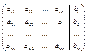
Будем выполнять над матрицей А элементарные преобразования так, чтобы привести её к виду, когда все элементы лежащие ниже диагонали будут равны нулю. Под элементарными преобразованиями понимают: изменение местами двух строк (столбцов) матрицы Ã; прибавление к элементам одной строки элементов другой умноженных на некоторое число.
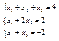 Ã = Ã =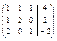
Расширенная матрица иногда называется присоединённой. Каждой системе линейных уравнений соответствует своя матрица Ã, зная матрицу Ã можно записать систему линейных уравнений, которая ей соответствует.
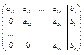
Если k¹n, то такой вид матрицы называется трапецевидный.
Если k=n, то такой вид матрицы называется треугольный.
Если получается трапецевидная матрица в процессе элементарных преобразований, это означает что система имеет не одно решение.
Если получается треугольный вид то матрица имеет одно решение.
Если матрица Ã приведена к трапецевидному виду, то перенося все неизвестные, которые расположены правее диагонали и придавая им произвольные значения, можно найти всевозможные решения первоначальной системы.
7. Однородные системы. Условия существования нулевых решений. Понятие ранга матрицы.
Рассмотрим АХ= , ,  = =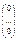 , Х= , Х= - векторстолбец. - векторстолбец.
Эта однородная система всегда является совместной, т.к. она всегда имеет решение х=0. Решения этой системы обладают свойствами:
Если х1
и х2
являются решениями системы, то 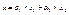 так же является решением этой системы. так же является решением этой системы.
Говорят, что решение однородной системы образует конечномерное линейное векторное пространство.
Пусть имеется 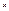 векторов: векторов: 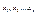 . .
Векторы 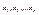 называют линейно независимыми, если из равенства называют линейно независимыми, если из равенства 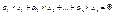 следует, что все следует, что все 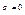 , в противном случае если векторы , в противном случае если векторы 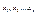 линейнозависимые. линейнозависимые.
Пусть матрица А имеет вид:
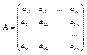 , , 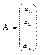 , , 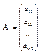 , , 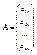
Тогда систему можно записать в виде 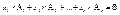 , из равенства видно что если система не имеет не нулевых решений, то векторы , из равенства видно что если система не имеет не нулевых решений, то векторы 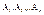 являются линейнонезависимыми. Если система имеет нулевое решение, то векторы являются линейнонезависимыми. Если система имеет нулевое решение, то векторы 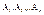 являются линейнозависимыми. являются линейнозависимыми.
Теорема:
Для того чтобы векторы 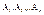 были линейнонезависимы, необходимо и достаточно чтобы ранг матрицы А образованный этими элементами равнялся n. Таким образом, чтобы решить однородную систему у-ий АХ= были линейнонезависимы, необходимо и достаточно чтобы ранг матрицы А образованный этими элементами равнялся n. Таким образом, чтобы решить однородную систему у-ий АХ=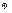 необходимо выполнить следующие действия: вычислить ранг матрицы А, если ранг совпадает с числом неизвестных, то однородная система линейных у-ий имеет одно решение. Если ранг матрицы А меньше числа неизвестных, то в матрице А можно найти S строк и S столбцов, таких, что определитель составленный из элементов лежащих на пересечении выбранных строк и столбцов не равнялся нулю. необходимо выполнить следующие действия: вычислить ранг матрицы А, если ранг совпадает с числом неизвестных, то однородная система линейных у-ий имеет одно решение. Если ранг матрицы А меньше числа неизвестных, то в матрице А можно найти S строк и S столбцов, таких, что определитель составленный из элементов лежащих на пересечении выбранных строк и столбцов не равнялся нулю.
Предположим для определённости, что определитель состоит из S строк и S столбцов отличных от нуля, тогда перенося слагаемые 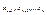 в правую часть и оставляя в системе первые S уравнений, получим систему: в правую часть и оставляя в системе первые S уравнений, получим систему:
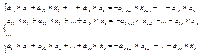 (3) (3)
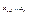 - свободные неизвестные (базисные неизвестные), придавая базисным неизвестным произвольные числовые значения из системы (3) можно найти - свободные неизвестные (базисные неизвестные), придавая базисным неизвестным произвольные числовые значения из системы (3) можно найти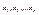 , таким образом однородная система линейных у-ий может иметь одно или бесконечное множество решений, отсюда следует, что , таким образом однородная система линейных у-ий может иметь одно или бесконечное множество решений, отсюда следует, что 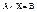 может иметь бесконечное кол-во решений или быть несовместной. может иметь бесконечное кол-во решений или быть несовместной.
Минором k-го порядка называют определитель размерностью (k´k), выбранный из матрицы размерностью (m´n).
Если в матрице А вычёркивается строка Ni
, а столбец Nj
, то минор, получающийся при удалении строки и столбца называется алгебраическим дополнением.
Наивысший порядок не вырожденных миноров называют – рангом (rang(A))
9. Векторные величины. Линейные операции с векторами.
Вектор – направленный отрезок, таким образом чтобы задать вектор необходимо задать его длину и направление.
Два вектора называют равными, если они имеют одинаковую длину и направление.
Вектор называют нулевым, если длна равна нулю (он не имеет направления).
Если на плоскости введена прямоугольная система координат, то для того чтобы задать вектор надо указать начало вектора т. А и его окончание т. В., в этом случае вектор обозначается 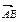
Пусть т. А имеет координаты 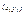 , т. В , т. В 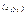

Тогда 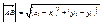
Пусть a и b обозначают углы, которые образует вектор 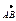 с положительным направлением координатных осей. a и b - углы определяющие направление вектора с положительным направлением координатных осей. a и b - углы определяющие направление вектора 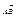 , cos этих углов называются направляющими: , cos этих углов называются направляющими:
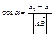 , , 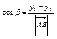
т.к. при параллельном переносе ни длина ни направление вектора не изменяется, то удобно расположить все векторы таким образом, чтобы они начинались в начале координат. В этом случае для задания вектора достаточно указать т., где он заканчивается.
Действия с векторами.

На основе полученных векторов, построим параллелограмм. Проведём диогональ АВ. Тогда 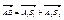 Для каждого вектора АВ не равного нулевому существует противоположный, который такой же длины но другого направления. Вектор обратный вектору АВ, обозначается (-АВ) Для каждого вектора АВ не равного нулевому существует противоположный, который такой же длины но другого направления. Вектор обратный вектору АВ, обозначается (-АВ)
Разностью двух векторов А1
В1
и А2
В2
называют вектор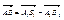 . .
Вектор АВ называется произведением вектора А1
В1
на вещественное число l и обозначается следующим образом:
а) если длина вектора АВ равна l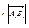 и вектор АВ имеет тоже направление что и вектор А1
В1
. и вектор АВ имеет тоже направление что и вектор А1
В1
.
б) если l=0, то l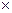 А1
В1
=0 А1
В1
=0
в) если l<0, то l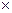 А1
В1
=(-( А1
В1
=(-(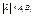 )) ))
10
. Скалярным произведением
векторов a и b называют число равное произведению длин этих векторов на cos угла между ними. Пусть ça çи çb ça - угол между векторами, тогда из определения следует ab = ça ç× çb çcos a. Пусть a1 – угол который образует вектор a с положительным направлением оси ОХ. a2 – угол который образует вектор b с положительным направлением оси ОХ. a=a1-a2 ab = êaê×êbêcos (a1-a2).
êa êcos a1 × êb êcos a2 + êa êsin a1 × êb êsin a2 = x1x2+y1y2. Таким образам скалярное произведение векторов a и b можно вычислить как сумму произведения их соответствующих координат. Это определение скалярного произведения эквивалентно первоначальному. Свойства векторов: 1.)ab = ba. 2.)a × 0 = 0. 3.) a(b +c) = ab + ac. 4.) (la) × (lb) = l(ab). 5.) aa = êa ê2
. 6.) aa ³ 0 aa = 0 Û a = 0. 7.) ab = 0 Û a ^ b. Предполагается, что нулевой вектор ^ любому вектору. Аналогичным образом определяется скалярное произведение для векторов расположенных в трехмерном пространстве свойства 1 –7 остаются неизменными.

11. Линейная зависимость и независимость векторов. Коллинеарные и компланарные вектора.
Два вектора называются коллинеарными, если они лежат на одной прямой или на || прямых.
Если векторы 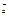 и и 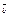 являются коллинеарными, то они наклонены под одним и тем же углом положительного направления оси ОХ, значит являются коллинеарными, то они наклонены под одним и тем же углом положительного направления оси ОХ, значит 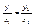 Þ Þ 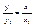 , ,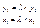 Þ Þ 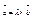 - условие коллинеарности векторов. - условие коллинеарности векторов.
Два вектора называются компланарными если они находятся в разных плоскостях и не пересекаются.
12. Декартовая
прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком – нибудь порядке. Точка пересечения осей называется началом координат, а сами оси – координатными осями. Первая из координатных осей называется осью абсцисс, а вторая – осью ординат. Начало координат обозначают буквой О
, ось абсцисс – символом ОХ,
ось ординат – символом ОУ.
Координатами произвольной точки М
в заданной системе называют числа Х
= ОМх, У = ОМу,
где Мх
и Му
суть проекции точки М
на оси ОХ
и ОУ, ОМх
обозначает величину отрезка ОМх
оси абсцисс, ОМу –
величину отрезка ОМу
оси ординат. Число Х
называется абсциссой точки М,
число У
называется ординатой этой же точки. Символ М (Х; У)
обозначает, что точка М
имеет абсциссой число Х
, а ординатой число У.
Ось ОУ
разделяет всю плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси ОХ,
называется правой, другая – левой. Точно так же ось ОХ
разделяет плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси ОУ
, называется верхней, другая нижней.
Обе координатные оси вместе разделяют плоскость на четыре четверти, которые номеруют по следующему правилу: первой координатной четвертью называется та, которая лежит одновременно в правой и в верхней полуплоскости, второй – лежащая в левой и в верхней полуплоскости, третьей – лежащая в левой ив нижней полуплоскости, четвертой – лежащая в правой и в нижней полуплоскости.
13. Векторным произведением
вектора a
на вектор b
называется вектор, обозначаемый символом [
ab
]
и определяемый следующими тремя условиями: 1) модуль вектора [
ab
]
равен ï
a
ï
×
ï
b
ï
sin
j
,
где j
- угол между векторами a
и b
; 2) вектор [
ab
]
не
неперпендикулярен к каждому из векторов a
и b
; 3) направление вектора [
ab
]
соответствует «правилу правой руки». Это означает, что если вектор a
,
b
и [
ab
]
приведены к общему началу, то вектор [
ab
]
должен быть направлен так, как направлен средний палец правой руки, большой палец которой направлен по первому сомножителю (т. е. по вектору a
), а указательный – по второму (т. е. по вектору b
). Векторное произведение зависит от порядка сомножителей, именно: [
ab
]
= -
[
ab
]
.
Модуль векторного произведения [
ab
]
равен S
параллелограмма, построенного на векторах a
и b
:
ê
[
ab
]
ê
=
S
. Само векторное произведение может быть выражено формулой [
ab
]
=
Se
,
где e
– орт векторного произведения. Векторное произведение [
ab
]
обращается в нуль тогда и только тогда, когда векторы a
и
b
коллинеарны. В частности [
aa
] = 0
. Если система координатных осей правая и векторы a
и
b
заданы в этой системе своими координатами:
a
= {
X
1;
Y
1;
Z
1},
b
=
{
X
2;
Y
2;
Z
2}
, то векторное произведение вектора a
на вектор b
определяется формулой [
ab
]
= 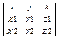 Свойства:1) aa =q
Свойства:1) aa =q 2) ab = (ba) 3) a(b1 + b2) = ab1 + ab2 4) (la)b = a(lb) = l(ab). 2) ab = (ba) 3) a(b1 + b2) = ab1 + ab2 4) (la)b = a(lb) = l(ab).
Смешанное произведение.
Пусть даны a
(
X
1;
Y
1;
Z
1),
b
(
X
2;
Y
2;
Z
2),
c
(
X
3;
Y
3;
Z
3).
Смешанным произведением трех векторов a
,
b
,
c
называется число, равное векторному произведению [
ab
],
умноженному скалярно на вектор c
, т. е. [
ab
]
c
.
Именно место тождество: [
ab
]
c
=
a
[
bc
],
ввиду чего для обозначения смешанного произведения [
ab
]
c
употребляется более простой символ:
abc
.
Таким образом, a
,
b
,
c
= [
ab
]
c
,
abc
=
a
[
bc
].
Смешанное произведение abc
равно объему параллелепипеда, построенного на векторах a
,
b
,
c
,
взятому со знаком плюс. Если векторы a
,
b
,
c
компланарны (и только в этом случае), смешанное произведение abc
рано нулю; иначе говоря, равенство abc
= 0
, есть необходимое и достаточное условие ком планарности векторов a
,
b
,
c
.
Если векторы a
,
b
,
c
заданы своими координатами: a
={
X
1;
Y
1;
Z
1},
b
= {
X
2;
Y
2;
Z
2},
c
= {
X
3;
Y
3;
Z
3;}
14. Простейшие задачи аналитической геометрии.
1) Вычислим расстояние между двумя точками на плоскости: 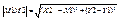
2) Деление отрезков в данном отношении. Пусть на плоскости даны две точки с координатами М1(X1;Y1) и M2(X2;Y2). Найти координаты точки М лежащей между М1 и М2 на отрезке М1М2, если выполняется условие: 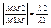 . Проекции точки М на ось абсцисс будет делить отрезок X1X2 в той же самой проекции, потому . Проекции точки М на ось абсцисс будет делить отрезок X1X2 в той же самой проекции, потому 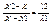 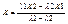 , l1X2 - l1X = l2X - l2X1. Аналогичным образом можно получить, что , l1X2 - l1X = l2X - l2X1. Аналогичным образом можно получить, что 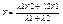 , , 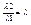 , , 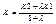 , , 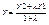
15. Полярные координаты.
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, луча ОА, исходящего из этой точки, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными. Полярными координатами произвольной точки М (относительно заданной системы) называются числа r = ОМ и q < АОМ. Угол q при этом следует понимать так, как принято в тригонометрии. Число r называется первой координатой, или полярным радиусом, число q- второй координатой, или полярным углом точки М. Символ М (r;q) обозначает, что точка М имеет полярные координаты r и q. Полярный угол q имеет бесконечно много возможных значений. Значение полярного угла, удовлетворяющее неравенствам -p < q ≤ +p, называется главным. В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1) пользоваться одним и тем же масштабом, 2)при определении полярных углов считать положительными повороты в том направлении, в каком следует вращать положительную полуось абсцисс, чтобы кратчайшим путем совместить ее с положительной полуосью ординат. При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки к декартовым координатам той же точки осуществляется по формулам 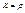 cosq, cosq, 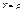 sinq. В этом же случае формулы sinq. В этом же случае формулы 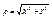 , tgq = , tgq = 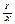 являются формулами перехода от декартовых координат к полярным. При одновременном рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштабов для обеих систем одинаковыми. являются формулами перехода от декартовых координат к полярным. При одновременном рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштабов для обеих систем одинаковыми.
16. Различные виды уравнения прямой.
Рассмотрим прямую проходящую через точки М1М2, пусть М произвольная точка лежащая на этой прямой тогда векторы ММ2 и М1М являются коллинеарными. Вектор ММ2 = (X2 – X; Y2 – Y), M1M = (X - X1; Y – Y1). Из условия коллинеарности векторов, следует, что 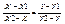 1).
1) -
уравнение прямой, проходящей через две заданные точки пусть X2 – X1 = K, Y2 – Y1 = L, тогда вектор a
= (K; L) параллельна данной прямой направляющий вектор 1)
может быть записано в виде: 1).
1) -
уравнение прямой, проходящей через две заданные точки пусть X2 – X1 = K, Y2 – Y1 = L, тогда вектор a
= (K; L) параллельна данной прямой направляющий вектор 1)
может быть записано в виде: 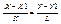 2). 2) -
уравнением прямой проходящей через данную точку М1 в заданном направлении 2)
каноническим уравнением прямой. Если три точки М1, М2 и М лежат на одной прямой, то площадь треугольника равна нулю. 2). 2) -
уравнением прямой проходящей через данную точку М1 в заданном направлении 2)
каноническим уравнением прямой. Если три точки М1, М2 и М лежат на одной прямой, то площадь треугольника равна нулю. 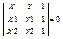 3). 3)
– уравнение прямой в виде определителя приравняем отношение равенства 1)
к некоторому числу T. X - X1 = (X2 – X) T, X –X1 = KT; Y – Y1 = (Y2 –Y1) T, Y – Y1 = LT. (X = X1 + KT , Y = Y1 + LT 4))
. 3). 3)
– уравнение прямой в виде определителя приравняем отношение равенства 1)
к некоторому числу T. X - X1 = (X2 – X) T, X –X1 = KT; Y – Y1 = (Y2 –Y1) T, Y – Y1 = LT. (X = X1 + KT , Y = Y1 + LT 4))
. 4) –
называется параметрическим уравнением. Пусть на плоскости заданы две точки A и B, лежащие на координатных осях A(a; 0), B(b; 0). Найдем уравнение прямой проходящей через точки A и B. 4) –
называется параметрическим уравнением. Пусть на плоскости заданы две точки A и B, лежащие на координатных осях A(a; 0), B(b; 0). Найдем уравнение прямой проходящей через точки A и B. 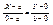 ; ; 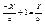 ; ; 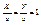 - 5) .
5) –
называется уравнением прямой на отрезке. - 5) .
5) –
называется уравнением прямой на отрезке.

Нормальное уравнение прямой.
Пусть прямая проходит через точку М(X; Y) перпендикулярно отрезку OP. Длина отрезка 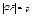 , , 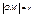 , , 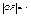 cos cos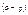 , p = r(cosacos + sinasinb), p = (r cosb)cosa + (r sinb)sina. X cosa + Y sinb = p – нормальное уравнение прямой. , p = r(cosacos + sinasinb), p = (r cosb)cosa + (r sinb)sina. X cosa + Y sinb = p – нормальное уравнение прямой.
17. Расстояние от точки до прямой.
Пусть дана какая – нибудь прямая и произвольная точка М*; обозначим через в расстояние точки М* от данной прямой. Отклонением в точки М* от прямой называется число +d, если данная точка и начало координат лежат по разные стороны от данной прямой, и –d, если данная точка и начало координат расположены по одну сторону от данной прямой. Если даны координаты X*, Y* точки М* и нормальное уравнение прямой X cosa + Y sina - p = 0, то отклонение в точки М* от этой прямой может быть вычислено по формуле в = X* cosa + Y* sina - p. Таким образом, чтобы найти отклонение какой – нибудь точки М* от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки М*. Полученное число будет равно искомому отклонению. Чтобы найти расстояние в от точки до прямой, достаточно вычислить отклонение и взять его модуль: в = 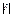 . Если дано общее уравнение прямой Ax + By + C = 0, то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель m, определяемый формулой . Если дано общее уравнение прямой Ax + By + C = 0, то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель m, определяемый формулой 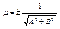 . Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения. . Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.
18. Взаимное расположение прямых на плоскости.
Пусть на плоскости заданы две прямые:A1x + B1y +C1 = 0 A2x + B2y + C2 = 0 – 1).
Возможны следующие случаи взаимного расположения этих прямых: 1) Прямые пересекаются в одной единственной точке, это означает, что система 1)
имеет единственное решение. 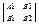 ¹ 0. 2) Прямые параллельны и не совпадают, это означает, что система 1)
не имеет решений. В соответствии с теоремой Капели – это возможно тогда и только тогда, когда rang ¹ 0. 2) Прямые параллельны и не совпадают, это означает, что система 1)
не имеет решений. В соответствии с теоремой Капели – это возможно тогда и только тогда, когда rang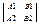 не совпадает с rang не совпадает с rang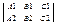 . . 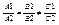 3) прямые совпадают, это означает, что система 1)
имеет множество решений. Это возможно тогда, когда rang 3) прямые совпадают, это означает, что система 1)
имеет множество решений. Это возможно тогда, когда rang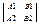 совпадает с rang совпадает с rang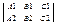 . Это возможно в том случае, когда коэффициенты пропорциональны: . Это возможно в том случае, когда коэффициенты пропорциональны: 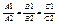 . .
19. Плоскость в пространстве.
В декартовых координатах каждая плоскость определяется уравнением первой степени, и каждое уравнение первой степени определяет плоскость. Всякий вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение A(X – Xo) + B(Y – Yo) + C(Z – Zo) = 0 – 1)
определяет плоскость, проходящую через точку Мо (Xo; Yo; Zo) и имеющую нормальный вектор n
= {
A
;
B
;
C
}.
Раскрывая в уравнении 1)
скобки и обозначая число – AXo – BYo – CZo буквой D, представим его в виде: AX + BY + CZ + в = 0. Это уравнение называется общим уравнением плоскости. Различные виды уравнения плоскости.
Пусть в пространстве заданы три различные точки М1(X1; Y1; Z1) M2(X2; Y2; Z2) M3(X3; Y3; Z3). Через эти три точки можно провести плоскость единственным образом. Рассмотрим точку M(X; Y; Z) лежащую в этой плоскости, тогда выполняется условие 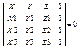  - 1).
Если условие 1)
не выполняется, то точка М не лежит в этой плоскости, поэтому 1)
называется уравнением плоскости проходящей через три заданные точки записанная в форме определителя. Раскроем определитель по элементам первой строки и обозначим коэффициенты, стоящие перед X,A; перед Y, B; перед Z, C, то тогда получим уравнение плоскости в виде AX + BY + CZ + в =0 – 2) – общее уравнение плоскости.
Предположим, что 2)
в ¹ 0 и рассмотрим плоскость, заданную уравнением AX + BY + CZ = 0 – 3).
Очевидно, что система линейных уравнений, состоящая из равенств 2) и 3)
не имеет решений. Это означает, что плоскости 2) и 3)
не пересекаются. Следовательно, плоскость 3)
êê
2).
Рассмотрим производную точку М лежащую в плоскости 3),
когда вектор ОМ целиком лежит в этой плоскости вектор ОМ (X; Y: Z), поэтому 3)
можно рассматривать как равное нулю, скалярного произведения векторов ОМ и N (A; B; C).Тогда из 3)
следует, что вектор N перпендикулярный плоскости 3).
Поэтому вектор М называется нормальным вектором плоскости, т. к. 2)
êê
3)
, то N ^ к этой плоскости, поэтому N называется нормальным вектором и для плоскости 2). - 1).
Если условие 1)
не выполняется, то точка М не лежит в этой плоскости, поэтому 1)
называется уравнением плоскости проходящей через три заданные точки записанная в форме определителя. Раскроем определитель по элементам первой строки и обозначим коэффициенты, стоящие перед X,A; перед Y, B; перед Z, C, то тогда получим уравнение плоскости в виде AX + BY + CZ + в =0 – 2) – общее уравнение плоскости.
Предположим, что 2)
в ¹ 0 и рассмотрим плоскость, заданную уравнением AX + BY + CZ = 0 – 3).
Очевидно, что система линейных уравнений, состоящая из равенств 2) и 3)
не имеет решений. Это означает, что плоскости 2) и 3)
не пересекаются. Следовательно, плоскость 3)
êê
2).
Рассмотрим производную точку М лежащую в плоскости 3),
когда вектор ОМ целиком лежит в этой плоскости вектор ОМ (X; Y: Z), поэтому 3)
можно рассматривать как равное нулю, скалярного произведения векторов ОМ и N (A; B; C).Тогда из 3)
следует, что вектор N перпендикулярный плоскости 3).
Поэтому вектор М называется нормальным вектором плоскости, т. к. 2)
êê
3)
, то N ^ к этой плоскости, поэтому N называется нормальным вектором и для плоскости 2). 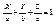 - Уравнение плоскости отрезка.
- Уравнение плоскости отрезка.
Взаимное расположение плоскостей
. 1) A1X + B1Y + C1Z + D1 = 0  2) A2X + B2Y + C2Z + D2 = 0. 1.
Пусть плоскости 1 и 2 пересекаются. В этом случае имеются точки, принадлежащие одновременно плоскостям 1и 2. Поэтому система линейных уравнений, составленная из 1и 2 имеет по крайней мере, одно решение. Для этого необходимо и достаточно выполнения условия:
2) A2X + B2Y + C2Z + D2 = 0. 1.
Пусть плоскости 1 и 2 пересекаются. В этом случае имеются точки, принадлежащие одновременно плоскостям 1и 2. Поэтому система линейных уравнений, составленная из 1и 2 имеет по крайней мере, одно решение. Для этого необходимо и достаточно выполнения условия: 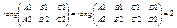
2.
Если плоскость 1 параллельна 2, то это означает, что с.л.у. составленная из 1и2 не имеет решений. Для этого необходимо и достаточно выполнения условия: 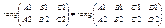  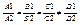 3.
Пусть плоскость 1и2 совпадают. 3.
Пусть плоскость 1и2 совпадают. 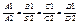 . .
Расстояние от точки до плоскости.
Пусть точка М* - какая угодно точка пространства, в – расстояние от нее до данной плоскости. Отклонением в точки М* от данной плоскости называется число +d, если точка М* и начало координат лежат по разные стороны от данной плоскости, и число –d, если они расположены по одну сторону от данной плоскости. Если даны координаты X*, Y*,Z* точки М* и нормальное уравнение плоскости X cosa + Y cosb + Z cosg - p = 0, то отклонение в точки М* от этой плоскости может быть вычислено по формуле в = X* cosa + Y* cosb + Z* cosg - p. Очевидно в = 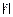 . Общее уравнение плоскости Ax + By + Cz + в = 0, приводится к нормальному виду умножением на нормирующий множитель, определяемый . Общее уравнение плоскости Ax + By + Cz + в = 0, приводится к нормальному виду умножением на нормирующий множитель, определяемый 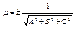 . Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения. . Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.
20. Прямая в пространстве.
Рассмотрим в пространстве две точки М1(X1; Y1; Z1) и M2(X2; Y2; Z2) можно провести единственную прямую. Пусть М(X; Y; Z) лежит на этой прямой, тогда векторы М1М2 и М1М каллинеарны М1М2(X2 – X1; Y2 –Y1; Z2 –Z1); M1M(X –X1; Y –Y1; Z – Z1). Из условия координат следует 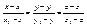 - 1).
1) –
уравнение прямой в пространстве проходящей через две заданные точки. X2 – X1 = k Y2 –Y1 = l Z2 – Z1 = m A(k; l; m) êêпрямой проходящей через М1 и М2. - 1).
1) –
уравнение прямой в пространстве проходящей через две заданные точки. X2 – X1 = k Y2 –Y1 = l Z2 – Z1 = m A(k; l; m) êêпрямой проходящей через М1 и М2. 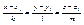 - 2) уравнение прямой проходящей через заданную точку М1 с заданным направляющим вектором. - 2) уравнение прямой проходящей через заданную точку М1 с заданным направляющим вектором.
Взаимное расположение прямых и плоскостей.
Пусть дана плоскость Ax + By + Cz + в = 0 - 3) .
Пусть дана прямая 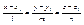 - 4).
A(l; m; n)– направляющий вектор для прямой. Тогда A * n = êA ê* ên êsina. sina = - 4).
A(l; m; n)– направляющий вектор для прямой. Тогда A * n = êA ê* ên êsina. sina = 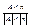 = = 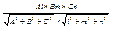 - 5).
Из 5)
следует, что прямая 4)
êê
3)
, тогда угол a = 0 следует Al + Bm + Cn = 0 – условие параллельности прямой плоскости. Если 4)
^
3)
, то a =90. - 5).
Из 5)
следует, что прямая 4)
êê
3)
, тогда угол a = 0 следует Al + Bm + Cn = 0 – условие параллельности прямой плоскости. Если 4)
^
3)
, то a =90. 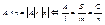 - условие перпендикулярности прямой и плоскости. - условие перпендикулярности прямой и плоскости.
21. Кривые второго порядка. Эллипс. Гипербола. Парабола.
Общее у-е кривых второго порядка: 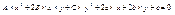
После изменения начала координат и переноса начала координат в новую т. или поворта координатных осей, кривые второго порядка могут быть преобразованы к более простому (каноническому) виду. В результате преобразований у-е может описывать следующие линии: эллипс; гиперболу; параболу; пару êêпрямых; пара пересекающихся прямых; точка.
Эллипс.
Эллипсом называют геометрическое место точек на плоскости, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная и большая чем расстояние между фокусами.
Пусть задан эллипс F1
и F2
– фокусы эллипса, выберем систему координат следующим образом, ось абсцисс проведём через фокусы, начало координат выберем между фокусами. F1
(c;0), F2
(-c,0), C>0.

Пусть т. М лежит на эллипсе êMF1
ê+êMF2
ê=const =2a>2c Þ a>c 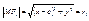 , , 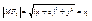 , r1
и r2
–фокальные радиусы. , r1
и r2
–фокальные радиусы. 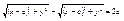 , , 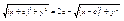 , , 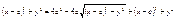 , , 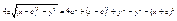 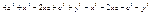 , , 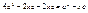 , , 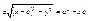 , , 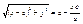 , , 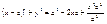 , , 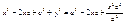 , , 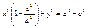 , , 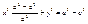 , , 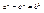 , , 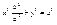 , , 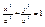 - каноническое у-е эллипса. - каноническое у-е эллипса.
Из канонического у-ия следует, что вместе с т. М лежащей на эллипсе, точки М1
(х;-у), М2
(-х;у), М3
(-х;-у) так же лежат на эллипсе, таким образом эллипс симметричен оси абсцисс и оси ординат. 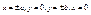 - вершины. - вершины.
Гиперболой называют геометрическое место точек на плоскости, модуль разности расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная и меньшая чем расстояние между фокусами.
Пусть дана гипербола, F1
и F2
– фокусы гиперболы, выберем систему координат следующим образом, ось абсцисс проведём через фокусы, начало координат выберем между фокусами. F1
(c;0), F2
(-c,0)

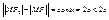 , , 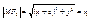 , , 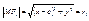 , , 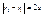 , , 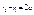 , , 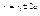 , , 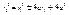 , , 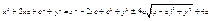 , , 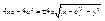 , , 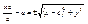 , , 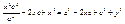 , , 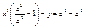 , , 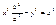 , , 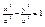 - каноническое у-е гиперболы. - каноническое у-е гиперболы.
Из канонического у-ия гиперболы получим 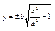 , ,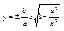 , ассимптоту гиперболы можно найти по формуле , ассимптоту гиперболы можно найти по формуле 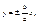 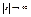
Параболой называют геометрическое место точек на плоскости, расстояние от которых до фиксированной точки, называемой фокусам, равно расстоянию до фиксированной прямой, называемой директрисой.
Выберем систему координат следующим образом, ось абсцисс проведём через фокус ^ директрисе, начало координат выберем посередине между фокусом и директрисой.

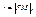 тогда из определения тогда из определения 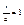 - экцентрисситет. - экцентрисситет.
| 1) 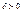 , элиптический тип , элиптический тип
|
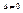
|
|
| 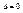
|
Пара пересекающихся прямых (точка)
|
| 2) 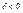 , гипербогический тип , гипербогический тип
|
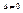
|
гипербола
|
| 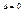
|
Пара пересекающихся прямых 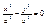
|
| 3) 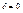 , параболический тип , параболический тип
|
|
парабола
|
| 
|
Пара êê прямых
|
23. Числовая последовательность. Основные понятия.
Пусть определено правило по которому каждому натуральному числу ставится в соответствии некоторое соответственное число, тогда говорят, что задана числовая последовательность. Мы будем рассматривать аналитический способ, в этом случае числовая последовательность задаётся с помощью математических выражений.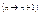 . .
Числа которые ставятся в соответствие натуральным числам, называются элементами последовательности.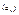 . .
Числовая последовательность может быть задана рекуррентным способом, в этом случае каждый элемент числовой последовательности определяется при помощи пред идущих элементов. 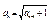
Числовая последовательность называется монотонно возрастающей, если каждый следующий элемент больше предыдущего.
Числовая последовательность называется монотонно убывающей, если каждый следующий элемент меньше предыдущего.
Числовая последовательность называется неубывающей, если выполняется условие 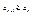
Числовая последовательность называется неубывающей, если выполняется условие 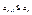
Числовая последовательность называется стационарной, если 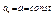 . .
Числовая последовательность называется ограниченной, если можно указать такое число А, что для всех n выполняется условие 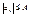
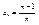 - убывающая ограниченная, - убывающая ограниченная, 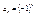 - ограниченная. - ограниченная.
Пусть задана числовая последовательность, изобразим элементы этой последовательности в виде точек на числовой оси 

тогда монотонное возрастание ч.п. означает, что каждая следующая тока расположена правее предыдущей.
Монотонное убывание ч.п. означает, что каждая следующая тока расположена левее предыдущей.
Очевидно, что числовая последовательность 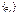 , будет ограниченной тогда и только тогда, когда можно указать отрезок , будет ограниченной тогда и только тогда, когда можно указать отрезок 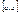 , такой, что " , такой, что " 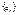 , , 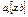
24. Сходящиеся последовательности. Свойства сходящихся последовательностей.


Ни для одного значения n для данной числовой последовательности не может выполнятся условие 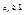 , действительно, если это условие выполнимо для данного , действительно, если это условие выполнимо для данного 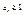 , , 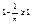
Элементы данной числовой последовательности могут сколь угодно близко располагаться около 1. 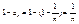 , значит расстояние от точек соответствующее элементам , значит расстояние от точек соответствующее элементам 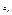 , до точки 1 равно , до точки 1 равно 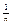 , поэтому какое бы не было положительное число в не было задано, всегда будет выполнятся условие , поэтому какое бы не было положительное число в не было задано, всегда будет выполнятся условие 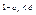 , d=0,01, , d=0,01, 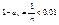 , n>100. , n>100.
e - окрестностью числа А называется множество чисел 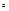 удовлетворяющих неравенству удовлетворяющих неравенству 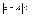 e - интервал (А-e,А+e) e - интервал (А-e,А+e)

Пусть дана числовая последовательность 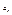 . А – называется пределом числовой последовательности, если для любого сколь угодно малого числа e можно указать такй номер N, что все эти элементы числовой последовательности . А – называется пределом числовой последовательности, если для любого сколь угодно малого числа e можно указать такй номер N, что все эти элементы числовой последовательности 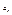 , будут попадать в e окрестности числа А при , будут попадать в e окрестности числа А при 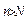 , , 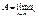 , , 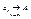 . .
Последовательность для которой существует предел, называется сходящейся.
Если число А является пределом числовой последовательности Аn
, то это означает, что все элементы числовой последовательности 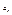 попадают в сколь угодно малую окрестность числа А, начиная с некоторого номера. попадают в сколь угодно малую окрестность числа А, начиная с некоторого номера.
Теорема 1: всякая сходящая числовая последовательность имеет единственный предел.
Теорема 2: всякая сходящая числовая последовательность ограничена.
Теорема 3: пусть даны три числовые последовательности, 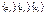 , предположим, что " n , предположим, что " n 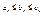 . .
Пусть последов. 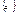 и и 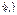 являются сходящими, причём являются сходящими, причём 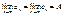 , тогда последовательность , тогда последовательность 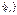 также является сходящейся и также является сходящейся и 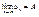 , теорема о двух милиционерах. , теорема о двух милиционерах.

Выберем произвольное положительное число e, "e найдём N1
и N2
, такие чтобы выполнялись Þ неравенства:
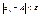 , , 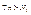 (1) (1)
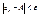 , , 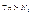 (2) (2)
N – max из (N1
, N2
), тогда "n>N одновременно выполняются неравенства:
А-e<an
<A+e (3)
А-e<cn
<A+e (4)
Поэтому "n>N выполняются неравенство:
А-e<an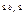 <A+e, А-e<bn
<A+e,
<A+e, А-e<bn
<A+e, 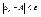 , таким образом , таким образом 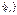 является сходящейся и имеет является сходящейся и имеет 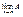 . .
Теорема 4: всякая монотонно возрастающая ограниченная числовая последовательность является сходящейся.
Всякая монотонно убывающая ограниченная числовая последовательность является сходящейся.
Арифметические св-ва сходящихся последовательностей.
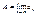 , , 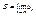 . .
Теоремы:
1) 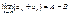
2) 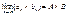
3) А¹0, 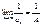
25.
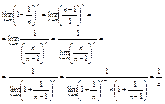
26. Понятие функции.
Пусть на некотором числовом множестве m определено правило, по которому каждому числу из множества m ставится в соответствии некоторое вещественное число. Тогда говорят, что на множество M задана функция. Множество M – называется областью определения этой функции. Обычно предполагают, что множество M представляет некоторый интервал, открытый или замкнутый ограниченный или ¥. Множество точек X принадлежащих множеству M будет образовывать на числовой оси некоторое множество. Это множество будет называться открытым, если вместе с любой точкой X из этого множества этому множеству M принадлежит некоторое ε окрестность X. Точка X Î M называется граничной точкой, если в любой e окрестности точки X можно указать точки, не принадлежащие множеству M. Множество М называется замкнутым, если дополнительное к нему множества является открытым R^\ M. Объединение любого числа отрытых множеств является открытым множеством, пересечение конечного числа множеств является открытым множеством. Следует, что пересечение любого числа замкнутых множеств являются замкнутым, объединение конечного числа замкнутых множеств являются замкнутыми. Пусть на множестве M определена функция. Это будем обозначать следующим образом: y = f(x), x Î M; x Î M . Величина x будет называться независимой переменной или аргументом y значение, которой зависит от x - называется зависимой переменной или функцией. Рассмотрим на координатной плоскости множество точек G = {(x; f(x)), x Î M}. Множество G – называется графиком функции. Пусть на множестве M определены две функции y = f(x); y = g(x), тогда функция h(x) значение, которой вычисляется по правилу h(x) = f(x) + g(x) – является суммой. Функция h(x) = f(x)g(x) называется произведением. Функция может быть задана различными способами: 1) Графический способ 2) Словесный или сательный 3) Аналитический. Пусть на множестве x определена функция y = f(x) со значениями во множестве Y предположим, что на множестве Y определена функция со значениями множествам X x = g(y). Пусть при этом выполнены условия x = g(f(x)), y = f(g(y)). Тогда функция x =g(y) – называется обратной функцией по отношению к функции y = f(x). Из определения следует, что функция y =f(x) так же является обратной функцией по отношению к функции x =g(y) по этому эти функции называются взаимно обратными. Примеры: 1) . Величина x будет называться независимой переменной или аргументом y значение, которой зависит от x - называется зависимой переменной или функцией. Рассмотрим на координатной плоскости множество точек G = {(x; f(x)), x Î M}. Множество G – называется графиком функции. Пусть на множестве M определены две функции y = f(x); y = g(x), тогда функция h(x) значение, которой вычисляется по правилу h(x) = f(x) + g(x) – является суммой. Функция h(x) = f(x)g(x) называется произведением. Функция может быть задана различными способами: 1) Графический способ 2) Словесный или сательный 3) Аналитический. Пусть на множестве x определена функция y = f(x) со значениями во множестве Y предположим, что на множестве Y определена функция со значениями множествам X x = g(y). Пусть при этом выполнены условия x = g(f(x)), y = f(g(y)). Тогда функция x =g(y) – называется обратной функцией по отношению к функции y = f(x). Из определения следует, что функция y =f(x) так же является обратной функцией по отношению к функции x =g(y) по этому эти функции называются взаимно обратными. Примеры: 1)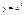 xÎ[0;¥] yÎ[0;¥]
xÎ[0;¥] yÎ[0;¥] 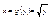 g(f(x)) =g g(f(x)) =g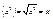 f(g(y))= f(g(y))=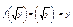 . 2)
Пусть дана функция . 2)
Пусть дана функция 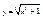 ; ; 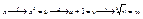 ; y = h(v) = h(g(u))®h(g(f(x))); y = f(x), x = g(y), y = f(g(y)), x = g(f(x)); g = lnx , ; y = h(v) = h(g(u))®h(g(f(x))); y = f(x), x = g(y), y = f(g(y)), x = g(f(x)); g = lnx , 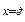 , f(x) = lnx, , f(x) = lnx, 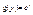 , , 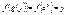 , , 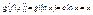 3) 3) 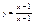 ,
, 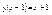 , , 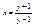 ; ; 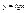 ,x = arctgy, tg(arctgy) = y, yÎ(-¥;¥), arctg (tgx) = x, ,x = arctgy, tg(arctgy) = y, yÎ(-¥;¥), arctg (tgx) = x, 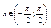 . . 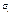 график функции y = f (x), график функции y = f (x),  график функции x = g(y), тогда график функции x = g(y), тогда  . Таким образом графики двух взаимно обратных функций совпадают, т. к. обычно через x обозначают независимую переменную, а через y зависимую переменную, то удобнее обратную функцию x = g(y) записывать в виде y = g(x) это приведет к тому, что график функции y = g(x) будет симметричен графику функции x =g(y), относительно биссектрисы одного координатного угла. . Таким образом графики двух взаимно обратных функций совпадают, т. к. обычно через x обозначают независимую переменную, а через y зависимую переменную, то удобнее обратную функцию x = g(y) записывать в виде y = g(x) это приведет к тому, что график функции y = g(x) будет симметричен графику функции x =g(y), относительно биссектрисы одного координатного угла.
27. Предел функции в точке.
x
= f(x), Xo ÎD(f) Xo – называется точкой сгущения, если в любой ее окрестности всегда можно указать точки из области определения функции y = f(x). Дальше всегда будем считать, что Xo точка сгущения. Число A называется пределом функции y =f(x), при 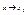 , если для любой числовой последовательности Xn сходящейся к Xo, , если для любой числовой последовательности Xn сходящейся к Xo, 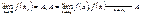 . Это определение эквивалентно следующему: A называется пределом функции f(x) при X ® Xo, если для любого числа e можно указать такое положительное число Δ, то из неравенства . Это определение эквивалентно следующему: A называется пределом функции f(x) при X ® Xo, если для любого числа e можно указать такое положительное число Δ, то из неравенства 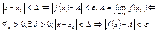 . Из свойств пределов следует: 1) . Из свойств пределов следует: 1) 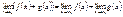 2) 2) 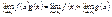 3) 3) 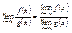 4) 4) 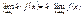 . .
28. Асимптоты. Опр.
Если точка (x; y) непрерывно перемещается по кривой y = f(x) так, что хотя бы одна из них координат точки стремится к бесконечности, и при этом расстояние точки от некоторой прямой стремится к нулю, то эта прямая называется асимптотой кривой. Если существует число a такое, что 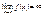 , то прямая x = a является вертикальной асимптотой. Если существуют пределы , то прямая x = a является вертикальной асимптотой. Если существуют пределы 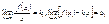 , то прямая , то прямая 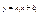 будет асимптотой (правая наклонная или, в случае K1 = 0, правая горизонтальная асимптота). Если существуют пределы будет асимптотой (правая наклонная или, в случае K1 = 0, правая горизонтальная асимптота). Если существуют пределы 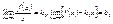 , то прямая , то прямая 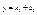 - асимптота (левая наклонная или, в случае K2 = 0, левая горизонтальная асимптота). График функции y = f(x) (функция предполагается однозначной) не может иметь более одной правой или левой асимптоты. - асимптота (левая наклонная или, в случае K2 = 0, левая горизонтальная асимптота). График функции y = f(x) (функция предполагается однозначной) не может иметь более одной правой или левой асимптоты.
3
0
.
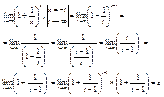 
31) Вычисление предела 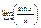 . .

Пусть X>0, угол измеренный в rad. AB=sinx, È AC=x, DC=tgx, очевидно, что AB<AC<ÈAC<DC, sinx<x<tgx, поделим обе части неравенства на sinx: 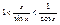 , , 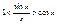 (1), (1), 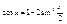 , , 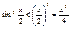 , , 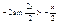 , , 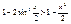 , , 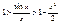 , т.к. при , т.к. при 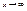 , , 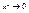 , то , то
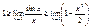 , , 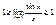 Þ Þ 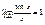 , таким образом, sinx и х являются эквивалентны бесконечно малым величинам, из доказанного предела следует, что , таким образом, sinx и х являются эквивалентны бесконечно малым величинам, из доказанного предела следует, что 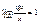
32. Непрерывность функции в точке и на интервале. Примеры.
Пусть ф-я y=f(x), определена на некотором интервале (a;b), пусть 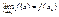 , тогда ф-я y=f(x) называется непрерывной на интервале (a;b). , тогда ф-я y=f(x) называется непрерывной на интервале (a;b).
Если ф-я y=f(x) является непрерывной в каждой точке интервала (a;b), то она непрерывна на интервале (a;b) из свойств lim Þ что если ф-я y=f(x) и y=g(x), являются непрерывными в точке, и на интервале (a;b), то их сумма, произведение, частное и произведение f(x) на константу k, также непрерывны в этой точке.
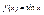 - докажем непрерывность этой ф-ии в некотррой точке х0
: - докажем непрерывность этой ф-ии в некотррой точке х0
:
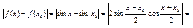 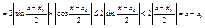 , ,
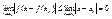 , , 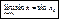
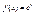
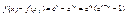 , , 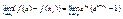 , , 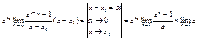 , , 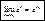
33. Свойства ф-ий, непрерывных на отрезке.
Теорема Больцано-Коши.
y=f(x), (a;b), x0
Î(a;b), для того чтобы ф-я y=f(x) была непрерывна в т. x0
, необходимо и достаточно, чтобы "e>0 $d(e)>0 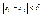 , , 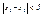 Þ Þ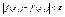
Первая теорема Больцано-Коши.
Пусть на отрезке 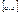 определена непрерывная ф-я y=f(x), предположим, что в точках а и b эта ф-я принимает значения разных знаков, тогда найдётся т. с, такая, что f(c)=0. определена непрерывная ф-я y=f(x), предположим, что в точках а и b эта ф-я принимает значения разных знаков, тогда найдётся т. с, такая, что f(c)=0.

Д-во.
Предположим для определённости, что f(b)>0. Пусьт  , если f(c1
)=0, то f(a)<0, тем самым т., существование которой утверждается в теореме найдена. Если f(c)¹0, то на концах одного из отрезков (a;c1
) или (c1
;b), ф-я y=f(x) принимает значения разных знаков. , если f(c1
)=0, то f(a)<0, тем самым т., существование которой утверждается в теореме найдена. Если f(c)¹0, то на концах одного из отрезков (a;c1
) или (c1
;b), ф-я y=f(x) принимает значения разных знаков.
Обозначим отрезок  и поступим с ним таким же образом, как и с отрезком и поступим с ним таким же образом, как и с отрезком  , продолжим этот процесс до бесконечности. Возможны два случая: , продолжим этот процесс до бесконечности. Возможны два случая:
а) на каком-нибудь конечном шаге найдётся точка сn
f(cn
)=0, тем самым будет найдена точка существования которой утверждается в теореме.
б) "cn
f(cn
)¹0, рассмотрим отр. 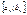 , cn
Î , cn
Î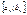 , f(an
)<0, f(bn
)>0, l - длина , f(an
)<0, f(bn
)>0, l - длина 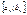 , тогда длина , тогда длина 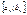 = =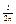 , , 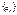 образует монотонно возрастающую последовательность, а последовательность образует монотонно возрастающую последовательность, а последовательность 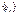 является ограниченной. является ограниченной.
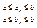 , , 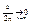 , ,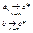 , ,
поэтому 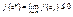 , , 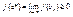 , f(c*)=0. , f(c*)=0.
Вторая теорема Больцано-Коши.
Пусть на отрезке 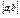 определена непрерывная ф-я y=f(x), f(a)=A, f(b)=B, A¹B, тогда ф-я y=f(x) принимает все промежуточные значения между А и В. определена непрерывная ф-я y=f(x), f(a)=A, f(b)=B, A¹B, тогда ф-я y=f(x) принимает все промежуточные значения между А и В.
Д-во.
Предположим для определённости, что B>A, пусть С произвольное число расположенное между А и В, тогда A<C<B. Докажем, что найдётся т. сÎ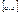 , такая, что f(c)=C, для этого рассмотрим ф-ю j(x)=f(x)-C, тогда j(a)=f(a)-C=A-C<0, j(b)=f(b)-C=B-C>0 Þ y=j(x), на концах отрезка , такая, что f(c)=C, для этого рассмотрим ф-ю j(x)=f(x)-C, тогда j(a)=f(a)-C=A-C<0, j(b)=f(b)-C=B-C>0 Þ y=j(x), на концах отрезка 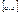 , принимает значения разных знаков. По первой теореме Больцано-Коши найдётся точка с, такая, что j(с)=0 Þ j(с)=f(c)-C=0 Þ f(c)=C , принимает значения разных знаков. По первой теореме Больцано-Коши найдётся точка с, такая, что j(с)=0 Þ j(с)=f(c)-C=0 Þ f(c)=C

Первая теорема Веерштрасса (19в).
Пусть на отрезке 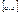 определена непрерывная ф-я y=f(x), тогда эта ф-я является ограниченной на отрезке определена непрерывная ф-я y=f(x), тогда эта ф-я является ограниченной на отрезке 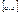 , $m, М,что , $m, М,что 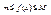 , , 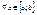 . .
Предположим, что утверждение теоремы не верно, тогда можно указать 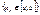 , такую, что , такую, что 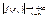 , т.к. , т.к. 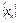 является ограниченной, то из неё можно выбрать сходящуюся подпоследовательность является ограниченной, то из неё можно выбрать сходящуюся подпоследовательность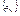 , , 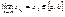 , , 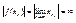 , что противоречит тому, что ф-я y=f(x) определена на отрезке , что противоречит тому, что ф-я y=f(x) определена на отрезке 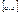 - теорема доказана. - теорема доказана.
Если отрезок 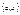 не является замкнутым, то утверждение теоремы может быть не верной. (y=1/x, yÎ(0;1]) не является замкнутым, то утверждение теоремы может быть не верной. (y=1/x, yÎ(0;1])

Вторая теорема Веерштрасса.
Пусть y=f(x), xÎ[a;b], тогда в некоторых точках отрезка [a;b] эта ф-я принимает наибольшее и наименьшее значения.

44. Инвариантность формы первого дифференциала.
Выражение f’(x)∆x представляет дифференциал в f(x), когда х рассматривается как аргумент. Если же сама величина х рассматривается как функция некоторого аргумента t, то выражение f’(x)∆x, как правило, не представляет дифференциала
; исключение составляет лишь случай линейной зависимости x=at+b.
Напротив, формула df(x)=f’(x)dx верна как в том случае, когда x есть аргумент (тогда dx=∆x), так и в случае, когда x есть функция от t. Это свойство выражения f’(x)dx называется его инвариантностью.
Например: Выражение 2x∆x представляет дифференциал функции y=x2
, когда х есть аргумент. Положим теперь x=t2
(2) и будем считать t аргументом. Тогда y=x2
=t4
(3). Из (2) находим: ∆x=2t∆t+∆t2
. Значит, 2x∆x=2t2
(2t∆t+∆t2
). Это выражение не пропорционально ∆t и потому теперь 2x∆x не является дифференциалом. Дифференциал функции y находим из (3): dy=4t3
∆t.
45. Теорема Ферма. Теорема Ролля, Лагранжа, Коши.
Теорема Ферма:
Пусть функция y=f(x) непрерывна на отрезке [a, b], причём наибольшего и наименьшего значения она достигает во внутренней точке отрезка a<c<b. Если в этой точке существует производная, то она равна нулю.
Доказательство: Пусть в точке с достигается наибольшее значение f(x)£f(c), и xÎ[a, b]. Вычислим односторонние производные:
По условию теоремы в точке с существует производная f’(c). Это означает, что левосторонняя и правосторонняя производные равны, т.е. f’(c)=0 Теорема Ролля:
Пусть функция f(x), дифференцируема в замкнутом промежутке (a, b), обращается в нуль на концах промежутка. Тогда производная f’(x) по меньшей мере один раз обращается в нуль внутри промежутка.
Теорема Лагранжа:
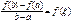
Если функция f(x) дифференцируема в замкнутом промежутке (a, b), то отношение (f(b)-f(a))/(b-a) равно значению производной f’(x) в некоторой точке x=x, лежащей внутри промежутка (a, b):
Пример: Пусть f(x)=x2
. Тогда f’(x)=2x. Формула принимает вид (b2
-a2
)/(b-a)=2x, откуда x=(a+b)/2, т.е. x лежит в точности на середине промежутка (a, b).
Теорема Коши:
Пусть производные f’(t) и j’(t) двух функций f(t) и j(t), дифференцируемых в замкнутом промежутке (a, b) , не обращаются одновременно в нуль нигде внутри этого промежутка. Пусть при этом одна из функций f(t), j(t) имеет неравные значения на концах интервала (например j(a)¹j(b)). Тогда приращения f(b)-f(a) и j(b)-j(a) данных функций относятся как их производные в некоторой точке t=t, лежащей внутри промежутка (a, b):
Пример: Рассмотрим функции f(t)=t3
и j(t)=t2
в промежутке (0, 2). На конце t=0 производные f’(t)=3t2
и j’(t)=2t обращаются в нуль, но внутри промежутка обе отличны от нуля. Каждая из функций f(t), j(t) имеет неравные значения на концах t=0 и t=2. Условия теоремы Коши выполнены. Значит, отношение
Должно равняться отношению В некоторой точке t=x, лежащей между a=0 и b=2. Действительно, уравнение (3/2)t=2 имеет корень t=4/3, лежащий внутри промежутка (0,2).
46. Применение производных для исследования функций. Условия монотонности.
1. Область определения.
2. Особые свойства функции: чётность или нечётность, периодичность.
3. Корни, промежутки знакопостоянства.
4.
Непрерывность, характер точек разрыва (односторонние пределы), пределы на бесконечности. 5. Асимптоты.
6. Производная, исследование функции на монотонность и экстремумы.
7. Вторая производная, исследование функции на выпуклость и перегиб.
8.
Нахождение значения функции и ее производной в характерных точках (пересечения с осями координат, экстремума, перегиба), нахождение нескольких дополнительных точек графика (не обязательно, используется для построения более точного графика). 9. Построение эскиза графика.
Исследование дифференцируемой функции на максимум и минимум с помощью первой производной:
1) Ищем первую производную функции, т. е. f’(x)
2) Находим критические значения аргумента x; для этого:
а) приравниваем первую производную к нулю и находим действительные корни полученного уравнения f’(x)=0;
б) находим значение x, при которых производная f’(x) терпит разрыв.
3) Исследуем знак производной слева и справа от критической точки. Так как знак производной остается постоянным в интервале между двумя критическими точками, то для исследования знака производной слева и справа, например, от критической точки x2
достаточно определить знак производной в точках a и b (x1
<a<x2
, x2
<b<x3
, где x1
и x3
– ближайшие критические точки).
4) Вычисляем значение функции f(x) при каждом критическом значении аргумента.
Исследование функции на максимум и минимум с помощью второй производной:
1) Пусть при x=x1
производная функции y=f(x) обращается в нуль, т.е. f’(x1
)=0. Пусть, кроме того, вторая производная f’’(x) существует и непрерывна в некоторой окрестности точки x1
. Тогда справедлива следующая теорема: Пусть f’(x1
)=0; тогда при x=x1
функция имеет максимум, если f’’(x1
)<0, и минимум, если f’’(x1
)>0
Условие монотонности:
1) Последовательность (an
) называется возрастающей (неубывающей),
если "n<k, nÎN, kÎN an
£ak
2) Последовательность (an
) называется убывающей (невозрастающей),
если "n<k, nÎN, kÎN an
³ak
47. Понятие локального экстремума. Необходимое и достаточное условие существования экстремума.
Функция f(x) имеет максимум (минимум) в точке x=a, если значение f(a) больше (меньше) всех соседних значений. Максимум и минимум объединяются наименованием экстремум
.
Необходимое условие максимума и минимума:
Если функция f(x) имеет экстремум в точке x=a, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует.
Первое достаточное условие экстремума:
Если в достаточной близости от точки x=a производная f’(x) положительна слева от a и отрицательна справа от a, то в самой точке x=a функция f(x) имеет максимум при условии, что функция f(x) здесь непрерывна.
Второе достаточное условие экстремума:
Пусть в точке x=a первая производная f’(x) обращается в нуль; если при этом вторая производная f’’(a) отрицательна, то функция f(x) имеет в точке x=a максимум, если положительна, то – минимум.
48. Выпуклые функции. Условия выпуклости.
Кривая обращена выпуклостью вверх на интервале (a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале. Кривая обращена выпуклостью вниз на интервале (b, c), если все точки кривой лежат выше любой ее касательной на этом интервале.
Теорема 1.
Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f’’(x)<0, то кривая y=f(x) на этом интервале обращена выпуклостью вверх (кривая выпукла).
Теорема 1'.
Если во всех точках интервала (b, c) вторая производная функции f(x) положительна, т.е. f’’(x)>0, то кривая y=f(x) на этом интервале обращена выпуклостью вниз (кривая вогнута).
Теорема 2.
Пусть кривая определяется уравнением y=f(x). Если f’’(a)=0 или f’’(a) не существует и при переходе через значение x=a производная f’’(x) меняет знак, то точка кривой с абсциссой x=a есть точка перегиба.
49.Формула Тейлора. Формулы Тейлора для элементарных функций. Примеры.
Теорема:
Если функция f(x) обладает в замкнутом промежутке (a, b) производными до (n+1)-го порядка включительно, то
где x - некоторое число, лежащее между a и b. Последнее слагаемое в формуле, называемое остаточным членом в форме Лагранжа, дает точное выражение разности Rn
между f(b) и выражением
(многочлен Тейлора):
Формула Тейлора устанавливает что уравнение, в котором за неизвестное принимается x, имеет, по меньшей мере, одно решение, лежащее между a и b.
Пример: Пусть f(x)=ex
. Все производные этой функции равны ex
. Нам известно значение ex
в точке х=0 (именно e0
=1). Эту точку мы примем за начальную. В многочлене Тейлора надо положить: a=0, f(a)=f’(a)=…=f(
n
)
(a)=1, и он принимает такой вид(5):
Заменив значение ex
значением многочлена (5), мы допустим некоторую ошибку Rn
; она равна
Число x лежит где-то между нулём и x (оно зависит и от x и от n). Значит, ex
лежит между e0
=1 и ex
. Этого достаточно, чтобы оценить ошибку.
34. Точка разрыва ф-ии. Односторонние пределы.
Пусть задана ф-я y=f(x), х0
ÎХ, для данной ф-ии можно определить односторонний предел.
Число А называют правосторонним пределом ф-ии y=f(x), если " числовой последовательности 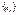 сходящейся к точке х0
и такокй, что xn
>x0
. сходящейся к точке х0
и такокй, что xn
>x0
.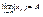 . .
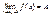

Аналогичным образом определяется левосторонний предел.
Нарушение условий непрерывности для ф-ии y=f(x), может происходить как в отдельных точках, так и в точках образующих одну или несколько линий.
35. Задачи приводящие к понятию производной. Производная ф-ии в точке. Геометрический смысл производной. У-ие касательной и нормали к графику ф-ий.
Пусть на отр. [a;b] определена ф-ия y=f(x), х0
Î(a;b), рассмотрим 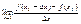 (1) (1)
Пусть существует конечное значение lim (1), - это число называют производной ф-ии y=f(x), х=х0
.Обозначается (f’(x), 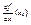 , , 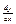 ) )
При изменении т. х0
будет манятся значение предела, таким образом можно рассмотреть ф-ию 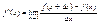 , , 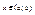

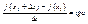 , поэтому , поэтому 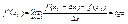 , , 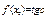 . .
Уравнение касательной: 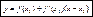
36. Дифференциал.
Пусть на отрезке (a; b) определена функция y = f(x), которая имеет в точке Xo, Xo Î (a; b), тогда принадлежит функции Δf(Xo) = f(Xo + ΔX) – f(Xo) = f ’(Xo)ΔX + 0(ΔX) – 1).
Из 1)
следует, что принадлежит функции можно представить в виде суммы двух слагаемых. Первые из них являются линейные функции, относят ΔX, а второе является величиной ¥ < более высокого порядка, чем DX. Рассмотрим схему о возможности предоставления приделу произвольной функции. y = f(x) в виде суммы двух слагаемых. Одно из которых является линейным – относительно превращения независимой переменной, а другая является ¥ < более высокого порядка, т. е. f(Xo + DX) – f(Xo) = A + DX + 0(DX) - 2)
. Первое слагаемое A´ DX – называется главной линейной частью превращения. Опр.
Главная линейная часть превращения называется дифференциалом и обозначается следующим образом dy, df(Xo). Разделим левую и правую часть 2)
на DX и перейдем к пределу при DX ® 0. 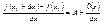 . . 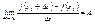 - 3).
Если для функции y = f(x) выполняется равенство 2),
то существует - 3).
Если для функции y = f(x) выполняется равенство 2),
то существует 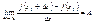 , т. е. A = f ’(Xo). Главная линейная часть превращения функции имеет вид f ‘ (Xo)DX. Функция, для которой можно написать разложение 2)
называется дифференцируемой. Из 3)
следует, что если функция является дифференцируемой, то она имеет конечную производную. Верно и обратное утверждение, если функция y = f(x) имеет конечную производную, то она является дифференцируемой. Это следует из равенства 1).
Для того, что бы функция была дифференцируемой необходимо и достаточно, чтобы она имела конечную производную. Обозначим превращение независимой переменой через dx = DX, тогда дифференциал функции можно записать в виде dy = в ´ f(x) = f(x)dx. В этом случае равенство 1)
можно переписать в виде Df(Xo) = df(Xo) – 0(DX) – 4).
Из 4)
следует, что если функция y = f(x) является дифференцируемой в Xo, то она является непрерывной в этой точке. , т. е. A = f ’(Xo). Главная линейная часть превращения функции имеет вид f ‘ (Xo)DX. Функция, для которой можно написать разложение 2)
называется дифференцируемой. Из 3)
следует, что если функция является дифференцируемой, то она имеет конечную производную. Верно и обратное утверждение, если функция y = f(x) имеет конечную производную, то она является дифференцируемой. Это следует из равенства 1).
Для того, что бы функция была дифференцируемой необходимо и достаточно, чтобы она имела конечную производную. Обозначим превращение независимой переменой через dx = DX, тогда дифференциал функции можно записать в виде dy = в ´ f(x) = f(x)dx. В этом случае равенство 1)
можно переписать в виде Df(Xo) = df(Xo) – 0(DX) – 4).
Из 4)
следует, что если функция y = f(x) является дифференцируемой в Xo, то она является непрерывной в этой точке.
37. Геометрический смысл дифференциала.
Пусть задана функция g = f(x), проведем через точку с координатами (Xo; f(Xo)) касательную. Уравнение касательной имеет вид 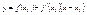 . Подставим вместо x значение Xo + DX, тогда получим . Подставим вместо x значение Xo + DX, тогда получим 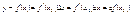 . Дифференциал df(Xo) равен превращению ординаты касательной, при изменении x от Xo до DX + Xo. . Дифференциал df(Xo) равен превращению ординаты касательной, при изменении x от Xo до DX + Xo.
38. Непрерывность.
Предел функции. Число A называется пределом функции z = f(x; y) при стремлении точки 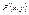 к точке P(a,b), если для любого e > 0 существует такое в > 0, что при 0 < r < d, где к точке P(a,b), если для любого e > 0 существует такое в > 0, что при 0 < r < d, где 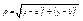 - расстояние между точками P и P’, имеет место равенство - расстояние между точками P и P’, имеет место равенство 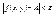 . В этом случае пишут: . В этом случае пишут: 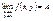 . Непрерывность и точки разрыва. Функция z = f(x, y) называется непрерывной в точке P(a, b), если . Непрерывность и точки разрыва. Функция z = f(x, y) называется непрерывной в точке P(a, b), если 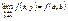 . Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области. Нарушение условий непрерывности для функции f(x, y) может происходить как в отдельных точках (изолированная точка разрыва), так и в точках, образующих одну или несколько линий (линий разрыва), а иногда и более сложные геометрические образы. . Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области. Нарушение условий непрерывности для функции f(x, y) может происходить как в отдельных точках (изолированная точка разрыва), так и в точках, образующих одну или несколько линий (линий разрыва), а иногда и более сложные геометрические образы.
39. Правила вычисления производных.
40. Производные от элементарных ф-ий.
а) f(x)=xn
, 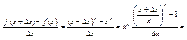 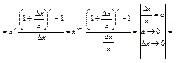 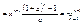 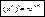
б) f(x)=sinx, 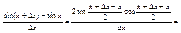 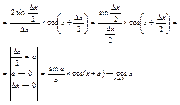 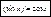
в) y=ax
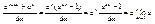 , , 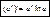
43. Производные высших порядков.
Пусть на отрезке (a; b) определена функция y = f(x). Предположим, что эта функция имеет производную на отрезке (a; b). В свою очередь f’(x) является функцией, от переменной величены x, поэтому можно рассмотреть задачу по вычислению производной от производной функции. Если эта производная существует, то ее называют второй производной и обозначим следующим образом: f “ (x) или 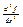 . Аналогичным образом определим третью производную и т.д. Производная порядка n обозначим . Аналогичным образом определим третью производную и т.д. Производная порядка n обозначим 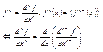 Т.к. (f(x) + g(x))’ = f’(x) +g’(x), то следует Т.к. (f(x) + g(x))’ = f’(x) +g’(x), то следует 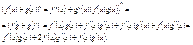 Аналогичным образом: Аналогичным образом: 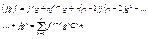
|