| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
"Гомельский государственный университет имени Франциска Скорины"
Математический факультет Кафедра алгебры и геометрии
Допущена к защите
Зав. кафедрой Шеметков Л.А.
" " 2005г.
Дипломная работа
Свойство централизаторов конгруэнций универсальных алгебр
Исполнитель
студентка группы М-51
Шутова И.Н.
Руководитель
Д., ф-м н., профессор Монахов В.С.
Гомель 2005
Содержание
Введение
1. Основные определения и используемые результаты
2. Свойство централизаторов универсальных алгебр
3. Мультикольцо
Заключение
Список использованных источников
Введение
В теории формаций конечных групп, мультиколец и многих других алгебраических систем исключительно важную роль играют такие понятия, как локальные экраны, локальные формации, основанные на определении центральных рядов. Впервые понятие централизуемости конгруэнций было введено Смитом в работе [5]. Возникает задача согласованности определения централизуемости Смита с определением в группах и мультикольцах.Такая задача была решена в указанной работе Смита [5], где было показано:нормальная подгруппа 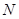 группы группы 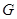 централизует подгруппу централизует подгруппу 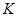 тогда и только тогда, когда конгруэнции,индуцированные этими нормальными подгруппами, централизуют друг друга в смысле Смита. тогда и только тогда, когда конгруэнции,индуцированные этими нормальными подгруппами, централизуют друг друга в смысле Смита.
Возникает следующий вопрос: справедливо ли аналогичное утверждение для мультиколец, т.е. будут ли выполнятся свойства централизуемости, изложенные в работе [3], для универсальных алгебр.
В настоящей дипломной работе решается задача взаимосвязи структуры мультиколец и универсальных алгебр, получен новый результат: идеал 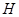 тогда и только тогда централизуется идеалом тогда и только тогда централизуется идеалом 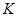 , когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита. , когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита.
Дипломная работа включает в себя введение, три параграфа и список литературы из 10 наименований.
Перейдем к краткому изложению содержания дипломной работы.
Раздел 1 является вспомогательным и включает в себя все необходимые определения и используемые результаты.
Раздел 2 носит реферативный характер. Здесь приводятся свойства централизаторов конгруэнций, доказательства которых изложены в работах [5, 6, 7].
Раздел 3 является основным. Здесь вводится определение мультикольца, определение идеала мультикольца, определение централизатора идеала и с использованием данных определений доказывается основной результат работы (теоремы 3.4. и 3.5).
1. Основные определения и используемые результаты
Определение 1.1.
[1] Универсальной алгеброй, или, короче, алгеброй называется пара 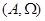 , где , где 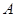 - непустое множество, - непустое множество, 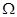 - (возможно пустое) множество операций на - (возможно пустое) множество операций на 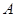 . .
Определение 1.2.
[1] Конгруэнцией на универсальной алгебре 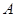 называется всякое отношение эквивалентности на называется всякое отношение эквивалентности на 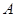 , являющееся подалгеброй алгебры , являющееся подалгеброй алгебры 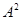 . .
Определение 1.3.
[1] Если 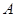 и и 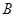 - алгебры сигнатуры - алгебры сигнатуры 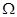 , то отображение , то отображение 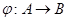 называется гомоморфизмом, если для любой называется гомоморфизмом, если для любой 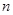 -арной операции -арной операции 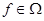 и любых элементов и любых элементов 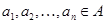 выполняется равенство: выполняется равенство:
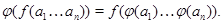
Взаимно однозначный гомоморфизм называется изоморфизмом.
Теорема 1.1.
[1] Пусть 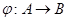 - гомоморфизм универсальных алгебр, тогда множество - гомоморфизм универсальных алгебр, тогда множество
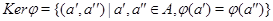
является конгруэнцией на алгебре 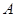 и называется ядром гомоморфизма и называется ядром гомоморфизма 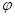
Теорема 1.2.
[1] Пусть 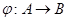 - гомоморфное наложение, тогда - гомоморфное наложение, тогда 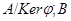 . .
Теорема 1.3.
[1] Пусть 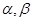 - конгруэнции на алгебре - конгруэнции на алгебре 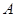 и и 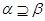 , тогда , тогда 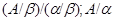 . .
Определение 1.4.
[2] Непустой абстрактный класс алгебр 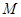 сигнатуры сигнатуры 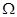 называется многообразием, если называется многообразием, если 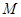 замкнут относительно подалгебр и прямых произведений. замкнут относительно подалгебр и прямых произведений.
Многообразие 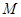 называется мальцевским, если конгруэнции любой алгебры из называется мальцевским, если конгруэнции любой алгебры из 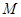 попарно перестановочны. попарно перестановочны.
Теорема 1.4.
[2] Конгруэнции любой алгебры многообразия 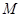 попарно перестановочны тогда и только тогда, когда существует термальная операция попарно перестановочны тогда и только тогда, когда существует термальная операция 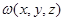 , что во всех алгебрах из , что во всех алгебрах из 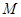 справедливы тождества справедливы тождества
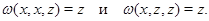
Определение 1.5.
[3] Пусть  и и 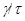 - факторы алгебры - факторы алгебры 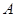 . Тогда они называются: . Тогда они называются:
1) перспективными, если либо 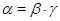 и и 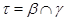 , либо , либо 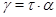 и и 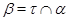 ; ;
2) проективными, если в 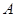 найдутся такие факторы найдутся такие факторы 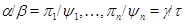 , что для любого , что для любого 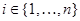 факторы факторы 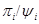 и и 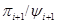 перспективны. перспективны.
Теорема 1.5.
[4] Между факторами произвольных двух главных рядов алгебры 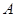 , принадлежащей мальцевскому многообразию, можно установить такое взаимно однозначное соответствие, при котором соответствующие факторы проективны и централизаторы в , принадлежащей мальцевскому многообразию, можно установить такое взаимно однозначное соответствие, при котором соответствующие факторы проективны и централизаторы в 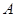 равны. равны.
Теорема 1.6.
[2] (Лемма Цорна). Если верхний конус любой цепи частично упорядоченного множества 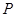 не пуст, то не пуст, то 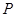 содержит максимальные элементы. содержит максимальные элементы.
2. Свойство централизаторов конгруэнций универсальных алгебр
Под термином ``алгебра'' в дальнейшем будем понимать универсальную алгебру. Все рассматриваемые алгебры предполагаются входящими в фиксированное мальцевское многообразие 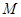 . Используются определения и обозначения из работы [1]. Дополнительно отметим, что конгруэнции произвольной алгебры обозначаются греческими буквами. Если . Используются определения и обозначения из работы [1]. Дополнительно отметим, что конгруэнции произвольной алгебры обозначаются греческими буквами. Если 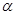 - конгруэнция на алгебре - конгруэнция на алгебре 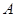 , то , то 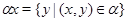 - класс эквивалентности алгебры - класс эквивалентности алгебры 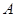 по конгруэнции по конгруэнции 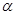 , , 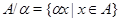 - факторалгебра алгебры - факторалгебра алгебры 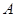 по конгруэнции по конгруэнции 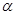 . Если . Если 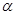 и и 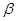 - конгруэнции на алгебре - конгруэнции на алгебре 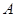 , , 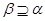 , то конгруэнцию , то конгруэнцию 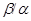 на алгебре на алгебре 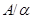 назовем фактором на назовем фактором на 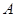 . Очевидно, что . Очевидно, что 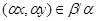 тогда и только тогда, когда тогда и только тогда, когда 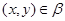 . . 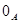 или или  и и 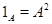 или или 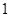 - соответственно наименьший и наибольший элементы решетки конгруэнций алгебры - соответственно наименьший и наибольший элементы решетки конгруэнций алгебры 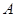 . .
Будем пользоваться следующим определением централизуемости конгруэнций, эквивалентность которого определению Смита [5] доказана в работе [6].
Определение 2.1.
Пусть 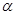 и и 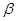 - конгруэнции на алгебре - конгруэнции на алгебре 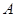 . Тогда . Тогда 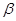 централизует централизует 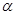 (записывается: (записывается: 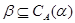 ), если на ), если на 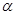 существует такая конгруэнция существует такая конгруэнция 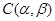 , что: , что:
1) из 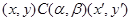 всегда следует всегда следует 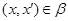 ; ;
2) для любого элемента 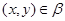 всегда выполняется всегда выполняется
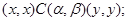
3) если 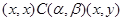 , то , то 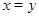 . .
Следующие свойства централизуемости, полученные Смитом [5], сформулируем в виде леммы.
Лемма 2.1.
Пусть 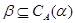 . Тогда: . Тогда:
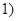 существует единственная конгруэнция существует единственная конгруэнция 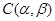 , удовлетворяющая определению 2.1; , удовлетворяющая определению 2.1;
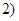 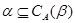 ; ;
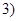 если если 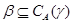 , то , то 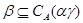 . .
Из леммы 2.1 и леммы Цорна следует, что для произвольной конгруэнции 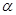 на алгебре на алгебре 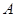 существует такая единственная наибольшая конгруэнция существует такая единственная наибольшая конгруэнция 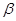 , что , что 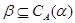 . Эту конгруэнцию . Эту конгруэнцию 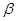 будем называть централизатором конгруэнции будем называть централизатором конгруэнции 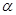 в в 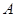 и обозначать и обозначать 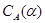 . .
Лемма 2.2.
Пусть 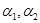 - конгруэнции на алгебре - конгруэнции на алгебре 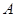 , , 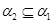 , , 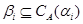 , , 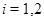 . Тогда справедливы следующие утверждения: . Тогда справедливы следующие утверждения:
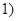 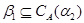 ; ;
  , где , где 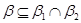 ; ;
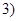 если, если, 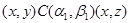 , либо , либо
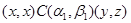 , либо , либо
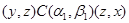 , то всегда , то всегда 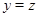 ; ;
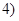 из из  всегда следует всегда следует 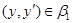 . .
Доказательство. 1).
Очевидно, что 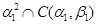 - конгруэнция на - конгруэнция на 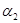 , удовлетворяющая определению 1. Значит, в силу п.1) леммы 2.1 , удовлетворяющая определению 1. Значит, в силу п.1) леммы 2.1 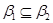 . .
2).
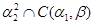 - конгруэнция на - конгруэнция на 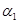 , удовлетворяющая определению 2.1. Значит, , удовлетворяющая определению 2.1. Значит, 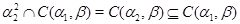 . .
3).
Пусть 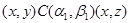 . Тогда . Тогда
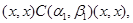
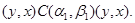
Применим к последним трем соотношениям мальцевский оператор  такой, что такой, что 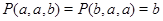 , для любых элементов , для любых элементов  . Тогда получим . Тогда получим
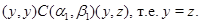
Аналогичным образом доказываются остальные случаи п.3).
4).
Пусть 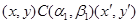 . Тогда справедливы следующие соотношения: . Тогда справедливы следующие соотношения:
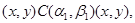
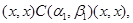
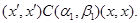
Следовательно, 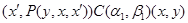 , где , где 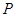 - мальцевский оператор. Тогда - мальцевский оператор. Тогда 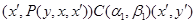 , т.е. , т.е. 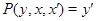 . Так как . Так как 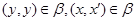 и и 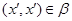 , то , то 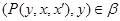 . Таким образом . Таким образом 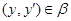 . Лемма доказана. . Лемма доказана.
В дальнейшем мы будем часто ссылаться на следующий хорошо известный факт (доказательство см., например [6]).
Лемма 2.3.
Любая подалгебра алгебры 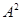 , содержащая конгруэнцию , содержащая конгруэнцию 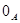 , является конгруэнцией на , является конгруэнцией на 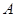 . .
Доказательство следующего результата работы [5] содержит пробел (следствие 224 [5] неверно, см. [7]), поэтому докажем его.
Лемма 2.4.
Пусть 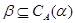 . Тогда для любой конгруэнции . Тогда для любой конгруэнции 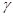 на на 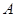
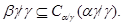
Доказательство.
Обозначим 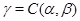 и определим на алгебре и определим на алгебре 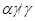 бинарное отношение бинарное отношение 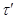 следующим образом: следующим образом:
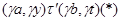
тогда и только тогда, когда 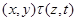 , где , где 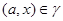 , , 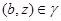 . Используя лемму 2.3, нетрудно показать, что . Используя лемму 2.3, нетрудно показать, что 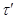 - конгруэнция на алгебре - конгруэнция на алгебре 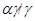 , причем , причем 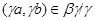 . .
Пусть 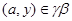 , т.е. , т.е. 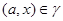 , , 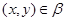 . Тогда . Тогда 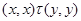 и, значит, и, значит, 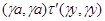 . .
Пусть, наконец, имеет место  и и 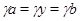 . Тогда справедливы следующие соотношения: . Тогда справедливы следующие соотношения:
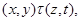
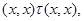
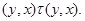
Применяя мальцевский оператор 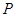 к этим трем соотношениям, получаем: к этим трем соотношениям, получаем: 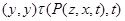 . Из леммы 2.2 следует, что . Из леммы 2.2 следует, что 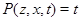 . Так как . Так как 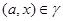 и и 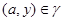 , то , то 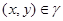 . Значит, . Значит, 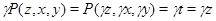 . Но . Но  , следовательно, , следовательно, 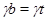 . Итак, . Итак, 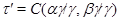 и удовлетворяет определению 2.1. Лемма доказана. и удовлетворяет определению 2.1. Лемма доказана.
Лемма 2.5.
Пусть  и и 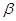 - конгруэнции на алгебре - конгруэнции на алгебре 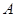 , , 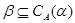 и и 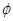 - изоморфизм, определенный на - изоморфизм, определенный на 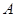 . Тогда для любого элемента . Тогда для любого элемента 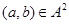 отображение отображение 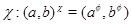 определяет изоморфизм алгебры определяет изоморфизм алгебры 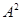 на алгебру на алгебру 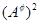 , при котором , при котором 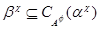 . В частности, . В частности, 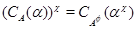 . .
Доказательство.
Очевидно, что 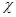 - изоморфизм алгебры - изоморфизм алгебры 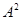 на алгебру на алгебру 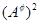 , при котором конгруэнции , при котором конгруэнции 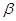 , ,  изоморфны соответственно конгруэнциям изоморфны соответственно конгруэнциям 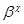 и и 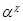 . Так как . Так как 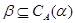 , то определена конгруэнция , то определена конгруэнция 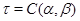 , удовлетворяющая определению 2.1. Изоморфизм , удовлетворяющая определению 2.1. Изоморфизм 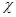 алгебры алгебры  на алгебру на алгебру 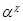 индуцирует в свою очередь изоморфизм индуцирует в свою очередь изоморфизм 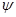 алгебры алгебры 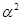 на алгебру на алгебру 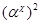 такой, что такой, что 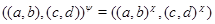 для любых элементов для любых элементов 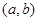 и и 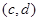 , принадлежащих , принадлежащих 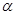 . Но тогда легко проверить, что . Но тогда легко проверить, что 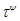 - конгруэнция на алгебре - конгруэнция на алгебре 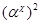 изоморфная конгруэнции изоморфная конгруэнции 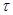 . Это и означает, что . Это и означает, что 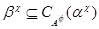 . Лемма доказана. . Лемма доказана.
Если 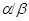 и и 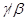 - факторы на алгебре - факторы на алгебре 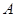 такие, что такие, что 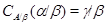 , то конгруэнцию , то конгруэнцию 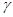 обозначим через обозначим через 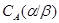 и назовем централизатором фактора и назовем централизатором фактора 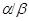 в в 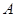 . .
Напомним, что факторы 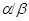 и и  на алгебре на алгебре 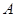 называются перспективными, если либо называются перспективными, если либо 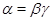 и и 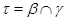 , либо , либо 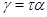 и и 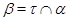 . .
Докажем основные свойства централизаторов конгруэнций.
Теорема 2.1.
Пусть 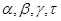 - конгруэнции на алгебре - конгруэнции на алгебре 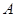 . Тогда: . Тогда:
 если если 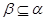 , то , то 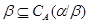 ; ;
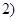 если если 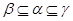 , то , то 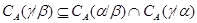 ; ;
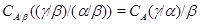 ; ;
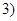 если если 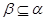 , , 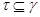 и факторы и факторы 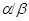 , ,  перспективны, то перспективны, то
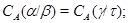
 если если 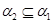 - конгруэнции на - конгруэнции на 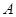 и и 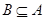 , то , то
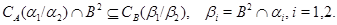
Доказательство. 1).
Так как конгруэнция 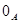 централизует любую конгруэнцию и централизует любую конгруэнцию и 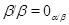 , то , то 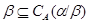 . .
2).
Из п.1) леммы 2.2 следует, что 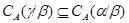 , а в силу леммы 2.4 получаем, что , а в силу леммы 2.4 получаем, что 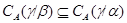 . .
Пусть  - изоморфизм - изоморфизм 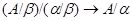 . Обозначим . Обозначим
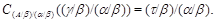
По лемме 2.5 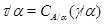 , а по определению , а по определению
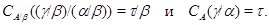
Следовательно, 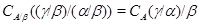 . .
3).
Очевидно, достаточно показать, что для любых двух конгруэнций 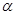 и и 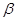 на алгебре на алгебре  имеет место равенство: имеет место равенство:
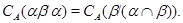
Покажем вначале, что
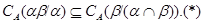
Обозначим 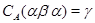 . Тогда, согласно определения 2.1, на алгебре . Тогда, согласно определения 2.1, на алгебре 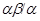 существует такая конгруэнция существует такая конгруэнция 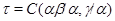 , что выполняются следующие свойства: , что выполняются следующие свойства:
а) если 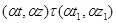 , то , то 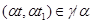 ; ;
б) для любого элемента 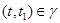 , , 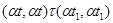 ; ;
в) если 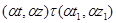 и и 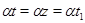 , то , то 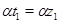 . .
Построим бинарное отношение 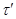 на алгебре на алгебре 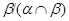 следующим образом: следующим образом:
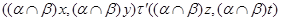
тогда и только тогда, когда 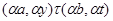 и и 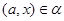 , , 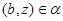 . Покажем, что . Покажем, что 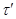 - конгруэнция на - конгруэнция на 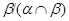 . Пусть . Пусть 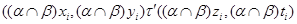 , , 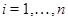 . Тогда . Тогда 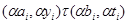 и и 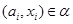 , , 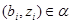 . Так как . Так как  - конгруэнция, то для любой - конгруэнция, то для любой 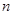 -арной операции -арной операции 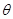 имеем: имеем:
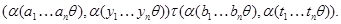
Очевидно, что (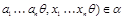 , , 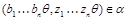 и и 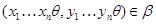 , , 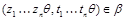 . Следовательно, . Следовательно, 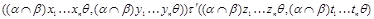 . Очевидно, что для любой пары . Очевидно, что для любой пары 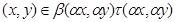 . Значит, . Значит, 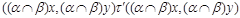 . Итак, по лемме 2.3, . Итак, по лемме 2.3, 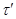 - конгруэнция на - конгруэнция на 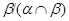 . Покажем теперь, что . Покажем теперь, что 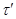 удовлетворяет определению 2.1, т.е. удовлетворяет определению 2.1, т.е. 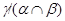 централизует централизует 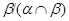 . .
Пусть
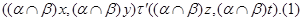
Тогда 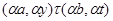 и и 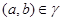 . Так как . Так как 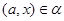 , , 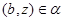 и и 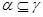 , то , то 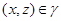 . Следовательно, . Следовательно, 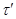 удовлетворяет определению 2.1. удовлетворяет определению 2.1.
Если 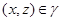 , то , то 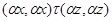 , значит, , значит,
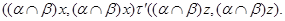
Пусть, наконец, имеет место (1) и
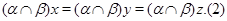
Тогда 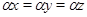 . Так как . Так как  и и 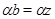 , то , то 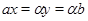 , следовательно, , следовательно, 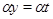 . Из (2) следует, что . Из (2) следует, что 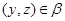 , а по условию , а по условию 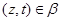 . Значит, . Значит, 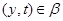 и поэтому и поэтому 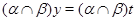 . Тем самым показано, что конгруэнция . Тем самым показано, что конгруэнция 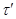 удовлетворяет определению 2.1, т.е. удовлетворяет определению 2.1, т.е. 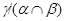 централизует централизует 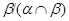 . Докажем обратное включение. Пусть . Докажем обратное включение. Пусть 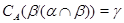 . Тогда на алгебре . Тогда на алгебре 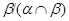 определена конгруэнция определена конгруэнция 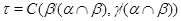 , удовлетворяющая определению 2.1. Построим бинарное отношение , удовлетворяющая определению 2.1. Построим бинарное отношение 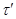 на алгебре на алгебре 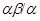 следующим образом: следующим образом:

тогда и только тогда, когда
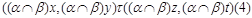
и 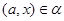 , , 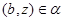 . Аналогично, как и выше, нетрудно показать, что . Аналогично, как и выше, нетрудно показать, что 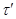 - конгруэнция на алгебре - конгруэнция на алгебре 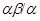 . Заметим, что из доказанного включения . Заметим, что из доказанного включения  следует, что следует, что 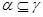 . Покажем поэтому, что . Покажем поэтому, что 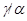 централизует централизует 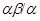 . Так как . Так как 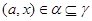 , , 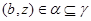 и и 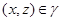 , то , то 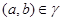 , т.е. , т.е. 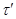 удовлетворяет условию 1) определения 2.1. удовлетворяет условию 1) определения 2.1.
Если 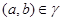 , то , то 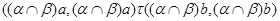 , следовательно, , следовательно,  . .
Пусть имеет место (3) и 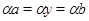 . Так как . Так как 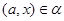 , , 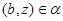 , то , то 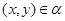 и и 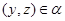 . Из (4) следует, что . Из (4) следует, что 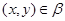 , следовательно, , следовательно, 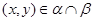 , т.е. , т.е. 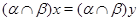 . На основании леммы 2.2 заключаем, что . На основании леммы 2.2 заключаем, что 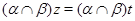 . Следовательно, . Следовательно, 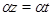 . Но так как . Но так как 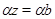 , то , то 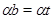 , т.е. , т.е. 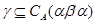 . .
4)
Обозначим 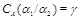 . Пусть . Пусть 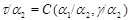 и удовлетворяет определению 2.1. Определим бинарное отношение и удовлетворяет определению 2.1. Определим бинарное отношение 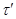 на на 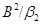 следующим образом следующим образом  тогда и только тогда, когда тогда и только тогда, когда 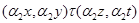 . Аналогично, как и выше, нетрудно показать, что . Аналогично, как и выше, нетрудно показать, что 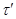 - конгруэнция, удовлетворяющая определению 2.1. Это и означает, что - конгруэнция, удовлетворяющая определению 2.1. Это и означает, что 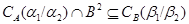 . Теорема доказана. . Теорема доказана.
Как следствие, из доказанной теоремы получаем аналогичные свойства централизаторов в группах и мультикольцах.
3 Мультикольцо
Согласно [2] алгебра  сигнатуры сигнатуры 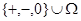 называется мультикольцом,если алгебра называется мультикольцом,если алгебра 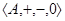 -группа(не обязательно абелева).Все операции из -группа(не обязательно абелева).Все операции из 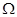 имеют ненулевые арности и для любой имеют ненулевые арности и для любой 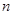 -арной операции -арной операции 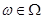 и любых элементов и любых элементов 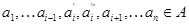 имеет место имеет место 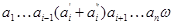 = =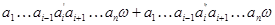 ,для любого ,для любого 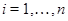 . Заметим,что мультикольцо является дистрибутивной . Заметим,что мультикольцо является дистрибутивной 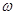 -группой в смысле определения Хиггинса [10] или мультиоператорной группой согласно А.Г.Куроша [9]. Для мультиколец справедливы следующие равенства: -группой в смысле определения Хиггинса [10] или мультиоператорной группой согласно А.Г.Куроша [9]. Для мультиколец справедливы следующие равенства:
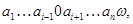
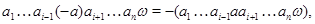
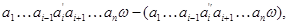
где 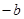 ,как обычно, обозначается элемент,противоположный к элементу ,как обычно, обозначается элемент,противоположный к элементу 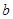 . .
Докажем,например,первое равенство.
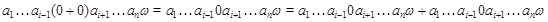
Прибавляя к обеим частям равенства элемент,противоположный к элементу
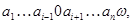
получаем требуемое равенство.
Определение.
Подалгебра 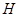 мультикольца мультикольца  называется идеалом [9],если называется идеалом [9],если 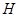 -нормальная подгруппа группы -нормальная подгруппа группы  и для любой и для любой 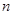 -арной операции -арной операции 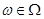 , произвольного , произвольного 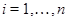 и любых и любых 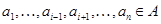 , ,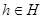 имеет место имеет место
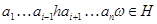
В частности,если 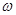 -нульарная или унарная операция,то это означает,что -нульарная или унарная операция,то это означает,что
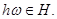
Как следует из примера [8] конгруэнции на мультикольце перестановочны. Следующая теорема устанавливает соответствие между идеалами и конгруэнциями мультикольца.
Теорема 3.1 [2]
Пусть 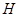 -идеал мультикольца -идеал мультикольца  и и
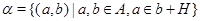
Тогда 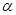 -конгуэнция на -конгуэнция на  и любая конгруэнция на и любая конгруэнция на 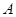 имеет такой вид для подходящего идеала имеет такой вид для подходящего идеала 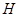 . .
Доказательство.
Так как
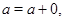
то 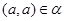 . Покажем,что . Покажем,что 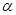 -подалгебра алгебры -подалгебра алгебры 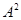 .Проверим вначале замкнутость .Проверим вначале замкнутость 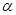 относительно групповых операций. Пусть относительно групповых операций. Пусть 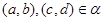 , т.е. , т.е. 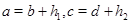 . Тогда в силу того,что . Тогда в силу того,что 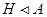 ,получаем ,получаем
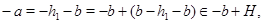
т.е.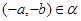
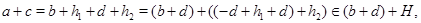
т.е.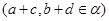 . Пусть теперь . Пусть теперь 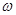 -n-арная операция и -n-арная операция и 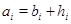 , ,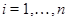 Так как Так как 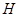 -идеал,то получаем -идеал,то получаем

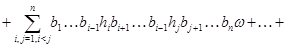
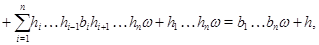
т.е. 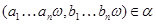 . Теперь из леммы [8] следует,что . Теперь из леммы [8] следует,что 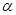 -конгруэнция на -конгруэнция на 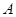 . Обратно,пусть . Обратно,пусть 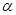 -конгруэнция на -конгруэнция на  . Положим . Положим
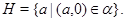
Из [8] следует,что 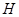 -нормальная подгруппа группы -нормальная подгруппа группы 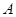 . Аналогичным образом,как и в [8],показывается,что . Аналогичным образом,как и в [8],показывается,что 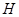 -идеал мультикольца -идеал мультикольца 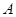 . Теорема доказана. . Теорема доказана.
Следствие 3.2.
Решетка идеалов мультикольца  изоморфна решетке его конгруэнций. изоморфна решетке его конгруэнций.
Определение 3.3
[3].Пусть 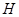 -идеал мультикольца -идеал мультикольца 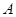 .Тогда централизатором .Тогда централизатором 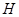 в в  называется наибольший идеал называется наибольший идеал 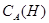 в в  такой,что для любого такой,что для любого 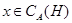 и любого и любого 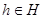 выполняются следующие условия: выполняются следующие условия:
1) 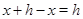 ; ;
2) для любой 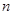 -арной операции -арной операции 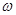 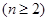 ,любых различных ,любых различных 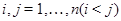 ,произвольных ,произвольных 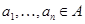 справедливо справедливо
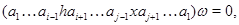
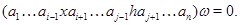
Теорема 3.4.
Пусть 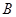 и и 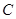 -идеалы мультикольца -идеалы мультикольца  и и 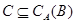 . Тогда . Тогда 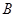 и и 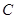 индуцируют на индуцируют на  соответственно конгруэнции соответственно конгруэнции 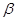 и и 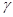 , где , где
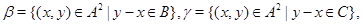
тогда
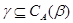
Доказательство :
Определим бинарное отношение  на на  следующим образом следующим образом 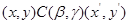 тогда и только тогда, когда найдутся такие элементы тогда и только тогда, когда найдутся такие элементы 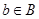 и и 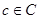 ,что справедливы равенства ,что справедливы равенства
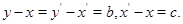
Очевидно,что  -отношенме эквивалентности на -отношенме эквивалентности на 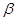 , удовлетворяющее условиям 1)-3) определения 2.1.,замкнутость которого относительно групповых операций доказана в примере [8] , удовлетворяющее условиям 1)-3) определения 2.1.,замкнутость которого относительно групповых операций доказана в примере [8]
Пусть теперь 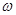 - -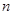 -арная операция и -арная операция и 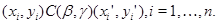 Тогда Тогда
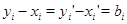 и и 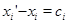
для любых 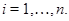 Следовательно, Следовательно,
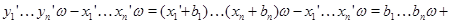
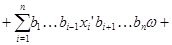 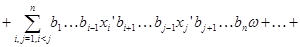
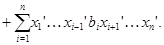
Подставляя в правую часть последнего равенства значения 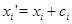 и учитывая,что после раскрытия скобок члены,одновременно содержащие элементы и учитывая,что после раскрытия скобок члены,одновременно содержащие элементы 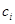 и и 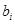 ,равны нулю ,равны нулю 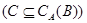 , получаем в правой части равенства выражение , получаем в правой части равенства выражение
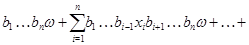 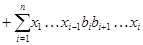 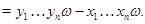
Так как 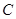 -идеал,то -идеал,то
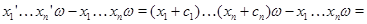
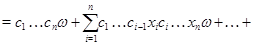
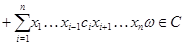
Итак,
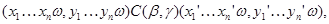
тогда 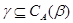 . .
Теорема 3.5
Пусть 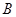 и и 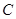 -идеалы мультикольца -идеалы мультикольца 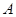 , , 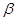 , ,  -конгруэнции,определенные в теореме 3.4. и -конгруэнции,определенные в теореме 3.4. и 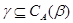 .Тогда .Тогда 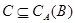 . .
Доказательство :
Пусть 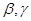 -конгруэнции мультикольца -конгруэнции мультикольца 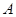 и и 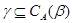 . Обозначим смежные классы по . Обозначим смежные классы по 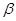 и и 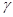 ,являющиеся идеалами мультикольца, соответственно ,являющиеся идеалами мультикольца, соответственно 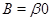 и и 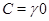 . Возьмем произвольные элементы . Возьмем произвольные элементы 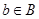 , , 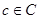 , ,  . Тогда . Тогда
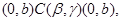
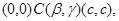
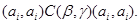
Следовательно,для любой 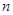 -арной операции -арной операции 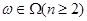 , любых различных , любых различных  получаем получаем
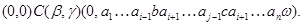
Из определения 2.1. следует,что
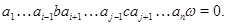
Очевидно,что справедливо и другое аналогичное равенство определения [8] Т.к. из примера [8] следует,что 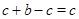 ,то это означает, что ,то это означает, что 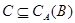 . .
Очевидно,что из теорем 3.4. и 3.5. и результатов раздела 2 следуют все известные свойства централизаторов подгрупп,а так же свойства централизаторов идеалов мультиколец работы [3](Лемма 2.8).
ЗАКЛЮЧЕНИЕ
В настоящей дипломной работе решается задача взаимосвязи структуры мультиколец и универсальных алгебр, получен новый результат: идеал 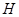 тогда и только тогда централизуется идеалом тогда и только тогда централизуется идеалом 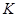 , когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита. , когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита.
Результаты данной дипломной работы могут быть использованы при чтении спецкурса для студентов математического факультета,а так же аспирантами и научными сотрудниками,занимающимися проблемами современной алгебры.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Кон П.М. Универсальная алгебра. - М.: Мир, 1968. - 351 с.
2. Скорняков Л.А. Элементы общей алгебры. - М.Наука, 1983. - 272 с.
3. Шеметков Л.А., Скиба А.Н. Формации алгебраических систем. - М.: Наука, 1989. - 256 с.
4. Ходалевич А.Д. Универсальные алгебры с 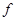 -централизаторными рядами конгруэнций // Весцi Акадэмii навук Беларусi. Сер. фiз.-мат. навук. - 1994. - № 1. - с. 30--34. -централизаторными рядами конгруэнций // Весцi Акадэмii навук Беларусi. Сер. фiз.-мат. навук. - 1994. - № 1. - с. 30--34.
5. Smith D.H. Mal'cev varieties // Lect. Notes Math. - 1976. - V. 554. - 158 p.
6. Ходалевич А.Д. Формационные свойства нильпотентных алгебр // Вопросы алгебры. - Гомель: Изд-во Гомельского ун-та, 1992. - Вып. 7. - с.76--85.
7. Ходалевич А.Д. Класс нильпотентных универсальных алгебр / Ред. ж. Изв. АН БССР. Сер. физ.-мат.н. - Минск, 1991. - 19 с. - Деп. в ВИНИТИ 10.02.91: 4555 - В91.
8. Ходалевич А.Д. Прикладная алгебра //Спецкурс.-Гомель:Изд-во Гомельского ун-та,2002.-с.30
9. Курош А.Г. Лекции по общей алгебре.- М.:Наука,1973.-339с.
10. Higgins P.J. Groups with multiple operators //Proc. London math.Soc.-1956.-V.6,--№3.-p. 366--416.
Отзыв
на дипломную работу
``Свойства централизаторов конгруэнций универсальных алгебр''
студентки 5 курса математического
факультета Шутовой И.Н.
Дипломная работа Шутовой И.Н. посвящена решению задачи изучения формационных свойств подалгебр универсальных алгебр.В отличии от теории многообразий, где основным методом изучения является понятие тождеств, в теории формаций одним из основных является понятие централизуемости. Это связано с определением локальных формаций.
В дипломной работе ''Свойства централизаторов конгруэнций универсальных алгебр'' решена задача взаимосвязи структуры мультиколец и универсальных алгебр, получен новый результат: идеал 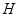 тогда и только тогда централизуется с идеалом тогда и только тогда централизуется с идеалом 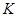 , когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита. , когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита.
В процессе работы над дипломной работой студентка Шутова И.Н. проявила способность к самостоятельным исследованиям, умение работать с научной литературой.
Считаю, что дипломная работа студентки Шутовой И.Н. удовлетворяет необходимым требованиям, предъявляемым к дипломным работам, и заслуживает оценки "отлично", а студентка Шутова И.Н. заслуживает присвоения ей квалификации "Математик. Преподаватель математики."
Научный руководитель,
к.ф.-м.н., доцент А.Д.Ходалевич
Рецензия
на дипломную работу
``Свойства централизаторов конгруэнций универсальных алгебр''
студентки 5 курса математического
факультета Шутовой И.Н.
Теория универсальных алгебр вплоть до 70-х годов развивалась исключительно в рамках теории многообразий. Появление в свет книги Л.А.Шеметкова и А.Н.Скибы ''Формации алгебраических систем'' указало на новые возможности в исследовании универсальных алгебр. Особую значимость в указанной теории играет понятие локальных формаций, в основе которых лежит понятие централизуемости.
В рецензируемой дипломной работе решается проблема адаптирования понятия ''централизуемость идеалов мультиколец'' работы [3] с работой Смита [5] и получен новый результат: идеал 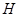 тогда и только тогда централизуется с идеалом тогда и только тогда централизуется с идеалом 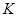 , когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита. , когда соответствующие этим идеалам конгруэнции централизуют друг друга в смысле Смита.
Дипломная работа аккуратно оформлена. Полученные здесь результаты являются новыми и представляют научный интерес.
Считаю, что дипломная работа студентки Шутовой И.Н. удовлетворяет необходимым требованиям, предъявляемым к дипломным работам, и заслуживает оценки ``отлично''.
Рецензент
к.ф.-м.н.,доцент Харламова В.И.
|