| 
Государственная (итоговая) аттестация 2010 года (в новой форме) по МАТЕМАТИКЕ обучающихся, освоивших основные общеобразовательные программы
Демонстрационный вариант
экзаменационной работы для проведения в 2010 году
государственной (итоговой) аттестации (в новой форме) по МАТЕМАТИКЕ обучающихся, освоивших основные
общеобразовательные программы основного общего образования
подготовлен Федеральным государственным научным учреждением
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»
1
Демонстрационный вариант экзаменационной работы для проведения в 2010 году государственной (итоговой) аттестации (в новой форме) по МАТЕМАТИКЕ обучающихся, освоивших основные общеобразовательные программы основного общего образования
Демонстрационный вариант 1
Пояснения к демонстрационному варианту экзаменационной работы
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включенные в него задания не отражают всех элементов
содержания, которые будут проверяться с помощью вариантов КИМ в 2010
году
. Полный перечень элементов содержания и умений, которые могут контролироваться на экзамене 2010 года, приведен в кодификаторах, размещенных на сайте www.fipi.ru.
Демонстрационный вариант предназначен для того, чтобы дать возможность любому участнику экзамена и широкой общественности составить представление о структуре будущей экзаменационной работы, числе и форме заданий, а также их уровне сложности. Приведенные критерии оценивания выполнения заданий с развернутым ответом, включенные в этот вариант, позволят составить представление о требованиях к полноте и правильности записи развернутого ответа.
Эти сведения дают выпускникам возможность выработать стратегию подготовки к сдаче экзамена по математике.
2
Демонстрационный вариант 2010 года
Инструкция по выполнению работы
Работа состоит из двух частей. В первой части 16 заданий, во второй – 5. На выполнение всей работы отводится 4 часа (240 минут).
При выполнении заданий первой части ответы укажите сначала на листах с заданиями экзаменационной работы, а затем перенесите в бланк № 1. Все необходимые вычисления, преобразования и т.д. выполняйте в черновике. Если задание содержит рисунок, то на нем можно проводить дополнительные построения.
Ответы на задания второй части указываются на бланке № 2 с развернутой записью хода решения. Текст задания можно не переписывать, необходимо лишь указать его номер.
Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у вас останется время, вы можете вернуться к пропущенным заданиям.
Правильный ответ в зависимости от сложности каждого задания оценивается одним или несколькими баллами. Баллы, полученные вами за все выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать как можно больше баллов.
Желаем успеха!
3
Часть 1
Площадь территории Испании составляет 506 тыс. км2
. Как эта величина записывается в стандартном виде?
1) 5,06 · 102
км2
3) 5,06 · 104
км2
2) 5,06 · 103
км2
4) 5,06 · 105
км2
Из 59 девятиклассников школы 22 человека приняли участие в городских спортивных соревнованиях. Сколько приблизительно процентов девятиклассников приняли участие в соревнованиях?
1) 0,37 % 2) 27 % 3) 37 % 4) 2,7 %
Числа a
и b
отмечены точками на координатной прямой. Расположите в
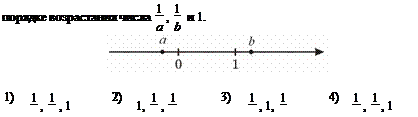
a b b a a b b a
x
4 x
3
 Найдите значение выражения + −1 при х
= 1. Найдите значение выражения + −1 при х
= 1.
4 3
Ответ: ________________________
t
Из формулы периода обращения T
=  выразите время вращения t
. выразите время вращения t
.
N
Ответ: ________________________
Какое из приведенных ниже выражений тождественно равно произведению (x
− 4)(x
− 2)?
1) (x
− 4)(2 − x
)
2) −(x
− 4)(2 − x
) 3) (4 − x
)(x
− 2)
4) −(4 − x
)(2 − x
)
2
3− 7m
Представьте выражение 6m
+  в виде дроби. m в виде дроби. m
Ответ: ________________________
4
Какое из данных выражений не равно
выражению  ? ?
 1) 2 5 2) 20
3) 10
4) 1) 2 5 2) 20
3) 10
4)
  3 3 20 3 5 3 3 20 3 5
Решите уравнение x
2
+ − =7x
18 0.
Ответ: ________________________
Окружность, изображенная на рисунке, задается уравнением x
2
+ y
2
= 4.
Используя рисунок, установите соответствие между системами уравнений и утверждениями: к каждому элементу первого столбца подберите элемент из второго столбца.
A) ⎧⎪x
2 + y
2 = 4 1) система имеет одно решение
⎨
⎪⎩y
= −x
Б) ⎧⎪x
2 + y
2 = 4 2) система имеет два решения
⎨
⎪⎩y
= x
− 4
В) ⎧⎪x
2 + y
2 = 4 3) система не имеет решений
⎨
⎪⎩y
= −2
Запишите в таблицу выбранные цифры.
Ответ:
Прочитайте задачу:
«Фотография имеет форму прямоугольника со сторонами 10 см и 15 см. Ее наклеили на белую бумагу так, что вокруг фотографии получилась белая окантовка одинаковой ширины. Площадь, которую занимает фотография с окантовкой, равна 500 см2
. Какова ширина окантовки?»
Пусть ширина окантовки равна х
см. Какое уравнение соответствует условию задачи?
1)  (10 + 2 )(15x
+ 2 )x
= 500 (10 + 2 )(15x
+ 2 )x
= 500
2) (10 + x
)(15+ x
) = 500
3) 10 15⋅ + (10x
+15 ) 2x
⋅ = 500
4) (10 + 2 )(15x
+ x
) = 500
5
Решите неравенство 20 −3(x
+ 5) < −1 7x
. Ответ: ________________________
При каких значениях х
верно неравенство x
2
+ 2x
−3< 0?
Ответ: ________________________
Из арифметических прогрессий, заданных формулой n
-го члена, выберите ту, для которой выполняется условие a
25
< 0.
| |
| 1) an
= 2n
|
3) an
= −2n
+100
|
| 2) an
=− +2n
50
|
4) an
= −2n
100
|
 График какой из перечисленных ниже функций изображен на рисунке? График какой из перечисленных ниже функций изображен на рисунке?
1) y
= x
2
+ 4
2) y
= x
2
+ 4x
3) y
=− −x
2
4x
4) y
= −x
2
− 4
Компания предлагает на выбор два разных тарифа для оплаты телефонных разговоров: тариф А и тариф В. Для каждого тарифа зависимость стоимости разговора от его продолжительности изображена графически. На сколько минут хватит 550 р., если используется тариф В?

Ответ: ________________________ мин.
Не забудьте перенести все ответы в бланк ответов № 1.
6
Часть 2
Для ответов на задания 17–21 используйте бланк ответов № 2. Укажите сначала номер задания, а затем запишите его решение.
Решите уравнение x
3
− 6x
2
− 4x
+ 24 = 0.
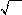 Решите неравенство ( 19 − 4,5)(5−3 )x
> 0. Решите неравенство ( 19 − 4,5)(5−3 )x
> 0.
В геометрической прогрессии сумма первого и второго членов равна 108, а сумма второго и третьего членов равна 135. Найдите первые три члена этой
прогрессии.
6
Прямая 2х
+ 3у
= с
, где с
– некоторое число, касается гиперболы у
=  в x
точке с отрицательными координатами. Найдите с
. в x
точке с отрицательными координатами. Найдите с
.
Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?
7 8
Система оценивания экзаменационной работы Решения и критерии оценивания к заданиям части 2
Ответы к заданиям части 1
Решите уравнение x
3 −6x
2 − + =4x
24 0.

| Номер задания
|
Правильный ответ
|
| 1
|
4
|
| 2
|
3
|
| 3
|
1
|
| 4
|
−
|
| 5
|
t
=TN
|
| 6
|
2
|
| 7
|
3−m
2

m
|
| 8
|
4
|
| 9
|
x
1
= 2, x
2
= −9
|
| 10
|
231
|
| 11
|
1
|
| 12
|
x
< −1
|
| 13
|
( 3− ;1)
|
| 14
|
4
|
| 15
|
2
|
| 16
|
220
|
| Баллы
|
Критерии оценивания выполнения задания
|
| 2
|
Ход решения верный, оба его шага выполнены, получен верный ответ.
|
| 1
|
Ход решения правильный, многочлен в левой части уравнения разложен на множители, но при этом допущена ошибка в знаке, например, получен двучлен x
2
+ 4, ответ дан с учетом этой ошибки.
Или допущена описка на последнем шаге.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
 //Ответ
: –2; 2; 6. //Ответ
: –2; 2; 6.
//Решение. Разложим на множители левую часть уравнения. Получим: x
2
(x
− 6) − 4(x
− 6) = 0, (x
− 6)(x
2
− 4) = 0, x
− 6 = 0 или x
2
− 4 = 0. Значит, уравнение имеет корни: –2; 2; 6.

2) Получаем неравенство 5−3x
< 0. Отсюда x
>1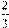 . .
| Баллы
|
Критерии оценивания выполнения задания
|
| 3
|
Ход решения верный, оба его шага выполнены, получен верный ответ.
|
| 2
|
Ход решения верный, правильно выполнен первый шаг, но при решении линейного неравенства допущена вычислительная ошибка или описка.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
В геометрической прогрессии сумма первого и второго членов равна 108, а сумма второго и третьего членов равна 135. Найдите первые три члена этой прогрессии.

//Ответ
: 48, 60, 75.
9 10
//Решение. 1) Пусть (bn
) – данная геометрическая прогрессия. Составим
⎧
⎪
b
1
+ b q
1
=108
⎧b
1
(1+ q
) =108 ⎧b
1
(1+ q
) =108 систему ⎨⎪⎩b q
1
+ b q
1
2 =135. Далее: ⎨⎩bq
1 (1+ q
) =135 , ⎩⎨q
⋅108 =135 .
Отсюда q
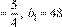 . .
| Баллы
|
Критерии оценивания выполнения задания
|
| 3
|
Ход решения верный, оба его шага выполнены, получен верный ответ.
|
| 2
|
Ход решения верный, решение доведено до конца, но допущена одна вычислительная ошибка и ответ отличается от правильного.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
 2) 2) . .
6
Прямая 2х
+ 3у
= с
, где с
– некоторое число, касается гиперболы у
=  в x в x
точке с отрицательными координатами. Найдите с
.
2  c c
//Решение. Из уравнения 2х
+ 3у
= с
выразим у
: у
= − x
+ . Графики
3 3
2 c
6
 функций у
= − x
+ и y
= функций у
= − x
+ и y
=  имеют единственную общую точку в том и имеют единственную общую точку в том и
3 3 x
2 c
6
 только в том случае, когда уравнение − x
+ = имеет один корень. только в том случае, когда уравнение − x
+ = имеет один корень.
3 3 x
Получаем: 2х
2
– сх
+ 18 = 0; D
= с
2
– 144 = 0; с
= ±12. Так как точка касания имеет отрицательные координаты, то с
< 0 (учащиеся могут прийти к этому выводу хотя бы из геометрических соображений). Поэтому условию задачи удовлетворяет только с
= –12 (в этом случае получаем прямую у
= − −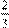 x
4, x
4,
которая касается ветви гиперболы, расположенной в третьей четверти, т.е. в точке с отрицательными координатами).
Комментарий. Подробное обоснование, почему выбрано значение с < 0, не требуется. Возможно наличие схематического рисунка.
| Баллы
|
Критерии оценивания выполнения задания
|
| 4
|
Ход решения верный, все его шаги выполнены правильно, получен верный ответ.
|
| 3
|
Ход решения верный, все его шаги выполнены, но допущена вычислительная ошибка или описка.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
11
Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?

//Ответ
: плот пройдет 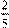 всего пути. всего пути.
//Решение. Пусть скорость течения реки (и плота) х
км/ч. Тогда скорость катера против течения равна 4х
– х
= 3х
км/ч, а по течению 4х
+ х
= 5х
км/ч. Следовательно, скорость катера против течения в 3 раза больше скорости плота, а по течению – в 5 раз больше скорости плота. Если плот до встречи проплыл S
км, то катер – в 3 раза больше, т.е. 3S
км. После встречи катер
3S
пройдет 3S
км, а плот – в 5 раз меньше, т.е.  км. Всего плот пройдет км. Всего плот пройдет
5
3S
8S
S
+ =  . Отношение пройденного плотом пути ко всему пути равно . Отношение пройденного плотом пути ко всему пути равно
5 5
8S
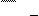 5
= 2 . 5
= 2 .
4S
5
Другое возможное решение
. Пусть скорость течения реки (и плота) х
км/ч. Тогда скорость катера против течения равна 4х
– х
= 3х
км/ч, а по течению 4х
+ х
= 5х
км/ч. Скорость сближения катера и плота равна
AB
х
+ 3х
= 4х
км/ч. Встреча произошла через  ч. За это время плот проплыл ч. За это время плот проплыл
4x
AB AB
3AB
x
⋅ = км, а катер –  км. Обратный путь катер пройдет за км. Обратный путь катер пройдет за
4x
4 4
3AB
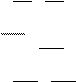 4
= 3AB
ч. Плот за это время проплывет расстояние, равное 4
= 3AB
ч. Плот за это время проплывет расстояние, равное
5x
20x
 3AB
3AB AB
3AB
2AB x
⋅ = км, а всего он проплывет + = км. 20x
20 4 20 5 3AB
3AB AB
3AB
2AB x
⋅ = км, а всего он проплывет + = км. 20x
20 4 20 5
| Баллы
|
Критерии оценивания выполнения задания
|
| 4
|
Ход решения верный, все его шаги выполнены, получен верный ответ.
|
| 3
|
Ход решения верный, все его шаги выполнены, но допущена одна ошибка – в преобразованиях или вычислениях, с ее учетом дальнейшие шаги выполнены правильно.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
12
|