| СОДЕРЖАНИЕ
Введение…………………………………………………………………………3
1.
Основные понятия теории вероятностей…………………………..…5
2.
Классическое определение вероятности……………………………..10
3.
Аксиомы теории вероятности…………………………………………19
Заключение……………………………………………………………………..23
Список используемой литературы………………………………………….24
Введение
Математику многие любят за её вечные истины: дважды два всегда четыре, сумма четных чисел четна, а площадь прямоугольника равна произведению его смежных сторон. В любой задаче, которую вы решали на уроках математики, у всех получался один и тот же ответ – нужно было только не делать ошибок в решении.
Реальная жизнь не так проста и однозначна. Исходы многих явлений заранее предсказать невозможно, какой бы полной информацией мы о них не располагали. Нельзя, например, сказать наверняка, какой стороной упадет подброшенная вверх монета, когда в следующем году выпадет первый снег или сколько человек в городе захотят в течение ближайшего часа позвонить по телефону. Такие непредсказуемые явления называются случайными
.
Однако случай тоже имеет свои законы, которые начинают проявляться при многократном повторении случайных явлений. Если подбросить монету 1000 раз, то «орёл» выпадет приблизительно в половине случаев, чего никак нельзя сказать о двух или даже десяти бросаниях. Следует обратить внимание на слово «приблизительно» – закон не утверждает, что число «орлов» будет в точности 500 или окажется в промежутке от 490 до 510. Он вообще ничего не утверждает наверняка, но дает определенную степень уверенности в том, что некоторое случайное событие произойдет. Такие закономерности изучает специальный раздел математики – теория вероятностей.
Теория вероятностей неразрывно связана с нашей повседневной жизнью. Это дает замечательную возможность установить многие вероятностные законы опытным путем, многократно повторяя случайные эксперименты. Материалами для этих экспериментов чаще всего будут обыкновенная монета, игральный кубик, набор домино, рулетка и даже колода карт. Каждый из этих предметов, так или иначе, связан с играми. Дело в том, что случай здесь предстает в наиболее чистом виде, и первые вероятностные задачи были связаны с оценкой шансов игроков на выигрыш.
Современная теория вероятностей ушла от азартных игр так же далеко, как геометрия от задач землеустройства, но их реквизит по-прежнему остается наиболее простым и надежным источником случая. Можно научиться вычислять вероятность случайных событий в реальных жизненных ситуациях, что позволит оценивать шансы на успех, проверять гипотезы, принимать решения не только в играх и лотереях.
Целью
курсовой работы является рассмотрение элементов теории вероятностей, а также пространства элементарных частиц.
1.
Основные понятия теории вероятностей
Как любой другой раздел математики, теория вероятностей имеет свой понятийный аппарат, который используется при формулировке определений, доказательстве теорем и выводе формул. Рассмотрим понятия, которые будем использовать при дальнейшем изложении теории.
Испытание
– осуществление комплекса условий.
Исход испытания (элементарное событие)
– любой результат который может произойти при проведении испытания.
Примеры.
1) Испытание:
подбрасывается игральный кубик.
Исходы испытания:
ω1
– на верхней грани кубика появилось одно очко;
ω2
– на верхней грани кубика появилось два очка;
ω3
– на верхней грани кубика появилось три очка;
ω4
– на верхней грани кубика появилось четыре очка;
ω5
– на верхней грани кубика появилось пять очков;
ω6
– на верхней грани кубика появилось шесть очков.
Всего возможно 6 исходов испытания (или 6 элементарных события).
2) Испытание:
ученик сдает экзамен.
Исходы испытания:
ω1
– ученик получил двойку;
ω2
– ученик получил тройку;
ω3
– ученик получил четверку;
ω4
– ученик получил пятерку.
Всего возможно 4 исхода испытания (или 4 элементарных события).
3) Испытание:
покупается лотерейный билет.
Исходы испытания:
ω1
– появился выигрышный билет;
ω2
– появился невыигрышный билет.
Всего возможно 2 исхода испытания (или 2 элементарных события).
4) Испытание:
производится выстрел по мишени.
Исходы испытания:
ω1
– мишень поражена;
ω2
– мишень осталась целой.
Всего возможно 2 исхода испытания (или 2 элементарных события).
Замечание.
Обозначение ω – является стандартным обозначением для элементарного события, в дальнейшем мы будем пользоваться этим обозначением.
Будем называть исходы данного испытания равновозможными
, если исходы испытания имеют одинаковые шансы на появление (примеры 1, 3, 4)
Пространство элементарных событий
– множество всех элементарных событий (исходов испытания), которые могут появиться при проведении испытания.
В примерах, которые были рассмотрены выше, фактически были описаны пространства элементарных событий данных испытаний.
Замечание.
Число точек в пространстве элементарных событий (ПЭС), т.е. число элементарных событий в дальнейшем будем обозначать буквой n
.
Массовые однородные испытания
– многократное повторение испытания в одинаковых условиях.
Теперь можно более точно определить круг вопросов, которыми занимается теория вероятностей.
Теория вероятностей
изучает закономерности имеющие место при проведении массовых однородных испытаний.
Рассмотрим основные определения, которыми мы будем пользоваться в дальнейшем.
Определение 1.
Событием
называется совокупность некоторого числа точек ПЭС.
События в дальнейшем мы будем обозначать большими латинскими буквами: А, В, С
.
Определение 2.
Событие, которое может произойти, а может и не произойти при проведении испытания, называется случайным событием
.
Замечание.
Любое элементарное событие так же является случайным событием.
Определение 3.
Событие, которое происходит при любом исходе испытания, называется достоверным событием
.
Определение 4.
Событие, которое не может произойти ни при каком исходе испытания, называется невозможным событием
.
Примеры.
1) Испытание:
подбрасывается игральный кубик.
Событие А:
на верхней грани кубика выпало четное число очков;
Событие В:
на верхней грани кубика выпало число очков, кратное 3;
Событие С:
на верхней грани кубика выпало 7 очков;
Событие D:
не верхней грани кубика выпало число очков меньшее 7.
События А
и В
могут произойти, а могут и не произойти при проведении испытания, поэтому это случайные события.
Событие С
не может произойти никогда, поэтому оно является невозможным событием.
Событие D
происходит при любом исходе испытания, значит это достоверное событие.
2) Испытание:
из коробки, содержащей 3 красных, 3 желтых, 3 зеленых шара, наудачу вынимают 4 шара.
Событие А:
все вынутые шары одного цвета;
Событие В:
все вынутые шары разных цветов;
Событие С:
среди вынутых шаров есть шары разных цветов;
Событие D:
среди вынутых есть шары всех трех цветов.
Событие А
– невозможное: нельзя вытащить из коробки четыре шара одного цвета, так как в ней только по три шара каждого цвета.
Событие В
– тоже невозможное: шары в коробке трех цветов, а вынимаем мы четыре шара.
Событие С
– достоверное: все четыре шара не могут быть одного цвета, поэтому среди них обязательно есть шары хотя бы двух цветов.
Событие D
– случайное: может произойти (например, когда появятся красный, красный, желтый, зеленый шары), а может и не произойти (например, когда появятся красный, красный, зеленый, зеленый шары).
Определение 5.
Элементарное событие ω называется благоприятствующим для события А
, если когда происходит элементарное событие ω, происходит и событие А
.
Замечание.
Число элементарных событий, благоприятствующих для данного события А
, в дальнейшем будем обозначать буквой m
.
Пример.
Испытание:
подбрасывается игральный кубик.
Событие А:
на верхней грани кубика выпало четное число очков;
Событие В:
на верхней грани кубика выпало число очков, кратное 3.
Благоприятствующими для А
событиями являются: ω2
– на верхней грани кубика появилось два очка; ω4
– на верхней грани кубика появилось четыре очка; ω6
– на верхней грани кубика появилось шесть очков; m
= 3.
Благоприятствующими для В
событиями являются: ω3
– на верхней грани кубика появилось три очка; ω6
– на верхней грани кубика появилось шесть очков; m
= 2
Определение 6.
Два события А
и В
называются несовместными
, если они не могут произойти при одном исходе испытания. Другими словами, если появление одного события исключает появление другого.
Определение 7.
Два события А
и В
называются совместными
, если они могут произойти при одном исходе испытания, или появление одного из них не исключает появление другого.
Примеры.
1) Испытание:
подбрасывается игральный кубик.
Событие А:
на верхней грани кубика выпало четное число очков;
Событие В:
на верхней грани кубика выпало число очков, кратное 3;
Событие С:
на верхней грани кубика выпало нечётное число очков;
Событие D:
на верхней грани кубика выпало число очков меньшее трех:
Событие Е:
на верхней грани кубика выпало простое число очков.
События А
и В
являются совместными, так как если на верхней грани кубика появится 6, то произойдет и событие А
и событие В
.
События А
и С
являются несовместными, так как не могут произойти одновременно при одном подбрасывании кубика.
События А, D, Е
являются совместными, так как число 2 одновременно является четным, меньшим чем 3 и простым.
События С, в
то же являются совместными, так как 1 является одновременно нечетным и меньшим 3.
2.
Классическое определение вероятности
Ранее рассмотрено, что случайные события при одних и тех же условиях могут произойти, а могут и не произойти. При этом у одних случайных событий шансов произойти больше (значит, они более вероятные – ближе к достоверным), а у других меньше (они менее вероятные – ближе к невозможным). Поэтому в первом приближении можно определить вероятность, как степень возможности наступления того или иного события.
Понятно, что более вероятные события будут происходить чаще, чем менее вероятные. Так что сравнивать вероятности можно по частоте, с которой события происходят.
Попытаемся расположить на специальной вероятностной шкале следующие события в порядке возрастания вероятности их появления.
Событие А:
в следующем году первый снег в Хабаровске выпадет в воскресенье;
Событие В:
свалившийся со стола бутерброд упал маслом вниз;
Событие С:
при подбрасывании игрального кубика выпадет 6 очков;
Событие D:
при подбрасывании игрального кубика выпадет четное число очков;
Событие Е:
при подбрасывании игрального кубика выпало 7 очков;
Событие F:
при подбрасывании игрального кубика выпадет число очков, меньшее 7.
Итак, в начальной точке нашей шкалы расположим невозможные события, так как степень возможности их наступления (вероятность) практически равна 0.
Таким образом, это будет событие Е
. В конечной точке нашей шкалы расположим достоверное событие – F
. Все остальные события являются случайными, попробуем расположить их на шкале в порядке возрастания степени возможности их появления. Для этого мы должны выяснить какие из них менее вероятные, а какие более вероятные. Начнем с события D
: когда мы подбрасываем игральный кубик, каждая из 6 граней имеет равные шансы оказаться верхней. Четное число очков – на трёх гранях кубика, на трёх других – нечетное. Значит, ровно половина шансов (3 из 6) за то, что событие D
произойдет. Поэтому расположим событие D
в середине нашей шкалы.
У события С
только один шанс из 6, в то время как у события D
– три шанса из 6 (как мы выяснили). Поэтому С
менее вероятно и будет расположено на шкале левее события D
.
Событие А
еще менее вероятно, чем С
, ведь в неделе 7 дней и в любой из них с равной вероятностью может выпасть первый снег, поэтому у события А
один шанс из 7. Событие А
, таким образом, будет расположено еще левее, чем событие С
.
Труднее всего расположить на шкале событие В
. Здесь нельзя точно подсчитать шансы, но можно призвать на помощь жизненный опыт: бутерброд гораздо чаще падает на пол именно маслом вниз (есть даже «закон бутерброда»), поэтому событие В
гораздо вероятнее, чем D
, поэтому на шкале расположим его правее, чем D
. Таким образом, получим шкалу:
Е А С в В F

невозможное случайные достоверное
Построенная вероятностная шкала не совсем настоящая – на ней нет числовых меток, делений. Тогда встает задача научиться вычислять степень возможности наступления (вероятность) того или иного события.
В теории вероятностей в зависимости от того, каким условиям удовлетворяют испытания, существует несколько определений вероятности. Рассмотрим только одно из них и научимся решать задачи на вычисление такой вероятности.
Пусть проводится одно испытание, удовлетворяющее следующим условиям:
1) число исходов испытания конечно (равно n
);
2) исходы испытания являются несовместными;
3) исходы испытания являются равновозможными.
Перечисленные условия составляют так называемую классическую схему испытаний (КСИ).
Определение 8.
Вероятностью события в классической схеме испытаний
называется число, равное отношению числа исходов испытания, благоприятствующих для данного события, к числу всех исходов испытания.
Обычно вероятность события А
обозначают Р(А)
. Таким образом,
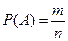 ………………………………(1), ………………………………(1),
где m
– число исходов испытания, благоприятствующих для события А
;
n
– число всех исходов данного испытания.
Решение задач на вычисление вероятности в классической схеме испытаний обычно осуществляется по следующему алгоритму.
Алгоритм вычисления вероятности в КСИ
1) Формулируется испытание.
2) Определяется ПЭС данного испытания и число n
- число точек в нём.
3) Проверяется, удовлетворяет ли испытание (КСИ).
4) Формулируется событие А
, вероятность которого нужно найти.
5) Определяется число m
– число элементарных событий, благоприятствующих событию А
.
6) Вычисляется вероятность события А
по формуле (1).
Задача 1.
Абонент забыл последнюю цифру телефонного номера и набрал её наудачу, помня только, что эта цифра нечетная, найдите вероятность того что, номер набран правильно.
Решение.
Воспользуемся предложенным алгоритмом.
1) Испытание.
Наудачу выбирают одну из нечетных цифр.
2) ПЭС:
каждое элементарное событие ω – появление какой-то из нечетных цифр. Так как нечетных цифр всего 5, то n
= 5.
3) Проверим условия КСИ:
1) число исходов испытания конечно n
= 5;
2) так как при выборе одной цифры не может появиться одновременно две различных цифры, то исходы испытания несовместны;
3) так как выбор происходит наудачу, то шанс выбора конкретной цифры одинаков для каждой цифры, т.е. исходы испытания равновозможные. Таким образом, все условия КСИ выполнены.
4) Событие. А
: выбрали правильную цифру.
5) Среди пяти нечетных цифр только одна правильная, поэтому число исходов благоприятствующих Соб. А m
= 1.
6) 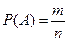 = = 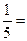 0,2 0,2
Ответ:
Р(А)
= 0,2.
Замечание.
Из определения 8 ясно, что вероятность это число всегда не меньшее нуля и не большее 1.
Задача 2.
В классе учится 10 мальчиков и 20 девочек.
а) На класс дали один билет в цирк, который решено разыграть по жребию. Какова вероятность того, что в цирк пойдет девочка?
б) Учитель истории знает, что 3 мальчика и 5 девочек из класса были накануне в кино, поэтому не выучили домашнее задание. К сожалению, он не знает их фамилий, но очень хочет поставить кому-нибудь двойку. Кого ему лучше вызвать к доске – мальчика или девочку?
Решение.
а) Непосредственно воспользуемся алгоритмом.
1) Испытание.
По жребию разыгрывается один билет среди 30 учеников.
2) ПЭС
: каждое элементарное событие ω – билет достался одному из 30 учеников, поэтому число точек в ПЭС n
= 30.
3) Проверяем условия КСИ
: 1) число точек в ПЭС конечно n
= 30;
2) исходы испытания несовместны, т.к. жребий выпадает только одному ученику;
3) т.к. выбор происходит по жребию, все ученики имеют равные шансы пойти в цирк, т.е. исходы испытания равновозможные.
4) Событие А.
Билет достался девочке.
5) Так как в классе 20 девочек, то число исходов испытания, благоприятствующих Событию А
m
= 20.
6) 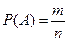 = = 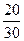 = = 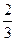 . .
Ответ:
Р(А) =
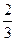 . .
б) Для ответа на вопрос задачи вычислим вероятность того, что вызванная к доске девочка не выучила урок; и вероятность того, что вызванный к доске мальчик не выучил урок. Вычислять эти вероятности будем по алгоритму.
1) Испытание.
Наудачу к доске вызывается девочка.
2) ПЭС
: каждое элементарное событие ω – появление у доски какой-то девочки из 20, поэтому число точек в ПЭС n
= 20.
3) Проверим условия КСИ
: 1) число точек в ПЭС конечно n
= 20.
2) исходы испытания несовместны;
3) так как выбор происходит наудачу, то исходы испытания равновозможные.
4) Событие А
. Вызванная девочка не выучила домашнего задания.
5) Так как домашнее задание не выучили 5 девочек, то число исходов, благоприятствующих для Событию А
m
= 5.
6) 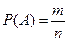 = = 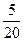 =0,25. =0,25.
Таким образом, вероятность того, что вызванная к доске девочка, оказалась той самой, которая ходила в кино, равна 0,26. Найдем вероятность того, что вызванный к доске мальчик не выучил урок.
1) Испытание:
наудачу к доске вызывается мальчик.
2) ПЭС
: n
= 10.
3) КСИ выполняется
.
4) Соб
ытие А
: Вызванный мальчик не выучил домашнего задания.
5) m =
3.
6) 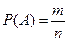 = = 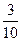 . .
Сравним полученные вероятности 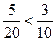 , поэтому обиженный тем, что в кино ходили без него учитель должен вызвать к доске мальчика, так как в этом случае у него больше шансов поставить двойку. , поэтому обиженный тем, что в кино ходили без него учитель должен вызвать к доске мальчика, так как в этом случае у него больше шансов поставить двойку.
Задача 3.
Одновременно подбрасывают три монеты. А) Найти вероятность того, что все монеты упадут на одну сторону. Б) Найти вероятность того, что выпадет хотя бы один «герб».
Решение.
А)
1) Испытание
Подбрасывается 3 монеты одновременно.
2) ПЭС
: выпишем все возможные исходы испытания, обозначив буквой Г – появление «герба», а буквой Ц – появление «цифры»:
{ГГГ; ГГЦ; ГЦГ; ЦГГ; ЦЦГ; ЦГЦ; ГЦЦ; ЦЦЦ}, n
= 8.
3) Проверим условия КСИ
: 1) число исходов испытания n
= 8 конечно;
2) так как при однократном подбрасывании трех монет может появиться только один из перечисленных исходов, то исходы испытания несовместны;
3) так как шансы на выпадение «герба» или цифры» на каждой из монет одинаковые, то исходы испытания равновозможные.
4) Событие А
: все три монеты упали на одну сторону.
5) Среди перечисленных исходов испытания только два – ГГГ; ЦЦЦ – благоприятствуют Событию А
, поэтому m
= 2.
6) 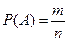 = = 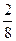 = 0,25. = 0,25.
Решим задача под буквой Б).
1) Испытание
Подбрасывается 3 монеты одновременно.
2) ПЭС
: выпишем все возможные исходы испытания, обозначив буквой Г – появление «герба», а буквой Ц – появление «цифры»:
{ГГГ; ГГЦ; ГЦГ; ЦГГ; ЦЦГ; ЦГЦ; ГЦЦ; ЦЦЦ}, n
= 8.
3) Проверим условия КСИ
: 1) число исходов испытания n
= 8 конечно;
2) так как при однократном подбрасывании трех монет может появиться только один из перечисленных исходов, то исходы испытания несовместны;
3) так как шансы на выпадение «герба» или «цифры» на каждой из монет одинаковые, то исходы испытания равновозможные.
4) Событие А
: при однократном подбрасывании трех монет появился хотя бы один «герб».
5) Событие А
среди перечисленных исходов благоприятствуют следующие: ГГГ; ГГЦ; ГЦГ; ЦГГ; ЦЦГ; ЦГЦ; ГЦЦ, поэтому m =
7.
6) 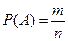 = = 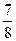 . .
Ответ:
А) Р(А) =
0,25; Б) Р(А) =
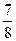 . .
Замечание.
Эта задача имеет и другое решение. Если иметь ввиду, что проводится не одно испытание, а три, то эти испытания удовлетворяют так называемой схеме Бернулли, решение задач в которой осуществляется по другому алгоритму.
Как было выяснено, для вычисления вероятности в КСИ необходимо знать два числа: m
- число исходов, благоприятствующих событию и n
– число всех исходов данного испытания. В рассмотренных задачах мы эти числа находили непосредственным подсчетом. Однако, при решении многих вероятностных задач для вычисления этих чисел рационально применять комбинаторные формулы.
Рассмотрим решение таких задач.
Задача 4.
Какова вероятность того, что при случайном расположении в ряд кубиков, на которых нанесены буквы а, г, и, л, м, о, р, т, получится слово алгоритм?
Решение.
Проводим по алгоритму.
1) Испытание
Случайным образом располагают 8 кубиков в ряд.
2) ПЭС
: каждое элементарное событие ω – слово из восьми букв, поэтому, чтобы подсчитать число элементарных событий нужно решить комбинаторную задачу: Скольким числом способов можно переставить 8 кубиков, на которых написаны буквы а, г, и, л, м, о, р, т
.
1) Определим число элементов во множестве из которого выбираем n
= 8.
2) Определим число элементов в выборке m
= 8.
3) Определим характер выборки: 1) упорядоченная; 2) без повторений.
4) Каждое расположение кубиков, т.е. каждое слово, есть перестановка без повторений, поэтому 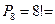 40320. 40320.
Таким образом, решив сформулированную комбинаторную задачу, мы нашли, что ПЭС данного испытания содержит n
= 40320 точек.
3) Проверим условия КСИ
: 1) число точек в ПЭС конечно n
= 40320;
2) одновременно два разных слова при однократном расположении в ряд кубиков появиться не могут, поэтому исходы испытания несовместны;
3) так как располагаем кубики случайным образом, то исходы испытания равновозможные. Условия КСИ выполняются.
4) Событие А
: появилось слово алгоритм
.
5) Этому событию благоприятствует только один исход испытания, т.е. m
= 1.
6) 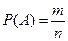 = = 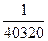 . .
Ответ: Р(А) =
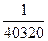
Задача 5.
Имеется 25 российских и 15 зарубежных марок. Какова вероятность того, что из пяти выбранных наугад марок окажется 3 российские и 2 зарубежные марки?
Решение.
1) Испытание
Из 40 марок наудачу извлекают 5.
2) ПЭС
: каждое элементарное событие ω – появление определенной пятерки марок, поэтому чтобы определить число точек в ПЭС, нужно решить комбинаторную задачу: скольким числом способов из 40 марок можно выбрать 5? Эту задачу решим по известному алгоритму:
1) Число элементов во множестве, из которого выбираем n
= 40.
2) Длина выборки m
= 5.
3) Характер выборки: 1) неупорядоченная; 2) без повторений.
4) Каждый набор из 5 марок есть сочетание без повторений, поэтому имеем 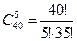 = 658008. = 658008.
Таким образом, число точек в ПЭС равно n
= 658008.
3) КСИ выполняется
.
4) Событие А
: появились 3 российские и 2 зарубежные марки.
5) Чтобы определить число исходов, благоприятствующих данному событию нужно решить комбинаторную задачу: скольким числом способов можно выбрать 3 российские марки из 25 и 2 зарубежные марки из 15? В результате решения получаем, что число исходов, благоприятствующих для События А
m
= 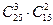 = 241500. = 241500.
6) 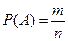 = = 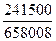 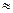 0,367. 0,367.
Ответ:
Р(А) =
0,367.
Замечание.
Может показаться, что совсем не нужно каждый раз останавливаться на проверке условий КСИ, так как они все равно выполняются. Но это очень важный момент при решении вероятностной задачи.
3.
Аксиомы теории вероятности
Определение 9.
Суммой
двух событий А и В называется событие АÈВ (А+В), заключающееся в том, что произойдет хотя бы одно из событий А или В (либо событие А, либо событие В либо А и В одновременно).
Определение 10.
Произведением (
или пересечением) двух событий А и В называется событие АÇВ (АВ), состоящее в одновременном появлении и события А и события В.
Определение 11.
Вероятность суммы
двух событий вычисляется по формуле (теорема сложения)
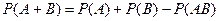 . .
Определение 12.
События А1
,А2
,...,Ак
образуют полную группу событий
, если в результате испытания непременно произойдет одно из них , т.е. 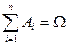 . .
События А и В называются несовместными
(непересекающимися), если они не могут произойти одновременно АÇВ=Æ. Если события несовместны, то
Р(АВ) = 0 и Р(А + В) = Р(А) + Р(В).
Задача 6.
В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?
Решение
. Событие A={вынуты пуговицы одного цвета} можно представить в виде суммы 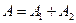 , где события , где события 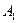 и и 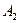 означают выборку пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна означают выборку пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна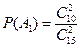 , а вероятность вытащить две синие пуговицы , а вероятность вытащить две синие пуговицы 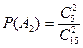 . Так как события . Так как события 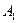 и и 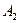 не могут произойти одновременно, то в силу теоремы сложения не могут произойти одновременно, то в силу теоремы сложения
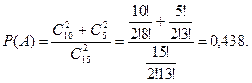
Помимо обычной (безусловной) вероятности можно рассматривать так называемую условную вероятность
, вычисляемую при условии, что событие B произошло. Такую вероятность (вероятность А при условии В) обозначают Р(А|В) и вычисляют с помощью одной из двух формул:
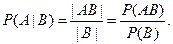
Из этой формулы вытекает формула для вероятности произведения двух событий (теорема умножения)
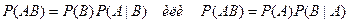 . .
Формула умножения для трех событий:
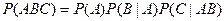 . .
Задача 7.
В семье – двое детей. Какова вероятность, что старший ребенок – мальчик, если известно, что в семье есть дети обоего пола?
Решение.
Пусть А={старший ребенок – мальчик}, B={в семье есть дети обоего пола}. Будем считать, что рождения мальчика и рождение девочки – равновероятные события. Если рождение мальчика обозначить буквой М, а рождение девочки – Д, то пространство всех элементарных исходов состоит из четырех пар: 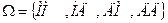 . В этом пространстве лишь два исхода (МД и ДМ) отвечают событию B. Событие AB означает, что в семье есть дети обоего пола и старший ребенок – мальчик, это значит, что второй (младший) ребенок – девочка. Этому событию AB отвечает один исход – МД. Таким образом, |AB|=1, |B|=2 и . В этом пространстве лишь два исхода (МД и ДМ) отвечают событию B. Событие AB означает, что в семье есть дети обоего пола и старший ребенок – мальчик, это значит, что второй (младший) ребенок – девочка. Этому событию AB отвечает один исход – МД. Таким образом, |AB|=1, |B|=2 и
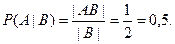
Задача 8.
Мастер, имея 10 деталей, из которых 3 – нестандартных, берет и проверяет детали одну за другой, пока нему не попадется стандартная. Какова вероятность, что он проверит ровно две детали.
Решение.
Событие А={мастер проверил ровно две детали} означает, что при такой проверке первая деталь оказалась нестандартной, а вторая – стандартная. Значит, 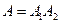 , где , где 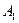 ={ первая деталь оказалась нестандартной } и ={ первая деталь оказалась нестандартной } и 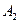 ={вторая деталь – стандартная}. Очевидно, что вероятность ={вторая деталь – стандартная}. Очевидно, что вероятность 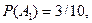 кроме того, кроме того, 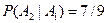 (так как перед взятием второй детали у мастера осталось 9 деталей, из которых только 2 нестандартные и 7 стандартных). По теореме умножения (так как перед взятием второй детали у мастера осталось 9 деталей, из которых только 2 нестандартные и 7 стандартных). По теореме умножения
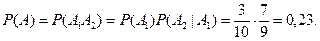
Событие А не зависит от
В, если появление события В не меняет значения вероятности события А, т.е. условная вероятность равна безусловной: Р(А/В) = Р(А).
Аналогично определяется независимость события B от A. Оказывается, что свойство независимости на самом деле симметрично относительно событий A и B, и потому определение независимости двух событий принимает более простой вид:
два события A и B независимы,
если справедливо равенство
Р(АВ) = Р(А)
×
Р(В).
Это равенство можно использовать также как удобный критерий независимости при практической проверке независимости двух событий.
Задача 9.
В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут один белый шар, если из каждого ящика вынуто по одному шару.
Решение
. Событие A={хотя бы из одного ящика вынут белый шар} можно представить в виде суммы 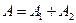 , где события , где события 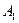 и и 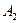 означают выборку одного белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна означают выборку одного белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна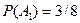 , а вероятность вытащить белый шар из второго ящика , а вероятность вытащить белый шар из второго ящика 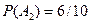 . Кроме того, в силу независимости . Кроме того, в силу независимости 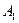 и и 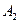 имеем: имеем: 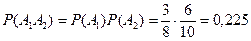 . По теореме сложения получаем: . По теореме сложения получаем:
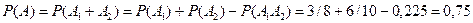 . .
Пусть событие А может быть реализовано только при условии появления одного из событий Hi
, i = 1,..., n. Предположим, что события Hi
несовместны, образуют полную группу (т.е. в результате испытания непременно произойдет одно из них) и вероятности их до опыта известны.. Такие события Hi
называются гипотезами.
Тогда вероятность события А можно вычислить с помощью формулы полной вероятности:
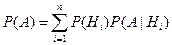 .
.
Заключение
Итак, в работе были рассмотрены вероятность как событие, классическая вероятностная модель, аксиомы теории вероятности.
Опыт, эксперимент, наблюдение явления называются испытанием. Испытаниями, например, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенным на каждую грань числом очков — от одного до шести).
Результат (исход) испытания называется событием. Событиями являются: выпадение герба или выпадение цифры, попадание в цель или промах, появление того или иного числа очков на брошенной игральной кости.
Можно ли как-то измерить возможность появления некоторого случайного события? Другими словами, можно ли охарактеризовать эту возможность некоторым числом? Всякое испытание влечет за собой некоторую совокупность исходов — результатов испытания, т. е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания.
Из приведенного классического определения вероятности вытекают следующие ее свойства: 1. Вероятность достоверного события равна единице. Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т.е. m = n, и, следовательно,
2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е. m = 0, откуда

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Список используемой литературы
1. Баврин И.И. Теория вероятностей и математическая статистика - М.: Высш. шк., 2005.— 160 с.
2. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М.: Наука, 2005. — 200 с.
3. Боровков А.А. Математическая статистика. М.: Наука, 2004. — 440 с.
4. Вентцель Е. С. Задачи и упражнения по теории вероятностей: Учеб. пособие для студ. втузов / Е. С. Вентцель, Л. А. Овчаров. — 5-е изд., испр. — М.: Издательский центр «Академия», 2006. — 448 с.
5. Вуколов Э.А., Ефимов А.В., Земсков В.Н., Поспелов А.С. Сборник задач по математике для втузов. В 4-х ч. ч. 4. - М., Физматлит, 2004- 432 с.
6. Гмурман В. Е. Теория вероятностей и математическая статистика - М., Высш.шк., 2003.- 479 с.
7. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. - М., Высш.шк., 2004.- 404 с.
8. Гнеденко Б.В. Курс теории вероятностей: Учебник. Изд. 8-е, испр. и доп. — М.: Едиториал УРСС, 2005. — 448 с. (Классический университетский учебник.).
9. Кибзун и др. Теория вероятностей и математическая статистика. базовый курс с примерами и задачами. М.: Физматлит, 2007. - 224 с.
10. Коршунов Д.А., Чернова Н.И. Сборник задач и упражнений по математической статистике. Новосибирск: Изд-во Института математики им. С.Л.Соболева СО РАН, 2008.
11. Феллер В. Введение в теорию вероятностей и ее приложения. М.: Мир, Т.2, 2004.
12. Теория вероятностей: Учеб. для вузов. - 3-е изд., испр. / А.В. Печинкин, О.И. Тескин, Г.М. Цветкова и др.; Под ред. B.C. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2004. -456 с.
|