Министерство образования Российской Федерации
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им. Р.Е. АЛЕКСЕЕВА
Выксунский филиал
Кафедра «Прикладная информатика»
Курсовая работа по информатике
«Численное моделирование и анализ переходных процессов в электрической цепи»
Вариант №
3
Выполнил:
студент гр. ЭПА-06
Братица Д.П.
Проверил:
старший преподаватель
Атаманов А.А
2007 г.
Содержание
1. Постановка задачи
1.1 Схема электрической цепи
1.2 Параметры элементов цепи
1.3 Описание работы электрической цепи
2. Вывод системы дифференциальных уравнений
3. Численное решение дифференциальных уравнений
3.1 Блок-схема решения системы дифференциальных уравнений
3.2 Реализация алгоритма на языке программирования высокого уровня Pascal
3.3 Решение дифференциальных уравнений в пакете MathCAD
4. Решение интерполяции в пакете Excel
5. Численное интегрирование
5.1 Блок-схема для нахождения выделившийся теплоты на резисторе R4
5.2 Реализация алгоритма на языке программирования высокого уровня Pascal
5.3 Вычисление количества теплоты в пакете MathCAD
Заключение
1. Постановка задачи
1.1
Схема электрической цепи
Дана схема электрической цепи, содержащая источник переменного тока, катушку индуктивности, конденсатор, набор резисторов и ключ.
1.2 Параметры элементов цепи
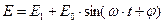 - гармонический источник тока - гармонический источник тока
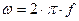 - циклическая частота - циклическая частота
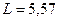 мГн - катушка индуктивности мГн - катушка индуктивности
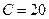 мкФ - конденсатор мкФ - конденсатор
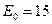 В - амплитуда колебаний В - амплитуда колебаний
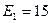 В – амплитуда колебаний В – амплитуда колебаний
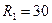 Ом - резистор Ом - резистор
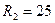 Ом - резистор Ом - резистор
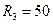 Ом - резистор Ом - резистор
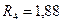 Ом - резистор Ом - резистор
 Ом - резистор Ом - резистор
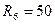 Ом - резистор Ом - резистор
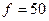 Гц - линейная частота
Гц - линейная частота
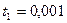 с. - текущее время с. - текущее время
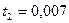 с. - текущее время с. - текущее время
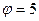 Рад - фаза Рад - фаза
1.3 Описание работы электрической цепи
В начальный момент времени 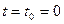 ключ находится в положении ключ находится в положении 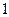 . При этом цепь разомкнута, напряжение на конденсаторе и ток на катушке равны нулю . При этом цепь разомкнута, напряжение на конденсаторе и ток на катушке равны нулю 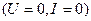 . Происходит первое переключение ключа, т.е. ключ мгновенно переводится в положение . Происходит первое переключение ключа, т.е. ключ мгновенно переводится в положение 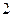 . При этом происходит заряд конденсатора, меняются значения . При этом происходит заряд конденсатора, меняются значения  и и 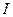 . .
В момент 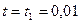 с. ключ мгновенно переводится в положение с. ключ мгновенно переводится в положение 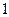 . Конденсатор разряжается, вновь меняются параметры . Конденсатор разряжается, вновь меняются параметры  и и 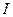 . Анализ схемы заканчивается в момент времени . Анализ схемы заканчивается в момент времени 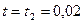 с. с.
2. Вывод системы дифференциальных уравнений
В соответствии с рисунком запишем выражения для 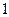 и и 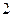 законов Кирхгоффа для положения ключа законов Кирхгоффа для положения ключа 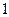 . .
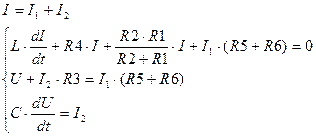
Систему 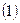 можно преобразовать, исключив токи можно преобразовать, исключив токи 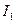 и и  . Тогда для величин . Тогда для величин  и и 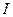 получим систему двух дифференциальных уравнений первого порядка. получим систему двух дифференциальных уравнений первого порядка.
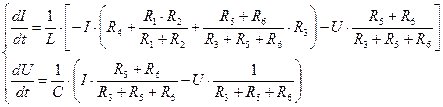
Начальные условия 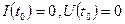
Аналогично может быть получена система дифференциальных уравнений для величин  и и 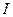 при положении ключа при положении ключа 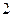 . В этом случае имеем: . В этом случае имеем:
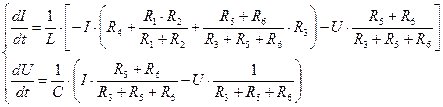
3. Численное решение дифференциальных уравнений
3.1 Блок-схема решения системы дифференциальных уравнений
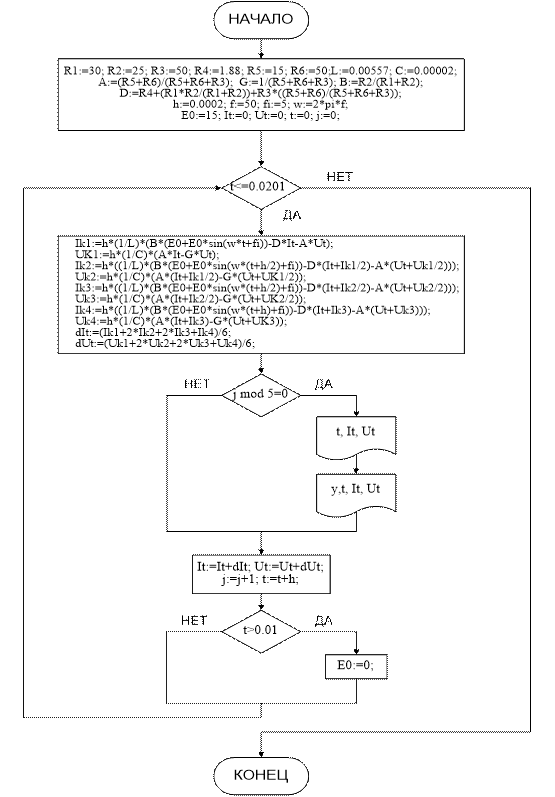
3.2 Реализация алгоритма на языке программирования высокого уровня
Pascal
Program
DIFFERENTSIAL;
uses
wincrt;
var
R1,R2,R3,R4,R5,R6,L,C,E0,h,w,f,fi,t,A,B,D,G,
Ik1,Ik2,Uk1,Uk2,Ik3,Uk3,Ik4,Uk4,It, Ut, dIt, dUt: real;
j:integer;
y: text;
Begin
clrscr;
assign(y,'c:\rezyltat.txt');
rewrite(y);
R1:=30; R2:=25; R3:=50; R4:=1.88; R5:=15; R6:=50;
L:=0.00557; C:=0.00002;
A:=(R5+R6)/(R5+R6+R3); G:=1/(R5+R6+R3); B:=R2/(R1+R2);
D:=R4+(R1*R2/(R1+R2))+R3*((R5+R6)/(R5+R6+R3));
h:=0.0002; f:=50; fi:=5; w:=2*pi*f;
E0:=15; It:=0; Ut:=0; t:=0; j:=0;
While
t<=0.0202 do
begin
Ik1:=h*(1/L)*(B*(E0+E0*sin(w*t+fi))-D*It-A*Ut);
UK1:=h*(1/C)*(A*It-G*Ut);
Ik2:=h*((1/L)*(B*(E0+E0*sin(w*(t+h/2)+fi))-D*(It+Ik1/2)-A*(Ut+Uk1/2)));
Uk2:=h*(1/C)*(A*(It+Ik1/2)-G*(Ut+UK1/2));
Ik3:=h*((1/L)*(B*(E0+E0*sin(w*(t+h/2)+fi))-D*(It+Ik2/2)-A*(Ut+Uk2/2)));
Uk3:=h*(1/C)*(A*(It+Ik2/2)-G*(Ut+UK2/2));
Ik4:=h*((1/L)*(B*(E0+E0*sin(w*(t+h)+fi))-D*(It+Ik3)-A*(Ut+Uk3)));
Uk4:=h*(1/C)*(A*(It+Ik3)-G*(Ut+UK3));
dIt:=(Ik1+2*Ik2+2*Ik3+Ik4)/6;
dUt:=(Uk1+2*Uk2+2*Uk3+Uk4)/6;
if
j mod
5=0 then
Writeln(y,'t=',t:6:4,' It=',It:9:6,' Ut=',Ut:6:5);
Writeln('j=',j:3,' t=',t:6:4,' It=',It:9:6,' Ut=',Ut:6:5);
It:=It+dIt; Ut:=Ut+dUt; j:=j+1; t:=t+h;
if
t>0.01 then
E0:=0;
end;
Close(y);
readln;
End
.
Таблица результатов
| t |
I |
U |
| 0.000 |
0.000000 |
0.000000 |
| 0.001 |
0.021116 |
0.28271 |
| 0.002 |
0.045202 |
0.95006 |
| 0.003 |
0.074067 |
1.99946 |
| 0.004 |
0.104367 |
3.36451 |
| 0.005 |
0.132911 |
4.92721 |
| 0.006 |
0.156807 |
6.54132 |
| 0.007 |
0.173674 |
8.05172 |
| 0.008 |
0.181844 |
9.31183 |
| 0.009 |
0.180509 |
10.19881 |
| 0.010 |
0.169796 |
10.62609 |
| 0.011 |
-0.074194 |
5.16433 |
| 0.012 |
-0.032145 |
2.22256 |
| 0.013 |
-0.013829 |
0.95612 |
| 0.014 |
-0.005949 |
0.41131 |
| 0.015 |
-0.002559 |
0.17694 |
| 0.016 |
-0.001101 |
0.07612 |
| 0.017 |
-0.000474 |
0.03275 |
| 0.018 |
-0.000204 |
0.01409 |
| 0.019 |
-0.000088 |
0.00606 |
| 0.020 |
-0.000038 |
0.00261 |
3.3 Решение дифференциальных уравнений в пакете
MathCAD
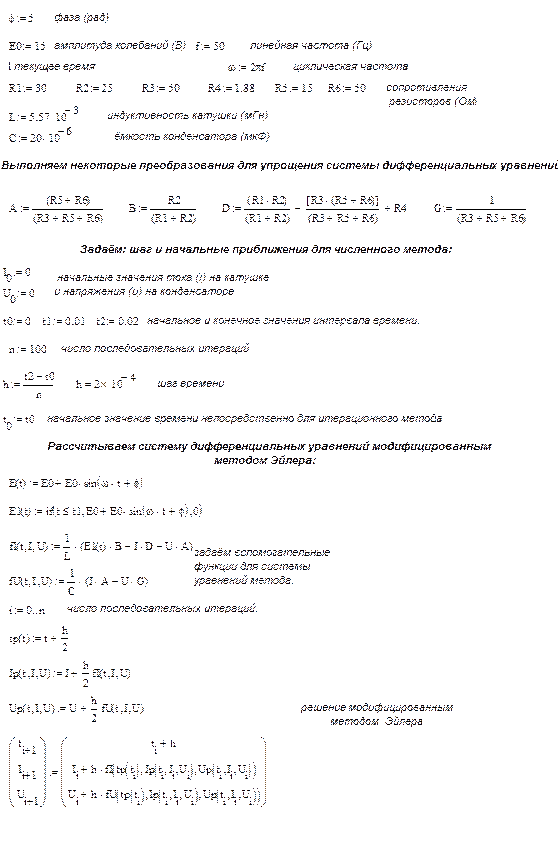
Графики зависимости I(t) и U(t)
.
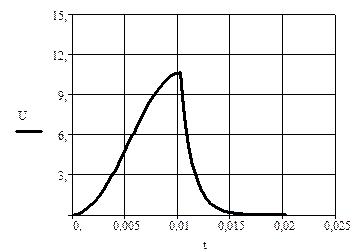
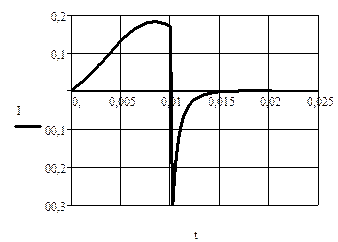
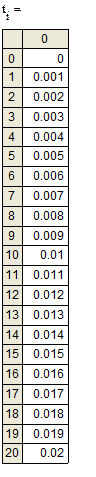
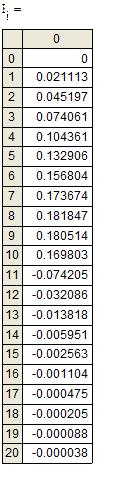
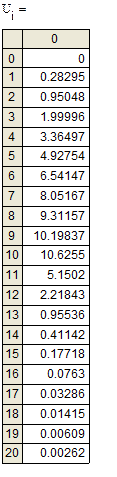
Результаты значений I и U в зависимости от времени t
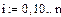
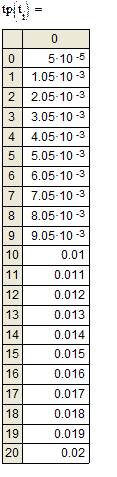
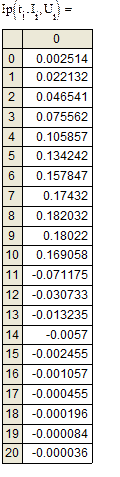
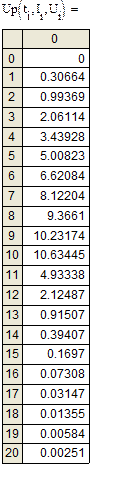
4. Решение интерполяции в пакете
Excel
| t
|
I
|
| 0,001
|
0.021116
|
| 0,002
|
0.045202
|
| 0,003
|
0.074067
|
| 0,004
|
0.104367
|
| 0,005
|
0.132911
|
| 0,006
|
0.156807
|
| 0,007
|
0.173674
|

5. Численное интегрирование
5.1 Блок-схема для нахождения выделившийся теплоты на резисторе
R
4
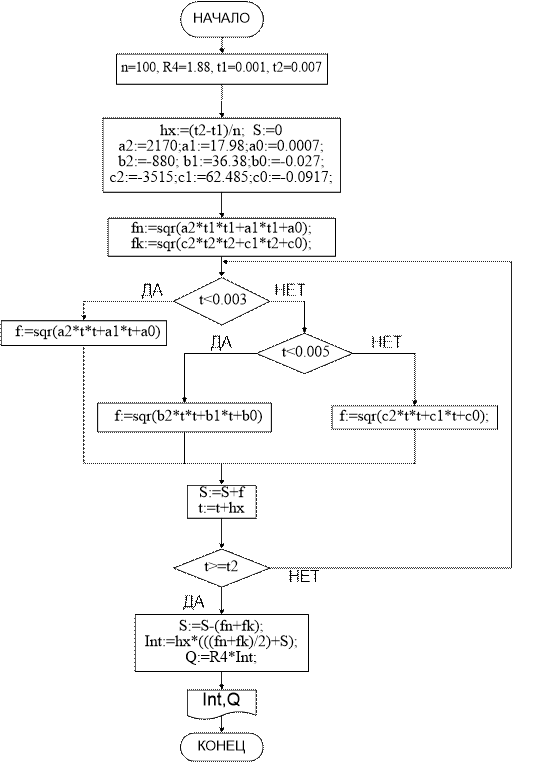
5.2 Реализация алгоритма на языке программирования высокого уровня
Pascal
Program
teplota;
uses
wincrt;
var
R4,Q,f,f1,f2,hx,t,t1,t2,S,Int,a2,a1,a0,b2,b1,b0,c2,c1,c0,fn,fk:Real;
n:Integer;
begin
R4:=1.88;
t1:=0.001;
t2:=0.007;
n:=100;
hx:=(t2-t1)/n;
a2:=2170;a1:=17.98;a0:=0.0007;
b2:=-880; b1:=36.38;b0:=-0.027;
c2:=-3515;c1:=62.485;c0:=-0.0917;
t:=t1;
S:=0;
fn:=sqr(a2*t1*t1+a1*t1+a0);
fk:=sqr(c2*t2*t2+c1*t2+c0);
repeat
if
t<=0.003 then
f:=sqr(a2*t*t+a1*t+a0)
else
if
t<=0.005 then
f:=sqr(b2*t*t+b1*t+b0)
else
f:=sqr(c2*t*t+c1*t+c0);
S:=S+f;
t:=t+hx;
until
t>=t2;
S:=S-(fn+fk);
Int:=hx*(((fn+fk)/2)+S);
Q:=R4*Int;
writeln(' Int=',Int:2:8,' Q=',Q:2:7);
end.
Результат:
Int
=0.00007562
Q
=0.0001422
5.3 Вычисление количества теплоты в пакете
MathCAD

Заключение
В данной курсовой работе преследовалась цель - провести аналитический анализ
работы электрической схемы (получить графики зависимости тока и напряжения), а так же количество теплоты, выделяющейся на резисторе за указанный промежуток времени.
Эти расчеты проводились в три этапа:
· выводы системы дифференциальных уравнений.
· аппроксимация полученных результатов.
· нахождение количества теплоты, выделяющейся на резисторе R4.
Все расчеты и вычисления осуществлялись на языке программирования Pascal
и в пакете Excel, входящем в семейство Microsoft
Office. Параллельно этому производились такие же вычисления в специальном математическом пакете MathCad, но координально другими методами.
Решение системы дифференциальных уравнений:
· метод Рунге-Кутта (Pascal)
· модифицированный метод Эйлера (MathCad)
Количество теплоты, выделяющееся на резисторе:
· методом трапеций (Pascal)
· методом трапеций (MathCad)
После сравнения результатов сделали вывод: что они аналогичны.
|