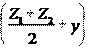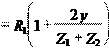Книга: Проектирование планетарного механизма и зубчатой передачи
|
Название: Проектирование планетарного механизма и зубчатой передачи Раздел: Промышленность, производство Тип: книга | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ФГОУ ВПО «ТЮМЕНСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТ- ВЕННАЯ АКАДЕМИЯ» МЕХАНИКО-ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ Кафедра: "Общетехнические дисциплины" ТЕОРИЯ МЕХАНИЗМОВ И МАШИНметодические указания по выполнению расчетно-графической работы на тему: «Проектирование планетарного механизма и зубчатой передачи»для студентов инженерных специальностей очного отделения Тюмень - 2006 Теория механизмов и машин: Методические указания по выполнению расчетно-графической работы «Проектирование планетарного механизма и зубчатой передачи». - Тюмень, ТГСХА, 2006. – 27 с. Составители: канд. тех. наук, доцент Т.В. Рожкова, ст. преподаватель А.Н. Верещагин; преподаватель М.Н. Моисеева. Рецензенты: канд. тех. наук, доцент В.А. Сапухин. Данное пособие предназначено для студентов очного отделения инженерных специальностей; может быть использовано при выполнении курсовых проектов и для подготовки к экзамену по курсу «Теория механизмов и машин». Рекомендовано методической комиссией Механико-технологического института. Работа издается по решению редакционно-издательского совета Тюменской ГСХА. © Тюменская государственная сельскохозяйственная академия ВВЕДЕНИЕРасчетно-графическая работа выполняется на формате А1 в соответствии с требованиями ГОСТ 2.109-73 «Основные требования к чертежам». В левой части формата вычерчивается схема планетарного редуктора (рис. 2) в двух проекциях. В правой части формата изображается зубчатое зацепление в выбранном масштабе (рис. 3). Масштаб построения выбираем таким способом, чтобы высота зуба на чертеже была не менее 40 мм . Обязательным является построение трех зубьев 1-го и 2-го колес. Конечным этапом расчетно-графической работы является выполнение расчетно-пояснительной записки (см. п. 4). 1. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ1.1. ПРОЕКТИРОВАНИЕ ПЛАНЕТАРНОГО МЕХАНИЗМА1. Определить передаточное отношение планетарного редуктора (планетарной ступени), если оно не задано. 2. Задавшись числом зубьев z1 = 17, 18… n, через передаточное отношение U1Н определить число зубьев z3 . 3. Из условия соосности определить число зубьев сателлита. 4. Из условия соседства определить максимально возможное число сателлитов. 5. Из условия сборки определить все возможные числа сателлитов. 6. Задавшись произвольным модулем, определить диаметры делительных окружностей всех колес планетарной ступени по формуле d = mz . 7. Выбрать масштаб, вычертить схему редуктора в двух проекциях. 1.2. ПРОЕКТИРОВАНИЕ ЗУБЧАТОЙ ПЕРЕДАЧИ1. Определить передаточное отношение зубчатой передачи. 2. По передаточному числу, количеству зубьев колес и типу зубчатого зацепления найти коэффициенты смещения (по таблицам в конце методических указаний). 3. Определить межосевое расстояние передачи. 4. Определить радиусы всех окружностей шестерни и колеса. 5. Определить шаг по делительной окружности. 6. Определить толщину зубьев по делительной окружности. 7. Вычертить зубчатое эвольвентное зацепление колес передачи, на котором показать все основные размеры. 8. Показать теоретическую и практическую линии зацепления. 9. Построить рабочие участки профилей зубьев и дуги зацепления для обоих колес. 10. Определить коэффициент перекрытия. 11. Произвести расчет коэффициентов удельных скольжений и построить их диаграммы. 2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ2.1. ВИДЫ ЗУБЧАТЫХ ПЕРЕДАЧПередачей называется механизм, служащий для передачи или преобразования вращательного движения. Зубчатые передачи подразделяются на два основных вида: - механизмы, у которых оси некоторых колес перемещаются в пространстве относительно стойки (планетарные и дифференциальные редукторы); - зубчатые механизмы с неподвижными осями всех колес (цилиндрические, конические и червячные редукторы). 2.2. ПРОЕКТИРОВАНИЕ ПЛАНЕТАРНЫХ ПЕРЕДАЧ2.2.1. Виды планетарных передачТакие многозвенные зубчатые механизмы (рис. 1 а , б ) обязательно имеют колеса с подвижным осями, которые называют сателлитами (z2 ) . Подвижное звено, в котором закреплена ось сателлита, называется водилом (H) . Колеса, геометрические оси которых неподвижные, называют центральными или солнечными (z1 ) . Неподвижное центральное колесо называется опорным (z3 ) .
Рис. 1. Схемы планетарных передач: а - планетарный редуктор; б - дифференциальный редуктор Планетарные механизмы подразделяются на: - планетарные редукторы и мультипликаторы , которые обладают одной степенью подвижности и обязательно имеют опорное колесо (рис. 1, а ); - зубчатые дифференциальные механизмы , число степеней подвижности которых два и более, и которые не имеют опорного колеса (рис. 1, б ). Планетарные механизмы, изображенные на рис.1, а, б , получили широкое применение в силовых передачах средней и большей мощности при высоком КПД (0,96…0,98). Наличие нескольких сателлитов позволяет значительно снизить габариты, улучшить уравновешивание, разгрузить опоры центральных колес и водила, уменьшить массу по сравнению с другими видами передач при тех же передаточных отношениях. 2.2.2. Передаточное отношение планетарной передачиПередаточным отношением планетарной передачи является отношение угловых скоростей на ведущем и ведомом валах, которое обычно выражают через числа зубьев колес
U 12 z 1 Сумма передаточных отношений планетарного редуктора всегда равна единице
Запишем формулы без вывода для определения передаточного отношения для обеих схем, представленных на рис. 1, а, б
U(3) 1H ==1-UH 13 =1+ z 2 z 3 ' - для схемы б ; (4) z 1 z 2 Обозначение U3 1Н соответствует передаточному отношению планетарной передачи от ведущего (центрального) колеса 1 к ведомому звену (водилу Н ) при неподвижном (опорном) колесе 3 . Обозначение UН 13 соответствует передаточному отношению зубчатой передачи от ведущего звена 1 к ведомому звену 3 при неподвижном звене Н . 2.2.3. Определение чисел зубьев планетарной передачиПосле выбора схемы планетарной передачи, назначения числа сателлитов (k ) и модуля (m ) производится определение числа зубьев колес так, чтобы наиболее точно обеспечить заданное передаточное отношение, а также следующие условия: - соосности; - соседства; - сборки; - заклинивания колес передачи. Заданное передаточное отношение обеспечивают подбором чисел зубьев так, чтобы при подстановке их значений в выражения (3) и (4) получаемое фактическое значение передаточного отношения максимально приближалось к заданному. Допустимое отклонение фактического передаточного отношения от заданного 1- 4 %. В исходных данных числа зубьев не заданы и их необходимо найти в процессе проектирования кинематической схемы. В формулах (3) и (4) известной величиной является только передаточное отношение, поэтому нахождение чисел зубьев является задачей неопределенной, допускающей большое число вариантов. Чтобы решение было однозначным, наложим следующие ограничения: 1. Числа зубьев z1 , z2 , z3 должны быть целыми числами, а модули всех колес одинаковыми. 2. Все зубчатые колеса должны быть нулевыми (неисправленными). А это значит, что во избежание подрезания ножки зуба для колес с внешним зацеплением z 1 ≥ z min = 17, для колес с внутренним зацеплением z 3 ≥ z min = 85 , в обоих случаях коэффициент исправления формы зуба ha * =1, количество зубьев сателлита z2 =z2 ' ≥20 . 3. Оси центральных колес и водила должны совпадать между собой, т.е. должно соблюдаться условие соосности , которое выражается так: z1 +2z2 = z3 - для схемы а ; (5) z1 + z2 = z3 -z2 ' - для схемы б . (6) 4. Сателлиты должны быть расположены с таким окружным шагом, чтобы между окружностями вершин соседних сателлитов обеспечивался гарантированный зазор - условие соседства : 1800 z 2 2
где k - число сателлитов. Для схемы 1, б вместо z2 следует подставлять z2 ' , если z2 ' >z2 . 5. Сборка сателлитов должна осуществляться без натягов при равных окружных шагах между ними. Это возможно при выполнении следующего условия (условие сборки ): z
1
= C, (8) k где С = 1, 2,… - целое число. Пример 1. Подобрать числа зубьев z1 , z2 и z3 для передачи (рис.1, а ) с передаточным отношением U1H =5,6 иопределить количество сателлитов k . Задаемся числом зубьев z1 , из ряда z1 = 17, 18, 19, 20… Пусть z1 =18. Число зубьев z3 найдем из выражения (3): U1H (3) -1=z3 /z1 , откуда z3 =z1 (U1H -1)=18(5,6-1)=82,8. Условие z3 ≥ zmin =85 не выполняется, поэтому задаемся новым числом зубьев z1 . Пусть z1 =19, тогда z3 =z1 (U1H -1)=19(5,6-1)=87,4 . Округляем z3 до целого, чтобы z3 было бы одинаковой четности с z1 , т.е. z3 =87 . Из условия соосности (5) найдем z2 z2 =(z3 -z1 )/2=(87-19)/2=34. Из условия соседства (7) определяем возможное число сателлитов в механизме
Значит, для этого механизма число сателлитов может быть взято равное 2, 3 и 4. Принимаем k = 4. Проверяем условие сборки из выражения (8) (z1 +z3 )/k= C, (19+87)/4=26,5. Число в ответе получилось не целое, значит, при этих числах зубьев механизм без натягов не соберется. Назначаем новое число z1 . Пусть z1 =20 , тогда z3 =z1 (U1H -1)=20(5,6-1)=92, z2 =(z3 -z1 )/2=(92-20)/2=36.
Принимаем k = 4 и проверяем условие сборки по формуле (8) z
3
Все условия выполняются, значит, окончательно принимаем k = 4, z1 =20, z2 =36, z3 =92 . Пример 2
(
рис.1, б
). Подобрать числа зубьев z1
, z2
, z
z 2 z
z 1 z 2 Передаточное отношение многоступенчатых редукторов равно произведению передаточных отношений отдельных ступеней (см. п. 2.3, уравнение (10)) U1n=U12∙U23∙…∙U(n-1)n. Согласно выражению (10) находим z 2/z 1=U 12H , z 3/z 2'=U 23H . Пусть U12 H =3 , значит, U23 H =9,18/3=3,06. Тогда z2 =3z1 и z3 =3,06 z2 ' . Задаемся числом зубьев z1 . Из условия (►2.) (см. выше) z1 нужно выбирать из ряда 17, 18, 19, 20…. Пусть z1 =17, тогда z2 =3·17=51. Запишем условие соосности (6) z 1 + z 2 = z 3 - z 2' . Из условия (6) найдем z2 : 17+51=3,06 z2 ' -z2 ' , т.е. 68=2,06z2 ' . Откуда z2 ’ = 33,0097. Принимаем z2 ' =33, тогда
Значит, в схеме механизма может быть либо 2, либо 3 сателлита. Принимаем k=3 . Проверяем, возможна ли сборка механизма по условию: z
3
тогда (17+101)/3=39,33 - число не целое, значит, механизм без натягов не может быть собран. Назначаем новое число зубьев z1 =18, тогда z2 =3·18=54. Из условия соосности (6) найдем z2 ' ·2,06z2' =18+54=72, z2 ' =34,95. Принимаем z2 ' =35, тогда z3 =3,06 z2 ' =3,06·35=107,1. Принимаем z3 =108, чтобы z3 было бы одной четности с z1 . Определяем возможное число сателлитов k
т.е. получим тот же результат, что и при z1 =17. Проверяем возможность сборки из условия (8) z
3
тогда (108+18)/3=42. Число в ответе целое, значит, сборка механизма возможна. Итак, окончательно имеем: k=3, z1 =18, z2 =54, z2 ' =35, z3 =108 . 2.2.4. Построение планетарного редуктораПосле подбора чисел зубьев планетарного редуктора определяем делительные радиусы колес по формуле, предварительно задавшись модулем m , который выбираем из ряда (см. п.2.3.3) mz
2 Затем вычерчиваем в масштабе схему планетарной передачи в двух проекциях (рис. 2).
Рис. 2. Построение планетарного редуктора 2.3. ПРОЕКТИРОВАНИЕ ЗУБЧАТОЙ ПЕРЕДАЧИ2.3.1. Передаточное отношение цилиндрических редукторовПередаточным отношением зубчатой передачи называется отношение угловой скорости ведущего вала к угловой скорости ведомого вала, т.е. U1k =ω1 /ωk , или U1k = n1 /nk , так как ω = πn/30. (9) Зубчатые передачи могут быть одноступенчатыми и многоступенчатыми. Передаточное отношение многоступенчатой передачи равно произведению передаточных отношений отдельных ступеней U1n =U12 ·U23 ·…·U(n-1)n . (10) Количество ступеней равно числу неподвижных осей минус единица. Одноступенчатые передачи делятся на передачи с внешним зацеплением и с внутренним зацеплением. Передаточное отношение для внешнего зацепления U12 =- ω1/ω2 =-z2/z1=-r2/r1. Передаточное отношение для внутреннего зацепления U12 = +ω1 /ω2 =+z2 /z1 = +r2 /r1 . Имея схему передачи и зная числа зубьев или радиусы начальных окружностей колес, можно всегда определить общее передаточное отношение редуктора. 2.3.2. Виды зубчатых колесПри проектировании зубчатой передачи возникает вопрос о выборе коэффициентов смещения, которые определяют положение делительной прямой зубчатой инструментальной рейки (режущего инструмента) относительно делительной окружности нарезаемого колеса. В реечном зацеплении делительная прямая рейки может располагаться различным образом по отношению к делительной окружности колеса. В зависимости от сдвига рейки зубчатые колеса бывают: -Нулевые. -Положительные. -Отрицательные. Если нет смещения (а = 0 ), то такое колесо называется нулевым .
S = e, S =p. -Если смещение а направлено в сторону от оси нарезаемого колеса, то колесо называется положительным .
-Если смещение a рейки направлено в сторону оси нарезаемого колеса, это колесо называется отрицательным .
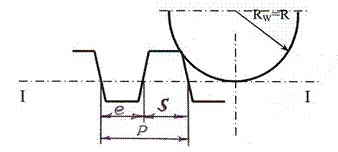
2.3.3. Виды зацепления зубчатых передач в зависимости от смещения рейкиВ зависимости от величин смещения каждого колеса можно получить три вида зацепления передач, отличающихся расположением начальных и делительных окружностей. а ). Нулевое зацепление . Данная передача составлена из нулевых колес. Начальные и делительные окружности совпадают, действительный угол зацепления равен стандартному (αw = α= 20o ). б ). Равносмещенное зацепление . Эта передача составлена из положительного и отрицательного колеса с одинаковыми по абсолютной величине коэффициентами смещения. Начальные и делительные окружности совпадают и угол зацепления равен 20 о . Отличие от нулевого зацепления заключается в том, что толщина зуба шестерни увеличивается, а у второго колеса - уменьшается, поэтому шаг остается таким же, как и при нулевой передаче (S1 = e2 ; S2 = e1 , где е – ширина впадины). в ). Неравносмещенное зацепление . Эта передача может быть составлена из положительного и нулевого колеса или из двух положительных колес. Делительные окружности не совпадают с начальными и действительный угол зацепления больше стандартного (αw > 20о ). Сумма толщин зубьев не равна шагу (S1 + S2 > P ). Поэтому, чтобы вписать данную передачу в заданный шаг, применяют коэффициент уравнительного смещения Δу . 2.3.4. Определение размеров зубчатой передачиРазмеры колес, а так же всего зацепления, зависят от чисел зубьев колес Z1 и Z2 , от модуля m зацепления, общего для обоих колес, а также от метода их обработки. Формулы для определения размеров элементов цилиндрического зацепления с прямым зубом представлены в табл. 1 приложения. На основании известных Z1 , Z2 , и U12 определим коэффициенты смещения Х1 , Х2 , для равносмещенного зацепления по таблице приложения 6, а для неравносмещенного зацепления коэффициенты Х1 , Х2 и Δу в зависимости от передаточного отношения: а ) если 2≥ U12 ≥1, то Х1 , Х2 определяются по таблице приложе- ния 4, Δу - по таблице 2. б ) если 2≤U11 ≤5, то Х1 и Δу по таблице 3, Х2 - по таблице 5. 2.3.5. Геометрические элементы зубчатых колесРадиусы начальных окружностей RW – радиусы окружностей колес, соприкасаемых в точке полюса р , перекатываемых без скольжения. Поэтому, межосевое расстояние аW можно вычислить по формуле аW =[O1 O2 ] = RW1 + RW2 . (11) Радиус делительной окружности R – радиус, который делит высоту зуба на ножку и головку (рис. 3). Для нулевой (стандартной) передачи радиус делительной окружности равен радиусу начальной, т.е. R = RW . Модуль зубчатого зацепления m
– отношение шага Р
к числу π
: m
Модуль – это стандартная величина, выбираемая их ряда рациональных чисел согласно ГОСТ 9563-60; измеряется в мм . В первом, предпочтительном ряду предусмотрены следующие модули в мм : 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1,0; 1,25; 1,5; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; 50; 60; 80; 100. Во втором ряду предусмотрены модули, промежуточные между модулями первого ряда, например: 3,5; 4,5; 5,5; 7; 9; 11 и др. Шаг зубчатого зацепления Р – расстояние по делительной окружности между одноименными точками двух соседних зубьев. Высота зуба h – расстояние между окружностями впадин Rf и выступов Ra . Высота зуба складывается из высоты ножки зуба hf и высоты головки зуба hа h= hf + hа . (13) Для нулевого (стандартного) колеса ha =m , hf = 1,25m , тогда h=2,25m. Радиус основной окружности Rb – радиус, с которого начинается построение эвольвенты. Эвольвента – развертка круга, боковая поверхность зуба. Радиус окружности впадин Rf – радиус, ограничивающий ножку (впадину) зуба. Радиус окружности выступов Rа – радиус, ограничивающий головку (вершину) зуба. 2.3.6. Вычерчивание элементов зубчатого зацепленияПодсчитав все размеры элементов зацепления по формулам (табл. 1 приложения), приступаем к вычерчиванию зубчатого зацепления. Масштаб построения выбираем таким способом, чтобы высота зуба на чертеже была не менее 40 мм . Профили зубьев вычерчиваем в следующей последовательности (рис. 3.): 1) На линии центров колес от точек О 1 и О 2 строим радиусы начальных окружностей Rw 1 , Rw 2 , и находим полюс зацепления (•) р . 2) Строим основные окружности Rв 1 , Rв 2 . Из полюса р проводим линию зацепления – касательную к основным окружностям. Из центров О 1 и О 2 опустим перпендикуляры на эту касательную. Обозначим точку касания с окружностью Rв 1 через А , а точку касания с окружностью Rв 2 -точкой В . 3) Строим окружности выступов обоих колес Rа 1 , Rа 2 . 4) Строим окружности впадин обоих колес Rf 1 и Rf 2 . Следует заметить, что радиус окружности впадин может быть больше, равен или меньше радиуса основной окружности. Это зависит от числа Z зубьев колеса, коэффициента смещения Х и вида зацепления. 5) Отмечаем высоту зуба h . При этом нужно иметь ввиду, что высота зуба обеих колес должна быть одинакова ! 6) Справа от точки В построение аналогично. Получаем точки 4; 5 …Соединяем последовательно точки р, 1// , 2// , 3// , 4// , 5// … плавной кривой - получаем эвольвенту для второго колеса. Таким же способом строим эвольвенту для шестерни. 7) Профиль ножки у основания зубьев строится упрощенно. Если Rf ≥ Rв , то получают точку пересечения окружности впадин с эвольвентой, а затем у основания делают закругление дугой радиуса r=0,25m . ЕслиRf < Rв , то от основания эвольвенты до окружности впадин проводят радиальный отрезок, а затем у основания зуба делают закругление радиусом 0,25m . 8) Построим радиусы делительных окружностей R1 и R2 , если они не совпадают с радиусами начальных окружностей Rw 1 и Rw 2 и находим точку пересечения эвольвенты с радиусами окружностей (точка С ). 9) 10) Обязательным является построение трех зубьев – первого, профиль которого построен по точкам, и двух, находящихся справа и слева от первого. Аналогично строятся три зуба для первого колеса. 2.3.7. Построение активной части линии зацепления, дуг зацепления и рабочих участков профилей зубьевРазличают теоретическую и активную часть зацепления. Теоретической частью зацепления называют отрезок, заключенный между точками А и В . Итак, теоретическая линия зацепления АВ - геометрическое место точек на неподвижной поверхности. Активной частью линии зацепления называют отрезок [ав] теоретической линии зацепления, заключенный между точками пересечения ее с окружностями выступов колес Rа1 и Rа2 . Активная часть линии зацепления является геометрическим местом точек зацепления профилей зубьев на неподвижной плоскости. Те участки профилей, которые непосредственно участвуют в зацеплении, называют рабочими . Чтобы найти эти участки, нужно на профиле зуба первого колеса найти точку, сопряженную с крайней точкой головки второго колеса, а на профиле зуба второго колеса найти точку, сопряженную с крайней точкой головки первого колеса. Для этого, через точку в из центра О2 проводим дугу радиусом О2 в до пересечения с профилем зуба (точка F2 ). На шестерне рабочий профиль строим аналогично. Чтобы обозначить на чертеже эти участки, нужно провести линии, параллельные эвольвентам на расстоянии 2…5 мм и заштриховать. Так как сопряженные профили перекатываются друг по другу со скольжением, то длины рабочих участков не равны между собой. Каждую из дуг начальных окружностей, которые перекатываются одна по другой за время зацепления одной пары сопряженных профилей без скольжения, называют дугой зацепления . Дуги зацепления для обоих зацепляющихся колес равны между собой. Построение дуги производится следующим образом. Через крайние точки Н2 и F2 рабочего профиля проводим в сторону вогнутости касательные к основным окружностям Rb1 и Rb2 . Находим точку а2 и в2 пересечения нормали с начальной окружностью второго колеса. Дуга а2 в2 является дугой зацепления. Аналогичным построением находим дугу зацепления первого колеса. Длину lк дуги зацепления определяют по формуле: l
К
где lав - длина активной части линии зацепления. 2.3.8. Определение качественных показателей зацепления
Коэффициент перекрытия ε показывает, сколько пар зубьев одновременно может находиться в состояние контакта. Если, например ε =1,45, то это значит, что во время движения зуба по дуге зацепления, безусловно, в зацеплении находиться одна пара зубьев, а 45% интервала движения по дуге в зацеплении находятся две пары. Коэффициент перекрытия для внешнего эвольвентного зацепления должен находится в пределах 1,1≤ε ≤ 2. Коэффициент перекрытия считается формулам:
При сравнении двух результатов разница не должна превышать 5%. Так как рабочие участки профилей зубьев перекатываются друг по другу со скольжением, то на этих участках возникают силы трения и происходит процесс изнашивания. Характеристикой вредного влияния скольжения является коэффициент удельного скольжения
где lАВ - длина теоретической линии зацепления; Х - расстояние от точки А касания теоретической линии зацепления с основной окружностью первого колеса, отсчитываемое в направлении к точке В . Полученные значения сводим в таблицу:
Строим графики удельных скольжений, применяя масштабный коэффициент:
Рис. 3. Построение картины внешнего эвольвентного зацепления и графиков удельных скольжений зубьев 3. ПРИМЕР ВЫПОЛНЕНИЯ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ3.1. ОФОРМЛЕНИЕ ТИТУЛЬНОГО ЛИСТАМИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ФГОУ ВПО «ТЮМЕНСКАЯ ГОСУДАРСТВЕННАЯ СЕЛЬСКОХОЗЯЙСТ- ВЕННАЯ АКАДЕМИЯ» Механико-технологический институт Кафедра «Общетехнические дисциплины» ПОЯСНИТЕЛЬНАЯ ЗАПИСКАк расчетно-графической работе по курсу «Теория механизмов и машин» на тему: «Проектирование планетарного редуктора и зубчатой передачи » Выполнил: студент (Ф.И.О.) ГруппаШифр_______ Проверил:________________ Тюмень – 20___ 3.2. РЕШЕНИЕ3.2.1. Исходные данные для проектирования- - Тип редуктора - дифференциальный. 3.2.2. Проектирование планетарного редуктораИз выражения U1Н
= 1
+ z 2 z
z 1 z 2 Передаточные отношения каждой ступени редуктора определятся по формулам z 2/z 1=U 12H , z 3/z 2'=U 23H . Пусть U12 H =3 . Значит, U23 H =9,18/3=3,06. Тогда z2 =3z1 и z3 =3,06 z2 ' . Задаемся числом зубьев z1 . Пусть z1 =18, тогда z2 =3·18=54. Из условия соосности z1 + z2 = z3 - z2 ' найдем z2 ' 18+54=3,06 z2 '- z2 ', т.е. 72=2,06z2 , откуда z2 ' =34,95. Принимаем z2 ' =35, тогда z3 =3,06 z2 ' =3,06·35=107,1. Принимаем z3 =108, чтобы z3 было бы одной четности с z1 . Определяем возможное число сателлитов k
Значит, в схеме механизма может быть либо 2 , либо 3 сателлита. Принимаем k =3 . Проверяем возможность сборки из условия z
3
тогда (108+18)/3=42. Число в ответе целое, значит, сборка механизма возможна. Итак, окончательно имеем: k=3, z1 =18, z2 =54, z2 ' =35, z3 =108 . Определяем делительные диаметры колес по формуле d= mz = (мм ).
3.2.3. Проектирование зубчатой передачиШаг зубчатого зацепления по делительной окружности Р= m=3,14 6=18,84 мм. Радиусы делительных окружностей
2 2 2 2 Межосевое расстояние аW = R1 + R2 = 54 + 162 = 216 мм. Радиусы основных окружностей
Rb2 = R2 cosα = 162 cos20о = 152,28 мм . Радиусы окружностей впадин
Rа1 = R1 + m=54+6=60 мм ; Rа2 = R2 + m=162+6=168 мм .
Строим зубчатую передачу в масштабе М 1 4. 20 4. ПРИЛОЖЕНИЯТаблица 1 Формулы для определения размеров зубчатых колес
Таблица 2 Значения коэффициента уравнительного смещения ∆У для неравносмещенного внешнего зацепления при 2≥U12>1 по В.Н. Кудрявцеву
Таблица 3 Значения коэффициентов уравнительного смещения ∆У и относительного смещения Х1 для неравносмещенного внешнего зацепления при 5≥U12>2 по В.Н. Кудрявцеву
22
23
Таблица 5 Значения коэффициента относительного смещения Х2 для неравносмещенного внешнего зацепления при 5≥U12>2 по В.Н. Кудрявцеву
Таблица 6 Значения коэффициента Х=Х1=-Х2 > 0 для равносмещенного внешнего зацепления с выровненными коэффициентами относительного скольжения
5. ПРИМЕРНЫЕ ВОПРОСЫ К ЗАЩИТЕ РАСЧЕТНОГРАФИЧЕСКОЙ РАБОТЫ1. Виды зубчатых передач (механизмов). 2. Передаточное отношение одноступенчатого и многоступенчатого цилиндрического редуктора, внешнего и внутреннего зацеплений. 3. Покажите на чертеже основные элементы зубчатого колеса: толщину зуба, высоту зуба, головку и ножку зуба, шаг зубчатого зацепления, боковую поверхность зуба, угол зацепления. По какой кривой очерчена главная боковая поверхность зуба? 4. Чему равна высота головки зуба? Ножки зуба? Всего зуба (для нулевого колеса)? 5. Что такое эвольвента? Свойства эвольвенты. 6. Расскажите о последовательности графических построений эвольвентного зацепления. 7. Дать названия и определения радиусам. Написать формулы для нахождения радиусов (для нулевого зацепления). 8.Что такое модуль и шаг зубчатого зацепления? 9. Расскажите о подрезании зубьев. Какие элементы зуба подрезаются и при каких условиях возникает явление подрезания? 10. Для каких целей производят смещение режущего инструмента от нарезаемого колеса? 11. Какие колеса и передачи бывают в зависимости от смещения рейки? 12. Что называют коэффициентом перекрытия? Покажите отрезки на чертеже, отношение которых равно коэффициенту перекрытия. 13. Линия зацепления (теоретическая и практическая), ее определение и построение. 14. Рабочий профиль зуба, его определение и построение. 15. Дуга зацепления, ее определение и построение. Записать формулу длины дуги. 16. Что характеризует коэффициент удельного скольжения профилей в зубчатом зацеплении? В открытых передачах что изнашивается интенсивней – головка или ножка зуба? 17. Зубчатые механизмы с подвижными осями. Их классификация и применение. 18. Обозначения звеньев планетарного редуктора. Показать на схеме редуктора. 19. Показать, какие колеса входят во внешнее, а какие во внутреннее зацепление. 20. Записать передаточное отношение заданной схемы планетарного редуктора. 21. Записать условие соосности для данного планетарного редуктора. Что из этого условия можно найти? 22. При каких условиях возможна сборка планетарного редуктора? 23. Как определили количество сателлитов? 31 СОДЕРЖАНИЕ1. Порядок выполнения лабораторной работы 3 2. Методические указания по выполнению работы 4 2.1. Виды зубчатых передач4 2.2. Проектирование планетарных передач4 2.3. Проектирование зубчатой передачи 11 3. Пример выполнения пояснительной записки19 4. Приложения 22 5.Вопросы к защите 30 32 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

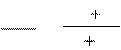 sin( )> ,
(7) k z
1 z
2
sin( )> ,
(7) k z
1 z
2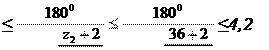 Находим возможное число сателлитов из условия (7) k .
arcsinarcsin
Находим возможное число сателлитов из условия (7) k .
arcsinarcsin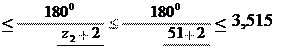 z3
=3,06·33=100,98.
Округляем z3
до целого, чтобы z3
было бы одинаковой четности с z1
,
т.е. принимаем z3
=101.
Определяем число сателлитов k
.arcsinarcsin
z3
=3,06·33=100,98.
Округляем z3
до целого, чтобы z3
было бы одинаковой четности с z1
,
т.е. принимаем z3
=101.
Определяем число сателлитов k
.arcsinarcsin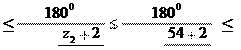 k 3,6,
arcsinarcsin
k 3,6,
arcsinarcsin
 Толщина зуба S
больше, чем ширина впадины е: S > e, S >
Толщина зуба S
больше, чем ширина впадины е: S > e, S >
 Толщина зуба S
меньше, чем ширина впадины е S < e, S <
Толщина зуба S
меньше, чем ширина впадины е S < e, S <
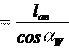 , (14)
, (14) 
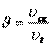 .
.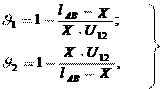 (17)
(17) 
 Передаточное отношение U1H
=10,18. -Модуль зацепления m=6 мм
.
Передаточное отношение U1H
=10,18. -Модуль зацепления m=6 мм
. 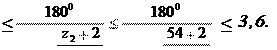 k
arcsinarcsin
k
arcsinarcsin
 R
1 mz
1 6 18 54 мм
; R
1 mz
2 6 54 162 мм
.
R
1 mz
1 6 18 54 мм
; R
1 mz
2 6 54 162 мм
.