МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
СУМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Курсовая работа
по программированию по теме:
«Решение системы линейных уравнений методом Гаусса и Жордана-Гаусса
»
Сумы 2005
ПЛАН
Постановка задачи
Теоретическая часть
Методы решения примененные в программе
Метод Гаусса.
Метод Жордана-Гаусса.
Краткое описание среды визуальной разработки Delphi
Таблица основных обозначений программы.
Описание процедур и алгоритм роботы программы
Текст программы.
Файл-модуль unit1.pas
Файл-модуль unit2.pas
Файл проекта - Project1.dpr:
Результат работы программы.
Инструкция по работе с программой
Использованная Литература
Составить программу для решения систем линейных уравнений размером n на n методом Гауса и Жордана-Гаусса.
Метод Гаусса
Метод Гаусса решения систем линейных уравнений состоит в последовательном исключении неизвестных и описывается следующей процедурой.
С помощью элементарных преобразований над строками и перестановкой столбцов расширенная матрица  системы системы  может быть приведена к виду может быть приведена к виду

Эта матрица является расширенной матрицей системы

которая эквивалентна исходной системе 
Заметим, что перестановка столбцов означает перенумерацию переменных. На практике обычно избегают этой процедуры, приводя расширенную матрицу к ступенчатому виду путем элементарных преобразований над строками.
Если хотя бы одно из чисел  отлично от нуля, то система отлично от нуля, то система  несовместна. Если же несовместна. Если же  , то система , то система  совместна и можно получить явное выражение для совместна и можно получить явное выражение для  базисных неизвестных базисных неизвестных  через через  свободных неизвестных свободных неизвестных 
Элементарные преобразования этого метода аналогичны методу Гаусса, только матрица при использовании этого метода приводится к виду, тоесть столбец свободных коэффициентов превращается в столбец корней.

Среда Delphi - это сложный механизм, обеспечивающий высокоэффективную работу программиста. Визуально она реализуется несколькими одновременно раскрытыми на экране окнами. Окна могут перемещаться по экрану, частично или полностью перекрывая друг друга, что обычно вызывает у пользователя, привыкшего к относительной “строгости” среды текстового процессора Word или табличного процессора Excel, ощущение некоторого дискомфорта. После приобретения опыта работы с Delphi это ощущение пройдет, и вы научитесь быстро отыскивать нужное окно, чтобы изменить те или иные функциональные свойства создаваемой вами программы, ибо каждое окно несет в себе некоторую функциональность, т. е. предназначено для решения определенных задач.
Запустите Delphi - и вы увидите нечто, похожее на
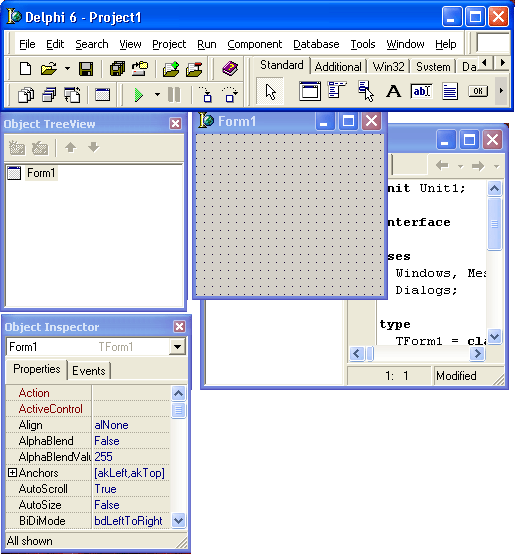
На рисунке изображены шесть наиболее важных окон Delphi: главное окно, окно Дерева объектов (Object Tree View), окно Инспектора объектов, окно браузера, окно формы и окно кода программы.
Чтобы упорядочить окна так, как они показаны на рисунке, вам придется вручную изменять их положение и размеры, т. к. обычно окно кода программы почти полностью перекрыто окном формы. Впрочем, добиваться максимального сходства того, что вы видите на экране вашего ПК, с изображением, показанным на рисунке, вовсе не обязательно: расположение и размеры окон никак не влияют на их функциональностью.
Замечу, что при первом запуске Delphi поверх всех окон появится окно
С помощью этого окна вы сможете получить доступ к Web-страницам корпорации Inprise для просмотра самой свежей информации о корпорации и ее программных продуктах, копирования дополни тельных файлов, чтения ответов на наиболее часто задаваемые вопросы и т. д. При повторных запусках Delphi это окно появляется автоматически с некоторой периодичностью, определяемой настройками на странице окна Tolls | Environment Options, связанной с закладкой Delphi Direct. Вы также сможете его вызвать в любой момент с помощью опции Help | Delphi Direct главного меню.
| Обозначение
|
Описание |
Модуль |
| maxr |
Константа для ограничения максимального размера системы |
Unit2 |
| arys, ary2s |
Типы данных для переменных, в которых хранятся значения коэффициентов системы |
Unit2 |
| Gauss1 |
Процедура для решения системы линейных уравнений методом Гаусса |
Unit2 |
| Gaussj |
Процедура для решения системы линейных уравнений методом Жордана-Гаусса |
Unit2 |
| i,j,l |
Счетчики |
Unit1 |
| prover |
Промежуточная переменная типа String, используется для проверки наличия букв среди коэффициентов системы, а также для замены «.» на «,». |
Unit1 |
| S |
Переменная для хранения размера матрицы |
Unit1 |
| k |
Переменная для хранения длины строчки хранящейся в переменной prover. |
Unit1 |
| dl |
Переменная для проверки размера системы. |
Unit1 |
| MainMenu1 |
Меню программы. |
Unit1 |
| File1, New1, Save1, Exit1 |
Пункты меню. |
Unit1 |
| Matrix, Coef, Gauss, Jgauss |
Таблицы для ввода элементов системы и вывода результатов расчета. |
Unit1 |
| XPManifest1 |
Компонент, который дает программе возможность использовать оформление Windows. |
Unit1 |
| SaveDialog1 |
Диалоговое окно для сохранения результатов. |
Unit1 |
| Button1, Button2 |
Кнопки для запуска процедур решения системы. |
Unit1 |
| New1Click |
Процедура, которая выполняется после выбора пункта меню New. |
Unit1 |
| Button1Click |
Процедура, которая выполняется после нажатия кнопки Gauss. |
Unit1 |
| Button2Click |
Процедура, которая выполняется после нажатия кнопки J-Gauss. |
Unit1 |
| Save1Click |
Процедура, которая выполняется после выбора пункта меню Save. |
Unit1 |
| Exit1Click |
Процедура, которая выполняется после выбора пункта меню Exit. |
Unit1 |
| Form1 |
Собственно окно программы. |
Unit1 |
В программу включены следующие процедуры : «
gauss
1», «
gaussj
», «New1Click», «
Button
1
Click
», «
Button
2
Click
», «Save1Click», «
Exit
1
Click
».
С каждой из них мы ознакомимся ниже.
Процедура «
gauss
1»
выполняет проверку системы на сходимость и решение методом Гаусса.
Процедура «
gaussj
»
выполняет проверку системы на сходимость и решение методом Жордана-Гаусса.
Процедура «New1Click»
выполняется после выбора пункта меню «New» или сразу после запуска программы и выполняет чтение размера системы и устанавливает размер таблиц для ввода коэффициентов системы.
Процедура «
Button
1
Click
»
считывает коэффициенты системы, проверяет корректность ввода коэффициентов и заменяет при необходимости «.» на «,». Потом запускает процедуру «
gauss
1»
для решения системы и выводит результаты.
Процедура «
Button
2
Click
»
считывает коэффициенты системы, проверяет корректность ввода коэффициентов и заменяет при необходимости «.» на «,». Потом запускает процедуру «
gaussj
»
для решения системы и выводит результаты.
Процедура «Save1Click»
запускает диалог сохранения файлов и выполняет сохранение результатов.
Процедура «
Exit
1
Click
»
- Выход из программы.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, Menus, XPMan, StdCtrls, Grids, unit2;
type
TForm1 = class(TForm)
Coef: TStringGrid;
Gauss: TStringGrid;
Jgauss: TStringGrid;
Button1: TButton;
Button2: TButton;
XPManifest1: TXPManifest;
SaveDialog1: TSaveDialog;
MainMenu1: TMainMenu;
File1: TMenuItem;
New1: TMenuItem;
Save1: TMenuItem;
Exit1: TMenuItem;
Matrix: TStringGrid;
procedure New1Click(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Save1Click(Sender: TObject);
procedure Exit1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
s:integer;
implementation
{$R *.dfm}
procedure TForm1.Exit1Click(Sender: TObject);
begin
close;
end;
procedure TForm1.New1Click(Sender: TObject);
var i,dl:integer;
prover:string;
begin
form1.Enabled:=false;
repeat
prover:=inputbox('Введитеразмерсистемы','Значениемежду 2 и 20','2');
dl:=length(prover);
if dl=0 then showmessage('Введитеразмерсистемы') else
begin
if (dl=1) and (prover<'9') and (prover>'0') then s:=trunc(strtofloat(prover))
else
begin
for i:=1 to dl do
begin
if prover[i]>'9' then
begin
showmessage('Введитечисло');
break;
end
else if i=dl then s:=trunc(strtofloat(inputbox('Введитеразмерсистемы','Значениемежду 2 и 20','2')));
end;
end;
end;
until (s>=2) and (s<=maxr);
form1.Enabled:=true;
matrix.RowCount:=s+1;
matrix.ColCount:=s+1;
gauss.colCount:=s+1;
coef.rowCount:=s+1;
jgauss.colCount:=s+1;
coef.Cells[1,0]:='B';
gauss.Cells[0,1]:='Gauss';
jgauss.Cells[0,1]:='J-Gauss';
for i:=1 to s do
begin
matrix.Cells[0,i]:=floattostr(i);
matrix.Cells[i,0]:='A'+floattostr(i);
coef.Cells[0,i]:=floattostr(i);
gauss.Cells[i,0]:='X'+floattostr(i);
jgauss.Cells[i,0]:='X'+floattostr(i);
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
var a:ary2s;
x,y:arys;
error:boolean;
i,j,l,K:integer;
prover:string;
begin
{Считывание массивов с исходными данными и проверка '.' или ','}
{***********************************************}
for i:=1 to s do
for j:=1 to s do
begin
prover:=matrix.Cells[j,i];
k:=length(prover);
if k=0 then
begin
showmessage('Вы не ввели один или несколько элементов системы.');
exit;
end;
for l:=1 to length(prover) do
if prover[l]='.' then prover[l]:=','
else if prover[l]>'9' then
begin
showmessage('В качестве одного или нескольких элементов системы введена буква. Заменитеихначисла!');
exit;
end;
matrix.Cells[j,i]:=prover;
a[i,j]:=strtofloat(matrix.cells[j,i]);
end;
for i:=1 to s do
begin
prover:=coef.cells[1,i];
for l:=1 to length(prover) do
if prover[l]='.' then prover[l]:=','
else if prover[l]>'9' then
begin
showmessage('В качестве одного или нескольких элементов системы введена буква. Заменитеихначисла!');
exit;
end;
coef.cells[1,i]:=prover;
y[i]:=strtofloat(coef.cells[1,i]);
end;
{***********************************************}
{Решение и вывод результатов}
{***********************************************}
gauss1(a,y,x,s,error);
if not error then
for i:=1 to s do
gauss.cells[i,1]:=floattostr(x[i])
else
begin
showmessage('Система решения не имеет');
new1.Click;
end;
{***********************************************}
end;
procedure TForm1.Button2Click(Sender: TObject);
var a:ary2s;
x,y:arys;
error:boolean;
i,j,l,k:integer;
prover:string;
begin
{Считывание массивов с исходными данными}
{***********************************************}
{Считывание массивов с исходными данными и проверка '.' или ','}
{***********************************************}
for i:=1 to s do
for j:=1 to s do
begin
prover:=matrix.Cells[j,i];
k:=length(prover);
if k=0 then
begin
showmessage('Вы не ввели один или несколько элементов системы.');
exit;
end;
for l:=1 to length(prover) do
if prover[l]='.' then prover[l]:=','
else if prover[l]>'9' then
begin
showmessage('В качестве одного или нескольких элементов системы введена буква. Заменитеихначисла!');
exit;
end;
matrix.Cells[j,i]:=prover;
a[i,j]:=strtofloat(matrix.cells[j,i]);
end;
for i:=1 to s do
begin
prover:=coef.cells[1,i];
for l:=1 to length(prover) do
if prover[l]='.' then prover[l]:=','
else if prover[l]>'9' then
begin
showmessage('В качестве одного или нескольких элементов системы введена буква. Заменитеихначисла!');
exit;
end;
coef.cells[1,i]:=prover;
y[i]:=strtofloat(coef.cells[1,i]);
end;
{***********************************************}
{***********************************************}
{Решение и вывод результатов}
{***********************************************}
gaussj(a,y,x,s,error);
if not error then
for i:=1 to s do
jgauss.cells[i,1]:=floattostr(x[i])
else
begin
showmessage('Система решения не имеет');
new1.Click;
end;
{***********************************************}
end;
procedure TForm1.Save1Click(Sender: TObject);
var f:textfile;
i,j:integer;
begin
savedialog1.Filter:='Text files (*.txt)|*.txt|';
if savedialog1.Execute then
begin
assignfile(f,savedialog1.filename+'.txt');
rewrite(f);
for i:=1 to s do
begin
writeln(f);
for j:=1 to s do
write(f,matrix.cells[i,j]:4,' ');
write(f,'|',coef.cells[1,i]);
end;
writeln(f);
writeln(f);
writeln(f,'Gauss');
for i:=1 to s do
writeln(f,'X'+floattostr(i)+'='+gauss.cells[i,1],' ');
writeln(f);
writeln(f,'J-Gauss');
for i:=1 to s do
writeln(f,'X'+floattostr(i)+'='+jgauss.cells[i,1],' ');
closefile(f);
end;
end;
end.
Файл
-модуль unit2.pas
unit unit2;
interface
const maxr=20;
type arys=array[1..maxr] of real;
ary2s=array[1..maxr,1..maxr] of real;
procedure gauss1(a:ary2s; y:arys; var coef:arys; ncol:integer; var error:boolean);
procedure gaussj(var b:ary2s; y: arys; var coef:arys; ncol:integer; var error: boolean);
implementation
{Решение системы линейных уравнений методом Гаусса}
{**********************************************************}
procedure gauss1(a:ary2s; y:arys; var coef:arys; ncol:integer; var error:boolean);
var b:ary2s;
w:arys;
i,j,i1,k,l,n:integer;
hold,sum,t,ab,big: real;
begin
error:=false;
n:=ncol;
for i:=1 to n do
begin
for j:=1 to n do
b[i,j]:=a[i,j];
w[i]:=y[i]
end;
for i:=1 to n-1 do
begin
big:=abs(b[i,i]);
l:=i;
i1:=i+1;
for j:=i1 to n do
begin
ab:=abs(b[j,i]);
if ab>big then
begin
big:=ab;
l:=j
end
end;
if big=0.0 then error:= true
else
begin
if l<>i then
begin
for j:=1 to n do
begin
hold:=b[l,j];
b[l,j]:=b[i,j];
b[i,j]:=hold
end;
hold:=w[l];
w[l]:=w[i];
w[i]:=hold
end;
for j:=i1 to n do
begin
t:=b[j,i]/b[i,i];
for k:=i1 to n do
b[j,k]:=b[j,k]-t*b[i,k];
w[j]:=w[j]-t*w[i]
end
end
end;
if b[n,n]=0.0 then error:=true
else
begin
coef[n]:=w[n]/b[n,n];
i:=n-1;
repeat
sum:=0.0;
for j:=i+1 to n do
sum:=sum+b[i,j]*coef[j];
coef[i]:=(w[i]-sum)/b[i,i];
i:=i-1
until i=0
end
end;
{**********************************************************}
{Решение системы линейных уравнений методом Жордана-Гаусса}
{**********************************************************}
procedure gaussj(var b:ary2s; y: arys; var coef:arys; ncol:integer; var error: boolean);
var w:array[1..maxr,1..maxr] of real;
index:array[1..maxr,1..3] of integer;
i,j,k,l,nv,irow,icol,n,l1:integer;
determ,pivot,hold,sum,t,ab,big:real;
{++++++++++++++++++++++++++++++++++++++++++++}
procedure swap(var a,b: real);
var hold:real;
begin
hold:=a;
a:=b;
b:=hold
end;
{++++++++++++++++++++++++++++++++++++++++++++}
{@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@}
procedure gausj2;
var i,j,k,l,l1:integer;
{===============================================}
procedure gausj3;
var l:integer;
begin
if irow<>icol then
begin
determ:=-determ;
for l:=1 to n do
swap(b[irow,l],b[icol,l]);
if nv>0 then
for l:=1 to nv do
swap(w[irow,l],w[icol,l])
end
end;
{===============================================}
begin
error:=false;
nv:=1;
n:=ncol;
for i:=1 to n do
begin
w[i,1]:=y[i];
index[i,3]:=0
end;
determ:=1.0;
for i:=1 to n do
begin
big:=0.0;
for j:=1 to n do
begin
if index[j,3]<>1 then
begin
for k:=1 to n do
begin
if index[k,3]>1 then
begin
error:=true;
exit;
end;
if index[k,3]<1 then
if abs(b[j,k])>big then
begin
irow:=j;
icol:=k;
big:=abs(b[j,k])
end
end
end
end;
index[icol,3]:=index[icol,3]+1;
index[i,1]:=irow;
index[i,2]:=icol;
gausj3;
pivot:=b[icol,icol];
determ:=determ*pivot;
b[icol,icol]:=1.0;
for l:=1 to n do
b[icol,l]:=b[icol,l]/pivot;
if nv>0 then
for l:=1 to nv do
w[icol,l]:=w[icol,l]/pivot;
for l1:=1 to n do
begin
if l1<>icol then
begin
t:=b[l1,icol];
b[l1,icol]:=0.0;
for l:=1 to n do
b[l1,l]:=b[l1,l]-b[icol,l]*t;
if nv>0 then
for l:=1 to nv do
w[l1,l]:=w[l1,l]-w[icol,l]*t;
end
end
end;
end;
{@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@}
begin
gausj2;
if error then exit;
for i:=1 to n do
begin
l:=n-i+1;
if index[l,1]<>index[l,2] then
begin
irow:=index[l,1];
icol:=index[l,2];
for k:=1 to n do
swap(b[k,irow],b[k,icol])
end
end;
for k:=1 to n do
if index[k,3]<>1 then
begin
error:=true;
exit;
end;
for i:=1 to n do
coef[i]:=w[i,1];
end;
{**********************************************************}
end.
Файл
проекта - Project1.dpr:
program Project1;
uses
Forms,
Unit1 in 'Unit1.pas' {Form1},
Unit2 in 'Unit2.pas';
{$R *.res}
begin
Application.Initialize;
Application.Title := 'Gauss&J-Gauss';
Application.CreateForm(TForm1, Form1);
Application.Run;
end.
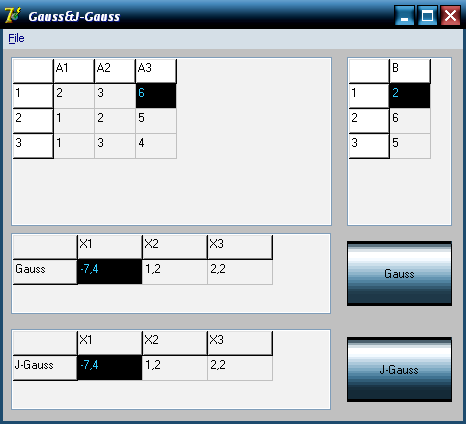
Результаты сохраненные в файле:
2 1 1 |2
3 2 3 |6
6 5 4 |5
Gauss
X1=-7,4
X2=1,2
X3=2,2
J-Gauss
X1=-7,4
X2=1,2
X3=2,2
Инструкция по работе с программ
ой
1. Сразу после запуска файла программы (pragramma.exe) перед вами появиться окно с запросом размера системы. Введите нужный размер и нажмите «ОК»(поскольку система размера n на n нужно ввести только одно число).
2. После ввода размера перед вами появится рабочее окно программы. Введите в него данные по следующей схеме:
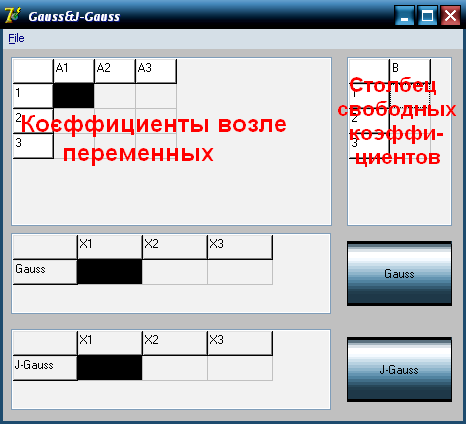
3. Для решения нужным методом нажмите соответствующую кнопку, и в таблице возле нее будут выведены корни системы.
4. Для сохранения результатов в меню «File» выберите «Save», перейдите в нужную папку и введите имя файла. Нажмите «ОК».
5. Для начала новых рассчетов «File» выберите «New», введите новый размер системы, нажмите «ОК».
6. Для выхода в меню «File» выберите пункт «Exit».
· Волков Е.А. численные методы: Учебное пособие для вузов. – 2-е изд., испр. – М.:Наука, 1987. – 248 с.
· Роганин А.М. Основные формулы высшей математики. – Х.:Торсинг, 2002
· Справочная система Borland Delphi 7.
· http://delphi.vitpc.com/
· http://www.fortunecity.com/campus/beverly/963/
· http://www.delphi.agava.ru/
· http://www.interface.ru/delphi/delphi_page.htm
· http://pog.da.ru/
|