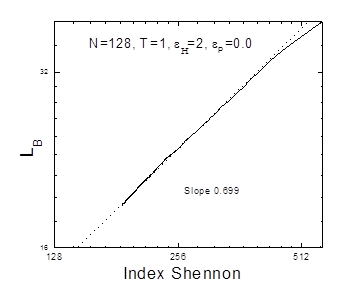Дипломная работа: Мутации структуры белковоподобного сополимера Компьютерное моделирование
|
Название: Мутации структуры белковоподобного сополимера Компьютерное моделирование Раздел: Рефераты по химии Тип: дипломная работа | ||||||||||
Государственное образовательное учреждение высшего профессионального образования Тверской государственный университет Химический факультет Кафедра неорганической и аналитической химии Направление 510500 – Химия Новиков Виктор Викторович Мутации структуры белковоподобного сополимера. Компьютерное моделирование Магистерская диссертация Научный руководитель д.ф.-м.н. проф. Халатур П.Г. ______________________ Работа допущена к защите « ___ » __________ 2003 г. Декан химического факультета д.х.н. профессор Лапина Г.П. _________________________ Тверь – 2003 План 1. Введение 2. Литературный обзор 2.1. Механическая модель молекулы 2.2. Методы компьютерного моделирования полимеров. Метод Монте Карло. Метод Молекулярной динамики 2.2.1 Основные подходы к математическому моделированию макромолекул 2.2.2. Методы молекулярной динамики (МД) 2.2.3. Метод Монте-Карло (МК) 2.2.4. Особенности компьютерного эксперимента 2.2.5. Решёточные и континуальные модели 2.2.6. Трудности машинного эксперимента Периодические граничные условия 2.2.7. Модернизированные методы компьютерного моделирования 2.3. Мотивы укладки цепи в белковых молекулах 2.4. Методы анализа белковых структур 2.4.1. Определение гомологии первичных структур 2.4.2. Нахождение вторичной структуры 2.4.3.Метод протягивания 2.4.4. Дизайн белковых молекул 2.5. Конформационно-зависимый дизайн последовательностей цепи 2.5.1. НР – сополимеры, «приспособленные к адсорбции» 2.5.2. Молекулярные диспергаторы 2.5.3. Моделирование мембранных белков 2.7. Белковоподобные сополимеры. Дизайн, структура, свойства 2.8. Оптимизация последовательностей белковоподобных сополимеров глобулярных белков 2.9. Дальнодействующие корреляции в белковоподобных сополимерах 3. Экспериментальная часть 3.1. Модель и метод моделирования 3.2.Модель молекулярной эволюции 3.3. Методы анализа 4. Результаты и обсуждение 5. Заключение 6. Список литературы 1. ВведениеКонцепция эволюции является одним из краеугольных камней в современных естественных науках: в космологии обсуждается эволюция вселенной, в геологии эволюция Земли, в биологии эволюция живого мира. Эту идею можно использовать и в полимерной науке [1,2]. Соответствующие положения этой проблемы достаточно ясны. В настоящее время биополимеры ( белки, ДНК, РНК) обладают сложной первичной структурой (последовательность мономерных звеньев ) которая определяет их функции и структуру ( в том числе и третичную структуру глобулярных белков). Поэтому эти последовательности ( 20-ти буквенный алфавит в случае белков и 4-х буквенный в случае ДНК и РНК) должны значительно отличаться от случайных и часто проявляют значительные корреляции на различных массштабах. Другими словами, естественно ожидать, что количество информации в таких последовательностях относительно высоко сравнительно высоко по сравнению со случайными (ДНК содержит всю генетическую информацию). С другой стороны, на начальном этапе до биологической эволюции могли образовываться только случайные последовательности или последовательности с короткодействующими корреляциями. Можно добавить, что по ходу молекулярной эволюции первичные структуры сополимеров становились всё сложнее и сложнее, пока не достигли уровня сложности современных биополимеров. Исследование различных возможностей эволюции последовательностей сополимеров является областью, где концепцию эволюции можно использовать в контексте науки оп полимерах. Стоит заметить, что, так как количество информации последовательности можно определить количественно, то весь процесс эволюции биополимерных последовательностей может быть точно определён в математических терминах, которые не всегда применимы для других случаях эволюции. С другой стороны, сформулированные фундаментальные проблемы чрезвычайно сложны из-за отсутствия прямой информации о ранней добиологической эволюции. Поэтому особый интерес представляют модельные системы эволюции последовательностей, которые показывают различные возможности появления сложной статистики и дальнодействующих корреляций в последовательностях. Так как при помощи случайных мутаций невозможно увеличить количество информации последовательности, то такие модельные системы должны принимать во внимание связь между конформацией полимерной цепи и эволюцией последовательности. Один из вариантов конформационно-зависимого дизайна сополимеров, который ведёт к статистически достаточно сложным последовательностям рассмотрен в статьях [3,4,5]. Подход заключается в модифицировании поверхности глобулы. Звеньям, находящимся на поверхности присваивается индекс Р (гидрофильные звенья), а находящимся в ядре глобулы – Н (гидрофобные). Конформация полученного сополимера зависит от Н-Н, Н-Р и Р-Р взаимодействий. Такие сополимеры были названы в статье [3] белковоподобными сополимерами, так как они отражают одну из важных особенностей реальных глобулярных белков: возможность образования плотного гидрофобного ядра, стабилизированным гидрофильными петлями, в глобулярной конформации. Благодаря этой особенности эти белки в глобулярной конформации.не выпадают в осадок в растворе Следует отметить, что образование гидрофильных звеньев является только одним из свойств белков, поэтому белковоподобные сополимеры не имеют общего с реальными белками. Можно говорить только о сходстве белковоподобных сополимеров и сополимеров, появляющиеся на ранних этапах эволюции. Были предложены простые различные компьютерные модели, описывающие эволюцию сополимерных последовательностей. Однако, цель большинства этих моделей – решить различные модели физики белка, т.е. проблему конструирования специфической аминокислотной последовательности, которая будет термодинамически стабильна в третичной глобулярной структуре и будет способна быстро сворачиваться в эту конформацию при данной температуре.[6,7] Мы предлагаем другой подход. Именно: 1. Мы предлагаем модельную систему молекулярной эволюции последовательностей сополимеров, в которой возможны две основные возможности: восходящая и нисходящая ветви эволюции ( в терминах количества информации последовательности), зависящей от параметров взаимодействий между звеньями. 2. Мы исследовали применимость теоретико-информационных характеристик для описания молекулярной эволюции. 2. Литературный обзор2.1. Механическая модель молекулыПод моделью системы понимают выбор правил, описывающих взаимодействие частиц между собой и/или с внешними полями, то есть в формулировке вида и способа вычисления функции потенциальной энергии.[8] В ряде задач физической химии удобно рассматривать молекулу не как электронно-ядерную систему, а как систему взаимодействующих атомов (механическая модель молекулы). Механическая модель не противоречит квантовой механике, а при некоторых ограничениях (среди них, прежде всего, следует упомянуть теорему Борна-Оппергеймера) может быть выведена из неё. В приближении МО ЛКАО ССП энергия молекулярной системы выражается как сумма одно-центровых взаимодействий (ea ), двуцентровых взаимодействий (ea b ), трёхцентровых взаимодействий ( ea b g ) и т.д.
Одно-центровые и двуцентровые интегралы естественно отнести к парам ядер (атомов), трёхцентровые интегралы- к тройкам ядер (атомов) и т. д .Тогда получаем энергию молекулы в атом-атомном приближении здесь суммирование ведётся по всем парам атомов, по всем тройкам атомов и т.д.
Многочастичные взаимодействия вносят малый вклад в энергию системы, и ими часто пренебрегают. Парные взаимодействия удобно разбить на взаимодействия атомов, валентно связанных между собой, и взаимодействия атомов, валентно между собой не связанных. Предполагается, что энергию взаимодействия можно разделить на ряд составляющих. 1. Энергия деформации связи. При отклонении длин связей от их нормального значения возникает энергия деформация связи (Есв ). Обычно связь рассматривают как гармонический осциллятор. При этом можно предположить, что при малых деформациях энергия ковалентных связей подчиняется следующей зависимости. U ( R ) = K ´ ( R - Ri )2 (2.3) Где К – силовая постоянная, R – равновесная длина связи Ri – мгновенная длина связи Рассмотрим вопрос о способе описания валентных связей. Здесь существует альтернатива[9]: 1) моделировать связи каким-либо гладким потенциалом (например гармоническим или потенциалом Морзе), 2) учитывать их как абсолютно жёсткие (геометрические) ограничения. Оба способа имеют свои преимущества и недостатки. В первом случае справедливы простые уравнения Ньютона. Однако из-за высокой "жёсткости" обычных валентных потенциалов связанные частицы могут совершать быстрые колебательные движения, учесть которые можно при очень малом шаге интегрирования. Поэтому даже после весьма большого числа шагов эволюции системы будет на самом деле прослежена лишь в течении короткого интервала времени. Проблема решается путём удаления соответствующих степеней свободы при рассмотрении химических связей как постоянных геометрических ограничений. При этом в системе действует единственный невалентный потенциал, который и задаёт минимальный временной масштаб. Однако в подобной постановке движение частиц описывается уже не уравнениями Ньютона, а уравнениями Лагранжа, что усложняет вычислительную схему и делает её более трудоёмкой. Кроме того, абсолютно жёсткие связи не вполне правильно отвечают реальной ситуации. Оптимальный вариант состоит в подборе таких валентных потенциалов, жёсткость которых мало отличается от невалентных. Один из них, известный как потенциал FENE, имеет вид
Uij ( r) = (2.4) 0 при r > r0 Здесь r – расстояние между парой связанных частицi и j , а параметры k и r0 принимаются равными 10e/s2 и 1.95s. Другой удачной аппроксимацией является конструкция из двух потенциалов Леннарда-Джонса, действующих навстречу друг к другу и описывающих только отталкивание. e0 [( b/ r)12 – 2( b/ r)6 +1 при r < b
(2 b- r)12 (2 b- r)6 Здесь b – заданная длина связи между частицами i и j . Данная функция имеет нулевой минимум при r = b и становится бесконечной при r = 0 и r = 2b . 2. Энергия деформации углов. Для каждого атома в молекуле существуют некоторые идеальные углы, отклонение от которых требуют затрат энергии угловых деформаций (Еугл ). Предполагается, что эта энергия аддитивна, причём при малых отклонениях справедлив закон Гука. Аналогично энергии деформации связей можно записать. U ( q ) = C ´ ( q i - q )2 (2.6) Где С – силовая константа, q- идеальное значение угла связи, qi – мгновенное значение угла связи Деформация углов происходит значительно легче, чем деформация связей ( константа К на порядок выше, чем С). Для описания угловых напряжений можно использовать потенциал (2.5), если в качестве параметра b взять расстояние между атомами, разделенными двумя связями. 3. Невалентные взаимодействия атомов (Ес ).
В попарно аддитивном приближении стерический вклад в потенциальную энергию молекулы выражается через взаимодействия отдельных атомов[10]. Ec = åå fij ( r ) (2.7) i < j Взаимодействия валентно не связанных атомов складывается из дисперсионного (а также индукционного и ориентационного) притяжения и отталкивания, возникающего из-за перекрывания электронных оболочек на малых расстояниях. На рис. 2.1 показана потенциальная функция f(r) взаимодействия двух атомов в зависимости от расстояния r между ними. Отталкивание между атомами апроксимируется обычно функциями вида B / rn или Cexp (- Dr ), а притяжение – функцией A / rm (A, B, C, D, m, n – постоянные). Отсутствие строгого выражения для f ( r ) вынуждает искать приближённые аналитические формы. Наибольшее распространение получили потенциалы типа "6-12" и "6 - exp". Потенциал Леннарда – Джонса ( m – n ) f(r) = n e (n-m)-1 (n/m)m/(n-m) [( s /r)n – ( s /r)m ] = n e (n-m) –1 [(m/n)(r0 /r)n – (r0 /r)m ] , где r 0 = 21/6 ´s, m и n – численные коэффициенты. Коэффициент m выбирается равным 6. Величина n лежит в интервале от 10 до 14 и чаще всего принимается равной 12. В этом случае данный потенциал называют потенциалом "6-12". При m = 6 и n = 12 имеем f ( r ) = 4 e [( s / r )12 – ( s / r )6 ] (2.8) Для малых r функция f ( r ) имеет большое положительное значение, а с ростом r – становится отрицательной, проходя при r = r 0 через минимум ( где f ( r 0 ) = - e ) и асимптотически приближается к нулю. Значение r при котором функция f ( r ) пересекает ось r , обозначено s . Наличие дальнодействующей части создаёт расчётные трудности, ибо в плотной системе для каждой частицы становится необходимым учёт её взаимодействий с большим числом окружающих частиц. Поэтому функцию 2.8. обрывают на некотором заранее выбранном расстоянии rc , полагая, что при r > rc f(r) = 0. Однако более целесообразно использовать такой потенциал, который сам по себе является короткодействующим. Кроме того, желательно, чтобы его производная по расстоянию обращалась в нуль на границе действия. В качестве примера представлена подобная функция, первая и вторая части которой сшиваются в точке r = 21/6 s, где f(r) = -e, а производная df(r)/dr обращается в нуль при r = 21/6 s и r = rc :
f(r) = e3( r-21/6 s)2 _ 2( r-21/6 )3 - 1 при 21/6 s < r < rc (rc -21/6 s)2 (rc -21/6 )3 (2.9) 0 при r > rc Ван-дер-ваальсовые взаимодействия имеют тот же порядок, что и тепловое движение атомов (кТ). Если ещё учесть, что число этих взаимодействий равно N(N-1)/2, то можно сделать вывод, что при согласованном действии этих сил могут происходить значительные крупномасштабные конформационные перестройки макромолекулы. 4. Торсионная энергия. Потенциалы невалентных взаимодействий дают слишком малые значения барьеров внутреннего вращения. Это обстоятельство можно изменить, если в конформационную энергию ввести член, зависящий от взаимного расположения связей, присоединённых к оси вращения. Суммарные энергетические затраты, характеризующие отклонения от оптимальной взаимной ориентации связей, определяются как торсионная (или ориентационная) составляющая (ЕТ ) конформационной энергии. U( j) = U0 /2(1 – cos( n j)) (2.10) Где U0 – барьер внутреннего вращения. Для карбоцепных полимеров этот барьер (между транс- и гош- состоянием) составляет примерно 3 ккал/моль n – порядок вращения. Для карбоцепных полимеров n =3. j -значение двухгранного угла. 5. Электростатические взаимодействия (Еэл ). Для энергии электростатических взаимодействий в монополь-монопольном приближении Eэл =K åå qi qj /r e (2.11) i < j Где qi и qj – парциальные заряды ( в долях заряда электрона) на атомах i и j, разделённых расстоянием r; e - эффективная диэлектрическая постоянная среды; K = 332 – переводной множитель, позволяющий выразить Eэл в ккал/моль, если r – в A°. Парциальные заряды получаются из дипольных моментов связей q = 0,208 m/ l (2.12) где l – длина связи (в А°), m - дипольный момент связи (в Дебаях), вычисляемый из опытных дипольных моментов соединений по аддитивной векторной схеме. Парциальные заряды на связанных атомах A и B могут быть также получены по приближённой формуле Смита q = 0,16( XA – XB ) + 0.035( XA – XB )2 (2.13) Здесь X – относительные электроотрицательности атомов ( по Полингу). Если расстояние, разделяющее два точечных заряда, превышает толщину мономолекулярного слоя растворителя, в котором находятся рассматриваемая молекула, то коэффициент e в 2.11 близок к диэлектрической постоянной этого растворителя. В противном случае e@ 1- 4. Чаще всего принимают s = e. Электростатические взаимодействия могут проявляются в полиэлектролитах. За счёт ионизации ионогенных групп на полимерной цепочке возникают заряды, а следовательно электростатические взаимодействия. В этом случае эти взаимодействия являются дальнодействующими ( убывают пропорционально 1/r) и определяют значительные крупномасштабные конформационные перестройки. 6. Другие составляющие энергии молекулы. Водородная связь носит донорно-акцепторный характер. Она проявляется главным образом при взаимодействии атомов О и Н групп С=О и HN, входящих, в частности в молекулы пептидов. Гораздо реже возникает необходимость вводить потенциал внутримолекулярной водородной связи для учёта взаимодействий О...Н в простых или сложных эфирах. Для описания зависимости энергии водородной связи от расстояния наибольшее распространение получила трёхпараметрическая функция Морзе. Взаимодействие двух неподелённых электронных пар (принадлежащим атомам O, S, N и др.) описываются эмпирическим потенциалом, аналогичным (2.11). Неподелённая пара представляется точечным зарядом (q = 0.1 e), расположенным на расстоянии l от ядра. Для атомов O, S,.. расстояние l отсчитывается в направлении продолжения биссектрисы угла с вершиной при данном атоме. Для атома N направление неподелённой пары совпадает с продолжением нормали к плоскости, отсекающей равные отрезки связей при атоме N. Величина l определяется сортом атома.. Если расстояние r, разделяющее две неподелённые пары, превышает 3 А°, то параметр e в (2.11) равен единице; в противном случае e = (3.5r2 – 21r + 32.5) –1 Не все вклады одинаковы важны. Для каждого класса задач выбираются наиболее важные составляющие потенциальной энергии молекулы, а другие не учитываются. 2.2. Методы компьютерного моделирования полимеров. Метод Монте Карло. Метод Молекулярной динамикиПри моделировании методами молекулярной динамики или Монте-Карло интересующее нас свойство системы большого числа молекул вычисляется через статистические средние по положениям и движениям молекул. Как и в методах молекулярной механики, здесь также необходимо перечислить все частицы системы и задать потенциалы межчастичных взаимодействий. Однако в отличие от молекулярной механики в данных подходах области задания межчастичных потенциалов взаимодействия должны быть достаточно протяженными, и они не должны ограничиваться малыми смещениями от положений равновесия. Это накладывает существенно более высокие требования на способы расчета потенциалов. 2.2.1 Основные подходы к математическому моделированию макромолекулОсновная задача статистической теории - вычисление средних значений различных величин, которые характеризуют поведение системы в состоянии равновесия. Существуют два подхода к решению этой общей задачи. В первом случае среднее значение <А> некоторого свойства A ( r, v ),которое предполагается зависящим от совокупности координат- {r} и скоростей {v} частиц, определяют путем усреднения множества "мгновенных" значений A [r(t),v(t)], наблюдаемых в последовательные моменты времени t на достаточно протяженном интервале t:[11] А =
Этот подход, называемый усреднением по времени, исходит из того, что нам известны законы движения частиц системы. Альтернативный путь вычисления средних значений параметров системы был намечен еще Больцманом, а затем развит Гиббсом в стройную теорию. Идея этого подхода заключается в том, что наблюдаемое свойство рассматривается не как среднее по времени, а как среднее по множеству различных состояний системы, которые возникают с определенной вероятностью. Такой подход называют усреднением по ансамблю. Вероятность (или частота) возникновения того или иного состояния пропорциональна его статистическому весу w=e- U / kT , где U - потенциальная энергия данной конфигурации, k - константа Больцмана, Т - абсолютная температура. В этом случае наблюдаемые средние значения даются общим выражением А =∫… ∫ A ( r ) w ( r ) dr / ∫… ∫ w ( r ) dr (2.15) Оба фундаментальных принципа определения средних значений могут быть положены в основу вычислительных схем, реализуемых на компьютере. При этом необходимо знать лишь способ расчета потенциальной энергии системы как функции координат r. Результаты расчетов, какого - либо свойства одной системы вычисляемые по одному и другому пути должны совпадать при длительном времени наблюдения за системой в первом подходе и при очень большом числе испытаний во втором подходе. 2.2.2. Методы молекулярной динамики (МД)Метод математического моделирования, основанный на подходе усреднения по времени наблюдения называют методом молекулярной динамики. Суть его состоит в следующем: Рассмотрим систему, состоящую из заданного числа частиц (атомов или молекул). В классической механике движение каждой частицы i с массой mi может быть описано уравнением Ньютона mi ai ( t ) = fi ( t ) (масса ´ускорение = сила). (2.16) Здесь f i (t)- сила, действующая в данный момент времени t на частицу iсо стороны всех остальных частиц системы (эта сила связана с потенциальной энергией известным соотношением f i (t) = -¶U/¶r i ); ускорение определяется как аi (t) = dv i (t)/dt или ai (t) = d2 r i /dt2 . Если эти производные заменить их конечно-разностными аналогами, то систему уравнений Ньютона, записанных для всех частиц, можно решить на компьютере. То есть, зная координаты частиц r (t) и отвечающие им силы f (t)в некоторый момент времени t, можно через небольшой промежуток времени Dt найти новые координаты r (t+Dt) и силы f (t+Dt) в следующий момент времени t+Dt и т.д., шаг за шагом. Очевидно, что скорости оцениваются как v » [r(t+Dt)-r(t)]/Dt. Вычисляя на каждом шаге интересующий нас параметр А можно проследить его эволюцию во времени, а усреднив по достаточно большому числу сделанных шагов s получаем искомые равновесные свойства. Такую схему расчета принято называть численным экспериментом динамического типа или просто методом молекулярной динамики (МД). Используются также различные вариации метода МД, в которых наряду с "внутренними" силами, обусловленными взаимодействием атомов друг с другом, включаются те или иные внешние силы. Подобные схемы моделирования составляют группу методов неравновесной молекулярной динамики. 2.2.3. Метод Монте-Карло (МК)Вычислительнуюсхему, в основе которой лежит альтернативный (вероятностный) принцип определения средних значения, называют методом статистических испытаний или методом Монте-Карло (МК). В этом методе переходы между состояниями системы осуществляются следующим образом. На каждом шаге случайным образом выбирается частица (или группа частиц) и перемещается на небольшое расстояние в случайном направлении. Это приводит к изменению потенциальной энергии системы на некоторую величину DU, которая и определяет вероятность перехода р ~ е- D U / kT из "старого" в "новое" состояние системы. Интересующие характеристики вычисляются на каждом шаге и усредняются по большому числу сделанных шагов. 2.2.4. Особенности компьютерного экспериментаВ обоих рассмотренных методах отсутствуют какие-либо физические упрощения. Эти методы основываются на общих принципах классической физики и, в сущности, представляют собой лишь математическую (численную) реализацию соответствующих фундаментальных подходов к определению макроскопических характеристик системы исходя из заданных микроскопических законов взаимодействия частиц. В определенном смысле компьютерную программу, по которой ведутся расчеты методами МД или МК, можно рассматривать просто как некую "формулу" (хотя, возможно, и чрезвычайно громоздкую). По этой формуле шаг за шагом (то есть оператор за оператором) отслеживается вся логическая цепочка переходов от исходных соотношений, составляющих базис современного естествознания, к конечному результату. Поэтому если в программе нет ошибок и предусмотрен надлежащий контроль статистических погрешностей (неизбежных при машинных вычислениях), то полученные результаты будут строгими, то есть имеющими силу аксиомы для выбранной математической модели физической системы. Компьютерная имитация методами молекулярной динамики или Монте-Карло модели физической системы с целью изучения ее характеристик в зависимости от заданных параметров представляет собой численный (компьютерный) эксперимент с этой моделью Как уже упоминалось, что число частиц при моделировании методами Монте-Карло и молекулярной динамики с помощью современных суперкомпьютеров может достигать колоссальных величин. Даже без суперкомпьютеров достаточно типичны численные эксперименты для значений N порядка десятков и сотен тысяч. Примеры успешного применения методов Монте-Карло и молекулярной динамики для моделирования равновесных составов смесей при постоянном давлении, фазовых равновесий, адсорбции на поверхности твердых тел, свойств жидкостей в микропорах и т.д. достаточно многочисленны. Этими же методами решаются задачи поиска устойчивых конформаций (поворотных изомеров) полимерных молекул, чрезвычайно важные для биохимических приложений.[12,13] N,V, U(r1 , r2 , ...,rn )
N, V, TN, V, E
движений F = ma
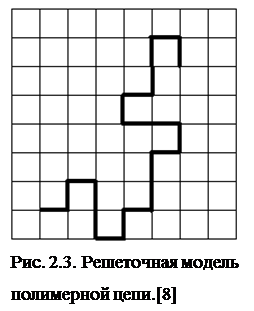
Равновесные свойства Равновесные и неравновесные свойства РИС. 2.2. Схема расчетов методами Монте-Карло и молекулярной динамики. 2.2.5. Решёточные и континуальные моделиНа основе решёточной модели выполнено множество теоретических построений, в частности связанных с решением классической и, в каком то смысле, основной задачи физикохимии полимеров о влиянии объемных взаимодействий на конформацию и, соответственно, на свойства гибкой полимерной цепи. Под объемными взаимодействиями обычно подразумевают короткодействующие силы отталкивания, которые возникают между удаленными вдоль по цепи звеньями, когда они сближаются в пространстве за счет случайных изгибов макромолекулы [14,15]. В решеточной модели реальную цепь рассматривают как ломаную траекторию, которая проходит через узлы правильной решетки заданного типа: кубической, тетраэдрической и др. Занятые узлы решетки соответствуют полимерным звеньям (мономерам), а соединяющие их отрезки - химическим связям в скелете макромолекулы. Запрет самопересечений траектории (или, иными словами, невозможность одновременного попадания двух и более мономеров в один решеточный узел) моделирует объемные взаимодействия (Рис. 2.3.). В методе МК при смещении случайно выбранного звена оно попадает в уже занятый узел, то такая новая конформация отбрасывается и уже не учитывается в вычислении интересующих параметров системы. Различные расположения цепи на решетке соответствуют конформациям полимерной цепи. По ним и проводится усреднение требуемых характеристик, например расстояния между концами цепи R. Исследование такой модели позволяет понять, как объемные взаимодействия влияют на зависимость среднеквадратичной величины <R2 > от числа звеньев в цепи N. Конечно величина <R2 >, определяющая средние размеры полимерного клубка, играет основную роль в разных теоретических построениях и может быть измерена на опыте; однако до сих пор не существует точной аналитической формулы для расчета зависимости <R2 > от N при наличии объемных взаимодействий. Можно также ввести дополнительно энергию притяжения между теми парами звеньев, которые попали в соседствующие узлы решетки. Варьируя эту энергию в компьютерном эксперименте, удается, в частности, исследовать интересное явление, называемое переходом "клубок — глобула", когда за счет сил внутримолекулярного притяжения развернутый полимерный клубок сжимается и превращается в компактную структуру - глобулу, напоминающую жидкую микроскопическую каплю. Понимание деталей такого перехода важно для развития наиболее общих представлений о ходе биологической эволюции, приведшей к возникновению глобулярных белков [16]. Существуют различные модификации решеточных моделей, например, такие, в которых длины связей между звеньями не имеют фиксированных значений, но способны меняться в определенном интервале, гарантирующем лишь запрет самопересечений цепи именно так устроена широко распространенная модель с "флуктуирующими связями". Однако все решеточные модели объединяет то, что они являются дискретными, то есть число возможных конформаций такой системы всегда конечно (хотя и может составлять астрономическую величину даже при сравнительно небольшом количестве звеньев в цепи). Все дискретные модели обладают очень высокой вычислительной эффективностью, но, как правило, могут исследоваться только методом Монте-Карло.
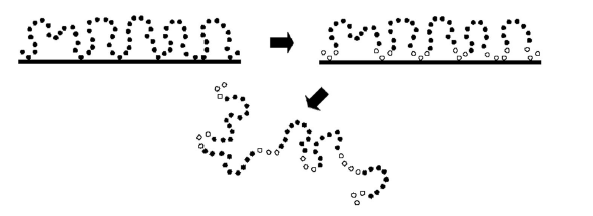
Для ряда случаев используются континуальные обобщенные модели полимеров, которые способны менять конформацию непрерывным образом. Простейший пример - цепь, составленная из заданного числа N твердых шаров, последовательно соединенных жесткими или упругими связями. Такие системы могут исследоваться как методом Монте-Карло, так и методом молекулярной динамики. 2.2.6. Трудности машинного эксперимента. Периодические граничные условияЛюбой современный компьютер способен оперировать таким количеством частиц N, которое обычно неизмеримо меньше, чем в реальных макроскопических системах, где Nимеет порядок числа Авогадро (~1023 ). Пределом технических возможностей наиболее мощных ЭВМ являются совокупности из N~106 -107 частиц. Поэтому если речь идет не о замкнутых микрообъемах вещества (например, микрокаплях, то есть кластерах) или об отдельных полимерных молекулах, то необходимо решение вопроса о том, как исходя из моделирования совокупности сравнительно малого числа частиц, интерпретировать свойства макросистемы. Такая проблема решается с помощью специального технического приема, суть которого состоит в том, что из макроскопического объема вещества мысленно вырезается небольшой объем, называемый расчетной (или базовой) ячейкой, а затем отслеживается поведение частиц только внутри этого выделенного объема. Базовую ячейку определяют как прямоугольный параллелепипед с ребрами длиной Lx , Ly , и Lz ,которые ориентированы по осям X, У и Zлабораторной системы координат. Объем ячейки V = Lx · Ly · Lz выбирается таким, чтобы среднечисленная плотность частиц p=N/V равнялась заданной макроскопической плотности. Основной вопрос при конструировании базовой ячейки связан с описанием поведения частиц вблизи ее границ. Нетрудно понять, что если сделать грани ячейки проницаемыми, то в ходе эволюции системы, движущиеся частицы со временем покинут первоначально занимаемый объем. Вместе с тем, в случае непроницаемых границ система, по сути, является малой и конечной, причем значительная доля частиц будет взаимодействовать со стенками (например, при N=1000 и ρ=1 вблизи стенок кубической ячейки размещено около 60% всех частиц). Поэтому для устранения поверхностных эффектов чаще всего используют так называемые тороидальные или периодические граничные условия (ПГУ). При таком описании противоположные грани ячейки объявляются тождественными. Иначе говоря, производится воображаемое попарное "склеивание" противоположных граней, в результате чего ячейка замыкается сама на себя и преобразуется в некую торообразную фигуру, у которой вовсе нет границ. Поясним суть этого приема на примере двумерной системы. Рассмотрим двумерную ячейку - квадрат, в которой находится единственная частица. Поскольку границы квадратной области проницаемы, то движущаяся частица рано или поздно выйдет за пределы выделенной области. Чтобы предотвратить это, преобразуем плоскую поверхность в цилиндр. Теперь частица, перемещаясь по внутренней поверхности цилиндра, может покинуть ячейку только через свободные торцы. Если теперь соединить противоположные торцы цилиндра друг другом и тем самым замкнем его в трехмерный тор. В результате частица оказывается заключенной в безграничном двумерном пространстве. Ту же процедуру мы можем мысленно проделать для исходной трехмерной кубической ячейки, свернув ее в четырехмерный тор. Любая частица, пересекающая при движении стенку базовой ячейки, входит обратно через ее противоположную грань. Тем самым сохраняется постоянной плотность системы. Кроме того, в динамических методах возвращающаяся частица имеет ту же самую скорость (импульс) что и уходящая (в итоге сохраняется кинетическая энергия). 2.2.7. Модернизированные методы компьютерного моделированияРазработаны также имитационные методы, сочетающие принципы динамического и вероятностного (стохастического) моделирования. Они предназначены для изучения влияния растворителя на конформацию и динамические свойства растворенной макромолекулы без явного учета малых молекул растворителя. Такой подход, основанный на численном решении диффузионных уравнений, позволяет расширить вычислительные возможности за счет резкого уменьшения общего числа атомов в системе. В этом случае сила, входящая в правую часть уравнений (2.16.), складывается из обычных потенциальных сил взаимодействия атомов рассматриваемой цепи, сил вязкого трения, пропорциональных скорости движения атомов в среде с заданной вязкостью, а также случайных сил, отражающих хаотичные толчки со стороны молекул среды. Соответствующие расчеты называют моделированием методом стохастической динамики (СД).[17] Поскольку плотная среда изменяет взаимодействие атомов по сравнению с их взаимодействием в вакууме, возникает вопрос о вычислении эффективных потенциалов, которые описывают такое влияние. В настоящее время эта непростая задача чаще всего решается с привлечением специальных представлений статистической теории жидкостей - метода интегральных уравнений. В таком комбинированном ("гибридном") подходе представляющая главный интерес подсистема - макромолекула - моделируется обычными методами, а влияние окружающих её малых молекул учитывается путем численного решения интегральных уравнений. На пути построения комбинированных вычислительных схем возможны и разного рода "логические инверсии": например, для выделенной (не слишком большой) молекулы можно проводить квантово-химические расчеты. а окружающую среду моделировать стандартными методами МД или МК. Таким образом, удается, в частности, исследовать химические реакции, протекающие в конденсированных средах. 2.3. Мотивы укладки цепи в белковых молекулахТретичная структура белка – это расположение всех атомов в пространстве. Для каждого белка третичная структура достаточно специфична и выявить общую тенденцию построения белковой молекулы достаточно сложно на этом уровне организации. Поэтому постараемся выяснить лишь общие моменты построения, то есть расположение отдельных частей белковой молекулы. В основном нас интересуют глобулярные белки. Это наиболее изученные молекулы, и когда говорят о строении белка, в основном подразумевают их. Рассмотрим некоторые особенности строения глобулярных белков. [18] 1. Глобулярные белки образуют достаточно компактную глобулу. Структура глобулы очень плотная и строго организована. В этом смысле белковая молекула очень похожа на кристалл. Так говоря словами Шрёдингера, белковая структура – это трёхмерный «апериодический кристалл». 2. Ядро белковой глобулы состоит из неполярных аминокислотных остатков. В образовании такой структуры большую роль играют гидрофобные взаимодействия. Они имеют энтропийную природу. Так при введении в воду неполярной группы происходит упорядочение молекул воды на поверхности раздела, что приводит к снижению энтропии системы. Обычно ядро образуют b - слои. При этом боковые группы аминокислот прячутся внутри, образуя «каплю масла». Преимущественное расположение вторичных структур внутри глобулы связано с возможностью образования водородных связей между аминокислотными остатками. Неупорядочным структурам цепи выгоднее находиться на поверхности, где аминокислотные остатки образуют водородные связи с водой. 3. Полярные и заряженные аминокислотные остатки преимущественно располагаются на поверхности белковой глобулы. Это объясняется во – первых резким повышением свободной энергии при введении заряда во внутрь глобулы (диэлектрическая постоянная белка на много меньше диэлектрической постоянной воды), 4. Во – вторых возможностью образованию связей с молекулами воды. 5. Это особенность связана с первичной структурой белковой цепи. Плотной и стабильной глобуле соответствует достаточно большое количество первичных структур. Конечно можно придумать первичные структуры, которым будут соответствовать очень стабильная структура ( стабильность выше, чем у других глобулярных структур), но их будет немного. То есть в природе заложена определённая вариативность первичной структуры. Важно, чтобы глобула была не только стабильной, но и ей соответствовало достаточное количество последовательностей цепи. Отметим ещё некоторые особенности денатурации белковой молекулы. Переход глобула - клубок описывается как фазовый переход первого рода, то есть сходен с плавлением кристалла. Это очень важный момент в физике белка. Так например клубок – глобула для гибкоцепных полимеров происходит плавно и описывается как фазовый переход второго рода. Подобное поведение белка говорит о кооперативности перехода. Это значит, что разрушение части белковой молекулы ведёт к разрушению остальных связей, поддерживающих нативную структуру. Поэтому такой переход осуществляется в небольшом температурном интервале. Это отражается в резком повышении свободной энергии при повышении температуры, а также в узком пике зависимости теплоёмкости от температуры. Затронем некоторые моменты строения мембранных белков. Эти белки встроены в мембрану клетки и выполняют функцию пропускания веществ через мембрану и могут участвовать в окислении органических веществ. Их включение в липидный бислой отражается в следующих мотивах строения. 1. Гидрофобные аминокислотные остатки расположены в середине белковой молекулы, подобно гамбургеру. То есть прослойка образована из неполярных остатков. 2. Гидрофильные и полярные остатки образуют полярные опушки с обеих сторон, взаимодействуя с полярной средой внутри и снаружи клетки. Такая особенность строения мембранных белков позволяет максимально эффективно удерживаться в мембране клетки. Понимание общих черт строения белков необходимо для создания адекватных моделей. Основные мотивы строения закладываются в математические модели и служат базой для построения структур белков. 2.4. Методы анализа белковых структурВ настоящее время не вызывает сомнения тот факт, что первичная структура белка определяет третичную. Поэтому возникает проблема предсказания пространственной структуры по аминокислотной последовательности. Основной метод – рентгенострруктурный анализ достаточно трудоёмок и поэтому с помощью него нельзя определить все пространственные структуры белка. Так при помощи этого метода определено всего несколько процентов пространственных структур белка. Поэтому для определения третичной структуры используют другие экспериментальные методы, а также мощный набор теоретических подходов. Рассмотрим некоторые математические подходы в решении этой задачи. 2.4.1. Определение гомологии первичных структурРазные программы по-разному оценивают, чего стоит совпадение остатков, чего — сходство, чего — несовпадение, чего — начало разрыва, чего — каждый дополнительный остаток в разрыве. Все эти оценки оптимизируются авторами так, чтобы удовлетворительно выделять белки, сходство которых уже известно из других данных, и потом "зашиваются" в программу. Поэтому конечный результат может варьироваться. При установлении структуры "нового" белка по его гомологии с уже изученным надо ясно отдавать себе отчет, что сходство пространственных структур может не распространяться на районы, где последовательности сильно разошлись. В основном это районы петель, нерегулярных конформаций белковой цепи. Здесь, с весьма переменным пока успехом, приходится прибегать к конформационным расчетам и другим методам гомологического моделирования. 2.4.2. Нахождение вторичной структурыЗная вклады отдельных взаимодействий в стабильность a-спирали, мы можем рассчитать свободную энергию спирализации любого участка цепи, а следовательно — и Больцмановскую вероятность образования спирали в любом месте полипептидной цепи, еще не свернувшейся в глобулу. Суммируя и усредняя эти вероятности, мы можем рассчитать и среднюю спиральность такого "несвернутого" полипептида. Потом результат можно сравнить с опытными данными — например, с КД спектрами. Переходя к расчету и предсказанию вторичной структуры белков, глобулярных белков, необходимо учесть, что здесь к взаимодействиям, существующим в несвернутых цепях, добавляется взаимодействие каждого участка цепи с глобулой, строения которой мы не знаем. Точнее, мы не знаем ее детального строения, но знаем, что участки цепи как-то примыкают к гидрофобному ядру белка. В простейшем приближении взаимодействие с ядром можно аппроксимировать взаимодействием с "гидрофобным озером", на котором плавает белковая цепь. Зная из опыта силу гидрофобных взаимодействий, а из стереохимии a- и b-структуры — мотивы чередования в цепи боковых групп, глядящих в одну и ту же сторону и способных, следовательно, одновременно взаимодействовать с гидрофобной поверхностью, — мы можем сосчитать вероятность образования a-спирали и b-структуры в каждом месте белковой цепи. В этом направлении достигнуты определённые результаты. Степень предсказания может достигать до 72%. 2.4.3.Метод протягиванияПредсказывая структуру белка, не имеющего видимой гомологии с белками уже расшифрованными, можно попробовать взять, одну за другой, все пространственные структуры из Банка, наложить (возможно, с некоторыми выпетливаниями) цепь этого белка на каждую из них, и посмотреть, какая из этих пространственных структур даст — для нашей цепи — наибольший энергетический выигрыш. При этом мы должны разрешать цепи то идти по скелету структуры, то выпетливаться или "сокращать" имеющиеся в скелете выпетливания — если это увеличивает энергетический выигрыш. Такой подход называют "методом протягивания" (threading method). Он был предложен Б.А.Ревой в 1990 г. и — независимо, в более простом и более удобном варианте — Д. Айзенбергом и его группой в 1991 г. Сейчас метод протягивания стал весьма популярным методом опознавания структур "новых" белков по их аналогии со "старыми". В общем, работа по протягиванию напоминает поиск гомологии, — только на этот раз "выравниваются" не две первичные структуры, "новая" и "старая", а "новая" первичная структура со "старым" белковым скелетом. Здесь возникают аналогичные проблемы, как в любом предсказательном методе. Во первых, конформацию даже тех кусков цепи, что наложены на скелет, мы знаем с большой погрешностью: ведь мы не знаем конформации боковых групп, — а именно они, в основном, и взаимодействуют. Далее, мы не знаем конформации всех выпетливаний. Оценка показывает, что при протягивании мы знаем примерно половину взаимодействий в белковой цепи, а вторую — не знаем. Значит, опять мы вынуждены судить о структуре белка по части взаимодействий, действующих в его цепи. Значит, опять наши предсказания могут носить только вероятный характер. Во-вторых, как перебрать все наложения и найти лучшие. Здесь приходит на помощь динамическое программирование и его вариант — статистическая механика одномерных систем (цепных молекул) — для расчета протягивания цепи через скелет; теория самосогласованного поля — для расчета действующего на цепь молекулярного поля в каждой точке скелета; стохастическая минимизация энергии методом Монте-Карло; а также — разные варианты метода ветвей и границ, и т.д. 2.4.4. Дизайн белковых молекулЗадача дизайна — обратная по отношению к задаче предсказания структуры. Если при предсказании мы должны найти пространственную структуру, наиболее пригодную для рассматриваемой последовательности — то при дизайне мы должны найти, сконструировать последовательность, годную для создания желаемой пространственной структуры. В этом подходе используют как экспериментальные методы, так и методы компьютерного моделирования. Олигонуклеотидный синтез и техника рекомбинантных ДНК дали возможность получения генов белков, не существовавших в природе; рентген и ЯМР позволили увидеть трехмерные структуры белков; а мощные ЭВМ и компьютерная графика позволили вступить в интерактивный диалог с этими пространственными структурами, — менять в них что-то и оценить последствия этих изменений. Остановимся на методах компьютерного моделирования и рассмотрим некоторые модели, используемые для создание первичной последовательности цепи. Можно сказать, что термин дизайн применим не только к белкам, но и к любым последовательностям, обладающих специфическими свойствами. 2.5. Конформационно-зависимый дизайн последовательностей цепиВ этой главе рассмотрим НР - сополимеры, то есть полимеры состоящие из двух типов звеньев, и компьютерную реализацию дизайна различных моделей. 2.5.1. НР – сополимеры, «приспособленные к адсорбции»Такие сополимеры получают по следующей схеме. Гомополимерную цепь, состоящую из звеньев Н, адсорбируем на плоской поверхности. Для этого вводится сильное притяжение между звеньями цепи и поверхностью. Затем звенья, лежащие ближе к поверхности, обозначаем как Н, другие звенья как Р. В компьютерном эксперименте это значит, что eН >eР . Таким образом, звенья Н считаются лиофобными, то есть избегают взаимодействия с растворителем, а звенья Р лиофильными. [19] На рис. 2.4 проиллюстрирована схема получения таких сополимеров.
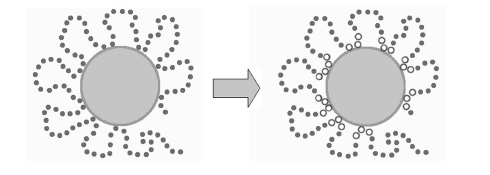
Рис. 2.4. Получение первичной структуры НР -сополимера, «приспособленного к адсорбции».[19] Если говорить о реальном эксперименте, то модифицирование звеньев цепи происходит на каталитической поверхности. Таким образом, можно видеть основную идею молекулярного дизайна. Сначала мы получаем пространственную структуру адсорбированного сополимера, а затем исследуем свойства полученной цепи. Поведение такой структуры сравнивали со случайными и случайно-блочными последовательностями. Оказалось, что число адсорбированных звеньев у таких сополимеров гораздо выше. То есть такие последовательности сохраняют «память» о своей адсорбированности. Таким образом, процесс адсорбции протекает более полно. 2.5.2. Молекулярные диспергаторыПодобную схему можно применить для получения другого класса сополимеров. На рис. 2.5. показана схема получения.
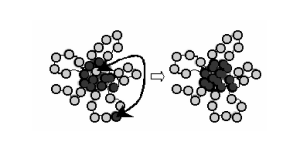
Рис. 2.5. Получение «молекулярных диспергаторов». [19] Такие сополимеры, приспособленные к адсорбции на коллоидных частицах или маленьких органических молекулах, обладают следующей спецификой. Такие структуры чувствительны к размеру частицы, то есть проявляют определённую селективность. При адсорбции сополимера происходит стабилизирование частицы лиофильными петлями цепи. Это препятствует слипанию коллоидных частиц. 2.5.3. Моделирование мембранных белков Рассмотрим получение модели НР – сополимера, имитирующей мембранные белки. В этом случае неполярную прослойку обозначим как Н-звенья, а полярные опушки как Р. На долю Н – звеньев приходится 30 %, а на долю Р – 70%. Введём различные энергетические параметры (eРР , eНР , eРР ). При этом eНН >eРР . При моделировании происходит диффузия Н и Р звеньев. Поэтому для улучшения структуры процедуру модифицирования производят много раз. [20]
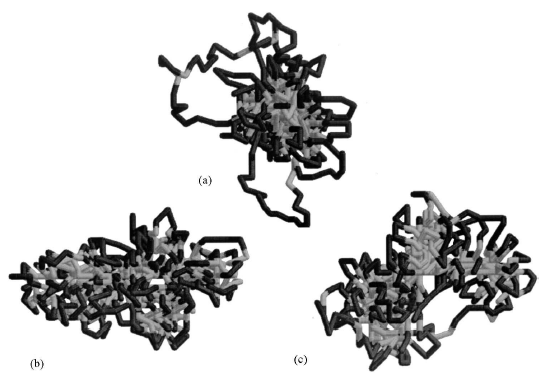
Рис. 2.6. Нативная конформация мембранного белковоподобного сополимера (слева) и конформация, полученная после равновесия в компьютерном моделировании (справа);N = 256.[20] Из рис. 2.6. можно видеть главную особенность таких структур – эффект стабильности микросегрегированной структуры. Таким образом, можно сказать, что подобная модель «наследует» свойства мембранных мелков. 2.7. Белковоподобные сополимеры. Дизайн, структура, свойстваИзучение структур НР сополимеров, состоящих из двух типов звеньев Н и Р, представляет достаточно большую область полимерной физики. Наиболее интенсивно изучаются блок-сополимеры и случайные сополимеры. Иногда исследуют сополимеры с близкодействующими корреляциями вдоль цепи. Такие корреляции всегда появляются после процесса полимеризации, если вероятность присоединения Н или Р звена к растущей цепи зависит от типа звена, которое присоединилось на предыдущем шаге. Тип подобной первичной структуры можно охарактеризовать как "случайная с близкодействующими корреляциями". С другой стороны глобулярные белки можно грубо считать как разновидность НР сополимеров. В самом деле, мономерные звенья этих белков различаются тем, что одни аминокислотные остатки являются гидрофильными или заряженными, в то время как другие гидрофобными. Мы можем очень грубо приписать первым из них индекс Р, и индекс Н остальным. Если проанализировать первичную структуру белковоподобного сополимера, полученного таким образом, и сравнить с простой первичной структурой описанной выше, то можно сделать вывод, что белковая НР последовательность более информативна и специфична. Обычно считают, что в глобулярных белках гидрофильные Р звенья покрывают поверхность глобулы, делая её устойчивой к межмолекулярной агрегации, а гидрофобные звенья Н в основном формируют ядро глобулы. Можно считать, что такое требование является достаточно ограничивающим, то есть справедливо только для малой доли всех возможных первичных структур. Следовательно, А/В корреляции, определённые в этом случае, зависят от конформации глобулы в целом , и их следует характеризовать как дальнодействующие. Вопрос состоит в том, могут ли быть получены такие первичные структуры НР сополимеров, не имеющих биологическое происхождение. Это легко сделать при помощи компьютерного моделирования, и гораздо труднее в реальном эксперименте. Однако, в обоих случаях соответствующие процедуры включают следующие шаги: Шаг 1. Берётся гомополимерный клубок с взаимодействиями с исключённым объёмом в хорошем растворителе. Шаг 2. За счёт сильных взаимодействий между всеми мономерными звеньями образуется гомополимерная глобула. В реальном эксперименте в этом случае подразумевается скачок температуры, добавление плохого растворителя и т.д. Шаг 3. Этот шаг легче всего реализовать в компьютерном эксперименте. Следует рассмотреть "мгновенное фото" и модифицировать поверхность, т.е. приписать индекс Р звеньям, находящимся на поверхности, и индекс Н – звеньям, образующим ядро. В реальном эксперименте поверхность модифицируется химическим реагентом, который изменяет её из гидрофобной в гидрофильную. Если количество реагента мало, то модифицируется только поверхность, а ядро остаётся гидрофобным. Важной особенностью является достаточно быстрая модификация поверхности и достаточно медленная агрегация. Шаг 4. Этот последний шаг необходим в компьютерном эксперименте. Вместо сильных одинаковых взаимодействий между звеньями, следует ввести различные потенциалы взаимодействия для Н и Р звеньев.
Рис. 2.7. Основные этапы схемы дизайна белковоподобных сополимеров. а) гомополимерная глобула b) глобула с модифицированной поверхностью c) белковоподобный сополимер в состоянии клубка. В статье [3] представлены результаты компьютерного моделирования методом Монте Карло перехода клубок-глобула, который происходит при увеличении притяжения между гидрофобными звеньями В. Было показано, что по сравнению со случайными сополимерами с тем же А/В составом поведение белковоподобных сополимров значительно отличается. Также анализировались особенности первичной структуры. В эксперименте используется цепь из N звеньев, состоящая из мономеров типа Н и Р (N = NН +NР ), которые занимают ячейки в кубической решётке. Молекулы растворителя представлены как вакантные ячейки. Для моделирования используется стандартная модель с флуктуирующими связями. В этой модели считается, что каждое мономерное звено цепи занимает восемь соседних ячеек кубической решётки и длина связи может флуктуировать от 2 до Ö10. Каждая конфигурация цепи характеризуется определённой энергией короткодействующих взаимодействий U, которые определяются следующим образом. Во-первых, эффект исключённого объёма заключается в том, что если два мономерных звена занимают одну и ту же ячейку, то потенциальная энергия приравнивается бесконечности. Во-вторых, пусть na b - это общее число контактов между ближайшими соседними звеньями Н и Р или между мономерными звеньями и частицами растворителя S. Таким образом, U = åa b ea b na b , где ea b - соответствующий энергетический параметр. Ясно такими параметрами, определяющие глобулярную организацию являются eРР , eНН , eР S , eН S , eНР . . В этой модели eРР = eНР = 0, также eР S < 0, eН S > 0, eНН < 0. Параметры eНН и eН S описывают гидрофобные взаимодействия между неполярными звеньями В и частицами полярного растворителя. Поэтому eBB nBB + eBS nBS – вклад гидрофобных взаимодействий в общую энергию системы. Таким образом общая энергия системы U = eBB nBB + eBS nBS + eAS nAS . Так как физическая природа взаимодействий сходна, то |eР S | = |eН S | = |eНН |. Однако интенсивность этих взаимодействий различна. Это обусловлено тем, что максимальное число Н-Н контактов между соседними мономерами равно 26, в то время как максимальное число контактов между Н и Р звеньями с вакантными ячейками растворителя S равно 98. Поэтому вводим нормализующий фактор равный 26/98. В конце концов считали, eР S = -1, eН S = 1, eНН = -1 и определяли температуру как главный параметр системы. Время t выражено в шагах Монте Карло на мономерное звено. Расмотрим следующие три модели цепи сополимера. 1. Соответствующая схема получения белковоподобных сополимеров включает следующие шаги. Берётся полимерный клубок и вводятся сильные взаимодействия между всеми звеньями цепи, в результате чего образуется гомополимерная глобула. Температура Т =1. NР = N/2 звеньям, которые имеют максимальное число контактов с частицами растворителя, приписывается индекс Р (гидрофильные). Остальным NН =N/2 звеньям, которые формируют ядро, приписывается индекс В (гидрофобные). Полученную первичную структуру можно охарактеризовать средними длинами непрерывных гидрофильных и гидрофобных участков (LР и LН ) , а также специфическим распределением Р и Н звеньев вдоль цепи. Для получения гетерополимерной глобулы при данной температуре требуется (2-3)´106 шагов Монте Карло, после чего в течении 4´106 шагов рассчитываются средние характеристики. Такая схема дизайна многократно повторяется. В эксперименте главный параметр – средняя длина Н блоков (L). 2. Цепь со случайным распределением Р и Н звеньев вдоль цепи характеризуется как случайная. В этом случае NР = NН и LР = LН = 2. Начальное конфигурация системы – гомополимерная глобула, которая при данной температуре приходит к равновесию после (2-3)´106 шагов Монте Карло. 3. Первичная структура случайно блочного сополимера характеризуется Пуасоновским распределением f(x) = e- l /x!, (x =0, 1, ..., l>0), где l = L. Также NР = NН = N/2. Начальное состояние системы – гомополимерная глобула. После наступления равновесия в течении 4´106 шагов рассчитывались характеристики системы. Все результаты представлены для достаточно длинной цепи, состоящая из Т = 512 звеньев. Таким образом, для гетерополимера NН = NР = 256. В приложении 1 представлены типичные распределения Р и Н звеньев вдоль цепи для белковоподобных, случайных и случайноблочных сополимеров. При сравнении первичных структур случайных и белковоподобных сополимеров можно видеть, средняя длина Р и Н блоков у протеиноподобных больше. С другой стороны, случайноблочные соплимеры, имеющие ту же среднюю длину Р и Н блоков как у белковоподобных, имеют другое распределение этих блоков вдоль цепи. Главная особенность белковоподобных сополимеров – это наличие в первичной структуре достаточно длинных однородных Р и Н последовательностей. Таким образом, первичную структуру этих полимеров можно охарактеризовать как ²случайная с дальнодействующими корреляциями. Сравним особенности перехода клубок-глобула для протеиноподобных сополимеров по сравнению с со случайными, имеющие тот же А/В состав. Во время счёта вычислялись средняя удельная энергия <U/N>, а также средний размер агрегата глобулярного ядра <m>. В приложении 2 представлены зависимости <U/N> и <m> от температуры для трёх типов сополимеров. В приложении 3 представлены производные по температуре d<U/N>/dT и d<m>/dT , полученные численным дифференцированием соответствующих кривых, представленных в приложении 2. Следует отметить, что производная d<U/N>/dT представляет собой удельную теплоту на одно мономерное звено и характеризует флуктуации внутренней энергии U в состоянии равновесия. Во всех случаях можно наблюдать переход из глобулярного состояния в клубок в небольшом температурном интервале, кривая d<m>/dT от Т имеет ярко выраженный пик. Однако можно видеть, что переход клубок-глобула для белковоподобных сополимеров находится при более высокой температуре и более резкий, чем для случайных и случайноблочных сополимеров. Таким образом можно сделать вывод, что специфическая первичная структура, которую протеиноподобные сополимеры ²наследуют² от глобулярных белков, отражается в сдвиге перехода кубок-глобула в сторону больших температур и делает глобулу более стабильной по сравнению с глобулами, образованными случайными сополимерами. Рассмотрим морфологию гетерополимерных глобул. В приложении 4 представлены типичные мгновенные фотографии глобулярных структур, полученные для трёх типов сополимеров при низкой температуре Т = 1.5 при состоянии равновесия. Можно видеть, что глобулы белковоподобных сополимеров имеют специфичную мицеллоподобную структуру, состоящую из плотного ядра из гидрофобных звеньев Н и длинных гидрофильных петель из гидрофильных звеньев Р. С другой стороны глобулы случайных сополимеров имеют большое рыхлое ядро и короткие поверхностные петли. Также изучалась кинетика перехода клубок-глобула. Было показано, что для белковоподобных сополимеров этот переход происходит быстрее, чем для случайных. 2.8. Оптимизация последовательностей белковоподобных сополимеров глобулярных белковОдин из методов получения белковоподобных сополимеров заключается в следующем. Начальная конфигурация – это гомополимерная глобула (Состоит из Н – звеньев). Затем выьирается несколько мономерных звеньев, имеющих наибольшее число контактов с растворителем, и им присваивается индекс Р ( eРР <eНН ). Следующий шаг заключается в релаксации полученной структуры. Затем модификации подвергаются следующие звенья. Такая процедура повторяется несколько раз. На рис. 2.8. можно видеть схематичное представление такой процедуры. Показано, что подобная схема дизайна более эффективна, чем процедура однократного модифицирования поверхности. Также следует сказать, что такая процедура дизайна наиболее близка к реальному процессу, чем другие схемы, так как происходит постепенное взаимодействие с реагентом в растворе и диффузия звеньев цепи в растворитель.
Рис. 2.8. Схематичное представление итеративной схемы дизайна.[19] Другая схема дизайна реализуется методом Монте Карло. Начальная структура – белковоподобный сополимер. Затем выбираются два звена разных типов и пытаемся поменять их. Согласно схеме Метрополиса, вероятность того, что такой обмен будет иметь место пропорционален ехр (DЕ/RT). После этого система релаксирует некоторое время. Такую схему повторяют много раз. Таким образом подбирается структура белковоподобного сополимера с наименьшей энергией. Рис. 2.9. Пробный шаг дизайна последовательности: выбираются два мономера различного типа и производится попытка поменять их тип. Вероятность обмена вычисляется согласно схеме Метраполиса. [19] 2.9. Дальнодействующие корреляции в белковоподобных сополимерахРассмотрим корреляции между Н и Р звеньями вдоль белковоподобных последовательностей, которые сконструированы по схеме показанной на рис. .В самом деле, белковоподобные последовательности не являются случайными, такие корреляции должны существовать и важно знать, как изучить их исходя из одномерной первичной последовательности, без моделирования складывания цепи. Было показано при помощи как компьютерного моделирования, так и точных аналитических вычислений, что такие корреляции действительно существуют и кроме того имеют дальнодействующий характер.[21] Более точно они принадлежат к так называемой статистике полёта Леви. Это значит, что эффект памяти нативной конформации выражается через специфичные и нетривиальные статистики первичных белковоподобных последовательностей. Анализ таких корреляций можно выполнить следующим образом. Нужно выбрать "окно" длинны L и двигать его вдоль сконструированной НР- последовательности. Число Н – звеньев в этом окне (hL )i является случайной переменной, зависящей от позиции i окна вдоль последовательности. Эта случайная переменная имеет определённое распределение. Её среднее <hL > определяется по всем по всей последовательности. Достаточно легко вычислить дисперсию этого распределения. [19] DL ~ < [( hL ) I - < hl >]2 >1/2 (2 .17) Для полностью случайной НР – последовательности значение DL имеет зависимость от ширины окна L как L1/2 . Зависимость DL ~ La , при a > ½ , явно показывает на существование дальнодействующих корреляций. В приложении 5 показана дисперсия DL для двух процедур модификации поверхности: ожнократное изменение поверхности и итеративный метод для N = 1024. Можно видеть , что для последовательности, полученной итеративным методом, кривая имеет больший угол наклона. Это означает, что дальнодействующие корреляции являются даже больше для этой последовательности, чем полученной первоначальным методом, описанным в статье [3]. Такое поведение DL может быть объяснено большей степенью блочности последовательностей, полученных при помощи итеративного алгоритма. В этом случае значение длины блока составляет примерно 10 звеньев, в то время как для не модифицированного первоначального метода она составляет около 8 звеньев. Можно легко понять такие изменения первичной структуры на количественном уровне: модифицированное мономерное звено становится более гидрофильным, поэтому существует тенденция к вытягиванию петель из глобулы. Это означает, что что следующие модификации будут более вероятно происходить в этой петле, что будет вести к увеличению длины блока. Сильные флуктуации величины DL при больших значениях L происходит из-за конечных размеров последовательностей. Самая верхняя кривая с тангенсом угла наклона равным 1 показывает поведение величины DL для максимально "неслучайной" последовательности (например для диблочного сополимера). 3. Экспериментальная часть3.1. Модель и метод моделированияГлобулярные белки можно грубо считать как разновидность НР- сополимеров. В самом деле, мономерные звенья этих белков различаются тем, что одни аминокислотные остатки являются гидрофильными или заряженными, в то время как другие гидрофобными. Мы можем очень грубо приписать первым из них индекс Р , и индекс Н остальным. Если проанализировать первичную структуру белково-подобного сополимера, полученного таким образом, и сравнить с простой первичной структурой описанной выше, то можно сделать вывод, что белковая НР последовательность более информативна и специфична. Обычно считают, что в глобулярных белках гидрофильные Р звенья покрывают поверхность глобулы, делая её устойчивой к межмолекулярной агрегации, а гидрофобные звенья Н в основном формируют ядро глобулы. Можно считать, что такое требование является достаточно ограничивающим, то есть справедливо только для малой доли всех возможных первичных структур. Следовательно, Р/Н корреляции, определённые в этом случае, зависят от конформации глобулы в целом и их следует характеризовать как дальнодействующие. Прежде всего, определим модель и алгоритм, используемый для моделирования эволюционного процесса. Мы рассмотрим модель сополимерной цепи, которая включает только два типа звеньев, Н (гидрофобные) и Р (гидрофильные или полярные). Для простоты зафиксируют НР состав последовательности как 1:1. Рассмотрим континуальную модель, противоположную широко используемой решёточной модели, так как динамика последней дискретна и релаксация плотной глобулы происходит достаточно медленно. Время эволюции системы определялись уравнениями Ньютона, которые решались при помощи метода молекулярной динамики (МД). Мономерные звенья, связанные упругими связями, образуют линейный НР сополимер длины N. Гамильтониан системы включает в себя только парные взаимодействия и имеет вид: N -1 N -2 N N Н = å Hb ( rij )+ å å [ Hev ( rij ) + Ha ( rij )] + 1/2 å pi 2 (3.1) i , j = i +1 i =1 j = i +2 i =1 где Hb – потенциал деформации связи, Hev принимает во внимание исключённый объём, Ha – характеризует энергию притяжения между мономерными звеньями, и i, j изменяются в диапазоне от 1 до N. Расстояние между звеньями определяется как rij = çri - rj ç, где ri обозначает расположение радиус-вектора звена в трёхмерном пространстве. Последнее значение в уравнении (3.1) – классическая кинетическая энергия цепи. Исключённый объём между всеми несвязанными звеньями моделировался при помощи отталкивающего Леннард-Джонсовского потенциала.
rij rij 4 Hev ( rij ) = (3.2) 0 , rij > r0 где s = e = 1 как для Н так и для Р мономерных звеньев и r0 = 21/6 s - расстояние «обрезки». Параметр e, входящий в уравнение контролирует шкалу энергии, тогда как s определяет расстояние на котором взаимодействуют мономерные звенья. Квазигармонический потенциал связанных звеньев цепи имеет вид:
rij rij Hb ( rij ) = (3.3)
b 0 b 0 где b0 и rij – равновесная и мгновенная длины связей соответственно. Это квазигармоническое уравнение с константами упругости Сb (1) и Cb (2) в гамильтониане (3.1) описывает взаимодействие связанных между собой звеньев. Мы использовали комбинированный потенциал вместо обычного квадратичного, так как использование простого гармонического потенциала увеличивает время достижения равновесия. Равновесная длина связи, как и другие величины длин, измерены в еденицах d,типичное значение для реальных полимеров составляет s» 5 А°. Присваиваем b0 = 1 и Cb (1) = Cb (2) = 1. Потенциал, описывающий притяжение между несвязанными мономерными звеньями имеет вид:
rij rc Ha ( rij ) = (3.4) 0, rij > rc Параметр ea b (=eНН, eРР, eНР ) устанавливают глубину минимума функции притяжения невалентно связанных звеньев от расстояния и rc = 2.8 – расстояние на котором «обрезают» потенциал, описывающий притяжение. В уравнении (3.4) параметр описывающий перекрёстные взаимодействия выбирается как: eНР = (eНН ´eРР )1/2 (энергия измерена в единицах kB T). В нашем эксперименте eРР – переменный энергетический параметр. При eНН = eРР = 2 фактически мы имеем гомополимерную глобулу, при этом образуется плотноупакованная конформация. При eНН = eРР = 0 не существует притяжения между звеньями. Для эффективного вычисления использовалась достаточно короткая цепь с N = 128. Предварительные результаты с N = 512 показали, что качественно большие системы сильно не отличаются. При моделировании системы не включали частицы растворителя. Чтобы сымитировать эффект растворителя и эволюцию системы в контакте с термостатом температуры T, в уравнение движения Ланжевена добавляют некоррелированный член. mi Fi = Fi – Г r + Ri , I = 1. 2, …, N(3.5) где mi = 1 – масса мономерного звена, Fi = -Ñri H (r) - (r) – постоянная сила действующая на звена i, R описывает случайные броуновские силы, действующие на каждое мономерное звено, Г – учитывает вязкость растворителя. Величины R и Г связаны между собой флуктационной-диссипативной теоремой, áRa i (0)´Ra i (t)ñ = 2Гi kB Td(t), a = x, y, z, и обеспечивает постоянство температуры. Заметим, что если Г включить в уравнение без члена R, то система просто диссипирует. Параметр Г зависит от площади доступной растворителю поверхности (SASA). Чтобы найти значение SASAдля данной конформации, производится аналитическое вычисление площади поверхности Ai для каждого заданного звена. Определив Ai можно найти Гi как Гi = Г0 Аi /Amax , где Amax – максимальное значение площади поверхности доступной растворителю мономера для изучаемой модели и стандартное значение Г0 принимается равным единице. Весовой коэффициент Ai /Amax показывает степень подверженности растворителю мономера i. Если значение SASA для данного мономера равно нулю, то броуновская сила и сила трения равны нулю и уравнение Ланжевена (3.5) редуцируется в уравнение движения Ньютона. Обычно это происходит, когда звено расположено в ядре глобулы. Наоборот, мономерное звено, находящееся на поверхности глобулы, сильно сольватировано. Это значит, что значение Ai становится близким к Amax , следовательно значение Гi становиться близким Г0 . Стандартная температура равна T = 1 e/kB . При интегрировании уравнения движения выбирается шаг интегрирования ∆t = sÖm/e , использовав численный алгоритм Верлета. 3.2.Модель молекулярной эволюцииПри моделировании эволюционного процесса используются следующий алгоритм:[22] 1. Чтобы сконструировать начальную конфигурацию (G = 0), нужно сгенерировать цепь (притяжение между мономерами отсутствует) со случайным распределением Н звеньев. Эта цепь является начальной для данного рассчёта. 2. Готовится набухший полимерный клубок, присваивая параметры eНН и eРР нулю. 3. Складывание цепи происходит при eНН = 2 и данном значении eРР . Эта конформация приходит к равновесию после 4´105 шагов интегрирования. 4. Одна половина звеньев, имеющих наибольшую площадь доступной растворителю (SASA) и одновременно удалённые от центра масс глобулярного ядра, модифицируются в тип Р, остальные звенья, имеющие меньшие значения SASA и находящиеся вблизи центра масс глобулярного ядра превращают в тип Н. Благодаря такому модифицированию последовательность мутирет и переходит в следующую генерацию G®G + 1. Состав последовательности строго определён, поэтому в цепи N/2 гидрофобных и N/2 гидрофильных звеньев. Чтобы вычислить статистические свойства данной последовательности, производят вычисление теоретико – информационные характеристик. 5. Чтобы вычислить термодинамические и структурные свойства, мы производили усреднение по большому числу шагов интегрирования, t2 = 4´105 . 6. Повторяем алгоритм по пунктам 2 – 5 для последней генерации. Это даёт класс глобулярных сополимеров с другой первичной НР структурой. В нашем исследовании шаги 2 –5 независимо повторяем 20 раз, начиная от различных случайных конформаций и тогда все результаты усредняются по этим расчетам, чтобы статистика была лучше. Каждую траекторию мы можем интерпретировать ряд последовательностей полученных по ходу эволюционного процесса, как различные ветви эволюции, получаемые от начльной конформации. Эти результаты могут быть важны для понимания основных возможностей эволюции последовательности. Существует два основных различия в методике между алгоритмом предложенным нами и который использовался в статьях [23-25]. Во первых, наша вычислительная схема основана на динамических принципах, в то время как в методе, описанном статьях [23-25], используется стохастическая динамика. Грубо говоря, алгоритм дизайна первичной структуры цепей отбирает те желаемые последовательности, чьи соответствующие конформации имеют наименьшую потенциальную энергию. Ясно, что такой подход позволяет оптимизировать энергию данной конформации,в то время как в нашем подходе энергия не является ограничивающим параметром и может в принципе увеличиваться. Конечно, следует помнить, что наша модель молекулярной эволюции включает стохастическую составляющую. Во вторых, каждый шаг процедуры, использующей метод Монте Карло, является попытка парной замены, заключающаяся в случайном выборе двух звеньев и обмене их между собой (модель «точечных мутаций»). Сущность процедуры модификации, используемой в нашем эксперименте, является химическая модификация всех звеньев, окружённых растворителем. В реальном эксперименте это можно произвести при помощи растворённого реагента. Подчеркнём, что даже единичное модифицирование поверхности глобулы может резко изменять одномерную первичную последовательность цепи. Поэтому число получаемых последовательностей строго ограничено, фактически составляя ничтожную часть всех возможных последовательностей. Таким образом, данный подход существенно отличается по своей сути, физической природе, и также по его экспериментальной осуществимости. Также следует помнить, что последовательности, полученные при помощи этого подхода, не являются уникальными и нативными. Так как при моделировании требуется существенное количество вычислении, наш анализ ограничивался только равновесными свойствами. В проведённом компьютерном эксперименте было обнаружено, что в области малых значениях параметра eр происходит вырождение глобулы и образование структуры типа ²головастик², который состоит из плотного ядра и длинного хвоста. Также возможно образование длинной петли или двух ²хвостов².Можно предположить, что на начальном этапе эволюции глобулы образуются длинные петли. Затем одна из длинных петель вырождается в длинный хвост.[26] На рис. 3.1. можно видеть типичную морфологии глобулы белково-подобного сополимера и структуру типа «головастик». Для количественного описания этого перехода было предложено ряд характеристик.
(а) (в) Рис. 3.1. (а) Мицелоподобная структура, (в) структура типа ²головастик². 3.3. Методы анализаРассмотрим поподробнее характеристики, которые были предложены для описания перехода «глобула – головастик». 1. Среднеквадратичный радиус инерции. Его можно рассчитать по формуле: <
R2
g
> =
N-1
где N – число частиц, r0 – радиус вектор центра масс, ri – радиус вектор i-й частицы Этот параметр характеризует размер макромолекулы. Косвенным образом может характеризовать форму молекулы. Часто используют для изучению перехода клубок - глобула. 2.Длины «хвостов» . Под «хвостом» понимают непрерывный участок Н или Р звеньев, который берёт начало с конца полимерной цепи. Так как в «головастике» длина хвоста достаточна велика, то вероятно это удачная характеристика для описания этого перехода. Однако, как будет показано в следующей главе, из-за недостаточного усреднения эта характеристика достаточно сильно флуктуирует. 3. Длины петель. Подобно длинам хвостов – это также непрерывный участок Н и Р звеньев, однако этот участок не имеет начало с конца полимерной молекулы. Так в первичной структуре можно выделить достаточное число петель, то усреднение будет лучше и характеристика меньше флуктуирует во времени. 4. Размер заархивированного файла характеристику можно объяснить следующим образом. Обозначим Н звенья как 0, а Р звенья - как 1. В результате первичную структуру сополимера можно представить как последовательность единиц и нулей. Такой цифровой код записывается в файл и подвергается архивированию. Размер заархивированного файла Lв , выраженным в байтах и характеризует первичную структуру, в частности, распределение в ней единиц и нулей. Мы использовали стандартный архиватор GZIP. Определение размера заархивированного файла показано на схеме в приложении 6. Эта характеристика удобна тем, что при вырождении глобулы в «головастик» значение её резко уменьшается. Это обусловлено увеличением длин петель и «хвостов». 5. Индекс Шеннона. ( I ) Индекс Шеннона (Shannon’sindex) вычисляется по формуле I
=
Nlog
2
N
-
где Ni - количество элементов сорта i, n - количество сортов элемента, N - общее количество элементов, Например в цепочке 10011111000000011110000001110111 имеется: блоков длиной 1 - 2 штуки (N1 =2) блоков длиной 2 - 1 штука (N2 =1) блоков длиной 3 - 2 штуки (N3 =2) блоков длиной 4 - 1 штука (N4 =1) блоков длиной 5 - 1 штука (N5 =1) блоков длиной 6 - 1 штука (N6 =1) блоков длиной 7 - 1 штука (N7 =1) всего блоков различной длины - 9 штук ( N=2+1+2+1+1+1+1=9), сортов блоков - 7 сортов (n=7) Индекс Шеннона равен: I = 9*log2 9 - (2*2*log2 2 + 7*1*log2 1 = 9*3.1699 - (2*2*1 + 7*1*0) = 24.5 Индекс Шеннона характеризует информационную энтропию. Индекс Шеннона, размер заархивированного файла и длины петель зависят друг от друга. На рис. 3.2. и 3.3 можно видеть, что в билогарифмических координатах эти зависимости можно апроксимировать прямой. |
 e0
b12
_ 2
b6
+1
при r > b
e0
b12
_ 2
b6
+1
при r > b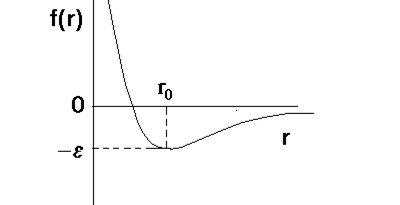
 f
(
r
) = 4
e
[(
s
/
r
)12
– (
s
/
r
)6
]
при r < 21/6
s
f
(
r
) = 4
e
[(
s
/
r
)12
– (
s
/
r
)6
]
при r < 21/6
s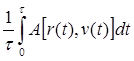 (2.14)
(2.14)