Введение
Все твердые тела в той или иной степени воспринимают воздействие внешних сил без разрушения и существенного изменения геометрических размеров и формы, то есть обладают свойствами прочности и жесткости. Сопротивление материалов – это наука о прочности, жесткости и устойчивости тел. Сопротивление материалов ставит своей целью создание инженерных методов расчетов типовых элементов конструкции. Методами сопротивления материалов выдуться практические расчеты по определению оптимальных размеров элементов конструкции. Методы сопротивления материалов опираются на законы теоретической механики и в особенности на законы статики.
Реферат
В данной курсовой работе производится расчет элементов статически неопределенных и статически определенных систем на прочность жесткость и устойчивость. Курсовая работа содержит 22 листа, 10 рисунков. Курсовая работа содержит расчеты при таких видах деформации, как растяжение, изгиб и сжатие, для каждого из вида деформаций построена соответствующая эпюра. В точках расчетов произведены выводы об удовлетворении конструкциями условиям прочности, жесткости и устойчивости.
Содержание
Реферат……………………………………………………………………..………….3 Введение………………….……………………………………………………………..4 1. РПР № 1.1.…………………………………………………………………………..5 2. РПР № 1.2.…………………………………………………………………………..9 3. РПР № 2.1…………………………………………………………………………..14 4. РПР № 3.1…………………………………………………………………………..16 5. РПР № 3.2…………………………………………………………………………..19 6. РПР № 3.3 ………………………………………………………………………….21 Список используемой литературы……………………………………………….24
РПР № 1.1
Дано: Р1=5 кН; Р2=-1 кН; Р3=-10 кН; 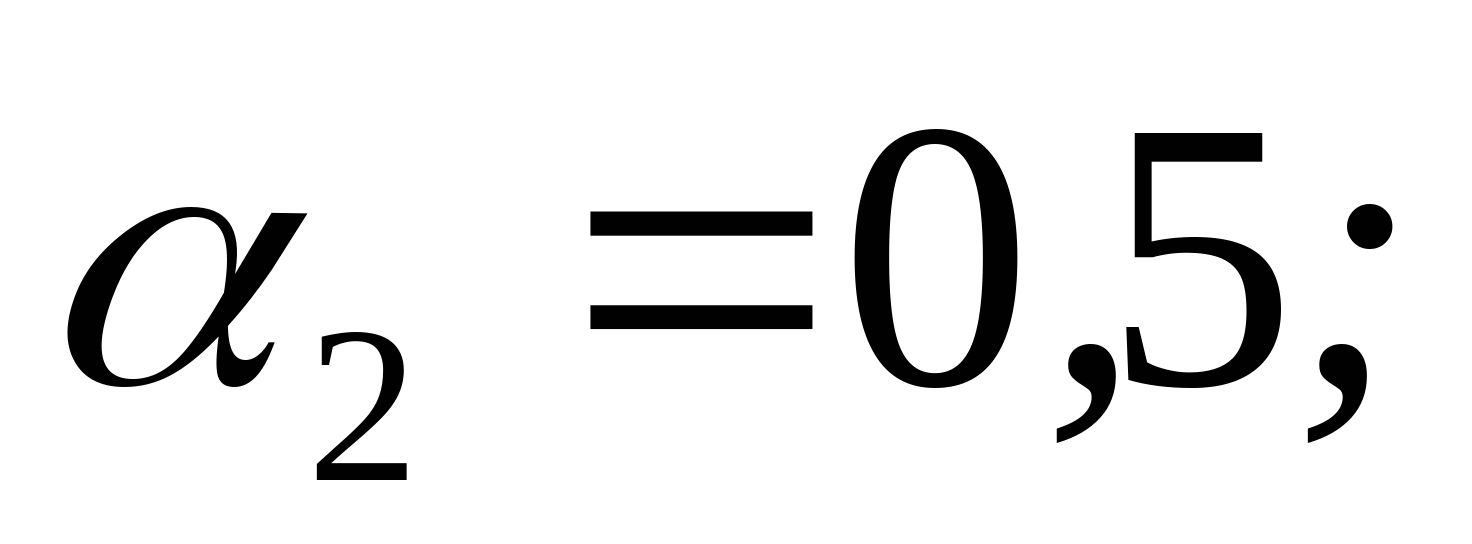 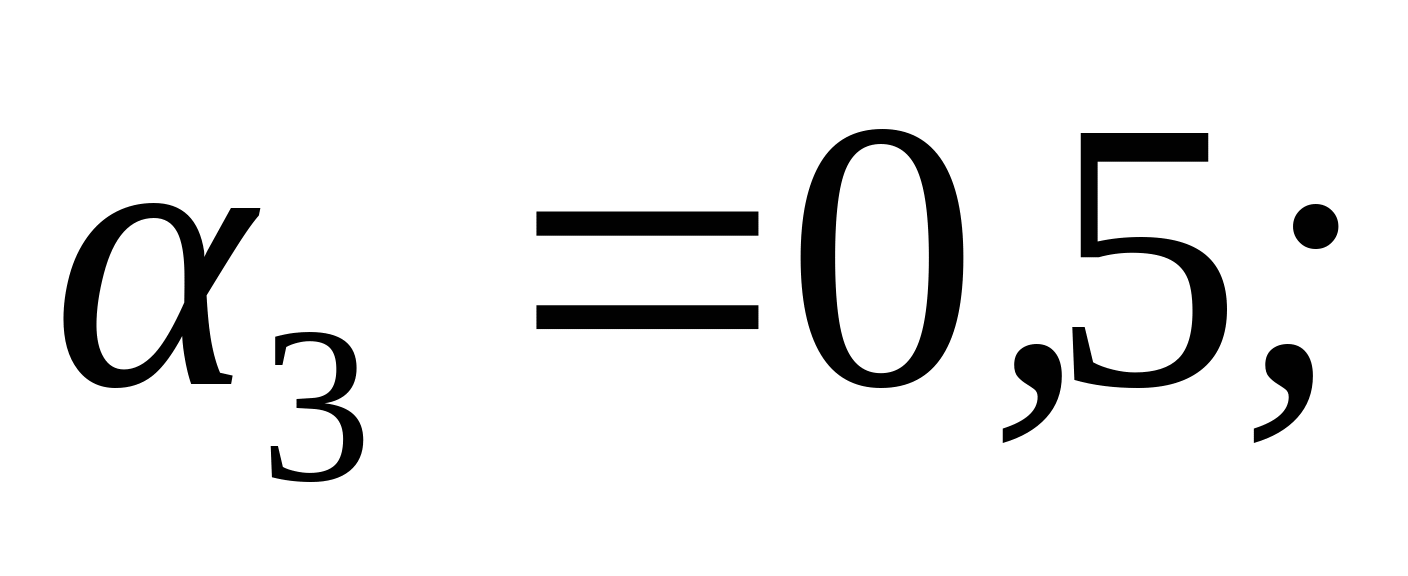 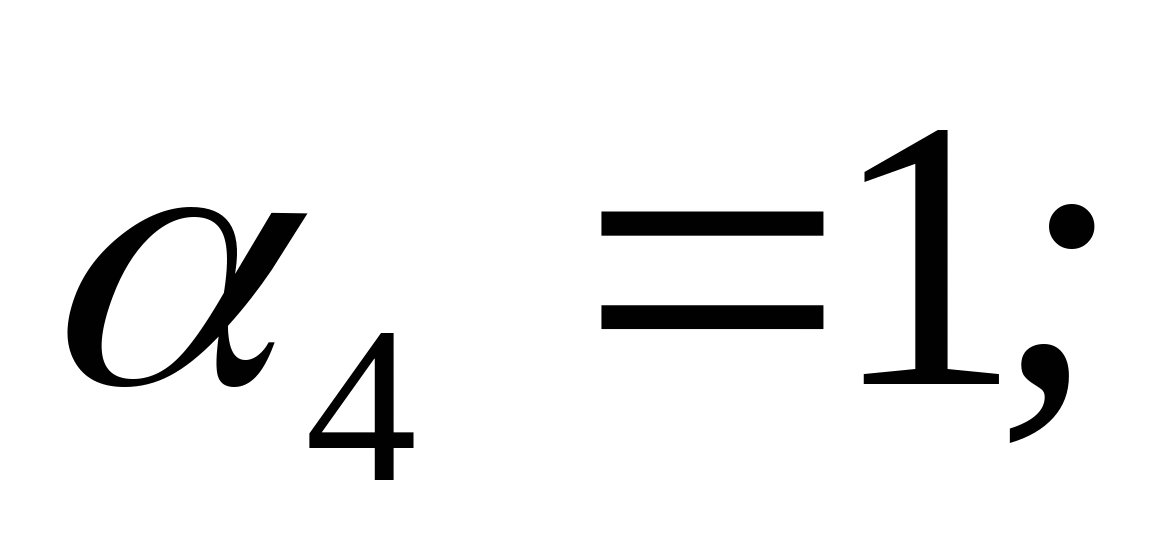 l1=0,6 м; l2=0,3 м; l3=0,6 м; l4=0,3 м l1=0,6 м; l2=0,3 м; l3=0,6 м; l4=0,3 м Сплав: Al13;  =0,7 =0,7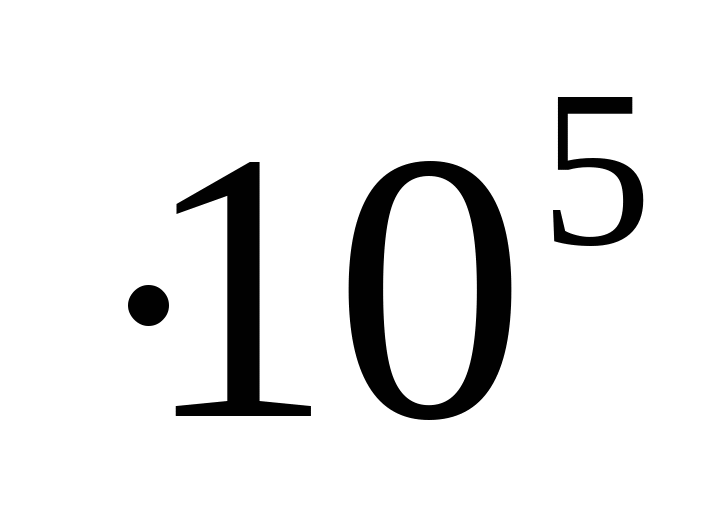 МПа; МПа; 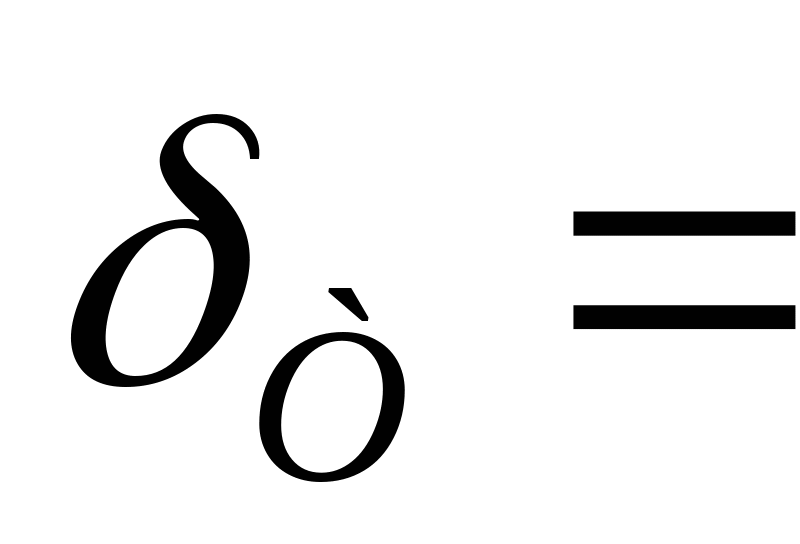 90 МПа; nT=1,5; 90 МПа; nT=1,5; 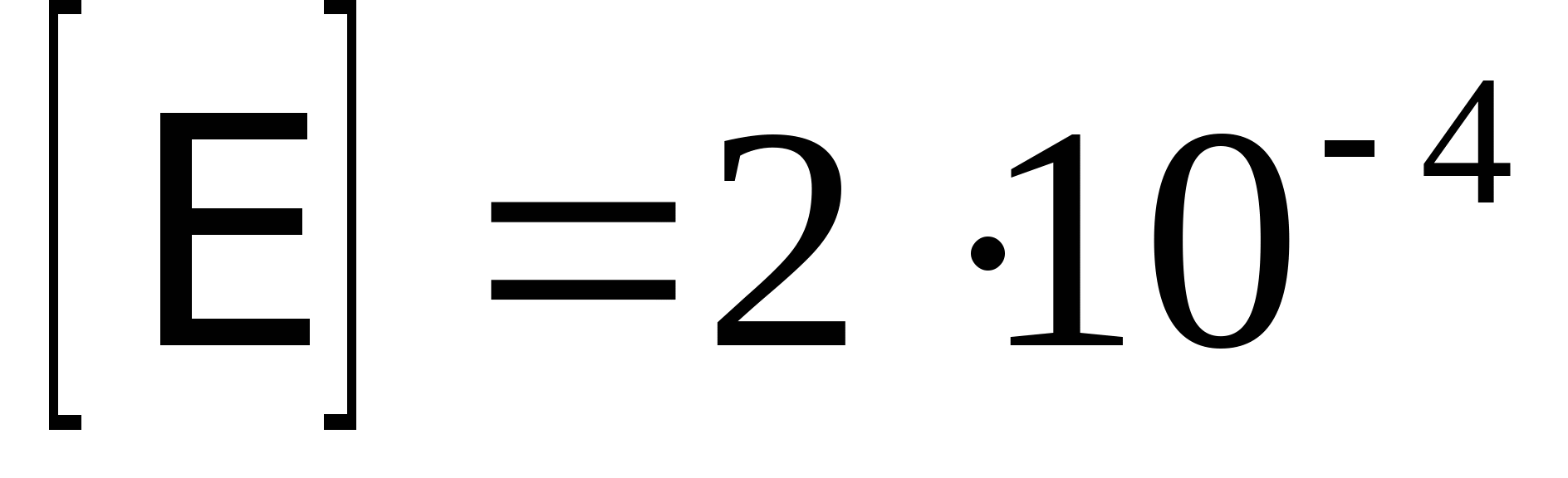
Решение: 1. Составим уравнение статики: 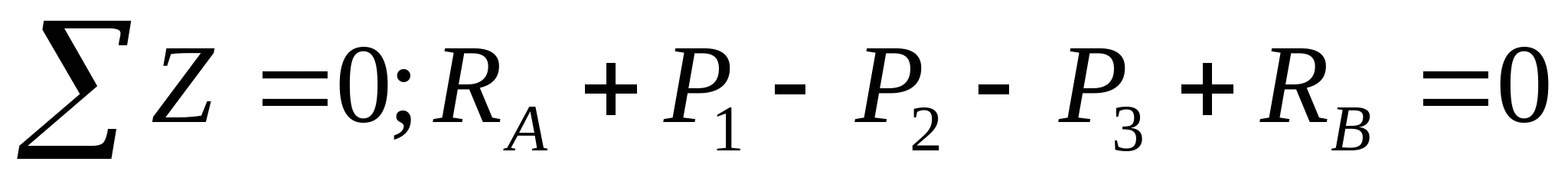 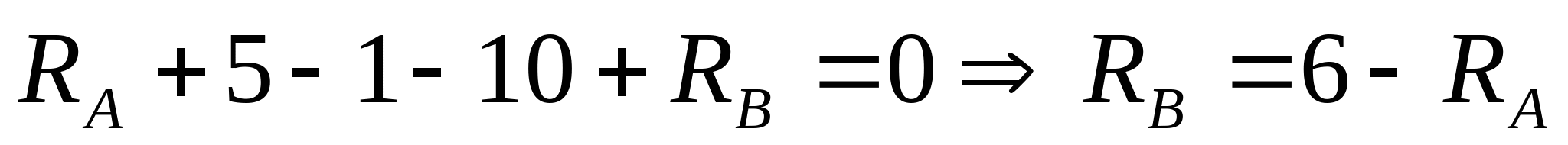 Степень статической неопределимости: n=2-1;
2. Отбросив опору А, строим схему перемещения: Уравнение совместимости деформации и перемещения: 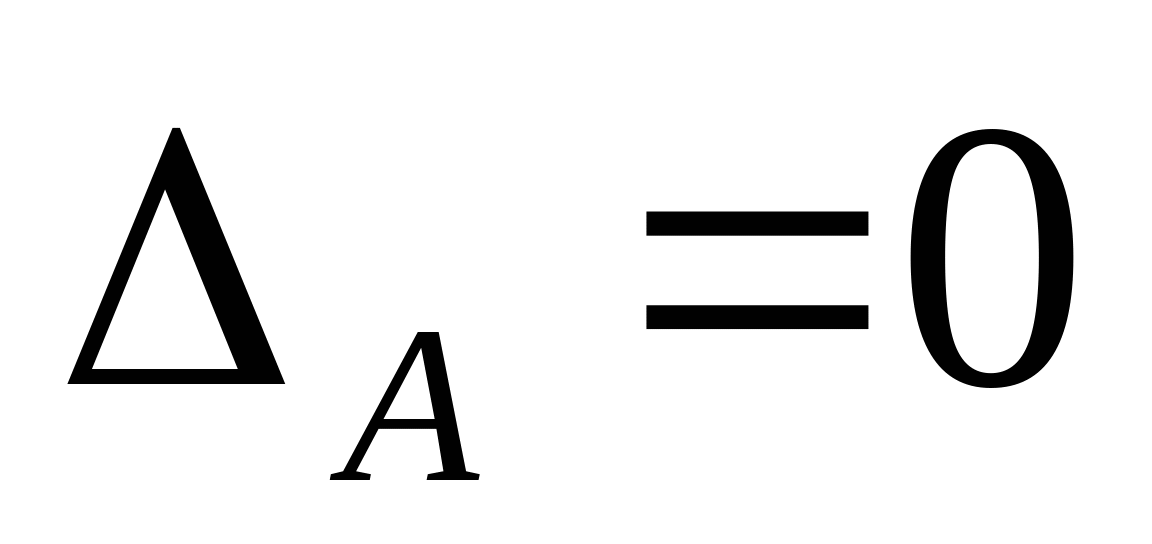 или или 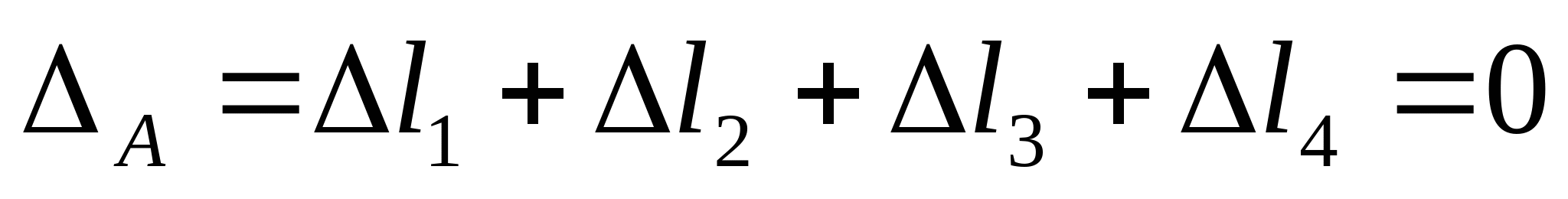 (2) (2) 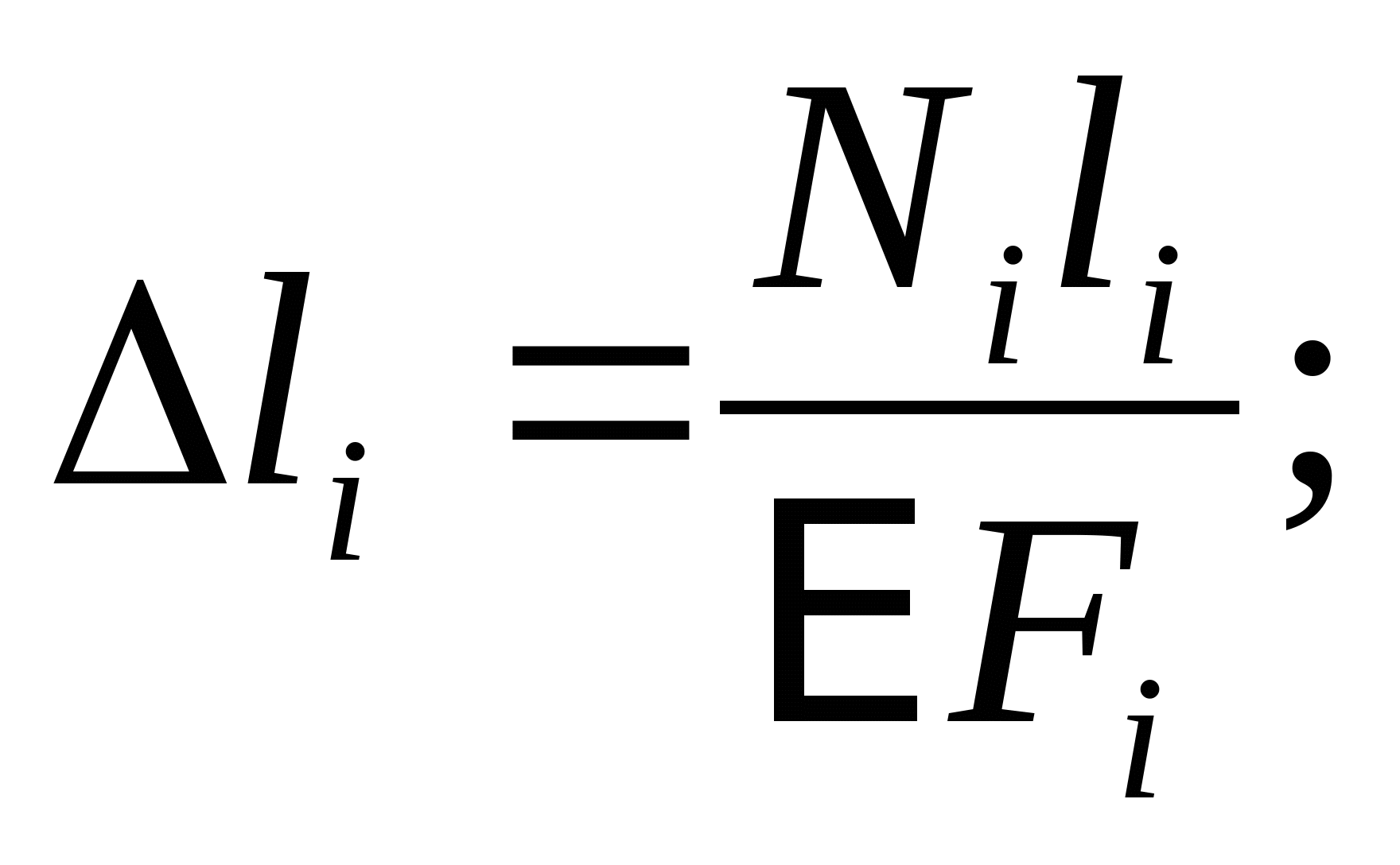 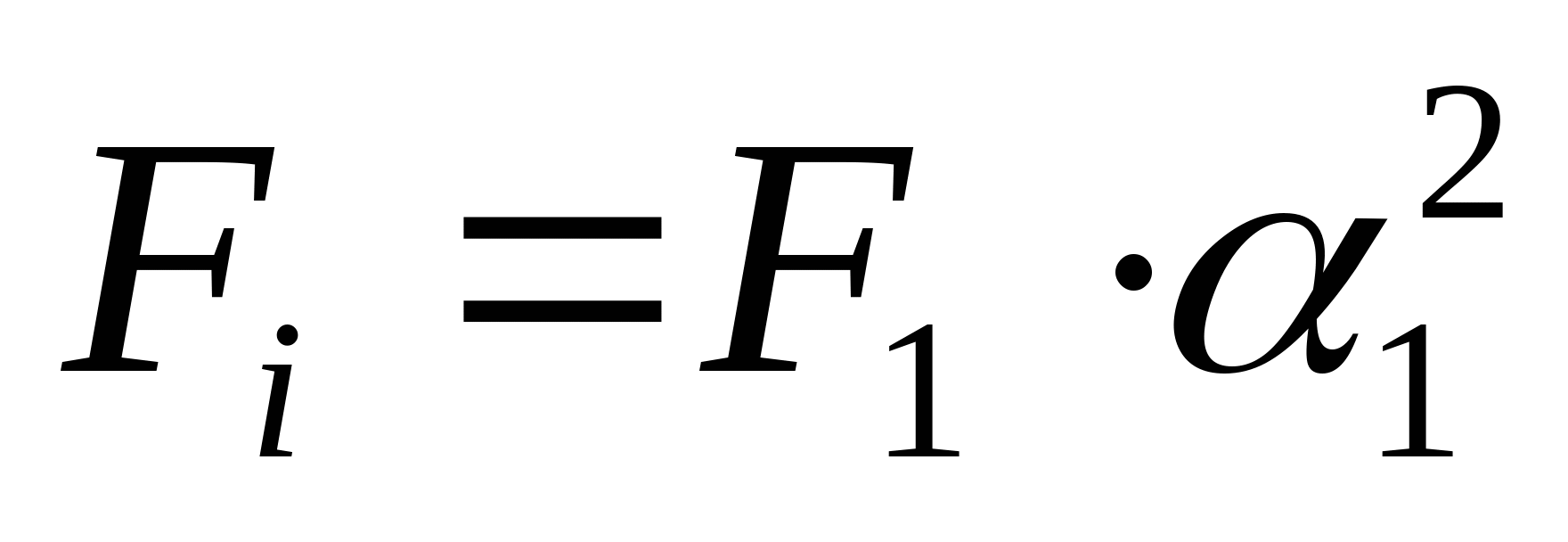 Выразим продольные силы N: 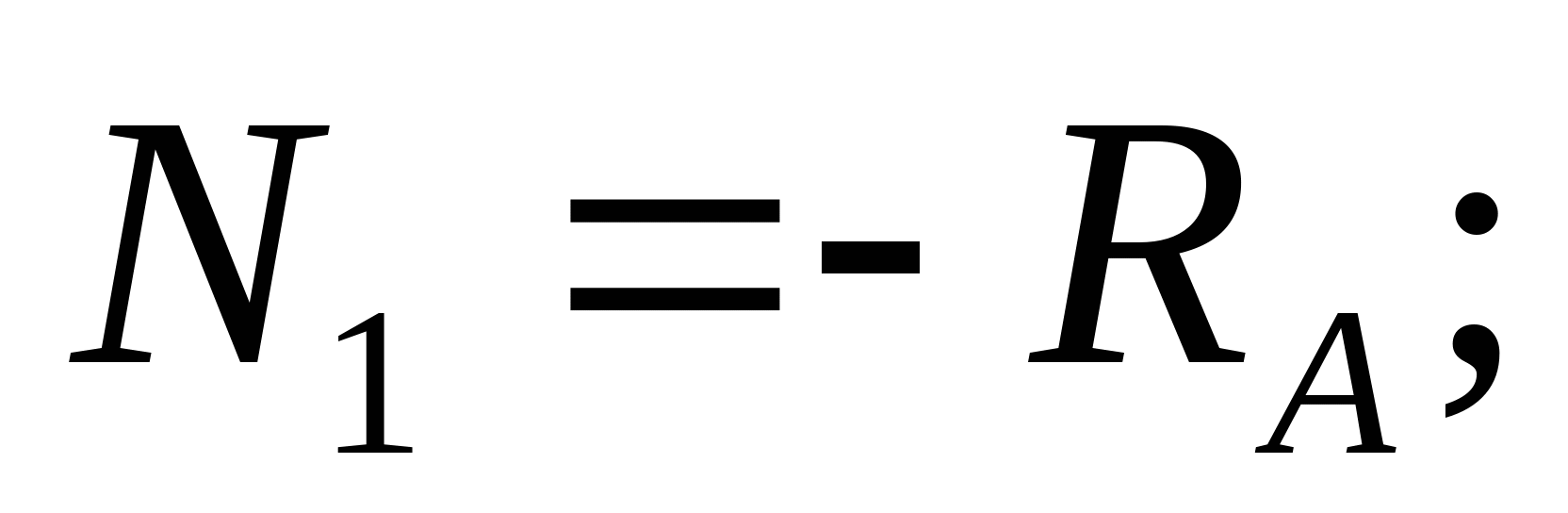  (3) (3) 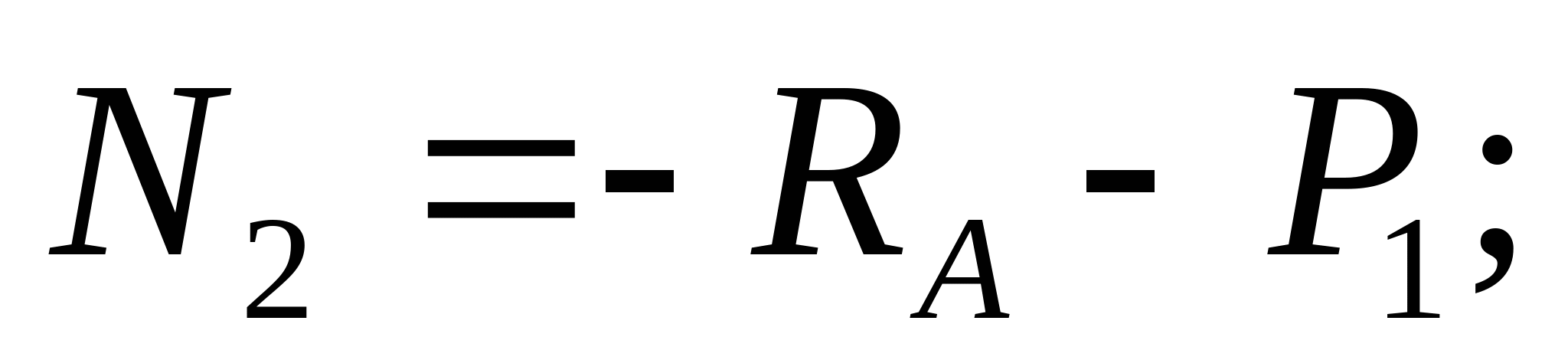 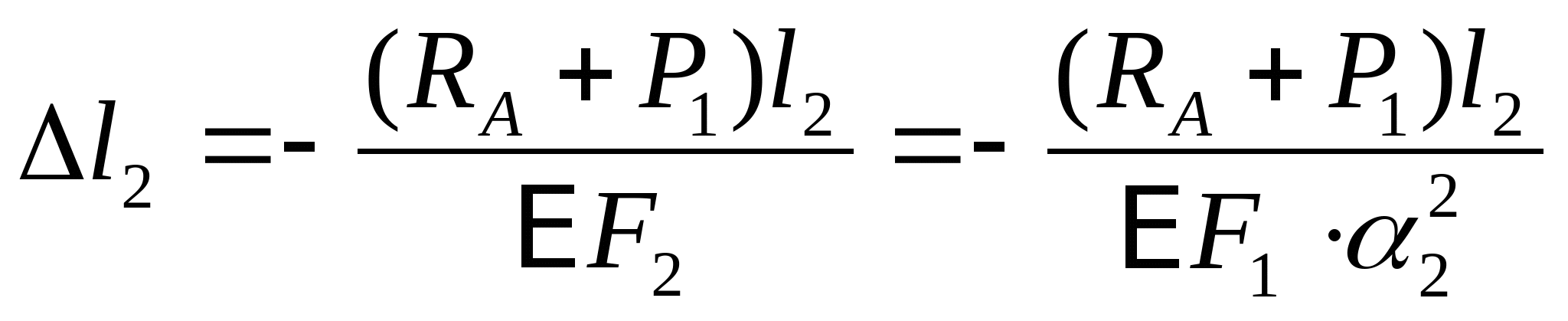 (4) (4) 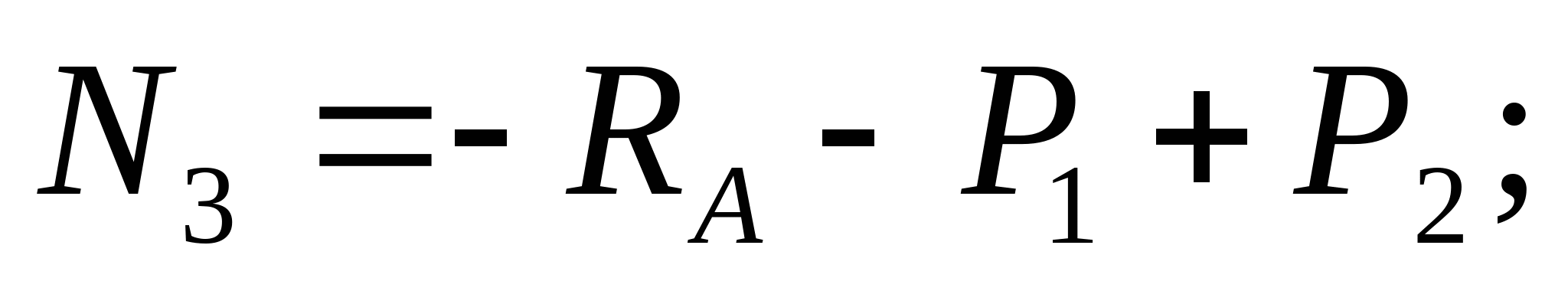 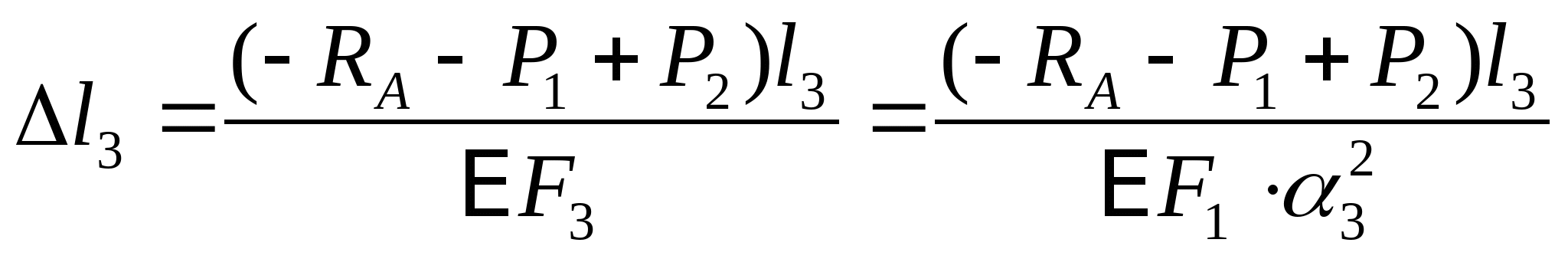 (5) (5) 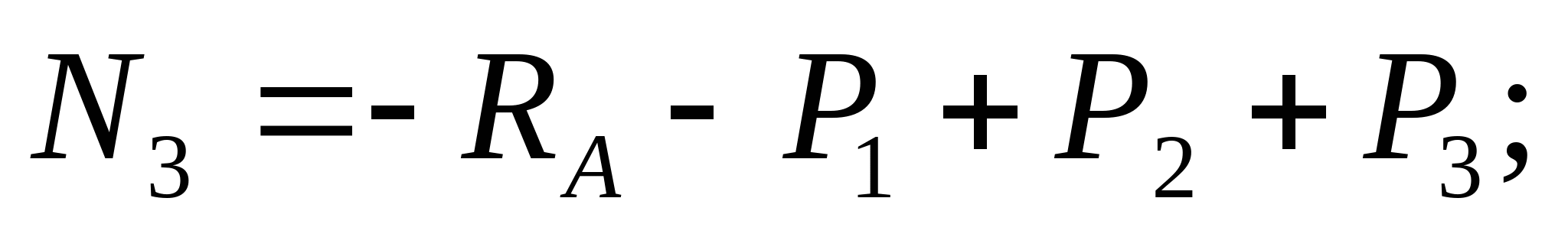 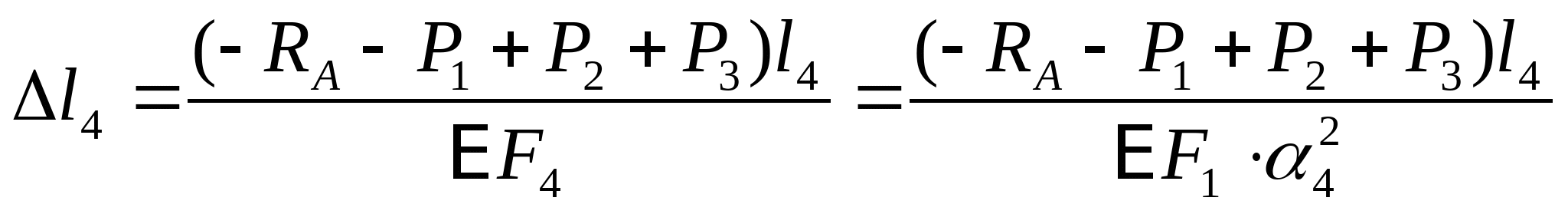 (6) (6)
Подставим полученные значения (3), (4), (5), (6) в (2): 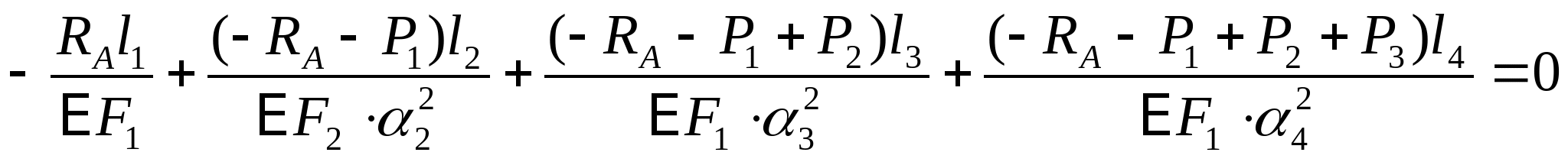 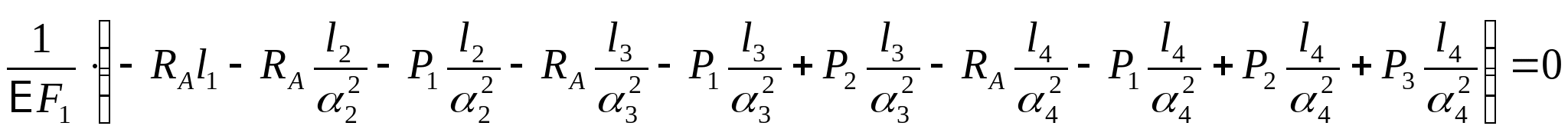 Так как  выражение в скобках: выражение в скобках: 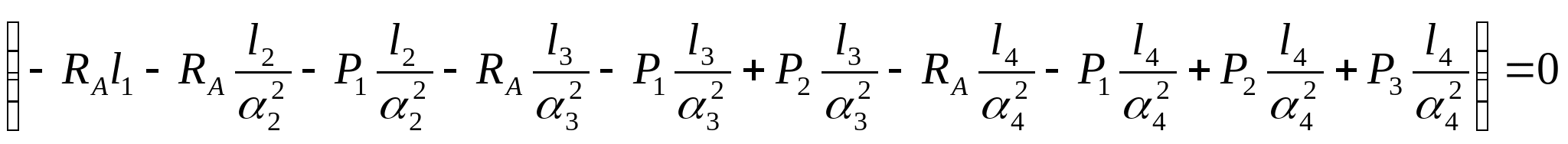 , тогда , тогда 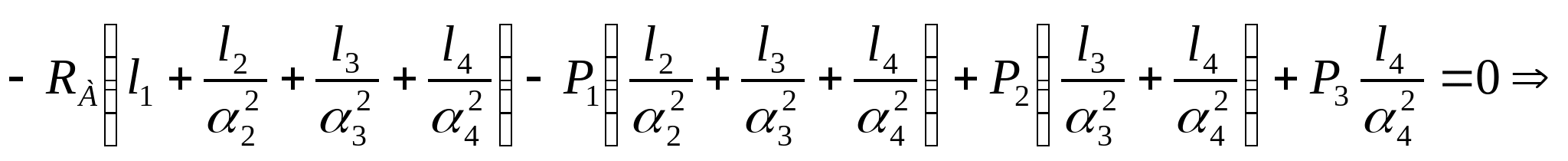 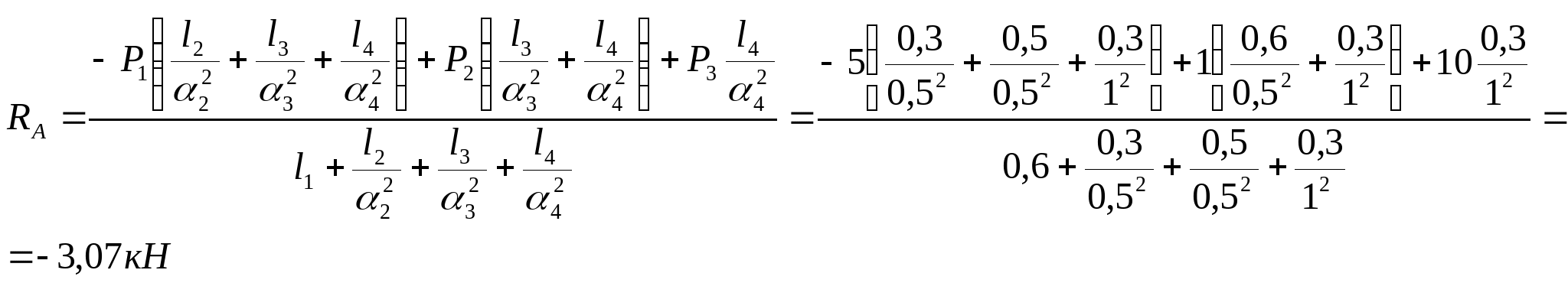 Знак «-» означает, что направление RА противоположно принятому на расчетной схеме. Из уравнения (1) вычисляем: RB=6-RA=6-(-3,07)=9,07 кН.
3. Строим эпюру нормальных сил: N1=-RA=-(-3,07)=3,07 кН 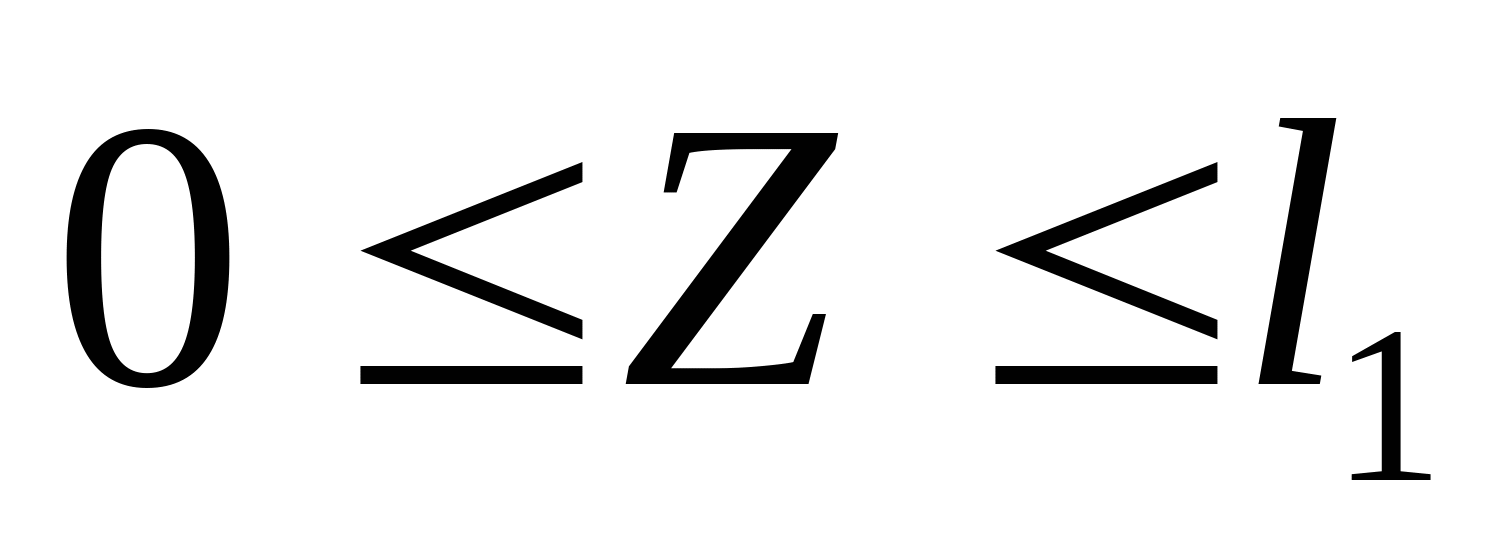 N2=- RA-P1=-(-3,07)-5=-1,93 кН 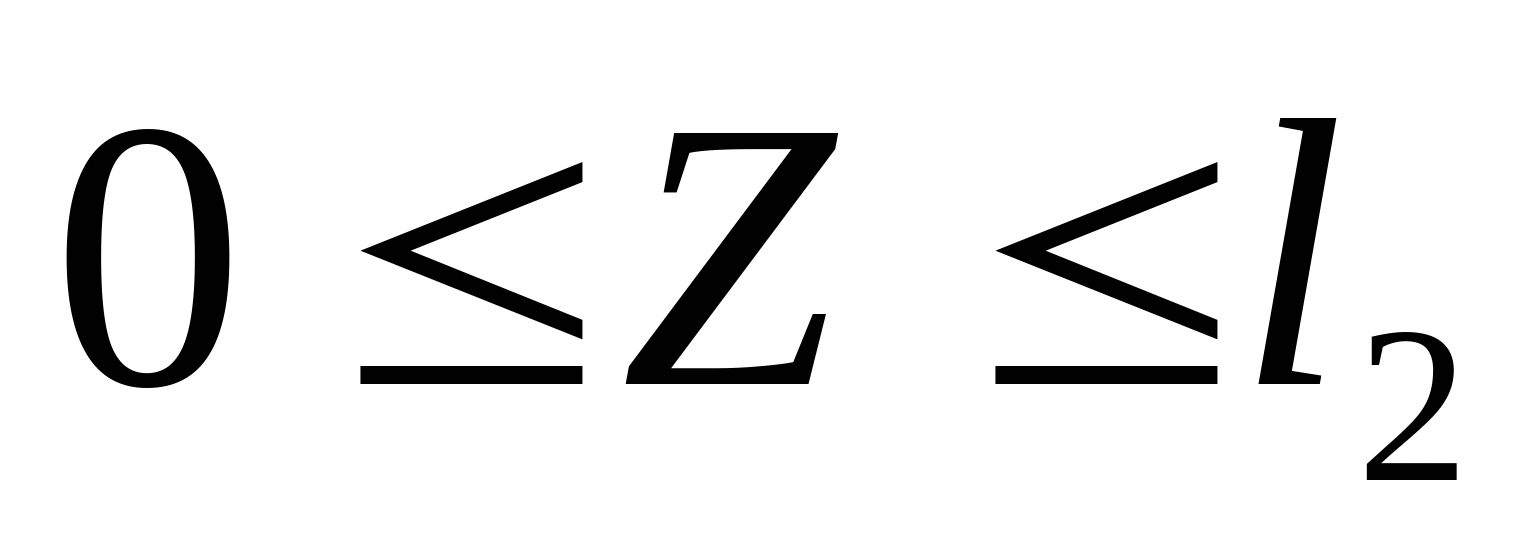 N3=- RA-P1+P2=-(-3,07)-5+1=-0,93 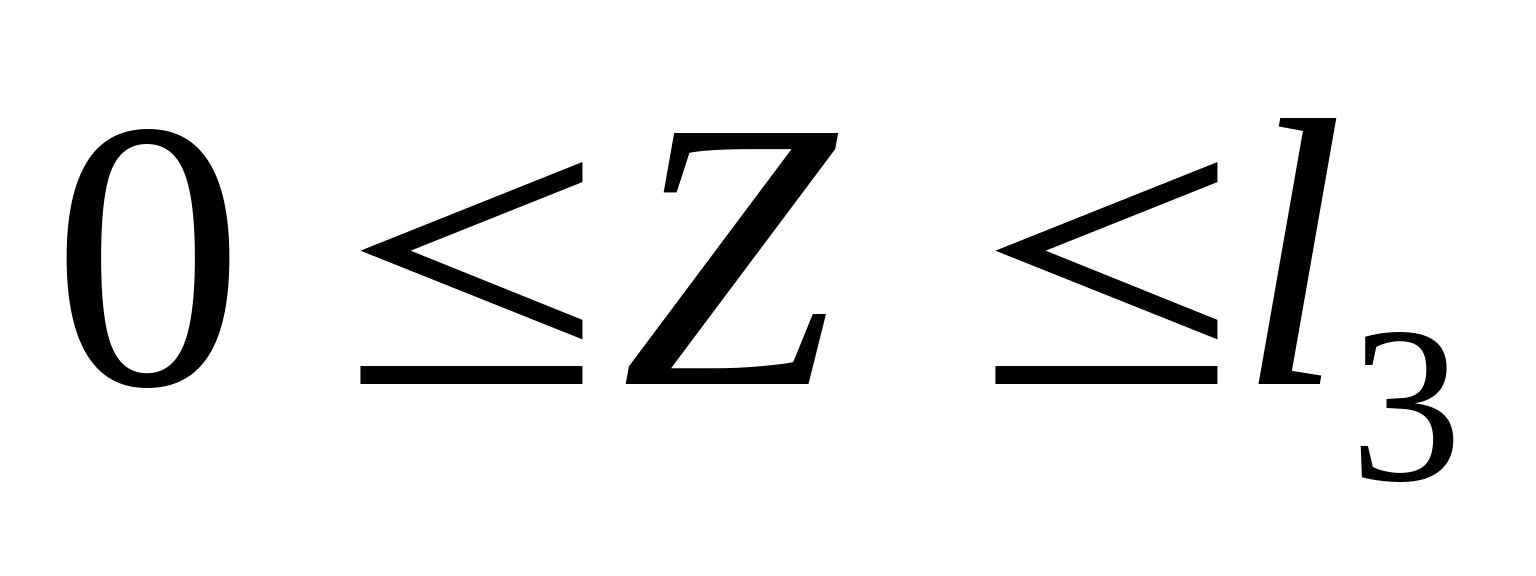 N4=- RA-P1+P2+P3=-(-3,07)-5+1+10=9,07 кН 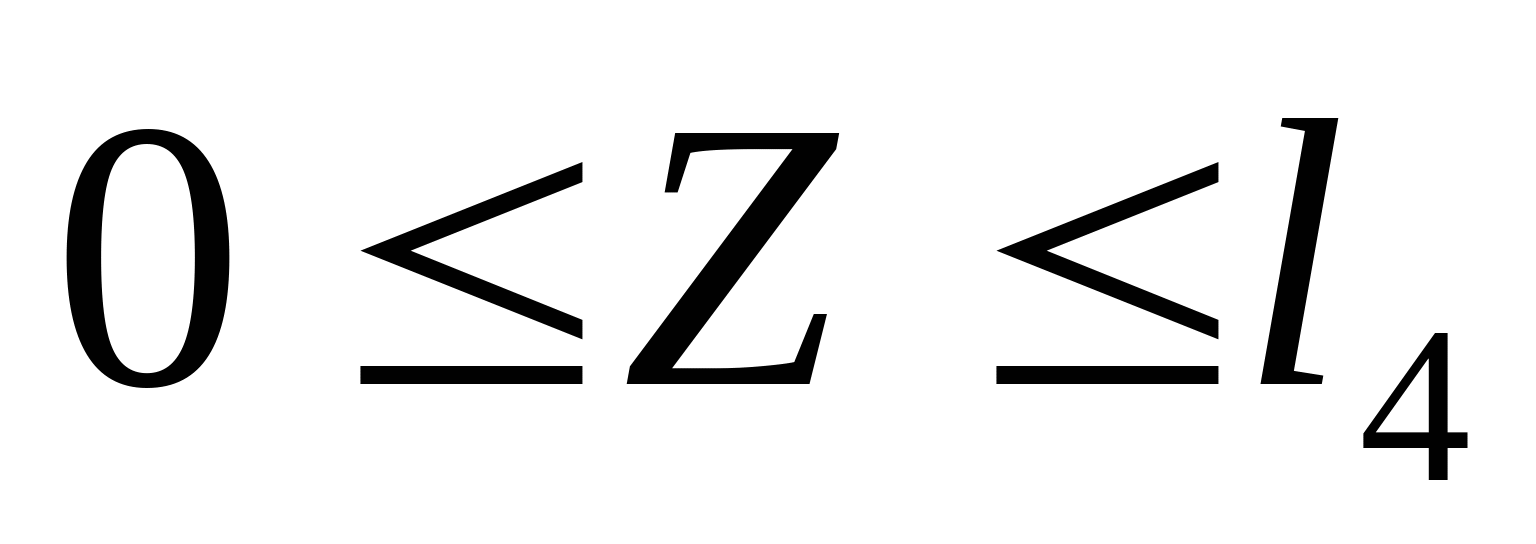
4. Строим эпюру приведенных нормальных напряжений 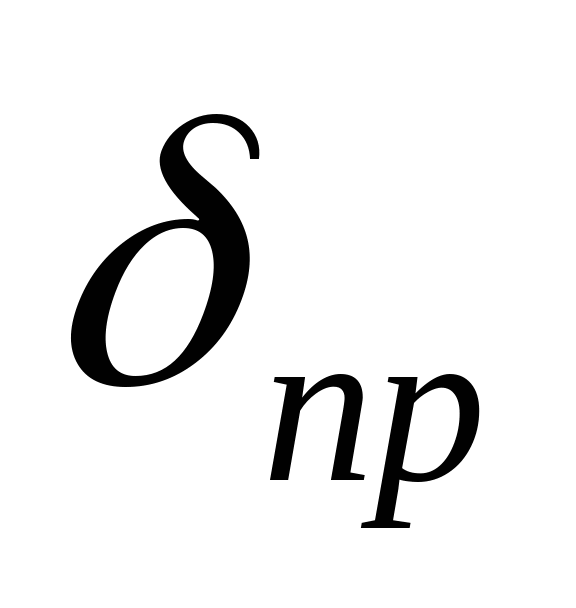 : :
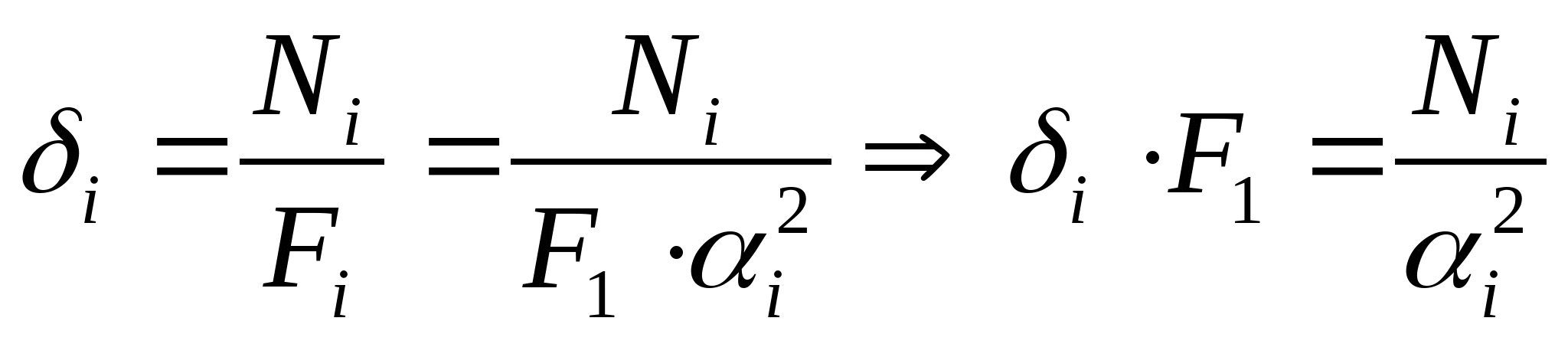 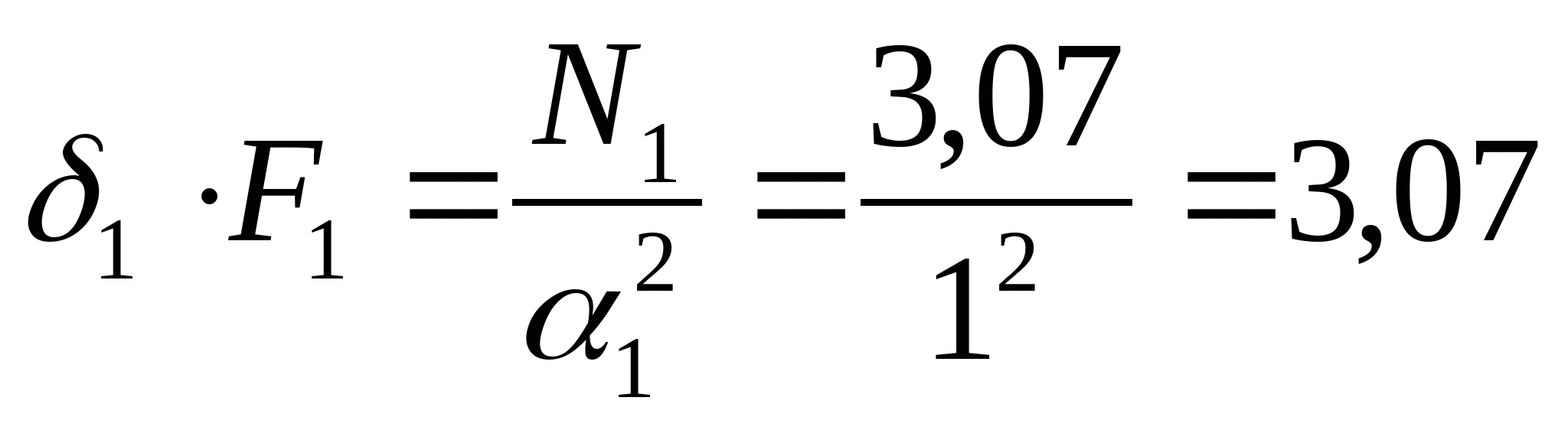 кН кН 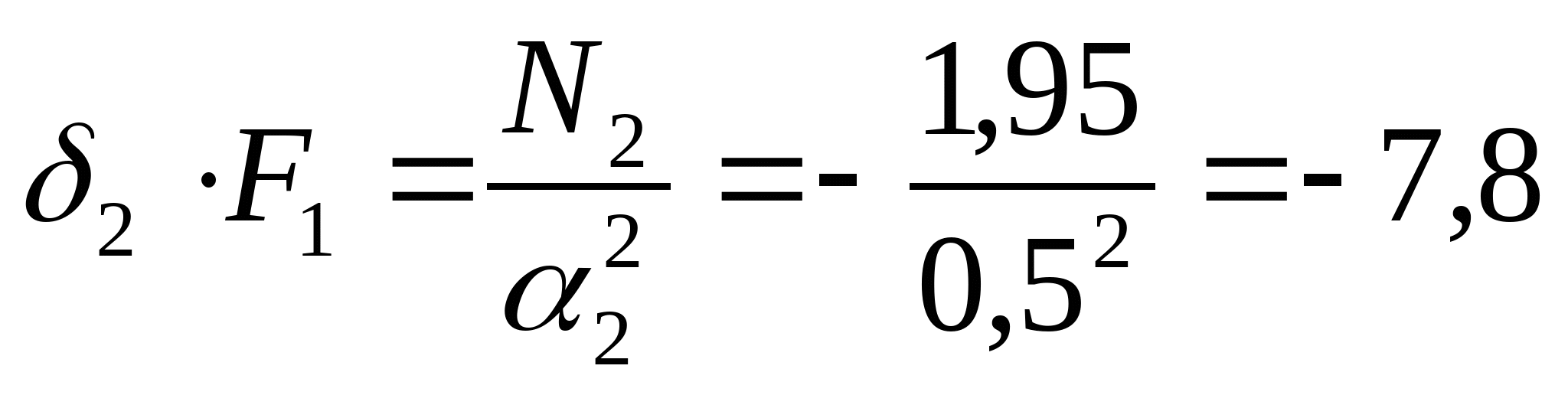 кН кН 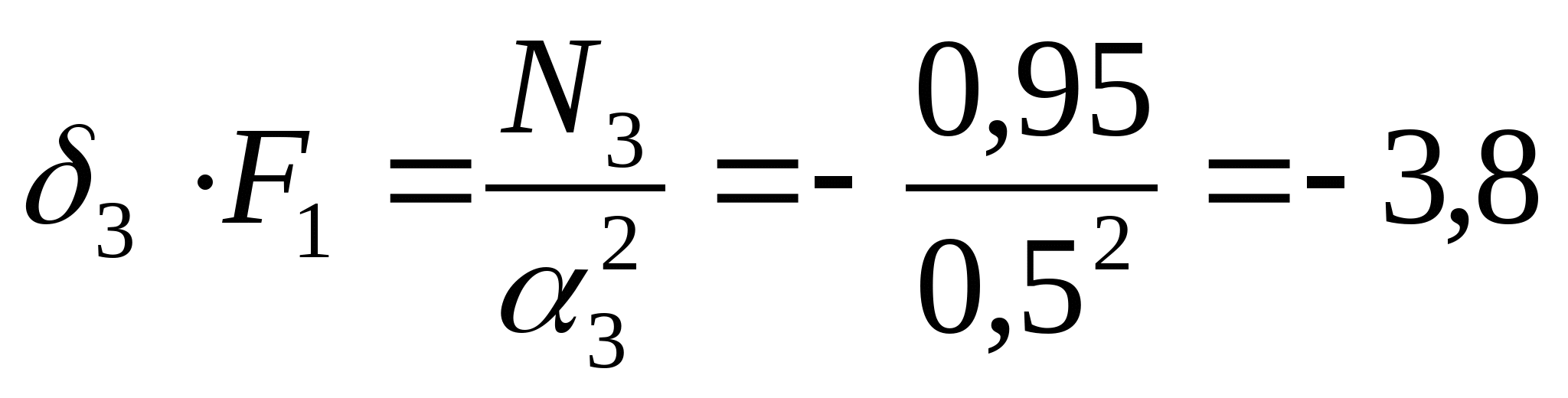 кН кН 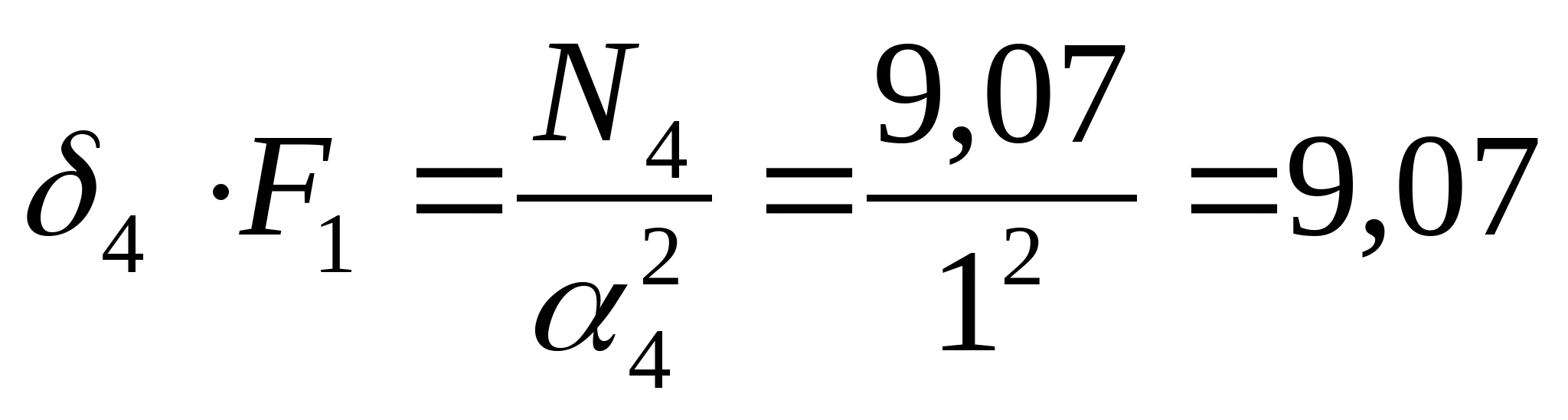 кН кН Из эпюры видно, что опасным участком является участок 4, где 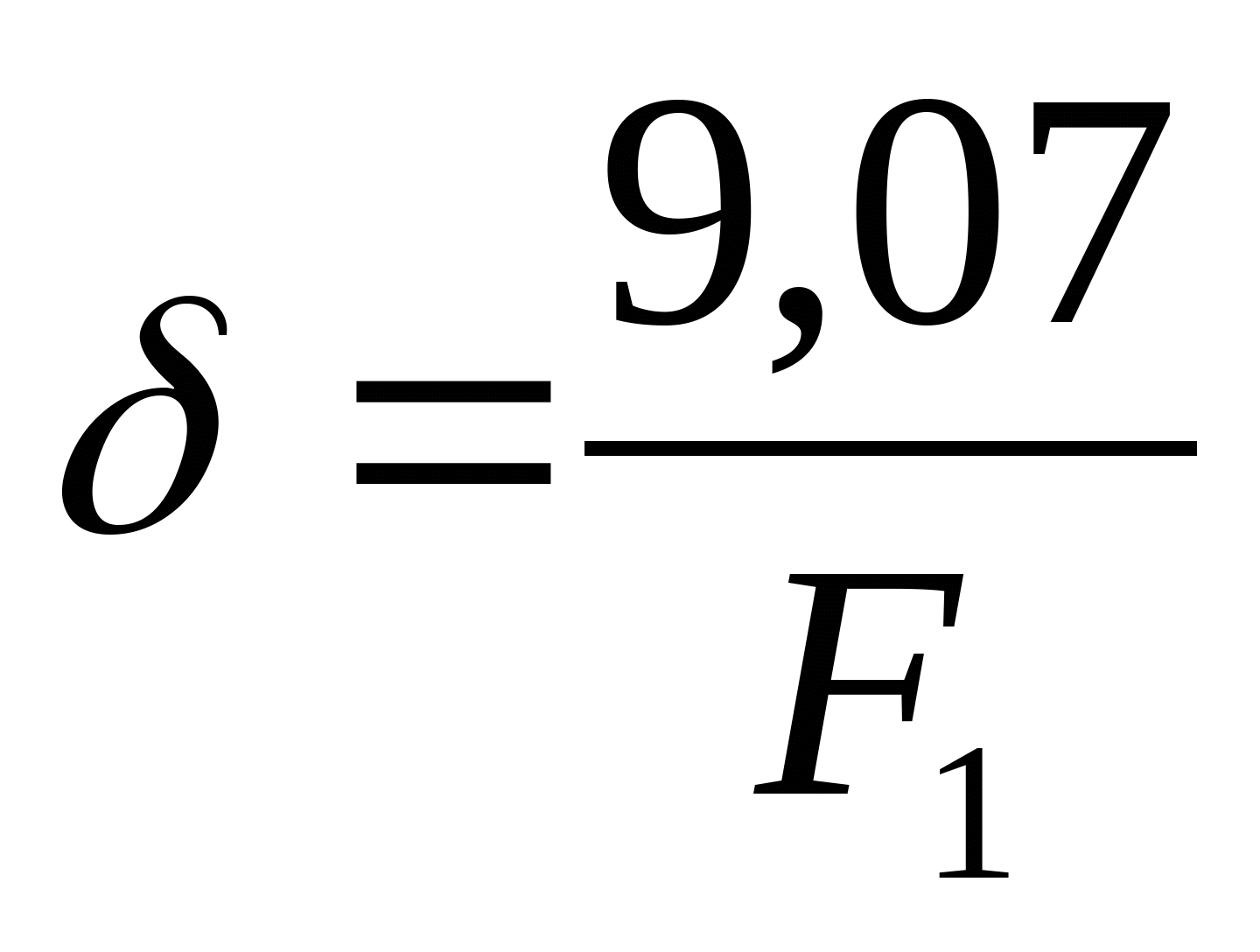 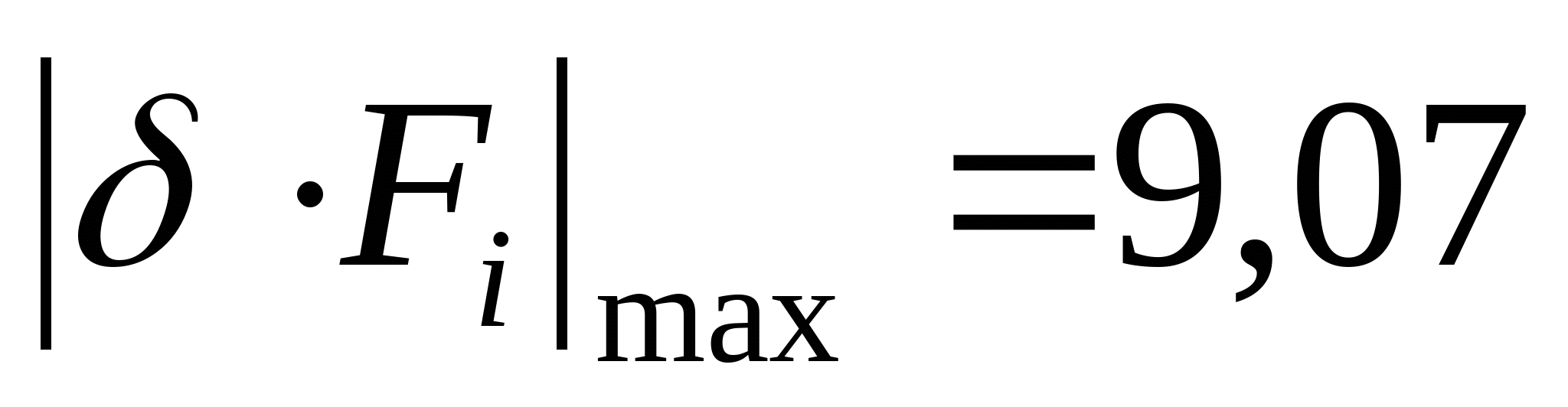 кН кН 5. Определяем размеры сечений di и Fi: из условия прочности 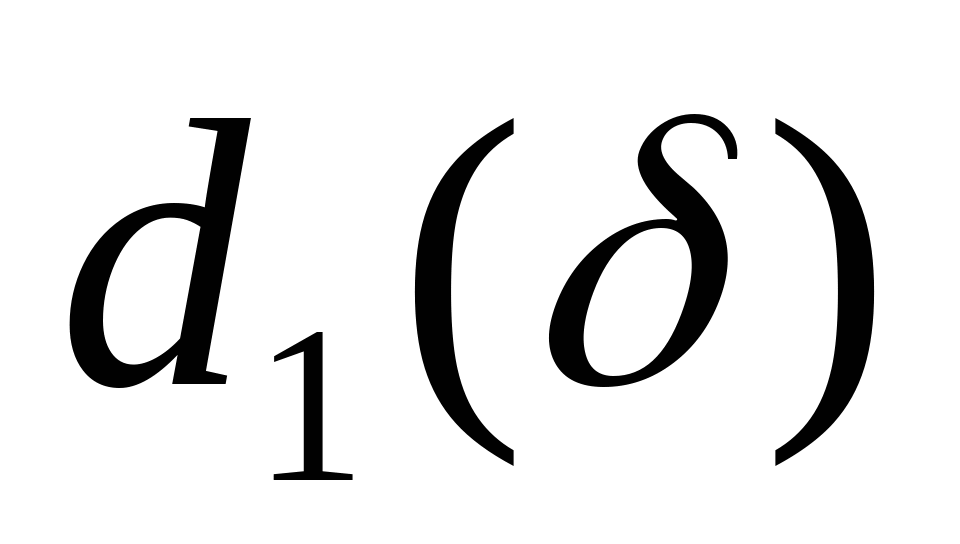 : : 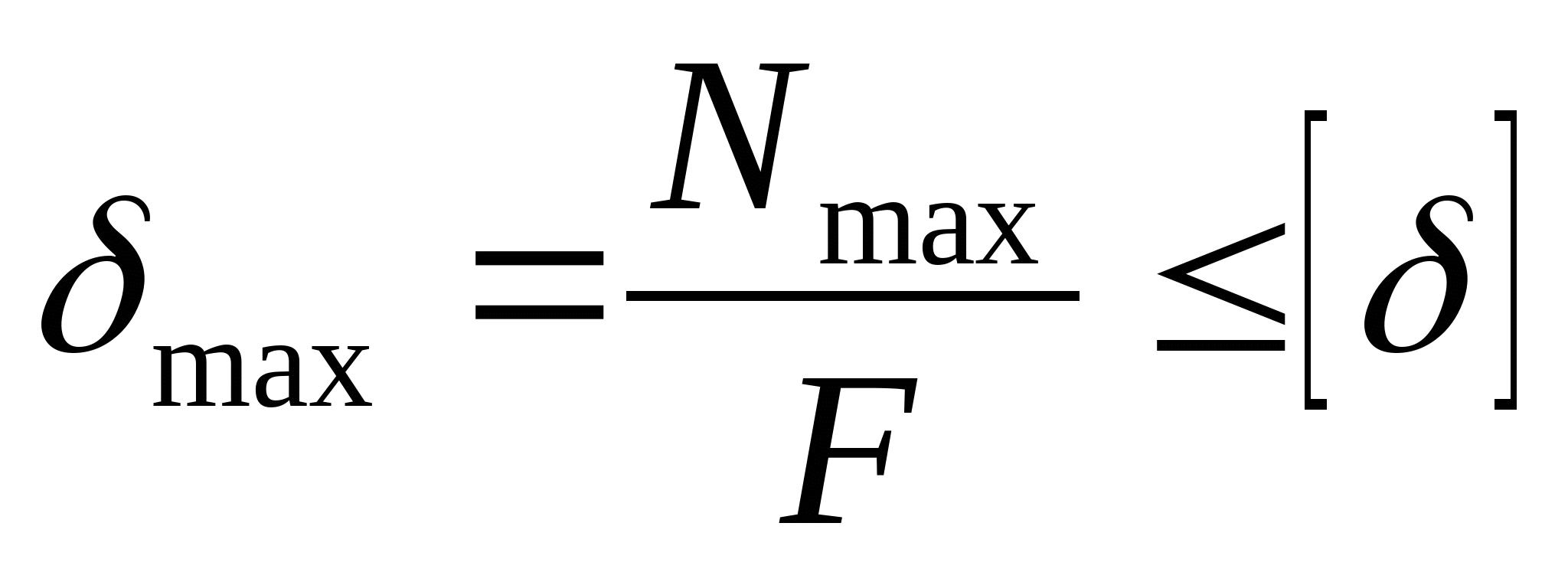 получаем: получаем: 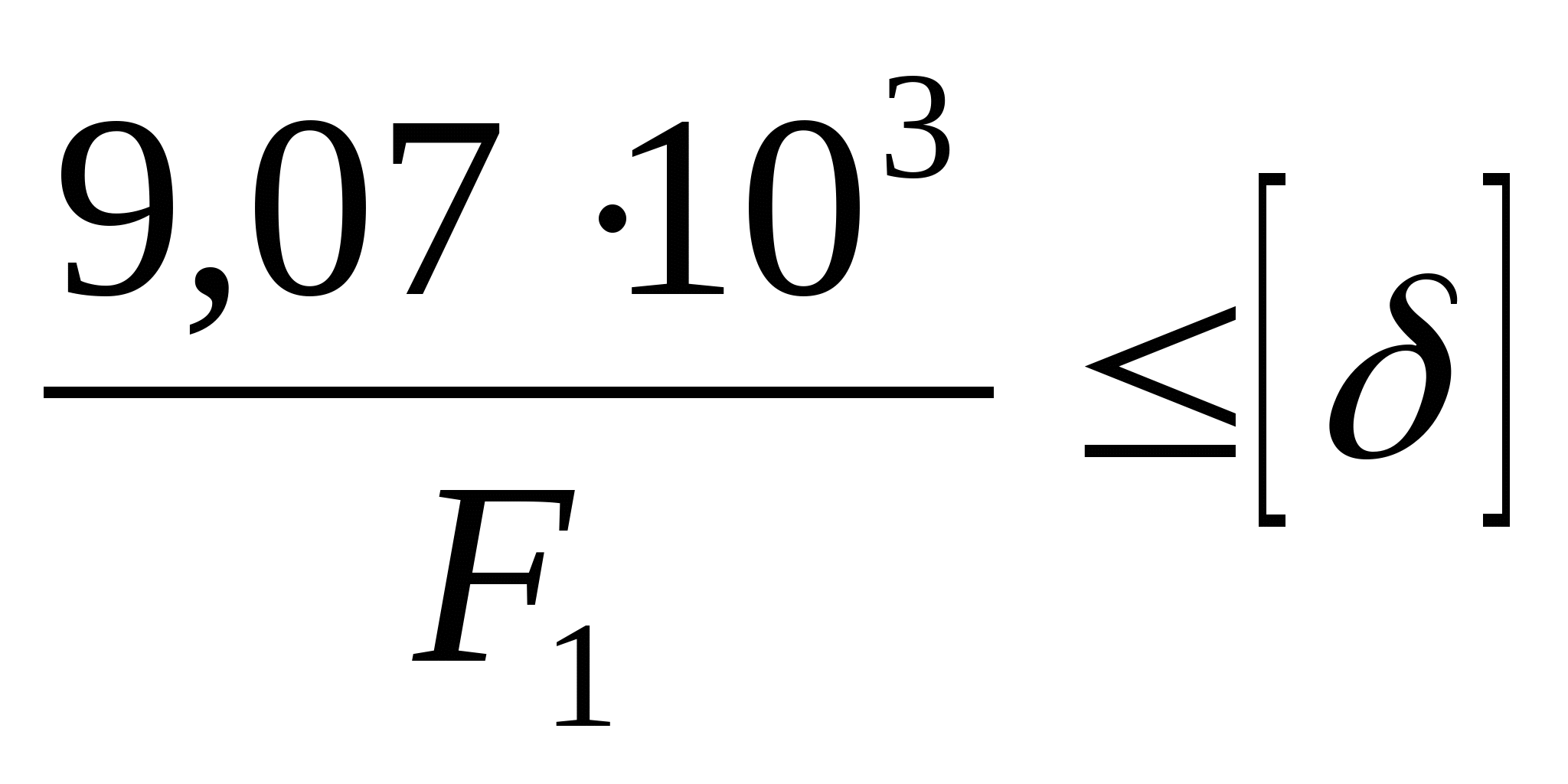 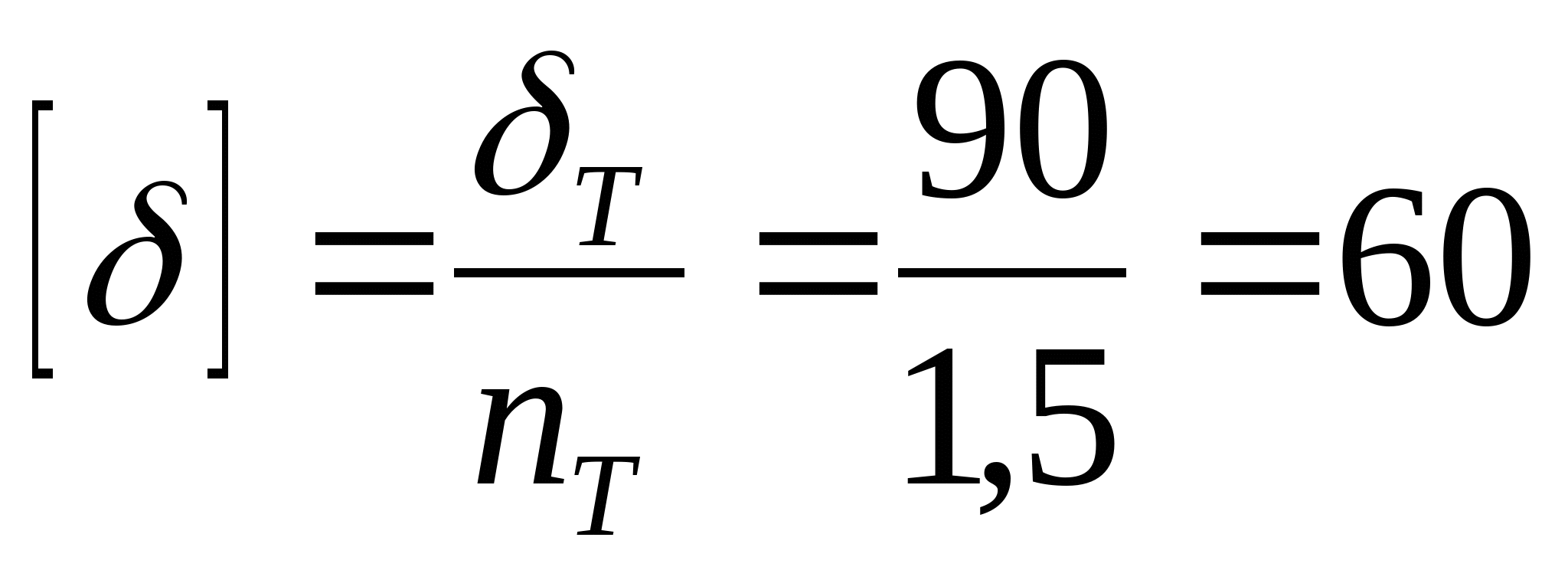 МПа; МПа; 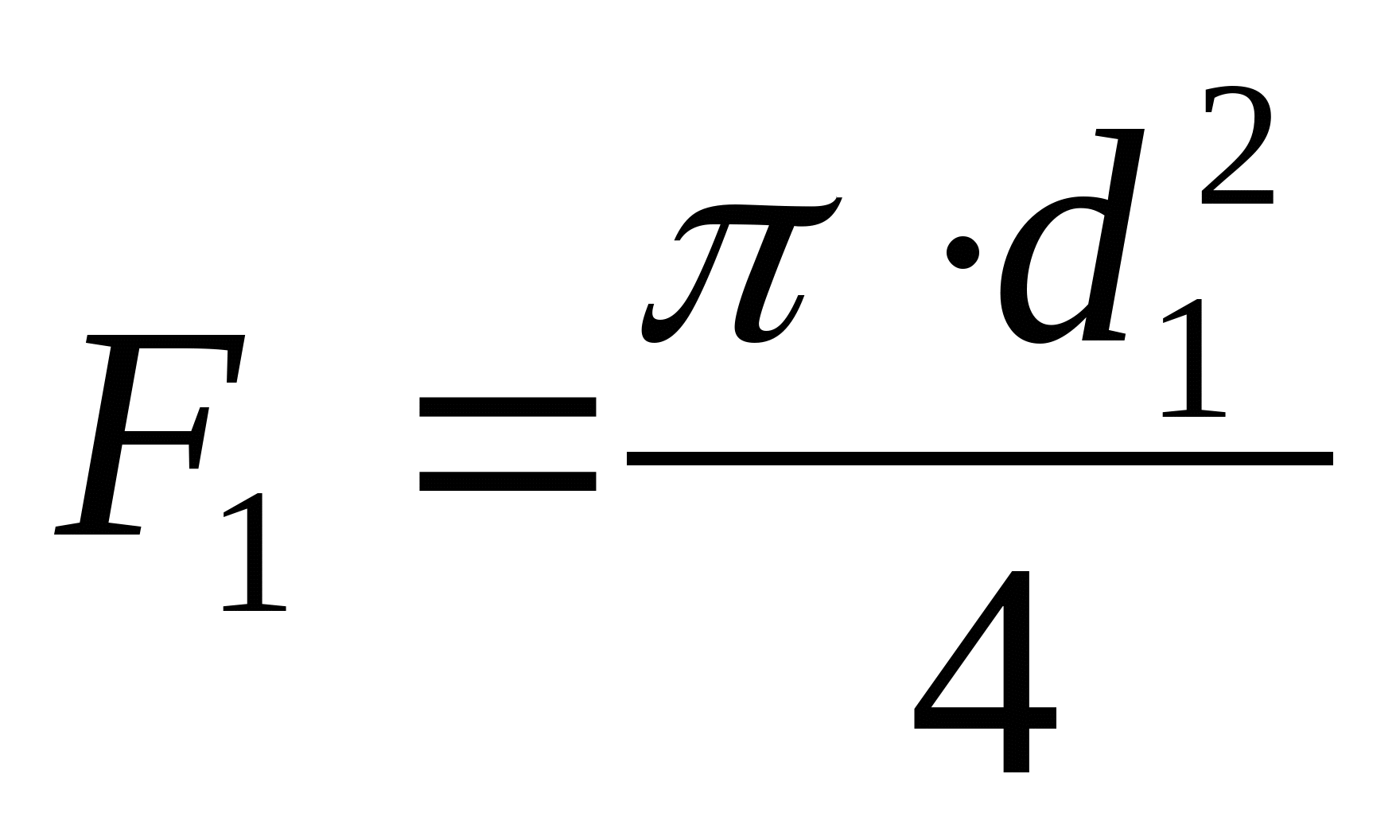 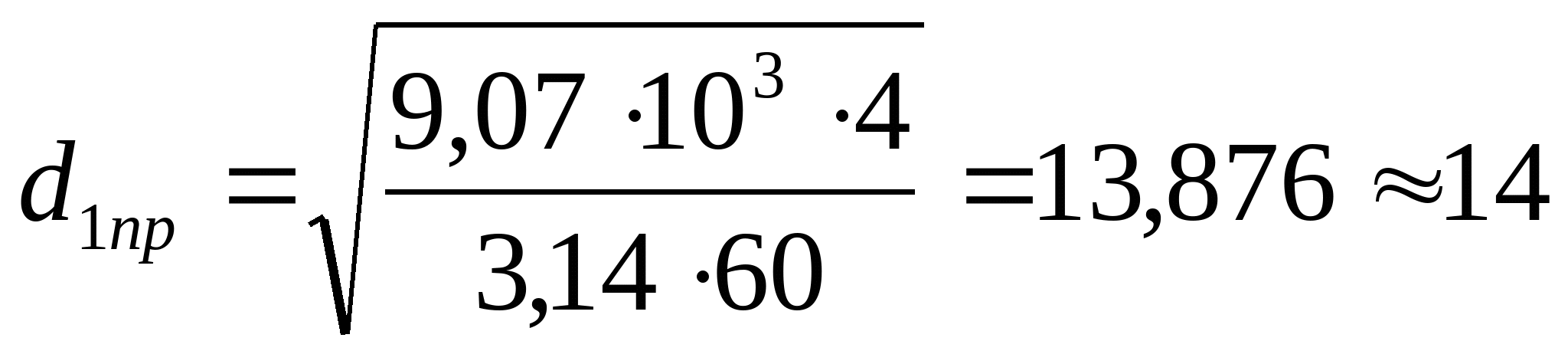 мм мм из условия жесткости d1(E) получим: 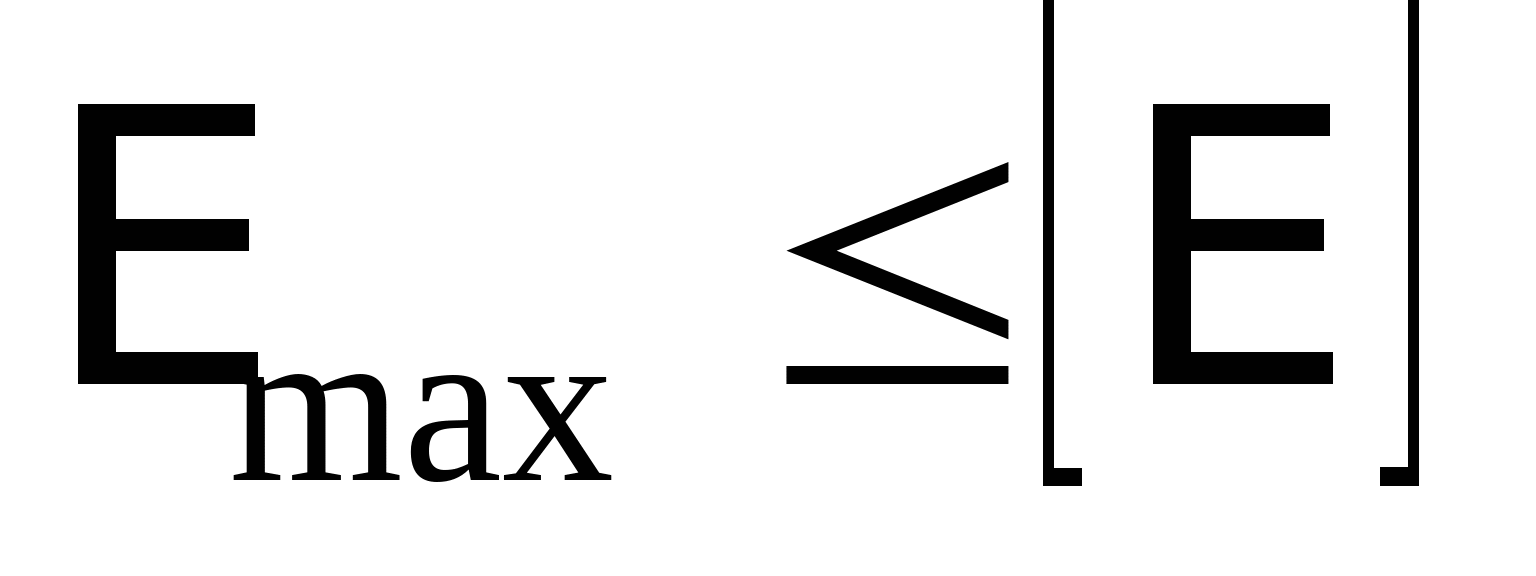 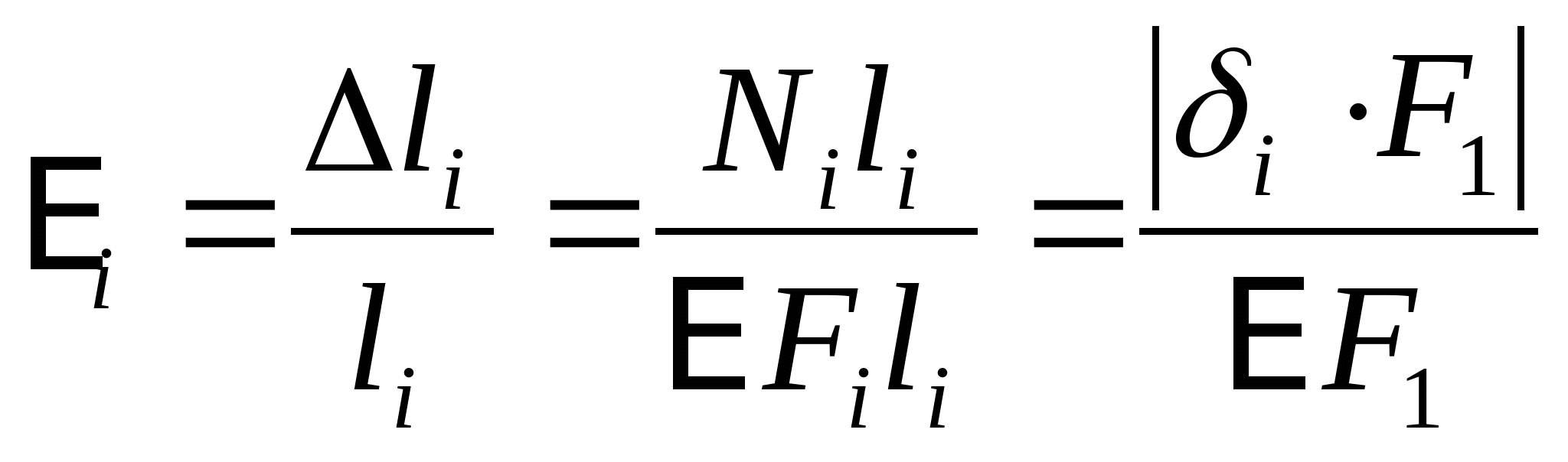
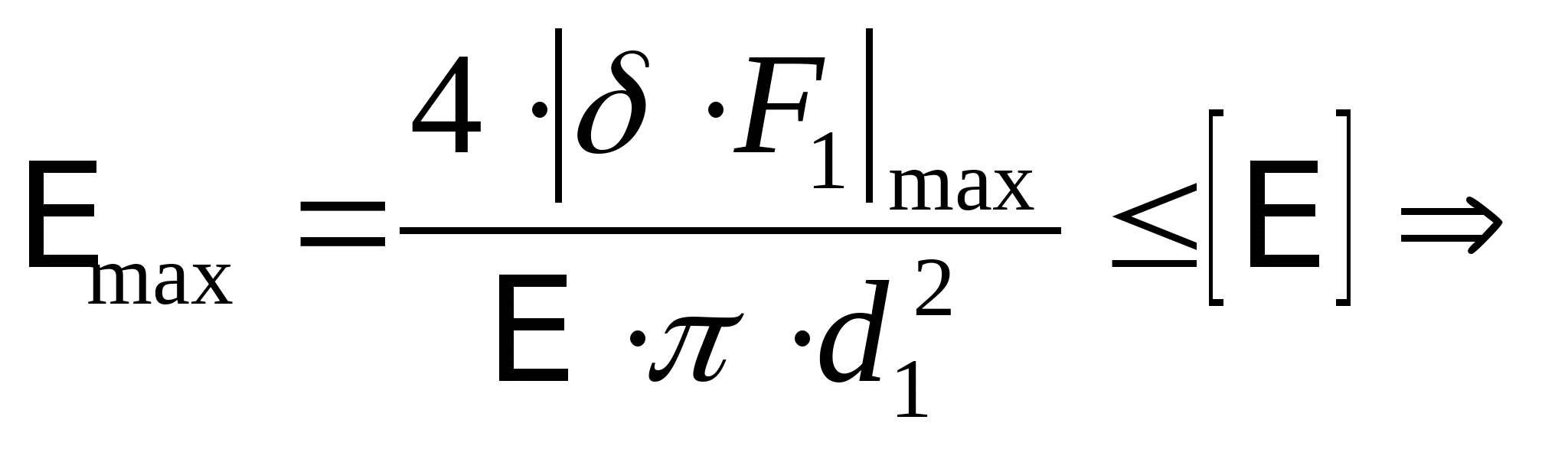 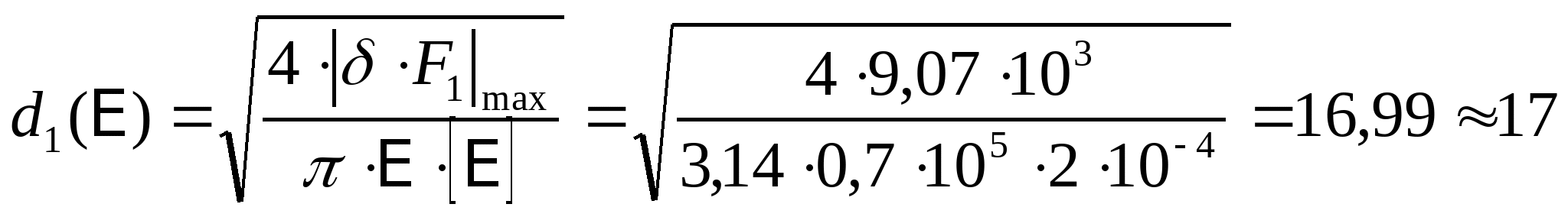 мм мм Так как 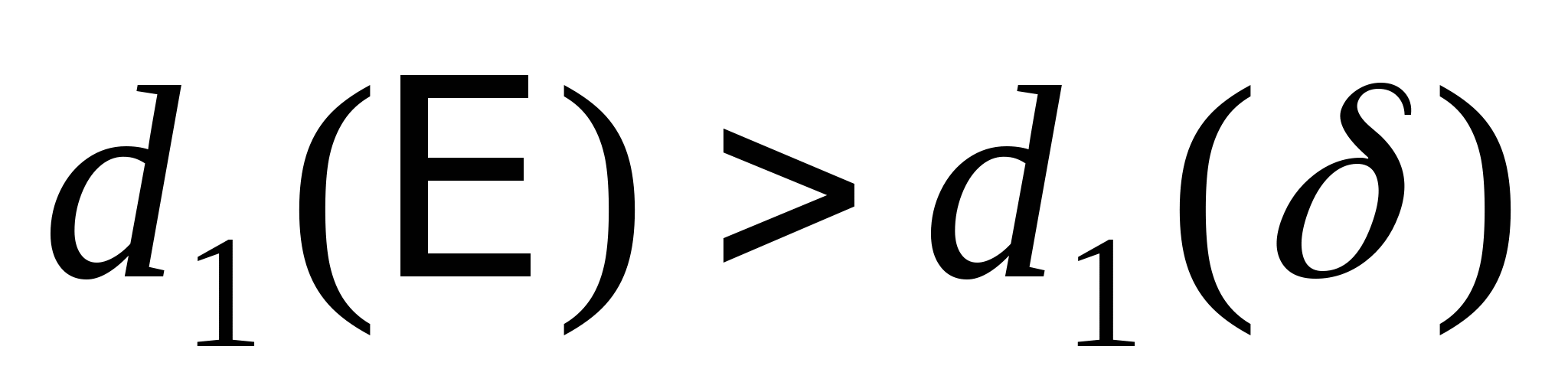 , то принимаем d1=17 мм. Тогда , то принимаем d1=17 мм. Тогда 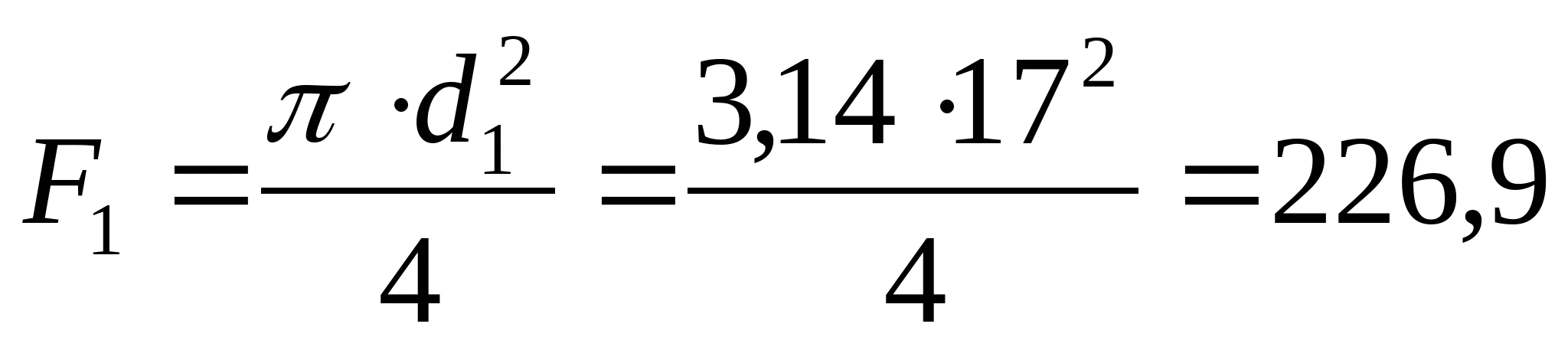 мм2 мм2 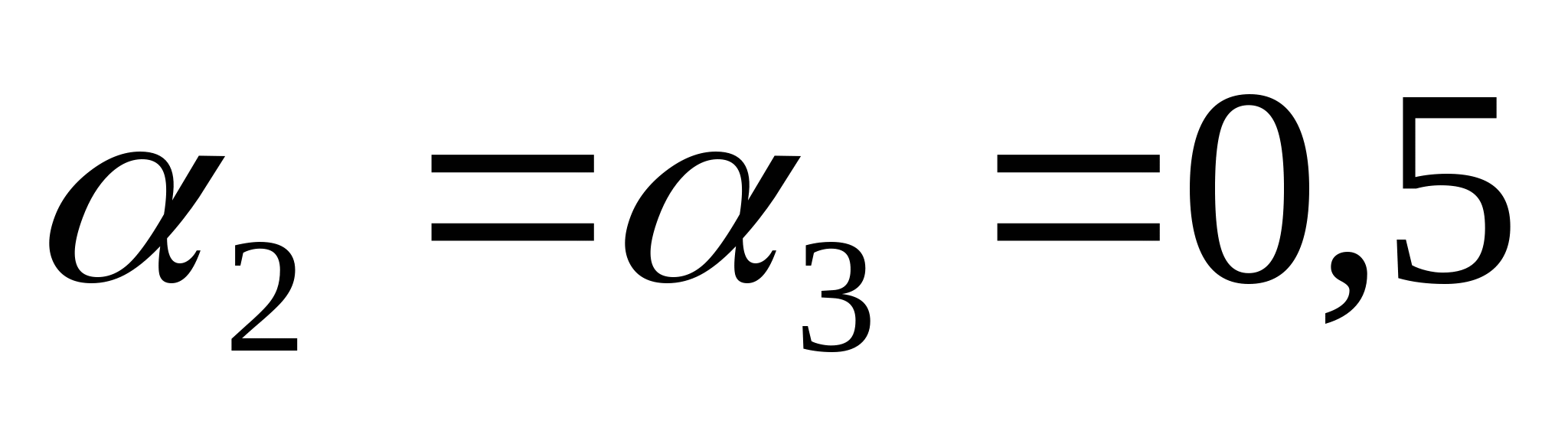 , , 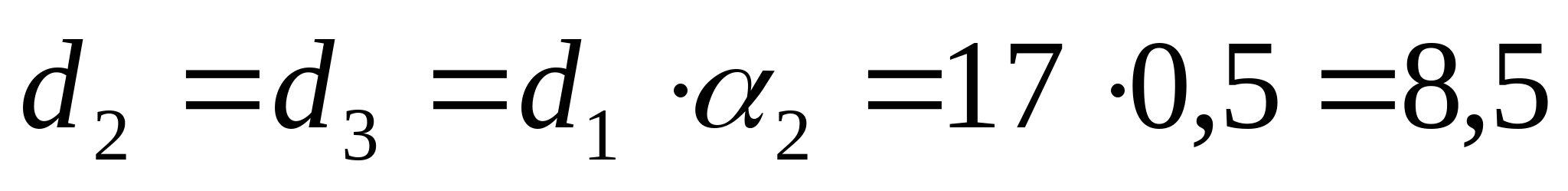 мм2 мм2 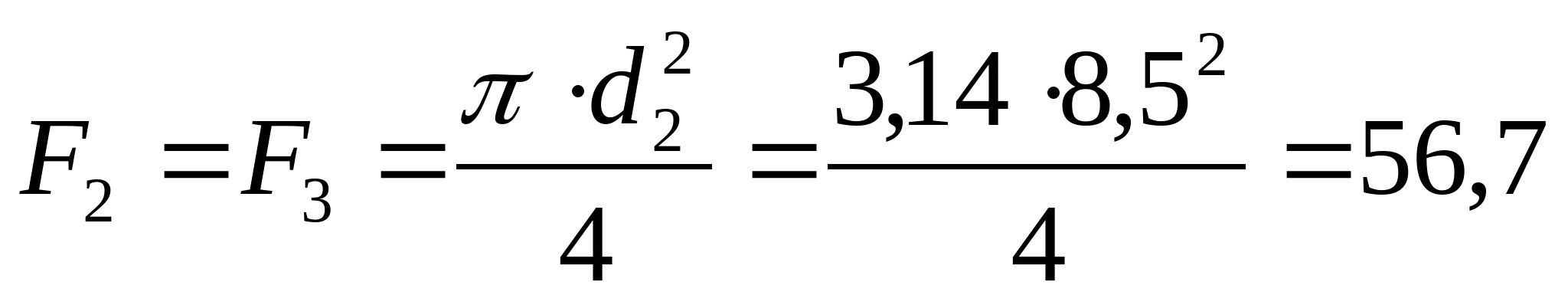 мм2 мм2 d4=17 мм, d4 =d1=17 мм и F4=F1=226,9 мм2
6. Рассчитаем эпюру истинных нормальных напряжений: 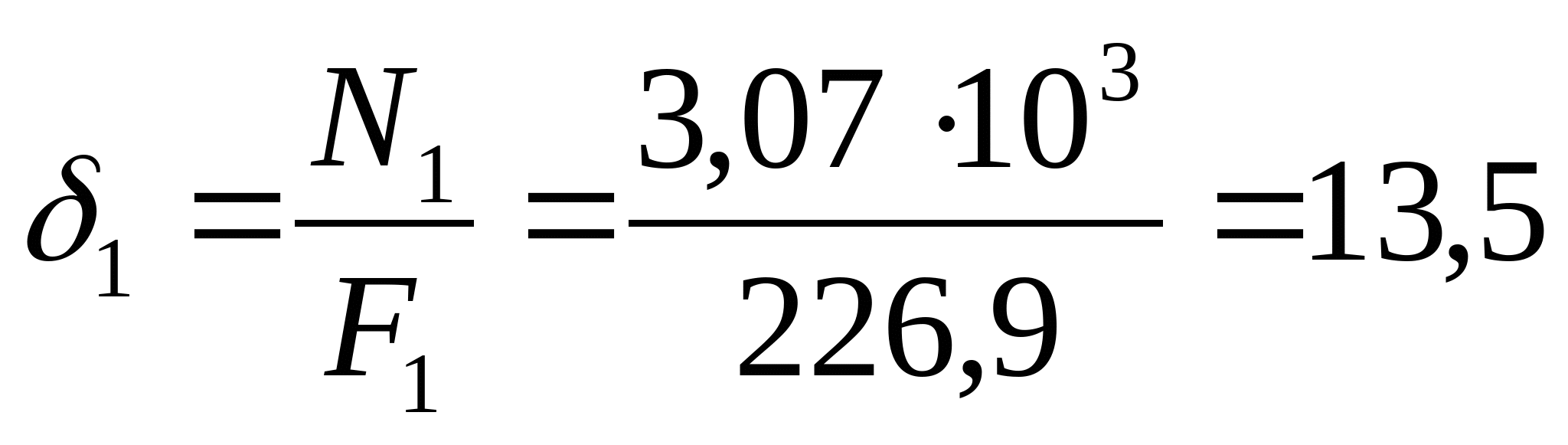 МПа МПа 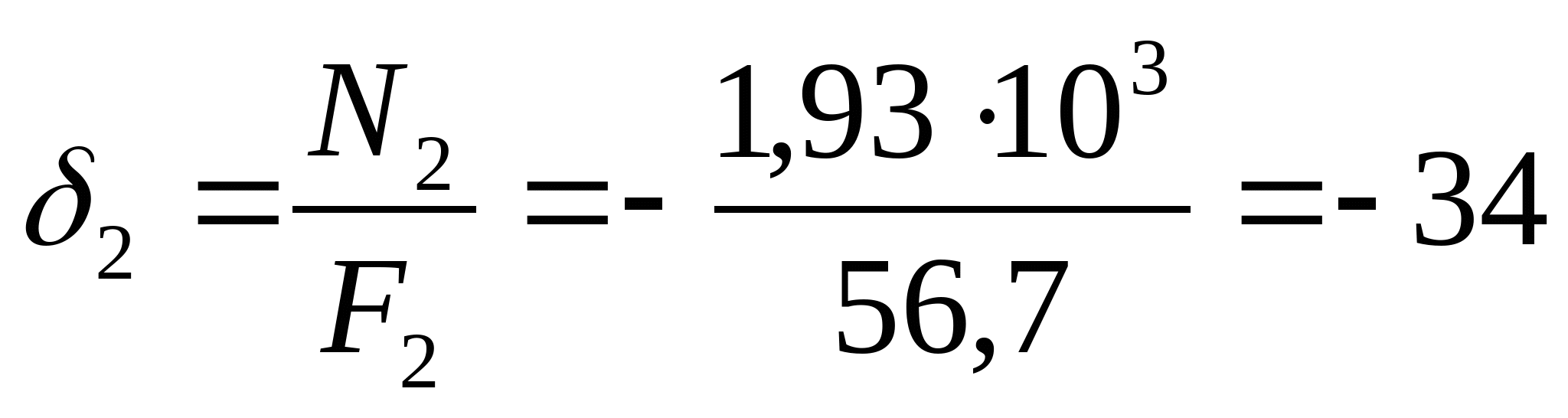 МПа МПа 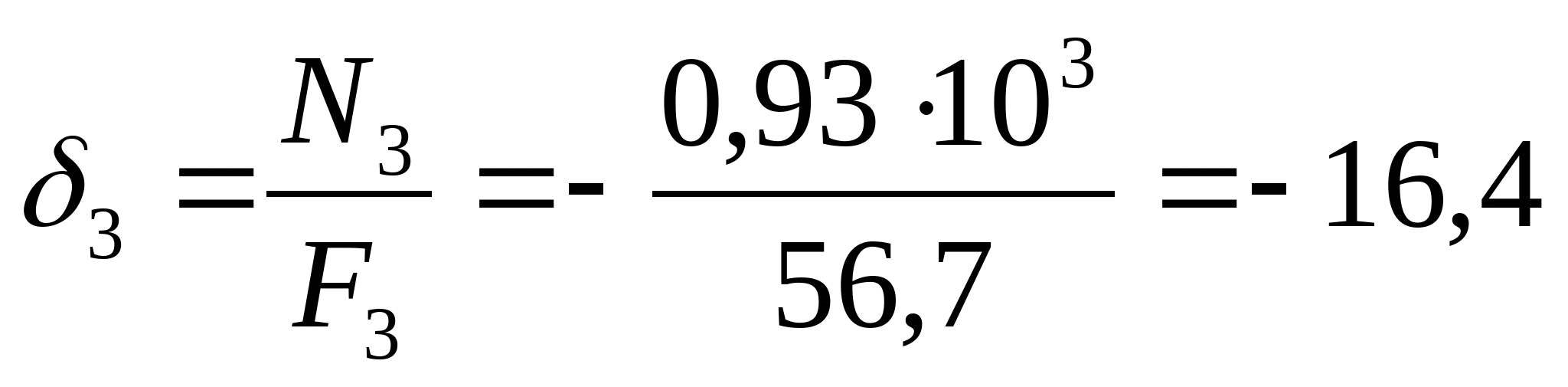 МПа МПа 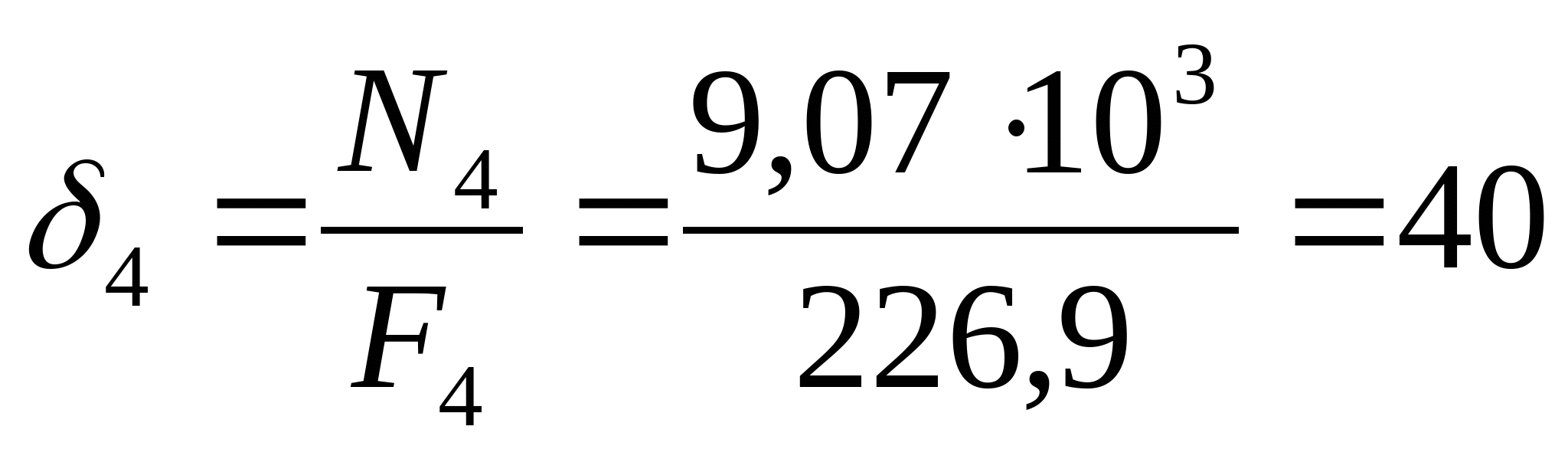 МПа МПа
7. Рассчитаем эпюру перемещений: 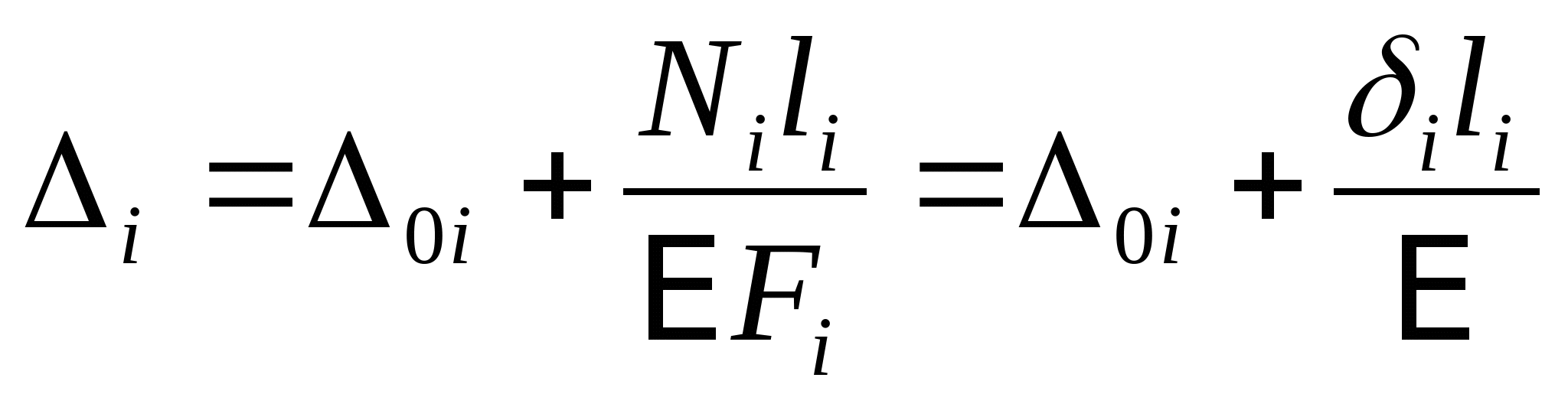 если строить от точки А, то тогда 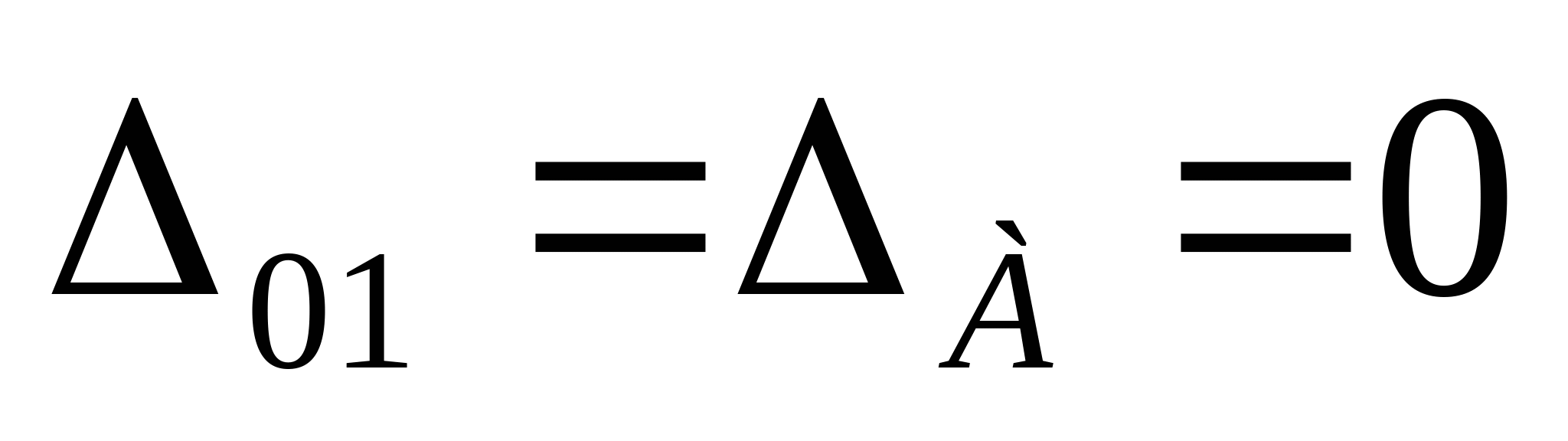 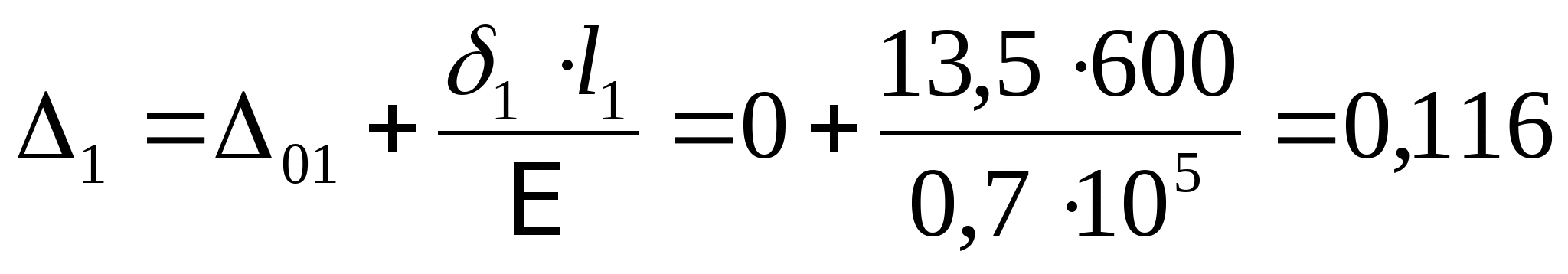 мм мм 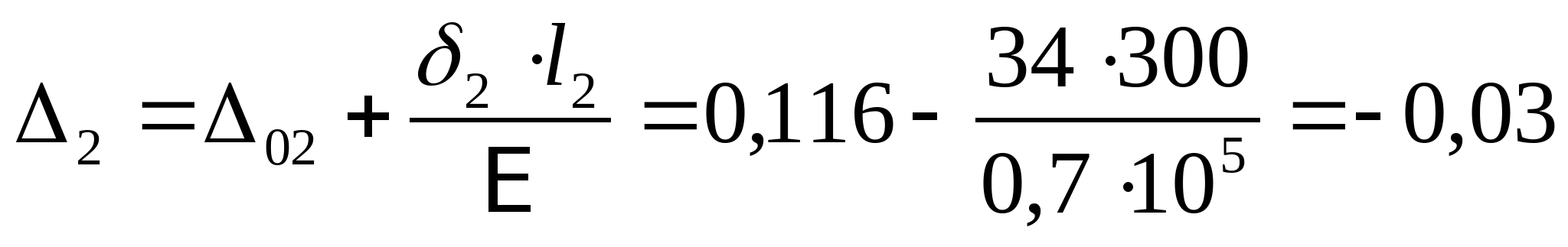 мм мм 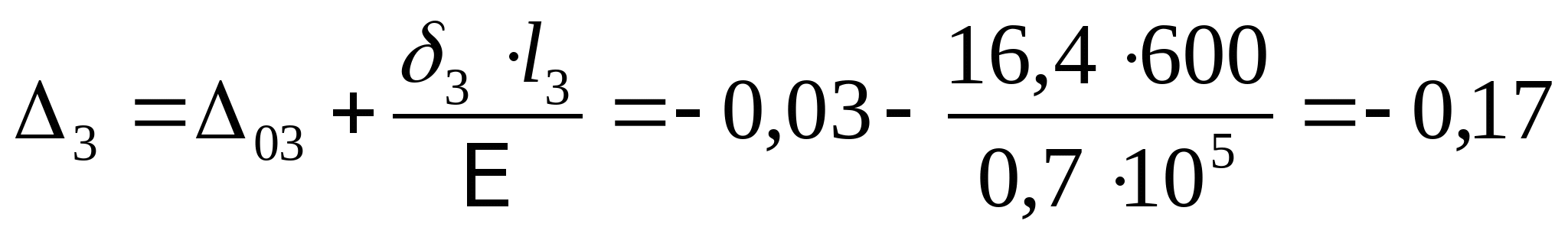 мм мм 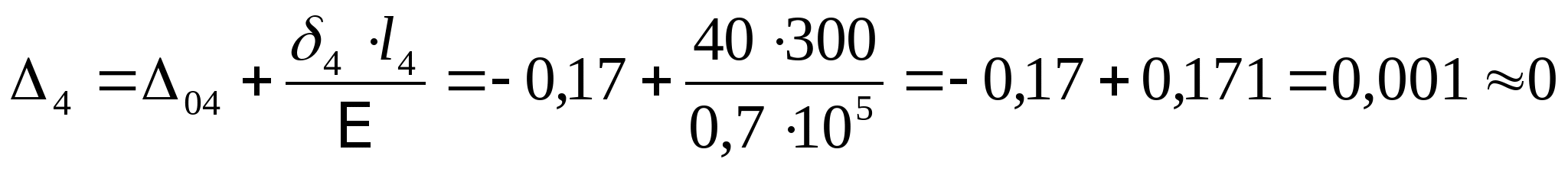 мм мм Вычислим отклонение: 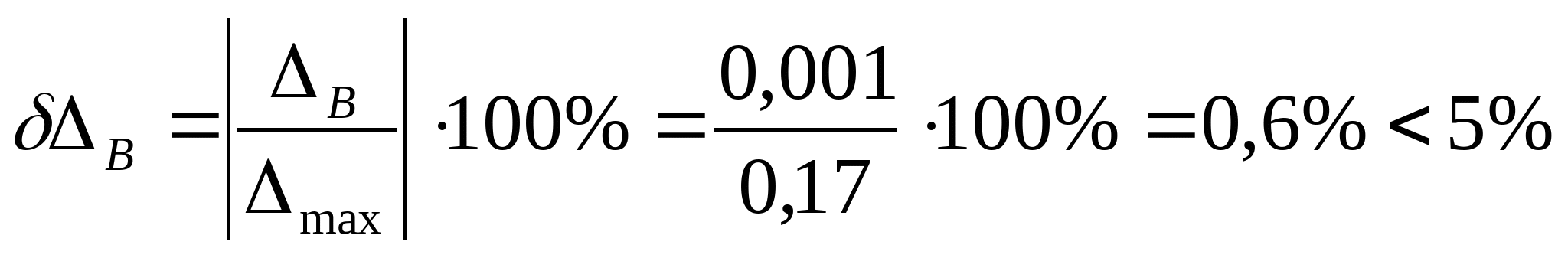 - статическая неопределимость раскрыта верно. - статическая неопределимость раскрыта верно. РПР № 1.2
Дано: а=1 м; b=1,2 м; с=0,5 м; Стержень 1: 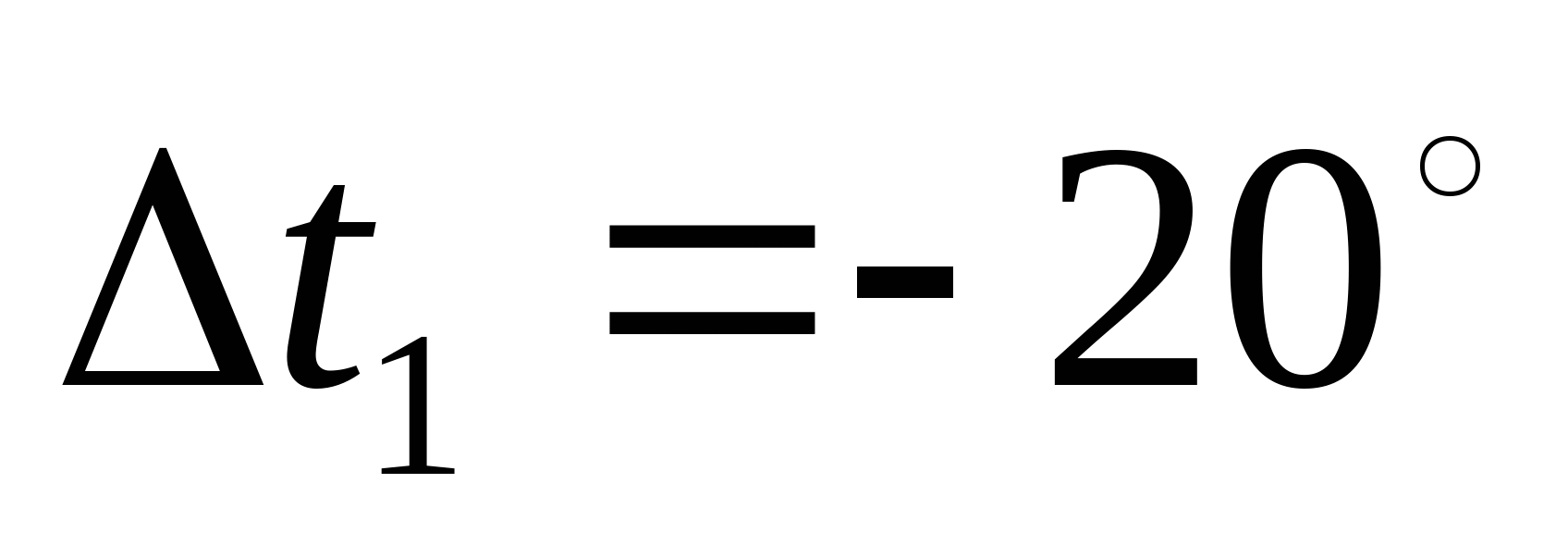 ; БрА5; ; БрА5; 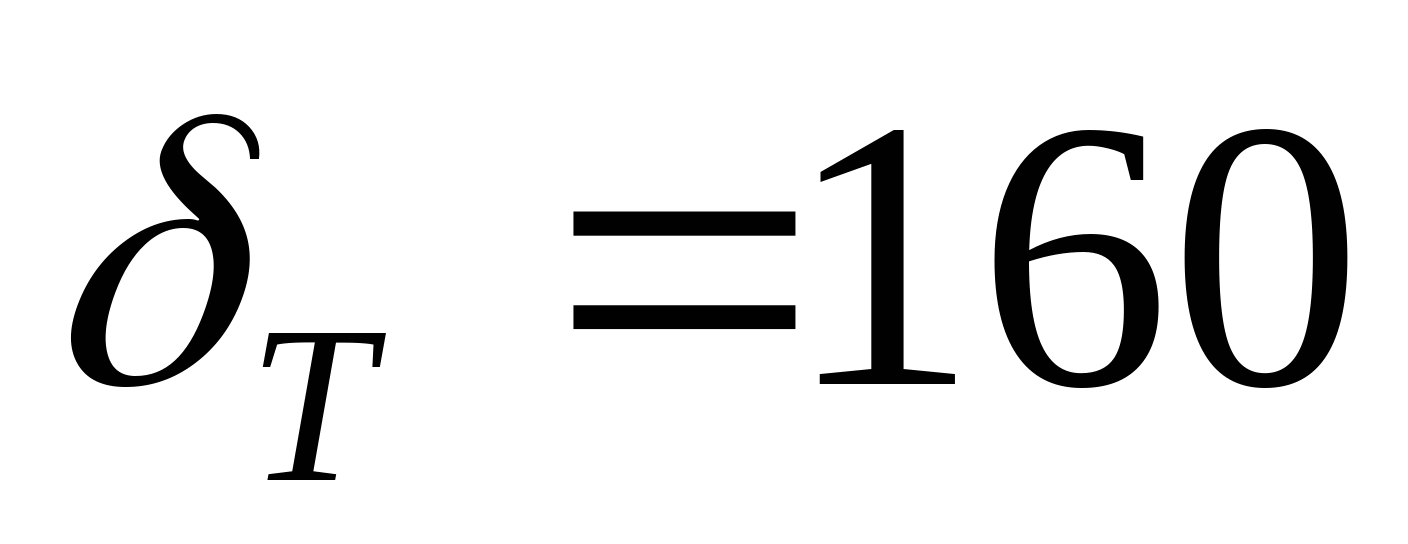 МПа; МПа; 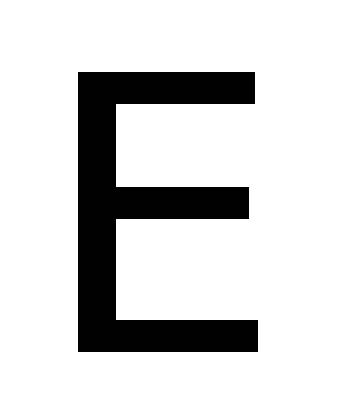 = =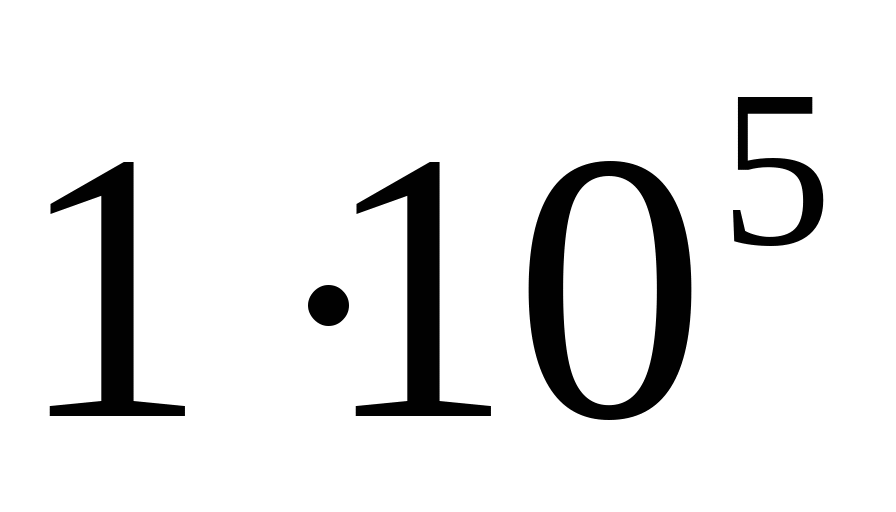 МПа; МПа; 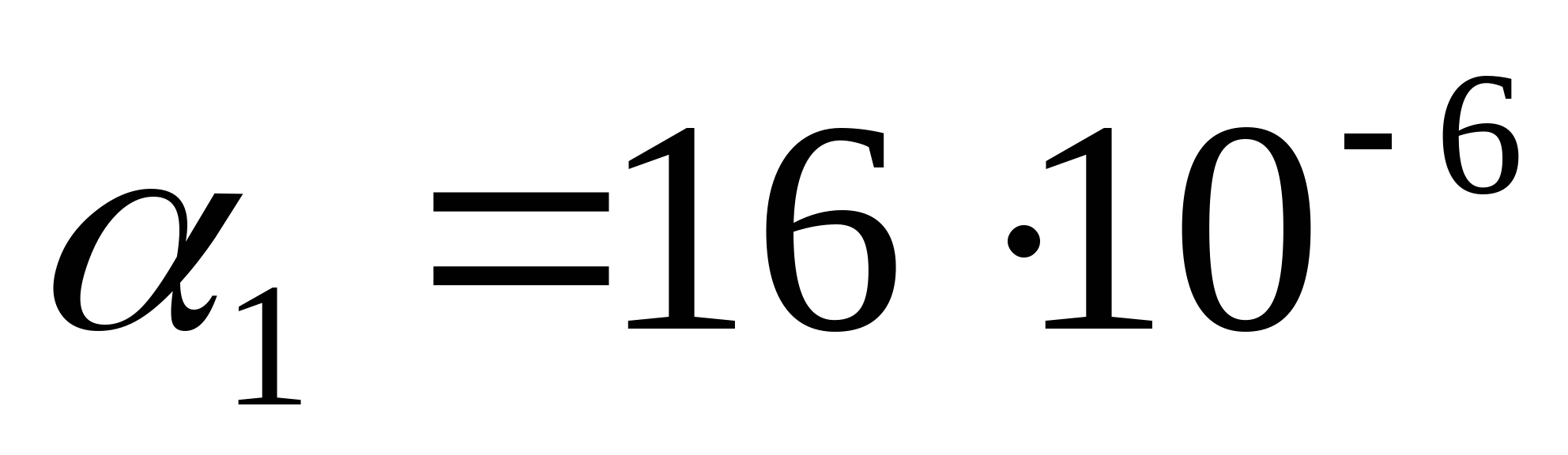 ; nТ1=1,5; ; nТ1=1,5; Стержень 2: 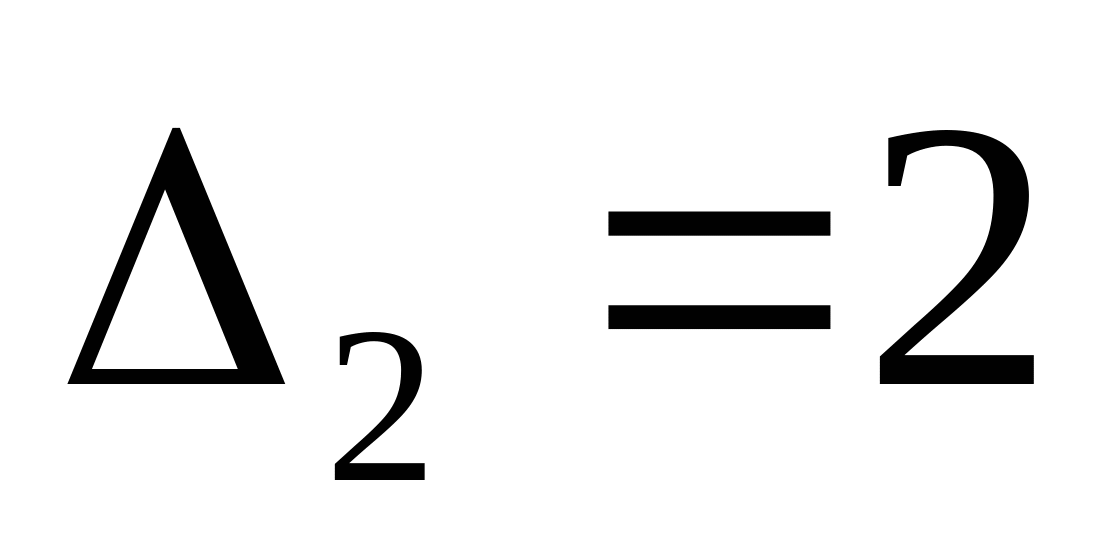 мм; Сталь 50; мм; Сталь 50; 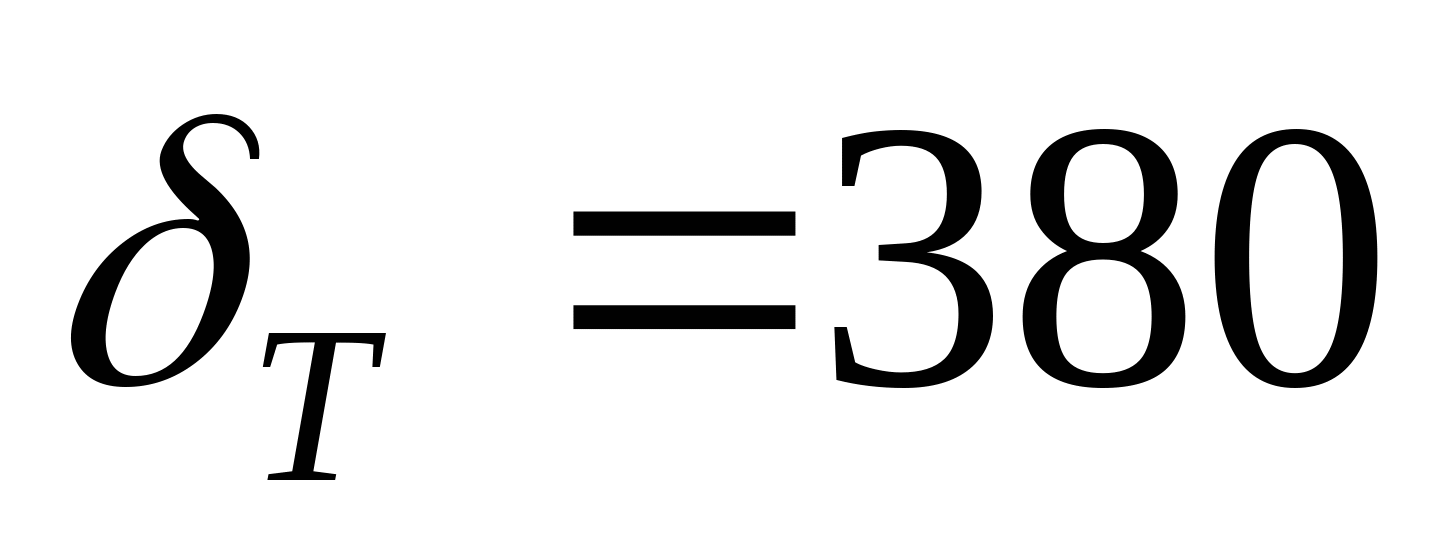 МПа; МПа; 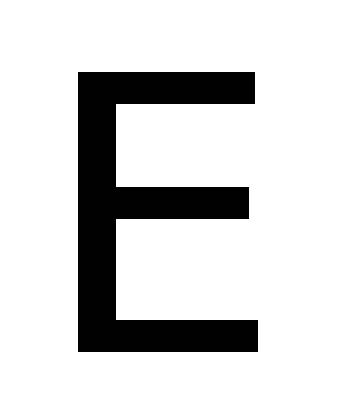 = =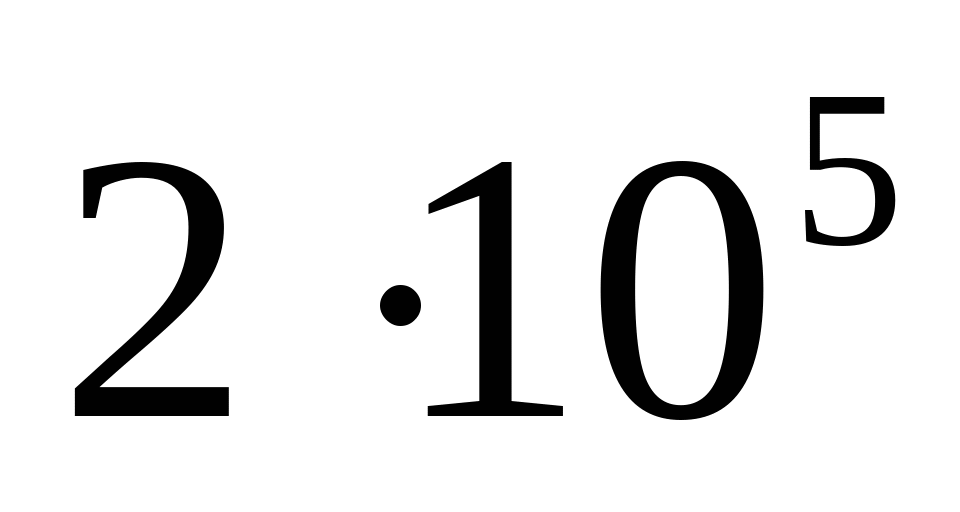 МПа; nТ2=1,5; МПа; nТ2=1,5;
Площади поперечных сечений: F1=F2=F
Отношение модулей упругости:
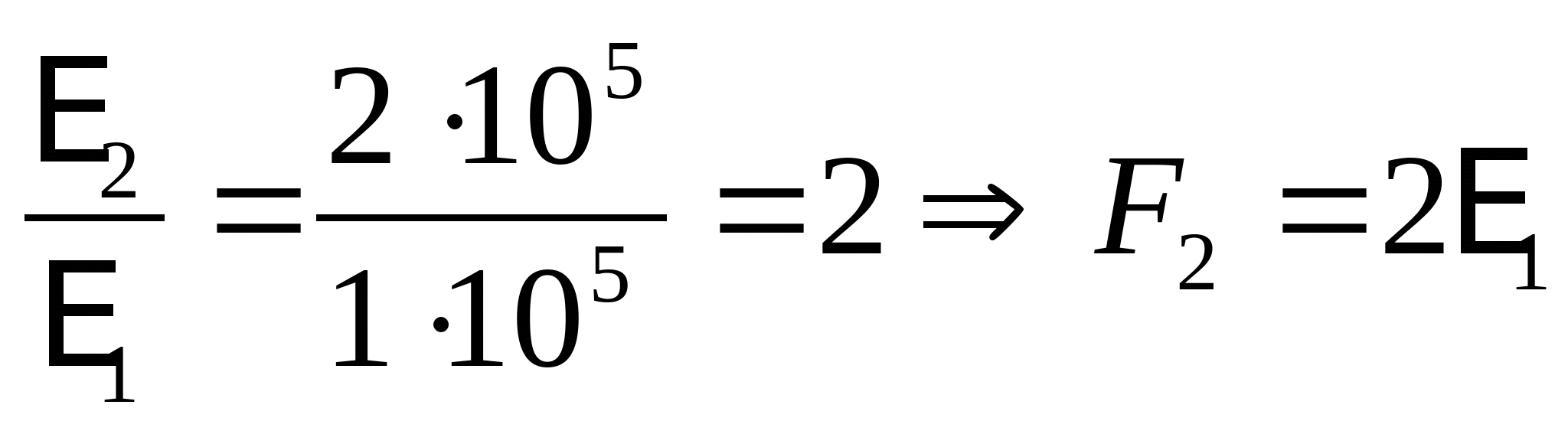 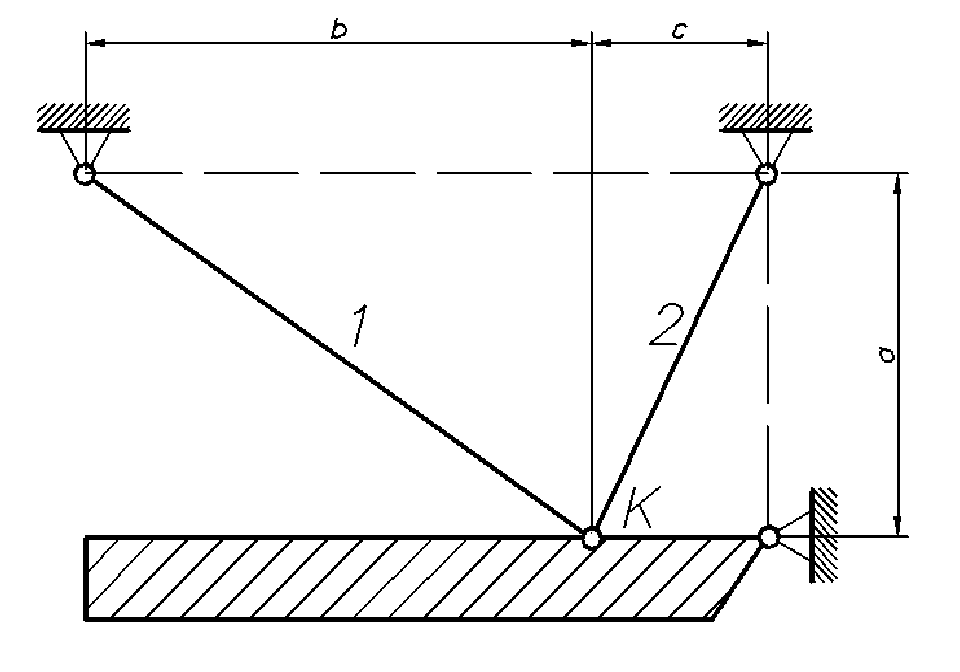
Рисунок 2. Общий вид конструкции.
Определяем углы 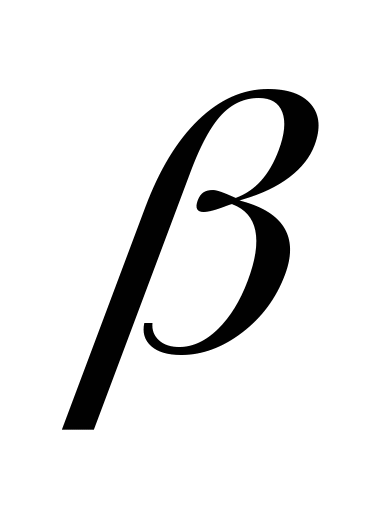 и и 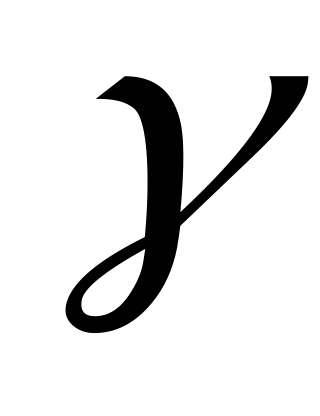 , и длины стержней: , и длины стержней:
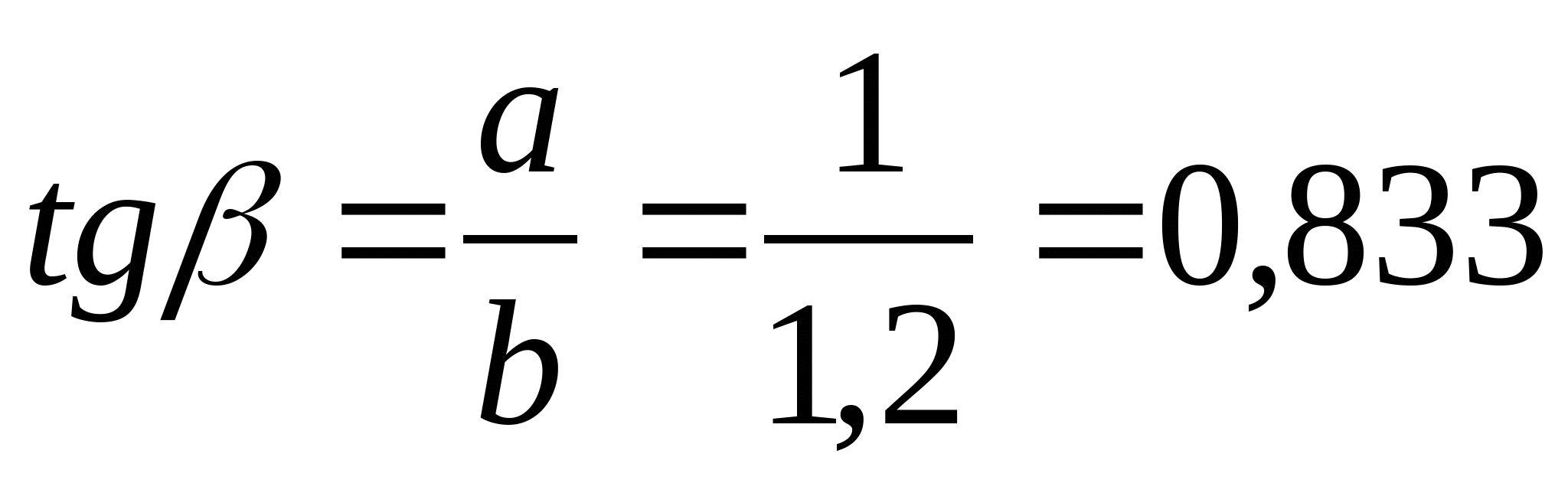 ; ; 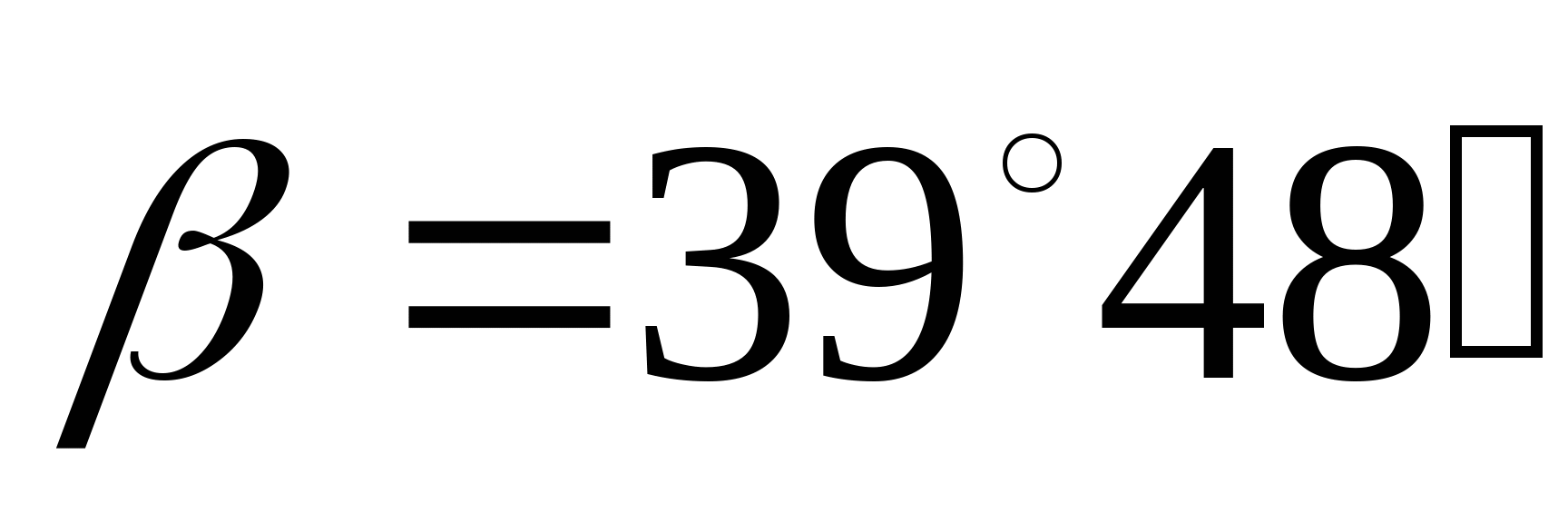 ; ; 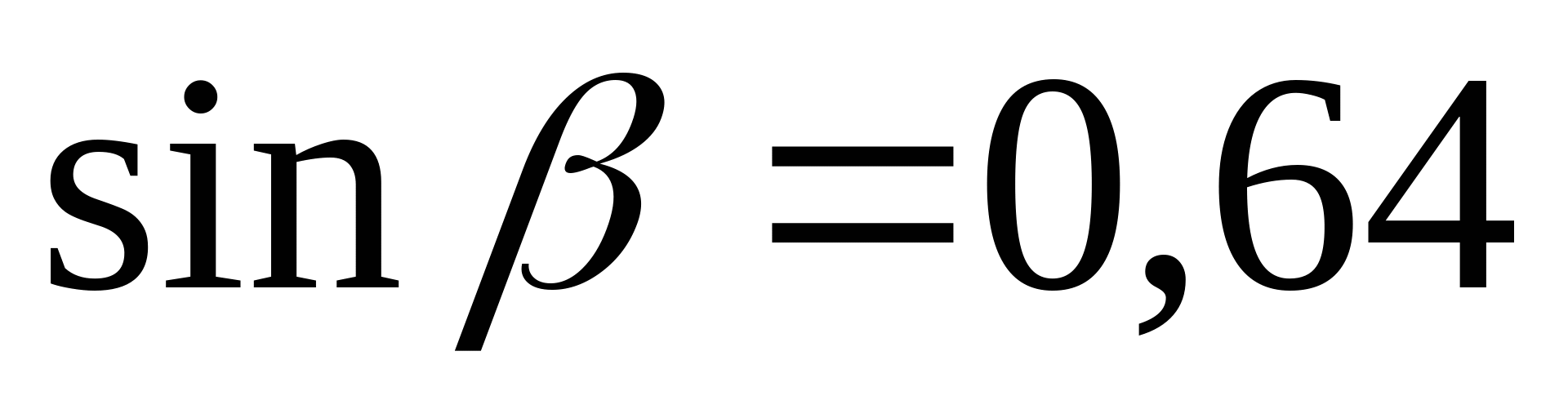 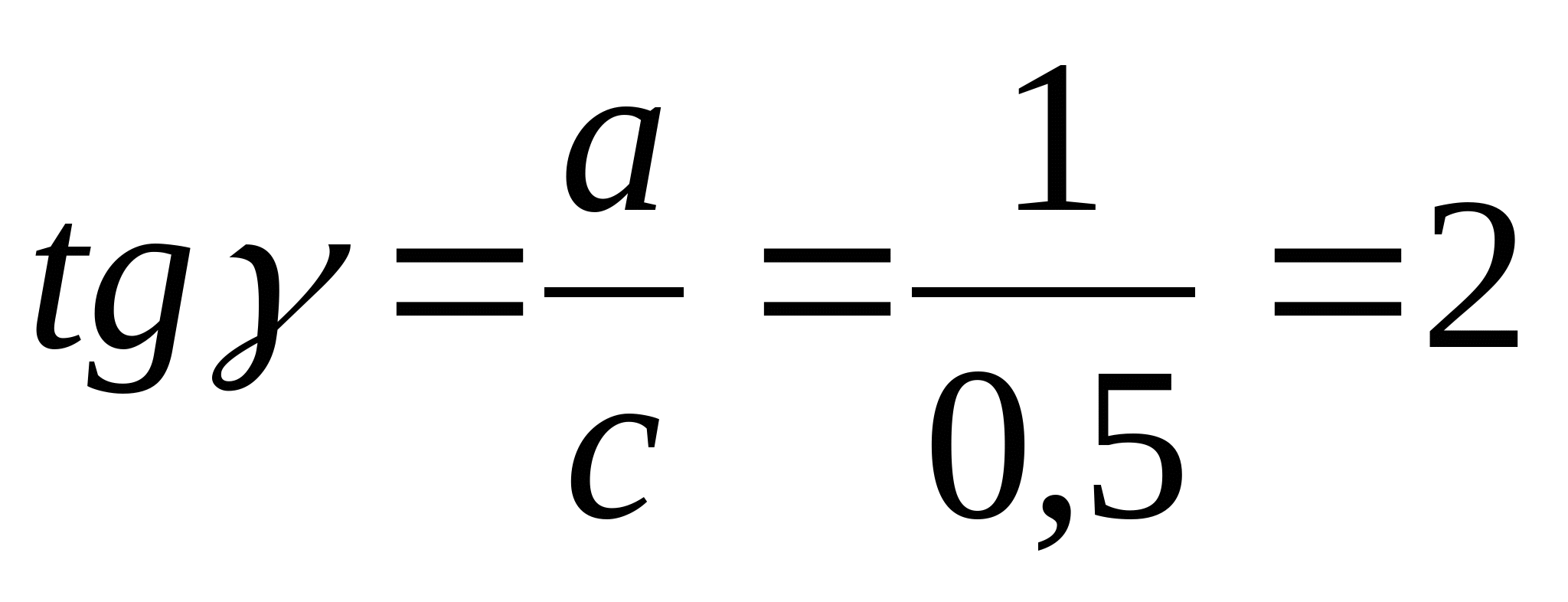 ; ; 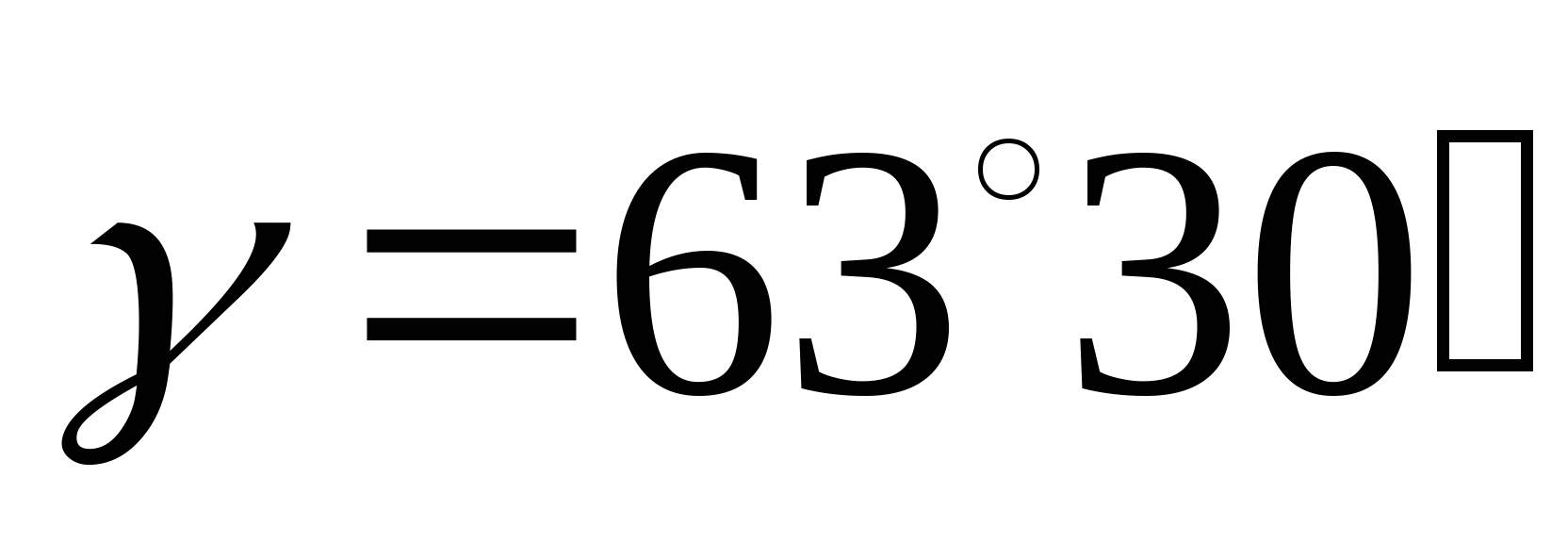 ; ; 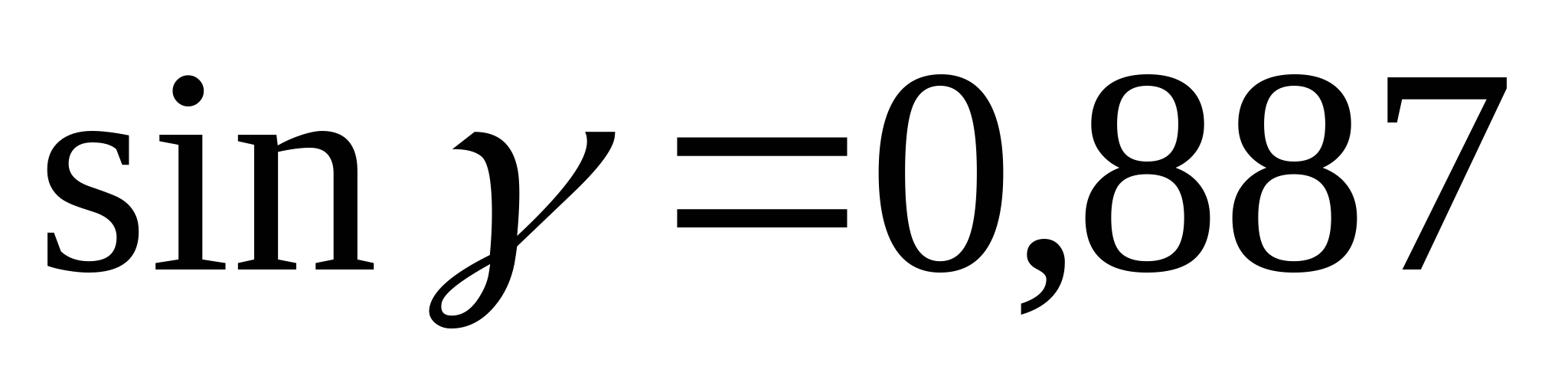 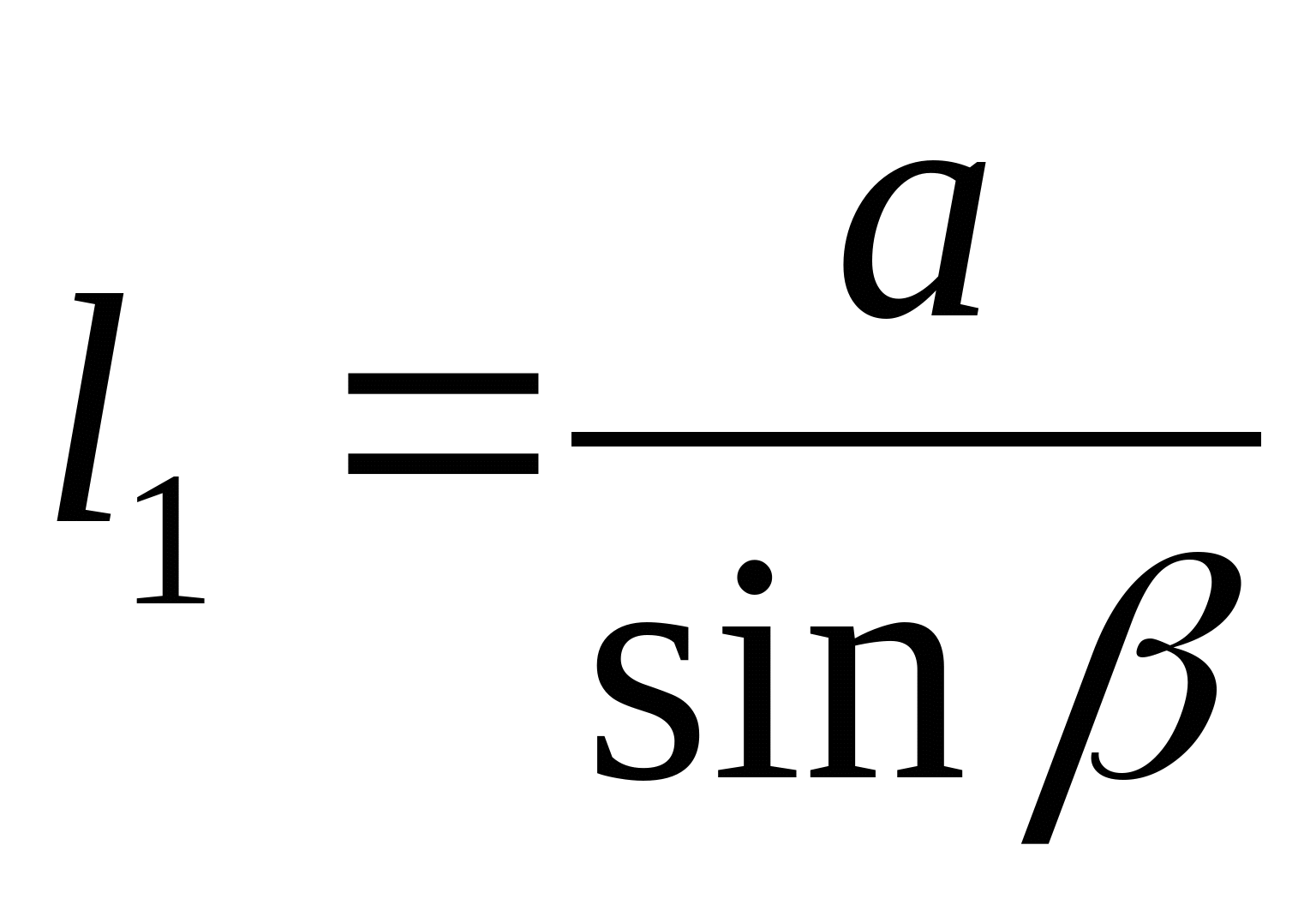 ; ; 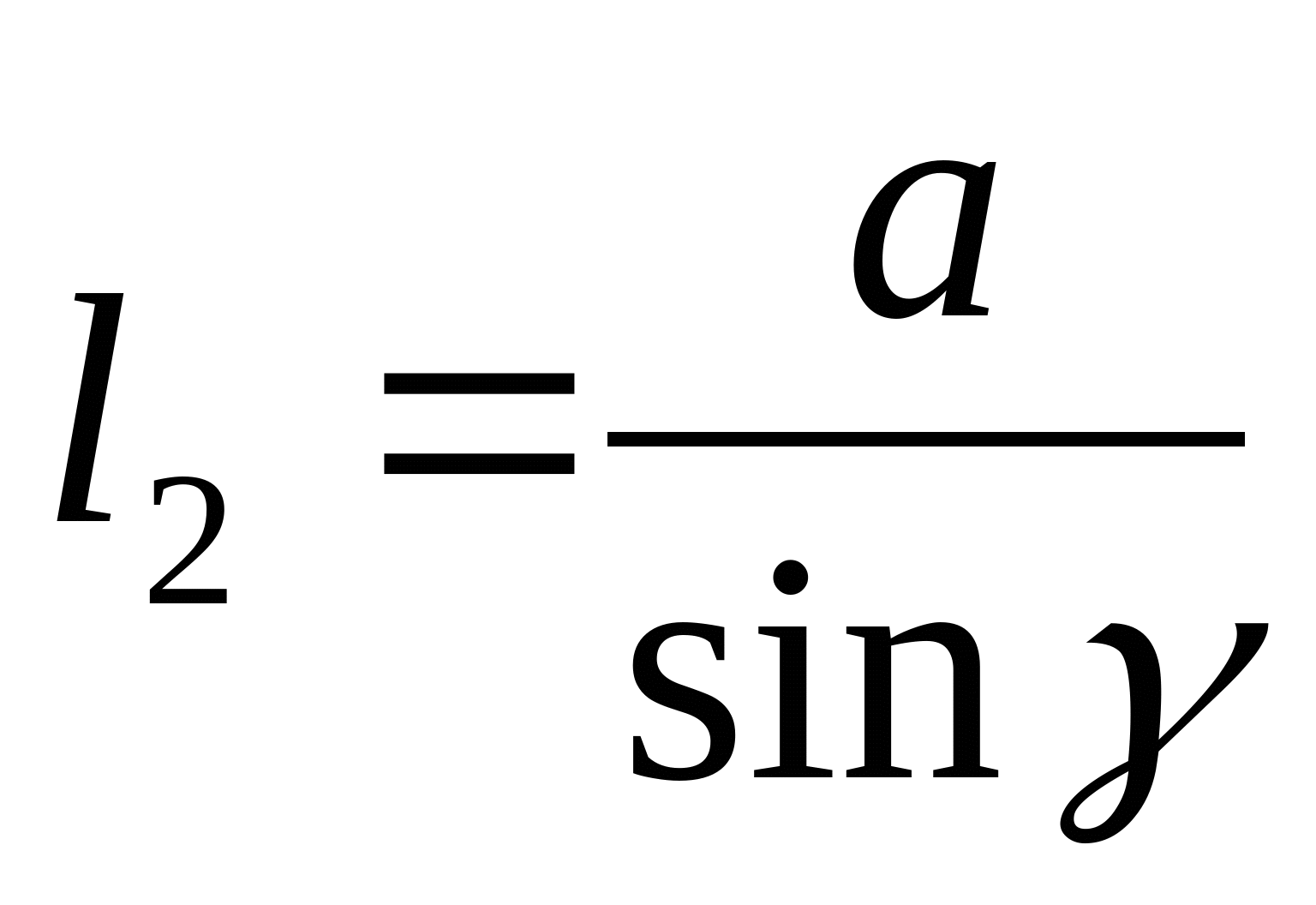
1. Температурная задача.
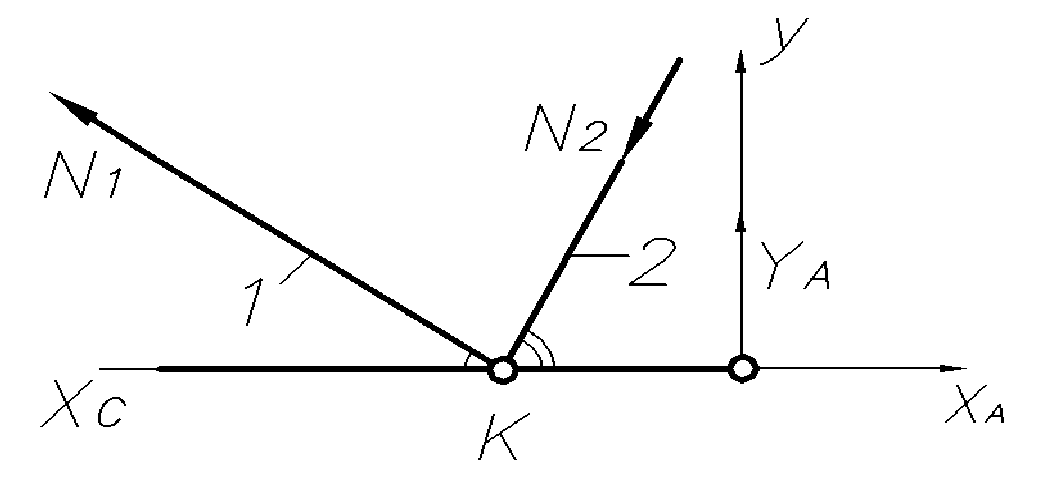
Рисунок 3.
Составим уравнение статики:
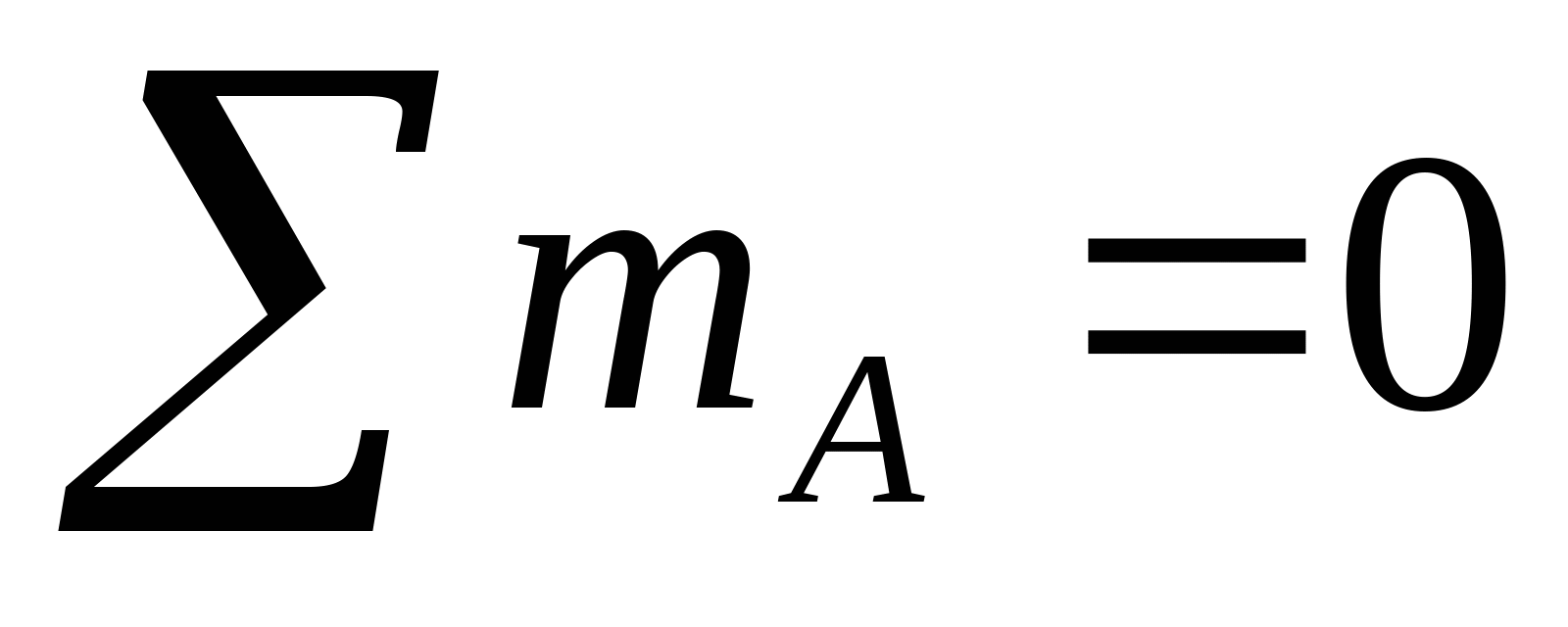 ; ; 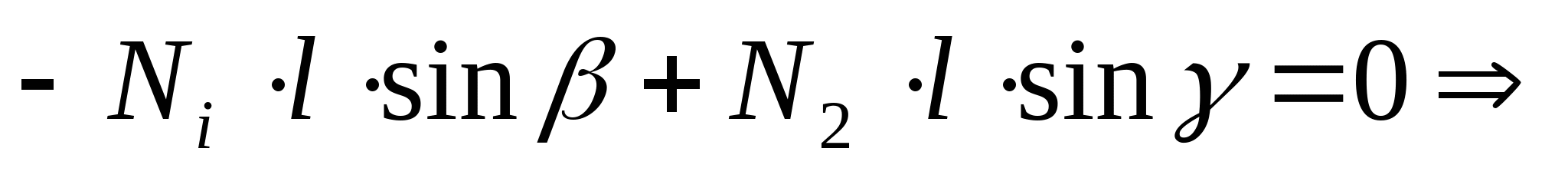 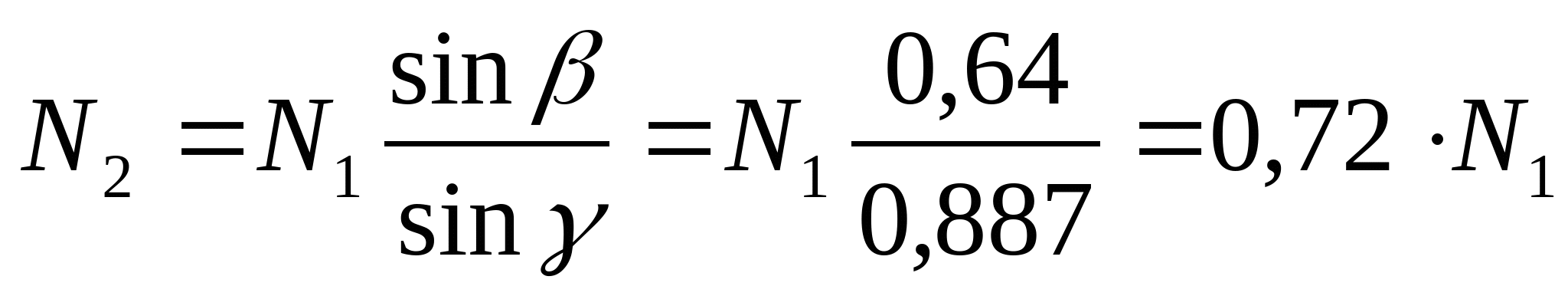 (1) (1) Определим степень статической неопределимости: n=2-1=1
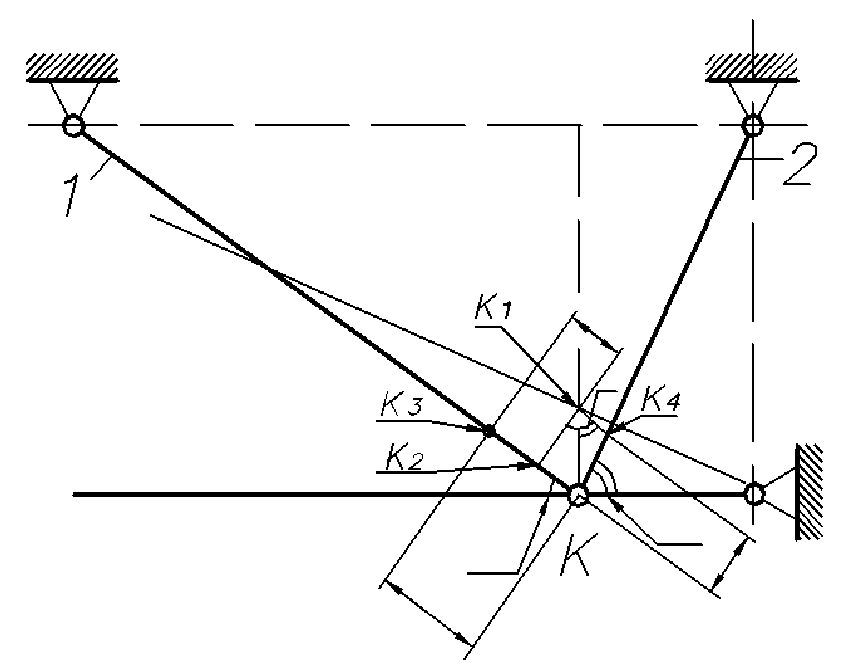
Рисунок 4. Схема перемещений. Составим уравнение совместности деформирования и перемещения:
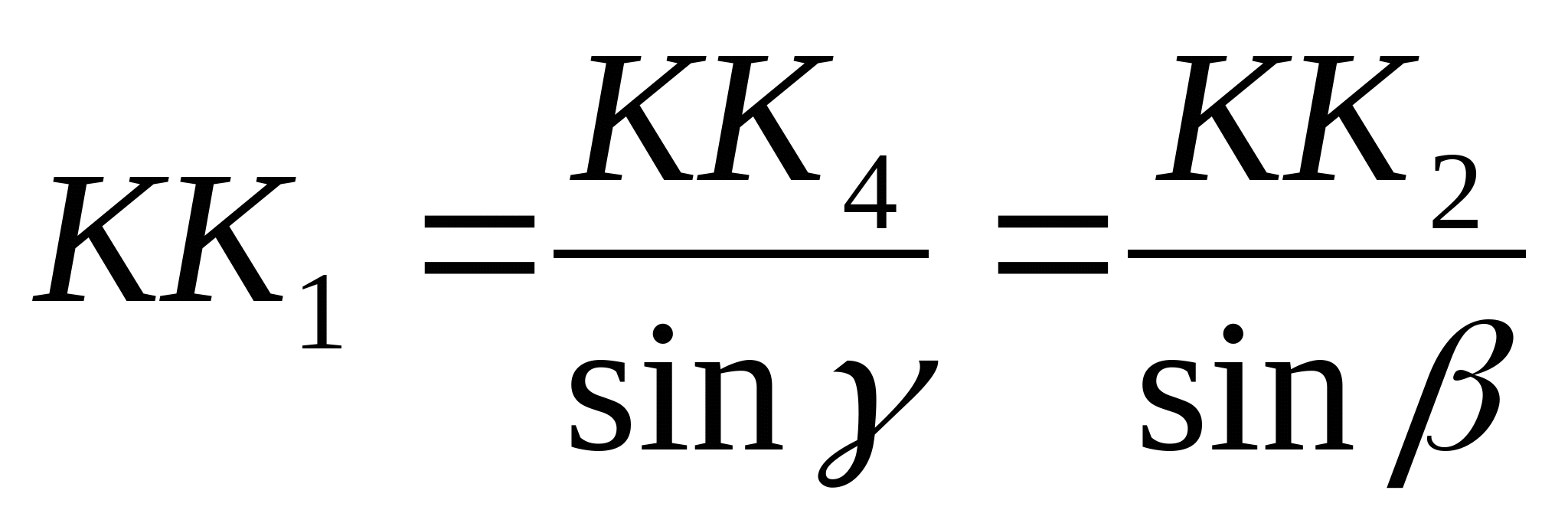 или или 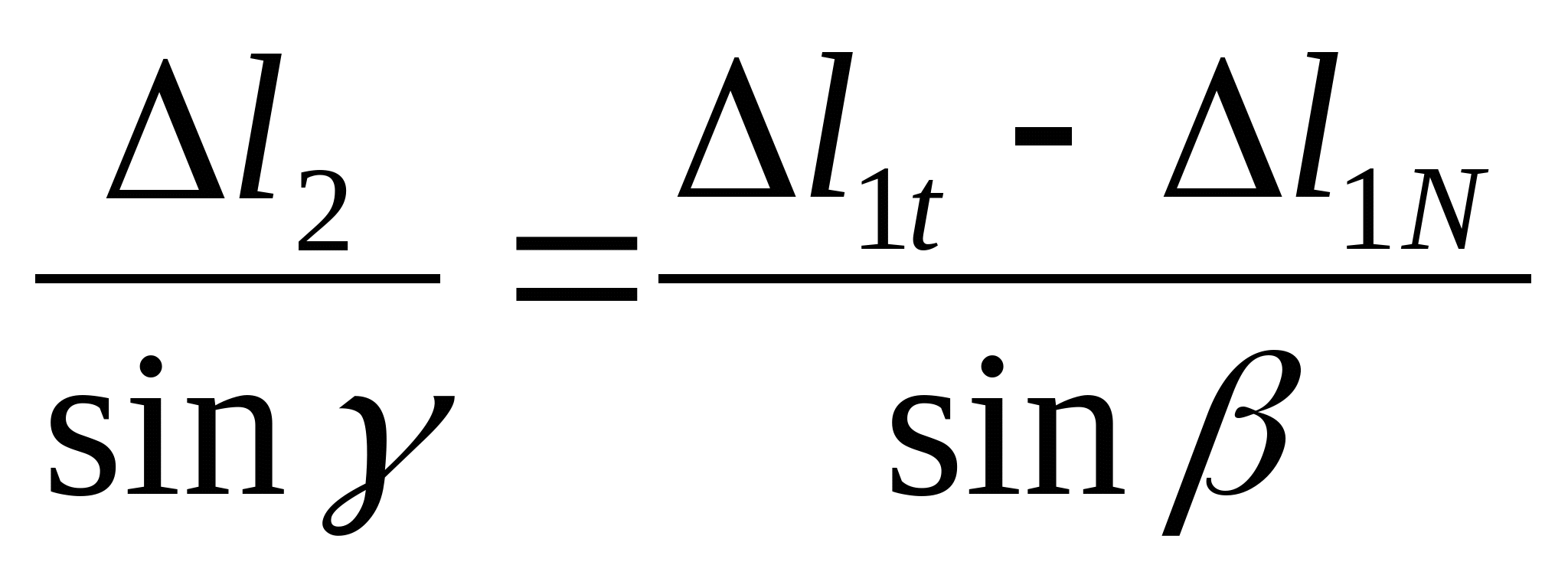 (2) (2) 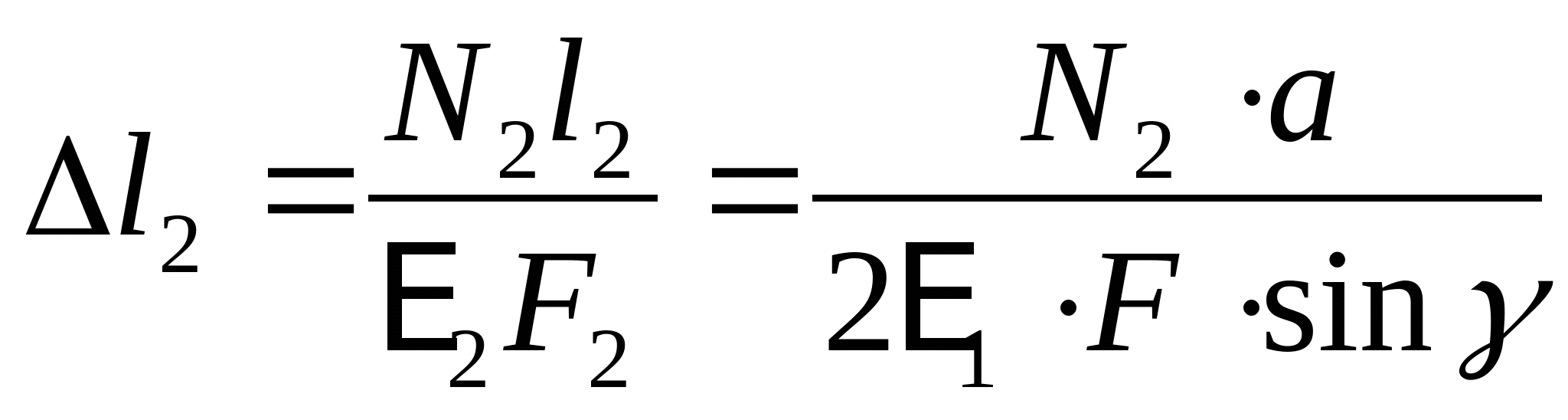 (3) (3) 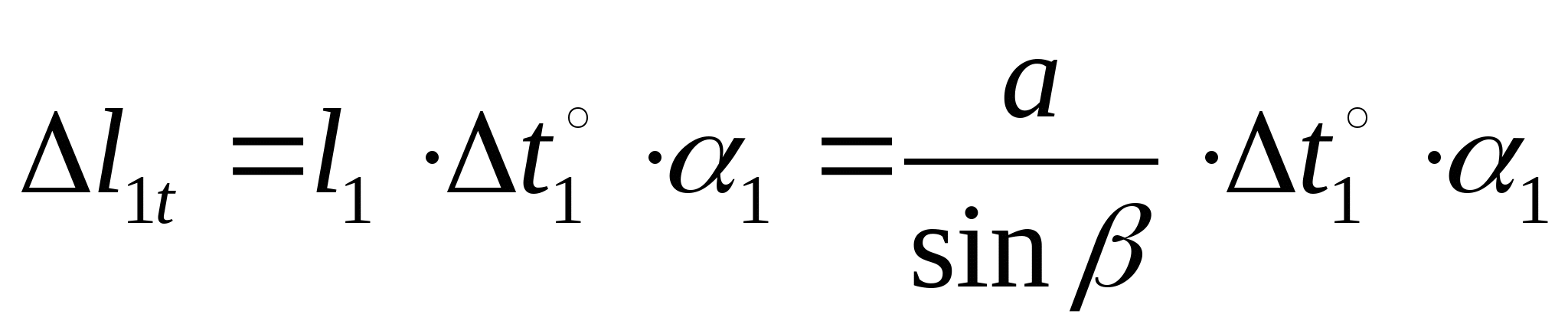 (4) (4)
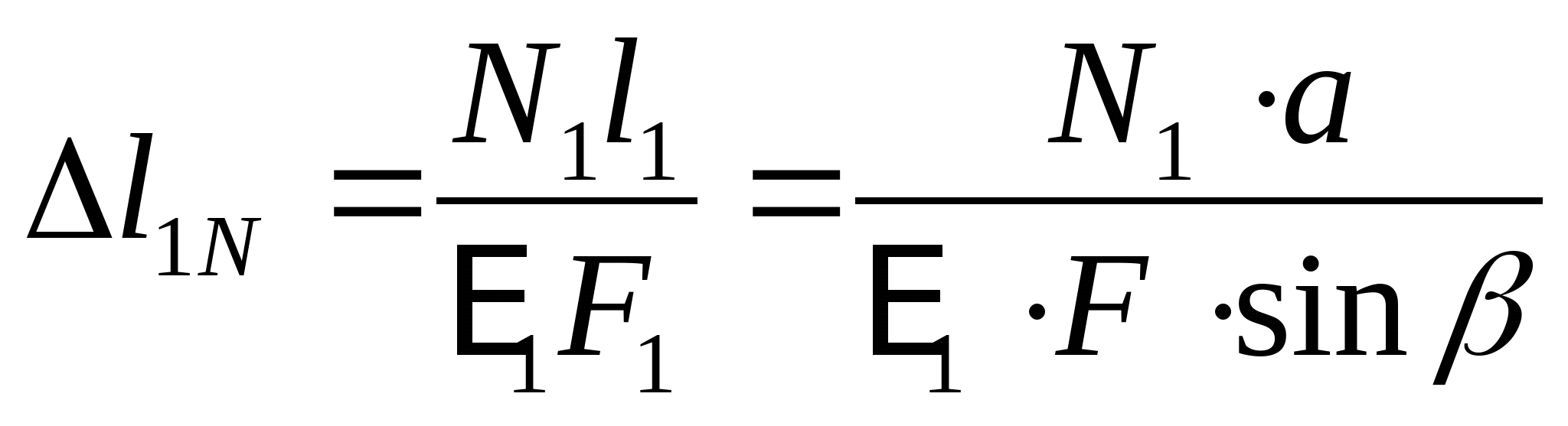 (5) (5)
Подставим полученные результаты (3), (4) и (5) в уравнение (2):
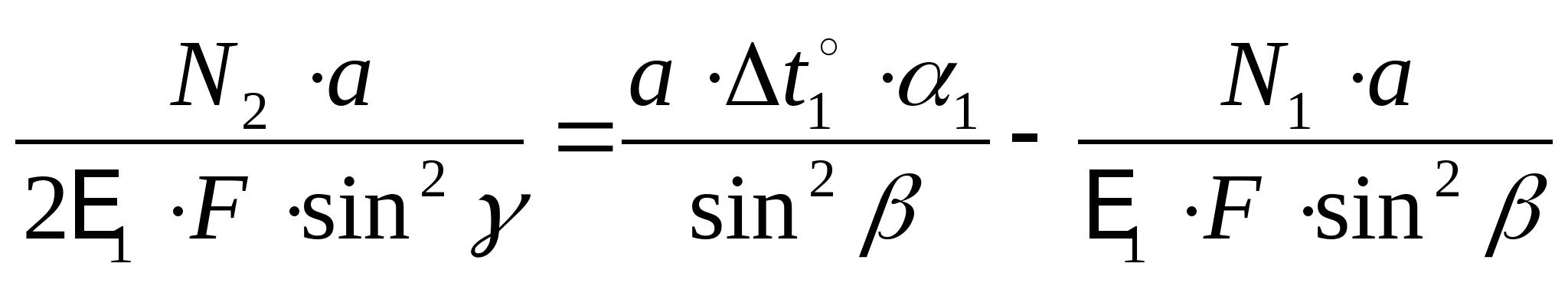 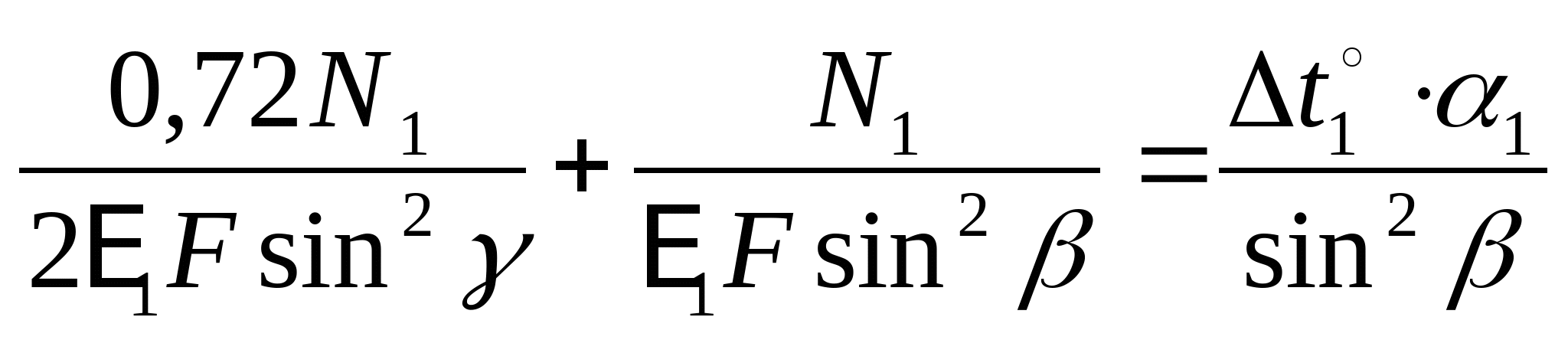 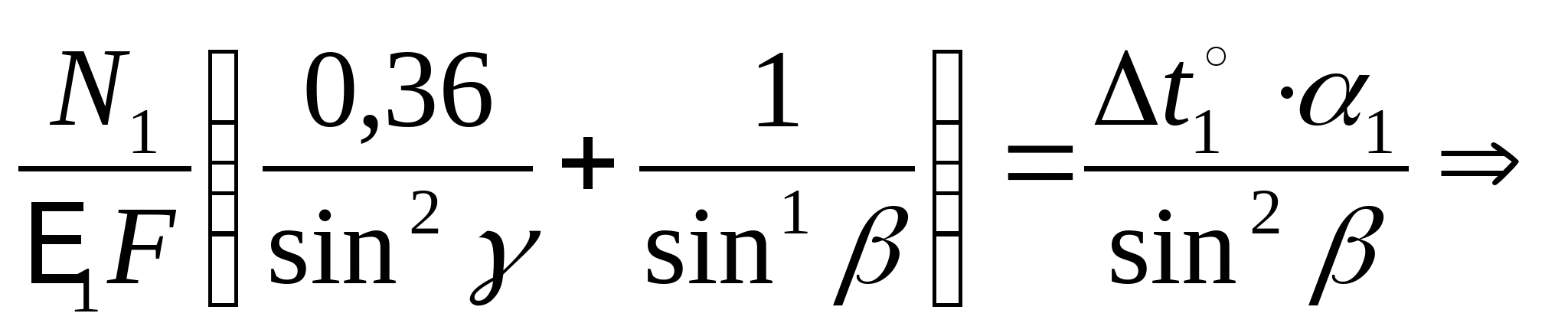 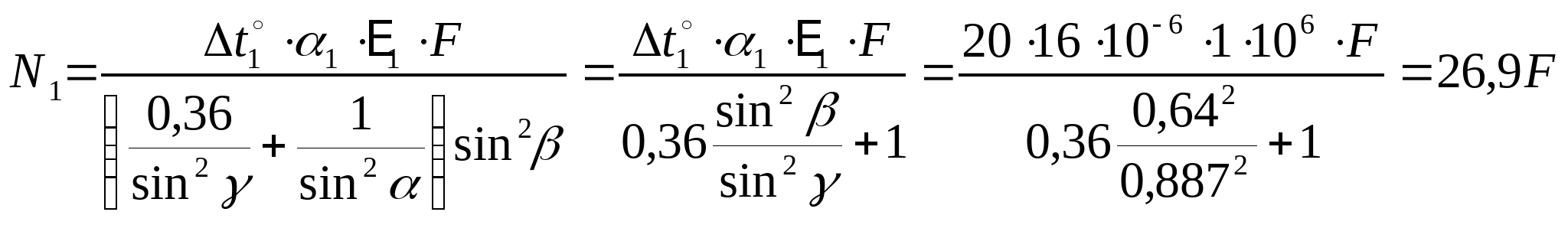
Полученный результат подставляем в (1) и получаем:
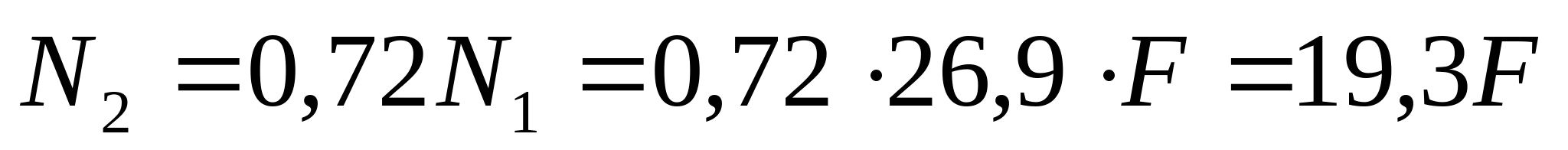
Так как сила N2 является сжимающей, то значение N2 примет значение -19,3F.
Составим уравнение температурных напряжений:
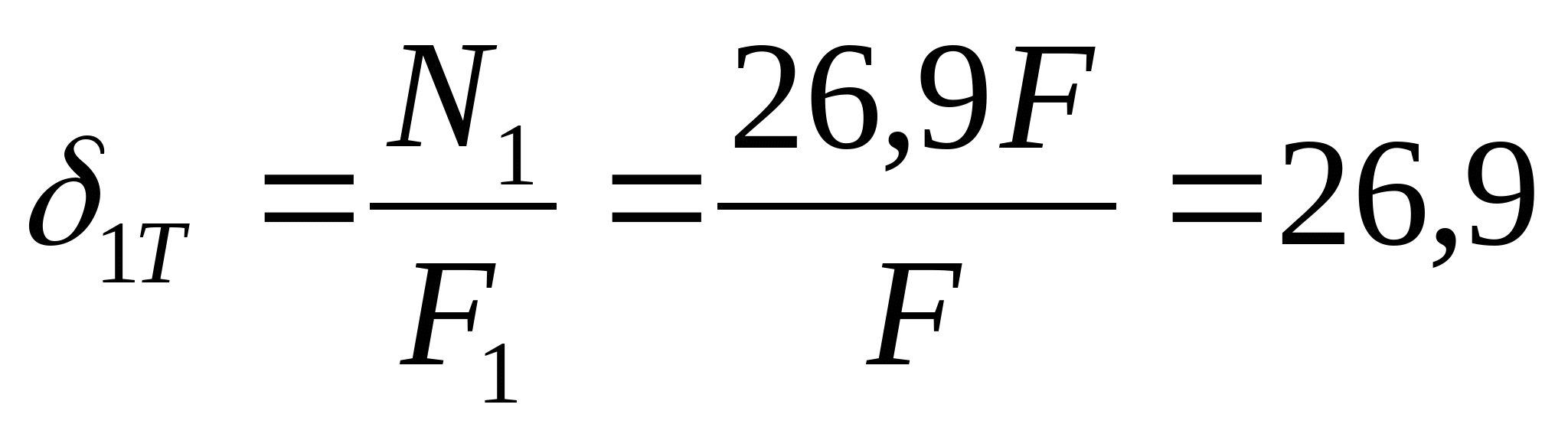 МПа МПа 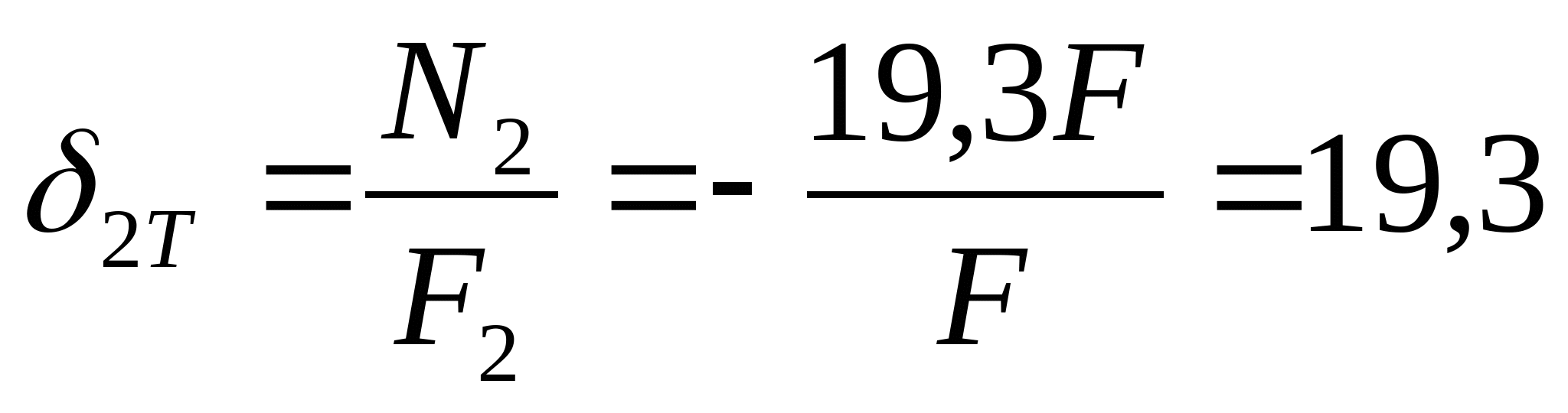 МПа МПа
2. Монтажная задача.
В нашей конструкции стержень 2 выполнен на 2 мм длиннее, чем 1, то при сборке стрежневой системы, он будет сжиматься, а стержень 1 – растягиваться. Это означает, что уравнение статики и схема сил будут аналогичны тем, что мы составили в температурной задаче, а из этого следует что: N2=0,72N1 (1)
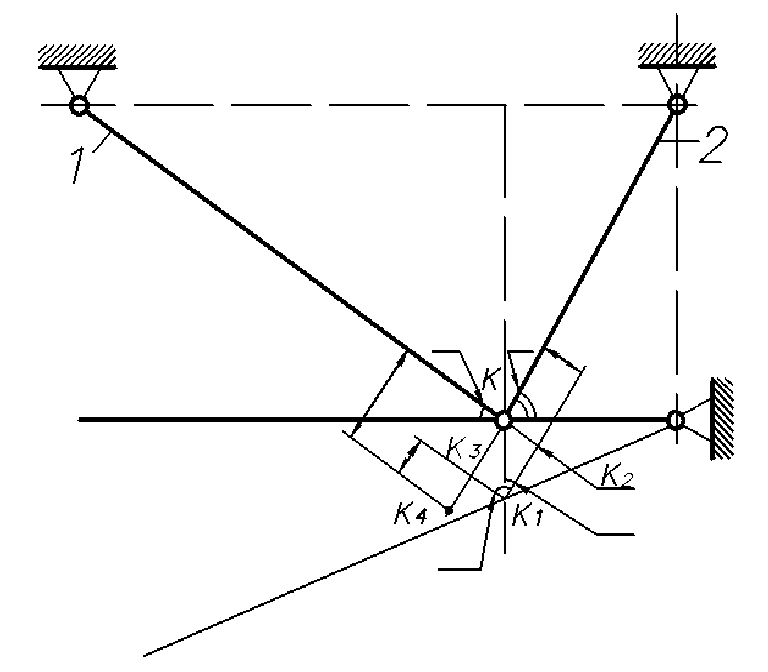
Рисунок 5. Схема перемещений.
Составим уравнение совместности деформаций и перемещений: 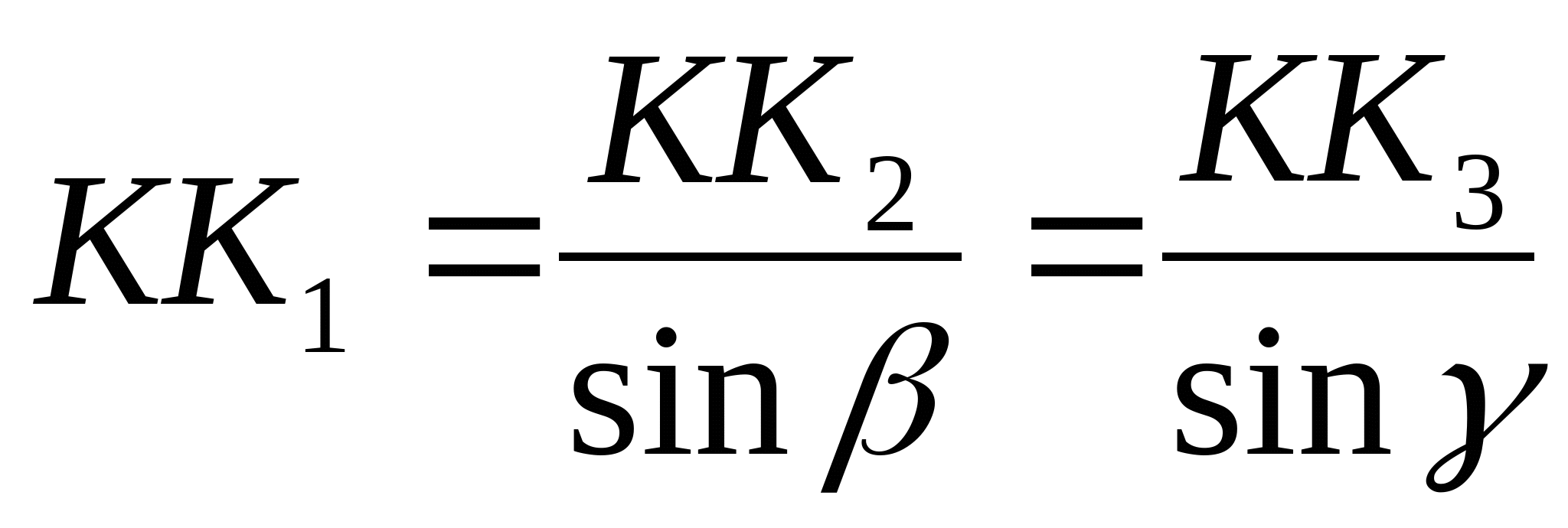 или или 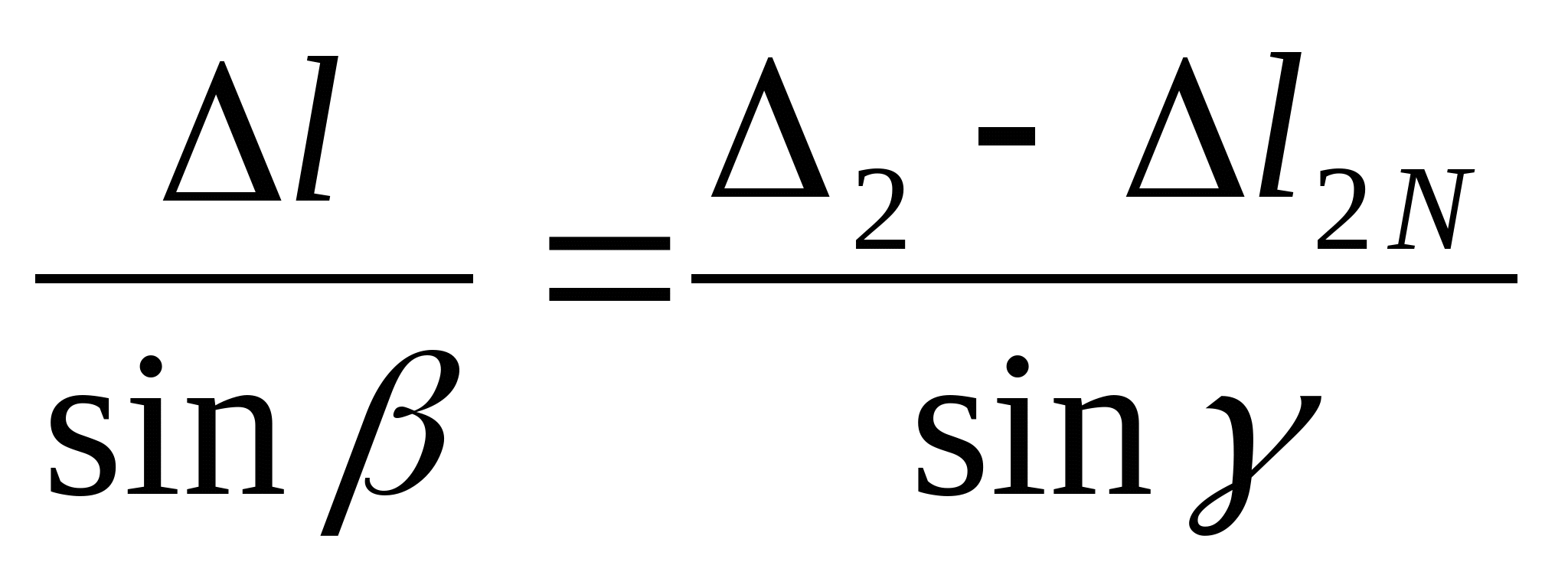 (2) (2) 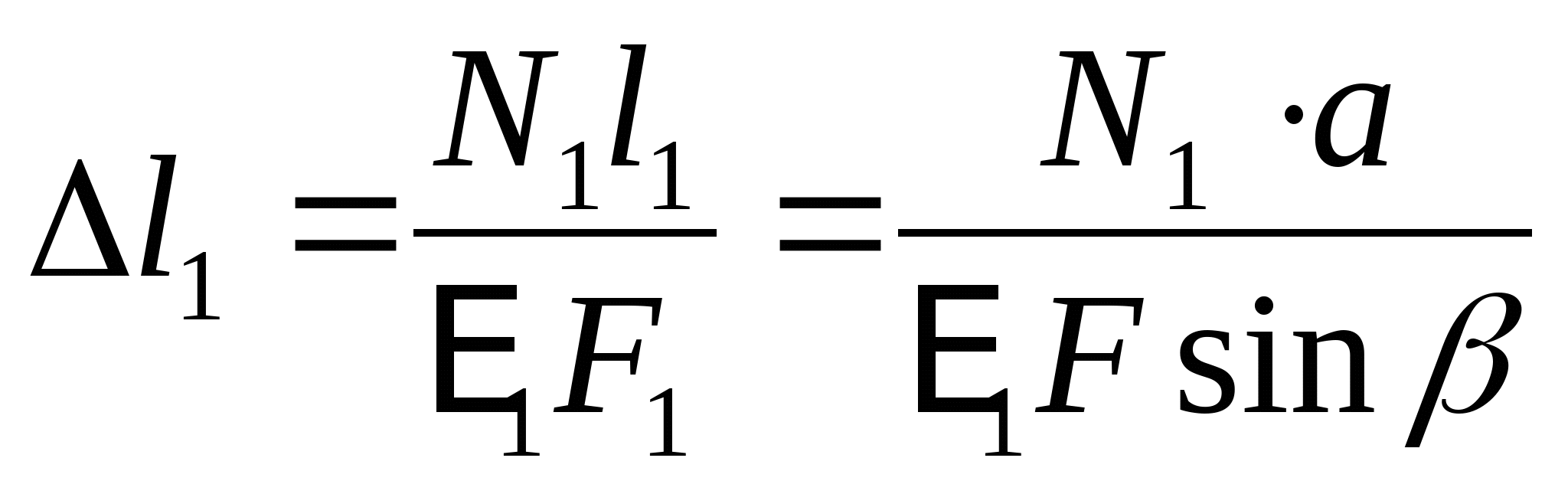 (3) (3) 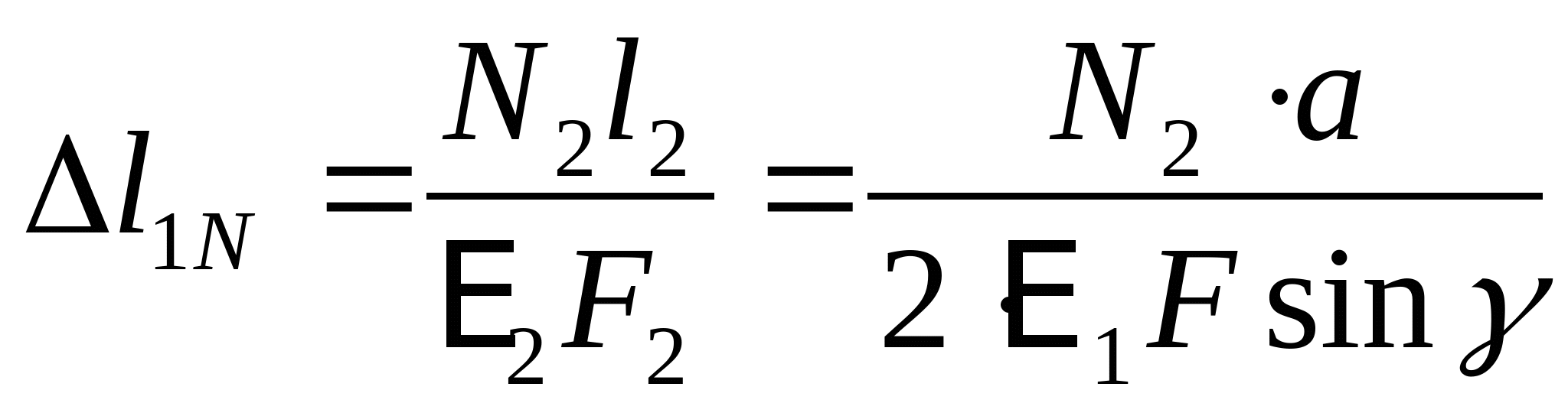 (4) (4) Подставим полученные уравнения (3) и (4) в (2): 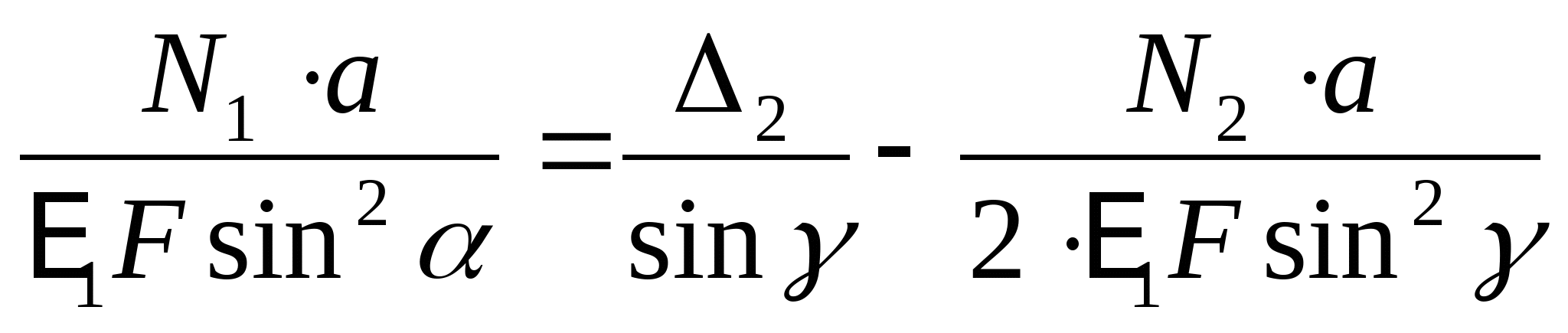
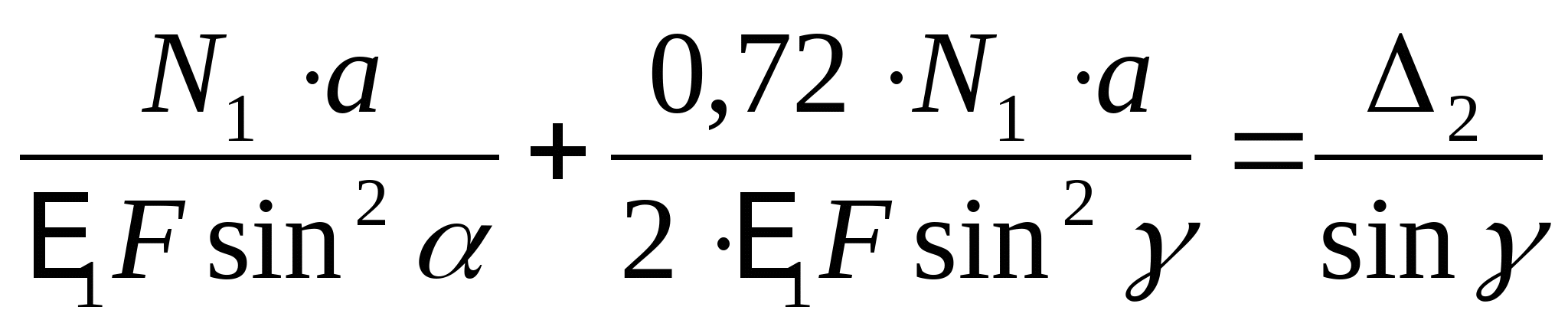 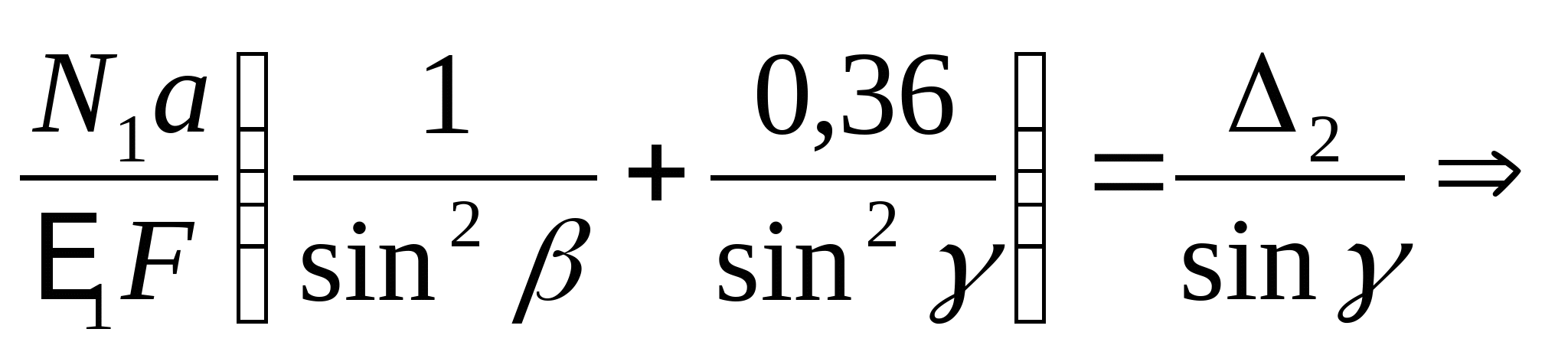 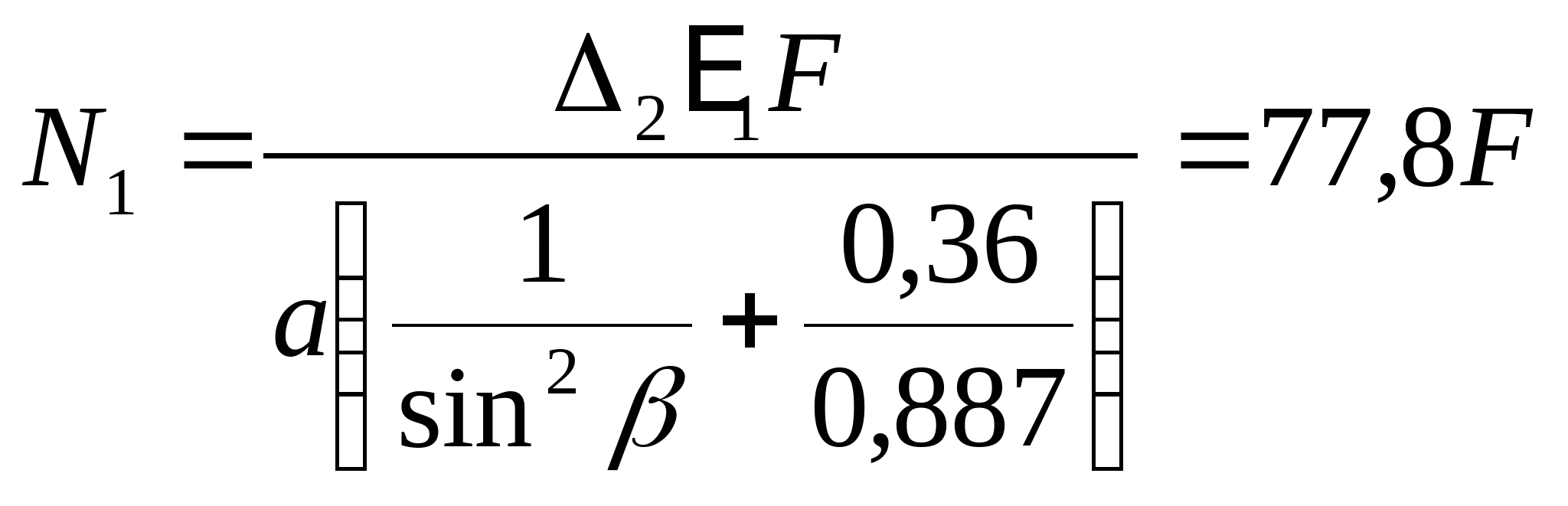 Подставив полученный результат в (1) получим: 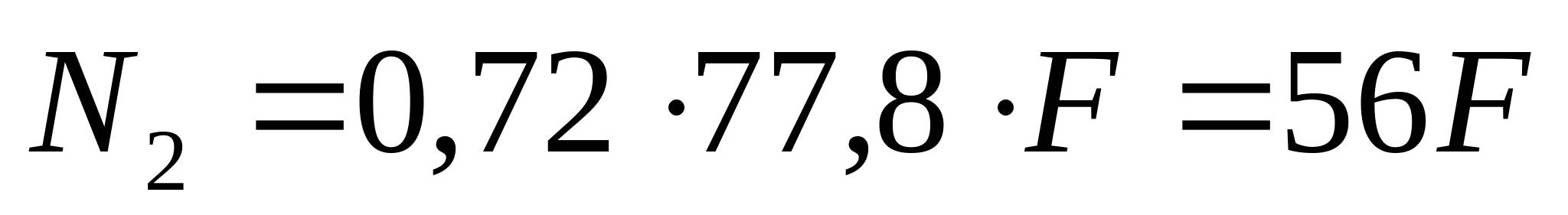 Так как сила N2 является сжимающей, то значение N2 примет значение -56F. Составим уравнения монтажных напряжений: 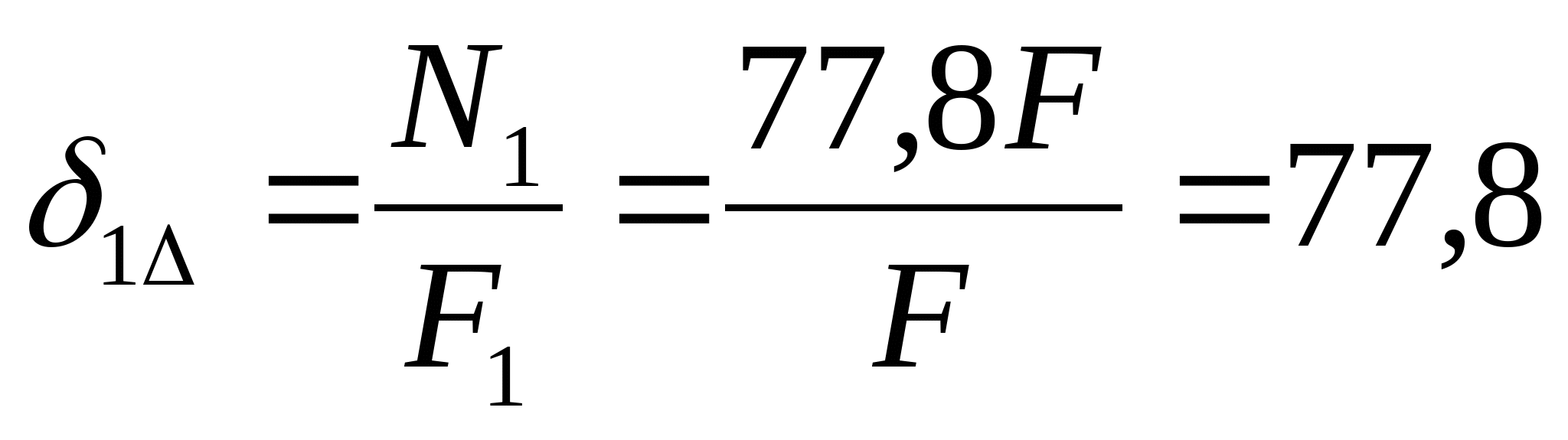 МПа МПа 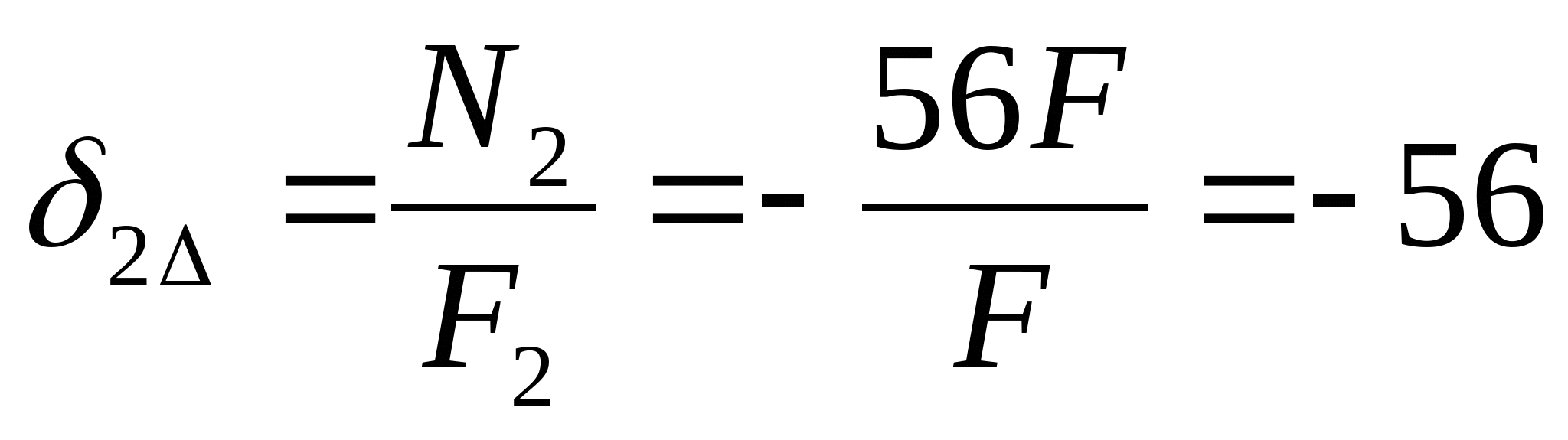 Мпа Мпа
3. Определяем суммарные напряжения. 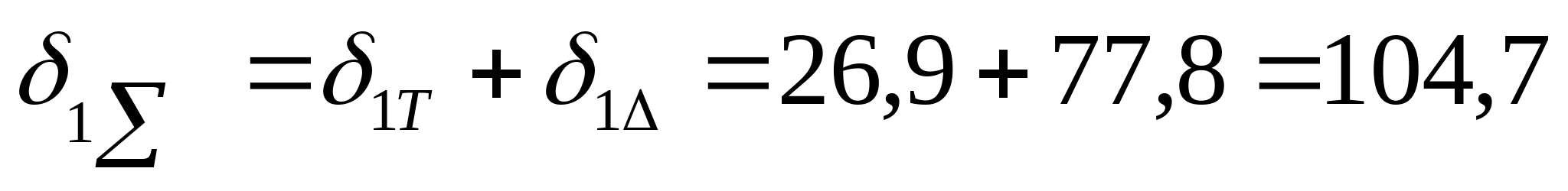 Мпа Мпа 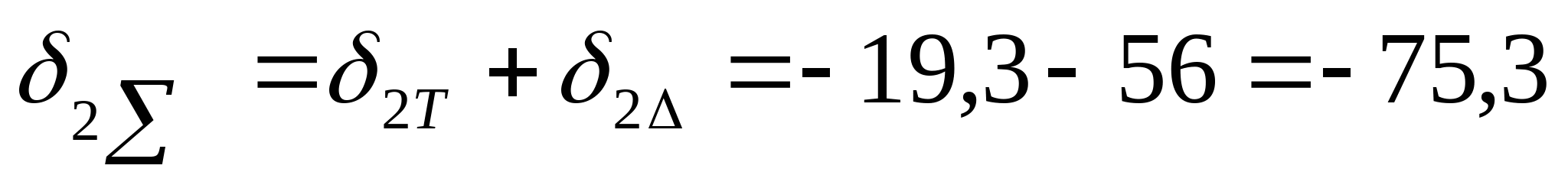 Мпа Мпа
4. Определяем допускаемые напряжения. Стержень 1: 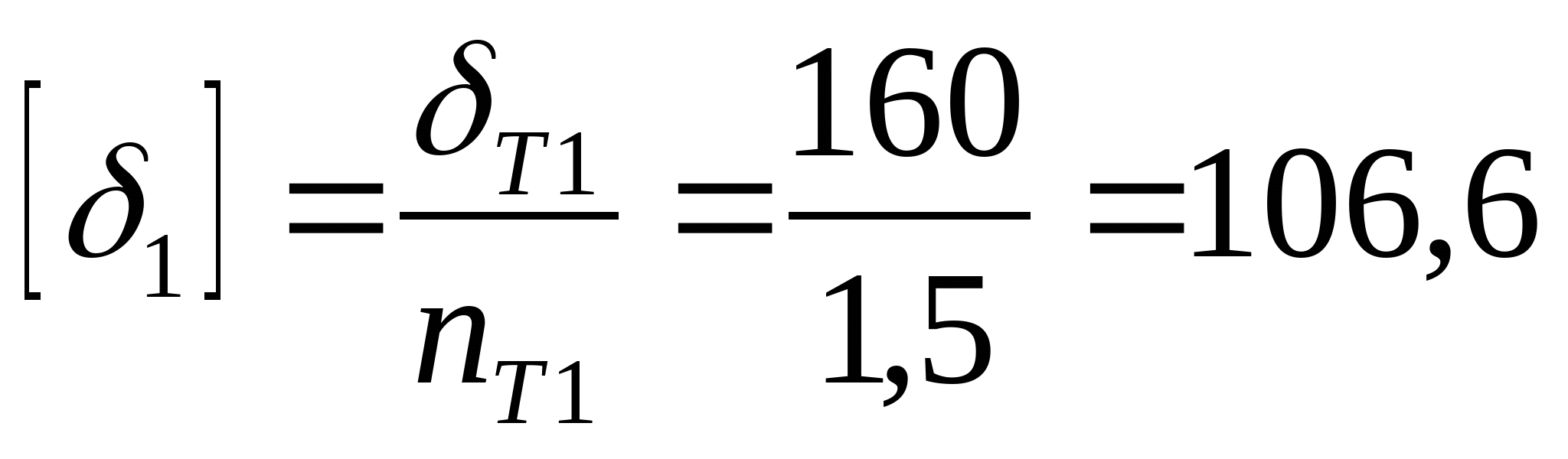 Мпа Мпа Получается, что 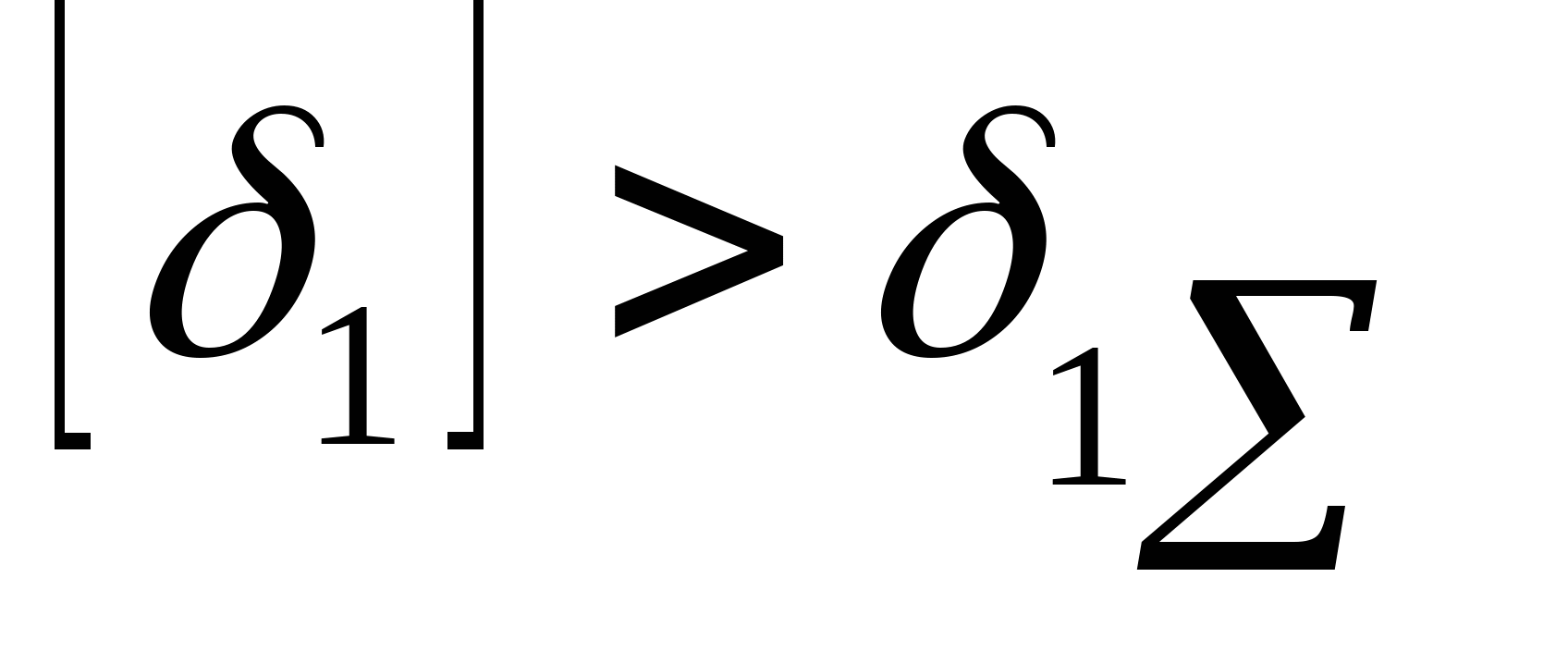 , значит, условие прочности выполняется. , значит, условие прочности выполняется. Стержень 2: 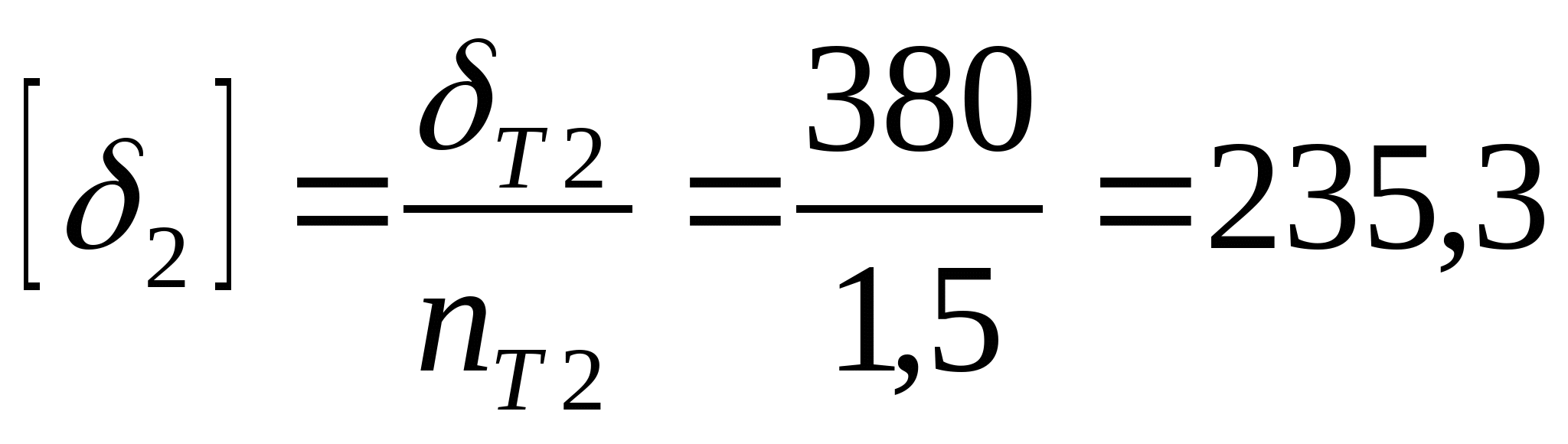 Мпа Мпа Получается, что 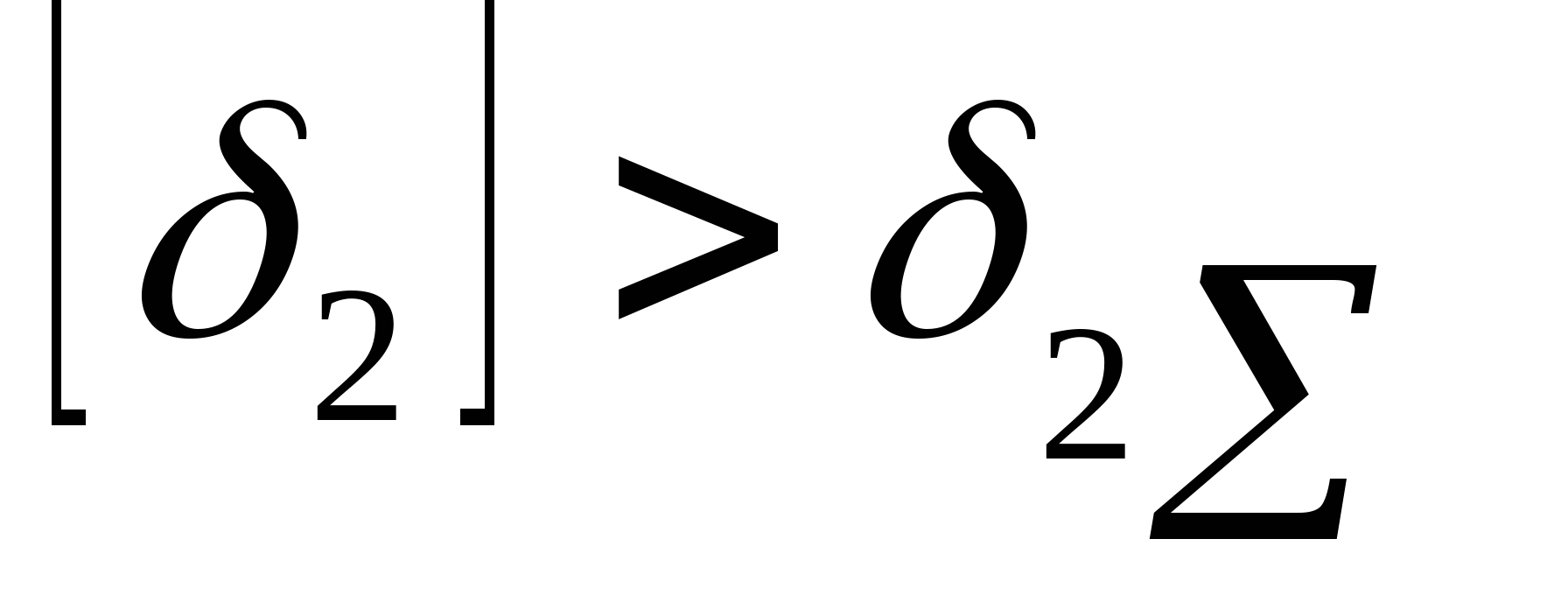 , значит, условие прочности выполняется. , значит, условие прочности выполняется. Рассчитаем истинные коэффициенты запаса прочности: 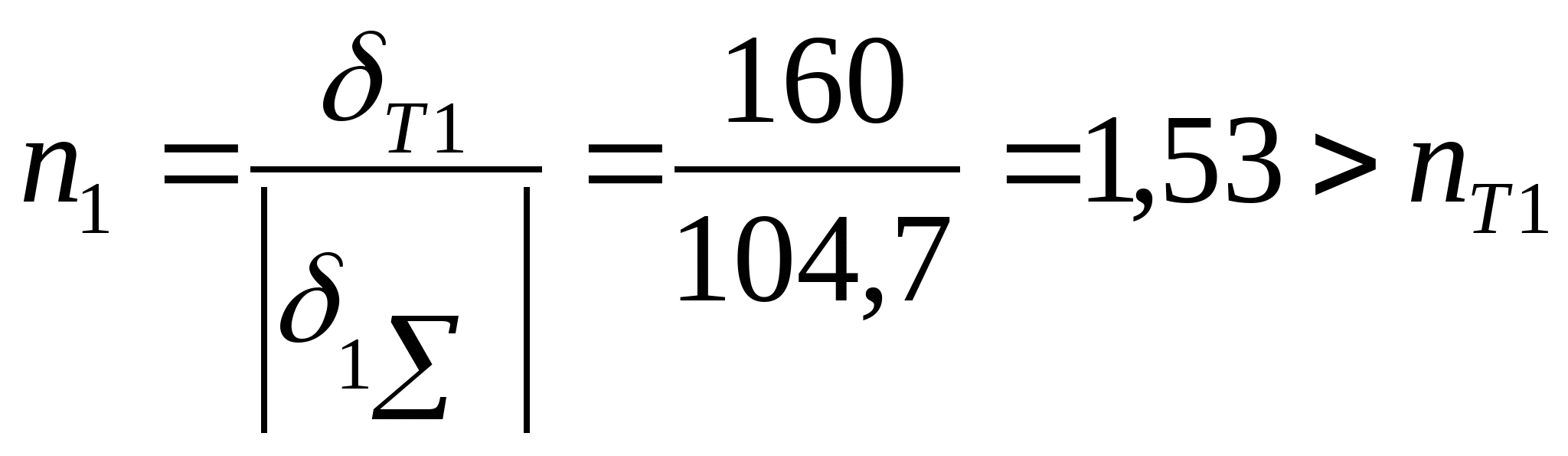 ; ; 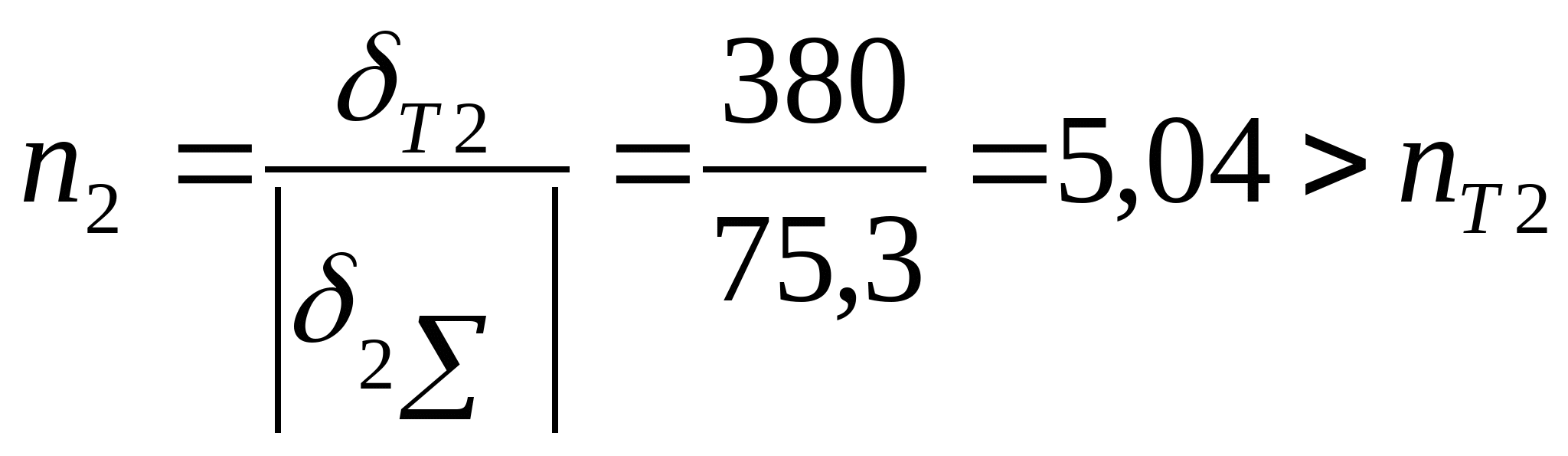 . .
Вывод: Запас прочности n1<n2 при суммарном напряжении 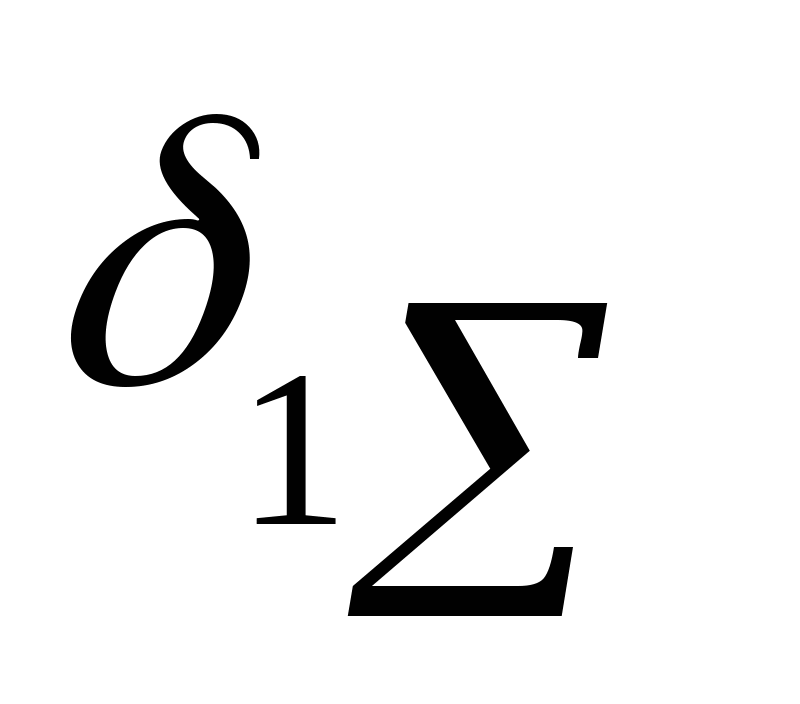 растягивающих, поэтому полезную нагрузку целесообразно приложить к балке АК так, чтобы она поворачивалась по часовой стрелке. Тогда стержень 1 будет сжиматься, компенсируя положительное значение растягивающих, поэтому полезную нагрузку целесообразно приложить к балке АК так, чтобы она поворачивалась по часовой стрелке. Тогда стержень 1 будет сжиматься, компенсируя положительное значение 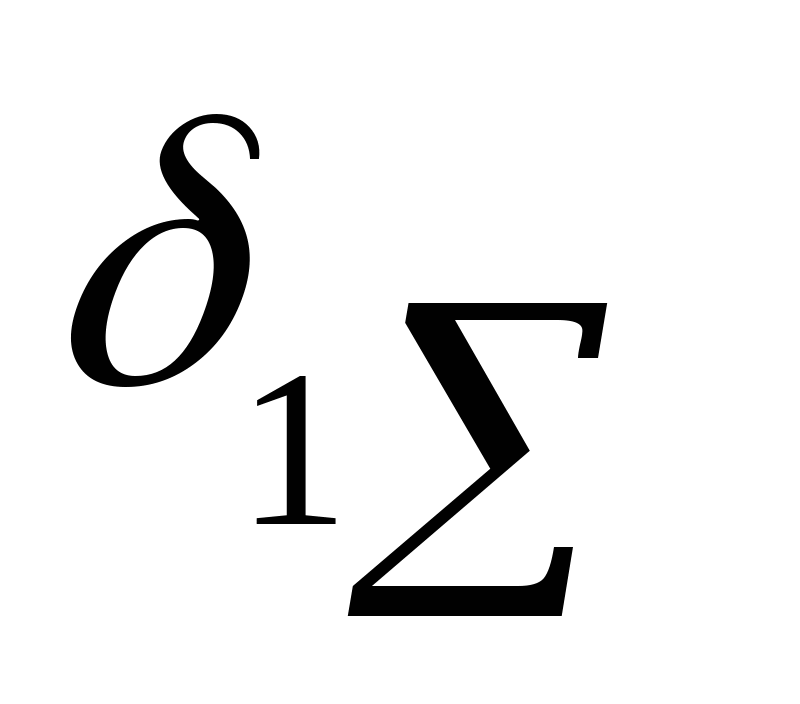 , и несущая способность стержневой системы будет наибольшей. , и несущая способность стержневой системы будет наибольшей. Р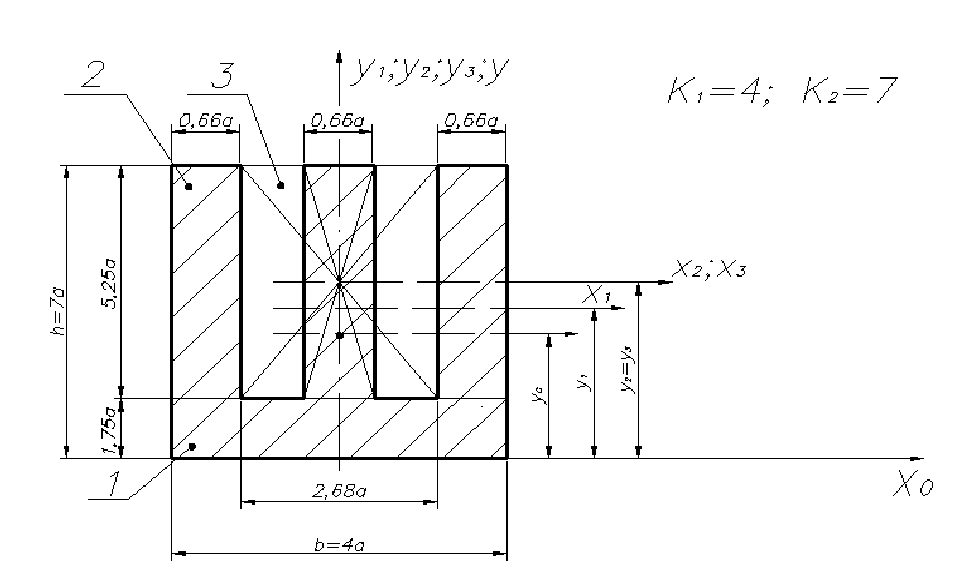 ПР № 2.1 ПР № 2.1
Рисунок 6.
Решение:
1. Разбиваем сечение на три простые фигуры. За исходную ось принимаем X0 – касательную к нижнему контуру сечения. Тогда: 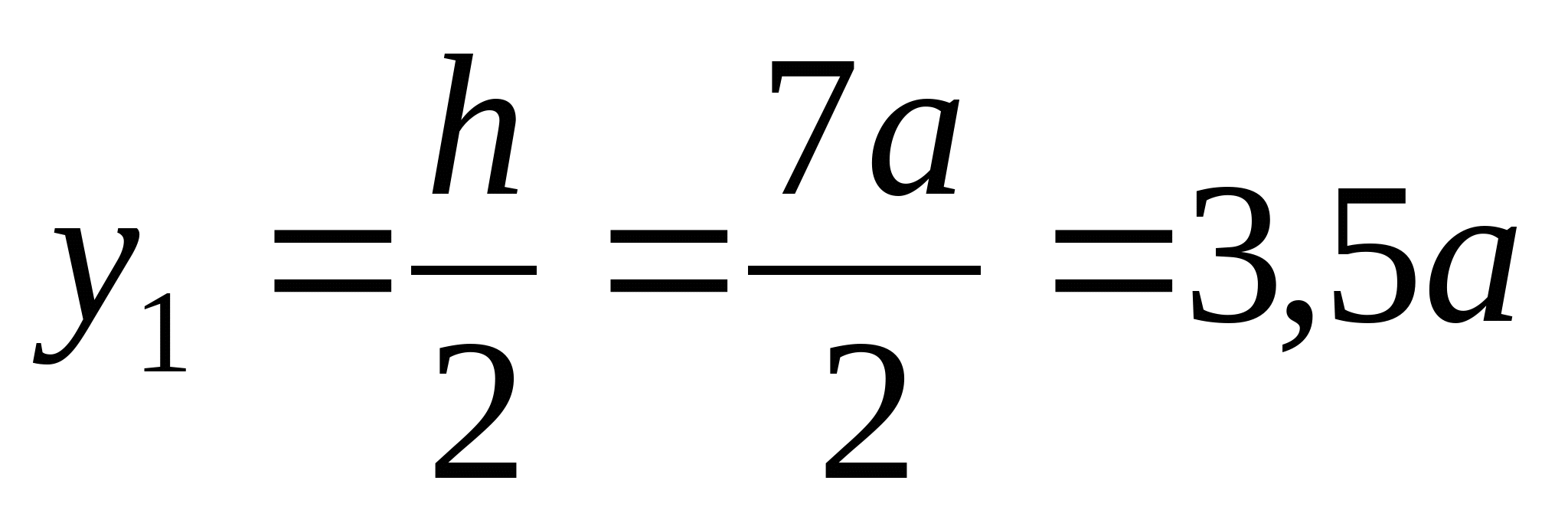 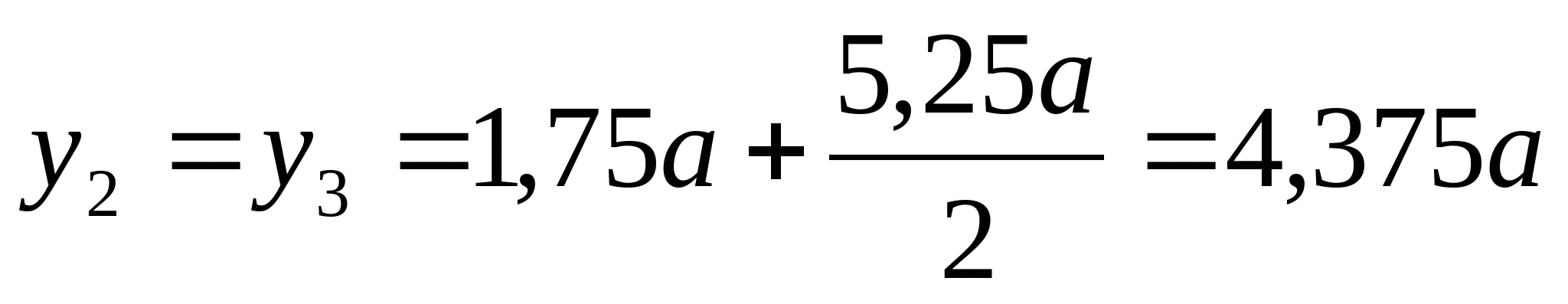
2. Найдем координату центра тяжести сечения: 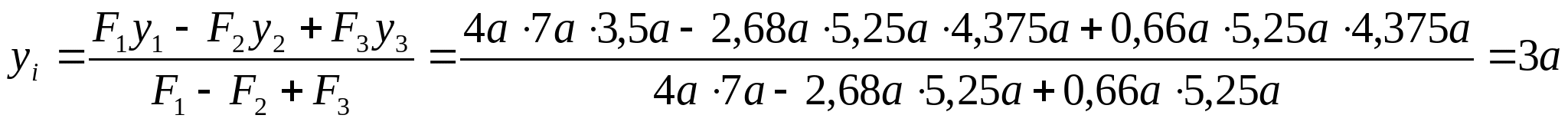
3. Определяем главные центральные моменты инерции сечения: 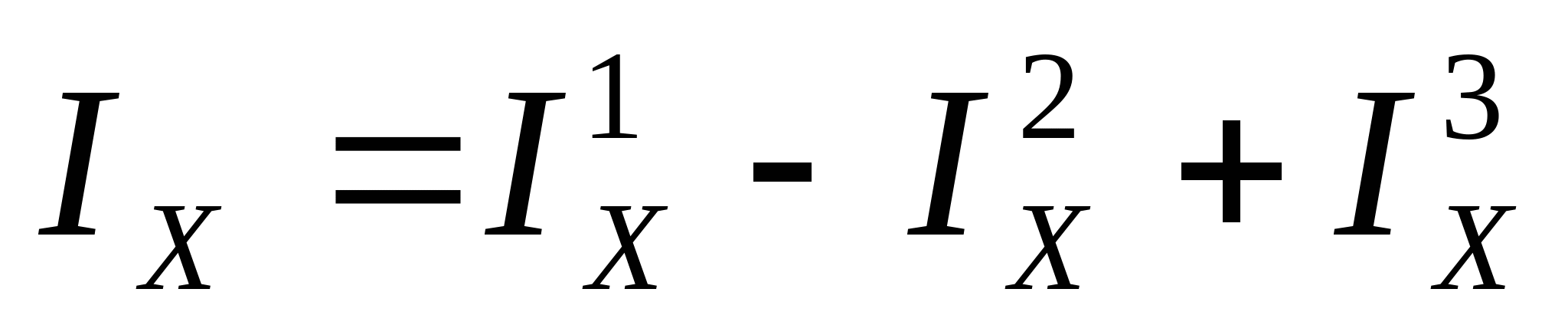 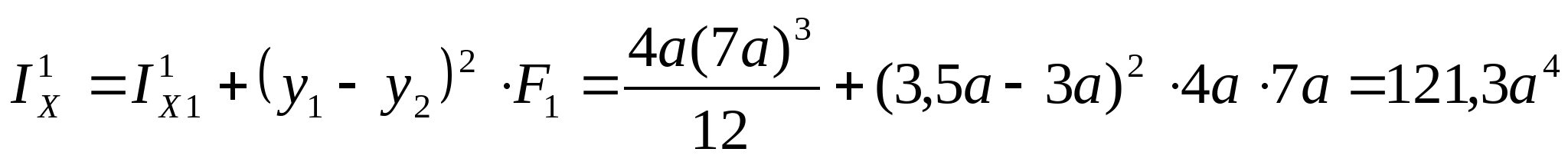 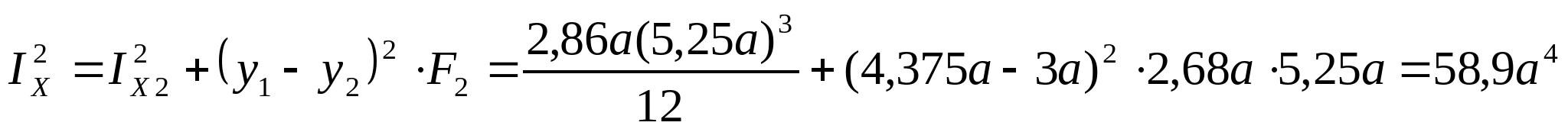 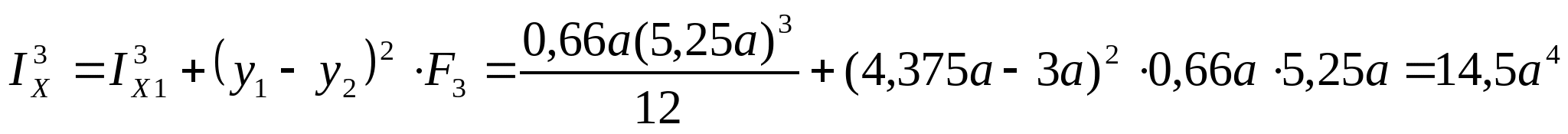 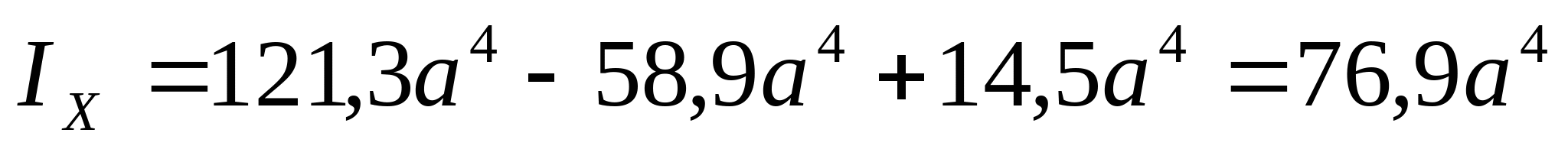
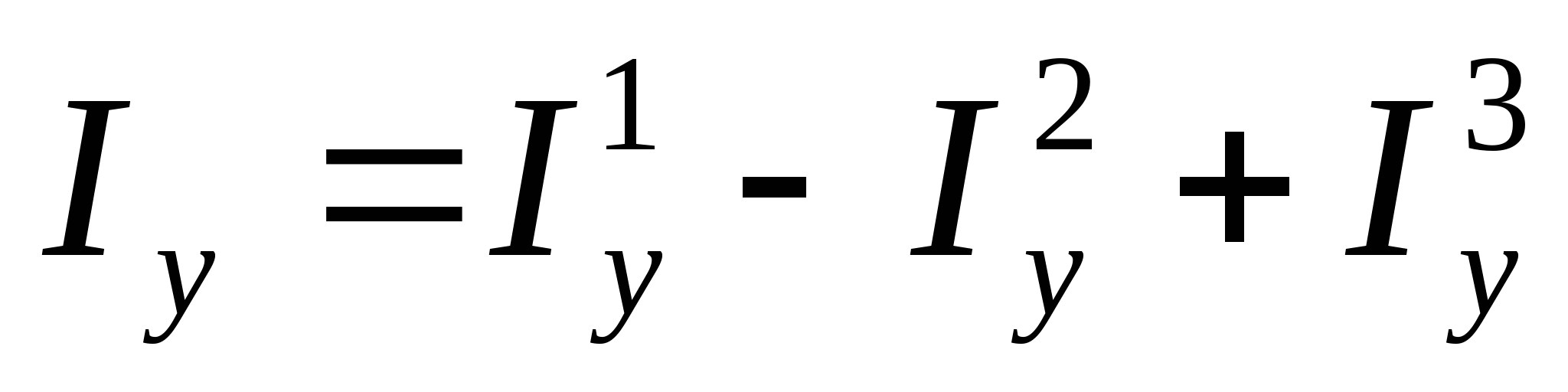 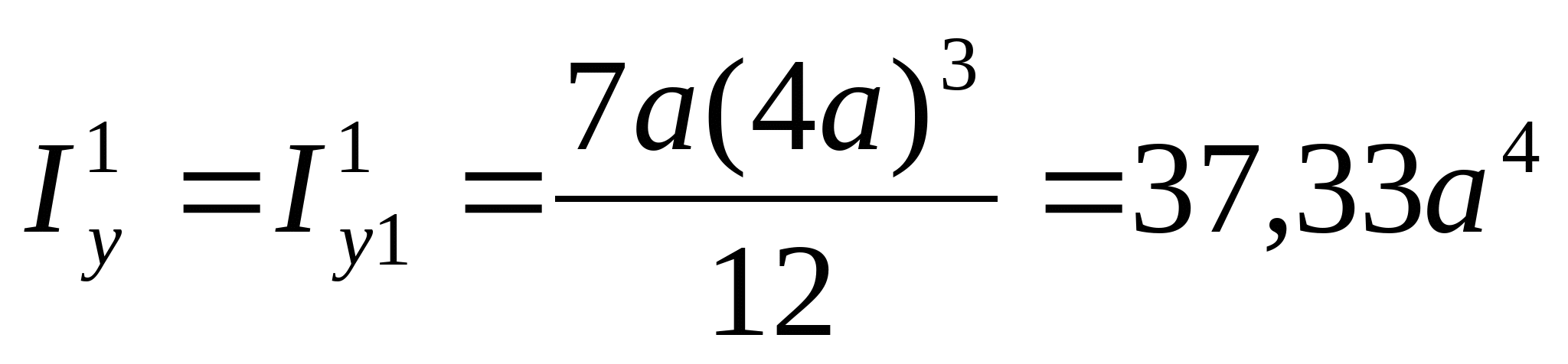 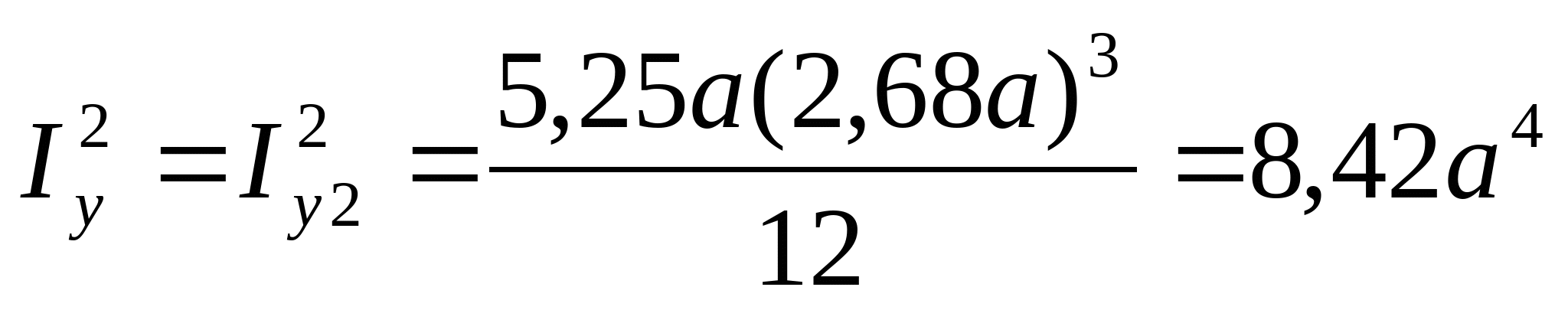 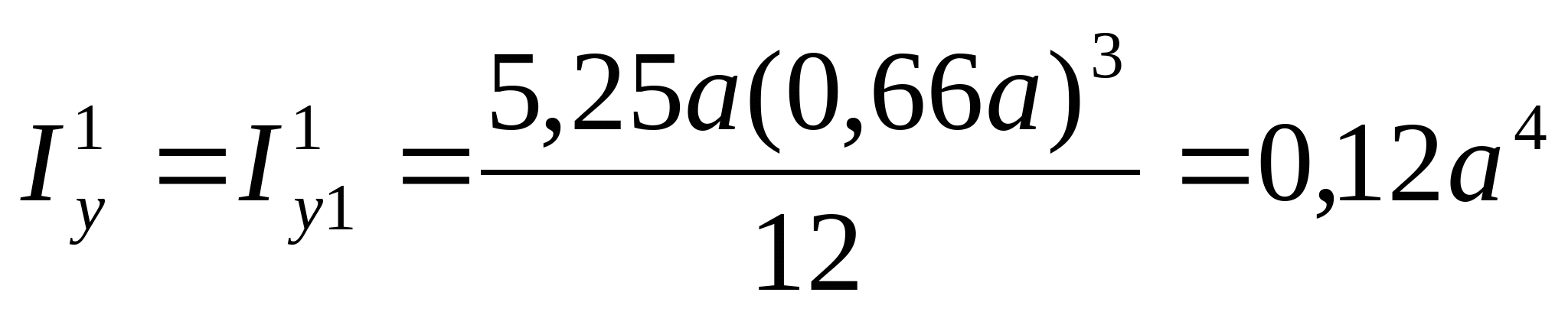 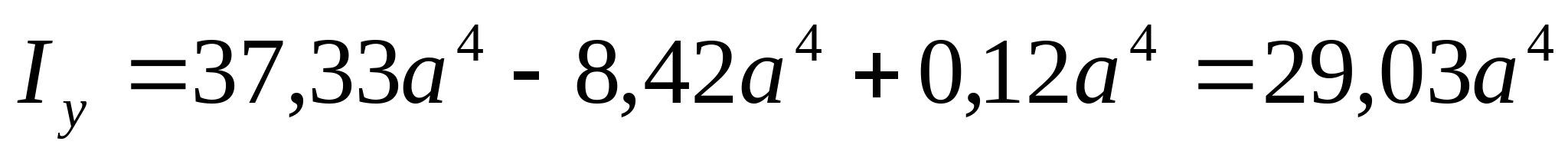
4. Определим моменты сопротивления поперечного сечения: 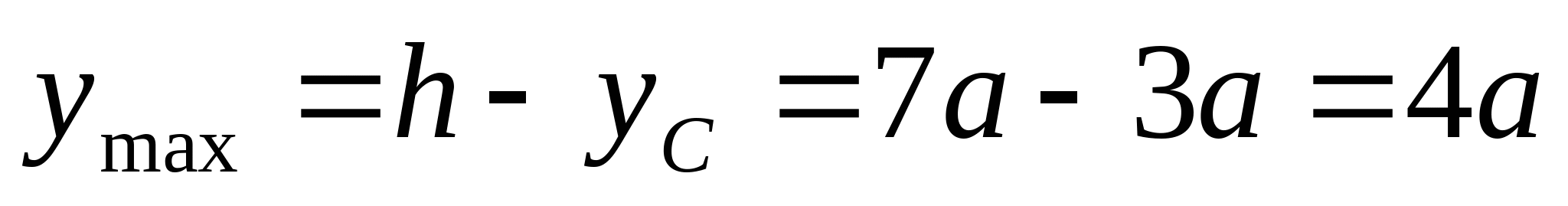 ; ; 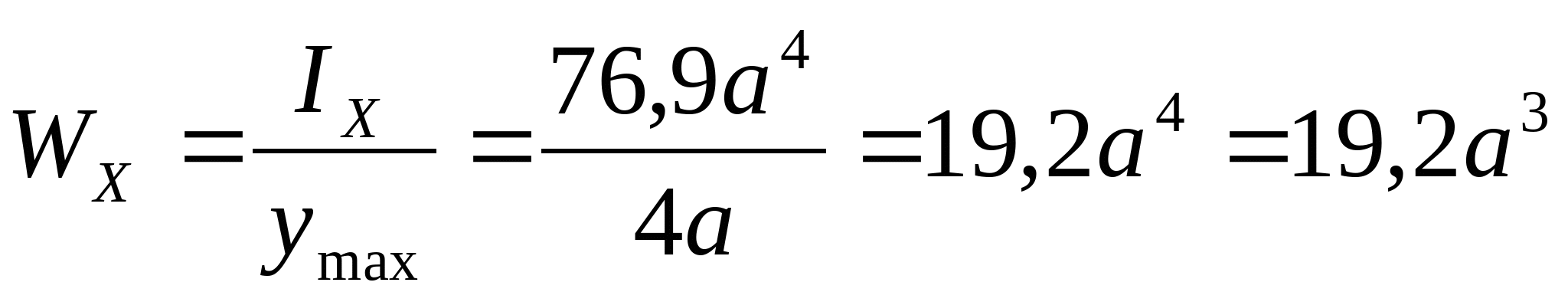 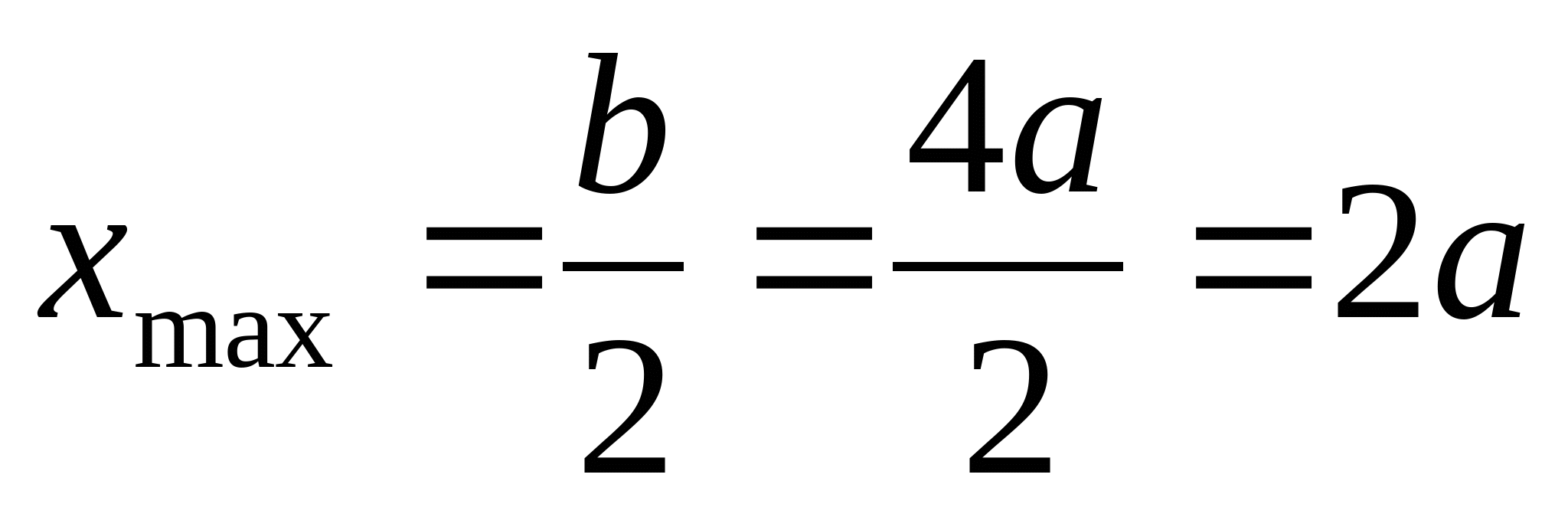 ; ; 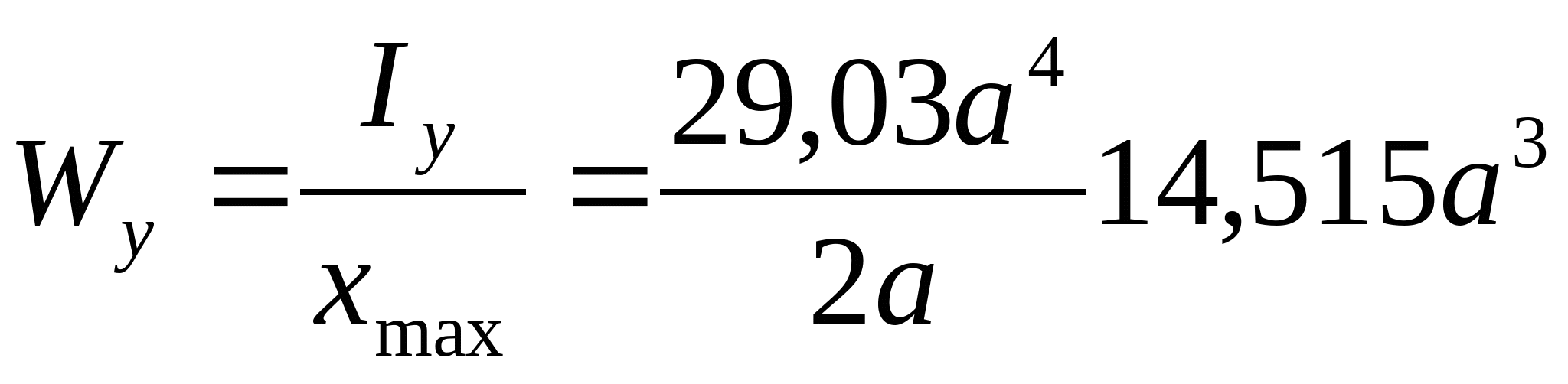 РПР № 3.1 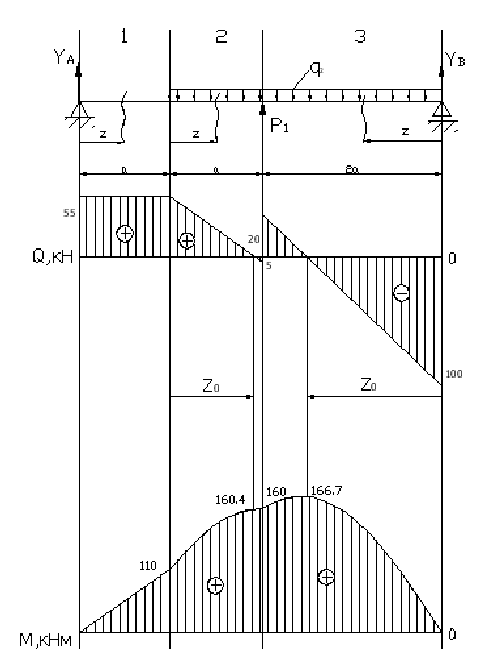
Дано: Р1=25 кН; 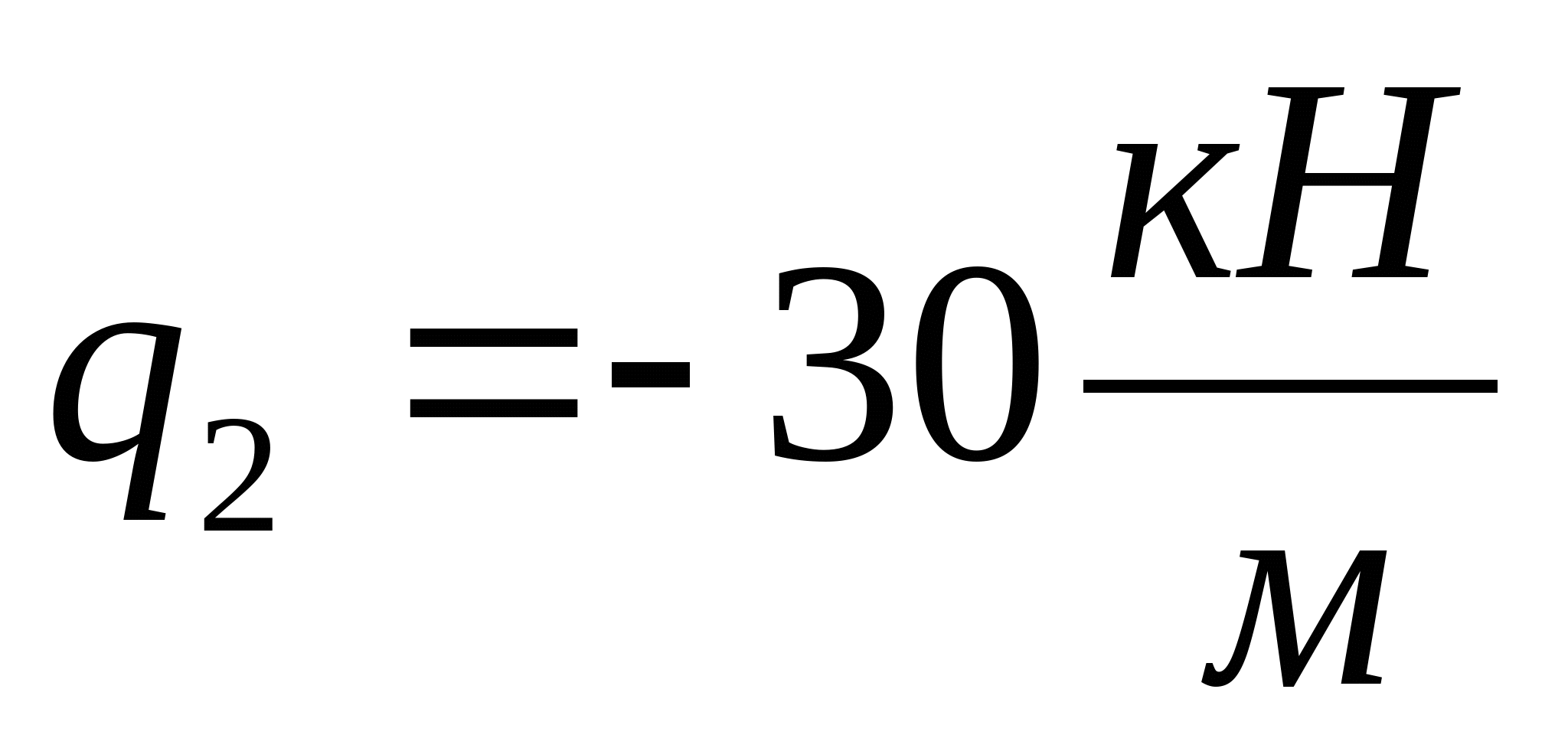 ; ; а=2 м; Сталь: Ст. 3; 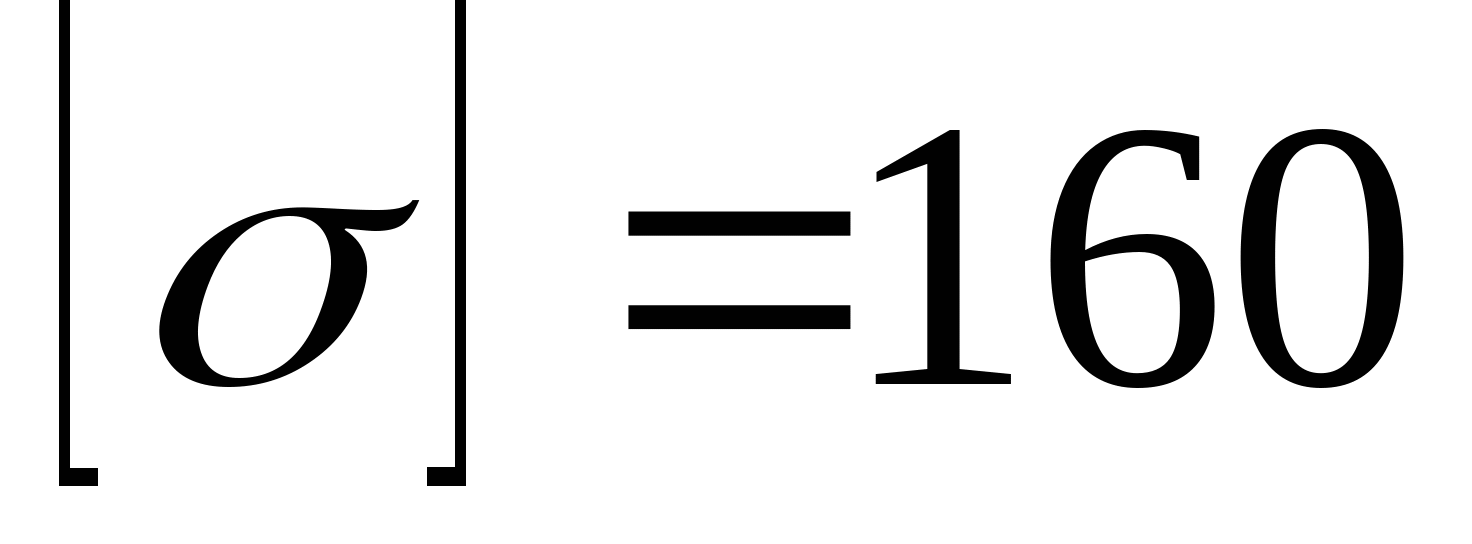 МПа; МПа;  = =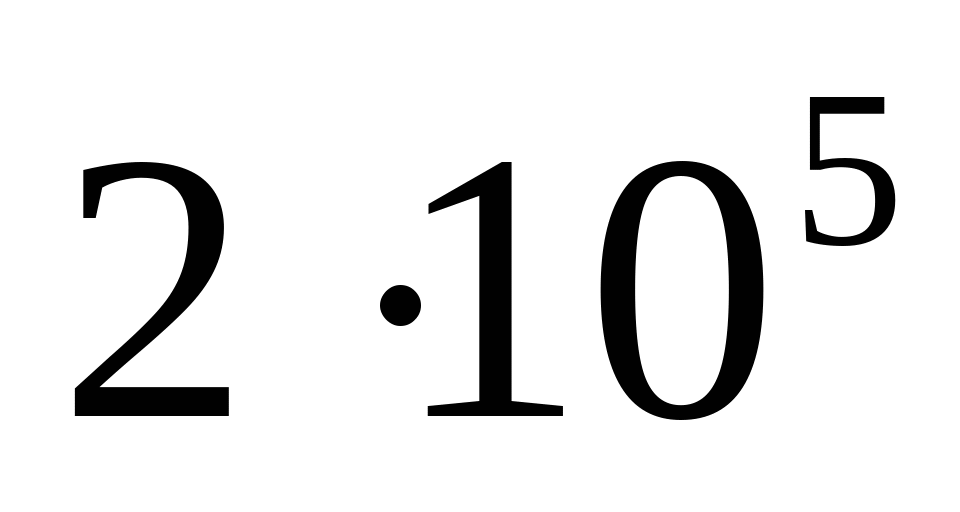 МПа. МПа.
Рисунок 7. Эпюра продольных сил и изгибающих моментов. 1. Определяем опорные реакции: 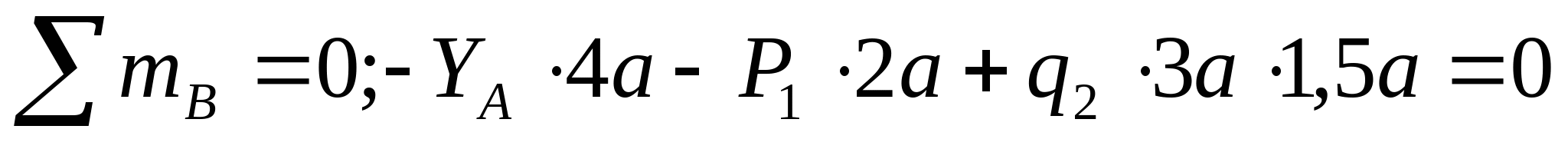 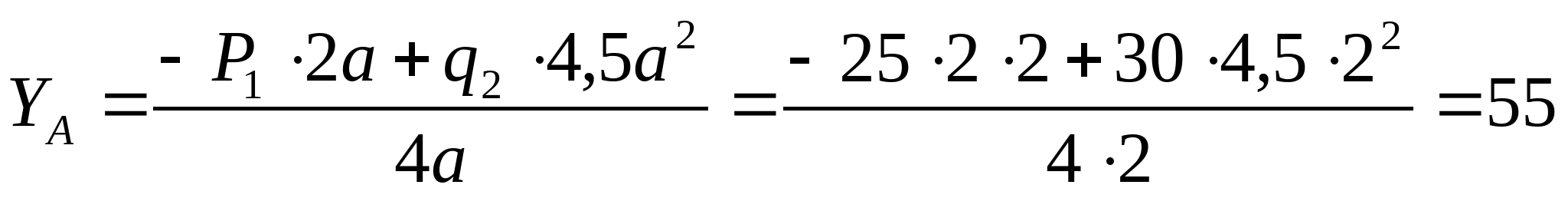 кН кН 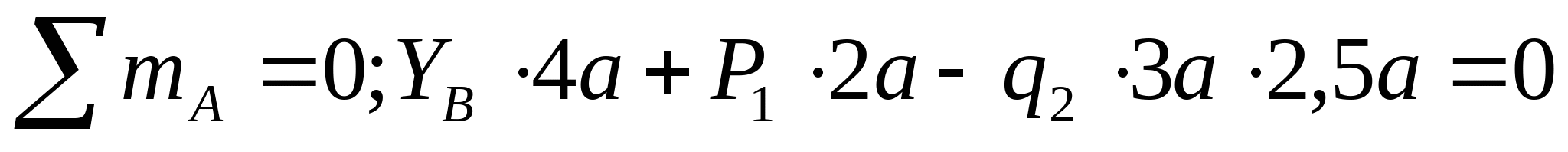 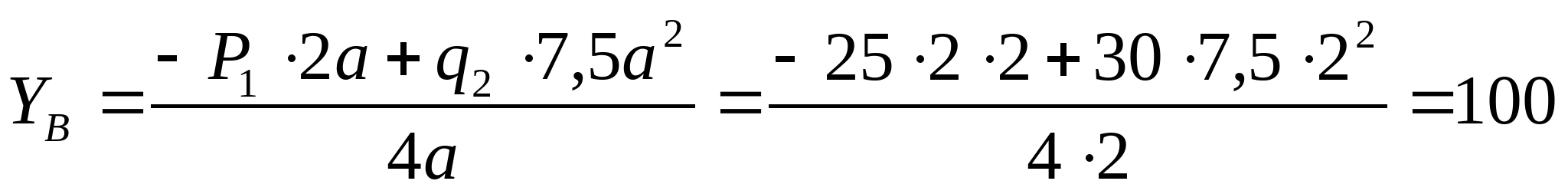 кН кН Проверка:  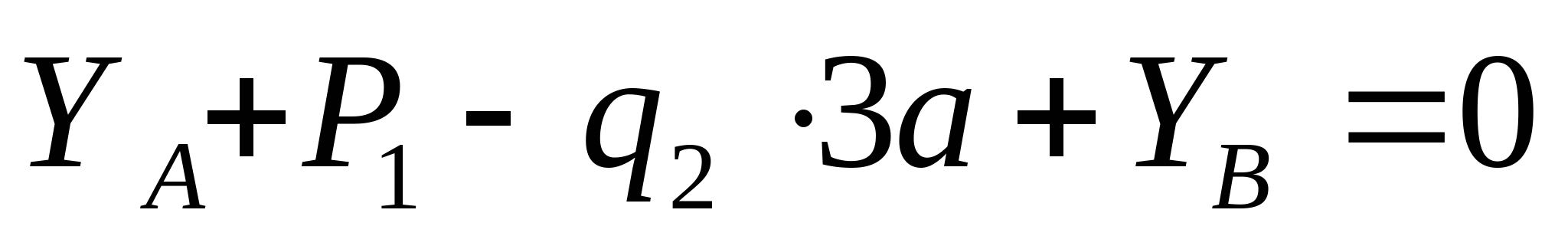 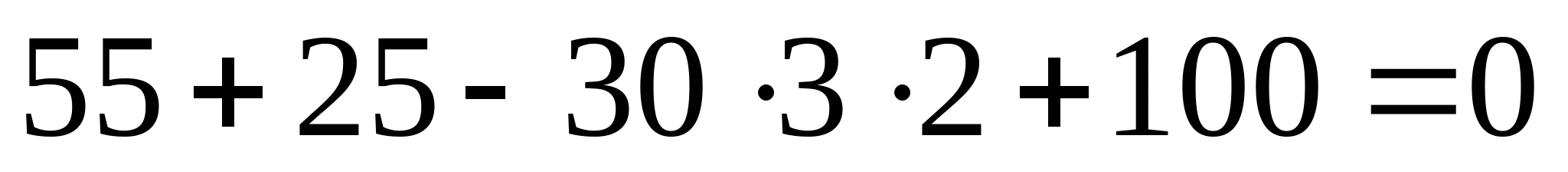
2. Рассчитаем координаты эпюры поперечных сил: Q1=YA=55 кН 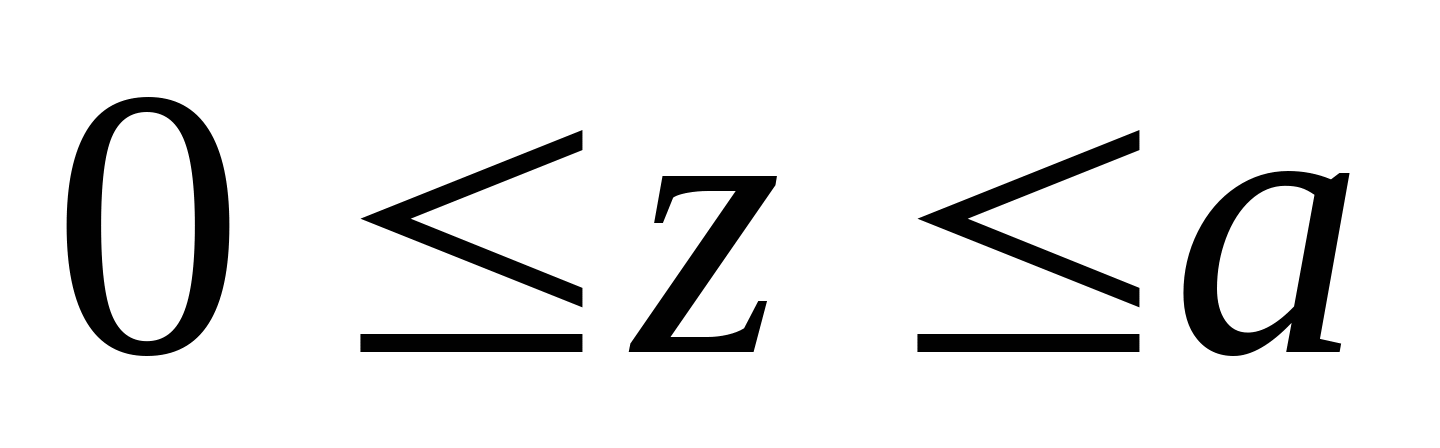 Q2=YA-q2z=55-30z 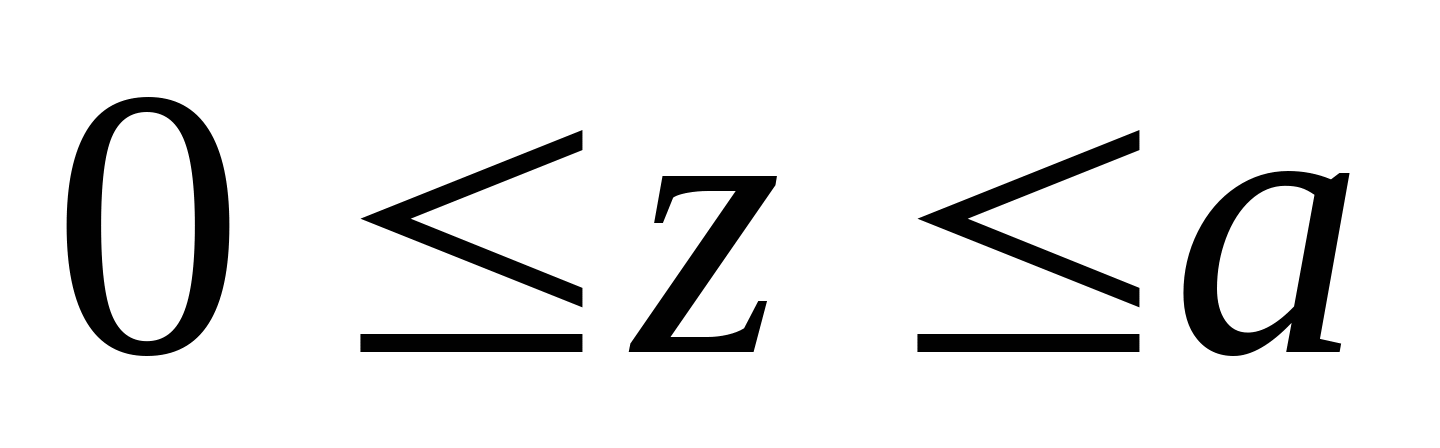 z=0; Q2=55 кН z=a=2 м; Q2=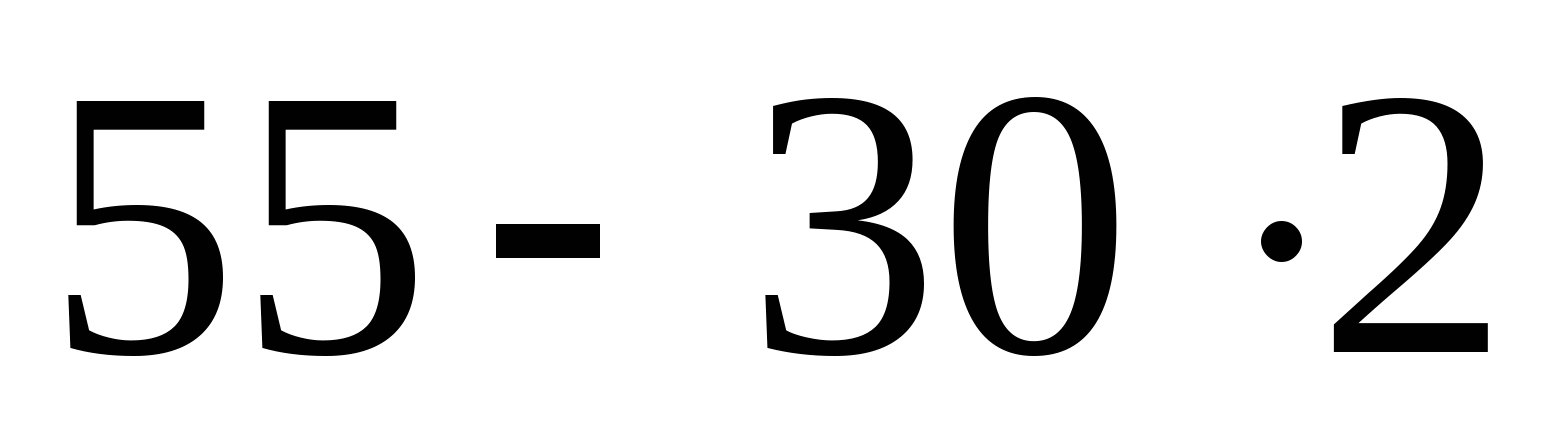 =-5кН =-5кН Q3=q2z-YB=30z-100 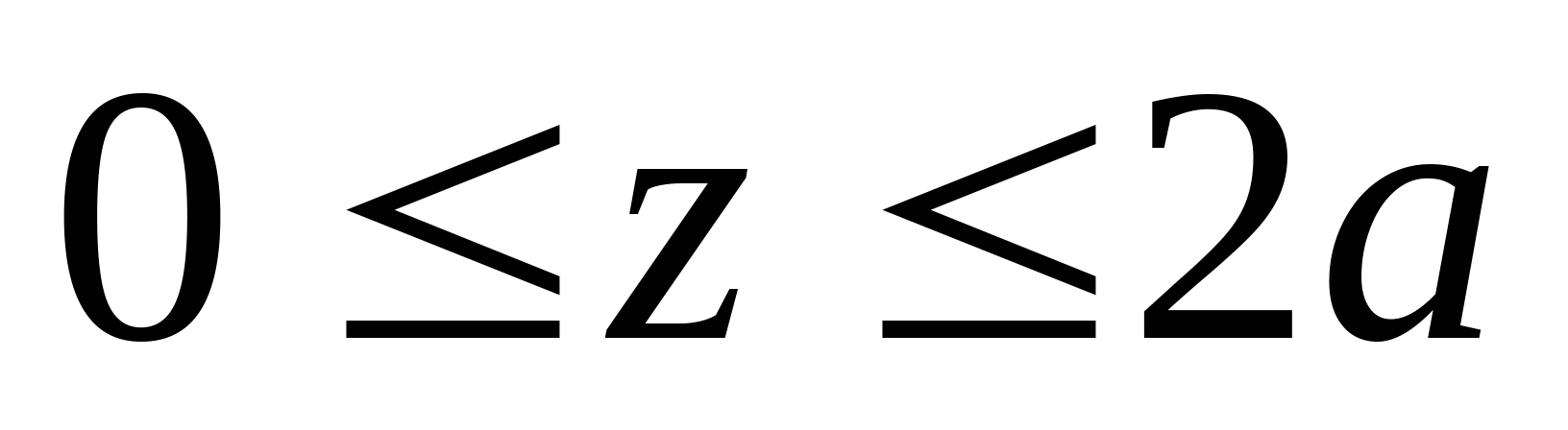 z=0; Q3=-100 кН; z=2a=4 м; Q3=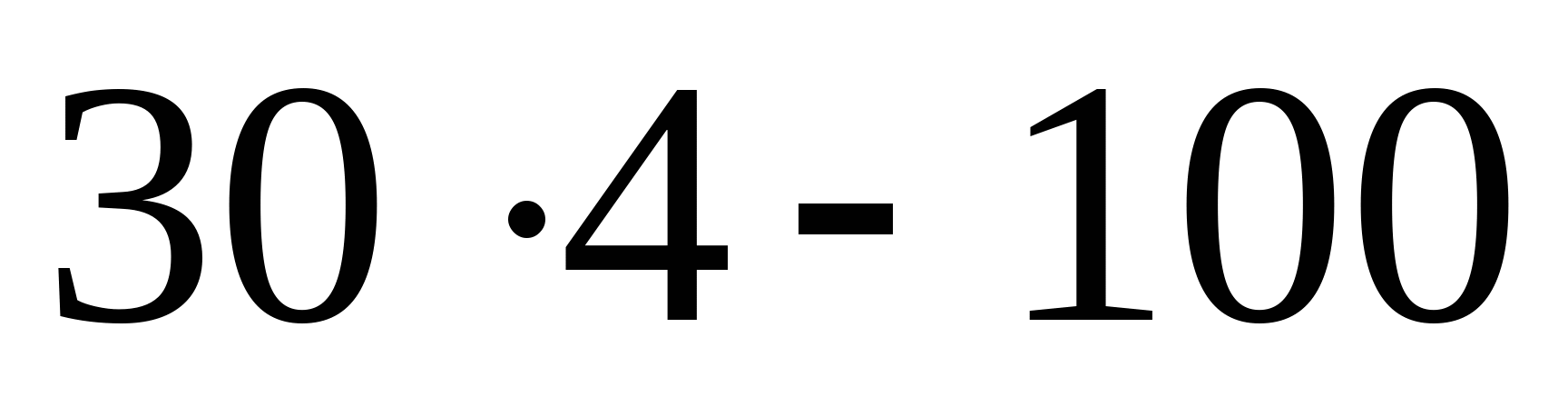 =20 кН =20 кН
3. Рассчитаем координаты эпюры изгибающих моментов: 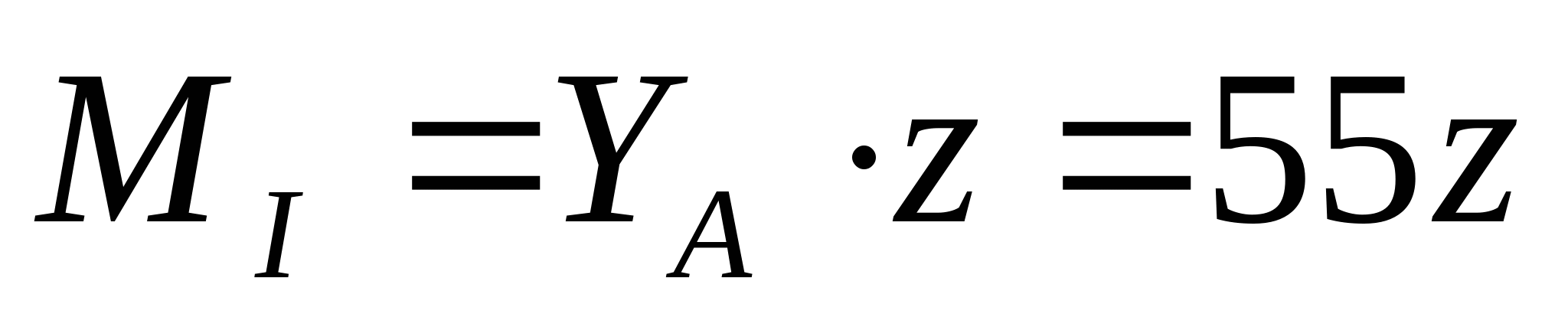 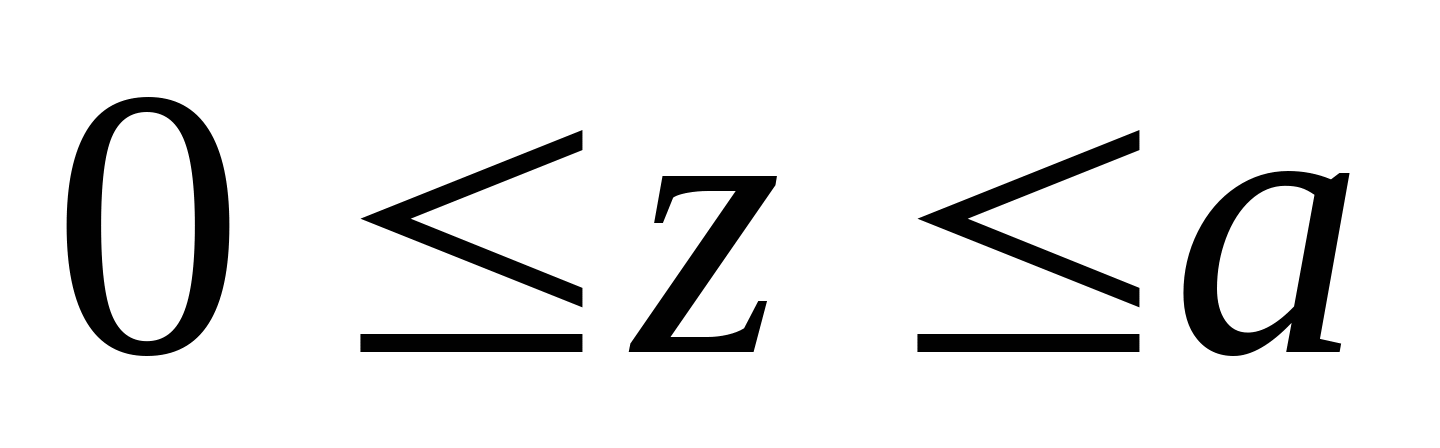 z=0; MI=0 z=a=2 м; 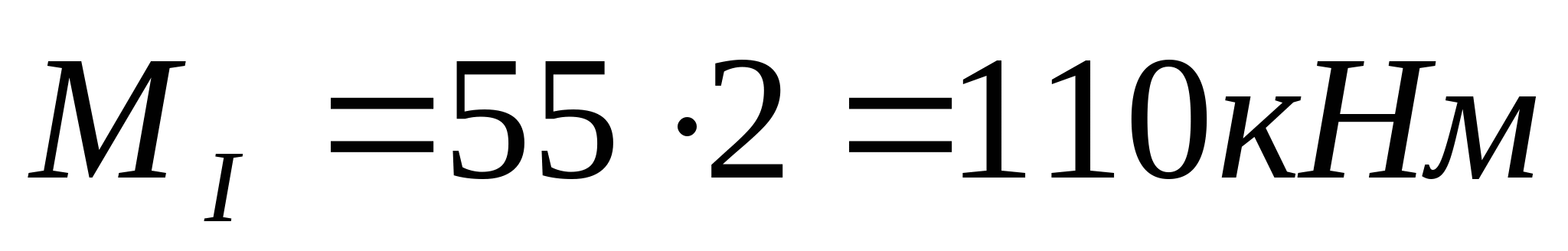 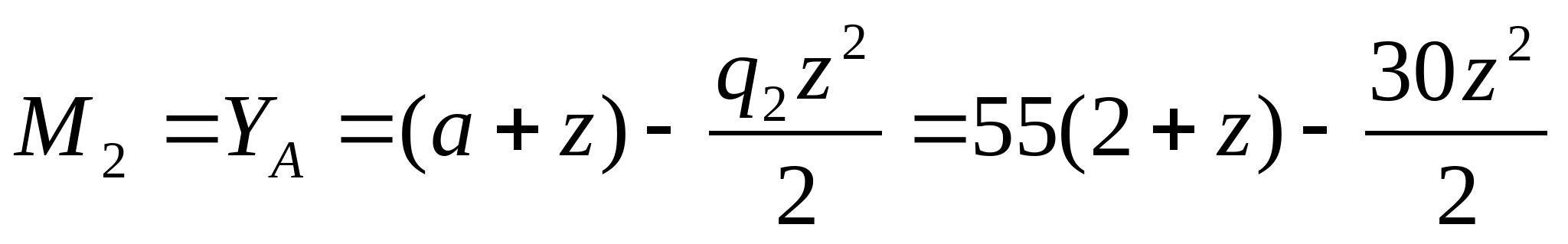 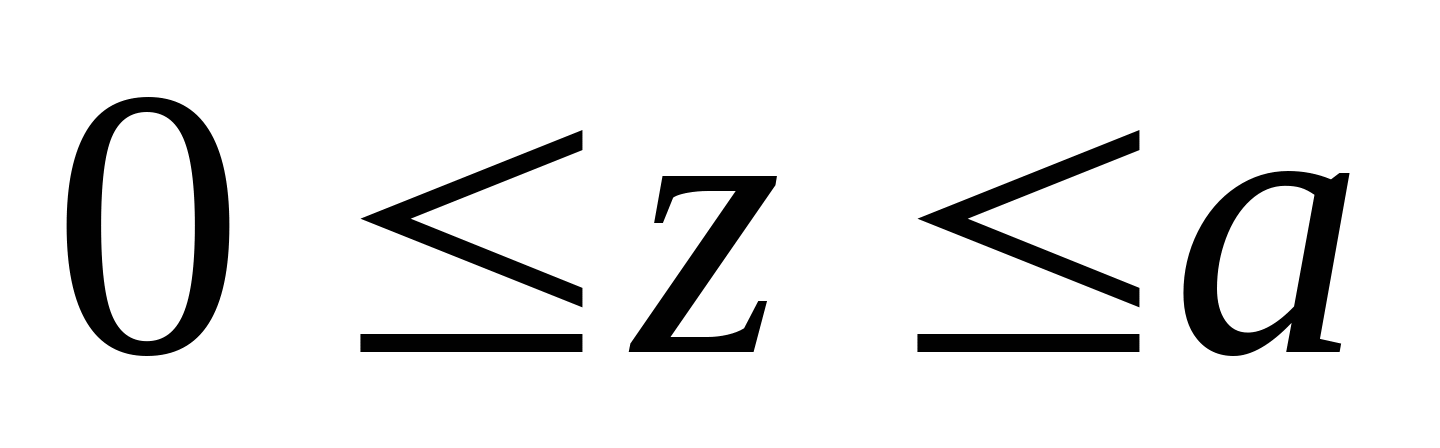 z=0; 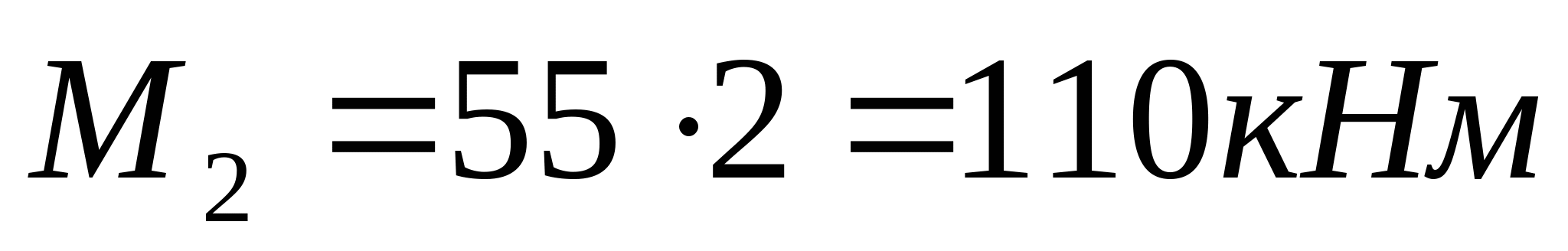 z=a=2 м; 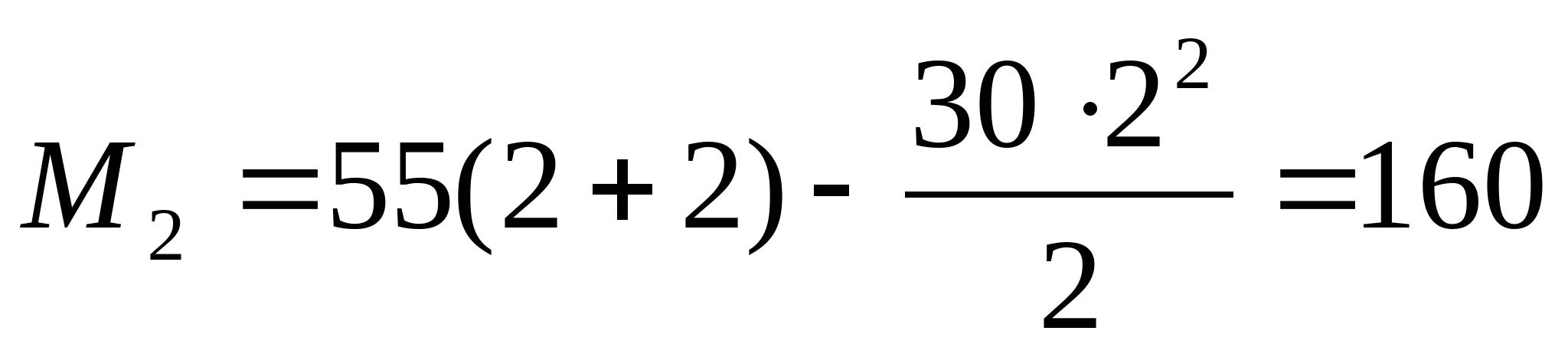 МПа МПа Координаты экстремума: 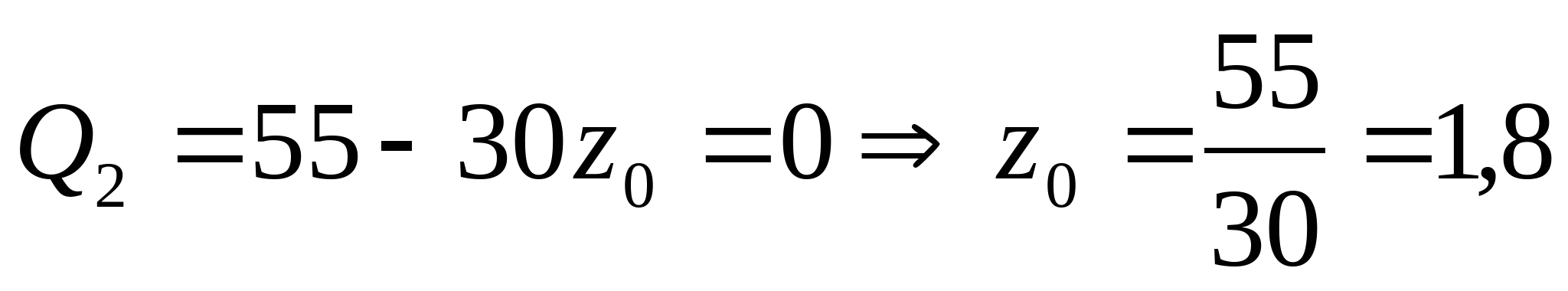 м м 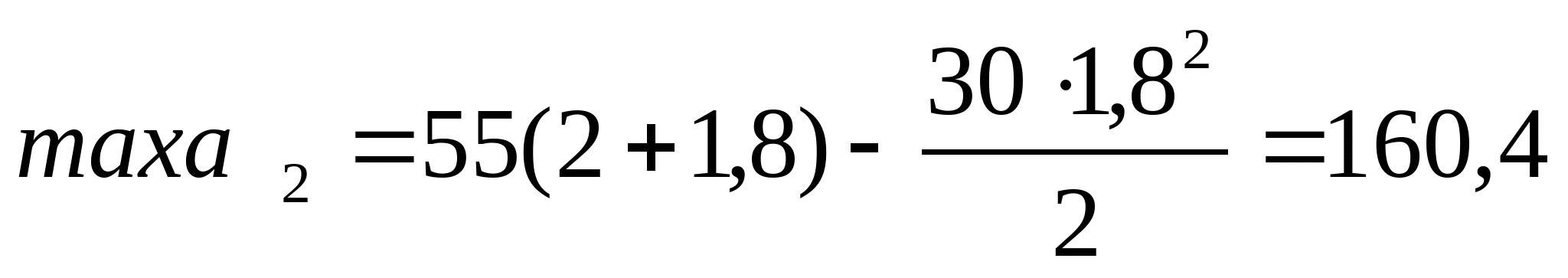 МПа МПа 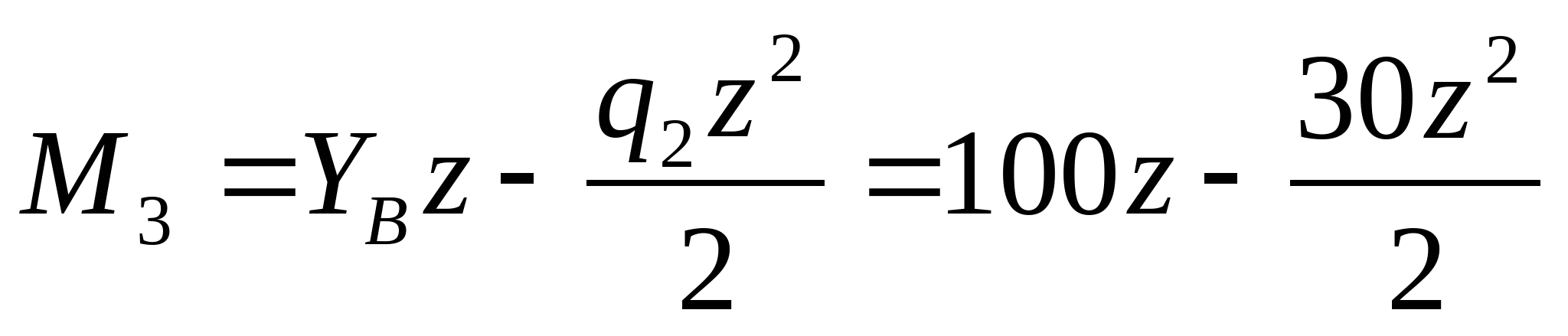 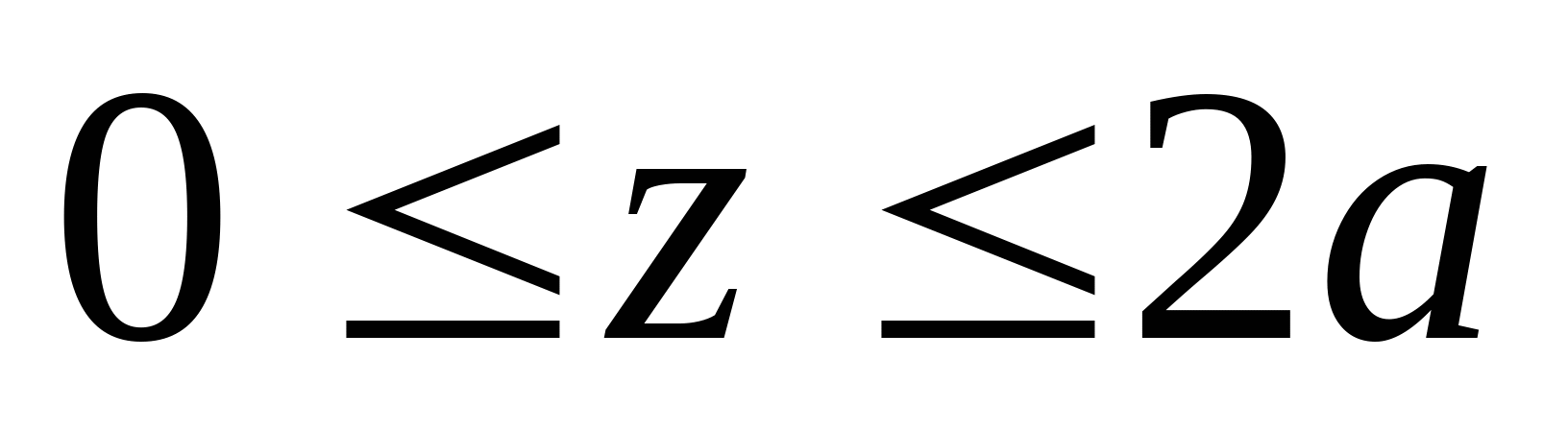 z=0; M3=0; z=2a=4 м 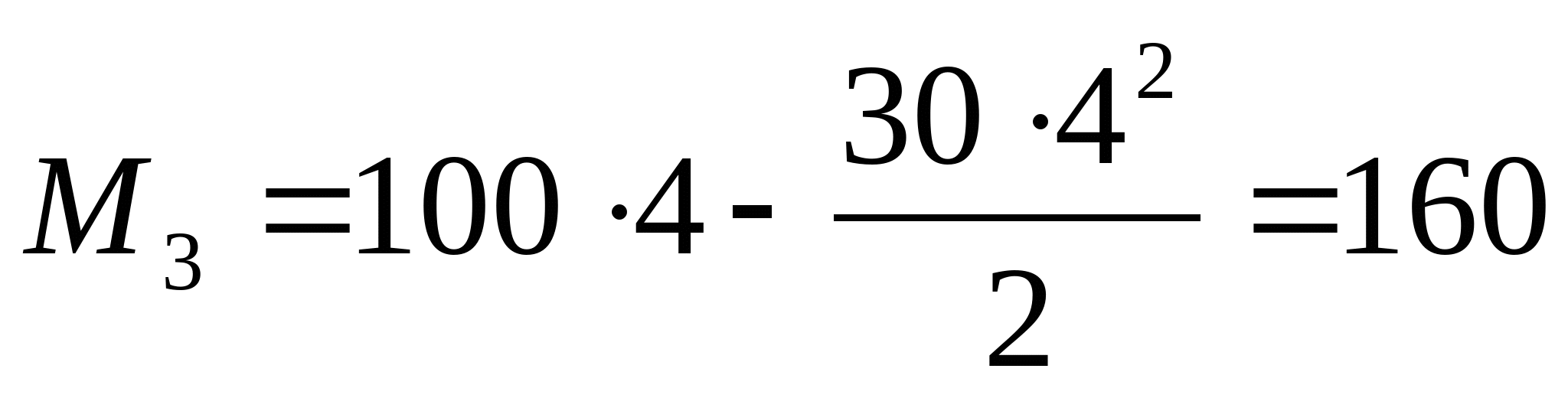 МПа МПа Координаты экстремума: 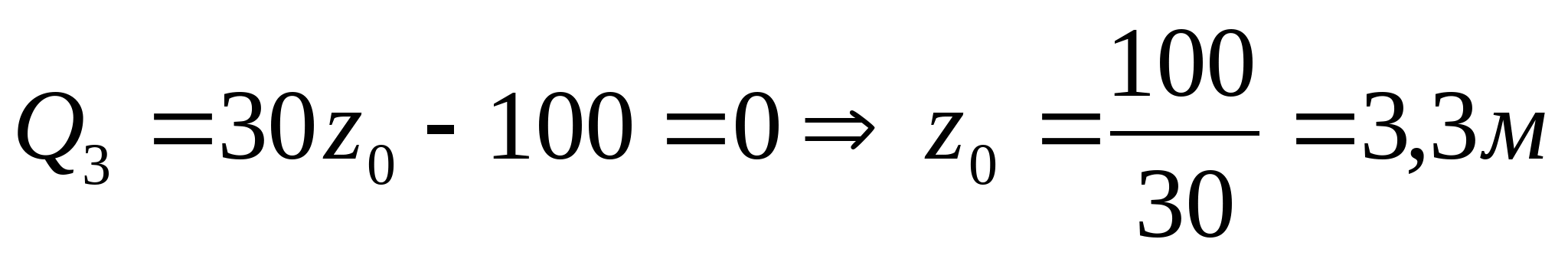  кНм кНм Из эпюры видно что в опасном сечении 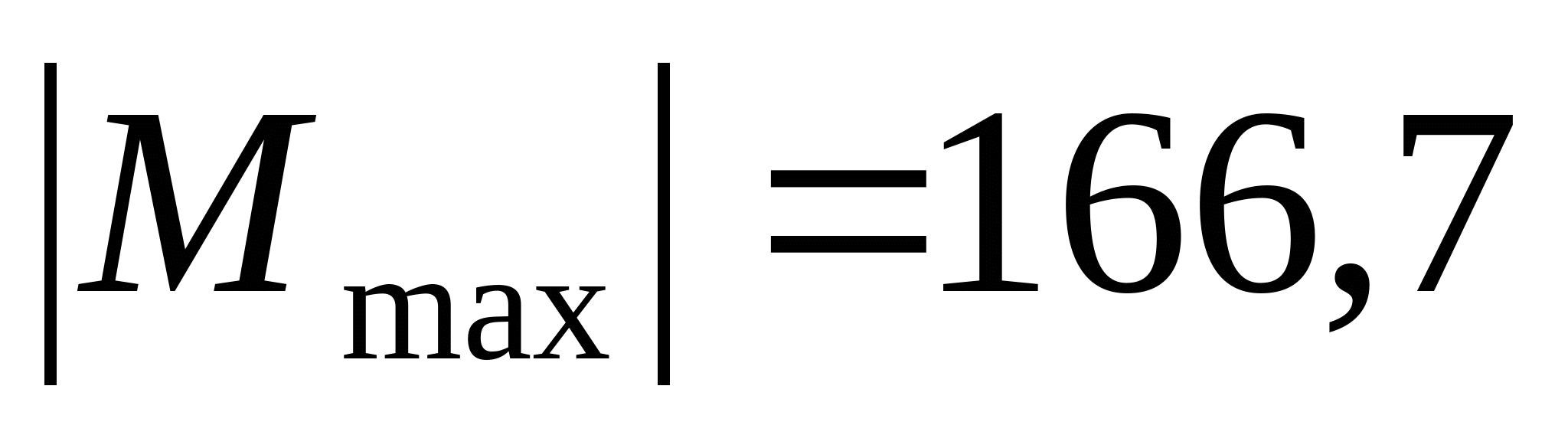 кНм кНм
4. Рассчитаем условие прочности: 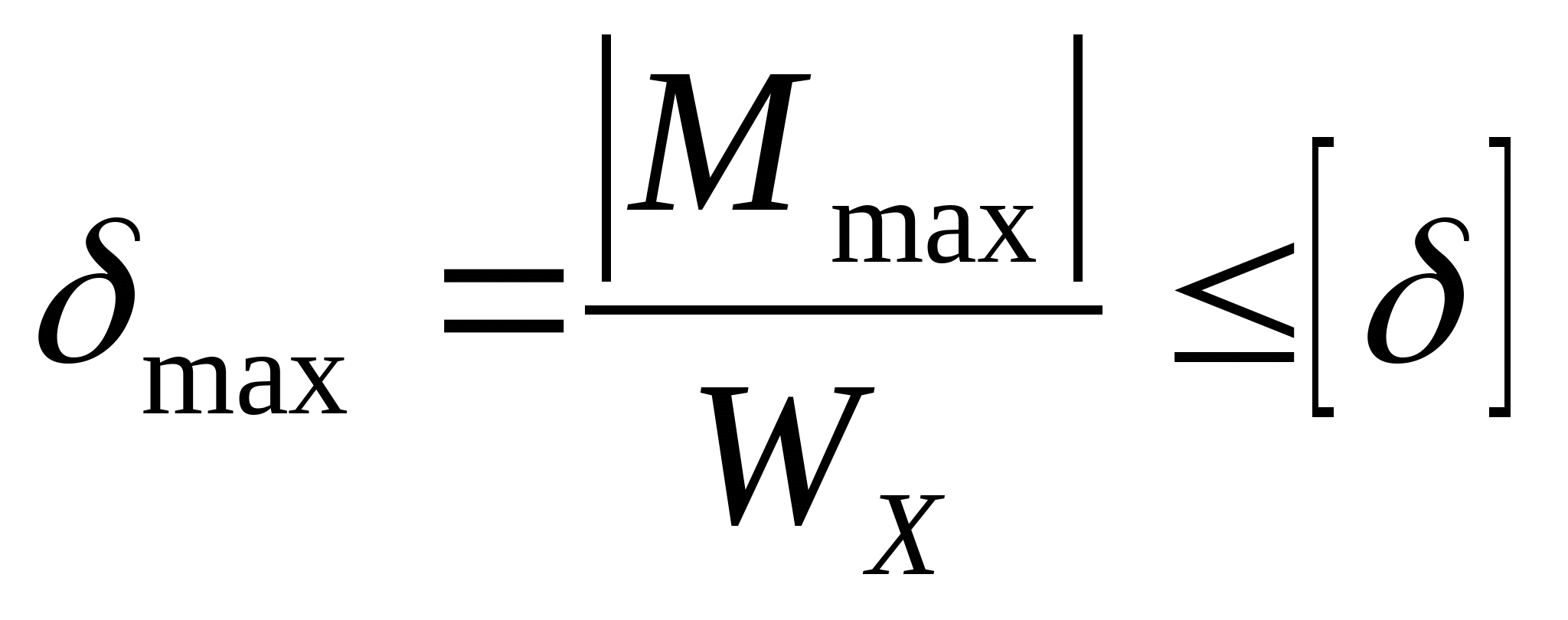 Подбор сечений: Двутавр 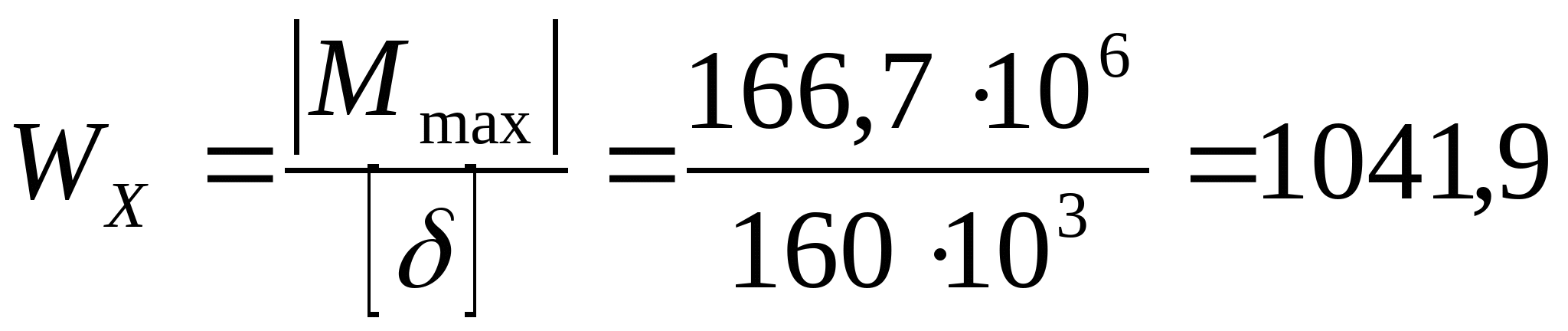 см3 см3 По ГОСТ 8239-89 I № 45, Wхтабл=1231 см3; F=84,7 см2
Круг 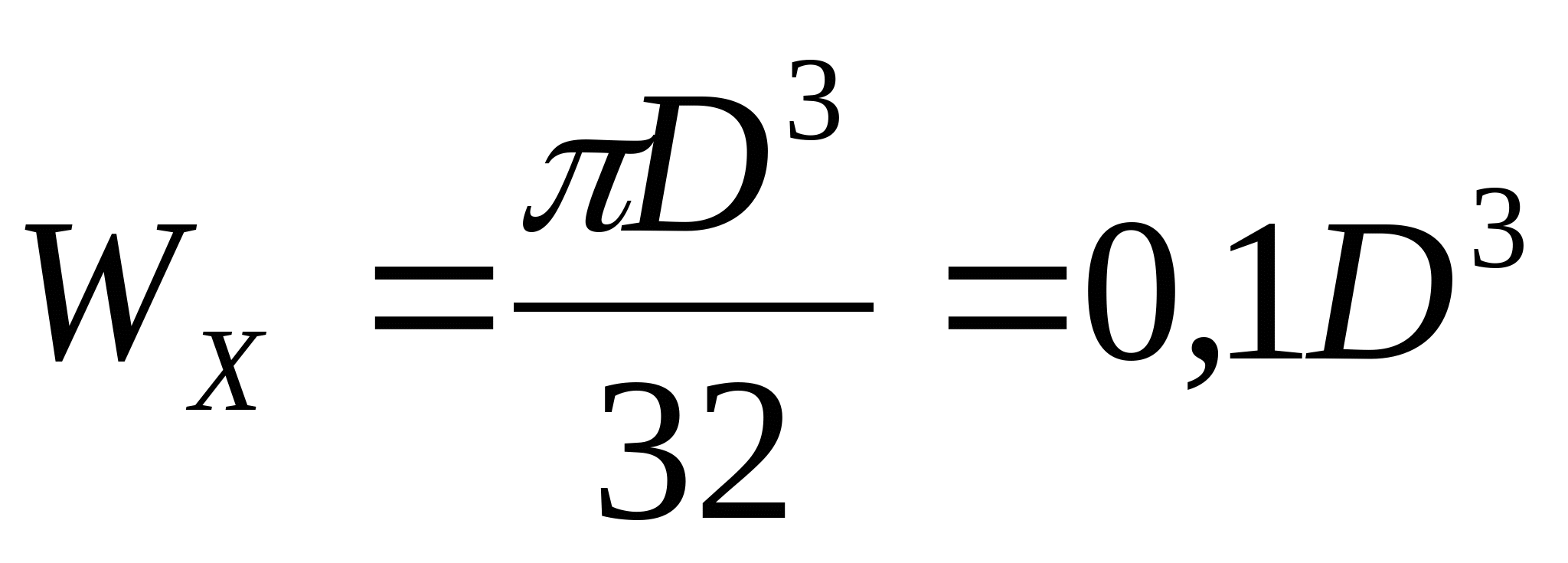 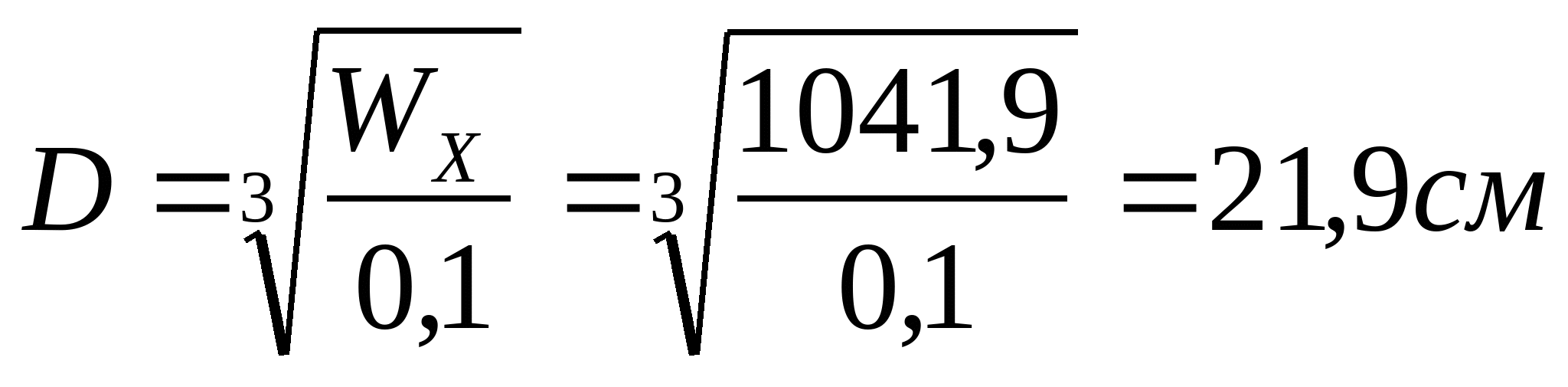
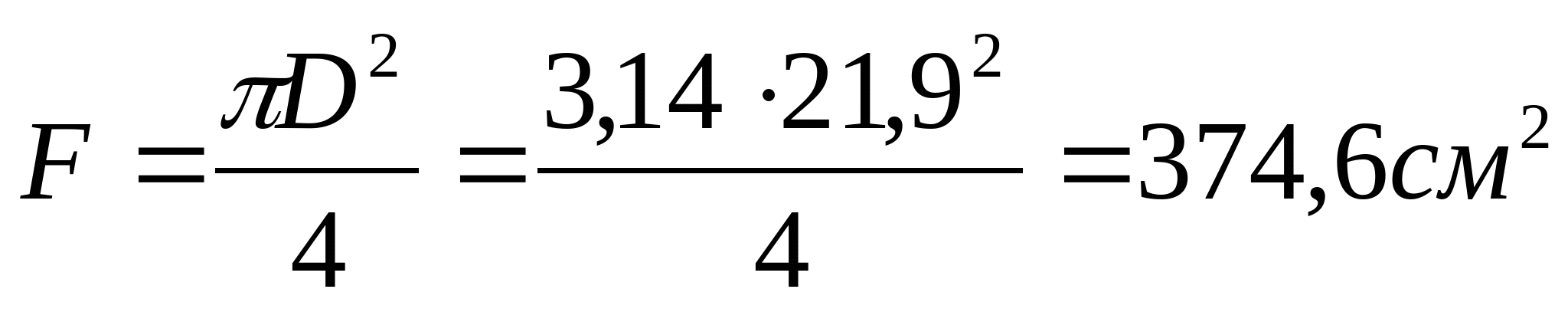
Кольцо при 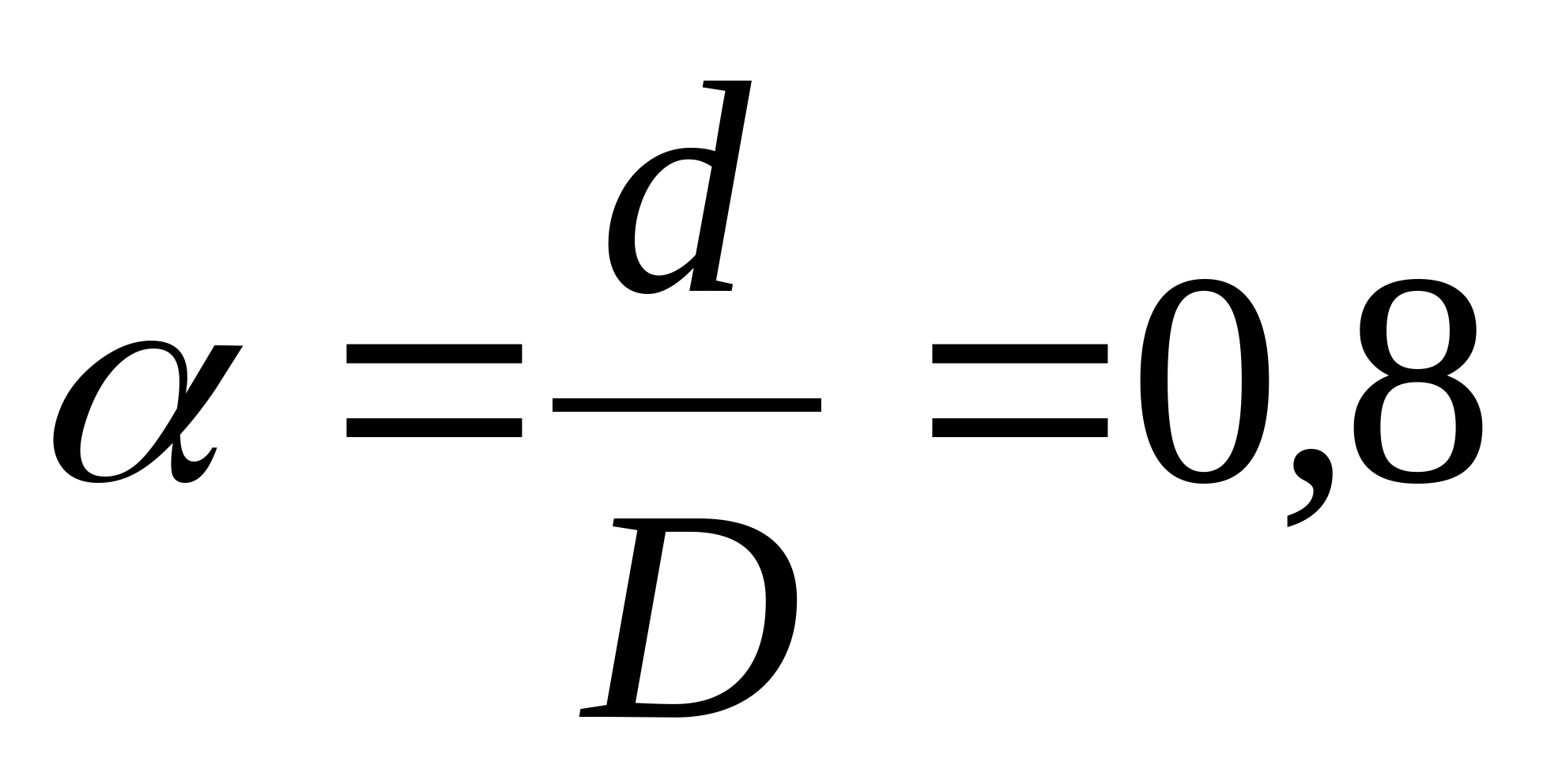 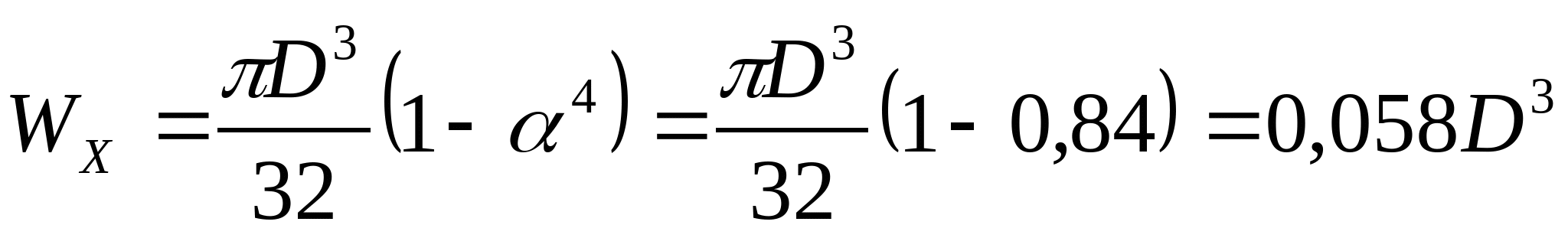 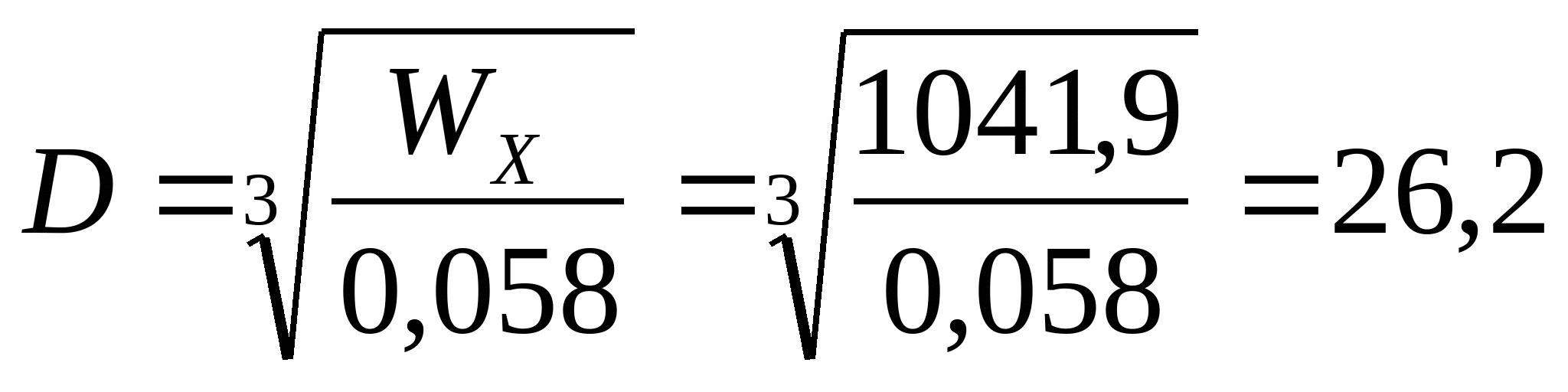 см см 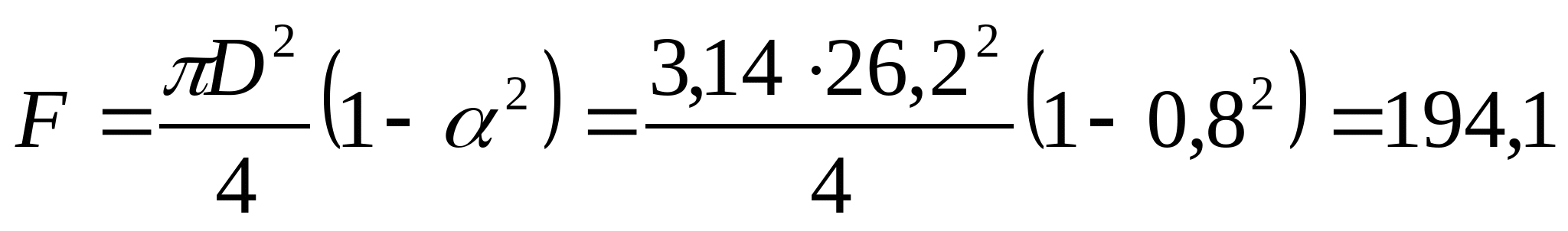 см3 см3
Прямоугольник при 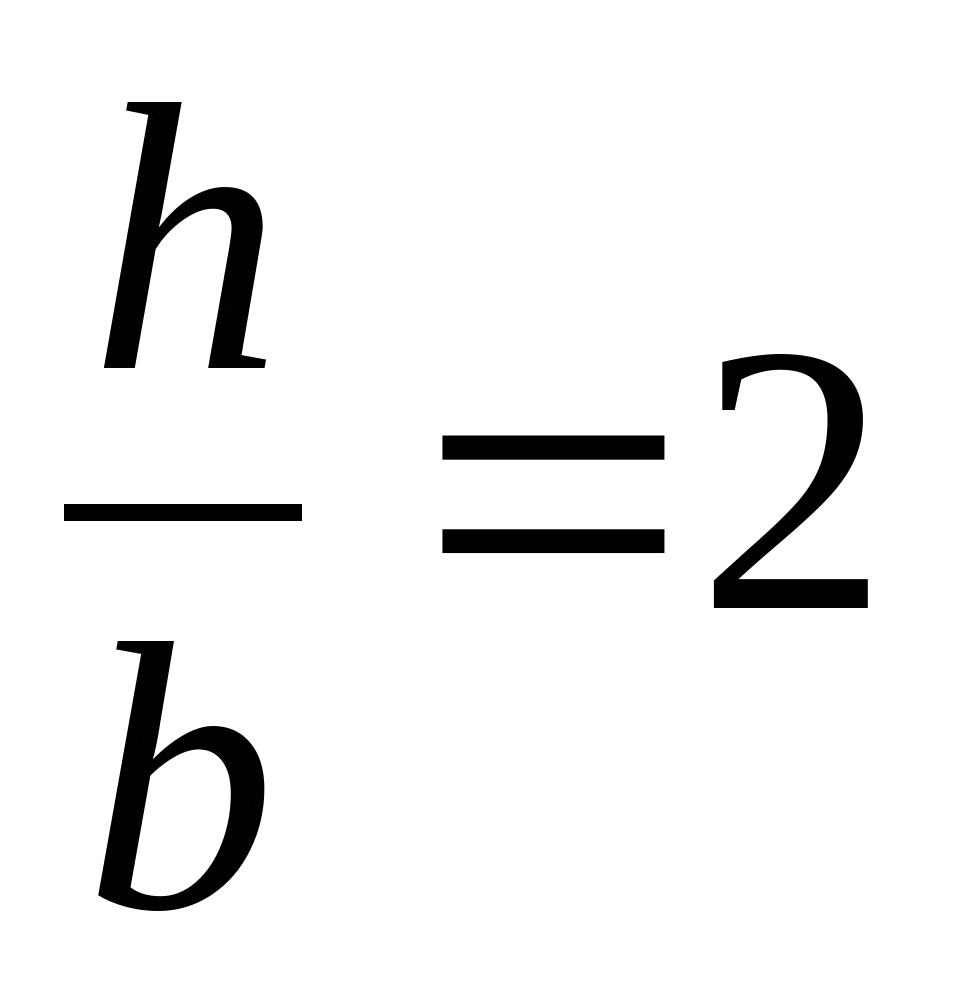 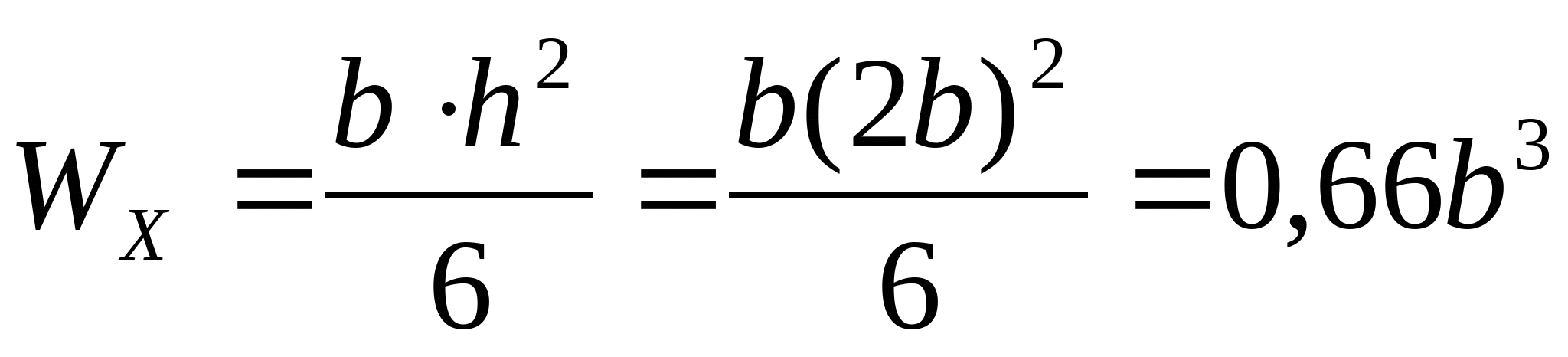 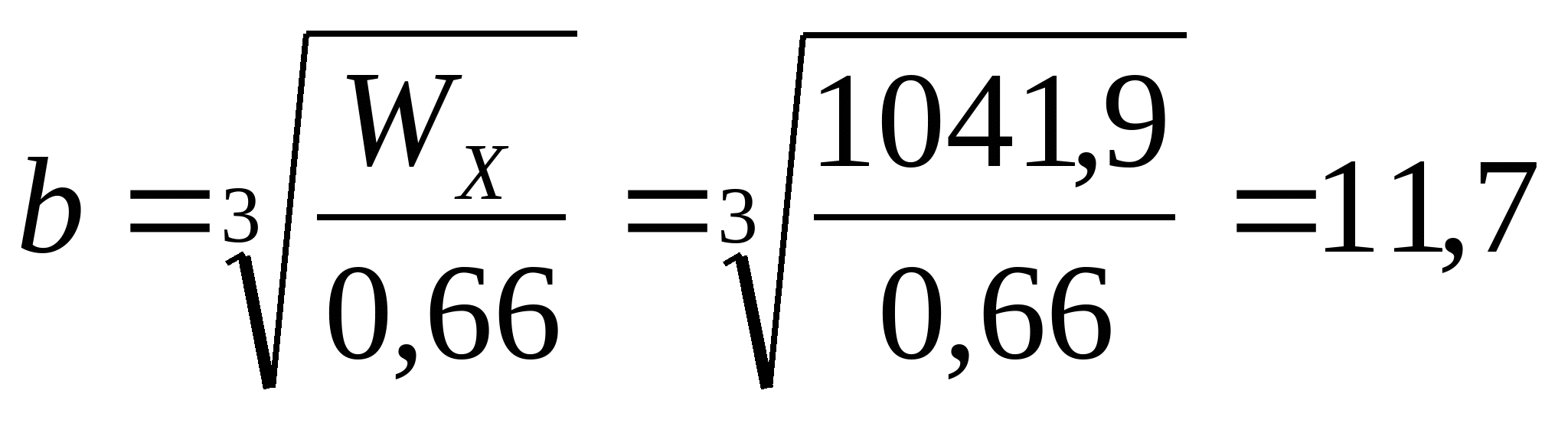 см см 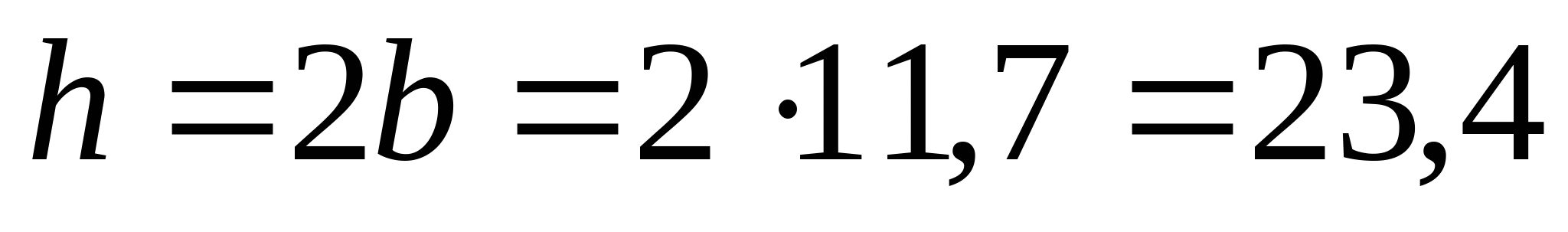 см; см; 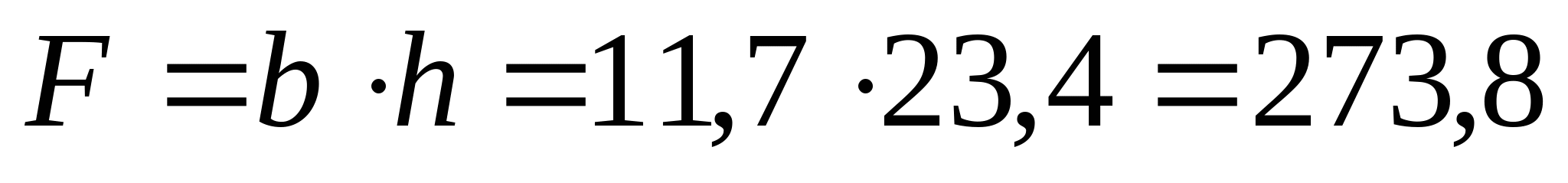 см3 см3
Сложное сечение из задачи 2.1 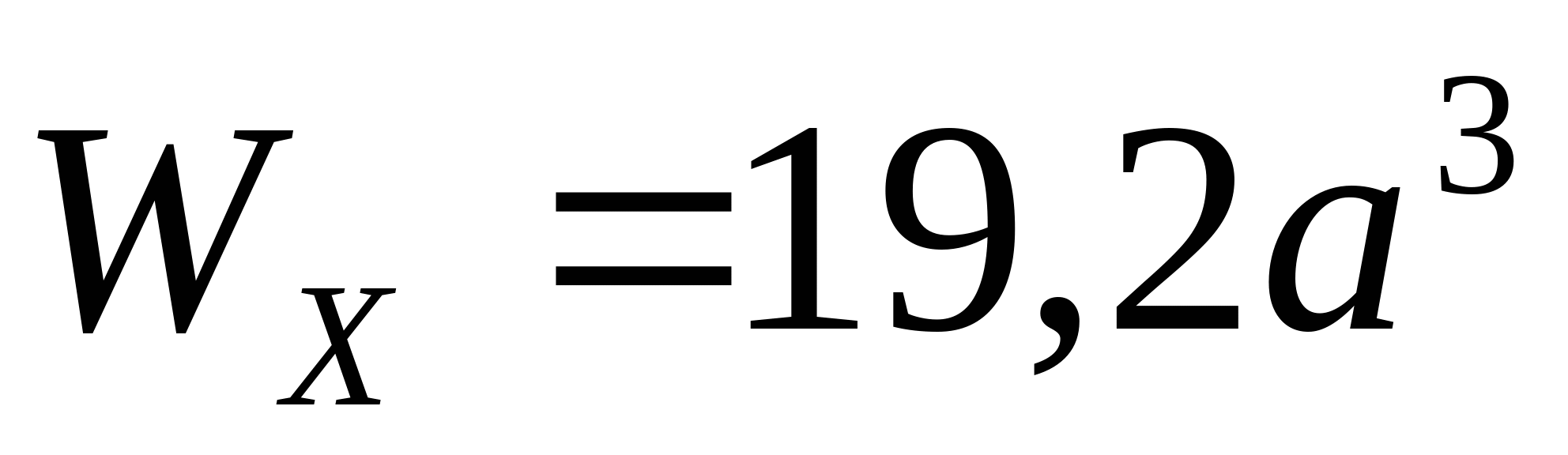 ; ; 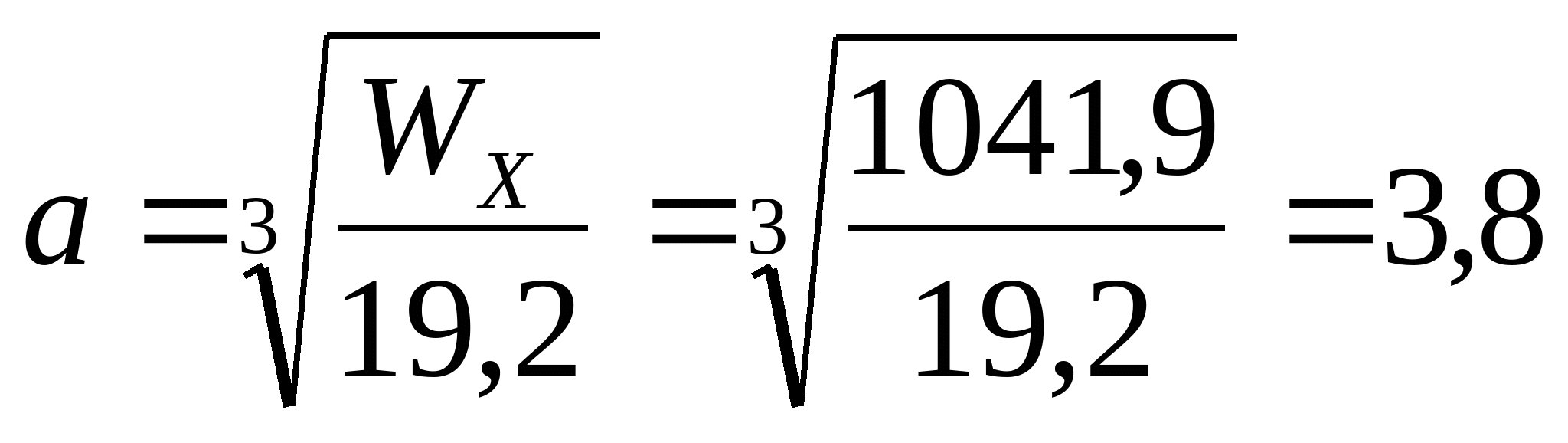 см см 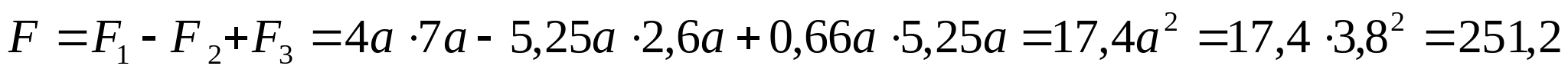 см2 см2 Все соотношения площадей полученных сечений сведем в одну таблицу:
| Тип сечения | Fi, см2 | Fi/FI | | Двутавр № 45 | 84,7 | 1 | | Круг | 374,6 | 4,42 | | Кольцо | 194,1 | 2,3 | | Прямоугольник | 273,8 | 3,2 | | Сложное сечение | 251,2 | 2,96 |
Из анализируя полученные результаты, получаем, что наименее материалоемким сечением будет – двутавровое сечение, а наиболее – круглое. РПР № 3.2
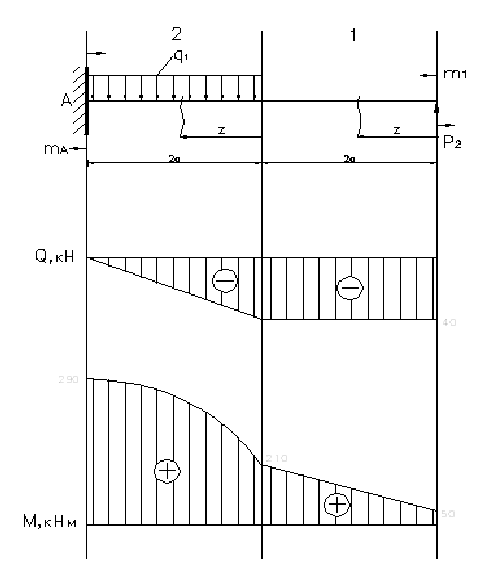
Дано: P2=-40 кН; m1=50 кН; q1=10  ; ; a=2 м;  =160МПа; =160МПа;  =90 МПа; =90 МПа;
Решение без определения опорных реакций.
Рисунок 8. Эпюра продольных сил и изгибающих моментов.
Решение:
1. Находим координаты эпюры поперечных сил и изгибающих моментов: 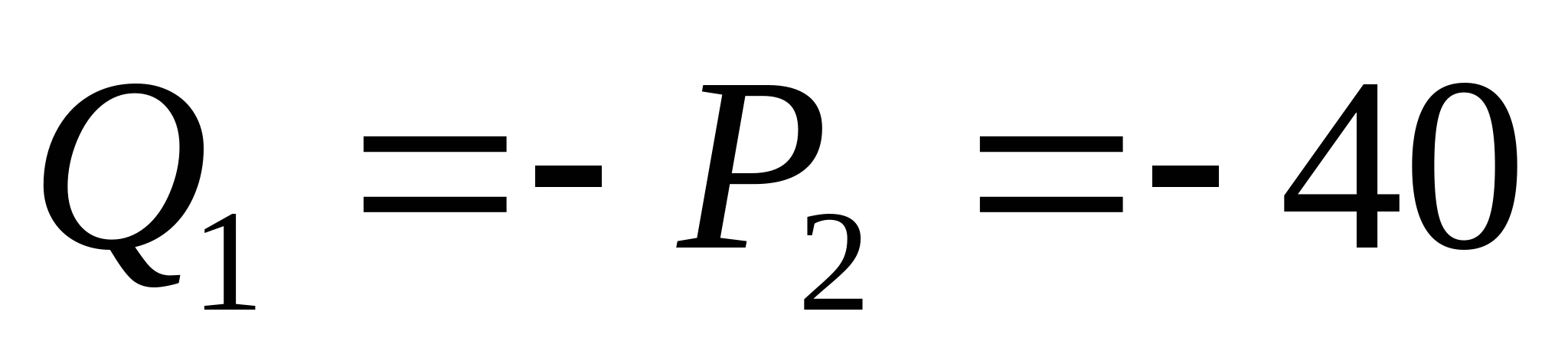 кН кН 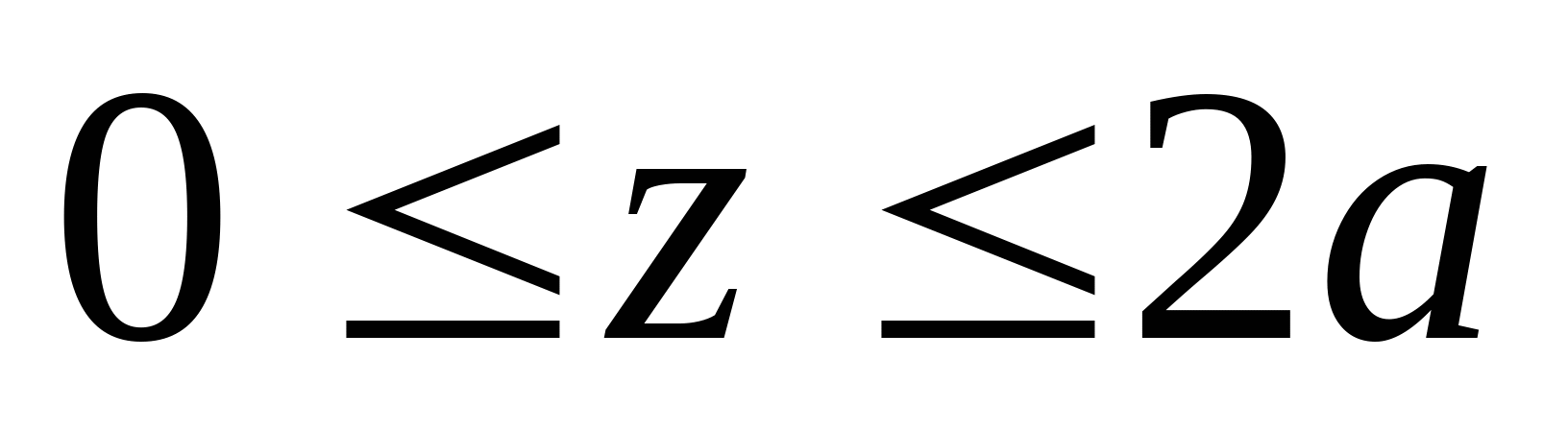 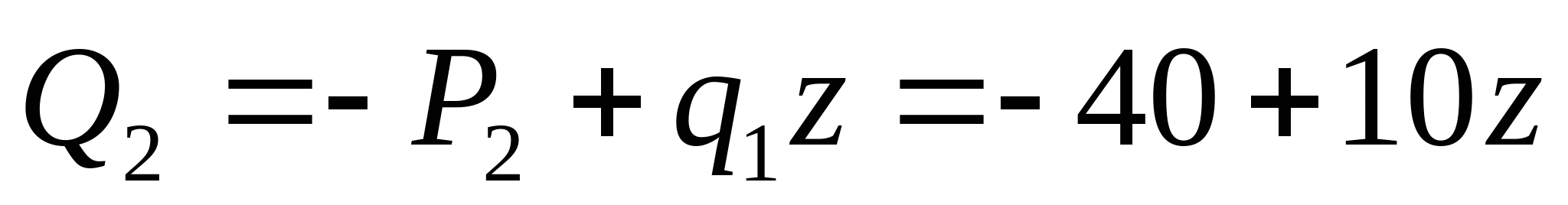 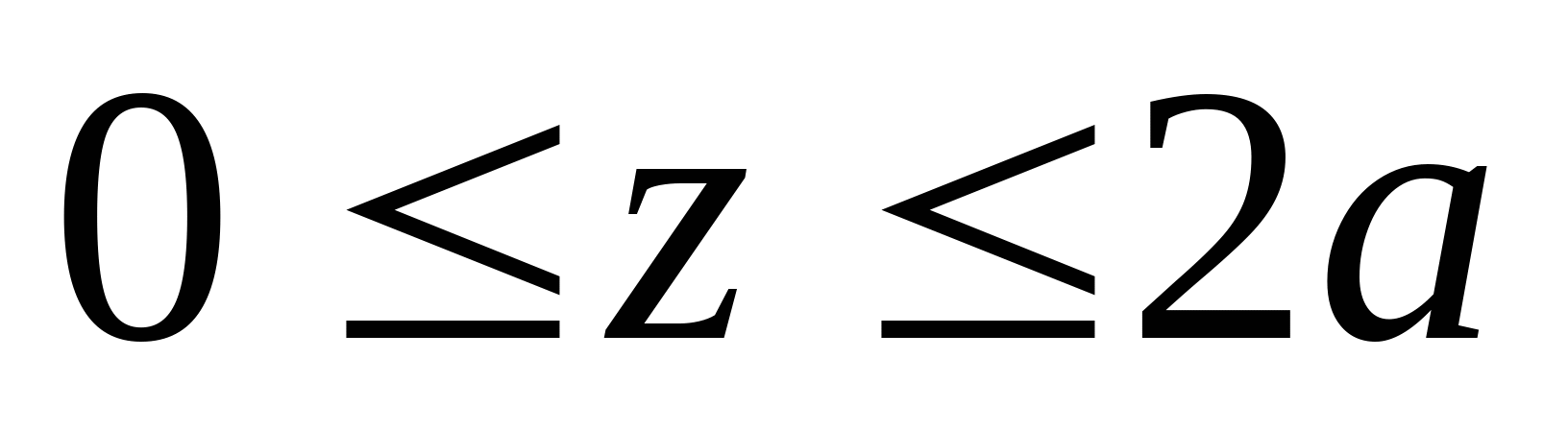 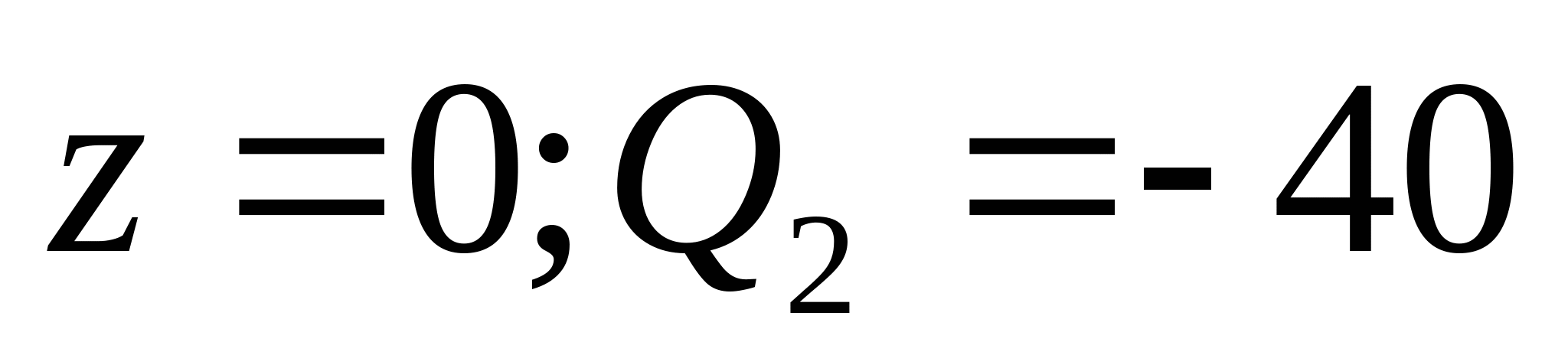 кН кН 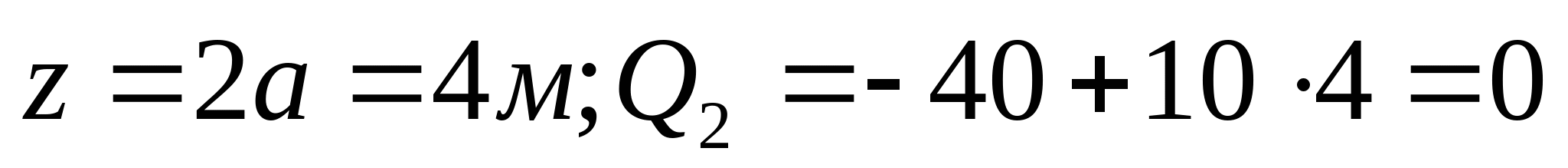
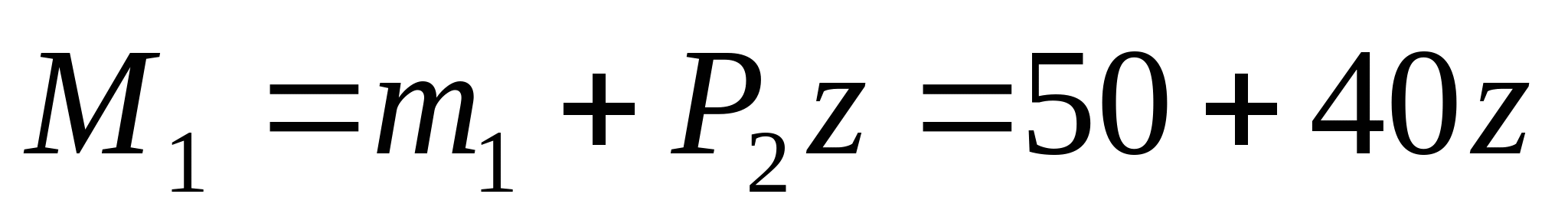 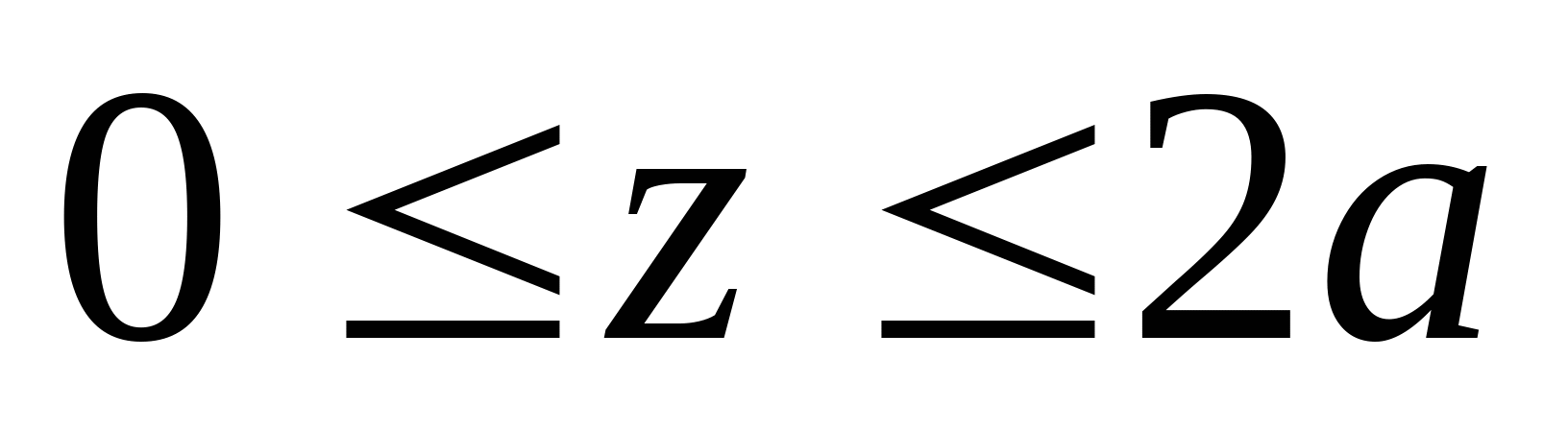 z=0; М1=50 кНм z=2а=4 м; М1=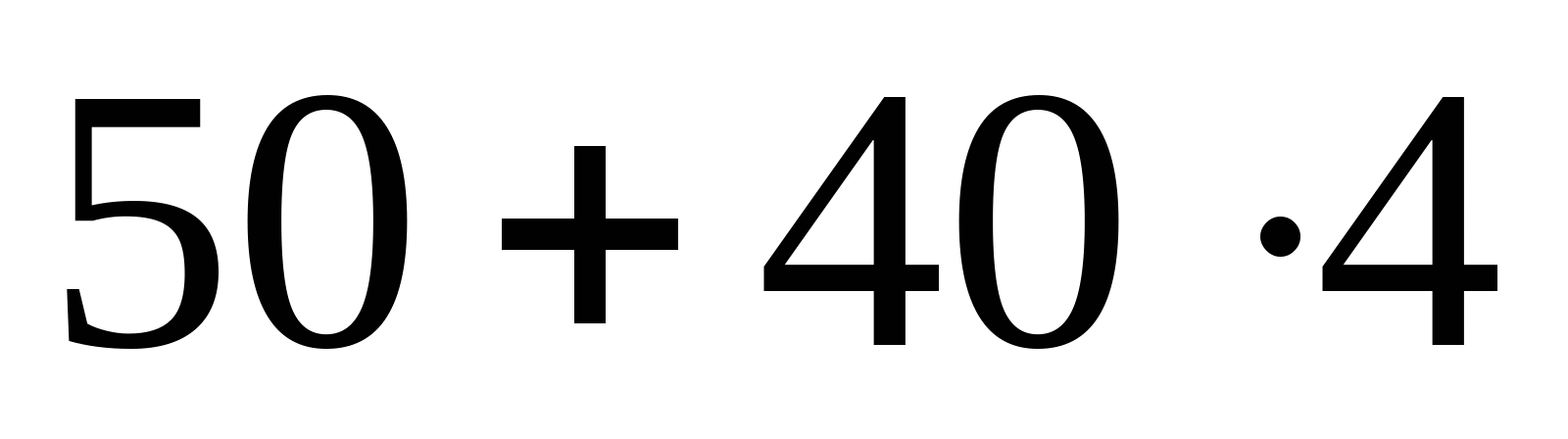 =210 МПа =210 МПа 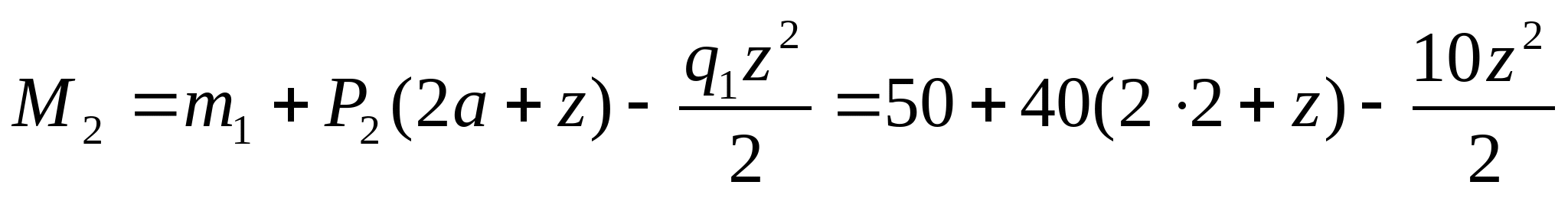  z=0; М2=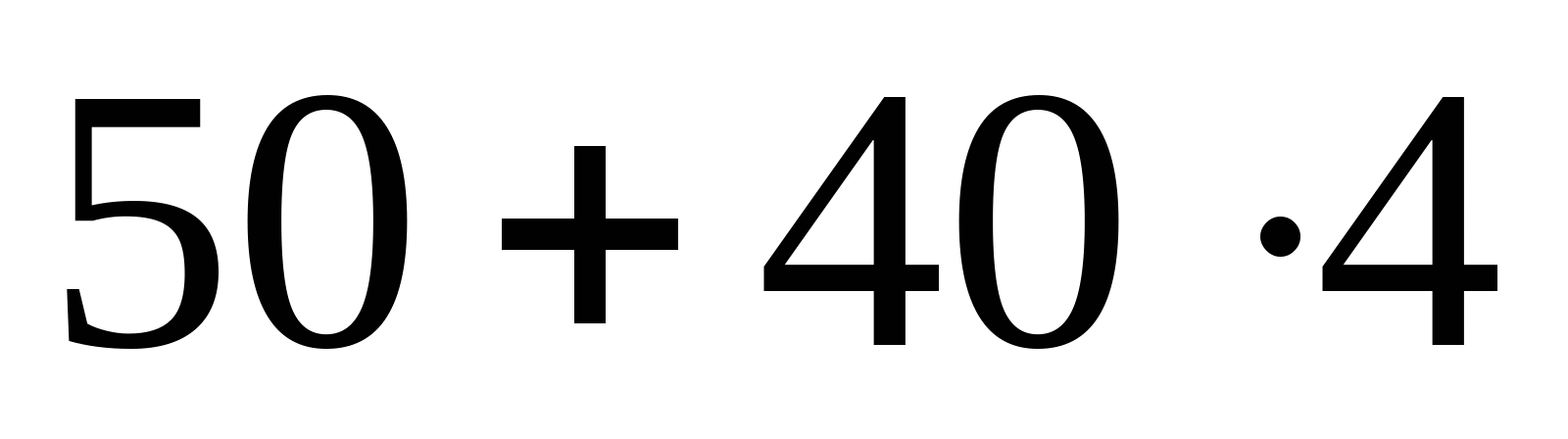 =210 МПа =210 МПа z=2а=4 м; 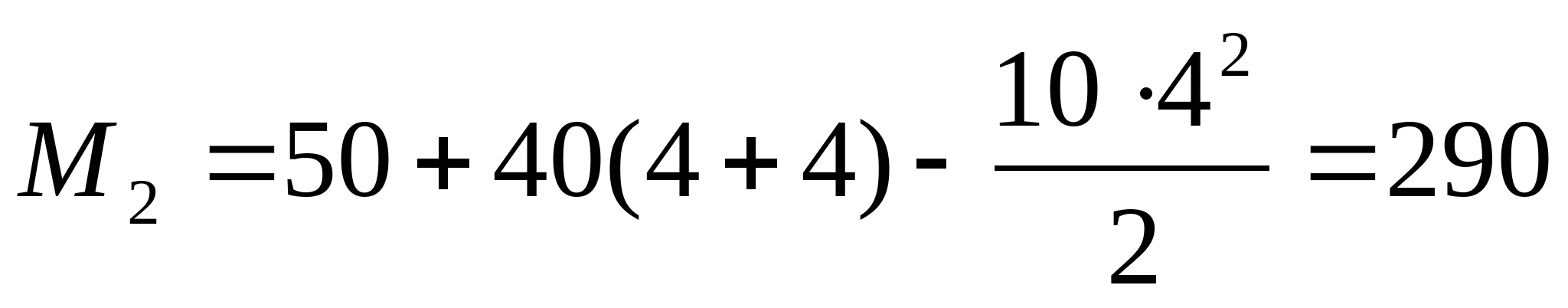 МПа МПа 2. Произведем подбор двутавровых сечений, исходя из условий прочности по нормальным напряжениям: 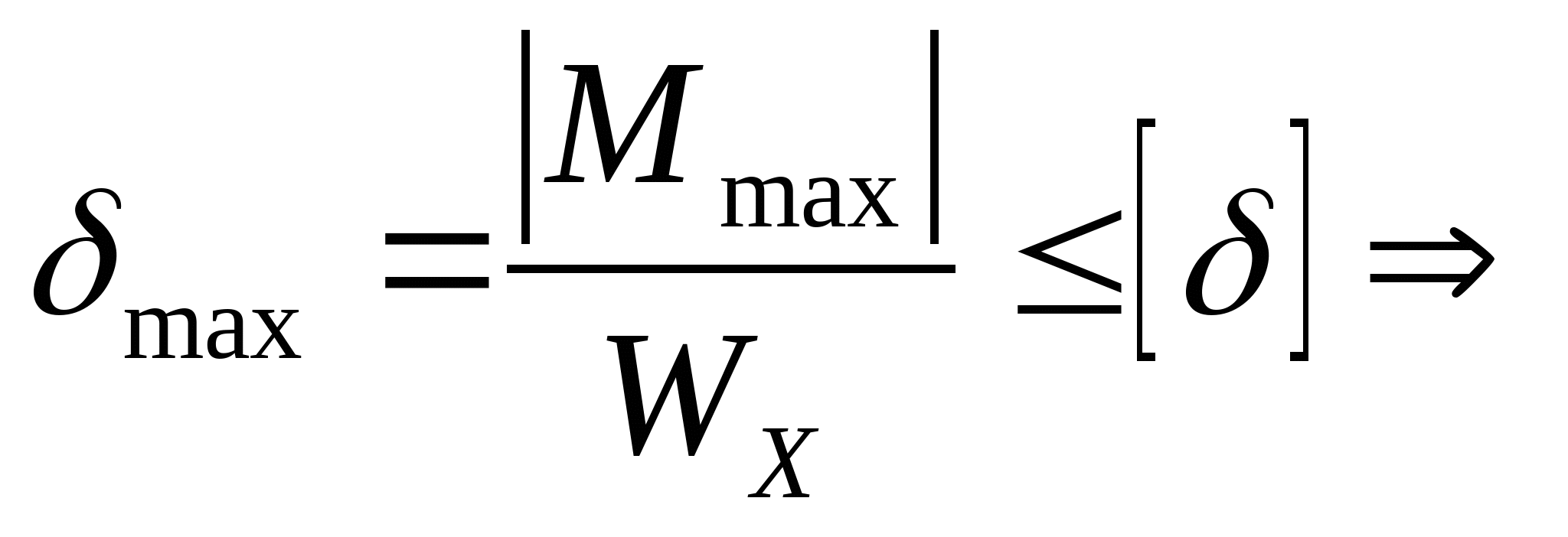 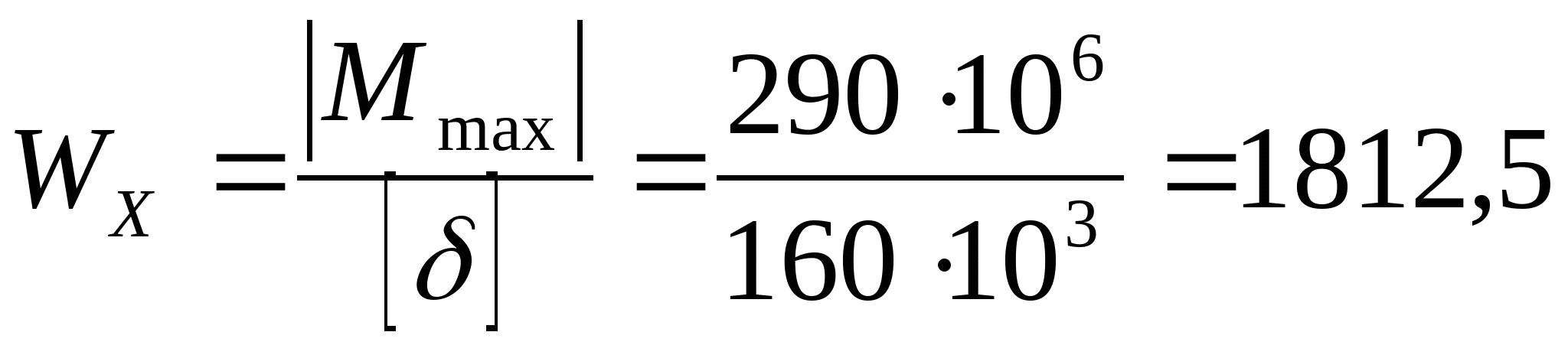 см3 см3 По ГОСТ 8239-89 I № 55; WХтабл=2035 см3; IX=55962 см4; SX=1181 см3; d=11 мм Проверка прочности по нормальным напряжениям: 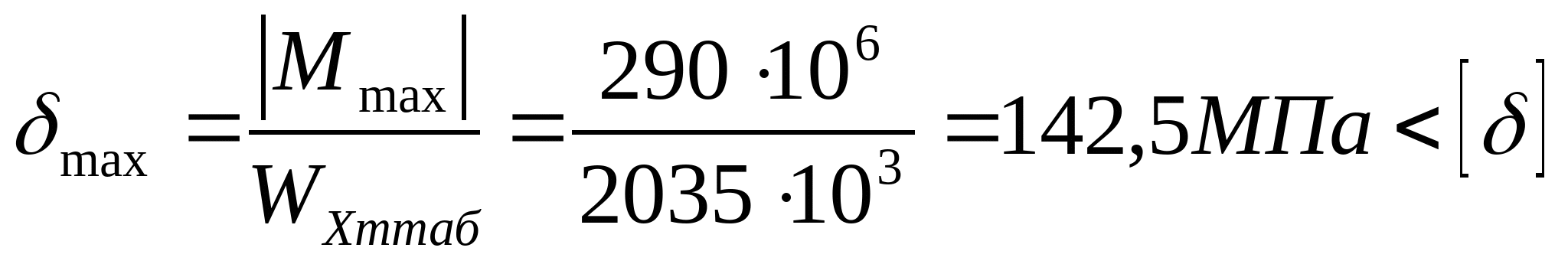 - условие прочности удовлетворяется. - условие прочности удовлетворяется.
3. Проверка прочности по касательным напряжениям: Условие прочности: 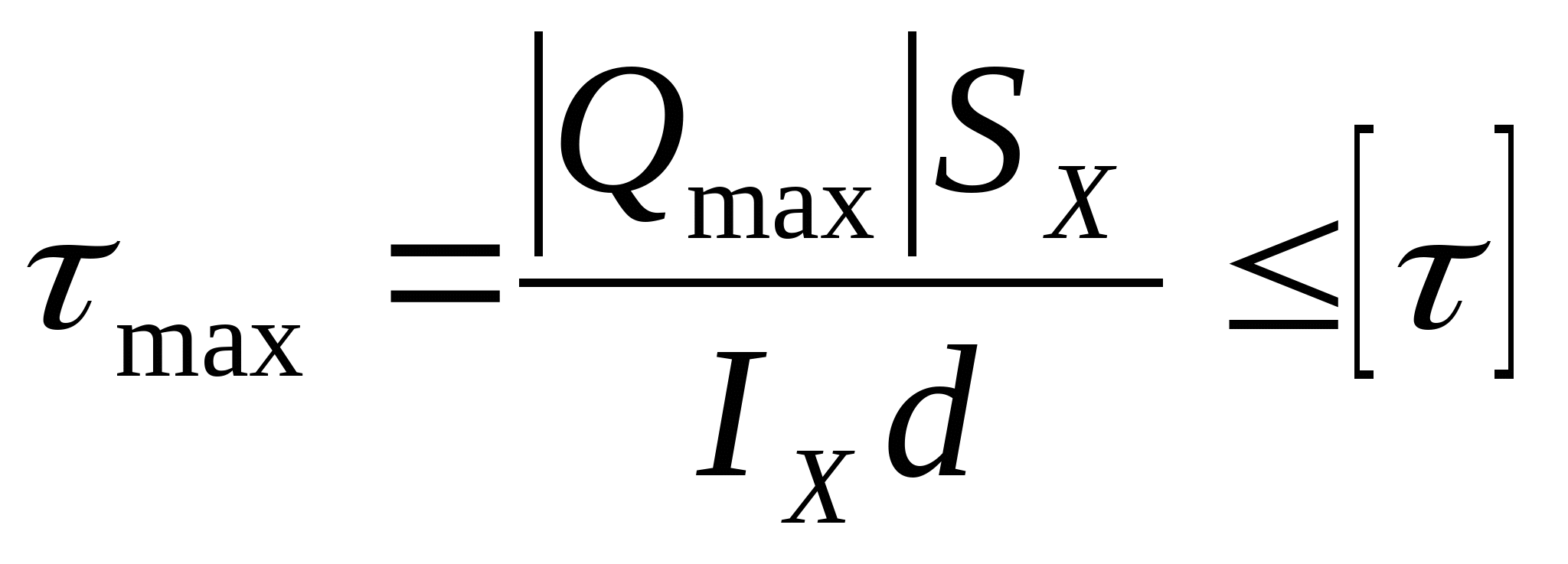 Из эпюры сил видно что опасным участком является участок 1, где  кН кН 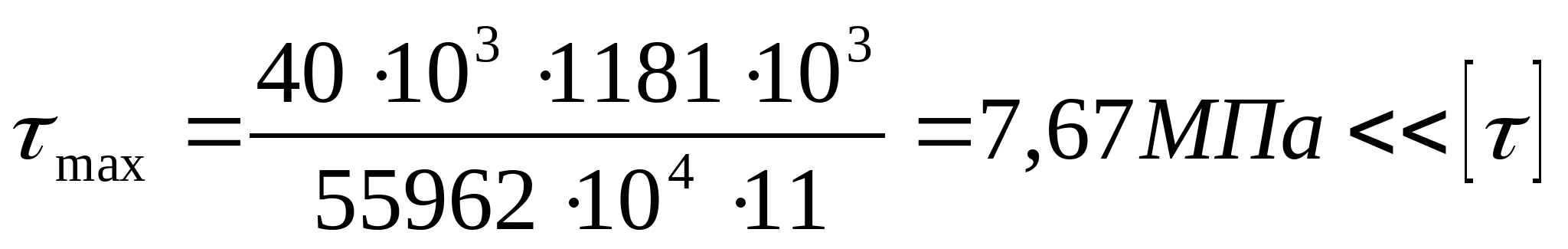 - т. е. условие прочности выполняется. - т. е. условие прочности выполняется. По  строим приближенно эпюру строим приближенно эпюру  : : 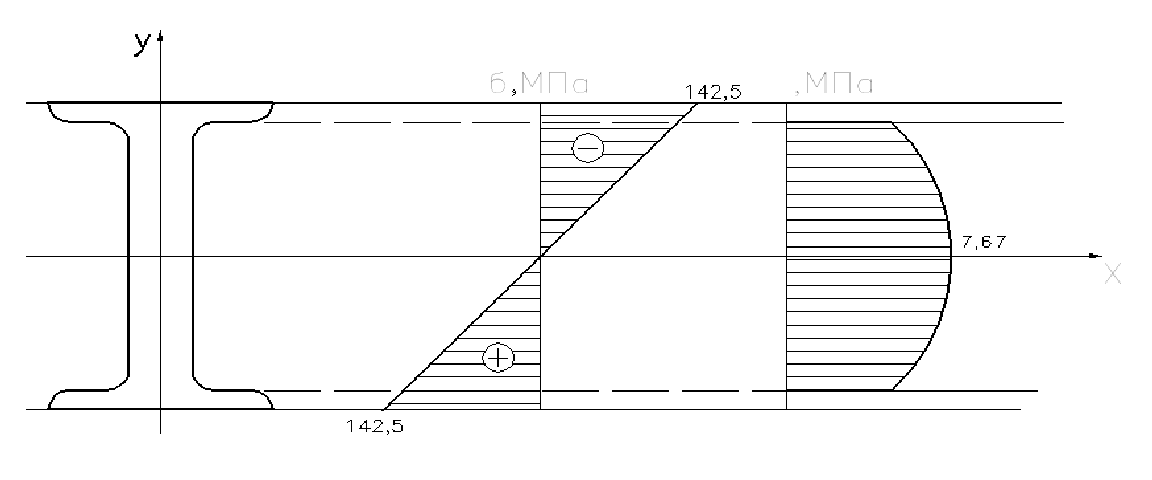
Рисунок 9. Эпюра. РПР № 3.3 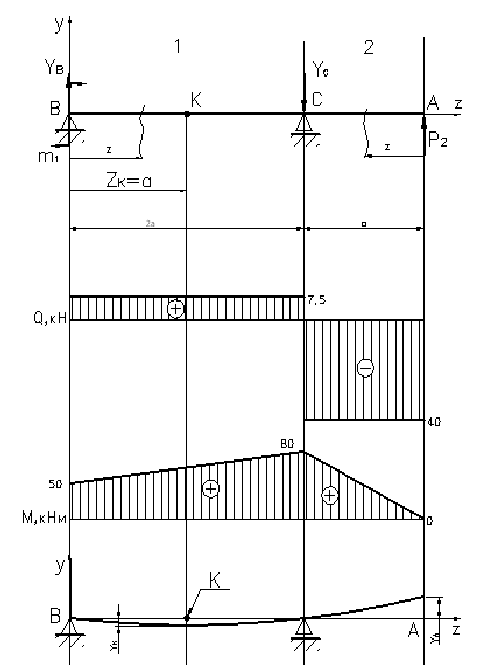 Дано: Дано: P2=-40 кН m1=50 кН а=2 м Ст. 3 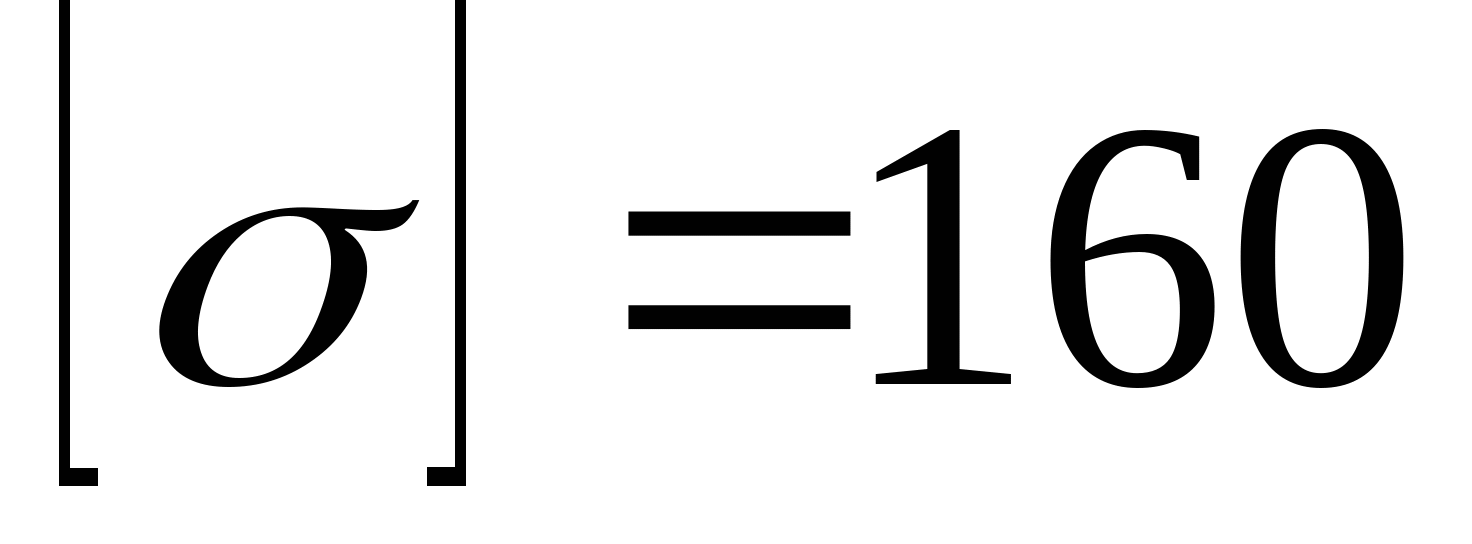 МПа МПа 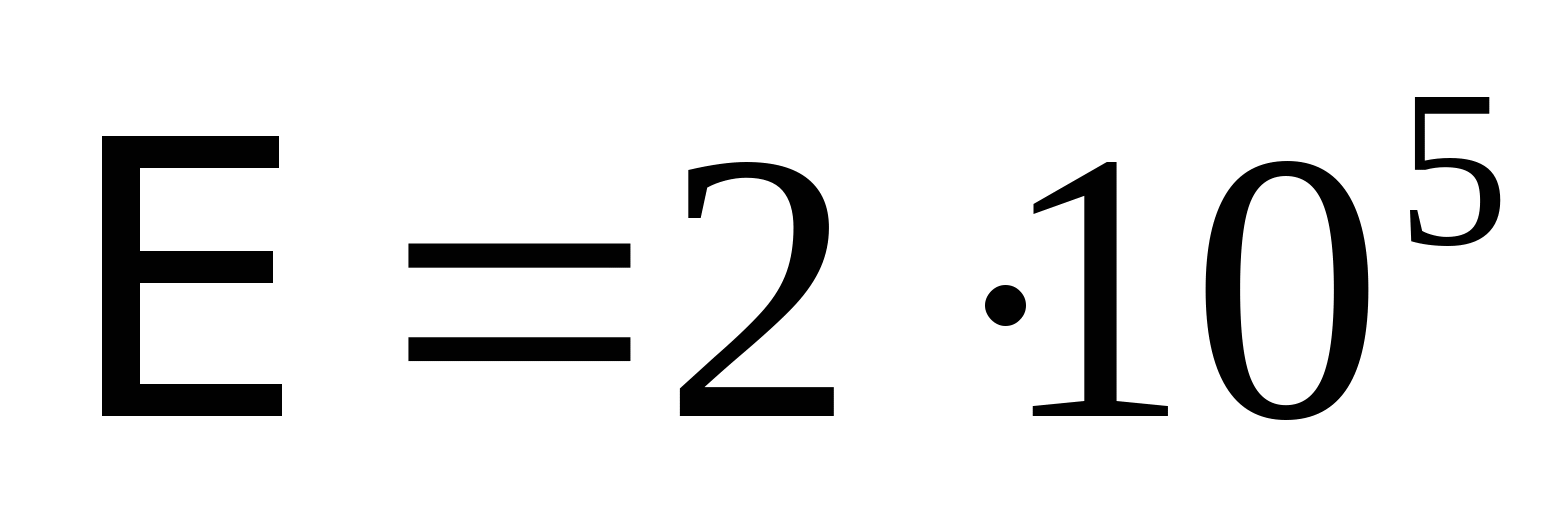 МПа МПа 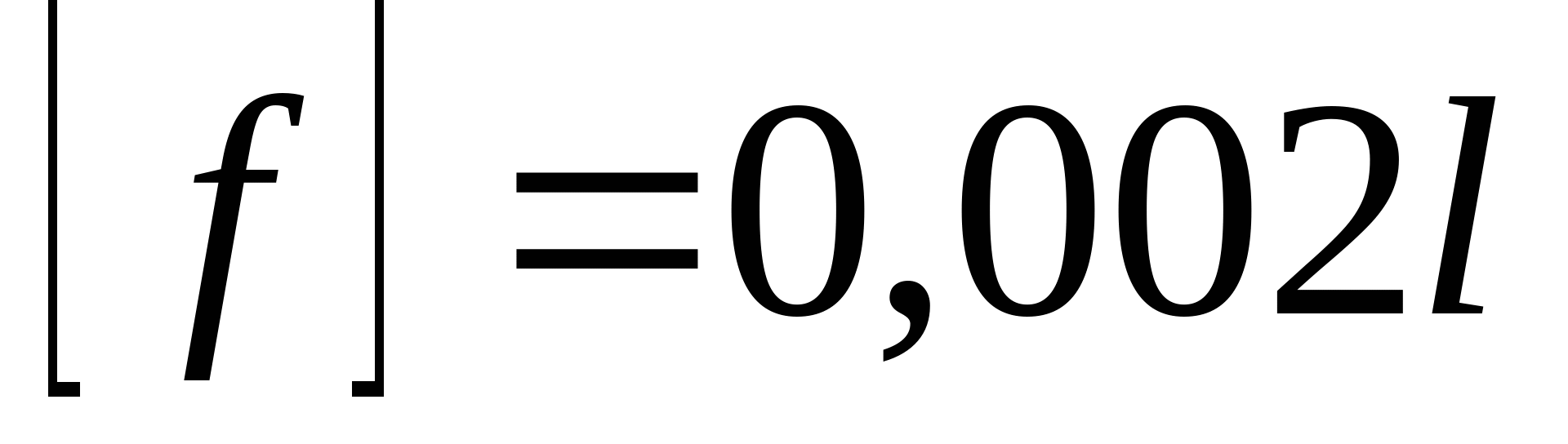
Рисунок 10. Эпюра продольных сил, изгибающих моментов и упругая линия.
1. Определяем опорные реакции: 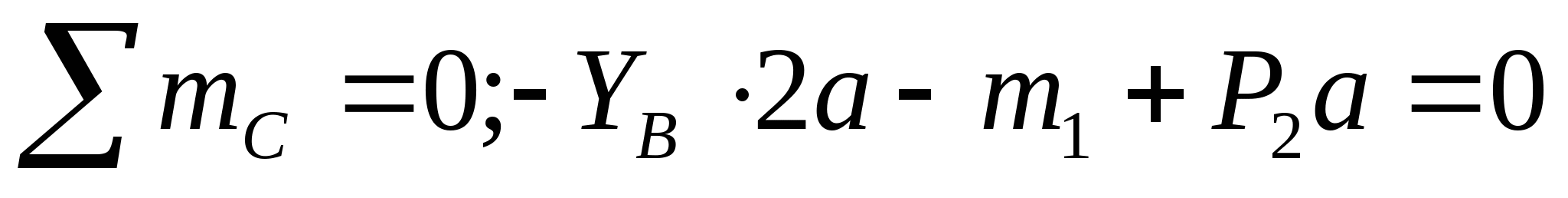 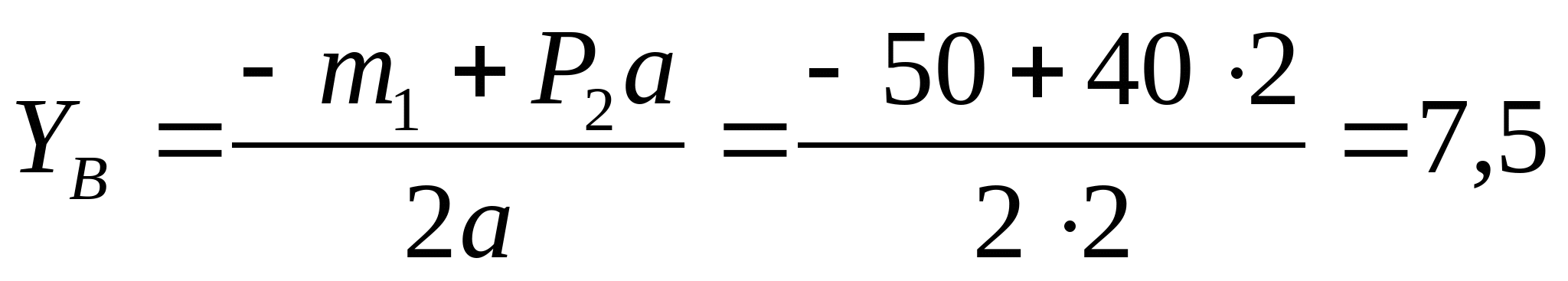 кН кН 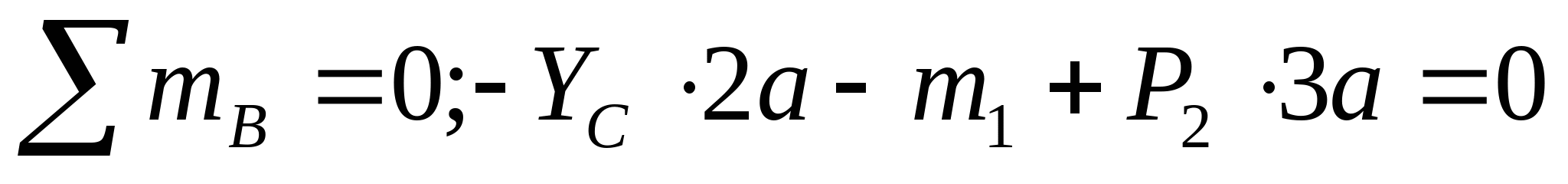 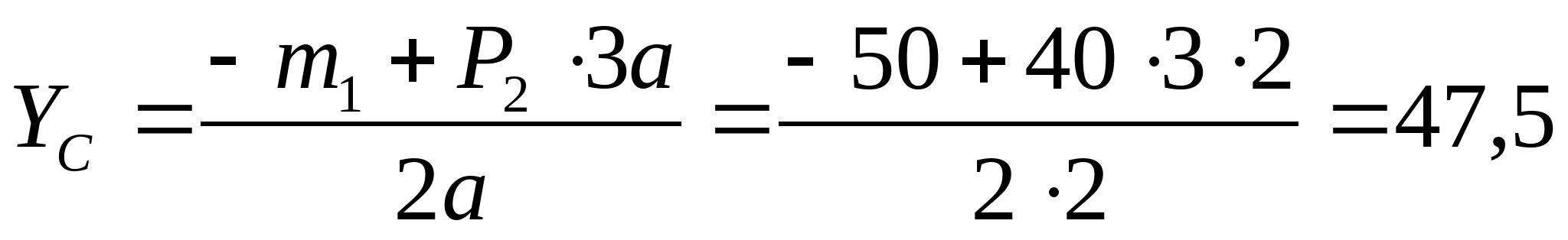 кН кН Проверка: 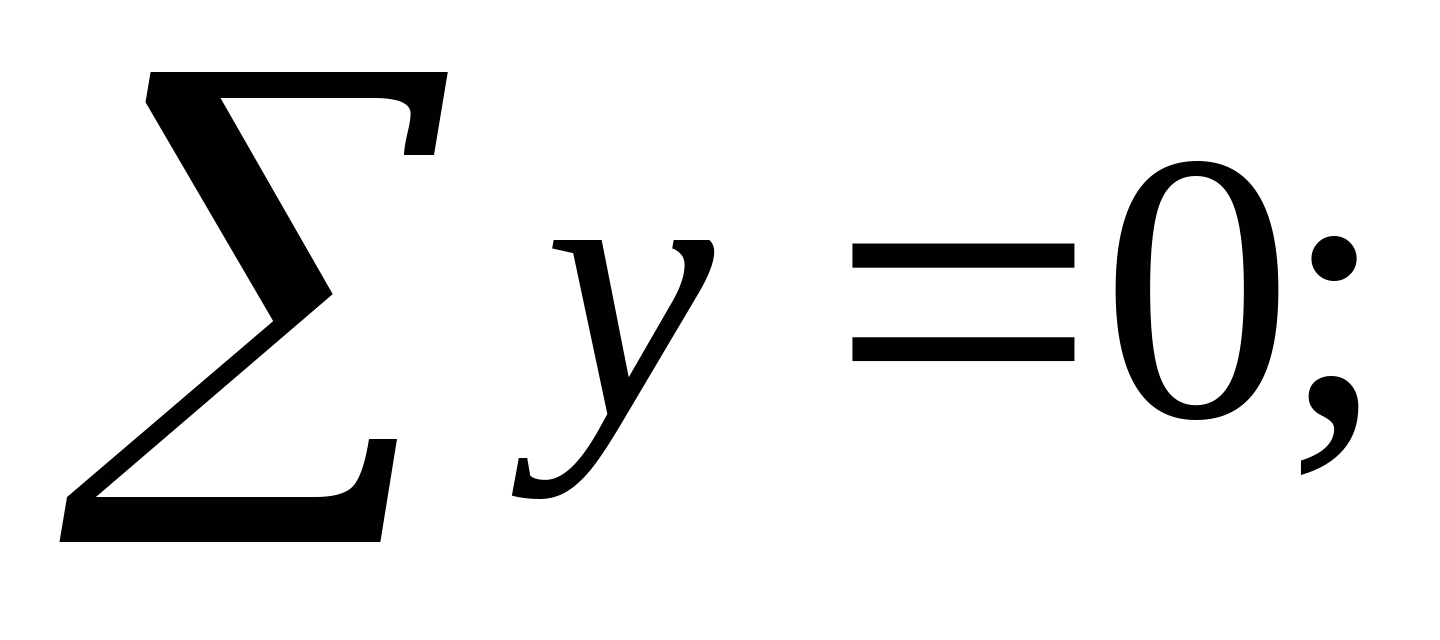 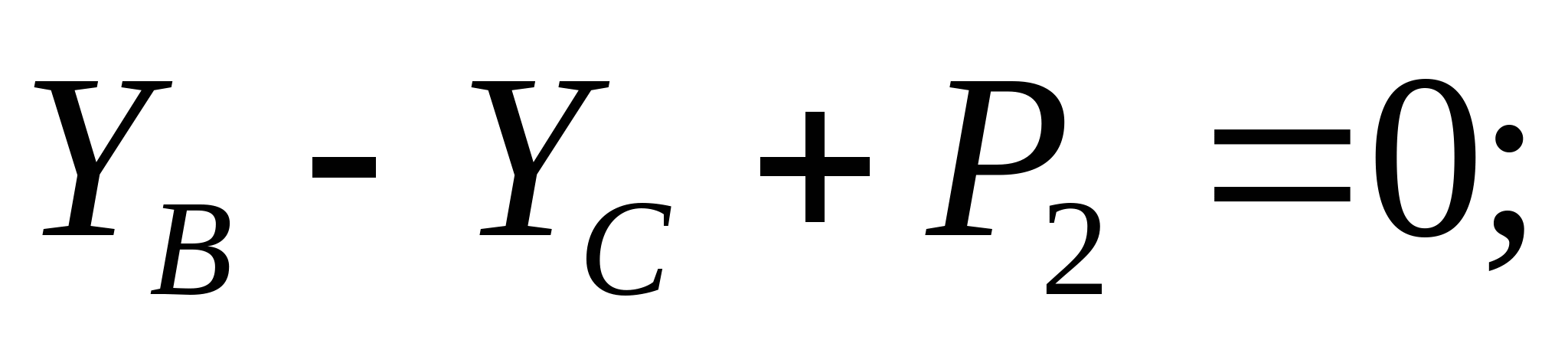 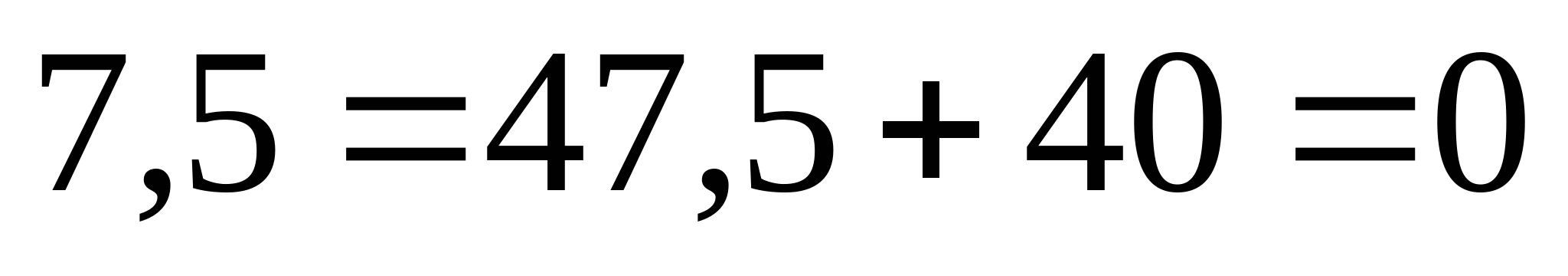
2. Рассчитаем координаты эпюры поперечных сил и изгибающих моментов: 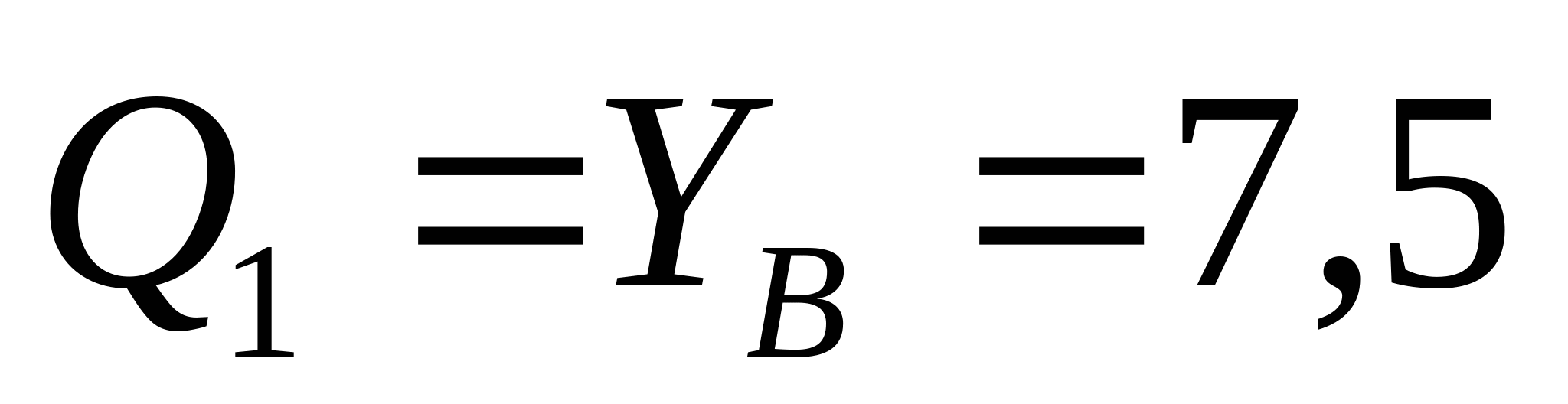 кН кН 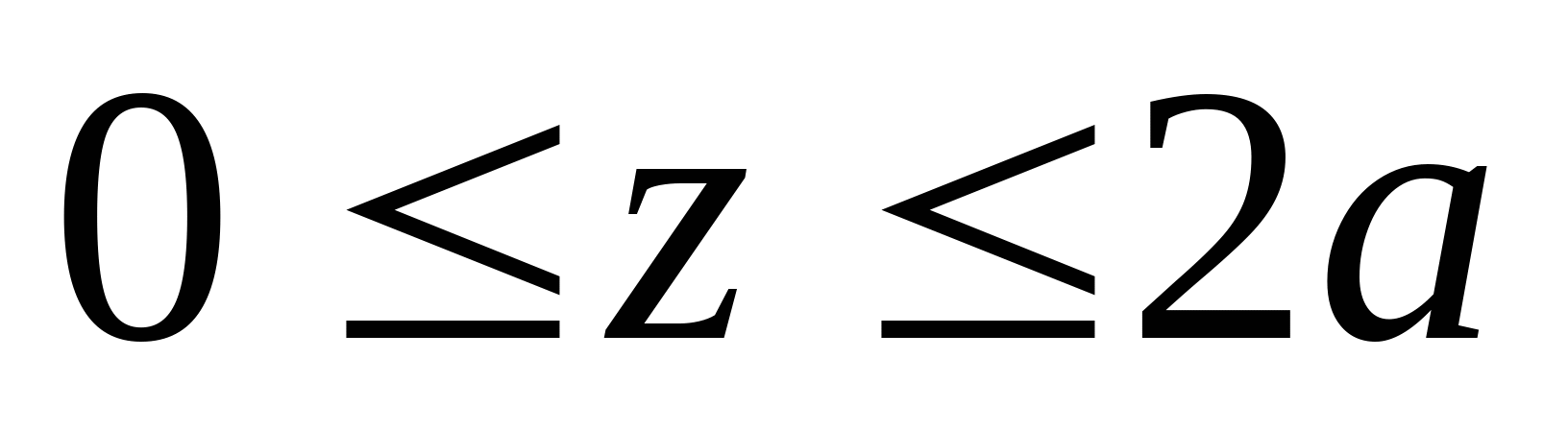 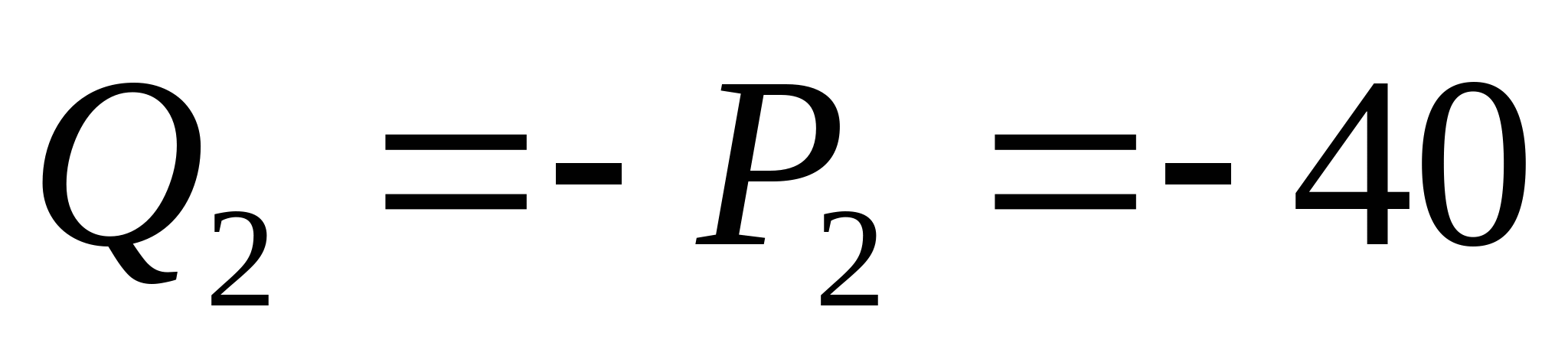 кН кН 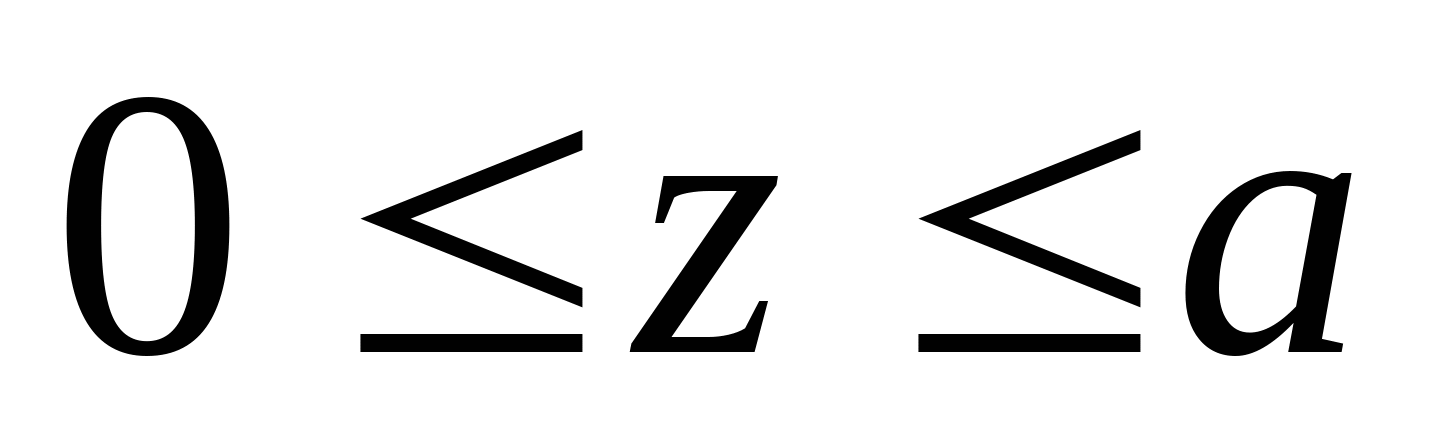 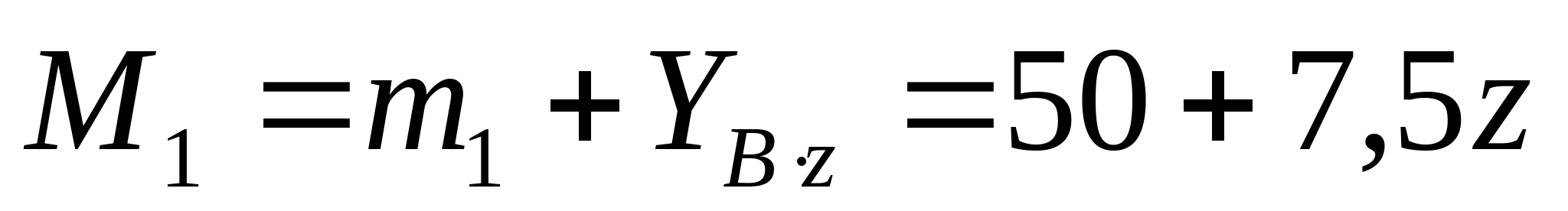 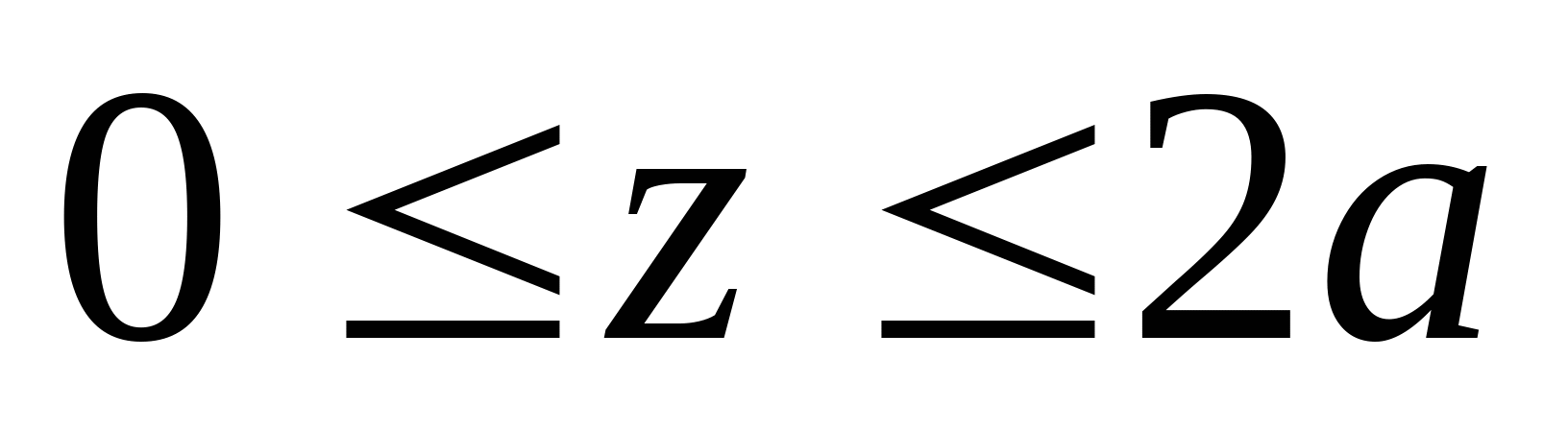 z=0; M1=50 кНм z=2a=4 м; 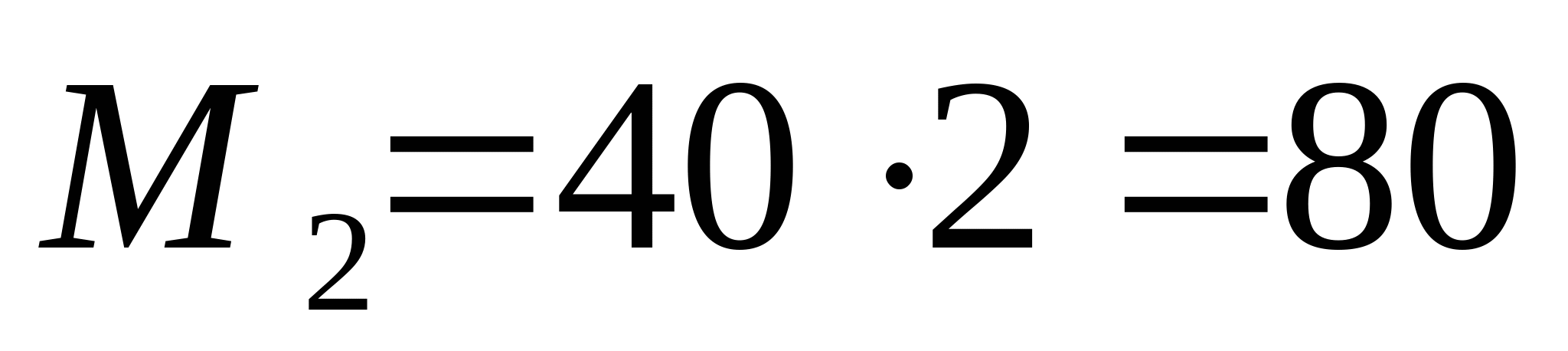 кНм кНм Из эпюры моментов получаем что опасное сечение находится в точке С, где 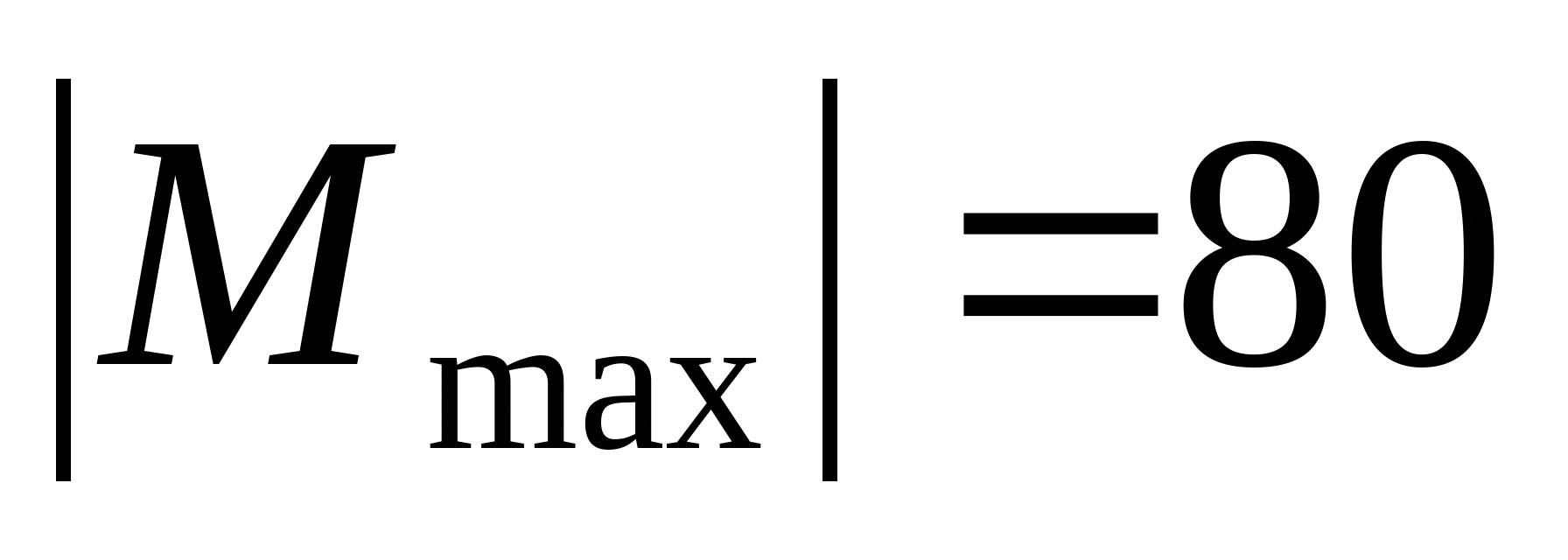 кНм кНм
3. Произведем подбор двутавровых сечений, исходя из условия прочности: 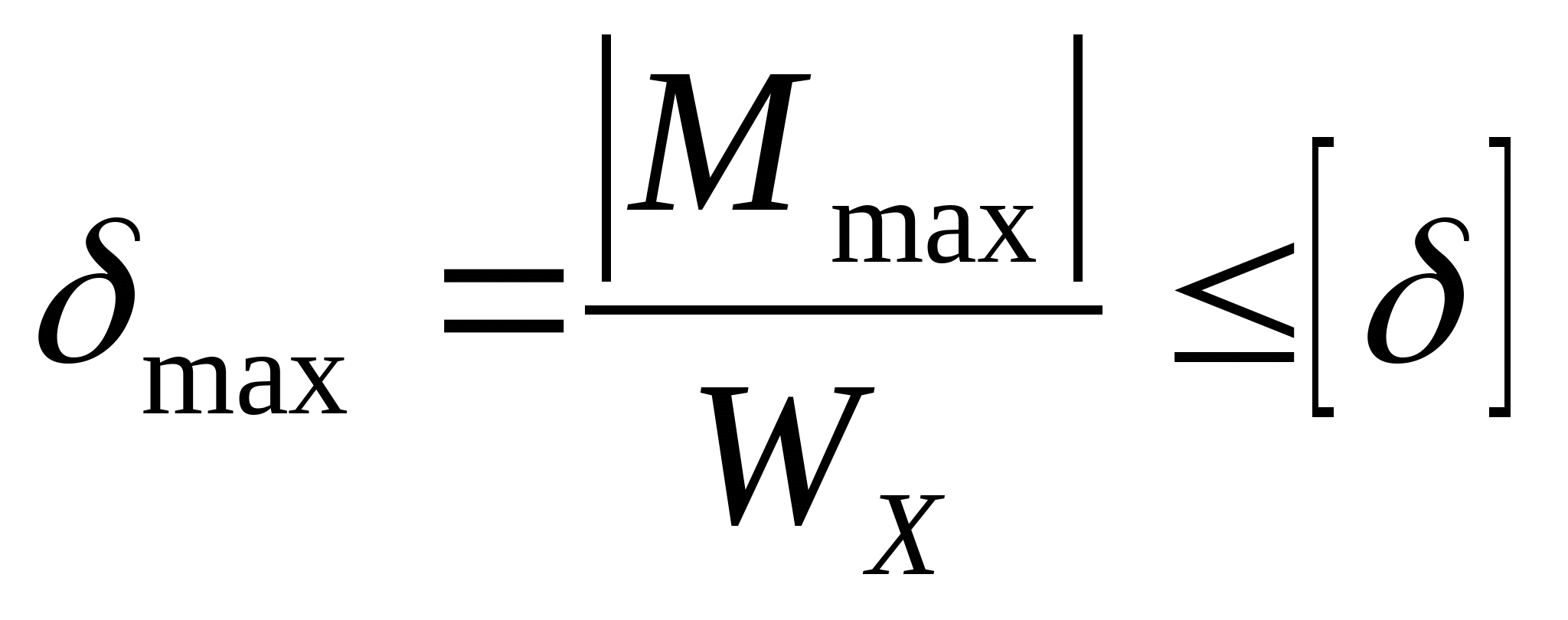 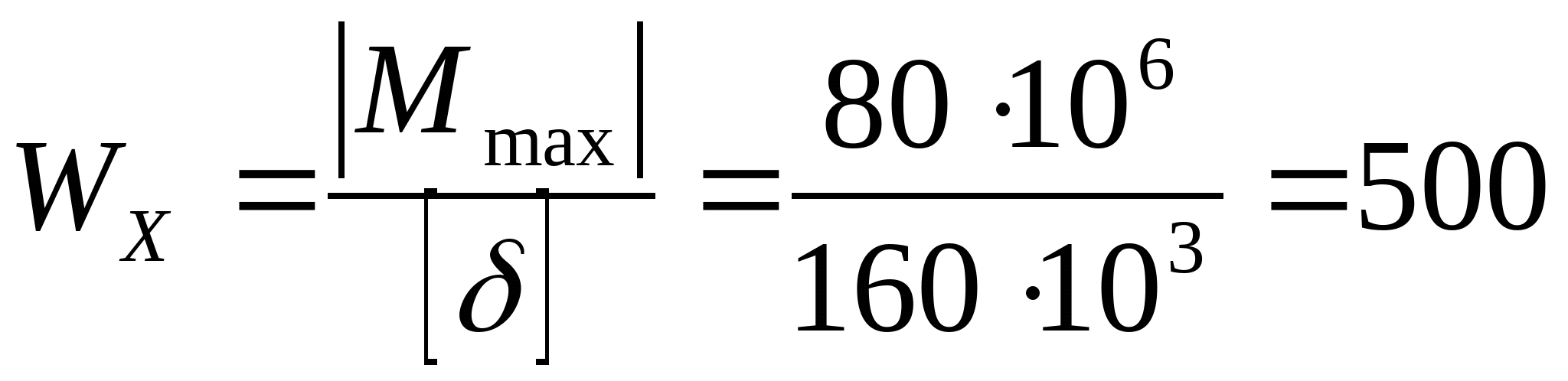 см3 см3 По ГОСТ 8239-89 I № 33, WXтабл=597 см3, IX=9840 см4, F=53,8 см2
4. произведем расчет на жесткость: Примем за начало координат точку В, положительные части осей y и z пойдут вверх и вправо соответственно. 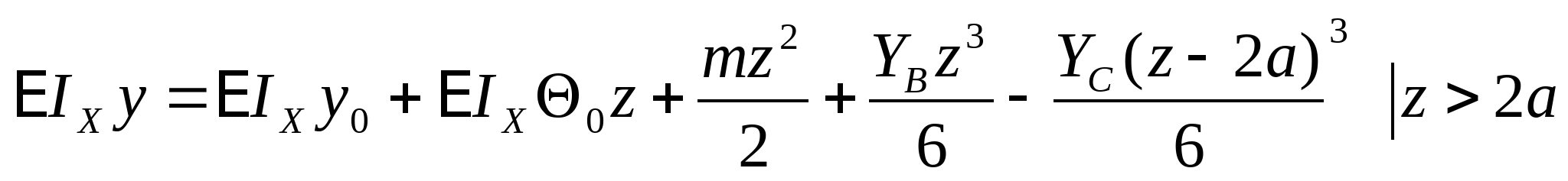 или
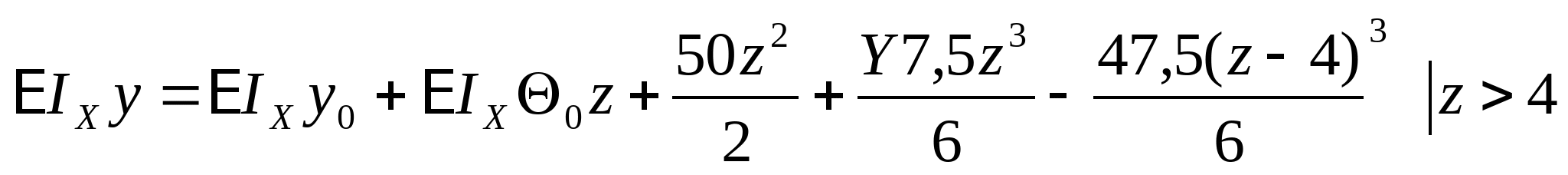 ; ; 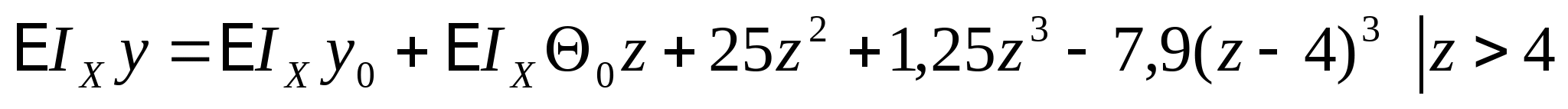 Определяем начальные параметры из граничных условий: z=0, y=0 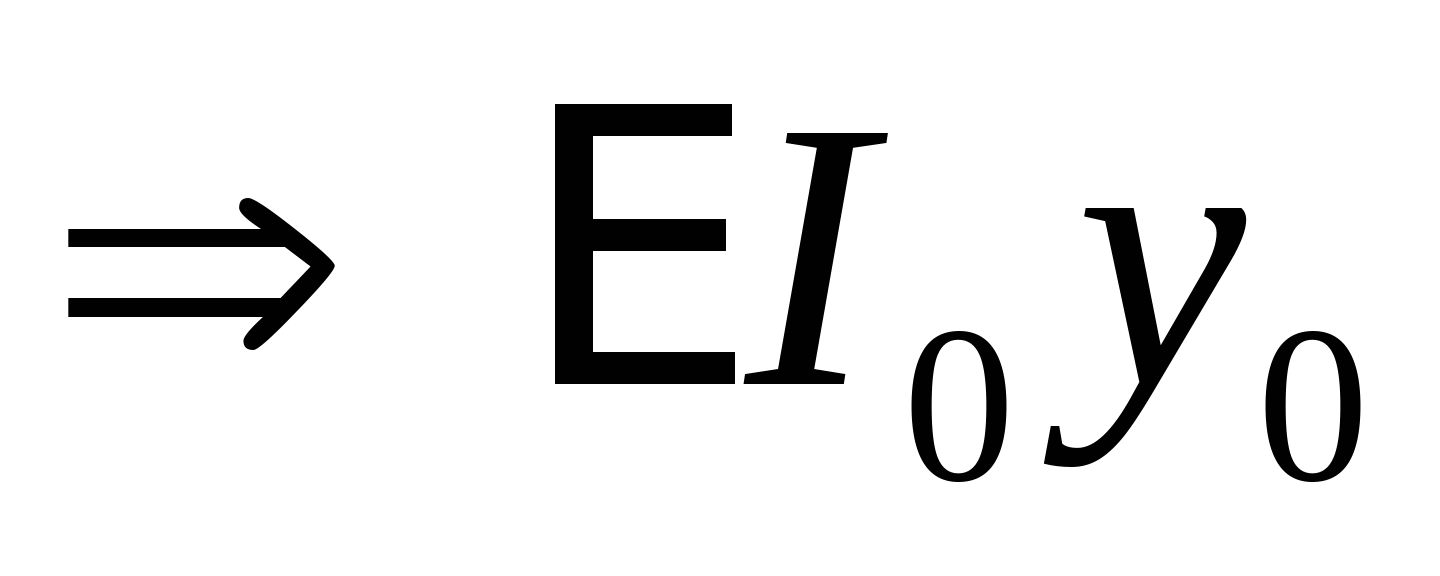 ; ; z=2a=4 м, y=0 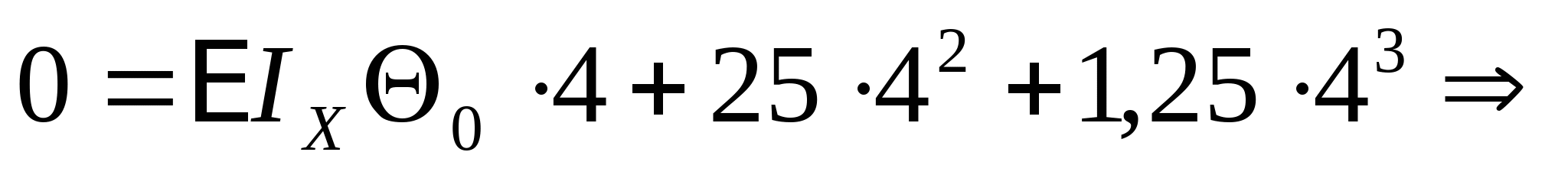
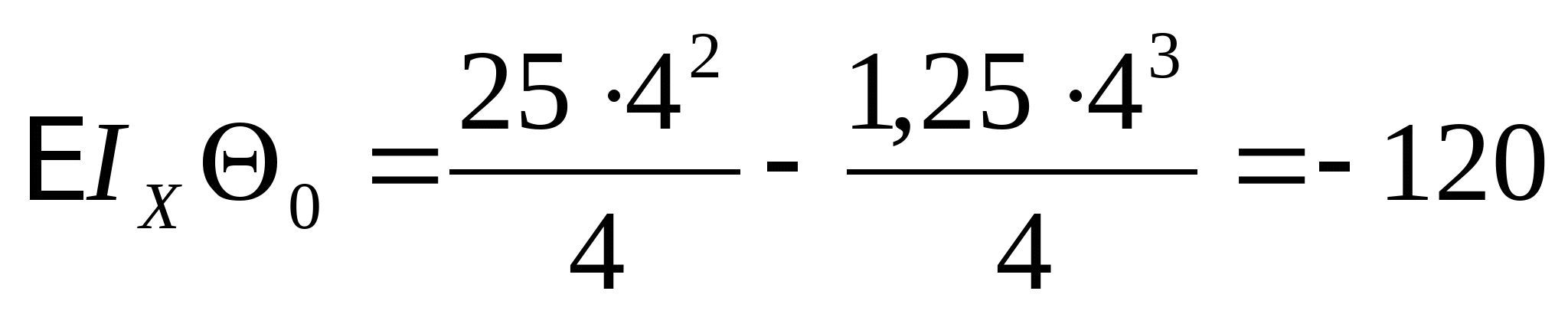 кНм2 кНм2 и окончательно получаем: 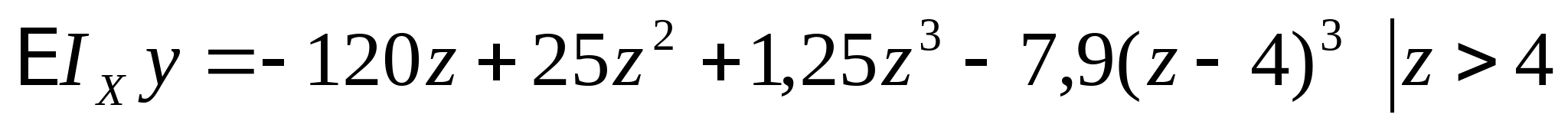 Далее определяем прогибы в характерных сечениях К и А: zK=a=2 м 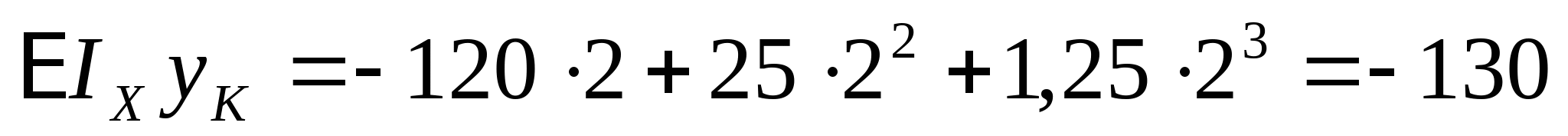 кНм3 кНм3 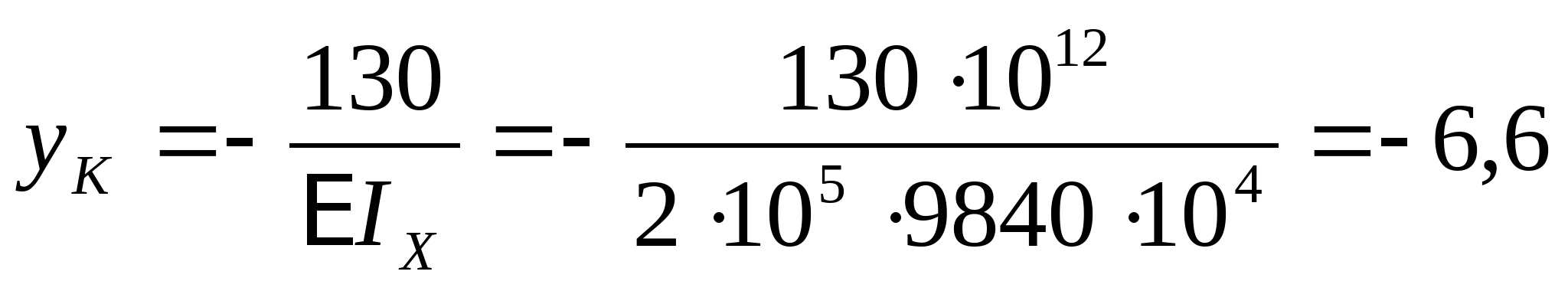 мм мм zA=3a=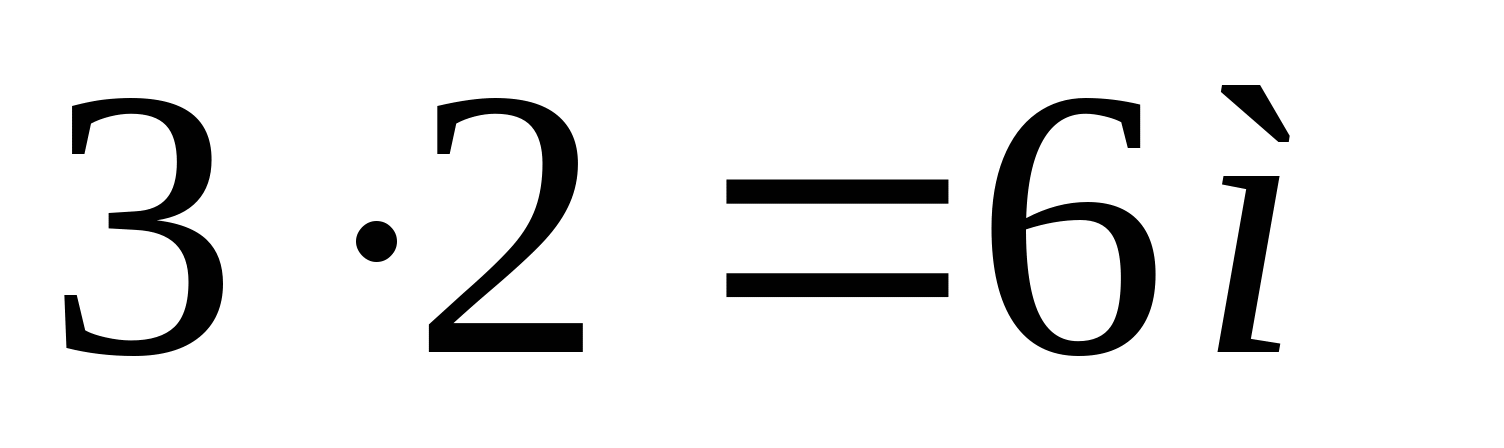 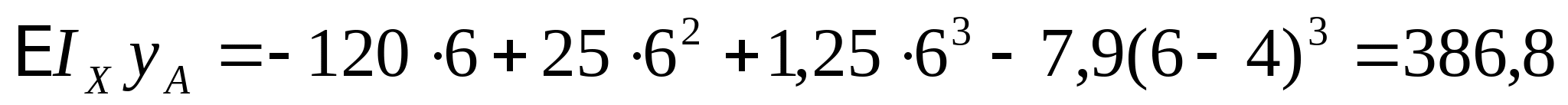 кНм3 кНм3 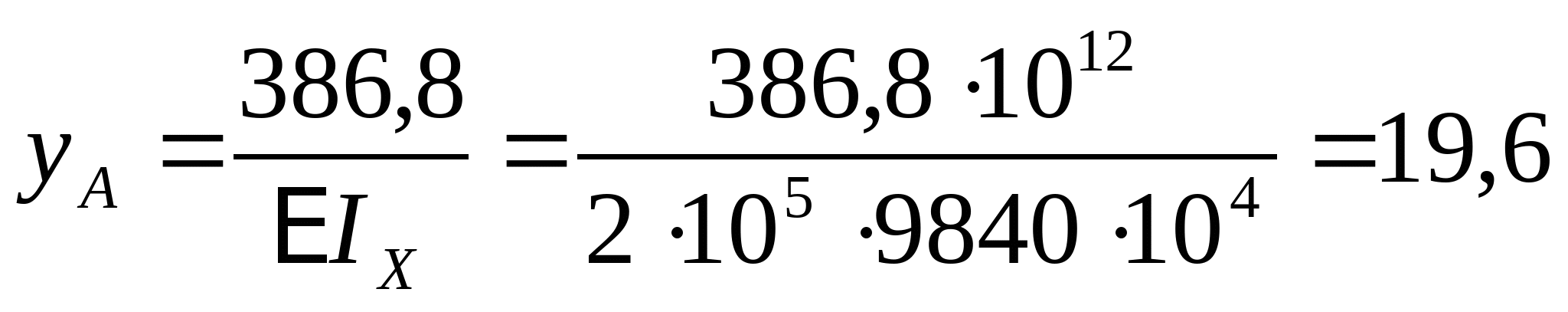 мм мм Из эпюры видно, что 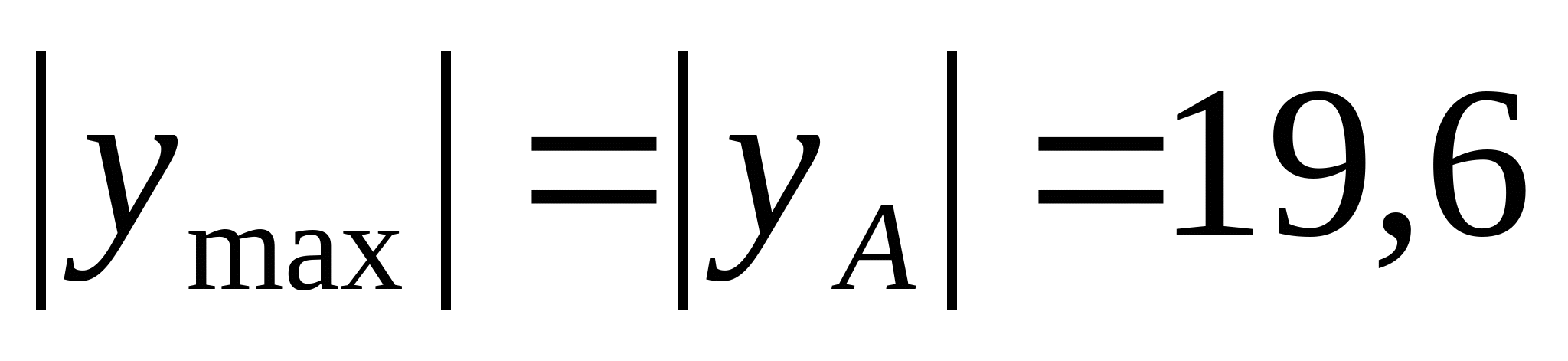 мм мм Проверка: жесткость должна удовлетворять следующему неравенству 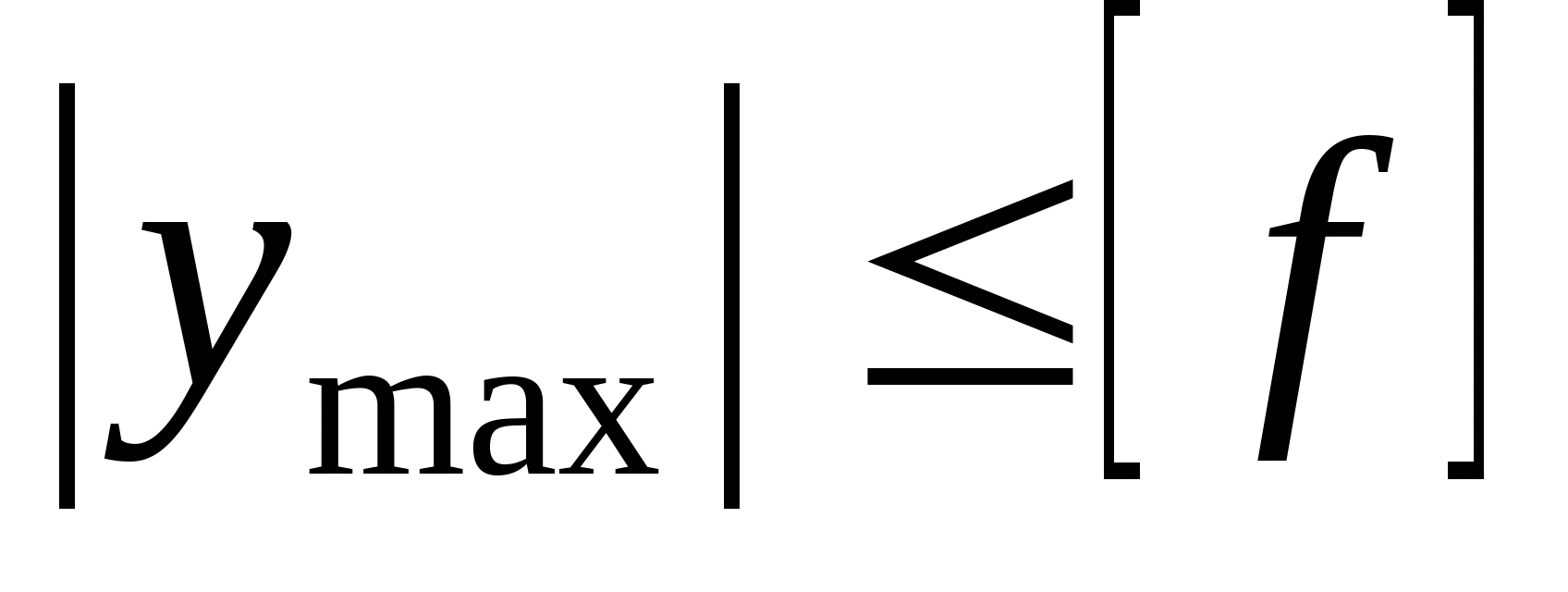 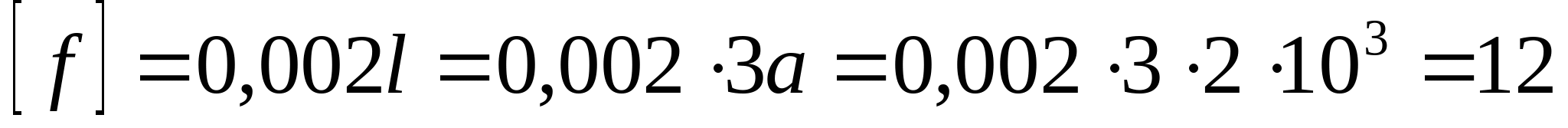 мм мм из полученного видно, что 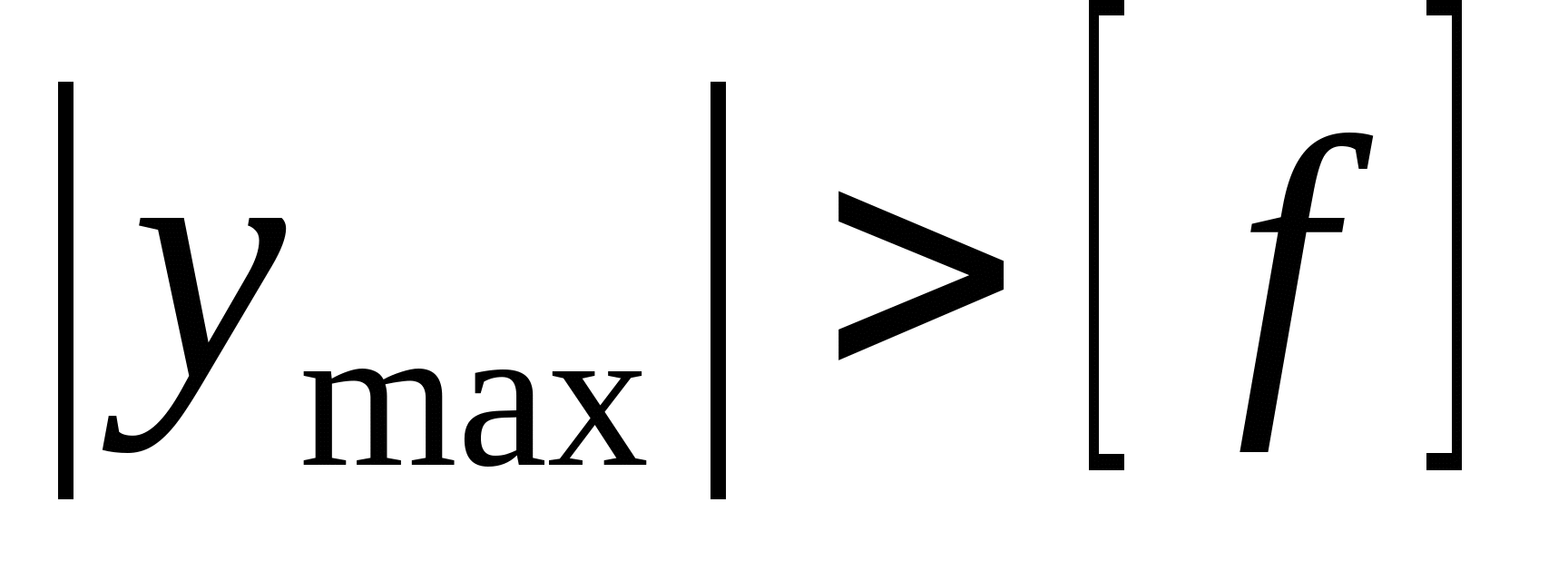 - это означает, что условие жесткости не выполняется. - это означает, что условие жесткости не выполняется. 5. Подбор двутаврового сечения из условия жесткости: 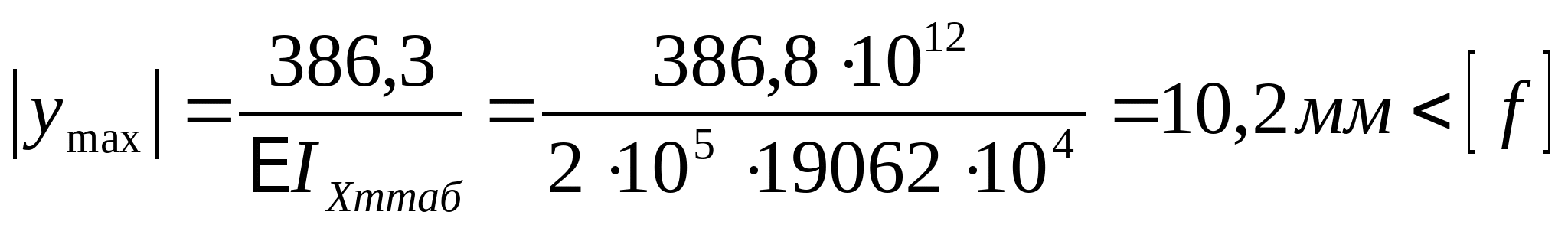 - условие жесткости выполняется. - условие жесткости выполняется. По полученным значениям yK и yА, с учетом знаков эпюры моментов, строим упругую линию балки. |