Океанов Е.Н.
В неподвижном
геометрическом трехмерном пространстве X Y Z
, ,
(с прямоугольными координатами) радиус-вектор:
r
( ) t
= i
x t
( ) + j
y t
( ) + k
z t
( ) (1)
определяет кривую в пространстве (годограф), по которой перемещается эта точка, являясь началом координат подвижного
трехмерного пространства X Y Z
m
,
m
,
m
(с иными прямоугольными координатами). Это подвижное пространство определено, как известно, сопровождающим трехгранником с базисом τ ,n,b
– ортами касательной, нормали и бинормали к указанному годографу, соответственно. В этом подвижном пространстве начало координат неподвижного пространства определяется радиусвектором:
r
m
=τ x
m
+ n
y
m
+ b
z
m
(2)
Представляется очевидным равенство:
r
=− r
m
, (3)
поскольку левая часть этого равенства выражает расстояние от начала неподвижного пространства до начала подвижного пространства, а правая часть, наоборот, расстояние от начала подвижного пространства до начала неподвижного пространства. Но это – одно и то же расстояние, и лишь в векторной интерпретации оно характеризуется разными векторами с одинаковым модулем и противоположными направлениями. Поэтому равенство (3) можно дополнить равенством:
 r
= r
m
(4) r
= r
m
(4)
Орты подвижного пространства можно выразить через орты неподвижного пространства:
τ= i
τ τ τ
x
+ j
y
+ k
z
, n
= i
n
x
+ j
n
y
+ k
n
z
, b
= i
b
x
+ j
b
y
+ k
b
z
(5)
и тогда равенство (3) преобразуется к виду:
i
( x
+ τ
x m
x
+ n y
x m
+ b z
x m
) + + j
( y
τ
y m
x
+ n y
y m
+ b z
y m
) + k
( z
+ τ
z m
x
+ n y
z m
+ b z
z m
) = 0, откуда следуют очевидные равенства:
τ z m x
+ n y
z m
+ b z
z m
= − x
τ
y m
x
+ n y
y m
+ b z
y m
= − y
, (6)
τ z m x
+ n y
z m
+ b z
z m
= − z
τ x n
x
Δ = τ
y
n
y
τ z n
z
и легко приводится к скалярному равенству:
|
b
x
b
y
(7)
b
z
|
  Эти равенства естественно рассматривать, как систему трех уравнений с тремя неизвестными x y z
m
,
m
,
m
, поскольку задание радиус-вектора (1) вполне определяет значение остальных величин в этой системе. Ее определитель равен: Эти равенства естественно рассматривать, как систему трех уравнений с тремя неизвестными x y z
m
,
m
,
m
, поскольку задание радиус-вектора (1) вполне определяет значение остальных величин в этой системе. Ее определитель равен:
Δ = τ
x
( n b
y z
− n b
z y
) + τ
y
( n b
z x
− n b
x z
) + τ
z
( n b
x y
− n b
y x
) , (8) которое в векторной форме принимает вид:
Δ = τ⋅ ( n b
× ) (9)
Но, в силу очевидного равенства:
τ = n b
× , определитель (7) принимает значение:
Δ =τ = 2
1 (10)
− x n
x
Δ x
= − y n
y
− z n
z
|
b
x
b
y
= − r n b
⋅ ( × ) (11)
b
z
|
  Первый частный определитель Δ x
системы равен: Первый частный определитель Δ x
системы равен:
и подвижная координата x
m
принимает значение:
 Δ x
( × ) (12) x
m
= = − r n b
⋅ Δ x
( × ) (12) x
m
= = − r n b
⋅
Δ
Второй частный определитель Δ y
системы равен:
  τ x
− x b
x τ x
− x b
x
Δ y
= τ
y
− y b
y
= r
⋅ τ× ( b
) (13)
τ z
− z b
z
Соответственно, вторая подвижная координата y
m
принимает значение:
τ x n
x
Δ z
= τ
y
n
y
τ z n
z
|
− x
− y
= − r
⋅ ( τ× n
) (15)
− z
|
  y
m y
m
 (14) Наконец, третий частный определитель Δ z
равен: (14) Наконец, третий частный определитель Δ z
равен:
и третья подвижная координата z
m
принимает значение: z
m
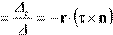 (16) (16)
Теперь необходимо принять во внимание равенства:
n b
× = τ
, τ
× b
= − n
, τ
× n
= b
, (17)
в соответствии с которыми подвижные координаты принимают вид скалярных произведений:
x
m
= − r
⋅τ , y
m
= − r n
⋅ , z
m
= − r b
⋅ (18)
Подстановка этих значений в уравнение (2) позволяет выразить радиус-вектор подвижного пространства через радиус-вектор неподвижного пространства:
r
m
= − r
⋅τ 2
− r n r b
⋅ 2
− ⋅ 2
= − r
( τ 2
+ n b
2
+ 2
) = − r
⋅ 1 = − r
, подтверждая равенство (3), если, конечно, учитывать работу [1] о сущности скаляра. Более того, полученный результат лишний раз подтверждает корректность, но – главное – актуальность этой работы. Потому, что теперь без всяких надуманных « мысленных экспериментов
» можно строго математически сравнивать скорости в неподвижной и подвижной системах отсчета. Действительно, скорость v
радиусвектора
(1) в неподвижной системе отсчета равна производной этого радиус-вектора по времени:
d
r
v
=  (19) dt (19) dt
В свою очередь, скорость v
m
радиус-вектора
(2) равна его производной по времени:
d
r
m
v
m
=  (20) dt
Но из равенства (3) следует очевидное равенство: (20) dt
Но из равенства (3) следует очевидное равенство:
v
= − v
m
, (21)
в котором нет и не может быть даже намека на преобразования Лоренца. Следует отметить, что на подвижную и неподвижную системы отсчета никакие ограничения не накладывались в ожидании, что исследование выведет на особенности, позволяющие отличать инерциальную систему от каких-либо иных. Не вывело.
Здесь полезно обратить внимание на принципиальное отличие физической
сущности скорости от ее математической
сущности. Физическая сущность скорости (например, некоторого тела) состоит в том, что скорость тела есть мера того, как быстро тело меняет свое положение относительно
выбранного репера (ориентира). На этом основании физическое понятие скорости тела можно полагать относительным
. Математическая сущность скорости состоит в том, что скорость есть производная вектора по времени, и, коль скоро вектор всегда является абсолютной величиной, математическое понятие скорости является абсолютным
. Обе сущности оказываются субъективным отображением объективной реальности, и, несмотря на различие, не являются взаимоисключающими. Поэтому они могут совпадать, или не совпадать в оценке объективной реальности. На этом основании можно говорить о наличии своеобразной интерференции понятий
в сознании исследователя. Когда физическая сущность совпадает с математической сущностью, вероятность заблуждений в изучении объективной реальности становится меньше. В противном случае возникают различные паразитные учения (например, о теплороде 200 лет назад, или о так называемых торсионных полях нынче), вплоть до «философского» отрицания генетики и кибернетики.
Так вот, если скорость (тела) понимать, как непосредственную характеристику
движущегося тела, то могут возникать проблемы интерференционного (в данном случае - терминологического) характера, приводящие к подмене понятий и, как следствие, к подмене решаемой задачи. Здесь скорость всегда понимается в ее строгом математическом смысле – производная вектора по времени
. Это единственный способ максимально уберечься от заблуждений. Тогда физическую « скорость тела
» следует понимать, как упрощение длинного определения:
– скорость тела есть производная по времени радиус-вектора из начала системы отсчета до центра масс этого тела и является не характеристикой тела, а только и исключительно характеристикой этого радиус-вектора
.
Но это упрощение повлекло за собой подмену
характеристики математического объекта (вектора) якобы характеристикой физического объекта (тела), а это уже – произвол, чреватый непредсказуемыми последствиями. Особенно с участием « мысленных экспериментов
», которые вполне могут оказаться совсем немыслимыми, хотя и красивыми.
Орты i,j,k
в качестве базиса неподвижного пространства являются векторами направлений и остаются неизменными константами в пределах своего пространства. Поэтому выражение скорости (19) в развернутом виде:
 v
( ) t
= в
r
= i
dx
+ j
dy
+ k
dz
(22) v
( ) t
= в
r
= i
dx
+ j
dy
+ k
dz
(22)
dt dt dt dt
не требует дифференцирования этих ортов. Орты τ ,n,b
в качестве базиса подвижного пространства в пределах своего подвижного пространства также являются константами, но в неподвижном пространстве они оказываются переменными векторами с неизменным единичным модулем. Поэтому выражение скорости (20) в развернутом виде:
d
r
m
d в d
 v
m
= =
( τ x
m
) + v
m
= =
( τ x
m
) +
 ( n
y
m
) + ( n
y
m
) +
 ( b
z
m
) (23) ( b
z
m
) (23)
dt dt dt dt
уже требует дифференцировать орты подвижного пространства по времени:
d
τ dx
m
d
n
dy
m
d
b
dz
m
  v
m
= v
m
=  x
m
+ τ + y
m
+ n
+ z
m
+ b x
m
+ τ + y
m
+ n
+ z
m
+ b
 (24) (24)
dt dt dt dt dt dt
в пределах неподвижного пространства, поскольку подвижное пространство движется в неподвижном пространстве. То есть, нет нужды « синхронизировать
» какие-либо « часы
» потому, что время t
оказывается единственным общим параметром
неподвижного и подвижного пространств, который и обеспечивает сопоставимость
этих пространств. С учетом известных формул Серре-Френе представляются очевидными равенства:
   d
τ = n
K dl
, в
n
= − ( τ K
+ b
T
)
dl
,
d
b
= − b
T d
τ = n
K dl
, в
n
= − ( τ K
+ b
T
)
dl
,
d
b
= − b
T
 dl
(25) dt dt dt dt dt dt dl
(25) dt dt dt dt dt dt
На основании равенств (18) в такой же мере очевидными представляются равенства: dx
m
d
r
d
τ dy
m
d
r
d
n
dz
m
d
r
d
b
 = −τ − r
, = − n
− r
, = − b
− r
(26) dt dt dt dt dt dt dt dt dt = −τ − r
, = − n
− r
, = − b
− r
(26) dt dt dt dt dt dt dt dt dt
Подстановка равенств (25) и (26) в равенство (24) приводит к уравнению:
2
d
τ dl
2
d
n
2
dl
2
d
b
v
m
= −τ v
− τ⋅ r
 − b n r
⋅ ⋅ T − b n r
⋅ ⋅ T
 − n v n r
− ⋅ − n v n r
− ⋅  + b r
⋅ T + b r
⋅ T
 − b v b r
− ⋅ − b v b r
− ⋅  , dt dt dt dt dt , dt dt dt dt dt
которое далее приводится к виду:
2 2 2
d
τ в
n
d
n
d
b
v
m
= − v
( τ + n b
+ ) − τ⋅ r
 − n r
⋅ − n r
⋅  − n r
⋅ − n r
⋅  − b r
⋅ − b r
⋅ 
dt dt dt dt
Остается в полученное выражение подставить равенства (25):
2 2 2
dl dl dl
2
dl
v
m
= − v
( τ + n b
+ ) − τ⋅ ⋅ n r
K
 + τ⋅ ⋅ n r
K + τ⋅ ⋅ n r
K
 − n b r
⋅ ⋅ T − n b r
⋅ ⋅ T
 + b r
⋅ T + b r
⋅ T
 = =
dt dt dt dt
(27) 2 2 2
dl
2 2 2 2
= − v
( τ + n b
+ ) + r
T
 ( b n b
− ⋅ ) = − v
( τ + n b
+ ) = − v ( b n b
− ⋅ ) = − v
( τ + n b
+ ) = − v
dt
Здесь опять учтена работа[1], а также очевидное равенство:
b
2
= n b
⋅ = 1
Полученное равенство (27), естественно, опять довольно сложным путем подтверждает установленное ранее простое равенство (21).
Эти неочевидные доказательства очевидных положений (3) и (21) выполнены под влиянием сомнений в знаменитой теории относительности, основанной на заблуждении о различных часах
. Все дело в том, что физическая сущность времени не совпадает с его математической сущностью
. Объективно время не существует. Объективно существует только последовательность неких физических состояний
. Чтобы осмысленно ориентироваться в этой последовательности, Человек Разумный придумал
способ неким счетным
образом упорядочить в своем сознании
эту последовательность, для чего придумал субъективную характеристику счета
– время. Математика (в качестве субъективного средства отображения объективной реальности) формализовала эту характеристику в статусе универсального параметра t
для всех физических явлений в данной среде обитания
. Таким образом, математическая сущность времени есть единая параметризация любых процессов
. А физической сущности времени не существует. Но существует физическая сущность самих процессов
, которой и адекватно понятие времени в части последовательности состояний в этих процессах. Необратимость времени является следствием необратимости последовательности состояний, а не причиной их. Поэтому у любых наблюдателей во Вселенной часы, если они исправны, всегда синхронизированы (точнее - когерентны
). Когда « мысленный эксперимент»
предполагает разные исправные часы у различных наблюдателей, он фактически по умолчанию
помещает этих наблюдателей в различные несопоставимые
Вселенные, из которых реально существует только одна. Так и превращается « мысленный эксперимент»
в абсолютно немыслимый.
Пусть теперь в рассмотренном неподвижном пространстве, кроме первой подвижной точки, начинает двигаться вторая материальная точка, определяемая радиус-вектором r
1
:
r
1
( ) t
= i
x t
1
( ) + j
y t
1
( ) + k
z t
1
( ) , (28) скорость v
1
которого равна его производной по времени:
d
r
1
v
1
=  (29) dt (29) dt
Это означает, что вдоль годографа этого второго радиус-вектора перемещается второе трехмерное подвижное пространство X
1 m
,
Y
1 m
,
Z
1 m
, в котором начало отсчета неподвижного пространства определено радиус-вектором
r
1 m
= τ 1
x
m
+ n
1 1
y
m
+ b
1 1
z
m
(30)
Скорость v
1 m
этого радиус-вектора равна его производной по времени:
d
r
1 m
v
1 m
=  (31) dt (31) dt
и теперь уже можно считать строго доказанным равенство: v
1 m
= − v
1
(32)
Поскольку в геометрическом неподвижном пространстве одновременно
движутся два различных геометрических подвижных пространства, например, A
и B
(соответственно, для первого и второго), постольку уже можно говорить о скорости v
A B
/
первого подвижного пространства относительно второго подвижного пространства. Очевидно, что эта скорость определяется разностью: d
v
A B
/
= v
m
− v
1 m
= −
( v
) ( − − v
1
) =
 ( r r
1
−
) (33) dt ( r r
1
−
) (33) dt
Не менее очевидно, что скорость v
B A
/
второго пространства относительно первого равна:
d
v
B A
/
= − v
A B
/
=  ( r r
− 1
) (34) dt ( r r
− 1
) (34) dt
Существенно, что подвижные пространства порождены
соответствующими математическими точками, а это значит, что выражения (33) и (34) характеризуют одну и ту же абсолютную
скорость одной математической точки относительно другой. Заметив, что разность R
:
R
= r
− r
1
(35)
представляет собой расстояние
между этими точками, можно сделать общее утверждение (достаточно очевидное, кстати):
– абсолютная скорость одного объекта относительно другого всегда
равна производной расстояния
между этими объектами по времени.
Литература
.
1. Океанов Е.Н.
- О сугубо математических противоречиях.
|