Федеральное агентство по образованию Российской Федерации
Южно-Уральский государственный университет
Кафедра «Радиотехнические системы»
Курсовой проект по курсу
«Устройства приема сигналов»
Тема: «Выделение огибающей АМ-сигнала»
Пояснительная записка ЮУрГУ-К 210304.481.01.ПЗ
Руководитель
Журавлёв А. В.
"___"__________ 2008 г.
Автор проекта студент группы ПС-481 Абдулин В. Ф.
"___"___________2008 г. Проект защищен с
оценкой____________
"___"__________ 2008 г.
Челябинск
2008
|
Техническое задание
Реализовать программно выделение огибающей АМ-сигнала, показать спектр огибающей и что такое аналитический сигнал.
|
| ЮУрГУ-К 210304.481.01.ПЗ |
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
| Разраб.
|
Абдулин В. Ф.
|
Выделение амплитудной огибающей.
Пояснительная записка.
|
Лит.
|
Лист
|
Листов
|
| Провер.
|
Журавлёв А. В.
|
2
|
14
|
| Реценз.
|
ЮУрГУ. Кафедра РТС
|
| Н. Контр.
|
| Утверд.
|
Аннотация
Абдулин В. Ф. Выделение огибающей АМ-сигнала. – Челябинск:
ЮУрГУ. ПС, 2008, 30с.
В данной работе программно реализован метод выделения огибающей АМ-сигнала при помощи преобразования Гильберта. Следует заметить, что данное преобразование в реальности не осуществимо, но благодаря программным технологиям его можно продемонстрировать. Программа также демонстрирует, что собой представляет аналитический сигнал, подтверждая теорию.
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 3
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
Содержание
ТЕХНИЧЕСКОЕ ЗАДАНИЕ .................................................................................... 2
АННОТАЦИЯ....................................................................................................... 3
СОДЕРЖАНИЕ ..................................................................................................... 4
1. ТЕОРЕТИЧЕСКИЕ ВЫКЛАДКИ ....................................................................... 5
2. ПРЕОБРАЗОВАНИЕ ГИЛЬБЕРТА ................................................................... 6
3. СИНТЕЗ АМ-СИГНАЛА .................................................................................. 7
4. СХЕМА РАБОТЫ ПРОГРАММЫ ...................................................................... 8
5. ПРИЕМНИК ................................................................................................... 9
6. ПРЕОБРАЗОВАТЕЛЬ ГИЛЬБЕРТА ................................................................. 9
7. ФОРМИРОВАТЕЛЬ ОГИБАЮЩЕЙ .................................................................. 10
8. УСТРОЙСТВО ГРАФИЧЕСКОГО ОТОБРАЖЕНИЯ ........................................... 10
9. ЛИСТИНГ ПРОГРАММЫ ................................................................................ 11
ЗАКЛЮЧЕНИЕ ..................................................................................................... 13
СПИСОК ЛИТЕРАТУРЫ ...................................................................................... 14
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 4
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
1. Теоретические выкладки
В различных системах передачи данных часто применяются узкополосные сигналы, спектр которых сосредоточен в окрестности некоторой частоты 0
. При анализе таких сигналов удобно пользоваться понятиями комплексной огибающей, амплитудой огибающей и фазовой функцией сигнала.
Рассмотрим сигнал, представленный в виде:
s
( t
) A
( t
)cos( 0
t
( t
)) .
Множитель A
( t
) называется амплитудной огибающей, а начальная
фаза ( t
) – фазовой функцией сигнала s
( t
) .
Сигнал можно представить как вещественную часть комплексной функции, заменив косинус комплексной экспонентой:
s
( t
) Re( A
( t
)exp( j
( 0
t
( t
)))) .
Здесь можно выделить два множителя: exp( j
0
t
) представляет немодулированное несущее колебание и является быстроменяющимся, а
A
( t
)exp( ( t
)) меняется значительно медленнее и содержит информацию об амплитудной огибающей и начальной фазе одновременно. Этот медленно меняющийся множитель и называется комплексной огибающей сигнала .
В техническом задании поставлена задача: выделить амплитудную огибающую сигнала s
( t
) . Способов существует множество, но остановимся
на одном – это преобразование Гильберта из-за ряда преимуществ:
- для гармонического сигнала данная структура даёт в результате постоянную амплитуду и начальную фазу;
- фазовая функция не меняется при умножении сигнала на произвольный постоянный множитель;
- данный способ дает понятие об аналитическом сигнале.
/1, с.55/
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 5
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
2. Преобразование Гильберта
Для выделения амплитуды произвольный сигнал s
( t
) представляется как вещественная часть комплексного сигнала s
& a
( t
) (он называется аналитическим сигналом ).
s
( t
) Re( s
& a
( t
))
Вещественная часть аналитического сигнала, естественно, должна совпадать с исходным сигналом s
( t
) . Мнимая же часть s
( t
) называется
сопряженным сигналом или квадратурным дополнением .
s
a
( t
) s
( t
) js
( t
)
Теперь вычислим спектр аналитического сигнала, учитывая, что преобразование Гильберта является линейным и его коэффициент передачи определяется формулой:
0, 0, S
& a
( ) S
& ( ) jS
&
( ) S
& ( )(1 K
&
( ))
S
& ( ), 0,
2 S
& ( ), 0.
В области положительных частот спектры вещественного и мнимого сигналов складываются, давая удвоенный результат. В области отрицательных частот спектр равен 0. В результате спектр оказывается односторонним (рис.1).

Рис.1. Амплитудные спектры вещественного сигнала(а) и
аналитического(б).
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 6
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
Итак, чтобы для произвольного сигнала определить амплитудную огибающую, необходимо, прежде всего сформировать аналитический сигнал, получив его мнимую часть с помощью преобразования Гильберта. Далее амплитудная огибающая находится как модуль аналитического сигнала:
 A
( t
) s
& ( t
) s
2
( t
) s
2
( t
) A
( t
) s
& ( t
) s
2
( t
) s
2
( t
)
Спектр комплексной огибающей представляет собой сдвинутый на 0
спектр аналитического сигнала.
3. Синтез АМ-сигнала
Для дальнейшей работы необходимо синтезировать АМ-сигнал с заданными параметрами. То есть с заранее выбранной несущей и парой боковых частот. Амплитуда боковых частот будут случайными величинами.
Спектр синтезируемого сигнала показан на рисунке 2:
 Рис.2. Спектр синтезируемого сигнала. Рис.2. Спектр синтезируемого сигнала.
Тогда АМ-сигнал запишем как:
A m A m
s
( t
) A
0
cos( 0
t
0
)  0
cos(( 0
1
) t
1
) 0
cos(( 0
1
) t
1
)  0
cos(( 0
1
) t
1
) 0
cos(( 0
1
) t
1
)
2 2
Построенный в программе сигнал выглядит следующим образом:
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 7
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|

Рис.3. Синтезированный АМ-сигнал (один из вариантов)
4. Схема работы программы
Разработанная программа реализует механизм работы эквивалентной схемы:
 Рис.4. Эквивалентная схема программного алгоритма Рис.4. Эквивалентная схема программного алгоритма
Данная схема состоит из трех компонентов: синтезатор АМ-сигнала, устройство обработки сигнала и устройство графического отображения. В нашем случае синтезатор АМ-сигнала необходим лишь только для генерации колебаний на заданной несущей частоте и со случайной амплитудой модулирующего колебания. Частота модулирующего колебания в каждом эксперименте так же задается случайно с небольшим интервалом разброса для разнообразия экспериментов.
Существуют различные виды АМ-сигнала. И самый подходящий по КПД
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 8
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
из них – это сигнал с подавленной несущей. Отказавшись от добавления постоянной составляющей к модулирующему сигналу, можно удалить бесполезное несущее колебание. Энергетический выигрыш при этом велик (КПД = 100%). Но этот способ не получил широкого применения, это связано с проблемами, возникающими при демодуляции. /1, с.439/
Остановимся на однотональной модуляции. Перемножитель и два генератора частот формируют нам требуемое колебание.
A
0
cos( 0
t
0
) - на рисунке 3 в точке 1,
A
1
(1 m
cos( 1
t
1
)) - на рисунке 3 в точке 2.
Здесь m
- коэффициент модуляции, задается в программе случайно в каждом эксперименте.
Перемножающее устройство формирует АМ-сигнал s
( t
) A
cos( 0
t
0
)(1 m
cos( 1
t
1
))
Am Am
A
cos( 0
t
0
)  cos(( 0
1
) t
1
) cos(( 0
1
) t
1
)  cos(( 0
1
) t
1
) cos(( 0
1
) t
1
)
2 2
5. Приемник
Устройство приемника в данном случае нас не очень интересует. Важно, чтобы усилитель промежуточной частоты был согласован с нашим сигналом, то есть настроен на несущую частоту и охватывал боковые.
Далее аналогово-цифровой преобразователь с частотой дискретизации, не менее, чем в 4 раза превосходящей частоту несущего колебания.
6. Преобразователь Гильберта
Преобразование Гильберта физически нереализуемое. Однако это ограничение можно обойти, если известны (точнее, считаются известными) будущие значения сигнала. Например, мы можем считать, что сигнал закончился (то есть все его будущие значения равны нулю). Именно поэтому это процедура осуществляется в программном виде.
Формирование аналитического сигнала осуществляется в частотной области. Вычисляется дискретное преобразование Фурье входного сигнала,
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 9
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
далее обнуляется половина спектра и, наконец, производится обратное преобразование Фурье. При этом задается частота дискретизации.
7. Формирователь огибающей
Здесь происходят простые алгебраические преобразования. Описывать не стоит:
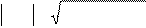 A
( t
) s
& ( t
) s
2
( t
) s
2
( t
) , A
( t
) s
& ( t
) s
2
( t
) s
2
( t
) ,
где s
( t
) - исходный сигнал, а s
( t
) - сигнал на выходе преобразователя Гильберта. A
( t
) и есть искомая амплитудная огибающая.
8. Устройство графического отображения
Реализованная программа все необходимые графики выводит в соответствующем окне(рис.5).
 Рис.5. Результат выполнения программы Рис.5. Результат выполнения программы
(графики сигналов по оси х - в секундах, графики спектров - в
герцах)
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 10
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
На первых двух графиках показаны исходный сигнал и его спектр
ДПФ, на второй паре графиков – сигнал с выхода преобразователя Гильберта и спектр ДПФ, на третьем – огибающая на фоне исходного сигнала и спектр огибающей.
По результатам выполнения программы визуально можно проверить, что сигнал прошедший через преобразователь Гильберта претерпел изменения: был симметричным относительно вертикальной оси в точке 0 (четным), стал – симметричным относительно точки 0 (нечетным). Спектр сигнала на выходе преобразователя получился с подавленными частотами справа от Fs/2.
9. Листинг программы
%константы%
pi = 3.14;
%частота выборки (дискредитизации)%
Fs = 400;
%временной интервал и разрешение% t = -1:1/Fs:1;
%несущая частота%
f0 = 10;
%модулирующая частота% f1 = f0*(0.5 - 0.4*rand(1));
%амплитуда сигнала%
A0 = 1;
%параметры поля для графиков% m = 2; n = 3; %кол-во столбцов и строчек%
%синтез АМ-сигнала%
AMsign = A0*(1+rand(1)*cos(2*pi*f1*t)).*cos(2*pi*f0*t);
%построение АМ-сигнала%
subplot(n,m,1);
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 11
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
plot(t, AMsign);
%ДПФ исходного сигнала%
SpectrAM = fft(AMsign,Fs); subplot(n,m,2);
%отображение спектра%
plot(abs(SpectrAM));
%преобразование Гильберта%
Hsign = hilbert(AMsign); subplot(n,m,3);
%построение графика%
plot(t,imag(Hsign));
%ДПФ после преобразования Гильберта % SpectrH = fft(Hsign,Fs); subplot(n,m,4);
%отборажение полученного спектра после преобразования
Гильберта%
plot(abs(SpectrH));
%Получение амплитудной огибающей%
Amplit = sqrt(AMsign.^2+imag(Hsign).^2); subplot(n,m,5);
%постоение огибающей на фоне исходного сигнала% plot(t, Amplit, 'r' ); %огибающая на графике красного цвета% hold on ; subplot(n,m,5);
plot(t, AMsign, '--' ); %исходный сигнал выделен пунктиром% hold off ;
%спектр огибающей%
SpectrA = specgram(Amplit); subplot(n,m,6);
%отображение спектра%
plot(abs(SpectrA));
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 12
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
Заключение
Проделанная работа показывает наглядно, что такое аналитический сигнал и как получить его квадратурное дополнение. А также была полученная амплитудная огибающая методом преобразования Гильберта.
Данная программа разработана в среде MathLab, и поэтому были использованы готовые функции, такие как hilbert(получение аналитического сигнала), fft(ДПФ), plot(построение графиков).
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 13
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
Список литературы
1. Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2002.
– 608с., ил.
2. Методические указания к курсовому проекту по курсу «Основы радиолокации» / сост. В.В. Милованов; под ред. А.В. Журавлева. – Челябинск.: ЧПИ, 1978. – 54 с.
3. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. – М.: Вильямс, 2003. – 1100с., ил.
4. Прокис Д. Цифровая связь. / Под. ред. Кловского Д. Д. – М.: Радио и связь, 2000 – 800с., ил.
|
| ЮУрГУ-К 210304.481.01.ПЗ |
Лист
|
| 14
|
| Изм.
|
Лист
|
№ докум.
|
Подпись
|
Дата
|
|