Содержание
1. Введение в анализ и дифференциальное исчисление функции одного переменного
2. Дифференциальное исчисление функций и его приложение
3. Интегральное исчисление функции одного переменного
1.
Введение в анализ и дифференциальное исчисление функции одного переменного
1. Вычислить предел:
 .
Решение.
При  имеем
Следовательно,
2. Найти асимптоты функции:
 .
Решение.
Очевидно, что функция не определена при  .
Отсюда получаем, что
Следовательно,  – вертикальная асимптота.
Теперь найдем наклонные асимптоты.
Следовательно,  – наклонная асимптота при  .
3. Определить глобальные экстремумы:
 при  .
Решение.
Известно, что глобальные экстремумы функции на отрезке достигаются или в критических точках, принадлежащих отрезку, или на концах отрезка. Поэтому сначала находим  .
 .
А затем находим критические точки.
Теперь найдем значение функции на концах отрезка.
 .
Сравниваем значения и получаем:
4. Исследовать на монотонность, найти локальные экстремумы и построить эскиз графика функции:
 .
Решение.
Сначала находим .
 .
Затем находим критические точки.
| x |
 |
–3 |
 |
0 |
 |
|
– |
0 |
+ |
0 |
+ |
 |
убывает |
min |
возрастает |
возрастает |
возрастает |
Отсюда следует, что функция
возрастает при  ,
убывает при  .
Точка  – локальный минимум.
5. Найти промежутки выпуклости и точки перегиба функции:
 .
Решение
Чтобы найти промежутки выпуклости и точки перегиба, найдем вторую производную функции.
 .
 .
 .
Отсюда следует, что функция
выпуклая при  ,
вогнутая при  .
Точки  ,  – точки перегиба.
2. Дифференциальное исчисление функций и его приложение»
1. Провести полное исследование свойств и построить эскиз графика функции  .
Решение.
1) Область определения функции
 .
2) Функция не является четной или нечетной, так как
 .
3) Теперь найдем точки пересечения с осями:
а) с о
x
:  , б) с oy
.
4) Теперь найдем асимптоты.
а) 
А значит,  является вертикальной асимптотой.
б) Теперь найдем наклонные асимптоты
Отсюда следует, что
 является наклонной асимптотой при  .
5) Теперь найдем критические точки
 не существует при  .
6) 
 не существует при
| x |
 |
0 |
 |
2 |
 |
4 |
 |
 |
+ |
0 |
– |
Не сущ. |
– |
0 |
+ |
|
– |
– |
– |
Не сущ. |
+ |
+ |
+ |
| y |
возрастает
выпуклая
|
max
|
убывает
выпуклая
|
не сущ. |
убывает
вогнутая
|
min
|
возрастает
вогнутая
|
Построим эскиз графика функции 
2. Найти локальные экстремумы функции
 .
Решение.
Сначала найдем частные производные
Известно, что необходимым условием существования экстремума является равенство нулю частных производных.
То есть мы получили одну критическую точку:  . Исследуем ее.
Далее проведем исследование этой точки.
Для чего найдем предварительно частные производные второго порядка
Для точки  :
 .
Следовательно, точка  не является точкой экстремума.
Это означает, что точек экстремума у функции
 нет.
3. Определить экстремумы функции  , если  .
Решение.
Сначала запишем функцию Лагранжа
 .
И исследуем ее
(Учитываем, что по условию  )
То есть мы получили четыре критические точки.
В силу условия  нам подходит только первая  .
Исследуем эту точку.
Вычислим частные производные второго порядка:
Отсюда получаем, что
Теперь продифференцируем уравнение связи
 .
Для точки
Далее получаем
То есть мы получили отрицательно определенную квадратичную форму.
Следовательно,  – точка условного локального максимума.
 .
3. Интегральное исчисление функции одного переменного
1–3. Найти неопределенный интеграл
1.  .
Решение.
 .
2.
 .
Решение.
 .
3.
Решение.
 .
4. Вычислить
 .
Решение.
 .
5. Определить площадь плоской фигуры, ограниченной кривыми
 .
Решение.
 .
|
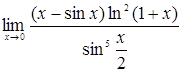
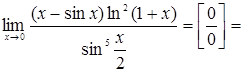
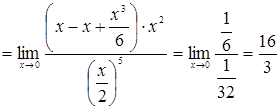
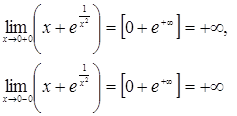
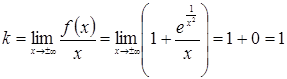
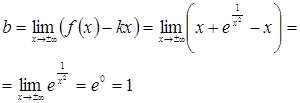
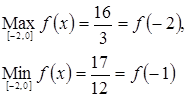
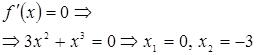
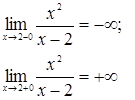
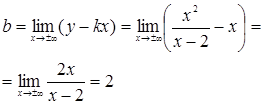
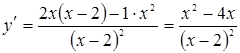
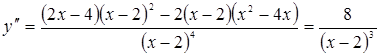
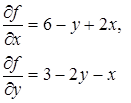
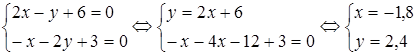
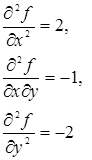
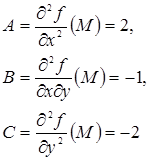
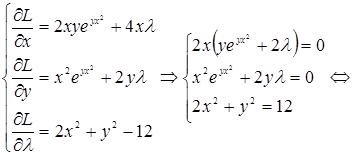
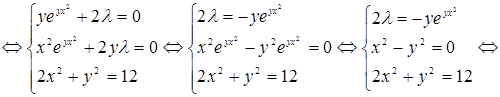
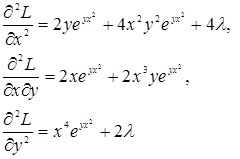
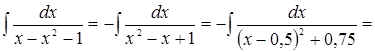
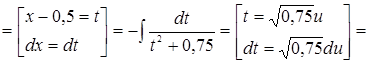
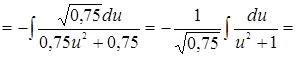
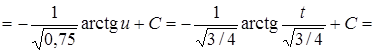
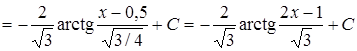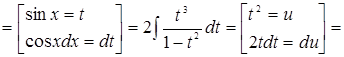
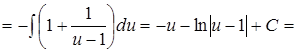
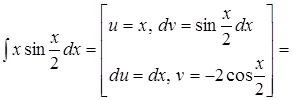
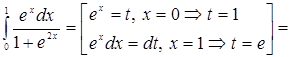
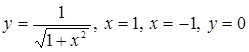
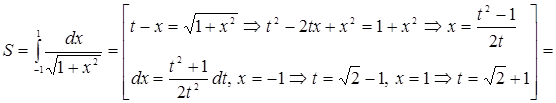
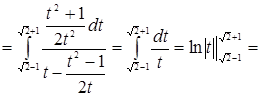
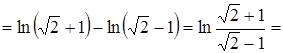
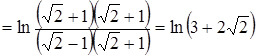