МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ КАЗАХСТАН
МЕЖДУНАРОДНАЯ ОБРАЗОВАТЕЛЬНАЯ КОРПОРАЦИЯ
КАЗАХСКАЯ ГОЛОВНАЯ
АРХИТЕКТУРНО-СТРОИТЕЛЬНА АКАДЕМИЯ
Факультет Дизайна
ПОСТРОЕНИЕ
ТЕНЕЙ
НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
Методические указания по дисциплине
« Инженерная графика-3 »
для студентов специальности 050421 – Дизайн
Алматы 20 10
УДК 515.2 (07)
Составитель: Шапрова Г.Г.
Построение теней . Методические указания по дисциплине « Инженерная графика-3 » для студентов специальности 050421 – Дизайн. - Алматы: КазГАСА, 20 10 . - 21 с.
Методические указания разработаны для самостоятельной работы студентов и позволяют выполнять задания по теме «Построение теней» .
Библиограф. 2 .
Рекомендовано к изданию методическим советом факультета дизайна КазГАСА, протокол № 5 от 11.03. 20 10 г.
Печатается по плану издания Казахской головной архитектурно-строительной академии на 200 9 -20 10 уч.год.
Рецензент: Сабитов А.Р. , д.арх., академический профессор КазГАСА
© Казахская головная
архитектурно-строительная
академия, 20 10 г.
1.
ЦЕЛЬ ЗАДАНИЯ
Целью работы является получение навыков построения теней и применение полученных знаний при выполнении самостоятельных заданий .
2
. ОБЩИЕ СВЕДЕНИЯ И ОПРЕДЕЛЕНИЯ
2.1 Построение теней
На архитектурных чертежах, для придания им большей наглядности, строят тени, благодаря которым получают более полное представление о рельефе здания, его отдельных объемах и деталях. Кроме того, построение теней на ортогональных проекциях уменьшает их основной недостаток – малую наглядность. Светотень как бы компенсирует отсутствие третьего измерения (на плане – высоты, а на фасаде – глубины). Тени также дают возможность лучше представить на чертеже взаимное расположение отдельных элементов, объемно-пространственную композицию здания.
Построение теней в полной мере соответствующих реальным условиям – достаточно сложная задача, но, при определенных условностях и упрощениях, данная задача решается с помощью методов начертательной геометрии.
Различают собственные и падающие тени. Собственные тени
– это затемненная часть освещенного предмета или это тени, которые получаются на неосвещенной поверхности самого тела. Линия, разделяющая на поверхности предмета освещенную и затененную части называется контуром собственной тени (на рис. 1(а, б) это линия ABCD на поверхности сферы). В свою очередь, данный предмет отбрасывает так называемые падающие тени
на плоскости и тела, находящиеся позади него. Внешняя граница падающей тени называется контуром падающей тени
(линия A о B о C о в о на плоскости π).
На архитектурно-строительных чертежах тени от изображаемого объекта могут быть построены как от искусственного
источника освещения
(лампа, прожектор, фонарь и т.п.) так и от естественного
(солнце), при этом считается, что свет распространяется прямолинейно.
При искусственном освещении
(рис. 1,а) источник света удален от объекта на незначительное расстояние. Лучи света при этом образуют связку лучей. Такое освещение еще называют факельным
.
При естественном
(солнечном) освещении
(рис. 1, б) источник света удален в бесконечность и световые лучи параллельны друг другу.
 
Рис. 1
Условно принято контуры теней в ортогональных проекциях строить при стандартном освещении параллельными лучами света. При этом за направление светового луча S
обычно принимают диагональ куба, грани которого параллельны плоскостям проекций. При этом наклон луча примерно равен 35°, а направление проекций лучей параллельно диагоналям граней куба и составляет с осями проекций на фасаде и на плане углы 45° (рис. 2).

Рис. 2
Для построения теней используются различные способы. Рассмотрим их на примере построения теней от точки, плоскости, поверхности.
2.2 Способ следа луча
2.2.1 Тень от точки
. Тенью точки
называется след светового луча, проходящего через данную точку. Следовательно, для построения падающей тени точки, необходимо через эту точку провести луч параллельно принятому направлению световых лучей и определить точку его пересечения с ближайшей встретившейся на его пути плоскостью или поверхностью.
Для построения тени от точки на ортогональном чертеже через проекции точки следует провести соответствующие проекции светового луча.
Рассмотрим построение тени от точки A
, расположенной в 1 четверти пространства, при заданном направлении светового луча (рис.3). Тень от точки на плоскость проекций определяется как след светового луча, проведенного через данную точку, поэтому рассматриваемый способ построения теней называется способом следа луча
. Тень от точки окажется на той плоскости проекций, которую световой луч встретит раньше. На рис.3 световой луч S , проведенный через точку А
, встречается с плоскостью π
2
раньше, чем с плоскостью π
1
. Точка А
π
2
для луча S
является горизонтальным следом, а для точки А
, через которую проходит этот луч, - тенью ее на плоскость проекций π
2
. Аналогично, точка А
π
1
для луча служит фронтальным следом, а для точки А
– тенью на плоскость π
1
. Из этих двух теней первая А
π
2
будет реальной, действительной, вторая – мнимой. Тень от точки на плоскость π
2
реальна потому, что световой луч пересекает плоскость π
2
раньше, чем π
1
. Для удобства условимся обозначать мнимую тень в круглых скобках.
Точка В
, напротив, расположена ближе к плоскости π
1
, следовательно, световой луч встретится с плоскостью π 1 раньше, чем с плоскостью π
2
. Построения реальной тени А
π
1
и мнимой А
π
2
понятны по чертежу.

Рис. 3
2.2.2 Тень прямой линии
. Для построения тени прямой
на какую-либо плоскость или плоскость проекций, необходимо построить тени двух ее точек. Тенью прямой будет прямая линия, соединяющая эти точки, за исключением случая, когда прямая параллельна световым лучам. На рисунке 4 приведен пример построения тени от отрезка прямой общего положения на горизонтальную плоскость проекций.

Рис. 4
На рис.5 показано построение теней от отрезка прямой общего положения на две плоскости проекций. Построения осуществляют в следующей последовательности:
- строят тень на одну из плоскостей проекций (в данном случае на плоскостью π
2
), предполагая, что второй не существует;
- если построенная тень пересекает ось проекций х
, отмечают точку преломления (точка Кх
);
- определяют, какая из построенных теней мнимая (в данном случае точка В
π
2
) и строят действительную тень от этой точки на вторую плоскость проекций π
1
(точку В
π
1
);
- соединяют действительные тени крайних точек отрезка прямой через точку преломления, т.е. А
π
2
КхВ
π
1.
Следовательно, тень от прямой линий, падающая на пересекающиеся плоскости, есть ломанная прямая, имеющая точку излома, лежащую на линии пересечения этих плоскостей.

Рис. 5
На рис. 6, 7, 8 показаны построения теней от прямых частного положения
. Рассмотрим каждый случай в отдельности.
Тень от отрезка прямой, занимающей горизонтально-проецирующее положение, построена в следующей последовательности (рис. 6, а). Строим тени от точек А
и В
и соединяем их прямой линией – получаем падающую тень А
π
2
В
π
2
. Построенная тень совпадает с горизонтальной проекцией светового луча. Аналогично строим тень от отрезка прямой CD
, перпендикулярного фронтальной плоскости проекций (рис.6, б). Как видно из чертежа, ее тень совпадает с фронтальной проекцией светового луча. Следовательно, можно сделать следующий вывод: если прямая перпендикулярна плоскости проекций, то тень, падающая от нее,
совпадает с проекцией светового луча.

Рис. 6
Из построений, сделанных на рис. 7, а, б, в можно также сделать вывод: если прямая параллельна какой-либо плоскости проекций, то тень, падающая от прямой на эту плоскость, параллельна самой прямой
.
 
Рис. 7
Построение тени от прямой, горизонтальная и фронтальная проекции которой наклонены к оси проекций x
под 45º, показано на рис. 8. Как видно из чертежа, тень от такой прямой на горизонтальной или фронтальной плоскостях проекций будет в виде прямой, параллельной оси х
.

Рис. 8
2.2.3 Тень плоской фигуры
. Контур падающей тени от плоской фигуры можно рассмотреть как совокупность теней характерных точек контура этой фигуры и соединенных между собой соответствующим образом. Так, например, для построения тени плоского непрозрачного треугольника, необходимо построить тени всех его вершин (рис. 9). Построения нужно вести в той же последовательности, что была рекомендована для построения тени прямой (пункт 2.2). Как видно из чертежа, тень от вершин А
и В
падают на плоскость π
2
, тень от вершины С
– на плоскость π
1
. Тени от сторон АС
и ВС
падают как на горизонтальную, так и на фронтальную плоскости проекций. Для определения направления теней от этих сторон на горизонтальной плоскости проекций, а также точек преломления Kx
и Lx
, используют мнимую тень С
π
2
.
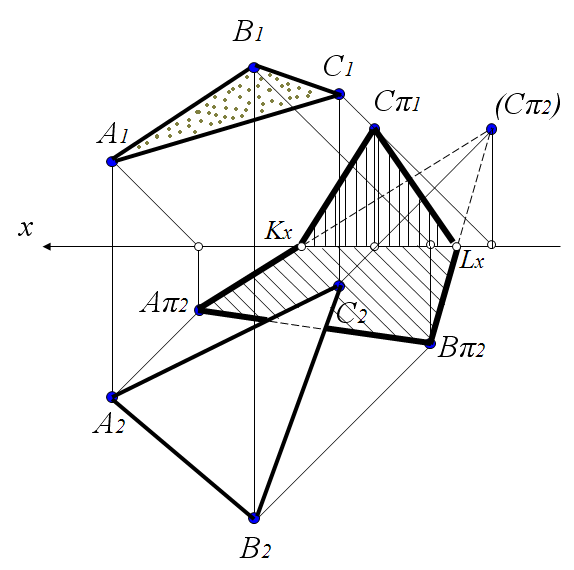
Рис. 9
В зависимости от положения плоской фигуры по отношению к направлению световых лучей и по отношению к плоскостям проекций, на ту или иную плоскость проекций может проецироваться освещенная или теневая сторона плоской фигуры. Чтобы определить, какая сторона плоской фигуры, т.е. освещенная или теневая, проецируется на данную плоскость проекций, следует сравнить порядок расположения проекций отдельных точек контура плоской фигуры с порядком расположения их теней. Если направление обхода проекций совпадает с направлением обхода падающей тени, то на проекции видна освещенная поверхность объекта (на горизонтальную плоскость проекций проецируется освещенная сторона треугольника АВС
, так как последовательность обозначений А 2 В 2 С 2 совпадает с обозначением контура его тени А
π
2
В
π
2
С
π
2
).
И, напротив, если направление обхода проекций и падающей тени не совпадают, то на проекции видна теневая сторона объекта (неосвещенная поверхность) – на фронтальную плоскость проекций проецируется неосвещенная сторона треугольника АВС
(рис. 9) .
Тень, падающая от плоской фигуры на плоскость, параллельную плоскости этой фигуры, равна самой фигуре. Это правило позволяет значительно сокращать построения. Например, для построения контура падающей тени от квадрата ABCD
на плоскость π
2
достаточно построить тень от одной из его вершин, имея в виду, что A
1
B
1
C
1
D
1
=
А
π
2
В
π
2
С
π
2
D
π
2
(рис. 10, а). Для построения тени в горизонтальной плоскости проекций от круга, расположенного параллельно этой плоскости, достаточно построить падающую тень О
π
2
от центра круга О(О
1
,О
2
)
и из полученной точки описать окружность с радиусом R
, равным радиусу данного круга (рис. 10, б).

Рис. 10
2.2.4 Тени геометрических тел.
При построении теней геометрических тел в первую очередь определяется контур собственной тени, т.е. линии раздела освещенных и находящихся в тени частей поверхностей тела. Контур собственной тени определит контур падающей тени. На рис. 11 при принятом направлении светового луча правая, задняя и нижняя грани куба находятся в собственной тени. Остальные грани освещены. Контуром собственной тени является замкнутая линия 1-2-3-4-5-6-1, т которой и строится контур падающей тени.

Рис. 11
Тень от призмы
. На рис. 12 а, б приведено построение падающих теней от призмы, основание которой рас положено в горизонтальной плоскости проекций. В собственной тени находятся задняя и правая боковые грани призмы. Ребра ,
ограничивающие эти грани, являются контуром собственной тени.
В первом слу чае (рис. 12,а) от призмы тень падает только на горизонтальную плоскость проекций, во втором (рис. 12,б) - тень падает частично и на фронтальную плоскость проекций.

Рис. 12
Тень от цилиндра.
Вначале строится падающая тень от верхнего основания цилиндра (рис. 13, а). Касательными прямыми соединим ее с нижним основанием. Получим контур падающей тени цилиндра. Касательные прямые являются падающими тенями от прямых образующих цилиндра, определяющие контур собственной тени.
Во втором случае (рис. 13, б) тень от цилиндра частично падает на фронтальную плоскость проекций. Для ее построения следует определить тени А
π
2
и С
π
2
от точек А
и С,
а также тени от ряда промежуточных точек контура верхнего основания цилиндра. На чертеже показано по строение тени от точки Е.

Рис. 13
Тень от конуса и пирамиды.
Построени е собственных и падающих теней конуса и пирамиды не имеют существенных отличий. При построении теней указанных тел в первую очередь строятся падающие тени, при помощи которых затем определяются контуры собственных теней.
Для построения падающей тени от конуса сначала строят падающую тень от вершины конуса на плоскость его основания ( рис. 14, а ). На чертеже такой тенью является мним ая тень S
π
2
.
Касательные, проведенные из этой точки к основанию конуса, определяют основания образующих AS
и BS
,
которые и являются контурными линиями собственной тени. Реальная тень от вершины конуса падает в данном случае на фронтальную плоскость проекций.
Построение тени пирамиды ( рис. 14, б ) понятны по чертежу.
а) б)

Рис. 15
3.
Задания для самостоятельного решения
3.1 Построить тени прямой АВ
на плоскости проекций.


3.2 Построить тени прямых на плоскости проекций.

3.3 Построить тень заданной поверхности на плоскости проекций
а) б)
 
в)

ЛИТЕРАТУРА
1. Н.В.Белов , А.А.Виксель. Начертательная геометрия . - Л ., Стройиздат, 200 0 .
2. Ю.И.Короев. Строительное черчение и рисование: Учебник для строительных специальностей вузов. – М., Высшая школа, 1999г.
СОДЕРЖАНИЕ
1. Цель задания 3
2. Общие сведения и определения 3
2.1 Построение теней 3
2.2 Способ следа луча 5
2.2.1 Тень от точки 5
2.2.2 Тень от прямой линии 6
2.2.3 Тень от плоской фигуры 10
2.2.4 Тени геометрических тел 12
3. Задачи для самостоятельного решения 16
Гульнара Габидуловна Шапрова
ПОСТРОЕНИЕ ТЕНЕЙ НА
КОМПЛЕКСНОМ ЧЕРТЕЖЕ
Редактор Таубалдиева Д.С.
Сводный план 2009-2010 уч.г., поз.№6
Формат 60х84 1/16. Бумага офсетная . Riso
Усл.печ.л. 1,5 . Уч.изд.л. 1,5 . Тираж 30 экз.
Заказ №
Цена договорная.
Издание Казахской головной архитектурно-строительной
академии
Издательский дом «Строительство и архитектура»
050043, г .Алматы, ул.К.Рыскулбекова, 28
|