Определенный интеграл
Содержание
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
2. Геометрический смысл определенного интеграла
3. Основные свойства определенного интеграла
4. Формула Ньютона–Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям
Лекция 2. Применение определенных интегралов. несобственные интегралы
1. Площадь криволинейной трапеции
2. Объем тела вращения
3. Длина дуги плоской кривой
4. Несобственные интегралы с бесконечными пределами интегрирования
5. Несобственные интегралы от неограниченных функций
Литература
Лекция 1.
Определенный интеграл
1.
Понятие определенного интеграла
Пусть функция  определена на отрезке определена на отрезке 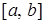 , , 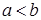 . Выполним следующие операции: . Выполним следующие операции:
1) разобьем отрезок 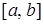 точками точками  на n частичных отрезков на n частичных отрезков 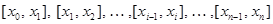 ; ;
2) в каждом из частичных отрезков 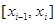 , , 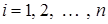 выберем произвольную точку выберем произвольную точку  и вычислим значение функции в этой точке: и вычислим значение функции в этой точке: 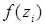 ; ;
3) найдем произведения  , где , где 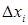 – длина частичного отрезка – длина частичного отрезка 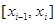 , , 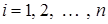 ; ;
4) составим сумму
 , (1) , (1)
которая называется интегральной суммой функции
y
=
f
(
x
) на отрезке
[
а,
b
].
С геометрической точки зрения интегральная сумма 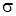 представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки  , а высоты равны , а высоты равны  соответственно (рис. 1). Обозначим через соответственно (рис. 1). Обозначим через 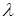 длину наибольшего частичного отрезка длину наибольшего частичного отрезка 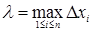 ; ;
5) найдем предел интегральной суммы, когда  . .

Рис. 1
Определение.
Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка 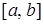 на частичные отрезки, ни от выбора точек на частичные отрезки, ни от выбора точек  в них, то этот предел называется определенным интегралом от функции в них, то этот предел называется определенным интегралом от функции  на отрезке на отрезке 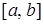 и обозначается и обозначается 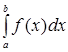 . .
Таким образом,  . .
В этом случае функция  называется интегрируемой на называется интегрируемой на 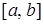 . Числа а и b называются соответственно нижним и верхним пределами интегрирования, . Числа а и b называются соответственно нижним и верхним пределами интегрирования,  – подынтегральной функцией, – подынтегральной функцией,  – подынтегральным выражением, – подынтегральным выражением,  – переменной интегрирования; отрезок – переменной интегрирования; отрезок 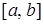 называется промежутком интегрирования. называется промежутком интегрирования.
Теорема 1.
Если функция  непрерывна на отрезке непрерывна на отрезке 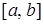 , то она интегрируема на этом отрезке. , то она интегрируема на этом отрезке.
2.
Геометрический смысл определенного интеграла
Пусть на отрезке 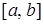 задана непрерывная неотрицательная функция задана непрерывная неотрицательная функция  . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции
y
=
f
(
x
), снизу – осью Ох, слева и справа – прямыми
x
=
a
и
x
=
b
(рис. 2). . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции
y
=
f
(
x
), снизу – осью Ох, слева и справа – прямыми
x
=
a
и
x
=
b
(рис. 2).

Рис. 2
Определенный интеграл 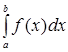 от неотрицательной функции от неотрицательной функции  с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции  , слева и справа – отрезками прямых , слева и справа – отрезками прямых  и и 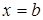 , снизу – отрезком , снизу – отрезком 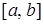 оси Ох. оси Ох.
3. Основные свойства определенного интеграла
1.
Значение определенного интеграла не зависит от обозначения переменной интегрирования:  . .
2.
Определенный интеграл с одинаковыми пределами интегрирования равен нулю: 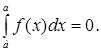
3.
Если  , то, по определению, полагаем , то, по определению, полагаем 
4.
Постоянный множитель можно выносить за знак определенного интеграла: 
5.
Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
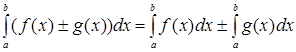 . .
6.
Если функция  интегрируема на интегрируема на 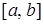 и и 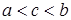 , то , то
 . .
7.
( теорема о среднем
). Если функция  непрерывна на отрезке непрерывна на отрезке  , то на этом отрезке существует точка , то на этом отрезке существует точка  , такая, что , такая, что  . .
4. Формула Ньютона–Лейбница
Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.
Теорема 2.
Если функция  непрерывна на отрезке непрерывна на отрезке  и и 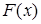 – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула: – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
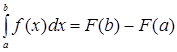 , (2) , (2)
которая называется формулой Ньютона–Лейбница.
Разность  принято записывать следующим образом: принято записывать следующим образом:
 , ,
где символ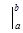 называется знаком двойной подстановки. называется знаком двойной подстановки.
Таким образом, формулу (2) можно записать в виде:
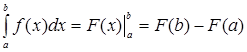 . .
Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную 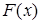 для подынтегральной функции для подынтегральной функции  ; на втором – находится разность ; на втором – находится разность 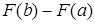 значений этой первообразной на концах отрезка значений этой первообразной на концах отрезка  . .
Пример 1.
Вычислить интеграл  . .
Решение. Для подынтегральной функции  произвольная первообразная имеет вид произвольная первообразная имеет вид 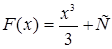 . Так как в формуле Ньютона-Лейбни-ца можно использовать любую первообразную, то для вычисления ин- . Так как в формуле Ньютона-Лейбни-ца можно использовать любую первообразную, то для вычисления ин-
теграла возьмем первообразную, имеющую наиболее простой вид: 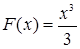 . Тогда . Тогда  . .
Пример 2.
Вычислить интеграл  . .
Решение. По формуле Ньютона-Лейбница имеем:
 . .
5. Замена переменной в определенном интеграле
Теорема 3.
Пусть функция  непрерывна на отрезке непрерывна на отрезке  . Тогда, если: 1) функция . Тогда, если: 1) функция 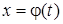 и ее производная и ее производная  непрерывны при непрерывны при 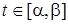 ; 2) множеством значений функции ; 2) множеством значений функции 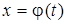 при при  является отрезок является отрезок  ; 3) ; 3) 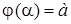 , ,  , то справедлива формула , то справедлива формула
 , (3) , (3)
которая называется формулой замены переменной в определенном интеграле.
Заметим, что как и в случае неопределенного интеграла, использование замены переменной позволяет упростить исходный интеграл, приблизив его к табличному. При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования 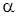 и и 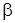 (для этого надо решить относительно переменной t уравнения (для этого надо решить относительно переменной t уравнения  и и 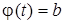 )). )).
На практике часто вместо подстановки 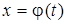 используют подстановку используют подстановку 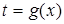 . В этом случае нахождение новых пределов интегрирования по переменной t упрощается: . В этом случае нахождение новых пределов интегрирования по переменной t упрощается: 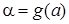 , , 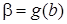 . .
Пример 3
. Вычислить интеграл 
Решение. Введем новую переменную по формуле  . Определим . Определим  и и 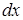 . Возведя в квадрат обе части равенства . Возведя в квадрат обе части равенства  , получим , получим  , откуда , откуда 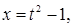 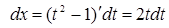 . Находим новые пределы интегрирования. Для этого в формулу . Находим новые пределы интегрирования. Для этого в формулу подставим старые пределы подставим старые пределы  и и 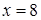 . Получим: . Получим:  , откуда , откуда  и, следовательно, и, следовательно, 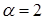 ; ; 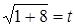 , откуда , откуда 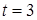 и, следовательно, и, следовательно, 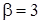 . Таким образом: . Таким образом:
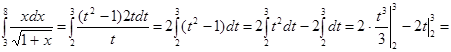
 . .
Пример 4.
Вычислить интеграл 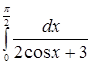 . .
Решение. Воспользуемся универсальной тригонометрической подстановкой. Положим  , откуда , откуда   , , 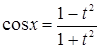 . Найдем новые пределы интегрирования: если . Найдем новые пределы интегрирования: если 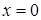 , то , то  ; если ; если  , то , то 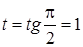 . Значит, . Значит, 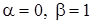 . Следовательно: . Следовательно:
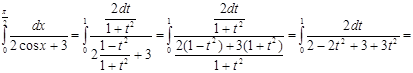
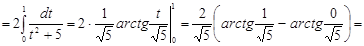
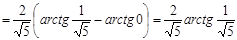 . .
Пример 5.
Вычислить интеграл  . .
Решение. Положим 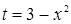 , тогда , тогда  , откуда , откуда 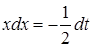 . Находим новые пределы интегрирования: . Находим новые пределы интегрирования: 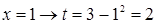 ; ;  . Имеем: . Имеем: 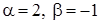 . Следовательно: . Следовательно:
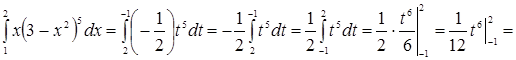
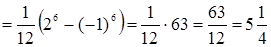 . .
6.
Интегрирование по частям
Теорема 4.
Пусть функции  и и  имеют непрерывные производные на отрезке имеют непрерывные производные на отрезке  . Тогда имеет место следующая формула интегрирования по частям: . Тогда имеет место следующая формула интегрирования по частям:
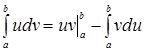 . (4) . (4)
Доказательство
Так как 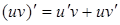 , то функция , то функция 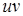 является первообразной для функции является первообразной для функции 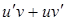 . Тогда по формуле Ньютона–Лейбница получаем . Тогда по формуле Ньютона–Лейбница получаем
 , ,
откуда
 . .
Пример 6.
Вычислить  . .
Решение. Положим 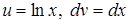 , отсюда , отсюда 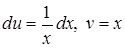 . По формуле (4) находим . По формуле (4) находим
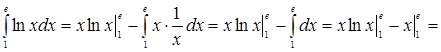
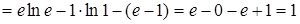 . .
Пример 7.
Вычислить 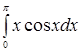 . .
Решение. Пусть  , тогда , тогда 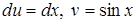 . Применяя формулу интегрирования по частям, получаем . Применяя формулу интегрирования по частям, получаем
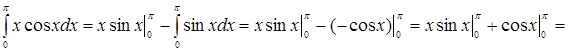
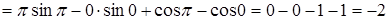 . .
Пример 8.
Вычислить  . .
Решение. Полагая  , определяем , определяем 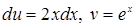 . Следовательно: . Следовательно:

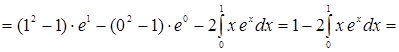 [к полученному интегра-лу снова применяем формулу интегрирования по частям: [к полученному интегра-лу снова применяем формулу интегрирования по частям: 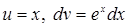 ; следовательно: ; следовательно:  ] = ] =  = = 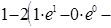
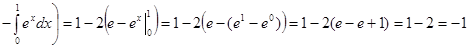 . .
Лекция 2.
Применение определенных интегралов. Несобственные интегралы
1.
Площадь криволинейной трапеции
Пусть функция  неотрицательна и непрерывна на отрезке неотрицательна и непрерывна на отрезке  . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью  , слева и справа – прямыми , слева и справа – прямыми 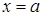 и и 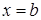 (см. рис. 2) вычисляется по формуле (см. рис. 2) вычисляется по формуле
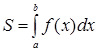 . (5) . (5)
Пример 9.
Найти площадь фигуры, ограниченной линией  и осью и осью 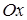 . .
Решение. Графиком функции 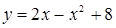 является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью 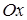 (прямой (прямой  ). Для этого решаем систему уравнений ). Для этого решаем систему уравнений
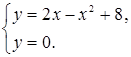
Получаем:  , откуда , откуда 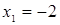 , , 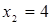 ; следовательно, ; следовательно,  , , 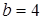 . .

Рис. 3
Площадь фигуры находим по формуле (5):

 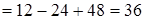 (кв. ед.). (кв. ед.).
Если функция  неположительна и непрерывна на отрезке неположительна и непрерывна на отрезке  , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью  , слева и справа – прямыми , слева и справа – прямыми 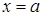 и и  , вычисляется по формуле , вычисляется по формуле
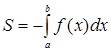 . (6) . (6)
В случае если функция  непрерывна на отрезке непрерывна на отрезке  и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов: и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:
 . (7) . (7)

Рис. 4
Пример 10.
Вычислить площадь фигуры, ограниченной осью  и графиком функции и графиком функции 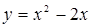 при при  . .
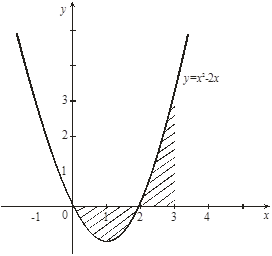
Рис. 5
Решение. Сделаем чертеж (рис. 5). Искомая площадь представляет собой сумму площадей  и и 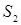 . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему  Получим Получим 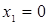 , , 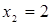 . Следовательно: . Следовательно:
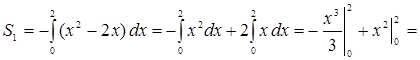 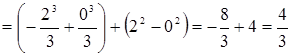 ; ;
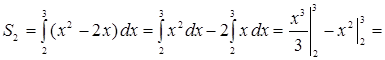
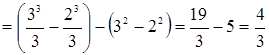 . .
Таким образом, площадь 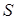 заштрихованной фигуры равна заштрихованной фигуры равна
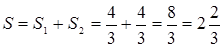 (кв. ед.). (кв. ед.).
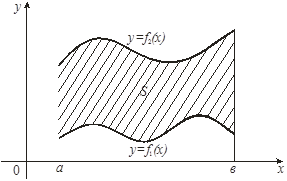
Рис. 6
Пусть, наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке  функций функций  и и  , ,
а слева и справа – прямыми 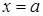 и и  (рис. 6). Тогда ее площадь вычисляется по формуле (рис. 6). Тогда ее площадь вычисляется по формуле
 . (8) . (8)
Пример 11.
Найти площадь фигуры, ограниченной линиями  и и  . .
Решение. Данная фигура изображена на рис. 7. Площадь ее вычислим по формуле (8). Решая систему уравнений  находим находим  , , 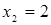 ; следовательно, ; следовательно, 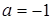 , ,  . На отрезке . На отрезке  имеем: имеем: 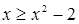 . Значит, в формуле (8) в качестве . Значит, в формуле (8) в качестве 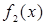 возьмем x , а в качестве возьмем x , а в качестве 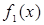 – – 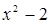 . Получим: . Получим:
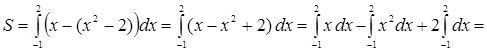 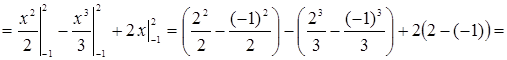  (кв. ед.). (кв. ед.).
Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.
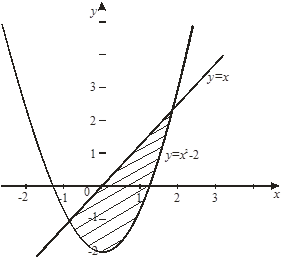
Рис. 7
Пример 12.
Найти площадь фигуры, ограниченной линиями  , , 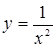 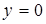 , ,  . .
Решение. Сделаем чертеж (рис. 8). Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью 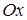 , слева и справа – прямыми , слева и справа – прямыми  и и 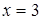 , сверху – графиками функций , сверху – графиками функций  и и 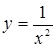 . Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой . Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой 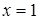 на две части (1 – это абсцисса точки пересечения линий на две части (1 – это абсцисса точки пересечения линий  и и 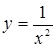 ). Площадь каждой из этих частей находим по формуле (4): ). Площадь каждой из этих частей находим по формуле (4):
 (кв. ед.); (кв. ед.);  (кв. ед.). Следовательно: (кв. ед.). Следовательно:
 (кв. ед.). (кв. ед.).

Рис. 8
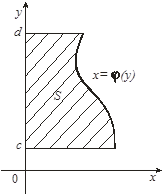 Рис. 9
В заключение отметим, что если криволинейная трапеция ограничена прямыми  и и  , осью , осью  и непрерывной на и непрерывной на  кривой кривой  (рис. 9), то ее площадь находится по формуле (рис. 9), то ее площадь находится по формуле
 . .
2.
Объем тела вращения
Пусть криволинейная трапеция, ограниченная графиком непрерывной на отрезке  функции функции  , осью , осью  , прямыми , прямыми 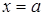 и и 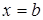 , вращается вокруг оси , вращается вокруг оси 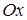 (рис. 10). Тогда объем полученного тела вращения вычисляется по формуле (рис. 10). Тогда объем полученного тела вращения вычисляется по формуле
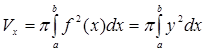 . (9) . (9)
Пример 13.
Вычислить объем тела, полученного вращением вокруг оси  криволинейной трапеции, ограниченной гиперболой криволинейной трапеции, ограниченной гиперболой  , прямыми , прямыми 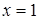 , , 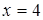 и осью и осью 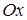 . .
Решение. Сделаем чертеж (рис. 11).
Из условия задачи следует, что 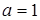 , , 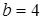 . По формуле (9) получаем . По формуле (9) получаем

 . .
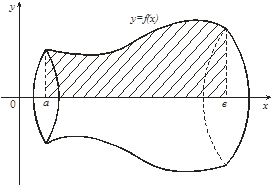
Рис. 10

Рис. 11
Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми у = с и у = в , осью Оу и графиком непрерывной на отрезке 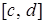 функции функции  (рис. 12), определяется по формуле (рис. 12), определяется по формуле
 . (10) . (10)
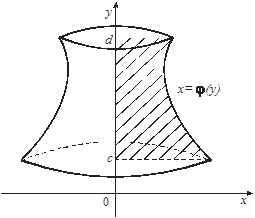 Рис. 12
Пример 14
. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х 2
= 4у, у = 4, х = 0 (рис. 13).
Решение. В соответствии с условием задачи находим пределы интегрирования: 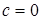 , , 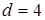 . По формуле (10) получаем: . По формуле (10) получаем:
 . .
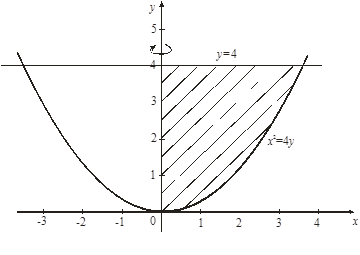
Рис. 13
3.
Длина дуги плоской кривой
Пусть кривая  , заданная уравнением , заданная уравнением 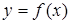 , где , где  , лежит в плоскости , лежит в плоскости  (рис. 14). (рис. 14).
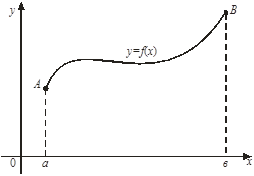
Рис. 14
Определение.
Под длиной дуги  понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю. понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
Если функция 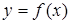 и ее производная и ее производная 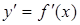 непрерывны на отрезке непрерывны на отрезке  , то длина дуги кривой , то длина дуги кривой 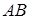 вычисляется по формуле вычисляется по формуле
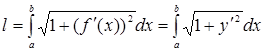 . (11) . (11)
Пример 15
. Вычислить длину дуги кривой 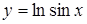 , заключенной между точками, для которых , заключенной между точками, для которых  . .
Решение. Из условия задачи имеем 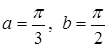 . По формуле (11) получаем: . По формуле (11) получаем:


 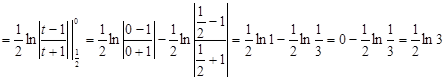 . .
4.
Несобственные интегралы с бесконечными пределами интегрирования
При введении понятия определённого интеграла  предполагалось, что выполняются следующие два условия: предполагалось, что выполняются следующие два условия:
а) пределы интегрирования а и 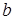 являются конечными; являются конечными;
б) подынтегральная функция 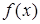 ограничена на отрезке ограничена на отрезке  . .
Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.
Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.
Определение.
Пусть функция  определена и непрерывна на промежутке определена и непрерывна на промежутке 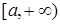 , тогда , тогда
 (12) (12)
называется несобственным интегралом
с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).
Если 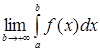 существует и конечен, то несобственный интеграл существует и конечен, то несобственный интеграл 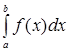 называется сходящимся
; если данный предел не существует или равен называется сходящимся
; если данный предел не существует или равен  , то несобственный интеграл называется расходящимся
. , то несобственный интеграл называется расходящимся
.
Геометрически несобственный интеграл 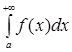 от неотрицательной функции от неотрицательной функции 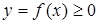 выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции  , снизу – осью , снизу – осью 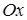 , слева – отрезком прямой , слева – отрезком прямой 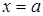 и неограниченной справа (рис. 15). и неограниченной справа (рис. 15).
Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.
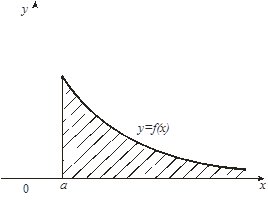
Рис. 15
Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:
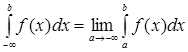 . (13) . (13)
Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:
 , (14) , (14)
где с – любая точка интервала 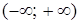 . Интеграл . Интеграл  сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14). сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).
Пример 16.
Исследовать на сходимость несобственные интегралы:
а) 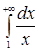 ; б) ; б)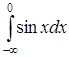 ; в) ; в)  ; г) ; г)  . .
Решение. а) 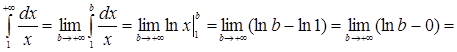  , следовательно, данный интеграл расходится; , следовательно, данный интеграл расходится;
б) 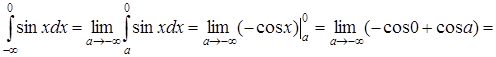
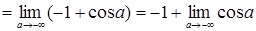 . Так как при . Так как при 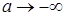 предел предел 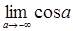 не существует, то интеграл не существует, то интеграл 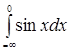 расходится; расходится;
в) 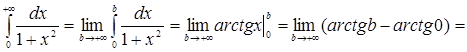
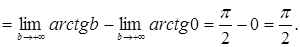 Значит, несобственный интеграл Значит, несобственный интеграл 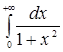 сходится и его значение равно сходится и его значение равно  ; ;
г) 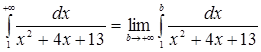 = [выделим в знаменателе полный квадрат: = [выделим в знаменателе полный квадрат:  ] = ] = 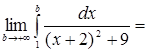 [замена: [замена: 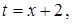
 ] = ] = 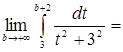
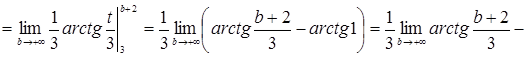 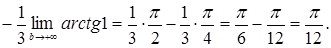
Значит, несобственный интеграл сходится и его значение равно 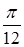 . .
5.
Несобственные интегралы от неограниченных функций
Пусть функция  непрерывна на конечном промежутке непрерывна на конечном промежутке 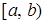 , но не ограничена на этом промежутке. , но не ограничена на этом промежутке.
Определение.
Несобственным интегралом  от функции у= f ( x ) на промежутке от функции у= f ( x ) на промежутке 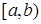 называется предел называется предел  , т.е. , т.е.
 . (15) . (15)
Если предел, стоящий в правой части равенства (15) существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
Интеграл (15) иногда называют несобственным интегралом второго рода.
Аналогично вводится понятие несобственного интеграла от функции 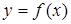 непрерывной, но не ограниченной на промежутке непрерывной, но не ограниченной на промежутке 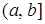 : :
 . (16) . (16)
Если функция  не ограничена при не ограничена при 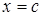 , где , где 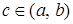 , и непрерывна при , и непрерывна при  и и 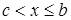 , то несобственный интеграл от функции у= f ( x ) на отрезке , то несобственный интеграл от функции у= f ( x ) на отрезке 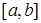 обозначается обозначается 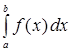 и определяется равенством и определяется равенством
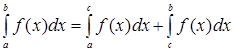 . (17) . (17)
Несобственный интеграл (17) называется сходящимся, если сходятся оба несобственных интеграла в правой части равенства (17).
В противном случае данный интеграл называется расходящимся.
Пример 17.
Исследовать на сходимость несобственные интегралы:
а)  ; б) ; б) 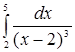 . .
Решение: а) данный интеграл является интегралом от неограниченной функции (подынтегральная функция  не определена в точке не определена в точке  , при , при 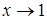 эта функция неограниченно возрастает). эта функция неограниченно возрастает).
По определению имеем
 [замена: [замена: 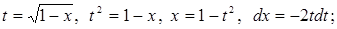 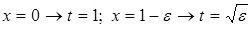 ] = ] =   , следовательно, данный интеграл сходится. , следовательно, данный интеграл сходится.
б) по определению

 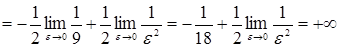 . .
Значит, данный интеграл является расходящимся.
Литература
1. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. I . – М.: Наука, 1982. – 616 с.
2. Гусак А.А. Математический анализ и дифференциальные уравнения. – Мн.: ТетраСистемс, 1998. – 416 с.
3. Гусак А.А. Высшая математика: Учеб. пособие для студентов вузов: В 2 т. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).
4. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2002. – 471 с.
5. Яблонский А.И., Кузнецов А.В., Шилкина Е.И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С.А. Самаля. – Мн.: Выш. шк., 2000. – 351 с.
|