| Министерство Образования Российской Федерации
Южно-Уральский Государственный Университет
Кафедра Системы Управления
КУРСОВАЯ РАБОТА
по дисциплине: Исследование операций
Вариант 8
Руководитель:
Плотникова Н.В.
«___»__________2004 г.
Автор проекта:
студентка группы
ПС – 317
Куликова Мария
«___»__________2004 г.
Проект защищен
с оценкой
«___»__________2004 г.
Челябинск
2004 г.
Содержание.
Задача 1………………………………………………………………….3
Задача 2………………………………………………………………….8
Задача 3…………………………………………………………………10
Задача 4…………………………………………………………………13
Задача 1 (№8)
Условие:
На производстве четырёх видов кабеля выполняется пять групп технологических операций. Нормы затрат на 1 км. кабеля данного вида на каждой из групп операций, прибыль от реализации 1 км. каждого вида кабеля, а также общий фонд рабочего времени, в течение которого могут выполняться эти операции, указаны в таблице.
Определить такой план выпуска кабеля, при котором общая прибыль от реализации изготовляемой продукции является максимальной.
| Технологическая операция
|
Нормы затрат времени на обработку 1 км кабеля вида
|
Общий фонд рабочего времени (ч)
|
| 1
|
2
|
3
|
4
|
| Волочение
|
а11
|
а12
|
а13
|
а14
|
А1
|
| Наложение изоляций
|
а21
|
а22
|
а23
|
а24
|
А2
|
| Скручивание элементов в кабель
|
а31
|
а32
|
а33
|
а34
|
А3
|
| Освинцовывание
|
а41
|
а42
|
а43
|
а44
|
А4
|
| Испытание и контроль
|
а51
|
а52
|
а53
|
а54
|
А5
|
| Прибыль от реализации 1 км кабеля
|
В1
|
В2
|
В3
|
В4
|
| №вар.
|
а11
|
а12
|
а13
|
а14
|
а21
|
а22
|
а23
|
а24
|
а31
|
а32
|
а33
|
а34
|
а41
|
| 1
|
1,5
|
1
|
2
|
1
|
1
|
2
|
0
|
2
|
4
|
5
|
5
|
4
|
2
|
| № вар.
|
а42
|
а43
|
а44
|
а51
|
а52
|
а53
|
а54
|
А1
|
А2
|
А3
|
А4
|
5
|
| 1
|
1
|
4
|
0
|
1
|
2
|
1,5
|
4
|
6500
|
4000
|
11000
|
4500
|
4500
|
Решение:
Составляем математическую модель задачи:
пусть x1 –длина 1-ого кабеля (км);
x2 – длина 2-ого кабеля (км);
x3 – длина 3-ого кабеля (км);
x4 – длина 4-ого кабеля (км)
тогда целевая функция L - общая прибыль от реализации изготовляемой продукции, будет иметь следующий вид
L= В1x1 + В2x2 + В3x3 + В4x4 = x1+ 2x2 + 1,5x3 + x4 → max
Получим систему ограничений:
1,5x1 + x2 + 2x3+ x4 £ 6500;
x1 + 2x2 + 0x3+2x4 £ 4000;
4x1 + 5x2 + 5x3+4x4 £11000;
2x1 + x2 +1,5x3+0x4 £ 4500;
x1 + 2x2 +1,5x3+4x4 £ 4500.
Приведём полученную математическую модель к виду ОЗЛП с помощью добавочных неотрицательных переменных, число которых равно числу неравенств:
1,5x1 + x2 + 2x3+ x4 + x5 = 6500;
x1 + 2x2 + 0x3+2x4 + x6= 4000;
4x1 + 5x2 + 5x3+4x4 + x7=11000;
2x1 + x2 +1,5x3+0x4 + x8 =4500;
x1 + 2x2 +1,5x3+4x4 + x9 =4500.
Итак, выберем x1, x2, x3, x4 - свободными переменными, а x5, x6, x7, x8, x9 - базисными переменными (каждая из них встречаются в системе лишь в одном уравнении с коэффициентом 1, а в остальных с нулевыми коэффициентами). Приведём систему к стандартному виду, выразив для этого все базисные переменные через свободные:
x5 = 6500 – (1,5x1 + x2 + 2x3+ x4 );
x6 = 4000 – ( x1 + 2x2 + 0x3+2x4);
x7 =11000 - ( 4x1 + 5x2 + 5x3+4x4);
x8 =4500 – ( 2x1 + x2 +1,5x3+0x4);
x9 =4500 – ( x1 + 2x2 +1,5x3+4x4)
L=0 –(- x1- 2x2 - 1,5x3 - x4)
Решим методом симплекс-таблиц:
Это решение опорное, т.к. все свободные члены положительны.
Выберем столбец в таблице, который будет разрешающим, пусть это будет x1, выберем в качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это x8).
| A
|

|

|

|

|
| L
|
0
2250
|
-1
0,5
|
-2
0,5
|
-1,5
2
|
-1
0
|
| 
|
6500
-3375
|
1,5
-0,75
|
1
-0,75
|
2
-3
|
1
0
|
| 
|
4000
-2250
|
1
-0,5
|
2
-0,5
|
0
-2
|
3
0
|
| 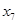
|
11000
-9000
|
4
-2
|
5
-2
|
5
-8
|
4
0
|
| x8
|
4500
2250
|
2
0,5
|
1
0,5
|
4
2
|
0
0
|
| x9
|
4500
-2250
|
1
-0,5
|
2
-0,5
|
1,5
-2
|
4
0
|
Меняем  и и 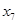
| A
|
x8
|

|

|

|
| L
|
2250
1000
|
0,5
-1
|
-1,5
0,5
|
0,5
-1,5
|
-1
2
|
| 
|
3125
-500/3
|
-0,75
1/6
|
0,25
-1/12
|
-1
0,25
|
1
-1/3
|
| 
|
1750
-1000
|
-0,5
1
|
1,5
-0,5
|
-2
1,5
|
3
-2
|
| 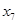
|
2000
2000/3
|
-2
-2/3
|
3
1/3
|
-3
-1
|
4
4/3
|
| 
|
2250
-1000/3
|
0,5
1/3
|
0,5
-1/6
|
2
0,5
|
0
-2/3
|
| x9
|
2250
-1000
|
-0,5
1
|
1,5
-0,5
|
-0,5
1,5
|
4
-2
|
Меняем  и x9 и x9
| A
|
x8
|
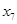
|
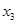
|

|
| L
|
3250
250
|
-0,5
0,5
|
0,5
-0,5
|
-1
1
|
1
2
|
| 
|
8875/3
187,5
|
-7/12
0,375
|
-1/12
-0,375
|
-0,75
0,75
|
2/3
1,5
|
| 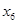
|
750
125
|
0,5
0,25
|
-0,5
-0,25
|
-0,5
0,5
|
1
1
|
| 
|
2000/3
250
|
-2/3
0,5
|
1/3
-0,5
|
-1
1
|
4/3
2
|
| 
|
5750/3
-625
|
5/6
-1,25
|
-1/6
1,25
|
2,5
-2,5
|
-2/3
-5
|
| x9
|
250
250
|
0,5
0,5
|
-0,5
-0,5
|
1
1
|
2
2
|
| A
|
x8
|
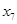
|
x9
|

|
| L
|
3500
|
0
|
0
|
1
|
3
|
| 
|
18875/6
|
-5/24
|
-11/24
|
0,75
|
13/6
|
| 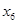
|
875
|
0,75
|
-0,75
|
0,5
|
2
|
| 
|
2750/3
|
-1/6
|
-1/6
|
1
|
10/3
|
| 
|
3875/3
|
-5/12
|
13/12
|
-2,5
|
-17/3
|
| 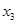
|
250
|
0,5
|
-0,5
|
1
|
2
|
Видим, что коэффициенты при переменных в целевой функции положительны, значит, найденное решение будет оптимальным.
Итак,  =0, =0,  =3875/3, =3875/3,  =2750/3, =2750/3, 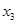 =250, L=3500. =250, L=3500.
Ответ: если предприятие будет изготавливать только три вида проволоки 1,2,3 причем 3875/3 км, 2750/3 км, 250 км соответственно, то общая прибыль от реализации изготовляемой продукции будет максимальной и равной 3500(ед).
Задача 2 (№28)
Условие:
С помощью симплекс–таблиц найти решение задачи линейного программирования: определить экстремальное значение целевой функции Q=CTx при условии Ax ³ £B,
где CT = [ c1 c2 . . . c6 ]T , ВT = [ b1 b2 . . . b6 ]T ,
XT = [ x1 x2 . . . x6]T , А= [aij] (i=1,6; j=1,3).
| № вар.
|
с1
|
с2
|
с3
|
с4
|
с5
|
с6
|
b1
|
b2
|
b3
|
Знаки ограничений
|
a11
|
a12
|
a13
|
a14
|
| 1
|
2
|
3
|
| 28
|
-6
|
0
|
1
|
-1
|
-1
|
0
|
8
|
2
|
3
|
=
|
=
|
=
|
4
|
1
|
1
|
2
|
| № вар.
|
a15
|
a16
|
a21
|
a22
|
a23
|
a24
|
a25
|
a26
|
a31
|
a32
|
a33
|
a34
|
a35
|
a36
|
Тип экстрем.
|
| 1. 34
|
1
|
0
|
2
|
-1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
max
|
Решение:
Получим систему:
4 x1 + x2 + x3+2x4 + x5 =8;
2x1 - x2 +x4=2;
x1 + x2+x5=3
L= -6x1+ x3 -x4 -x5 → max
Пусть x2, x4 – свободные переменные, а x1, x3, x5 - базисные переменные. Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
x5 =2-(1,5x2 -0,5 x4);
x3 =6-(1,5x2 +0,5 x4);
x1=1-(-0,5x2+0,5x4)
L=-2-(3x2- x4) → max
Составим симплекс-таблицу:
Выберем разрешающим столбцом x4,т.к. только перед этой переменной в целевой функции отрицательное число, выберем в качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это x1). Меняем x4 и x1
| b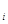
|
x2
|
x4
|
| L
|
-2
2
|
3
-1
|
-1
2
|
| x1
|
1
2
|
-0,5
-1
|
0,5
2
|
1/0,5=2
|
| 
|
6
-1
|
1,5
0,5
|
0,5
-1
|
6/0,5=12
|
| 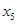
|
2
1
|
1,5
-0,5
|
-0,5
1
|
| b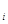
|
x2
|
x1
|
| L
|
0
|
2
|
2
|
| x4
|
2
|
-1
|
2
|
| 
|
5
|
2
|
-1
|
| 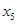
|
3
|
1
|
1
|
Получили оптимальное решение, т.к. все коэффициенты положительны.
Итак, x1= x2=0, x3 =5, x4=2, x5 =3, L=0.
Ответ: x1= x2=0, x3 =5, x4=2, x5 =3, L=0.
Задача 3 (№8)
Условие:
Решение транспортной задачи:
1. Записать условия задачи в матричной форме.
2. Определить опорный план задачи.
3. Определить оптимальный план задачи.
4. Проверить решение задачи методом потенциалов.
| №вар.
|
а1
|
а2
|
а3
|
b1
|
b2
|
b3
|
b4
|
b5
|
с11
|
с12
|
с13
|
| 8
|
200
|
200
|
600
|
200
|
300
|
200
|
100
|
200
|
25
|
21
|
20
|
| с14
|
с15
|
с21
|
с22
|
с23
|
с24
|
с25
|
с31
|
с32
|
с33
|
с34
|
с35
|
| 50
|
18
|
15
|
30
|
32
|
25
|
40
|
23
|
40
|
10
|
12
|
21
|
Решение:
Составим таблицу транспортной задачи. Заполним таблицу методом северо-западного угла:
| B1
|
B2
|
B3
|
B4
|
B5
|
ai
|
| A1
|
25
200
|
21
|
20
|
50
|
18
|
200
|
| A2
|
15
|
30
200
|
32
|
25
|
40
|
200
|
| A3
|
23
|
40
100
|
10
200
|
12
100
|
21
200
|
600
|
| bj
|
200
|
300
|
200
|
100
|
200
|
1000
|
Количество заполненных ячеек r=m+n-1=6.
Проверим сумму по столбцам, сумму по строкам и количество базисных (заполненных) клеток:
r =6, å ai=å bj=1000, всё выполняется, значит, найденный план является опорным.
L=25*200+30*200+40*100+10*200+12*100+21*200=22400
Постараемся улучшить план перевозок.
1) Рассмотрим цикл (1;1)-(1;2)-(2;2)-(2;1)
Подсчитаем цену цикла: j=15-30+21-25=-19<0
| B1
|
B2
|
B3
|
B4
|
B5
|
ai
|
| A1
|
25
|
21
200
|
20
|
50
|
18
|
200
|
| A2
|
15
200
|
30
|
32
|
25
|
40
|
200
|
| A3
|
23
|
40
100
|
10
200
|
12
100
|
21
200
|
600
|
| bj
|
200
|
300
|
200
|
100
|
200
|
1000
|
L=21*200+15*200+40*100+10*200+12*100+21*200=18600
2) Рассмотрим цикл (2;1)-(2;2)-(3;2)-(3;1)
j=-15+30+23-40=-2<0
| B1
|
B2
|
B3
|
B4
|
B5
|
ai
|
| A1
|
25
|
21
200
|
20
|
50
|
18
|
200
|
| A2
|
15
100
|
30
100
|
32
|
25
|
40
|
200
|
| A3
|
23
100
|
40
|
10
200
|
12
100
|
21
200
|
600
|
| bj
|
200
|
300
|
200
|
100
|
200
|
1000
|
L=21*200+15*100+30*100+23*100+10*200+12*100+21*200=18400
Проверим методом потенциалов:
Примем α1=0, тогда βj = cij – αi (для заполненных клеток).
Если решение верное, то во всех пустых клетках таблицы Δij = cij – (αi+ βj) ≥ 0
Очевидно, что Δij =0 для заполненных клеток.
В результате получим следующую таблицу:
| B1=6
|
B2=21
|
B3=-7
|
B4=-5
|
B5=4
|
ai
|
| A1=0
|
25-6>0
|
21-21=0
200
|
20+7>0
|
50+5>0
|
18-4>0
|
200
|
| A2=9
|
15-9-6=0
100
|
30-21-9=0
100
|
32-9+7>0
|
25+5-9>0
|
40-4-9>0
|
200
|
| A3=17
|
23-17-6=0
100
|
40-21-17>0
|
10+7-17=0
200
|
12+5-17=0
100
|
21-4-17=0
200
|
600
|
| bj
|
200
|
300
|
200
|
100
|
200
|
1000
|
Таким образом, решение верное, т.к. Δij > 0 для всех пустых клеток и Δij =0 для всех заполненных.
Тогда сумма всех перевозок:
L=18400
Ответ:
| B1
|
B2
|
B3
|
B4
|
B5
|
ai
|
| A1
|
25
|
21
200
|
20
|
50
|
18
|
200
|
| A2
|
15
100
|
30
100
|
32
|
25
|
40
|
200
|
| A3
|
23
100
|
40
|
10
200
|
12
100
|
21
200
|
600
|
| bj
|
200
|
300
|
200
|
100
|
200
|
1000
|
Задача 4 (№53)
Условие:
Определить экстремум целевой функции вида
F = c11x12+c22x22+c12x1x2+b1x1+b2x2
при условиях:
a11x1+a12x2<=>p1
a21x1+a22x2<=>p2.
1. Найти стационарную точку целевой функции и исследовать ее (функцию) на выпуклость (вогнутость) в окрестностях стационарной точки.
2. Составить функцию Лагранжа.
3. Получить систему неравенств в соответствии с теоремой Куна-Таккера.
4. Используя метод искусственных переменных составить симплекс-таблицу и найти решение полученной задачи линейного программирования.
5. Дать ответ с учетом условий дополняющей нежесткости.
| №
|
b1
|
b2
|
c11
|
c12
|
c22
|
extr
|
a11
|
a12
|
a21
|
a22
|
p1
|
p2
|
Знаки огр.
1 2
|
| 53
|
6
|
1,5
|
-2
|
-4
|
–1
|
max
|
2,5
|
-1
|
3
|
2,5
|
7
|
13
|
³
|
³
|
Решение:
Целевая функция:
F= -2x12-x22-4x1x2+6x1+1,5x2→max
Ограничения g1(x) и g2(x): 2,5x1-x2³7 2,5x1-x2–7³0
3x1+2,5x2³13 3x1+2,5x2-13³0
1) определим относительный максимум функции, для этого определим стационарную точку (х10, х20):
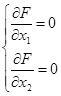 → →
2) Исследуем стационарную точку на максимум, для чего определяем выпуклость или вогнутость функции
F11 (х10, х20) = -4 < 0
F12 (х10, х20)=-4
F21 (х10, х20)=-4
F22 (х10, х20)=-2
F11 F12 -4 -4
F21 F22 -4 -2
Т.к. условие выполняется, то целевая функция является строго выпуклой в окрестности стационарной точки
3) Составляем функцию Лагранжа:
L(x,u)=F(x)+u1g1(x)+u2g2(x)=-2x12-x22-4x1x2+6x1+1,5x2+u1 (2,5x1-x2–7)+ u2 (3x1+2,5x2-13).
Получим уравнения седловой точки, применяя теорему Куна-Таккера:
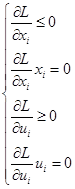 i=1;2 i=1;2
Объединим неравенства в систему А, а равенства в систему В:
Система А:
Система В:
Перепишем систему А:
6-4x1-4x2+2,5u1+3u2 <0
1,5-4x1-2x2-u1+2,5u2 <0
2,5x1-x2–7³0
3x1+2,5x2–13³0
4)Введем новые переменные
V={v1,v2}≥0; W={w1,w2}≥0
в систему А для того, чтобы неравенства превратить в равенства:
6-4x1-4x2+2,5u1+3u2 + v1=0
1,5-4x1-2x2-u1+2,5u2 + v2=0
2,5x1-x2–7- w1=0
3x1+2,5x2–13- w2=0
Тогда
- v1=6-4x1-4x2+2,5u1+3u2
- v2=1,5-4x1-2x2-u1+2,5u2
w1=2,5x1-x2–7
w2=3x1+2,5x2–13
Следовательно, система В примет вид:
 - это условия дополняющей нежесткости. - это условия дополняющей нежесткости.
5) Решим систему А с помощью метода искусственных переменных.
Введем переменные Y={y1; y2} в 1 и 2 уравнения системы
6-4x1-4x2+2,5u1+3u2 + v1 -y1=0
1,5-4x1-2x2-u1+2,5u2 + v2 -y2=0
2,5x1-x2–7- w1=0
3x1+2,5x2–13- w2=0
и создадим псевдоцелевую функцию Y=My1+My2→min
Y’=-Y= -My1-My2→max.
В качестве свободных выберем х1, х2, v1, v2, u1, u2;
а в качестве базисных y1, y2, w1, w2.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
y1=6-(4x1+4x2-2,5u1-3u2 - v1)
y2=1,5-(4x1+2x2+u1-2,5u2 -v2)
w1=-7-(-2,5x1+x2)
w2=-13-(-3x1-2,5x2)
Y’=-Y=-My1-My2=-7,5M-(-8x1-6x2+1,5u1+5,5u2+ v1+v2) M
Решим с помощью симплекс-таблицы. Найдем опорное решение:
| 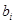
|
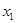
|

|

|

|

|
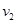
|
| 
|
-7,5M
4,5M
|
-8M
12M
|
-6M
3M
|
1,5M
3M
|
5,5M
-7,5M
|
M
0
|
M
-3M
|
| 
|
6
-3
|
4
-8
|
4
-2
|
-2,5
-2
|
-3
5
|
-1
0
|
0
2
|
| 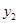
|
1,5
3/4
|
4
2
|
2
0,5
|
1
0,5
|
-2,5
-5/4
|
0
0
|
-1
-0,5
|
| 
|
-7
-3/4
|
-2,5
-2
|
1
-0,5
|
0
-0,5
|
0
5/4
|
0
0
|
0
0,5
|
| 
|
-13
15/8
|
-3
5
|
-2,5
5/4
|
0
5/4
|
0
-25/16
|
0
0
|
0
-5/4
|
Меняем и и 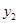
| 
|
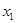
|
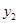
|

|

|

|
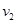
|
| 
|
-3M
3M
|
4M
-4M
|
3M
-2M
|
4,5M
-4,5M
|
-2M
M
|
M
-M
|
-2M
2M
|
| 
|
3
3/2
|
-4
-2
|
-2
-1
|
-4,5
-9/4
|
2
0,5
|
-1
-0,5
|
2
1
|
| 
|
3/4
15/8
|
2
-2,5
|
0,5
-5/4
|
0,5
-45/16
|
-5/4
5/8
|
0
-5/8
|
-0,5
5/4
|
| 
|
-31/4
-15/8
|
-4,5
2,5
|
-0,5
5/4
|
-0,5
45/16
|
5/4
-5/8
|
0
5/8
|
0,5
-5/4
|
| 
|
-89/8
75/32
|
2
-25/8
|
5/4
-25/16
|
5/4
-225/64
|
-25/16
25/32
|
0
-25/32
|
-5/4
25/16
|
Меняем  и и 
| 
|
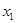
|
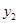
|

|

|

|
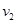
|
| 
|
0
0
|
0
0
|
M
0
|
0
0
|
M
0
|
0
0
|
0
0
|
| 
|
3/2
77/8
|
-2
-1
|
-1
-3/4
|
-9/4
-37/16
|
0,5
5/8
|
-0,5
-5/8
|
1
3/4
|
| 
|
21/8
77/32
|
-0,5
-1/4
|
-3/4
-3/16
|
-37/16
-37/64
|
5/8
5/32
|
-5/8
-5/32
|
3/4
-3/16
|
| 
|
-77/8
77/16
|
-2
-0,5
|
3/4
-3/8
|
37/16
-37/32
|
-5/8
5/16
|
5/8
-5/16
|
-3/4
3/8
|
| 
|
-281/32
693/128
|
-9/8
-9/16
|
-5/16
-27/64
|
-145/64
-333/256
|
25/32
45/128
|
-25/32
-45/128
|
5/16
27/64
|
Меняем 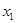 и и 
| 
|

|
|

|

|

|
|
| 
|
0
0
|
0
0
|
M
0
|
0
0
|
M
0
|
0
0
|
0
0
|
| 
|
89/8
431/18
|
-1
-16/9
|
-7/4
|
-73/16
|
9/8
|
-9/8
|
7/4
|
| 
|
161/32
431/72
|
-1/4
-4/9
|
-15/16
|
-185/64
|
25/32
|
-25/32
|
9/16
|
| 
|
77/16
431/36
|
-0,5
-8/9
|
-3/8
|
-37/32
|
5/16
|
-5/16
|
3/8
|
| 
|
-431/32
431/18
|
-9/16
-16/9
|
-47/64
|
-913/256
|
145/128
|
-145/128
|
47/64
|
Меняем  и и 
| 
|

|
|

|

|

|
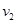
|
| 
|
0
|
0
|
M
|
0
|
M
|
0
|
0
|
| 
|
2525/72
|
| 
|
3173/288
|
| 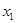
|
2417/144
|
| 
|
431/18
|
Итак,  = =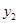 = = = = = = = =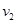 , , 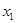 =16,785, =16,785,  =11,017, =11,017,  =23,944, =23,944,  =35,07 =35,07
6) Условия дополняющей нежесткости выполняются 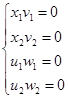 ,значит, решения исходной задачи квадратичного программирования существует. ,значит, решения исходной задачи квадратичного программирования существует.
Ответ: существует.
Литература.
1) Курс лекций Плотникова Н.В.
2) Пантелеев А.В., Летова Т.А. «Методы оптимизации в примерах и задачах».
|