СОДЕРЖАНИЕ
Задание 1
Задание 2
Задание 3
Задание 4
Список использованной литературы
Задание 1
Имеются данные за 12 месяцев года по району города о рынке вторичного жилья ( y
– стоимость квартиры (тыс. у.е.), x
– размер общей площади (м 2
)). Данные приведены в табл. 1.4.
Таблица 1
| Месяц |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| у |
22,5 |
25,8 |
20,8 |
15,2 |
25,8 |
19,4 |
18,2 |
21,0 |
16,4 |
23,5 |
18,8 |
17,5 |
| х |
29,0 |
36,2 |
28,9 |
32,4 |
49,7 |
38,1 |
30,0 |
32,6 |
27,5 |
39,0 |
27,5 |
31,2 |
Задание:
1. Рассчитайте параметры уравнений регрессий
 и и 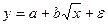 . .
2. Оцените тесноту связи с показателем корреляции и детерминации.
3. Рассчитайте средний коэффициент эластичности и дайте сравнительную оценку силы связи фактора с результатом.
4. Рассчитайте среднюю ошибку аппроксимации и оцените качество модели.
5. С помощью F -статистики Фишера (при  ) оцените надежность уравнения регрессии. ) оцените надежность уравнения регрессии.
6. Рассчитайте прогнозное значение  , если прогнозное значение фактора увеличится на 5% от его среднего значения. Определите доверительный интервал прогноза для , если прогнозное значение фактора увеличится на 5% от его среднего значения. Определите доверительный интервал прогноза для  . .
7. Расчеты должны быть подробны, как показано в примере 1, и сопровождены пояснениями.
Решение
Составим таблицу расчетов 2.
Все расчеты в таблице велись по формулам
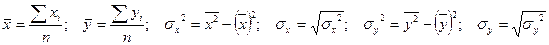 . .
Таблица 2
| х |
х 2
|
у |
ху |
у 2
|
 |
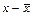 |
 |
 |
 |
 |
 |
А(%) |
| 29,0 |
841,0 |
22,5 |
652,5 |
506,3 |
2,1 |
-4,5 |
4,38 |
20,33 |
18,93 |
3,57 |
12,75 |
15,871 |
| 36,2 |
1310,4 |
25,8 |
934,0 |
665,6 |
5,4 |
2,7 |
29,07 |
7,25 |
21,28 |
4,52 |
20,40 |
17,506 |
| 28,9 |
835,2 |
20,8 |
601,1 |
432,6 |
0,4 |
-4,6 |
0,15 |
21,24 |
18,90 |
1,90 |
3,62 |
9,152 |
| 32,4 |
1049,8 |
15,2 |
492,5 |
231,0 |
-5,2 |
-1,1 |
27,13 |
1,23 |
20,04 |
-4,84 |
23,43 |
31,847 |
| 49,7 |
2470,1 |
25,8 |
1282,3 |
665,6 |
5,4 |
16,2 |
29,07 |
262,17 |
25,70 |
0,10 |
0,01 |
0,396 |
| 38,1 |
1451,6 |
19,4 |
739,1 |
376,4 |
-1,0 |
4,6 |
1,02 |
21,08 |
21,90 |
-2,50 |
6,27 |
12,911 |
| 30,0 |
900,0 |
18,2 |
546,0 |
331,2 |
-2,2 |
-3,5 |
4,88 |
12,31 |
19,26 |
-1,06 |
1,12 |
5,802 |
| 32,6 |
1062,8 |
21,0 |
684,6 |
441,0 |
0,6 |
-0,9 |
0,35 |
0,83 |
20,11 |
0,89 |
0,80 |
4,256 |
| 27,5 |
756,3 |
16,4 |
451,0 |
269,0 |
-4,0 |
-6,0 |
16,07 |
36,10 |
18,44 |
-2,04 |
4,16 |
12,430 |
| 39,0 |
1521,0 |
23,5 |
916,5 |
552,3 |
3,1 |
5,5 |
9,56 |
30,16 |
22,20 |
1,30 |
1,69 |
5,536 |
| 27,5 |
756,3 |
18,8 |
517,0 |
353,4 |
-1,6 |
-6,0 |
2,59 |
36,10 |
18,44 |
0,36 |
0,13 |
1,923 |
| 31,2 |
973,4 |
17,5 |
546,0 |
306,3 |
-2,9 |
-2,3 |
8,46 |
5,33 |
19,65 |
-2,15 |
4,62 |
12,277 |
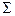 |
402,1 |
13927,8 |
244,9 |
8362,6 |
5130,7 |
0,0 |
0,0 |
132,7 |
454,1 |
- |
- |
79,0 |
129,9 |
| Среднее значение |
33,5 |
1160,7 |
20,4 |
696,9 |
427,6 |
- |
- |
- |
- |
- |
- |
6,6 |
10,8 |
 |
6,43 |
- |
3,47 |
- |
- |
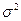 |
41,28 |
- |
12,06 |
- |
- |
Тогда
 , ,

и линейное уравнение регрессии примет вид:  . .
Рассчитаем коэффициент корреляции:
 . .
Связь между признаком 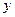 и фактором и фактором  заметная. заметная.
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
R 2
= 0,606 2
= 0,367
Средний коэффициент эластичности позволяет проверить, имеют ли экономический смысл коэффициенты модели регрессии.
позволяет проверить, имеют ли экономический смысл коэффициенты модели регрессии.

Для оценки качества модели определяется средняя ошибка аппроксимации:
 , ,
допустимые значения которой 8 - 10 %.
Вычислим значение  -критерия Фишера. -критерия Фишера.
 , ,
где
 – число параметров уравнения регрессии (число коэффициентов при объясняющей переменной – число параметров уравнения регрессии (число коэффициентов при объясняющей переменной  ); );
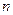 – объем совокупности. – объем совокупности.
 . .
По таблице распределения Фишера находим
 . .
Так как  , то гипотеза , то гипотеза  о статистической незначимости параметра о статистической незначимости параметра 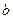 уравнения регрессии отклоняется. уравнения регрессии отклоняется.
Так как 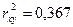 , то можно сказать, что 36,7% результата объясняется вариацией объясняющей переменной. , то можно сказать, что 36,7% результата объясняется вариацией объясняющей переменной.
Выберем в качестве модели уравнения регрессии  , предварительно линеаризовав модель. Введем обозначения: , предварительно линеаризовав модель. Введем обозначения:  . Получим линейную модель регрессии . Получим линейную модель регрессии  . .
Рассчитаем коэффициенты модели, поместив все промежуточные расчеты в табл. 3.
Таблица 3
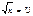 |
 |
y |
yU |
y 2
|
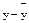 |
 |
 |
 |
 |
 |
 |
А(%) |
| 5,385 |
29,0 |
22,5 |
121,17 |
506,25 |
1,640 |
-0,452 |
2,69 |
0,20 |
13,74 |
8,76 |
76,7 |
38,92 |
| 6,017 |
36,2 |
25,8 |
155,23 |
665,64 |
4,940 |
0,180 |
24,40 |
0,03 |
14,01 |
11,79 |
139,0 |
45,70 |
| 5,376 |
28,9 |
20,8 |
111,82 |
432,64 |
-0,060 |
-0,461 |
0,004 |
0,21 |
13,74 |
7,06 |
49,9 |
33,95 |
| 5,692 |
32,4 |
15,2 |
86,52 |
231,04 |
-5,660 |
-0,145 |
32,04 |
0,02 |
13,87 |
1,33 |
1,8 |
8,72 |
| 7,050 |
49,7 |
25,8 |
181,89 |
665,64 |
4,940 |
1,213 |
24,40 |
1,47 |
14,42 |
11,38 |
129,5 |
44,11 |
| 6,173 |
38,1 |
19,4 |
119,75 |
376,36 |
-1,460 |
0,336 |
2,13 |
0,11 |
14,07 |
5,33 |
28,4 |
27,45 |
| 5,477 |
30,0 |
18,2 |
99,69 |
331,24 |
-2,660 |
-0,360 |
7,08 |
0,13 |
13,78 |
4,42 |
19,5 |
24,27 |
| 5,710 |
32,6 |
21,0 |
119,90 |
441 |
0,140 |
-0,127 |
0,02 |
0,02 |
13,88 |
7,12 |
50,7 |
33,89 |
| 5,244 |
27,5 |
16,4 |
86,00 |
268,96 |
-4,460 |
-0,593 |
19,89 |
0,35 |
13,68 |
2,72 |
7,4 |
16,58 |
| 6,245 |
39,0 |
23,5 |
146,76 |
552,25 |
2,640 |
0,408 |
6,97 |
0,17 |
14,10 |
9,40 |
88,3 |
39,98 |
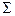 |
58,368 |
343,4 |
208,600 |
1228,71 |
4471,02 |
- |
- |
- |
- |
- |
- |
- |
313,567 |
| Среднее значение |
5,837 |
34,34 |
20,860 |
122,871 |
447,10 |
- |
- |
- |
- |
- |
- |
- |
31,357 |
 |
0,549 |
- |
3,646 |
- |
- |
- |
- |
 |
0,302 |
- |
13,292 |
- |
- |
- |
- |
Рассчитаем параметры уравнения:
 , ,
 , ,
   . .
Коэффициент корреляции
 . .
Коэффициент детерминации
 , ,
следовательно, только 9,3% результата объясняется вариацией объясняющей переменной  . .
 , ,
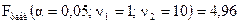
 , ,
следовательно, гипотеза  о статистической незначимости уравнения регрессии принимается. По всем расчетам линейная модель надежнее, и последующие расчеты мы сделаем для нее. о статистической незначимости уравнения регрессии принимается. По всем расчетам линейная модель надежнее, и последующие расчеты мы сделаем для нее.
Оценим значимость каждого параметра уравнения регрессии  . .
Используем для этого t -распределение (Стьюдента). Выдвигаем гипотезу 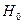 о статистической незначимости параметров, т.е. о статистической незначимости параметров, т.е.
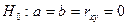 . .
 . .
Определим ошибки  . .
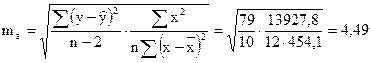 , ,
 , ,
 , ,
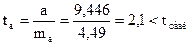 , ,
 , ,
 . .
Полученные оценки модели и ее параметров позволяют использовать ее для прогноза.
Рассчитаем
 . .
Тогда
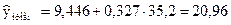 . .
Средняя ошибка прогноза
 , ,
где
 , ,
 . .
Строим доверительный интервал с заданной доверительной вероятностью  : :
 , ,
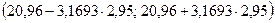 , ,
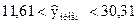 . .
Найденный интервальный прогноз достаточно надежен (доверительная вероятность 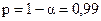 ) и достаточно точен, т.к. ) и достаточно точен, т.к.  . .
Оценим значимость каждого параметра уравнения регрессии
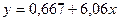 . .
Используем для этого t -распределение (Стьюдента). Выдвигаем гипотезу 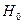 о статистической незначимости параметров, т.е. о статистической незначимости параметров, т.е.
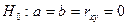 . .
 . .
Определим ошибки  . .
 , ,
 , ,
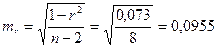 , ,  , ,
 , , 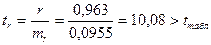 . .
Следовательно,  и и  не случайно отличаются от нуля, а сформировались под влиянием систематически действующей производной. не случайно отличаются от нуля, а сформировались под влиянием систематически действующей производной.
1.  , следовательно, качество модели не очень хорошее. , следовательно, качество модели не очень хорошее.
2. Полученные оценки модели и ее параметров позволяют использовать ее для прогноза.
Рассчитаем  . Тогда . Тогда  . .
3. Средняя ошибка прогноза
 , ,
где
 , ,
 . .
Строим доверительный интервал с заданной доверительной вероятностью  : :
 , ,
 , ,
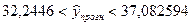 . .
Найденный интервальный прогноз достаточно надежен (доверительная вероятность  ) и достаточно точен, т.к. ) и достаточно точен, т.к. 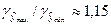 . .
Задание 2
Имеются данные о деятельности крупнейших компаний в течение двенадцати месяцев 199Х года. Данные приведены в табл. 4.
Известны – чистый доход ( у
), оборот капитала ( х
1
), использованный капитал ( х
2
) в млрд у.е.
Таблица 4
| у
|
х
1
|
х
2
|
| 1,5 |
5,9 |
5,9 |
| 5,5 |
53,1 |
27,1 |
| 2,4 |
18,8 |
11,2 |
| 3,0 |
35,3 |
16,4 |
| 4,2 |
71,9 |
32,5 |
| 2,7 |
93,6 |
25,4 |
| 1,6 |
10,0 |
6,4 |
| 2,4 |
31,5 |
12,5 |
| 3,3 |
36,7 |
14,3 |
| 1,8 |
13,8 |
6,5 |
| 2,4 |
64,8 |
22,7 |
| 1,6 |
30,4 |
15,8 |
Задание:
1. Рассчитайте параметры линейного уравнения множественной регрессии.
2. Дайте оценку силы связи факторов с результатом с помощью средних коэффициентов эластичности.
3. Оцените статистическую зависимость параметров и уравнения регрессии в целом с помощью соответственно критериев Стьюдента и Фишера (α=0,01).
4. Рассчитайте среднюю ошибку аппроксимации. Сделайте вывод.
5. Составьте матрицы парных и частных коэффициентов корреляции и укажите информативные факторы.
6. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение
Результаты расчетов приведены в табл. 5.
Таблица 5
| y
|
x
1
|
x
2
|
yx
1
|
yx
2
|
x
1
x
2
|
x
1
2
|
x 2
2
|
y 2
|
| 1,5 |
5,9 |
5,9 |
8,85 |
8,85 |
34,81 |
34,81 |
34,81 |
2,25 |
| 5,5 |
53,1 |
27,1 |
292,05 |
149,05 |
1439,01 |
2819,61 |
734,41 |
30,25 |
| 2,4 |
18,8 |
11,2 |
45,12 |
26,88 |
210,56 |
353,44 |
125,44 |
5,76 |
| 3 |
35,3 |
16,4 |
105,90 |
49,20 |
578,92 |
1246,09 |
268,96 |
9 |
| 4,2 |
71,9 |
32,5 |
301,98 |
136,50 |
2336,75 |
5169,61 |
1056,25 |
17,64 |
| 2,7 |
93,6 |
25,4 |
252,72 |
68,58 |
2377,44 |
8760,96 |
645,16 |
7,29 |
| 1,6 |
10 |
6,4 |
16,00 |
10,24 |
64,00 |
100,00 |
40,96 |
2,56 |
| 2,4 |
31,5 |
12,5 |
75,60 |
30,00 |
393,75 |
992,25 |
156,25 |
5,76 |
| 3,3 |
36,7 |
14,3 |
121,11 |
47,19 |
524,81 |
1346,89 |
204,49 |
10,89 |
| 1,8 |
13,8 |
6,5 |
24,84 |
11,70 |
89,70 |
190,44 |
42,25 |
3,24 |
| 2,4 |
64,8 |
22,7 |
155,52 |
54,48 |
1470,96 |
4199,04 |
515,29 |
5,76 |
| 1,6 |
30,4 |
15,8 |
48,64 |
25,28 |
480,32 |
924,16 |
249,64 |
2,56 |
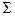 |
32,4 |
465,8 |
196,7 |
1448,33 |
617,95 |
10001,03 |
26137,30 |
4073,91 |
102,96 |
| Средн. |
2,7 |
38,8 |
16,4 |
120,69 |
51,50 |
833,42 |
- |
- |
65,80 |
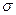 |
1,2 |
27,1 |
8,8 |
- |
- |
- |
- |
- |
- |
 |
1,4 |
732,4 |
77,2 |
- |
- |
- |
- |
- |
- |
Рассматриваем уравнение вида:
 . .
Параметры уравнения можно найти из решения системы уравнений:

Или, перейдя к уравнению в стандартизированном масштабе:
 , где , где
 – стандартизированные переменные, – стандартизированные переменные,
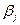 – стандартизированные коэффициенты: – стандартизированные коэффициенты:

Коэффициенты 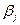 определяются из системы уравнений: определяются из системы уравнений:
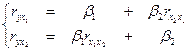 
 , , 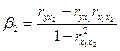 ; ;
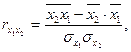  ; ;
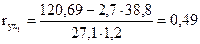 , ,  ; ;
 , , 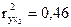 ; ;
 , ,  ; ;
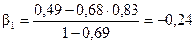 , ,  ; ;
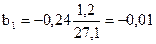 , ,  ; ;
 . .
Стандартизированная форма уравнения регрессии имеет вид:
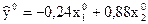 . .
Естественная форма уравнения регрессии имеет вид:
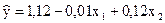 . .
Для выяснения относительной силы влияния факторов на результативный признак рассчитываются средние коэффициенты эластичности:
 , ,
 , ,
 . .
Следовательно, при увеличении оборота капитала ( x 1
) на 1% чистый доход ( y ) уменьшается на 0,14% от своего среднего уровня. При повышении использованного капитала на 1% чистый доход повышается на 0,73% от своего среднего уровня.
Линейные коэффициенты частной корреляции для уравнения определяются следующим образом:
 , ,
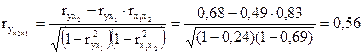 . .
Линейный коэффициент множественной корреляции рассчитывается по формуле
 . .
Коэффициент множественной детерминации 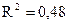 . .
 , ,
где
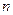 - объем выборки, - объем выборки,
 - число факторов модели. - число факторов модели.
В нашем случае
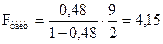 . .
Так как  , то , то 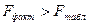 и потому уравнение незначимо. и потому уравнение незначимо.
Выясним статистическую значимость каждого фактора в уравнении множественной регрессии.
Для этого рассчитаем частные  -статистики. -статистики.
 . .
Так как  , то , то 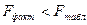 и следует вывод о нецелесообразности включения в модель фактора и следует вывод о нецелесообразности включения в модель фактора  после фактора после фактора  . .
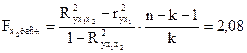 . .
Так как  , то следует вывод о нецелесообразности включения в модель фактора , то следует вывод о нецелесообразности включения в модель фактора  после фактора после фактора  . .
Результаты расчетов позволяют сделать вывод :
1) о незначимости фактора  и нецелесообразности включения его в уравнение регрессии; и нецелесообразности включения его в уравнение регрессии;
2) о незначимости фактора  и нецелесообразности включения его в уравнение регрессии. и нецелесообразности включения его в уравнение регрессии.
Задание 3
1. Используя необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое уравнение модели.
2. Определите тип модели.
3. Определите метод оценки параметров модели.
4. Опишите последовательность действий при использовании указанного метода.
5. Результаты оформите в виде пояснительной записки.
Модель денежного и товарного рынков:
R t
= a
1
+ b
12
Y
t
+ b
14
M
t
+ e 1
,
Y t
= a
2
+ b
21
R
t
+ b
23
I
t
+ b
25
G t
+ e 2
,
I t
= a
3
+ b
31
R
t
+ e 3
,
где
R
– процентные ставки;
Y
– реальный ВВП;
M
– денежная масса;
I
– внутренние инвестиции;
G – реальные государственные расходы.
Решение
1. Модель имеет три эндогенные ( R t
Y t
I t
) и две экзогенные переменные ( M t
G t
).
Проверим необходимое условие идентификации:
1-е уравнение: в =1, H =2, в +1= H - уравнение идентифицировано.
2-е уравнение: в =1, H =1, в +1=2 - уравнение сверхидентифицировано.
3-е уравнение: в =1, H =2, в +1= H - уравнение идентифицировано.
Следовательно, необходимое условие идентифицируемости выполнено.
Проверим достаточное условие:
В первом уравнении нет переменных I t
, G t
Строим матрицу:
| It |
Gt |
| 2 ур. |
b23 |
b23 |
| 3 ур. |
0 |
0 |
det M = det  , rank M =2. , rank M =2.
Во втором уравнении нет переменных M t
det M ¹ 0
В третьем уравнении нет переменных Y t
, M t
, G t
Строим матрицу:
det M / /
Следовательно, достаточное условие идентифицируемости выполнено.
Система точно идентифицируема.
2. Найдем структурные коэффициенты модели.
Для этого:
Запишем систему в матричной форме, перенеся все эндогенные переменные в левые части системы:
R t
-b 12
Y t
=a 1
+b 12
M t
Y t
-b 21
R t
-b 23
I t
=a 2
+b 25
G t
I t
-b 31
R t
=a 3
откуда
 , и , и  , ,  , , 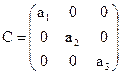 , , 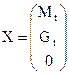 . .
Решаем систему относительно 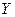 : :  . Найдем . Найдем
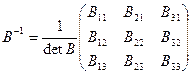 , где , где 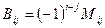 – –
алгебраические дополнения соответствующих элементов матрицы  , ,  – минор, т.е. определитель, полученный из матрицы – минор, т.е. определитель, полученный из матрицы 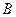 вычеркиванием i -й строки и j -го столбца. вычеркиванием i -й строки и j -го столбца.
 , ,
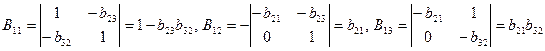 , ,
 , ,
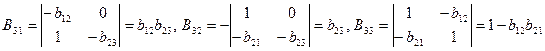 . .
Поэтому
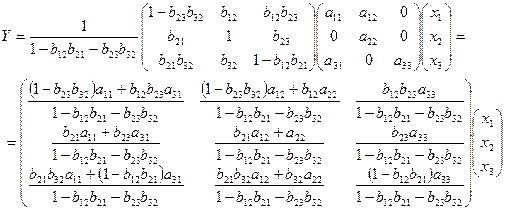
В данном случае эти коэффициенты можно найти значительно проще. Находим 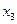 из второго уравнения приведенной системы и подставим его в первое уравнение этой системы. Тогда первое уравнение системы примет вид: из второго уравнения приведенной системы и подставим его в первое уравнение этой системы. Тогда первое уравнение системы примет вид:  , откуда , откуда   , , 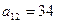 . Из третьего уравнения системы находим . Из третьего уравнения системы находим 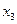 и подставляем во второе уравнение системы, получим: и подставляем во второе уравнение системы, получим:  , решая его совместно с уравнением , решая его совместно с уравнением  и, исключая и, исключая  , получим , получим  . Сравнивая это уравнение со вторым уравнением системы получим . Сравнивая это уравнение со вторым уравнением системы получим  . Выражая . Выражая  из второго уравнения, и подставляя в третье системы (3.2), получим из второго уравнения, и подставляя в третье системы (3.2), получим  . Сравнивая это уравнение с третьим уравнением системы, получим . Сравнивая это уравнение с третьим уравнением системы, получим  . .
Задание 4
Имеются данные за пятнадцать дней по количеству пациентов клиники, прошедших через соответствующие отделения в течение дня. Данные приведены в табл. 6 .
Таблица 6
| День |
Глазное отделение |
| 1 |
30 |
| 2 |
22 |
| 3 |
19 |
| 4 |
28 |
| 5 |
24 |
| 6 |
18 |
| 7 |
35 |
| 8 |
29 |
| 9 |
40 |
| 10 |
34 |
| 11 |
31 |
| 12 |
29 |
| 13 |
35 |
| 14 |
23 |
| 15 |
27 |
Требуется:
1. Определить коэффициенты автокорреляции уровней ряда первого и второго порядка.
2. Обосновать выбор уравнения тренда и определите его параметры.
3. Сделать выводы.
4. Результаты оформить в виде пояснительной записки.
Решение
Определим коэффициент корреляции между рядами 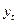 и и  . Ррасчеты приведены в таблице 7: . Ррасчеты приведены в таблице 7:

| год |

|

|

|
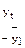 |
 |
 |
 |
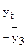 |
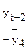 |
 |
 |
 |
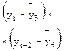 |
| 1 |
30 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
| 2 |
22 |
30 |
- |
-6,14 |
1,64 |
37,73 |
2,70 |
- |
- |
- |
- |
10,09 |
- |
| 3 |
19 |
22 |
30 |
-9,14 |
-6,36 |
83,59 |
40,41 |
-9,36 |
1,23 |
87,56 |
1,51 |
58,12 |
11,52 |
| 4 |
28 |
19 |
22 |
-0,14 |
-9,36 |
0,02 |
87,56 |
-0,36 |
-6,77 |
0,13 |
45,82 |
1,34 |
2,42 |
| 5 |
24 |
28 |
19 |
-4,14 |
-0,36 |
17,16 |
0,13 |
-4,36 |
-9,77 |
18,98 |
95,44 |
1,48 |
42,57 |
| 6 |
18 |
24 |
28 |
-10,14 |
-4,36 |
102,88 |
18,98 |
-10,36 |
-0,77 |
107,27 |
0,59 |
44,19 |
7,97 |
| 7 |
35 |
18 |
24 |
6,86 |
-10,36 |
47,02 |
107,27 |
6,64 |
-4,77 |
44,13 |
22,75 |
71,02 |
31,68 |
| 8 |
29 |
35 |
18 |
0,86 |
6,64 |
0,73 |
44,13 |
0,64 |
-10,77 |
0,41 |
115,98 |
5,69 |
6,92 |
| 9 |
40 |
29 |
35 |
11,86 |
0,64 |
140,59 |
0,41 |
11,64 |
6,23 |
135,56 |
38,82 |
7,62 |
72,54 |
| 10 |
34 |
40 |
29 |
5,86 |
11,64 |
34,31 |
135,56 |
5,64 |
0,23 |
31,84 |
0,05 |
68,19 |
1,30 |
| 11 |
31 |
34 |
40 |
2,86 |
5,64 |
8,16 |
31,84 |
2,64 |
11,23 |
6,98 |
126,13 |
16,12 |
29,68 |
| 12 |
29 |
31 |
34 |
0,86 |
2,64 |
0,73 |
6,98 |
0,64 |
5,23 |
0,41 |
27,36 |
2,27 |
3,36 |
| 13 |
35 |
29 |
31 |
6,86 |
0,64 |
47,02 |
0,41 |
6,64 |
2,23 |
44,13 |
4,98 |
4,41 |
14,82 |
| 14 |
23 |
35 |
29 |
-5,14 |
6,64 |
26,45 |
44,13 |
-5,36 |
0,23 |
28,70 |
0,05 |
34,16 |
1,24 |
| 15 |
27 |
23 |
35 |
-1,14 |
-5,36 |
1,31 |
28,70 |
-1,36 |
6,23 |
1,84 |
38,82 |
6,12 |
8,46 |
 |
120 |
- |
- |
- |
0,00 |
0,00 |
547,71 |
549,21 |
3,36 |
0,00 |
507,94 |
518,31 |
330,84 |
234,47 |
| Средн. |
8 |
28,14
28,36
|
28,36 |
28,77 |
Результат говорит о заметной зависимости между показателями и наличии во временном ряде линейной тенденции.
Определим коэффициент автокорреляции второго порядка:
 , , 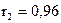
Результат подтверждает наличие линейной тенденции. Выбираем линейное уравнение тренда:  . .
Параметры определим, используя МНК. Результаты расчетов приведены в табл. 8.
Таблица 8
 |
 |
 |
 |
 |
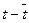 |
 |
 |
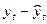 |
 |
| 1 |
30 |
1 |
900 |
30 |
-7,00 |
49 |
| 2 |
22 |
4 |
484 |
44 |
-6,00 |
36 |
| 3 |
19 |
9 |
361 |
57 |
-5,00 |
25 |
| 4 |
28 |
16 |
784 |
112 |
-4,00 |
16 |
| 5 |
24 |
25 |
576 |
120 |
-3,00 |
9 |
| 6 |
18 |
36 |
324 |
108 |
-2,00 |
4 |
| 7 |
35 |
49 |
1225 |
245 |
-1,00 |
1 |
| 8 |
29 |
64 |
841 |
232 |
0,00 |
0 |
| 9 |
40 |
81 |
1600 |
360 |
1,00 |
1 |
| 10 |
34 |
100 |
1156 |
340 |
2,00 |
4 |
| 11 |
31 |
121 |
961 |
341 |
3,00 |
9 |
| 12 |
29 |
144 |
841 |
348 |
4,00 |
16 |
| 13 |
35 |
169 |
1225 |
455 |
5,00 |
25 |
| 14 |
23 |
196 |
529 |
322 |
6,00 |
36 |
| 15 |
27 |
225 |
729 |
405 |
7,00 |
49 |
 |
120 |
424 |
1240 |
12536 |
3519 |
0 |
280 |
| Средн. |
8,00 |
28,27 |
82,67 |
835,73 |
234,6 |
- |
- |
 . .
Уравнение тренда примет вид:  , коэффициент корреляции , коэффициент корреляции
 . .
Расчетное значение критерия Фишера равно  , ,
 , ,
уравнение статистически значимо и прогноз имеет смысл.
Список использованной литературы
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 1998.
2. Катышев П.К., Пересецкий А.А. Сборник задач к начальному курсу эконометрики. – М.: Дело, 1999.
3. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: начальный курс. – М.: Дело, 2000.
4. Практикум по эконометрике. Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.
5. Эддоус М., Стэнсфилд Р. Методы принятия решения. – М.: ЮНИТИ, 1997.
6. Эконометрика. Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.
|