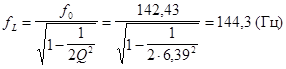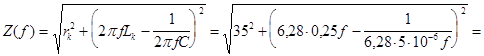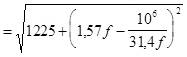Лабораторная работа: Исследование резонанса в одиночных колебательных контурах

Белорусский государственный университет информатики и радиоэлектроники

Кафедра теоретических основ электротехники

Отчёт по лабораторной работе №4

ПО ТЕМЕ: “ИССЛЕДОВАНИЕ РЕЗОНАНСА В ОДИНОЧНЫХ КОЛЕБАТЕЛЬНЫХ КОНТУРАХ”

Выполнил:

Студент группы 851003

Куликов С.С.

Проверил:

Преподаватель

Коваленко В.М.

Минск, 1999

1. ЦЕЛЬ РАБОТЫ

Экспериментально исследовать частотные и резонансные характеристики последовательного контура, влияние активного сопротивления на вид резонансных кривых. Ознакомиться с настройкой последовательного контура на резонанс с помощью ёмкости.

2. ПОСЛЕДОВАТЕЛЬНЫЙ КОНТУР

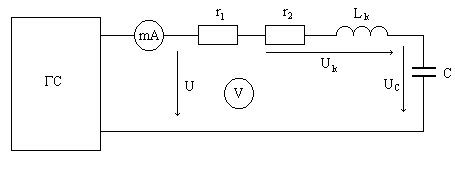
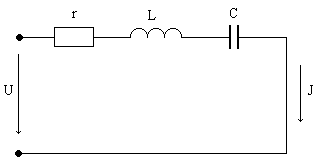
Рис. 1. Схема цепи

Таблица-1 (“Исходные данные”)

3. ТЕОРЕТИЧЕСКИЙ РАСЧЁТ

Определение угловой частоты:

Определение циклической частоты:

Определение характеристического сопротивления:

Определение добротности:

;

Резонансная характеристика тока:

;

Величина тока при резонансе:

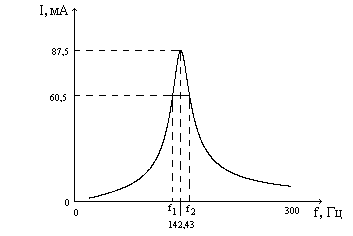
Рис. 2. Резонансная кривая тока.

Частотная характеристика напряжения на ёмкости:

;

Резонансная частота напряжения на ёмкости:

Напряжение на конденсаторе при резонансе:

;

Частотная характеристика напряжения на индуктивности:

;

Резонансная частота напряжения на индуктивности:

Напряжение на индуктивности при резонансе:

Полное сопротивление контура:

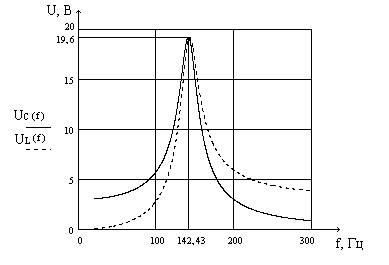
Рис. 3. Резонансные кривые напряжений на ёмкости и индуктивности

4. ПРАКТИЧЕСКИЙ РАСЧЁТ

Рис.4. Схема

Таблица 2.

Зависимость тока и напряжений на индуктивности и ёмкости от частоты при r1=0

Таблица 3.

Зависимости тока и напряжений на индуктивности и ёмкости от частоты при r1<>0

Частотные характеристики Xc(f), XL(f), ZK(f).

Реактивные сопротивления ёмкости и индуктивности и полное сопротивление цепи определяются по формулам:

Рис. 5. Зависимость реактивных сопротивлений элементов и полного сопротивления цепи от частоты.

Таблица 4.

Зависимость реактивных сопротивлений элементов и полного сопротивления цепи от частоты при r1=0.

Характеристическое сопротивление r.

Характеристическое сопротивление контура определяется по точке пересечения частотных характеристик на частоте 142 Гц. В точке пересечения реактивные сопротивления катушки индуктивности и ёмкости равны между собой и составляют примерно 210-220 Ом. Теоретическое расчётное значение характеристического сопротивления и экспериментальное значение совпадают с достаточной точностью.

Резонансные характеристики контура I(f), UK(f), UC(f):

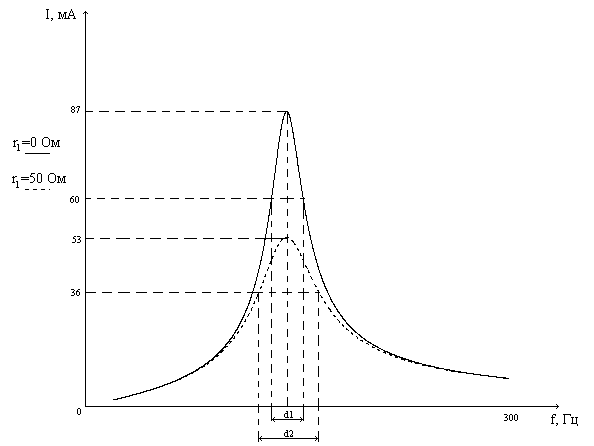
Рис.6. Зависимость тока от частоты сигнала

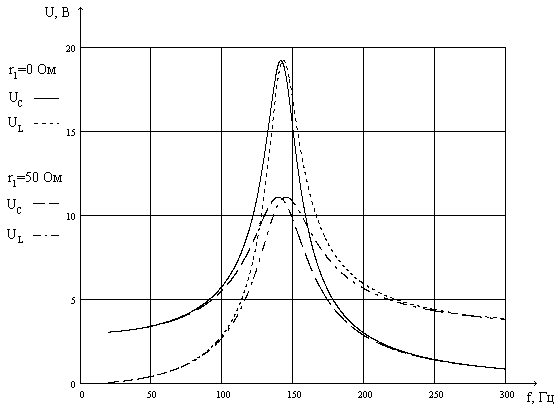
Рис.7. Зависимость напряжения на реактивных элементах от частоты сигнала

Определение добротности Q:

а) При r1=0

По напряжениям на катушке индуктивности и ёмкости в момент резонанса. f0=142 Гц

;

По ширине полосы пропускания резонансной кривой тока на уровне

I=0,7×I0=0,7×87= 60 мА.

б) При r1=50 Ом

По напряжениям на катушке индуктивности и ёмкости в момент резонанса

f0=142 Гц.

;

По ширине полосы пропускания резонансной кривой тока на уровне

I=0,7×I0=0.7*53= 36 мА.

По отношению характеристического и активного сопротивлений контура.

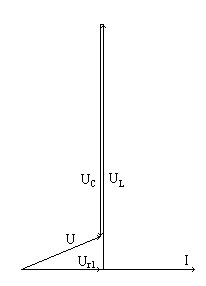
Векторная диаграмма тока и напряжений для частоты f<f0.

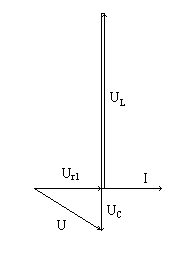
f=130 Гц, mU=2 В/см.

Векторная диаграмма тока и напряжений для частоты f=f0

f=142 Гц, mU=2 В/см, Ur1=U

Векторная диаграмма тока и напряжений для частоты f>f0

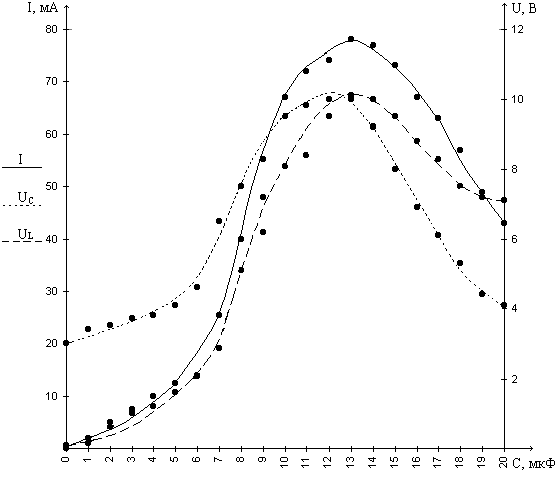
f=150 Гц, mU=2 В/см

Таблица 5.

Зависимости тока и напряжений на катушке и конденсаторе от ёмкости (f=100 Гц).

Рис. 8 Частотные характеристики тока и напряжений последовательного контура на частоте 100 Гц при изменении ёмкости

ВЫВОД

Последовательный контур представляет собой электрическую цепь, состоящую из последовательно соединённых активного сопротивления, ёмкости и индуктивности. Резонанс напряжений в последовательной цепи возникает на частоте, при которой реактивные сопротивления ёмкости и индуктивности равны. На резонансной частоте сопротивление последовательного контура минимально и равно активному сопротивлению цепи. Падения напряжений на ёмкости и индуктивности и ток в цепи достигают максимальных значений.

На частотах, ниже резонансной, сопротивление последовательного контура имеет ёмкостной характер. На частотах, выше резонансной, ¾ индуктивный характер.

Добротность последовательного контура зависит от величины активного сопротивления и возрастает с уменьшением сопротивления.

Резонанс напряжений в последовательном контуре достигается изменением реактивных параметров схемы или частоты сигнала. Изменение ёмкости ¾ наиболее применяемый способ достижения резонанса.
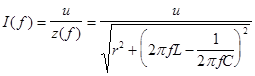
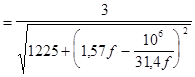
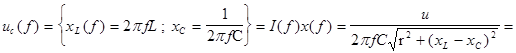
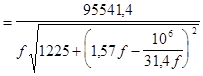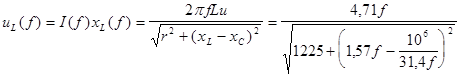