Реферат: Расчёт железобетонных конструкций многоэтажного производственного здания
|
Название: Расчёт железобетонных конструкций многоэтажного производственного здания Раздел: Рефераты по строительству Тип: реферат | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Нижегородский государственный архитектурно-строительныйуниверситет
Кафедра железобетонных и каменных конструкций
ПОЯСНИТЕЛЬНАЯ ЗАПИСКАК КУРСОВОЙ РАБОТЕ «Расчёт железобетонных конструкций многоэтажного производственного здания».
Выполнил студент гр.191: Е.И.Рябушева Проверил: А.Д.Макаров
г.Н.Новгород 2006 год Содержание Стр. 1. Расчет плиты на прочность ……………………………………………… 5 1.1 Расчёт полки плиты……………………………………………………………. 5 1.2 Расчёт поперечного торцевого ребра………………………………………… 6 1.3 Расчёт продольных рёбер……………………………………………………... 6 2. Расчет сборного ригеля поперечной рамы . ……………………………… 10 2.1 Дополнительные данные……………………………………………………… 10 2.2 Расчётные пролёты ригеля……………………………………………………. 10 2.3 Расчётные нагрузки…………………………………………………………… 10 2.4 Расчётные изгибающие моменты……………………………………………. 10 2.5 Расчёт ригеля на прочность по нормальным сечениям……………………. 11 2.7 Расчётные продольные силы………………………………………………… 11 2.6 Расчёт ригеля на прочность по наклонным сечениям на действие поперечных сил…………………………………………………………................ 12 2.8 Обрыв продольной арматуры в пролёте. Построение эпюры арматуры…. 16 3. Расчет сборного ригеля поперечной рамы ………………………………. 20 3.1 Расчёт колонны на сжатие…………………………………………………… 20 3.2 Расчёт колонны консоли……………………………………………………... 24 Литература ……………………………………………………………………. 27 1. Расчёт плиты на прочность
Для сборного железобетонного перекрытия, представленного на плане, требуется рассчитать сборную ребристую плиту с ненапрягаемой арматурой в продольных ребрах. Сетка колонн Расчетное сопротивление тяжёлого бетона класса В20
осевому сжатию при расчёте по предельным состояниям первой группы (на прочность) Основные размеры плиты:-длина плиты l П = l К - 50 мм =6400 – 50 = 6350 мм ; - нормальная ширина В = l /5 = 5700/5 = 1140 мм ; - конструктивная ширина В1 = В -15 мм = 1140 -15 = 1125 мм . Высоту плиты ориентировочно определяем по формуле, принимая всю нагрузку длительной:
с = 30 – при армировании сталью класса А300
b = 300 мм – предварительно принимаемая ширина сечения ригеля
θ = 1,5 Принимаем h = 450 мм > l п /15 = 423мм . 1.1 Расчёт полки плиты . Толщина полки принята h / f = 50 мм . Пролет полки в свету l 0 = В1 -240 мм = 1125-240 = 885 мм . Расчетная нагрузка на 1 м2 полки: Постоянная с а) вес полки б) вес пола и перегородок Итого постоянная нагрузка: g0 = 1,375+2,75 = 4,125 кН/м2 Временная нагрузка с
Полная постоянная нагрузка с
Изгибающий момент в полке (в пролете и на опорах) по абсолютной величине равен: Полка армируется сварными сетками из проволоки А400Расчетное сопротивление Rs = 355МПа
b = 1000 мм
Процент армирования полки: Проверяем усилие:
условие соблюдается, так как Нижние (пролётные) и верхние (надопорные) сетки принимаем:
1.2 Расчёт поперечного торцевого ребра
Каждое поперечное торцевое ребро армируется U –образными сварным каркасом с тремя продольными стержнями ø6А400 и поперечными стержнями ø4В500 с шагом 100 мм .
1.3 Расчёт продольных рёбер Продольные ребра рассчитываются в составе всей плиты, рассматриваемой как балка П-образного сечения с высотой h
= 450 мм
и конструктивной шириной В1
= =1125 мм
(номинальная ширина В
= 1,14 м
). Толщина сжатой полки Расчетный пролет при определении изгибающего момента, принимается равным расстоянию между центрами опор на ригелях: l = lК -0.5b = 6,4-0,5×0,3 = 6,25м Расчетный пролет при определении поперечной силы: l0 = lк – b = 6,4 - 0,3 = 6,1 м , где b = 0,3м – предварительно принимаемая ширина сечения ригеля. Нагрузка на 1пог. м плиты считаем только из условия прочности (первая группа предельных состояний). Постоянная
p = 25 кН/м Временная Полная Усилия от расчетной нагрузки для расчета на прочность:
Расчет прочности нормальных сечений . Продольная арматура в ребрах принята класса А300 , расчетное сопротивление RS = 270 МПа . Сечение тавровое с полкой в сжатой зоне; расчетная ширина полки b/ f = B1 – 40 мм = 1125 – 40 = 1085 мм ; h0 = h – a = 450 – 50 = 400 мм .Пологая, что нейтральная ось лежит в полке, имеем
Проверяем усилие:
условие соблюдается, так как Принимаем продольную арматуру 4ø20А300 Аs = 1256мм2 (+6,5%) Расчет прочности наклонных сечений на поперечную силу. Поперечная сила на грани опоры Бетон В20 ( Предварительно принимаем 1. Проверка на прочность наклонной сжатой полосы
т.е. прочность полосы обеспечена 2. Проверка прочности наклонного сечения
Поскольку
Поскольку
принимаем c = 3h 0 =1200 мм ; с0 = 2h 0 =800 мм .
Проверка условия
Проверка требования
Определение приопорного участка (аналитический способ). При равномерно распределённой нагрузке длина приопорного участка определяется в зависимости от:
Поскольку
Так как
поскольку
Таким образом длина приопорного участка будет:
2. Расчёт сборного ригеля поперечной рамы.
2.1. Дополнительные данные.
Бетон тяжелый, класса В20
, коэффициент условий работы бетона 2.2. Расчётные пролёты ригеля. Предварительно назначаем сечение колонн 400×400 мм (hc = 400 мм ), вылет консолей lc = 300 мм . Расчетные пролеты ригеля равны: -крайний пролет l1 = l - 1,5hc - 2lc = 5,7 - 1,5×0,4 - 2×0,3 = 4,5 м -средний пролет l 2 = l - hc - 2l c = 6,8 - 0,4 - 2×0,3 = 4,7 м. 2.3. Расчётные нагрузки.
Нагрузка на ригель собирается с грузовой полосы шириной lк = 6,4 м , равной расстоянию между осями ригелей. а) Постоянная нагрузка ( с вес железобетонных плит с заливкой швов: 0,95×1,1×3,0×6,4 = 20,064 кН/м вес пола и перегородок: 0,95×1,1×2,5×6,4 = 16,72 (кН/м) собственный вес ригеля сечением b × h = 0,3×0,65 м : 0,95×1,1×0,3×0,65×25=3,92 кН/м итого постоянная нагрузка g = 40,704 кН/м ; б) Временная нагрузка с коэффициентом снижения к1
=0,9 ( с р = 0,95×0,9×1,2×14×6,4 = 81,87 кН/м . Полная расчетная нагрузка: q = g + p = 122,57 кН/м . 2.4. Расчётные изгибающие моменты. В крайнем пролете:
На крайней опоре:
В средних пролетах и на средних опорах
Отрицательные моменты в пролетах при p/g = 81,87/40,704 =2,011 в крайних пролетах для точки 4 при
в среднем пролете для точки 6 при
2.5. Расчётные поперечные силы.
На крайней опоре На опоре В слева На опоре В справа и на средних опорах
2.6. Расчёт ригеля на прочность по нормальным сечениям.
Для бетона класса В20
и арматуры класса А300
h = h 0 + a = 411,975+65=476,975 мм , принимаем h = 600 мм (b/h = 0,5 мм ). Расчет арматуры Расчетное сопротивление арматуры класса A 300 : RS = 270 МПа . а)Крайний пролет . М1 = 206,83 кНм; b = 300 мм ; h = 600 мм ; h 0 = h - a = 600-60 = 540 мм (арматура расположена в два ряда по высоте)
принимаем арматуру: 2ø22 А300+2ø25 А300 Аs = 760+982=1742 мм2 (+5,34%) Проверяем выполнение условия б) Средний пролет . М2 = 169,223 кНм; b = 300 мм ; h = 600 мм ; h 0 = h - a = 600-55 = 545 мм (арматура расположена в два ряда по высоте)
принимаем арматуру: 2ø20 А300+2ø22 А300 Аs = 1388 мм2 (+8,86%) в) Средная опора . МВ = МС = М = 169,223 кНм ; b = 300 мм ; h = 600 мм ; h 0 = h - a = 600-65 = 535 мм (однорядная арматура);
принимаем арматуру: 2ø32 А300 Аs = 1609 мм2 (+19,5%). г) Крайняя опора. МА = 124,102 кНм ; h 0 = h - a = 600-65 = 535 мм (однорядная арматура);
принимаем арматуру: 2ø25 А300 Аs = 982 мм2 (+6,2%) д) Верхняя пролетная арматура среднего пролета по моменту в сечении 6. М6 = 62,27 кНм; b = 300 мм ; h = 600 мм ; h 0 = h - a = 600-35 = 565 мм (арматура однорядная);
принимаем арматуру: 2ø18 А300 Аs = 509 мм2 (+17%). е) Верхняя пролетная арматура крайнего пролета по моменту в сечении 4 . М4 = 49,64 кНм; b = 300 мм ; h = 600 мм ; h 0 = h - a = 600-35 = 565 мм (арматура однорядная);
принимаем арматуру: 2ø16 А300 Аs = 402 мм2 (+17%). 2.7. Расчёт ригеля на прочность по наклонным сечениям на действие поперечных сил.
Каждый ригель армируется одним плоским сварным каркасом с односторонним расположением рабочих продольных стержней при наибольшем диаметре их d=32мм. Поперечные стержни пролётных каркасов принимаем из арматуры класса А400. Из условия обеспечения доброкачественной точечной сварке при максимальном диаметре продольных стержней в = 32 мм
, во всех пролётах принимаем поперечную арматуру ø8 А400
с RSW
= 285 МПа
. Имеем: Бетон тяжелый, класса В20
(Rb
= 11,5 МПа
; Rbt
= 0,90 МПа
; Сечение балки при расчёте на Q рассматривается прямоугольное с размерами: b =300 мм и высотой h = 600 мм , рабочая высота h0 сечения берётся в зависимости от приопорного участка. Средняя опора.
Предварительно принимаем 1. Проверка обеспечения прочности по наклонной сжатой полосе между наклонными трещинами по условию:
303360 Н ≤ 450225 Н 2. Проверка прочности наклонного сечения
Поскольку
Поскольку
принимаем c = 1188,4 мм ; с0 = 2h 0 =1070 мм .
Проверка условия
Проверка требования
Определение приопорного участка (аналитический способ). При равномерно распределённой нагрузке длина приопорного участка определяется в зависимости от:
Поскольку Так как
Крайняя опора.
Предварительно принимаем 2. Проверка обеспечения прочности по наклонной сжатой полосе между наклонными трещинами по условию:
248200 Н ≤ 553725 Н 2. Проверка прочности наклонного сечения
Поскольку
Поскольку
принимаем c = 1188,4 мм ; с0 = 2h 0 =1070 мм .
Проверка условия
Проверка требования
Определение приопорного участка (аналитический способ). При равномерно распределённой нагрузке длина приопорного участка определяется в зависимости от:
Поскольку Так как
поскольку
Таким образом длина приопорного участка будет:
2.8. Обрыв продольной арматуры в пролёте. Построение эпюры арматуры.
По изложенному выше в пункте 2.6 расчету определяется площадь продольной рабочей арматуры в опасных участках сечения: в пролетах и на опорах, где действует наибольшие по абсолютной величине моменты. Для определения места обрыва продольной арматуры строятся огибающая эпюра изгибающих моментов от внешних нагрузок и эпюра арматуры, представляет собой изображение несущей способности сечений ригеля Мult . Моменты в пяти точках определяются по формуле:
Расчетные моменты эпюры арматуры, которые может воспринять балка в каждом сечении при имеющихся в этих сечениях растянутой арматуры, определяется по формуле:
AS - площадь арматуры в рассматриваемом сечении;
Место действия обрыва стержней отстоит от теоретического на расстоянии W , принимаемом не менее 20d и не менее величины, определяемой по формуле:
Q - расчетная поперечная сила в месте теоретического обрыва стержня; Qsw - усилие в поперечных стержнях на единицу длины элемента на рассматриваемом участке. d - диаметр обрываемого стержня. При правильном подборе и распределении продольной арматуры по длине ригеля эпюра арматура MU повсюду охватывает огибающюю эпюру моментов M , нигде не врезаясь в нее, но и не удаляясь от нее слишком далеко в расчетных сечениях. В таком случае во всех сечениях ригеля, будет выполнятся условие прочности по моменту M < MU и обеспечения экономичности расходование арматуры.
*Отрицательный момент Нулевые точки эпюры положительных моментов располагаются на расстояниях 0,1·l 1 = 0,45м от грани левой опоры и моментов и 0,125·l 1 = 0,5625 м от грани правой опоры. На положительные моменты На наибольший положительный момент M1 принята арматура 2ø22 А300+2ø25 А300 Аs = 760+982=1742 мм2 .
Ввиду убывания положительного момента к опорам, часть арматуры можно не доводить до опор, оборвав в пролете. Рекомендуется до опор доводить не менее 50% расчетной площади арматуры. Примем, что до опор доводится 2ø25 А300 с Аs = 982 мм2 . Момент М U , отвечающий этой арматуре, получим пропорционально ее площади
На отрицательные моменты На момент М4
принята арматура 2ø32 А300
с Аs
= 1609 мм2.
Принимаем
На момент МА принята арматура 2ø25 А300 с Аs = 982 мм2 .
На отрицательные пролетные моменты. На момент М4
принята арматура 2ø16 А300
с Аs
= 402мм2
.Принимаем
Ординаты Обрываемые пролетные и опорные стержни заводятся за место теоретического обрыва на величину W . Расстояние от опорных стержней до мест теоретического обрыва стержней определяется из эпюры графически. В сечении каркаса (dsw = 8 мм ; Аsw1 = 50,3мм2 ; А sw = 100,6 мм2 ; Rsw = 285 МПа )
Значения W будут: -для пролетных стержней 2ø25 А500 слева справа -для надопорных стержней слева 2ø28А300
справа 2ø32А300
Принято W1 = 600 мм; W2 =400 мм ; W3 =900мм; W4 =600 мм.
3. Расчёт сборной железобетонной колонны.
3.1. Расчёт колонны на сжатие.
Полная грузовая площадь для одной внутренней колонны составит
Подсчет нагрузок на грузовую площадь сведен в таблицу. Нагрузку от собственного веса конструкций покрытия и междуэтажных конструкций принимаем по данным предыдущего расчёта. Колонну принимаем сечением 500×500 мм . Собственный вес колонны длиной 6 м с учетом веса двухсторонней консоли будет: нормативный - 0,95[0,5×0,5×6,0+(0,3×0,6+0,3×0,3)·0,4]·25 = 38,19 кН расчетный - 1,1×38,19 = 42,009 кН . Расчет колонны по прочности на сжатие производим для двух схем загружения: Расчет колонны по условиям первой схемы загруженияЗа расчетное принимаем верхнее сечение колонны 1-го этажа, расположенное на уровне оси ригеля перекрытия этого этажа. Расчет выполняется на комбинацию усилий Mmax -N , отвечающую загружению временной нагрузкой одного из примыкающих к колонне пролетов ригеля перекрытия 1-го этажа и сплошному загружению остальных перекрытий и покрытия. а) Определение усилий в колонне. Расчетная продольная сила N . Постоянная и временная нагрузки на одну внутреннюю колонну от покрытия и всех межэтажных перекрытий, кроме того перекрытия 1-го этажа, собирается с полной грузовой площади 36,48 м2 . Постоянная нагрузка от перекрытия 1-го этажа собирается с полной грузовой площади.
Временная нагрузка на перекрытие 1-го этажа собирается с половины грузовой площади, учитывается полосовое ее расположение через пролет. Расчетная продольная сила N в расчетном сечении колонны с учетом собственного веса двух ее верхних этажей, расположенных выше рассматриваемого сечения:
Расчетный изгибающий момент М. Для определения момента М в расчетном сечении 1 колонны временную нагрузку на ригеле перекрытия 1-го этажа располагаем в одном из примыкающих к колонне пролетов. Величина расчетной временной нагрузки р на 1 м длины ригеля с учетом коэффициента снижения к2 = 0,85.
Расчетные высоты колонн будут: - для первого этажа Н1 =Н1эт +0.15- hпол -hпл -hРиг /2 = 6,0+0,15-0,1-0,45-0,5/2 = 5,35 м . для второго этажа Н2 =Н2эт = 6,0 м. Линейные моменты инерции: колонны сечением 500×500 мм : Для первого этажа Для второго этажа -ригеля сечением 300×600 мм , пролетом l = 5,7 м :
Расчетный изгибающий момент М в расчетном сечении колонны по формуле:
б) Расчет колонны по прочности . Принимая условно всю нагрузку длительно действующей, имеем Для тяжелого бетона класса В15 имеем расчетное сопротивление бетона Rb = 0,9×8,5 = 7,65 МПа , модуль упругости бетона Е b = 20500 МПа . Для продольной арматуры класса А300 расчетное сопротивление Rs =Rsc = 270 МПа; модуль упругости Еs = 200000 МПа. h0 =h-a = 500-50 = 450 мм (предварительно а = 50 мм ).
Так как Задаёмся μ
= 0,018 Жесткость колонны
Поскольку
Допускается принимать
Проверка
Расчет колонны по усилиям второй схемы загружения. За расчетное принимается нижнее сечение колонны 1-го этажа, расположенное на уровне верха фундамента. Расчет выполняется на комбинацию усилий Nmax -M , отвечающих сплошному загружению временной нагрузкой всех междуэтажных перекрытий и покрытия. а) Определение усилий в колонне. Расчетная продольная сила N. Постоянная и временная нагрузка на одну внутреннюю колонну от покрытия и всех перекрытий собираются с полной грузовой площади. Учитывается также собственный вес колонны высотой в четыре этажа. На основании данных таблицы получим: N=347,15+4×775,48+5×42,009=3313,85 кН. Расчетный изгибающий момент М. Поскольку здание имеет жесткую конструктивную схему и пролеты ригеля, примыкающие к рассматриваемой колонне слева и справа, равны, то при сплошном загружении временной нагрузкой покрытия и всех междуэтажных перекрытий изгибающий момент в сечении колонны будет равен нулю. б) Расчет колонны на прочность В нижнем сечении колонны 1-го этажа действует продольная сила N = 3313,85 кН. Изгибающий момент в сечении М=0 . Поскольку расчетный эксцентриситет с0 =М/ N =0, сечение рассчитывается на сжатие продольной силой N = 3313,85 кН , приложенной со случайным эксцентриситетом е0 . Расчётная длина колонны и фактическая длина l 0 = l = H 1 =5,35 м. Так как вся временная нагрузка принята длительной то Nl = N =3313,85 кН. При Nl
/
N
=1 и l
0
/
h
=16,7 для тяжелого бетона находим
Таким образом, в результате проведённых расчётов видим, что А s,tot = 6421 мм 2 > As +As ’ = 2×3149,852 = 6299,7 мм 2 Поэтому продольную рабочую арматуру подбираем по наибольшей требуемой площади А s , tot = 6421 мм2 Принимаем 8ø32А300 Аs = 6434 мм2 (+0,2%) 3.2.Расчет консоли колонны.
Консоль колонны предназначена для опирания ригеля рамы. Консоли колонны бетонируются одновременно с ее стволом, поэтому выполняется также из тяжелого бетона класса В15 имеем расчетное сопротивление бетона Rb =7,65 МПа , Rbt =0,675 МПа , модуль упругости бетона Е b =20500 МПа . Продольная арматура выполняется из стали класса A300 с расчетным сопротивлением R s =270 МПа . Поперечное армирование коротких консолей выполняется в виде горизонтальных двухветвевых хомутов из стержней диаметром 8 мм класса А240 . Модуль упругости поперечных стержней Еs =200000 МПа. Консоль воспринимает нагрузку от одного междуэтажного перекрытия с грузовой площади ω/2=18,36 м2 . Расчетная поперечная сила передаваемая на консоль, составляет: Q=764,164/2=382,082 кН . Принимаем вылет консоли lc
=300 мм
, высоту сечения консоли в месте примыкания ее к колонне, h
=600 мм
. Угол наклона сжатой грани консоли к горизонту h0 =h-a=600-35=565 мм . Поскольку lc =300<0.9h=513 мм , консоль короткая. Расстояние от приложения силы Q до опорного сечения консоли будет: a=lc -lsup /2=300-240/2=180 мм. Проверяем прочность бетона на смятие под опорной площадкой:
Проверяем условие прочности по наклонной сжатой полосе:
Принимаем шаг горизонтальных хомутов Sw =150 мм Asw =nAsw1 =2×50,3=100,6 мм2
Проверяем условие прочности:
Определяем площадь продольной арматуры Аs . Момент в опорном сечении, взятый с коэффициентом 1,25, равен: М=1,25×Q×a=1,25×382,082×0,18 = 85,968 кНм . Площадь сечения арматуры будет равна: Принимаем 2ø12А300 Аs = 628 мм2 (+0,3%) Список используемой литературы 1. СНиП 2.03.01-84* Бетонные и железобетонные конструкции /Госстрой России.- М.: ГУП ЦПП. 2000 2. СНиП 2.01.07-85* Нагрузки и воздействия /Минстрой России.- СССР.- М.: ГУП ЦПП. 1996. 3. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции. Общий курс. Издание пятое. – М.: Стройиздат, 1991. 4. Сахновский К.В. Железобетонные конструкции. Издание восьмое. – М.: Госстройиздат, 1959 5. Киселёв Н. Н., Ишаков В.И. Расчёт железобетонных конструкций многоэтажного производственного здания / Учебное пособие /Издание второе. – Н.Новгород, 2001 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

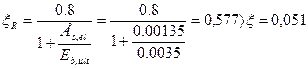
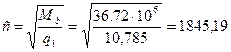 мм
> 3h
0
=1200 мм
мм
> 3h
0
=1200 мм
 мм
> S
1
= 125 мм
.
мм
> S
1
= 125 мм
.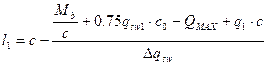 , где
, где 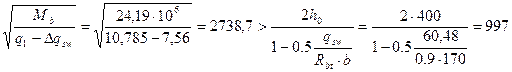 то:
то: , принимаем
, принимаем 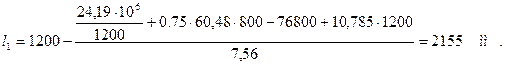
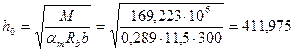 мм
мм
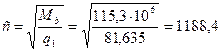 мм
< 3h
0
=1605 мм
мм
< 3h
0
=1605 мм
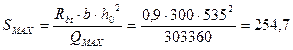 мм
> S
1
= 150 мм
.
мм
> S
1
= 150 мм
.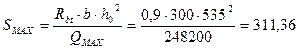 мм
> S
1
= 200 мм
.
мм
> S
1
= 200 мм
. , где
, где 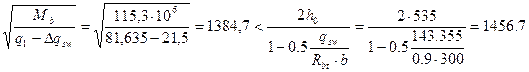 то:
то: , принимаем
, принимаем 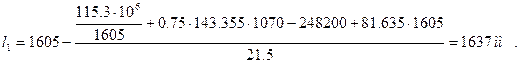
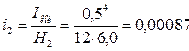 м3
.
м3
.
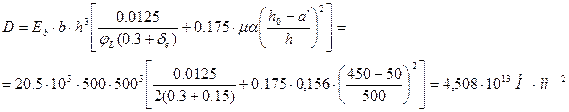
 ;
;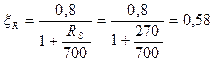

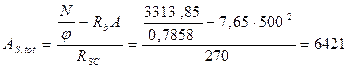 мм2
мм2