|
Р. А. Мартусевич
В статье доказывается возможность изъятия победителем конкурса за право быть естественным монополистом положительной монопольной ренты на рынке с линейным спросом. Для этого модифицируется модель конкурса за концессии с единственным критерием минимума цены, построенная для абсолютно неэластичного спроса. Определяется условие, когда верна гипотеза Г. Демсетца о равенстве цены победителя его ожидаемым удельным издержкам.
В 1968 г. на основе предложенной Эдвином Чадвиком идеи «конкуренции за рынок» [4, 381–420] американский экономист Гарольд Демсетц в статье «Why Regulate Utilities?» («Зачем регулировать коммунальные предприятия?») развил теорию торгов за франшизу, т. е. за право быть естественным монополистом, и предложил ее в качестве решения проблемы регулирования тарифов естественных монополий [6, 55–65]. Демсетц утверждает, что недостаток традиционного подхода к регулированию естественных монополий заключается в неспособности провести различие между ex ante количеством участников торгов за право поставки и ex post условиями последней.
Демсетц пришел к следующим важным выводам:
— если предположить, что имеется много квалифицированных и не склонных к сговору участников торгов за контракт (франшизу), который будет за-ключен с тем из них, кто предложит наименьшую удельную цену поставки, то «цена победителя будет незначительно отличаться от удельных издержек производства» (и таким образом, по его мнению, будет полностью решена проблема регулирования тарифов на продукцию и услуги естественных монополий);
— то есть даже если соображения эффективности могут требовать наличия ex post одного продавца в отрасли с естественной монополией, нерегулируемые рыночные цены могут быть свободными от элементов монополии (монопольной ренты).
В более поздней своей статье, опубликованной в 1971 г., Демсетц уже прямо заявляет о равенстве цены и удельных издержек и о нулевой экономической прибыли, получаемой победителем торгов, возможно, предполагая постоянное наличие совершенной конкуренции на исследуемом рынке прав быть естественным монополистом [5, 356–363]. Там же он приводит следующий график (рис. 1).
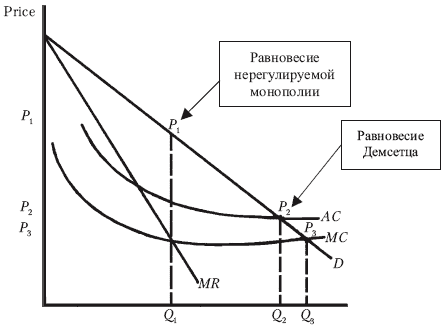
Рис. 1. Равновесия Демсетца и нерегулируемой монополии:
P 1 и Q 1 — цена и выпуск нерегулируемой монополии; P 2 и Q 2 — равновесие Демсетца; P 3 и Q 3 — идеал теории общественного благосостояния; MR — кривая предельного дохода (marginal revenue); MC — кривая предельных издержек (marginal cost); в — кривая спроса (см.: Demsetz. On the Regulation of Industry...)
Конкурс с единственным критерием минимума цены при абсолютно неэластичном спросе на продукцию концессионера
В работе [1] доказано, что в конкурсе с единственным критерием минимума цены при абсолютно неэластичном спросе в ситуации, когда все участники конкурса максимизируют математическое ожидание прибыли, ожидаемой от реализации выставленного на конкурс концессионного проекта, в отсутствие какого-либо знания издержек конкурентов, гипотеза Демсетца неверна, поскольку победитель конкурса неизбежно получит положительную монопольную ренту [1, 43–78].
А равновесие, описанное Демсетцем (P* = P 2, Q* = Q 2), действительно до-стигается при абсолютно неэластичном спросе, когда все участники максимизируют вероятность выигрыша конкурса в отсутствие какого-либо знания об издержках конкурентов и их стратегий [1, 43–78].
Заметим, что предпосылка об абсолютно неэластичном спросе в отраслях естественной монополии имеет право на самостоятельное существование. Действительно, во многих отраслях естественной монополии, относящихся к отраслям жизнеобеспечения, спрос может быть абсолютно неэластичным. В част-ности, это весьма правдоподобная ситуация для концессий в инфраструктурных отраслях жизнеобеспечения (теплоснабжение, водоснабжение, водоотведение и т. д.). Например, речь может идти о строительстве по схеме ВОТ (Build-Operate-Transfer) или ВТО (Build-Transfer-Operate) станции очистки сточных вод, поступающих исключительно от жителей нового жилого микрорайона. Другой пример — реконструкция на концессионной основе котельной, поставляющей теплоноситель исключительно для отопления жилых домов этого микрорайона. Можно ожидать, что в этих случаях фактический годовой объем спроса будет постоянным либо незначительно или предсказуемо отклоняться от ожидаемой величины.
Таким образом предпосылка об абсолютно неэластичном спросе, использованная в модели Мартусевича (2007), вовсе не является надуманной.
Напомним также, что ситуацию естественной монополии определяет в первую очередь субаддитивность затрат [3], а вовсе не наклон кривой спроса, что делает удовлетворение рыночного спроса одной фирмой более дешевым в сопоставлении с двумя и более фирмами.
Однако предпосылка об абсолютно неэластичном спросе больше соответствует конкурсам за государственные контракты подряда. При абсолютно неэластичном спросе: а) выпуск нерегулируемого монополиста не ниже социально оптимального; б) в отсутствие регулирования отсутствуют потери в общественном благосостоянии (потери мертвого груза), происходит лишь перераспределение излишка потребителя в пользу производителя. Таким образом, в ситуации абсолютно неэластичного спроса теряют силу некоторые стандартные аргументы в пользу регулирования тарифов естественных монополий. Но ограниченность анализа, основанного на предпосылке об абсолютно неэластичном спросе, заключается не столько в том, что она не соответствует стандартному представлению о естественно-монопольных рынках, сколько в том, что она не отражает реальной ситуации во многих отраслях естественной монополии, сталкивающихся с эластичным спросом (рис. 1). Поэтому представляется актуальным рассмотреть также конкурсы за концессии в отраслях естественных монополий, реализация которых потребует от концессионера удовлетворения спроса, отличного от абсолютно неэластичного.
В настоящей статье мы покажем справедливость приведенных выше выводов относительно гипотезы Демсетца при линейном спросе.
Модель конкурса с единственным критерием минимума цены
при линейном спросе на продукцию концессионера
Откажемся от предпосылки об абсолютно неэластичном спросе. Чтобы быть способными рассуждать о величине монопольной ренты и результатах конкурса, мы вынуждены ввести дополнительные предпосылки о виде функций спроса и издержек. Предположим, что для каждого участника конкурса (например, i-го) верно следующее:
1) оценка обратной функции спроса представляет линейную функциональную зависимость: P в (x i ) = a — bx i , где a, b > 0; x i — планируемый объем выпуска i-го участника конкурса в случае победы;
2) фирмы различаются лишь постоянными издержками, тогда как переменные издержки определяются господствующей технологией (например, технология задается самой передаваемой в концессию системой (или объектом) инфраструктуры и/или достигнутым в обществе уровнем знаний) и одинаковы у всех фирм 1 ;
3) функция совокупных издержек есть сумма постоянных и переменных издержек: ТС i (x i ) = CF 0 + FC i + cx i , где c, FC i > 0; CF 0 — фиксированная величина взимаемой концедентом концессионной платы (для простоты положим CF 0 = 0); FC i — оцениваемые i-м участником конкурса постоянные издержки (не включают CF 0; с — его переменные (предельные) издержки, связанные с реализацией концессионного соглашения.
В модели мы рассмотрим две различные ситуации:
— все участники конкурса максимизируют ожидаемую прибыль в отсутствие какого-либо знания издержек своих конкурентов и их бизнес-стратегий (ситуация № 1);
— все участники конкурса максимизируют вероятность выигрыша в отсутствие какого-либо знания издержек конкурентов и их бизнес-стратегий (ситуация № 2).
Все остальные предпосылки (кроме предпосылки об абсолютно неэластичном спросе) модели Мартусевича (2007) остаются неизменными. В частности, предполагается, что в конкурсе с единственным критерием минимума цены принимает участие не менее двух фирм, и в соответствии с Федеральным законом от 21.07.2005 № 115-ФЗ «О концессионных соглашениях» концедент произвольно устанавливает максимально допустимый уровень цены P 0.
Сформулируем следующую лемму.
Лемма 1. Кривые удельных издержек участников конкурса не пересекаются. При этом чем выше постоянные издержки, тем выше проходит кривая удельных издержек.
Доказательство тривиально и вытекает из вида функций совокупных издержек участников конкурса.
Рассмотрим теперь логику принятия решений i-м 2 участником конкурса.
1. Возможны три случая: а) при любом значении выпуска максимальная готовность платить ниже средних издержек; б) максимальная готовность платить равна средним издержкам при единственном значении выпуска; в) на непустом множестве объемов выпуска максимальная готовность платить выше средних издержек (рис. 2).
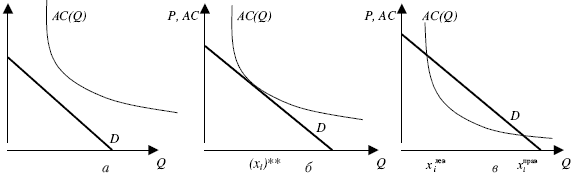
Рис. 2. Варианты расположения кривых спроса и удельных издержек
относительно друг друга:
P — цена; AC — удельные издержки; Q — объем выпуска; в — спрос
Рассмотрим наиболее эффективного участника конкурса. Сразу исключим из анализа случай на рис. 2, а, когда его кривая АС лежит выше кривой спроса, так как при этом при любом объеме производства даже самый эффективный потенциальный участник имел бы гарантированный убыток. Исключим также случай на рис. 2, б, при котором гарантированный убыток имел бы следующий по эффективности участник (в силу леммы 1) и наш самый эффективный участник остался бы один, тогда как, по предположению, в конкурсе участвуют не менее двух участников. Таким образом, необходимо рассмотреть лишь один случай, соответствующий рис. 2, в.
2. Найдем минимальную цену, которую может назначить i-й участник конкурса, и соответствующий ей объем выпуска.
Минимальная цена будет определяться равенством цены и удельных издержек: P в (x i ) = TC i (x i )/x i = АC i (x i ) (предложив цену ниже определяемого таким образом уровня, i-й участник конкурса будет терпеть убытки).
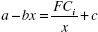 , (1.1) , (1.1)
bx 2 = (c - a) x + FC i = 0,
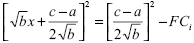 . (1.2) . (1.2)
Из условия (1.2) определяется объем выпуска, при котором пересекаются кривые спроса и удельных издержек. В зависимости от знака правой части равенства возможны три случая.
Случай 1. Для i-й фирмы 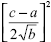 < FC i , т. е. кривая удельных издержек лежит выше кривой спроса, не имея точек касания или пересечения. Такая фирма отказывается от участия в конкурсе. Данный случай представлен на рис. 2, а, и мы его исключили из дальнейшего анализа. < FC i , т. е. кривая удельных издержек лежит выше кривой спроса, не имея точек касания или пересечения. Такая фирма отказывается от участия в конкурсе. Данный случай представлен на рис. 2, а, и мы его исключили из дальнейшего анализа.
Случай 2. Для i-й фирмы 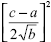 = FC i , т. е. кривые спроса и удельных издержек касаются в единственной точке с объемом выпуска = FC i , т. е. кривые спроса и удельных издержек касаются в единственной точке с объемом выпуска  . В этом случае единственное значение цены, которое такая фирма может указать в конкурсном предложении, это (Pi)** = AC i ((x i )**) = (a + c)/2. Для такой фирмы подобная комбинация цены и выпуска максимизирует как ожидаемую прибыль, так и вероятность выигрыша. Данный случай представлен на рис. 2, б, и его мы также исключили из дальнейшего анализа. . В этом случае единственное значение цены, которое такая фирма может указать в конкурсном предложении, это (Pi)** = AC i ((x i )**) = (a + c)/2. Для такой фирмы подобная комбинация цены и выпуска максимизирует как ожидаемую прибыль, так и вероятность выигрыша. Данный случай представлен на рис. 2, б, и его мы также исключили из дальнейшего анализа.
Случай 3. Для i-й фирмы 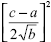 > FC i , т. е. кривые спроса и удельных издержек пересекаются в двух точках (x i лев и x i прав ), между которыми кривая удельных издержек лежит ниже кривой спроса. Заметим, что при объеме выпуска x i лев фирма получит ту же нулевую ожидаемую прибыль, что и при объеме выпуска x i прав , но при вероятности выигрыша существенно меньшем, чем при объеме выпуска x i прав . Следовательно, из двух точек она предпочтет именно правую –. Минимальная цена в этом случае будет определяться подстановкой в обратную функцию спроса объема выпуска . Данный случай представлен на рис. 2, в. > FC i , т. е. кривые спроса и удельных издержек пересекаются в двух точках (x i лев и x i прав ), между которыми кривая удельных издержек лежит ниже кривой спроса. Заметим, что при объеме выпуска x i лев фирма получит ту же нулевую ожидаемую прибыль, что и при объеме выпуска x i прав , но при вероятности выигрыша существенно меньшем, чем при объеме выпуска x i прав . Следовательно, из двух точек она предпочтет именно правую –. Минимальная цена в этом случае будет определяться подстановкой в обратную функцию спроса объема выпуска . Данный случай представлен на рис. 2, в.
3. Найдем теперь для случая 3 максимальную цену, которую может назначить i-й участник конкурса:
Максимальная цена есть минимум из цены нерегулируемой монополии P в ((x i )*) и цены P 0 , устанавливаемой концедентом. Иными словами, возможна ситуация, когда рациональный участник конкурса будет ориентироваться в качестве максимума цены не на Р 0 , как в случае абсолютно неэластичного спроса, а на некоторую более низкую (!) цену.
Найдем значение выпуска (x i )*, которое выбрала бы нерегулируемая монополия для максимизации своей прибыли. Для этого приравняем предельную выручку предельным издержкам: MR(x) = a — 2bx = c = МС(x). Откуда получаем
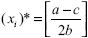 . (1.3) . (1.3)
Заметим, что в этой точке равенство (1.2) не выполняется (при подстановке (x i )* в (1.2), получим в левой части равенства нуль, а в правой его части величину, по условию больше нуля), следовательно, AC i ((x i )*) < P в ((x i )*). Значит, точка выпуска нерегулируемой монополии лежит внутри отрезка кривой спроса, ограниченного точками выпуска x i лев и x i прав .
Лемма 2. Для всех участников конкурса максимальная цена, которую каждый из них захотел бы установить в ситуации нерегулируемой естественной монополии, будет одинаковой.
Доказательство. Из выражения (1.3) видно, что объем выпуска, выбираемый каждым из участников конкурса в ситуации нерегулируемой естественной монополии, не зависит от его постоянных издержек, а следовательно, будет одинаковым у всех участников конкурса. Следовательно, в ситуации нерегулируемой монополии у каждого из них будет одинаковой цена, которую он захочет установить (P mon ) и которая определяется путем подстановки (x i )* в функцию обратного спроса P в (x): P mon = P в (x i )*. Q.E.D.
Ни одному из участников, какова бы ни была его целевая функция, не выгодно устанавливать цену выше P mon , так как это будет сокращать не только прибыль в случае победы, но и вероятность выигрыша. Однако может оказаться и так, что максимум цены, установленный концедентом, Р 0 будет ниже P mon . В этом случае участники конкурса будут ориентироваться не на P mon , а на Р 0 как на максимально возможную цену.
Таким образом, максимум цены, которую может установить каждый из участ-ников конкурса, определяется как минимум из P mon и Р 0 .
4. Найдем оптимальные значения конкурсных предложений для ситуаций 1 и 2, определенных выше.
То, что ни в одной из этих ситуаций ни одному из участников, какую бы целевую функцию он ни имел, не выгодно устанавливать цену выше P mon , показано выше. Покажем теперь, что ни одному из участников не выгодно устанавливать цену на уровне P mon . Для этого заметим, что пересечение кривых спроса и удельных издержек 3 означает доступность для выбора объемов выпуска на отрезке [(х)*, x i прав ].
Докажем следующее утверждение.
Утверждение 1. Участник конкурса, например, i-й, максимизирующий вероятность своего выигрыша при полном незнании издержек конкурентов (ситуация 2), в конкурсе с единственным критерием минимума цены установит цену на уровне правой точки пересечения кривых спроса и удельных издержек (x i прав ).
Доказательство. Действительно, любое отклонение от в сторону увеличения цены снижает вероятность выигрыша, что противоречит целевой функции участника, а любое отклонение в сторону снижения цены приводит к гарантированным убыткам в случае победы в конкурсе. Q.E.D.
Таким образом, для максимизирующих вероятность выигрыша участников конкурса оптимальная цена будет равна (P i )* = a — b x i прав , а экономическая прибыль (монопольная рента ex ante) — нулю.
Рассмотрим конкурсы с единственным критерием минимума цены и ситуацию, когда все участники конкурса максимизируют ожидаемую прибыль, ничего не зная о функциях издержек друг друга (ситуация 1). Этот случай требует построения математической модели конкурса.
Ключевым моментом такой модели является логика рассуждений участника конкурса. Сделаем рациональное предположение, что каждый участник конкурса (например, i-й) размышляет следующим образом.
1. Установив цену ( P i ) в своем конкурсном предложении на уровне своих удельных издержек (AC i (x i прав )), он получит максимальную вероятность своей победы в конкурсе, но экономическая прибыль при этом будет нулевой;
2. Установив цену чуть выше AC i (x i прав ) и пожертвовав, таким образом, некоторой вероятностью выигрыша, он сможет получить положительную экономическую прибыль.
3. Вопрос заключается в том, насколько цена P i должна превысить величину AC i (x i прав ), чтобы математическое ожидание величины прибыли, которую i-й участник конкурса ex ante ожидает получить от реализации выставленного на торги концессионного проекта, стало максимальным.
По аналогии с подходом, предложенным в модели Мартусевича (2007) для абсолютно неэластичного спроса, можно предположить, что i-й участник рационально считает, что значения ключевого параметра (цены), содержащиеся в конкурсных предложениях других участников, являются случайными величинами, которые независимы и одинаково равномерно распределены на отрезке 4 ( AC i (x i прав ), min{ P mon , P 0 }].
Далее предполагается, что все участники конкурса определяют оптимальные значения параметров своих конкурсных предложений, следуя представленной выше логике рассуждений. Если предположить наличие у рассматриваемого i-го участника N – 1 конкурентов ( N ≥ 2), модель будет выглядеть следующим образом.
Для любой цены товара (услуги) P i , указанной в конкурсном предложении i-го участника конкурса и превышающей его удельные издержки ( AC i ≤ P i ≤ P 0 ), его ожидаемая прибыль равна
E (Profit i ) = (P i - AC i (x i ) – CF 0 )*Prob i win + 0 · (1 - Prob i win ), (1.4)
где P i — цена единицы товара (услуги), указанная i-м участником в своем конкурсном предложении; x i — объем выпуска (находится из равенства P i = a — bx i ); AC i (x i ) — ожидаемые удельные издержки 5 i-го участника на производство единицы товара (услуги) при реализации концессионного проекта; Pr ob win i — (субъективно оцениваемая) вероятность выиграть данный конкурс и заключить концессионное соглашение; Pr ofit i = P i — AC i — экономическая прибыль, которую получит i-й участник в случае своей победы; E (Pr ofit i ) — математическое ожидание величины экономической прибыли, которую i-й участник конкурса ex ante ожидает получить от реализации выставленного на конкурс концессионного проекта, указав в своем конкурсном предложении цену на уровне P i .
При сделанных предположениях i-я фирма будет субъективно оценивать свою вероятность выиграть конкурс как
 . (1.5) . (1.5)
5. Докажем следующее утверждение.
Утверждение 2. В ситуации 1 максимизирующий свою ожидаемую прибыль победитель конкурса получит положительную монопольную ренту ex ante, т. е. оптимальная цена, указанная в его конкурсном предложении, будет строго выше цены, определяемой пересечением кривых спроса и удельных издержек при объеме выпуска x win прав.
Доказательство. Без потери общности допустим, что победил i-й участник конкурса. Выпишем функцию ожидаемой прибыли i-го участника конкурса, предполагающего, что значения конкурсных предложений его конкурентов есть независимые случайные величины, равномерно распределенные на отрезке [ AC i (x i прав); min{P 0, P в ((x i )*)}]. Для простоты далее откажемся от использования индекса i.
E(Profit) = [TR(x) – TC(x)]Prob win (P в (x)). (1.6)
Находя условие первого порядка (FOC), продифференцируем это равенство по х — объему выпуска:
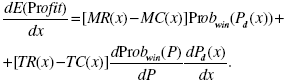 . (1.7) . (1.7)
Найдем значение этой производной в точке x i прав. При цене P = AC(x i прав) второе слагаемое равно нулю. Что касается первого слагаемого, то заметим:
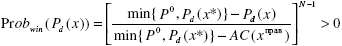 , ,
так как при цене P = AC(x i прав ) субъективно оцениваемая вероятность выиграть конкурс максимальна; MR(x) – MC(x) ≤ 0, поскольку объем выпуска х прав не ниже монопольного объема выпуска (х)*, при котором MR(x) = MC(x).
Таким образом, при х = х прав первое слагаемое не больше нуля, и dE (Pr ofit )/ dx ≤ 0.
Докажем, что для победителя конкурса, имеющего как минимум одного конкурента, это неравенство соблюдается как строгое. Для этого предположим обратное: при х = х прав dE (Pr ofit )/ dx = 0. Из этого следует, что MR(х прав ) – MC(х прав ) = 0. То есть х прав = (х)*, или, иными словами, кривая удельных издержек победителя конкурса лишь касается кривой спроса в точке х = (х)*. В силу леммы 1 кривые удельных издержек остальных участников конкурса лежат выше кривой победителя, а следовательно, выше кривой спроса. Таким образом, остальные участники конкурса, будучи рациональными, не стали бы участвовать в нем. По условию же в конкурсе принимают участие как минимум две фирмы. Мы пришли к противоречию. Следовательно, при х =х прав : dE (Pr ofit )/ dx < 0.
Итак, объем выпуска х = х прав , а следовательно и цена P = AC(х прав ), не оптимальны для победителя конкурса: с уменьшением объема выпуска его ожидаемая прибыль будет возрастать. Оптимальная же цена, при которой его ожидаемая прибыль будет максимальна, будет выше удельных издержек в точке х прав (при меньших объемах выпуска удельные издержки будут выше).
Так как при объеме выпуска х прав ожидаемая прибыль равна нулю, а уменьшение объема выпуска относительно х прав увеличивает прибыль, то, назначив цену, максимизирующую ожидаемую прибыль, победитель конкурса рассчитывает в случае победы получить положительную монопольную ренту ex ante. Q.E.D.
В условиях честной конкуренции обоснованность величины монопольной ренты ex ante, получаемой победителем такого конкурса с единственным критерием минимума цены, и нецелесообразность ее изъятия методами тарифного регулирования аргументируются в [1].
6. Докажем теперь следующее утверждение.
Утверждение 3. Даже если отказаться от предположения о равномерном распределении рассматриваемых независимых одинаково распределенных случайных величин на отрезке ACi(x i прав );min{P 0 , P в ((x i )*)} и допустить любое другое их независимое одинаковое распределение, такое, что субъективно оцениваемая неким участником конкурса случайная величина, равная цене, указанной в конкурсном предложении его соперника, может с ненулевой вероятностью принять значение выше уровня средних издержек рассматриваемого участника (и это будет верно для ценовых предложений каждого из его соперников), то в ситуации 1 данный участник конкурса может рассчитывать на получение положительной монопольной ренты ex ante.
Доказательство. Для простоты положим, что в конкурсе победил участник 1. Тогда формула вероятности его выигрыша в конкурсе примет вид 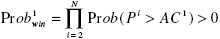 . При подстановке этой вероятности в (1.5) доказательство утверждения 2 сохраняет силу и для доказательства нашего утверждения. . При подстановке этой вероятности в (1.5) доказательство утверждения 2 сохраняет силу и для доказательства нашего утверждения.
Действительно, во-первых, при цене P = AC(х прав ) второе слагаемое в выражении (1.6) всегда равно нулю; во-вторых, и при цене P = AC(х прав ) вероятность выиграть конкурс будет максимальна и строго больше нуля по условию, тогда как при изменении формулы расчета вероятности выиграть конкурс все остальные слагаемые и сомножители в выражении (1.6) не меняют не только знак, но и значение. Таким образом, в точке х = х прав : dE (Pr ofit )/ dx < 0, а поэтому объем выпуска х = х прав , следовательно и цена P = AC(х прав ), не оптимальны для победителя конкурса; оптимальная же цена, при которой его ожидаемая прибыль будет максимальна, будет выше удельных издержек в точке х прав .
Итак, назначив цену, максимизирующую ожидаемую прибыль, победитель конкурса рассчитывает в случае победы получить положительную монопольную ренту ex ante. Q.E.D.
Заметим, что, как следует из модели, если ограничение на цену P ≤ P 0 становится активным, то размер монопольной ренты ex ante, получаемой концессионером, снижается. У концедента может возникнуть естественное желание снизить уровень P 0 по максимуму. Однако это чревато тем, что конкурс может не состояться в силу того, что все потенциальные участники сочтут невыполнимыми его условия (например, они просто не могут произвести требуемый товар (услугу) установленного минимального качества с издержками, не превышающими установленный максимум цены). В частности, нереально низкий потолок цены был одной из причин провала конкурса за концессию водоснабжения в Каракасе (Венесуэла) [3].
Напомним, что с практической точки зрения причиной, по которой российский законодатель ввел требование устанавливать в конкурсной документации максимальный порог цены, в первую очередь являются ограничения по приемлемости (affordability) тарифов, выход за которые сделает жизненно важные инфраструктурные ресурсы (услуги) недоступными для существенной доли населения с точки зрения их платежеспособности.
Решая практическую задачу выбора концедентами уровня P 0 , можно предложить следующее: если речь идет о передаче в концессию нормально функционирующей системы или объекта инфраструктуры (например, канализационных очистных сооружений) без обязательств по новому строительству, то максимальное значение цены целесообразно устанавливать на уровне цены, по которой до проведения конкурса продавала этот товар (услугу) фирма — естественный монополист 6 (чаще всего муниципальное или государственное предприятие, когда-то получившее право эксплуатировать коммунальную инфраструктуру без конкурса). Такой подход дает дополнительное преимущество: для потребителей он делает наглядными выгоды от проведения конкурса.
Практическая проблема с такой рекомендацией может, однако, заключаться в том, что регулируемые цены (тарифы), по которым муниципальное или государственное предприятие работало до конкурса, возможно, не позволяли ему полностью возмещать свои обоснованные издержки. В таком случае нет никакой уверенности, что даже самое эффективное предприятие сможет работать безубыточно с такими тарифами.
Следовательно, прежде чем проводить конкурс и устанавливать максимальное значение цены, следует дать возможность действующему в отрасли предприятию в течение нескольких лет (хотя бы двух-трех!) поработать на безубыточном уровне. Возможно, это потребует роста тарифов. Например, в Буэнос-Айресе перед проведением конкурса за концессию правительство подняло тарифы (на 25 % в феврале 1991 г. и на 29 % в апреле того же года). Такой рост тарифов усилил у участников конкурса уверенность в том, что эффективно функционирующая компания-концессионер сможет получить приемлемую отдачу на вложенный капитал [3].
В настоящей статье построена модель конкурсов за право быть естественным монополистом на рынке с линейным спросом, исследована зависимость результатов таких конкурсов от целевой функции, которую имеют его участники, — максимизации вероятности выигрыша или максимизации ожидаемой прибыли. Показано, что ряд выводов, полученных в модели Мартусевича (2007) для рынка с абсолютно неэластичным спросом, остается верным и в рамках модифицированной модели. Так, сохраняется условие, при котором верна гипотеза Демсетца (1968) о равенстве цены, предложенной победителем его ожидаемым удельным издержкам. Также при отказе от предпосылки об абсолютно неэластичном спросе в пользу линейного спроса остается верным вывод о том, что победитель конкурса, максимизирующий ожидаемую прибыль, неизбежно получит положительную монопольную ренту ex ante.
Примечания
1 На основе опыта автору эта предпосылка представляется более адекватной, чем предпосылка, сделанная в модели Риордана и Саппингтона, об одинаковых постоянных издержках, связанных с реализацией выставленного на конкурс проекта, у всех участников конкурса при различиях лишь в предельных издержках (см. [7, 377]). 
2 В силу симметрии результаты модели не зависят от выбора i. 
3 Выше мы установили, что для победителя конкурса невозможны ситуации, представленные на рис. 2, а и б, следовательно, кривая удельных издержек победителя конкурса обязательно пересечет кривую спроса. 
4 Важно, что в ситуации полной априорной неопределенности у участников конкурса нет оснований предпочитать одно распределение субъективной вероятности другому, равно как и нет оснований отвергать какое-либо распределение. Ведь только потом, по мере получения опыта, можно переоценивать вероятность (правдоподобие) того, что полученные наблюдения являются реализацией того или иного истинного распределения вероятности. Нередко в такой ситуации, т. е. в условиях полного отсутствия априорной информации об этом распределении, в качестве «нулевого приближения» выбирают равномерное распределение вероятностей на некотором отрезке (подробнее см.: Айвазян С. А., Мхиторян В. С. Теория вероятностей и прикладная статистика. М., 2001). При этом можно доказать, что результат конкурса — оптимальное значение цены и соответственно величина монопольной ренты ex ante — не изменится, если рассматриваемый участник будет предполагать, что цены, указанные в конкурсных предложениях его соперников, являются независимыми, одинаково распределенными случайными величинами, каждая из которых распределена равномерно на отрезке [0, min{ P mon, P 0}]. 
5 Следует уточнить, что речь идет об экономических издержках, которые известным образом отличаются от бухгалтерских. 
Список литературы
1.Мартусевич Р. А. Конкурсы за концессии в отраслях естественных монополий и рента победителя // Реформирование общественного сектора: проблемы эффективного управления: Сб. ст. / Под ред. Т. М. Скляр, И. Н. Баранова. СПб., 2007. С. 43–78.
2.Мартусевич Р. А., Сиваев С. Б., Хомченко Д. Ю. Государственно-частное партнерство в коммунальном хозяйстве. М., 2006.
3.Менар К., Крючкова П. В., Кудряшова Е. Н. и др. Контракты и издержки в ресурсоснабжающих подотраслях жилищно-коммунального хозяйства. М., 2000.
4.Chadwick E. Results of Different Principles of Legislation in Europe: Of Competition for the Field as Compared with Competition within the Field of Service // J. of the Royal Statistical Society. Ser. A22 (1859). Р. 381–420.
5.Demsetz H. On the Regulation of Industry: A Reply // J. of Political Economy. 1971. Vol. 79, № 2 (March/Apr.). Р. 356–363.
6.Demsetz H. Why Regulate Utilities? // J. of Law and Economics. 1968. Vol. 11 (Apr.). Р. 55–65.
7.Riordan M. H., Sappington D. Awarding Monopoly Franchises // American Economic Rev. 1987. Vol. 77, № 3 (June). Р. 377.
|