| Дифференциальные уравнения поля поляризации среды физического вакуума
В.В. Сидоренков
На основе концепции Единого поля силового пространственного взаимодействия материальных тел аналитически однозначно установлено, что в физическом вакууме реально и единственно существуют только волны его поляризации, переносящие в пространстве вакуумной среды энергию ее возбуждения, которая при силовом взаимодействии с определенной физической характеристикой (электрической, магнитной или гравитационной) материального тела, создает динамический отклик параметров этого тела, который регистрируется в эксперименте как реальный поток энергии соответствующей физической природы.
К настоящему времени достигнут существенный прогресс в изучения уникального феномена силового пространственного взаимодействия материальных тел, аналитически описываемого структурно тождественными законами Кулона в электромагнетизме и тяготения Мичелла-Кавендиша [1]. Главный результат успеха проведенных исследований [2] состоит в том, что на основе анализа физических характеристик сил пространственного взаимодействия материальных тел в стационарных условиях установлена объективность существования в Природе Единого поля силового взаимодействия этих тел в пространстве физического вакуума, обусловленного поляризацией вакуумной среды при наличии в ней Материи. При этом получены аналитические соотношения для указанного поля взаимодействия [2], структурно тождественно, а главное адекватно описывающие различные по физической природе электрические, магнитные и гравитационные силы в упомянутых выше законах:
 . (1) . (1)
Здесь  - модифицированная постоянная Планка, - модифицированная постоянная Планка,  - скорость света в вакууме [1], - скорость света в вакууме [1],  - потенциальная энергия, - потенциальная энергия, 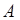 - безразмерный множитель [2]: - безразмерный множитель [2]:  , ,  и и  определяемый произведениям локальных физических параметров двух неподвижных взаимодействующих точечных тел (электрические определяемый произведениям локальных физических параметров двух неподвижных взаимодействующих точечных тел (электрические  и магнитные и магнитные  заряды, m - массы), нормируемого на квадрат той же размерности константы Планка ( заряды, m - массы), нормируемого на квадрат той же размерности константы Планка ( , ,  и и  ), составленных из комбинации других фундаментальных физических констант. ), составленных из комбинации других фундаментальных физических констант.
Чтобы подчеркнуть физическую сущность безразмерного множителя 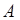 в соотношениях (1), он назван «амплитудой поляризации» среды физического вакуума, и именно только он единственно определяет физическую природу пространственного взаимодействия материальных тел и численное значение силы этого взаимодействия для данного расстояния в соотношениях (1), он назван «амплитудой поляризации» среды физического вакуума, и именно только он единственно определяет физическую природу пространственного взаимодействия материальных тел и численное значение силы этого взаимодействия для данного расстояния  между телами, а саму универсальную векторную силовую функцию между телами, а саму универсальную векторную силовую функцию  назовем «силой поляризации среды физического вакуума». Соответственно, в формулах (1) выражение назовем «силой поляризации среды физического вакуума». Соответственно, в формулах (1) выражение  есть потенциальная энергия взаимодействия частиц вакуумной среды, или говоря более конкретно, это энергия поляризации физического вакуума. Изучение поднятой здесь актуальной фундаментальной проблемы на наш взгляд вполне оправдано, особенно в перспективе при переходе от статических полей к полям динамическим. есть потенциальная энергия взаимодействия частиц вакуумной среды, или говоря более конкретно, это энергия поляризации физического вакуума. Изучение поднятой здесь актуальной фундаментальной проблемы на наш взгляд вполне оправдано, особенно в перспективе при переходе от статических полей к полям динамическим.
Продолжение таких исследований необходимо прежде всего для аналитического обоснования концепции Единого поля силового пространственного взаимодействия тел Материи [2] посредством построения системы дифференциальных уравнений силового поля поляризации физического вакуума, уравнения которой должны стать сущностной первоосновой описания динамических характеристик поведения полей, называемых, следуя существующим на сегодня традиционным представлениям, электрическим, магнитным или гравитационным полем (см. например, [3, 4]). Кстати, концепция Единого поля [2] уже использована опосредованно в работе [4] для вывода систем дифференциальных уравнений электрического, магнитного и гравитационного полей в «пустом» пространстве, где полученные системы уравнений структурно тождественны между собой, и согласно решениям которых, скорость распространения волн всех указанных полей в точности равна скорости света в вакууме.
Теперь же надо в явном виде подтвердить правомерность указанной концепции Единого поля. Говоря более предметно, анализ представленных в работах [2-4] результатов однозначно требует строгой аналитической аргументации по выяснению и обоснованию физического механизма переноса в пространстве физического вакуума потоков электрической, магнитной и гравитационной энергий посредством волн единого поля поляризации вакуумной среды.
Наши рассуждения начнем с того, что рассмотрим формулу поля вектора силы поляризации среды физического вакуума  . Для наглядности соотношение . Для наглядности соотношение  представим в структурно аналогичном, например, закону Кулона в электростатике виде: представим в структурно аналогичном, например, закону Кулона в электростатике виде:  . Здесь . Здесь  есть некая новая фундаментальная физическая величина, которую назовем условно «вакуумным зарядом», подобно электрическому заряду есть некая новая фундаментальная физическая величина, которую назовем условно «вакуумным зарядом», подобно электрическому заряду  в законе Кулона. Поскольку единица измерения электрического заряда в системе физических единиц СИ есть «Кулон»: в законе Кулона. Поскольку единица измерения электрического заряда в системе физических единиц СИ есть «Кулон»:  , то единицу измерения вакуумного «заряда» назовем «Кавендиш»: , то единицу измерения вакуумного «заряда» назовем «Кавендиш»:  . .
Продолжая наши рассуждения, введем понятие вектора напряженности поля поляризации среды физического вакуума  , размерность которого, согласно определению напряженности, должна быть равна , размерность которого, согласно определению напряженности, должна быть равна  - линейной плотности скалярного потенциала, в системе СИ - линейной плотности скалярного потенциала, в системе СИ . Для сравнения размерность напряженностей электромагнитного поля: . Для сравнения размерность напряженностей электромагнитного поля: и и  . При этом видно, что статическое поле . При этом видно, что статическое поле  потенциально, то есть интеграл от такой функции по произвольному замкнутому контуру потенциально, то есть интеграл от такой функции по произвольному замкнутому контуру  равен нулю. Соответственно это условие потенциальности, согласно равен нулю. Соответственно это условие потенциальности, согласно  - теореме Стокса, в дифференциальной форме имеет вид: - теореме Стокса, в дифференциальной форме имеет вид:  . .
Физически логично теперь ввести аналитически понятие отклика среды на воздействие силового поля  в виде вектора в виде вектора  , который назовем полем индукции физического вакуума (аналогично , который назовем полем индукции физического вакуума (аналогично  и и  – потоковым векторам электрической и магнитной индукции в пустоте) и проанализировать его. Здесь константа – потоковым векторам электрической и магнитной индукции в пустоте) и проанализировать его. Здесь константа  записана нами из логических соображений как наиболее физически приемлемая для реализации потокового вектора отклика вакуумной среды. В системе СИ потоковый вектор поля индукции физического вакуума с учетом структуры его аналитики имеет размерность записана нами из логических соображений как наиболее физически приемлемая для реализации потокового вектора отклика вакуумной среды. В системе СИ потоковый вектор поля индукции физического вакуума с учетом структуры его аналитики имеет размерность  с единицами измерения с единицами измерения  , который определяет поверхностную плотность вакуумного «заряда», в отличие от линейного (циркуляционного) вектора напряженности поля поляризации среды физического вакуума , который определяет поверхностную плотность вакуумного «заряда», в отличие от линейного (циркуляционного) вектора напряженности поля поляризации среды физического вакуума  - линейной плотности скалярного потенциала. - линейной плотности скалярного потенциала.
Затем с учетом структуры соотношения 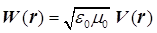 физически интересно найти величину потока вектора индукции вакуумной среды через произвольную замкнутую поверхность S в вакуумном пространстве, равную физически интересно найти величину потока вектора индукции вакуумной среды через произвольную замкнутую поверхность S в вакуумном пространстве, равную   . Как видим, результат мировоззренчески чрезвычайно любопытен, поскольку вне зависимости от объема охватывающей его поверхности S поток поля индукции физического вакуума . Как видим, результат мировоззренчески чрезвычайно любопытен, поскольку вне зависимости от объема охватывающей его поверхности S поток поля индукции физического вакуума  определяется с точностью до коэффициента определяется с точностью до коэффициента  (определяется системой физических единиц) фундаментальной величиной - вакуумным «зарядом» (определяется системой физических единиц) фундаментальной величиной - вакуумным «зарядом»  , индуцированным на этой поверхности. Таким образом, каждая точка пространства физического вакуума обладает «зарядом» , индуцированным на этой поверхности. Таким образом, каждая точка пространства физического вакуума обладает «зарядом»  , который силовым образом взаимодействует с окружением по закону , который силовым образом взаимодействует с окружением по закону  , реализуя поле поляризации вакуумной среды. Очевидно, что полученный результат в определенном смысле физически тривиален, так как это не что иное как аналог теоремы Гаусса в электростатике , реализуя поле поляризации вакуумной среды. Очевидно, что полученный результат в определенном смысле физически тривиален, так как это не что иное как аналог теоремы Гаусса в электростатике  , описывающей результат индуцированной электрической поляризации материальной среды. , описывающей результат индуцированной электрической поляризации материальной среды.
Поскольку значение потока поля индукции физического вакуума не зависит от величины, охватывающей объем пространства поверхности интегрирования, то из определения понятия дивергенции  (теорема Гаусса-Остроградского) следует дифференциальная форма формулы (теорема Гаусса-Остроградского) следует дифференциальная форма формулы  в виде уравнения в виде уравнения   - первого уравнения системы дифференциальных уравнений силового поля поляризации физического вакуума. - первого уравнения системы дифференциальных уравнений силового поля поляризации физического вакуума.
Соответственно из дивергентного уравнения  с учетом известного соотношения векторного анализа с учетом известного соотношения векторного анализа  получаем следующее дифференциальное уравнение получаем следующее дифференциальное уравнение   . Здесь функция . Здесь функция  - это векторный потенциал силового поля поляризации вакуума с единицами измерения в СИ - это векторный потенциал силового поля поляризации вакуума с единицами измерения в СИ  , определяющий линейную плотность вакуумного «заряда». И еще. Поскольку в уравнении , определяющий линейную плотность вакуумного «заряда». И еще. Поскольку в уравнении  вектор вектор  реализуется посредством векторного произведения векторного оператора «Набла» на векторную функцию: реализуется посредством векторного произведения векторного оператора «Набла» на векторную функцию:  , то тем самым однозначно устанавливается, что векторы , то тем самым однозначно устанавливается, что векторы  и и  ортогональны между собой. Во-вторых, в уравнении ортогональны между собой. Во-вторых, в уравнении   , а потому поле вектора , а потому поле вектора  чисто вихревое, и по этой причине можно записать еще одно уравнение для поля другого потокового вектора в виде соотношения кулоновской калибровки: чисто вихревое, и по этой причине можно записать еще одно уравнение для поля другого потокового вектора в виде соотношения кулоновской калибровки:   . .
Заметим, что единица измерения вектора  такова, что при частном дифференцировании по времени такова, что при частном дифференцировании по времени  функции такого потокового вектора функции такого потокового вектора  , он превращается в потоковый вектор поля индукции физического вакуума , он превращается в потоковый вектор поля индукции физического вакуума  . Результат данного рассуждения позволяет предположить наличие функциональной связи между вектором напряженности поля поляризации физического вакуума . Результат данного рассуждения позволяет предположить наличие функциональной связи между вектором напряженности поля поляризации физического вакуума  и его векторным потенциалом и его векторным потенциалом  в виде соотношения: в виде соотношения:
 . (2) . (2)
Данное соотношение очевидно является фундаментальным, поскольку оно структурно аналогично знаковым соотношениям в теории электромагнитного поля:  и и  , а также гравитационного поля , а также гравитационного поля  [4]. С практической точки зрения соотношение (2) должно помочь нам построить последнее уравнение в системе дифференциальных уравнений единого силового поля поляризации физического вакуума. [4]. С практической точки зрения соотношение (2) должно помочь нам построить последнее уравнение в системе дифференциальных уравнений единого силового поля поляризации физического вакуума.
В продолжение наших исследований рассмотрим последовательную цепочку, в которой сначала берется ротор от соотношения (2), а затем после учета уравнения  для векторного потенциала для векторного потенциала  сюда снова подставляется соотношение (2), но уже продифференцированное по времени сюда снова подставляется соотношение (2), но уже продифференцированное по времени  : :
 . (3) . (3)
В итоге имеем последнее четвертое уравнение в искомой системе дифференциальных динамических уравнений единого силового поля поляризации физического вакуума:   . .
Для проверки знака в уравнении  рассмотрим из соотношений (3) его промежуточную версию: рассмотрим из соотношений (3) его промежуточную версию:  . Соответственно, посредством соотношения (2), изменим уравнение . Соответственно, посредством соотношения (2), изменим уравнение  так, чтобы оно с точностью до знака стало структурно симметричным так, чтобы оно с точностью до знака стало структурно симметричным  : :  . В итоге мы получаем промежуточную версию полноправных уравнений поля поляризации физического вакуума в следующем виде: . В итоге мы получаем промежуточную версию полноправных уравнений поля поляризации физического вакуума в следующем виде:
a)  , b) , b)  , (4) , (4)
c) , d) , d)  . .
На вопрос о правомерности знаков при временных производных в уравнениях (4а) и (4c) нагляднее и проще всего можно ответить напрямую, записав эти по сути дела волновые уравнения для компонент волны поляризационного поля при некой ориентации ее векторных компонент 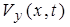 и и  . Не сложно убедиться частным дифференцированием по . Не сложно убедиться частным дифференцированием по 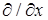 и по и по  функции плоской гармонической волны функции плоской гармонической волны  , распространяющейся со скоростью v в положительном направлении оси 0X, что ее волновое уравнение записывается в следующей форме: , распространяющейся со скоростью v в положительном направлении оси 0X, что ее волновое уравнение записывается в следующей форме:  . Тогда, расписав в уравнениях (4а) и (4c) функции ротора для предложенной ориентации векторов полевых компонент . Тогда, расписав в уравнениях (4а) и (4c) функции ротора для предложенной ориентации векторов полевых компонент  и и  , получим в итоге , получим в итоге
 и и  , ,
где константа  является скоростью распространения волн поляризации физического вакуума. Как видим, проверка показала, что знаки в представленных уравнениях (4а) и (4c) действительно верны. является скоростью распространения волн поляризации физического вакуума. Как видим, проверка показала, что знаки в представленных уравнениях (4а) и (4c) действительно верны.
Таким образом, мы можем теперь записать окончательную версию системы дифференциальных уравнений единого силового поля поляризации физического вакуума с векторными компонентами напряженности поля поляризации  и поля векторного потенциала и поля векторного потенциала  : :
a)  , b) , b) 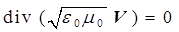 , (5) , (5)
c)  , d) , d) 
С математической точки зрения, соотношение (5a) и (5b) показывает, что, также как и  в (5c) и (5d), поле вектора в (5c) и (5d), поле вектора  является чисто вихревым. Итак, как следует из (5a), в статике ( является чисто вихревым. Итак, как следует из (5a), в статике ( ) поле поляризации вакуума ) поле поляризации вакуума  есть потенциальное поле: есть потенциальное поле:  , а в динамике ( , а в динамике ( ) )  – вихревое: – вихревое:  , соответственно, поле вектора , соответственно, поле вектора  – как в статике, так и в динамике вихревое, поскольку – как в статике, так и в динамике вихревое, поскольку  всегда. всегда.
Существенно, что представленные в системе (5) уравнения (5а) и (5c) в совокупности есть первичные волновые уравнения поля поляризации физического вакуума. В этом можно легко убедиться, взяв, как обычно, ротор от одного из роторных уравнений системы, и после чего подставить в него другое роторное уравнение этой же системы. Например, в качестве иллюстрации получим волновое уравнение относительно  : :
 . .
Аналогично рассуждая, получим волновое уравнение для  : :
 . .
Итак, имеем волновые уравнения для компонент поля поляризации физического вакуума:  и и  . Причем скорость распространения волн компонент поля поляризации физического вакуума . Причем скорость распространения волн компонент поля поляризации физического вакуума  определяется только лишь электрическими определяется только лишь электрическими 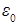 и магнитными и магнитными 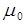 параметрами пространства физического вакуума и в точности равна скорости света (электромагнитных волн) в «пустом» пространстве: параметрами пространства физического вакуума и в точности равна скорости света (электромагнитных волн) в «пустом» пространстве:  . В итоге появляется физически принципиальный вопрос: что это за волны, и каковы характеристики распространения этих волн? Конечно здесь необходим подробный анализ решений указанных волновых уравнений, который следует провести в дальнейшем. Но уже сейчас можно с уверенностью сказать, что, согласно соотношению (2), где . В итоге появляется физически принципиальный вопрос: что это за волны, и каковы характеристики распространения этих волн? Конечно здесь необходим подробный анализ решений указанных волновых уравнений, который следует провести в дальнейшем. Но уже сейчас можно с уверенностью сказать, что, согласно соотношению (2), где  , колебания взаимно ортогональных компонент , колебания взаимно ортогональных компонент  и и  в плоской гармонической волне поля поляризации физического вакуума имеют относительно друг друга сдвиг по фазе на в плоской гармонической волне поля поляризации физического вакуума имеют относительно друг друга сдвиг по фазе на  . .
Физически для нас важно то, что система уравнений (5) структурно полностью идентична системам динамических уравнений электромагнитного поля и поля гравитации, полученным в работе [4] на основе опосредованного привлечения концепции Единого поля силового пространственного взаимодействия материальных тел [2]. Однако теперь потребуется напрямую и в явном виде подтвердить правомерность и фундаментальность концепции Единого поля.
В этой связи возникает еще один принципиальный вопрос: что переносят волны поля поляризации физического вакуума? Другими словами, необходимо прояснить физическое содержание представленной здесь системы дифференциальных векторных уравнений силового единого поля поляризации вакуума. На этот вопрос уравнения системы (5) также способны ответить посредством дифференциального соотношения энергетического баланса:
 . (6) . (6)
Чисто структурно уравнение баланса (6) представляет собой аналог известной энергетической теоремы Умова-Пойнтинга [1], при этом оно определяет в данной точке пространства скалярные в конечном итоге физические соотношения энергии поляризации физического вакуума с единицами измерения:  (слагаемые справа), поведение которых определяет транспорт в окружающее пространство энергетического потока поля вектора (слагаемые справа), поведение которых определяет транспорт в окружающее пространство энергетического потока поля вектора  (дивергентное слагаемое). Как и должно быть, новый с точки зрения ортодоксальных представлений потоковый вектор энергии поляризации физического вакуума (дивергентное слагаемое). Как и должно быть, новый с точки зрения ортодоксальных представлений потоковый вектор энергии поляризации физического вакуума  имеет размерность поверхностной плотности энергии имеет размерность поверхностной плотности энергии  , то есть в определенной мере подобен вектору Пойнтинга , то есть в определенной мере подобен вектору Пойнтинга  . .
Таким образом, построенная на основе концепции Единого поля силового пространственного взаимодействия материальных тел [2] система дифференциальных уравнений единого силового поля поляризации физического вакуума (5) однозначно описывает реально существующие в вакуумной среде волны ее возбуждения, переносящие в пространстве посредством потокового вектора  энергию возбуждения вакуума. Как видим, полученные здесь дифференциальные уравнения и результаты их предварительного анализа действительно являются сущностной первоосновой аналитического описания физического механизма реализации конкретных динамических характеристик поведения электрических, магнитных и гравитационных полей. энергию возбуждения вакуума. Как видим, полученные здесь дифференциальные уравнения и результаты их предварительного анализа действительно являются сущностной первоосновой аналитического описания физического механизма реализации конкретных динамических характеристик поведения электрических, магнитных и гравитационных полей.
В заключение подведем итог и отметим основные результаты:
 на основе концепции Единого Поля силового пространственного взаимодействия материальных тел построена и предварительно проанализирована система дифференциальных уравнений единого силового поля поляризации среды физического вакуума, описывающая характеристики реально и единственно существующих в вакуумной среде волн ее поляризации, переносящих в пространстве энергию возбуждения среды физического вакуума; на основе концепции Единого Поля силового пространственного взаимодействия материальных тел построена и предварительно проанализирована система дифференциальных уравнений единого силового поля поляризации среды физического вакуума, описывающая характеристики реально и единственно существующих в вакуумной среде волн ее поляризации, переносящих в пространстве энергию возбуждения среды физического вакуума;
 аналитически однозначно установлено, что в пространстве физического вакуума никаких других волн кроме волн поляризации вакуумной среды возбудить невозможно, при этом поток энергии возбуждения вакуума силовым образом взаимодействуя с определенной физической характеристикой (электрической, магнитной или гравитационной) материального тела, создает динамический отклик параметров этого тела, который регистрируется в эксперименте как реальный поток энергии соответствующей физической природы; аналитически однозначно установлено, что в пространстве физического вакуума никаких других волн кроме волн поляризации вакуумной среды возбудить невозможно, при этом поток энергии возбуждения вакуума силовым образом взаимодействуя с определенной физической характеристикой (электрической, магнитной или гравитационной) материального тела, создает динамический отклик параметров этого тела, который регистрируется в эксперименте как реальный поток энергии соответствующей физической природы;
 существенно подчеркнуть, что в реальных материальных средах (разного рода диэлектрики и проводники) электромагнитные, акустические и другие обычные волны конечно действительно существуют, хотя физический механизм их распространения в своей первооснове обусловлен все теми же волнами поляризации физического вакуума, взаимодействующими с материей пространства реальной среды, при этом скорость распространения обычных волн всегда принципиально меньше скорости света и зависит от физических характеристик этих материальных сред; существенно подчеркнуть, что в реальных материальных средах (разного рода диэлектрики и проводники) электромагнитные, акустические и другие обычные волны конечно действительно существуют, хотя физический механизм их распространения в своей первооснове обусловлен все теми же волнами поляризации физического вакуума, взаимодействующими с материей пространства реальной среды, при этом скорость распространения обычных волн всегда принципиально меньше скорости света и зависит от физических характеристик этих материальных сред;
 по нашему мнению, экспериментальным подтверждением механизма возбуждения единым силовым полем поляризации вакуума обычных волн различной физической природы в реальных материальных средах может служить известный эффект волны-предвестника, распространяющейся перед передним фронтом импульса при разного рода «ударных» воздействиях, который на сегодня не имеет однозначного физического объяснения. по нашему мнению, экспериментальным подтверждением механизма возбуждения единым силовым полем поляризации вакуума обычных волн различной физической природы в реальных материальных средах может служить известный эффект волны-предвестника, распространяющейся перед передним фронтом импульса при разного рода «ударных» воздействиях, который на сегодня не имеет однозначного физического объяснения.
Список литературы
1. Физический энциклопедический словарь / Гл. ред. А.М. Прохоров. - М.: Советская энциклопедия, 1983.
2. Сидоренков В.В. Единое поле силового пространственного взаимодействия материальных тел // XLVII Всероссийская конференция по проблемам физики частиц, физики плазмы и конденсированных сред, оптоэлектроники: Тезисы докладов. Секция «Теоретическая физика». - М.: РУДН, 2011. С. 67-69; // http://www.referat.ru/referats/view/31525.
3. Сидоренков В.В. Физические основы современной теории электромагнитного поля // http://www.referat.ru/referats/view/31773.
4. Сидоренков В.В. Динамические полевые уравнения взаимодействия материальных тел в среде физического вакуума // http://referat.ru/referats/view/31896.
|