Аксиоматика вещественных чисел. Алгебраические свойства вещественных чисел. На множестве вещественных чисел определена операция сложения, удовлетворяющая следующим аксиомам:    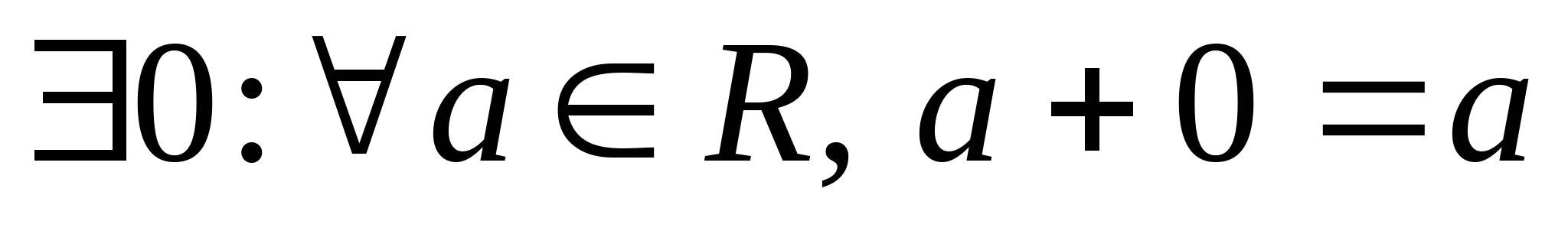  Введем операцию умножения:   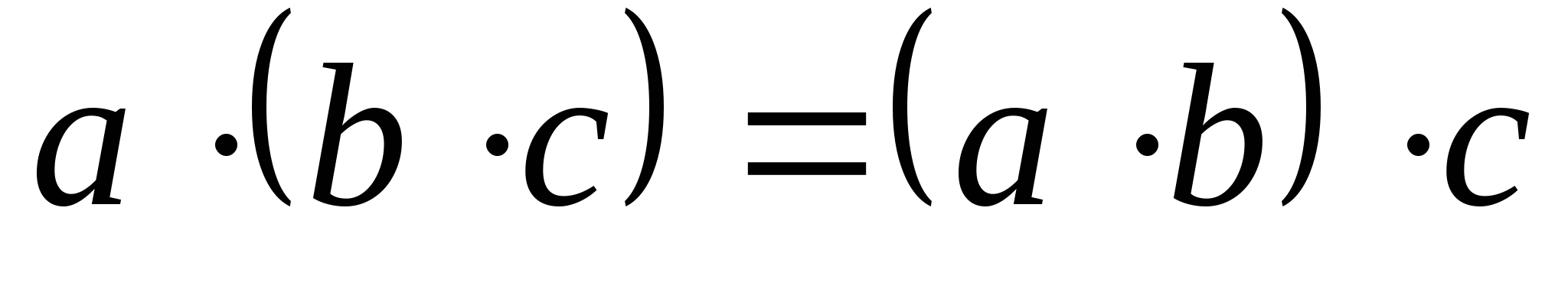   Дистрибутивность. Распределительный закон. 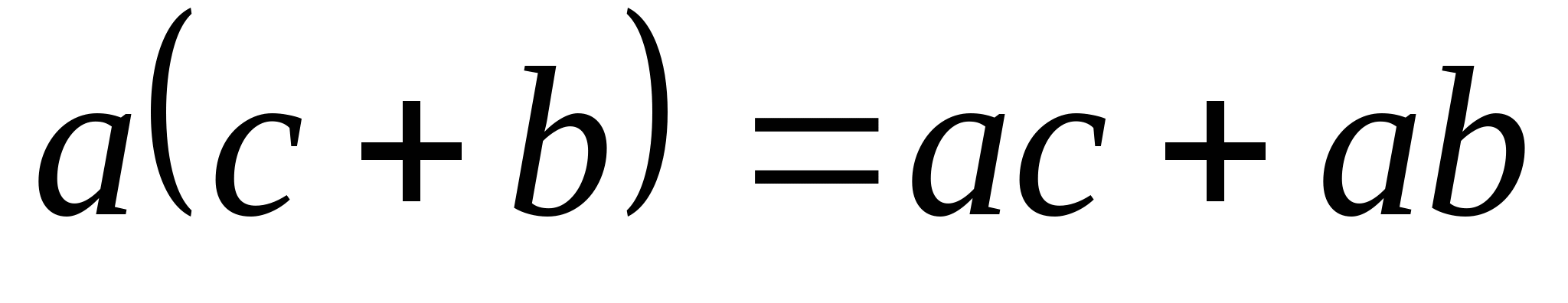 Множество, элементы которого удовлетворяют a, b, c – числовое поле. Примеры: множество вещественных и рациональных чисел. Отношение порядка. На множестве вещественных чисел вводится отношение порядка  , т.е. , т.е. 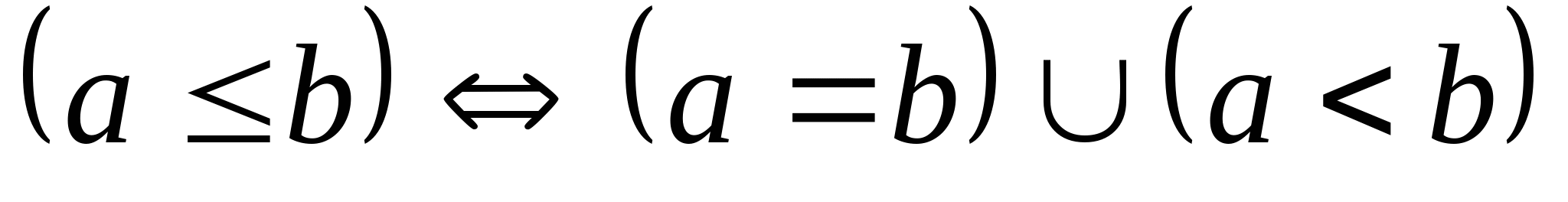 , которое удовлетворяет следующим аксиомам: , которое удовлетворяет следующим аксиомам:  выполняется выполняется 




 
Из этих аксиом следует, что для любого а и b  , выполняются три случая: , выполняются три случая: a <b (a =b) b<a Множество, на котором вводится отношение порядка, удовлетворяющее аксиомам 1-6, называется линейной упорядоченностью. И множество вещественных чисел, и множество рациональных чисел – линейно упорядоченное поле
Аксиома непрерывности вещественных чисел Пусть  , причем , причем  и и  : :  , тогда , тогда  Множеством вещественных чисел называется линейно упорядоченное непрерывное числовое поле. Замечание: Аксиома непрерывности гарантирует, что каждому вещественному числу соответствует единственный тип числовой прямой и, наоборот, каждой числовой прямой соответствует единственное вещественное число.
Представление (модель) вещественного числа.
Можно доказать, что аксиомам удовлетворяют десятичные дроби, причем конечные (периодические) соответствуют рациональным числам, а бесконечные (непериодические) – иррациональным числам. Т.к. бесконечные дроби нельзя использовать при вычислениях (не представимы в ЭВМ), то в реальных расчетах пользуются исключительно рациональными числами, но доказано, что любое вещественное число можно с любой степенью точности представить рациональным числом.
Свойство числового множества (следует из свойства упорядоченности). Множество  - ограничено сверху, если - ограничено сверху, если  . . Число M – верхняя граница множества X. Любое число  - точка верхней границы, т.к. - точка верхней границы, т.к.  Итак, верхних границ бесконечно много. Наименьшая из всех верхних границ – верхняя грань множества Х (sup X – супремум икс) 
Множество  - ограничено снизу, если - ограничено снизу, если  . . Число В – верхняя граница множества X. Любое число  - точка нижней границы, т.к. - точка нижней границы, т.к.  Наибольшая из всех нижних границ – нижняя грань множества Х (inf X). 
Множество  называется ограниченным, если оно ограничено и снизу и сверху. называется ограниченным, если оно ограничено и снизу и сверху. 
Теорема: Любое непустое, ограниченное сверху (снизу) множество, имеет верхнюю (нижнюю) грань. Понятие абсолютной величины вещественного числа. На упорядоченном числовом множестве введем понятие модуля (абсолютной величины) вещественного числа: 


Свойства: 




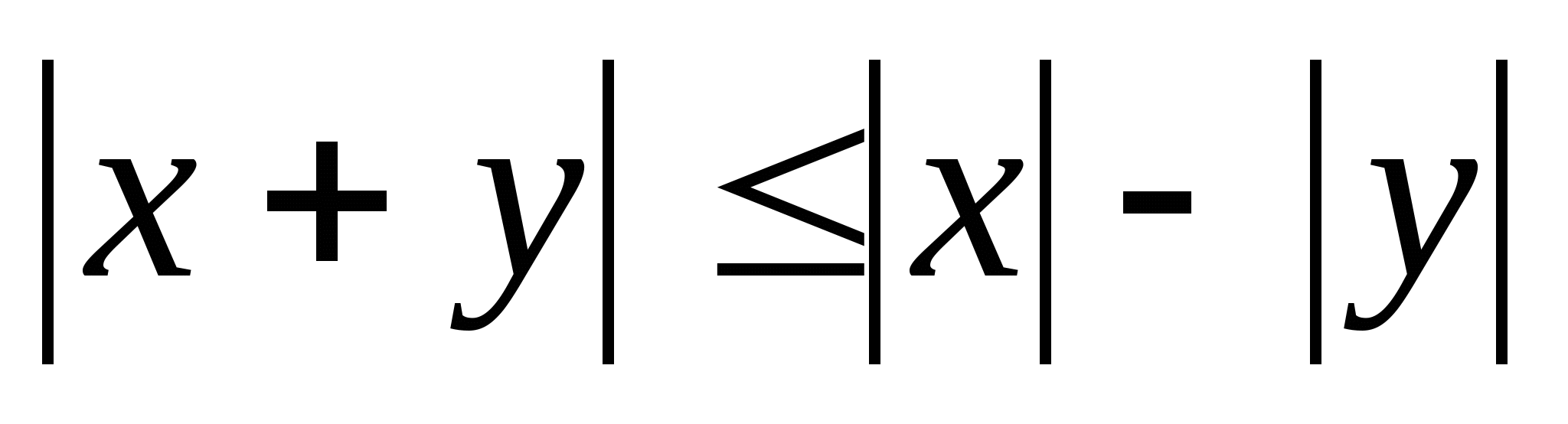

Решение простейших неравенств с модулем. Эквивалентность неравенств: 

геометрический смысл: 
 
 
Понятие окрестности в точке х0 окрестности в точке х0 (U (x0)) – симметричный интервал радиуса с центром в точке х0 
Приколотой окрестности в точке х0 называется окрестности этой точки без самой х0 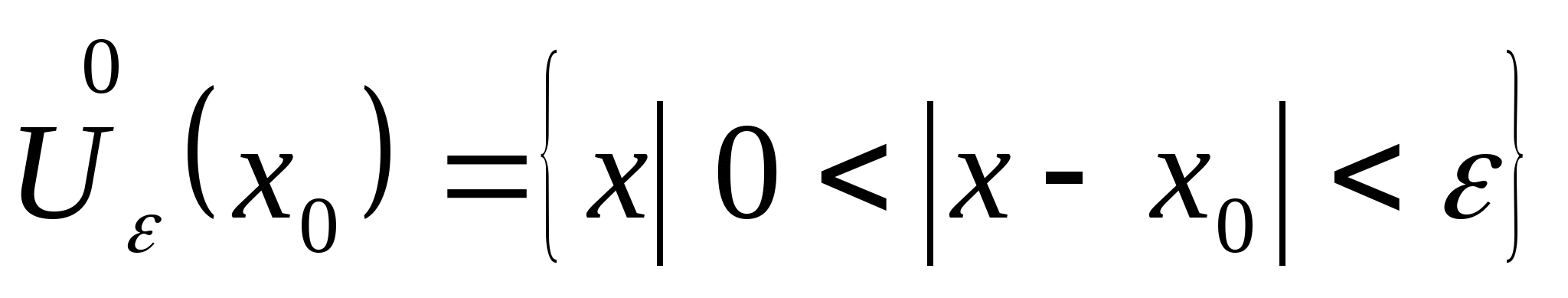
Открытые и замкнутые множества Множество  - называется открытым, если для любой точки этого множества найдется такая - называется открытым, если для любой точки этого множества найдется такая  , которая целиком содержится в этом множестве. , которая целиком содержится в этом множестве.  , точки, обладающие этими свойствами, называются внутренними точками. , точки, обладающие этими свойствами, называются внутренними точками. (a,b) – открытое множество: Точка x  X B любой окружности содержит – граничной точки множества X X B любой окружности содержит – граничной точки множества X
Точки a и b – граничные [a;b] или (a;b). Граничные точки могут и принадлежать, и не принадлежать множеству отрицательных. Множество своих границ не содержит. Точка x называется предельной точкой X, если любое  - окружности содержит хотя бы - окружности содержит хотя бы  точек X. точек X. (x-предельная для X)  ( (  (x) ( (x) ( x, x,  x) x)  (x, (x,   (x) ) (x) ) точки a,b являются предельными как для отрезка, так и для интервала ( [a;b] и (a;b) ) a,b  отрезку x отрезку x a,b  X X Граничных точек – 2 Предельных – целый отрезок (интервал) Точка изолирована – если найдётся  (x), которая (x), которая  . . Совокупность предельных и изолированных точек – называется точками соприкосновения множества X.
Множество X замкнутое, если оно содержит все свои точки прикосновения.
Замкнутым множеством является сегмент [a;b]. Открытость и замкнутость – не альтернативные понятия. Существуют множества, не являющиеся ни открытыми, ни замкнутыми. Например, [a;b) или (a;b]. Или одновременно открытые и замкнутые ().
Принципы существования предельной точки (Вейерштрасс)
Всякое ограниченное бесконечное множество определяет хотя бы одну предельную точку. Для неограниченных бесконечных множеств это утверждение неверно. (Множество целых чисел предельных точек не имеет, так как состоит их одних изолированных точек). _________________________ Для распространения принципа Вейерштрасса на неограниченное множество вводятся новые объекты: +бесконечность, - , которые числами не являются. Вводятся правила действия над ними. , которые числами не являются. Вводятся правила действия над ними. 
Бессмысленно: 
Понятие функции.
Основной объект - функция Основной предмет - предел.
Функция – закон, по которому элементу  ставится ставится  в соответствии ед. элемент  . . Д/з1: Область определения функции  Д/з2: Область значения функции  (f) – E[f] C Y, такое, что (f) – E[f] C Y, такое, что   (Каждый элемент множества E имеет прообраз во множестве.
Замечание 1: в определении не требуется, чтобы каждый элемент X имел прообраз в Y. Говорят, что функция  отображает множества X во отображает множества X во множество Y. Всегда  отображает множество X на отображает множество X на множестве E. Не требуется, чтобы элементы E имели единственный прообраз во множестве X.  Д/з: Отображение, осуществляемых функций  , называется взаимно однозначным отображением множества X на Y , если каждый элемент Y имеет единственный прообраз множества X. , называется взаимно однозначным отображением множества X на Y , если каждый элемент Y имеет единственный прообраз множества X.  . . Д/з: Две функции равны, если:  . .
совпадают законы соответствия.
Пример: 1) Равны ли функции  и и  Нет, так как  . . 2)  и и  
Д/з: Две функции совпадают на множестве X1, с вкл. в пересечение областей определения функций  , если для любой , если для любой  совпадает с совпадает с  . .

Пример:  и и 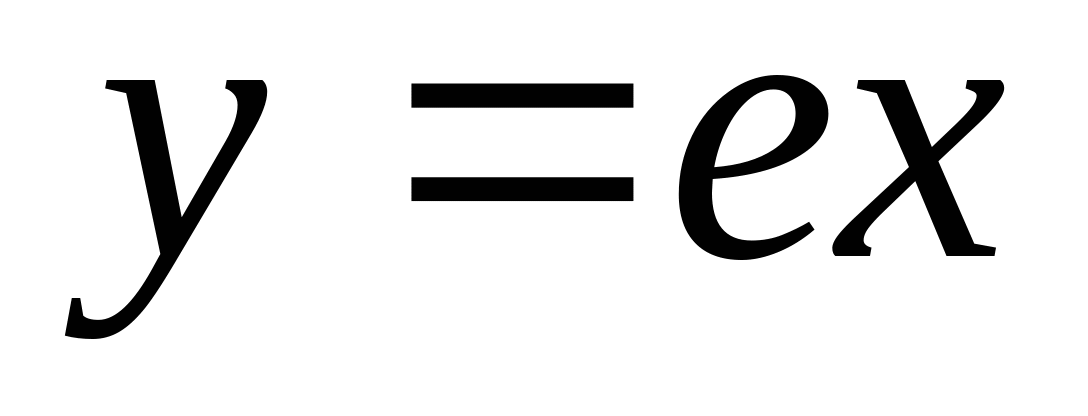 совпадают на множестве совпадают на множестве 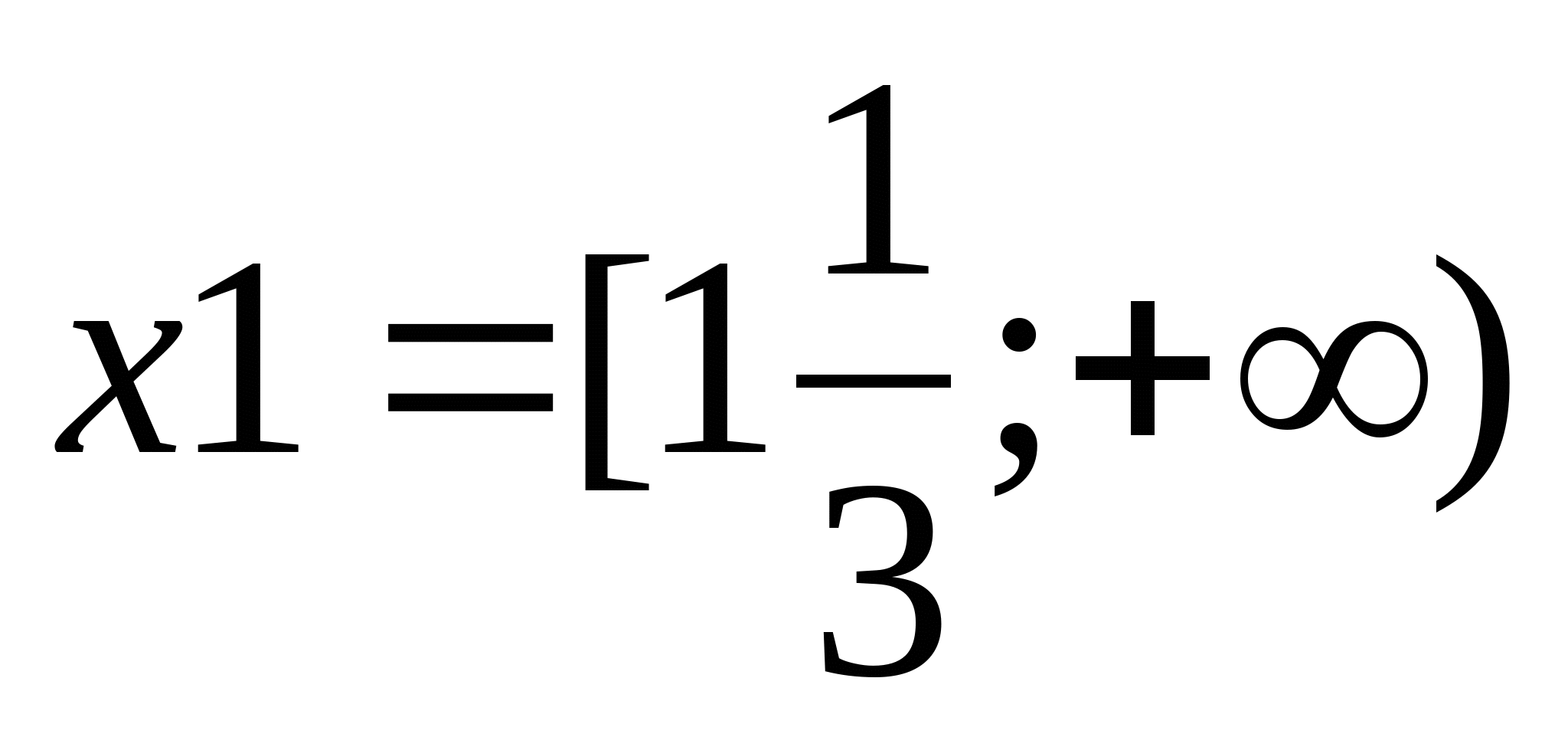 Д/з: выписать определения чётных, нечётных, периодичных функций; их свойства и свойства симметрии графиков, сп. зад. функций с примерами.
Общие свойства функций.
1) Ограниченность. Сводится к ограниченности множества значений. Функция ограничена, существует  , что для , что для  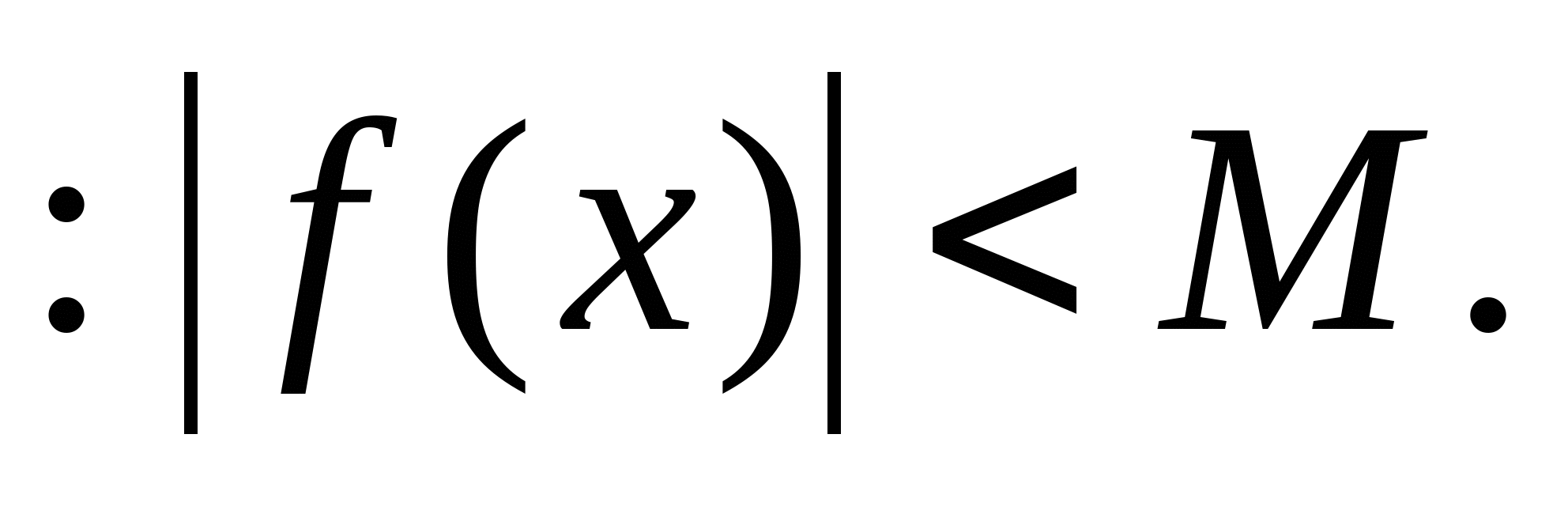
 - огранич. - огранич.
 - неогранич.; - неогранич.; 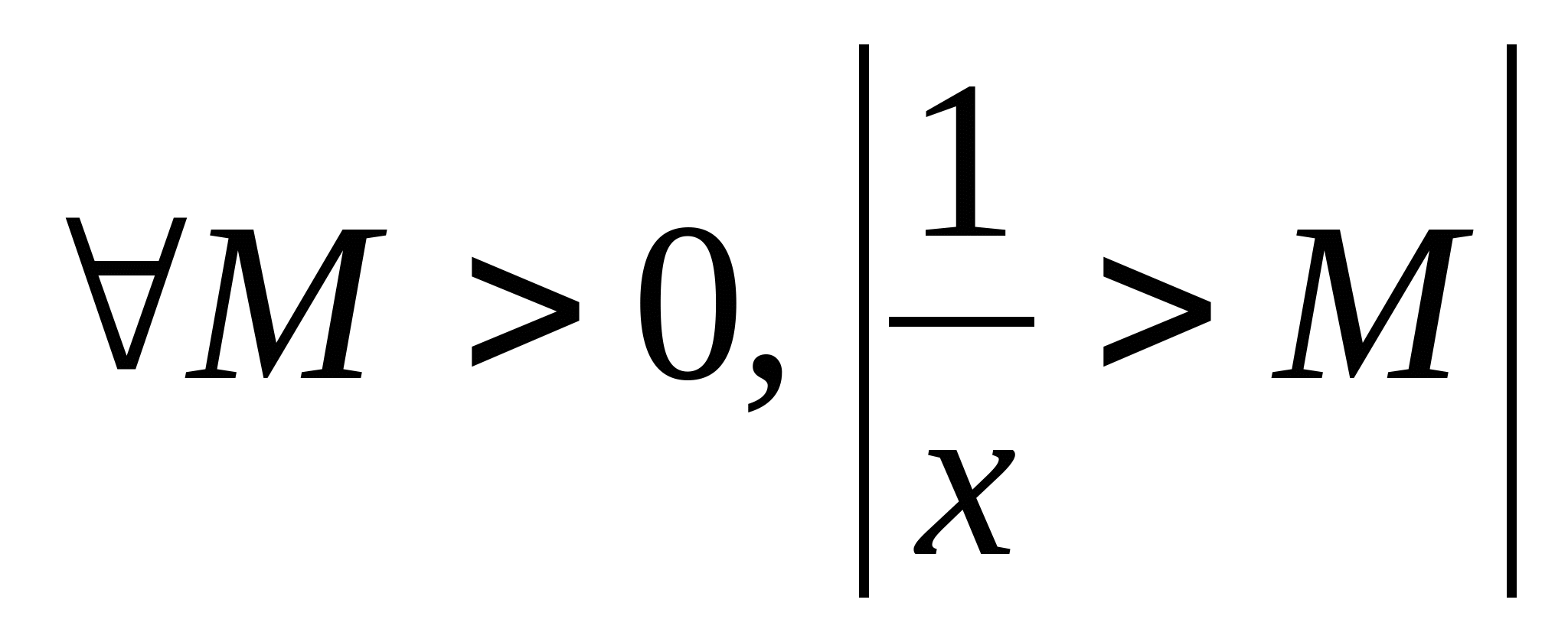 при при 
2) Монотонность. Д/з: Функция  называется возрастающей на промежутке X, если для любого называется возрастающей на промежутке X, если для любого  промежутку; промежутку;  Убывающей, если  Замечание: если неравенства нестрогие, то говорят о неубывании в 1 случае и невозрастании (либо неизм., убыв.) во 2 случае. Невозрастающие и неубывающие функции – монотонные. При строгом неравенстве строгомонотонные. Пример:  Докажем, что она убывающая на любом промежутке. Например:  Пусть   
Понятие монотонности только для промежутков. Промежуток – множество, обладающее свойством: наряду с любым 2-мя числами  и и  ему принадлежат все числа, заключённые между ними ему принадлежат все числа, заключённые между ними  . .
Понятие сложной функции. (композиции функции)
Пусть даны отображения  и и  , такие, что пересечения , такие, что пересечения  и и  - непустое множество - непустое множество 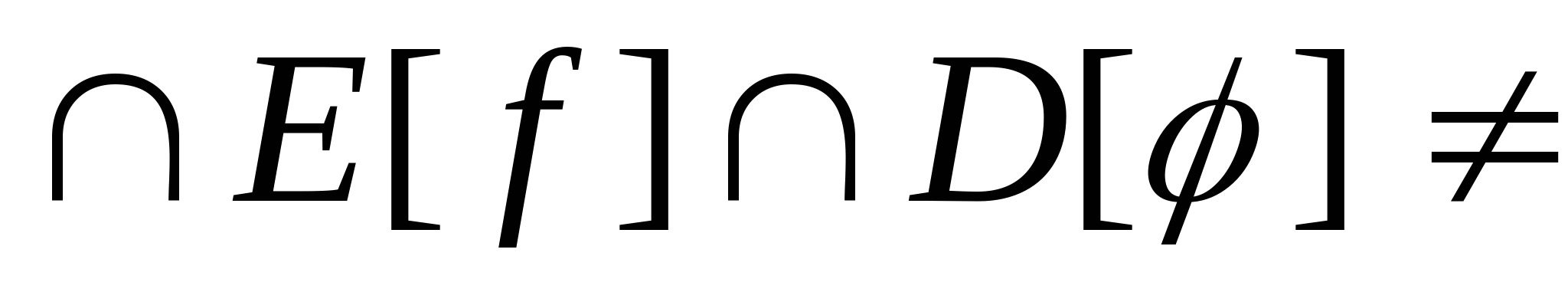 . . Тогда вводится новое отображение,  , которое включает , которое включает  новой функции новой функции    и закон соответствия получается по формуле: и закон соответствия получается по формуле:
 - отображ. сложная функция (композиция). - отображ. сложная функция (композиция).
Пример: 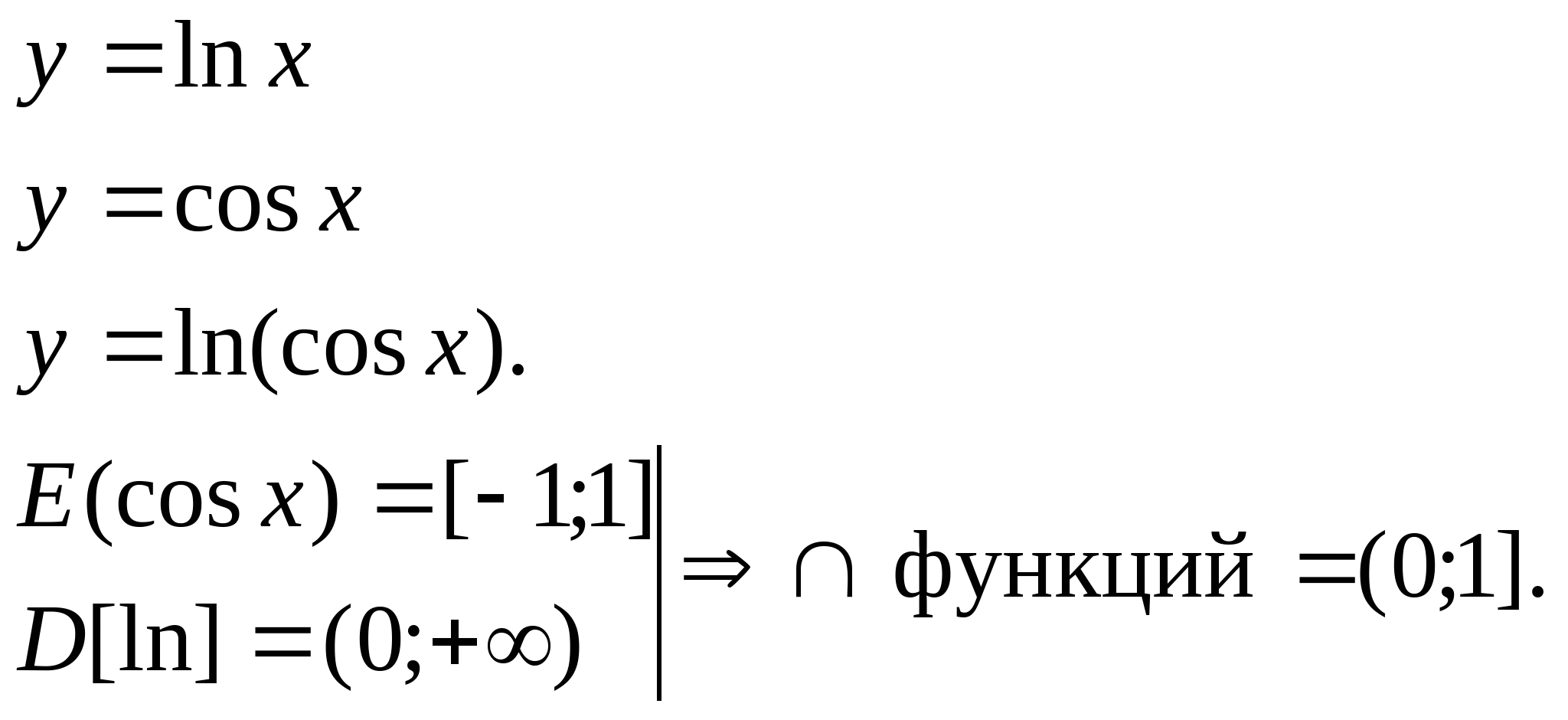 

Обратная функция:
При взаимооднозн. отображении X на Y с пом. функции  эти множествасимм. относительно этого отображения, т.е. наряду с функцией эти множествасимм. относительно этого отображения, т.е. наряду с функцией  существует обр. ф-я существует обр. ф-я  Д/з:  называется обратной взаимооднозн. ф-и называется обратной взаимооднозн. ф-и  , если каждому элементу , если каждому элементу  ставят в соотв. ставят в соотв.  так, что так, что  . . Замечание: y взаимнообр. ф-й D(f) и E(f) мен. местами Замечание 2: если для обр. функций сделать замену переменных 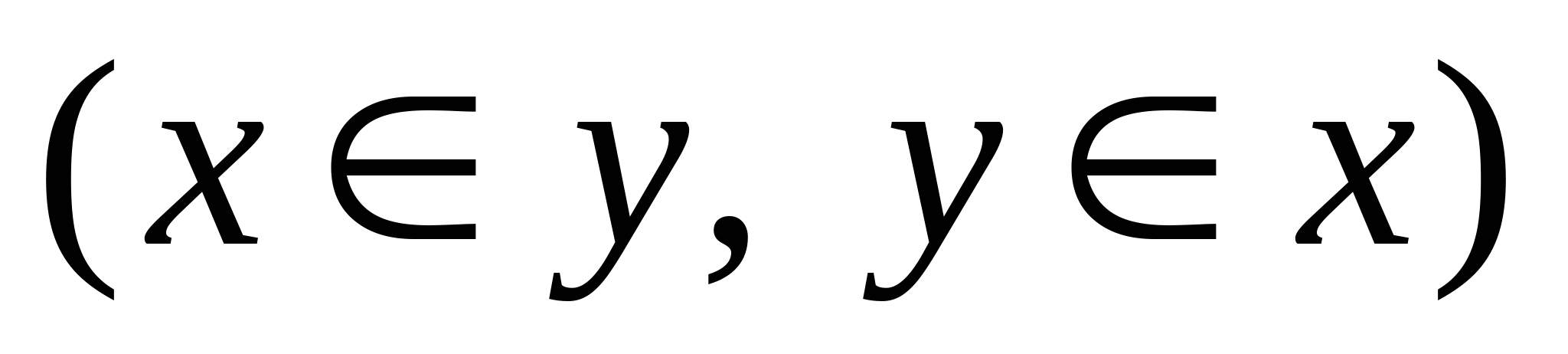 , чтобы , чтобы  то гр-ни функций то гр-ни функций  и и  симм. отн. бессектр. 1 и 3 квадратов. симм. отн. бессектр. 1 и 3 квадратов.
Пример:  обр. ф-я – обр. ф-я –    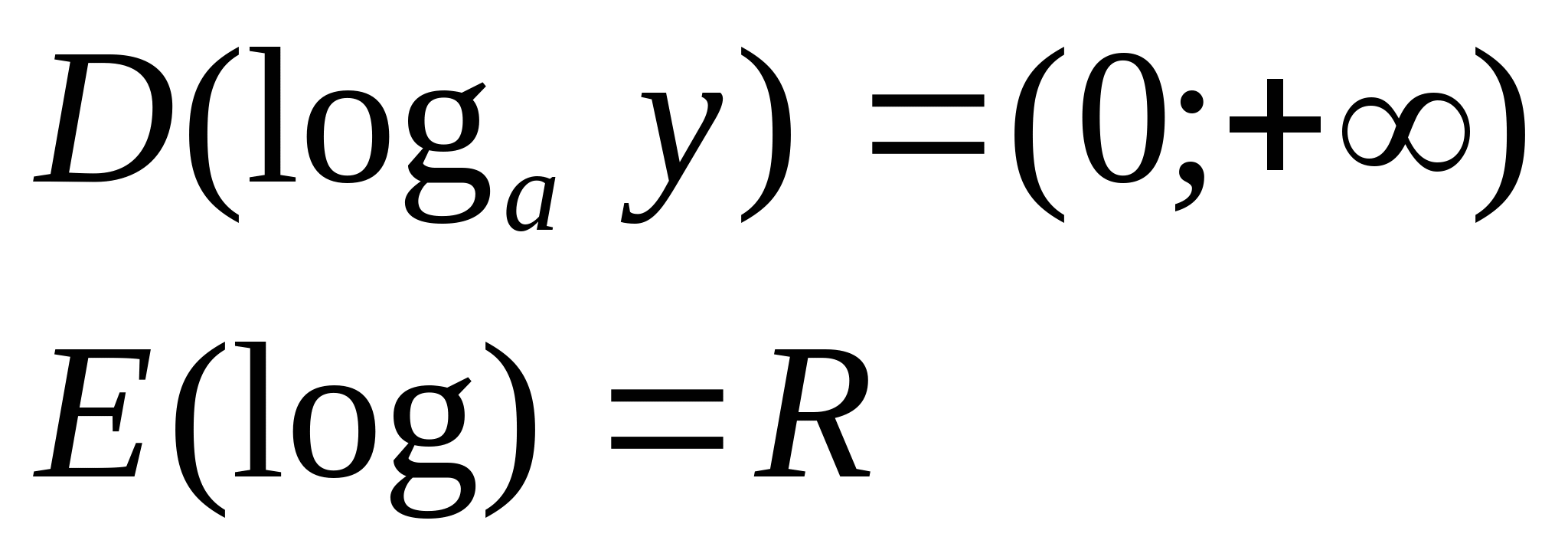

Элементы теории пределов. Теория пределов формализует (перев. на мат. яз.) фразы: и Зн-я  неогранич. приалинс-ся к числу A, когда x неогр. приалинс-ся к числу ф; или n Зн-я неогранич. приалинс-ся к числу A, когда x неогр. приалинс-ся к числу ф; или n Зн-я  неогр. приыл. к A тогда, когда неогр. приыл. к A тогда, когда 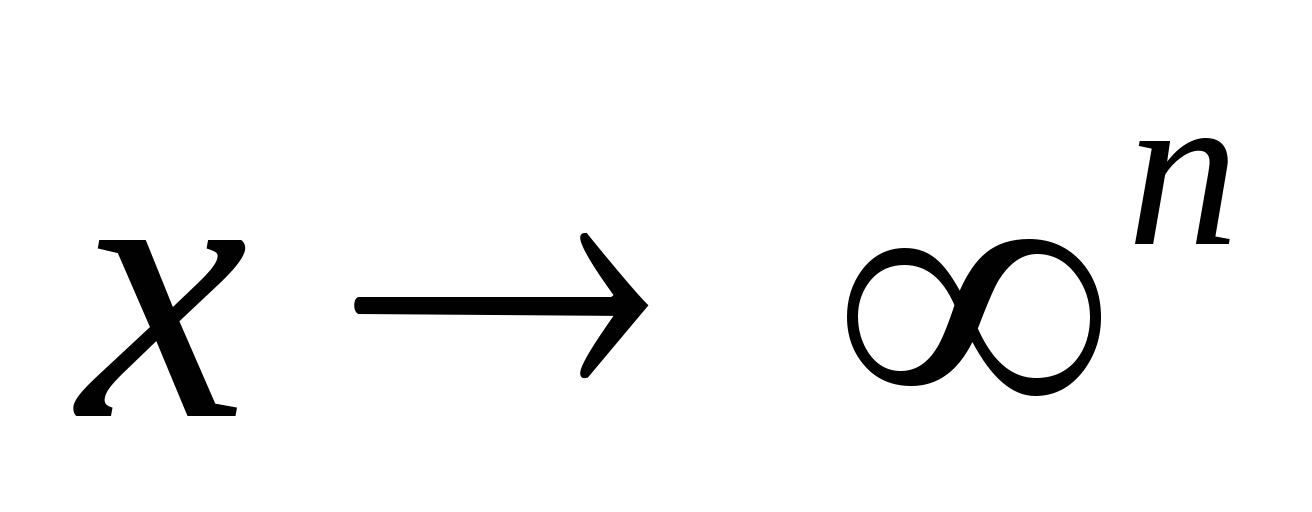 и т.д. и т.д. Д/з: Р/м  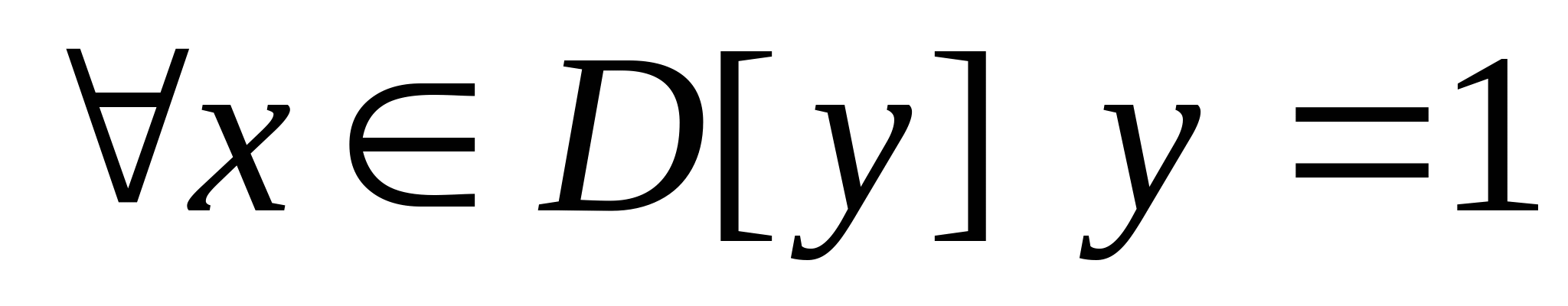 втом числе и для x, сколько угодно втом числе и для x, сколько угодно к 0, т.е. к 0, т.е.  хотя зн-я хотя зн-я  этой т. этой т.  не имеет. не имеет.
Определение предела в терминах окресностей. Число А называется пределом  при при  , и обозначается , и обозначается  , если для любой -окресности числа А найдется проколатая окресность, так что ля всех х из этой окресности значения , если для любой -окресности числа А найдется проколатая окресность, так что ля всех х из этой окресности значения  будут принадлежать -окресности числа А. будут принадлежать -окресности числа А. 
Конечный предел ф-ии (А-вещ. число) 
Число А-конечный предел ф-ии в т. а, если 
Частные случаи (геометрическая иллюстрация) Конечный предел в конечной т. а – вещественное число 
Общие свойства конечного предела Если  - const, то ее предел сущ. и равен этой же const. - const, то ее предел сущ. и равен этой же const.  , то , то Если конечный предел сущ., то он единственный  Для f(x), имеет конечный предел в т. а, сущ. такая прколотая окрестность этой т., в которой ф-ия ограничена. 
Если ф-ия имеет в т. а, конечный предел, неравный нулю то найдется такая  в т. а, в которой в т. а, в которой  - ограниченная. - ограниченная.  Если f(x), имеет в т. а отрицательный конечный предел, то найдется такое значение этой точки, в котором ф-ия отрицателная. 
Бесконечно малые ф-ии и их свойства:
Опр: - бесконечно малая при - бесконечно малая при  , если , если  
Свойства: Пусть  и и  являются бесконечно малыми при являются бесконечно малыми при  , а , а  - ограничена, то бесконечно малыми является алгебраическая сумма ф-ий f(x) и (x), произведения их и произведения ф-ий на ограниченную. - ограничена, то бесконечно малыми является алгебраическая сумма ф-ий f(x) и (x), произведения их и произведения ф-ий на ограниченную.



Представвление ф-ии, имеющей конечный предел. Теорема: Для того чтобы ф-ия  имела конечный предел А в точке х=а, небходимо и достаточно, чтобы имела конечный предел А в точке х=а, небходимо и достаточно, чтобы  =А+(х), где (х)- бесконечно малая при =А+(х), где (х)- бесконечно малая при  . . 
Доказательство: 
Алгебраические свойства фунцций имеющих конечный предел в точке а.
Пусть  , тогда: , тогда: Существует предел алгебраической суммы этих ф-ий,равный алгебраической сумме этих пределов. 
Существует предел произведения ф-ий произведение пределов 
Если предел знаменателя неравен 0 и B неравно 0 то  
Следствие. Из 1 и 2 следует, что константы можно выносить за знак предела 
Бесконечно большие и их свойства Опр. Ф-ия  называется бесконечно большой в точке а, если ее предел в этой точке равен бесконечности. называется бесконечно большой в точке а, если ее предел в этой точке равен бесконечности. 
Свойства Пусть  и и  - бесконечно большие ф-ии в точке а. - бесконечно большие ф-ии в точке а. Ф-ия (х) имеет предел в точке а, отличный от 0 Ф-ия (х) и (ч) – бесконечно малые Тогда справедливы следующие утверждения: Произведение двух бесконечно больших ф-ий – бесконечно большая ф-ия. 
Произведение бесконечно больших на ф-ию, имеющую отличный от нуля предел - бесконечно большая.  Ф-ия, обратная величине бесконечно большой – есть бесконечно малая, и наоборот. 
Доказательство 2):  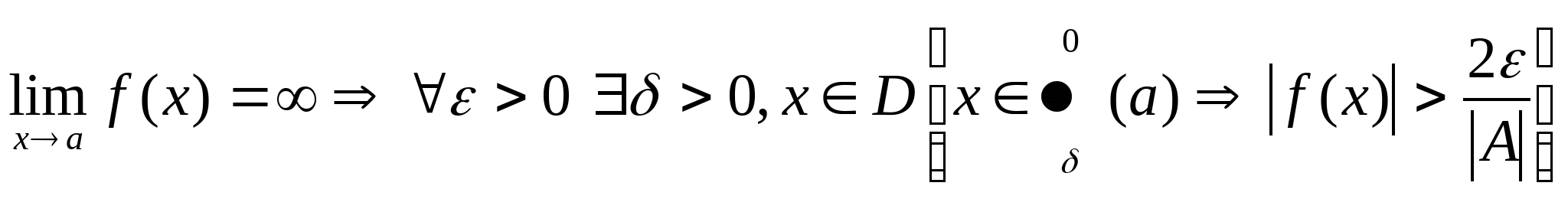


Доказательство 3):  
Односторонние пределы в конечной точке и их связь с пределом в этой точке.
В определении предела окрестности точки а – симметричный интервал с центром в этой точке, т.е. требуется существование значений ф-ий как справа от точки а , так и слева от нее. Когда а – граничная точка D(f)- такая ситуация невозможна. В этом, случае вводится понятие одностороннего предела, в определении которого фигурирует левые и правые полуокрестности точки а

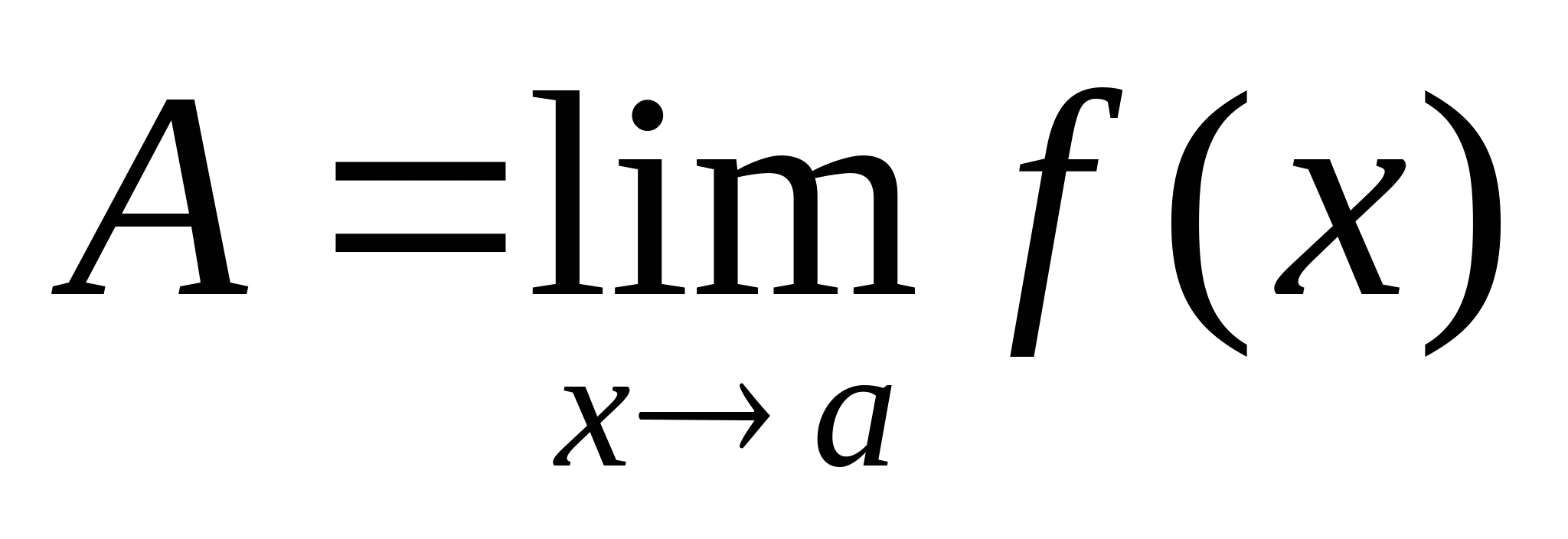 - левосторонний предел, если - левосторонний предел, если  в левой полуокружности точки А, значения ф-ии лежат в -окрестности точки А в левой полуокружности точки А, значения ф-ии лежат в -окрестности точки А
Аналогично дается определение правостороннего предела. 
Теорема: Для того, чтобы в точке а существовал предел ф-ии, необходимо и достаточно существования и равенства левостороннего и правостороннего пределов Доказательство: Необходимость: 
Достаточность: 
Числовые последовательности
Задача, по которой каждому N числу, ставится в соответствие единственное вещественное число – называется числовой последовательностью.
Числовая последовательность – ф-ия натурального аргумента. Обозначается: 
Последовательность, множество значений которой состоит из одного числа – стационарная.
Так как числовая последовательность – не симметричное множество, то для него не существует понятия четности, нечетности, периодичности. Зато сохраняются свойства, связанные с упорядоченностью. Свойства: Ограниченность. последовательность  ограничена сверху, если ограничена сверху, если  последовательность  ограничена снизу, если ограничена снизу, если  последовательность  ограничена, если ограничена, если  Монотонность. последовательность  возрастает, если возрастает, если  последовательность  убывает, если убывает, если  последовательность  не убывает, если не убывает, если  последовательность  не возрастает, если не возрастает, если 
Предел последовательности Т.к. N числа имеет 1 т. бесконечности, то для числовой последовательности существует  
Замечания: А может быть конечным или бесконечным Если последовательность имеет конечный предел, то она называется сходящейся, а если нет – расходящейся. Общие свойства сходящихся последовательностей аналогичны свойствам ф-ий, имеющих конечный предел. Арифметические свойства сходящихся последовательностей аналогичны свойствам ф-ий, имеют конечный предел Переход к пределам в неравенствах, для сходящихся последовательностей аналогичен ф-ям, имеющим конечный предел. Определение бесконечно малых и бесконечно больших последовательностей и их свойства аналогичны соответствующим определениям и свойствам ф-ии непрерывного аргумента.
Критерии существования предела последовательности
1. Критерии Коши (произведения последовательностей) Для существования предела последовательностей  необходимо и достаточно, чтобы для любой.............. необходимо и достаточно, чтобы для любой.............. 
Последовательность, для которой выполняется признак Коши – фундаменталная 2. Критерий Вейерштрасса (монотонность последовательности) а) неубывающие последовательности, ограниченные сверху, имеют предел. 
б) не возрастающие последовательности, ограниченные снизу, имеют предел.
Доказательство(а): 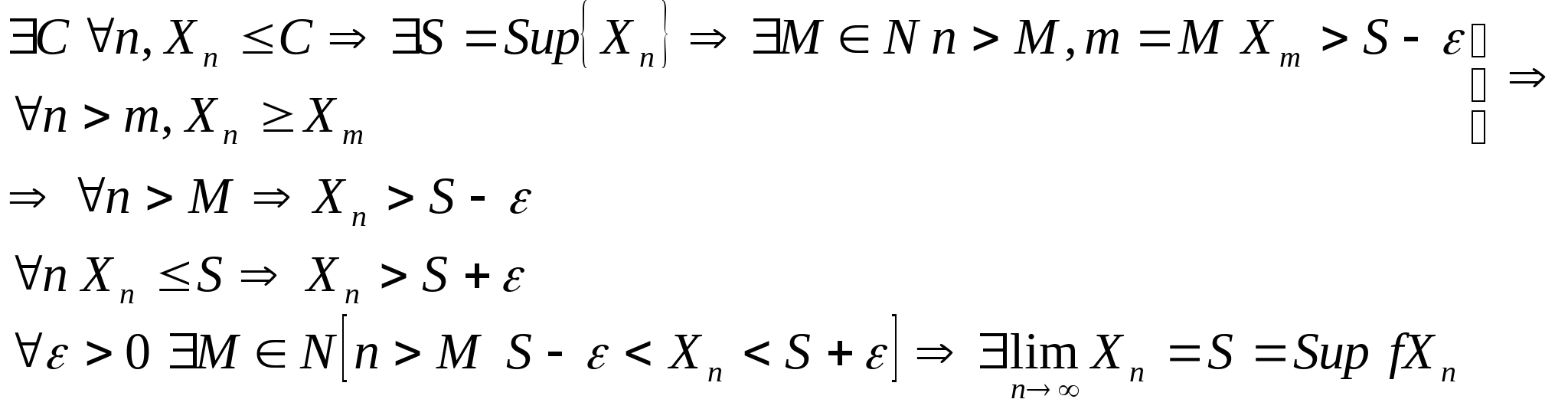
Переход к пределу в неравенстве Теорема: Пусть f(х) и (х) имеют конечные пределы в т. y=a, тогда справедливо: 



Доказательство: Пусть  , тогда по общему свойству №6 , тогда по общему свойству №6  , ,
а это противоречит 1 Замечание: Из утверждения №3 следует, что предел неотрицательной ф-ии является неотрицательным. При пределов к противоположным можно обе части умножать на (-1).
Теорема 2(о двух миллиционерах ) Пусть в некоторой области Д выполняется система неравенств  и а – предел точки. и а – предел точки. Пусть существуют равные пределы  , , тогда существует  . . Доказательство: 

Первый замечательный предел

Д оказательство: докажем для оказательство: докажем для  справедливость неравенства справедливость неравенства  В силу четности входящих в неравенство ф-ий, докажем это неравенство на промежутке Из рисунка видно, что площадь кругового сектора 
 , так как х>0, то , так как х>0, то  , ,
2. следовательно, что 


Покажем, что 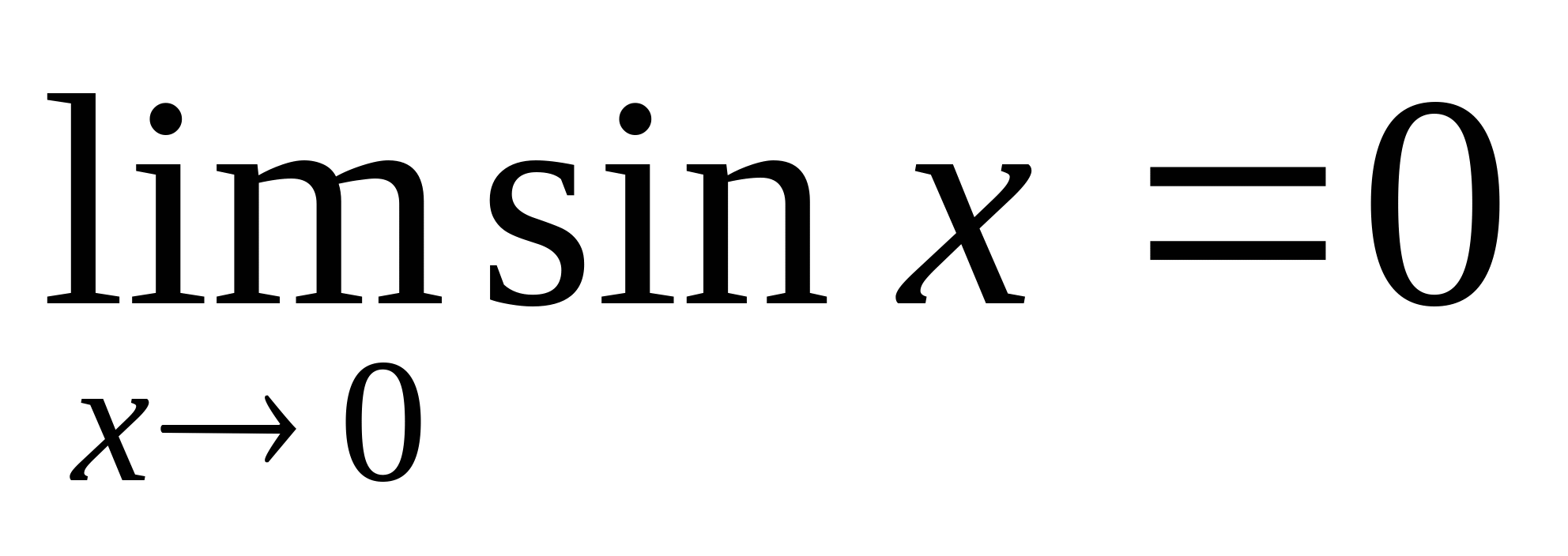 

Докажем, что  
Последнее утверждение: 
Второй замечательный предел
Понятие касательной к прямой.
П рямая, проходящая через две точки кривой – секущая. рямая, проходящая через две точки кривой – секущая. Предельное положение секущей, которое она занимает при стремлении т. М к т. М0 называется касательной к кривой в т. М0
Бесконечные пределы ф-ии.
Если в общем определении предела через окрестности положить в качестве А бесконечно удаленную точку, то получим определение бесконечного предела. Так как различают три вида бесконечно удаленных точек, то существуют три определения: 1. 
2. 
3. 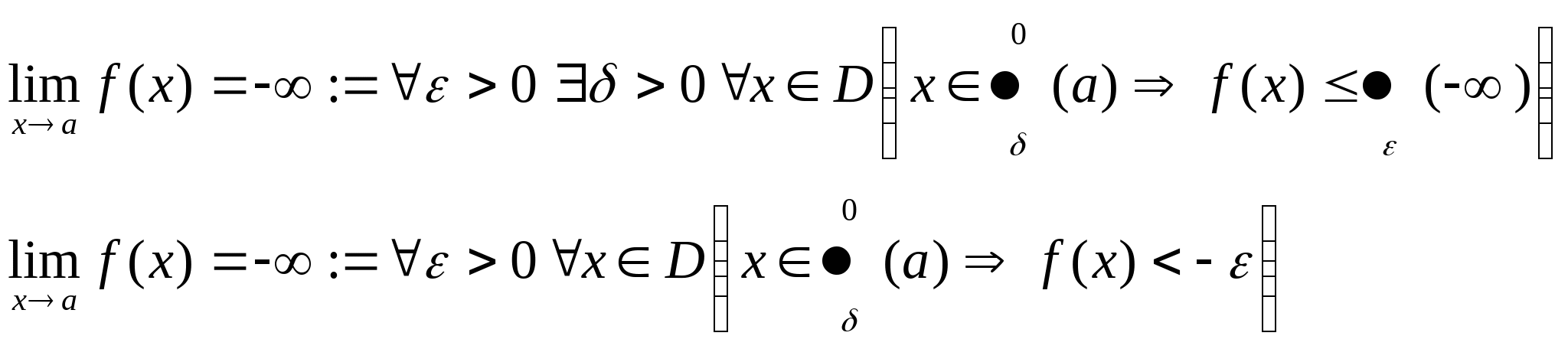
Понятие непрерывности ф-ии.
Непрерывность – такое свойство ф-ии, как отсутствие точек разрыва у графиков этой ф-ии. Т.е. строится единственной непрерывной линией.  
График непрерывной ф-ии ; График ф-ии, разрывной в т. С;
1.Ф-ия  называется непрерывной в точке х0 , если предел называется непрерывной в точке х0 , если предел  в данной точке совпадает со значением ф-ии в этой же точке в данной точке совпадает со значением ф-ии в этой же точке 
2. 3. Разность  -приращение аргумента в точке х0 -приращение аргумента в точке х0 4. Разность  - приращение ф-ии в точке х0 вызывает приращение аргумента - приращение ф-ии в точке х0 вызывает приращение аргумента  5. Ф-ия  называется непрерывной в точке х0 , если бесконечно малому аргументу соответствует бесконечно малое значение ф-ии в точке х0 . называется непрерывной в точке х0 , если бесконечно малому аргументу соответствует бесконечно малое значение ф-ии в точке х0 .
Общие свойства ф-ии, непрерывной в точке.
Представим ф-ию с помощью бесконечно малых 1.  2.Пусть ф-ия  непрерывна в точке х0 и ее значение в этой точке отлично от нуля, то существует целая окрестность х0 , в которой ф-ия не равна нулю и сохраняет знак f(x0) непрерывна в точке х0 и ее значение в этой точке отлично от нуля, то существует целая окрестность х0 , в которой ф-ия не равна нулю и сохраняет знак f(x0) 
sign(х)(сигнум) 
Доказательство: а)  б)  Из а) и б) следует: 
Непрерывность и арифметические операции Пусть  и и  непрерывна в т. х0 , тогда справедливо: непрерывна в т. х0 , тогда справедливо: Сумма этих ф-ий непрерывна в т. х0 ;  - непрерывна в точке х0 - непрерывна в точке х0 2. Произведение этих ф-ий непрерывно в т. х0  - непрерывна в точке х0 - непрерывна в точке х0 3. Отношение этих функций непрерывно в тех точках, в которых знаменатель отличен от нуля, т.е. если знаменатель 0. 
Доказательство: 
Непрерывность сложной ф-ии. Пусть: | Ф-ия  - непрерывна в т. y0 . - непрерывна в т. y0 . Ф-ия  - непрерывна в т. х0 . - непрерывна в т. х0 . 
|
тогда сложная ф-ия  - непрерывна в т. х0 . - непрерывна в т. х0 . |
Доказательство: А). 
Б).  из А) и Б) следует: 
Sl. 
Непрерывность ф-ии на множестве. Df. Ф-ия непрерывна на множестве Х , если она непрервна в каждой точке этого меожества. Непрерывность обратной ф-ии: Пусть  - непрерывна и строго монотонна на промежуте Х , тогда справедливо: - непрерывна и строго монотонна на промежуте Х , тогда справедливо: ***** На промежутке Y существует непрерыная обратная ф-ия  . . Характер монотонности обратной ф-ии такой же как и прямой. Непрерывность элементарной ф-ии: ********** Доказательство непрерывности основной элементарной ф-ии tg и ctg , следует из свойств непрерыности элементарных ф-ий. Непрерывность log, arcsin, arccos, arstg следует из определения непрерывности обратной ф-ии. Df Элементарные ф-ии, полученные из основных элементарных ф-ий с помощью арифметических операций, взятых в конечном числе,********
Характеристика точек разрыва ф-ии. 1. Точка устранимого разрыва. D(f) т. х0 называется точкой устранимого разрыва ф-ии  , если она не определена в этой точке, но имеет конечный предел. , если она не определена в этой точке, но имеет конечный предел.
Ф-ию можно сделать непрерывной в этой точке, доопределив ей значение в этой точке равным пределом. 
2. Точка разрыва первого рода. D(f) х0 – точка разрыва первого рода, если существует конечный левосторонний и правосторонний предел не равные между собой.  Разницу (b-a)называют скачком ф-ии в т. х0
3. Точка разрыва второго рода. *********************************
Односторонняя непрерывность ф-ии. Если в D(f)1 непрерывности предел заменить односторонним пределом, то получим определение односторонней непрерывности ф-ии. Ф-ия называется непрерывной в точке х0 справа, если правосторонний предел совпадает со значением ф-ии. Ф-ия называется непрерывной в точке х0 слева, есди левосторонний предел совпадает со значением ф-ии. Например:  - исследуем предел ф-ии справа и слева: - исследуем предел ф-ии справа и слева:  ф-ия непрепывна в точке х=0. ф-ия непрепывна в точке х=0. Для непрерывности в точке х0 необходимо и достаточно, чтобы она была непрерывна слева и справа в этой точке.
Свойства ф-й, непрерывных на отрезке Ф-ия называется непрерывной на отрезке [a,b], если она непрерывна на интервале(a,b) и в т. а непрерывна справа а в т. b – слева. Т1: Ф-ия  , непрерывная на [a,b], ограничена на этом отрезке. , непрерывная на [a,b], ограничена на этом отрезке.  - непрерывная на [a,b] - непрерывная на [a,b]  D(f) : число М называется наибольшим значением ф-ии на отрезке [a,b], если существует такое число  . . D(f) :точка называется наименьшим значекнием ф-ии на [a,b], если  Т2 : ф-ия  , непрерывная на [a,b],имеет на [a,b] наибольшее и наименьшее значения. , непрерывная на [a,b],имеет на [a,b] наибольшее и наименьшее значения. Т3 : *************
Sl1 : (f) ф-ии, непрерывной на отрезке, является отрезок Sl2 (Т3): ф-ия, непрерывная на отрезке [a,b], имеющая различные по знаку значения, на его границах обязательно обращается в ноль, хотя-бы в одной точке этого отрезка.
*******************************************
Дифференциальное счисление. Ф-ия одной переменной. 1. Задачи, приводящие к понятию производной. 3.1. Задача о вычислении скорости точки, движущейся вдоль прямой. Пусть точка движется вдоль прямой х. ****************************************** - l-единичный вектор, задающий направление вдоль прямой.    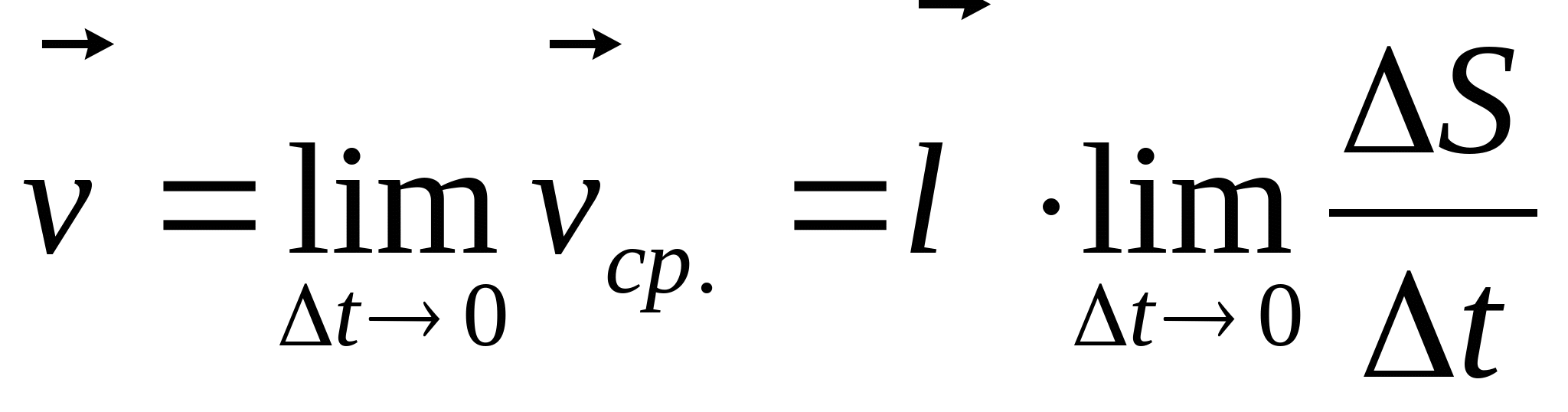 3.2 Построение касательной к кривой с уравнением  в т. х0 . в т. х0 . ********************  Задачи, различные по смыслу, из разных областей науки, свелись к вычислению одного и того же предела. В таких случаях в математике абстрагируются от крнкретных задач и изучают отдельно предел ф-й.
Определение призводной ф-ии в точке. Обозначение:  Df1 Производной ф-ии  в т. х называют предел отношения приращения ф-ии в этой т. к приращению аргумента, при стремлении последнего к нулю. в т. х называют предел отношения приращения ф-ии в этой т. к приращению аргумента, при стремлении последнего к нулю. 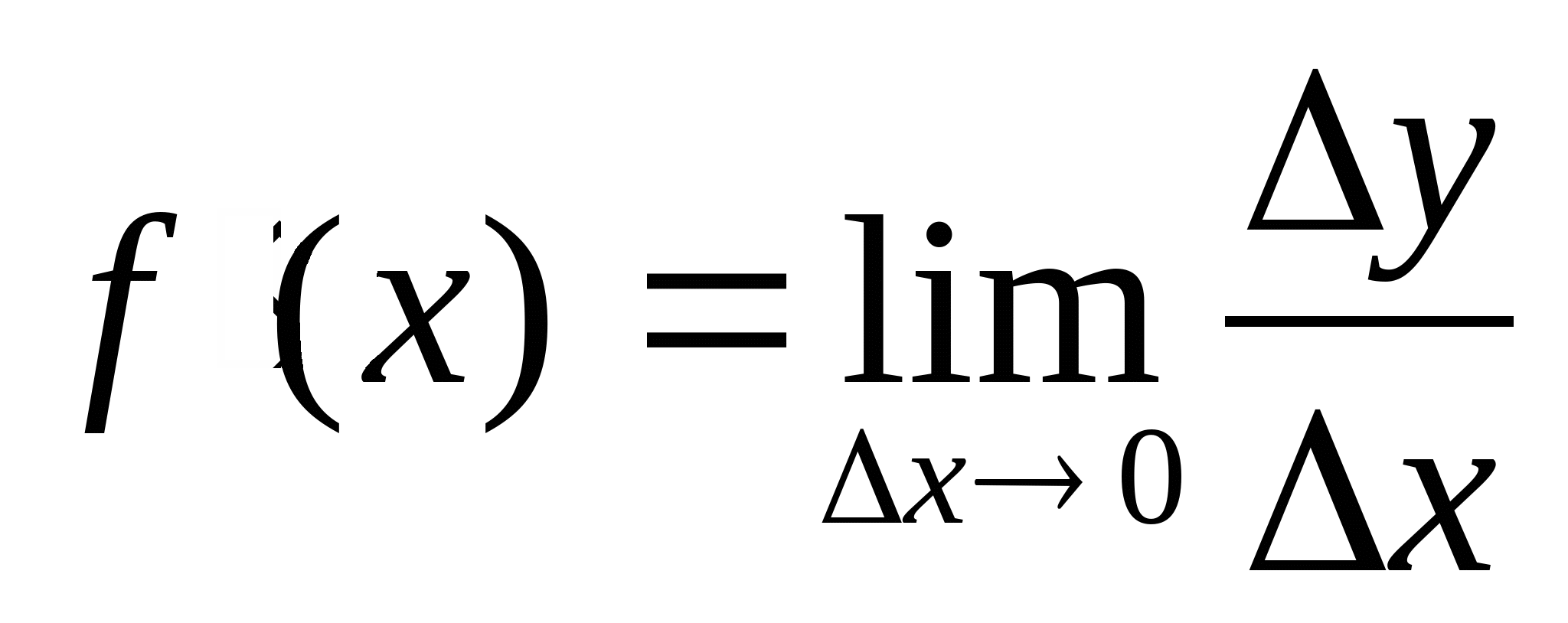
Пример: 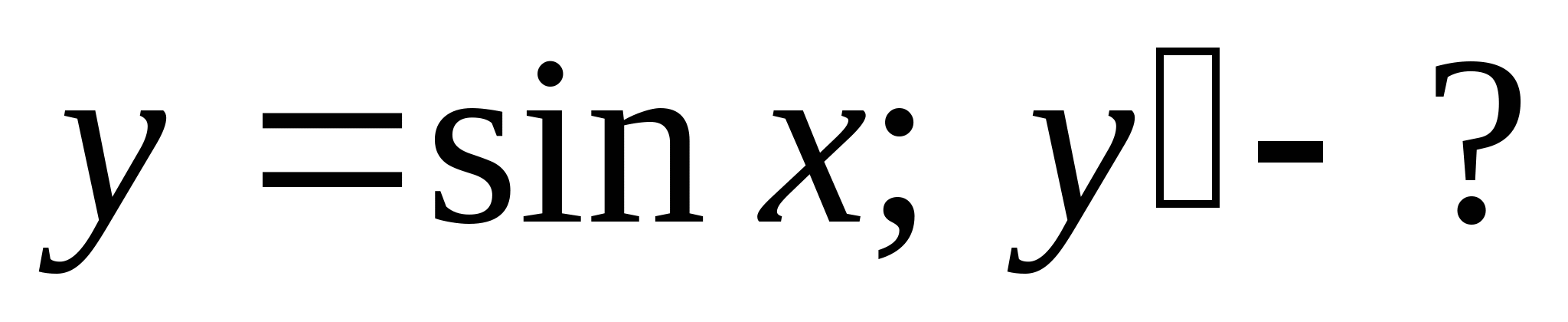   - непрерывная. - непрерывная. 
Степень ф-ии с вещественным показателем. Справка:  . .  Геометрический смысл производной. Из второй задачи следует, что поизводная ф-ии  в т. х0 =тангенсу угла наклона касательной, проведенной к графику ф-ии в этой точке. в т. х0 =тангенсу угла наклона касательной, проведенной к графику ф-ии в этой точке. Sl1 : Уравнение касательной к кривой. Его можно написать, зная точку, через которую она проходит, и угловой коэффициент   где x и y – координаты т. на касательной. где x и y – координаты т. на касательной. Sl2 : Уравнение нормали. Его можно написать, зная точку, через которую она проходит и угловой коэффициент  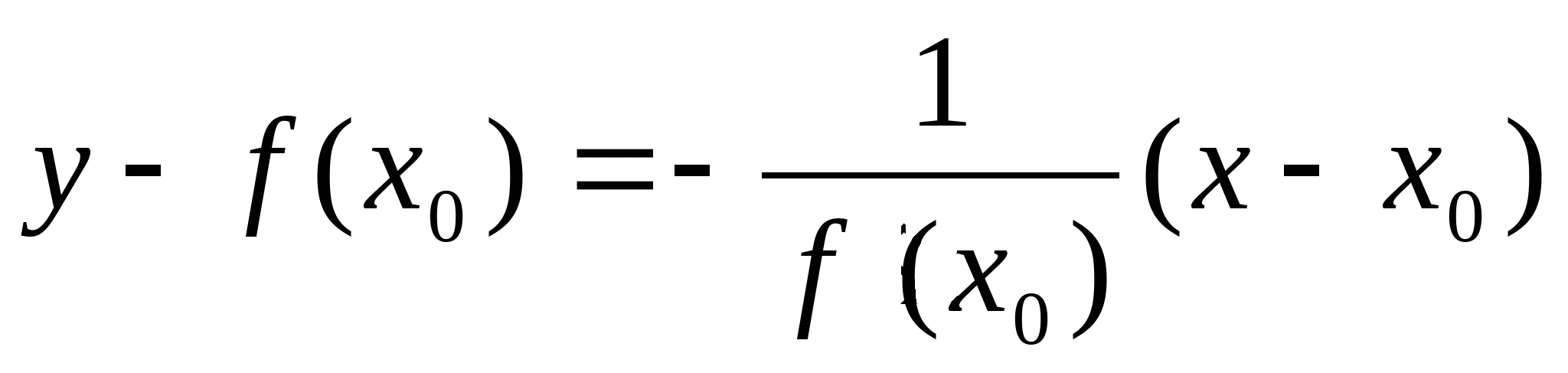 , x и y – точки на нормали. , x и y – точки на нормали.
Механический смысл производной. ************
Дифференцируемость ф-ии. Df : Ф-ия  дифференцируема в точке х0 , если приращение ф-ии в точке сможет быть представлено в виде: дифференцируема в точке х0 , если приращение ф-ии в точке сможет быть представлено в виде:  , А – const. , А – const. Dh: Для дифференцирования ф-ии в т. х0 , необходимо и достаточно, чтобы в этой точке существовала производная. Доказательство: (необходимость)  (достаточность): 
Производная суммы, произведения, частного. Dh:Пусть ф-ия  и и  дифференцируемы в точке х0 , тогда в этой точке дифференцируемы их сумма, произведение и частное, причем выполняются формулы: дифференцируемы в точке х0 , тогда в этой точке дифференцируемы их сумма, произведение и частное, причем выполняются формулы: 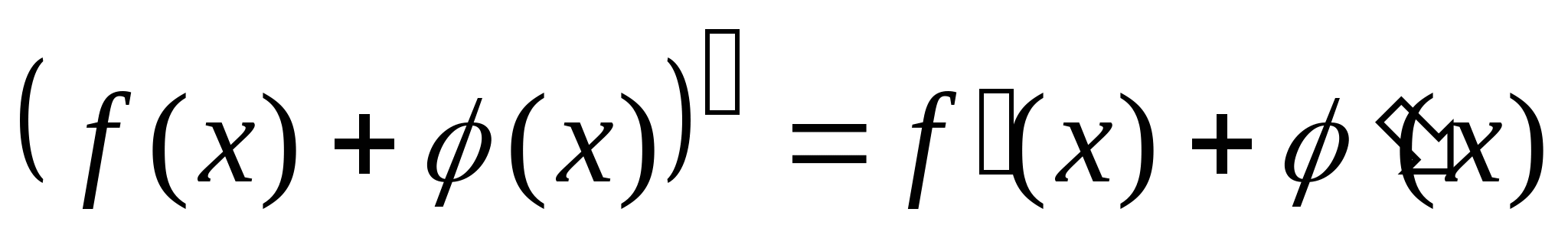   , если , если 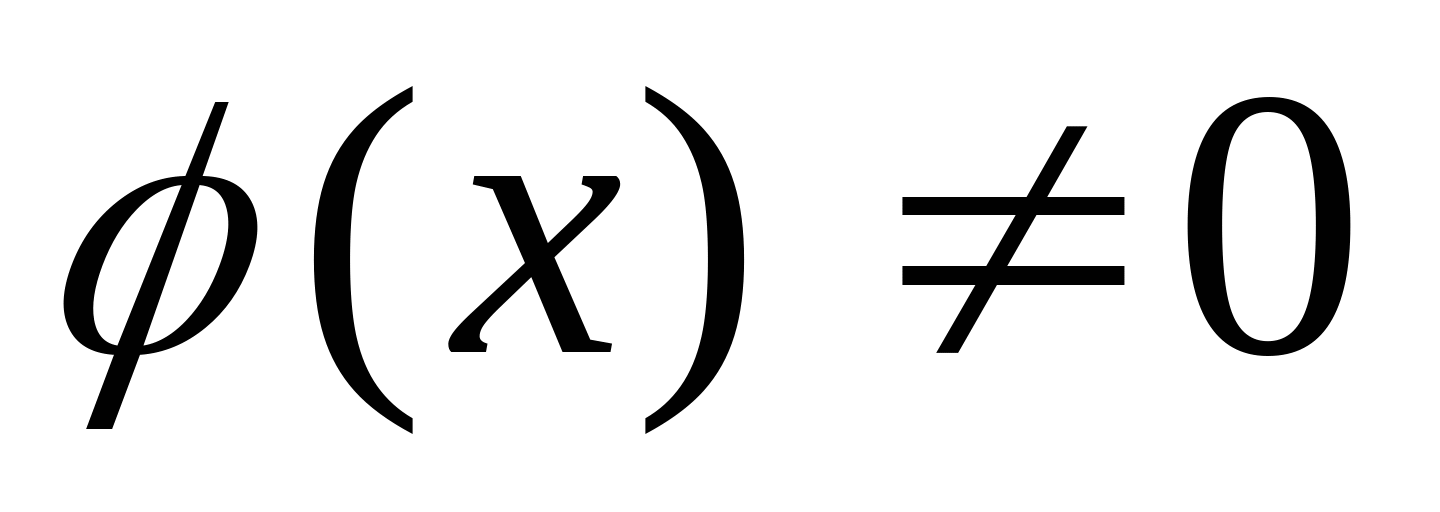 Лемма: Ф-ия, дифференцируема в точке х0 , непрерывнна в этой точке.  - дифф. в т. х0 - дифф. в т. х0  обратное утверждение неверно!!!
Производная от const ф-ии =0. Если  Доказательство: 
Zm1: При вычислении производной, константу можно выносить за знак производной.  Zm2: Данные формулы можно рассматривать на большее число слагаемых и сомножителей.
Df: Линейным колебанем системы из т. ф-ий называется сумма призведения этих ф-ий на производную и постоянную. называется сумма призведения этих ф-ий на производную и постоянную. 
Zm: Свойство линейности производной. Из доказанных свойств, следует, что производная от линейных колебаний ф-й = линейные комбинации призводных. 
Производная от обратной ф-ии. Dh: Пусть  в точке х0 имеет: в точке х0 имеет:  на промежутке, содержащем х0 , обратную ф-ию   тогда в точке х0 существует  , равная , равная 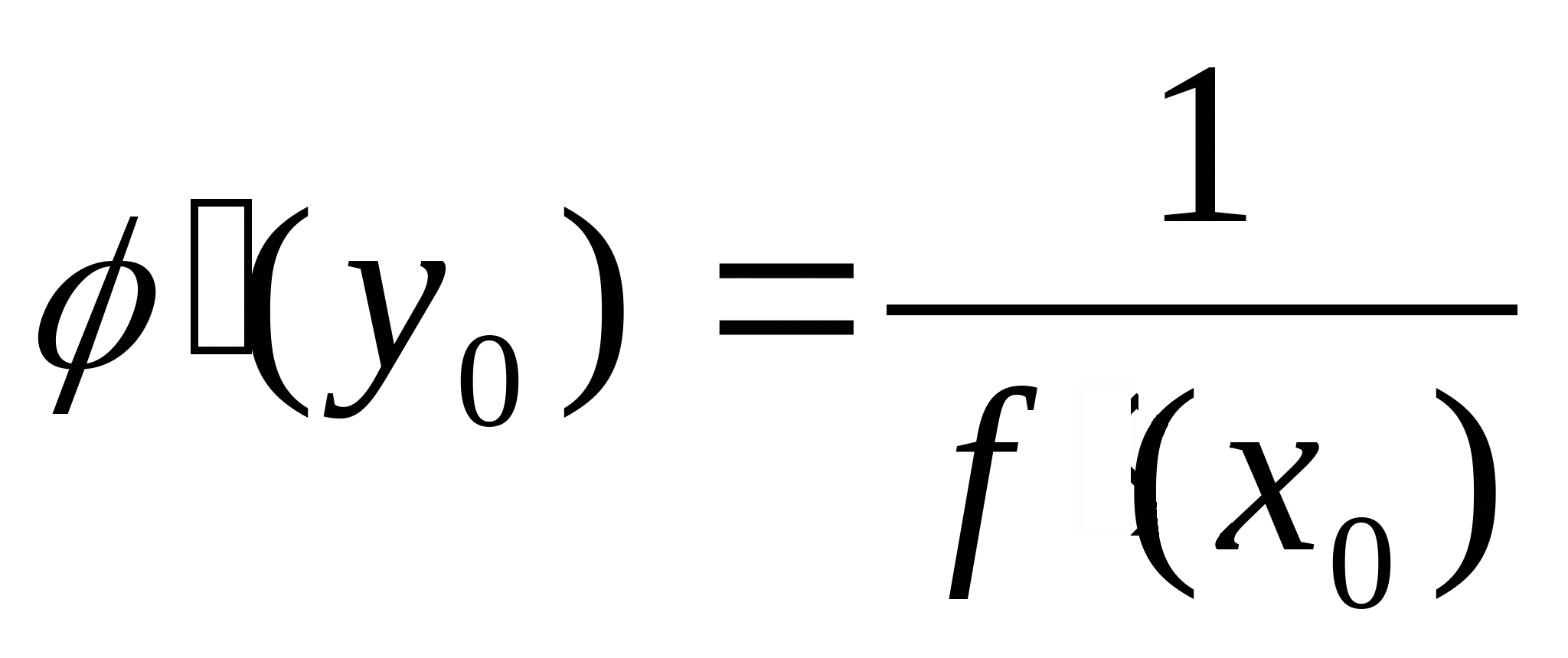
Производная от обратной ф-ии. Dh: Пусть  в точке х0 имеет: в точке х0 имеет:  на промежутке, содержащем х0 , обратную ф-ию   тогда в точке х0 существует 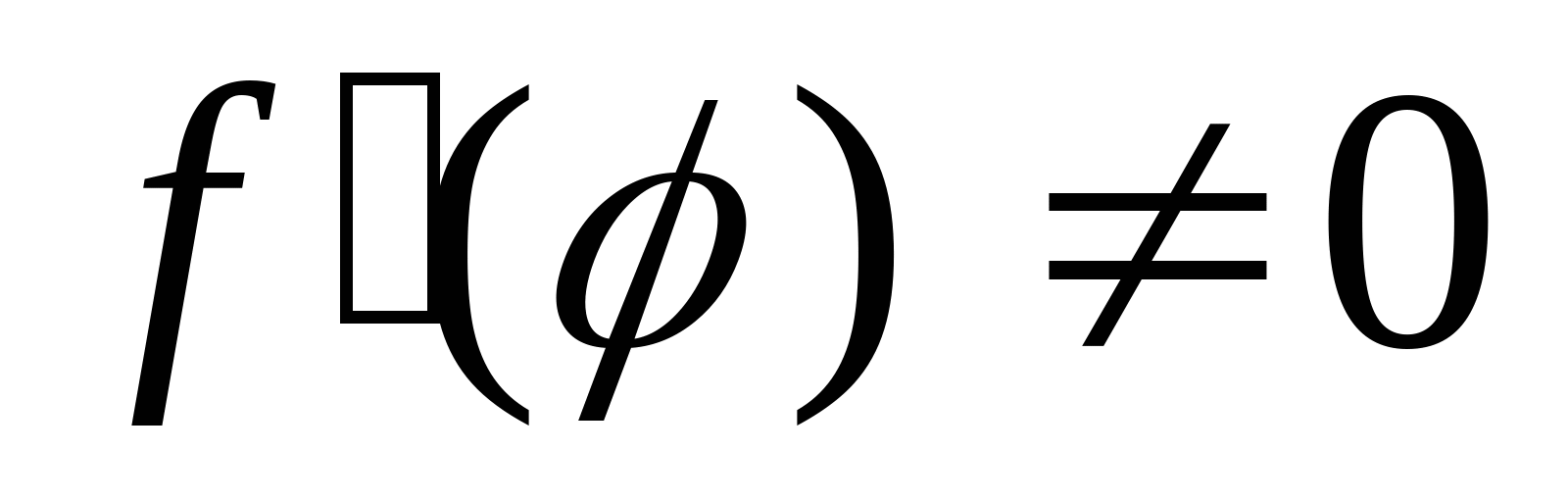 , равная , равная  Доказательство: 1. Пусть и двум различным значениям х соответствует е различных значений y . и двум различным значениям х соответствует е различных значений y .  2. Пусть  дифф. в точке х0 , тогда дифф. в точке х0 , тогда   3. т.к. 
Производная от сложной ф-ии. Dh: Пусть:  - дифф. в точке y0 . - дифф. в точке y0 .  - дифф. в точке х0 . - дифф. в точке х0 .  тогда сложная ф-ия  - дифф. в точке х0 и справедлива формула: - дифф. в точке х0 и справедлива формула:  Доказательство: 1.  - дифф. в точке y0 - дифф. в точке y0  2.  - дифф. в точке х0 - дифф. в точке х0   3.  - дифф. в точке х0 а значит непрерывна в этой точке - дифф. в точке х0 а значит непрерывна в этой точке . .   
Односторонние производные. Заменим в определении производной предел – односторонним пределом, получится определение односторонней производной.  
Производная от параметрически заданной ф-ии. Df: Ф-ия  называется заданной параметрически, если ее аналитическое выражение может быть представлено в виде: называется заданной параметрически, если ее аналитическое выражение может быть представлено в виде:  t- параметр. t- параметр. Dh: Пусть ф-ия задана параметрически, где  и и  дифф. в точке х0 , тогда дифф. в точке х0 , тогда  Доказательство: Предположим. что  имеет обратную ф-ию имеет обратную ф-ию  , тогда , тогда  - сложная ф-ия от х и определению сложной ф-ии имеет: - сложная ф-ия от х и определению сложной ф-ии имеет: 
Производные высших порядков. Df: Пусть ф-ия  дифф. на Х , то есть дифф. в каждой т. Х . дифф. на Х , то есть дифф. в каждой т. Х . Каждому значению Х соответствует единственное значение  , т.е. получаем , т.е. получаем  как ф-ию, заданную на Х. как ф-ию, заданную на Х. Если она окажется дифф. на Х, то мы можем вычислить следующую  , которая будет называться второй и т.д. , которая будет называться второй и т.д.  Df: Производной n-го порядка от ф-ии  называется первая производная от производной n-1 порядка. называется первая производная от производной n-1 порядка. 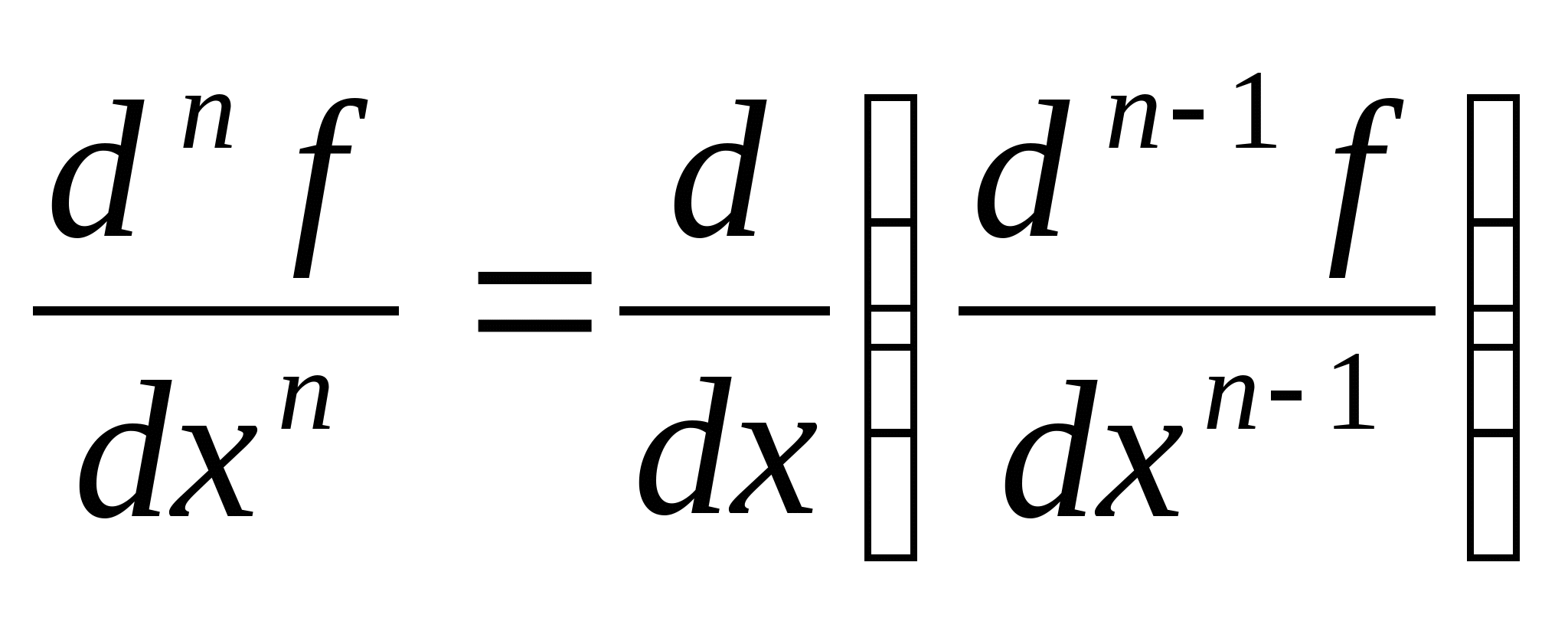 Пример:  Теоремы о дифф. ф-ях. Теорема Ферма: Пусть  дифф. на дифф. на  и наибольшее или наименьшее ее значение в т. х0 , тогда производная в этой точке равна нулю. и наибольшее или наименьшее ее значение в т. х0 , тогда производная в этой точке равна нулю. **************************
Доказательство: Пусть  - наибольшее на - наибольшее на 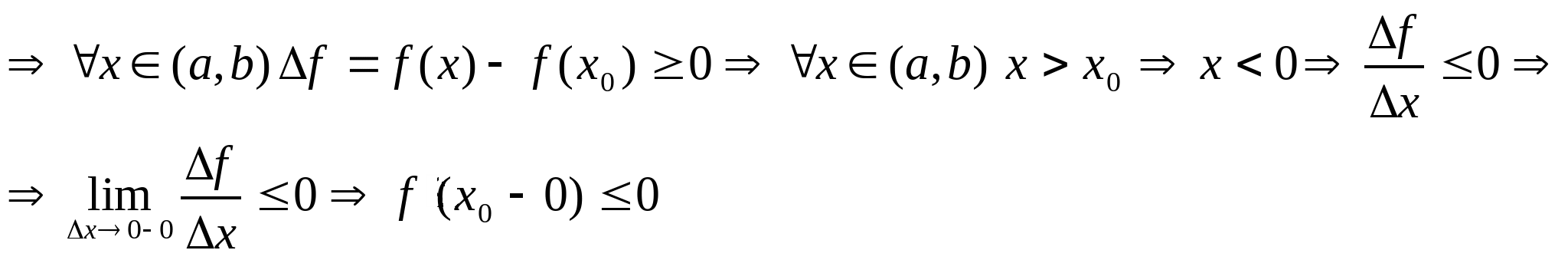 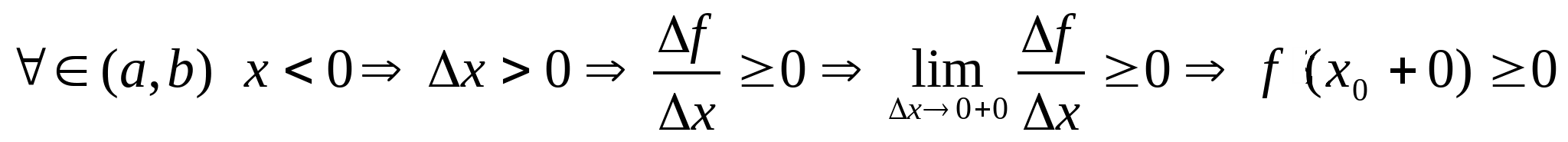 Но из дифф  в т. х0 в т. х0 
Zm: Из доказательства т. Ферма следует: Пусть  непрерывна на промежутке и внутренних точках этого промежутка принимает наибольшее и наименьшее значение, тогда если в этой точке ф-ия дифф., то непрерывна на промежутке и внутренних точках этого промежутка принимает наибольшее и наименьшее значение, тогда если в этой точке ф-ия дифф., то  . .
Теорема Ролля: Пусть ф-ия  : : непрерывна на  дифф. на  Принимает на концах этого отрезка одинаковые значения. Тогда на  существует т. х0 , в которой существует т. х0 , в которой  ************* Доказательство: Из непрерывности ф-ии на отрезке следует, что имеет на этом отрезке свои наименьшее(m) и наибольшее(M) значения. Возьмем два случая: m=M ; наименьшее значение совпадает с х0 следовательно:   ; из (3) следует: ; из (3) следует:  *********** ***********
Dh: Между двумя корнями ф-ии есть точка производной.
Теорема Лагранжа: Пусть ф-ия  непрерывна на промежутке непрерывна на промежутке  , дифф. на , дифф. на , тогда на , тогда на существует такая х0 такая, что верна формула: существует такая х0 такая, что верна формула:  Если ее переписать в виде  ************************** Доказательство: Рассмотрим вспомогательную ф-ию  . . Она непрерывна на  как сумма непрерывных ф-ий. как сумма непрерывных ф-ий. F(x) – дифф. на  как сумма дифф. на интервале ф-ий. как сумма дифф. на интервале ф-ий. F(а) = 0; F(b) = 0 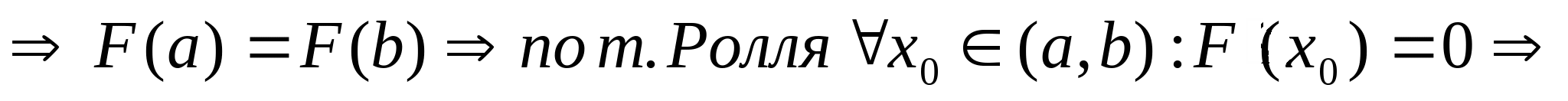  Sl: Пусть ф-ия  дифф. на дифф. на  , тогда для любой внутренней точки интервала справедлива формула Лагранжа: , тогда для любой внутренней точки интервала справедлива формула Лагранжа:
 х0 между х0 между 
Действительно ***************
Из дифф. ф-ии на  следует ее непрерывность на следует ее непрерывность на  
Теорема Коши: Пусть  и и  : : Непрерывны на  . . Дифф. на  Тогда на  существует т. х0 , для которой справедлива формула Коши: существует т. х0 , для которой справедлива формула Коши:  Доказывается как теорема Лагранжа. 
Приложение производной к исследованию ф-ий. 1. Исследование на монотонность. Пусть  дифф. на дифф. на  , тогда справедливо: , тогда справедливо: Ф-ия возрастает на  на на  . . Ф-ия не убывает на  на на  . . Ф-ия постоянна на  на на  . . Ф-ия не возрастает на  на на  . . Ф-ия убывает на  на на  . . 2. Исследование на экстремум. Df: т. х0 называется точкой локального минимума, если ф-ия непрерывна в этой точке и существует такая окрестность х0 , что для любого х  **************************
Исследование ф-ии на выпуклость графика.
************************** Df: График ф-ии  на на  направлен выпуклостью вниз (вогнутый), если он расположен выше касательной, проведенной в любой точке направлен выпуклостью вниз (вогнутый), если он расположен выше касательной, проведенной в любой точке  , а график ф-ии , а график ф-ии  - выпуклый, если он расположен ниже касательной, проведенной в любой точке - выпуклый, если он расположен ниже касательной, проведенной в любой точке  . . Df2: Точка х0 , в которой  непрерывна, называется точкой перегиба, если она отделяет интервал выпуклости от интервала вогнутости. непрерывна, называется точкой перегиба, если она отделяет интервал выпуклости от интервала вогнутости. Достаточные условия выпуклости ф-ии на интервале. Пусть ф-ия  дважды дифф. на дважды дифф. на  и и  сохраняет на нем свой знак, то: сохраняет на нем свой знак, то:  , то график на , то график на - вогнутый. - вогнутый.  , то график на , то график на - выпуклый. - выпуклый. Асимптоты графика ф-ии. В некоторых случаях, когда график ф-ии имеет бесконечные ветви, оказывается, что при удалении точки вдоль ветви к бесконечности, она неограниченно стремится к некоторой прямой. Такие прямые называют асимптотами. .Вертикальные асимптоты – прямая  называется вертикальной асимптотой графика ф-ии называется вертикальной асимптотой графика ф-ии  в точке b , если хотя бы один из разносторонних пределов равен бесконечности. в точке b , если хотя бы один из разносторонних пределов равен бесконечности. Если ф-ия задана дробно-рациональным выражением, то вертикальная асимптота появляется в тех точках, когда знаменатель равен нулю, а числитель не равен нулю. ******************** Наклонная асимптота – прямая  наклонная асимптота ф-ии наклонная асимптота ф-ии  , если эта ф-ия представлена в виде , если эта ф-ия представлена в виде  Необходимый и достаточный признак существования наклонной асимптоты: Для существования наклонной асимптоты  к графику ф-ии к графику ф-ии  необходимо и достаточно существование конечных пределов: необходимо и достаточно существование конечных пределов:   Доказательство: Пусть:  Пусть:  Следовательно существует асимптота.
Общая схема исследования ф-ий По ф-ии D(f) E(f) Непрерывность в области определения Четность, нечетность. Переодичность Асимптоты По первой производной Экстремумы Интервалы монотонности По второй производной Интервалы выпуклостей Точки перегиба Построение графика ф-ии.
Приложение производной к вычислению пределов. (Правило Лопиталя). Пусть: Ф-ии  и и  дифф. в проколотой окрестности точки х0 дифф. в проколотой окрестности точки х0   то справедливо: 
Доказательство: 1. Доопределим ф-ии  и и  в точке х0 так, чтобы они стали непрерывными, т.е. в точке х0 так, чтобы они стали непрерывными, т.е.  ф-ия непрерывна на всей окрестности ф-ия непрерывна на всей окрестности  2. применим т.Коши на интервале применим т.Коши на интервале  или или   , где ζ лежит между х и х0 следовательно , где ζ лежит между х и х0 следовательно  Zm:Если производная ф-ии удовлетворяет правилу Лопиталя, то можно вычислять последнюю несколько раз (2,3,4…), пока она удовлетворяет условию.Правило Лопиталя применимо, когда x0 – бесконечно удаленная точка.
Дифференциал ф-ии. Из Df дифференцируемости следует, что приращение дифф. ф-ии  можно представить в виде можно представить в виде  Из равенства нулю предела следует, что  - б.м. более высшего порядка малости, чем - б.м. более высшего порядка малости, чем 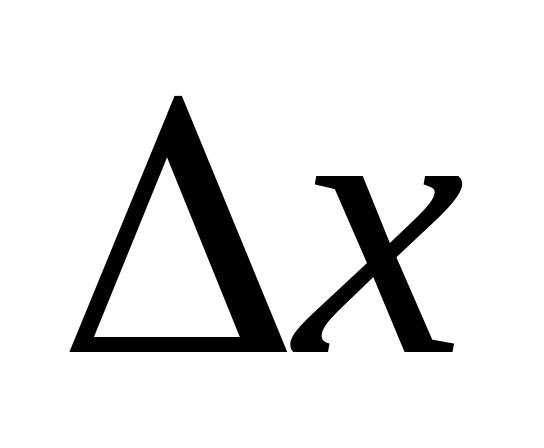 , и , и  Поскольку  - б.м. одного порядка малости. - б.м. одного порядка малости.  - б.м. одного порядка малости - б.м. одного порядка малости  - б.м. эквивылентные, т.е. - б.м. эквивылентные, т.е.  Пусть 
************** 
Zm1:  и х – независимые переменные, т.е. и х – независимые переменные, т.е. 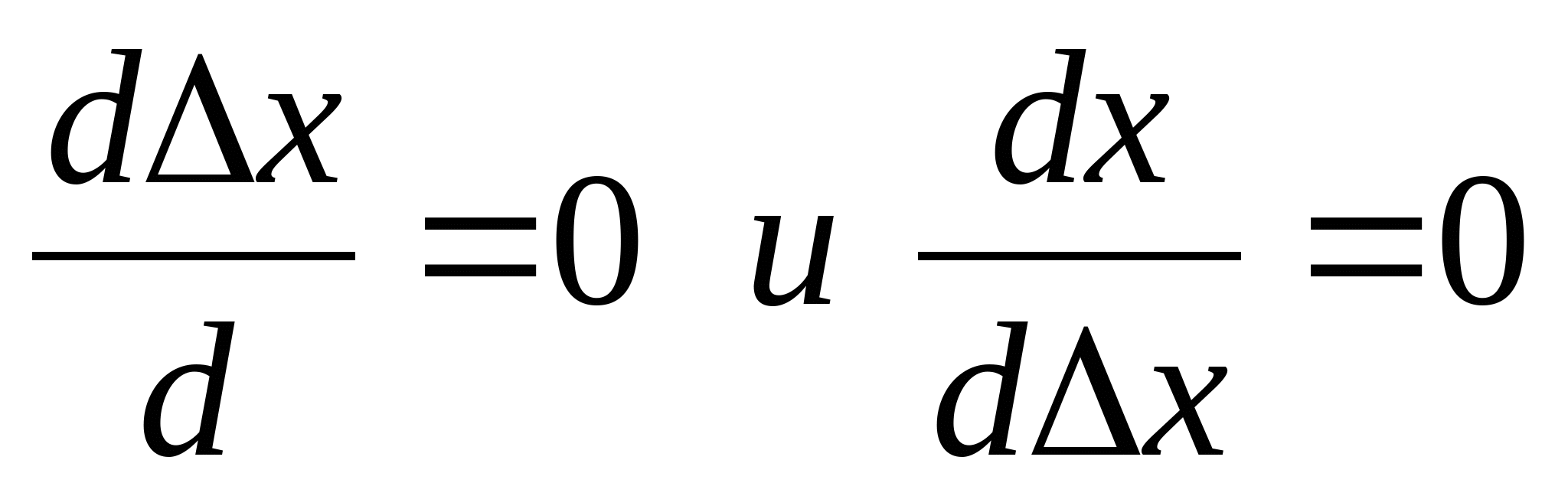 Zm1:  для независимых переменных. для независимых переменных. 
Свойства дифференциала:     
Дифференцирование сложных ф-ий. Инвариантность в форме дифференциала
Интегрирование с помощью подстановки. Пусть подынтегральная ф-ия в интеграле непрерывна на Х и ф-ия  дифф. на промежутке Т и имеет на нем обратную ф-ию дифф. на промежутке Т и имеет на нем обратную ф-ию 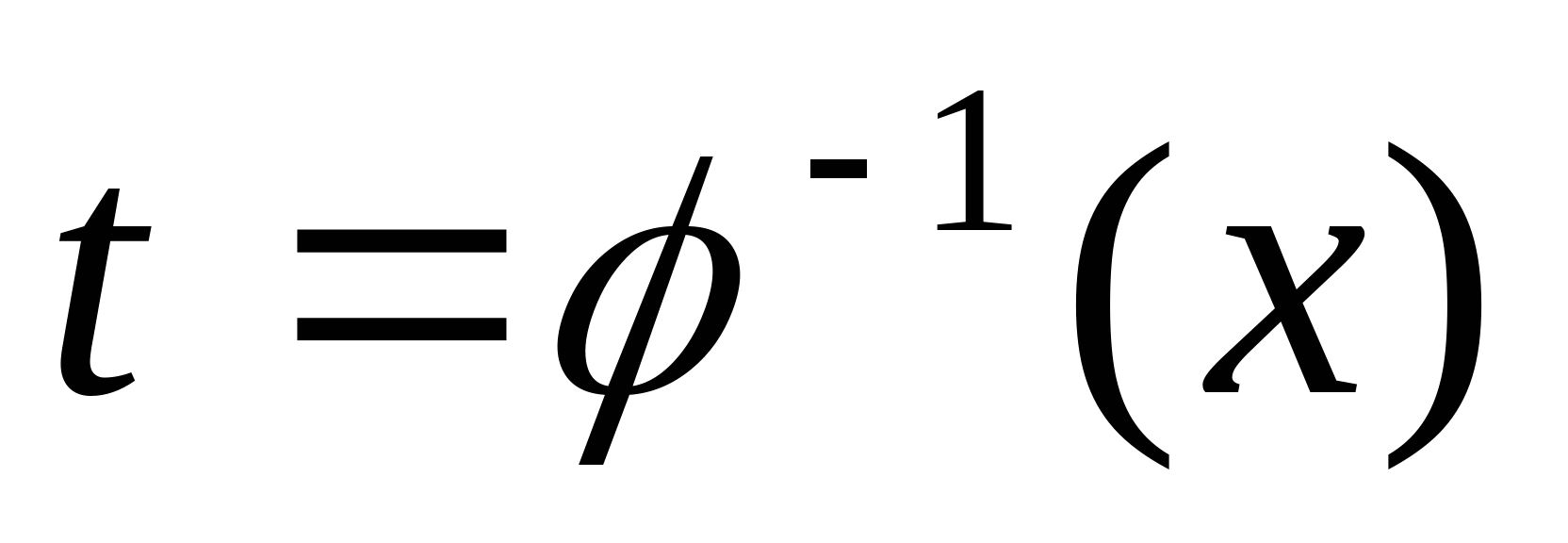 с с  на промежутке Х , тогда справедливо: на промежутке Х , тогда справедливо: 
Алгоритм интегрирования подстановкой. Для интеграла подынтегральная ф-ия  такая, что такая, что  является табличным или сводится к нему так, что легко находится является табличным или сводится к нему так, что легко находится  . . Нах. обратную ф-ию 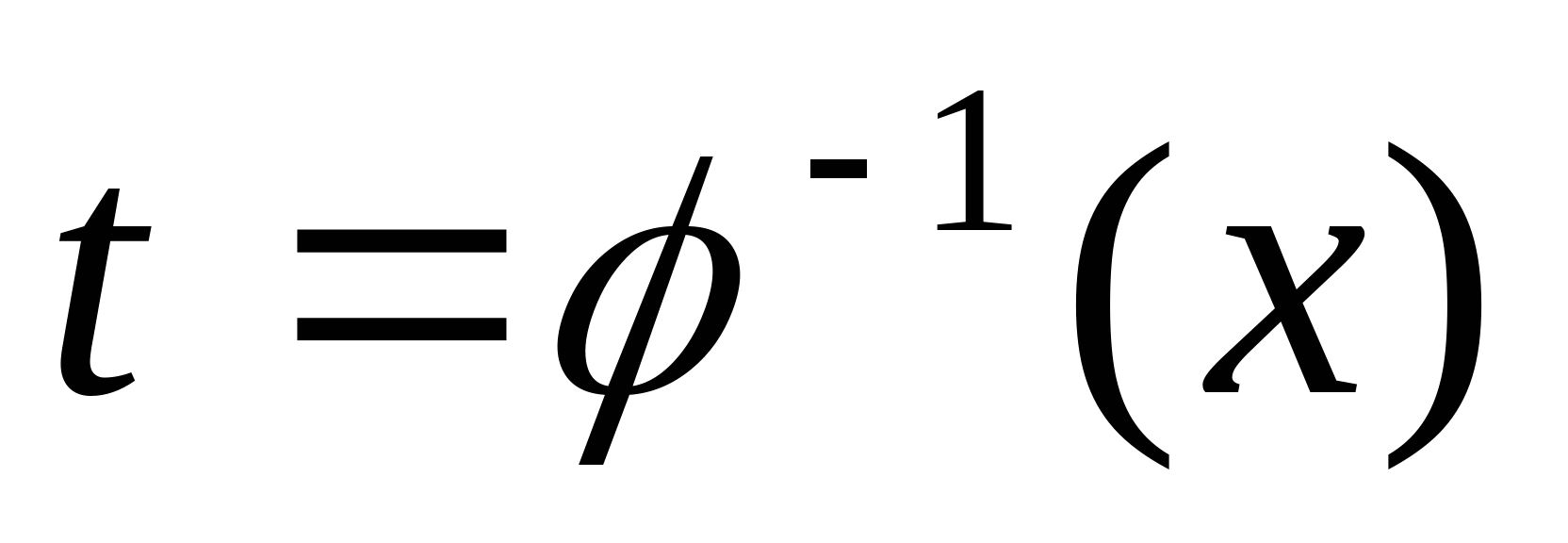 и подставляем в и подставляем в  , которая и будет первообразной для исходного интеграла. , которая и будет первообразной для исходного интеграла.
Алгоритм: Часть подынтегрального выражения вводится под знак дифференциала и полученное выражение под знаком дифференциала обозначается как новая переменная. В подынтегральной ф-ии делается замена переменной на новую, находится  от новой переменной. от новой переменной. В  возвращ. к старой переменной. возвращ. к старой переменной.
Интегрирование по частям. Интегрирую выражение любого дифференциала произведения, получим:  
Пример:  Рекомендации: В интегралах с подынтегральным выражением вида:  (Pn –многочлен степени n ) (Pn –многочлен степени n ) Pn принимается за u
В интегралах с подынтегральным выражением вида:  за u  Интегрирование с подстановкой выражений вида  после двукратного интегрирования по частям приводится к линейному уравнению относительно вычисляемого интеграла. после двукратного интегрирования по частям приводится к линейному уравнению относительно вычисляемого интеграла.
Интегрирование дробно-рациональных выражений Df Дробно-рациональная ф-ия  - отношение 2х многочленов - отношение 2х многочленов  - многочлены степени n и m соответственно. - многочлены степени n и m соответственно. Рациональная дробь правильная, если степень числителя строго меньше степени знаменателя, обратно - неправильная.
Zm Неправильная рациональная дробь путем выделения целой части приводится к сумме многочлена и правильной рациональной дроби; многочлен называется целой частью неправильной дроби.
Простейшие (элементарные) рациональные дроби и их применение. К простым рациональным дробям относятся рациональные дроби типов:  - вещественные постоянные - вещественные постоянные 2. - вещественные постоянные, - вещественные постоянные,  3. 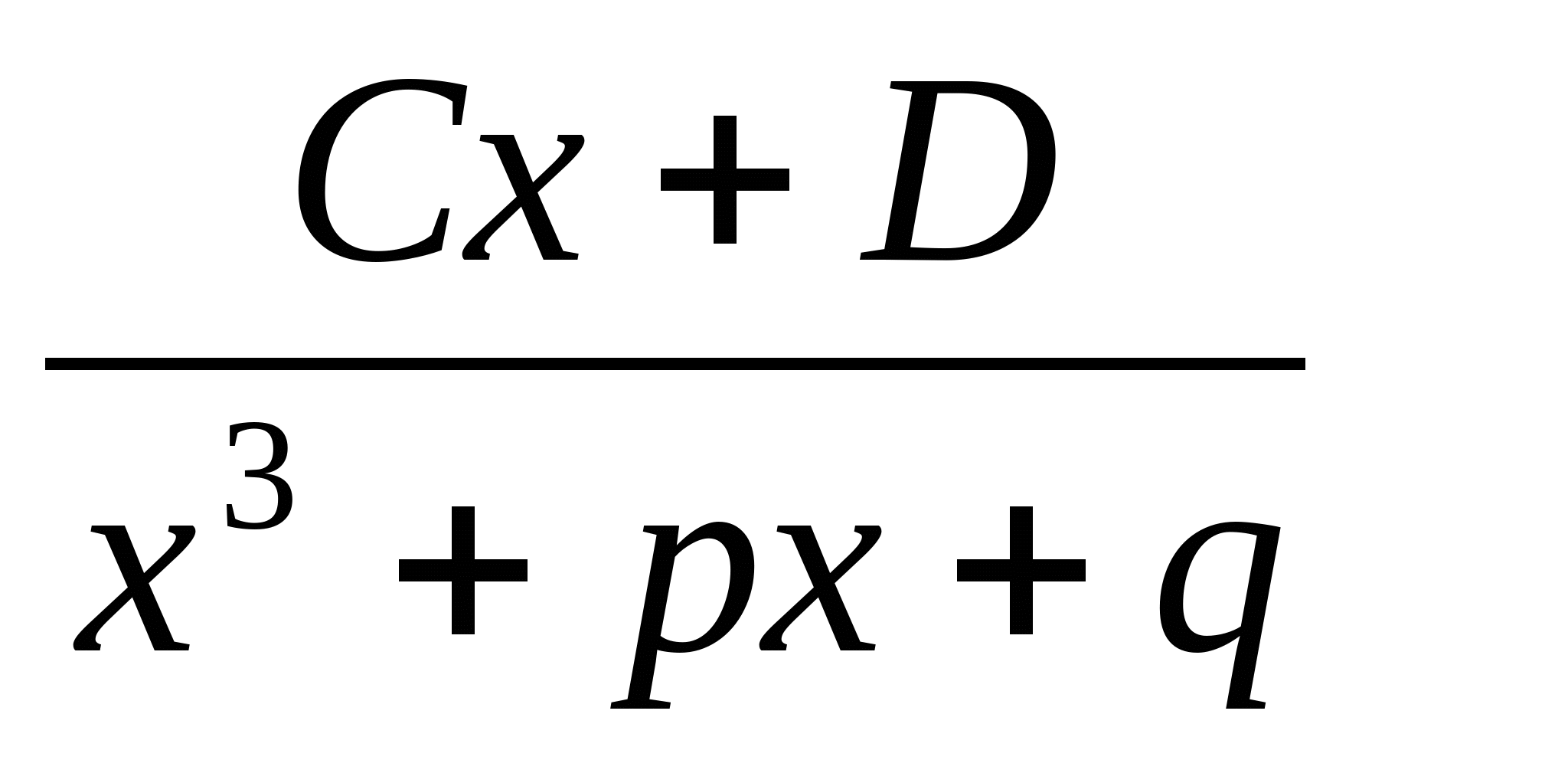 4. 
Интегрирование 1го типа: 
Интегрирование 2го типа: 
Интегрирование 3го типа: проводится в два этапа: 1. В числителе выделяется дифференциал знаменателя:   2. Выделение полного квадрата в знаменателе второго интеграла.   
Интегрирование 4го типа: 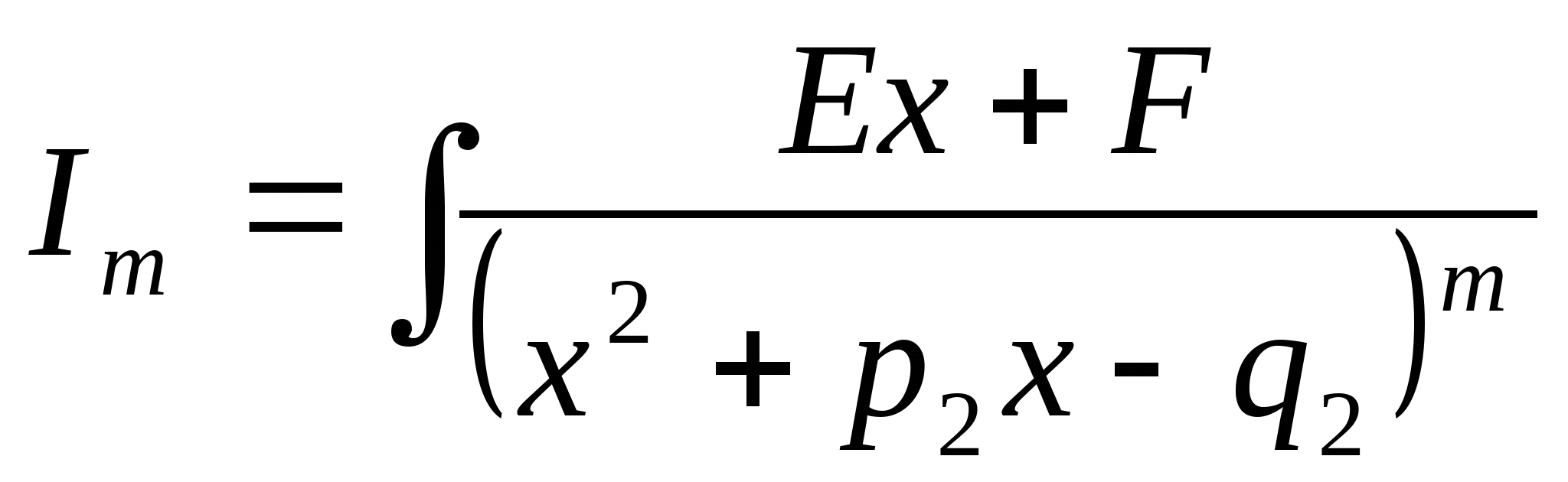 1. Выделяем в числителе *** знаменателя:  Выделяем в знаменателе 2го интеграла ф-лы квадрата: 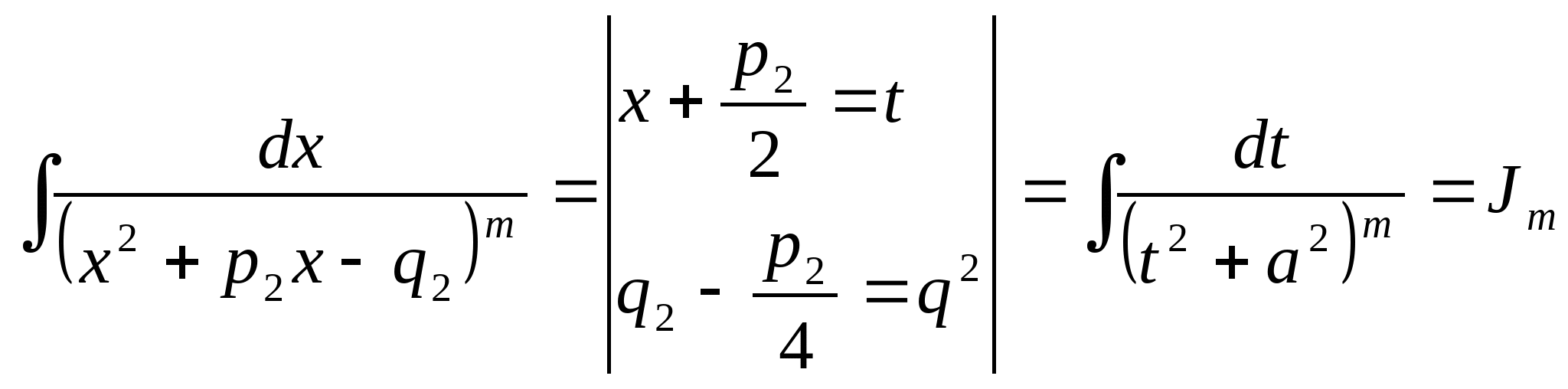 Рекуррентная формула для вычисления Jm (вычисление происходит путем подстановки в известную форму)

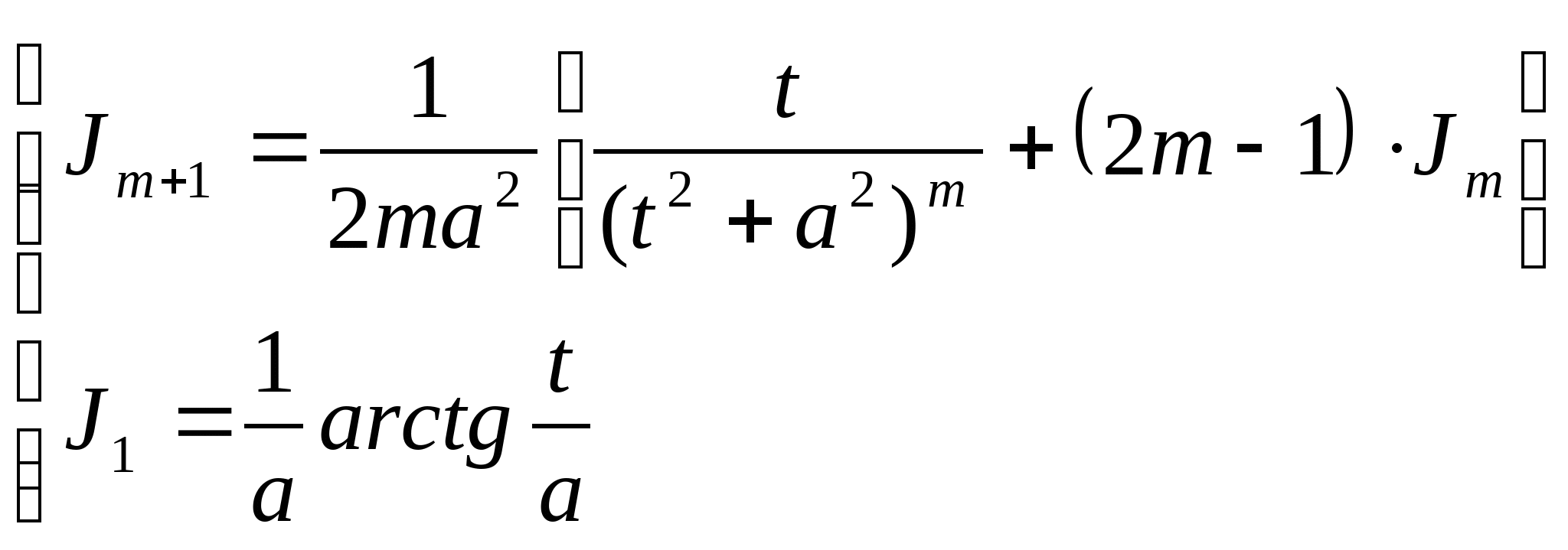
Метод неопределенных коэффициентов. 1. Разложим знаменатель на множители:  2. Правильная дробь разлагается в сумму простейших и каждому множителю вида  соотв. сумма из n простейших дробей вида: соотв. сумма из n простейших дробей вида:  с неопределенным коэф. A1 …n с неопределенным коэф. A1 …n Каждому множителю вида соот. сумма из m простейших дробей вида: соот. сумма из m простейших дробей вида: с неопределенным коэф.B1 C1…
3. Неизвестный коэф. находится методом неопределенных коэф., основанном на: определении, что 2 многочлена тождественно совпадают, если у них равные коэффициенты при одинаковых степенях. 4. Приравнивая коэф. при одинаковых степенях в левой и правой частях, получим систему линейных уравнений относительно неизвестного уравнения.
Определенный интеграл
Задача, приводящая к понятию определенного интеграла. Вычисление площади криволинейной трапеции: Df. Криволинейная трапеция – фигура на площади, ограниченной линиями с уравнениями  1. Отрезок  разобьем на n частей: разобьем на n частей:  ********* Длина каждого отрезка 2. Т.к.  - непрерывна на - непрерывна на  , то она непрерывна на каждом частичном отрезке, принад. **** , то она непрерывна на каждом частичном отрезке, принад. **** 3. Впишем в трапецию мн-к, состоящий из пр-в с основаниями, совпадающими с частичными отрезками и высотой mi Суммируем площади пр-в – получаем площадь трапеции.  Меняя n , получаем числовую последовательность площадей, вписанных в многоугольник. Меняя n , получаем числовую последовательность площадей, вписанных в многоугольник.  ********** **********
4. Опишем около трапеции многоугольник
**********************************
Необходимое условие существование определенного интеграла. Df. Пусть существует интеграл  подынтегральная ф-ия подынтегральная ф-ия  ограничена на ограничена на  Доказательство: Пусть  - неограниченна на - неограниченна на  , то при любом разбиении этого отрезка она неограниченна на каком-то из частичных отрезков *** , то при любом разбиении этого отрезка она неограниченна на каком-то из частичных отрезков *** на частичном отрезке, мы можем сделать значение ф-ии в т. на частичном отрезке, мы можем сделать значение ф-ии в т.  сколь угодно большим по модулю интегральная сумма, соотв. этому прозв. разб. будет неограниченна не имеет предела противоречит условию ф-ия сколь угодно большим по модулю интегральная сумма, соотв. этому прозв. разб. будет неограниченна не имеет предела противоречит условию ф-ия  ограничена на ограничена на 
Некоторые классы интегральных ф-ий. Df. Любая ф-ия, для которой существует определенный интеграл на  , интегрируема на этом промежутке. , интегрируема на этом промежутке. Множество таких ф-ий обозначают  К интегрируемым на  ф-иям относятся: ф-иям относятся: Ф-ии, непрерывные на  Монотонные на  Имеющие на отрезке конечное или счетное мн-во точек разрыва 1-го рода. Свойства определенного интеграла. Df. Промежуток с гранич. т. A и B ориентированным, если указано направление перехода от т. A к т. B. 1. Пусть сущ. определенный интеграл 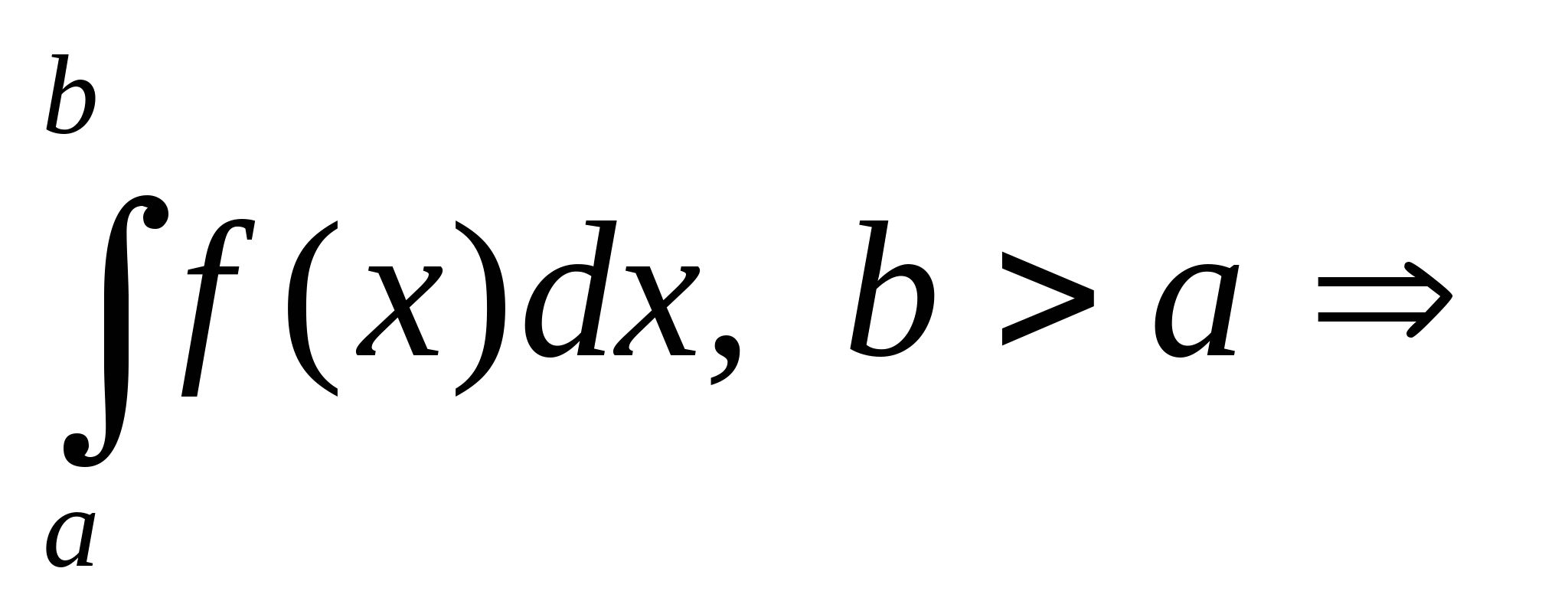 сущ. определенный интеграл сущ. определенный интеграл и справедливо равенство и справедливо равенство 
2.  Док-во:  
3. Свойство линейности определенного интеграла: 1. Пустьф-ии интегрируемы на интегрируемы на  *** ***  2. Пусть 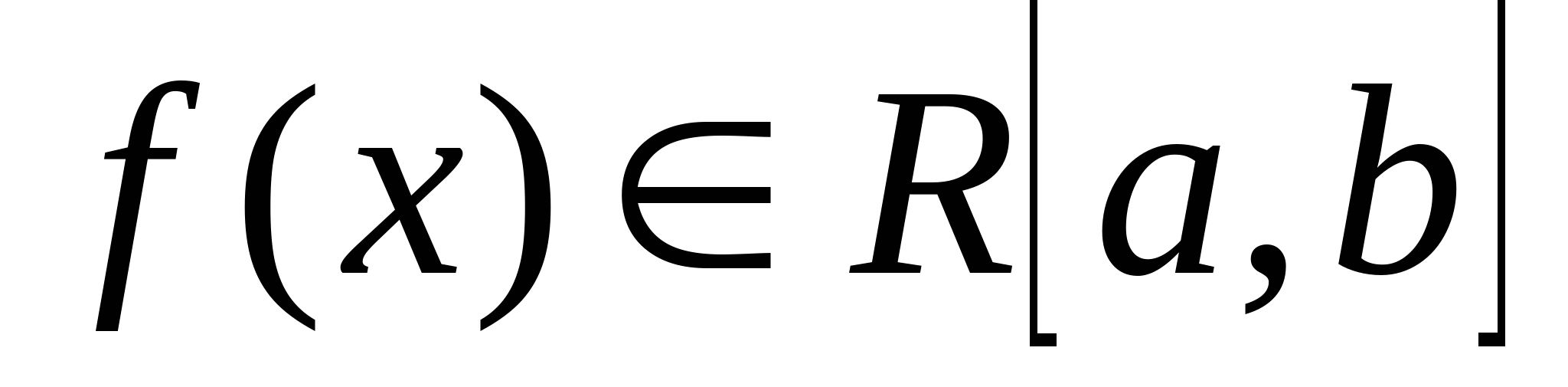 , то для любой произвольной постоянной , то для любой произвольной постоянной   - справедлива формула - справедлива формула  4. Аддитивность определенного интеграла: Пусть ф-ия  интегрируема на большем их трех помежутков интегрируема на большем их трех помежутков  , тогда она интегрируема на обоих меньших промежутках и справедлива формула: , тогда она интегрируема на обоих меньших промежутках и справедлива формула: 
Свойство монотонности. 1. Пусть ф-ия  неотрицательна на неотрицательна на  и интегрируема на нем, и интегрируема на нем,  Док-во: В силу н-ва для ф-ий любая интегрируема ф-ия неотрицательна любая последовательность интегрируемых сумм будет иметь неотрицательный предел интеграл будет неотрицательным.   2. Пусть ф-ия  на на  , искл. конечн. точек, и интегрируема на , искл. конечн. точек, и интегрируема на  , тогда , тогда  Док-во: Из интегрируемости следует, что предел не зависит от выбора разбиения на  . Достаточно строить инт. разбиения так, чтобы точки, в которых ф-ия равна нулю, являлись точками разбиения. А следовательно в силу аддитивности интеграл по всему прмежутку равен сумме интегралов по частичным промежуткам, т.к **** . Достаточно строить инт. разбиения так, чтобы точки, в которых ф-ия равна нулю, являлись точками разбиения. А следовательно в силу аддитивности интеграл по всему прмежутку равен сумме интегралов по частичным промежуткам, т.к ****  Df Две ф-ии  , заданные на , заданные на  , значения которых различны на , значения которых различны на  лишь в конечном ч. точек называются эквивалентными на этом отрезке. лишь в конечном ч. точек называются эквивалентными на этом отрезке.
3. Инт. от эквивалентных ф-ий совп. Пусть  эквивалентны и интегрируемы на эквивалентны и интегрируемы на  , тогда , тогда  (они не совпадают а интегралы совпадают). (они не совпадают а интегралы совпадают). Д-во:  на на  лишь в конеч. ч. точек отр. лишь в конеч. ч. точек отр.  , следовательно по 2му , следовательно по 2му   4. Пусть  на на  , кроме конечного ч. точек, , кроме конечного ч. точек,  инт. на инт. на  , ,  , то , то  5. Пусть  инт-ма на инт-ма на  модуль ф-ии тоже интегрируем на модуль ф-ии тоже интегрируем на  и справедливо неравенство: и справедливо неравенство:  6. Пусть  интегрируема на интегрируема на  , ,  , то существует М, такая что , то существует М, такая что  Интеграл как ф-ия переменного верх. предела. Пусть ф-ия  инт. на инт. на  , ,  , то она инт. на любом отрезке между , то она инт. на любом отрезке между  Рассмотрим определенный интеграл  . Из определения опр. интеграла следует,что любому х соот. единст. значние этого интеграла. . Из определения опр. интеграла следует,что любому х соот. единст. значние этого интеграла. Определенный интеграл с перемнного верх. предела – есть ф-ия своего предела 
1 теорема Гульдена Ph Гульдена Пусть криволинейная трапеция вращ. вокруг оси oX. Тогда она опишет тело вращения с массой  из формулы для центра масс знаем:     Объем тела, полученного вращением крив. трапеции, равно произведению площади этой трапеции на длину окружности, описанную из центра масс.
Однородная плоская дуга От точки с абсциссой х отложим дугу длины  . Тогда . Тогда  , ,  
2 теорема Гульдена Пусть плоская дуга вращается вокруг оси oX. Она опишет площадь:  Площадь поверхности, полученная вращением дуги, равна произведению длины этой дуги на длину окр-ти, описыв-ю ц. масс.
Несобств. интегралы. Для существования определенного интеграла должны выполняться два условия: Предел интегрирования конечный; Подынтегральная ф-ия ограничена. Нарушение этих двух условий приводит к несуществующему интегралу. В этом случае вводится обобщение определенного интеграла, который называется несобственным интегралом. 1. Несобственный интеграл с бесконечным пределом интегрирования. а)  - Пусть - Пусть  - интегрируема на любом - интегрируема на любом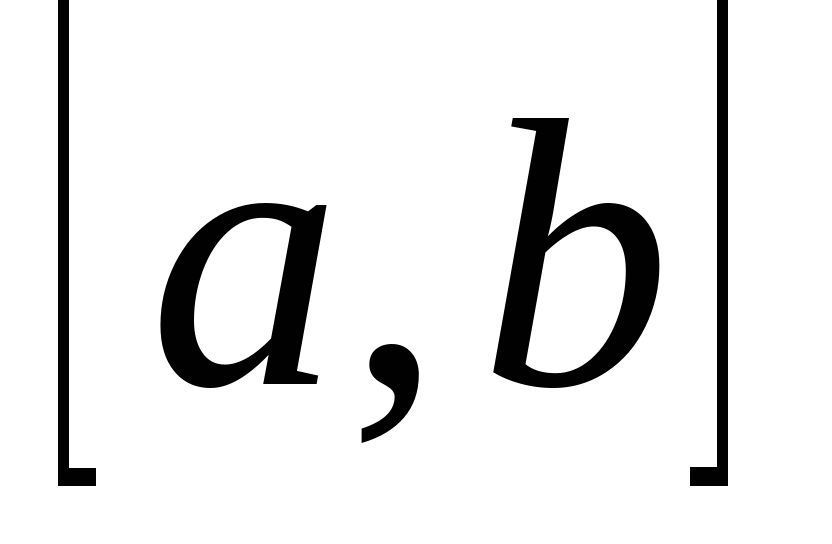 , где , где  , то по определению: , то по определению:  Если предел в правой части существует и конечен, говорят, что, инт. сходится; нет - расходятся. б)  в) 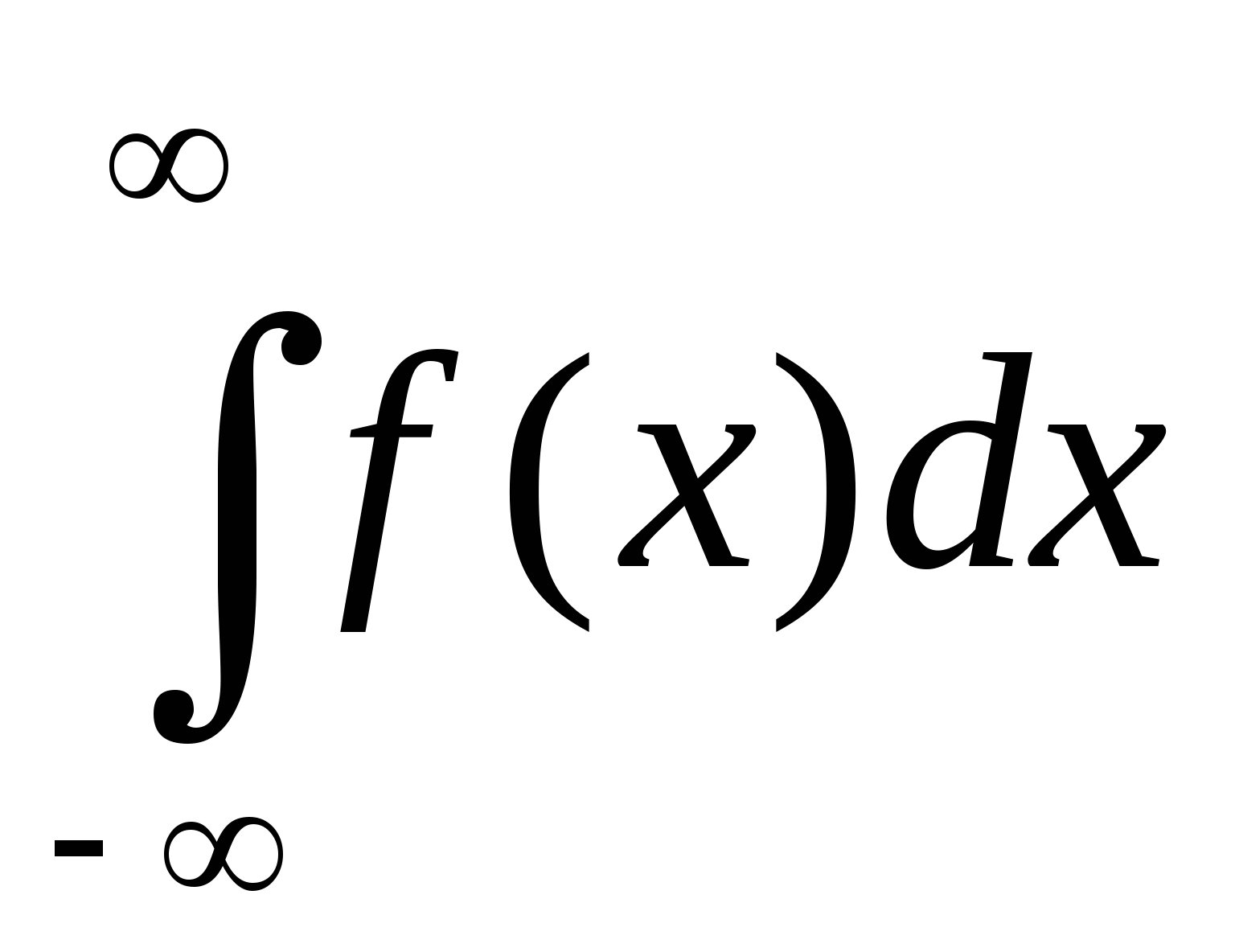 Этот случай сводится к предыдущему *** Этот случай сводится к предыдущему ***  , , 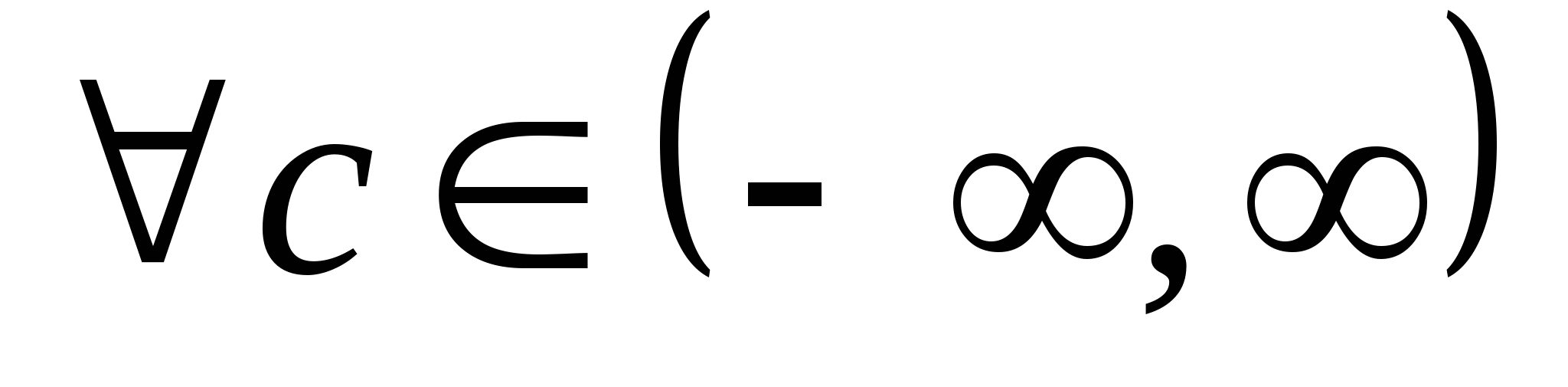 ; Результат от с не зависит ; Результат от с не зависит Zm: Инт. в левой части существует, если интеграл в правой части существует по отдельности, т.е. предел интегрирования в этих интервалах надо обозначать разными буквами. 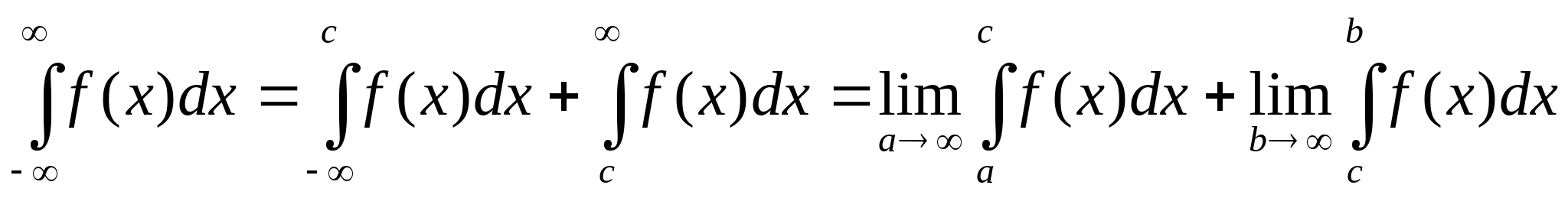 Признаки сходимости В некоторых случаях достаточно знать, сходится интеграл или нет, без его вычисления. Для этого применяется признак сравнения. 1). Пусть  и и  интегрируемы на интегрируемы на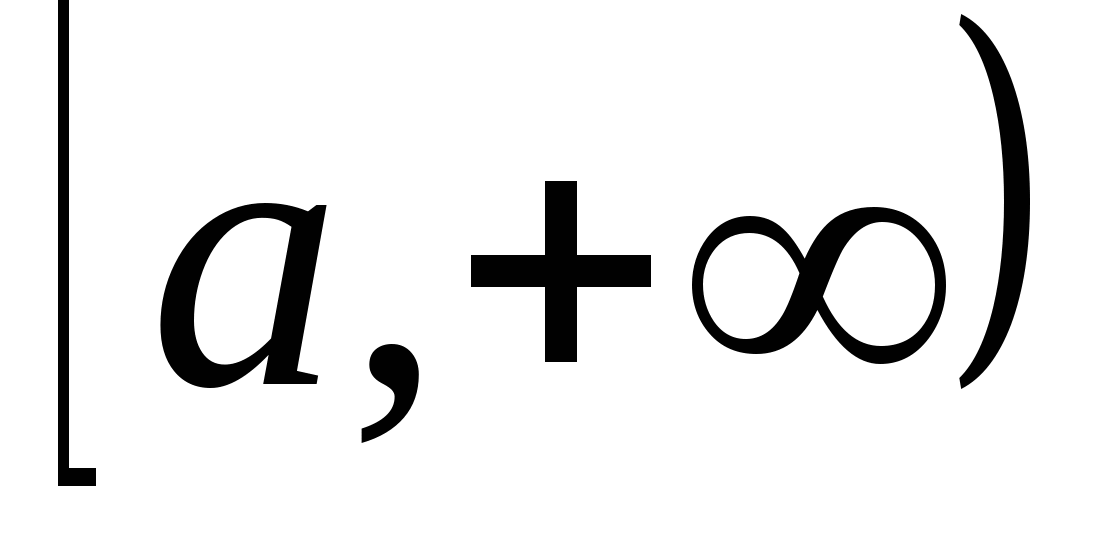 и удовлетворяют на этом промежутке неравенству: и удовлетворяют на этом промежутке неравенству: , то справедливо следующее утверждение: , то справедливо следующее утверждение:   Обратное утверждение неверно!!!
Rn *******     На арифм. эмерном пространстве метрика вводится по формуле:  , где , где 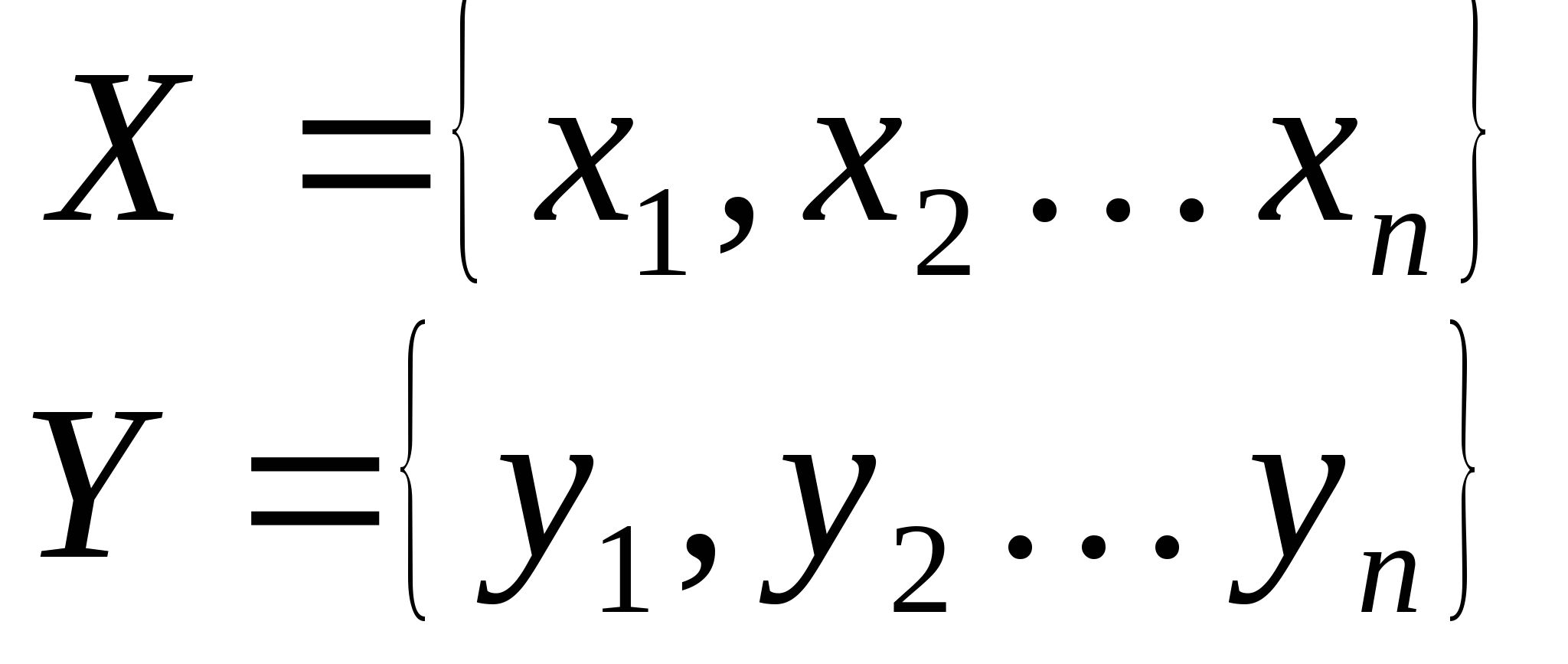 Арифм. эмерное пространство, сведенное с метрикой по формуле - евклидово пространство. Понятие окрестности в Rn
Интегрирование с помощью подстановки. Пусть подынтегральная ф-ия в интеграле непрерывна на Х и ф-ия 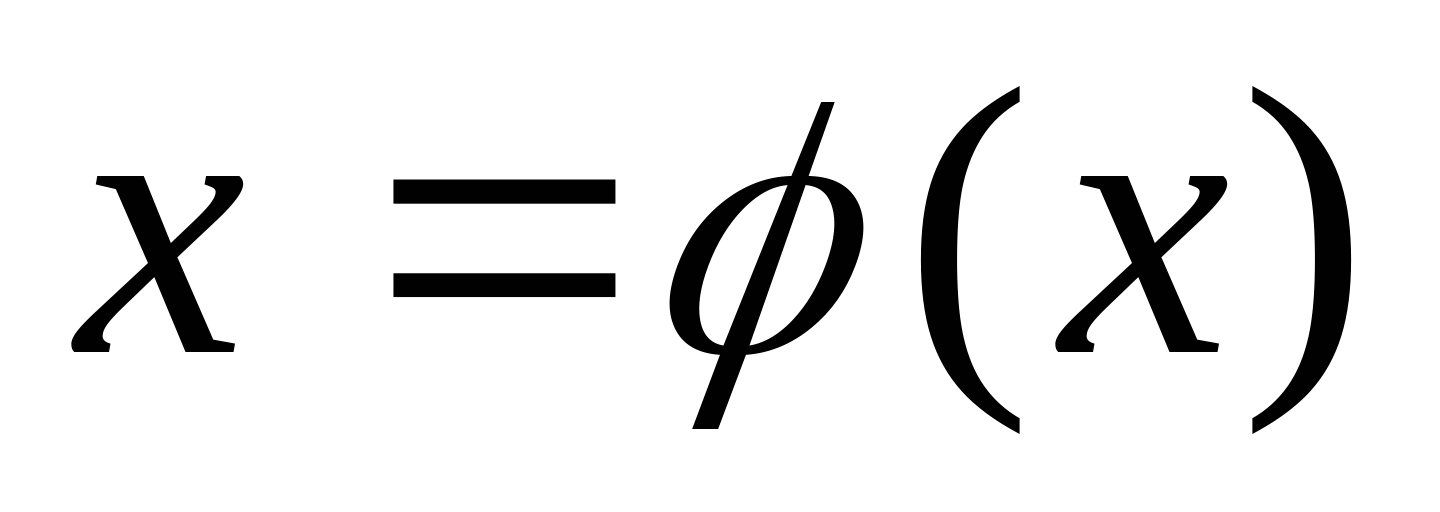 дифф. на промежутке Т и имеет на нем обратную ф-ию дифф. на промежутке Т и имеет на нем обратную ф-ию  с с  на промежутке Х , тогда справедливо: на промежутке Х , тогда справедливо: 
Алгоритм интегрирования подстановкой. Для интеграла подынтегральная ф-ия 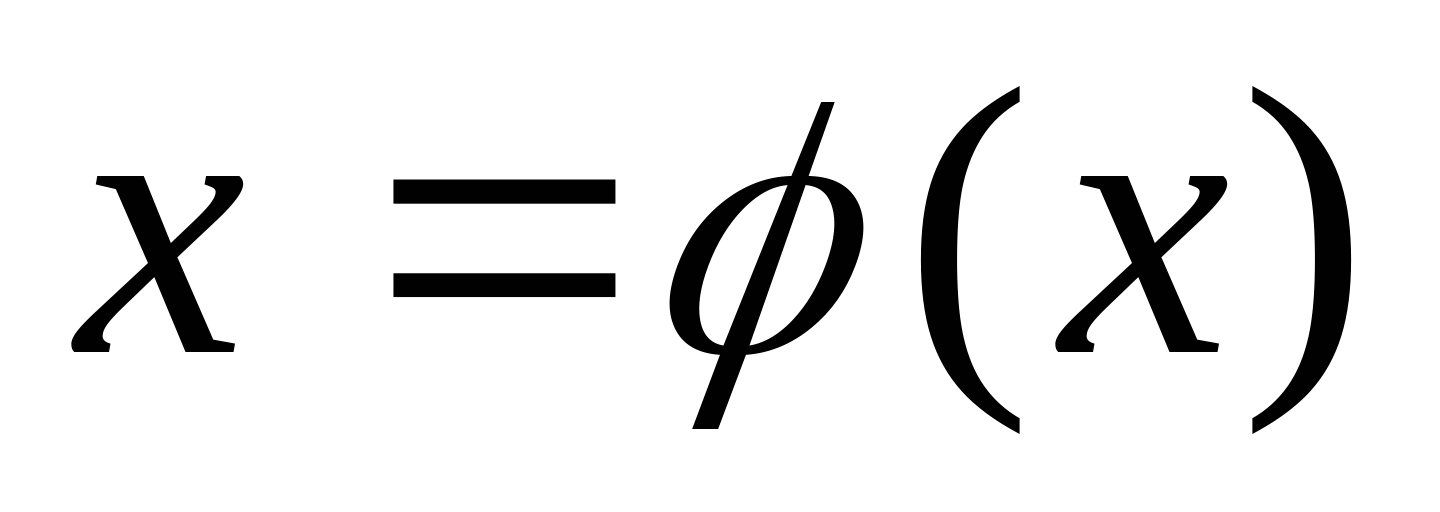 такая, что такая, что  является табличным или сводится к нему так, что легко находится является табличным или сводится к нему так, что легко находится  . . Нах. обратную ф-ию  и подставляем в и подставляем в  , которая и будет первообразной для исходного интеграла. , которая и будет первообразной для исходного интеграла.
Алгоритм: Часть подынтегрального выражения вводится под знак дифференциала и полученное выражение под знаком дифференциала обозначается как новая переменная. В подынтегральной ф-ии делается замена переменной на новую, находится  от новой переменной. от новой переменной. В  возвращ. к старой переменной. возвращ. к старой переменной.
Интегрирование по частям. Интегрирую выражение любого дифференциала произведения, получим:  
Пример:  Рекомендации: В интегралах с подынтегральным выражением вида:  (Pn –многочлен степени n ) (Pn –многочлен степени n ) Pn принимается за u
В интегралах с подынтегральным выражением вида:  за u  Интегрирование с подстановкой выражений вида  после двукратного интегрирования по частям приводится к линейному уравнению относительно вычисляемого интеграла. после двукратного интегрирования по частям приводится к линейному уравнению относительно вычисляемого интеграла.
Интегрирование дробно-рациональных выражений Df Дробно-рациональная ф-ия  - отношение 2х многочленов - отношение 2х многочленов  - многочлены степени n и m соответственно. - многочлены степени n и m соответственно. Рациональная дробь правильная, если степень числителя строго меньше степени знаменателя, обратно - неправильная.
Zm Неправильная рациональная дробь путем выделения целой части приводится к сумме многочлена и правильной рациональной дроби; многочлен называется целой частью неправильной дроби.
Простейшие (элементарные) рациональные дроби и их применение. К простым рациональным дробям относятся рациональные дроби типов:  - вещественные постоянные - вещественные постоянные 2. - вещественные постоянные, - вещественные постоянные, 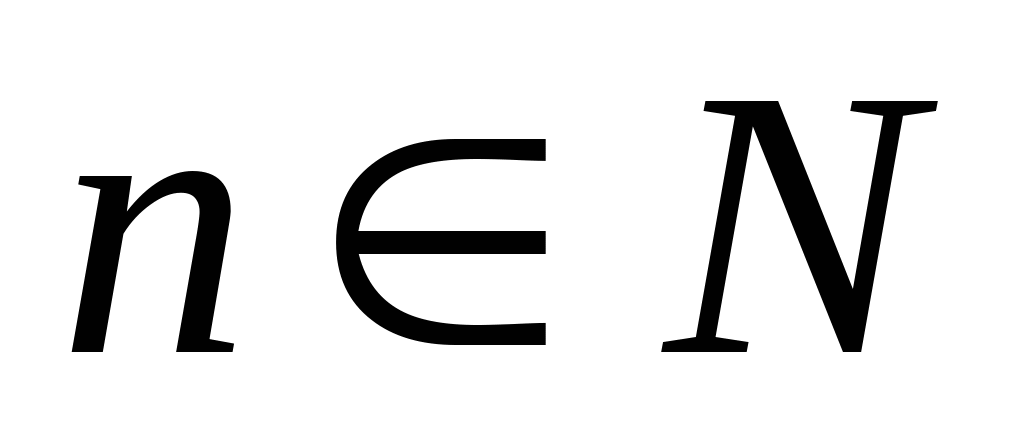 3.  4. 
Интегрирование 1го типа: 
Интегрирование 2го типа: 
Интегрирование 3го типа: проводится в два этапа: 1. В числителе выделяется дифференциал знаменателя:   2. Выделение полного квадрата в знаменателе второго интеграла.   
Интегрирование 4го типа:  1. Выделяем в числителе *** знаменателя:  Выделяем в знаменателе 2го интеграла ф-лы квадрата:  Рекуррентная формула для вычисления Jm (вычисление происходит путем подстановки в известную форму)


Разложение рациональной дроби на простейшие. В курсе алгебры доказываются утверждения |