|
1) свойство вероятности: 20 стр.
Свойство 1. Вероятность невозможного события равна 0, т.е. 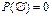 . . 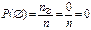 . .
Свойство 2. Вероятность достоверного события равна 1, т.е. 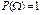 , , 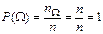
Свойство 3. Для любого события 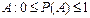 . . 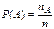 , т.к. , т.к. 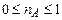 , то , то 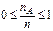 и следовательно и следовательно 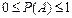 . .
Свойство 4. Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей:
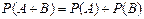
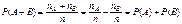
Свойство 5. (обобщенная теорема сложения вероятностей) 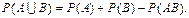 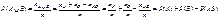 . .
Свойство 6. (теорема сложения k слагаемых) Если события А1, А2,…, Аk попарно несовместимы, то 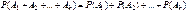 . .
Свойство 7. Если 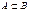 (А влечет В), то (А влечет В), то  . . 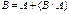 , тогда , тогда 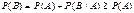
Свойство 8. Если 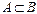 , то , то 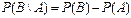 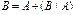 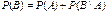 . Тогда . Тогда 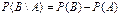
Свойство 9. 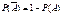 . . 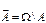 , , 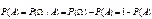 . .
Свойство 10. Если события Н1, Н2,…,Нk образуют полную группу, то 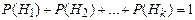 . Т.к. . Т.к. 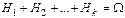 , то по свойству 6: , то по свойству 6:
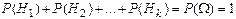
2)условная вероятность, независимость:
Условной вероятностью события B при условии A называется вероятность события B в предположении, что событие A наступило. Обозначение 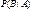 , (реже , (реже  ). ). 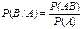 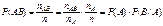 . .
Теорема (умножение вероятностей): 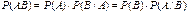 . .
Теорема (обобщенная теорема умножения).
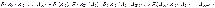
3)формулы полной вероятности и Баеса: 23 стр.
Теорема 1. Если события Н1, Н2,…,Нn образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности:
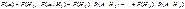 , или , или 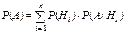 . .
Так как события образуют полную группу, то можно записать 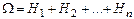 . .
Событие А может произойти только с одним из событий Hi, i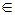 {1,2,…,n}, то А=АН1+АН2+…+АНn. По теореме сложения вероятностей {1,2,…,n}, то А=АН1+АН2+…+АНn. По теореме сложения вероятностей 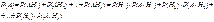
Замечание: при применении формулы полной вероятности события Н1,Н2,…,Нn , образующие полную группу, называются гипотезами.
Теорема 2. Пусть события Н1, Н2, …, Нn образуют полную группу, А–некоторое событие, причем P(A)≠0, тогда имеет место формула Байеса:
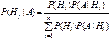 , ,
Замечание. При применении формулы Байеса вероятности 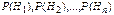 называются априорными вероятностями гипотез. Вероятности P(H1|A),…,P(Hn|A) называют апостериорными вероятностями гипотез. называются априорными вероятностями гипотез. Вероятности P(H1|A),…,P(Hn|A) называют апостериорными вероятностями гипотез.
4)схема независимых испытаний Бернули. Полиномиальное распределение:
Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы называем успехом и неудачей.
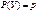 , , 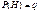 , p+q=1. , p+q=1.
Предположим, что мы производим независимо друг от друга n таких испытаний.
Последовательность n испытаний называется испытаниями Бернулли, если эти испытания
независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию.
Элементарным исходом будет являться:
(w1,w2,…,wn), 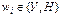 . .
Всего таких исходов 2n.
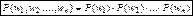 (1) (1)
Формула (1) показывает, что события независимы.
Обозначим через µ число успехов в n испытаниях Бернулли. 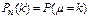 — вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие — вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие 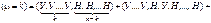 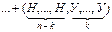 . .
По теореме сложения получим
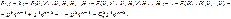
Таким образом, получим
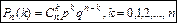 —формула Бернулли. —формула Бернулли.
Предположим, что в результате испытания возможны k исходов E1, E2, …, Ek,
P(Ei)=pi,  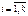 . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле: . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле:
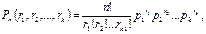 где где 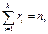 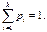
Эта формула полиномиальное распределения, обобщающая формулу Бернулли.
5)случайные велечины, функция распределения и её свойства.
Случайной величиной Х называется функция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R.
Множество значений случайной величины обозначается Ωх. Одной из важных характеристик случайной величины является функция распределения случайной величины.
Функцией распределения случайной величины Х называется функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате эксперимента значение, меньшее некоторого фиксированного числа х.
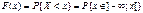 . .
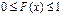 . .
Если рассматривать Х как случайную точку на оси ох, то F(x) с геометрической точки зрения—это вероятность того, что случайная точка Х в результате реализации эксперимента попадет левее точки х.
Свойства функции распределения.
1.Функция распределения F(x)–неубывающая функция, т.е. для 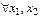 таких что x1<x2 таких что x1<x2 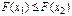 . .
Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е. 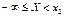 , представим в виде объединения двух несовместимых событий , представим в виде объединения двух несовместимых событий
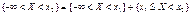
Тогда по теореме сложения вероятностей получим
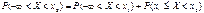 , т.е. , т.е.
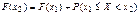 . Поскольку . Поскольку 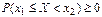 , то , то 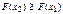 . .
2.Для любых 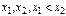 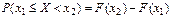
Замечание. Если функция распределения F(x) непрерывная, то свойство выполняется и при замене знаков ≤ и < на < и ≤.
3.
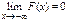 , , 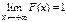 . .
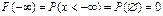 , , 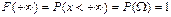 . .
4.Функция F(x) непрерывна слева. (т.е. 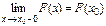 ). ).
5. Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.
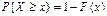 . .
Достоверное событие {-∞<x<+∞} представим в виде двух несовместимых событий. 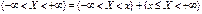 . Найдем их вероятности . Найдем их вероятности
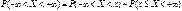 . .
Поскольку вероятность достоверного события равна единице, то
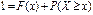 .Отсюда .Отсюда 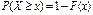 . .
6)мат. ожидание дискретной случайной велечины и его свойства (включая теорему 1)
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Если случайная величина Х принимает конечное число значений, то 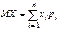 . .
Если случайная величина Х принимает счетное число значений, то 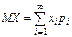 , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическое ожидание дискретной случайной величины—это неслучайная величина (т.е. число, постоянная).
1.Математическое ожидание постоянной величины равно самой постоянной
M(C)=C.
Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно, 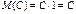 . .
Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х.
2.множитель можно выносить за знак математического ожидания:
M(CX)=CM(X).
Если случайная величин Х имеет ряд распределения
| X
|
x1
|
x2
|
…
|
xn
|
…
|
| P
|
p1
|
p2
|
…
|
pn
|
…
|
Ряд распределения случайной величины СХ
| СХ
|
Сx1
|
Сx2
|
…
|
Сxn
|
…
|
| Р
|
p1
|
p2
|
…
|
pn
|
…
|
Математическое ожидание случайной величины СХ 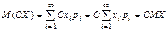 . .
Случайные величины X1,X2,…,Xn называются независимыми, если для любых числовых множеств B1,B2,…,Bn 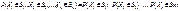
3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий
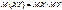 . .
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
4.Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых:
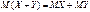 . .
Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: 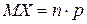 . .
Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события 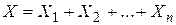 . По свойству 4: . По свойству 4:
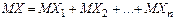 . .
Согласно примеру 2 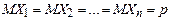 . Таким образом, получим . Таким образом, получим 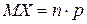 . .
7)дисперсия дискретной случайной велечины и её свойства (включая теорему2): 43 стр.
Дисперсией случайной величины называется число 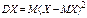 . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания. . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
Средним квадратическим отклонением случайной величины Х называется число 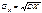 . .
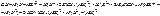
Свойства дисперсии.
1.Дисперсия постоянной величины С равна 0. DC=0.
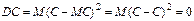
2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: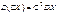 . .
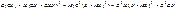 . .
3.Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: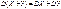 . .
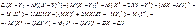
Следствие. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин.
Теорема 2. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании: 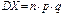 . .
Случайная величина Х—число появлений события А в n независимых испытаниях. 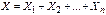 , где Хi—число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных. , где Хi—число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных.
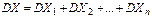 . .
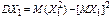 . Т.к. MX1=p. . Т.к. MX1=p. 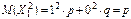 , то , то 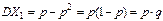 . Очевидно, что дисперсия остальных случайных величин также равна pq, откуда . Очевидно, что дисперсия остальных случайных величин также равна pq, откуда 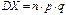 . .
|