Курсовая работа: Поиск максимума одной функции многих переменных методом покоординатного спуска и с помощью метода
|
Название: Поиск максимума одной функции многих переменных методом покоординатного спуска и с помощью метода Раздел: Рефераты по информатике Тип: курсовая работа | ||
РефератВ работе реализуется нахождение решения одной задачи на тему максимизации функций многих переменных. При этом рассматриваются методы дихотомии и покоординатного спуска. Пояснительная записка к курсовой работе состоит из двух основных частей: теоретической и практической. В теоретической части рассматривается поиск максимума одной функции многих переменных методом покоординатного спуска и с помощью метода дихотомии. Практическая часть содержит разработку программного обеспечения для решения заданной задачи выше указанными методами, реализованную на языке С++. Объем пояснительной записки: 1 Количество рисунков: 3 Количество используемых источников: 3 Содержание Введение1. Постановка задачи 2. Решение задачи с использованием метода дихотомии 2.1 Описание метода дихотомии 2.2 Алгоритм решения 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска 3.2 Алгоритм решения Заключение Список используемой литературы Приложение 1. Листинг программы№1 Приложение 2. Листинг программы №2 Приложение 3. Листинг программы №3 Приложение 4. Результаты работы программы №1 Приложение 5. Результаты работы программы №3 Введение В работе рассмотрены способы нахождения таких значений аргументов, при которых исходная функция максимальна, а вспомогательная (от которой зависит исходная) – минимальна. В параграфе 2 изложено решение задачи с использованием метода дихотомии. В параграфе 3 произведено исследование задачи методом покоординатного спуска. 1. Постановка задачи Исходная функция имеет вид:
xi
p, q с=c(x1 …xn ) –– вспомогательная функция, записанная в неявном виде
Задача: Найти xi
*
, Выполним следующую замену: xi
=axi
+b,
Таким образом, исходную область определения функции можно сузить до xi
Далее будем рассматривать задачу от n-2 переменных, т.к. x1 и xn являются константами. 2. Решение задачи с использованием метода дихотомии
2.1 Описание метода дихотомии Данный метод применяется для решения нелинейных уравнений. Если нелинейное уравнение достаточно сложное, то найти точно его корни удается весьма редко. Важное значение приобретают способы приближенного нахождения корней уравнения и оценка степени их точности. Пусть f(x)=0 (1) Где f(x) определена и непрерывна в некотором конечном и бесконечном интервале a<x<b.
Требуется найти все или некоторые корни уравнения (1).Всякое значение 1. Отделение корней, т.е. установление возможно более тесных промежутков [ 2. Нахождение приближенных (грубых) значений корней. 3. Вычисление корней с требуемой точностью. Первая и вторая задача решаются аналитическими и графическими методами. Отделение корней Если уравнение f(x) =
0 имеет только действительные корни, то полезно составить таблицу значений функции f(x).
Если в двух соседних точках Графические методы Действительные корни уравнения f(x) = 0 приближенно можно определить как абсциссы точек пересечения графика функции f(x) с осью x. Приближенные значения корней, найденные грубо, в дальнейшем уточняют с помощью какого-либо итерационного метода. Метод дихотомии Дихотомия означает деление пополам. Пусть нашли такие точки Если требуется найти корень с точностью Метод устойчив к ошибкам округления, но скорость сходимости невелика. К недостаткам метода следует отнести сходимость к неизвестно какому корню (если корни не отделены). Но указанный недостаток имеется у всех итерационных методов. Дихотомия применяется тогда, когда требуется высокая надежность счета, а скорость сходимости малосущественна. Метод иногда применяется для грубого нахождения корней с последующим уточнением по другому методу с большей скоростью сходимости. Этот метод относится к двусторонним (или к двух шаговым) методам, т.к. для вычисления очередного приближения необходимо знать два предыдущих. 2.2 Алгоритм решения Для нахождения максимума функции будем перебирать всевозможные переменные xi
, Затем будем находить значение функции с( Для этого вычислим производную функции
Найдем корень Подставим конкретный набор Перебирая все xi , найдем максимум функции. Перебирая всевозможные параметры p и q, получим некоторые наборы 3. Решение задачи с использованием метода покоординатного спуска
3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных Выберем нулевое приближение Затем из новой точки сделаем спуск по направлению, параллельному оси Будем повторять циклы. На каждом спуске функция не возрастает, и при этом значения функции ограничены снизу ее значением в минимуме Это зависит от функции и выбора нулевого приближения. Метод спуска по координатам несложен и легко программируется на ЭВМ. Но сходится он медленно. Поэтому его используют в качестве первой попытки при нахождении минимума. 3.2 Алгоритм решения Будем перебирать с с шагом какой-либо малой длины. Зададим нулевое приближение, например:
Найдем частные производные
Пусть при каком-то j Тогда k-ое приближение считаем по формулам:
Шаг t будем выбирать таким образом, чтобы
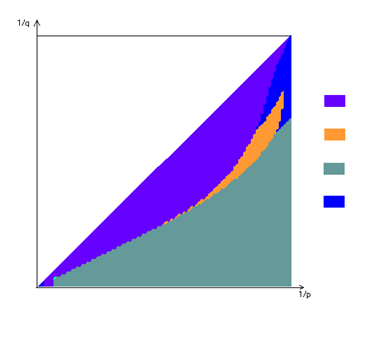
В результате, закончив процесс по критерию Подставим найденный набор Заключение В ходе решения поставленной задачи рассмотрены случаи, когда n=4,5,6. Были найдены две основные области наборов 1) xi =0 или 1(количество 0 и 1 одинаково) 2) xi
=0.5, Причем участок 1<p<1.5 покрыт первой областью, при q>>p На участке p>2 появлялись области вида: i<k => xi =0; i>n-k => xi =1; k-1<i<n-k+1=> xi =0.5. На участке 2<q<3 p xi =a => xn - i =1-a, 0<a<1. Список использованных источников 1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994. 543с. 2. Березин И.С. и Жидков Н. П. Методы вычислений. т.1. М.: “Наука”, 1965. 633c. 3. Подбельский В.В. и Фомин С.С. Программирование на языке Си. М.: “Финансы и статистика”, 2000. 599с. Приложение 1. Листинг программы №1 //вывод на экран областей максимума функции #include "stdafx.h" #include "KE2.h" #include "math.h" #include "KE2Doc.h" #include "KE2View.h" #ifdef _DEBUG #define new DEBUG_NEW #undef THIS_FILE static char THIS_FILE[] = __FILE__; #endif IMPLEMENT_DYNCREATE(CKE2View, CView) BEGIN_MESSAGE_MAP(CKE2View, CView) //{{AFX_MSG_MAP(CKE2View) // NOTE - the ClassWizard will add and remove mapping macros here. // DO NOT EDIT what you see in these blocks of generated code! //}}AFX_MSG_MAP // Standard printing commands ON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint) ON_COMMAND(ID_FILE_PRINT_DIRECT, CView::OnFilePrint) ON_COMMAND(ID_FILE_PRINT_PREVIEW, CView::OnFilePrintPreview) END_MESSAGE_MAP() CKE2View::CKE2View() { } CKE2View::~CKE2View() { } BOOL CKE2View::PreCreateWindow(CREATESTRUCT& cs) { return CView::PreCreateWindow(cs); } void CKE2View::OnDraw(CDC* pDC) { CKE2Doc* pDoc = GetDocument(); ASSERT_VALID(pDoc); drawPoint(pDC); // TODO: add draw code for native data here } BOOL CKE2View::OnPreparePrinting(CPrintInfo* pInfo) { // default preparation return DoPreparePrinting(pInfo); } void CKE2View::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) { // TODO: add extra initialization before printing } void CKE2View::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/) { // TODO: add cleanup after printing } #ifdef _DEBUG void CKE2View::AssertValid() const { CView::AssertValid(); } void CKE2View::Dump(CDumpContext& dc) const { CView::Dump(dc); } CKE2Doc* CKE2View::GetDocument() // non-debug version is inline { ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CKE2Doc))); return (CKE2Doc*)m_pDocument; } #endif //_DEBUG int sgn(float a) { int sg; if (a>0) sg=1; if (a==0) sg=0; if (a<0) sg=-1; return(sg); } #define n 6 void CKE2View::drawPoint(CDC *pDC) { double **c,*f1,*f,*x,*w,*e,max,p=2,q=2,xx,yy; int i=0,j=0,k,m,a,b,*l,bb=0; c=new double*[10000]; for(i=0;i<10000;i++) { c[i]=new double[3]; memset(c[i],0,sizeof(double)*3); } f=new double[10000]; e=new double[10000]; w=new double[10000]; f1=new double[10000]; x=new double[n]; l=new int[10000]; for(xx=0.5;xx<1;xx+=0.01) for(yy=xx;yy<1);yy+=0.01) { p=1./(1.-xx); q=1./(1.-yy); memset(w,0,sizeof(double)*10000); memset(e,0,sizeof(double)*10000); memset(f1,0,sizeof(double)*10000); memset(x,0,sizeof(double)*n); x[n-1]=1; j=0; for(i=0;i<10000;i++) {j=0; f1[i]=1;c[i][0]=0;c[i][1]=1;c[i][2]=0.5; while(fabs(f1[i])>0.00000001) { f1[i]=0; for(k=0;k<n;k++) { f1[i]+=pow((fabs(x[k]-c[i][2])),(p-1))*sgn(x[k]-c[i][2]);} if (f1[i]<-0.00000001) {max=c[i][2];c[i][2]=c[i][2]-(fabs(c[i][2]-c[i][1])/2.0);c[i][1]=max;} if (f1[i]>0.00000001) {max=c[i][2];c[i][2]=c[i][2]+(fabs(c[i][2]-c[i][1])/2.0);c[i][1]=max;} if (fabs(f1[i])<=0.00000001) {c[i][0]=c[i][2];goto B;} } B: c[i][0]=c[i][2]; for(a=0;a<n;a++) { for(b=0;b<n;b++) w[i]+=pow((fabs(x[a]-x[b])),q); e[i]+=pow((fabs(x[a]-c[i][0])),p); } f[i]=pow((e[i]/n),(1./p))/pow((w[i]/(n*n)),(1./q)); x[n-2]+=0.1; for(k=2;k<n;k++) { if(x[n-k]>1.04) { x[n-k-1]+=0.1; x[n-k]=x[n-k-1]; for(m=2;m<k;m++) x[n-m]=x[n-k-1]; } if (x[0]!=0) goto A; } } A: max=f[0];k=0; for(m=0;m<i;m++) { if (fabs(max-f[m])<0.001) {k++;l[k]=m;} if (max<f[m]) {k=0;max=f[m];l[k]=m;} } for(a=0;a<n-1;a++) x[a]=0; for(a=0;a<l[0];a++) { x[n-2]+=0.1; for(k=2;k<n;k++) if(x[n-k]>1.04) { x[n-k-1]+=0.1; x[n-k]=x[n-k-1]; for(m=2;m<k;m++) x[n-m]=x[n-k-1]; } } b=0; for(k=0;k<n;k++) { if((x[k]==0)||(fabs(x[k]-1)<0.04)) b++; else { if(fabs(x[k]-0.5)<0.04) b+=2; else b=-n; } } b-=n; if (b<0) b=24; if (b==0) b=58; if(b==bb) continue; bb=b; c=%f\n",p,q,l[0],l[k],k+1,max,c[l[0]][0]); COLORREF cr(RGB((b%3)*127,(b%4)*85,(b%5)*63)); CBrush r(cr); CPen rp(PS_SOLID,0,cr); pDC->SelectObject(&rp); pDC->SelectObject(&r); CPoint r1[3]={CPoint(0,360),CPoint(int(720./p),-int(720./q)+360),CPoint(int(720./p),360)}; pDC->Polygon(r1,3); } } Приложение 2. Листинг программы №2. //Покоординатный спуск #include<stdAfx.h> #include<stdio.h> #include<iostream.h> #include<conio.h> #include<math.h> #define n 4 void main() { //double ff(double v,double vv); int sgn(float a); double *aa,**x,*f1,f,e,w,w1,e1,q=7,p=7,*r,*z,f2,*r1,max,m=0,c,f20,f21; int bb,i,MAX,k,j,a,b,mm,ss; x=new double*[n]; for(i=0;i<n;i++) x[i]=new double[2]; z=new double[3]; aa=new double[n-2]; r=new double[n]; r1=new double[n]; //f2=new double[n]; f1=new double[n]; for(i=1;i<n-1;i++) //начальное прибл - все х от 1-го до n-2-го равны x[i][0]=0.1; // x[n-1][0]=1;x[n-1][1]=1;x[0][1]=0;x[0][0]=0;x[1][0]=0.9;//x[2][0]=0;//x[3][0]=0;x[4][0]=1;//начальное приближение for(c=0.5;c<0.7;c+=0.1) //Цикл по c { bb=0; for(k=1;;k++) //Цикл по k { // for(i=0;i<n;i++) // cerr<<"x["<<i<<"]="<<x[i][0]<<"\n"; // cerr<<"\n"; w=0;e=0;w1=0;e1=0; for(a=0;a<n;a++) r[a]=0; for(a=0;a<n;a++) { for(b=0;b<n;b++) { w+=pow((fabs(x[a][0]-x[b][0])),q); r[a]+=pow((fabs(x[a][0]-x[b][0])),q-1)*sgn(x[a][0]-x[b][0]); } e+=pow((fabs(x[a][0]-c)),p); } w=pow(w/(n*n),1./q);//знаменатель исх ф-ции e=pow(e/n,1./p);//числитель исх ф-ции f=e/w; //cerr<<"\n"<<f<<"\n"; f1[0]=0;f1[n-1]=0; MAX=0; for(j=1;j<n-1;j++) { f1[j]=pow(n,(2./q-1./p))*(pow(e,(1./p-1))*pow(fabs(x[j][0]-c),(p-1))*w *sgn(x[j][0]-c)-2.*pow(w,(1./q-1))*r[j])/(w*w); //производная исх. функции по x[j][0] в точке с координатами x[i][0] i=0..n-1 на k-ом приближении // cerr<<f1[j]<<"\n"; for(a=0;a<bb;a++) if(aa[a]==j) break; if(a!=bb) continue; if (fabs(f1[j])>fabs(f1[MAX])) MAX=j; } // т.к. x[0]=0 и x[n-1]=1 - cosnt mm=0;ss=0; for(i=0;;i++) { if (mm==0) z[0]=100000000./pow(1.2,i);//шаг if(mm==1) { z[0]=-1000000000./pow(1.2,ss); ss++; } /*if(z[0]<0.000000000000001) { z[0]=-0.5/pow(1.5,mm); mm++; }*/ for(a=0;a<n;a++) r1[a]=0; w1=0;e1=0; for(a=0;a<n;a++) { if(a==MAX) { for(b=0;b<n;b++) { w1+=pow(fabs(x[a][0]+f1[a]*z[0]-(x[b][0]+f1[b]*z[0])),q); r1[a]+=pow( fabs(x[a][0]+f1[a]*z[0] - (x[b][0]+f1[b]*z[0]) ),q-1)* sgn( x[a][0]+f1[a]*z[0] - (f1[b]*z[0]+x[b][0]) ); } e1+=pow((fabs(x[a][0]+f1[a]*z[0]-c)),p); } else { for(b=0;b<n;b++) { w1+=pow((fabs(x[a][0]-x[b][0])),q); r1[a]+=pow((fabs(x[a][0]-x[b][0])),q-1)*sgn(x[a][0]-x[b][0]); } e1+=pow((fabs(x[a][0]-c)),p); } } w1=pow(w1/(n*n),1/q);e1=pow(e1/n,1/p); //printf("\n f=%f f[a]=%f",e/w,e1/w1); a=0; //for(j=1;j<n-1;j++) //if (((x[j][0]+z[0]*f1[j])<1)&&((x[j][0]+z[0]*f1[j])>0)) a++; //if(a<n-2) continue; if (((x[MAX][0]+z[0]*f1[MAX])<1)&&((x[MAX][0]+z[0]*f1[MAX])>0)) a++; if(a!=1) continue; if (e1/w1>e/w) break; if ((e1/w1-e/w)>-0.00000001) { if(z[0]>0) { mm=1; continue; } for(a=1;a<n-1;a++) x[a][1]=x[a][0]; goto A; } } for(j=1;j<n-1;j++) if(j==MAX) x[j][1]=x[j][0]+z[0]*f1[j]; else x[j][1]=x[j][0]; if(fabs(x[MAX][1]-x[MAX][0])<0.00000001) { aa[bb]=MAX; bb++; } if(bb==n-2) break; for(j=1;j<n-1;j++) x[j][0]=x[j][1]; } //закрытие цикла по k A: cerr<<"K-vo iteratsiy: "<<k-1<<"\n\n"; for(i=0;i<n;i++) cerr<<"x["<<i<<"]="<<x[i][0]<<"\n"; cerr<<"\nf="<<f<<"\n"; }// закрытие цикла по с } int sgn(float a) { int sg; if (a>0) sg=1; if (a==0) sg=0; if (a<0) sg=-1; return(sg); } Приложение 3. Листинг программы №3 #include <stdAfx.h> #include <stdlib.h> #include <stdio.h> #include <conio.h> #include <math.h> #include <iostream.h> #define n 4 int sgn(float); main() { double **c,*f1,*f,*x,*w,*e,max,p=2,q=2,xx,yy; int i=0,j=0,k,m,a,b,*l; c=new double*[10000]; for(i=0;i<10000;i++) c[i]=new double[4]; f=new double[10000]; e=new double[10000]; w=new double[10000]; f1=new double[10000]; x=new double[n]; l=new int[10000]; for(xx=0.5;xx<1;xx+=0.01) for(yy=xx;yy<1;yy+=0.01) { p=1./(1.-xx); q=1./(1.-yy); for(i=0;i<10000;i++) { w[i]=0; e[i]=0; f1[i]=0; } for(i=0;i<10000;i++) for(j=0;j<3;j++) {c[i][j]=0; } for(i=0;i<n;i++) x[i]=0; x[n-1]=1; j=0; for(i=0;i<10000;i++) {j=0; f1[i]=1;c[i][0]=0;c[i][1]=1;c[i][2]=0.5; while(fabs(f1[i])>0.000000001) { f1[i]=0; for(k=0;k<n;k++) { f1[i]+=pow((fabs(x[k]-c[i][2])),(p-1))*sgn(x[k]-c[i][2]);} if (f1[i]<-0.000000001) {max=c[i][2];c[i][2]=c[i][2]-(fabs(c[i][2]-c[i][1])/2.0);c[i][1]=max;} if (f1[i]>0.000000001) {max=c[i][2];c[i][2]=c[i][2]+(fabs(c[i][2]-c[i][1])/2.0);c[i][1]=max;} if (fabs(f1[i])<=0.000000001) {c[i][0]=c[i][2];goto B;} } B: c[i][0]=c[i][2]; for(a=0;a<n;a++) { for(b=0;b<n;b++) w[i]+=pow((fabs(x[a]-x[b])),q); e[i]+=pow((fabs(x[a]-c[i][0])),p); } f[i]=pow((e[i]/n),(1./p))/pow((w[i]/(n*n)),(1./q)); x[n-2]+=0.1; for(k=2;k<n;k++) { if(x[n-k]>1.04) { x[n-k-1]+=0.1; x[n-k]=x[n-k-1]; for(m=2;m<k;m++) x[n-m]=x[n-k-1]; } if (x[0]!=0) goto A; } } A: max=f[0];k=0; for(m=0;m<i;m++) { if (fabs(max-f[m])<0.0001) {k++;l[k]=m;} if (max<f[m]) {k=0;max=f[m];l[k]=m;} } printf("p=%f q=%f max=%f\n",p,q,max); x[n-1]=1; for(a=0;a<=n-2;a++) x[a]=0; for(a=0;a<l[0];a++) { x[n-2]+=0.1; for(k=2;k<n;k++) { if(x[n-k]>1.04) { x[n-k-1]+=0.1; x[n-k]=x[n-k-1]; for(m=2;m<k;m++) x[n-m]=x[n-k-1]; } } } for(a=0;a<n;a++) printf("Nabor:x[%d]=%f ",a,x[a]); } getch(); return 0; } int sgn(float a) { int sg; if (a>0) sg=1; if (a==0) sg=0; if (a<0) sg=-1; return(sg); } Приложение №4 Результаты работы программы №1: n=6
n=5
n=4
Приложение №5. Результаты работы программы №3. p=2.000000 q=2.000000 max=0.707107 Nabor: x[0]=0.000000 x[1]=0.600000 x[2]=0.700000 x[3]=1.000000 p=2.000000 q=2.100000 max=0.696478 Nabor: x[0]=0.000000 x[1]=0.300000 x[2]=0.700000 x[3]=1.000000 p=2.000000 q=2.200000 max=0.686567 Nabor: x[0]=0.000000 x[1]=0.300000 x[2]=0.700000 x[3]=1.000000 p=2.000000 q=2.300000 max=0.677294 Nabor: x[0]=0.000000 x[1]=0.300000 x[2]=0.700000 x[3]=1.000000 p=2.000000 q=2.400000 max=0.668738 Nabor: x[0]=0.000000 x[1]=0.200000 x[2]=0.800000 x[3]=1.000000 p=2.000000 q=2.500000 max=0.660879 Nabor: x[0]=0.000000 x[1]=0.200000 x[2]=0.800000 x[3]=1.000000 p=2.000000 q=2.600000 max=0.653565 Nabor: x[0]=0.000000 x[1]=0.200000 x[2]=0.800000 x[3]=1.000000 p=2.000000 q=2.700000 max=0.646741 Nabor: x[0]=0.000000 x[1]=0.200000 x[2]=0.800000 x[3]=1.000000 p=2.000000 q=2.800000 max=0.640603 Nabor: x[0]=0.000000 x[1]=0.100000 x[2]=0.900000 x[3]=1.000000 p=2.000000 q=2.900000 max=0.635019 Nabor: x[0]=0.000000 x[1]=0.100000 x[2]=0.900000 x[3]=1.000000 |
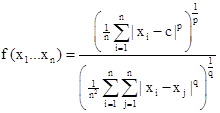 , где:
, где:
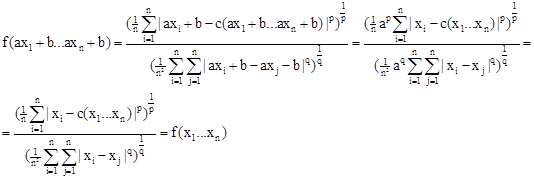
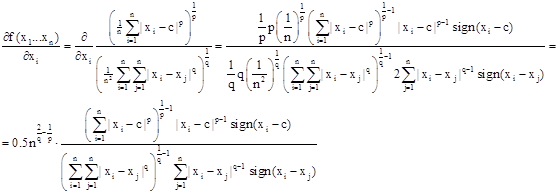
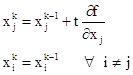
 и
и