| Содержание
1.Введение в анализ и дифференциальное исчисление функции одного переменного. 2
2. Дифференциальное исчисление функций и его приложение 5
3. Интегральное исчисление функции одного переменного 8
1.Введение в анализ и дифференциальное исчисление функции одного переменного
1. Вычислить предел
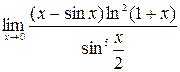
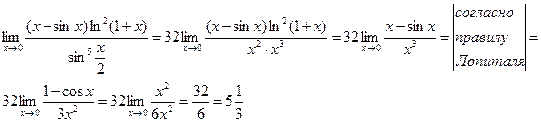
2. Найти асимптоты функции
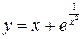
Отметим, что данная функция не существует при 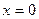 . .
Исследуем прямую 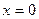 на вертикальную асимптотичность: на вертикальную асимптотичность:
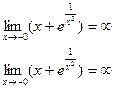
Отсюда следует, что прямая 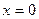 является вертикальной асимптотой. является вертикальной асимптотой.
Проверим функцию на существование горизонтальных асимптот:
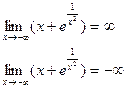
Отсюда следует, что горизонтальные асимптоты отсутствуют.
Проверим функцию на существование наклонной асимптоты:
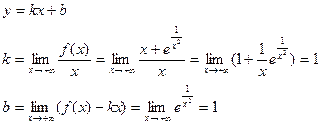
Отсюда следует, что функция имеет наклонную асимптоту 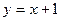
Таким образом, данная функция имеет вертикальную асимптоту 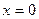 и наклонную асимптоту и наклонную асимптоту 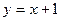
3. Определить глобальные экстремумы
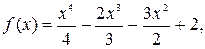 при х
Î[-2,0] при х
Î[-2,0]
Для определения глобальных экстремумов, вычислим производную 1-го порядка для данной функции:
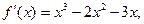
Найдем значения аргумента, при которых данная производная будет равна 0:
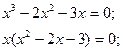
Отсюда имеем 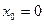 ; ;
Продолжая решение: 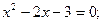
По теореме Виета, получим:
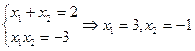
По условию задания глобальные экстремумы определяются на отрезке х
Î[-2,0]. Таким образом, имеем, что на отрезке [-2, -1] значение производной отрицательно, на отрезке
[-1, 0] – положительно. Таким образом, при 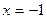 , функция принимает минимальное значение на заданном отрезке: , функция принимает минимальное значение на заданном отрезке: 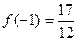
Исследуем значения функции на концах заданного отрезка: 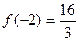 , , 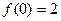
Таким образом, при 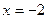 функция принимает максимальное значение на заданном отрезке. функция принимает максимальное значение на заданном отрезке.
Ответ: 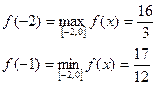
4. Исследовать на монотонность, найти локальные экстремумы и построить эскиз графика функции
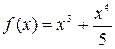
Для исследования функции на монотонность, найдем производную 1-го порядка:
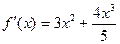 , Определим значения аргумента, при которых производная равна 0 , Определим значения аргумента, при которых производная равна 0
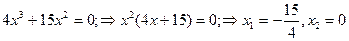
На промежутке 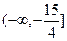 - функция монотонно убывает - функция монотонно убывает
На промежутке 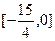 - функция монотонно убывает - функция монотонно убывает
На промежутке 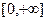 - функция монотонно возрастает - функция монотонно возрастает
То есть при х=0, функция принимает минимальное значение у=0
Таким образом, эскиз графика функции, выполненный по условию задания, выглядит следующим образом:

5. Найти промежутки выпуклости и точки перегиба функции
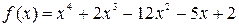
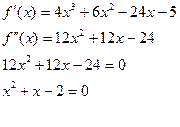
По теореме Виета:
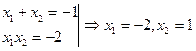
Далее определим промежутки выпуклости функции
На промежутке 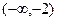 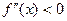 ; - выпуклость вверх ; - выпуклость вверх
На промежутке 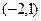 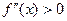 ; - выпуклость вниз ; - выпуклость вниз
На промежутке 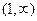 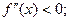 - выпуклость вверх - выпуклость вверх
Значения функции в точках перегиба: 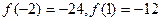
Тогда точки перегиба функции: 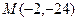 и N и N 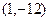
2.
Дифференциальное исчисление функций и его приложение
1. Провести полное исследование свойств и построить эскиз графика функции
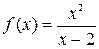
1) Функция 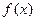 не является четной, не является нечетной. Функция не периодична. не является четной, не является нечетной. Функция не периодична.
2) Функция 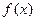 не существует при не существует при 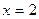 . Проверим гипотезу об асимптоте . Проверим гипотезу об асимптоте 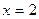 : :
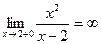
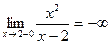
Таким образом 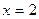 является вертикальной асимптотой данной функции является вертикальной асимптотой данной функции
3) Проверим гипотезу о существовании горизонтальной асимптоты:
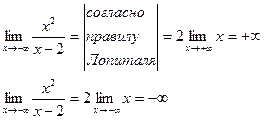
Отсюда следует, что горизонтальные асимптоты отсутствуют.
4) Проверим гипотезу о существовании наклонной асимптоты:
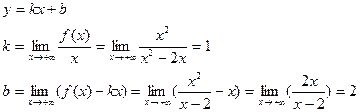
аналогично при 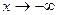
Таким образом, наклонная асимптота имеет вид: 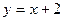
5) 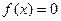 единственно при единственно при 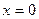 , и не существует при , и не существует при 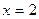 Исследуем знаки постоянства функции: Исследуем знаки постоянства функции:
на промежутке 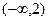 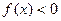
на промежутке 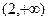 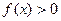
6) Исследуем функцию на монотонность:
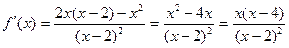 ; ;
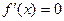 при при 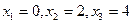
На интервале 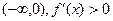 - функция возрастает - функция возрастает
На интервале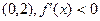 - функция убывает - функция убывает
На интервале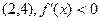 - функция убывает - функция убывает
На интервале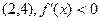 - функция убывает - функция убывает
На интервале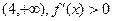 -функция возрастает -функция возрастает
Точки экстремума: 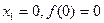 - локальный максимум - локальный максимум
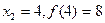 - локальный минимум - локальный минимум
7) Исследуем функцию на выпуклость:
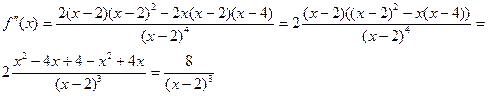
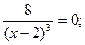 данное уравнение корней не имеет; данное уравнение корней не имеет;
Производная второго порядка не существует при 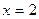
На промежутке 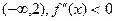 - функция выпукла вверх - функция выпукла вверх
На промежутке 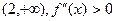 - функция выпукла вниз - функция выпукла вниз
Таким образом, учитывая все вышеуказанное, эскиз графика функции будет выглядеть следующим образом:
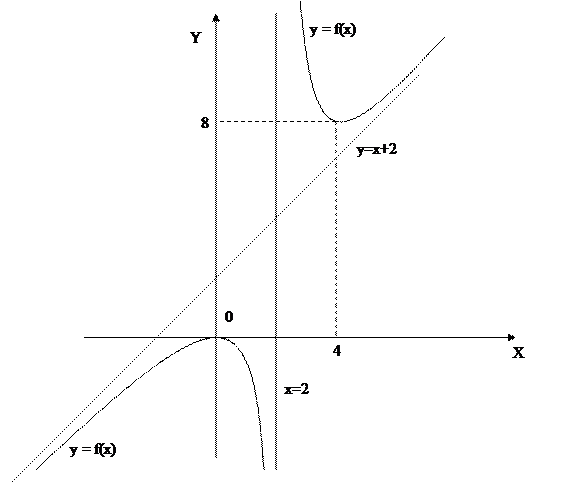
2. Найти локальные экстремумы функции
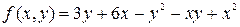
Найдем первые производные:
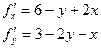
Составим систему:
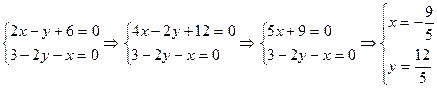
Найдем вторые производные:
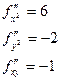
Поскольку производные 2-го порядка для данной функции не существуют, то вопрос о локальных экстремумах остается открытым.
3. Определить экстремумы функции
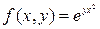 , если у2
+
2х2
=12, х
>0, у
>0 , если у2
+
2х2
=12, х
>0, у
>0
- Составляем функцию Лагранжа:
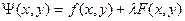
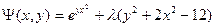
- Найдем первые частные производные функции Лагранжа:
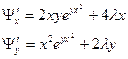
- Составим систему уравнений:

По условию: х
>0, у
>0
Таким образом: х = у
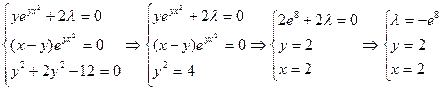
- Определи вторые производные функции Лагранжа:
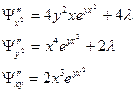
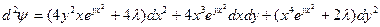
- Учитывая значения переменных, полученные в п.3, имеем:
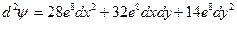
- Найдем производные условной функции:
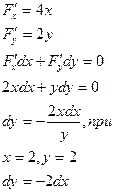
- Таким образом:
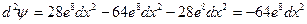
Видим, что в точке (2,2) исходная функция 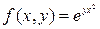 при условии у2
+
2х2
=12, х
>0, у
>0, будет иметь строгий условный максимум, при этом при условии у2
+
2х2
=12, х
>0, у
>0, будет иметь строгий условный максимум, при этом 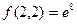
3. Интегральное исчисление функции одного переменного
1-3 Найти неопределенный интеграл:
а.
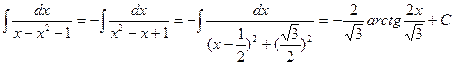
б.
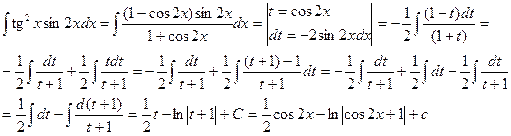
в.
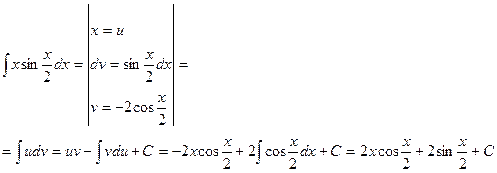
4 Вычислить
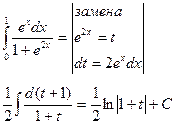
Таким образом:
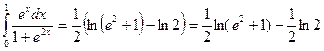
5. Определить площадь плоской фигуры, ограниченной кривыми
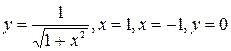
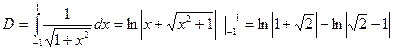
|