| Министерство образования и молодежной политики ЧР
ГОУ «Чувашский республиканский Институт образования»
КУРСОВАЯ РАБОТА
Параметры в школьном курсе математики. Элективный курс.
Выполнила учитель математики МОУ СОШ № 29 г. Чебоксары Морушкина Вера Васильевна
Чебоксары 2009
Оглавление
Пояснительная записка. 3
Структура курса планирования учебного материала. 4
Краткое содержание курса. 4
I. Первоначальные сведения. 4
II. Решение линейных уравнений (и уравнений приводимых к линейным), содержащих параметр. 5
III. Решение линейных неравенств, содержащих параметр. 7
IV. Квадратные уравнения и неравенства, содержащие параметр. 9
V. Свойства квадратичной функции в задачах с параметрами. 9
VI. Тригонометрия и параметр. Иррациональные уравнения. 10
VII. Показательные и логарифмические уравнения, содержащие параметр. Рациональные уравнения. 10
VIII. Производная и ее применение. 10
IX. Нестандартные задачи. 10
Х. Текстовые задачи с использованием параметра. 11
Планирование. 11
Заключение. 12
Задачи для самостоятельного решения. 13
Литература. 15
Цель профильного обучения в старших классах - обеспечение углубленного изучения предмета и подготовка учащихся к продолжению образования.
В заданиях ЕГЭ по математике с развернутым ответом (часть С), а также с кратким ответом (часть В), встречаются задачи с параметрами.
Появление таких заданий на экзаменах далеко не случайно, т.к. с их помощью проверяется техника владения формулами элементарной математики, методами решения уравнений и неравенств, умение выстраивать логическую цепочку рассуждений, уровень логического мышления учащегося и их математической культуры.
Решению задач с параметрами в школьной программе уделяется мало внимания. Большинство учащихся либо вовсе не справляются с такими задачами, либо приводят громоздкие выкладки. Причиной этого является отсутствие системы заданий по данной теме в школьных учебниках. Трудности при решении задач с параметрами обусловлены тем, что наличие параметра заставляет решать задачу не по шаблону, а рассматривать различные случаи, при каждом из которых методы решения существенно отличаются друг от друга.
В связи с этим возникла необходимость в разработке и проведении элективного курса для старшеклассников по теме: «Решение задач с параметрами».
Многообразие задач с параметрами охватывает весь курс школьной математики. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления.
При проведении занятий на первое место выходят следующие формы организации работы: лекционно-семинарская, групповая и индивидуальная. Рекомендуемые методы работы: исследовательский и частично-поисковый. Задачи с параметрами дают прекрасный материал для настоящей учебно-исследовательской работы.
Задачи курса
1. Сформировать у учащихся устойчивый интерес к предмету;
2. Выявить и развить математические способности;
3. Подготовить к ЕГЭ и к обучению в вузе
Цель курса
1. Формировать у учащихся умения и навыки по решению задач с параметрами, сводящихся к исследованию линейных и квадратных уравнений, неравенств для подготовки к ЕГЭ и к обучению в вузе.
2. Изучение курса предполагает формирование у учащегося интереса к предмету, развитие их математических способностей, подготовку к ЕГЭ, централизованному тестированию и к вступительным экзаменам в вузы
3. Развивать исследовательскую и познавательную деятельность учащегося.
4. Обеспечить условия для самостоятельной творческой работы.
В результате изучения курса учащиеся должны
1. Усвоить основные приемы и методы решения уравнений, неравенств систем уравнений с параметрами.
2. Применять алгоритм решения уравнений, неравенств, содержащих параметр.
3. Проводить полное обоснование при решении задач с параметрами.
4. Овладеть навыками исследовательской деятельности.
I. Первоначальные сведения. 2ч
II. Решения линейных уравнений, содержащих параметры. 2ч
III. Решения линейных неравенств, содержащих параметры. 2ч
IV. Квадратные уравнения и неравенства, содержащие параметры. 7ч
V. Свойства квадратичной функции в задачах с параметрами. 4ч
VI. Тригонометрия и параметры. 2ч
Иррациональные уравнения. 2ч
VII. Показательные и логарифмические уравнения, содержащие параметры.
Рациональные уравнения. 2ч
VIII. Производная и ее применения. 4ч
Графические приемы решения. 2ч
IX. Нестандартные задачи с параметрами. 6ч
- количество решений уравнений;
- уравнения и неравенства с параметрами с некоторыми условиями
X. Текстовые задачи с использованием параметра. 4 ч
Определение параметра. Виды уравнений и неравенств, содержащие параметр.
Основные приемы решения задач с параметрам.
Решение простейших уравнений с параметрами.
Цель:
Дать первоначальное представление учащемуся о параметре и помочь привыкнуть к параметру, рассмотреть понятие «параметр», его существенный признак и двойственная природа, особенности записи ответов при решении заданий с параметром.
Примерное содержание
.
Решить уравнение с параметром
- это значит найти все те и только те значения параметра, при которых задача имеет решения.
Условимся считать, что параметры в уравнениях принимают действительные значения, в задачах с параметрами отыскиваются действительные решения.
Другими примерами равенств с параметрами могут служить общие виды функций, изучаемых в основной школе.
- линейная функция y=k
x+b
, (k
, b
- параметры, x, y- переменные);
- квадратичная функция y= a
x²+b
x+c
, где а
≠0 (a
, b
, c
-параметры, x, y -переменные).
Задачи с параметрами мы встречаем и в геометрии. Уравнение окружности с центром в начале координат имеет вид 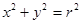 , где x, y- координаты точек - переменные, r- радиус окружности – параметр. , где x, y- координаты точек - переменные, r- радиус окружности – параметр.
Моделируя различного вида задачи, можно получить различного вида уравнения, для которых нужно уметь выбирать ответы.
Общие подходы к решению линейных уравнений. Решение линейных уравнений, содержащих параметр.
Решение уравнений, приводимых к линейным.
Решение линейно-кусочных уравнений.
Применение алгоритма решения линейных уравнений, содержащих параметр.
Геометрическая интерпретация.
Решение системных уравнений.
Цель:
Поиск решения линейных уравнений в общем, виде; исследование количества корней в зависимости от значений параметра.
Примерное содержание.
1. Алгоритм решения уравнений вида Ах=В.
| Решением является любое действительное число
|
При А=0 и В=0
|
| Нет решений
|
При А=0, 
|
| Единственное решение 
|
При 
|
2. Рассмотреть примеры.
ПРИМЕР 1: Решить уравнение: 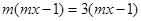
Решение.
Приведём данное уравнение к виду Ах=В
и воспользуемся алгоритмом.
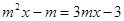 , ,
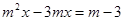 , ,

Рассмотрим случаи:
Если 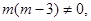 т.е. т.е. 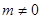 и и 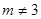 , то обе части уравнения разделим на , то обе части уравнения разделим на  . Получим . Получим 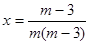 , сократим дробь и получим единственное решение уравнения: , сократим дробь и получим единственное решение уравнения: 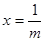 . .
Если 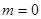 , то подставив это значение параметра в уравнение, получим , то подставив это значение параметра в уравнение, получим 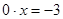 или или 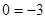 - неверное числовое равенство, следовательно, данное уравнение решений не имеет. - неверное числовое равенство, следовательно, данное уравнение решений не имеет.
Если 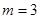 , то подставив это значение параметра в уравнение, получим , то подставив это значение параметра в уравнение, получим  или или 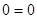 - верное числовое равенство, следовательно, решением данного уравнения является любое действительное число. - верное числовое равенство, следовательно, решением данного уравнения является любое действительное число.
Ответ:
при 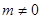 и и 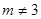 - единственное решение уравнения: - единственное решение уравнения: 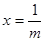
при 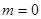 - нет
решений - нет
решений
при 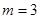 - любое действительное число. - любое действительное число.
ПРИМЕР 2: Решить уравнение: 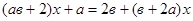
Решение.
Приведём данное уравнение к виду Ах=В
и воспользуемся алгоритмом.
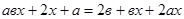 , ,
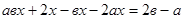 , ,
 , ,
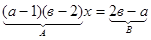 . .
Рассмотрим случаи:
Если 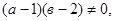 т.е. т.е.  и и  , тогда получим единственное решение уравнения: , тогда получим единственное решение уравнения: 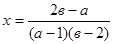 . .
Если  , то подставив это значение параметра в уравнение, получим , то подставив это значение параметра в уравнение, получим 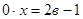 Решение этого уравнения зависит от выражения, стоящего в правой части. Рассмотрим случаи: а) 2в – 1 = 0, т.е. Решение этого уравнения зависит от выражения, стоящего в правой части. Рассмотрим случаи: а) 2в – 1 = 0, т.е.  то подставив это значение параметра в уравнение, получим то подставив это значение параметра в уравнение, получим 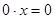 - верное числовое равенство, следовательно, решением данного уравнения является любое действительное число. - верное числовое равенство, следовательно, решением данного уравнения является любое действительное число.
в) 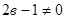 , т.е. , т.е.  то подставив это значение параметра в то подставив это значение параметра в
уравнение, получим 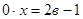 или или 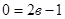 - неверное числовое равенство, - неверное числовое равенство,
следовательно, данное уравнение решений не имеет.
3. Если  , то подставив это значение параметра в уравнение, получим , то подставив это значение параметра в уравнение, получим
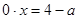 Решение этого уравнения зависит от выражения, стоящего в правой Решение этого уравнения зависит от выражения, стоящего в правой
части.
Рассмотрим случаи: а) 4 – а = 0, т.е. 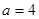 то подставив это значение параметра в то подставив это значение параметра в
уравнение, получим 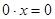 - верное числовое равенство, следовательно, - верное числовое равенство, следовательно,
решением данного уравнения является любое действительное число.
в) 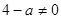 , т.е. , т.е. 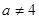 то подставив это значение параметра в то подставив это значение параметра в
уравнение, получим 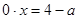 или или  - неверное числовое равенство, - неверное числовое равенство,
следовательно, данное уравнение решений не имеет.
4. Если  и и  , то подставив эти значения параметров в уравнение, получим , то подставив эти значения параметров в уравнение, получим
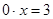 - неверное числовое равенство, следовательно, данное уравнение решений - неверное числовое равенство, следовательно, данное уравнение решений
не имеет.
Ответ:
при  и и  - единственное решение уравнения: - единственное решение уравнения: 
при  , ,  или или  , , 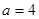 - любое действительное число - любое действительное число
при  , ,  или или  , , 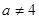 - нет
решений. - нет
решений.
Определение линейного неравенства.
Алгоритм решения неравенств.
Решение стандартных линейных неравенств, простейших неравенств с параметрами.
Исследование полученного ответа.
Обработка результатов, полученных при решении.
Цель:
Выработать навыки решения стандартных неравенств и приводимых к ним, углубленное изучение методов решения линейных неравенств.
Примерное содержание
.
1.На доске записаны следующие неравенства:
Задание. Решите неравенства и запишите ответ.
2.Сформулируйте свойства неравенств, которые использованы при решении.
Неравенства вида ax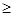 b ax b ax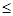 b, где a и b действительные числа или выражения, зависящие от параметров, а x – неизвестное, называются линейными неравенствами. b, где a и b действительные числа или выражения, зависящие от параметров, а x – неизвестное, называются линейными неравенствами.
В зависимости от коэффициентов a и b решением линейного неравенства может быть либо неограниченный промежуток, либо числовая прямая, либо пустое множество.
3.. Решение линейных неравенств вида aх>b.
если a>0, то 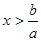 . .
если a<0, то 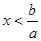 . .
если a=0 и b<0, то 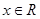 . .
Если a=0 и b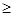 0, то решений нет. 0, то решений нет.
Пример 1.
Решите неравенство ах>1.
1) если a>0, то 
2) если a<0, то 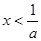
3) если a=0, то решений нет.
4. Решение линейных неравенств вида aх<b.
если a>0, то 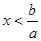 . .
если a<0, то 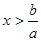 . .
если a=0 и b>0, то 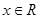 . .
если a=0 и b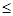 0, то решений нет. 0, то решений нет.
Пример 2
. Решите неравенство ах<5.
1) если a>0, то 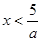
2) если a<0, то 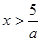
3) если a=0, то 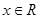 . .
5. Решение линейных неравенств вида ax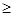 b. b.
если a>0, то 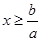 . .
если a<0, то  . .
если a=0 и b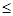 0, то 0, то 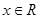 . .
если a=0 и b>0, то решений нет.
Пример 3.
Решите неравенство ax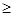 4. 4.
1) если a>0, то 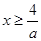
2) если a<0, то 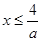
3) если a=0, то решений нет.
6. Решение линейных неравенств вида ax 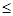 b b
если a>0, то  . .
если a<0, то 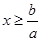 . .
если a=0 и b 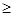 0, то 0, то 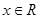 . .
если a=0 и b<0, то решений нет.
Пример 4. Решите неравенство ах 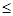 6. 6.
1) если a>0, то 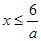 ; ;
2) если a<0, то  ; ;
3) если a=0, то 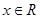 . .
7. Решить неравенства.
(m-1)x<5m
если m-1>0, т.е. m>1, то 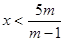 , ,
2 если m-1<0, т.е. m<1, то 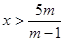 , ,
3. если m-1=0, т.е. m=1, то 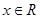 . .
(a-1)x>6
если a-1>0, т.е. a>1, то 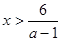 , ,
2. если a-1<0, т.е. a<1, то 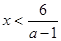 , ,
3. если a-1=0, т.е. а=1, то решений нет.
При каких значениях параметра b уравнение 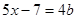 имеет положительный корень? имеет положительный корень?
Решение.
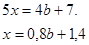 Так как корень х>0, то 0,8 b+14>0; 0,8 b>-14; b>-1,75. Так как корень х>0, то 0,8 b+14>0; 0,8 b>-14; b>-1,75.
Ответ: при b>-1,75
Актуализация знаний о квадратном уравнении. Исследования количества корней, в зависимости от дискриминанта. Использование теоремы Виета. Исследование трехчлена.
Алгоритм решения уравнений.
Аналитический способ решения.
Графический способ.
Классификация задач, с позиций применения к ним методов исследования.
Цель:
Формировать умение и навыки решения квадратных уравнений с параметрами.
Примерное содержание.
1.Повторить
Теорему Виета.
Тождество 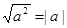
Свойства функций 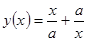 и и 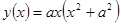
При каких значениях a, b, c и Д корни квадратного уравнения одного или разных знаков.
5. Выделение полного квадрата из квадратного трёхчлена.
2.Решить уравнения: 1)a
x² + 2x + 4=0,
2)(a
+ 3)x²+2x(a
+5)+2a
+7=0.
Ответ: 1) x=-2 при а=
0; х=-4 при а
=1/4;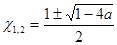 при при  ; не имеет корней при а
>1/4 .2) х=-1/4 при а
=-3; х=1, х=-3/2 ; не имеет корней при а
>1/4 .2) х=-1/4 при а
=-3; х=1, х=-3/2
при а
=-4,а
=1; 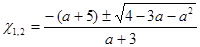 при при  ; не имеет корней при ; не имеет корней при 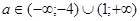 . .
Область значений функции.
Область определения функции.
Монотонность. Координаты вершины параболы.
Цель:
Познакомить с многообразием задач с параметрами.
Примерное содержание.
Квадратичная функция задаётся формулой y=a
x²+b
x+c
, где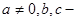 параметры, x и y- переменные. Графиком квадратичной функции является парабола. параметры, x и y- переменные. Графиком квадратичной функции является парабола.
Коэффициент a
определяет направление ветвей параболы. Если а
>0 , то они направлены вверх, если а
<0, то направлены вниз. Дискриминант квадратного трёхчлена D=b²-4ac
определяет наличие и количество общих точек с осью Ох. Если D
<0, то парабола не пересекает ось абсцисс. Если D
=0, то парабола и ось имеют одну общую точку. Если D
>0, то общих точек две.
Графический способ решения задач с параметрами является универсальным, а значит (обратная сторона любой универсальности), есть конкретные случаи, когда задачу можно решить несколько проще.
Пусть для функции y=a
x²+b
x+c
, где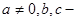 параметры, x и y — переменные. Числа параметры, x и y — переменные. Числа  и и  – нули функции, в = b – нули функции, в = b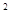 – 4ac, D
> 0, – 4ac, D
> 0, 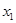 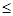  , ,  = - = -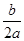 - абсцисса вершины параболы. В этих задачах, как правило, требуется определить те значения параметра, при которых выполняется некоторое условие для расположения корней. - абсцисса вершины параболы. В этих задачах, как правило, требуется определить те значения параметра, при которых выполняется некоторое условие для расположения корней.
Использование основных свойств тригонометрических функций в задачах с параметрами. Тригонометрические уравнения, содержащие параметр.
Тригонометрические неравенства, содержащие параметр.
Область значений тригонометрических функций.
Цель:
Сформировать умение использования свойств тригонометрических функций при решении тригонометрических уравнений и неравенств с параметрами.
Исследование дробно-рациональных уравнений, содержащих параметры.
V
II. Показательные и логарифмические уравнения, содержащие параметр. Рациональные уравнения.
Свойства степеней и показательной функции. Решение показательных уравнений и неравенств, содержащих параметры.
Свойства логарифмов и логарифмической функции. Решение логарифмических уравнений и неравенств с параметрами.
Цель:
Сформировать умение решать показательные и логарифмические уравнения и неравенства с параметрами, рациональные уравнения
Касательная к функции.
Критические точки.
Монотонность.
Наибольшие и наименьшие значения функции.
Построение графиков функций.
Цель:
Познакомить учащихся с типом задач с параметрами на применение методов дифференциального исчисления.
Уравнения высших степеней. Теорема Безу. Симметрические уравнения. Система однородных уравнений и приводящиеся к ним. Аналитические способы решения уравнений высших степеней с параметрами. Графический способ решения уравнений высших степеней с параметром
Задачи физического содержания. Задачи на объемные доли и концентрации вещества. Задачи на проценты.
В этом разделе формируются навыки решения текстовых задач.
(34 часа)
| № урока
|
Тема
|
| 1
|
Основные понятия уравнений с параметрами
|
| 2
|
Основные понятия неравенств с параметрами
|
| 3-4
|
Уравнения с параметрами (первой степени)
|
| 5-6
|
Неравенства с параметрами (первой степени)
|
| 7-11
|
Уравнения с параметрами (второй степени)
|
| 12-14
|
Неравенства с параметрами (второй степени)
|
| 15-16
|
Рациональные уравнения с параметрами
|
| 17-18
|
Графические приемы при решении
|
| 19-20
|
Свойства квадратичной функции
|
| 21-23
|
Текстовые задачи с использованием параметра
|
| 24-25
|
Иррациональные уравнения с параметрами
|
| 26-28
|
Параметр и количество решений уравнений, неравенств и их систем
|
| 29-30
|
Уравнения и неравенства с параметрами с различными условиями
|
| 31-32
|
Нестандартные задачи
|
| 33
|
Итоговая контрольная работа по курсу
|
| 34
|
Защита индивидуальных проектов
|
Введение элективного курса «Решение задач с параметрами» необходимо учащимся в наше время, как при подготовке к ЕГЭ, так и к вступительным экзаменам в вузы. Владение приемами решения задач с параметрам можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления.
Решение задач, уравнений с параметрами, открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях и на любом другом математическом материале. Именно такие задачи играют большую роль в формировании логического мышления и математической культуры у школьников, Поэтому учащиеся, владеющие методами решения задач с параметрами, успешно справляются с другими задачами.
1. Решить уравнение: 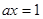
2. Решить уравнение: 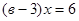
3. Решить уравнение: 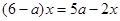
4. Решить уравнение: 
5. Решить уравнение: 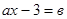
6. Решить уравнение: 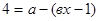
7. Решить уравнение: 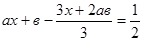
8. Решить уравнение: 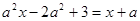
9. Решить уравнение: 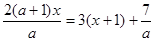
10. Решить уравнение: 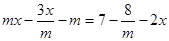
11. При каких значениях параметра в
уравнение 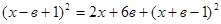 : :
а) имеет бесконечно много корней; в) имеет корень, равный единице;
б) не имеет корней; г) имеет ненулевые корни?
12. При каких значениях а
уравнение 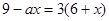 имеет: имеет:
а) только положительные корни; б) только отрицательные корни?
13. Решить уравнение: 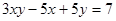 : :
а) относительно х
и найдите значение параметра, при котором корень равен нулю;
б) относительно у
и найдите значение параметра, при котором корень равен единице?
14. При каких значениях параметра в
число 1 является корнем уравнения 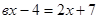 ? ?
15. При каких значениях параметра а
уравнение 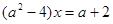 имеет корни не равные имеет корни не равные
3?
16. Решить уравнение х2
+а
2
- 1 =0.
Ответ: при │а
│>1 корней нет, при других а
х=±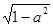 . .
17. Решить уравнение а
х2
-х+3 =0.
Ответ: при а
=0 х=3, при а
=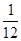 х=6, при а
> х=6, при а
>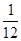 корней нет, при других а корней нет, при других а
х= . .
18. Решить неравенство а
х2
+( а
+1)х+1>0 при различных значениях а
.
Ответ: при а
=0 х>-1; при а
=1 х Є (-∞; -1)U(-1; +∞), при а
>1 х Є (-∞; -1)U( -1/а
; +∞),
при а
<0 х Є (-1; -1/а
); при а
Є (0;1) х Є (-∞; -1/а
)U(-1; +∞).
19. При каких значениях параметра а
неравенство х2
+а
х+1<0 не имеет решений?
Ответ: а
Є[-1;1].
20. Решить неравенство х2
-4а
х+9 ≤0.
Ответ: при │а
│>1,5 решений нет, при а
=1,5 х=3, при а
=-1,5 х=-3, при других а
хє[2а
- ; 2а
+ ; 2а
+ ]. ].
21. При каком значении параметра а
система 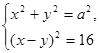 имеет ровно два решения? имеет ровно два решения?
Ответ: а
=2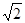 . .
22. Решить неравенство х2
- 2а
х + 1>0 для всех значений параметра а
.
Ответ: при |а
|>1 х Є R,
при а
=1 х Є R, где х ≠ 1,
при а
=-1 х Є R, где х ≠ -1,
при -1<a
<1 х Є (-∞;-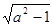 )U(а
+ )U(а
+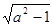 ; +∞). ; +∞).
23. При каких значениях а
неравенство а
х2
+4а
х +а
+3<0 выполняется для всех действительных значений х?
Ответ: а
Є (-∞; -4).
24. При каких значениях параметра m
двойное неравенство
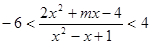 выполняется при всех действительных значениях х? выполняется при всех действительных значениях х?
Ответ: m
Є (-2; 4).
1. Агалаков.С.А Математика. Единый экзамен- 2004. Часть С. Омск; НОУ НОК Образование плюс, 2004.
2. Азаров А.И., Барвенов С.А., Федосеенко В.С. Методы решения задач с параметрами. Минск: Аверсэв, 2003.
3. БашмаковМ., Резник Н. Задачник по алгебре для 7класса общеобразователь-ной школы. Санкт – Петербург, 2001.
4. Галицкий М.Л., Гольдман А.М., Звавич Л.И.. Сборник задач по алгебре. 8-9кл. М.: Просвещение, 1994.
5. Горбачев В.И. Методы решения уравнений и неравенств с параметрами, Брянск, 1999
6. Горнштейн П.И. Задачи с параметрами. - М.: Гимназия, 2002.
7. ГорнштейнП.И., Полонский В.Б., Якир М.С.. Задачи с параметрами. Илекса. Гимназия. Москва- Харьков, 2002.
8. Далингер В.А.. Всё для обеспечения успеха на выпускных и вступительных экзаменах по математике, выпуск 4. ОГПИ, Омск, 1995.
9. Евсеева А.И.. Уравнения с параметрами.// ж. «Математика в школе», 2003, №7.
10. Ерина Т.М.. Линейные и квадратные уравнения с параметром.// ж. «Матема-тика для школьников», 2004, №2.
11. Крамор В.С. Математика. Типовые примеры на вступительных экзаменах. - М.: Аркти, 2000.
12. Крамор В.С. Примеры с параметрами и их решение. Аркти, Москва, 2000.
13. Математика для поступающих в вузы //Сост. Тырымов А.А.. – Волгоград: Учитель, 2000.
14. Математика. Задачи Сканави М.И. – Минск 1998г.
15. Математика. «Первое сентября».№ 4, 22, 23-2002 г; №12,38-2001 г
16. Материалы по подготовке к ЕГЭ 2001-2008 г
17. Мочалов В.В. Сильвестров В.В. Уравнения и неравенства с параметрами: Чебоксары – Издательство Чувашского университета, 2006.
18. Нырко В.А.,Табуева В.А. Задачи с параметрами. - Екатеринбург; УГТУ,2001.
19. Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Уравнения и неравенства с параметрами. Издат МГУ, 1992г
20. Е.М. Родионов. Справочник по математике для поступающих в ВУЗы. Изд – во МЦ «Аспект», 1992.
21. Ястребинецкий Г.А. Задачи с параметрами. – М. Просвещение, 1988г
22. Ю.Ф. Фоминых. Прикладные задачи по алгебре для 7-9 классов. М.: Просве-щение, 1999.
23. А.В. Шевкин. Задачи с параметром. Линейные уравнения и их системы. 8-9 классы. М.: Русское слово, 2003.
24. Тысяча и один пример. Под ред. О.М. Назаренко, Л.Д. Назаренко. Изд – во «Слобожаницина», 1994.
25. 514 задач с параметрами. Под ред. С.А. Тынянкина. Волгоград, 1991.
|