| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
фгоувпо «МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра высшей математики
и программного обеспечения ЭВМ
Методические рекомендации к выполнению контрольных
работ для студентов 1 курса вечерне-заочного факультета
по дисциплине «Математика»
Часть
3
.
Интегральное исчисление функции одной переменной.
Дифференциальные уравнения.
Мурманск
2006 г.
УДК 514.2 + 512.64 + 514.144.2 (075.8)
ББК 22.151.5 + 22.143Я73
М 33
Составители – Великая Елена Евгеньевна, старший преподаватель кафедры высшей математики и программного обеспечения ЭВМ МГТУ;
Мостовская Любовь Григорьевна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ;
Хохлова Людмила Ивановна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой ВМ и ПО ЭВМ 15 февраля 2006 г
., протокол № 4
Рецензент – Кацуба В.С., канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Редактор
Корректор
ÓМурманский государственный технический университет, 2006
Оглавление
Стр.
Введение…………………………………………………………………………. 4
Методические указания по темам «Интегральное исчисление функции
одной переменной» и «Дифференциальные уравнения»...……………………5
Справочный материал по теме «Интегральное исчисление функции одной
переменной»……………………………………………………………………… 7
1. Первообразная и неопределенный интеграл. Таблица интегралов……..7
2. Свойства неопределенного интеграла. Замена переменной под
знаком неопределенного интеграла………………………………….…………. 8
3. Интегрирование по частям …………………………………………… … 9
4. Интегрирование рациональных дробей……………………………….. 10
5. Интегрирование некоторых тригонометрических функций………….. 10
6. Определенный интеграл. Формула Ньютона–Лейбница …………...... 11
7. Несобственные интегралы первого и второго рода…………………….11
8. Вычисление площади плоской фигуры в декартовой системе
координат (ДСК)…………………………………………………………...…… 13
9. Вычисление площади в полярной системе координат (ПСК)……..…..13
10. Вычисление объема тела вращения…………………………………..... 14
11. Вычисление длины дуги плоской кривой…..………………………….. 14
Примерный вариант и образец выполнения контрольной работы №5 ...........15
Справочный материал по теме «Дифференциальные уравнения»………….. 21
1. Дифференциальные уравнения 1-го порядка…………………….......... 21
2. Методы решения основных типов дифференциальных уравнений
1-го порядка……………………………………………………………………...22
3. Дифференциальные уравнения 2-го порядка…………….……………. 29
4. Решение дифференциальных уравнений 2-го порядка,
допускающих понижение порядка ……………………………………………. 30
5. Решение линейных дифференциальных уравнений 2-го порядка с
постоянными коэффициентами …………………………………………..…… 34
6. Системы двух линейных дифференциальных уравнений и их
решение порядка методом повышения порядка …………………………….. 40
Примерный вариант и образец выполнения контрольной работы №6….….. 41
Варианты контрольных работ………………………………………………….. 49
Рекомендуемая литература …………………………………………….............. 56
Введение
В настоящем пособии содержатся методические рекомендации к изучению теоретического материала и выполнению контрольных работ по темам «Интегральное исчисление функции одной переменной» и «Дифференциальные уравнения», варианты этих контрольных работ и список рекомендуемой литературы.
В результате изучения этих тем студенты должны:
• изучить основные методы интегрирования – интегрирование методом замены переменной и интегрирование по частям, научиться интегрировать рациональные дроби и тригонометрические функции;
• получить представление об определенном интеграле и его свойствах, научиться вычислять его по формуле Ньютона–Лейбница;
• научиться исследованию несобственных интегралов первого и второго рода на сходимость и расходимость;
• научиться использовать определенный интеграл для решения геометрических задач, таких как вычисление площади плоской фигуры, объема тела вращения, длины дуги плоской кривой.
• знать основные понятия теории дифференциальных уравнений (порядок дифференциального уравнения, его общее и частное решения, начальные условия и др.) и уметь определять тип дифференциального уравнения;
• знать и уметь использовать методы решения основных типов дифференциальных уравнений 1-го порядка а также дифференциальных уравнений 2-го порядка, допускающих понижение порядка;
• уметь решать линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и системы линейных дифференциальных уравнений 1-го порядка методом повышения порядка.
Данные методические рекомендации включают также справочный материал, необходимый для выполнения контрольных работ по темам «Интегральное исчисление функции одной переменной» и «Дифференциальные уравнения», и подробные решения примерных вариантов работ со ссылками на используемый справочный материал.
Методические указания по темАМ
«Интегральное исчисление функции одной переменной»
И «Дифференциальные уравнения»
В таблице 1 приведены наименования тем в соответствии с содержанием контрольных работ и ссылки на литературу по этим темам. Перед выполнением каждой из контрольных работ рекомендуется изучить соответствующий теоретический материал и решить указанные в таблице задачи.
Таблица 1.
| №
к.раб.
|
№
задачи
|
Содержание (темы)
|
Литература
|
| 5
|
2
|
3
|
4
|
| 5
|
1
|
Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица интегралов. Основные методы интегрирования: метод замены переменной, интегрирование по частям
|
[1], гл.VII, §29, 30; [3], гл.7, §1-4;
[4], гл.IX, №1337-1350, 1368-1371, 1373-
1375; 1392-1396;
[6], гл.6, № 2-14, 36-50, 102, 103, 108, 109,
114, 118-120
|
| 5
|
2
|
Интегрирование рациональных дробей. Интегрирование некоторых тригонометрических функций
|
[1], гл.VII, §31, 32; [3], гл.7, §5, 6.3;
[4], гл.IX, №1410-1416, 1428-1434, 1489-
1490, 1494-1505; [6], гл.6, № 172, 177-180,
193, 194-199, 230-242
|
| 5
|
3
|
Определенный интеграл и его свойства. Вычисление определенного интеграла по формуле Ньютона–Лейбница. Несобственные интегралы первого и второго рода
|
[1], гл.VIII, §35-40; [3], гл.8, §1, 4-9, 11;
[4], гл.X, №1552-1554, 1559-1560; 1572-
1578;
[6], гл.6, № 255-266, 355-360, 366-369
|
| 5
|
4
|
Приложение определенного интеграла: вычисление площади плоской фигуры
|
[1], гл.VIII, §41.1, 41.2; [3], гл.8, §10.1, 10.2; [4], гл.X, №1596-1601;
[6], гл.6, № 290-294,301, 302
|
Окончание таблицы 1.
| 1
|
2
|
3
|
4
|
| 5
|
5
|
Приложение определенного интеграла: вычисление объема тела вращения
|
[1], гл. VIII, §41.4; [3], гл.8, §10.4;
[4], гл.X, №1628-1631;
[6], гл.6, № 319-323
|
| 5
|
6
|
Приложение определенного интеграла: вычисление длины дуги плоской кривой
|
[1], гл. VIII, §41.3; [3], гл.8, §10.3;
[4], гл.X, №1613-1618;
[6], гл.6, № 307-312
|
| 6
|
1
|
Дифференциальные уравнения 1-го порядка
|
[2], гл.I, §1.1, 1.2, 2.1-2.4; [3], гл.15, § 1.1-
1.6; [5], гл.IV, № 515-517, 550-556,603-608;
[6], гл.14, № 32-38, 43-54, 61-64, 139-140
|
| 6
|
2
|
Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
|
[2], гл.I, §3.1, 3.2; [3], гл.15, § 2.1-2.2;
[5], гл. IV, № 651, 652, 654, 659-665
|
| 6
|
3
|
Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
|
[2], гл.I, §3.4, 4.1, 5.1-5.3; [3], гл.15, § 3-4;
[5], гл.IV, № 696-699; 721-726;
[6], гл.14, № 98-111, 180, 184, 185
|
| 6
|
4
|
Системы линейных дифференциальных уравнений 1-го порядка
|
[2], гл.I, § 6.1-6.2;
[5], гл. IV, № 778-782; [6], гл.14, № 208-213
|
Примечание. Ссылки на литературу в таблице даны в соответствии с номерами в списке рекомендуемой литературы.
Справочный материал по теме «Интегральное
исчисление функции одной переменной»
1.
Первообразная и неопределенный интеграл. Таблица интегралов
Функция F
(x
) называется первообразной
для функции f
(x
) на интервале (a
, b
), если для всех x
из этого интервала выполняется равенство
 . (1) . (1)
Неопределенным интегралом
от функции f
(x
) называется множество всех первообразных этой функции, то есть неопределенный интеграл – это выражение вида  , где , где  . .
Процедуру нахождения неопределенного интеграла называют интегрированием
. При интегрировании используют: таблицу интегралов (таблица 2), свойства интегралов и специальные методы интегрирования, основные из которых – замена переменной и интегрирование по частям.
Таблица 2.
| 1. ; ;
2. ; ;
3.  ; ;
4.  ; ;
5.  ; ;
6. 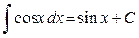 ; ;
7.  ; ;
8. 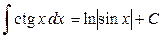 ; ;
9.  ; ;
|
10.  ; ;
11. 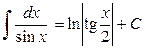 ; ;
12.  ; ;
13. 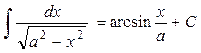 ; ;
14.  ; ;
15.  ; ;
16.  . .
|
2.
Свойства неопределенного интеграла. Замена переменной под знаком неопределенного интеграла
При интегрировании функций наиболее часто используются следующие его свойства:
1)  ; ;
2) 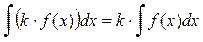 ; ;
3)  . .
Пример 1
. Найти 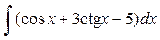 . .
Решение. Воспользуемся свойствами 1-3, а также таблицей интегралов:
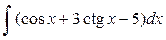 = = +3 +3 = =  . .
Ответ:  = = . .
Одним из основных методов интегрирования является метод замены переменной
(метод подстановки), который в некоторых случаях позволяет свести заданный интеграл к табличному интегралу.
Замена переменной под знаком неопределенного интеграла осуществляется по формулам:

или
 . (2) . (2)
Пример 2
. Найти  . .
Решение. Воспользуемся формулой (2) и таблицей интегралов:
 Ответ: Ответ:  . .
Этот интеграл можно взять, используя подведение под знак дифференциала части подинтегральной функции (не прописывая замену переменной)
 = = = = . .
Наиболее часто прием подведения под знак дифференциала используется при линейной замене переменной интегрирования:
 , (3) , (3)
так как 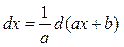 . .
Пример 3
. Найти  . .
Решение. Согласно формуле (3) можно записать:
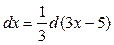  . .
Теперь воспользуемся свойством 2, а также таблицей интегралов:
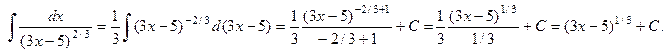 Ответ: Ответ:  = = . .
3.
Интегрирование по частям
Формулой интегрирования по частям
называют следующую формулу:
 .
(4) .
(4)
Обычно за  принимают такое выражение, интегрирование которого не вызывало бы трудностей, а за u
– функцию, дифференцирование которой приводит к ее упрощению. принимают такое выражение, интегрирование которого не вызывало бы трудностей, а за u
– функцию, дифференцирование которой приводит к ее упрощению.
Можно выделить два основных класса интегралов, берущихся по частям:
1) 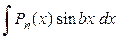 ; ;  ; ; 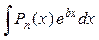 ; ; 
– здесь за u
принимают целый многочлен  , за , за  – оставшееся выражение, то есть, например – оставшееся выражение, то есть, например  . .
2)  ; ;  ; ; 
– здесь за u
принимают обратную функцию, например, arcsinbx
, за  – оставшееся выражение, то есть – оставшееся выражение, то есть  . .
4.
Интегрирование рациональных дробей
Рациональной дробью
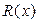 называют отношение двух целых многочленов называют отношение двух целых многочленов  и и  , т.е. , т.е. 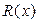 = = . Для интегрирования рациональной дроби необходимо предварительно разложить ее, т.е. представить . Для интегрирования рациональной дроби необходимо предварительно разложить ее, т.е. представить 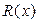 в виде суммы простейших дробей видов: в виде суммы простейших дробей видов:

где k
, r
– целые положительные числа, а трехчлен 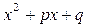 не имеет действительных корней. не имеет действительных корней.
Если дробь  неправильная ( неправильная ( ), то необходимо предварительно выделить целую часть дроби. ), то необходимо предварительно выделить целую часть дроби.
5.
Интегрирование некоторых тригонометрических функций
Для нахождения интегралов видов  и и  используют тригонометрические формулы: используют тригонометрические формулы:
  (5)
(5)
Для нахождения интегралов вида 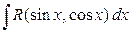 , где R
– рациональная функция (не содержащая sinх
и cosx
под знаком корней), используют универсальную подстановку: , где R
– рациональная функция (не содержащая sinх
и cosx
под знаком корней), используют универсальную подстановку: 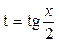 , которая сводит , которая сводит 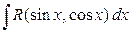 к интегралу от рациональной функции, т.к. к интегралу от рациональной функции, т.к.
 и и  (6) (6)
5.
Формула Ньютона–Лейбница
Формула Ньютона–Лейбница для вычисления определенного интеграла имеет вид:
 , (7)
, (7)
если  и и  непрерывна на непрерывна на 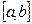 . .
Пример 4.
Вычислить определенный интеграл . .
Решение. Это определенный интеграл, берущийся по частям, поэтому, применяя формулу (4), а затем формулу Ньютона–
Лейбница, получаем:
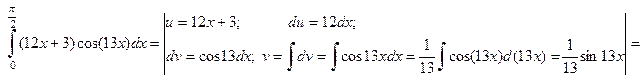 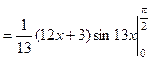  
= . .
Ответ:  = = . .
7. Несобственные интегралы первого и второго рода
Примером несобственного интеграла первого рода
является интеграл
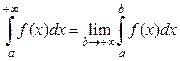 (8) (8)
Интегралы
 , (9) , (9)
где a
– точка бесконечного разрыва функции  , и , и
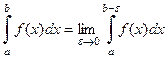 , (10) , (10)
где b
– точка бесконечного разрыва функции  , относятся к несобственным интегралам второго рода
. , относятся к несобственным интегралам второго рода
.
Несобственный интеграл называется сходящимся
, если существует конечный предел в правой части равенства. Если же предел не существует или равен бесконечности, то интеграл называется расходящимся
.
Пример 5
. Исследовать на сходимость интеграл 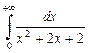 . .
Решение. Это несобственный интеграл первого рода, поэтому
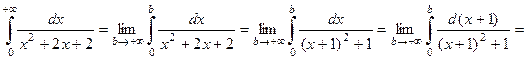
 . .
Ответ: интеграл  сходится и равен сходится и равен  . .
Пример 6.
Исследовать на сходимость интеграл 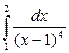 . .
Решение. Это несобственный интеграл второго рода, так как х
= 1 –
точка разрыва второго рода подинтегральной функции, поэтому
  , ,
следовательно, интеграл расходится.
Ответ: интеграл 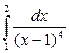 расходится. расходится.
8.
Вычисление площади плоской фигуры в декартовой системе
координат (ДСК)
 Криволинейной трапецией
в ДСК называется фигура, ограниченная прямыми x
=
a
, x
=
b
, y
= 0 и кривой y
= f
(x
), где Криволинейной трапецией
в ДСК называется фигура, ограниченная прямыми x
=
a
, x
=
b
, y
= 0 и кривой y
= f
(x
), где  для для  (рис. 1). (рис. 1).
Формула для вычисления площади криволинейной трапеции:
 . (11) . (11)

Если фигура Ф
ограничена в ДСК линиями x
=
a
, x
=
b
, y
= f
1
(x
) и y
= f
2
(x
) где 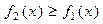 для для  (рис. 2), то площадь Ф
можно вычислить по формуле: (рис. 2), то площадь Ф
можно вычислить по формуле:
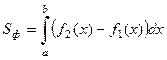 . (12) . (12)
9.
Вычисление площади плоской фигуры в полярной системе координат (ПСК)
 Криволинейным сектором
в ПСК называется фигура, ограниченная лучами Криволинейным сектором
в ПСК называется фигура, ограниченная лучами  и кривой и кривой  , где , где 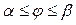 (рис. 3). (рис. 3).
Формула для вычисления площади криволинейного сектора:
 . (13)
. (13)
10.
Вычисление объема тела вращения
Пусть криволинейная трапеция, ограниченная прямыми x
=
a
, x
=
b
,
y
= 0 и непрерывной кривой y
= f
(x
), где  для для  , вращается вокруг оси О
X
. Объем полученного при этом тела вращения (рис. 4) вычисляется по формуле: , вращается вокруг оси О
X
. Объем полученного при этом тела вращения (рис. 4) вычисляется по формуле:
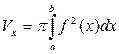 .
(14)
.
(14)
Если плоская фигура ограничена линиями x
=
a
, x
=
b
, y
1
= f
1
(x
) и
y
2
= f
2
(x
) где 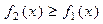 для для 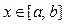 , то объем полученного при ее вращении вокруг О
X
тела (рис. 5) можно вычислить по формуле: , то объем полученного при ее вращении вокруг О
X
тела (рис. 5) можно вычислить по формуле:
 . (15)
. (15)

11.
Вычисление длины дуги плоской кривой
Пусть плоская кривая АВ
задана уравнением y
= f
(x
), где 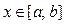 . Если функция f
′
(x
) и ее производная f
·′
(x
) непрерывны на промежутке [a
; b
], то длина кривой АВ
вычисляется по формуле: . Если функция f
′
(x
) и ее производная f
·′
(x
) непрерывны на промежутке [a
; b
], то длина кривой АВ
вычисляется по формуле:
 .
(16)
.
(16)
Примерный вариант и образец выполнения
контрольной работы №5
Задача 1.
Найти неопределенные интегралы:
 , ,  , ,  , ,  . .
В примерах  правильность полученных результатов проверить дифференцированием. правильность полученных результатов проверить дифференцированием.
Задача 2.
Вычислить несобственные интегралы или доказать их расходимость:
а
) , б
) , б
) 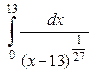 . .
Задача 3.
Вычислить с помощью определенного интеграла площадь плоской фигуры:
а
) ограниченной в ДСК линиями l
1
:  и l
2
:
и l
2
:  ;
;
б
)
ограниченной в ПСК линией l
:  .
.
Сделать чертежи.
Задача 4.
Вычислить с помощью определенного интеграла объем тела, полученного вращением вокруг оси OX
фигуры, ограниченной линиями
l
1
: 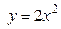 и l
2
: y =
6x
. Сделать чертеж.
и l
2
: y =
6x
. Сделать чертеж.
Задача 5.
Вычислить с помощью определенного интеграла длину дуги кривой, заданной в ДСК уравнением  , где , где  . .
Решение задачи 1
.
а
) Так как 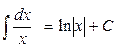 , то используя формулу (3), получим: , то используя формулу (3), получим:
 . .
Проверим результат дифференцированием:

следовательно, выполнено условие (1).
Ответ:  = = . .
б
) Интеграл  относится к типу интегралов, берущихся по частям; это интеграл так называемого второго типа. Используя формулу (4), получим: относится к типу интегралов, берущихся по частям; это интеграл так называемого второго типа. Используя формулу (4), получим:
  . .
Проверим результат дифференцированием:
 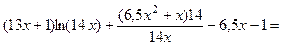
 . .
Ответ:  = = . .
в
) Подинтегральная функция является правильной рациональной дробью, поэтому ее можно представить в виде суммы простейших дробей:
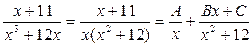 , отсюда , отсюда
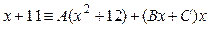 , или , или 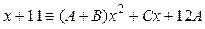 . .
Неопределенные коэффициенты А
, В
, С
найдем, приравнивая коэффициенты при одинаковых степенях х
в левой и правой частях тождества:

Коэффициенты А
, В
, С
можно найти другим способом –
подставляя в тождество «удобные» значения х
(метод частных значений):

Из первого уравнения получим:  . Почленно вычитая два последних равенства, получим: . Почленно вычитая два последних равенства, получим:  , и из последнего уравнения , и из последнего уравнения
 . .
Таким образом, 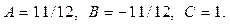
Переходим к интегрированию:

 . .
Здесь использовано:  , ,
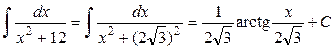 . .
Проверим результат дифференцированием: 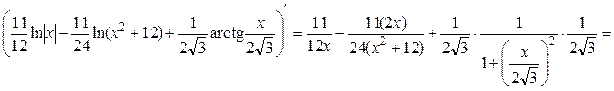
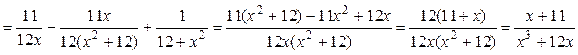 . .
Ответ:  = =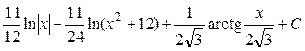 . .
г
) Применим универсальную тригонометрическую подстановку:

  . .
Возвращаясь к переменной х
, получаем:
  . .
Ответ: 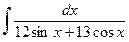 = = . .
Решение задачи 2
.
а
) Данный интеграл является несобственным интегралом первого рода, поэтому

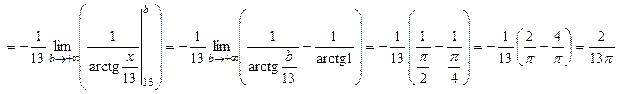 , ,
следовательно, интеграл сходится и равен 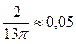 . .
Здесь использовано:  . .
Ответ: интеграл  сходится и равен сходится и равен  . .
б
) Данный интеграл является несобственным интегралом второго рода, т.к. х=
13 – точка бесконечного разрыва подинтегральной функции. Поэтому
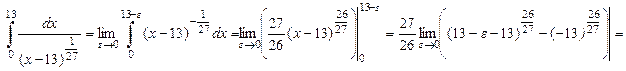 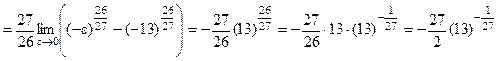 , ,
следовательно, интеграл сходится и равен  . .
Ответ: интеграл  сходится и равен сходится и равен  . .
Решение задачи 3
.
 а
) Найдем точки пересечения кривых, для чего составим и решим систему а
) Найдем точки пересечения кривых, для чего составим и решим систему  . Приравнивая правые части, получаем уравнение . Приравнивая правые части, получаем уравнение 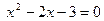 , решив которое, найдем абсциссы точек пересечения: x
= –
1, x
= 3. , решив которое, найдем абсциссы точек пересечения: x
= –
1, x
= 3.
Построим чертеж (рис. 6). На рисунке видно, что 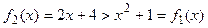 на промежутке [–
1; 3]. на промежутке [–
1; 3].
Используя формулу (12), вычислим площадь фигуры, ограниченной заданными линиями:

 . .
Ответ: 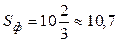 единиц площади. единиц площади.
б
) Для построения кривой 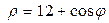 в ПСК составим таблицу значений функции на промежутке в ПСК составим таблицу значений функции на промежутке 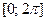 . .
| 
|
0
|
π
/4
|
2π
/4
|
3π
/4
|
π
|
5π
/4
|
6π
/4
|
7π
/4
|
2π
|
| 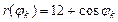
|
13
|
12,7
|
12
|
11,3
|
11
|
11,3
|
12
|
12,7
|
13
|
Построим чертеж в ПСК (рис. 7). Так как фигура ограничена кривой,
заданной в полярной системе координат, то площадь фигуры, ограниченной заданной линией, вычислим по формуле (13):  .
.
 Для Для  получаем: получаем:
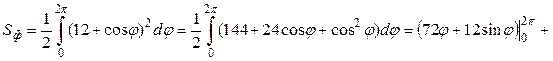
 . .
Ответ: 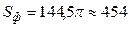 единицы площади. единицы площади.
Решение задачи 4
.
Для построения фигуры Ф
, ограниченной кривыми l
1
и l
2
, нужно найти точки их пересечения, т.е. решить систему:  . Приравнивая правые части равенств, получаем уравнение . Приравнивая правые части равенств, получаем уравнение  , решив которое, найдем абсциссы точек пересечения кривых: , решив которое, найдем абсциссы точек пересечения кривых: 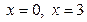 . .
 Объем тела вращения, полученного вращением фигуры Ф
вокруг оси OX
(рис. 8), можно найти как разность объемов двух тел по формуле (15): Объем тела вращения, полученного вращением фигуры Ф
вокруг оси OX
(рис. 8), можно найти как разность объемов двух тел по формуле (15):


 . .
Ответ:  единиц объема. единиц объема.
Решение задачи 5
.
Кривая задана уравнением 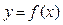 где где 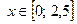 , поэтому ее длина вычисляется по формуле (16): , поэтому ее длина вычисляется по формуле (16):  .
.
Для 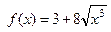 получаем: получаем:  ,
,
тогда длина дуги кривой
 .
.
Ответ: 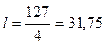 единиц длины. единиц длины.
Справочный материал по теме
«Дифференциальные уравнения»
1.
Дифференциальные уравнения 1-го порядка
Дифференциальным уравнением 1-го порядка
называется уравнение вида
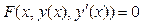 , (17) , (17)
где x
– независимая переменная, y
(х
) – неизвестная функция этой переменной,  – ее первая производная. – ее первая производная.
Часто дифференциальное уравнение первого порядка встречается в разрешенной относительно  форме: форме:
 , ,
или в дифференциальной форме (в дифференциалах):
P
(x, y
)dx+Q
(x, y
)dy =
0.
Решением дифференциального уравнения
называется функция y
=
g
(x
), которая при подстановке в дифференциальное уравнение обращает его в тождество.
Процесс нахождения решения дифференциального уравнения называется его интегрированием. В результате интегрирования дифференциального уравнения первого порядка получают не одно решение, а семейство решений, зависящих от одной произвольной постоянной С
:
y
=
g
(x
, С
)
– общее решение дифференциального
уравнения 1-го порядка
.
Если решение получено в виде, не разрешенном относительно у
:
G
(x
, y
, C
) = 0,
то его называют общим интегралом
дифференциального уравнения 1-го порядка
.
Всякое решение, получающееся из общего при конкретном числовом значении произвольной постоянной C
= C
0
, называется частным решением
:
y
=
g
(x
, С
0
).
Чтобы найти частное решение дифференциального уравнения (17), удовлетворяющее некоторому начальному условию
y
(x
0
) = y
0
, (18)
нужно в общее решение уравнения y
=
g
(x
, С
) подставить x
= x
0
, y
= y
0
:
y
0
=
g
(x
0
, С
), (19)
из полученного уравнения (19) найти C
= C
0
, затем найденное значение C
0
подставить в общее решение. В результате получим частное решение
y
=
g
(x
, С
0
).
Задача нахождения частного решения уравнения (17), удовлетворяющего начальному условию (18), называется задачей Коши
.
Общее решение y
=
g
(x
, С
) задает на плоскости XOY
семейство интегральных кривых
данного дифференциального уравнения, поскольку каждому значению  соответствует кривая с уравнением соответствует кривая с уравнением  Решению задачи Коши y
=
g
(x
, С
0
) соответствует одна интегральная кривая из этого семейства, проходящая через точку (x
0
; y
0
). Решению задачи Коши y
=
g
(x
, С
0
) соответствует одна интегральная кривая из этого семейства, проходящая через точку (x
0
; y
0
).
2. Методы решения основных типов д
ифференциальных уравнений
1-го порядка
2.1. Дифференциальные уравнения с разделяющимися переменными
.
Дифференциальное уравнение вида
 (20)
(20)
называется дифференциальным уравнением с разделяющимися переменными
. Отличительной особенностью уравнений этого типа является то, что в правой их части находится произведение функций 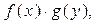  одна из которых зависит только от x
, другая только от y
. одна из которых зависит только от x
, другая только от y
.
Для того, чтобы найти решение уравнения (20), нужно разделить переменные x
и y
, собрав в левой и правой его частях функции, зависящие только от одной переменной.
Для разделения переменных в уравнении (20) заменим производную 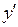 на на  и умножим обе части уравнения на и умножим обе части уравнения на 

Получили уравнение с разделенными переменными. Общий интеграл этого уравнения, а следовательно, и уравнения (20) находится почленным интегрированием его левой и правой частей:

где С
– произвольная постоянная, С
= С
2
– С
1
.
Таким образом, чтобы найти общее решение или общий интеграл уравнения (20), нужно разделить переменные x
и y
и почленно проинтегрировать полученное равенство с добавлением произвольной постоянной С
.
Пример 1.
Решить дифференциальное уравнение: 
Решение. Сравнивая данное уравнение с уравнением (20), замечаем, что оно является уравнением с разделяющимися переменными. Заменим  на на 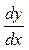 и разделим переменные, умножая обе части уравнения на и разделим переменные, умножая обе части уравнения на 
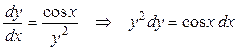 . .
Интегрируя полученное равенство, получим:

Отсюда  – общий интеграл данного уравнения (константы интегрирования включены в общую константу С
). Разрешая его относительно у
, можно записать общее решение данного уравнения в виде – общий интеграл данного уравнения (константы интегрирования включены в общую константу С
). Разрешая его относительно у
, можно записать общее решение данного уравнения в виде
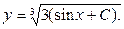
Ответ: 
З а м е ч а н и е. Уравнение вида
 (21) (21)
также является уравнением с разделяющимися переменными, т.к. здесь коэффициенты при dx
и dy
являются произведениями функций, каждая из которых зависит только от одной переменной. Уравнение вида (21) решается тем же способом, что и уравнение (20).
2.2. Линейные дифференциальные уравнения 1-го порядка.
Дифференциальное уравнение вида
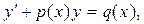 (22) (22)
где p
(x
), q
(x
) – заданные функции, называется линейным дифференциальным уравнением 1-го порядка
.
Отличительной особенностью линейного уравнения (22) является то, что искомая функция y
и ее первая производная  входят в уравнение линейно – в первых степенях и не перемножаются между собой. входят в уравнение линейно – в первых степенях и не перемножаются между собой.
Для решения уравнения (22) воспользуемся способом подстановки. Будем искать неизвестную функцию y
в виде произведения двух тоже пока неизвестных функций: положим y
= u
(x
)v
(x
). Тогда  Подставив значения y
и Подставив значения y
и  в уравнение (22), получим: в уравнение (22), получим:

 (23) (23)
Если выбрать v
(x
) так, чтобы выражение, стоящее в скобках, обратилось в нуль, т.е.
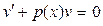 , (24) , (24)
то для второй функции u
(x
) из равенства (23) получится уравнение
 (25) (25)
Таким образом, решение линейного дифференциального уравнения (22) сводится к решению двух уравнений (24) и (25), каждое из которых является дифференциальным уравнением с разделяющимися переменными. Общее решение уравнения (22) есть произведение какого-либо частного решения уравнения (24) и общего решения уравнения (25):
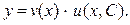 (26) (26)
Пример 2
. Найти решение дифференциального уравнения 
которое удовлетворяет условию 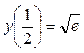 (задача Коши). (задача Коши).
Решение. Разделив все члены уравнения на х
, перепишем уравнение в виде
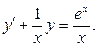 Сравнивая его с уравнением (22), убеждаемся, что оно является линейным дифференциальным уравнением. Сравнивая его с уравнением (22), убеждаемся, что оно является линейным дифференциальным уравнением.
Положим y
= u
(x
)v
(x
), тогда  Подставив y
и Подставив y
и  в уравнение, получим: в уравнение, получим: 
 (*) (*)
Найдем функцию v
, решая уравнение 

(в данном случае удобно использовать логарифмическую константу интегрирования, положив 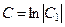 ). ).
Из последнего уравнения следует:  – общее решение, а при соответствующем подборе – общее решение, а при соответствующем подборе  получаем получаем 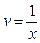 – частное решение уравнения – частное решение уравнения 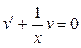 . .
Подставив найденную функцию 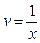 в уравнение (*), получим уравнение для функции u
: в уравнение (*), получим уравнение для функции u
:  . Найдем функцию . Найдем функцию  – общее решение – общее решение
этого уравнения:
 . .
Общим решением исходного уравнения является функция
 . .
Найдем частное решение, удовлетворяющее заданному начальному условию  Для этого подставим в общее решение вместо x
, y
числа Для этого подставим в общее решение вместо x
, y
числа 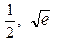 соответственно: соответственно:
Подставляя найденное значение С
в общее решение, получим искомое частное решение (решение задачи Коши): 
Ответ: 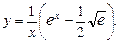
2.3. Уравнения Бернулли.
Дифференциальное уравнение вида
 (27) (27)
где n
– действительное число,  , называется уравнением Бернулли
. , называется уравнением Бернулли
.
Уравнение Бернулли является обобщением линейного дифференциального уравнения (22) и может быть решено тем же способом.
Пример решения уравнения Бернулли приведен в образце выполнения контрольной работы.
2.4.Однородные уравнения.
Функция f
(
x
,
y
)
называется однородной функцией
m
-го порядка (измерения)
, если 
Дифференциальное уравнение вида
P
(x,y
)dx+Q
(x,y
)dy =
0 (28)
называется однородным
, если P
(x
,
y
) и Q
(x
,
y
) – однородные функции одного порядка.
Однородное дифференциальное уравнение может быть приведено к виду
 (29) (29)
С помощью подстановки  , т.е. , т.е.  однородное дифференциальное уравнение (29) приводится к уравнению с разделяющимися переменными относительно новой неизвестной функции t
(x
). однородное дифференциальное уравнение (29) приводится к уравнению с разделяющимися переменными относительно новой неизвестной функции t
(x
).
Пример 3.
Решить дифференциальное уравнение: 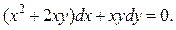
Решение. Здесь  , обе функции – однородные, 2-го порядка, так как выполнено , обе функции – однородные, 2-го порядка, так как выполнено
 . .
Разрешим данное уравнение относительно  . Для этого запишем его в виде . Для этого запишем его в виде  и разделим обе части на xydx
, заменяя при этом и разделим обе части на xydx
, заменяя при этом 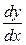 на на  ; в результате получим исходное уравнение в виде (29): ; в результате получим исходное уравнение в виде (29):  . .
Введем подстановку y
=
tx
, откуда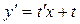 . Тогда уравнение примет вид: . Тогда уравнение примет вид:
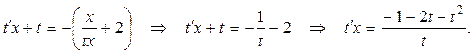
Это дифференциальное уравнение с разделяющимися переменными относительно новой неизвестной функции t
(х
).
Разделяем переменные t
и х
:
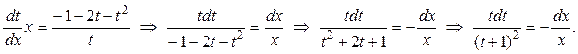
Переходим к интегрированию:

Здесь использовано:

Заменяя t
на 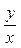 и упрощая результат, получаем: и упрощая результат, получаем:
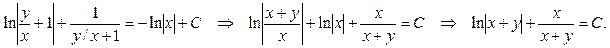
Поскольку функцию y
(x
) сложно выразить явным образом через х
и С
, запишем решение в форме общего интеграла уравнения.
Ответ: 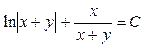 – общий интеграл уравнения. – общий интеграл уравнения.
Для определения типа дифференциального уравнения 1-го порядка и выбора метода его решения можно использовать таблицу 3.
Таблица 3.
| Тип дифференциального уравнения
|
Вид, к которому
приводится уравнение
|
Метод решения
|
| Дифференциальное уравнение с разделяющимися переменными
|

|
Разделение переменных:

|
| Линейное дифференциальное уравнение 1-го порядка
|

|
Замена:
y
= u
(x
)v
(x
),

|
| Уравнение Бернулли
|
 
|
Замена:
y
= u
(x
)v
(x
),

|
| Однородное дифференциальное уравнение 1-го порядка
|

|
Замена:
y
=
tx
,
 . .
|
3. Дифференциальные уравнения 2-го порядка
Дифференциальным уравнением
2-го порядка
называется уравнение вида
 (30) (30)
где х
– независимая переменная, y
(х
) – неизвестная функция этой переменной,  и и  – ее первая и вторая производные. – ее первая и вторая производные.
Иногда уравнение 2-го порядка встречается в форме, разрешенной относительно второй производной:
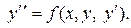
Общее решение уравнения
2-го порядка
имеет вид:
y
= g
(x
, C
1
, C
2
), (31)
где С
1
и С
2
– две произвольные постоянные.
Решение, полученное в неявном виде
G
(x
, y
, C
1
, C
2
) = 0,
называется общим интегралом
уравнения
2-го порядка
.
Всякое решение, получающееся из общего решения при конкретных числовых значениях произвольных постоянных С
1
и С
2
, является его частным решением.
Задача Коши для дифференциального уравнения 2-го порядка (30) состоит в нахождении частного решения уравнения, удовлетворяющего двум начальным условиям:
 , (32) , (32)
где  – заданные числа. – заданные числа.
Для решения задачи Коши нужно подставить в общее решение (31) и его производную заданные начальные условия
 , ,
решить полученную систему двух уравнений относительно неизвестных С
1
и С
2
и подставить найденные значения постоянных 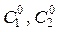 в общее решение: в общее решение:
 – решение задачи Коши. – решение задачи Коши.
4. Решение дифференциальных уравнений 2-го порядка, допускающих понижение порядка
В некоторых случаях дифференциальное уравнение 2-го порядка можно решить методом понижения порядка
. Использование этого метода позволяет свести решение уравнения 2-го порядка к решению уравнения 1-го порядка.
4.1. Дифференциальные уравнения 2-го порядка, не содержащие искомой функции.
Уравнение такого типа имеет вид:
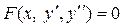 . (33) . (33)
Отличительной особенностью этого уравнения является то, что в него не входит явно искомая функция у
, а входят только ее производные  и и 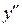 . .
Для решения уравнения (33) используется способ подстановки. Вместо производной  введем новую неизвестную функцию введем новую неизвестную функцию  = z
(x
), тогда = z
(x
), тогда  . Подставляя в (33) вместо . Подставляя в (33) вместо  и и  соответственно z
и соответственно z
и  , получим дифференциальное уравнение 1-го порядка относительно новой неизвестной функции z
(x
): , получим дифференциальное уравнение 1-го порядка относительно новой неизвестной функции z
(x
):
 . .
Определив тип этого уравнения и решив его, следует записать его общее решение в виде  , а затем вернуться к функции у
: , а затем вернуться к функции у
: 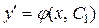 . Полученное уравнение является дифференциальным уравнением 1-го порядка. Решая его, получаем общее решение уравнения (33): . Полученное уравнение является дифференциальным уравнением 1-го порядка. Решая его, получаем общее решение уравнения (33):
 . .
Таким образом, решение уравнения 2-го порядка (33) сводится к последовательному решению двух дифференциальных уравнений 1-го порядка.
Пример 4.
Найти частное решение уравнения  , удовлетворяющее начальным условиям , удовлетворяющее начальным условиям 
Решение. Данное дифференциальное уравнение – это дифференциальное уравнение 2-го порядка, не содержащее явно у
. Полагаем  = z
(x
), = z
(x
),  , тогда уравнение примет вид: , тогда уравнение примет вид:
 . .
Это линейное дифференциальное уравнение 1-го порядка относительно функции z
(x
). Положим 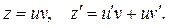 Подставив z
и Подставив z
и  в уравнение, получим в уравнение, получим 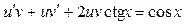 , или , или
 (**) (**)
Найдем функцию v
(x
) решая уравнение 
 Из последнего уравнения, полагая Из последнего уравнения, полагая 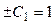 получаем: получаем:  – частное решение уравнения – частное решение уравнения  . .
Подставим найденную функцию  в уравнение (**) и найдем общее решение этого уравнения: в уравнение (**) и найдем общее решение этого уравнения:
 
– общее решение уравнения  . .
Запишем общее решение уравнения  : :
 . .
Так как z
=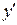 , то получаем дифференциальное уравнение для функции у
(х
): , то получаем дифференциальное уравнение для функции у
(х
):
 (***) (***)
Прежде чем интегрировать это уравнение, целесообразно определить значение постоянной С
, используя начальное условие 

Подставив значение  в дифференциальное уравнение (***), получим: в дифференциальное уравнение (***), получим:

Проинтегрируем:

Найдем значение постоянной С
1
, используя начальное условие 

Запишем частное решение исходного дифференциального уравнения, удовлетворяющее заданным начальным условиям:  . .
Ответ: 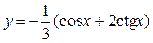 . .
4.2. Дифференциальные уравнения 2-го порядка, не содержащие независимой переменной.
Уравнение такого типа имеет вид:
 . (34) . (34)
Отличительной особенностью этого уравнения является то, что в него не входит явно независимая переменная x
.
Способ решения уравнения (34) состоит в следующем. Примем переменную y
за новую независимую переменную, вместо неизвестной функции y
(х
) введем новую неизвестную функцию p
(y
) по формуле  = p
(y
). Тогда, пользуясь правилом дифференцирования сложной функции, получим = p
(y
). Тогда, пользуясь правилом дифференцирования сложной функции, получим
 , где , где  . .
Подставляя в (34) выражения для  и и  , получим дифференциальное уравнение 1-го порядка относительно неизвестной функции p
(y
): , получим дифференциальное уравнение 1-го порядка относительно неизвестной функции p
(y
):
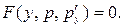
Определив тип этого уравнения и решив его, следует записать его общее решение в виде 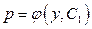 . Так как p
= . Так как p
=  , полученное выражение является дифференциальным уравнением 1-го порядка относительно искомой функции y
(х
): , полученное выражение является дифференциальным уравнением 1-го порядка относительно искомой функции y
(х
):
 . .
Это уравнение с разделяющимися переменными, которое следует решать по обычной схеме (см. п.2.1).
Таким образом, решение уравнения 2-го порядка (34) сводится к последовательному решению двух дифференциальных уравнений 1-го порядка.
Пример решения уравнения 2-го порядка, не содержащего независимой переменной, приведен в образце выполнения контрольной работы.
5. Решение линейных дифференциальных уравнений 2-го порядка с
постоянными коэффициентами
5.1. Линейные дифференциальные уравнения 2-го порядка.
Уравнение вида
 (35) (35)
где p
(x
), q
(x
) и f
(x
) – заданные функции, называется линейным дифференциальным уравнением 2-го порядка
.
Отличительной его особенностью является то, что искомая функция у
, и ее производные 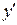 и и  входят в уравнение линейно – в первых степенях и не перемножаются между собой. входят в уравнение линейно – в первых степенях и не перемножаются между собой.
Если  , то уравнение (35) называется линейным однородным дифференциальным уравнением
и имеет вид: , то уравнение (35) называется линейным однородным дифференциальным уравнением
и имеет вид:
 . (36) . (36)
если же  , то уравнение (35) называется линейным неоднородным дифференциальным уравнением 2-го порядка
. , то уравнение (35) называется линейным неоднородным дифференциальным уравнением 2-го порядка
.
Общее решение линейного однородного уравнения 2-го порядка (36) имеет вид:
 , ,
где у
1
и у
2
– два линейно независимых частных решения этого уравнения 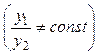 , а С
1
и С
2
– произвольные постоянные. , а С
1
и С
2
– произвольные постоянные.
Общее решение линейного неоднородного уравнения (35) имеет вид:
 , ,
где 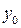 – общее решение соответствующего однородного уравнения (36), – общее решение соответствующего однородного уравнения (36),
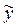 – какое-либо частное решение неоднородного уравнения (35). – какое-либо частное решение неоднородного уравнения (35).
5.2. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
Если коэффициенты при у
,  и и  – постоянные, то уравнение – постоянные, то уравнение
 (37) (37)
где p
и q
– вещественные числа, называется линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами
.
Общее решение уравнения (37) имеет вид:  , ,
где у
1
и у
2
– два линейно независимых частных решения этого уравнения,
С
1
и С
2
– произвольные постоянные.
Для нахождения линейно независимых частных решений у
1
и у
2
уравнения (37) используется квадратное уравнение вида
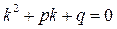 , ,
которое называется характеристическим
уравнением
для уравнения (37).
В таблице 4 приведены виды функций у
1
и у
2
и вид общего решения уравнения (37) в зависимости от вида корней характеристического уравнения.
Таблица 4.
| Корни характеристического уравнения
|
Вид функций у
1
и у
2
|
Вид общего решения уравнения
|
| Вещественные
различные 
|
 , ,

|
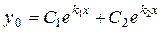
|
| Вещественные равные 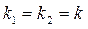
|
 , ,

|

|
| Комплексно-сопряженные 
|
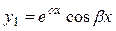 , ,

|

|
Пример 5.
Найти общее решение уравнения  . .
Решение. Характеристическое уравнение для данного однородного уравнения имеет вид  (коэффициент при (коэффициент при  равен нулю). Его корнями являются комплексные числа равен нулю). Его корнями являются комплексные числа  Здесь Здесь 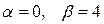 . Тогда . Тогда  , ,  и общее решение данного уравнения: и общее решение данного уравнения: 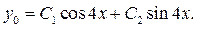
Ответ: 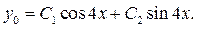
5.3. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
Уравнение вида
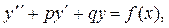 (38) (38)
где p
и q
– вещественные числа, называется линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами
.
Общее решение линейного неоднородного уравнения (38) имеет вид:
 (39) (39)
где  – общее решение соответствующего однородного уравнения (37), а – общее решение соответствующего однородного уравнения (37), а  – какое-либо частное решение неоднородного уравнения (38). – какое-либо частное решение неоднородного уравнения (38).
Построение общего решения неоднородного уравнения состоит из двух этапов. Сначала нужно найти общее решение соответствующего однородного уравнения  , затем найти частное решение , затем найти частное решение 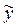 неоднородного уравнения. неоднородного уравнения.
Решение  для линейного однородного дифференциального уравнения (37) находят, используя характеристическое уравнение (п. 5.1), а для нахождения частного решения для линейного однородного дифференциального уравнения (37) находят, используя характеристическое уравнение (п. 5.1), а для нахождения частного решения 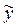 уравнения (38) можно использовать либо метод вариации произвольных постоянных, либо метод неопределенных коэффициентов. уравнения (38) можно использовать либо метод вариации произвольных постоянных, либо метод неопределенных коэффициентов.
Метод вариации произвольных постоянных.
Метод вариации произвольных постоянных применяется для нахождения частного решения  линейного неоднородного дифференциального уравнения в тех случаях, когда известно общее решение линейного неоднородного дифференциального уравнения в тех случаях, когда известно общее решение  соответствующего однородного уравнения. соответствующего однородного уравнения.
Если известно  , то функция , то функция  будет частным решением уравнения будет частным решением уравнения  , если функции с
1
(х
) и с
2
(х
) удовлетворяют так называемым «условиям вариации»: , если функции с
1
(х
) и с
2
(х
) удовлетворяют так называемым «условиям вариации»:
 (40) (40)
Для нахождения частного решения 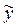 необходимо решить систему уравнений (40), затем проинтегрировать полученные функции: необходимо решить систему уравнений (40), затем проинтегрировать полученные функции:
 (41) (41)
и записать частное решение:  . Константы интегрирования в (41) можно взять равными нулю, так как мы находим частное решение. . Константы интегрирования в (41) можно взять равными нулю, так как мы находим частное решение.
Пример использования метода вариации произвольных постоянных приведен в образце выполнения контрольной работы.
Метод неопределенных коэффициентов.
Метод неопределенных коэффициентов применяется для нахождения частного решения  неоднородного уравнения с постоянными коэффициентами в тех случаях, когда функция f
(x
), стоящая в правой части этого уравнения, имеет один из двух «специальных» видов: неоднородного уравнения с постоянными коэффициентами в тех случаях, когда функция f
(x
), стоящая в правой части этого уравнения, имеет один из двух «специальных» видов:
 , (42) , (42)
где Pn
(x
) – многочлен степени n
: Pn
(x
) = a
0
xn
+ a
1
xn
-1
+….+ an
-1
x
+
an
,
или
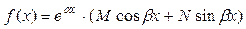 , (43) , (43)
где M
и N
– числа.
1) Если 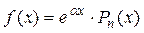 , то частное решение можно искать в виде: , то частное решение можно искать в виде:
 (44) (44)
где k
1
, k
2
– корни характеристического уравнения, Qn
(x
) – многочлен степени n
, записанный с неопределенными коэффициентами, подлежащими определению, например,
 , и т.д. , и т.д.
2) Если  , то частное решение , то частное решение 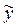 можно искать в виде: можно искать в виде:
 (45) (45)
где k
1
, k
2
– корни характеристического уравнения, А
и В
– неизвестные постоянные, подлежащие определению.
Пример 6.
Найти общее решение уравнения  . .
Решение.
1 этап. Построим общее решение  соответствующего однородного уравнения соответствующего однородного уравнения  . Составим для него характеристическое уравнение . Составим для него характеристическое уравнение  и найдем корни: и найдем корни:  – корни вещественные и различные. По таблице 4 определим вид линейно независимых частных решений однородного уравнения: – корни вещественные и различные. По таблице 4 определим вид линейно независимых частных решений однородного уравнения:  , , 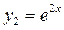 и запишем его общее решение: и запишем его общее решение:
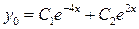 . .
2 этап. Построим частное решение данного неоднородного уравнения  . В заданном уравнении . В заданном уравнении 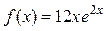 – правая часть 1-го специального вида: – правая часть 1-го специального вида: 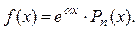 Здесь Здесь 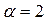 , Pn
(x
) = 12x
, т.е. многочлен в правой части – , Pn
(x
) = 12x
, т.е. многочлен в правой части –
1-й степени (n
= 1). Число 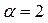 совпадает с одним корнем характеристического уравнения совпадает с одним корнем характеристического уравнения 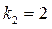 . Следовательно, согласно (44) частное решение . Следовательно, согласно (44) частное решение  будем искать в виде: будем искать в виде:
 , ,
где А,
B
– неизвестные коэффициенты, подлежащие определению.
Найдем производные  и подставим и подставим 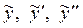 в данное неоднородное уравнение в данное неоднородное уравнение  , при этом для простоты используем следующую форму записи: , при этом для простоты используем следующую форму записи:

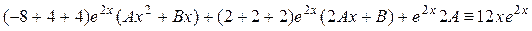 . .
Здесь слева от черты записаны коэффициенты, с которыми  входят в уравнение, а под чертой приравниваются (тождественно) левая и правая части уравнения после подстановки в него входят в уравнение, а под чертой приравниваются (тождественно) левая и правая части уравнения после подстановки в него  с группировкой подобных членов. с группировкой подобных членов.
После сокращения обеих частей тождества на 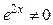 , получаем: , получаем:
 , откуда, приравнивая коэффициенты при х
1
и при х
0
в обеих частях тождества, получаем: , откуда, приравнивая коэффициенты при х
1
и при х
0
в обеих частях тождества, получаем: 
Решая систему, находим  . Подставляя найденные значения в . Подставляя найденные значения в  , получим: , получим: 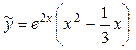 . .
Объединяя результаты 2-х этапов, получаем общее решение уравнения: 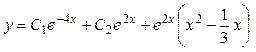 . .
Ответ: 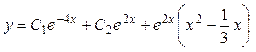 . .
Пример использования метода неопределенных коэффициентов для случая, когда функция, стоящая в правой части уравнения, имеет 2-й специальный вид, приведен в образце выполнения контрольной работы.
6. Системы двух линейных дифференциальных уравнений и их решение порядка методом повышения порядка
Нормальная система двух линейных дифференциальных уравнений 1-го порядка имеет вид:
 (46) (46)
где х
– независимая переменная, y
(x
) и z
(x
) – неизвестные функции, f
1
(x
) и f
2
(x
) – известные функции a
1
, a
2
, b
1
, b
2
– коэффициенты. Общее решение системы (46) имеет вид:
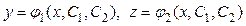 , ,
где С
1
и С
2
– произвольные постоянные.
Для решения системы (46) методом повышения порядка необходимо исключить одну из неизвестных функций. Для этого можно выразить одну из функций, например, z
(x
), из одного уравнения системы:
 , (47) , (47)
продифференцировать ее и подставить z
и  во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида во второе уравнение системы. После упрощения получаем дифференциальное уравнение 2-го порядка вида 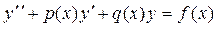 . После получения его решения . После получения его решения  , следует, используя (47), найти вторую неизвестную функцию: , следует, используя (47), найти вторую неизвестную функцию:  и записать ответ. и записать ответ.
Если в системе (46) коэффициенты a
1
, a
2
, b
1
, b
2
– постоянные, то в результате применения метода повышения порядка получается линейное неоднородное уравнение с постоянными коэффициентами:
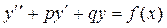 , ,
решение которого рассмотрено в п.5.
Пример использования метода повышения порядка для решения системы двух линейных дифференциальных уравнений 1-го порядка приведен в образце выполнения контрольной работы.
Примерный вариант и образец выполнения
контрольной работы №6
Задача 1.
Дано дифференциальное уравнение 1-го порядка: и точка и точка  . Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М
и уравнения еще 4-х интегральных кривых (любых). Построить все эти кривые в системе координат. . Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М
и уравнения еще 4-х интегральных кривых (любых). Построить все эти кривые в системе координат.
Задача 2.
Дано дифференциальное уравнение 1-го порядка: 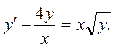 Определить тип дифференциального уравнения и найти его общее решение. Определить тип дифференциального уравнения и найти его общее решение.
Задача 3.
Дано дифференциальное уравнение 2-го порядка:  и начальные условия: и начальные условия:  Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям. Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
Задача 4.
Дано дифференциальное уравнение 2-го порядка:  . Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных. . Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных.
Задача 5.
Дано дифференциальное уравнение 2-го порядка: 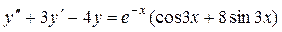 . Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов. . Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
Задача 6.
Дана система линейных дифференциальных уравнений 1-го порядка:  Найти общее решение системы методом повышения порядка. Найти общее решение системы методом повышения порядка.
Решение задачи 1.
Данное дифференциальное уравнение 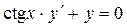 – уравнение с разделяющимися переменными. Заменим – уравнение с разделяющимися переменными. Заменим  на на  и разделим переменные, умножая обе части уравнения на и разделим переменные, умножая обе части уравнения на 
 . .
Интегрируя полученное равенство, получим:

откуда 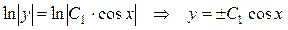 . Заменяя . Заменяя  , запишем общее решение данного уравнения: , запишем общее решение данного уравнения: 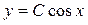 . .
Найдем уравнение интегральной кривой, проходящей через точку
 , т.е. частное решение, удовлетворяющее заданному начальному условию: , т.е. частное решение, удовлетворяющее заданному начальному условию:  Для этого подставим в общее решение вместо x
, y
числа Для этого подставим в общее решение вместо x
, y
числа
 соответственно: соответственно:  . Подставляя найденное значение С
в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М
): . Подставляя найденное значение С
в общее решение, получим искомое частное решение (уравнение интегральной кривой, проходящей через точку М
):  . .
Найдем уравнения еще нескольких интегральных кривых.

 Построим все эти кривые в системе координат (рис. 9). Построим все эти кривые в системе координат (рис. 9).
Ответы:  ; ;
 
Интегральные кривые изображены на рис. 9.
Решение задачи 2.
Данное дифференциальное уравнение  – это уравнение Бернулли (см. (27)), в котором – это уравнение Бернулли (см. (27)), в котором 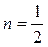 . Применим подстановку . Применим подстановку 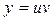 , тогда , тогда  Подставив значения y
и Подставив значения y
и  в уравнение, получим в уравнение, получим  , или , или
 (****) (****)
Найдем функцию v
(x
), решая уравнение 
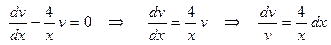 . .
Проинтегрируем левую и правую части этого уравнения:

при соответствующем подборе  получаем получаем  – частное решение уравнения – частное решение уравнения 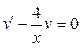 . .
Подставляя найденную функцию   в (****), получим дифференциальное уравнение для функции u
: в (****), получим дифференциальное уравнение для функции u
:  , или , или 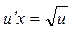 . .
Найдем функцию  – общее решение этого уравнения: – общее решение этого уравнения:
 Общим решением исходного уравнения является функция Общим решением исходного уравнения является функция
 . .
Ответ:  . .
Решение задачи 3.
Данное дифференциальное уравнение  – это дифференциальные уравнения 2-го порядка, не содержащие независимой переменной x
(см. (34)). Полагаем – это дифференциальные уравнения 2-го порядка, не содержащие независимой переменной x
(см. (34)). Полагаем  = p
(y
), тогда = p
(y
), тогда  и уравнение примет вид: и уравнение примет вид:

Решая первое уравнение, получим:  – первое семейство решений. Оно не удовлетворяет начальному условию – первое семейство решений. Оно не удовлетворяет начальному условию 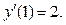
Второе уравнение  есть уравнение с разделяющимися переменными. Разделим переменные, заменяя есть уравнение с разделяющимися переменными. Разделим переменные, заменяя 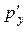 на на  и проинтегрируем: и проинтегрируем:


где  . Производя обратную замену p
= . Производя обратную замену p
=
 , получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y
: , получим дифференциальное уравнение 1-го порядка относительно неизвестной функции y
:

Это уравнение с разделяющимися переменными. Прежде чем его интегрировать, целесообразно определить значение постоянной С
1
, используя начальные условия (y
= 3,  = 2 при х
= 1): = 2 при х
= 1): 
Подставив значение  в дифференциальное уравнение, получим: в дифференциальное уравнение, получим:

Разделяя переменные и интегрируя, найдем

Здесь использовано:  . .
Определим значение постоянной С
2
, соответствующее начальному условию y
(1) = 3: 
Отсюда получим частный интеграл, удовлетворяющий заданным начальным условиям (решение задачи Коши):  . .
Получим частное решение уравнения, выразив y
(x
):

Ответ: 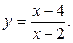
Решение задачи 4.
Данное дифференциальное уравнение  – это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид – это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид  . Найдем его в 2 этапа (см. п. 5.3.). . Найдем его в 2 этапа (см. п. 5.3.).
1 этап. Построим общее решение 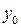 соответствующего однородного уравнения соответствующего однородного уравнения  . Составим для него характеристическое уравнение . Составим для него характеристическое уравнение  и найдем его корни: и найдем его корни:  По таблице 4 определим вид его общего решения По таблице 4 определим вид его общего решения 
2 этап. Построим частное решение  данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь данного неоднородного уравнения при помощи метода вариации произвольных постоянных. Здесь  , т.е. , т.е.  , тогда частное решение , тогда частное решение  будем искать в виде будем искать в виде  . .
Составим условиям вариации согласно (40):

Поделив оба уравнения почленно на  , получим систему с неизвестными , получим систему с неизвестными 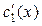 и и  : :

Для решения этой системы можно использовать метод исключения. Выразим  из первого уравнения и подставим во второе: из первого уравнения и подставим во второе:

затем найдем 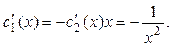
Переходим к интегрированию:

(константы интегрирования считаем равными нулю).
Тогда  , и общее решение , и общее решение  . .
Ответ: 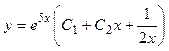 . .
Решение задачи 5.
Данное дифференциальное уравнение  – это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид – это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид  . Найдем его в 2 этапа. . Найдем его в 2 этапа.
1 этап. Построим общее решение 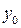 соответствующего однородного уравнения соответствующего однородного уравнения  Составим для него характеристическое уравнение Составим для него характеристическое уравнение  и найдем его корни: и найдем его корни:  По таблице 4 определим вид его общего решения По таблице 4 определим вид его общего решения 
2 этап. Построим частное решение  данного неоднородного уравнения при помощи метода неопределенных коэффициентов. В заданном уравнении данного неоднородного уравнения при помощи метода неопределенных коэффициентов. В заданном уравнении  – правая часть 2-го специального вида: – правая часть 2-го специального вида:  , где , где  . Числа . Числа  , тогда, согласно (45), частное решение , тогда, согласно (45), частное решение 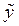 будем искать в виде: будем искать в виде:

где А
и В
– неизвестные постоянные. Подставим  в данное неоднородное уравнение: в данное неоднородное уравнение:

Сократим обе части тождества на  и приравняем коэффициенты при cos3x
и при sin3x
в левой и правой частях тождества. и приравняем коэффициенты при cos3x
и при sin3x
в левой и правой частях тождества.

Решая полученную систему двух уравнений с двумя неизвестными, находим 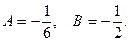 Подставив найденные значения А
и В
в выражение Подставив найденные значения А
и В
в выражение  , получим частное решение неоднородного уравнения: , получим частное решение неоднородного уравнения:

Объединяя результаты 2-х этапов, запишем ответ – общее решение данного уравнения.
Ответ: 
Решение задачи 6.
Для решения системы  методом повышения порядка исключим из нее одну из функций – z
(x
). методом повышения порядка исключим из нее одну из функций – z
(x
).
Выразим z
(x
) из первого уравнения системы:  , продифференцируем ее: , продифференцируем ее:  и подставим z
и и подставим z
и  во второе уравнение системы: во второе уравнение системы:
 . .
После упрощения получаем дифференциальное уравнение 2-го порядка относительно функции у
(х
):
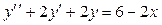 . .
Это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами (см. (38)). Его общее решение имеет вид  . Найдем его в 2 этапа. . Найдем его в 2 этапа.
1 этап. Построим общее решение 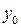 соответствующего однородного уравнения соответствующего однородного уравнения  . Составим для него характеристическое уравнение . Составим для него характеристическое уравнение  и найдем корни: и найдем корни:  – корни комплексные сопряженные: – корни комплексные сопряженные:  . Здесь . Здесь 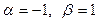 , тогда по таблице 4 определим вид общего решения однородного уравнения: , тогда по таблице 4 определим вид общего решения однородного уравнения:
 . .
2 этап. Построим частное решение  неоднородного уравнения. Здесь неоднородного уравнения. Здесь  – правая часть 1-го специального вида: – правая часть 1-го специального вида:  , где , где  , n
= 1. Число , n
= 1. Число  не совпадает с корнями характеристического уравнения не совпадает с корнями характеристического уравнения  , тогда, согласно (44), частное решение , тогда, согласно (44), частное решение  будем искать в виде: будем искать в виде:
 , ,
где А,
B
– неизвестные коэффициенты, подлежащие определению.
Найдем производные  и подставим и подставим  в неоднородное уравнение в неоднородное уравнение 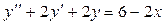 , при этом для простоты используем следующую форму записи: , при этом для простоты используем следующую форму записи:
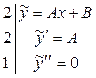
(здесь слева от черты записаны коэффициенты, с которыми 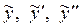 входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него входят в уравнение). Приравниваем левую и правую части уравнения после подстановки в него 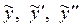 : :
 . .
Приравнивая коэффициенты при х
1
и при х
0
в обеих частях тождества, получаем:

откуда находим: A
= –1, B
= 4. Подставляя найденные значения в  , получим: , получим:  . .
Объединяя результаты 2-х этапов, получаем общее решение уравнения  : :
 . .
Найдем вторую неизвестную функцию:
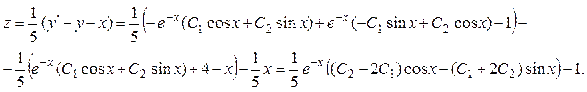
Ответ:

Варианты контрольнЫХ работ
Каждый вариант контрольной работы №5 для студентов-заочников 1 курса всех специальностей содержит 5 задач, охватывающих материал по теме «Интегральное исчисление функции одной переменной». Каждый вариант контрольной работы №6 содержит 6 задач по теме «Дифференциальные уравнения».
Перед выполнением каждой контрольной работы студенту необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания для всех вариантов общие; студенту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление контрольных работ должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).
Интегрирование в контрольной работе №5 должно сопровождаться необходимыми ссылками на таблицы интегралов, их свойства, а также указанием метода интегрирования. При использовании замены переменной следует привести формулы замены всех элементов подинтегрального выражения через новую переменную.
Решение всех дифференциальных уравнений в контрольной работе №6 следует приводить подробно, указывая тип уравнения, способ получения решения и используемые методы интегрирования.
Варианты контрольной работы №5
Задача 1.
Найти неопределенные интегралы:
| № варианта
|
Интегралы
|
| n
|
 ; ;  ; ;
 ; ; 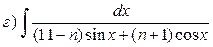
|
В примерах  правильность полученных результатов проверить дифференцированием. правильность полученных результатов проверить дифференцированием.
Задача 2.
Вычислить несобственные интегралы или доказать их расходимость:
| № варианта
|
Интегралы
|
|
n
|
а
)  ; б
) ; б
) 
|
Задача 3.
Вычислить с помощью определенного интеграла площадь плоской фигуры:
а
) ограниченной в ДСК линиями l
1
и l
2
;
б
)
ограниченной в ПСК линией l
.
Сделать чертежи.
| № варианта
|
Уравнения линий
|
| а
)
|
б
)
|
| n
|

|

|
Задача 4.
Вычислить с помощью определенного интеграла объем тела, полученного вращением вокруг оси OX
фигуры, ограниченной линиями
l
1
и l
2
. Сделать чертеж.
| № варианта
|
Уравнения линий
|
| n
|
 
|
Задача 5.
Вычислить с помощью определенного интеграла длину дуги кривой, заданной в ДСК уравнением y
= f
(x
), где  . .
| № варианта
|
Уравнение кривой
|
Промежуток
|
| n
|

|

|
Варианты контрольной работы №6
Задача 1.
Дано дифференциальное уравнение 1-го порядка и точка М
. Определить тип дифференциального уравнения. Найти общее решение дифференциального уравнения, уравнение интегральной кривой, проходящей через точку М
и уравнения еще 4-х интегральных кривых (любых). Построить все эти кривые в системе координат.
| № варианта
|
Дифференциальное уравнение
|
Точка
|
| 1
|

|
M
(–2; 4)
|
| 2
|

|
M
(0; 3)
|
| 3
|
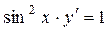
|
M
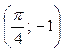
|
| 4
|
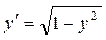
|
M
(0; 1)
|
| 5
|

|
M
(1; 2)
|
| 6
|

|
M

|
| 7
|

|
M
(0; –1)
|
| 8
|
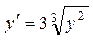
|
M
(0; 1)
|
| 9
|

|
M
(2; 1)
|
| 10
|

|
M
(–1; 2)
|
Задача 2.
Дано дифференциальное уравнение 1-го порядка. Определить тип дифференциального уравнения и найти его общее решение.
| № варианта
|
Дифференциальное уравнение
|
№ варианта
|
Дифференциальное уравнение
|
| 1
|

|
6
|

|
| 2
|

|
7
|
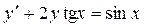
|
| 3
|

|
8
|

|
| 4
|

|
9
|
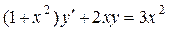
|
| 5
|

|
10
|

|
Задача 3.
Дано дифференциальное уравнение 2-го порядка и начальные условия. Определить тип дифференциального уравнения и найти его частное решение, удовлетворяющее заданным начальным условиям.
| № варианта
|
Дифференциальное уравнение
|
Начальные условия
|
| 1
|

|

|
| 2
|

|

|
| 3
|
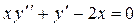
|

|
| 4
|
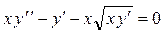
|

|
| 5
|

|

|
| 6
|

|
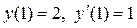
|
| 7
|
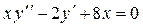
|

|
| 8
|

|
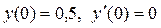
|
| 9
|
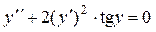
|

|
| 10
|

|

|
Задача 4.
Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод вариации произвольных постоянных.
| № варианта
|
Дифференциальное уравнение
|
№ варианта
|
Дифференциальное уравнение
|
| 1
|

|
6
|
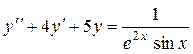
|
| 2
|

|
7
|

|
| 3
|

|
8
|

|
| 4
|
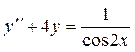
|
9
|

|
| 5
|
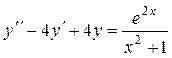
|
10
|

|
Задача 5.
Дано дифференциальное уравнение 2-го порядка. Определить тип дифференциального уравнения и найти его общее решение, используя метод неопределенных коэффициентов.
| № варианта
|
Дифференциальное уравнение
|
№ варианта
|
Дифференциальное уравнение
|
| 1
|

|
6
|

|
| 2
|

|
7
|
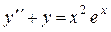
|
| 3
|

|
8
|
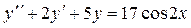
|
| 4
|

|
9
|

|
| 5
|

|
10
|

|
Задача 6.
Дана система линейных дифференциальных уравнений 1-го порядка. Найти общее решение системы методом повышения порядка.
| № варианта
|
Система
дифференциальных уравнений
|
№ варианта
|
Система
дифференциальных уравнений
|
| 1
|

|
6
|

|
| 2
|

|
7
|
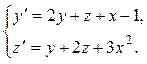
|
| 3
|

|
8
|

|
| 4
|

|
9
|
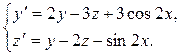
|
| 5
|

|
10
|

|
Рекомендуемая литература
1. Письменный, Д. Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д. Т. Письменный. –М. : Айрис-пресс, 2003. – 288 с.
2. Письменный, Д. Т. Конспект лекций по высшей математике. В 2 ч. Ч. 2 / Д. Т. Письменный. –М. : Рольф, 2002. – 256 с.
3. Щипачев, В. С. Высшая математика: учебник для вузов / В. С. Щипачев.– М.: Высш. шк., 1998.– 479 с.
4. Данко, П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова.– М. : Высш. шк., 1999.– 304 с.
5. Данко, П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова.– М. : Высш. шк., 1999.– 416 с.
6. Щипачев, В. С. Задачник по высшей математике / В. С. Щипачев.– М. : Высш. шк., 2001.– 304 с.
|