| РЕФЕРАТ
Записка с., 4 табл., 2 приложения, 5 источников.
АЛГЕБРАИЧЕСКОЕ УРАВНЕНИЕ, КОРНИ УРАВНЕНИЯ, ЧИСЛО ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ УРАВНЕНИЯ, ТЕОРЕМА ШТУРМА, МЕТОД ЛОБАЧЕВСКОГО–ГРЕФФЕ, МЕТОД ЛИНА, МЕТОД БЕРНУЛЛИ, МЕТОД БРОДЕТСКОГО–СМИЛА.
В курсовом проекте рассмотрен способ приближенного нахождения корней алгебраического уравнения – метод Лобачевского–Греффе. В работе определена идея метода, его вычислительная схема, найдены условия применимости метода, условия сходимости к точному решению, дана характеристика метода с точки зрения его точности. Приведена программная реализация метода Лобачевского–Греффе для случая пары комплексно–сопряженных корней на ЭВМ.
СОДЕРЖАНИЕ
РЕФЕРАТ 3
СОДЕРЖАНИЕ 4
ВСТУПЛЕНИЕ 6
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 8
1.1 Постановка задачи 8
1.2 Алгебраических уравнений 9
1.2.1 Основные понятия об алгебраическом уравнении 9
1.2.2 Оценка границ модулей корней уравнения 10
1.2.3 Корни алгебраического уравнения 11
1.2.4 Число корней полинома в некоторой области 12
1.2.5 Число действительных корней полинома 13
1.2.6 Теорема Бюдана–Фурье 16
1.3 Метод Лобачевского–Греффе для приближенного решения алгебраических уравнений 19
1.3.1 Идея метода 19
1.3.2 Квадрирование корней 21
1.3.3 Метод Лобачевского-Греффе для случая комплексных корней 24
1.3.4 Модификация метода Лобачевского–Греффе. Метод Бродетского–Смила 25
1.3.5 Потеря точности в методе Лобачевского–Греффе 28
1.4 Другие методы решения алгебраических уравнений с комплексными корнями 28
1.4.1 Метод Бернулли 29
1.4.2 Метод Лина 30
2.1 Задание 1 32
2.2 Задание 2 35
2.3 Описание программного продукта 38
2.3.1 Программа Strum 38
2.3.2 Программа MLG 38
2.4 Анализ полученных результатов 39
ВЫВОД 40
ПЕРЕЧЕНЬ ССЫЛОК 41
ПРИЛОЖЕНИЕ А 42
ПРИЛОЖЕНИЕ В 45
ВСТУПЛЕНИЕ
Вычислительная техника наших дней представляет собой мощные средства для фактического выполнения счетной работы. Благодаря этому во многих случаях стало возможным отказаться от приближенной трактовки прикладных вопросов и перейти к решению задач в точной постановке. Разумное использование современной вычислительной техники не мыслимо без умелого применения методов приближенного и численного анализа.
Курс “Численные методы” занимает одно из ведущих мест среди дисциплин, которые изучают студенты специальностей ПМ, САУ, ИНФ.
Численные методы направлены на решение задач, которые возникают на практике. Решение задачи численными методами сводятся к арифметическим и логическим действиям над числами, что требует применение вычислительной техники. Условия и решения задач чаще всего являются приблизительными, т.е. имеют погрешности, причиной которых являются несоответствие построенной математической модели реальному объекту, погрешность исходных данных, погрешность метода решения, погрешность округления и т.д. Целью дисциплины “Численные методы” является поиск наиболее эффективных методом решения конкретной задачи.
Решение уравнений – алгебраических или трансцендентных – представляет собой одну из существенных задач прикладного анализа, потребность в которой возникает в многочисленных и самых разнообразных разделах физики, механики, техники и естествознания в широком смысле этого слова.
Настоящий курсовой проект посвящен одному из методов решения алгебраических уравнений – методу Лобачевского–Греффе.
Цель работы данной рассмотреть идею метода Лобачевского–Греффе для решения алгебраических, привести вычислительную схему нахождения действительных и комплексных корней, определить условия применимости метода, условия сходимости метода к точному решению, привести условную погрешность вычислений.
В курсовом проекте рассмотрены основные теоретические вопросы, связанные нахождением корней алгебраических уравнений. Помимо метода Лобачевского–Греффе рассмотрены методы Лина, метод Бернулли, метод Бродетского–Смила, приведены основные принципы этих методов, указаны условия применимости.
В практической части данной работы приведен комплекс программ, реализующий решение алгебраических уравнений методом Лобачевского–Греффе. Рассмотрены примеры нахождения приближенного решения уравнений данным методом.
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.1 Постановка задачи
Пусть даны множество X элементов x и множество Y с элементами y. Допустим, кроме того, что на множестве X определен оператор  , который ставит в соответствие каждому элементу x из Х некоторый элемент y из Y. Возьмем какой-нибудь элемент , который ставит в соответствие каждому элементу x из Х некоторый элемент y из Y. Возьмем какой-нибудь элемент  и поставим себе целью найти такие элементы и поставим себе целью найти такие элементы  , для которых , для которых  является изображением. является изображением.
Такая задача равносильна решению уравнения
 (1.1) (1.1)
Для него могут быть поставлены следующие проблемы.
1. Условия существования решения уравнения.
2. Условие единственности решения уравнения.
3. Алгоритм решения, следуя которому, можно было бы найти, в зависимости от поставленной цели и условий, точно или приближенно все решения уравнения (1.1), или какое-либо одно решение, заранее указанное, или любое из числа существующих.
Далее будем рассматривать уравнения, в которых x и y будут численными величинами, X, Y – множествами их значений, а оператором  будет некоторая функция. В этом случае уравнение (1.1) можно будет записать в виде будет некоторая функция. В этом случае уравнение (1.1) можно будет записать в виде
 (1.2) (1.2)
В теории численных методов стремятся построить вычислительный процесс, при помощи которого можно найти решение уравнения (1.2) с наперед заданной точностью. Особенно большое значение имеют сходящиеся процессы, позволяющие решить уравнение с любой, сколь угодно малой погрешностью.
Наша задача – нахождение, вообще говоря, приближенное, элемента  . Для этой цели разрабатывается алгоритм, который выдает последовательность приближенных решений . Для этой цели разрабатывается алгоритм, который выдает последовательность приближенных решений   , причем так, что имеет место соотношение , причем так, что имеет место соотношение

Такое описание действий, конечно, является несколько идеализированным. Обычно получают какой-либо алгоритм построения последовательности  , но фактически реализуется лишь несколько его шагов, т.е. получают только несколько первых членов этой последовательности. , но фактически реализуется лишь несколько его шагов, т.е. получают только несколько первых членов этой последовательности.
1.2 Алгебраических уравнений
1.2.1 Основные понятия об алгебраическом уравнении
Рассмотрим алгебраическое уравнение n-й степени 
 , (1.3) , (1.3)
где коэффициенты  – действительные числа, причем – действительные числа, причем  . .
В общем случае будем считать, что  – комплексная переменная. – комплексная переменная.
Теорема 1.1 (основная теорема алгебры). Алгебраическое уравнение n-й степени (1.3) имеет ровно n корней, действительных и комплексных, при условии, что каждый корень считается столько раз, какова его кратность.
При этом говорят, что корень  уравнения (1.3) имеет кратность s, если уравнения (1.3) имеет кратность s, если
 , ,  . .
Комплексные корни уравнения (1.3) обладают свойством парной сопряженности.
Теорема 1.2. Если коэффициенты алгебраического уравнения (1.3) – действительные, то комплексные корни этого уравнения попарно комплексно-сопряженные, т.е. если  ( ( – действительные числа) есть корень уравнения (1.3), кратности s, то число – действительные числа) есть корень уравнения (1.3), кратности s, то число  также является корнем этого уравнения и имеет ту же кратность s. также является корнем этого уравнения и имеет ту же кратность s.
Следствие. Алгебраическое уравнение нечетной степени с действительными коэффициентами имеет по меньшей мере один действительный корень.
1.2.2 Оценка границ модулей корней уравнения
Можно дать грубую оценку модулей корней уравнения (1.3)
Теорема 1.3. Пусть
 , ,
где  – коэффициенты уравнения (1.3). – коэффициенты уравнения (1.3).
Тогда модули всех корней  (k=1,…,n) уравнения удовлетворяют неравенству (k=1,…,n) уравнения удовлетворяют неравенству
 , (1.4) , (1.4)
т.е. корни этого уравнения на комплексной плоскости   расположены внутри круга расположены внутри круга  . .
Следствие. Пусть  и и  . Тогда все корни . Тогда все корни  уравнения (1.3) удовлетворяют неравенству уравнения (1.3) удовлетворяют неравенству
 , (1.5) , (1.5)
т.е. корни уравнения (1.3) расположены в круговом кольце  . .
1.2.3 Корни алгебраического уравнения
Если  – корни уравнения (1.3), то для левой части справедливо разложение – корни уравнения (1.3), то для левой части справедливо разложение
 . (1.6) . (1.6)
Произведя перемножение биномов в формуле (1.6) и приравнивая коэффициенты при одинаковых степенях x в левой и правой частях равенства (1.6), получим соотношения между корнями и коэффициентами алгебраического уравнения (1.3):
 (1.7) (1.7)
Если учитывать кратности корней, то разложение (1.6) принимает вид
 , ,
где  –различные корни уравнения (1) и –различные корни уравнения (1) и  – их кратности, причем – их кратности, причем  . .
Производная  выражается следующим образом: выражается следующим образом:

где Q(x) – полином такой, что
 при k=1,2,…,m при k=1,2,…,m
Поэтому полином

является наибольшим общим делителем полинома  и его производной и его производной  , и может быть найден с помощью алгоритма Евклида [4]. Составим частное , и может быть найден с помощью алгоритма Евклида [4]. Составим частное
 , ,
и получим полином

с действительными коэффициентами  , А1
, A2
,…, Am
, корни которого , А1
, A2
,…, Am
, корни которого  различны. различны.
Таким образом, решение алгебраического уравнения с кратными корнями сводится к решению алгебраического уравнения более низкого порядка с различными корнями.
1.2.4 Число корней полинома в некоторой области
Полное число корней  уравнения уравнения  , расположенных на комплексной плоскости внутри простого замкнутого контура Г, можно определить на основании следующей теоремы , расположенных на комплексной плоскости внутри простого замкнутого контура Г, можно определить на основании следующей теоремы
Теорема 1.4. Если полином P(x) не имеет корней на замкнутом контуре Г, то число корней N этого полинома внутри контура Г в точности равно изменению Arg P(x) при положительном обходе контура Г, деленному на  , т.е. , т.е.
 Arg P(x), Arg P(x),
причем каждый корень считается столько раз, какова его кратность.
Если уравнение контура Г есть
 , ,  , ,
где t – параметр, то для определения числа N на плоскости XOY строят кривую
 , ,   , (1.8) , (1.8)
где

(X(t), Y(t) – действительные функции), и подсчитывают, сколько оборотов N делает кривая (1.9) делает вокруг начала координат.
1.2.5
Число действительных корней полинома
Общее представление о числе действительных корней уравнения (1.3) на интервале (a,b) дает график функции  , где корнями , где корнями  являются абсциссы точек пересечения графика с осью Ox. являются абсциссы точек пересечения графика с осью Ox.
Отметим некоторые свойства полинома P(x):
1. Если P(a)P(b)<0, то на интервале (a, b) имеется нечетное число корней полинома P(x) с учетом их кратностей.
2. Если P(a)P(b)>0, то на интервале (a, b) существует четное число или не существует вообще корней полинома P(x).
Вопрос о числе действительных корней алгебраического уравнения на данном промежутке решается методом Штурма.
Определение. Пусть дана упорядоченная конечная система действительных чисел, отличных от нуля:
 , , ,…, ,…,  (1.9) (1.9)
Говорят, что для пары рядом стоящих элементов  , ,  системы (1.9) имеется изменение знака, если эти элементы обладают противоположными знаками, т.е. системы (1.9) имеется изменение знака, если эти элементы обладают противоположными знаками, т.е.
 , ,
и нет изменения знака, если знаки их одинаковы, т.е.
 . .
Определение. Общее число изменений знаков всех пар соседних элементов  , ,   системы (1.9) называется числом перемен знаков в системе (1.9). системы (1.9) называется числом перемен знаков в системе (1.9).
Определение. Для данного полинома P(x) системой Штурма называется система полиномов [1]
 , ,  , ,  , ,  ,…, ,…,  , ,
где  , ,  – взятый с обратным знаком остаток при делении полинома – взятый с обратным знаком остаток при делении полинома  на на  , ,  – взятый с обратным знаком остаток при делении полинома – взятый с обратным знаком остаток при делении полинома  на на  и т.д. и т.д.
Замечание 1. Если полином  не имеет кратных корней, то последний элемент не имеет кратных корней, то последний элемент  системы Штурма есть отличное от нуля действительное число. системы Штурма есть отличное от нуля действительное число.
Замечание 2. Элементы системы Штурма можно вычислять с точностью до положительного числового множителя.
Обозначим через N(c) число перемен знаков в системе Штурма при x=c, при условии, что нулевые элементы этой системы вычеркнуты.
Теорема 1.5. (теорема Штурма). Если полином P(x) не имеет кратных коней и  , ,  , то число его действительных корней , то число его действительных корней  на интервале на интервале  в точности равно числу потерянных перемен знаков в системе Штурма полинома в точности равно числу потерянных перемен знаков в системе Штурма полинома  при переходе от при переходе от  до до  , т.е. , т.е.
 . .
Следствие 1. Если  , то число , то число  положительных и число положительных и число  отрицательных корней полинома отрицательных корней полинома  соответственно равны соответственно равны
 , ,
 . .
Следствие 2. Для того чтобы все корни полинома P(x) степени n, не имеющего кратных корней, были действительны, необходимо и достаточно, чтобы выполнялось условие
 . .
Таким образом в уравнении (1.3) все корни будут действительными тогда и только тогда, когда:
1) система Штурма имеет максимальное число элементов n+1, т.е. m=n;
2) выполнены неравенства   , т.е. старшие коэффициенты всех функций Штурма , т.е. старшие коэффициенты всех функций Штурма  должны быть положительными. должны быть положительными.
С помощью системы Штурма можно отделять корни алгебраического уравнения, разбивая интервал (a,b), содержащий все действительные корни уравнения, на конечное число частичных интервалов  таких, что таких, что
 . .
1.2.6 Теорема Бюдана–Фурье
Так как построение системы Штурма, вообще говоря, требует громоздких вычислений, то на практике ограничиваются более простыми частными приемами подсчета числа действительных корней алгебраический уравнений.
Определение. Пусть дана конечная упорядоченная система действительных чисел
 , ,  , …, , …,  , (1.10) , (1.10)
где  и и  . .
С одной стороны, назовем нижним числом перемен знаков системы (1.10) число перемен знаков в преобразованной системе (1.10), где нулевые элементы

( , ,  ) заменены элементами ) заменены элементами   такими, что такими, что
 . .
Очевидно, что если система (1.10) не имеет нулевых элементов, то число N перемен знаков в этой системе по смыслу совпадает с ее нижним  и верхним и верхним  числами перемен знаков: числами перемен знаков:
 , ,
вообще же говоря,  . .
Теорема 1.6. (теорема Бюдана–Фурье). Если числа a и b (a<b) не являются корнями полинома P(x) степени n, то число N(a, b) действительных корней уравнения P(x)=0, содержащихся между а и b, равно минимальному числу  перемен, знаков потерянных в системе последовательных производных перемен, знаков потерянных в системе последовательных производных
 , ,  , ,  , …, , …,  , …, , …,  (1.11) (1.11)
при переходе от x=a к x=b, или меньше числа  на четное число, т.е. на четное число, т.е.
 , ,
где

и  – нижнее число перемен знаков в системе (1.13) при x=a, – нижнее число перемен знаков в системе (1.13) при x=a,  – верхнее число перемен знаков в этой системе при x=b – верхнее число перемен знаков в этой системе при x=b  . .
Предполагается, что каждый корень уравнения (1.3) считается столько раз, какова его кратность. Если производные   не обращаются в нуль при x=a и x=b, то подсчет знаков упрощается, а именно: не обращаются в нуль при x=a и x=b, то подсчет знаков упрощается, а именно:
 . .
Следствие 1. Если  , то между a и b нет действительных корней уравнения (1.3) , то между a и b нет действительных корней уравнения (1.3)
Следствие 2. Если  , то между a и b имеется ровно один действительный корень уравнения (1.3). , то между a и b имеется ровно один действительный корень уравнения (1.3).
Замечание. Для подсчета числа потерянных знаков  в системе (1.11), пользуются схемой Горнера, составляют два разложения: в системе (1.11), пользуются схемой Горнера, составляют два разложения:
 (1.12) (1.12)
и
 . (1.13) . (1.13)
Пусть  – нижнее число перемен знаков коэффициентов разложения (1.12) и соответственно – нижнее число перемен знаков коэффициентов разложения (1.12) и соответственно  – верхнее число перемен знаков коэффициентов разложения (1.13). Так как – верхнее число перемен знаков коэффициентов разложения (1.13). Так как
 , ,   , ,
то знаки чисел  и и  совпадают со знаками системы (1.13) при x=a и x=b. Поэтому совпадают со знаками системы (1.13) при x=a и x=b. Поэтому
 . .
Теорема Декарта. Число положительных корней алгебраического уравнения (1.3) с учетом их кратностей равно числу перемен знаков в системе коэффициентов
 , ,  , …, , …, (1.14) (1.14)
(где коэффициенты, равные нулю, не учитываются), или меньше этого числа на четное число.
Теорема Декарта представляет собой применение теоремы Бюдана–Фурье к интервалу  . .
Следствие. Если коэффициенты уравнения (1.3) отличны от нуля, то число отрицательных корней этого уравнения, с учетом их кратностей, равно числу постоянств знака в системе (1.14) его коэффициентов или меньше этого числа на четное число. (Доказательство этого утверждения следует из применения теоремы Декарта к полиному  ). ).
Укажем также признак вещественности всех корней полинома  . .
Теорема Гюа. Если уравнение (1.3) имеет действительные коэффициенты и все корни его действительны, то квадрат каждого не крайнего коэффициента этого уравнения больше произведения двух его соседних коэффициентов, т.е. выполнены неравенства
  . .
Следствие. Если при каком-нибудь k выполнено неравенство
 , ,
то уравнение (1.3) имеет по меньшей мере одну пару комплексных корней.
1.3 Метод Лобачевского–Греффе для приближенного решения алгебраических уравнений
1.3.1 Идея метода
Рассмотрим алгебраическое уравнение (1.3).
Предположим, что
 , (1.15) , (1.15)
т.е. корни различные по модулю, причем модуль каждого предыдущего корня значительно больше модуля последующего. Другими словами, предположим, что отношение любых двух соседних корней, считая в порядке убывания их номеров, есть величина, малая по модулю:
 , (1.16) , (1.16)
где  и и  – малая величина. Такие корни называются отделенными. – малая величина. Такие корни называются отделенными.
Далее из системы (1.7) соотношений между корнями и коэффициентами уравнения (1.3) получаем:
 (1.17) (1.17)
где  , ,  ,…, ,…,  – малые по модулю величины по сравнению с единицей. Пренебрегая в системе (1.17) величинами – малые по модулю величины по сравнению с единицей. Пренебрегая в системе (1.17) величинами   , будем иметь приближенные соотношения , будем иметь приближенные соотношения
 (1.18) (1.18)
Откуда находим корни
 (1.19) (1.19)
Точность корней в системе равенств (1.20) зависит от того, насколько малы по модулю величины  в соотношениях (1.16) в соотношениях (1.16)
Чтобы добиться отделения корней, исходя из уравнения (1.3), составляют преобразованное уравнение
 , (1.20) , (1.20)
корнями которого  , ,  ,…, ,…,  являются m-e степени корней являются m-e степени корней  , ,  ,…, ,…,  уравнения (1.3). уравнения (1.3).
Если все корни уравнения (1.3) различны и их модули удовлетворяют условию (1.17), то при достаточно большом m корни  , ,  ,…, ,…,  уравнения (1.20) будут отделенными, т.к. уравнения (1.20) будут отделенными, т.к.
 при при  . .
Очевидно, что достаточно построить алгоритм нахождения уравнения, корни которого будут квадратами корней заданного уравнения. Тогда можно будет получить уравнение, корни которого будут равны корням исходного уравнения в степени  . .
1.3.2 Квадрирование корней
Многочлен (1.3) запишем в следующем виде

И умножим его на многочлен вида

Тогда получим

Сделав замену  и умножив на и умножив на  , будет иметь , будет иметь
 . (1.21) . (1.21)
Корни многочлена (1.21) связаны с корнями многочлена  (1.3) следующим соотношением (1.3) следующим соотношением
 . .
Следовательно, интересующее нас уравнение есть
 , ,
коэффициенты которого вычисляются по формуле (1.22)
  , (1.22) , (1.22)
где предполагается, что  при при  . .
Применяя последовательно k раз процесс квадрирования корней к многочлену (1.3) , получим многочлен
 , (1.23) , (1.23)
в котором  , ,  , и т.д. , и т.д.
При достаточно больших k можно добиться чтобы для корней уравнения (1.23) выполнялась система
 (1.24) (1.24)
Определим число k, для которого система (1.24) выполняется с заданной точностью.
Допустим, что нужное k уже достигнуто и равенства (1.24) выполняются с принятой точностью. Проделаем еще одно преобразование и найдем многочлен
 , ,
для которого также выполнена система (1.24) при  . .
Так как в силу формулы (1.22)
 , (1.25) , (1.25)
то, подставив (1.25) в систему (1.24), получим, что абсолютные величины коэффициентов  должны быть в принятой точности равны квадратам коэффициентов должны быть в принятой точности равны квадратам коэффициентов  . Выполнение этих равенств и будет свидетельствовать о том, что необходимое значение k уже было достигнуто на k-м шаге. . Выполнение этих равенств и будет свидетельствовать о том, что необходимое значение k уже было достигнуто на k-м шаге.
Таким образом квадрирование корней уравнения (1.3) следует прекратить, если в принятой точности в правой части формулы (1.24) сохраняется только квадраты коэффициентов, а удвоенная сумма произведений окажется ниже границы точности.
Тогда действительные корни уравнения получаются отделенными и их модули находятся по формуле
 (1.26) (1.26)
Знак корня можно определить грубой прикидкой, подставив значения  и и  в уравнение (1.3). в уравнение (1.3).
1.3.3 Метод Лобачевского-Греффе для случая комплексных корней
Рассмотрим теперь случай когда среди корней уравнения (1.3) содержаться одинаковые по модулю, тогда из предположения, что уравнение (1.3) не содержит кратных корней, следует, что если  , то , то  и и  – коплексно-сопряженные. – коплексно-сопряженные.
Характерным признаком этого является тот факт, что при квадрировании корней коэффициент при  в уравнении (1.25), меняет знак, так как при наличии лишь действительных корней все коэффициенты преобразованных уравнений неотрицательны. в уравнении (1.25), меняет знак, так как при наличии лишь действительных корней все коэффициенты преобразованных уравнений неотрицательны.
Согласно общей теории отделенных корней [1] корни  и и  , соответствующие комплексным корням , соответствующие комплексным корням  и и  , приближенно удовлетворяют квадратному уравнению , приближенно удовлетворяют квадратному уравнению
 . .
Откуда получаем модули корней по формуле
 (1.27) (1.27)
Относительную погрешность модуля найденного по формуле (1.27), без учета погрешности округлений при преобразованиях многочлена, можно оценить следующей величиной [2]
 , (1.28) , (1.28)
где

Комплексные корни можно найти воспользовавшись первым и последним равенством из системы (1.7). Откуда
 , (1.29) , (1.29)
 . (1.30) . (1.30)
Тогда  и и  находятся из квадратного уравнения находятся из квадратного уравнения
 . (1.31) . (1.31)
1.3.4 Модификация метода Лобачевского–Греффе. Метод Бродетского–Смила
Пусть  – неопределенный параметр, малый настолько, что его первой степенью еще нельзя пренебрегать в вычислениях, а второй и более высокими степенями можно пренебрегать. – неопределенный параметр, малый настолько, что его первой степенью еще нельзя пренебрегать в вычислениях, а второй и более высокими степенями можно пренебрегать.
Для простоты предположим, что
 (1.32) (1.32)
Разложим многочлен (1.3) по степеням  : :
 . .
Проделаем преобразования Лобачевского–Греффе над многочленом  . Как легко доказать [2], коэффициенты многочлена, полученного после k-го преобразования, будут иметь следующий вид . Как легко доказать [2], коэффициенты многочлена, полученного после k-го преобразования, будут иметь следующий вид
 . .
Пусть  – корень однократного модуля. Тогда при достаточно малом – корень однократного модуля. Тогда при достаточно малом   представляет собой корень однократного модуля многочлена представляет собой корень однократного модуля многочлена  . Его можно найти по формуле . Его можно найти по формуле

При выполнении операций деления и извлечения корней над числами вида  можно пользоваться следующими формулами: можно пользоваться следующими формулами:
 , ,
 . .
Тогда
 , (1.33) , (1.33)
где
 . .
Так как  , то приравнивая модули коэффициентов при , то приравнивая модули коэффициентов при  , получим: , получим:
 . .
Заменяя  через через  , будем иметь , будем иметь  . .
Перепишем теперь равенство (1.33) в виде  . .
Из соотношения  следует, что при положительном следует, что при положительном  и положительном и положительном   . Из соотношения (1.33) видно тогда, что . Из соотношения (1.33) видно тогда, что  должно быть отрицательным. Аналогично получаем, что при отрицательном должно быть отрицательным. Аналогично получаем, что при отрицательном  и положительном и положительном  должно быть должно быть  , так что , так что
 . .
Эта формула дает возможность вычислить корни однократного модуля без извлечения корней степени  и без неопределенности в знаке. и без неопределенности в знаке.
Рассмотрим теперь, как вычислить корни двукратного модуля  , ,  (по ранее сделанному предположению эти корни являются комплексно сопряженными). Для этого найдем квадратичный делитель (по ранее сделанному предположению эти корни являются комплексно сопряженными). Для этого найдем квадратичный делитель  , где , где

1.3.5 Потеря точности в методе Лобачевского–Греффе
Коэффициенты многочлена в методе Лобачевского–Греффе растут неодинаково быстро и вскоре становятся величинами разного порядка.
Число преобразований многочлена обычно бывает невелико, и точность коэффициентов последнего многочлена по сравнению с точностью коэффициентов первого многочлена уменьшается за счет ошибок округления не более чем на две-три значащие цифры.
Разность между корнем последнего многочлена, взятым с обратным знаком, и соответствующей степенью корня исходного многочлена не превосходит, очевидно, безусловной погрешности корня последнего многочлена, обусловленной погрешностью округления.
Относительная безусловная погрешность корня довольно часто бывает величиной примерно такого же порядка, как и погрешность коэффициентов многочлена. Таким образом, относительная погрешность корня последнего многочлена лишь на несколько порядков превосходит погрешность округления.
При извлечении корня степени  относительная погрешность уменьшается в относительная погрешность уменьшается в  раз, так что относительная погрешность найденного по методу Лобачевского–Греффе модуля корня оказывается величиной такого же порядка, что и погрешность округления. Таким образом метод Лобачевского–Греффе для однократных корней дает очень малую потерю точности. раз, так что относительная погрешность найденного по методу Лобачевского–Греффе модуля корня оказывается величиной такого же порядка, что и погрешность округления. Таким образом метод Лобачевского–Греффе для однократных корней дает очень малую потерю точности.
1.4 Другие методы решения алгебраических уравнений с комплексными корнями
Иногда для нахождения корней уравнения целесообразно использовать другие методы вычислений. В ряде случаев, например при слабой сходимости метода, к найденному с меньшей точностью корню применяются методы уточнения корней. В данном разделе рассмотрены некоторые из существующих методов, которые обладают более простой чем в методе Лобачевского–Греффе вычислительной схемой.
1.4.1 Метод Бернулли
Метод Бернулли [2] позволяет найти наибольший и наименьший по модулю корень алгебраического уравнения, но и несколько ближайших к нему (по модулю) корней.
Вычисления по методу Бернулли сводятся в основном к построению некоторой последовательности чисел  , для построения которой выбираются вначале некоторые, вообще говоря, произвольные значения , для построения которой выбираются вначале некоторые, вообще говоря, произвольные значения  . После этого значения . После этого значения  вычисляются с помощью рекуррентной формулы: вычисляются с помощью рекуррентной формулы:
 , , 
Далее по виду последовательности определяется вид наибольшего (наименьшего) по модулю корня и значение этого корня.
Далее после того, как наибольший корень вычислен с достаточной степенью точности, определяется второй по величине модуля корень. Для второго корня строиться новая последовательность  , вид которой определяется на основании типа сходимости последовательности построенной для предыдущего корня. , вид которой определяется на основании типа сходимости последовательности построенной для предыдущего корня.
После того как найден второй по модулю корень, аналогично находятся третий и последующие корни.
Пусть погрешность округления во всех вычислениях постоянна и равна  . Тогда относительная погрешность первого корня равна [2] . Тогда относительная погрешность первого корня равна [2]
 , где , где  . .
Потеря точности для последующих корней может быть значительно больше.
Таким образом, метод Бернулли обладает очень простой вычислительной схемой. Основные вычисления сводятся к повторению операции накопления, что делает метод удобным для вычисления на ЭВМ. Но с другой стороны для реализации метода необходим более сложный, чем для метода Лобачевского–Греффе, логический аппарат, определяющий тип сходимости последовательности  . Кроме того, корни в методе Бернулли определяются не все сразу, а один или несколько наибольших (наименьших) по модулю корней, что приводит к потере точности для остальных корней. . Кроме того, корни в методе Бернулли определяются не все сразу, а один или несколько наибольших (наименьших) по модулю корней, что приводит к потере точности для остальных корней.
1.4.2 Метод Лина
Метод Лина [2] служит для нахождения делителей любой степени для заданного многочлена. Чаще всего этот метод используется для нахождения квадратичных делителей, определяющих пару комплексных сопряженных корней многочлена. Этот метод также можно применить для вычисления наибольшего по модулю корня.
Метод Лина может не привести к нахождению делителя, либо привести к нахождению не того делителя, который предполагалось вычислить.
Рассмотрим многочлен (1.3) и найдем его делитель k-й степени
 . .
Для этого возьмем какой-нибудь приведенный многочлен  степени k и разделим степени k и разделим  на на  . Тогда полученный остаток будет иметь, вообще говоря, ту же степень k. Разделив его на коэффициент при старшем члене получим приведенный многочлен . Тогда полученный остаток будет иметь, вообще говоря, ту же степень k. Разделив его на коэффициент при старшем члене получим приведенный многочлен  . Проделав с многочленом . Проделав с многочленом  те же операции, что и с те же операции, что и с  получим получим  и т.д. Последовательность многочленов и т.д. Последовательность многочленов  , ,  , ,  ,… сходится к ,… сходится к  при условии, что для всех k при условии, что для всех k

где  – корни многочлена – корни многочлена  . .
Вычислительная схема метода Лина достаточно проста, но вычисление корней может потребовать довольно большой вычислительной работы, а иногда может даже не привести к результату. При использовании метода Лина для вычисления комплексных корней целесообразно применять метод ускорения сходимости Хеда [2].
2 ПРАКТИЧЕСКАЯ ЧАСТЬ
2.1 Задание 1
Методом Лобачевского–Греффе решить уравнение:
 . (2.1) . (2.1)
Сначала установим количество действительных и комплексных корней в уравнении (2.1). Для этого воспользуемся теоремой Штурма.
Система Штурма для уравнения (2.1) будет иметь следующий вид:

Откуда получаем
Таблица 2.1.
| Многочлен
|
Точки на действительной оси
|
| 
|

|
| 
|
+
|
+
|
| 
|
–
|
+
|
| 
|
–
|
–
|
| 
|
–
|
+
|
| 
|
–
|
–
|
| Число перемен знаков
|
1
|
3
|
Таким образом, получаем, что число действительных корней в уравнении (2.1) равно
 , ,
т.е. уравнение (2.1) содержит 2 действительных и два комплексных корня.
Для нахождения корней уравнения воспользуемся методом Лобачевского–Греффе для пары комплексно–сопряженных корней.
Произведем квадрирование корней уравнения. Вычисления коэффициентов производились по следующей формуле
 , (2.2) , (2.2)
где
 , (2.3) , (2.3)
а  считается равным 0 при считается равным 0 при  . .
Результаты вычислений с восьмью значащими цифрами приведены в таблице 2.2
Таблица 2.2.
| i
|
0
|
1
|
2
|
3
|
4
|
| 
|
| 
|
0
|
-3.8000000E+01
|
3.5400000E+02
|
3.8760000E+03
|
0
|
| 
|
1
|
4.3000000E+01
|
7.1500000E+02
|
4.8370000E+03
|
1.0404000E+04
|
| 
|
| 
|
0
|
-1.4300000E+03
|
-3.9517400E+05
|
-1.4877720E+07
|
0
|
| 
|
1
|
4.1900000E+02
|
1.1605100E+05
|
8.5188490E+06
|
1.0824322E+08
|
| 
|
| 
|
0
|
-2.3210200E+05
|
-6.9223090E+09
|
-2.5123467E+13
|
0
|
| 
|
1
|
-5.6541000E+04
|
6.5455256E+09
|
4.7447321E+13
|
1.1716594E+16
|
| 
|
| 
|
0
|
-1.3091051E+10
|
5.3888712E+18
|
-1.5338253E+26
|
0
|
| 
|
1
|
-9.8941665E+09
|
4.8232776E+19
|
2.0978658E+27
|
1.3727857E+32
|
| 
|
| 
|
0
|
-9.6465552E+19
|
4.1513541E+37
|
-1.3242653E+52
|
0
|
| 
|
1
|
1.4289776E+18
|
2.3679142E+39
|
4.3877982E+54
|
1.8845406E+64
|
| 
|
| 
|
0
|
-4.7358285E+39
|
-1.2540130E+73
|
-8.9248610+103
|
0
|
| 
|
1
|
-4.7337865E+39
|
5.6070053E+78
|
1.9252683+109
|
3.5514932+128
|
| 
|
| 
|
0
|
-1.1214011E+79
|
1.8227619+149
|
-3.9826483+207
|
0
|
| 
|
1
|
1.1194724E+79
|
3.1438509+157
|
3.7066582+218
|
1.2613104+257
|
Как видно из таблицы 2.2 на 7-м шаге корни  , ,  (считая в порядке убывания модулей) можно считать отделенными. Модули корней находим по формуле (1.27) и грубой прикидкой определяем их знак: (считая в порядке убывания модулей) можно считать отделенными. Модули корней находим по формуле (1.27) и грубой прикидкой определяем их знак:


Так как преобразованный коэффициент при  меняет знак, то данное уравнение имеет комплексные корни, которые определяются из уравнения (1.31) с использованием формул (1.29) и (1.30): меняет знак, то данное уравнение имеет комплексные корни, которые определяются из уравнения (1.31) с использованием формул (1.29) и (1.30):
 i. i.
Относительная погрешность корней, вычисленная по формуле (1.28) равна
 , ,
 , ,
 . .
2.2 Задание 2
Методом Лобачевского–Греффе решить уравнение:
 . (2.4) . (2.4)
Для начала с помощью теоремы Штурма определим количество действительных и комплексных корней в уравнении (2.2).
Для данного уравнения система Штурма имеет вид


Откуда получаем
Таблица 2.3.
| Многочлен
|
Точки на действительной оси
|
| 
|

|
| 
|
+
|
+
|
| 
|
–
|
+
|
| 
|
+
|
+
|
| 
|
–
|
+
|
| 
|
–
|
–
|
| Число перемен знаков
|
3
|
1
|
Таким образом, получаем, что число действительных корней в уравнении (2.2) равно
 , ,
т.е. уравнение (2.2) содержит 2 действительных и два комплексных корня.
Для приближенного нахождения корней уравнения воспользуемся методом Лобачевского–Греффе для пары комплексно–сопряженных корней.
Произведем квадрирование корней уравнения. Вычисления коэффициентов произведем по формулам (2.2) и (2.3) .
Результаты вычислений с восьмью значащими цифрами приведены в таблице 2.4
Таблица 2.4.
| i
|
0
|
1
|
2
|
3
|
4
|
| 
|
| 
|
0
|
-9.2000000E+00
|
-3.3300000E+01
|
1.3800000E+02
|
0
|
| 
|
1
|
1.6900000E+00
|
-1.2140000E+01
|
1.3825000E+02
|
2.2500000E+02
|
| 
|
| 
|
0
|
2.4280000E+01
|
-1.7285000E+01
|
5.4630000E+03
|
0
|
| 
|
1
|
2.7136100E+01
|
1.3009460E+02
|
2.4576062E+04
|
5.0625000E+04
|
| 
|
| 
|
0
|
-2.6018920E+02
|
-1.2325470E+06
|
-1.3172078E+07
|
0
|
| 
|
1
|
4.7617872E+02
|
-1.2156224E+06
|
5.9081077E+08
|
2.5628906E+09
|
| 
|
| 
|
0
|
2.4312447E+06
|
-5.5753725E+11
|
6.2310144E+15
|
0
|
| 
|
1
|
2.6579909E+06
|
9.2020050E+11
|
3.5528838E+17
|
6.5684084E+18
|
| 
|
| 
|
0
|
-1.8404010E+12
|
-1.8886934E+24
|
-1.2088505E+31
|
0
|
| 
|
1
|
5.2245148E+12
|
-1.0419245E+24
|
1.2621774E+35
|
4.3143988E+37
|
| 
|
| 
|
0
|
2.0838490E+24
|
-1.3188529E+48
|
8.9905555E+61
|
0
|
| 
|
1
|
2.9379403E+25
|
-2.3324632E+47
|
1.5930919E+70
|
1.8614037E+75
|
| 
|
| 
|
0
|
4.6649263E+47
|
-9.3608180E+95
|
8.6833113+122
|
0
|
| 
|
1
|
8.6361583E+50
|
-8.8167795E+95
|
2.5379418+140
|
3.4648238+150
|
Как видно из таблицы 2.4 на 7-м шаге корни  , ,  (считая в порядке убывания модулей) можно считать отделенными. Модули корней находим по формуле (1.27) и грубой прикидкой определяем их знак: (считая в порядке убывания модулей) можно считать отделенными. Модули корней находим по формуле (1.27) и грубой прикидкой определяем их знак:


Так как преобразованный коэффициент при  меняет знак, то данное уравнение имеет комплексные корни, которые определяются из уравнения (1.31) с использованием формул (1.29) и (1.30): меняет знак, то данное уравнение имеет комплексные корни, которые определяются из уравнения (1.31) с использованием формул (1.29) и (1.30):
 i. i.
Относительная погрешность корней, вычисленная по формуле (1.28) равна
 , ,
 . .
2.3 Описание программного продукта
Программный продукт, разработанный в курсовом проекте, включает в себя две независимые программы Sturm и MLG, выполненные на алгоритмическом языке Fortran и среде разработки Compaq Visual Fortran.
2.3.1 Программа
Strum
Программа Strum предназначена для построения системы Штурма для заданного полинома 4-го порядка.
Входные данные: коэффициенты исходного полинома 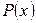 4-го порядка. 4-го порядка.
Выходные данные: коэффициенты многочленов  , ,  , … с четырьмя значащими цифрами, которые образуют вместе с полиномом , … с четырьмя значащими цифрами, которые образуют вместе с полиномом  систему Штурма. систему Штурма.
Ограничения использования: многочлен  должен удовлетворять условию теоремы Штурма. должен удовлетворять условию теоремы Штурма.
Область применения: решение задач связанных с определением числа действительных корней многочлена, принадлежащих некоторому интервалу (a,b).
Листинг программы представлен в Приложении А.
2.3.2 Программа
MLG
Программа MLG предназначена для приближенного нахождения корней уравнения 4-го порядка методом Лобачевского–Греффе.
Входные данные: коэффициенты многочлена, корни которого необходимо найти.
Выходные данные: коэффициенты всех вспомогательных полиномов, полученных в ходе квадрирования исходного многочлена, корни уравнения полученные с заданной точностью, оценка относительной условной погрешности найденных корней.
Ограничение использования: количество комплексно–сопряженных корней должно быть не менее двух. При слабой начальной отделенности корней, рекомендуется использовать другие методы решения.
Область применения: задачи связанные с нахождением всех корней заданного многочлена 4-го порядка. С незначительными изменениями программу можно использовать для решения уравнений методом Лобачевского–Греффе любого порядка.
Листинг программы приводится в Приложении В к данному курсовому проекту.
2.4 Анализ полученных результатов
Из полученных при решении уравнений (2.1) и (2.4) уравнений можно судить о следующих особенностях метода Лобачевского–Греффе.
С помощью рассматриваемого метода можно найти все корни многочлена с достаточно высокой точностью, при не большом количестве итераций.
Величина погрешности полученных корней в высокой степени зависит от отделенности корней в исходном многочлене, так, например, в уравнении (2.1) минимальная разность между различными по модулю корнями равна  и и  в уравнении (2.4), что в результате дает погрешности разных порядков (4.52958089E–11 и 4.22229789E-06 соответственно) при одинаковом количестве итераций. в уравнении (2.4), что в результате дает погрешности разных порядков (4.52958089E–11 и 4.22229789E-06 соответственно) при одинаковом количестве итераций.
Таким образом, метод Лобачевского–Греффе дает хорошую точность при отделенных корнях, и значительно теряет при кратных или близких по модулю корнях.
ВЫВОД
Метод Лобачевского–Греффе, который был рассмотрен в данном курсовом проекте, имеет простую схему вычислений и позволяет с помощью небольших по объему вычислений найти с большой точностью модулю всех корней алгебраического уравнения, исключая разве только кратные или очень близкие по модулю корни. Однако окончательное нахождение корней требует значительной вычислительной работы, особенно в случае комплексных корней.
Затруднительным для метода является нахождение кратных корней. Однако метод можно применять и в этом случае, если предварительно избавиться от кратных корней с помощью алгоритма, описанного в данной работе.
Наибольшую проблему представляют корни близкие по модулю, т. к. в этом случае происходит большая потеря точности вычислений, что влечет за собой необходимость в увеличении затрат ресурсов. В данном случае рекомендуется пользоваться другими методами нахождения корней алгебраического уравнения.
Метод Лобачевского–Греффе один из самых эффективных методов вычислений, который при небольшом количестве итераций дает результат с довольно хорошей точностью, поэтому сфера использования этого метода на практике очень широкая. Методом можно пользоваться при построении математических моделей химических и физических процессов, в методах оптимизации.
ПЕРЕЧЕНЬ ССЫЛОК
1. В.П. Демидович, И.А. Марон. Основы вычислительной математики.– М.: Наука, 1966.–664с.
2. В.Л. Загускин. Справочник по численным методам решения алгебраических и трансцендентных уравнений.– М.: Государственное издательство физико-математической литературы, 1960.–216с.
3. В.И. Крылов, В.В. Бобков, П.И. Монастырский. Вычислительные методы высшей математики.–Минск: Вышэйшая школа, 1972, т. 1.–584с.
4. А.Г. Курош. Курс высшей алгебры.–М.: Наука,1971,–432с.
5. Ю.И. Рыжиков. Программирование на Фортране PowerStation для инженеров. Практическое руководство.–СПб.: КОРОНА принт, 1999.–160с.
ПРИЛОЖЕНИЕ А
Листинг программы Sturm. Применяется для построения системы Штурма.
! Sturm.f90
!
!************************************************************************
!
! PROGRAM: Sturm
!
! PURPOSE: Построение системы Штурма.
!
!************************************************************************
program Sturm
implicit none
double precision, dimension(1:5,0:4) ::a
double precision, dimension(0:4) ::c
double precision, dimension(0:4,0:4) ::maxmas
integer i,j,l
double precision a1
print *,'vvedite koeffitsienty mnogochlena', ' '
read *, c !чтение данных
a(1,0:4) = c
!вычисление производной
do i=0,3
a(2,i)=a(1,i)*(4-i)
end do
a1 = abs(a(2,0))
do i=0,3
a(2,i) = a(2,i)/a1
end do
print '(en13.3)',a(2,0:3)
! вычисление первого частного
a(3,0:4) = a(1,0:4)
do i=0,1
a1 = a(3,i)/a(2,0)
do j=0,3
a(3,j+i) = a(3,j+i)-a1*a(2,j)
end do
end do
a(3,0:2) = a(3,2:4)
a(3,3:4) = 0
a1 = abs(a(3,0))
do i=0,2
a(3,i) = a(3,i)/a1
end do
a(4,0:4) = a(2,0:4)
print *,' '
print '(en13.3)',a(3,0:2)
! вычисление второго частного
do i=0,1
a1 = a(4,i)/a(3,0)
do j=0,3
a(4,j+i) = a(4,j+i)-a1*a(3,j)
end do
end do
a(4,0:2) = a(4,2:4)
a(4,3:4) = 0
a1 = abs(a(4,0))
do i=0,2
a(4,i) = a(4,i)/a1
end do
a(5,0:4) = a(3,0:4)
print *,' '
print '(en13.3)',a(4,0:1)
! вычисление третьего частного
do i=0,1
a1 = a(5,i)/a(4,0)
do j=0,3
a(5,j+i) = a(5,j+i)-a1*a(4,j)
end do
end do
a(5,0:2) = a(5,2:4)
a(5,3:4) = 0
print *,' '
print '(en13.3)',a(5,0)
end program Sturm
ПРИЛОЖЕНИЕ В
Программа MLG. Решение алгебраического уравнения.
! MLG.f90
!
!***********************************************************************
!
! PROGRAM: MLG
!
! PURPOSE: Решение алгебраического уравнения методом Лобачевского-Греффе
!
!***********************************************************************
program MLG
implicit none
double precision, dimension(0:4) ::a1,b2,eps,summa
double precision, dimension(0:8) ::b1
double precision, dimension(1:4) ::y,lg,dx
double precision, dimension(1:3) ::b3
double precision koef,v,sumcmplx,prcmplx,e1,e2, epsilon
double complex deskr
double complex, dimension(1:4) ::x
logical, dimension(0:4) ::mask
logical, dimension(1:4) ::flags
logical flag
integer i,k,m
! задание начальных значений
epsilon = 1e-3
print *,'vvedite koeffitsienty mnogochlena', ' '
read *, a1 !чтение данных
!открытие файла для записи данных
open (3, file='res2.txt', status='replace')
write (3,10) a1
10 format (t3,'коэффициенты исходного многочлена',5(2x,es15.7))
write (3,11) epsilon
11 format (t3,'ограничение точности ',es15.7)
y = 0.0
mask = .true.
b1 = 0.0
b1(0:4) = a1
flag = .true.
k=0
!операция квадрирования корней
do while (flag)
k = k + 1 !считаем номер итерации
write (3,1) k
1 format (t60,'итерация № ',t75,i2)
b2 = b1(0:4)*b1(0:4)
summa = (/(2*s(i),i=0,4)/)
write (3,2) summa
2 format (t3,'удвоенная сумма',5(2x,es15.7))
print *,' '
b2 = (/(b2(i)+2*s(i),i=0,4)/) !вычисление коэффициентов
write (3,3) b2
3 format (t3,'коэффициенты ',5(2x,es15.7))
mask = mask .and. (b2 > 0) !определение действительных корней
eps = 0.0
where (mask) eps = abs(b2/(b1(0:4)*b1(0:4))-1)
flag = maxval(eps)>epsilon !ограничение точности
if (.not. flag) then
k = k-1
do i=1,4
if (.not. mask(i)) then
e1 = abs(b2(i-1) - b1(i-1)*b1(i-1))
e2 = abs(b2(i+1) - b1(i+1)*b1(i+1))
koef = 1/exp((k+1)*LOG(2.0))
dx(i) = koef*(e1/(b1(i-1)*b1(i-1))+e2/(b1(i+1)*b1(i+1)))
else
e1 = abs(b2(i-1) - b1(i-1)*b1(i-1))
e2 = abs(b2(i) - b1(i)*b1(i))
koef = 1/exp((k+1)*LOG(2.0))
dx(i) = koef*(e1/(b1(i-1)*b1(i-1))+e2/(b1(i)*b1(i)))
end if
end do
else
b1(0:4) = b2 !запоминаем значение коэффициентов на текущей итерации
end if
write (3,4)
4 format (t3,' ')
end do
!определение номеров комплексных корней
do i=1,4
if (.not. mask(i)) m=i
end do
mask(m+1) = .false.
dx(m+1) = dx(m)
!вычисление корней в уравнении Q(y) = 0
do i=1,4
if (mask(i)) y(i) = b1(i)/b1(i-1)
end do
!вычисление действительных корней
koef = 1/exp(k*LOG(2.0))
where (mask(1:4)) lg = exp(koef*log(y))
!определение знака действительных корней
flags = .false.
do i=1,4
if (mask(i)) then
v = polinom(lg(i))/polinom(-1.0*lg(i))
flags(i) = (v > 1.0)
end if
end do
where (flags) lg = -1.0*lg
x = lg
!составляем уравнение для нахождения комплексных корней
sumcmplx = -a1(1)/a1(0)
do i=1,4
if (mask(i)) then
sumcmplx = sumcmplx - x(i)
end if
end do
v = -1.0
prcmplx = extent_int(v,4)*a1(4)/a1(0)
do i=1,4
if (mask(i)) then
prcmplx = prcmplx/x(i)
end if
end do
b3(1) = 1.0
b3(2) = -1.0*sumcmplx
b3(3) = prcmplx
!нахождение комплексных корней
v = b3(2)*b3(2)-4*b3(1)*b3(3)
deskr = dcmplx(-1.0*b3(2),sqrt(abs(v)))/(2*b3(1))
x(m) = deskr
x(m+1) = CONJG(x(m))
!вывод результата
write (3,5)
5 format (t3,'-------------------------------------')
write (3,6)
6 format (t3,'полученый результат')
do i=1,4
write (3,7) x(i)
7 format (t20,2(es15.8,3x))
write (3,8)
8 format (t3,'')
end do
write (3,9) dx
9 format (t3,'относительная погрешность корней ',4(es15.8,2x))
print *,'vse vychisleniya vypolneny uspeshno', ' ', 'rezultat sohranen v faile res2.txt'
close (3, status='keep')
contains
real(8) function s(a)
integer a,j
real(8) sum
sum = 0.0
do j=1,a
if (mod(j,2) == 0) then
sum = sum + b1(a-j)*b1(a+j)
else
sum = sum - b1(a-j)*b1(a+j)
end if
end do
s=sum
end function s
real(8) function polinom(xp)
real(8) xp,p,xs
integer j,l
p = 0.0
do j=0,4
p = p+ extent_int(xp,j)*a1(4-j)
end do
polinom = p
end function polinom
real(8) function extent_int(num,ext)
real(8) num
integer ext,l
real(8) w
w=1.0
do l=1,ext
w = w*num
end do
extent_int = w
end function extent_int
end program MLG
|