|
Федеральное агентство по образованию
ГОУ ВПО «Саратовский государственный университет
имени Н.Г. Чернышевского»
Кафедра нелинейной физики
Колебания в системе связанных осцилляторов
Курсовая работа
студентки 1 курса факультета нелинейных процессов
****
Научный руководитель
профессор, д. ф.-м. н., ______________Ю. П. Шараевский
Заведующий кафедрой,
чл.-кор. РАН, проф.,
д. ф.-м. н. ______________ Ю. П. Шараевский
Саратов-2008
Введение. 3
1. Два связанных осциллятора. 4
1.1.
Анализ системы двух связанных осцилляторов
. 4
1.2
. Затухание в системе связанных осцилляторов
. 7
1.3
. Связанные осцилляторы под действием гармонической силы
. 9
2. Колебания системы со многими степенями свободы.. 11
2.1. Колебания системы
N связанных осцилляторов
. 11
2.2. Колебательные цепи
. 12
3. Переход к сплошной среде. 15
4. Заключение. 16
5. Список используемой литературы.. 17
В теории колебаний движение заряда в электрическом контуре или груза на пружине, можно описать уравнением линейного гармонического осциллятора. Но на практике в большинстве случаев приходится иметь дело не с одним осциллятором, а с более сложными системами - взаимодействующими между собой осцилляторами. В качестве примеров таких систем можно рассматривать колебания молекул в жидкостях и твердых телах, электрические цепи, состоящие из нескольких взаимосвязанных контуров, два математических маятника, связанные между собой пружиной.
Многие эффекты, проявляющиеся в системе с двумя степенями свободы, характерны для более сложных систем, поэтому осуществляется подробный анализ системы двух связанных осцилляторов. Такой подход позволяет перейти к рассмотрению большого, а затем и бесконечного числа связанных осцилляторов, осуществить переход к сплошной среде.
1.1
.
Анализ системы двух связанных осцилляторов
 Рассмотрим систему двух связанных осцилляторов на примере двух электрических контуров. Каждый контур состоит из конденсаторов с емкостью C
, катушек индуктивности L1
и L2
, связан с другим посредством общего конденсатора C1
(рис.1). Рассмотрим систему двух связанных осцилляторов на примере двух электрических контуров. Каждый контур состоит из конденсаторов с емкостью C
, катушек индуктивности L1
и L2
, связан с другим посредством общего конденсатора C1
(рис.1).
Пусть в первом контуре течет ток I1
, во втором - I2
. Пренебрегаем потерями энергии в контурах.
Тогда по первому закону Кирхгофа:
I =
I1
+
I2
Рис.1
или после интегрирования
q =
q1
+
q2
, (1)
где q
– заряд на обкладках конденсатора C1
, q1
,
q2
– заряды на конденсаторах C; 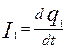 , ,  . .
Совершая обходы по каждому контуру в указанных на рис. 1 направлениях, получим уравнения:
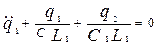 и и  (2) (2)
Уравнения (2) описывают систему связанных осцилляторов. Если 1/
C = 0
, т.е. отсутствует связь, тогда (2) переходит в систему двух независимых осцилляторов с собственными частотами  и
и 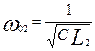 .
.
 Рассматривая колебания в системе двух связанных математических маятников (рис.2), соединенных пружиной k, длиной l1
и l2
с одинаковыми массами m =
m1
=
m2
, тогда уравнения движения запишутся в виде: Рассматривая колебания в системе двух связанных математических маятников (рис.2), соединенных пружиной k, длиной l1
и l2
с одинаковыми массами m =
m1
=
m2
, тогда уравнения движения запишутся в виде:
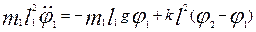
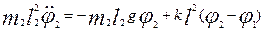 (3) (3)
Как видно, уравнения (2) для контуров эквивалентны уравнениям (3), описывающим механическую систему. Рис.2
Способ связи осцилляторов, при котором в каждом из уравнений для несвязанных
систем появляются слагаемые, пропорциональные координате
второй системы, называется силовой
связью (механические системы) или емкостной
связью (колебательный контур) [1].
Аналогичным образом можно записать уравнения для системы двух связанных контуров с индуктивной связью:
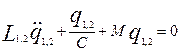
Для механических систем такой способ связи называют инерционным
[1].
Тип связи зависит от выбора обобщенных координат.[2 (лекция 22)] или другими словами выбором динамических переменных [1].
В общем виде уравнения движения для системы связанных маятников можно записать так [2]:
 , ,
 . .
Уравнения (2) можно получить, исходя из уравнений Лагранжа – Максвелла (уравнения Лагранжа второго рода) [2]:
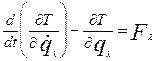  , ,
где T
- энергия, 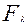 - это обобщенная сила. Выражение - это обобщенная сила. Выражение 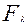 называют так по аналогии с тем, что имеет место в декартовых координатах, где работа определяется как произведение называют так по аналогии с тем, что имеет место в декартовых координатах, где работа определяется как произведение  (X – сила, (X – сила, 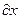 - перемещение) [2]. - перемещение) [2].
Если 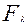 - такие потенциальные силы, зависящие от - такие потенциальные силы, зависящие от 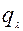 , что , что
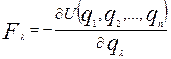
То уравнения для электрической цепи становятся следующими:
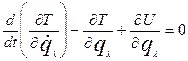 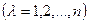 , ,
Где U
- электрическая, а T
– магнитная энергия,  - токи, - токи, 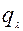 - заряды. При подстановки значений T
и U
в полученные уравнения приходим к уравнениям (2). - заряды. При подстановки значений T
и U
в полученные уравнения приходим к уравнениям (2).
Сложим и вычтем уравнения (2), получим:
 , ,
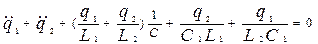 . .
Для упрощения дифференциальных уравнений введем обозначения
 и
и  ,
,
откуда
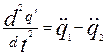 и и 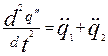 . .
Пусть для простоты  , тогда , тогда 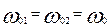 . И после преобразований получим: . И после преобразований получим:
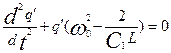 ,
(4) ,
(4)
 , (5) , (5)
где 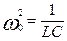 . .
Т.о. q’
и q”
- линейные комбинации обычных координат q1
и
q2
,
которые
называются нормальными координатами
, и которым соответствуют нормальные частоты
:
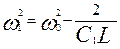 и и  , ,
а соответствующие нормальным координатам гармонические колебания - собственные моды
системы.
Следует отметить, что число независимых (нормальных) координат, необходимое и достаточное для однозначного определения положения системы называется числом степеней свободы системы.[2 (лекция 22)]
В случае, когда q’ = 0 (
q1
=
q2
),
колебания системы описываются уравнением (5), т.е. первая нормальная мода с частотой 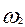 . Ток I1
= I2
,
в обоих контурах направлены либо по часовой стрелке, либо против нее. Следовательно, ток через конденсатор C1
не протекает. Если же q” = 0 (
q1
= -
q2
),
рассматривая уравнение (4), то возбуждается вторая мода с частотой . Ток I1
= I2
,
в обоих контурах направлены либо по часовой стрелке, либо против нее. Следовательно, ток через конденсатор C1
не протекает. Если же q” = 0 (
q1
= -
q2
),
рассматривая уравнение (4), то возбуждается вторая мода с частотой  и в любой момент времени через конденсатор C проходит удвоенный ток I1
(
I2
)
. и в любой момент времени через конденсатор C проходит удвоенный ток I1
(
I2
)
.
Т. о. уравнения (4), (5) можно свести к уравнениям двух независимых осцилляторов.
Обобщая: линейная консервативная система с N
степенями свободы может быть представлена в виде набора N
независимых осцилляторов.
Рассмотрим парциальные частоты в колебательном контуре.
Парциальной системой
, соответствующей данной координате, является система, получаемая из исходной “закреплением” всех остальных координат [3].
“Закрепление” координат на примере уравнений (2) означает, что либо q1
= 0
, либо q2
= 0
.
В первом случае получим  , во втором , во втором 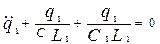 . .
Т.о. парциальные частоты определяются следующим образом:
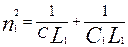 и и 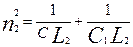 . (6) . (6)
При  эти частоты равны эти частоты равны 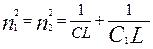 . Сравним их с нормальными частотами: . Сравним их с нормальными частотами:
 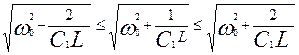 , (7) , (7)
т.о. парциальные частоты всегда лежат между нормальными.( ). ).
Двойное неравенство (7) наглядно демонстрирует, что введение связи в систему связанных осцилляторов увеличивает интервал между собственными частотами.
Перепишем уравнения (2) в соответствии с (6) в виде (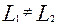 ): ):
 и и 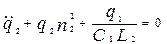 (8) (8)
Общее решение выглядит следующим образом:
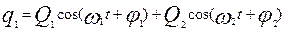 , ,
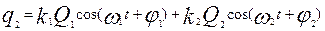 , (9) , (9)
При этом
 , ,
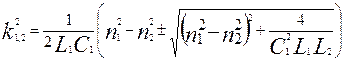 . .
Введем обозначение 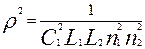 , коэффициент связи. Тогда последнее слагаемое, стоящее под корнем будет равным: , коэффициент связи. Тогда последнее слагаемое, стоящее под корнем будет равным:
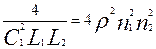 . .
Связь между осцилляторами мала, если  . При этом их колебания не зависят друг то друга. В случае . При этом их колебания не зависят друг то друга. В случае 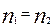 амплитуда колебаний осцилляторов одинакова. амплитуда колебаний осцилляторов одинакова.
Сильная связь может возникнуть если 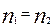 при любых ρ,
или при при любых ρ,
или при 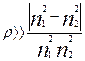 . .
Рассмотрим передачу энергии в системе связанных осцилляторах.
Пусть в начальный момент времени 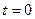 был возбужден первый контур, полагая был возбужден первый контур, полагая 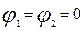 , имеем: , имеем:
 , ,  , , 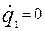 , , 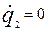 . .
 Тогда, подставляя начальные условия в (9) и выражая Тогда, подставляя начальные условия в (9) и выражая 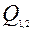 через через  , получим решения: , получим решения:
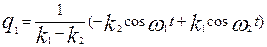 , ,
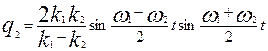 . .
Во второй формуле амплитуда переменная. Передача энергии от одного колебательного контура к другому за время 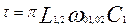 сопровождается уменьшением амплитуды первого контура и увеличением Рис.3 сопровождается уменьшением амплитуды первого контура и увеличением Рис.3
амплитуды
второго. Получаются биения
(рис.3).
1.2
. Затухание в системе связанных осцилляторов
Введём затухания в линейную колебательную систему. В общем случае уравнения движения выглядят следующим образом [4]:
 , ,
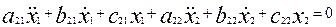 . (10) . (10)
Полагая, что 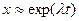 , получаем характеристическое уравнение для системы 10: , получаем характеристическое уравнение для системы 10:

Пусть 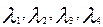  - корни, тогда общее решение запишется в виде: - корни, тогда общее решение запишется в виде:
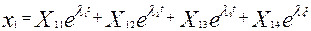 , ,
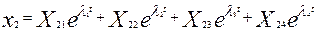 . (11) . (11)
Коэффициенты при каждой экспоненте связаны друг с другом соотношениями:
 ( ( ). ).
Когда нет трения, то 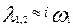 и и 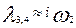 . Наличие затухания приводит к тому, что корни либо действительные, либо комплексно сопряженные. При малых . Наличие затухания приводит к тому, что корни либо действительные, либо комплексно сопряженные. При малых  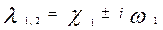 и и 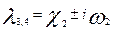 , (11) примет вид: , (11) примет вид:
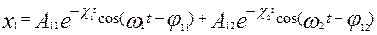 , ,
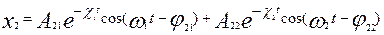 , ,
где
 , , 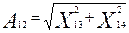 , ,
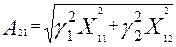 , ,  , ,
 , , 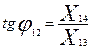 , ,  , , 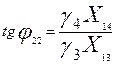 . .
Таким образом, если в системе есть затухания, то общее решение – сумма двух колебаний с частотами  и и 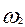 , с комплексными амплитудами. , с комплексными амплитудами.
Рассмотрим затухающие колебания в LC – контуре.
Отличие такого контура от рассмотренного ранее – наличие электрического сопротивления, т.е. в колебательной системе происходит потеря энергии (в механических системах из-за трения).
В каждое уравнение добавляется новое слагаемое – падение напряжения на сопротивлении  [2]: [2]:
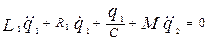 и и 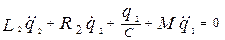
Будем искать решение в виде  , ,  . При подстановки которых, получим . При подстановки которых, получим
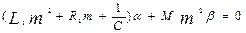 , ,
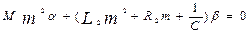 . .
Причем, α
, β
и m
– не известны. По отношению к α
, и β
эти уравнения линейны, имеют нетривиальное решение, когда детерминант равен нулю:
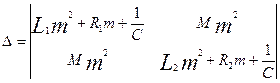 . .
Развертывая детерминант, получаем уравнение 4-й степени: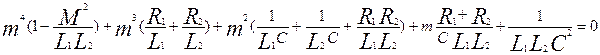
В отсутствии сопротивления (трения) оба корня  отрицательны, отрицательны,  , где , где 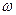 - действительная частота. - действительная частота.
При наличии сопротивления корни либо действительные, либо комплексные, попарно сопряженные. Общее решение состоит из суммы двух колебаний с возрастающими или затухающими амплитудами.
В случае системы с сопротивлением происходит сдвиг фаз между колебаниями каждой из частот в обеих координатах.
Затухание в системе связанных осцилляторов может быть неодинаковым для разных мод, поскольку, например, конденсаторы “работают” для различных нормальных колебаний по-разному[6]. Наконец, небольшое затухание никак не может повлиять на фундаментальные свойства нормальных колебаний – соответствие между числом нормальных мод и количеством колебательных степеней свободы.
1.3
. Связанные осцилляторы под действием гармонической силы
.
Пусть на осцилляторы действует внешняя гармоническая сила с частотой p
.
Тогда уравнения движения в общем случае:
 , ,
 . (12) . (12)
Общее решение системы - сумма однородного (собственные колебания) и частного (правые части системы ненулевые) решений [1].
Решение ищем в виде:
 , ,
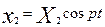 . .
Подставляя эти выражения в (12), получим:
 , ,
 . (13) . (13)
Детерминант системы
 . .
Если ∆=0
, то в системе установятся свободные колебания, рассматривались ранее и также были определены для них нормальные частоты. Если ∆≠0
, то для всех p
система (13) имеет решение, причем однородные уравнения не имеют решения.
Решение уравнений системы (13):
 , , 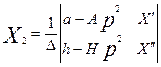 . .
Резонансные кривые, изображенные на рис.4 позволяют сделать следующие выводы.
1. Пусть сила действует на первую парциальную систему, т.е. 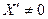 , , 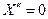 , тогда возможно совпадение частоты внешней силы и парциальной частоты второго осциллятора - динамическое демпфирование [2], первый осциллятор не колеблется: , тогда возможно совпадение частоты внешней силы и парциальной частоты второго осциллятора - динамическое демпфирование [2], первый осциллятор не колеблется:
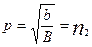 , , 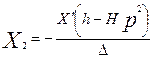 . .
2. Резонанс наступает при совпадении частоты внешней силы с одной из собственных частот системы, происходит неограниченный рост амплитуд в обоих осцилляторах.
 3. при частоте внешней силы 3. при частоте внешней силы  второй осциллятор не колеблется, это возможно, если связь носит смешанный характер. второй осциллятор не колеблется, это возможно, если связь носит смешанный характер.
Пусть сила действует на второй осциллятор, т.е.  , , 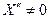 , тогда , тогда
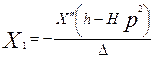 . .
Для линейных систем справедлива теорема взаимности
[2]: если на второй осциллятор действует сила  , то движение первой координаты – такое же, как Рис.4 , то движение первой координаты – такое же, как Рис.4
движение второй координаты, когда на первый осциллятор действует сила  . .
Она справедлива для линейных систем с любым числом степеней свободы, в том числе и для сплошных сред.
В электродинамике, например, теорема взаимности применяется в теории антенн.
Рассмотрим систему n
связанных осцилляторов.
Для этого воспользуемся уравнением Лагранжа [4]:
 , , 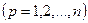 , ,
где каждому значению p
соответствует одно из уравнений движения
Подставим в него значения кинетической и потенциальной энергий, которые определяются формулами:
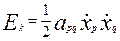 и и  . (14) . (14)
Где 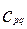 и и 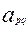 - симметрические матрицы, - симметрические матрицы, 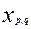 - обобщенные координаты. Кинетическая и потенциальная энергии положительны при колебания вблизи положения равновесия. - обобщенные координаты. Кинетическая и потенциальная энергии положительны при колебания вблизи положения равновесия.
Подставляя (14) в уравнения Лагранжа, уравнения движения примут вид:
 . (15) . (15)
Делая подстановку  , получаем систему алгебраических уравнений , получаем систему алгебраических уравнений
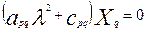 , (16) , (16)
которая имеет ненулевые решения, если детерминант равен нулю:
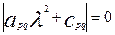 . (17) . (17)
Корни уравнения (17) действительные или комплексные попарно сопряженные (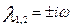 ). ).
Если известны собственные значения, т.е. решение (16), то общее решение уравнений движения представляется в виде:
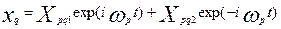 (18) (18)
Положим  , и , и 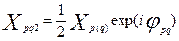 , тогда (18) примет вид: , тогда (18) примет вид:
 . (19) . (19)
Уравнение (19) содержит 2n
постоянных  и и  . Подстановка частного решения . Подстановка частного решения 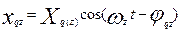 позволяет получить две системы уравнений, откуда в свою очередь, общее решение (19) содержит 2n независимых постоянных: позволяет получить две системы уравнений, откуда в свою очередь, общее решение (19) содержит 2n независимых постоянных:
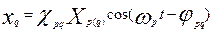 . (20) . (20)
Согласно формулам (20), общее решение представлено n
гармониками, входящими в каждую координату. При сложении эти гармоники не влияют друг на друга.
 - коэффициенты распределения
[4], матрица которых определяет распределение амплитуд отдельных гармоник во всех координатах. - коэффициенты распределения
[4], матрица которых определяет распределение амплитуд отдельных гармоник во всех координатах.
Из уравнения (16) для z
-го колебания
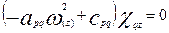 , ,
зная распределение амплитуд z
-го колебания (элементы z
-го столбца матрицы  ), можно перейти к выражению для частоты: ), можно перейти к выражению для частоты:
 (21) (21)
Формула (21) позволяет установить зависимость частоты от условий задачи [2].
Если уравнение 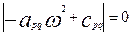 имеет корень n
-ой кратности, т.е. существует единственная частота, следует обращение в нуль всех элементов детерминанта и имеет корень n
-ой кратности, т.е. существует единственная частота, следует обращение в нуль всех элементов детерминанта и
 . .
Такое соотношение между кинетической и потенциальной энергиями выполняется, например, когда связи между координатами отсутствуют либо в системе присутствуют как инерционная, так и силовая связи. При наличии связей одного типа корней n-ой кратности в системе нет.
Таким образом, у системы с N
степенями свободы имеется N
мод. Каждой моде соответствует своя частота и своя фазовая постоянная, определяемая начальными условиями.
Система связанных осцилляторов, в которой они упорядочены так, что каждый из осцилляторов связан только с двумя соседями (за исключением двух крайних), называется цепочкой осцилляторов
[1].
 На рис.5 изображены примеры колебательных цепей с силовой связью (а, б
) и индукционной (в, г
). На рис.5 изображены примеры колебательных цепей с силовой связью (а, б
) и индукционной (в, г
).
Колебательные цепи – в зависимости от их реакции на периодические возмущения на входе – называют фильтрами высоких и низких частот [4].
Фильтры низких частот
(рис. 5а, 5б), через которые могут проходить только возмущения с частотами, лежащими ниже определенной граничной частоты. Фильтры высоких частот
(рис. 5в, 5г) пропускают колебания, частота которых лежит выше . Рис. 5
некоторой граничной частоты
В качестве примеров фильтров можно привести широко распространенные радиотехнические цепочки, электронные приборы СВЧ диапазона и модель кристалла, в котором пружины заменяют межатомные связи.
Рассмотрим схему, изображенную на рис. 5а. Пусть имеется N+2
шара, и оба конца цепи закреплены. Масса каждого шара – m
и жесткость пружины k
. Тогда уравнение движения для n-ой массы можно записать так:
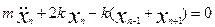 . (22) . (22)
Введем комплексные амплитуды 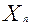 : :
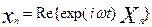 . .
Подставляя это решение в (22):
 , , 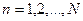 , (23) , (23)
Положим распределение амплитуд колебаний в виде  , где A и , где A и  - некоторые постоянные. Тогда из уравнения (23) следует: - некоторые постоянные. Тогда из уравнения (23) следует:
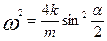 (24) (24)
Если цепочка состоит из механических маятников, то при 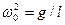 , (24) примет вид: , (24) примет вид:
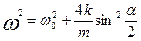 (24’) (24’)
Оба конца цепи находятся в положении равновесия:  и и  . Из этого условия находим, что . Из этого условия находим, что 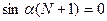 , или , или
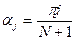 , ,  . (25) . (25)
Тогда собственные частоты определяются следующим образом:
 . .
 Спектр – совокупность всех собственных частот системы [1]. Расстояние между любыми двумя точками спектра равно Спектр – совокупность всех собственных частот системы [1]. Расстояние между любыми двумя точками спектра равно  . На рисунке 6, демонстрирующем зависимость . На рисунке 6, демонстрирующем зависимость  , точками отмечено положение собственных частот, лежащих в интервале между крайними точками , точками отмечено положение собственных частот, лежащих в интервале между крайними точками
 и и  . .
Рис.6
Распределение собственных частот вдоль оси  неоднородно. Увеличивая количество осцилляторов N
, плотность проекций точек, изображающих собственные частоты, на эту ось будет возрастать быстрее около крайних точек. неоднородно. Увеличивая количество осцилляторов N
, плотность проекций точек, изображающих собственные частоты, на эту ось будет возрастать быстрее около крайних точек.
Если  , а движущиеся элементы находятся в ограниченном объеме, то расстояние между соседними элементами стремится к нулю. Система ведет себя так, как если бы она была непрерывной, т.е. движение соседних элементов почти одинаково. , а движущиеся элементы находятся в ограниченном объеме, то расстояние между соседними элементами стремится к нулю. Система ведет себя так, как если бы она была непрерывной, т.е. движение соседних элементов почти одинаково.
Если в нашем случае увеличивать количество масс и пружин, а их самих уменьшать, то рассматриваемая цепь переходит в струну. Картина колебаний принимает вид стоячих
волн
.
Стоячие волны являются нормальными модами непрерывных систем [5]. Непрерывная система имеет бесконечное число степеней свободы и соответственно бесконечным числом мод.
Общее движение системы может быть описано как суперпозиция ее мод. Амплитуды и фазовые константы определяются из начальных условий.
Назовем длиной волны – расстояние вдоль системы между двумя осцилляторами, которые колеблются в одинаковой фазе [1].
Тогда для j
-го колебания можно записать:
 , ,
где d
– расстояние меду соседними осцилляторами,  определяется формулой (25), определяется формулой (25),  - длина волны j
-го колебания. Этот параметр для колебаний в пространстве имеет такой же смысл, что и период T для колебаний во времени. - длина волны j
-го колебания. Этот параметр для колебаний в пространстве имеет такой же смысл, что и период T для колебаний во времени.
Длина всей цепочки равна (N
+1)d
. По длине системы должно укладываться целое число полуволн – условие резонанса, которое выглядит следующим образом:
 . .
Учитывая предыдущее уравнение, получим (25).
Вводя волновое число k, равное  ,
имеем ,
имеем  . .
Следовательно, колебания цепочки осцилляторов можно описывать в терминах стоячих волн.
Рассмотрим спектр колебаний цепочки с большим числом элементов, например модель кристалла. В любом бесконечно малом интервале частот  будет содержаться большое число собственных мод будет содержаться большое число собственных мод  . Поэтому вводится функция . Поэтому вводится функция  - плотность распределения
собственных частот [1]: - плотность распределения
собственных частот [1]:
 . .
Тогда средняя энергия осциллятора, находящегося в состоянии теплового равновесия при температуре T определяется как:
 , ,
где  - постоянная Планка, - постоянная Планка,  - постоянная Больцмана. - постоянная Больцмана.
Откуда энергия внутренней среды равна

Это полученное соотношение применяется, например, в теории теплоемкости кристаллов при известном  . .
При  , используя формулы (24) и (25) и , используя формулы (24) и (25) и  , получаем: , получаем:
 . .
Вблизи границ спектра  обращается в бесконечность(рис.7): обращается в бесконечность(рис.7):
  , ,  , ,
 , ,  . .
Обращение в бесконечность функции  в критических точках – особенность одномерных цепочек. Для колебаний в двумерных (пластины, мембраны) и трехмерных кристаллических решеток - в критических точках – особенность одномерных цепочек. Для колебаний в двумерных (пластины, мембраны) и трехмерных кристаллических решеток -  остается конечной, а ее производная терпит разрыв. Рис.7 остается конечной, а ее производная терпит разрыв. Рис.7
Вид функция  зависит от структуры колебательной цепи, т.е. от количества элементов цепи разных типов на одном периоде системы и от их масс. зависит от структуры колебательной цепи, т.е. от количества элементов цепи разных типов на одном периоде системы и от их масс.
3. Переход к сплошной среде
Рассмотрим цепочку связанных осцилляторов – одномерную кристаллическую решетку, представляющую собой упорядоченную структуру. Другими примерами такой структуры являются цепочка, состоящая из LC
-элементов, набор связанных пружинами маятников. Смещая в такой системе один элемент от положения равновесия, получаем смещение соседних элементов, т.е. по всей структуре побежит волна.
Если в уравнении Клейна-Гордона, которое описывает распространение одномерных волн в среде с дисперсией [1]:
 , (26) , (26)
где  (связанные маятники массой m
, имеющие собственную частоту (связанные маятники массой m
, имеющие собственную частоту  , связь между которыми осуществляется пружинами с жесткостью , связь между которыми осуществляется пружинами с жесткостью  ), устремить ), устремить  к нулю, то получим к нулю, то получим
 . (27) . (27)
Это классическое волновое уравнение. Любая одномерная волна может быть описана решением (27).
Подставляя  в (26) имеем в (26) имеем
 . (28) . (28)
 - сдвиг фазы волны при смещении вдоль цепочки осцилляторов на одну ячейку. - сдвиг фазы волны при смещении вдоль цепочки осцилляторов на одну ячейку.
Уравнение (28) получается из (24’), если  . .
Дисперсионное уравнение, описывающее связь  и k
, в общем случае выглядит следующим образом: и k
, в общем случае выглядит следующим образом:
 . .
Дисперсия существует, описывается уравнением (28), что обусловлено существованием пространственного и временного собственного масштабов ( и a).. и a)..
ka
<<1, (a
<< ) справедливо для достаточно длинных волн, т.е. цепочку осцилляторов можно рассматривать как одномерную сплошную среду, описываемую уравнением (26). ) справедливо для достаточно длинных волн, т.е. цепочку осцилляторов можно рассматривать как одномерную сплошную среду, описываемую уравнением (26).
Наличие дисперсии обусловлено существованием собственного временного масштаба  . .
При  , ,  , т.е. длина маятника , т.е. длина маятника  и не влияет на его колебание, следовательно, получаем сплошную среду без дисперсии (отсутствие пространственного и временного масштабов). Каждый маятник имеет собственный период и не влияет на его колебание, следовательно, получаем сплошную среду без дисперсии (отсутствие пространственного и временного масштабов). Каждый маятник имеет собственный период  , «среда» не будет воспринимать частоту меньше собственной. , «среда» не будет воспринимать частоту меньше собственной.
В случае  в уравнении (24’) соотношение между a
и в уравнении (24’) соотношение между a
и  может быть любым ( может быть любым ( ), тогда получаем цепочку связанных шариков. Дисперсия в системе сохраняется, она существенна, пока a
не мало по сравнению с ), тогда получаем цепочку связанных шариков. Дисперсия в системе сохраняется, она существенна, пока a
не мало по сравнению с  . .
Существование дисперсии в среде связанно с наличием в ней собственных, не зависимых от параметров волны пространственных и временных масштабов.
В данной работе были рассмотрены колебания в системе двух связанных осцилляторов, проведен анализ этой системы в случае свободных колебаний и при воздействии внешней силы. Рассмотрено явление внутреннего резонанса, при котором отдельные подсистемы (парциальные) обмениваются энергией друг с другом, а также явление динамического демпфирования, которое используется на практике для гашения «вредных» колебаний.
Выводы, относящиеся к колебаниям в системе с двумя степенями свободы, обобщаются на случай колебаний в более сложных электрических схемах или механических вибраций.
В работе осуществлен переход от колебательной цепочки, набора элементарных осцилляторов, к одномерной сплошной среде.
С помощью некоторых цепочек можно реализовать практически любую дисперсионную зависимость, на основе которых исследуется распространение волн в различных средах.
5
. Список используемой литературы
[1] Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны. – М.: Физматлит, 2001.
[2] Мандельштам Л.И. Лекции по колебаниям. Полное собрание трудов. Т. 4. –М.:Изд-во АН СССР, 1957.
[3]Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. – М.: Ижевск: НИЦ Регулярная и хаотическая динамика. 2000.
[4] Магнус К. Колебания. – М.:Изд-во Мир, 1982.
[5] Крауфорд Ф. Волны. Берклеевский курс физики. Т. 3. – М.: Наука, 1974.
[6] Козлов С.Н., Зотеев А.В. колебания и волны. Волновая оптика. – М.: Физический факультет МГУ, 2006.
|