| ГОУ Гимназия №1505
«Московская городская педагогическая гимназия-лаборатория»
Реферат
Числа Фибоначчи и Золотое сечение
автор
: ученица 9 класса «Б»
Карпова Анастасия
Руководитель:
Шалимова М.Н.
Москва
2012
Содержание
Введение
………………………………………………….……………...2
Глава 1
Свойства Чисел Фибоначчи.………………………………..……...........4
Глава 2
Теоретико-числовые свойства чисел Фибоначчи………...…...……………………………………..…..............7
Глава 3
Числа Фибоначчи и геометрия…………………………………………..9
Заключение
…………………………………………………...………….12
Список литературы
……………………………………………………..13
Введение.
Из школьного курса математики хорошо известны такие ученые, как Евклид, Архимед и Герон.
Если же мы обратимся к математике средневековья, то не обнаружим такого большого количества выдающихся математических деятелей. Это связано с тем, что математика в эту эпоху развивалась крайне медленно.
Однако стоит обратить внимание на сочинение “Liber abacсi”, написанное знаменитым итальянским математиком Леонардо Фибоначчи в 1202 году, которое дошло до нас в издании от 1228 года. В данной книге содержатся почти все арифметические и алгебраические сведения того времени. Данная работа сыграла большую роль в развитии математики в Западной Европе в течение нескольких следующих столетий.
Данный трактат примечателен тем, что материал поясняется на большом числе интересных математических задач. Обратимся к одной из задач, разобранной в этой книге.
[1]
Исходная формулировка задачи – «Сколько пар кроликов в один год от одной пары рождается?» Рассмотрим предлагаемое автором решение. Представим, что некто поместил пару кроликов в огороженном со всех сторон месте и хочет узнать, сколько пар кроликов родится при этом в течение года. По условию задачи природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Проведем мысленный эксперимент и узнаем, сколько пар кроликов будет в каждом последующем месяце. Так как первая пара в первом месяце даст потомство, то всего будет 2 пары, причем первая пара рождает и в следующем месяце. То есть во втором месяце окажется три пары и две из них в следующем месяце дадут потомство. Получится, что в третьем месяце будет пять пар кроликов и три пары дадут потомство в следующем месяце. То есть в четвертом месяце будет 8 пар кроликов, и пять из них будут давать потомство. Это значит, что в пятом месяце будет 13 пар, из которых 8 дадут потомство в следующем месяце. Проведя аналогичные рассуждения, получим, что в шестом месяце будет 21 пара, в седьмом 34 пары, в восьмом 55 пар, в девятом 89 пар, в десятом 144 пары, в одиннадцатом 233 пары, в двенадцатом 377 пар – столько пар произвела первая пара в данном месте к концу одного года. Можно заметить, что число пар кроликов в текущем месяце равняется сумме пар кроликов за два предшествующих месяца.
Математически решение этой задачи приводит к появлению последовательности чисел
[2]
u1
, u2
, …
un
в которой каждый член равен сумме двух предыдущих, то есть для любого n>2
[3]
un
= un
-1
+ un
-2
Эта последовательность была названа числами Фибоначчи. В школьном курсе математики не изучаются числа Фибоначчи, поэтому возникает вопрос: какие это числа и какими свойствами они обладают? Поэтому я поставила следующие задачи:
1) Проанализировать в чем состоят свойства чисел Фибоначчи
2) возможности их применения к решению задач.
Для того чтобы получить сведения по данным вопросам, я выбрала и проанализировала первоисточник: книгу Н.Н.Воробьева «Числа Фибоначчи».
§ 1. СВОЙСТВА ЧИСЕЛ ФИБОНАЧЧИ
В первой главе описываются простейшие свойства чисел Фибоначчи. Зная особенности суммарной последовательности Фибоначчи ученые смогли выяснить, что им подчиняются многие особенности жизни, времени, деятельности человека. В законах природы, как и в законах математики имеется важнейший элемент – ритмичность. Свойства чисел последовательности используются не только в математике и физике, но и в природе, архитектуре, биологии, астрономии, изобразительном искусстве. При помощи этих чисел описываются разнообразные процессы во вселенной. Свойства чисел последовательности Фибоначчи, сделал их основой технического анализа. Я изучила простейшие свойства чисел Фибоначчи и проверила их верность на примерах. Рассмотрим некоторые из них:
1. Сумма первых n чисел Фибоначчи равна:
[4]
u1
+ u2
+… + un
= un+2
– u2
где u2
= 1
Рассмотрим это на простейшем примере. Пусть n = 5, тогда:
u1
= 1; u2
= 1; u3
= 2; u4
= 3; u5
= 5; un
+2
= 13
1 + 1 + 2 + 3 + 5 = 13 - 1
12=12 Свойство верно
2. Сумма чисел Фибоначчи с нечетными номерами равна:
[5]
u1
+ u3
+ u5
… + u2
n
-1
= u2
n
Например, n = 5, тогда:
u1
= 1; u3
= 2; u5
= 5; u7
= 13; u2
n
-1
= 34; u2
n
= 55
1 + 2 + 5 + 13 + 34 = 55
55 = 55 Свойство верно
3. Сумма чисел Фибоначчи с четными номерами равна:
[6]
u2
+ u4
+ … + u2
n
= u2
n
+1
– 1
Например, n = 5, тогда:
u2
= 1; u4
= 3; u6
= 8; u8
= 21; u2
n
= 55; u2
n
+1 =
89
1 + 3 + 8 + 21 + 55 = 89 - 1
88 = 88 Свойство верно
4. Формула суммы квадратов первых n чисел Фибоначчи выглядит так:
[7]
u1
2
+ u2
2
+… + un
2
= un
un
+1
Например, n = 5, тогда:
u1
2
= 1; u2
2
= 1; u3
2
= 4; u4
2
= 9; un
2
= 25; un =
5; un+1
= 8
1 + 1 + 4 + 9 + 25 = 5 * 8
40 = 40 Свойство верно
5. [8]
Соотношения между числами Фибоначчи удобно доказывать при помощи метода полной индукции. Сущность метода заключается в том, что для доказательства, что некоторого утверждения справедливого для всякого натурального числа достаточно двух условий
А) Утверждение имеет место для числа 1
Б) Из справедливости доказываемого утверждения для произвольного числа n, следует его справедливость для числа n+1.
Иногда применяется индуктивное рассуждение, которое можно назвать переходом «от всех чисел, меньших n, к n». Именно таким является доказательство возможности разложения любого натурального числа на простые множители.
6. Простейшей реализацией идеи индукции в применении к числам Фибоначчи является само определение чисел Фибоначчи. Оно состоит в указании двух первых чисел Фибоначчи: u1
= 1 и u2
= 1 и в индуктивном переходе от un
и un
+1
к un
+2
, даваемым рекуррентным соотношением
un
+ un
+1
= un
+2
,
Отсюда автоматически следует, что если некоторая последовательность чисел начинается с двух единиц, а каждое из следующих получается
сложением двух предыдущих, то эта последовательность является последовательностью чисел Фибоначчи.
7. Аналогично только что доказанным свойствам чисел Фибоначчи можно установить еще и такие свойства этих чисел:
[9]
u1
u2
+ u2
u3
+ u3
u4
+ …+ u2n - 1
u2n =
u2
2n
u1
u2
+ u2
u3
+ u3
u4
+ …+ u2n+1
u2n =
u2
2n+1
– 1
nu1
+ (n-1)u2
+(n-2) u3
+ …+2un – 1
+ un =
un+4
- (n-3)
u1
+ 2
u2
+ 3u3
+ …+ nun =
nun+2
– un+3
+2.
8. [10]
Любое число Фибоначчи можно определить и непосредственно, как некоторую функцию его номера. для этого исследуют различные последовательности u1
, u2
, ..., un
, ..., удовлетворяющие соотношению
un
= un-2
+ un-1
9. Числа Фибоначчи могут составить основу своеобразно «фибоначчисвой» системы счисления, т. е., представления любого натурального числа а в виде некоторой последовательности «цифр» ф1
ф2
.. .фг
.
Рассмотренные мною свойства являются не всеми свойствами занимательных чисел, они требуют более глубокого знания математики.
§ 2. ТЕОРЕТИКО-ЧИСЛОВЫЕ СВОЙСТВА ЧИСЕЛ ФИБОНАЧЧИ
Вторая глава рассматривает свойства чисел Фибоначчи, касающиеся их делимости.
Если существует хотя бы одно число Фибоначчи un
делящееся на m, то таких делящихся на m чисел Фибоначчи можно найти сколь угодно много. Ими будут, кроме un
, например, числа u2
n
, u3
n
., u4
n
…
Оказывается, что по заданному числу m можно найти хотя бы одно делящееся на него число Фибоначчи. Это доказывает следующая теорема: [11]
Каково бы ни было целое число
m, среди первых
m2
—1 чисел Фибоначчи найдется хотя бы одно, делящееся на
m.
Эта теорема не утверждает ничего о том, какое именно число Фибоначчи разделится на m. Она говорит только, что первое число Фибоначчи, делящееся на m, не должно быть особенно большим. Рассмотрим справедливость этой теоремы на конкретном примере. Пусть m = 5, тогда m2
—1 = 24, то есть n = 24
| № п-п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
| Числа
|
1
|
1
|
2
|
3
|
5
|
8
|
13
|
21
|
34
|
55
|
89
|
144
|
| № п-п
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
| Числа
|
233
|
377
|
610
|
987
|
1597
|
2584
|
4181
|
6765
|
10946
|
17711
|
28657
|
46368
|
Вывод:
Приняв за m число 5. Из 24 чисел последовательности Фибоначчи на m делится 4 числа. Теорема верна.
[12]
Теорема. Соседние числа Фибоначчи взаимно просты.
Возьмем два соседних числа. Например, u5
= 5 и u6
= 8.
Пусть вопреки утверждению теоремы 5 и 8 имеют некоторый общий делитель d> 1. Тогда и их разность 8 - 5 будет делиться на d. А так как 8 — 5 = 3(u4
), на в должно делиться и 3. Числа 8 и 5 не имеют общего делителя.
Имеет место равенство (um
, un
)= u(
m,
n)
.
[13]
О делимости чисел Фибоначчи можно судить, рассматривая делимость их номеров. Рассмотрим, несколько «признаков делимости» чисел Фибоначчи. Под признаком делимости мы понимаем здесь признак, по которому можно определить, делится или нет то или иное число Фибоначчи на некоторое данное число.
Число Фибоначчи четно тогда и только тогда, когда его номер делится на 3.
Число Фибоначчи делится на 3 тогда и только тогда, когда его номер делится на 4.
Число Фибоначчи делится на 4 тогда и только тогда, когда его номер делится на 6.
Число Фибоначчи делится на 5 тогда и только тогда, когда его номер делится на 5.
Число Фибоначчи делится на 7 тогда и только тогда, когда его номер делится на 8.
Число Фибоначчи делится на 16 тогда и только тогда, когда его номер делится на 12. Доказательства всех этих признаков делимости и всех других, подобных им, легко могут быть проведены читателем при помощи предложения, приведенного в начале этого пункта, и рассмотрения соответственно третьего, четвертого, пятого, шестого, восьмого, двенадцатого и т. д. чисел Фибоначчи. Пусть заодно читатель докажет, что не существует чисел Фибоначчи, дающих при делении на 8 в остатке 4, а также, что нет нечетных чисел Фибоначчи, делящихся на 17.
[14]
Рассмотрим следующее свойство: Если число Фибоначчи имеет нечетный номер, то все его нечетные делители имеют вид 4
t+1.
Вернемся к нечетным номерам рассматриваемой последовательности чисел Фибоначчи.
| № п-п
|
5
|
7
|
11
|
13
|
17
|
19
|
23
|
| Числа
|
5
|
13
|
89
|
233
|
1597
|
4181
|
28657
|
| 4t+1
|
5:4= 1+1
|
13:4=3+1
|
89:4=22+1
|
233:4=58+1
|
1597:4=399+1
|
4181:4=1045+1
|
28657:4=7164+1
|
Вывод: свойство верно
[15]
Теорема. Всякое натуральное число разлагается на простые множители лишь одним способом.
§ 3. ЧИСЛА ФИБОНАЧЧИ И ГЕОМЕТРИЯ
[16]
Последовательность Фибоначчи стремится к постоянному соотношению. Это отношение иррационально, представляет собой число с бесконечной последовательность десятичных чисел в дробной части. Члены последовательности связаны между собой соотношениями. Если член последовательности разделить на предшествующий ему, то величина будет колебаться примерно Ф = 1,618. Число Фи. При делении каждого числа Фибоначчи на последующее отношение стремится к 0,382. Эти соотношения называются фибоначчиевыми коэффициентами. Золотое сечение не проходится в школьном курсе математики, поэтому оно известно далеко не всем. Золотое сечение с древности рассматривалось, как эстетически самое благоприятное отношение. Через Золотое сечение числа Фибоначчи проявляют свои свойства. Посколько целое всегда состоит из частей, то части находятся в определенном отношении к друг другу и к целому. Принц Золотого сечения – это принцип гармоничной пропорции. Рассмотрим пример деления отрезка:
1. Разделим отрезок АВ единичной длины на две части точкой C так, чтобы большая из его частей являлась средним пропорциональным между меньшей его частью и всем отрезком. Обозначим искомую длину большей части отрезка через х. Тогда условие нашей задачи дает пропорцию:

Положительным корнем является  . Получаем, что отношения в пропорции равны . Получаем, что отношения в пропорции равны 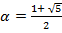 ( (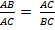 ). Это деление и есть Золотое сечение или деление отрезка в крайнем и среднем отношении. Отрезки Золотой пропорции выражаются бесконечными и рациональными дробями b = 0,618; a = 0,382. Числа 0,618: 0,382 – коэффициенты последовательности Фибоначчи. На этой последовательности базируются все геометрические фигуры. ). Это деление и есть Золотое сечение или деление отрезка в крайнем и среднем отношении. Отрезки Золотой пропорции выражаются бесконечными и рациональными дробями b = 0,618; a = 0,382. Числа 0,618: 0,382 – коэффициенты последовательности Фибоначчи. На этой последовательности базируются все геометрические фигуры.
Рассмотрим правильный пятиугольник.
 [17]
Можно доказать, что точка С делит отрезок AD золотым сечением. То есть: [17]
Можно доказать, что точка С делит отрезок AD золотым сечением. То есть:  . Таким образом, среди отрезков ВС, АВ, AC, AD каждый последующий в α раз больше предыдущего. . Таким образом, среди отрезков ВС, АВ, AC, AD каждый последующий в α раз больше предыдущего.
Рассмотрим прямоугольник, у которого отношение сторон равно α. Такие прямоугольники будем называть прямоугольниками золотого сечения. Можно доказать, что, вписав в такой прямоугольник наибольший возможный квадрат, мы снова получим прямоугольник золотого сечения.
Можно говорить и о треугольниках золотого сечения: остроугольном — с углами 36°, 72° и 72° и тупоугольном— с углами 108°, 36° и 36°. Интересно, что остроугольный треугольник золотого сечения разбивается на меньшие три треугольника золотого сечения. Соотношение длины боковой стороны к длине основания такого треугольника равно 1,618.
В Природе мы часто видим, что расположение предметов можно описать соотношениями чисел Фибоначчи и соответствующими величинам Золотого деления. Например, это спирально закрученные раковины и спиралевидная паутина, и спирально закрученный торнадо, и спиралевидная молекула ДНК. 
Числа спиралей того и другого типов часто оказываются соседними числами Фибоначчи. 
Золотое сечение применяли художники и архитекторы, астрономы описывали закономерности планет солнечной системы.
Числа Фибоначчи появляются также в вопросах, связанных с исследованием путей в различных геометрических конфигурациях.
Заключение
Изучив и проанализировав первоисточник Н.Н.Воробьева «Числа Фибоначчи», а так же дополнительную литературу я пришла к следующим выводам:
1) Все в природе подчиняется цикличности и закономерности, которую можно объяснить при помощи последовательности Фибоначчи и Золотого сечения.
2) Изучение свойств последовательности Фибоначчи позволяет применять ее для решения многих практических и теоретических задач в различных сферах деятельности человека
3) Многие свойства чисел Фибоначчи до конца не изучены.
[1]
Воробьев Н.Н. «Числа Фибоначчи», М: Наука 1978.
[2]
Там же
[3]
Там же
[4]
Воробьев Н.Н. «Числа Фибоначчи», М: Наука 1978.
[5]
Там же
[6]
Там же
[7]
Там же
[8]
Там же
[9]
Там же
[10]
Там же
[11]
Там же
[12]
Там же
[13]
Там же
[14]
Там же
[15]
Там же
[16]
Фибоначчи. [Электронный ресурс]. Числа Фибоначчи. Режим доступа: http://forexaw.com Свободный. Данные соответствуют – 01.05.2012г.
[17]
Воробьев Н.Н. «Числа Фибоначчи», М: Наука 1978.
|