| Аннотация.
Данная курсовая работа содержит вариант расчёта комбинированной САУ (выбор передаточной функции объекта управления, выбор параметров настроек регулятора и компенсатора и расчёт НЦУ). Пояснительная записка выполнена в программном приложении Microsoft Word. К работе прилагаются все необходимые графики.
The summary.
The given course activity contains version of calculation of a combined ACS (selection of a transfer function of object of control, selection of parameters of adjustments of the regulator both compensator and calculation DNC). The explanatory slip is executed in the programmatic appendix Microsoft Word. To activity all indispensable schedules are appended.
Содержание.
Введение………………………………………………………….………….стр.2
1. Идентификация объекта управления по экспериментальной переходной
характеристике …………………………………………………………..……..стр.3
1.1. Аппроксимация переходной характеристики объекта по
регулирующему каналу…………………………………………………………стр.3
1.2. Аппроксимация переходной характеристики объекта по
возмущающему каналу………………………………………………………….стр.6
2. Выбор ПИ-алгоритма управления и расчёт параметров ПИ-регулятора…….стр.9
3. Получение передаточной функции физически реализуемого компенсатора..стр.13
4. Расчёт переходных процессов в САУ на ПЭВМ ……..…………………..……стр.15
5. Определение показателей качества ……………………………………………..стр.17
6. НЦУ ……………………………………………………………………………….стр.19
7. Список используемой литературы………………………………………………стр.24
Введение.
Промышленные объекты управления, как правило, представляют собой сложные агрегаты со многими входными и выходными величинами, характеризующими технологический процесс. Зависимости выходных величин от входных, как правило, нелинейные, и изменение одной из них приводит к изменению других. Таким образом, создаётся сложная система взаимозависимостей, которую трудно, а подчас и невозможно строго математически описать.
Задачу можно существенно упростить, если считать зависимости выходных величин от входных линейными или линеаризуемыми в окрестностях малых отклонений от статических, рабочих режимов объекта. Поскольку при устойчивой работе автоматической системы регулирования (АСР) отклонения параметров в системе малы, такая линеаризация почти всегда оказывается допустимой. Кроме того, сложные объекты часто можно разбить на отдельные «регулируемые участки» («каналы»), взаимным влиянием отдельных каналов друг на друга можно пренебречь и рассматривать их как самостоятельные.
1. Идентификация объекта управления по экспериментальной переходной характеристике.
1.1. Аппроксимация переходной характеристики объекта по регулирующему каналу.
Исследуемый объект по каналу регулирования является объектом с самовыравниванием (рис.1.1). Объекты с самовыравниванием аппроксимируют дробно-рациональными передаточными функциями с введением звена запаздывания [1]:
 , (1.1) , (1.1)
где Коб
– коэффициент передачи; t - время запаздывания; То
– постоянная времени.
Простейшим частным случаем оператора (1.1), имеющим в инженерной практике наибольшее применение, является передаточная функция вида:
 . (1.2) . (1.2)
Проведём касательную к экспериментальной переходной характеристике в точке перегиба с координатами (hп
; tп
) (рис.1.1). Определим параметры передаточной функции:
Коб
= hуст
= 1,6; tо
= 2,2с; То
= 10,1с; hп
= 0,4; tп
= 4,85с.
В этом случае передаточная функция принимает вид:
 . .
Параметры передаточной функции могут быть найдены следующим образом. Обозначив  , получим: , получим:
 (1.3) (1.3)
Из (1.3) определяются параметры аппроксимирующей характеристики:
Тa
= (1 - b)То
; (1.4)
 . (1.5) . (1.5)
В нашем случае:
 ; ;
Тa
= (1 – 0,25)×10,1 = 7,54с;

После подстановки параметров передаточная функция примет вид:
 . .
Более точную аппроксимацию переходной функции ОУ даёт передаточная функция вида:
 . (1.6) . (1.6)
Для определения параметров передаточной функции используем
специальную номограмму [1].
По номограмме по известному значению  находим: находим:
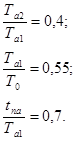
Из данных отношений определяем параметры передаточной функции:

Так как tпа
< tп
(tп
= 4,85с), то при аппроксимации следует учесть запаздывание:
tа
= tп
– tпа
= 4,85 – 3,88 = 0,97с. И тогда третья аппроксимирующая функция будет иметь вид: 
 . .
При условии b = 0,265 в выражении (1.6) постоянная времени Тa1
= Тa2
. В этом случае (Тa
= Тa1
= Тa2
) аппроксимирующее выражение имеет вид:
 , (1.7) , (1.7)
где  ; tп
– переходное запаздывание, tп
= 0,107×То. ; tп
– переходное запаздывание, tп
= 0,107×То.
Определим значения параметров передаточной функции:

  - -  1,08с; 1,08с;
Итак, четвертая аппроксимирующая функция имеет вид:
 . .
Графики всех аппроксимирующих функций, а также график
экспериментальной переходной характеристики представлены на рис.1.1.
Вычислим погрешности аппроксимации всех четырёх функций. Погрешность аппроксимации может быть найдена по формуле:
 , (1.8) , (1.8)
где SA,i
– площадь, заключённая между экспериментальной и i-той кривой; Sисх
– площадь под экспериментальной кривой.


Из расчётов видно, что наименьшую погрешность аппроксимации даёт функция Wоб,4
(р). Следовательно, она наилучшим образом аппроксимирует экспериментальную характеристику.

1.2. Аппроксимация переходной характеристики объекта по возмущающему каналу.
Исследуемый объект по возмущающему каналу также является объектом с самовыравниванием (рис.1.2). Поэтому первая аппроксимирующая передаточная функция примет форму оператора (1.2).
Проведём касательную к экспериментальной переходной характеристике в точке перегиба с координатами (hп
; tп
) (рис.1.2). Определим параметры передаточной функции:
Коб
= hуст
= 1,45; tо
= 4,5с; То
= 14,15с; hп
= 0,35; tп
= 8с.
В этом случае передаточная функция принимает вид:
 . .
Параметры передаточной функции могут быть найдены следующим образом.
Обозначив  и используя формулы (1.3), (1.4), (1.5), найдём параметры передаточной функции: и используя формулы (1.3), (1.4), (1.5), найдём параметры передаточной функции:
 ; ;
Тa
= (1 – 0,24)×14,15 = 10,75с;

После подстановки параметров передаточная функция примет вид:
 . .
Более точную аппроксимацию переходной функции ОУ даёт передаточная функция вида (1.6).
Для определения параметров передаточной функции используем
специальную номограмму [1].
По номограмме по известному значению  находим: находим:

Из данных отношений определяем параметры передаточной функции:

Так как tпа
< tп
(tп
= 8с), то при аппроксимации следует учесть запаздывание:
tа
= tп
– tпа
= 8 – 5,09 = 2,91с. И тогда третья аппроксимирующая функция будет иметь вид: 
 . .
При условии b = 0,265 в выражении (1.6) постоянная времени Тa1
= Тa2
. В этом случае (Тa
= Тa1
= Тa2
) аппроксимирующее выражение имеет вид (1.7).
Определим значения параметров передаточной функции:

ta
= tо
- tп
= 1,51с.
Итак, четвертая аппроксимирующая функция имеет вид:
 . .
Графики всех аппроксимирующих функций, а также график экспериментальной переходной характеристики представлены на рис.1.2.
Вычислим погрешности аппроксимации всех четырёх функций. Погрешность аппроксимации может быть найдена по формуле (1.8).


Из расчётов видно, что наименьшую погрешность аппроксимации даёт функция Wоб,4
(р). Следовательно, она наилучшим образом аппроксимирует экспериментальную характеристику.

2. Выбор ПИ-алгоритма управления и расчёт параметров ПИ-регулятора по параметрам объекта Wo
u-y
(p) (по регулирующему каналу графоаналитическим методом Ротача).
В качестве показателя оптимальности АСР принимается минимум интеграла от квадрата ошибки системы при действии на объект наиболее тяжелого ступенчатого возмущения по регулирующему каналу (интегральный квадратичный критерий) с учетом добавочного ограничения на запас устойчивости системы, т.е.
 . (2.1) . (2.1)
Такой критерий допускает значительное перерегулирование  и увеличивает время регулирования, но он обеспечивает наименьшее максимальное динамическое отклонение регулируемой величины. и увеличивает время регулирования, но он обеспечивает наименьшее максимальное динамическое отклонение регулируемой величины.
При практических расчётах запас устойчивости удобно характеризовать показателем колебательности системы М, значение которого в САУ, имеющих интеграл в алгоритме управления, совпадает с максимумом амплитудно-частотной характеристики системы:
 (2.2) (2.2)
где wр
- резонансная частота, на которой Аз
(w) имеет максимум.
Чтобы максимум не превышал некоторой заданной величены М, амплитудно-фазовая характеристика (АФХ) разомкнутой системы Wраз
(jw) не должна заходить внутрь “запретной” области ограниченной окружностью,центр uo
и радиус Ro
которой определяется через М формулами (рис.2.1):
 (2.3) (2.3)
 . (2.4) . (2.4)

Рис.2.1.
Определение центра и радиуса окружности, соответствующей заданному показателю колебательности М.
Если же Wраз
(jw) касается указанной окружности, то это означает, что САУ находится на границе заданного запаса устойчивости.
На практике чаще всего принимают  . При этом в САУ перерегулирование g £ 30%, максимальное отклонение регулируемого параметра при внутренних возмущениях (возмущениях по регулирующему воздействию) не превышает 10%. . При этом в САУ перерегулирование g £ 30%, максимальное отклонение регулируемого параметра при внутренних возмущениях (возмущениях по регулирующему воздействию) не превышает 10%.
С помощью прикладной программы «СС» рассчитываем и строим АФХ объекта по заданию. Результаты расчёта приведены в табл.2.1.
Таблица2.1
| w
|
0,331
|
0,93
|
0,5016
|
0,349
|
0,266
|
0,18
|
0,0758
|
0,0439
|
0,0162
|
| А
|
0,01
|
0,123
|
0,36
|
0,59
|
0,81
|
1,10
|
1,48
|
1,55
|
1,59
|
| j
|
360 
|
-207,5о
|
-155,5о
|
-127о
|
-106о
|
-79,24о
|
-36,21о
|
-21,26о
|
-7,92о
|
Рассмотрим ПИ-алгоритм управления, передаточная функция которого имеет вид:
 , (2.5) , (2.5)
а параметрами, подлежащими определению, являются коэффициент усиления Кр
и постоянная интегрирования Ти
.
1. По АФХ объекта Wоб
u
-y
(jω) строим семейство характеристик разомкнутой системы Wраз
(jω) для Кр
= 1 и нескольких фиксированных значений постоянной интегрирования Ти
.
Для этого сначала строим несколько векторов характеристики объекта Wоб
u
-y
(jω), например, векторы  для частоты ω1
, для частоты ω1
,  для ω2
и т.д. (рис.2.2). К их концам надо пристроить векторы для ω2
и т.д. (рис.2.2). К их концам надо пристроить векторы  , ,  ,…, ,…,  , повернутые по отношению к векторам , повернутые по отношению к векторам  , ,  ,…, ,…,  на угол 90°. Длина векторов на угол 90°. Длина векторов  , ,  ,…, ,…,  выбирается из соотношения выбирается из соотношения  (где в числителе (где в числителе  - длина вектора АФХ объекта для определённого значения частоты wi
, которую можно измерить непосредственно в миллиметрах; в знаменателе – произведение указанной частоты на фиксированное значение Ти
). Через полученные точки С1
, С2
,…, Сn
проводим плавную кривую, которая является характеристикой Wраз1
(jω) для выбранного значения Ти
. - длина вектора АФХ объекта для определённого значения частоты wi
, которую можно измерить непосредственно в миллиметрах; в знаменателе – произведение указанной частоты на фиксированное значение Ти
). Через полученные точки С1
, С2
,…, Сn
проводим плавную кривую, которая является характеристикой Wраз1
(jω) для выбранного значения Ти
.
Аналогичные построения проводим для других значений Ти
. В итоге получаем семейство характеристик Wраз1
(jω) для различных значений Ти
.
2. Из начала координат проводим прямую ОЕ под углом b, характеризующим запас устойчивости по фазе и определяемым как:
 . (2.6) . (2.6)
3. С помощью циркуля вычерчиваем окружности с центром на отрицательной вещественной полуоси, каждая из которых касается одновременно как прямой ОЕ, так и одной из характеристик Wраз1
(jω) (центр каждой окружности и ее радиус находим подбором).
4. Отношение требуемого радиуса R0
, определяемого по формуле (2.3)
 , ,
к полученному в каждом отдельном случае значению ri
показывает, во сколько раз нужно изменить единичный коэффициент передачи регулятора (Кр
=1), чтобы каждая характеристика Wраз1
(jω) касалась окружности с заданным М, т.е.
или  . (2.7) . (2.7)
Для вычисления Кр. пред
использована формула
 , (2.8) , (2.8)
где Rо
– радиус, определяемый по формуле (2.3); r – радиус окружности (на рис.2.2), который находим методом подбора; m к
– масштабный коэффициент, из рис.2.2 равный mк
= 0,023.
Все результаты вычислений представлены в таблице 2.2.
Таблица 2.2
| Ти
, с
|
ri
, мм
|
Кр
|
| 5
|
92
|
1,10
|
| 6
|
77
|
1,32
|
| 7
|
72
|
1,45
|
| 8
|
65
|
1,57
|
5). В результате в плоскости варьируемых параметров алгоритма Кр
и Ти
строится граница области заданного запаса устойчивости, вид которой представлен на рис.2.3.
Максимум отношения Кр
/Ти
, определяющего оптимальную настройку регулятора при низкочастотных возмущениях, соответствует точке пересечения касательной с границей заданного запаса устойчивости, проведённой через начало координат (точка А на рис.2.3).
Передаточная функция регулятора, после определения координат точки А (Кр.опт
= 1,2 и Ти опт
= 5,5 с), имеет вид:
 . .
Следует отметить, что найденные таким образом параметры являются оптимальными только при низкочастотном характере возмущений. По мере расширения полосы частот возмущений точка оптимума в плоскости параметров (рис.2.3) смещается вправо от точки А, причём сначала это смещение идёт вдоль границы заданного запаса устойчивости, а затем, при достаточно высокочастотных воздействиях, она уходит вглубь области. Это означает, что с ростом частоты воздействий ПИ-алгоритм должен всё более приближаться к П-алгоритму, Кр
которого также снижается. Это сопровождается ухудшением эффективности управления.
3. Получение передаточной функции физически реализуемого компенсатора, обеспечивающего компенсацию возмущения f
.
Одной из главных целей синтеза автоматической системы является обеспечение требуемой точности в установившихся и переходных режимах. Точность систем в установившихся режимах можно улучшить, увеличивая порядок астатизма и коэффициент разомкнутого контура. Но при этом, как правило, уменьшается запас устойчивости, увеличивается колебательность и, как следствие, ухудшается точность системы в переходных процессах. Эффективным средством устранения противоречия между условиями точности в установившихся и переходных режимах служит компенсация внешних воздействий путём осуществления инвариантности (независимости одной физической величины от другой).
Инвариантность в автоматических системах достигается при помощи управления по возмущению: управляющее воздействие формируется в зависимости от изменений возмущающего воздействия.
Рассмотрим схему комбинированной системы (рис.1). Уравнение такой системы имеет вид:
 , (3.1) , (3.1)
где -передаточная функция системы по задающему воздействию; а -передаточная функция системы по задающему воздействию; а  - передаточная функция системы по возмущению. - передаточная функция системы по возмущению.
Управляемая величина не зависит от возмущения, если передаточная функция по возмущению равна нулю. А это возможно, если равен нулю её числитель. Отсюда условие инвариантности стабилизируемой величины по отношению к возмущению:
 . .
Согласно условию инвариантности передаточная функция компенсирующего устройства:
 . (3.2) . (3.2)
На основании вышеизложенного получим передаточную функцию компенсатора: 
где  учтено повышением порядка передаточной функции компенсатора. учтено повышением порядка передаточной функции компенсатора.
Параметры передаточной функции компенсатора находим по методу Смольникова:


После подстановки численных значений параметров передаточная функция компенсатора примет вид:
 . .
4. Расчёт переходных процессов в САУ на ПЭВМ.
Переходные процессы в САУ целесообразно рассчитывать при наличии нескольких конкурирующих вариантов параметров САУ с целью выбора наилучшего. Быстро это можно сделать на ЭВМ частотным методом [1].
На первом этапе по заданной на ЭВМ передаточной функции замкнутой системы Wз
(р) рассчитывается вещественная частотная характеристика замкнутой системы. Для этого в выражение Wз
(р) подставляют  и, меняя частоту w от 0 до ¥, вычисляют вещественную часть и, меняя частоту w от 0 до ¥, вычисляют вещественную часть  : :
 при w = 0; w1
; w2
, …, wmax
. (4.1) при w = 0; w1
; w2
, …, wmax
. (4.1)
Поскольку практически невозможно вычислить (4.1) для всего диапазона частот от 0 до ¥, приходится ограничиться некоторой максимальной частотой wmax
, которая выбирается таким образом, чтобы при w > wmax
вещественная частотная характеристика принимала пренебрежимо малые значения, например менее 5% от начального значения Рз
(0).
Второй этап расчёта заключается в получении переходного процесса по найденной на первом этапе Рз
(w) в диапазоне 0 £ w £ wmax
. Для этого используется известное выражение:
 при t > 0. (4.2) при t > 0. (4.2)
Интеграл (4.2) вычисляется приближённым (численным) методом для ряда значений времени t: от t = 0 до t = tmax
. Максимальное значение времени tmax
выбирают таким образом, чтобы к моменту t = tmax
переходный процесс y(t) практически закончился.
В соответствии с заданием для проверки правильности выполненных расчётов нужно построить переходные процессы в САУ по задающему и возмущающему воздействиям.
Для построения переходной характеристики по задающему воздействию запишем передаточную функцию по заданию:
 . .
Заменив р = jw, получим:
  . .
Представим 
где Р(w) – вещественная часть  ; Q(w) – мнимая часть ; Q(w) – мнимая часть  . .
Берём Р(w), строим её, выделяя диапазон 0 £ w £ wmax
. Делим этот диапазон на n интервалов. Далее находится Р(w1
) для частоты w1
и подставляется в интеграл (4.2), который рассчитывается численным методом. И так для всех частот диапазона 0 £ w £ wmax
. Все расчёты выполняются на ПЭВМ. Результаты расчётов представлены на рис.5.1.
Переходные процессы по возмущающему воздействию без компенсатора и с компенсатором строятся аналогично, только за исходную передаточную функцию принимается:
а) для построения переходного процесса без компенсатора:
 ; ;
б) для построения переходного процесса с компенсатором:

Результаты расчётов представлены на рис.5.2.
5. Определение показателей качества
.
Переходные характеристики по задающему и возмущающему воздействиям представлены на рисунках 5.1 и 5.2 соответственно.
5.1. Рассмотрим переходную характеристику по управляющему воздействию.
1.Статическое отклонение:
 . .
2.Время регулирования:

3. Перерегулирование:
 . .
4.Степень затухания:

5.2 Для переходной характеристики по возмущающему воздействию без компенсатора.
1.Статическое отклонение:
 . .
2.Время регулирования:

3.Степень затухания:

5.3 Для переходной характеристики по возмущающему воздействию с компенсатором.
1.Статическое отклонение:
 . .
2.Время регулирования:

3.Степень затухания:

Вывод:
Оценив переходные процессы по задающему и возмущающему воздействиям, можно сказать, что рассчитанные параметры регулятора и компенсатора удовлетворяют заданным показателям качества.
Структурная схема САУ с рассчитанными параметрами представлена на рис.5.3.
6. Непосредственное цифровое управление.
Система автоматического регулирования с НЦУ (рис.6.1) содержит объект управления и автоматический регулятор. Роль последнего выполняет ЭВМ, снабжённая рядом устройств, для преобразования сигналов из аналоговой формы в цифровую (АЦП), а также из цифровой формы в аналоговую (ЦАП). На рис.6.1 аналоговые сигналы обозначены как функции времени y(t), g(t), f(t). Соответствующие цифровые сигналы отличаются от них не только формой представления величин, но и дискретным характером изменения во времени. Изменения значений цифровых сигналов производится в моменты времени  где Тд
– интервал дискретности; i = 0, 1, 2, … где Тд
– интервал дискретности; i = 0, 1, 2, …
Цифровые сигналы обозначены на схеме как переменные с индексами y[n], g[n], f[n], причём y[n] = y(nTд
); g[n] = g(nТд
); f[n] = f(nТд
). Интервал дискретности Тд
выбирается из условия: Тд
£ Ти
/ 20, где Ти
– постоянная времени интегрирования непрерывного регулятора. В нашем случае: Тд
= 5,22/20 = 0,26с.
f(t)
f[n]
g(t) g[n] u[n] u(t) y(t)       

y[n]
Рис.6.1.
Структурная схема системы НЦУ.
Алгоритм работы ЭВМ, осуществляющий автоматическое регулирование, может быть получен из уже найденного закона регулирования непрерывного
регулятора [3].
Принимаем за исходный ПИ-закон:
 (6.1) (6.1)
где u1
(t) – регулирующее воздействие на объект; e(t) – сигнал ошибки,
e(t) = g(t) – y(t); Кр
и Ти
– параметры настройки непрерывного ПИ-регулятора.
Замена непрерывных сигналов цифровыми, взятыми в дискретные моменты, может быть проведена по следующей схеме:
e(t) ® e[n]; u1
(t) ® u1
[n]; 
Поэтому ПИ-закон регулирования в цифровой форме имеет вид:
 (6.2) (6.2)
Более удобна для реализации на ЭВМ другая, так называемая скоростная форма этого алгоритма. Для её получения запишем значение u1
на предыдущем интервале дискретности:
 
Вычитая его из предыдущего, получим:

Отсюда:

После подстановки e[n] = g[n] – y[n]; e[n-1] = g[n] – y[n-1] получим:

Подставив значения всех постоянных коэффициентов, получим:
 (6.3) (6.3)
Алгоритм работы ЭВМ, осуществляющий компенсацию возмущающего воздействия, может быть получен на основании передаточной функции компенсатора следующим образом [3].
Пусть, например, сигнал компенсатора u2
(t) подаётся на вход объекта (вместе с сигналом регулирования u1
) и пусть передаточная функция компенсатора:
 . (6.4) . (6.4)
Тогда соответствующее операторное выражение имеет вид:

и в дифференциальной форме записывается в виде:

Переход к цифровым сигналам, взятым в дискретные моменты времени, может быть проведён по следующей схеме:

В результате перехода получим:

Отсюда:
 . .
Подставив значения всех постоянных коэффициентов, получим:

 
 (6.5) (6.5)
Окончательно управляющее воздействие цифрового регулятора с компенсацией возмущений получают суммированием регулирующего u1
(t) и компенсирующего u2
(t) воздействий:
 (6.6) (6.6)
 (6.7) (6.7)
Полученное выражение используется для составления программы НЦУ.
Алгоритм непосредственного цифрового регулирования (рис.6.2), кроме расчёта управляющего воздействия, выполняет следующие дополнительные функции:
1) анализ входных сигналов и вычисленных управляющих сигналов на корректность (на схеме алгоритма – “Анализ”);
2) сигнализация о некорректных значениях и недопустимых отклонениях (на схеме – “Сигнализация”).
Рис.6.2.
Схема алгоритма НЦУ.
7. Список используемой литературы.
1. Теория автоматического управления. Расчёт САУ горного производства с использованием ЭВМ: Метод, указания для студентов спец. 2105 / ЛГИ Сост.: В.И. Златкин, С.В. Стороженко. Л., 1991г. 46 с.
2. Лукас В.А. Основы теории автоматического управления. Л.: Недра, 1977г.376 с.
3. Медведев Р.Б., Бондарь Ю.Д., Романенко В.Д. АСУ в металлургии. М.: Металлургия, 1987г. 253 с.
4. Марюта А.Н., Качан Ю.Г., Бунько В.А. Автоматическое управление технологическими процессами обогатительных фабрик. М.: Недра, 1983г. 248 с.
5. Теория автоматического управления: Программа, методические указания, контрольные задания и задания к курсовой работе / ЛГИ Сост.: В.И. Златкин, С.В. Стороженко. СПб, 1992г. 40 с.
6. Конспект лекций по ТАУ Стороженко С.В.
|