| ЛИПЕЦКИЙ ИНСТИТУТ РАЗВИТИЯ ОБРАЗОВАНИЯ
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА СТ. ДРЯЗГИ
Из опыта работы
«Задачи на процентные вычисления».
Выпускная квалификационная работа
Работу выполнила:
Кобзева Н.Д.
Усмань 2008
Содержание
| Введение………………………………………………………………………
|
3
|
| 1.
|
Изучение процентов в основной школе……………………………………
|
3
|
| 2.
|
Классификация задач на проценты и методы их решения………………..
|
6
|
| Рабочая тетрадь по теме «Задачи на проценты»…………………………...
|
20
|
| Литература……………………………………………………………………
|
29
|
Введение
Теме «Проценты» в математике отводится очень мало времени и места, в результате учащиеся не умеют решать задачи на проценты. Наблюдения действительно показывают, что многие учащиеся испытывают трудности, когда встречаются с понятием процента. Поэтому желательно к этой теме обращаться постоянно, учитывая, что проценты тесно связаны с повседневной жизнью и с ними приходится иметь дело. Ученики не разбираются в вопросах инфляции, ценообразования, банковских вкладах и кредитах.
Кроме того, при поступлении в различные техникумы, колледжи, институты и университеты требуются знания, связанные с процентами. А сейчас при сдаче ЕГЭ нужны знания о процентах, так как задачи на проценты включены в его состав. При подготовке к экзамену по математике учителю предстоит повторить с учащимися процентные вычисления, а что-то придётся объяснить заново. Это очень важная работа, так как учащиеся впервые с процентами знакомились в 5 классе, а среди заданий экзамена есть задачи на процентные вычисления.
В этой работе я хочу поделиться своим опытом подготовки учащихся к сдаче экзамена, а именно повторению темы «Проценты». Ниже изложенный материал может служить помощью учителю, да и самому ученику. Здесь предлагается учебно-методическое пособие «Тетрадь с печатной основой», где находятся задачи на процентные вычисления: сначала к задаче предлагается почти целое решение, затем нужно заполнить пропуски в решении, а затем решить задачу полностью.
1.
Изучение процентов в основной школе.
Тема «Проценты» является одной из самых сложных в школьном курсе математики. К тому же для её изучения отводится очень мало времени. В результате, если ещё в 5-6 классах учащиеся могут решать простейшие задачи на проценты, то к 9-11 классам они забывают самые элементарные понятия темы «Процент» (что такое один процент числа, 100% числа, как перевести процент в десятичную или обыкновенную дроби и наоборот и др.) Такие проблемы, как правило, возникают с отстающими ребятами. Поэтому считаю, что изучению и, особенно, повторению процентов следует уделять больше времени. Может, например, для повторения один раз в неделю или хотя бы один раз в месяц задавать учащимся задачи на проценты в качестве домашнего задания с последующей проверкой их решения; время от времени включать задачи на проценты в контрольные, самостоятельные работы, математические диктанты и т.п.
На начальном этапе изучения этой темы очень важна мотивация. Зачем нам нужны проценты? Для чего нам их нужно изучать и откуда они взялись? Такие вопросы задают себе школьники, впервые знакомясь с процентами. Чтобы ответить на эти вопросы, следует обратиться к истории возникновения процентов.
Проценты были известны индусам ещё в пятом веке нашей эры. В Индии с давних пор вёлся счёт в десятичной системе. В Европе десятичные дроби появились на 1000 лет позже, их ввел бельгийский учёный Симон Стевин. Он же в 1584 году впервые опубликовал таблицу процентов. Введение процентов оказалось удобным для оценки содержания одного вещества в другом. В процентах стали измерять изменения производства товаров, денежный доход… Что только не измеряют в процентах, даже двоечников в школе!
В переводе с латыни «pro centum» - это « на сто». Была придумана и специальная запись 23%, 34%...
Интересно происхождение символа %. Как предполагается, он стал использоваться благодаря опечатке. В рукописях словосочетание «pro centum» часто заменяли словом «cento» - «сто» и писали его сокращенно « ». В 1685 году в Париже была напечатана книга «Руководство по коммерческой арифметике», где по ошибке наборщик в место « ». В 1685 году в Париже была напечатана книга «Руководство по коммерческой арифметике», где по ошибке наборщик в место « » набрал %. » набрал %.
Учитель может сам рассказать ученикам о возникновении процентов, а может и дать доклады и самим ученикам. Сообщения учащихся могут быть более обширными, содержать больше информации. Это вызовет интерес школьников к данной теме. Изучение темы станет более осмысленным. Ребята узнают, что проценты – это не только значок, что они имеют свою историю и тесно связаны с повседневной жизнью. Такой урок не забудется ученикам, а следовательно и то о чём на нём говорилось. При введении процентов, считаю очень важным, чтобы учащиеся поняли, что 1% - это одна сотая часть, а 100% - это 1, то есть вся величина. Затем ребята должны научиться представлять проценты в виде десятичной и обыкновенной дробях и наоборот. Здесь можно предлагать следующие задачи:
1) Представьте в виде десятичной дроби: 12%, 43%, 63%, 87%, 124%, 347% и т.д.
2) Выразите процент обыкновенной дробью и если сокращается сократите: 34%, 58%, 120%, 60%, 100% и т.д.
3) Выразите в процентах:
а) три сотых всех книг библиотеки;
б) восемьдесят сотых всех учащихся школы;
в) шестьдесят сотых всей зарплаты.
При изучении процентов ребятам полезно заполнить следующую таблицу
| Проценты
|
1%
|
2%
|
60%
|
| Десятичные
дроби
|
0,01
|
0,04
|
0,1
|
| Обыкновенные
дроби
|
 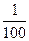
|

|
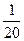
|
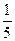
|
Следующие задания помогут ребятам наглядно представить себе проценты.
1.Какая часть заштрихована? Выразите в процентах?
      
2. Сколько процентов круга заштриховано?
2.
3.
При подготовке к экзамену по математике учителю предстоит повторить с учащимися процентные вычисления, а что-то придётся объяснить заново. Это очень важная работа, так как учащиеся впервые с процентами знакомились в 5 классе, а среди заданий экзамена есть задачи на процентные вычисления. Задания, предлагаемые для повторения должны быть расположены в порядке нарастания: от простых к сложным. Для экономии времени следует заранее готовить на доске упражнения и тексты задач, а многие выполнять устно. Устный счёт приучает к рациональным вычислениям, помогает сопоставлять, сравнивать, прикидывать в уме результаты действий. На уроках можно использовать фронтальный опрос, который охватывает большую часть учащихся класса. Можно порекомендовать комментированные упражнения, самостоятельные и групповые задания, тестирование и т.д.
2. Классификация задач на проценты и методы их решения.
Проанализировав методическую литературу и учебники можно выделить следующие виды задач на проценты:
1) задачи на нахождение процентов от числа;
2) задачи на нахождение числа по его процентам;
3) задачи на нахождение процентного отношения;
4) задачи на увеличение и уменьшение числа на несколько процентов;
5) задачи на смеси и сплавы;
6) задачи на вычисление простых и сложных процентов.
1. Задачи на нахождение процентов от числа.
В учебнике Г. В. Дорофеева, И. Ф. Шарыгина «Математика» за
6 класс есть задача: «Зимняя куртка стоит 2500 рублей. На весенней распродаже её можно купить на 33% дешевле. Сколько стоит куртка на распродаже?»
К этой задаче приводится такое решение:
1 способ
1) сначала находится 1% стоимости куртки: 2500:100=25(р.)
2) теперь находится 33% её стоимости: 25*33=825(р.)
2 способ
Можно было рассуждать и иначе: 33% величины – это 33 её сотых доли, т.е 33% выражается в виде дроби 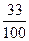 . Чтобы найти . Чтобы найти 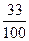 , надо число умножить на дробь: 2500* , надо число умножить на дробь: 2500*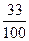 =825(р.). Следовательно, куртка будет стоить 825 рублей. =825(р.). Следовательно, куртка будет стоить 825 рублей.
В учебнике Э. Р. Нурка, А. Э. Тельгмаа
«Математика»
за 6 класс приводится такая задача: «При переработке сахарной свёклы можно получить 13% сахара от всей массы свёклы. Сколько сахара получится из 50 тонн свёклы?».
И ниже в учебнике приводится её решение: для решения задачи нужно найти 13% от числа 50. Выражаем 13% обыкновенной или десятичной дробью: 13%= =0,13. Умножаем данное число на эту дробь: 50* =0,13. Умножаем данное число на эту дробь: 50*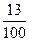 = =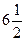 или 50*0,13=6,5. Следовательно, из 50 тонн получится 6,5 тонн сахара. или 50*0,13=6,5. Следовательно, из 50 тонн получится 6,5 тонн сахара.
Здесь, в учебнике, после задачи приводится правило, чтобы найти проценты от данного числа, надо:
1) выразить проценты обыкновенной или десятичной дробью;
2) умножить данное число на эту дробь.
Для прочного усвоения метода решения задач данного вида можно да и нужно дать ученикам ряд задач:
1. В 6 «б» классе 35 учеников, а в 6 «а» - 80% этого количества. Сколько учеников в 6 «а» классе?
2. Тело человека содержит примерно 64% воды. Сколько килограммов воды в человеке массой 60 кг?
3. При сушке яблоки теряют 91% своей массы. Сколько килограммов сушёных яблок получится из 160 кг свежих?
4. По плану токарь должен изготовить 400 деталей за день. Он выполнил план на 110%. Сколько деталей он изготовил?
5. Луч, проведённый из вершины прямого угла, делит его на два угла. Один из них составляет 65% прямого угла. Вычислите градусные меры этих углов.
6. Сберегательный банк начисляет на каждый вклад 123% в год. Сколько денег будет на счету через год, если на нём было 100 тыс.р.?
2. Задачи на нахождение числа по его процентам.
Возьмём задачу из учебника Э. Р. Нурка, А. Э. Тельгмаа: «За контрольную работу по математике оценку «4» получили 9 человек. Это составляет 36% от всех учащихся класса. Сколько учащихся в классе?».
Разбирается решение: при решении задачи нужно найти такое число 36% которого равны 9; для этого выразим проценты обыкновенной или десятичной дробью: 36%=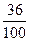 =0,36. Далее поступим по правилу нахождения числа по его дроби, т.е. разделим число на дробь: =0,36. Далее поступим по правилу нахождения числа по его дроби, т.е. разделим число на дробь: 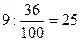 или 9:0,36=25. Значит, в классе 25 учеников. или 9:0,36=25. Значит, в классе 25 учеников.
После этой задачи ниже приводится правило, чтобы найти число по его процентам, нужно:
1) выразить проценты обыкновенной или десятичной дробью;
2) разделить данное число на эту дробь.
Для прочного усвоения метода решения задач данного вида нужно дать ученикам ряд задач:
1. 8 учеников, что составляет 25% учащихся класса, за контрольную работу получили оценку «5». Сколько учащихся в классе?
2. В коробке лежали лампочки, 4 из которых оказались разбитыми. Разбитые лампочки составляют 2% от числа всех лампочек. Сколько всего лампочек было в коробке?
3. В школе 125 учеников учатся на «5». Это составляет 5% всех учеников школы. Сколько учеников в школе?
4. Кладовщик выдал маляру 18% количества всей краски, после чего на складе ещё осталось 492 кг. Сколько килограммов краски выдали маляру?
5. Мужчины на заводе составляют 75% всего количества рабочих. Женщин на заводе 216. Сколько мужчин работает на заводе?
6. Товар вместе с упаковкой стоит 40,8р.Стоимость упаковки составляет 2% стоимости товара. Сколько стоит товар без упаковки?
3.Задачи на нахождение процентного отношения.
Рассмотрим решения задач данного вида.
Задача №1.
Каково процентное содержание меди в руде, если на 225 кг руды приходится 34,2 кг меди?
Решение.
1 способ.
Содержание меди в руде составляет дробь: 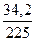 .
Обратим данную дробь в десятичную .
Обратим данную дробь в десятичную 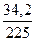 =0,152. Умножаем получившуюся дробь на 100% и находим процентное содержание 0,152*100%=15,2%. =0,152. Умножаем получившуюся дробь на 100% и находим процентное содержание 0,152*100%=15,2%.
Ответ:15,2%.
2 способ.
Руда 225 кг - 100%
Медь 34,2 кг - ? %
 =15,2% =15,2%
Следовательно, получается правило: чтобы найти процентное отношение первого числа от второго (и обратно), нужно найти отношение первого ко второму (и обратно) и полученное отношение умножить на 100%.
Возьмём задачу из учебника Э.Р.Нурка, А.Э.Тельгмаа.
Задача №2.
До снижения цен книга стоила 250 р., после снижения она стала стоить 230 р. На сколько процентов понизилась цена?
Решение.
Для решения задачи узнаем сначала, на сколько рублей изменилась цена книги:
1) 250-230=20 (р.) Теперь найдём, сколько процентов составляет полученная разность:
2)  *100%=0,08*100%=8%. *100%=0,08*100%=8%.
Значит, стоимость книги понизилась на 8%.
Ответ: на 8%.
Для прочного усвоения метода решения задач данного вида нужно дать ученикам ряд задач:
1. Колхоз планировал получить с 1 га в среднем 29 ц зерновых, а получил – 32 ц. На сколько процентов колхоз перевыполнил план? На сколько процентов выполнил план?
2. Среди жителей села 350 человек имеют право участвовать в голосовании. На избирательный участок в день выборов пришло 189 человек. Какой процент избирателей принял участие в голосовании?
3. Из 2150 телевизоров, выпущенных за месяц на заводе А, в первый же год потребовали ремонта 48 штук, а из 725 телевизоров, сделанных на заводе В, в первый год ремонт потребовали 31 телевизор. На каком заводе процент некачественных телевизоров выше?
4. На соревнования спортсмены завоевали 96 медалей, из них 35 медалей бронзовые и 31 медаль серебряная. Сколько процентов от общего числа составили золотые медали?
5. Число дождливых дней в июне обычно равно 12. Сколько процентов не дождливых дней в июне?
6. Из 30000 жителей города 6900 – дети. Какой процент всего населения составляют дети?
4.
Задачи на увеличение и уменьшение числа на несколько процентов.
Задача №1.
Товар стоимостью 250 рублей уценён на 10%. Определите новую стоимость товара.
Решение.
Данную задачу можно решить двумя способами:
1 способ.
Сначала находим на сколько рублей уценили товар , для этого находим сначала 1 %:
1) 250:100=2,5 (р.) – в одном проценте. Далее уже находим 10% уценки:
2) 2,5*10=25 (р.) – на столько уценили товар. А теперь находим новую цену:
3) 3) 250-25=225 (р.) – новая цена.
2 способ.
Сначала находим сколько процентов стал стоить товар:
1) 100% - 10%=90% - стал стоить товар. Далее находим сколько рублей приходится на 1%.
2) 250:100=2,5 (р.) – на 1%. Теперь узнаем новую цену товара:
3) 90*2,5=225 (р.) – новая цена.
Ответ: 225 рублей.
Задача №2.
Цена товара повысилась на 20% , а затем ещё на 50%. На сколько процентов повысилась цена по сравнению с первоначальной ценой?
Решение.
Первоначальную цену примем за 100%. После первого повышения цена стала равна:
1) 100%+20%=120% . Второе повышение происходит от новой цены, то есть:  =60%. =60%.
Ответ: на 60%.
Для прочного усвоения метода решения задач данного вида нужно дать ученикам ряд задач:
1. В магазине книга стоит 50 руб. Определите её новую цену, если стоимость книги увеличилась на 120%.
2. Цену товара увеличили на 10 %. Какова цена товара?
3. Флеш-карта стоит 500 рублей. Сначала цена уменьшилась на 20 %, а затем увеличилась на 10%. Сколько стала стоить флеш-карта?
4. Весной цена товара была повышена на 10 % , а осенью – ещё на 5%. Сколько стал стоить товар, если его первоначальная стоимость была 300 руб.?
5. Цену на калькулятор сначала повысили на 25% , а потом ещё на 65% . Во сколько раз увеличилась цена на калькулятор?
5.Задачи на смеси и сплавы.
Задача №1.
Для проведения опыта научный сотрудник химической лаборатории смешал 4% раствор некоторого химического вещества и 10% раствора этого же вещества и получил 75 мл. 8% раствора . сколько миллилитров 4% раствора и сколько 10% раствора было взято.
Решение.
Обозначим через x – количество 4% раствора, а через y – количество 10% раствора. Запишем первое уравнение системы, т.к. должно получится 75 мл. раствора: x + y=75.
Второе уравнение системы связывает количество соли в 4%, 10% и получившимся растворах: 0,04x + 0,1y =0,08(x+y).
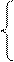 Решим получившуюся систему уравнений: Решим получившуюся систему уравнений:
x+y=75,
0,04x+0.1y=0,08(x+y);
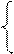 x=25, x=25,
y=50.
Значит, 25 мл взяли 4% раствора и 50 мл 10% раствора.
Ответ: 25 мл; 50 мл.
Задача №2.
Кусок сплава золота и серебра весом 3 кг содержит 30% золота. Сколько кг чистого золота нужно прибавить к этому куску, чтобы получившийся новый сплав содержал 40% золота?
Решение.
Пусть добавили x кг чистого золота; 3*0,3=0,9(кг) – чистого золота было в сплаве. Всего чистого золота стало (x+0,9) кг, а сплав массой 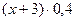 (кг) – чистого золота. Составим и решим уравнение:
(кг) – чистого золота. Составим и решим уравнение:  ,
x=0,5, т. е. 0,5 (кг) – надо добавить чистого золота. ,
x=0,5, т. е. 0,5 (кг) – надо добавить чистого золота.
Ответ: 0,5 кг.
Данный вид задач представляет собой сложный вид, т.к. эти задачи учащиеся решают очень плохо. Думаю, что после объяснения решения таких задач целесообразно прорешать аналогичные как индивидуально, так и со всеми вместе.
1. До какого веса надо выпарить 800 г 10% раствора соли, чтобы довести её содержание до 16%?
2. На складе имеются две ёмкости с 5% и 25% содержанием уксуса. Сколько надо взять литров из каждой ёмкости, чтобы получить 80 литров 10% уксуса?
3. Сколько килограммов пресной воды надо прибавить к 80 кг морской воды, содержащей 5% соли ( по массе), чтобы содержание соли стало 2%?
4. Кусок сплава меди и цинка массой 36 кг содержит 455 меди. Какую массу меди нужно добавить к этому куску, чтобы полученный сплав содержал 60% меди?
5. В сплав входит медь, олово и сурьма в отношении 4:15:6. Сколько процентов сплава составляет каждый металл?
6. Задачи на вычисление простых и сложных процентов.
Тема «Проценты», как было уже сказано выше, связана с повседневной жизнью. Мы часто сталкиваемся с банковскими операциями: различные вклады, ссуды. Между тем, многие ребята, да и мы взрослые, при столкновении с этими задачами боимся их, потому что не умеем их решать. В учебниках не вводятся формулы простых и сложных процентов. Учащиеся должны решать задачи, опираясь не на формулы, а на понимание, на смысл понятия «процент», на умение находить процент от числа, число по его проценту. Вообще, данный вид задач применяется во многих областях хозяйственной деятельности и бухгалтерского учёта, а также в различных статистических расчётах, где используются формулы простых и сложных процентов.
Для нахождения простых процентов служит формула простых процентов: если с величины «а» нарастает «р»% за год (или другой период), то через t лет, полученную сумму можно получить по формуле:
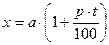 . .
При этом предполагается, что по истечении каждого года доход за этот год исчисляется с первоначальной величины.
Если же доход причисляют к первоначальной величине и, следовательно, доход за новый год исчисляется с наращенной суммы, то говорят о сложных процентах; в этом случае величина, в которую превращается «а» через t лет вычисляется по формуле сложных процентов:
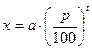 . .
Задача №1.
Клиент положил в банк на год 4000 рублей. Какая сумма у него будет через год, если банк выплачивает 8% годовых?
Решение.
Данную задачу можно решить двумя способами.
1 способ.
Сначала находим сколько рублей приходится на 1%:
1) 4000:100=40 ( р.) – на 1%.
Далее находим, сколько рублей будет составлять 8%:
2) 40*8=320 (р.) – на 8%.
А теперь найдём, какая сумма получится в конце года:
3) 4000+320=4320 (р.) – получилась сумма к концу года.
2 способ.
Сначала находим, сколько процентов будет в конце года:
1) 100+8=108% - к концу года.
Находим, сколько приходится на 1%:
2) 4000:100=40 (р.) – на 1%.
А теперь найдём нужную нам сумму:
3) 40*108=4320 (р.) – сумма в конце года.
Ответ: 4320 рублей.
Задача №2.
Владелец садового участка взял в банке ссуду 300000 рублей для постройки дома на участке. Он должен был вернуть эти деньги через год с надбавкой 9%. Какую сумму он должен был вернуть?
Решение.
1) 100+9=109% - должен вернуть в банк владелец.
109:100*300000=327000 (р.) – должен вернуть.
Ответ: 327000 рублей.
Задача №3.
Ирина внесла в январе 100 рублей на счёт, по которому ежемесячно начисляется 2%. И затем каждый месяц в течение года она вносила ещё по 100 рублей, не снимая с него никаких сумм. Сколько рублей на её счете будет в конце декабря?
Решение.
Выразим процент десятичной дробью: 2% - 0,02. Вклад ежемесячно увеличивается в 1,02 раза и идёт последовательное накопление вклада:
январь – 100 р;
февраль – 100*1,02+100 р;
март – 100*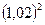 +100*1,02+100 р; +100*1,02+100 р;
………………………………………
декабрь – 100*(1,02) +100*(1,02) +100*(1,02)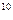 +……..+100=100*((1,02) +……..+100=100*((1,02) + (1,02) + (1,02)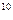 + +1) =100* + +1) =100* =1341(р.) =1341(р.)
Ответ: 1341 рубль.
В ходе решения подобных задач учащиеся видят, что формула суммы геометрической прогрессии – это не просто абстракция, отвлечённая формула, а конкретные математическое знание, необходимое в жизни.
Задача №4.
Вклад, положенный в сбербанк два года назад, достиг 1312500 р. Каков был первоначальный вклад при 25% годовых?
Решение.
Пусть x (р.) – первоначальный размер вклада. В конце первого года вклад составит:
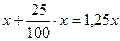 (р.)
(р.)
1,25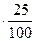 (р.) – на столько увеличился вклад к концу второго года по сравнению с первым; (р.) – на столько увеличился вклад к концу второго года по сравнению с первым;
 (р.) – таким станет вклад к концу второго года, т.е. составит по условию 1312500 р. Имеем: (р.) – таким станет вклад к концу второго года, т.е. составит по условию 1312500 р. Имеем:  , откуда , откуда 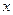 =840000. Значит 840000 (р.) – первоначальный вклад. =840000. Значит 840000 (р.) – первоначальный вклад.
Ответ: 840000 рублей.
Как было уже выше написано, что вычисление процентов необходимо в банковских расчётах. Например, есть такие вклады в банках, как вклад «Сберегательный сбербанка России»:
на 1 месяц – 5%,
на 2 месяца и 1 день – 5%,
на 3 месяца и 1 день – 7%,
на 6 месяцев– 9%,
на 1 год – 11 %;
по которым процентные начисления как в предыдущей задаче.
Очень трудно вычисляются проценты при взятии клиентом ссуды в банке на несколько лет.
Задача.
Клиент берёт ссуду в размере 10000 рублей на 5 лет при 19% годовых. Сколько ему нужно будет платить ежемесячно, если он взял ссуду в октябре?
Решение.
При выплачивании ссуды клиент начинает платить, т.е. делать первое погашение через 2 месяца. Ниже приведена таблица погашения данной ссуды.
| Дата операции
|
Ежемесячный платёж
|
Платёж %%
|
Всего платёж
|
Остаток после платежа
|
| 31.12.2003
|
198
|
432.05
|
630.05
|
9802
|
| 31.01.2004
|
169
|
157.74
|
326.74
|
9633
|
| 29.02.2004
|
169
|
145.02
|
314.02
|
9464
|
| 31.03. 2004
|
169
|
152.3
|
321.30
|
9295
|
| 30.04. 2004
|
169
|
144.76
|
313.76
|
9126
|
| 31.05.2004
|
169
|
146.86
|
315.86
|
8957
|
| 30.06.2004
|
169
|
139.49
|
308.49
|
8788
|
| 31.07.2004
|
169
|
141.42
|
310.42
|
8619
|
| 31.08.2004
|
169
|
138.7
|
307.70
|
8450
|
| 30.09.2004
|
169
|
131.6
|
300.6
|
8281
|
| 31.10.2004
|
169
|
133.27
|
302.27
|
8112
|
| 30.11. 2004
|
169
|
126.33
|
295.33
|
7943
|
| 31.12. 2004
|
169
|
127.83
|
296.83
|
7774
|
| 31.01.2005
|
169
|
125.45
|
294.45
|
7605
|
| 28.02.2005
|
169
|
110.85
|
279.85
|
7436
|
| 31.03.2005
|
169
|
119.99
|
288.99
|
7267
|
| 30.04.2005
|
169
|
113.48
|
282.48
|
7098
|
| 31.05.2005
|
169
|
114.54
|
283.54
|
6929
|
| 30.06.2005
|
169
|
108.21
|
277.21
|
6760
|
| 31.07.2005
|
169
|
109.09
|
278.09
|
6591
|
| 31.08.2005
|
169
|
196.36
|
275.36
|
6422
|
| 30.09.2005
|
169
|
100.29
|
269.29
|
6253
|
| 30.10.2005
|
169
|
100.9
|
269.9
|
6084
|
| 30.11.2005
|
169
|
95.01
|
264.01
|
5915
|
| 31.12.2005
|
169
|
95.45
|
264.45
|
5746
|
| 31.01.2006
|
169
|
92.72
|
261.72
|
5577
|
| 28.02.2006
|
169
|
81.25
|
250.29
|
5408
|
| 31.03.2006
|
169
|
87.27
|
256.27
|
5239
|
| 30.04.2006
|
169
|
81.81
|
250.81
|
5070
|
| 31.05.2006
|
169
|
81.81
|
250.81
|
4901
|
| 30.06.2006
|
169
|
76.54
|
245.54
|
4732
|
| 31.07.2006
|
169
|
76.36
|
245.36
|
4563
|
| 31.08.2006
|
169
|
73.63
|
242.63
|
4394
|
| 30.09.2006
|
169
|
68.62
|
237.62
|
4225
|
| 30.10.2006
|
169
|
68.18
|
237.18
|
4056
|
| 30.11.2006
|
169
|
63.34
|
232.34
|
3887
|
| 31.12.2006
|
169
|
62.72
|
231.72
|
3718
|
| 31.01.2007
|
169
|
60
|
229
|
3549
|
| 28.02.2007
|
169
|
51.73
|
220.73
|
3380
|
| 31.03.2007
|
169
|
54.54
|
223.54
|
3211
|
| 30.04.2007
|
169
|
50.14
|
219.14
|
3042
|
| 31.05.2007
|
169
|
49.09
|
218.09
|
2873
|
| 30.06.2007
|
169
|
44.87
|
213.87
|
2704
|
| 31.07.2007
|
169
|
43.63
|
212.63
|
2535
|
| 31.08.2007
|
169
|
40.91
|
209.91
|
2366
|
| 30.09.2007
|
169
|
36.95
|
205.95
|
2197
|
| 30.10.2007
|
169
|
35.45
|
204.45
|
2028
|
| 30.11.2007
|
169
|
31.67
|
200.67
|
1859
|
| 31.12.2007
|
169
|
30
|
199
|
1690
|
| 31.01.2008
|
169
|
27.2
|
196.2
|
1521
|
| 28.02.2008
|
169
|
22.9
|
191.9
|
1352
|
| 31.03.2008
|
169
|
21.76
|
190.76
|
1183
|
| 30.04.2008
|
169
|
18.42
|
187.42
|
1014
|
| 31.05.2008
|
169
|
16.32
|
185.32
|
845
|
| 30.06.2008
|
169
|
13.16
|
182.16
|
676
|
| 31.07.2008
|
169
|
10.88
|
179.88
|
507
|
| 31.08.2008
|
169
|
8.16
|
177.16
|
338
|
| 30.09.2008
|
169
|
5.26.
|
176.02
|
287
|
| 30.10.2008
|
169
|
2.08
|
174.26
|
169
|
| 09.10.2008
|
169
|
0.79
|
169.79
|
0
|
| Итого
|
10000
|
5005.11
|
15005.11
|
Нижеприведённые задачи можно будет использовать при индивидуальной работе с сильными учащимися, а также на факультативах по математике.
1. Сбербанк выплачивает вкладчикам 6% годовых. Сколько выплатил сбербанк дополнительно к вкладу, если вклад составил:
а) 200000 р. в) 1000000 р.
б) 300000 р. г) 4000000 р.?
2. Клиент положил в банк вклад из расчёта 3% годовых. Какой доход в процентах принесёт вклад через 4 года?
3.Банк начисляет ежегодно 5% от суммы вклада. Найти наименьшее число лет, за которое вклад вырастет более чем на 10%?
4.Через сколько лет остаток вклада под 100% годовых превзойдёт 2400 р., стартовая сумма 1000 р. и если вкладчик берёт 900 р. в конце каждого года?
5. В банк положен вклад из расчёта 10% годовых. Через два года со счёта была снята сумма, составляющая 21% от суммы первоначального вклада. Через какое наименьшее число лет после этого сумма вклада больше первоначальной в 1,4 раза?
Рабочая тетрадь по теме
«Задачи на проценты».
Данное учебно-методическое пособие является дополнительным материалом для подготовки учащихся 11 классов к сдаче ЕГЭ по математике и может быть использована учителем на уроках или дополнительных занятиях по математике.
Цель данного учебного пособия состоит в том, чтобы помочь учителю подготовить учеников к экзамену. Ведь на изучение процентов отводится очень мало времени, а к 11 классу они забывают, как решать самые элементарные задачи на проценты, не говоря уже о сложных.
В данном пособии предлагаются задачи разных видов на процентные вычисления. К каждому виду задач предлагается сначала просмотреть, практически решённую задачу, затем вставить пропуски в решении задачи, а потом полностью самому её решить.
Думаю, что многих заинтересует данное пособие и они будут использовать его на своих уроках, а может разработают аналогичное по другой теме.
I
.
Задачи на нахождение процентов от числа.
Задача №1.
В школе 425 учащихся, 56% из них девочки. Сколько девочек в школе?
Решение.
1) 56%=0,56
2) 425*0,56=-------(д.)
Ответ:-------- девочек.
Задача №2.
В классе 30 учащихся, 80% из них хорошисты. Сколько хорошистов в классе?
Решение.
1) 80%=-------
2) 30*------=-------(уч.)
Ответ: ---------
Задача №3.
Тело человека содержит 64% воды. Сколько килограммов воды в человеческом теле, если он весит 80 килограмм?
Решение.
1)--------------------
2)--------------------
Ответ:-----------
4. В 6 «б» классе 35 учеников, а в 6 «а» - 80% этого количества. Сколько учеников в 6 «а» классе?
5.Тело человека содержит примерно 64% воды. Сколько килограммов воды в человеке массой 60 кг?
6. При сушке яблоки теряют 91% своей массы. Сколько килограммов сушёных яблок получится из 160 кг свежих?
7. По плану токарь должен изготовить 400 деталей за день. Он выполнил план на 110%. Сколько деталей он изготовил?
8. Луч, проведённый из вершины прямого угла делит его на два угла. Один из них составляет 65% прямого угла. Вычислите градусные меры этих углов.
9. Сберегательный банк начисляет на каждый вклад 123% в год. Сколько денег будет на счету через год, если на нём было 100 тыс.р.?
II
. Задачи на нахождение числа по его процентам.
Задача №1.
8 учеников, что составляет 20% учащихся класса, за контрольную работу получили оценку «52. Сколько учащихся в классе?
Решение.
1) 20%=
2) 8:  =-------(уч.) =-------(уч.)
Ответ: -------учеников.
Задача №2.
В посёлке 1650 квартир имеют центральное отопление. Это составляет 55% всех квартир в посёлке. Сколько квартир в посёлке?
Решение.
1) 55%=-------
2) 1650:-------=---------(к.)
Ответ:--------- квартир.
Задача №3.
Масса крови взрослого человека составляет в среднем 7,5% от его общей массы. Сколько крови у человека, если его масса 72 килограмма?
Решение.
1)----------------------
2)----------------------
Ответ:----------------
4. 6 учеников, что составляет 25% учащихся класса, за контрольную работу получили оценку «5». Сколько учащихся в классе?
5. В коробке лежали лампочки, 4 из которых оказались разбитыми. Разбитые лампочки составляют 2% от числа всех лампочек. Сколько всего лампочек было в коробке?
6. В школе 125 учеников учатся на «5». Это составляет 5% всех учеников школы. Сколько учеников в школе?
7. Кладовщик выдал маляру 18% количества всей краски, после чего на складе ещё осталось 492 кг. Сколько килограммов краски выдали маляру?
8. Мужчины на заводе составляют 75% всего количества рабочих. Женщин на заводе 216. Сколько мужчин работает на заводе?
9. Товар вместе с упаковкой стоит 40,8р. Стоимость упаковки составляет 2% стоимости товара. Сколько стоит товар без упаковки?
III
. Задачи на нахождение процентного отношения.
Задача №1.
Каково процентное отношение золота в серебре, если на 100 г серебра приходится 21 г золота?
Решение.
Содержание золота в серебре составляет: 
Находим процентное отношение:
 *100%=--------- *100%=---------
Ответ:---------
Задача №2.
На выборы на избирательный участок пришло 654 человека из 963 человек, живших на данном участке. Какой процент избирателей приняло участие в выборах?
Решение.
Часть избирателей, пришедших на голосование выражается дробью:---------
Обращаем эту дробь в десятичную: -----------
Находим процентное отношение:
--------*100%=-----------%
Ответ:------------
Задача №3.
Число морозных дней в декабре обычно равно 21. Сколько процентов не морозных дней в декабре?
Решение.
1)-----------------
2)-----------------
Ответ: -----------
4. Колхоз планировал получить с 1 га в среднем 29 ц зерновых, а получил – 32 ц. На сколько процентов колхоз перевыполнил план? На сколько процентов выполнил план?
5. Среди жителей села 350 человек имеют право участвовать в голосовании. На избирательный участок в день выборов пришло 189 человек. Какой процент избирателей принял участие в голосовании?
6. Из 2150 телевизоров, выпущенных за месяц на заводе А, в первый же год потребовали ремонта 48 штук, а из 725 телевизоров, сделанных на заводе В, в первый год ремонт потребовали 31 телевизор. На каком заводе процент некачественных телевизоров выше?
7. На соревнования спортсмены завоевали 96 медалей, из них 35 медалей бронзовые и 31 медаль серебряная. Сколько процентов от общего числа составили золотые медали?
8. Число дождливых дней в июне обычно равно 12. Сколько процентов не дождливых дней в июне?
9. Из 30000 жителей города 6900 – дети. Какой процент всего населения составляют дети?
IV
. Задачи на увеличение и уменьшение числа на несколько процентов.
Задача №1.
Книга стоила 120 рублей. В связи с инфляцией книга стала стоить на 15% дороже. Сколько стала стоить книга?
Решение.
1)120:100=1,2 (р.) – на 1%.
2)1,2*15=-------(р.) – стоит книга.
Ответ:---------- рублей.
Задача №2.
Под кукурузу отвели участок в форме прямоугольника. Через некоторое время длину увеличили на 35%, а ширину на 14% уменьшили. На сколько процентов изменилась площадь?
Решение.
Пусть x – длина, y – ширина, тогда площадь x*y. После изменения длины, она стала – 1,35x, а после изменения ширины, она стала - ----------.
Площадь нового участка стала равна 1,35x*0,86y=----------
-------- - xy=0,161xy
0,161*100%= --------
Ответ:----------
Задача №3.
На ковёр цену повысили на 10%, а потом ещё на 15%. На сколько больше стал стоить ковёр?
Решение.
1)---------------
2)---------------
3----------------
Ответ:----------------
4. В магазине книга стоит 50 руб. Определите её новую цену, если стоимость книги увеличилась на 120%.
5. Цену товара увеличили на 10 %. Какова цена товара?
6. Флеш-карта стоит 500 рублей. Сначала цена уменьшилась на 20 %, а затем увеличилась на 10%. Сколько стала стоить флеш-карта?
7. Весной цена товара была повышена на 10 % , а осенью – ещё на 5%. Сколько стал стоить товар, если его первоначальная стоимость была 300 руб.?
8. Цену на калькулятор сначала повысили на 25% , а потом ещё на 65% . Во сколько раз увеличилась цена на калькулятор?
V
. Задачи на смеси и сплавы.
Задача №1.
Слиток серебра с цинком весом в 3,5 кг содержал 75% серебра. Его сплавили с другим слитком и получили вес 10,5 кг, содержание серебра в котором 84%. Сколько процентов серебра содержалось во втором слитке?
Решение.
1) 3,*0,75=2,66 (кг) – серебра в первом слитке.
2) 10,5*0,84=--------(кг) – в 10,5 кг сплава.
3) --------- - 2,66 =6,16 (кг) – серебра во втором слитке.
4) 10,5 – 3,5= 7 (кг) – вес второго слитка.
5) 6,16:------=0,88=--------% - во втором слитке серебра.
Ответ:--------%
Задача №2.
Один раствор содержит 30% по объёму азотной кислоты, а второй – 55% азотной кислоты. Сколько нужно взять первого и второго раствора, чтобы получить 100 литров 50% раствора азотной кислоты?
Решение.
Обозначим через x – количество 30% раствора, а через y – 55% раствора.
Составим первое уравнение:
-----------------------------
Второе уравнение связываем с процентным содержанием азотной кислоты:
0,3x+0,55y=0,5(x+y)
Составим и решим систему уравнений:
----------------------------
----------------------------
----------------------------
----------------------------
----------------------------
Ответ: ----------------
Задача №3.
Смешали 30% раствор соляной кислоты с 10% и получили 600 г 15% раствора. Сколько граммов каждого раствора было взято?
Решение.
-------------------------
-------------------------
-------------------------
-------------------------
Ответ:---------------------
4. До какого веса надо выпарить 800 г 10% раствора соли, чтобы довести её содержание до 16%?
5. На складе имеются две ёмкости с 5% и 25% содержанием уксуса. Сколько надо взять литров из каждой ёмкости, чтобы получить 80 литров 10% уксуса?
6. Сколько килограммов пресной воды надо прибавить к 80 кг морской воды, содержащей 5% соли ( по массе), чтобы содержание соли стало 2%?
7. Кусок сплава меди и цинка массой 36 кг содержит 455 меди. Какую массу меди нужно добавить к этому куску, чтобы полученный сплав содержал 60% меди?
8. В сплав входит медь, олово и сурьма в отношении 4:15:6. Сколько процентов сплава составляет каждый металл?
VI
. Задачи на вычисление простых и сложных процентов.
Задача №1.
Получив премию, сотрудник фирмы положил её на счёт с доходом 8%. Если бы банк выплачивал 11% годовых, то для получения такого же дохода потребовалось бы на 900 рублей меньше. Определите сколько рублей составляла премия?
Решение.
Пусть x руб. сумма, которая составила премию, тогда 0,08x руб. – было бы на вкладе. Если бы выплачивались 11% годовых на сумму-------------, то доход составил бы 0,11*--------------, что равно 0,08x рублей.
0,11*-----------=0,08x
11*------------ 8x
--------------------
x=----------------
Ответ: 3300 рублей.
Задача №2.
Сбербанк выплачивает вкладчикам 9% годовых, Сколько выплатил Сбербанк дополнительно к вкладу 250000 р.?
Решение.
1)-----------------
2)-----------------
Задача №3.
Вкладчик взял из Сбербанка 25% своих денег, потом 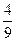 оставшихся и ещё 64000 руб. После этого у него осталось 15% всех денег. Как велик вклад? оставшихся и ещё 64000 руб. После этого у него осталось 15% всех денег. Как велик вклад?
Решение.
1)---------------
2)---------------
Ответ:---------------
4. Сбербанк выплачивает вкладчикам 6% годовых. Сколько выплатил сбербанк дополнительно к вкладу, если вклад составил:
а) 200000 р. в) 1000000 р.
б) 300000 р. г) 4000000 р
5. Клиент положил в банк вклад из расчёта 3% годовых. Какой доход в процентах принесёт вклад через 4 года?
6. Банк начисляет ежегодно 5% от суммы вклада. Найти наименьшее число лет, за которое вклад вырастет более чем на 10%?
7. Через сколько лет остаток вклада под 100% годовых превзойдёт 2400 р., стартовая сумма 1000 р. и если вкладчик берёт 900 р. в конце каждого года?
8. В банк положен вклад из расчёта 10% годовых. Через два года со счёта была снята сумма, составляющая 21% от суммы первоначального вклада. Через какое наименьшее число лет после этого сумма вклада больше первоначального в 1,4 раза?
Литература:
1. Дорофеев Г.В., Кузнецова Л.В., Минаева С.С., Суворова С.Б.. Изучение процентов в основной школе / Математика в школе. - №1, 2002.
2. Дорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и др. Математика, 6 класс. – М.: Дрофа, 2008.
3. Ивлев Б.М., Саакян С.М., Шварцбурд С.И. «Дидактические материалы по алгебре и началам анализа для 11 класса». – М.: Просвещение, 2005.
4. Канашева Н.А. О решении задач на проценты/ Математика в школе. - №5, 1995.
5. Нагорнова А.В. Изучаем проценты/ Математика в школе. - №26, 2000.
6.Нурк Э.Р., Тельгмаа А.Э. Математика, 6 класс. – М.: Просвещение, 2000.
7. Петров В. Коварные проценты. // Квант. - №3, 1999г.
8. Райхмист Р. Б. Задачник по математике. – М.: Московский лицей.2002.
9. Математика. ЕГЭ – 2007. Учебно-тренировочные тесты/ под редакцией Ф.Ф. Лысенко. Ростов-на-Дону: Легион, 2007.
10. Единый государственный экзамен 2007. Математика. Учебно-тренировочные материалы для подготовки учащихся / ФИПИ авторы-составители: Л.О.Денищева, Ю.А.Глазков, К.А.Краснянская, А.Р. Рязановский, П.В. Семенов – М.: Интеллект-Центр, 2007.
|