| Московский Государственный Университет Путей Сообщения (МИИТ)
Кафедра «Управление и информатика в технических системах»
Курсовая работа на тему:
Расчет оценок показателей достоверности приема дискретной информации. Проектирование кодера и декодера БЧХ-кода.
Студент:
Группа: ВУИ-411
Вариант №4
(Задание №1
Определение вероятности ошибки на символ)
Москва 2006
Реферат
В курсовой работе использовались следующие понятия:
ВЕРОЯТНОСТЬ ОШИБКИ НА СИМВОЛ, ПОРОГ, СОГНАЛ, ПОМЕХА, ЛОГИЧЕСКАЯ ЕДИНИЦА, ЛОГИЧЕСКИЙ НОЛЬ, ДИСПЕРСИЯ ПОМЕХИ, ВЕРОЯТНОСТЬ ТРАНСФОРМАЦИИ, ВЕРОЯТНОСТЬ ПОДАВЛЕНИЯ, ВЕРОЯТНОСТЬ ПРАВИЛЬНОГО ПРИЕМА, КОД, КОДОВАЯ КОМБИНАЦИЯ, ТРАНСФОРМАЦИЯ КОДОВОЙ КОМБИНАЦИИ, МИНИМАЛЬНОЕ КОДОВОЕ РАССТОЯНИЕ, ПРИЕМНИК, ПЕРЕДАТЧИК, КОДЕР, ДЕКОДЕР, ФУНКЦИОНАЛЬНАЯ СХЕМА.
Определена вероятность ошибки на символ, оценены вероятность трансформации кодовой комбинации, вероятность подавления и вероятность правильного приема разрабатываемого кода, рассчитана вероятность правильного приема, рассчитано минимальное кодовое расстояние, выбран систематический циклический БЧХ код, обеспечивающий заданную величину вероятности трансформации кодовой комбинации при условии, что детектор работает только в режиме обнаружения ошибок, рассмотрен алгоритм работы данного кода, по которому в дальнейшем построены блок-схемы кодера и декодера систематического циклического кода, построены функциональные схемы кодера определенного нами кода и схемы обнаружения ошибок.
Содержание:
1.
Исходные данные и задание на курсовую работу………………………..4
2.
Введение…………………………………………………………………… 5
3.
Определение вероятности ошибки на символ……………………………6
4.
Оценки вероятности трансформации кодовой комбинации Ртр
, вероятности подавления Рпод
и вероятности правильного приема Рпр
….9
5.
Расчет вероятности правильного приема………………………………..10
6.
Расчет
dmin
– минимального кодового расстояния. Расчет оценок Ртр
, Рпод
, Рпр
……………………………………………………………………..11
7.
Выбор БЧХ кода…………………………………………………………..12
8.
Алгоритм работы кодера БЧХ кода……………………………………...13
9.
Кодер систематического циклического кода……………………………15
10.
Схема обнаружения ошибки……………………………………………..18
11.
Заключение………………………………………………………………
..20
Список использованной литературы………………………………………
..20
Исходные данные для выполнения курсовой работы.
- На входе порогового устройства приемника сигнал S0
и аддитивная гауссова помеха ξ.
- Отношение мощности сигнала
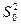 к мощности помехи к мощности помехи  = =
- Логическая «1» соответствует S0
, логический «0» соответствует 0.
- Уровень порогового устройства
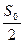 . .
- Структура передаваемых данных такова, что вероятность передачи «1» - P(1) и вероятность передачи «0» - P(0), равны, т.е. P(1)=P(0)=0,5.
- Допустимая вероятность трансформации равна Pтр
.
- Разрядность кода равна n.
таблица данных для расчета
| Вар.
|
№4
|
| λ
|
60
|
| Pтр
|
10-11
|
| n
|
31
|
Задание
1. Определить вероятность ошибки на символ Рош
.
2. Выбрать код БЧХ, обеспечивающий заданную величину Ртр
при условии, что декодер работает только в режиме обнаружения ошибки.
3. Рассчитать при этом оценку вероятности отказа от декодирования (вероятность подавления) Рпод
.
4. Рассчитать вероятность правильного приема.
5. Построить блок-схему кодера.
6. Построить блок-схему декодера-определителя ошибки.
7. Построить функциональные схемы кодера и декодера.
Введение
В данной работе необходимо спроектировать кодер и декодер БЧХ-кода. Для чего в начале определяется вероятность ошибки на символ, вероятность трансформации кодовой комбинации, вероятность подавления кодовой комбинации. Определяется минимальное кодовое расстояние dmin. После этого выбирается генераторный полином определяющий БЧХ-код.
Далее стоятся блок-схемы кодера и декодера по которым строятся функциональные схемы.
1.
Определение вероятности ошибки на символ
Пусть на входе порогового устройства с порогом П
сигнал S0
, соответствующий логической единице и аддитивная гауссова помеха ξ.
Закон распределения плотности вероятности помехи гауссовский с нулевым математическим ожиданием (смотрите рис. 1).

Рис. 1
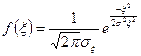 где где   дисперсия помехи.
дисперсия помехи.
Если при передаче логической «1» сумма сигнала и помехи больше или равна величине порога П
, т.е. на выходе «1» - данный элементарный сигнал принят правильно.
Если при подаче логической «1» сумма сигнала и помехи меньше порога П
, на выходе устройства «0» - сигнал принят ошибочно.
Таким образом, вероятность ошибки при условии подачи «1» определяется следующим выражением:
Р(Ош|1)=Р(S0
+ξ<П)
Соответственно вероятность ошибки при условии передачи «0»
Р(Ош|0)=Р(ξ>=П)
И вероятность ошибки на передаваемый сигнал определяется по формуле полной вероятности:
Рош
=Р(0)Р(Ош|0)+Р(1)Р(Ош|1)=Р(0) Р(ξ>=П)+Р(1) Р(S0
+ξ<П)
Т.к. помеха распределена по гауссовскому закону:
P(ξ≥П)=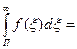  
P(S0
+x<П)=Р(x<П-S0
)=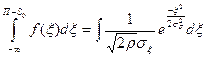
Вероятности передачи логических «0» и «1» равны т.е. Р(0)=Р(1)=1/2 отсюда
Рош
=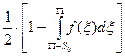
Следовательно при заданных П, S0
и f(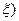 может быть определена вероятность ошибки на символ. может быть определена вероятность ошибки на символ.
При f(п)=f(п-S0
) функция pош
(П) достигает минимума (смотрите рис. 2).
Исследуем зависимость вероятности ошибки на символ от величины порога, для этого функция Рош
(П) исследуется на экстремум.

При f(П)=f(П-S0
) – функция Рош
достигает минимума при П=
S0
/2
.
Таким образом, для минимизации вероятности ошибки на символ величина порога выбирается равной S0
/2. В этом случае вероятность ошибочного приема «1» при условии передачи «0» равна вероятности ошибочного приема «0» при условии передачи «1». Такой канал связи называется двоичным (бинарным) симметричным каналом.
При П=S0
/2 Рош=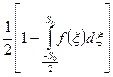
Рис.
2
Так как гауссовский закон распределения f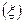 при нулевом математическом ожидании – четная функция при нулевом математическом ожидании – четная функция  , то , то
Рош
=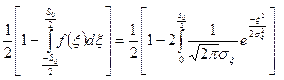
Введем обозначения:
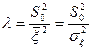 - отношение мощности сигнала к мощности помехи - отношение мощности сигнала к мощности помехи  , x= , x=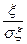 . .
Тогда dξ=σξ
dx и 2
Запишем интеграл в следующем виде:
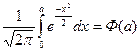
отсюда Рош
=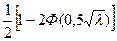
Ф(а)=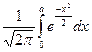
Значение функции Ф(а) табулированы
| а
|
Ф(а)
|
| 2,74
|
0,4969280
|
| 3,162
|
0,4992112
|
| 3,555355
|
0,4997922
|
| 4,183
|
0,4999854
|
| 4,472
|
0,4999963
|
| 5
|
0,4999997
|
В данной задаче воспользуемся методом трапеций:
Разобьем отрезок от нуля до 3,873 на 10 частей, шаг найдем по формуле h=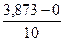
и вычислим интеграл
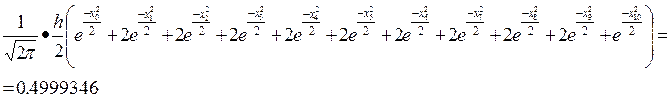
Где x0
, x1
……xn
- значения от нуля до 3,873 с шагом h=0.387
Выполним расчет вероятности ошибки на символ в следующем порядке:
λ=60
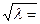 7,746 7,746
а=0,5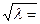 3,8 3,8
Ф(а)= 0.4999346
Pош
=1/2(1-2Ф(а))= 6.54*10-5
Ответ: Вероятность ошибки на символ Рош
=6,54*10-5
2. Оценки вероятности трансформации кодовой комбинации Ртр
,
вероятности подавления Рпод
и вероятности правильного приема Рпр
.
Для расчета показателей достоверности приема кодовой информации разрядности n принята биномиальная модель источника ошибок в канале связи. Эта модель характеризуется следующим:
· Ошибки симметричны, т.е. Р(1)=Р(0)=0,5
· Ошибки независимы, т.е. вероятность ошибочного приема символа на j-ой позиции кодовой комбинации не зависит от наличия или отсутствия ошибок на ранее переданных позициях кодовой комбинации.
При этих двух условиях вероятность любой ошибки i-ой кратности в канале связи в случае передачи n-разрядной кодовой комбинации определяется выражением
Рн
=(i)= где рош
– вероятность ошибки при приеме символа. где рош
– вероятность ошибки при приеме символа.
Число всех ошибок i-ой кратности равно числу сочетаний из n по i
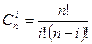
Вероятность всех ошибок i-ой кратности:
P(
i)=
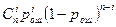 - зто выражение есть биномиальный закон распределения лучайной величины i. Отсюда название модели – биномиальная.
- зто выражение есть биномиальный закон распределения лучайной величины i. Отсюда название модели – биномиальная.
Если при передаче информации используется код с обнаружением ошибок, то трансформация кодовой комбинации происходит только тогда, когда ошибка, произошедшая в канале связи не обнаруживается кодом. Вероятность трансформации определяется выражением
Ртр
=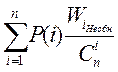 где Wi
необн
число необнаруживаемых ошибок i-ой кратности: где Wi
необн
число необнаруживаемых ошибок i-ой кратности:
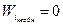 при 1 при 1 где dmin
– минимальное кодовое расстояние избыточного кода и где dmin
– минимальное кодовое расстояние избыточного кода и 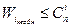 , при i , при i величину Ртр
можно оценить сверху величину Ртр
можно оценить сверху
Pтр
=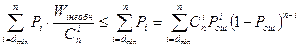
Вероятность того, что приемник обнаружит наличие ошибок при приеме кодовой последовательности и откажется от декодирования(подавление кодовой последовательности) определяется по формуле:
Pпод
=
Pпод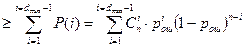
Вероятность правильного приема определяется по формуле:
Pпр
=P(i=0)=(1-pош
)n
=(1-6,54*10-5
)31
=0.998
3. Расчет вероятности правильного приема
Вероятность правильного приема определяется выражением
Pпр
=(1-pош
)n
Pпр
=(1-6.54*10-5
)31
=0.999
И в соответствии с биномом Ньютона
Pпр
=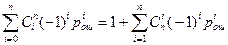 . .
Если эту функцию разложить в ряд Маклорена, то получится степенной знакопеременный ряд с числом членов n+1, совпадающий с разложением по биному Ньютона. Поэтому для расчета Pпр
с конечной точностью , при учете что 0<Pош
<1, можно ограничиться вычислением не всех членов ряда. Полученный сходящийся (область сходимости pош
<1) и знакопеременный, следовательно остаток Ri
=Pпр
-Pпр
l
, где Pпр
– сумма всех членов ряда, Pпр
l
– сумма первых l членов ряда, имеет знак первого отброшенного члена и меньше его по абсолютной величине.
Величина δPпр
=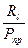 - относительная погрешность вычислений вероятности правильного приема Pпр. - относительная погрешность вычислений вероятности правильного приема Pпр.
Тогда δPпр
=
Учитывая что Rl
<<Pпр
l
получим δPпр . .
Если 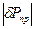 задано, например как задано, например как  , то к - число членов ряда необходимое для вычислений с заданной точностью, можно определить из неравенства: , то к - число членов ряда необходимое для вычислений с заданной точностью, можно определить из неравенства:
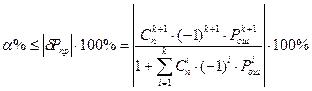 где где 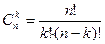
Выполним расчет с одним членом ряда
Возьмем к=1, разрядность кода n=31 и Рош
=6,54*10-5
 = =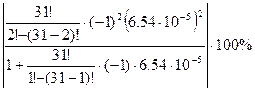
=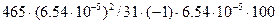 =0.02 =0.02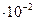 <1% <1%
Следовательно k=1 оказалось достаточно.
Получаем расчет с допустимой погрешностью.
Отсюда Pпр
=(1-Рош
)n
=1-nPОш
=0.999
4. Расчет dmin
минимального кодового расстояния. Расчет оценок P
тр
, P
под
, P
пр
.
При фиксированном n-числе разрядов, вычисленном значении Pош
и заданной вероятности трансформации Pтр зад
величина минимального кодового расстояния определяется из формулы верхней оценки Pтр.
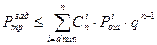 где q=1-Pош где q=1-Pош
Отсюда dmin не получается в явном виде, и требуется много вычислительной работы.
Поэтому найдем dmin из неравенства
 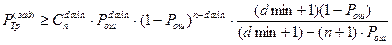
Будем задаваться различными значениями dmin, до тех пор, пока не подберем походящее. И каждый раз будем рассчитывать (1-Pош
)n-
dmin
с допустимой точностью 1 %.
Возьмем
dmin=1
Тогда
(1-Pош
)n-1
=1-(n-dmin)Pош
=0.99804

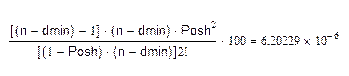
6.20229*10-6
%<1%, следовательно, вычисления сделаны с допустимой точностью.
Оценим вероятность трансформации кодовой комбинации сверху:
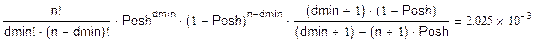
Так, как  <2.025*10-3
dmin=1 не подходит. <2.025*10-3
dmin=1 не подходит.
Возьмем
dmin=2
(1-Pош
)n-2
=1-(n-dmin)Pош
=0.9981
 =5.98842*10-6
%<1% =5.98842*10-6
%<1%
следовательно, вычисления сделаны с допустимой точностью.
Оценим вероятность трансформации кодовой комбинации сверху:
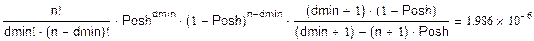
dmin=2 тоже не подходит так, как 10-11
< 1.986*10-6
Возьмем
dmin=3
(1-Pош
)n-3
=1-(n-dmin)Pош
=0.99817
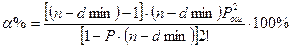 =5.77454*10-6
%<1% =5.77454*10-6
%<1%
следовательно, вычисления сделаны с допустимой точностью.
Оценим вероятность трансформации кодовой комбинации сверху:
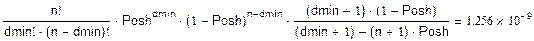
dmin=3 тоже не подходит так, как 10-11
< 1.256*10-9
Возьмем
dmin=4
(1-Pош
)n-4
=1-(n-dmin)Pош
=0.99823
 =5.56067*10-6
%<1% =5.56067*10-6
%<1%
следовательно, вычисления сделаны с допустимой точностью.
Оценим вероятность трансформации кодовой комбинации сверху:
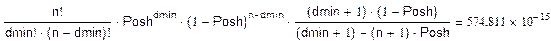
dmin=4 подходит так, как 10-11
> 574.811*10-15
Отсюда оценки показателей достоверности имеют вид:
Pтр
=574.811*10-15
Pпр
=0.99823
Вычислив  , оценку вероятности подавления кодовой комбинации определим по формуле , оценку вероятности подавления кодовой комбинации определим по формуле
Рпод
=1-Рпр
-Ртр
=1-0.99823- 574.811*10-15
=1.77*10-3
5.
Выбор БЧХ кода
В примитивном двоичном БЧХ-коде n=2m
-1. Откуда при заданном n выбирается величина m. Если в результате расчета получено dmin
– нечетное число, выбираем генераторный полином g(x) из следующих соображений: dmin
=2t+1; корнями многочлена g(x) являются α, α3
,…α2
t-1
. По таблицам Марша при полученном m находим m1
(x), m3
(x),...,m2
t-1
(x) – минимальные функции для α, α3
,…α2
t-1
. После чего g(x) определяется как наименьшее общее кратное минимальных функции.
g(x)=НОК[m1
(x), m3
(x),...,m2
t-1
(x)].
Если в результате расчета получено dmin
– четное число, то dmin
=2t+2. корнями многочлена g(x) являются 1, α, α3
,…α2
t-1
. И g(x)=НОК[(x+1)m1
(x), m3
(x),...,m2
t-1
(x)].
генераторный полином полностью определяет БЧХ – код, его кодер и декодер (в режиме обнаружения ошибок).
В нашем случае dmin
=4, следовательно dmin
=2t+2 и g(x)=НОК[(x+1)m1
(x), m3
(x),...,m2
t-1
(x)].
Т.к. dmin
=4 то 4=2t+2, отсюда t=1 и 31=2m
-1, m=5
g(x)=НОК[(x+1)m1
].
m1(x)=45=100101=x5
+x2
+1=x6
+x5
+x3
+x2
+x+1
(x+1)*( x5
+x2
+1)=
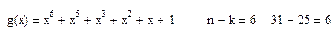
Число информационных символов k=25, а число проверочных символов n=6. И емкость кода С=2к
=3.355*107
Итак, мы получили генераторный полином g(x)= x6
+x5
+x3
+x2
+x+1, который полностью определяет БЧХ-код, его кодер и декодер (в режиме обнаружения ошибок).
6. Алгоритм работы кодера БЧХ-кода
Выбранный БЧХ-код задается своей разрядностью n и генераторным полиномом g(x), степень которого равна n-k, где k-число информационных символов. Емкость БЧХ-кода C=2k
.
Пусть a(X)=a0
+a1
X+...+ak
-1
Xk
-1
– k-разрядный вектор информационных символов, V(X)=b0
+b1
X+b2
X2
+...+bn
-1
Xn
-1
- n-разрядный вектор кода. Кодер преобразует вектор a(X) в вектор V(X), реализует процедуру получения систематического кода т.е.:
V(X)=ak
-1
Xn
-
k
+ak
-2
Xn
-2
+...+a0
Xn
-
k
+bn
-
k-1
Xn
-
k-1
+b1
X+b0
;
Таким образом, в векторе V(X) коэффициенты при старших степенях X-информационные символы, при младших степенях проверочные.
Вектор V(X) для выбранного циклического кода при заданном a(X) получаем следующим образом:
1 шаг: - a(X)*Xn
-
k
2 шаг: a(X)*Xn
-
k
/ g(x) – получим остаток от деления R(X) (результат деления нас не интересует). Отметим, что степень многочлена R(X) меньше степени многочлена g(x).
3 шаг: - получаем вектор систематического кода как сумму a(X)*Xn
-
k
и R(X), т.е.
V(X)= a(X)*Xn
-
k
+ R(X); отметим, что степень многочлена a(X)*Xn
-
k
не меньше n-k, поэтому их сложение это по существу «приписывание» R(X) за a(X)*Xn
-
k
.
| x30
+x29
+x28
+ x27
+x26
+x25
+ x24
+x23
+x22
+ x21
+x20
+x19
+ x18
+x17
+x16
+x15
+x14
+ x13
+x12
+x11
+ x10
+x9
+x8
+ x7
+x6
|
x6
+x5
+x3
+ x2
+x+1
|
| x30
+x29
+x27
+ x2
6
+x2
5
+x2
4
|
x24
+x22
+x21
+x19
+x18
+x14
+x7
+x5
+x4
+x3
|
| x28
+x26
+x23
+x22
+ x21
+x20
+x19
+ x18
+x17
+x16
+x15
+x14
+ x13
+x12
+x11
+ x10
+x9
+x8
+ x7
+x6
x28
+x2
7
+x25
+ x2
4
+x2
3
+x2
2
|
| x27
+x26
+x25
+x24
+ x21
+x20
+x19
+ x18
+x17
+x16
+x15
+x14
+ x13
+x12
+x11
+ x10
+x9
+x8
+ x7
+x6
x27
+x26
+x24
+ x2
3
+x2
2
+x21
|
| x25
+ x23
+x22
+x20
+x19
+ x18
+x17
+x16
+x15
+x14
+ x13
+x12
+x11
+ x10
+x9
+x8
+ x7
+x6
x25
+x24
+x22
+x21
+x20
+x19
|
| x24
+x23
+x21
+x18
+x17
+x16
+x15
+x14
+ x13
+x12
+x11
+ x10
+x9
+x8
+ x7
+x6
|
| x24
+x23
+x21
+x20
+x19
+x18
|
| x20
+x19
+ x17
+x16
+x15
+x14
+ x13
+x12
+x11
+ x10
+x9
+x8
+ x7
+x6
x20
+x19
+ x17
+x16
+x15
+x14
|
| x13
+x12
+x11
+ x10
+x9
+x8
+ x7
+x6
x13
+x12
+ x10
+x9
+x8
+ x7
|
| x11
+x6
x11
+x10
+x8
+ x7
+x6
+x5
|
| x10
+x8
+ x7
+x5
x10
+x9
+ x7
+x6
+x5
+x4
|
| x9
+x8
+x6
+x4
x9
+x8
+x6
+x5
+x4
+x3
|
| x5
+x3
|
Получаем остаток от деления равный R(X)= x5
+x3
.Таким образом
V(X)=a(X)Xn-k
+R(X)= x30
+x29
+x28
+ x27
+x26
+x25
+ x24
+x23
+x22
+ x21
+x20
+x19
+ x18
+x17
+x16
+x15
+x14
+ x13
+x12
+x11
+ x10
+x9
+x8
+ x7
+x6
+ x5
+x3
При n равном 31 получим n-разрядный вектор кода.
| 1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
xn
................................................................................................................................................x0
7 .Кодер систематического циклического кода
Кодер систематического циклического кода реализует следующий алгоритм:
- шаг: a(X)Xn-k
- шаг: a(X)Xn-k
/g(x)
- шаг: V(X)= a(X)Xn
-
k
+R(X), где V(X)-вектор кодового слова, R(X)-остаток от деления a(X)Xn
-
k
/g(x).
И строится на линейной переключательной схеме одновременного умножения (на Xn
-
k
) и деления (на g(X)) многочленов.
Построим схему кодера для кода, у которого:
n=31, g(x)=x6
+x5
+x3
+x2
+x+1
Линейная переключательная схема одновременного умножения a(X) на многочлен b(X)=b6
X6
+ b5
X5
+ b4
X4
+ b3
X3
+ b2
X2
+ b1
X+b0
и деления на многочлен g(X)= g6
X6
+ g5
X5
+ g4
X4
+ g3
X3+ g2
X2
+ g1
X+g0
приведена ниже. Прямоугольниками на схеме обозначены элементы памяти, кружочками – устройства умножения на константу, записанную в кружочке, кружочками со знаком «+» обозначены сумматоры. Число элементов памяти равно степени равно степени многочленов b(X) и g(X). Цепи сдвига на схеме не показаны.
Все математические операции выполняются в поле GF(2), где –gi
=gi
, 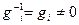 . А gi
=0 или bi
=0 соответствует разрыву в схеме, gi
=1 или bi
=1 соответствует наличию соединения. . А gi
=0 или bi
=0 соответствует разрыву в схеме, gi
=1 или bi
=1 соответствует наличию соединения.
На вход схемы поступают последовательно во времени все коэффициенты (включая и нулевые) многочлена a(X), начиная со старшей степени.
Общая схема одновременного умножения и деления
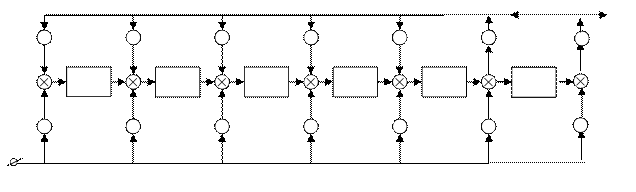
Рис.
3
Схема одновременного умножения на b(X)=Xn
-
k
=X31-25
=X6
и деления на многочлен g(x)= x6
+x5
+x3
+x2
+x+1 имеет вид:

Рис.
3
В этой схеме –g0
=-g1
=-g2
=-g3
=1; -g4
=0; -g5
=1; -g6
=1.
Суммирование осуществляется по модулю два.
Блок-схема кодера
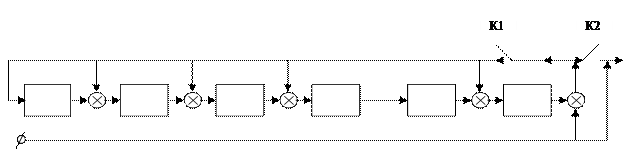
Рис.
5
В начале ключ К1 замкнут, а К2 разомкнут.На вход схемы поступают коэффициенты многочлена a(X), начиная со старше степени. Эти символы поступают на выход схемы и в цепь обратной связи (деление). После поступления символа a0
ключ К1 размыкается(обрывается обратная связь схемы деления), ключ К2 замыкается и содержимое регистра(проверочные символы) последовательно во времени передаются на выход. Таким образом на выходе получаем вектор кода V(X).
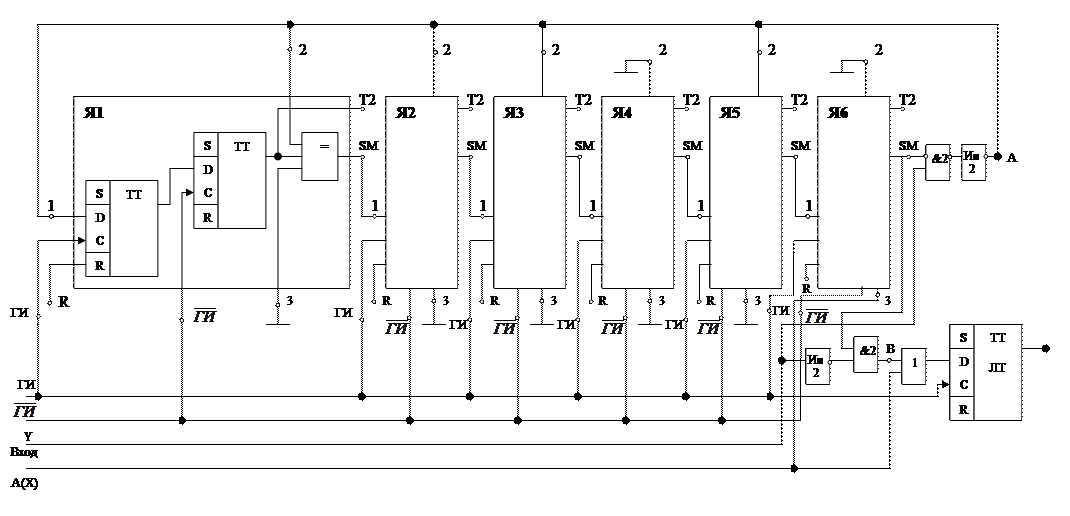
Функциональная схема, соответствующая блок-схеме (рис. 5), приведена на рис. 6.
На вход схемы подаются сигналы: с прямого (ГИ) и инверсного (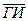 ) выхода генератора импульсов, управления (У), информационные символы a(x) последовательно во времени, начиная с a24
. Информационные символы синхронизированы с ГИ. Каждая ячейка состоит из двух Д-триггеров и сумматора по модулю 2. На «нижний» Д-триггер информация записывается по переднему фронту ГИ, на «верхний» Д-триггер информация переписывается с «нижнего» Д-триггера по переднему фронту ) выхода генератора импульсов, управления (У), информационные символы a(x) последовательно во времени, начиная с a24
. Информационные символы синхронизированы с ГИ. Каждая ячейка состоит из двух Д-триггеров и сумматора по модулю 2. На «нижний» Д-триггер информация записывается по переднему фронту ГИ, на «верхний» Д-триггер информация переписывается с «нижнего» Д-триггера по переднему фронту  , то есть по заднему фронту ГИ. Схемы «И1» и «Ин1» выполняют функцию ключа К1 (смотрите блок-схему кодера 31,25 БЧХ кода на рис. 3). При поступлении информационных символов с a24
по a0
(первые 25 тактов) Y=1 и обратная связь включена. При этом на выходе инвертора «Ин2» сигнал равен 0, следовательно, на выходе схемы «&2» B=0. Сигналы a24
…a0
через схему «ИЛИ» поступают на вход линейного триггера (ЛТ), выход которого – выход кодера. После поступления всех информационных символов (25 тактов), на входе a(x) сигнал, соответствующий логическому «0», на входе «Y» сигнал также соответствует логическому «0». При этом А=0, то есть обратная связь отключена. С выхода шестой ячейки коэффициенты R(x) - остатка от деления a(x)xn
-
k
на g(x), которые к этому времени уже получены, поступают через схему &2 при Ин2=1 на вход ЛТ. С выхода ЛТ получаем проверочные символы – коэффициенты R(x), вслед за информационными. Таким образом, формируем кодовый вектор V(x). , то есть по заднему фронту ГИ. Схемы «И1» и «Ин1» выполняют функцию ключа К1 (смотрите блок-схему кодера 31,25 БЧХ кода на рис. 3). При поступлении информационных символов с a24
по a0
(первые 25 тактов) Y=1 и обратная связь включена. При этом на выходе инвертора «Ин2» сигнал равен 0, следовательно, на выходе схемы «&2» B=0. Сигналы a24
…a0
через схему «ИЛИ» поступают на вход линейного триггера (ЛТ), выход которого – выход кодера. После поступления всех информационных символов (25 тактов), на входе a(x) сигнал, соответствующий логическому «0», на входе «Y» сигнал также соответствует логическому «0». При этом А=0, то есть обратная связь отключена. С выхода шестой ячейки коэффициенты R(x) - остатка от деления a(x)xn
-
k
на g(x), которые к этому времени уже получены, поступают через схему &2 при Ин2=1 на вход ЛТ. С выхода ЛТ получаем проверочные символы – коэффициенты R(x), вслед за информационными. Таким образом, формируем кодовый вектор V(x).
Функциональная схема кодера 31,25
Рис. 6
8.
Схема обнаружения ошибки
При передаче информации по каналу связи к вектору кода V(x) прибавляется вектор ошибки e(x). Если e(x)=0, ошибки в канале связи не было. При e(x)≠0 в канале связи была ошибка.
Кодовое слово принадлежит коду, если оно делится на g(x). Поэтому принятый кодовый вектор V1
(x)=V(x)+e(x) в приемнике делим на g(x). Если V1
(x) делится на g(x) без остатка, то V1
(x) – вектор кода. В противном случае обнаруживается ошибка.
В нашем случае линейная переключательная схема деления многочлена V(x) на g(x)= x6
+x5
+x3
+x2
+x+1 имеет вид:
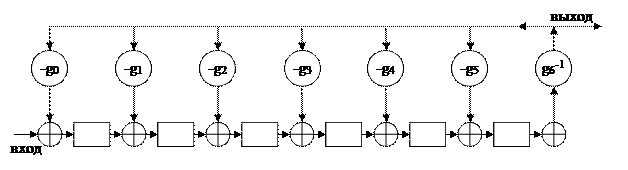
Рис. 7
На этой схеме –gi
– элеимент, обратный по сложению элементу gi
в поле GF(p), g6
-1
– элемент, обратный по умножению элементу g6
≠0 в поле GF(p).
На вход схемы подают коэффициенты многочлена V1
(x), начиная с коэффициента при старшей степени х. Для n,k кодаэта степень равна n–1. При использовании двоичных кодов значение коэффициента может быть равно либо 1, либо 0.
После поступления всех n коэффициентов V1
(x) в элементах памяти находится остаток от деления – R(x). Результат деления, получаемый на выходе схемы, не используется. Если R(x)=0, кодовое слово принадлежит коду. Если R(x)≠0, то обнаружена ошибка, и приемник отказывается от декодирования.
Схема деления на многочлен приведена на рис. 8.

Рис. 8
Функциональная схема, соответствующая схеме на рис. 8 приведена на рис. 9
Рис. 9

Типовые ячейки от Я1 до Я6 в этой схеме и включение генератора импульсов ГИ то же, что и в схеме кодера. В качестве сумматора по модулю 2 на входе первой ячейки, один вход которого подключен к точке, на которую последовательно во времени поступают сигналы кода, второй – к выходу ячейки Я6, используется сумматор по модулю 2, имеющийся в составе ячейки Я6.
После приема кодового вектора V1
(x) в ячейках памяти при наличии обнаруживаемой ошибки получен остаток R(x)≠0. Факт наличия остатка фиксируется схемами «ИЛИ1» и «И2». При R(x)≠0 после приема всех разрядов кода А=1. В это время на второй вход схемы «И2» подается сигнал устройства управления Y1, равный 1. В течение времени, когда Y1=1 и A=1, выход в схеме «И2» также равен 1. Этот сигнал подключается к устройству запрета считывания принятой информации. После Y1=1 формируется Y2=1, сбрасывающий схему деления в исходное состояние.
На первых 31 тактах осуществляется прием V1
(x) и вычисление остатка.
На первой половине 32 такта сигналом Y2=1 все ячейки схемы деления сбрасываются в исходное состояние, равное 0, после чего эта схема готова к приему нового вектора.
9.
Заключение
В данной курсовой работе был выбран БЧХ-код, определена вероятность ошибки на символ, вероятность трансформации кодовой комбинации, вероятность подавления и вероятность правильного приема, минимальное кодовое расстояние. По этим параметрам построен генераторный полином, который полностью определяет БЧХ-код.
Был рассмотрен принцип работы кода, по которому построены блок-схемы кодера и декодера кода. Далее по полученному алгоритму были построены функциональные схемы кодера и декодера.
Список используемой литературы
1. Методические указания к курсовой работе «Расчет оценок показателей достоверности приема дискретной информации. Проектирование кодера и декодера БЧХ-кода». Л. А. Баранов, МИИТ 2000 г.
2. Лекции по курсу «Статистическая теория связи» Л. А. Баранов. 2006.
|