| Комитет по образованию администрации города Майкопа
Реферат на тему:
«Геометрические решения экстремальных геометрических задач »
Номинация - математика
Выполнила:
ученица 11 «М» класса
гимназии №22
Соловей Екатерина
Руководитель:
Учитель математики
Захарьян А.А.
Майкоп
2008 г.
Содержание
Содержание. 2
Введение. 3
Задачи…………………………………………………………………………………………….4
Задача1(МЭСИ).………………………………………………………………………….4
Задача2(МАИ)……………………………………………………………………………5
Задача3(МАИ)……………………………………………………………………………6
Задача4(МИСиС)………………………………………………………………………...7
Задача5(УрГУ)…………………………………………………………………………...8
Задача6(МФТИ)..………………………………………………………………………...9
Задача7(МАИ)..…………………………………………………………………………10
Задача8(ЕГЭ-2007)...……………………………………………………………………11
Заключение. 13
Список использованной литературы. 14
Введение.
Большую часть своих усилий человек тратит на поиск наилучшего, т.е. оптимального решения поставленной задачи. Как, располагая определенными ресурсами, добиваться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени. Так ставятся вопросы, над которыми приходится думать каждому члену общества.
Математикам удалось разработать методы решения задач на наибольшее и наименьшее значение, или, как их еще называют, задач на оптимизацию (от латинского «оптимум» - наилучший). Многие задачи, поиска оптимальных решений, могут быть решены только с использованием методов дифференциального исчисления. Ряд задач такого типа решается с помощью специальных методов линейного программирования, но существуют и такие экстремальные задачи, которые решаются средствами элементарной математики и геометрии.
Задачи, связанные с нахождением наибольших и наименьших значений геометрических величин, неспроста пользуются большой популярностью у составителей экзаменационных заданий: ведь чтобы решить подобную задачу, абитуриенту приходится комбинировать приемы и методы из весьма различных разделов школьного курса математики. Первое, что приходит в голову,— составить с помощью заданных параметров функцию и исследовать ее на максимум и минимум. У такого подхода, тем не менее, есть недостаток: во многих геометрических задачах этот привычный путь решения сопряжен со значительными техническими трудностями. Часто, однако, удается избавиться от громоздких выкладок, обойдясь чисто геометрическими рассуждениями.
Задача моей работы заключается в следующем:
· Изучить данный способ решения геометрических экстремальных задач
· Научиться решать такие задачи геометрическим способом
Также сейчас в заданиях Единого Государственного Экзамена встречаются задачи на нахождение наименьшего и набольшего значений, которые легко решаются данным способом. И в своей работе я представлю решения некоторых подобных задач.
Далее представлены примеры и решения геометрических экстремальных задач геометрическим способом.
Задачи
Задача 1 (МЭСИ).
На отрезках АВ и АС как на диаметрах построены полуокружности. В общую часть двух образовавшихся полукругов вписана окружность максимального радиуса. Найдите радиус этой окружности, если АВ=4, АС = 2, 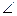 ВАС = 120°. ВАС = 120°.
Решение.
 Пусть Пусть  и и — середины соответственно отрезков АВ и АС (рис. 1). Тогда — середины соответственно отрезков АВ и АС (рис. 1). Тогда 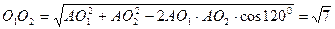 . Пусть r — радиус окружности, о которой говорится в условии задачи, О — ее центр. Для точек . Пусть r — радиус окружности, о которой говорится в условии задачи, О — ее центр. Для точек  , , , , 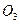 имеем имеем 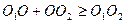 , или 1 - r + 2 , или 1 - r + 2  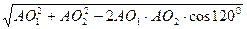 . .
Отсюда 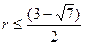 . Очевидно, знак равенства достигается лишь в том случае, когда точка O принадлежит отрезку . Очевидно, знак равенства достигается лишь в том случае, когда точка O принадлежит отрезку   . .
Ответ:
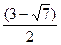
Задача 2 (МАИ).
Найдите периметр треугольника наибольшей площади, образованного большим основанием и продолжением боковых сторон трапеции, если известно, что длина верхнего основания трапеции в два раза меньше длины ее нижнего основания, а диагонали равны 5 и 6.

Решение.
Пусть ВС и AD —основания трапеции (рис. 2), ВС = 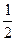 AD. Выходит, что ВС — средняя линия треугольника AED. Тогда AD. Выходит, что ВС — средняя линия треугольника AED. Тогда 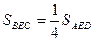
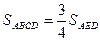

Следовательно, площадь треугольника AED достигает максимального значения при максимальной площади трапеции ABCD. Очевидно, 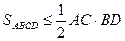 , т. е. площадь данной трапеции максимальна, если ее диагонали перпендикулярны. Итак, искомый периметр — это периметр треугольника с перпендикулярными медианами: , т. е. площадь данной трапеции максимальна, если ее диагонали перпендикулярны. Итак, искомый периметр — это периметр треугольника с перпендикулярными медианами: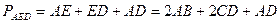  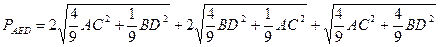 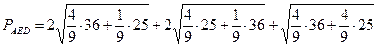 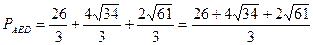
Ответ
:
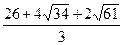
Задача 3 (МАИ).
В треугольнике ABC биссектриса, проведенная из вершины А, имеет длину 2, и АВ= 2АС. На стороне АВ взята точка М, а на стороне АС — точка N так, что BM=AN. Найдите наименьшее возможное расстояние от середины отрезка MN до вершины А.
 Решение
. Решение
.
Пусть Q — середина отрезка MN, К — точка пересечения биссектрисы угла ВАС и ВС. Спроектируем точки М, N, Q и В на биссектрису угла ВАС (рис.3).
Тогда  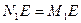 . .
Пусть AC=m, AB = 2m,  . Тогда . Тогда
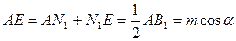
Отсюда 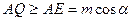
Следовательно, искомое расстояние принимает наименьшее значение, когда середина Q отрезка MN лежит на биссектрисе.
Для площади треугольника ABC имеем 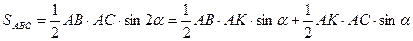
Или 
Отсюда 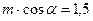
Ответ
: 1,5
Задача 4 (МИСиС).
В параболу 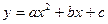 вписан четырехугольник ABCD наибольшей площади с диагоналями АС и BD. Найдите координаты вершины С, если А(-3; -4), В(-2; -1), D(1;-4) . вписан четырехугольник ABCD наибольшей площади с диагоналями АС и BD. Найдите координаты вершины С, если А(-3; -4), В(-2; -1), D(1;-4) .
Решение.
Так как точки А, В, в лежат на параболе, то их координаты удовлетворяют ее уравнению: 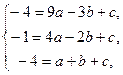 откуда a= -1, b= -2, c= -1. откуда a= -1, b= -2, c= -1.
Итак, уравнение заданной параболы найдено: 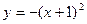 . В условии указано, что АС — диагональ четырехугольника ABCD, значит, точка С лежит на дуге BD параболы (рис. 4). . В условии указано, что АС — диагональ четырехугольника ABCD, значит, точка С лежит на дуге BD параболы (рис. 4).

Для решения задачи достаточно найти координаты точки С, при которых площадь треугольника DBC максимальна, что, в свою очередь, равносильно поиску на дуге BD точки, максимально удаленной от прямой BD. Пусть l
— касательная к параболе, параллельная BD. В силу характера выпуклости квадратичной функции все точки параболы лежат в одной полуплоскости относительно прямой l
. Следовательно, точкой, максимально удаленной от прямой BD, будет точка касания.
Так как прямая BD невертикальная, то ее уравнение имеет вид y=kx+d. Зная координаты точек В и D, легко установить, что k = - 1. Значит, угловой коэффициент касательной l
равен -1, т. е. производная квадратичной функции, задающей параболу, в точке касания равна -1. Имеем -2(х0
+ 1)= —1, где х0
—абсцисса точки касания; отсюда х0
= - . .
Ответ:

Задача 5 (УрГУ).
К кривой 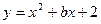 в точках с абсциссами в точках с абсциссами 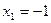 и и 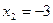 проведены касательные. При каком значении b периметр треугольника, образованного проведенными касательными и осью Oy, будет наименьшим? проведены касательные. При каком значении b периметр треугольника, образованного проведенными касательными и осью Oy, будет наименьшим?
Решение.
 Уравнения касательных к заданной параболе в точках с абсциссами Уравнения касательных к заданной параболе в точках с абсциссами 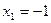 и и 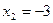 соответственно имеют вид y1
=(b-2)x+1, у2
=(b-2)х -7. соответственно имеют вид y1
=(b-2)x+1, у2
=(b-2)х -7.
Отсюда две вершины треугольника, о котором говорится в условии, имеют координаты M(0;1) и N(0;-7), а третья — К(-2; 5-2b) (рис. 5). Следовательно, нужно найти такое положение точки К на прямой х = - 2, при котором сумма MK + KN была бы наименьшей.
Покажем, что искомая точка — это точка пересечения прямых х=-2 и РМ, где точка Р симметрична точке N относительно прямой х = - 2. Пусть К' произвольная точка прямой х = — 2, отличная от К. Имеем
МК' +
K'N=MK'+PK'>MP = РК + КМ = KN + КМ.
Поскольку средняя линия треугольника PMN лежит на прямой х = — 2, треугольник MKN равнобедренный; тогда ордината точки К равна —3. Отсюда 5—2b = —3, b = 4.
Ответ
: b = 4.
Задача 6 (МФТИ).
В основании прямой призмы 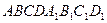 лежит ромб ABCD с углом лежит ромб ABCD с углом  . Длины всех ребер призмы равны 1. Точка F — середина ребра DC, а точка М лежит на прямой A . Длины всех ребер призмы равны 1. Точка F — середина ребра DC, а точка М лежит на прямой A F. Определите наименьшее значение суммы площадей треугольников МВВ1
и МСС1 F. Определите наименьшее значение суммы площадей треугольников МВВ1
и МСС1
Решение
.
Пусть МК и ML — высоты соответственно треугольников МВВ1
и МСС1
(рис. 6), М1
— проекция точки М на плоскость ABC. Тогда М1
В=МК, M1
C=ML и
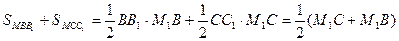
Как и в предыдущей задаче, сумма M1
B + M1
C принимает наименьшее значение, если M1
— точка пересечения прямых AF и BE, где Е — точка, симметричная точке С относительно прямой AF (рис. 7).
Осталось найти длину отрезка
BE. По теореме косинусов
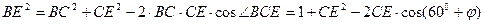 , ,
где 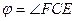 . Проведем в треугольнике ADF высоту DN. Видно, что СЕ=2DN и . Проведем в треугольнике ADF высоту DN. Видно, что СЕ=2DN и 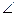 FCE= FCE=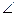 NDF. Но NDF. Но
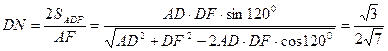
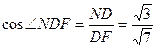
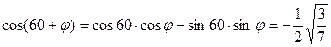
Из 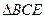 по Т. косинусов по Т. косинусов

Ответ
:
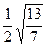


Задача 7 (МАИ).
В треугольной пирамиде SABC все ребра имеют одинаковую длину, равную l
. На ребре SA взята точка М так, что SM =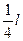 , на ребре SB взята точка N, а на плоскости ABC взята точка Р. Найдите наименьшую величину суммы длин отрезков MN и NP. , на ребре SB взята точка N, а на плоскости ABC взята точка Р. Найдите наименьшую величину суммы длин отрезков MN и NP.
Решение.
 Длина отрезка NP минимальна, если Р — проекция точки N на плоскость ABC. Очевидно, что Р принадлежит медиане BE правильного треугольника ABC (рис. 8). Теперь нужно найти кратчайшее расстояние от данной точки М до прямой BE по поверхности двугранного угла, образованного плоскостями ABS и BSE. Это все равно, что найти расстояние от точки до прямой на плоской развертке этого двугранного угла. Длина отрезка NP минимальна, если Р — проекция точки N на плоскость ABC. Очевидно, что Р принадлежит медиане BE правильного треугольника ABC (рис. 8). Теперь нужно найти кратчайшее расстояние от данной точки М до прямой BE по поверхности двугранного угла, образованного плоскостями ABS и BSE. Это все равно, что найти расстояние от точки до прямой на плоской развертке этого двугранного угла.
Рассмотрим такую развертку. Для этого в плоскости SBE построим треугольник SA1
В, равный треугольнику ASB (рис. 9). На стороне SA1
отметим точку M1
, в которую при раз- разворачивании двугранного угла пере- переходит точка М, так что SM1
=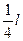 . Как известно, кратчайшее расстояние от точки до прямой есть перпендикуляр, опущенный из данной точки на данную прямую. Поэтому проведем М1
P1 . Как известно, кратчайшее расстояние от точки до прямой есть перпендикуляр, опущенный из данной точки на данную прямую. Поэтому проведем М1
P1 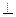 BE. Очевидно, что сумма
BE. Очевидно, что сумма
MN+NP=M1
N+NP минимальна тогда и только тогда, когда Р=Р1
и N = Q. Осталось выяснить, чему равна длина отрезка М1
Р1
.

Проведем SK 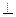 M1
P1
. Пусть
M1
P1
. Пусть  KSB = KSB = SBE = α. Высота SO пирамиды равна SBE = α. Высота SO пирамиды равна 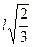 . Тогда M1
P1
= M1
K+SO= . Тогда M1
P1
= M1
K+SO=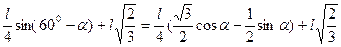 . .
Выразив sin α и cos α из треугольников SBE и SBO, получим ответ: 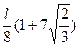
Ответ:
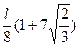
Задача 8. (ЕГЭ-2007)
Отрезок АВ – диаметр сферы. Точки С и в лежат на сфере так, что объем пирамиды ABCD наибольший. Найдите этот объем, если радиус сферы равен 1 см.
Решение
.
Чтобы объем пирамиды был наибольший, должна быть наибольшей высота этой пирамиды и площадь основания, так как 
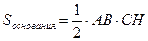
Так как A и B принадлежат диаметру сферу, то  опирается на диаметр, а значит опирается на диаметр, а значит
 =900
=> =900
=>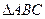 - прямоугольный. - прямоугольный.
Наибольшую площадь из всех прямоугольных треугольников имеет равнобедренный прямоугольный треугольник; т.к. АВ- const, то высота СН должна быть наибольшей, а значит СН=R и 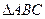 - прямоугольный равнобедренный. - прямоугольный равнобедренный.
Аналогично рассуждаем для 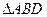 , т.е. получаем, что DH=R. , т.е. получаем, что DH=R.
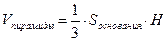 = =

Ответ:
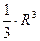
Задачи для самостоятельного решения
Конечно, все эти задачи можно решать путем составления функции и исследования ее на экстремум. Но решение будет куда более громоздким.
Также для решения рекомендуются задачи, собранные по этой теме из вступительных экзаменов прошлых лет в различные Российские ВУЗы.
1. (МАИ).
Найдите длины сторон параллелограмма ABCD наибольшей площади, если известно, что его вершина А удалена от середины сторон ВС и CD на 6 и 8 единиц соответственно.
2.
Две дуги окружностей радиусами R с центрами в точках А и В таких, что AB=R, пересекаются в точке С. Впишите в криволинейный треугольник ABC равнобедренную трапецию наибольшей площади.
3. (ЛГУ).
Даны точки А(0;3), В(4;5)На оси Ох найдите такую точку С, чтобы периметр треугольника ABC был наименьшим.
4. (ЛГУ).
Боковые стороны трапеции перпендикулярны. Какое наибольшее значение может иметь площадь треугольника, образованного диагоналями и средней линией трапеции, если известно, что длины оснований трапеций равны a и b?
5.
На координатной плоскости рассматриваются правильные треугольники, у которых две вершины лежат на прямой y=х+2, а координаты третьей вершины удовлетворяют неравенству  .Найдите наибольшее возможное значение площади рассматриваемых треугольников. .Найдите наибольшее возможное значение площади рассматриваемых треугольников.
6. (УГУ).
К кривой у=x-3
+bx в точках c абсциссами x1
=0 и x2
=-3/2 проведены 2 касательные. При каком значении b периметр треугольника, образованного проведенными касательными и осью Оу, будет наименьшим?
7. (МФТИ).
Точка в является серединой ребра BB1
правильной треугольной призмы АВСА1
В1
С1
. На боковой грани AA1
C1
C взята точка Е, на основании ABC — точка F так, что прямые ЕВ1
и FD параллельны. Какой наибольший объем может иметь призма АBСА1
В1
С1,
если ЕВ1
= 1, FD=3/4, EF=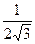 . .
8. (МАИ).
В основании четырехугольной пирамиды SABCD лежит параллелограмм ABCD. Известно, что расстояния от точек А, B, С, S до середины ребра ВС равны 4. При какой величине угла, образованного плоскостями ACS и SCD, объем пирамиды будет наибольшим?
Заключение
.
В настоящее время получило всеобщее признание то, что успех развития многих областей науки и техники существенно зависит от развития многих направлений математики. Математика становится средством решения проблем организации производства, поисков оптимальных решений и, в конечном счете, содействует повышению производительности труда и устойчивому поступательному развитию народного хозяйства.
Использование экстремальных задач при изучении математики оправдано тем, что они с достаточной полнотой закладывают понимание того, как человек ищет, постоянно добивается решения жизненных задач, чтобы получающиеся результаты его деятельности были как можно лучше. Решая задачи указанного типа, наблюдаем, с одной стороны, абстрактный характер математических понятий, а с другой большую эффективную их применимость к решению жизненных практических задач.
Экстремальные задачи помогают ознакомиться с некоторыми идеями и прикладными методами школьного курса математики, которые часто применяются в трудовой деятельности, в познании окружающей действительности. Решение экстремальных задач способствует углублению и обогащению наших математических знаний.
Список использованной литературы.
1. Горнштейн П., Полонский В., Якир М. Геометрические решения экстремальных геометрических задач. Журнал «Квант» № 9/1992. – М.: Бюро «Квантум», 1992.
2. Лысенко Ф.Ф. ЕГЭ вступительные экзамены. Математика – Ростов-на-Дону, 2004.
3. Лаппо Л.Д., Попов М.А. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ – М.: «Экзамен», 2008
4. Возняк Г. М., Гусев В. А. Прикладные задачи на экстремумы. М.: Просвещение, 1985.
5. Готман Э.Г. Поиск рационального решения задачи на экстремум //Математика в школе. – 1997. - № 6. – С. 40.
6. Прасолов В.В. Задачи по планиметрии. Часть I. – 2-е изд. – М.: Наука, 1991, с. 282.
7. Тихомиров В.М. Рассказы о максимумах и минимумах. – М.: Наука, 1986 (Библиотечка «Квант»)
|