ФЕДЕРАЛЬНАЯ СЛУЖБА ПО НАДЗОРУ В СФЕРЕ ОБРАЗОВАНИЯ И НАУКИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ НАУЧНОЕ УЧРЕЖДЕНИЕ
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»
Учебно-методические материалы для председателей и
членов региональных предметных комиссий
по проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ 2010 года
ЧАСТЬ 1
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ОЦЕНИВАНИЮ ВЫПОЛНЕНИЯ ЗАДАНИЙ ЕГЭ
С РАЗВЕРНУТЫМ ОТВЕТОМ
МАТЕМАТИКА
Москва
2010
Научный руководитель: А.Л. Семёнов, чл.-корр. РАН, ректор МИОО
Руководитель: И.В. Ященко, в.н.с. ФИПИ
Авторы-составители: И.Р. Высоцкий, В.С. Панфёров, А.В. Семенов, И.Н. Сергеев, В.А. Смирнов
СОДЕРЖАНИЕ
| Введение
|
| §1.
|
Задания с развернутым ответом повышенного уровня сложности С1. Критерии проверки и оценки решений
|
7
|
| §2.
|
Задания с развернутым ответом повышенного уровня сложности С2. Критерии проверки и оценки решений
|
23
|
| §3.
|
Задания с развернутым ответом повышенного уровня сложности С3. Критерии проверки и оценки решений
|
34
|
| §4.
|
Задания с развернутым ответом повышенного уровня сложности С4. Критерии проверки и оценки решений
|
45
|
| §5.
|
Задания с развернутым ответом высокого уровня сложности С5. Критерии проверки и оценки решений
|
56
|
| §6.
|
Задания с развернутым ответом высокого уровня сложности С6. Критерии проверки и оценки решений
|
ВВЕДЕНИЕ.
Учебно-методические материалы для председателей и членов региональных предметных комиссий по проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ 2010 года по математике разработаны в соответствии с Тематическим планом работ Федерального государственного научного учреждения «Федеральный институт педагогических измерений» по заданию Федеральной службы по надзору в сфере образования и науки в 2009 году (в целях научно-методического обеспечения мероприятий общероссийской системы оценки качества образования). Пособие предназначено для подготовки экспертов по оцениванию заданий с развернутым ответом, которые являются частью контрольных измерительных материалов (КИМ) для сдачи единого государственного экзамена (ЕГЭ) по математике. Пособие состоит из трех частей.
В первой части («Методические рекомендации по оцениванию выполнения заданий ЕГЭ с развернутым ответом. Математика») дается краткое описание структуры контрольных измерительных материалов 2010 года по математике, характеризуются общие подходы к применению предложенных критериев оценки решений математических заданий с развернутым ответом, приводятся примеры оценивания решений и даются комментарии, объясняющие выставленную оценку.
Во второй части («Материалы для самостоятельной работы экспертов») в целях организации самостоятельной и групповой работы экспертов приводятся примеры решений, которые эксперты должны по результатам коллективного обсуждения оценить в соответствии с критериями оценивания выполнения заданий с развернутым ответом.
В третьей части («Материалы для проведения зачета») приведены примеры решений заданий с развернутым ответом, предназначенные для проведения индивидуальных зачетных работ по проверке подготовки экспертов.
Структура контрольно-измерительных материалов ЕГЭ-2010 по математике изменилась по сравнению с 2001-2009 гг., см. подробнее Спецификацию КИМ
, www.fipi.ru/view/sections/211/docs/471.html
Кратко перечислим основные параметры этих изменений, которые относятся к проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ 2010 года.
Во-первых, вместо 5 заданий с развернутым ответом среди полного набора из 26 заданий в каждом варианте, как это было в последние годы, в вариантах ЕГЭ-2010 будет по 6 заданий с развернутым ответом, а всего в варианте будет 18 заданий. При этом каждый вариант теперь состоит не из трех, а из двух частей и не содержит заданий с выбором ответа. Тем самым, набор заданий с развернутым ответом изменен и количественно, и качественно, и занимает новое положение в структуре всей работы.
В частности, если по статистике предыдущих лет, к выполнению заданий С1-С5 части 3 прежних КИМ приступало примерно 40% выпускников, то можно ожидать, что задания С1-С6 части 2 контрольно-измерительных материалов ЕГЭ-2010 по математике начнет выполнять заметно большее число участников экзамена, например, до 60%. Такое изменение имеет непосредственное отношение к работе членов региональных предметных комиссий, так как приведет к увеличению количества работ, подлежащих проверке экспертами. Видимо, в основном это коснется заданий уровня сложности С1 и С2.
Во-вторых, изменения коснулись шкалы оценивания заданий с развернутым ответом. Выполнение каждого из двух первых заданий С1 и С2 оценивается в 0 баллов, 1 балл или 2 балла. За выполнение каждого из двух следующих заданий С3 и С4 учащийся может получить оценку от 0 до 3 баллов. Выполнение заданий С5 и С6 оценивается от 0 до 4 баллов.
Напомним при этом, что шкалы оценивания заданий с развернутым ответом в 2005-2009 гг. были существенно смещены к своей верхней границе. Например, для заданий С1 и С2 оценка в 1 балл ставилась только за практически полное и верное решение и отличалась от 2 баллов наличием лишь небольших неточностей. Аналогично, 3 балла для заданий С3-С5 отличались от 4 баллов только вычислительными ошибками на последних этапах выполнения заданий. В 2010 году шкала оценивания имеет тенденцию к более равномерному распределению баллов в зависимости от продвижений учащихся в решении задачи. Подробнее это положение разъяснено ниже в §§1-6 на конкретных примерах.
В-третьих, предложен новый подход не только к формальной шкале оценивания, но и к самим критериям оценивания заданий с развернутым ответом. Напомним, что в 2001-2009 гг. членам региональных предметных комиссий для оценивания работ учащихся предлагались общие критерии и конкретизированные критерии. По мнению разработчиков КИМ ЕГЭ-2010, общие критерии предыдущих лет были слишком
общими: они были составлены для проверки любого решения вообще любой задачи по математике и при применении их к конкретным решениям конкретных учащихся возникали различные несостыковки. В свою очередь, конкретизированные критерии были излишне
конкретизированными: они относились лишь к единственному способу решения конкретной задачи, указанному разработчиками и в заметном числе случаев была неясна их применимость к другим способам решения той же самой задачи. Кроме того, текст критериев (к каждой из задач С3-С5) занимал около страницы текста, и понимание самих критериев требовало заметного времени у эксперта.
При разработке критериев для проверки работ учащихся в 2010 г. был выбран в некоторый промежуточный вариант. Пара (общие критерии; конкретизированные критерии) была заменена на один вид критериев, которые в определенном смысле одновременно являются и конкретными, и общими. А именно, для каждого конкретного типа из заданий С1-С6 ЕГЭ-2010 были составлены общие критерии проверки, не зависящие ни от тематической интерпретации задания в том или ином варианте КИМ, ни от способа решения, выбранного выпускником. Объем каждого из критериев составляет не более трети страницы текста.
В материалах этого пособия использованы оригиналы решений учащихся из различных диагностических работ в новом формате ЕГЭ-2010, которые были проведены в 2009 г.
В заключение отметим, что первоначальный вариант настоящего пособия прочли сотрудники лаборатории современных методов математического образования НИИСО Московского городского педагогического университета О. В. Кирюшкина, М. В. Шуркова, А. Р. Рязановский, П. В. Семенов. Авторы признательны им за проведенную апробацию и за высказанные (и не высказанные) многочисленные замечания и предложения.
§1. Задания с развернутым ответом повышенного уровня сложности С1.
Критерии проверки и оценки решений.
Задача 1.
Решите систему уравнений 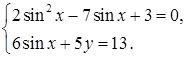
Решение №1
.
Из первого уравнения находим, что 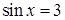 или или 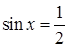 . .
Уравнение 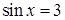 не имеет решений. не имеет решений.
Подставим 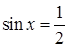 во второе уравнение и получим, что во второе уравнение и получим, что 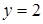 . .
Ответ
: 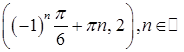 . .
Решение №2
.
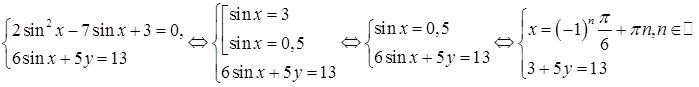
Ответ
: 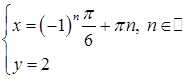 . .
Решение №3
.
Из второго уравнения 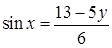 . Подставляем в первое уравнение . Подставляем в первое уравнение
 , , 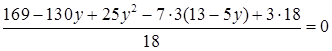 , ,
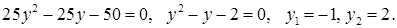
Поэтому 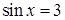 , что невозможно, так как , что невозможно, так как 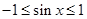 или или 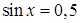 , т.е. , т.е.
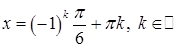 . .
Ответ
:  . .
Комментарий
.
К каждому из приведенных решений №№1-3 могут быть предъявлены в той или иной мере существенные претензии. Например, в решениях №1 и №2 нет никакого упоминания о множестве значений синуса, т.е., формально, не обосновано, почему отброшен случай 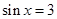 . В решении №1 много ненужных слов, а решение №3, как это принято называть, «не рационально». В решениях №№2 и 3 в ответ выписаны, формально, уравнения, а не множество решений системы уравнений, да и в решении №1 полагалось бы написать . В решении №1 много ненужных слов, а решение №3, как это принято называть, «не рационально». В решениях №№2 и 3 в ответ выписаны, формально, уравнения, а не множество решений системы уравнений, да и в решении №1 полагалось бы написать 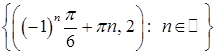 . В решении №3 запись . В решении №3 запись 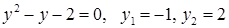 , вообще говоря, неясно, что означает, и корректнее следовало бы писать , вообще говоря, неясно, что означает, и корректнее следовало бы писать 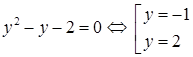 . .
Обсуждения решений этой задачи показали, что многие учителя, кроме того, считают совершенно необходимым введение новой переменной 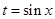 , явное выписывание дискриминанта и т.д. , явное выписывание дискриминанта и т.д.
Поиски некоего «оптимального», самого правильного, идеального решения – вещь затягивающая и в определенной степени увлекательная. Тут можно заострить методические копья, развернуть дискуссию на страницах печати, обвинить оппонента в полнейшей математической безграмотности и т.п.
Все это, однако, имеет довольно косвенное отношение к работе эксперта при проверке работ выпускников на ЕГЭ. Представим, что Вам при конкретной работе в качестве эксперта встретилось бы одно из решений №№1-3. В каждом из них ясно видна логика и конструкция всего решения, неверных утверждений, ошибок или описок нет, получен верный ответ.
Как же следует оценить эти решения? Можно пойти от противного, и переформулировать вопрос так. Если за такие
решения не
ставить 2 балла, то за что же их (2 балла) ставить? Только за те тексты, в которых есть явная ссылка на неравенство 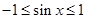 , а ответ выписан именно, как множество?? В таком случае, очевидно, что максимальный балл за решение этой задачи получат лишь несколько процентов всех участников экзамена. Напомним, что в силу новой структуры ЕГЭ-2010 по математике, к выполнению задания С1 вполне может приступить около 60-70% всех выпускников, т.е. более полумиллиона учеников. Поэтому излишне жесткие критерии оценивания выполнения этого задания могут в целом по стране дать лишь отрицательный эффект. Другими словами, позиция разработчиков КИМ ЕГЭ-2010 состоит в том, что за решения №№1-3 нельзя ставит 0 баллов, не следует ставить 1 балл, и, тем самым, эти решения заслуживают оценки в 2 балла. , а ответ выписан именно, как множество?? В таком случае, очевидно, что максимальный балл за решение этой задачи получат лишь несколько процентов всех участников экзамена. Напомним, что в силу новой структуры ЕГЭ-2010 по математике, к выполнению задания С1 вполне может приступить около 60-70% всех выпускников, т.е. более полумиллиона учеников. Поэтому излишне жесткие критерии оценивания выполнения этого задания могут в целом по стране дать лишь отрицательный эффект. Другими словами, позиция разработчиков КИМ ЕГЭ-2010 состоит в том, что за решения №№1-3 нельзя ставит 0 баллов, не следует ставить 1 балл, и, тем самым, эти решения заслуживают оценки в 2 балла.
Как уже отмечалось выше, в КИМ ЕГЭ-2010 по математике для всех типов заданий С1 предложено использовать унифицированные критерии оценивания. Выглядят они весьма кратко.
| Критерии оценивания выполнения задания С1
|
Баллы
|
| Обоснованно получен правильный ответ
|
2
|
| Получен ответ, но решение неверно только из-за того, что не учтены ограничения на знак или величину выражения cosx
(sinx
)
|
1
|
| Решение не соответствует ни одному из критериев, перечисленных выше
|
0
|
Отметим, что характер и критерии выставления 1 балла за выполнение задания С1 в 2010 году отличаются от предыдущих лет (2005-2009), когда оценка в 1 балл была очень сильно смещена к оценке в 2 балла. По критериям 2005-2009 гг. оценка в 1 балл выставлялась в тех случаях, когда задача по существу была решена полностью («…приведена верная последовательность всех шагов решения…»), но решение отличалось от «двубалльного» лишь наличием неточностей («…допущена одна описка и/или вычислительная ошибка, не влияющая на дальнейший ход решения…»).
В соответствии с критериями этого года при получении 1 балла вполне возможна ситуация, когда, решая систему уравнений, ученик после равенства 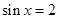 напишет напишет 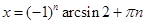 и включит «такие» и включит «такие» 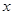 в ответ. В то же время, если ученик при решении квадратного уравнения, скажем, относительно в ответ. В то же время, если ученик при решении квадратного уравнения, скажем, относительно 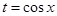 допускает вычислительную ошибку, «… не влияющую на дальнейший ход решения…», то решение неверно не
только
«…из-за того, что не учтены ограничения на знак или величину выражения cosx
(sinx
)..» и по этой причине такое решение оценивается в 0 баллов. Грубо говоря, имеется некоторый приоритет ошибок: ошибки начального, первого рода (арифметические, в вычислениях) наказываются весьма сурово, ошибки в более продвинутом учебном материале (множества значений тригонометрических функций) оцениваются не так жестко. допускает вычислительную ошибку, «… не влияющую на дальнейший ход решения…», то решение неверно не
только
«…из-за того, что не учтены ограничения на знак или величину выражения cosx
(sinx
)..» и по этой причине такое решение оценивается в 0 баллов. Грубо говоря, имеется некоторый приоритет ошибок: ошибки начального, первого рода (арифметические, в вычислениях) наказываются весьма сурово, ошибки в более продвинутом учебном материале (множества значений тригонометрических функций) оцениваются не так жестко.
Для конкретности приведем четыре возможные ситуации в записях учащихся:
А) … 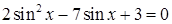  …. ….
Б) … 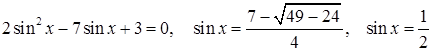 …. ….
В) … 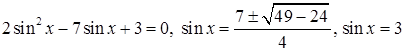 или или  , т.е. , т.е. 
Г) ….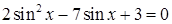  …. ….
В случае А) ошибок нет, и не следует настаивать на явном текстуальном обосновании того, что уравнение 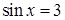 не имеет корней. В случае Б) явно приведено неверное решение квадратного уравнения, и, тем самым, решение неверно не
«…только из-за того, что не учтены ограничения на знак или величину выражения cosx
(sinx
)..». По этой причине такое решение оценивается в 0 баллов, хотя ответ вполне может оказаться и верным. В случае В) есть арифметическая ошибка и опять же решение неверно не
«…только из-за того, что не учтены ограничения на знак или величину выражения cosx
(sinx
)..». Значит, и тут 0 баллов. не имеет корней. В случае Б) явно приведено неверное решение квадратного уравнения, и, тем самым, решение неверно не
«…только из-за того, что не учтены ограничения на знак или величину выражения cosx
(sinx
)..». По этой причине такое решение оценивается в 0 баллов, хотя ответ вполне может оказаться и верным. В случае В) есть арифметическая ошибка и опять же решение неверно не
«…только из-за того, что не учтены ограничения на знак или величину выражения cosx
(sinx
)..». Значит, и тут 0 баллов.
Случай Г) – «пограничный», такие случаи практически всегда возникают при небольшой шкале оценок, примененных к большому массиву работ. Если трактовать его как неверное решение квадратного уравнения относительно синуса, то это – 0 баллов. Если его интерпретировать, как уравнение, верно решенное относительно 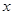 , («…а корень , («…а корень 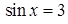 отброшен в уме…»), то при отсутствии ошибок в дальнейшем – это 2 балла. По крайней мере, при возможной апелляции работы учеником, у эксперта будет довольно большая головная боль: ведь ошибки в равносильностях из Г) нет. отброшен в уме…»), то при отсутствии ошибок в дальнейшем – это 2 балла. По крайней мере, при возможной апелляции работы учеником, у эксперта будет довольно большая головная боль: ведь ошибки в равносильностях из Г) нет.
Никто, кроме конкретного эксперта, оценивающего целиком всю конкретную работу конкретного ученика, не сможет принять тут (только по фрагменту Г) ) однозначного решения относительно оценивания.
Примеры оценивания выполнения заданий С1.
Пример 1.1.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий
.
Предложенное учащимся решение похоже на решение №1, но гораздо подробнее его. Явно описана замена переменных, явно указан ход решения квадратного уравнения. Все преобразования выполнены верно.
При описании двух независимых тригонометрических серий для переменной 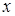 учащийся использовал два разных целочисленных параметра, хотя в ответе записал обе серии с помощью одного выражения с одним параметром. Поскольку оба способа задают одно и то же множество решений, такую запись в решении нельзя считать ошибочной. учащийся использовал два разных целочисленных параметра, хотя в ответе записал обе серии с помощью одного выражения с одним параметром. Поскольку оба способа задают одно и то же множество решений, такую запись в решении нельзя считать ошибочной.
Учащийся обосновал все этапы решения, верно выполнил преобразования, получил верный ответ.
Оценка эксперта:
2 балла.
Пример 1.2.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий
.
В целом, ясна логика решения.
Для решения первого уравнения сделана замена. В полученном квадратном уравнении выписан дискриминант и только один корень, но никаких оснований для отбрасывания второго корня в решении не прослеживается. Поэтому в тексте не удается отследить верное решение первого уравнения.
Второе уравнение системы выписано с ошибкой: совершенно неясно как синус вдруг стал косинусом. Кроме того, и в дальнейшем переход от синуса к косинусу содержит ошибку. Тригонометрическое уравнение 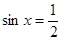 решено верно (судя по ответу). решено верно (судя по ответу).
Указанное в ответе значение у
никак не следует из предложенного решения.
Несмотря на правильный ответ, решение может быть оценено только в 0 баллов, так как оно неверно по многим причинам, из которых неучет множества значений синуса – лишь одна из них.
Оценка эксперта: 0 баллов.
Пример 1.3.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий.
Все замечательно. Однако, конечный ответ не получен (не выписан). Тем самым, 2 балла ставить нельзя. Но и 0 баллов поставить невозможно: ведь задача по существу решена верно и полностью.
Тут типичный пример оценивания «по дополнению». Остается ставить 1 балл, несмотря на некоторое формальное несоответствие с предлагаемыми критериями выставления 1 балла.
Оценка эксперта:
1 балл.
В следующем примере задания С1 мы ограничимся лишь одним способом записи его решения, аналогичным решению №1 предыдущей задачи. Ясно, как будут выглядеть аналоги решений №2 и №3.
Задача
2.
Решите систему уравнений 
Решение
.
Из первого уравнения находим, что 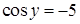 или или 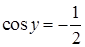 . .
Уравнение 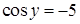 не имеет решений. не имеет решений.
Из уравнения 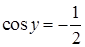 находим: находим:  . .
Подставим 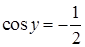 во второе уравнение и получим: во второе уравнение и получим: 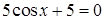 , откуда , откуда 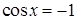 , и , и 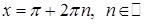 . .
Ответ
: 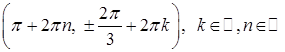 . .
В целом, по своей структуре задача 2 практически совпадает с задачей 1. Однако, есть и серьезное отличие: для нахождения значений переменной 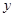 требуется решать не линейное, а простейшее тригонометрическое уравнение. Нетрудно предугадать типичную ошибку даже неплохо подготовленных учеников. Она связана с тем, что для выписывания корней уравнения требуется решать не линейное, а простейшее тригонометрическое уравнение. Нетрудно предугадать типичную ошибку даже неплохо подготовленных учеников. Она связана с тем, что для выписывания корней уравнения 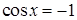 и корней уравнения и корней уравнения 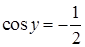 многие выберут один и тот же целочисленный параметр, скажем, многие выберут один и тот же целочисленный параметр, скажем,  . К этому нельзя отнестись, как к простой формальной описке: ведь получается просто неверный ответ. . К этому нельзя отнестись, как к простой формальной описке: ведь получается просто неверный ответ.
Поэтому, эта задача, хотя в целом и находится в рамках сложности для заданий С1, несколько сложнее для учащихся, чем предыдущая. Дело в том, что задача 1 и задача 2 взяты из разных диагностических работ, проводившихся в разное время и их «выравнивание» по сложности производилось лишь приближенно. Критерии выставления 0, 1 или 2 баллов для задачи 2 были несколько иными.
| Баллы
|
Критерии оценивания выполнения задания С1
|
| 2
|
Обоснованно получен правильный ответ
|
| 1
|
Верно решено первое уравнение, но система решена неверно.
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше
|
Подчеркнем, что условие «Верно решено первое уравнение, но система не решена верно.» отличается от условия «Верно решено первое уравнение, но система решена неверно.» достаточного для получения 1 балла. В последнем случае подразумевается, что решение (быть может, и неверное) доведено до конца, а в первом случае разрешалось бы полностью остановиться после решения только первого уравнения.
Пример 2.1.
Решение задачи 2, комментарий и оценка этого решения.
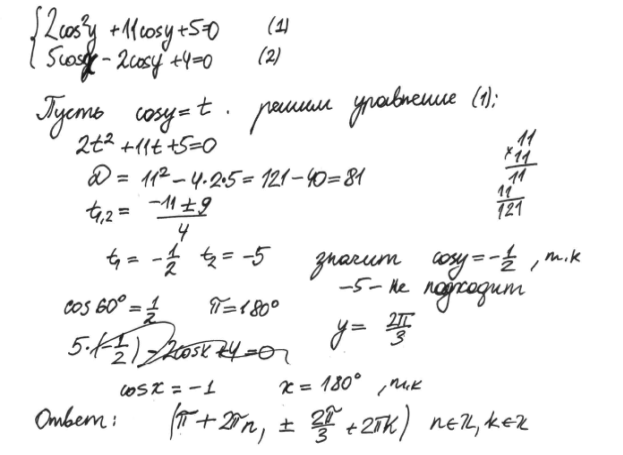
Комментарий
.
Довольно непростой случай. Ясна последовательность шагов решения и логика решения прослеживается.
Технические преобразования выполнены верно. При решении тригонометрических уравнений внутри текста явно не выписаны корни. Более точно, указаны лишь «основные» корни, причем для  ответ вообще в градусах(!). Но, в итоге, все корни верно указаны при выписывании ответа. ответ вообще в градусах(!). Но, в итоге, все корни верно указаны при выписывании ответа.
Имеется попытка неверной подстановки во второе уравнение, но она зачеркнута учеником. В решении есть и посторонние записи (умножение столбиком), что может быть оценено как несформированная культура записи решения математических задач, но формально оснований для снижения баллов нет.
Оценка
эксперта:
2 балла.
Пример 2.2.
Решение задачи 2, комментарий и оценка этого решения.

Комментарий
.
Технические преобразования выполнены верно, однако при записи серий решений для  и и 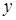 учащийся допустил ошибку: общий целый параметр учащийся допустил ошибку: общий целый параметр 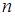 формально связывает серии. Таким образом, учащийся нашел не все множество решений, а только часть. формально связывает серии. Таким образом, учащийся нашел не все множество решений, а только часть.
Несмотря на это, следует отметить владение техникой решения тригонометрических уравнений, логикой преобразований, корректное использование равносильных переходов.
Формально «Верно решено первое уравнение, но система решена неверно.», что соответствует критерию в 1 балл.
Оценка
эксперта:
1 балл.
Пример 2.3.
Решение задачи 2, комментарий и оценка этого решения.
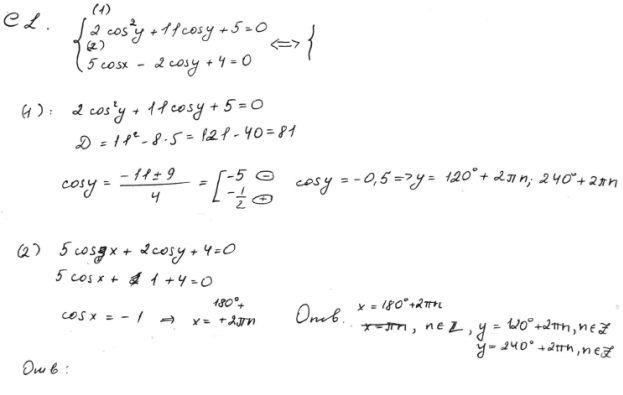
Комментарий.
Крайне неприятная ситуация. Работа явно «не пустая».
Учащийся продемонстрировал некоторую технику преобразований при решении системы уравнений. Однако допустил серьезную ошибку, выразив переменные в градусах. Это говорит о непонимании природы тригонометрических функций числовых аргументов. Выражения вида 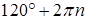 формально не имеют смысла. формально не имеют смысла.
Кроме того, при записи серий решений для  и и 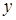 учащийся допустил стандартную ошибку: общий целый параметр учащийся допустил стандартную ошибку: общий целый параметр 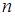 формально связывает серии. Таким образом, учащийся нашел не все множество решений, а только часть. формально связывает серии. Таким образом, учащийся нашел не все множество решений, а только часть.
Формально условие «Верно решено первое уравнение…» не выполнено, но содержательно (по картинке, по числовой окружности) оно как раз таки выполнено.
Оценка эксперта:
1 балл.
Рассмотрим еще один пример задания уровня сложности С1 и три примера его решений учащимися. Как и в предыдущем примере, мы ограничимся лишь одним способом записи его решения.
Задача
3.
Решите систему уравнений 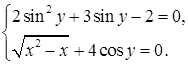
Решение
.
Пусть 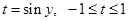 . Тогда . Тогда 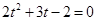 и и 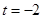 , что невозможно, или , что невозможно, или 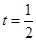 , т.е. , т.е.
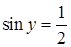 , , 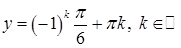 . Но . Но 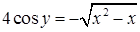 , т.е. , т.е. 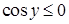 . Поэтому . Поэтому
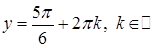 и и 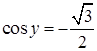 . .
Тогда 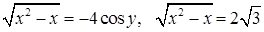 ; ; 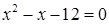 , т.е. , т.е. 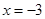 или или  . .
Ответ
: 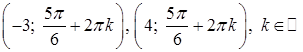 . .
Как и предыдущая задача, задача 3 по своей структуре практически совпадает с задачей 1: тоже система, тоже «квадратно-тригонометрическое» уравнение. Однако, существенным отличием является необходимость отбора корней уравнения 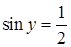 с учетом знака косинуса из второго уравнения. Ясно, что ответ с учетом знака косинуса из второго уравнения. Ясно, что ответ 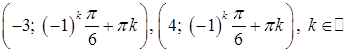 является весьма типичной ошибкой. Кроме того, наличие двух серий пар в ответе весьма непривычно для действующих школьных УМК, т.е. для многих учеников сам вид ответа в такой задаче также является весьма необычным. Поэтому, эта задача, находится, пожалуй, на верхней допустимой грани сложности для заданий уровня С1. Это задача с еще одной диагностической работы, и вопрос ее «уравнивания» по сложности предыдущим задачам 1 и 2 в полной мере не рассматривался. является весьма типичной ошибкой. Кроме того, наличие двух серий пар в ответе весьма непривычно для действующих школьных УМК, т.е. для многих учеников сам вид ответа в такой задаче также является весьма необычным. Поэтому, эта задача, находится, пожалуй, на верхней допустимой грани сложности для заданий уровня С1. Это задача с еще одной диагностической работы, и вопрос ее «уравнивания» по сложности предыдущим задачам 1 и 2 в полной мере не рассматривался.
Тем не менее, критерии оценивания выставления 0, 1 или 2 баллов остаются неизменными. Отметим, что многие учителя считают необходимым в данном случае выписывание «ОДЗ подкоренного выражения». Если это сделать верно, то вреда не будет. Правда, не будет и никакой пользы: ведь корни 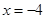 и и 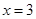 найдены из уравнения найдены из уравнения 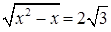 или или 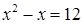 , т.е. подкоренное выражение автоматически положительно. Тем самым, снижение оценки за отсутствие ОДЗ здесь недопустимо. , т.е. подкоренное выражение автоматически положительно. Тем самым, снижение оценки за отсутствие ОДЗ здесь недопустимо.
| Баллы
|
Критерии оценивания выполнения задания С1
|
| 2
|
Обоснованно получен правильный ответ
|
| 1
|
Верно решено первое уравнение, но система решена неверно
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше
|
Пример 3.1.
Решение задачи 3, комментарий и оценка этого решения.

Комментарий
.
Что-то весьма разумное в этой работе есть: введение новой переменной, решение квадратного уравнения, верно найдены значения неизвестной 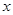 , в целом ход решения правильный , в целом ход решения правильный
В то же время, вообще ничего не сказано про отбрасывание корня -2 в квадратном уравнении относительно 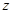 . Учет условия . Учет условия 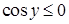 отсутствует. Более того, косинус формулой выражен через синус просто неверно, хотя ниже, для конкретного отсутствует. Более того, косинус формулой выражен через синус просто неверно, хотя ниже, для конкретного 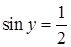 , косинус выражен верно. Все-таки, основной ошибкой здесь следует считать принципиально неверное решение простейшего тригонометрического уравнения , косинус выражен верно. Все-таки, основной ошибкой здесь следует считать принципиально неверное решение простейшего тригонометрического уравнения 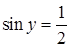 (хоть с учетом (хоть с учетом 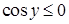 , хоть без учета). Поэтому условие «Верно решено первое уравнение» (относительно , хоть без учета). Поэтому условие «Верно решено первое уравнение» (относительно 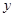 ) из критериев на 1 балл не выполнено. ) из критериев на 1 балл не выполнено.
Оценка:
0 баллов.
Пример 3.2.
Решение задачи 3, комментарий и оценка этого решения

Комментарий
.
Ситуацию удобно сравнить с предыдущим примером 3.1. Тут положение даже лучше: есть условие 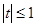 и его использование, есть учет отрицательности косинуса. Однако учащийся демонстрирует незнание табличных значений тригонометрических функций. При условиях и его использование, есть учет отрицательности косинуса. Однако учащийся демонстрирует незнание табличных значений тригонометрических функций. При условиях 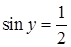 и и 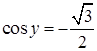 учащийся заявляет, что учащийся заявляет, что 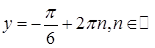 , а в ответе значения , а в ответе значения  вообще зависят от значений вообще зависят от значений 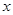 . Таким образом, даже первое уравнение не решено. . Таким образом, даже первое уравнение не решено.
Оценка:
0 баллов.
Пример 3.3.
Решение задачи 3, комментарий и оценка этого решения.

Комментарий
.
Нет учета знака косинуса, ответ неверен и поэтому – это точно не 2 балла.
Кроме того, неприятность в том, что в самом начале (вторая строка текста) утверждается, что 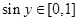 и ниже использовано именно это утверждение. Если трактовать это как локальное помутнение рассудка (ведь ниже рассмотрен случай отрицательных значений косинуса!), то условие «Верно решено первое уравнение» из критериев на 1 балл выполнено. Если же интерпретировать это как принципиальное незнание основ тригонометрии, то тогда следует ставить 0 баллов. и ниже использовано именно это утверждение. Если трактовать это как локальное помутнение рассудка (ведь ниже рассмотрен случай отрицательных значений косинуса!), то условие «Верно решено первое уравнение» из критериев на 1 балл выполнено. Если же интерпретировать это как принципиальное незнание основ тригонометрии, то тогда следует ставить 0 баллов.
Никто, кроме конкретного эксперта, оценивающего целиком всю конкретную работу конкретного ученика, не сможет принять тут однозначного решения.
Оценка:
1 балл (возможно, и 0 баллов).
Пример 3.4.
Решение задачи 3, комментарий и оценка этого решения.

Комментарий.
Логика решения понятна. Отбор решений в соответствии с условием 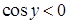 , вероятно, не сделан. Тем не менее, первое уравнение решено верно, а вся система решена (получены значения неизвестных), но, скорее всего, неверно: : полностью судить нельзя, поскольку ответ не выписан. , вероятно, не сделан. Тем не менее, первое уравнение решено верно, а вся система решена (получены значения неизвестных), но, скорее всего, неверно: : полностью судить нельзя, поскольку ответ не выписан.
Оценка:
1 балл.
§2. Задания с развернутым ответом повышенного уровня сложности С2.
Критерии проверки и оценки решений.
Задача 1.
В правильной шестиугольной призме A
… F
1
, все ребра которой равны 1, найдите угол между прямыми AB
1
и BE
1
. 
Решение №1.
Так как основание призмы – правильный шестиугольник, то 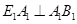 . Так как призма прямая, то . Так как призма прямая, то 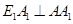 . Поэтому . Поэтому , т.е. , т.е. 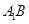 есть проекция наклонной есть проекция наклонной 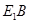 на плоскость на плоскость 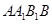 . Диагонали в квадрате . Диагонали в квадрате 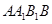 перпендикулярны между собой. По теореме о трех перпендикулярах наклонная перпендикулярны между собой. По теореме о трех перпендикулярах наклонная 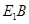 и прямая и прямая 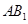 , перпендикулярны между собой, т.е. искомый угол равен 90о
. Ответ.
90°. , перпендикулярны между собой, т.е. искомый угол равен 90о
. Ответ.
90°.
 Решение №2.
Через точку B
проведем прямую, параллельную прямой AB
1
, и обозначим G
1
ее точку пересечения с прямой A
1
B
1
. Тогда по Решение №2.
Через точку B
проведем прямую, параллельную прямой AB
1
, и обозначим G
1
ее точку пересечения с прямой A
1
B
1
. Тогда по 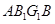 есть параллелограмм, а искомый угол равен углу E
1
BG
1
. есть параллелограмм, а искомый угол равен углу E
1
BG
1
.
Вычислим стороны треугольника E
1
BG
1
1) 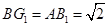 . .
2) В прямоугольном треугольнике BEE
1
катеты BE
и EE
1
равны соответственно 2 и 1. Следовательно, гипотенуза BE
1
равна 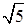 . .
3) Так как 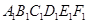 – правильный шестиугольник, то – правильный шестиугольник, то 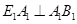 и и  . Следовательно, . Следовательно, 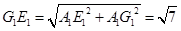 . Поэтому . Поэтому 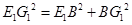 . По теореме, обратной к теореме Пифагора, получаем, что угол E
1
BG
1
равен 90о
. Ответ.
90°. . По теореме, обратной к теореме Пифагора, получаем, что угол E
1
BG
1
равен 90о
. Ответ.
90°.
Решение № 3.
Пусть точка А – начало прямоугольной системы координат, АВ – единичный отрезок по оси Ox, а 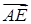 и и 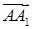 – направления осей Oy и Oz. Тогда – направления осей Oy и Oz. Тогда  . Так как в нижнем основании лежит правильный шестиугольник, то . Так как в нижнем основании лежит правильный шестиугольник, то 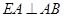 и и 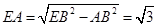 . Поэтому . Поэтому 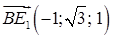 , , 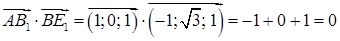 , и , и 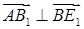 . .
Ответ: 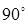 . .
Комментарий
.
На втором месте в задачах с развернутым ответом разработчики КИМ ЕГЭ-2010 сознательно поставили именно геометрическую, и именно стереометрическую задачу. Положение дел, сложившееся с преподаванием геометрии в российских школах крайне тяжелое, а положение стереометрии, мягко говоря, катастрофическое.
Среди множества различных причин выделим отсутствие на протяжении многих лет геометрической (стереометрической) составляющей в получении выпускниками аттестационной оценки за курс математики средней школы. Формат КИМ ЕГЭ предыдущих лет, когда аттестационная оценка выставлялась только по разделу «Алгебра и начала математического анализа», закрепил дополнительность, определенную необязательность изучения стереометрии в старшей школе. Во многих выпускных классах различных регионов в последние несколько лет учащиеся фактически переставали изучать стереометрию, особенно во втором полугодии 11-го класса.
Восстанавливать нормальное положение дел довольно сложно. Получение оценки на ЕГЭ-2010, как оценки именно по математике
, а не только по алгебре и началам математического анализа, является, очевидно, первым необходимым шагом.
Следующий шаг состоит в позиционировании стереометрической задачи, как задачи для большинства нормально успевающих учеников, а не только для избранных. Реализация этого положения состоит в том, что в КИМ предлагается задача по стереометрии с минимальными техническими вычислениями, и располагается она на одном из первых мест среди задач с развернутым ответом.
При разработке критериев оценивания выполнения заданий С2 разработчики существенно ослабили (по сравнению с привычными «советскими» временами и традиционными математическими стандартами) условия получения максимального балла. Достаточными являются верное изображение, описание, констатация положения искомого угла и верно проведенное вычисление. Не являются необходимыми точные обоснования того, почему именно та или иная прямая является, например, проекцией другой прямой, или же что она параллельна (перпендикулярна) другой прямой или плоскости.
Подчеркнем, что никто не против присутствия этих обоснований (например, они в минимальном, но достаточно полном объеме приведены выше в решениях №№1-3). При наличии таких обоснований (и верных вычислений), разумеется, следует выставлять 2 балла. Но те же 2 балла, по мнению разработчиков, следует выставлять и в тех случаях, когда в решении учащегося лишь продемонстрирована верная конструкция. Дело в том, что, к сожалению, даже такое условие для нынешней российской школы является весьма ограничительным, и сама постановка вопроса о грамотной обоснованности такого построения – есть вещь экзотическая для многих выпускников (и некоторых учителей). Грубо говоря, многие достаточно хорошие выпускники за время своего обучения вполне могли просто отвыкнуть (или не привыкнуть) приводить необходимые доказательства верности своих конструкций: они их «видят», и по школьной своей привычке считают это достаточным.
| Критерии оценивания выполнения задания С2
|
Баллы
|
| Обоснованно получен правильный ответ
|
2
|
| Способ нахождения искомого угла верен, но получен неверный ответ или решение не закончено
|
1
|
| Решение не соответствует ни одному из критериев, перечисленных выше
|
0
|
Примеры оценивания заданий
C
2.
Пример 1.1.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий
.
Довольно необычная ситуация. В тексте, написанном, очевидно, хорошо подготовленным учеником, нет ошибок, верно проведены многие построения и доказаны некоторые факты. Однако нет главного – самого решения задачи, так как отсутствует построение или описание плоского угла, равного искомому. Решение не доведено до конца и не видно, каким образом автор предполагал бы продолжить свое решение. Нет ответа.
Оценка эксперта:
0 баллов.
Пример 1.2.
Решение задачи 1, комментарий и оценка этого решения.
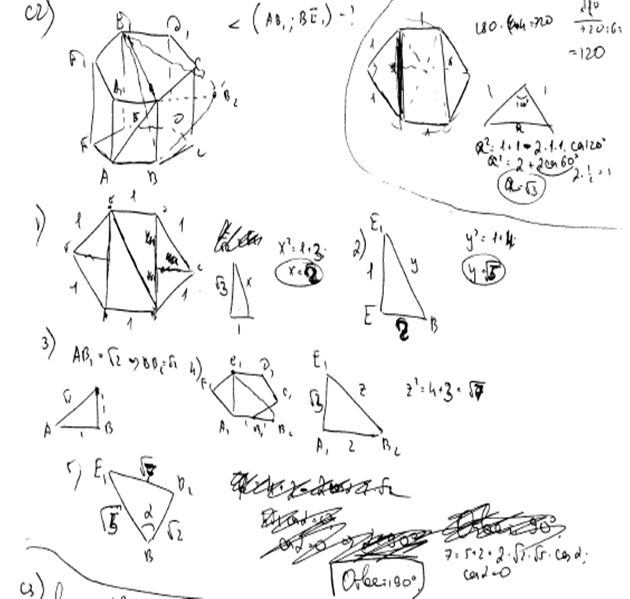
Комментарий
.
Первая реакция проверяющих на этот текст понятна. «Да это издевательство, комикс какой-то!», «Руки бы поотрывать за такую запись!!» - вот примеры относительно вежливых высказываний.
Тем не менее, следует признать, что автор, несомненно, верно решил задачу и, например, при устной апелляции легко обоснует все пункты 1)-3). Почему он не оформил свое решение в более пристойном виде, теперь уже не узнает никто.
Итак, получен правильный ответ, все приведшие к нему вычисления проиллюстрированы (не слишком адекватными) рисунками, имеется верное изображение искомого угла. Собственно, не хватает только описания и обоснования того, как именно построен этот угол. Скорее всего, конкретный преподаватель в «своем» конкретном классе вряд ли оценит эту «мазню» максимальным баллом, но по критериям на ЕГЭ-2010 это именно максимальный балл, см. комментарии выше.
Оценка эксперта:
2 балла.
Пример 1.3.
Решение задачи 1, комментарий и оценка этого решения.
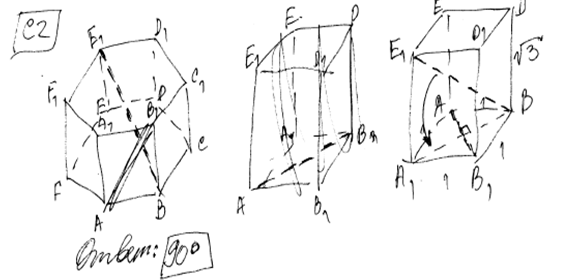
Комментарий
.
По трем приведенным рисункам ход решения автора восстанавливается однозначно. Он вырезает из призмы «центральный» прямоугольный параллелепипед, ставит его на боковую грань, на эту грань проецирует диагональ и использует теорему о трех перпендикулярах.
Вообще говоря, эксперт оценивает в основном не замыслы автора, а их реализацию в тексте работы. В данном случае, с реализацией - дело неважное. А именно, отсутствует обоснование нахождения искомого угла. Тем не менее, как и в предыдущем примере, по критериям на ЕГЭ-2010 это - именно максимальный балл.
В некотором смысле, включение именно этого ученического решения, на наш взгляд ярко демонстрирует «нижнюю грань» для возможного выставления максимального балла.
Оценка эксперта:
2 балла.
Пример 1.4.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий
.
Это – типичный пример того, что происходит со сканированием текста, записанного не
гелевой, и к тому же, синей шариковой ручкой. Легкомысленное отношение к этому обстоятельству может создать совершенно ненужные сложности эксперту, вплоть до того, что он просто откажется проверять такой текст. И кстати, имеет на это право.
Так как задача нам хорошо известна, то по читаемым фрагментам текста видно, что это по существу версия решения №2, только диагональ из передней грани переносится на заднюю грань, и тем самым строится нужный плоский угол. Тем самым, способ нахождения искомого угла верен. В то же время, получен неверный ответ. Ошибка ясно видна: при вычислении  диагональ диагональ 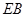 «приравняна» автором к диагонали «приравняна» автором к диагонали 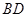 . .
Довольно ясный случай получения 1 балла.
Оценка эксперта:
1 балл.
Пример 1.5.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий
.
Этот пример решения удобно сравнить с примером 1.2. По крайней мере, степень неряшливости примерно такая же. Но тут есть и существенное отличие. А именно, полностью прописано построение плоского угла, равного искомому углу между прямыми. Ясно, что оценка тут не может быть хуже, чем в примере 1.2 или 1.3. Значит, это 2 балла.
Оценка эксперта:
2 балла.
В качестве еще одного примера задания уровня сложности С2 рассмотрим задачу, в которой требуется найти угол между плоскостями, а не угол между скрещивающимися прямыми.
Задача 2.

 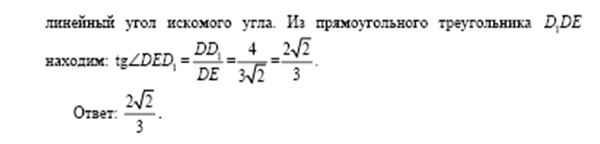
Комментарий
.
Обратим внимание на то, что при более грамотном изложении решения полагалось бы сослаться на равнобедренность треугольников, совпадение в них медианы с высотой, признак перпендикулярности прямой и плоскости, теорему Пифагора и, может быть, еще на что-нибудь.
Однако, если все эти условия включить в качестве необходимых для получения максимального балла, то, во-первых, это будет большой неожиданностью для очень многих, даже весьма успевающих, школьников, во-вторых, приведет к резкому снижению интереса к выполнению стереометрических заданий и, наконец, существенно снизит общую оценку на ЕГЭ-2010 за выполнение задания С2.
Пример 2.1.
Решение задачи 2, комментарий и оценка этого решения.

Комментарий
.
Это несомненно (по критериям ЕГЭ-2010) максимальный балл. Угол изображен верно, вычисления и ответ верны. Более того, есть, быть может и неполные, обоснования: ссылка на использование параллельности верхней и нижней граней, равенство угла между плоскостями некоторому плоскому углу, явное указание на то, что в основании лежит квадрат.
Оценка эксперта:
2 балла.
Пример 2.2.
Решение задачи 2, комментарий и оценка этого решения.

Комментарий
.
Так как ответ неверен, то тут не может идти речи о выставлении 2 баллов. Остается небольшой выбор: 1 балл или 0 баллов. С одной стороны, имеются некоторые вполне разумные построения, записанные достаточно грамотным образом. Более того, в конце п. 2) явно описан нужный линейный угол двугранного угла. С другой стороны, для нахождения тангенса угла автор зачем-то вычисляет гипотенузу и делит друг на друга длины равных отрезков, что вообще не дает никакого тангенса. Поэтому условие «Способ нахождения искомого угла верен…» необходимое для получения 1 балла, формально, здесь выполнено: сам угол указан на рисунке верно (см. конец 2)), а вычисляется, почему-то, совсем не он.
Оценка эксперта:
1 балл (хотя, возможно, кто-то сочтет верной и оценку 0 баллов).
Пример 2.3.
Решение задачи 2, комментарий и оценка этого решения.

Комментарий
.
Это еще один пример того, как при сканировании может выглядеть текст, написанный не
гелевой ручкой.
Ученик ясно и довольно подробно (по любым меркам) обосновал построение нужного линейного угла. Однако, он «сэкономил» на вычислениях, не привел их и, видимо, не проверял. Это привело к неверному ответу. Может быть, он вообще не проводил вычислений, по рисунку «увидел», что угол похож на стандартный угол в 30 градусов и сразу написал ответ. Странно, что его не остановил тот факт, что в условии речь идет о тангенсе угла, а он в ответе дает сам угол.
Все же, решение закончено, ответ (неверный) имеется, способ нахождения угла приведен верно.
Оценка эксперта:
1 балл.
Пример 2.4.
Решение задачи 2, комментарий и оценка этого решения.

Комментарий
.
Вряд ли тут нужные особые комментарии. По нынешним реалиям так и хочется сказать: «Бывает же!»
Оценка эксперта: 2 балла
.
§3. Задания с развернутым ответом повышенного уровня сложности С3.
Критерии проверки и оценки решений.
Задача 1.
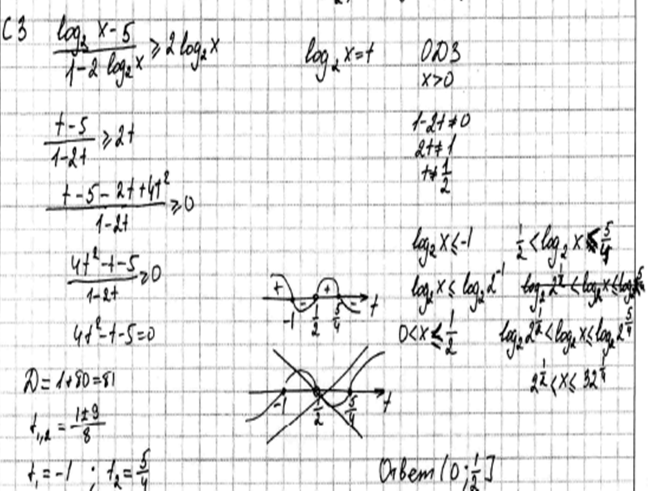
Решите неравенство 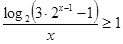 . .
Решение №1
.
1) Неравенство определено, если 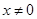 и если и если 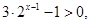 т.е. если т.е. если 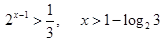 . .
2) Пусть 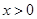 . Тогда . Тогда 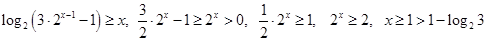 . .
3) Пусть 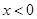 . Тогда . Тогда 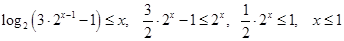 . Поэтому в этом случае . Поэтому в этом случае 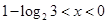 . Объединяя множества решений из 2) и 3), получаем ответ. . Объединяя множества решений из 2) и 3), получаем ответ.
Ответ:
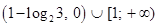 . .
Решение №2
. Используем следующее утверждение: «Если функция 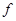 возрастает на множестве, то выражения возрастает на множестве, то выражения 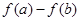 и и 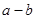 имеют одинаковый знак для всех имеют одинаковый знак для всех 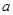 и и 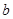 из этого множества». Сначала используем его для из этого множества». Сначала используем его для 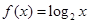 , а затем для , а затем для 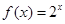 . .
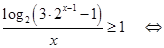 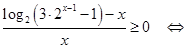 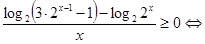
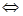 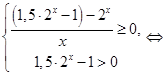  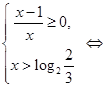 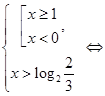 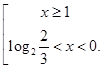 . .
Ответ
: 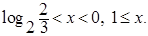
Решение №3
.
Рассмотрим непрерывную функцию 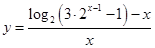 . Она определена при . Она определена при 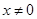 и и 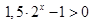 , т.е. , т.е. 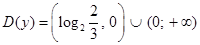 . Найдем нули функции: . Найдем нули функции: 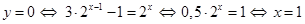 . .
Если 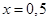 , то , то 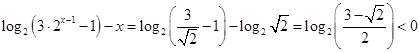 и и 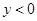 . Поэтому . Поэтому 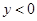 на всем промежутке на всем промежутке 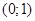 . Если . Если 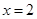 , то , то 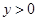 . Поэтому . Поэтому 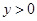 на всем промежутке на всем промежутке 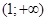 . В итоге, непрерывная функция меняет свой знак при прохождении через точку . В итоге, непрерывная функция меняет свой знак при прохождении через точку 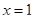 (нуль числителя) и через точку (нуль числителя) и через точку 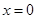 (нуль знаменателя). Поэтому (нуль знаменателя). Поэтому 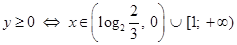 . .
Ответ:
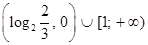 . .
Комментарий.
Существует много различных способов оформления решения этого неравенства. Выше выбраны три, в определенном смысле «экстремальных» способа. Решение №1 (перебор случаев) крайне традиционно. Решение №2 использует так называемый «метод замены множителей», довольно широко известный в весьма узких кругах (следящих за тенденциями вступительных экзаменов в МГУ), но практически неизвестный рядовым пользователям школьных УМК. Решение №3 по существу есть обобщенный метод интервалов.
«У каждого – свои недостатки». Есть они и у решений №№1-3. В решении №1 грамотнее было бы вместо запятых между неравенствами или системами неравенств расставить значки 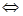 . Более того, словесный оборот «Пусть…Тогда…» подразумевает импликацию «из А следует В», в то время как для решения существенна именно равносильность. В решении №2 ответ записан (по мнению некоторых методистов) в ужасной форме: это не множество, а два неравенства, причем без указания связи между ними. Кроме того, в описании метода замены множителей, формально, отсутствует случай . Более того, словесный оборот «Пусть…Тогда…» подразумевает импликацию «из А следует В», в то время как для решения существенна именно равносильность. В решении №2 ответ записан (по мнению некоторых методистов) в ужасной форме: это не множество, а два неравенства, причем без указания связи между ними. Кроме того, в описании метода замены множителей, формально, отсутствует случай  . В решении №3 нет обоснований непрерывности введенной функции, как нет и явных ссылок на те места, где эта непрерывность необходима. . В решении №3 нет обоснований непрерывности введенной функции, как нет и явных ссылок на те места, где эта непрерывность необходима.
Поиск «абсолютно идеальной» записи – красиво звучащая проблема, процесс решения которой является довольно увлекательной деятельностью, но весьма далекой от реалий работы экспертов при проверке работ на ЕГЭ по математике. Представим, что Вам при конкретной работе в качестве эксперта встретилось бы одно из решений №№1-3. В каждом из них ясно видна логика и конструкция всего решения, неверных утверждений, ошибок или описок нет, получен верный ответ. Все это соответствует случаю выставления максимального балла. Для заданий уровня С3 – это 3 балла.
Обратим внимание на то, что зачастую в представленных ниже решениях учеников полностью отсутствуют комментарии–слова и не всегда корректно используются знаки импликаций. Поэтому эксперту необходимо внимательно просмотреть все формулы и понять, правильна или нет общая логика решения и без особых причин не «наказывать» учеников за неправильное использования логических знаков.
Тонкость в данный момент состоит в том, что задача 1 взята, разумеется, не из реальных КИМ ЕГЭ-2010, эта задача предлагалась на одной из диагностических работ и для оценивания ее выполнения критерии несколько отличались от тех, которые будут на реальном ЕГЭ. Выглядели они вот так.
| Баллы
|
Критерии оценивания выполнения задания С3
|
| 3
|
Обоснованно получен правильный ответ
|
| 2
|
Ответ не точен т.к. допущена описка или при в основном правильном решении в ответ включены значения переменной, при которых логарифмируемое выражение обращается в 0
|
| 1
|
Решение содержит верные преобразования. Из-за ошибок потеряны промежутки решения, либо в ответ включены лишние промежутки
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше.
|
Процитируем и критерии, которые будут использоваться на реальном ЕГЭ-2010.
| Критерии оценивания выполнения задания С3
|
Баллы
|
| Обоснованно получен правильный ответ
|
3
|
| Обоснованно получен ответ, отличающийся от верного только конечным числом точек.
|
2
|
| Полученный ответ неверен, но решение содержит переход от исходного неравенства к верным рациональным неравенствам.
|
1
|
| Решение не соответствует ни одному из критериев, перечисленных выше
|
0
|
Последние критерии при выставлении 1 балла не всегда могут быть применены к решениям задачи 1, см. выше решения №№1 и 3, в которых просто нет никаких рациональных неравенств. Поэтому ниже будем использовать именно критерии из диагностической работы.
Примеры оценивания заданий С3.
Пример 1.1.
Решение задачи 1, комментарий и оценка этого решения.
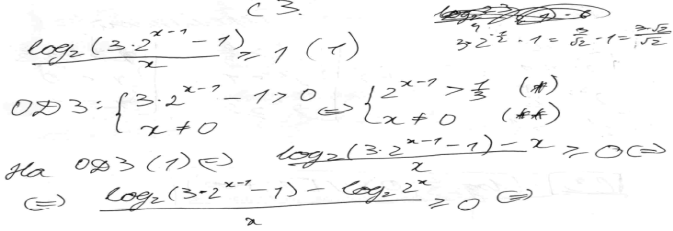

Комментарий
.
Предложенное учащимся решение по своей структуре напоминает смесь решений №1 и №2, однако гораздо подробнее и того, и другого.
Учащийся подробно обосновал все этапы решения, верно выполнил преобразования, получил верный ответ.
Оценка эксперта:
3 балла.
Пример 1.2.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий
.
Формально, это наглядный пример того, что получается при сканировании текста, написанного не
гелевой ручкой. Вообще говоря, эксперт может просто отказаться проверять подобного качества текст, сославшись на невозможность его прочтения.
Содержательно, логика решения верна. Для  в тексте получен верный ответ в тексте получен верный ответ  , но в ответе почему-то стоит , но в ответе почему-то стоит  . При нахождении ОДЗ есть арифметическая ошибка при переносе -1 в другую часть неравенства. По критериям, арифметическая ошибка (ошибка базового уровня) «наказывается» строже, нежели ошибка, связанная, например, с «пропущенным делением на ноль», т.е. чем ошибка в более сложном учебном материале. . При нахождении ОДЗ есть арифметическая ошибка при переносе -1 в другую часть неравенства. По критериям, арифметическая ошибка (ошибка базового уровня) «наказывается» строже, нежели ошибка, связанная, например, с «пропущенным делением на ноль», т.е. чем ошибка в более сложном учебном материале.
Оценка эксперта:
1 балл.
Пример 1.3.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий
.
Формально, это еще один наглядный пример того, что получается при сканировании текста, написанного не
гелевой ручкой. Чтобы разобрать текст, его пришлось при включении в это пособие увеличивать в полтора раза.
Содержательно, логика решения верная, напоминает решение №3 приведенное выше. Неясно, почему зачеркнуто верно найденное и нужное ограничение 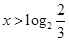 . .
Решая неравенство методом интервалов, учащийся «забывает» о знаке знаменателя дроби, поэтому получает правильное решение только для 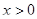 . Такое решение неравенства, согласно критериям, оценивается 1 баллом. . Такое решение неравенства, согласно критериям, оценивается 1 баллом.
Оценка эксперта:
1 балл.
Пример 1.4.
Решение задачи 1, комментарий и оценка этого решения.
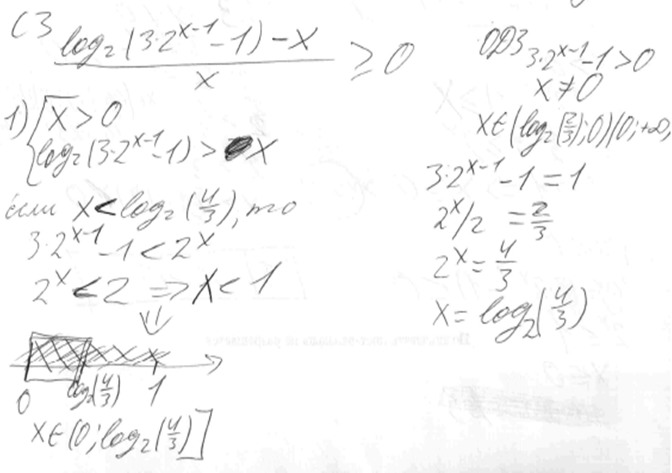
Комментарий
.
Верно найдена ОДЗ.
Все остальное содержит ошибки почти в каждой строке:
а) неясно, что для решения может дать точка 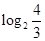 и зачем ее находить; и зачем ее находить;
б) есть случай 1) 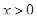 , но нет случая , но нет случая 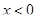 ; ;
в) нестрогое неравенство «превращается» в строгое;
г) «избавление» от логарифмов произведено с ошибкой в знаке неравенства.
Другими словами, учащийся лишь имитирует верную схему решения подобного сорта неравенств, но ошибается в выполнении простейших алгебраических преобразований.
Ответ получается неверный.
Оценка эксперта:
0 баллов.
Рассмотрим еще один пример логарифмического неравенства уровня сложности С3. Приведем только один из возможных подходов к его решению.
Задача
2.
Решите неравенство 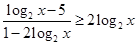 . .
Решение
.
1) Обе части неравенства определены, если 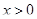 и если и если 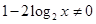 , т.е. если , т.е. если 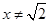 . .
2) Сделаем замену переменной 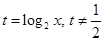 . Решаем неравенство относительно . Решаем неравенство относительно 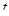
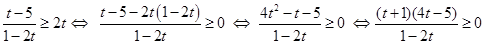
По методу интервалов получаем 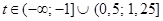 . .
3) Возвращаемся к переменной 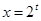 : :
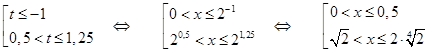
Ответ
: 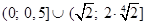 . .
Обратим внимание на два момента.
Во-первых, при использовании стандартного метода интервалов допустимо лишь приведение верного итогового результата, т.е. не является необходимым даже рисование числовой оси с отмеченными точками, не говоря уже о выписывании совокупностей и систем линейных неравенств и т.п. Разумеется, из этого совсем не
следует, что кто-то запрещает рисовать схемы или (если ученик привык так делать) составлять цепочки простейших равносильностей. Такие операции, конечно же, полезны и разумны, но разрешается проводить их на черновике, а в промежуточный ответ на чистовике выписывать только результат.
Во-вторых, к приведенному решению можно попробовать предъявить претензии про отсутствие ОДЗ: 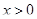 и и 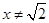 . Однако при выбранном способе решения оба эти условия выполнены автоматически: . Однако при выбранном способе решения оба эти условия выполнены автоматически: 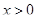 , так как , так как 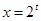 , а , а 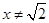 , так как по методу интервалов , так как по методу интервалов 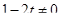 . Поэтому требование о том, что решение непременно следует начинать с нахождения ОДЗ является излишне догматическим и, по крайней мере, в данном случае, за отсутствие ОДЗ оценку снижать не следует. . Поэтому требование о том, что решение непременно следует начинать с нахождения ОДЗ является излишне догматическим и, по крайней мере, в данном случае, за отсутствие ОДЗ оценку снижать не следует.
Ниже используем реальные критерии оценивания задания С3.
| Критерии оценивания выполнения задания С3
|
Баллы
|
| Обоснованно получен правильный ответ
|
3
|
| Обоснованно получен ответ, отличающийся от верного только конечным числом точек.
|
2
|
| Полученный ответ неверен, но решение содержит переход от исходного неравенства к верным рациональным неравенствам.
|
1
|
| Решение не соответствует ни одному из критериев, перечисленных выше
|
0
|
Пример 2.1.
Решение задачи 2, комментарий и оценка этого решения.

Комментарий
.
Предложенное учащимся решение отличается от решения разработчиков только тем, что метод интервалов использован с явной подстановкой значений и более подробно произведен обратный возврат к переменной 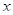 . .
Учащийся подробно обосновал все этапы решения, верно выполнил преобразования, получил верный ответ.
Можно, конечно, обсуждать смысл неравенства 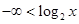 между числом и символом. Аналогично, при переходе между числом и символом. Аналогично, при переходе 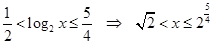 можно было бы потребовать формально необходимой ссылки на возрастание (и, даже, непрерывность) показательной функции с основанием 2>1. Все это – тема для интересной методической дискуссии, но вряд ли выяснение тут отношений может сказаться на общей оценке работы. можно было бы потребовать формально необходимой ссылки на возрастание (и, даже, непрерывность) показательной функции с основанием 2>1. Все это – тема для интересной методической дискуссии, но вряд ли выяснение тут отношений может сказаться на общей оценке работы.
Оценка эксперта:
3 балла.
Пример 2.2.
Решение задачи 2, комментарий и оценка этого решения.
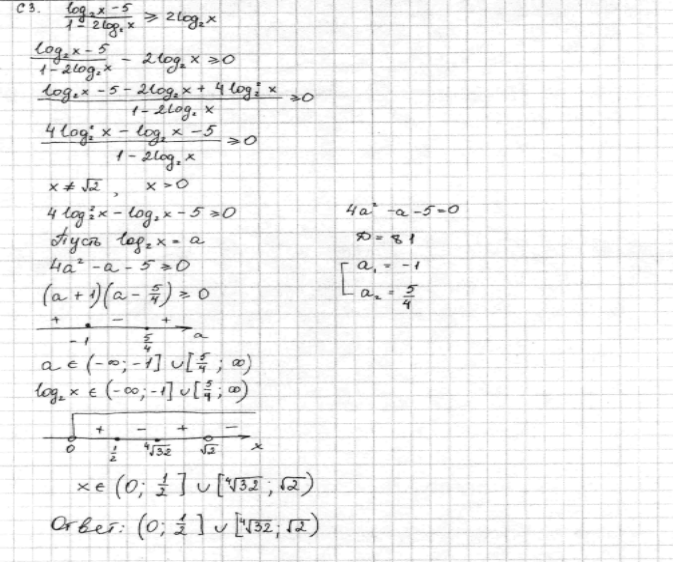
Комментарий
.
Ход решения верный.
Учащийся обосновал основные этапы решения, верно выполнил преобразования, но ошибся в сравнении чисел 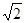 и и 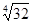 , что привело к неправильному ответу. , что привело к неправильному ответу.
Секретом является «отбрасывание» знаменателя 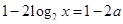 при решении рационального неравенства: ведь в решении есть только квадратное неравенство. Но еще большим секретом является, тем не менее, верная расстановка знаков всего рационального выражения при прохождении через точку при решении рационального неравенства: ведь в решении есть только квадратное неравенство. Но еще большим секретом является, тем не менее, верная расстановка знаков всего рационального выражения при прохождении через точку 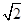 . .
Наверняка найдутся эксперты, которые интерпретируют это как тот факт, что ученик «в уме» учел знаки рационального выражения, и будут настаивать на выставлении 2 баллов. Но факт состоит в том, что в тексте рациональное неравенство решается неверно
, а уж как потом автор получил почти что верный ответ, «в уме» или просто поменял + на -, теперь уже не выяснить.
Отметим, что абсолютно скрупулезное следование приведенным выше критериям может привести и к оценке в 0 баллов.
Оценка эксперта:
1 балл.
Пример 2.3.
Решение задачи 2, комментарий и оценка этого решения.
Комментарий
.
Ход решения верный.
Часть правильно найденного решения по непонятным причинам не включена в ответ. Так что это – точно не 3 балла. Ставить только 1 балл – невозможно, так как в принципе в этом решении всё правильно. Быть может, не помешали бы несколько слов про то, как применен метод интервалов: видно, что у автора тут были сомнения.
Опять же, если следовать критериям буква в букву, то ставить 2 балла нельзя, так как выписанный ответ отличается от верного на бесконечное
множество точек.
Тут больной вопрос о «глупой» ошибке при выписывании ответа. Больше 1 балла за такой ляп снимать с ученика нельзя.
Оценка эксперта:
2 балла.
Пример 2.4.
Решение задачи 2, комментарий и оценка этого решения.
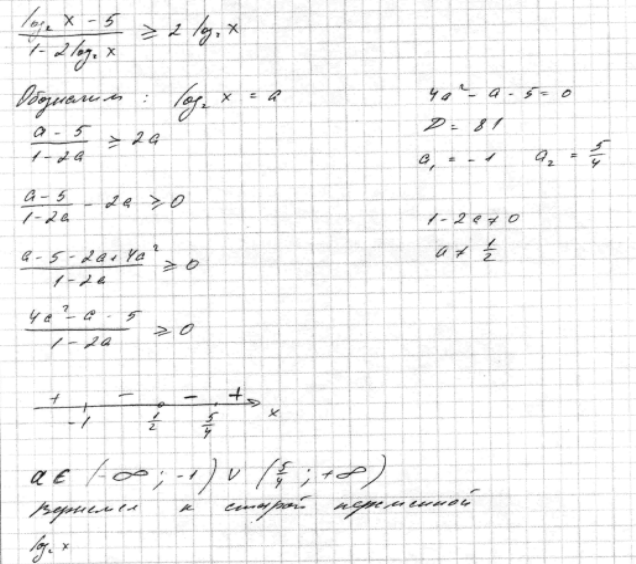
Комментарий
.
В работе продемонстрирован переход к новой переменной. Относительно нее решалось дробное рациональное неравенство методом интервалов.
Однако метод интервалов применен неверно, точнее - допущены ошибки в определении знаков выражения на промежутках. Переход к старой переменной «х
» обещан, но в итоге не выполнен. В итоге, ответ вообще отсутствует и это есть решающий аргумент для того, чтобы не ставить в данном случае даже 1 балл.
Оценка эксперта:
0 баллов.
§4. Задания с развернутым ответом повышенного уровня сложности С4.
Критерии проверки и оценки решений.
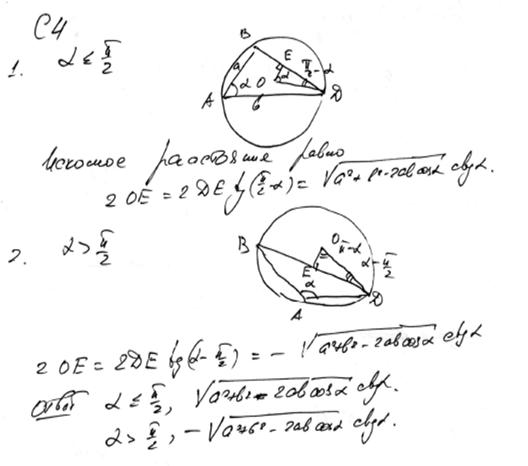
Задача 1.
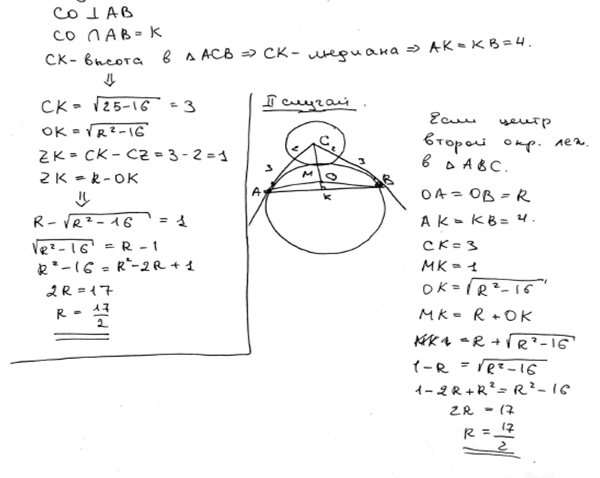
Основание равнобедренного треугольника равно 8, а боковые стороны равны 5. Вершина треугольника, в которой пересекаются боковые стороны, служит центром данной окружности радиуса 2. Найти радиус окружности, касающейся данной и проходящей через концы основания треугольника.
Решение
.
Пусть 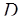 – середина основания. Обозначим через – середина основания. Обозначим через 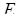 и и 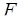 – точки пересечения данной окружности с прямой – точки пересечения данной окружности с прямой 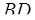 (см. рисунок). (см. рисунок).
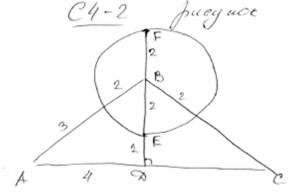
Искомых окружностей две: это окружности, описанные вокруг треугольников  и и 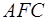 . Их радиусы найдем по формуле . Их радиусы найдем по формуле 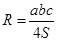 . .
В треугольнике  : : 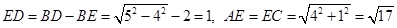 и и
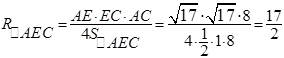
В треугольнике 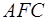 : : 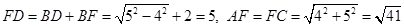 и и
 . .
Ответ
: 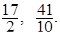
Комментарий.
Эта задача — по планиметрии. В ней требуется найти радиусы двух окружностей, касающихся заданной в задаче окружности. Задача не очень проста, так как необходимо рассмотреть два случая касания: привычное – внешнее и непривычное – внутреннее.
· для вычисления искомых радиусов используются некоторые хотя и стандартные, но не слишком часто употребляемые в задачах факты – формулы.
· разумеется, возможны другие способы решения, в которых будут определять положение центра окружности как точку пересечения «серединных перпендикуляров», составлять уравнение относительно радиуса, определять углы и применять теорему синусов и др.; примеры таких ученических решений приведены ниже.
При любом подходе к решению этой задачи от выпускника требуется понимание реализуемости различных геометрических конфигураций и умение вычислять стандартные элементы в заданном треугольнике.
Как и во всякой геометрической, и особенно, достаточно сложной геометрической задаче весьма деликатным является вопрос о степени и характере обоснованности построений и утверждений. Излишняя требовательность к обоснованиям в принципе ведет к необходимости текста, изложение в котором начинается, грубо говоря, с аксиом, продолжается формулировками теорем, приведением нужных формул, и в котором только после этого происходит собственно решение задачи. В данном случае взыскательный и внимательный эксперт может задать, например, такие вопросы:
- почему, окружности, проходящие через точки А, С, Е или А, С, F действительно касаются данной окружности, где тут доказательство?
- почему искомых окружностей ровно две, а не больше, где тут обоснование??
Вопросы резонные. Если трактовать эту задачу как пару задач («первая» – на построение, «вторая» – на вычисление), то в решении «первой» задачи приведена конструкция, но пропущены анализ и доказательство. Позиция разработчиков КИМ ЕГЭ-2010 состоит в том, что в задании С4 такой формальный пропуск является допустимым. Невозможно от выпускников школ на ЕГЭ требовать изложения, приближающегося к стилю учебников и научно-методических статей. Достаточным является наличие ясного понимания возможности разных геометрических конфигураций искомых объектов, верного описания (предъявления) этих конфигураций и грамотно проведенных вычислений.
Обратим также внимание на то, что часто при решении геометрических задач школьники ссылаются на весьма невразумительный чертёж, а иногда чертёж вообще отсутствует (если рисунок сделан на бланке карандашом, то эта область не сканируется).
Снижать оценку только
за это не рекомендуется.
Наконец, специально отметим, некоторую несогласованность единственного и множественного числа в постановке вопроса задачи и в ответе на этот вопрос. Традиции отечественного геометрического образования таковы, что вопрос «Найти геометрический объект
, удовлетворяющий некоторым условиям (или найти его числовую характеристику)», всегда трактовался как полное решение, т.е. отыскание всех объектов
, удовлетворяющих условиям задачи. Мы следуем традиционному подходу и считаем нецелесообразным вопрос «Найти радиус окружности, касающейся данной и…» задачи 1 приводить в формулировке, скажем, «Найти радиусы всех окружностей, касающихся данной и…»
| Критерии оценивания выполнения задания С3
|
Баллы
|
| Рассмотрены все возможные геометрические конфигурации, и получен правильный ответ
|
3
|
| Рассмотрена хотя бы одна возможная конфигурация, для которой получено правильное значение искомой величины
|
2
|
| Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неправильное из-за арифметической ошибки
|
1
|
| Решение не соответствует ни одному из критериев, перечисленных выше
|
0
|
Примеры оценивания выполнения заданий
C
4.
Пример 1.1.
Решение задачи 1, комментарий и оценка этого решения.
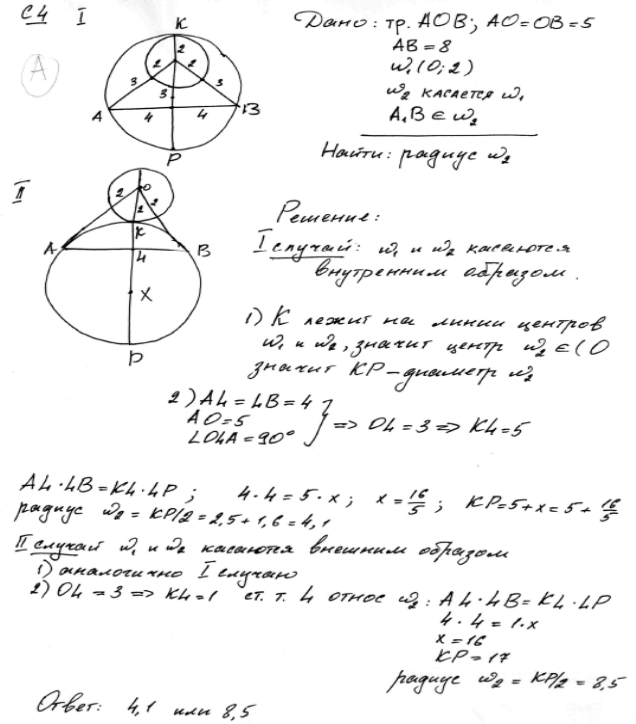
Комментарий
.
В предложенном решении реализованы все геометрические конфигурации.
Получен верный ответ.
Формально, нет описания точки L и она не указана на первом рисунке. Но зато – указана на втором рисунке.
Решение оценивается максимальным баллом.
Оценка эксперта:
3 балла.
Пример 1.2.
Решение задачи 1, комментарий и оценка этого решения.
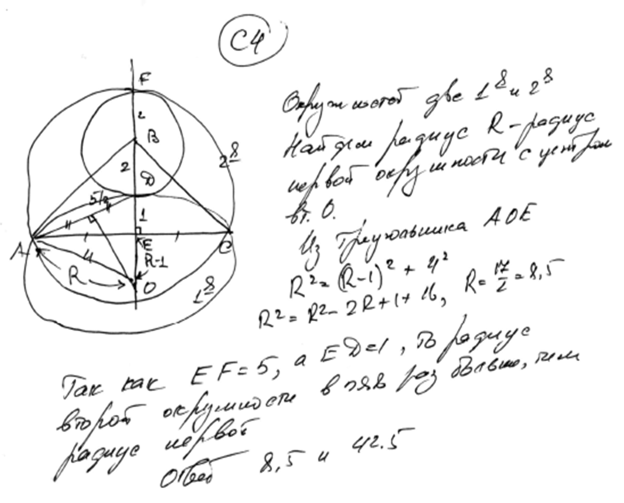
Комментарий
.
В решении рассмотрены все возможные геометрические конфигурации.
Правильно найден радиус одной окружности, а радиус второй находится из неверного предположения: радиус второй окружности в 5 раз больше радиуса первой. Ясно, что тут нельзя поставить 3 балла, как нельзя и поставить 0 баллов.
Конечно, предположение о пятикратном увеличении радиуса удивительно несуразно и, честно говоря, безумно. Из неких общих соображений и привычек, следовало бы за это при проверке серьезно «наказать» автора, т.е. поставить 1 балл.
Однако, по приведенным критериям это решение следует оценить в 2 балла. По мнению разработчиков КИМ ЕГЭ-2010, в первую очередь, оцениваются успехи и положительные результаты выпускника, а при дальнейших ошибках возможна «амнистия».
Оценка эксперта:
2 балла.
Пример 1.3.
Решение задачи 1, комментарий и оценка этого решения.
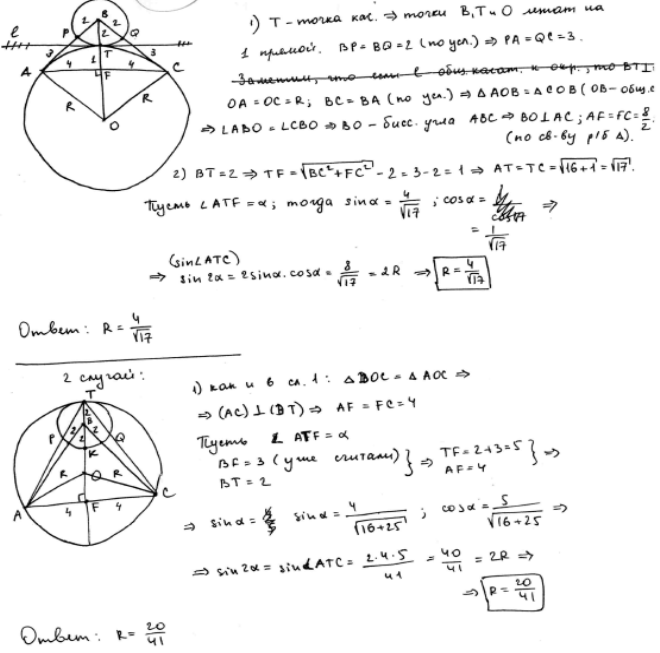
Комментарий
.
Сложный случай. Рассмотрены и верно описаны все геометрические конфигурации. Для каждой из них верно найдены необходимые тригонометрические величины.
Но, оба раза – одна и та же ошибка в вычислении радиуса, а именно, в теореме синусов «забыта» сторона, на которую опирается вписанный угол. Оба радиуса найдены в итоге неверно и поэтому 2 балла по приведенным критериям выставить невозможно. Более того, если абсолютно строго придерживаться критериев, то поставить и 1 балл нельзя: ученик сделал, формально, не
арифметическую ошибку.
Однако, оценить это решение в 0 баллов недопустимо: ведь автор для обеих конфигураций практически верно разобрал все геометрические детали и (дважды) ошибся лишь в заключительном шаге.
Оценка эксперта:
1 балл.
Пример 1.4.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий
.
В решении рассмотрена только одна из двух геометрических конфигураций. Для случая внешнего касания окружностей задача решена верно.
Авторское указание двух случаев относится к двум способам решения задачи для одного и того же способа расположения окружностей.
Оценка эксперта:
2 балла.
Рассмотрим еще одну планиметрическую задачу уровня сложности С4 и примеры оценивания ее выполнения.
Задача 2.
В параллелограмме  известны стороны известны стороны  , ,  и угол и угол 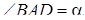 . Найдите расстояние между центрами окружностей, описанных около треугольников . Найдите расстояние между центрами окружностей, описанных около треугольников 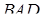 и и 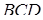 . .
Решение №1
.
Треугольники  расположены в разных полуплоскостях относительно прямой расположены в разных полуплоскостях относительно прямой  . Поэтому также по разные стороны от нее расположены и центры . Поэтому также по разные стороны от нее расположены и центры 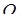 и и 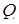 описанных около них окружностей, лежащие на серединном перпендикуляре описанных около них окружностей, лежащие на серединном перпендикуляре 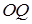 к их общей стороне к их общей стороне  , следовательно, , следовательно, 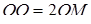 , где , где 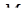 — середина — середина  . .
Возможны три случая:
1.  , ,
тогда 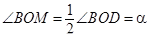 (теорема о вписанном угле), (теорема о вписанном угле),
2. 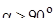 , , тогда 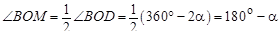 (теорема о вписанном угле),
(теорема о вписанном угле),
3. 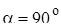 , тогда точки , тогда точки  и и 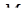 совпадают. совпадают.
Во всех рассмотренных случаях имеем
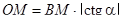 . .
Найдем 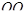 : :
а) 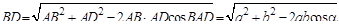 (теорема косинусов для (теорема косинусов для 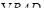 ), ),
б)  , ,
в) 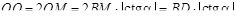 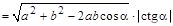 . .
Ответ
: 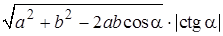 . .
Решение №2
.
Треугольники 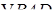 и и 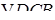 симметричны относительно точки симметричны относительно точки  – середины – середины 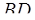 . Поэтому при любом расположении центров . Поэтому при любом расположении центров 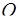 и и 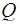 окружностей ( окружностей ( ; см. рисунки) искомое расстояние ; см. рисунки) искомое расстояние 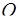 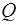 в два раза больше, чем расстояние от точки в два раза больше, чем расстояние от точки 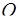 до до 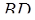 , т.е. , т.е.  . .
Из прямоугольного треугольника 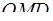 : : 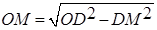 . .
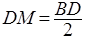 , а , а 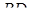 находим из теоремы косинусов, применённой к треугольнику находим из теоремы косинусов, применённой к треугольнику 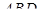 : :  . .
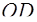 – радиус окружности, который находим по теореме синусов, применённой к треугольнику – радиус окружности, который находим по теореме синусов, применённой к треугольнику 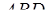 : : 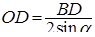 . .
В итоге, 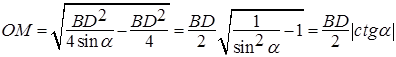 . .
Ответ
: 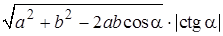 . .
Комментарий.
Эта задача — по планиметрии. В ней требуется найти расстояние между некоторыми точками в заданной геометрической фигуре.
Задача не очень проста по следующим причинам:
· для вычисления искомого расстояния используются некоторые хотя и стандартные, но не слишком часто употребляемые в задачах факты, такие как местонахождение центра описанной окружности, соотношение между вписанным и центральным углами, еорема синусов (для нахождения радиусов окружности);
· условие задачи, ввиду недостаточной определенности данного в ней угла, не совсем однозначно задает расположение центров, между которыми ищется расстояние, — они могут лежать как внутри соответствующих треугольников, так и снаружи, или даже на их границе, от чего могут зависеть (см. решение №1) рассуждения, необходимые для решения задачи;
· возможно решение (см. решение №2), в котором различные конфигурации аналитически описываются одинаково: расстояние между центрами в два раза больше, чем расстояние от одного из них до диагонали, относительно которой центры симметричны, а расстояние до диагонали ищется из прямоугольного треугольника с гипотенузой, равной радиусу, и катетом, равным половине диагонали, – такая аналитика автоматически даёт модуль котангенса.
При любом подходе к решению этой задачи от выпускника требуется понимание реализуемости различных геометрических конфигураций и умение вычислять стандартные элементы в заданном треугольнике.
Отметим, что в обоих решениях имеется доказательство равенства  (в решении №1 – несколько менее обоснованное). Однако, для учащихся при выполнении заданий С4 на ЕГЭ считается допустимым предъявление этого равенства и без подробных обоснований. (в решении №1 – несколько менее обоснованное). Однако, для учащихся при выполнении заданий С4 на ЕГЭ считается допустимым предъявление этого равенства и без подробных обоснований.
Критерии оценивания остаются такими же, как и в задаче 1.
Примеры оценивания выполнения заданий
C
4
Пример 2.1.
Решение задачи 2, комментарий и оценка этого решения.
Комментарий
.
В решении представлены рисунки, верно отражающие обе конфигурации.
Пояснения краткие, но верные, получен верный ответ. Некоторая напряженность есть в случае  , так как тогда нет , так как тогда нет  . .
Однако, ответ полученный автором, верен и в этом случае.
Решение можно оценить максимальным баллом.
Оценка эксперта:
3 балла.
Пример 2.2.
Решение задачи 2, комментарий и оценка этого решения.

Комментарий
.
Ход решения понятен. Автор допускает ошибку в одной формуле: 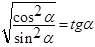 , вместо , вместо 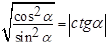 , что приводит к неправильному ответу. , что приводит к неправильному ответу. Из текста невозможно однозначно понять, рассматривает ли ученик обе конфигурации, или ограничивается только случаем острого угла. По крайней мере, отсутствует даже минимальное указание на то, что для тупых углов подсчет аналогичен. Из текста невозможно однозначно понять, рассматривает ли ученик обе конфигурации, или ограничивается только случаем острого угла. По крайней мере, отсутствует даже минимальное указание на то, что для тупых углов подсчет аналогичен.
Тем самым, «Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неправильное из-за арифметической ошибки».
Оценка эксперта:
1 балл.
Пример 2.3.
Решение задачи 2, комментарий и оценка этого решения.
Комментарий
.
В решении есть принципиально неверное утверждение: расстояние между центрами окружностей одинакового радиуса равно диаметру. В записи теоремы косинусов пропущена вторая степень, что повлекло за собой измерение длины отрезка в квадратных единицах длины. О различных геометрических конструкциях нет упоминаний.
Оценка эксперта:
0 баллов.
§5. Задания с развернутым ответом высокого уровня сложности С5.
Критерии проверки и оценки решений
За выполнение задания С5 эксперт должен выставить 0 баллов, 1 балл, 2 балла, 3 балла или 4 балла. В этом, чисто арифметическом смысле, оценивание похоже на характер оценивания задач С3-С5 предыдущего формата ЕГЭ. Однако, аналогия тут весьма условна. А именно, оценки от 0 до 4-х баллов в версии 2001-2009 гг. были сильно смещены к своей верхней границе.
В отличие от этого, в нынешнем формате оценку в 2 балла можно выставить и в тех случаях, когда в решении есть существенные изъяны, т.е., например, в случаях, когда полностью не учтены некоторые возможные случаи. Аналогично, 1 балл можно выставить и в тех случаях, когда ученик продемонстрировал лишь тот или иной фрагмент (явно указанный в критериях) решения и, скорее всего, даже и не имел представления о том, как проводить решение задачи в дальнейшем. Характер выставления 3 баллов в целом совпадает с прежними критериями: он соответствует тем случаям, когда оцениваемое и верное по существу решение, закончено, полно, но содержит неточности, приводящие к ответу «почти» совпадающему с правильным ответом.
Ниже представлены примеры из двух диагностических работ. Примеры эти довольно различны, как различны на текстовом уровне и критерии оценивания. Отметим, что во второй диагностической работе критерии оценивания более близки к критериям оценивания реальных вариантов ЕГЭ-2010.
Задачи С5 из этих двух диагностических работ объединяет, пожалуй, лишь наличие параметра и возможность в каждой из задач приводить решение, активно использующее графики функций, т.е. так называемый функционально-графический метод решения.
Задача 1.
Найти все значения 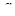 , при каждом из которых уравнение , при каждом из которых уравнение
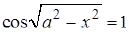 имеет ровно 8 решений. имеет ровно 8 решений.
Решение.
1. Преобразуем уравнение
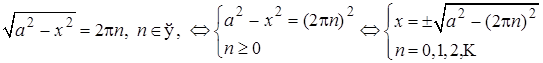
2. Если 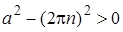 , то уравнение имеет два корня, отличающихся знаком. Если , то уравнение имеет два корня, отличающихся знаком. Если 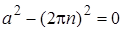 , то имеется ровно один корень , то имеется ровно один корень 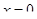 . Если . Если 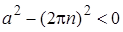 , то корней нет. Поэтому для выполнения условия задачи, необходимо и достаточно, чтобы , то корней нет. Поэтому для выполнения условия задачи, необходимо и достаточно, чтобы 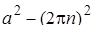 было положительно при было положительно при 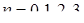 и отрицательно при и отрицательно при 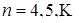
3. Получаем систему неравенств: 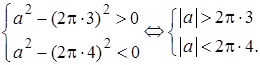
Ответ
: 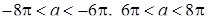 . .
Комментарий.
1. Для решения задачи можно к уравнению 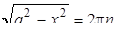
применить графическую иллюстрацию. Например, можно нарисовать графики отдельно левой части 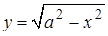 (верхняя полуокружность с центром в начале координат и переменным радиусом (верхняя полуокружность с центром в начале координат и переменным радиусом 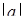 ) и отдельно правой части ) и отдельно правой части 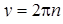 (фиксированные горизонтальные прямые), а затем, указав границы для радиуса полуокружности, обеспечить нужное количество точек их пересечения. (фиксированные горизонтальные прямые), а затем, указав границы для радиуса полуокружности, обеспечить нужное количество точек их пересечения.
2. Легко ошибиться, включив в ответ также и значения  , не заметив, что каждое из них при , не заметив, что каждое из них при 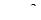 задает лишь одно значение неизвестной (а не два!). задает лишь одно значение неизвестной (а не два!).
3. Если забыть про отрицательные значения неизвестной (задаваемые уравнением наряду с положительными), то количество корней уравнения будет сосчитано неверно, от чего ответ сильно исказится.
4. Неравенство 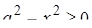 автоматически вытекает из условия автоматически вытекает из условия 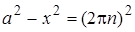 . Поэтому «нахождение ОДЗ» в данном случае вовсе не обязательно (и даже, нежелательно). . Поэтому «нахождение ОДЗ» в данном случае вовсе не обязательно (и даже, нежелательно).
Баллы
|
Критерии оценивания выполнения задания С5
|
| 4
|
Обоснованно получен правильный ответ
|
| 3
|
Ответ обоснован и состоит из верных промежутков, но дополнительно содержит хотя бы один из их концов
|
| 2
|
Решение опирается на верное рассуждение, в котором только не учтены возможные отрицательные значения неизвестной  или имеются другие существенные изъяны. В результате, возможно, получен неверный ответ или имеются другие существенные изъяны. В результате, возможно, получен неверный ответ
|
| 1
|
Ответ неверен или не получен, но найдено верное выражение для неизвестной или ее квадрата
|
| 0
|
Решение не соответствует ни одному из критериев, перечисленных выше.
|
Примеры оценивания выполнения заданий С5.
Пример 1.1.
Решение задачи 1, комментарий и оценка этого решения.

Комментарий
В принципе, полностью аргументированное решение, соответствующее максимальному баллу. Имеется некоторая неприятность с тем, что оно излишне
аргументировано. А именно из 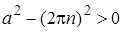 следует следует 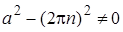 и неясно, с какой стати автор вообще рассматривает случай Б). Правда, такая излишность гарантированно позволила избежать возможного включения концевых точек в ответ. и неясно, с какой стати автор вообще рассматривает случай Б). Правда, такая излишность гарантированно позволила избежать возможного включения концевых точек в ответ.
Оценка эксперта:
4 балла.
Пример 1.2.
Найти все значения  , при каждом из которых уравнение , при каждом из которых уравнение
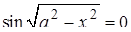 имеет ровно 8 решений. имеет ровно 8 решений.
Ответ
: 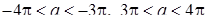 . .
Решение задачи, комментарий и оценка этого решения.

Комментарий
По существу, решение верно. Грамотно и вовремя использовано убывание 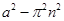 относительно относительно 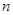 . Однако, при переводе на язык систем неравенств нужные строгие неравенства ошибочно заменены нестрогими. По этой причине, ответ неверен, но отличается от верного лишь конечным числом точек. . Однако, при переводе на язык систем неравенств нужные строгие неравенства ошибочно заменены нестрогими. По этой причине, ответ неверен, но отличается от верного лишь конечным числом точек.
Оценка эксперта:
3 балла.

Пример 1.3.
Решение задачи, комментарий и оценка этого решения.
Комментарий.
В целом, решение очень похоже на предыдущий пример 1.2. В ответе некоторые строгие неравенства ошибочно заменены нестрогими.
Но есть и еще один существенный изъян: в решении фигурирует неверное неравенство 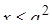 , из него сделан непонятный и впоследствии никак не учтенный вывод , из него сделан непонятный и впоследствии никак не учтенный вывод 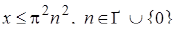 . .
Оценка эксперта:
2 балла.
Пример 1.4.
Найти все значения  , при каждом из которых уравнение , при каждом из которых уравнение
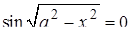 имеет ровно 8 решений. имеет ровно 8 решений.
Ответ
:  . .
Решение задачи, комментарий и оценка этого решения.
Комментарий
В решении приведена формула для неизвестной, причем с ошибкой (забыт знак  ). Дальнейшее рассуждение позволяет для полученного (искаженного) уравнения найти верный ответ, однако для параметра ). Дальнейшее рассуждение позволяет для полученного (искаженного) уравнения найти верный ответ, однако для параметра  найдена только одна граница, которая и принята за ответ. найдена только одна граница, которая и принята за ответ.
Разумеется, тут реальный выбор – между 0 баллов и 1 баллом. По критерию «Ответ неверен или не получен, но найдено верное выражение для неизвестной или ее квадрата» допустимо поставить 1 балл. Хотя положение шаткое: для квадрата неизвестной выражение верно, а для самой неизвестной – нет.
Оценка эксперта:
1 балл (возможно, и 0 баллов).
Пример 1.5.
Найти все значения  , при каждом из которых уравнение , при каждом из которых уравнение
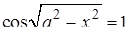 имеет ровно 10 решений. имеет ровно 10 решений.
Ответ
:  . .
Комментарий.
Уравнение приведено к формуле для квадрата неизвестной, правда, с ошибкой (потерян множитель 2 при решении простейшего тригонометрического уравнения).
Далее, из этой формулы сделан вывод об искомых значениях параметра (гарантирующих наличие не ровно 10 корней, а не более 10 корней). При этом не учтены возможные отрицательные значения неизвестной и, к тому же, верхняя граница значений параметра ошибочно включена в ответ.
По критерию условие «Ответ неверен или не получен, но найдено верное выражение для неизвестной или ее квадрата» выставления 1 балла не выполнено.
Оценка эксперта:
0 баллов.
Задача 2.
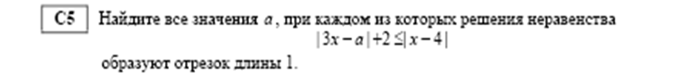
Решение №1.
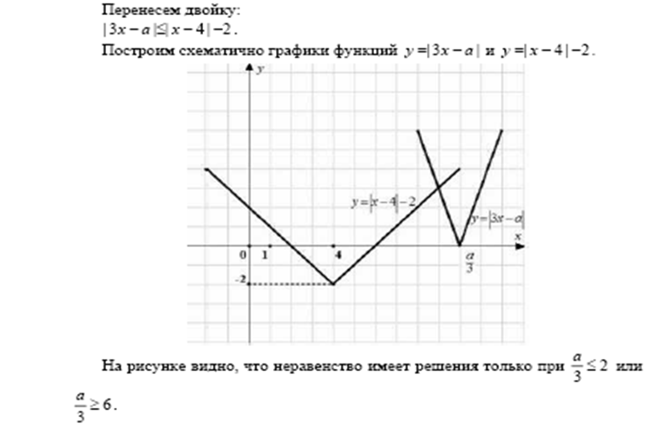
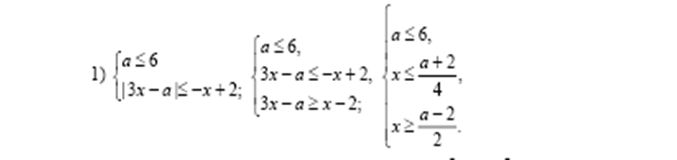

Решение №2.
1) 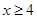 . Тогда . Тогда 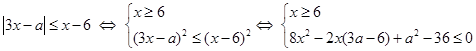 . .
Ветви параболы направлены вверх, а  . Значит, . Значит, 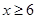 и и  принадлежит отрезку с концами принадлежит отрезку с концами 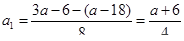 и и 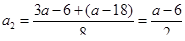 . .
Если  , то , то 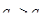 и для выполнения условия задачи необходимо, чтобы и для выполнения условия задачи необходимо, чтобы 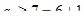 . Но тогда . Но тогда 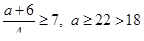 . Противоречие. . Противоречие.
Если  , то , то  и и 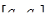 - множество решений неравенства. Получаем, что - множество решений неравенства. Получаем, что 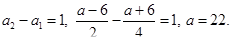
2) 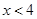 . Тогда . Тогда 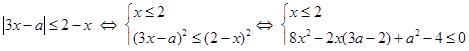 . .
 . Значит, . Значит, 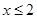 и при этом и при этом  принадлежит отрезку с концами принадлежит отрезку с концами 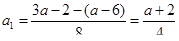 и и 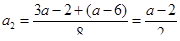 . .
Если 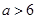 , то , то 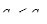 и для выполнения условия задачи необходимо, чтобы и для выполнения условия задачи необходимо, чтобы 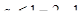 . Но тогда . Но тогда 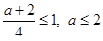 . Противоречие. . Противоречие.
Если  , то , то  и и  - множество решений неравенства. Получаем, что - множество решений неравенства. Получаем, что 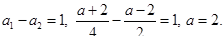
Ответ:
 . .
| Критерии оценивания выполнения задания С5
|
Баллы
|
| Обоснованно получен правильный ответ
|
4
|
| Получен верный ответ. Решение в целом верное, но либо имеет пробелы (например, не описаны необходимые свойства функции), либо содержит вычислительные ошибки
|
3
|
| Верно рассмотрены все случаи раскрытия модулей. При составлении или решении условий на параметр допущены ошибки, в результате которых в ответе либо приобретены посторонние значения, либо часть верных значений потеряна
|
2
|
| Хотя бы в одном из случаев раскрытия модуля составлено верное условие на параметр, либо построен верный эскиз графика функции в целом
|
1
|
| Решение не соответствует ни одному из критериев, перечисленных выше.
|
0
|
Пример 2.1.
Решение задачи 2, комментарий и оценка этого решения.
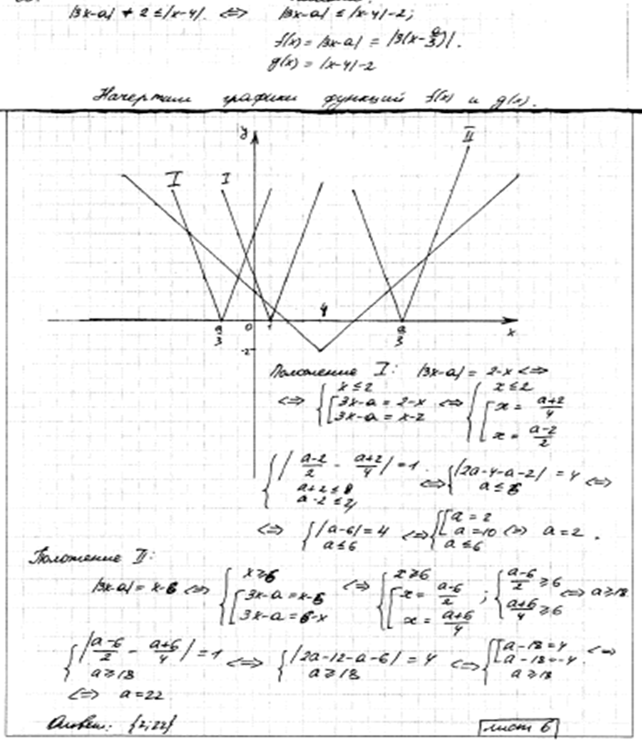
Комментарий.
Понятно, что речь тут о 3 баллах, или о 4 баллах. Вычислительных ошибок нет. Вопрос о том, описаны или «не описаны необходимые свойства функции» - деликатный, в силу неформализуемости термина «описаны». Конечно, неплохо бы явно сослаться на то, что 3>1, наклон одних прямых больше наклона других и поэтому… Но автор ограничился ясным графическим истолкованием этих соображений. Так есть тут «описания» или их нет? На наш взгляд – есть, в данном случае это понятные и верные графические описания.
Оценка эксперта:
4 балла.
Пример 2.2.
Решение задачи 2, комментарий и оценка этого решения.

Комментарий.
Каким образом из двух совокупностей неравенств были составлены две системы неравенств, как минимум, неясно. Более того, и по существу неясно, как такой переход можно аккуратно оформить. Неверный ответ 6 связан с неверно выбранным (и никак не обоснованным) расположением концов отрезка, образованного решениями неравенства.
Тем не менее, на первом фрагменте текста (до систем) - все верно: использована равносильность 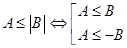 . Есть и арифметическая ошибка во втором неравенстве второй совокупности в первом случае. Тем не менее, «Верно рассмотрены все случаи раскрытия модулей. При составлении или решении условий на параметр допущены ошибки, в результате которых…» . Есть и арифметическая ошибка во втором неравенстве второй совокупности в первом случае. Тем не менее, «Верно рассмотрены все случаи раскрытия модулей. При составлении или решении условий на параметр допущены ошибки, в результате которых…»
Оценка эксперта:
2 балла.
Пример 2.3
Решение задачи 2 (условие, см. в тексте), комментарий и оценка этого решения.

Комментарий.
Пойдем «по дополнению».
4 балла или 3 балла нельзя поставить, так как (даже на формальном уровне) представлен лишь частичный ответ на поставленный вопрос.
2 балла нельзя поставить, так как никаких случаев раскрытия модуля не рассмотрено вообще.
Поэтому тут - выбор между 0 баллов и 1 баллом. Так как «…построен верный эскиз графика функции в целом…», то стоит рассмотреть возможность выставления 1 балла. Однако, в тексте есть прямая ошибка: изменение параметра приводит к перемещению по Ох, а не по Оy, как утверждает автор.
Оценка эксперта:
0 баллов.
|