| Реферат
Тема: «Решение задач с параметрами»
Выполнила ученица 10 класса МОУ СОШ №1 г.Карталы Челябинской области, Алтынбаева Дарина.
Оглавление.
Введение.
1. Аналитический способ решения задач с параметрами.
1.1. Линейные уравнения с одной переменной, содержащие параметр.
1.2. Квадратные уравнения, содержащие параметр.
1.3. Системы линейных уравнений с параметрами.
2. Применение графического способа при решении задач с параметрами.
Заключение.
Список литературы.
Введение.
Большинство жизненных задач
решаются как алгебраические
уравнения: приведением их к
самому простому виду.
Толстой Л. Н. “Круг чтения”.
Толковый словарь определяет параметр как величину, характеризующую какое - нибудь основное свойство машины, устройства, системы или явления, процесса. (Ожегов С.И.
, Шведова Н.Ю.
Толковый словарь русского языка. Москва. 1999). Рассмотрение параметров - это всегда выбор. Покупая какую-то вещь, мы внимательно изучаем ее основные характеристики. Перед выбором мы стоим и в различных жизненных ситуациях.
Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами.
Решение задач с параметрами можно считать деятельностью, близкой по своему значению к исследовательской. Это обусловлено тем, что выбор метода решения, процесс решения, запись ответа предполагают определённый уровень сформированности умений наблюдать, сравнивать, анализировать, выдвигать и проверять гипотезу, обобщать полученные результаты.
Выполняя данную работу, я ставила цель расширить свои математические представления о приёмах и методах решения задач с параметрами, развивать логическое мышление и навыки исследовательской деятельности.
В своем реферате я рассмотрела основные типы задач с параметрами:
· уравнения и их системы, которые необходимо решить либо для любого значения параметра, либо для значений параметра, принадлежащих заранее оговоренному множеству;
· уравнения и их системы, для которых требуется определить количество решений в зависимости от значения параметра;
· уравнения и их системы, для которых требуется найти все те значения параметра, при которых указанные уравнения и их системы имеют заданное число решений.
В первой части моего реферата я рассматриваю наиболее стандартный аналитический способ решения уравнений и систем уравнений с параметрами, а во второй – графический метод.
Я думаю, что знания, полученные мной в процессе работы, помогут мне при сдаче ЕГЭ по математике.
1. Аналитический способ решения задач с параметрами.
Задачи с параметрами встречаются фактически с самого начала изучения математики, когда начинают оперировать с буквами, как с числами. Они связаны с решением уравнений и неравенств, в запись которых наряду с переменными входят буквы, называемые параметрами.
Предполагается, что эти параметры могут принимать любые числовые значения, т.е. одно уравнение с параметром задает множество уравнений.
Решить уравнение с параметрами означает следующее:
· исследовать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметров;
· найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения.
1.1. Линейные уравнения с одной переменной, содержащие параметр.
Уравнение вида ах + в = 0, где а и в – некоторые постоянные, называется линейным уравнением.
Если а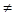 0, то линейное уравнение имеет единственный корень: х= 0, то линейное уравнение имеет единственный корень: х=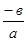 . .
Если а=0 и в=0, переписав исходное уравнение в виде ах=-в, легко видеть, что любое х является решением линейного уравнения.
Если а=0 и в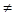 0, то линейное уравнение не имеет корней. 0, то линейное уравнение не имеет корней.
Пример 1
. Решить уравнение с параметром:
1) ах=0.
Решение. Если а=0, то 0 х=0; х - любое действительное число. х=0; х - любое действительное число.
Если а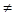 0, то х = 0, то х =  = 0. = 0.
Ответ: если а=0, х - любое действительное число;
если а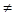 0, то х = 0. 0, то х = 0.
2) х + 2 = ах.
Решение. Преобразуем данное уравнение к виду х(1-а) = -2.
Если 1-а =0,т.е. а=1, то получим уравнение х 0=-2, которое не имеет корней. 0=-2, которое не имеет корней.
Если 1-а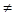 0,т.е. а 0,т.е. а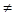 1, то уравнение имеет единственный корень 1, то уравнение имеет единственный корень
х= . .
Ответ: если а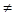 1, то х= 1, то х= ; ;
если а=1,то уравнение не имеет корней.
3) (а2
-1)х=2 а2
+ а -3.
Решение. Приведем данное уравнение к виду (а-1)(а+1)х=(2а+3)(а-1).
Если а=1, то уравнение принимает вид 0 х=0, его решением является любое действительное число. х=0, его решением является любое действительное число.
Если а=-1, то уравнение принимает вид 0 х=-2, это уравнение не имеет решений. х=-2, это уравнение не имеет решений.
Если а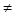  1, то уравнение имеет единственное решение х= 1, то уравнение имеет единственное решение х= . .
Это значит, что каждому допустимому значению а соответствует единственное значение х.
Ответ: если а=1, то х- любое действительное число;
если а=-1, то уравнение не имеет решений;
если а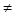  1, то х= 1, то х=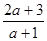 . .
Пример 2
. Решить относительно х уравнение
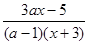 + + 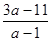 = =  . .
Решение. Из условия следует, что (а-1)(х+3)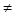 0, т.е. а 0, т.е. а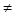 1, х 1, х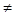 -3. -3.
Умножив обе части данного уравнения на (а-1)(х+3), получим уравнение
3ах-5+ (3а-11)(х+3)=(2х+7)(а-1), или х(4а-9)=31-2а.
При а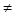 2,25 х= 2,25 х=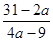 . .
Теперь необходимо проверить, нет ли таких значений а, при которых найденное значение х=-3.
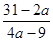 =-3 при а=-0,4. =-3 при а=-0,4.
Таким образом, при а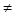 2,25, а 2,25, а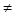 1 и а 1 и а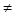 -0,4 данное уравнение имеет единственное решение х= -0,4 данное уравнение имеет единственное решение х=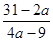 . .
При а=2,25, а=-0,4 и а=1 уравнение решений не имеет.
Замечание: если при каком-либо значении параметра данное уравнение не имеет смысла, то оно при этом значении параметра и не имеет решения. Обратное утверждение не верно.
Ответ: если а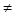 2,25, а 2,25, а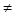 1 и а 1 и а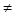 -0,4, то х= -0,4, то х=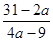 ; ;
если а=2,25, а=-0,4 и а=1,то уравнение решений не имеет.
Пример 3
. При каких значениях параметра а уравнение имеет бесконечное множество решений?
6(ах-1)-а=2(а+х)-7.
Решение. Приведем данное уравнение к виду 2х(3а-1)=3а -1.
Если 3а-1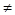 0,т.е. а 0,т.е. а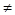 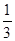 , то х= , то х=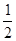 . .
Если 3а-1=0, т.е. а=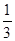 , то уравнение примет вид 2х , то уравнение примет вид 2х 0=0, его решением является любое число. 0=0, его решением является любое число.
Ответ: уравнение имеет бесконечное множество решений при а=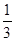 . .
Пример 4
. При каких значениях параметра а уравнение не имеет решений?
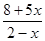 =2а. =2а.
Приведем данное уравнение к виду х(5+2а)=4а-8.
Если 5+2а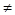 0,т.е. а 0,т.е. а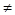 - -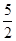 , то х= , то х=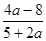 . .
Если 5+2а =0,т.е. а =-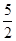 , то уравнение примет вид х , то уравнение примет вид х 0=-18, это уравнение не имеет решений. 0=-18, это уравнение не имеет решений.
Ответ. уравнение не имеет решений при а =-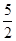 . .
1.2. Квадратные уравнения, содержащие параметр.
Уравнение вида ах2
+вх+с=0, где а,в,с –некоторые числа (а 0), х-переменная, называется квадратным уравнением. 0), х-переменная, называется квадратным уравнением.
Для решения квадратного уравнения следует вычислить дискриминант
D= b2
-4ac.
Если D=0, то квадратное уравнение имеет единственный корень:
х=-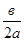 (или два, но сливающихся корня х1
=х2
). (или два, но сливающихся корня х1
=х2
).
Если D>0, то квадратное уравнение имеет два корня:
х1
= 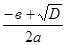 ; х2
= ; х2
= 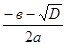 . .
Если D<0, то квадратное уравнение не имеет корней.
Если один из коэффициентов в или с равен нулю, то квадратное уравнение можно решать, не вычисляя дискриминанта:
1. в=0, с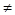 0; 0;  <0, то х1,2
= <0, то х1,2
= 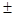 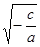 . .
2. в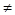 0, с=0, то х1
=0, х2
=- 0, с=0, то х1
=0, х2
=-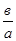 . .
Следующие теоремы также помогают при решении квадратных уравнений с параметрами.
Теорема Виета
(прямая) утверждает: если х1
и х2
являются корнями квадратного уравнения ах2
+вх+с=0, то выполняются соотношения:
х1
+х2
=-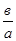 и х1 и х1
 х2
= х2
= . .
Обратная теорема
утверждает: если для некоторых постоянных а, в, с существуют числа х1
и х2
, удовлетворяющие соотношениям
х1
+х2
=-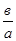 и х1 и х1
 х2
= х2
= , то эти числа х1
и х2
являются корнями уравнения ах2
+вх+с=0. , то эти числа х1
и х2
являются корнями уравнения ах2
+вх+с=0.
Пример 5
. Решить относительно х:
ах2
-2х+4=0
Если а=0, тогда уравнение примет вид -2х+4=0, отсюда х=2.
Если а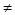 0, то D=4-16а. 0, то D=4-16а.
Если 4-16а≥0, т.е а≤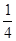 , х1,2
= , х1,2
= 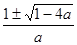
Если 4-16а<0, т.е. а>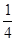 , то уравнение не имеет решений. , то уравнение не имеет решений.
Ответ: если а=0, то х=2;
если а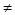 0 и а≤ 0 и а≤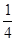 , то уравнение имеет два решения х1,2
= , то уравнение имеет два решения х1,2
= 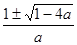
если а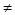 0 и а> 0 и а>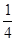 , то уравнение не имеет решений. , то уравнение не имеет решений.
Пример 6
. При каких значениях а уравнение ах2
-х+3=0 имеет единственное решение?
Если а=0, тогда уравнение примет вид –х+3=0, отсюда х=3.
Если а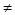 0, то D=1-12а. 0, то D=1-12а.
Уравнение будет иметь единственное решение при D=0.
1-12а=0, отсюда а=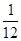 . .
Ответ: уравнение имеет единственное решение при а=0 или а=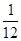 . .
Пример 7.
При каких значениях а уравнение ах2
+4х+а+3=0 имеет более одного корня?
Если а=0, то уравнение примет вид 4х+3=0, которое имеет единственный корень, что не удовлетворяет условию задачи.
Если а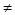 0, то D=16-4а2
-12а. 0, то D=16-4а2
-12а.
Уравнение имеет более одного корня при D>0.
16-4а2
-12а>0.
Рассмотрим функцию у=16-4а2
-12а.
Найдем нули этой функции, решая уравнение 16-4а2
-12а=0.
а1
=-4; а2
=1.
Функция принимает положительные значения, если -4<а<1.
Ответ: уравнение имеет более одного корня, если -4<а<0 и 0<а<1.
Пример 8.
Найти коэффициент а, если корни уравнения х2
-2х+а=0.
связаны соотношением 2х1
+х2
=3.
х2
-2х+а=0.
По теореме Виета х1
+х2
=а и х1
 х2
=2. х2
=2.
Составляю систему:
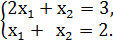
Решая эту систему, получаю, что х1
=1, х2
=1.
Тогда а=1.
Ответ: а=1.
1.3. Системы линейных уравнений с параметром.
Системы линейных уравнений вида
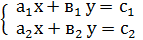
1) имеют единственное решение, если  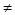 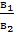 ; ;
2) не имеют решений, если 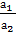 = =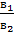 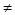 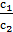 ; ;
3) имеют бесконечное множество решений, если 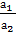 = =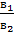 = =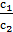 . .
Пример 9.
Найти все значения параметра а, при котором система имеет бесконечное множество решений:
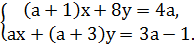
Система имеет бесконечное множество решений, если выполняется условие:
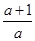 = = 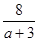 = = 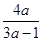 . .
1) 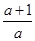 = = 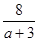 ; ;
ОДЗ: а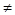 0, а 0, а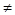 -3. -3.
(а+1)(а+3)=8а, отсюда а2
-4а+3=0.
D>0, а1
=1 и а2
=3. Оба значения входят в область допустимых значений.
2) 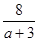 = = 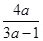 ; ;
ОДЗ: а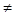 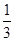 ; а ; а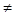 -3. -3.
4а(а+3)=8(3а-1), отсюда а2
-3а+2=0.
D>0, а1
=2 и а2
=1. Оба значения входят в область допустимых значений.
3) 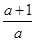 = =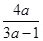 ; ;
ОДЗ: а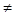 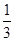 ; а ; а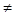 0. 0.
4а2
=(а+1)(3а-1), отсюда а2
-2а+1=0, (а-1)2
=0, а=1.
Ответ: при а=1 система имеет бесконечное множество решений.
Пример 10.
При каких m и n система
а) имеет единственное решение;
б) не имеет решений.
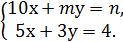
а) система имеет единственное решение, если 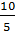 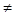 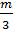 ; ;
Это условие выполняется при m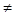 6. 6.
б) система не имеет решений, если 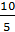 = =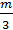 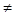  ; ;
1) 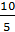 = =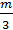 , отсюда m=6. , отсюда m=6.
2) 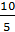 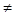  , отсюда n , отсюда n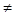 8. 8.
3) 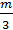 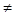  , отсюда n , отсюда n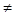  ; т.е. при m=6 n ; т.е. при m=6 n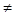 8. 8.
Ответ: а) при m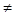 6 система имеет единственное решение; 6 система имеет единственное решение;
б) при m=6 и n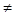 8 система не имеет решений. 8 система не имеет решений.
2.Применение графического способа при решении задач с параметрами.
Пример 11
. Решить уравнение х2
-4х+2=а.
Рассмотрим функцию у1
= х2
-4х+2, графиком которой является парабола, ветви направлены вверх. Для удобства построения выделим полный квадрат у=(х-2)2
-2. Вершиной параболы является точка с координатами (2;-2).
Рассмотрим функцию у2
=а. Графиком этой функции является прямая, параллельная оси ОХ.
Так как параметр содержится в уравнении прямой, то решение уравнения будет зависеть от расположения данной прямой. Построим графики рассматриваемых функций: у1
= х2
-4х+2 и у2
=а. 
По графикам построенных функций можно сделать следующий вывод:
при а<-2 уравнение не имеет корней;
при а=-2 уравнение имеет единственный корень, х=2;
при а>-2 уравнение имеет два корня.
При графическом способе решения данного уравнения мы легко определили количество корней в зависимости от значения а. Однако не всегда удается найти их аналитическое значение, как в случае при а>-2.
Найдем значение этих корней аналитическим способом.
Если а>-2, то в > 0.
Находим корни по формуле: х1,2
= 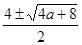
х1,2
=2±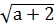
Ответ: если а<-2, то уравнение не имеет корней;
если а=-2, то х=2;
если а>-2, то х1,2
=2±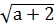 . .
Пример12
. Найти все значения параметра а, для которых вершины парабол у1
= х2
-2(а+1)х+1 и у2
= ах2
-х+а лежат по разные стороны от прямой у= . .
Решение данной задачи начнем с анализа графической модели.
Рассмотрим функцию у1
= х2
-2(а+1)х+1, графиком которой является парабола, ветви направлены вверх. Графиком функции у2
= ах2
-х+а является парабола, направление ветвей которой будет зависеть от значения параметра а.
Согласно условию задачи схематично можно изобразить четыре возможных варианта:

Найдем координаты вершин парабол:
хв1
=а+1; ув1
=1-(а+1)2
.
хв2
=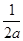 ; ув2
= 4а2-14а. ; ув2
= 4а2-14а.
Согласно схематичным чертежам записываем четыре системы неравенств:

Рассмотрим более подробно решение первой системы . Преобразование остальных систем аналогично , отличается только знаками:

Рационально далее решить систему методом интервалов:

Система решений не имеет.
Объединяя решения систем получаем ответ:

Пример 13.
Найти все значения параметра а, при которых корни уравнения х2
+х+а=0 действительные, различные и оба больше а.
Рассмотрим функцию у= х2
+х+а, графиком которой является парабола. Ветви параболы направлены вверх. Абсцисса вершины параболы хв
=-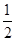 . .
Графическая интерпретация данной задачи:
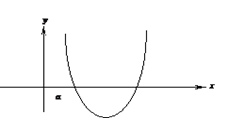
По условию задачи уравнение имеет два различных действительных корня, которые одновременно больше а, тогда и только тогда, когда:
D>0,fa>0,xв>a;⇒ D>0,fa>0,xв>a;

Ответ: (-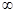 ; -2). ; -2).
Пример 14
. Найти все значения параметра а, при которых корни уравнения ах2
+2(а+3)х+а+2=0 неотрицательны.
Корни уравнения неотрицательны, значит они могут принимать значения больше либо равные нулю, не сказано, что корни различны, следовательно это могут быть два совпавших корня.
Графическая интерпретация данной задачи:

Чтобы выполнялось условие задачи, необходимо и достаточно
D≥0,f0≥0,xв>0, a>0. или D≥0,f0≤0,xв>0, a<0.
Решая системы методом интервалов, получаем, что решением первой системы является пустое множество, а решением второй системы - -2,25;-2
Ответ: а 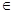  -2,25;-2. -2,25;-2.
Пример15.
Найти все значения параметра а, при которых корни уравнения ах2
-(а+1)х+а+3=0 имеют разные знаки.
Для того, чтобы парабола, являющаяся графиком функции у= ах2
-(а+1)х+а+3, пересекала ось абсцисс в точках, между которыми располагается начало координат, необходимо и достаточно, чтобы квадратный трехчлен ах2
-(а+1)х+а+3 принимал в точке х = 0 отрицательное или положительное значение, в зависимости от направления ветвей параболы. Графическая интерпретация данной задачи:

Тогда искомое условие задачи имеет вид:

Ответ: а 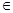  (-3;0). (-3;0).
Пример16.
При каких значениях параметра а, корни уравнения х2
-ах+2=0 принадлежат отрезку 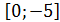 ? ?
При требуемом условии расположения корней квадратного трехчлена х2
-ах+2 соответствующая парабола располагается следующим образом:

Решение данной задачи определяется условием:
D≥0,f0≥0; f3≥0,0≤xв≤3;⇔ а2-8≥0,11-3а≥0,0≤а2≤3.
Решаем систему методом интервалов, откуда получаем, что а 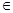 22;113 . 22;113 .
Ответ: а 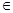 22;113 . 22;113 .
Заключение.
Таким образом, я рассмотрела часто встречающиеся типы уравнений и системы уравнений с параметрами и сделала следующие выводы:
· при решении многих задач с параметрами удобно воспользоваться геометрическими интерпретациями. Это часто позволяет существенно упростить анализ задач, а в ряде случаев представляет собой единственный «ключ» к решению задачи;
· существенным этапом решения задач с параметрами является запись ответа. Особенно это относится к тем задачам, где решение как бы «ветвится» в зависимости от значения параметра. В подобных случаях составление ответа – это сбор ранее полученных результатов.
Подготовка реферата позволила мне узнать много нового и интересного, подробно познакомиться с вопросами, которые на уроках изучаются кратко.
Оформление реферата способствовало совершенствованию и закреплению полученных мною на уроках информатики умений и навыков по редактированию и форматированию текстовых документов.
Я могу сказать, что научилась решать уравнения с параметрами, но не хочу останавливаться на достигнутом и в следующем году собираюсь продолжить работу по этой теме и рассмотреть примеры тригонометрических, логарифмических и показательных уравнений с параметрами.
Список литературы.
1. Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. – М.: Просвещение, 1990.
2. Шарыгин И.Ф. Факультативный курс по математике: Решение задач.Учеб. пособие для 10 кл. средней школы – М.: Просвещение, 1989.
3. Васильев Ю.С., Витовтов П.Г. и др. Математика. Система дистанционного образования. Часть 1. Учебно-практическое пособие. – Челябинск: 2000.
4. Горнштейн Ш. Квадратные трехчлены и параметры. – Математика. -1999, №5.
5. Мещерякова Г.В. Задачи с параметрами, сводящиеся к квадратным уравнениям. –Математика в школе. №5, 2001.
6. Большой энциклопедический словарь. Математика. – М.: Научное издательство «Большая Российская энциклопедия», 1998.
|