| Пензенский государственный педагогический университет
имени В. Г. Белинского
УДК 53(075)
А. А. Марко,
ИЗБРАННЫЕ ВОПРОСЫ КИНЕМАТИКИ
МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЕРДОГО ТЕЛА
Пенза, 2010
Печатается по решению редакционно-издательского совета Пензенского государственного педагогического университета имени В. Г. Белинского
УДК 53(075)
Марко А. А. Избранные вопросы кинематики материальной точки и твердого тела. / А. А. Марко – Пенза: ПГПУ, 2010. – 40 с.
Учебно-методическое пособие предназначено студентам физико-математического факультета, учителей школ и абитуриентов. Пособие содержит краткое обсуждение теоретических основ кинематического описания движения точки и твердого тела, подборку тестовых заданий и базовых задач для организации самостоятельной работы. В пособие приведены методические рекомендации по решению задач, а так же приведены примеры решения задач по кинематике в рамках векторно-координатного метода решения.
Ó Пензенский государственный
педагогический университет
имени В. Г. Белинского, 2010
Ó А. А. Марко, 2010
Ó Л. С. Иванова, 2010
Ó Н. В. Кирпичева, 2010
1.1. Основные вопросы.
Механическое движение. Относительность механического движения. Материальная точка. Система отсчета. Траектория. Вектор перемещения и его проекции. Путь.
Скорость. Сложение скоростей. Ускорение.
Прямолинейное равномерное и равнопеременное движение. Зависимости скорости, координат и пути от времени.
Средняя скорость. Свободное падение тел.
Криволинейное движение.
Равномерное движение по окружности. Угловая скорость. Период и частота обращения. Ускорение тела при движении по окружности.
Свободное падение тел. Ускорение свободно падающего тела. Движение тела, брошенного под углом к горизонту. Дальность
и высота полета.
Поступательное и вращательное движение твердого тела.
1.2. Поступательное движение и его характеристики
Механическим движением тела
называется изменение его положения в пространстве с течением времени относительно других тел или его отдельных частей.
Механическое движение относительно, т.е. если говорить, что тело совершает механическое движение, то необходимо указать тело отсчета, относительно которого происходит это движение.
В классической механике рассматриваются механические движения тел, происходящие со скоростями, значительно меньшими скорости света в вакууме ( ). ).
Для описания механического движения необходимо указать тело, относительно которого рассматривается движение. Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчета. С телом отсчета связывается система координат. Чаще всего для определения положения тела используется правая декартова прямоугольная система координат.
Система отсчёта
– совокупность тела отсчёта и связанная с этим телом система координат и прибор для измерения времени (часы).
Тело, размерами, формой и структурой которого можно пренебречь при изучении данного механического движения, называется материальной точкой
.
 Положение материальной точки М задаётся либо радиус-вектором Положение материальной точки М задаётся либо радиус-вектором  , проведенным из начала системы координат: , проведенным из начала системы координат:
 , (1.2.1) , (1.2.1)
либо координатами  (рис. 1). (рис. 1).
При движении точки радиус-вектор и координаты изменяются с течением времени. Говорят, что задан закон движения, если известна векторная функция времени
Рис. 1  (1.2.2) (1.2.2)
или три эквивалентные ей скалярные функции:
 (1.2.3) (1.2.3)
Линия, описываемая движущейся точкой в пространстве, называется траекторией
. Движения разделяются на прямолинейные и криволинейные в зависимости от вида траектории.
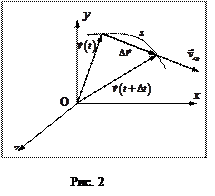 Перемещение
точки за промежуток времени Перемещение
точки за промежуток времени  – вектор – вектор  , соединяющий положения точки в моменты , соединяющий положения точки в моменты  и и 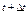 . Из . Из
рис, 2 видно, что
 (1.2.4) (1.2.4)
Путь
 , пройденный точкой за тот же промежуток времени , пройденный точкой за тот же промежуток времени 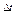 , это длина соответствующего отрезка траектории. При прямолинейном движении в одном направлении , это длина соответствующего отрезка траектории. При прямолинейном движении в одном направлении 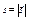 , при криволинейном – , при криволинейном –  . .
Путь  , пройденный точкой к моменту времени , пройденный точкой к моменту времени  , это длина траектории от некоторого начального положения до положения , это длина траектории от некоторого начального положения до положения
в момент  . Если точка меняла направление движения по той же траектории, то её путь . Если точка меняла направление движения по той же траектории, то её путь  – это полное расстояние, пройденное вдоль траектории. – это полное расстояние, пройденное вдоль траектории.
Вектором средней скорости
за время 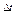 называется отношение вектора перемещения материальной точки ко времени, за которое оно совершено: называется отношение вектора перемещения материальной точки ко времени, за которое оно совершено:
 (1.2.5) (1.2.5)
Направление вектора  совпадает с совпадает с  (рис. 2). (рис. 2).
Средней путевой скоростью
за время называется скалярная величина равная отношению отрезка пути  к к 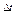
 (1.2.6) (1.2.6)
При прямолинейном движении в одном направлении  , при криволинейном – , при криволинейном –  . .
Мгновенная скорость
в данной точке траектории равна пределу отношения перемещения на участке траектории, включающем эту точку, к промежутку времени, в течение которого это перемещение совершается:
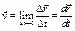 . (1.2.7) . (1.2.7)
Скорость в каждой точке направлена по касательной к траектории. Проекции скорости на оси координат:
 , (1.2.8) , (1.2.8)
модуль скорости
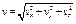 , (1.2.9) , (1.2.9)
причем
 , (1.2.10) , (1.2.10)
где 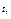 и и  – фиксированные моменты времени при движении тела по заданной траектории. – фиксированные моменты времени при движении тела по заданной траектории.
В случае произвольного криволинейного движения вектор скорости 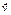 может изменяться с течением времени как по модулю, так и по направлению (рис. 3). может изменяться с течением времени как по модулю, так и по направлению (рис. 3).
Вектором среднего ускорения
за время 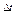 называется отношение приращения вектора скорости называется отношение приращения вектора скорости  ко времени, за которое оно совершено: ко времени, за которое оно совершено:
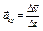 , (1.2.11) , (1.2.11)
 Направление вектора Направление вектора  совпадает с направлением совпадает с направлением  (рис. 3). (рис. 3).
Предельный переход в выражении (1.2.11) при  , определяет вектор ускорения материальной точки в момент времени , определяет вектор ускорения материальной точки в момент времени  : :
 . (1.2.12) . (1.2.12)
Проекции вектора ускорения на координатные оси равны:
 , (1.2.13) , (1.2.13)
модуль ускорения
 . (1.2.14) . (1.2.14)
Если движение материальной точки плоское (будем считать, что траектория материальной точки лежит в плоскости  ),
то вектор ускорения ),
то вектор ускорения  всегда можно разложить на две взаимно перпендикулярные составляющие (рис. 4) всегда можно разложить на две взаимно перпендикулярные составляющие (рис. 4)
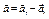 , (1.2.15) , (1.2.15)
где  – тангенциальное (касательное) и – тангенциальное (касательное) и  – нормальное (центростремительное) ускорения материальной точки. – нормальное (центростремительное) ускорения материальной точки.
 Вектор Вектор  всегда направлен к центру кривизны траектории О', а вектор всегда направлен к центру кривизны траектории О', а вектор 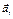 лежит на касательной к траектории и может быть направлен как в сторону движения, так и в противоположную сторону. лежит на касательной к траектории и может быть направлен как в сторону движения, так и в противоположную сторону.
Нормальное ускорение  характеризует быстроту изменения направления вектора скорости материальной точки. Тангенциальное ускорение характеризует быстроту изменения направления вектора скорости материальной точки. Тангенциальное ускорение
 характеризует быстроту изменения величины скорости материальной точки. характеризует быстроту изменения величины скорости материальной точки.
Абсолютные значения нормального и тангенциального ускорений определяются соотношениями
 , (1.2.16) , (1.2.16)
 , (1.2.17) , (1.2.17)
где 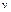 модуль скорости материальной точки; модуль скорости материальной точки;  — радиус кривизны траектории в данный момент времени. — радиус кривизны траектории в данный момент времени.
Абсолютные значения величин ускорений связаны между собой соотношением
 . (1.2.18) . (1.2.18)
1.3. Равномерное и равноускоренное движения
Равноускоренным движением
тела называется движение, при котором его скорость за любые равные промежутки времени изменяется одинаково.
Если направление векторов  и и 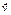 совпадают, движение называется равноускоренным
, если противоположны – равнозамедленным
. совпадают, движение называется равноускоренным
, если противоположны – равнозамедленным
.
При прямолинейном движении
координатная ось обычно совмещается с направлением движения. Тогда при движении с постоянным ускорением координата и скорость материальной точки, при этом изменяются по кинематическим формулам:
 , (1.3.1) , (1.3.1)
 . (1.3.2) . (1.3.2)
Путь, пройденный телом при равноускоренном движении:
 , (1.3.3) , (1.3.3)
при равнозамедленном движении:
 (1.3.4) (1.3.4)
где  , ,  – модуль начальной скорости и модуль ускорения соответственно; – модуль начальной скорости и модуль ускорения соответственно;  – путь пройденный телом до остановки; – путь пройденный телом до остановки;  – путь, пройденный телом после остановки, при его движении в другую сторону. – путь, пройденный телом после остановки, при его движении в другую сторону.
Графическая иллюстрация соотношений (1.3.3) и (1.3.4) представлена на рисунках 5 и 6.
Движение тела с постоянным ускорением включает в себя равномерное и равноускоренное движение. При равномерном прямолинейном движении скорость тела не изменяется и в уравнениях (1.3.1), (1.3.2) и (1.3.3) нужно положить  . .
При плоском криволинейном движении
мгновенная скорость тела в любой точке направлена по касательной к траектории, при этом ее проекции на оси координат и координаты материальной точки меняются со временем:
 (3.1.5) (3.1.5)
Простейшими случаями криволинейного движения являются движение тела, брошенного под углом к горизонту, и движение тела с постоянной по величине скоростью по окружности (см. §1.4.)
Если тело начинает движение в поле силы тяжести Земли со скоростью  ,
составляющей угол ,
составляющей угол  с горизонтом, то его траектория будет криволинейной, лежащей в плоскости перпендикулярной к поверхности земли. Удобно выбрать прямоугольную систему координат с горизонтом, то его траектория будет криволинейной, лежащей в плоскости перпендикулярной к поверхности земли. Удобно выбрать прямоугольную систему координат
с осью  , направленной горизонтально и осью , направленной горизонтально и осью  , направленной вертикально (рис. 7). Движение представляет собой комбинацию равномерного движения в горизонтальном направлении и равнозамедленного и равноускоренного в вертикальном направлении с ускорением свободного падения , направленной вертикально (рис. 7). Движение представляет собой комбинацию равномерного движения в горизонтальном направлении и равнозамедленного и равноускоренного в вертикальном направлении с ускорением свободного падения  . .
 Система начальных условий имеет вид: Система начальных условий имеет вид:
 . (1.3.6) . (1.3.6)
Проекции скорости на координатные оси c учетом (1.3.6) в любой момент времени  равны: равны:
 , (1.3.7) , (1.3.7)
 . (1.3.8) . (1.3.8)
Из (1.3.7) и (1.3.8) получаем для модуля скорости
 . (1.3.9) . (1.3.9)
Направление вектора скорости можно определить из соотношения 
 . (1.3.10) . (1.3.10)
Координаты тела в момент времени  равны: равны:
 , (1.3.11) , (1.3.11)
 . (1.3.12) . (1.3.12)
Время полета до момента падения определяется из (1.3.12) при  : :
 . (1.3.13) . (1.3.13)
Время подъема до максимальной высоты определяется из (1.3.8) при 
 . (1.3.14) . (1.3.14)
Максимальная высота подъема определяется из (1.3.12) при  : :
 . (1.3.15) . (1.3.15)
Дальность полета получаем из (1.3.11) при  : :
 . (1.3.16) . (1.3.16)
Исключая из (1.3.11) и (1.3.12) получаем уравнение траектории:
 . (1.3.17) . (1.3.17)
1.4. Равномерное движение по окружности
Движение по окружности – простейший пример криволинейного движения. Скорость  движения по окружности называется линейной скоростью. При равномерном движении по окружности модуль движения по окружности называется линейной скоростью. При равномерном движении по окружности модуль  мгновенной скорости материальной точки с течением времени не изменяется ( мгновенной скорости материальной точки с течением времени не изменяется ( на рис. 8). на рис. 8).
 Изменение положения точки на окружности может быть охарактеризовано изменением угловой координаты точки: Изменение положения точки на окружности может быть охарактеризовано изменением угловой координаты точки:  .
Угол .
Угол  называется углом поворота радиус-вектора точки (рис. 8). называется углом поворота радиус-вектора точки (рис. 8).
При равномерном движении точки по окружности за любые равные промежутки времени углы поворота её радиус-вектора одинаковы. Поэтому угловой скоростью  движения точки движения точки
по окружности вокруг заданного
центра (или оси) называется отношение угла поворота  радиус-вектора точки за промежуток времени радиус-вектора точки за промежуток времени  к длительности этого промежутка: к длительности этого промежутка:
 . (1.4.1) . (1.4.1)
Угол поворота  радиус-вектора точки, равномерно движущемся по окружности, равен: радиус-вектора точки, равномерно движущемся по окружности, равен:
 . (1.4.2) . (1.4.2)
Промежуток времени  , в течение которого точка совершает один полный оборот по окружности, называется периодом
обращения (периодом вращения), а величина обратная периоду , в течение которого точка совершает один полный оборот по окружности, называется периодом
обращения (периодом вращения), а величина обратная периоду
 (1.4.3) (1.4.3)
– частотой
вращения.
За один период угол поворота радиус-вектора точки равен  рад, поэтому рад, поэтому
 , (1.4.4) , (1.4.4)
 . (1.4.5) . (1.4.5)
Путь  , пройденный точкой, равномерно движущейся по окружности, за промежуток времени , пройденный точкой, равномерно движущейся по окружности, за промежуток времени  при при  равен равен  . Путь, пройденный точкой за один период по окружности радиуса . Путь, пройденный точкой за один период по окружности радиуса  , равен , равен  , а угол поворота радиус-вектора точки за тот же промежуток времени равен , а угол поворота радиус-вектора точки за тот же промежуток времени равен  рад. Отсюда находим связь между линейной и угловой скоростью: рад. Отсюда находим связь между линейной и угловой скоростью:
 . (1.4.6) . (1.4.6)
Всякое перемещение плоской фигуры, происходящее в плоскости расположения этой фигуры, можно рассматривать в любой момент времени как результат наложения поступательного движения тела вместе с некоторой произвольной точкой  тела (называемой полюсом) и вращательного движения тела относительно этой точки. тела (называемой полюсом) и вращательного движения тела относительно этой точки.
Выбирая полюс в различных точках тела, можно по-разному осуществлять разложение плоского движения на поступательное и вращательное. В каждом из этих случаев перемещение и скорость в поступательном движении могут быть различными, а угловое перемещение и угловая скорость одинаковые.
В случае плоско-параллельного движения твердого тела существует такая точка, скорость которой в данный момент времени равна нулю. Эту точку называют мгновенным центром скоростей. Мгновенный центр скоростей можно найти по следующим рекомендациям:
1. при качении без проскальзывания плоской фигуры по неподвижной поверхности мгновенный центр скоростей совпадает с точкой соприкосновения тела с поверхностью
(рис 9).
2. мгновенный центр скоростей находится на пересечении перпендикуляров, восставленных из двух данных точек тела к линиям векторов абсолютной скорости этих точек.
3. в том случае, когда перпендикуляры, проведенные из указанных точек сливаются, сливаются в один, мгновенный центр скоростей лежит в точке пересечения перпендикуляра с линией, проведенной через концы векторов скоростей этих
точек (рис. 9).
1.5. Методический аспект решения задач по кинематике
При решении задач по кинематике необходимо выработать общие подходы к решению задач этого класса обобщенные в алгоритм решения задачи.
1. Внимательно прочитать задачу, проанализировать условие, выяснить характер движения.
2. Сделать схематический чертеж, отображающий описанное в задаче движение. Изобразить на нем траекторию движения, векторы скорости, ускорения, перемещения.
3. Выбрать систему отсчета.
4. Сформировать краткие данные задачи (выписать числовые значения заданных величин, ввести необходимые обозначения)
5. Составить для данного движения уравнения, отражающие математическую связь между проекциями векторов на оси координат. (Число уравнений должно быть равно числу неизвестных величин).
6. Решить составленную систему относительно искомых величин (получить расчетные формулы).
7. Подставить в расчетные формулы числовые значения физических величин и произвести вычисления. Оценить реальность полученного результата.
1.6. Контрольные вопросы
1. Что называют системой отсчета?
2. При каких условиях тело можно рассматривать как материальную точку?
3. Как определить координаты точки на плоскости, в пространстве?
4. Как по координатам двух точек на плоскости определить расстояние между ними?
5. Сумма какого минимального числа векторов неодинаковой длины может равняться нулю?
6. Что такое механическое движение? Какое движение тела называют поступательным?
7. Что называют траекторией движения материальной точки?
8. Зависит ли траектория движения от выбора системы отсчета?
9. Что такое вектор перемещения, скорости, ускорения?
10. Что называют длиной пути?
11. Может ли модуль вектора перемещения материальной точки быть больше пути, пройденного ей за тот же промежуток времени?
12. Что показывает счетчик километров автомобиля (путь или перемещение)?
13. Что такое мгновенная и средняя скорость?
14. Какую скорость (мгновенную, среднюю) показывает спидометр автомобиля?
15. Какое движение называют равномерным?
16. Если известна траектория движения, можно ли указать направление мгновенной скорости и ускорения в произвольной точке этой траектории?
17. Может ли материальная точка в один и тот же момент времени иметь: скорость, направленную вправо, и ускорение направленное влево; равную нулю скорость и не равное нулю ускорение?
18. Как по графику зависимости скорости от времени для прямолинейного движения найти перемещение материальной точки и пройденный ей путь?
19. Какое движение называют равноускоренным?
20. Как выглядит график зависимости скорости от времени для равноускоренного прямолинейного движения материальной точки?
21. Какое движение называют свободным падением?
22. В какой точке траектории скорость снаряда составляет с его ускорением прямой угол? (Сопротивлением воздуха пренебречь).
23. В какой точке траектории снаряд имеет наименьшую скорость, наименьшее ускорение?
24. Какой может быть траектория материальной точки, если она движется с постоянным по величине и направлению ускорением?
25. Что такое угловая скорость и как она связана с частотой и периодом обращения при движении по окружности?
26. Зависит ли угловая скорость и ускорение точек равномерно вращающегося диска от расстояния до оси вращения?
27. При каком движении мгновенная скорость материальной точки в любой момент времени перпендикулярна ускорению?
28. Могут ли совпадать направления мгновенной скорости и ускорения при движении по криволинейной траектории?
29. При движении по окружности модуль скорости движения материальной точки возрастает. Будет ли ускорение направлено к центру окружности?
30. Какие точки колеса телеги имеют наибольшее и наименьшее значение скорости относительно Земли и относительно телеги?
31. Поезд движется прямолинейно с ускорением  . Чему равно ускорение камня выброшенного из окна вагона относительно поезда и относительно Земли? . Чему равно ускорение камня выброшенного из окна вагона относительно поезда и относительно Земли?
32. В чем состоит принцип независимого движения тел?
1.7. Примеры решения задач
Пример 1.
По взаимно перпендикулярным дорогам движутся два автомобиля с постоянными скоростями  и и  . В момент начала наблюдения первый автомобиль находился на перекрестке, а второй на расстоянии . В момент начала наблюдения первый автомобиль находился на перекрестке, а второй на расстоянии  от него. Определить наименьшее расстояние между автомобилями. от него. Определить наименьшее расстояние между автомобилями.
РЕШЕНИЕ:
| Дано:





|
Схема задачи:
Решение:
Запишем законы движения для каждого из тел в координатной форме:
 , ,  ; (1) ; (1)
с учетом данных задачи получим
 , ,  . (2) . (2)
Расстояние между точками определим
 , (3) , (3)
с учетом (2), имеем
 . (4) . (4)
Найдем момент времени  соответствующий минимуму расстояния между телами. Условие минимума расстояния имеет вид соответствующий минимуму расстояния между телами. Условие минимума расстояния имеет вид
 . (5) . (5)
Находя производную и приравнивая ее к нулю, получаем уравнение:
 . (6) . (6)
Из (6) находим
 . (7) . (7)
Подстановка (7) в (4) дает ответ задачи
 . (8) . (8)
Ответ:

|
| Найти:

|
Пример 2.
Лифт поднимается с ускорением  , В тот момент, когда его скорость стала равна , В тот момент, когда его скорость стала равна  , с потолка лифта начал падать болт. Высота лифта , с потолка лифта начал падать болт. Высота лифта  . Вычислить время падения болта и расстояние, пройденное болтом относительно шахты. . Вычислить время падения болта и расстояние, пройденное болтом относительно шахты.
РЕШЕНИЕ:
| Дано:





|
 Схема задачи: Схема задачи:
Решение:
Рассмотрим движение болта (точка Б – индексы «2») и точки пола лифта (точка Л – индексы «1») относительно шахты.
Запишем законы движения для каждой точки в координатной форме:
 , ,  ; (1) ; (1)
с учетом данных задачи получим
 , ,  . (2) . (2)
В момент падения болта на пол
 , (3) , (3)
с учетом (2) имеем
 . (4) . (4)
Найдем время 
 . (5) . (5)
Расстояние, пройденное болтом относительно шахты:
 , (6) , (6)
Из (6) с учетом (2) и (5) находим
 . (7) . (7)
Подстановка числовых данных в (5) и (7) дает числовой ответ задачи.
Ответ:
 , ,  . .
|
| Найти:


|
Пример 3.
Со скалы высоты  в горизонтальном направлении бросают тело с начальной скоростью в горизонтальном направлении бросают тело с начальной скоростью  . Одновременно с поверхности земли под углом . Одновременно с поверхности земли под углом 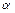 к горизонту навстречу бросают второе тело с такой же начальной скоростью. Определить на каком расстоянии от скалы бросали второе тело, если тела столкнулись в воздухе. Определить скорость второго тела относительно первого. к горизонту навстречу бросают второе тело с такой же начальной скоростью. Определить на каком расстоянии от скалы бросали второе тело, если тела столкнулись в воздухе. Определить скорость второго тела относительно первого.
РЕШЕНИЕ:
| Дано:

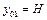








|
Схема задачи:
Решение:
С учетом начальных условий законы движения тел можно записать в виде:
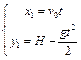 , ,  . (1) . (1)
В момент «встречи» тел
 , (2) , (2)
или с учетом (1)
 . (3) . (3)
Исключив из системы уравнений (3) время, найдем
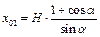 . (4) . (4)
Закон изменения скорости для каждого тела, с учетом начальных условий имеет вид
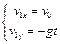 , , 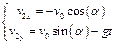 . (5) . (5)
Относительная скорость движения  равна: равна:
 , (6) , (6)
или в проекциях
 . (7) . (7)
Модуль относительной скорости определим как
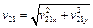 . (8) . (8)
Окончательно, при подстановке (7) в (8) получим
 . (9) . (9)
Ответ:
 ,. ,. . .
|
| Найти:


|
Пример 4.
Шарик радиуса  катится со скоростью катится со скоростью  по двум рельсам, расположенным на расстоянии по двум рельсам, расположенным на расстоянии  . Определить скорости верхней (А
) и нижней (B
) точек шара относительно рельсов. . Определить скорости верхней (А
) и нижней (B
) точек шара относительно рельсов.
РЕШЕНИЕ:
| Дано:

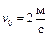

|
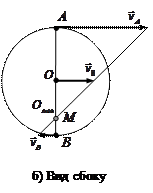 Схема задачи: Схема задачи:
Решение:
Мгновенная ось вращения в данном случае определена на рисунке ( ). Угловая скорость шара относительно мгновенной оси ). Угловая скорость шара относительно мгновенной оси
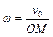 , (1) , (1)
где
 . (2) . (2)
Скорости точек А
и В
определим как
 (3) (3)
С учетом (1) и (2) из (3), найдем
 . (4) . (4)
Подставляя в (4) числовые значения величин, получим
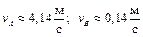 . (5) . (5)
Ответ:
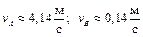 . .
|
| Найти:
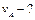
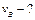
|
1.8. Задания с выбором ответа для самостоятельной работы
1.1. Лодка плывет по течению реки. Если скорость течения 1 м/с, а скорость лодки относительно берега 4 м/с, то скорость лодки относительно воды равна:
| 1). 4 м/с
|
2). 5 м/с
|
3).1 м/с
|
4). 2,5 м/с
|
5). 3 м/с
|
1.2. Лодка плывет по течению реки. Если скорость течения 1 м/с, а скорость лодки относительно воды 4 м/с, то скорость лодки относительно берега равна:
| 1). 4 м/с
|
2). 5 м/с
|
3).1 м/с
|
4). 2,5 м/с
|
5). 3 м/с
|
1.3. Лодка плывет против течения реки. Если скорость течения 1 м/с, а скорость лодки относительно воды 4 м/с, то скорость лодки относительно берега равна:
| 1). 4 м/с
|
2). 5 м/с
|
3).1 м/с
|
4). 2,5 м/с
|
5). 3 м/с
|
1.4. Лодка плывет против течения реки. Если скорость течения 1 м/с, а скорость лодки относительно берега 4 м/с, то скорость лодки относительно воды равна:
| 1). 4 м/с
|
2). 5 м/с
|
3).1 м/с
|
4). 2,5 м/с
|
5). 3 м/с
|
1.5. Лодка движется по реке со скоростью 3 м/с относительно воды перпендикулярно берегу. Если ширина реки 60 м, а скорость течения реки 2 м/с, то время, за которое лодка переплывет реку, равно:
| 1). 12 с
|
2). 20 с
|
3). с с
|
4). 30 с
|
5).  с с
|
1.6. Плот равномерно плывет по реке со скоростью 4 км/ч. Человек движется поперек плота со скоростью 3 км/ч. Скорость человека в системе отсчета, связанной с берегом будет равна:
| 1). 1 км/ч
|
2). 3 км/ч
|
3).7 км/ч
|
4). 4 км/ч
|
5). 5 км/ч
|
1.7. Пассажирский катер проходит расстояние 120 км по течению реки за 2 ч, а против течения за 3 ч. Скорость катера в стоячей воде равна:
| 1). 50 км/ч
|
2). 60 км/ч
|
3).40 км/ч
|
4). 30 км/ч
|
5). 24 км/ч
|
1.8. Если при движении моторной лодки по течению реки её скорость относительно берега 8 м/с, а при. движении против течения 6 м/с, то скорость течения реки равна:
| 1). 1 м/с
|
2). 2 м/с
|
3). 3 м/с
|
4). 4 м/с
|
5). 5 м/с
|
1.9. Если при движении моторной лодки по течению реки её скорость относительно берега 8 м/с, а при движении против течения 6 м/с, то скорость лодки в стоячей воде равна:
| 1). 2 м/с
|
2). 6 м/с
|
3). 7 м/с
|
4). 8 м/с
|
5). 10 м/с
|
1.10. Тело равномерно вращается по окружности. Период обращения Т.
Через какую часть периода путь, пройденный телом, будет максимальным?
1.11. Тело равномерно вращается по окружности. Период обращения Т.
Через какую часть периода вектор перемещения тела будет максимальным?
1.12. Тело равномерно вращается по окружности. Период обращения Т.
Через какую часть периода вектор перемещения тела будет численно равен радиусу окружности?
1.13. Тело равномерно вращается по окружности. Период обращения Т.
Через какую часть периода путь, пройденный телом, будет
в  раз больше модуля вектора перемещения? раз больше модуля вектора перемещения?
1.14. Модуль перемещения материальной точки, начавшей двигаться по окружности и совершившей за 1,5с 1,5 полных оборота, равен:
1.15. Модуль перемещения материальной точки, начавшей двигаться по окружности за время 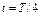 , равен: , равен:
1.16. Если человек прошёл по горизонтальному полю 400 м строго на север, затем ещё 300 м на запад, то модуль вектора перемещения человека будет равен:
| 1). 700 м
|
2). 100 м
|
3). 300 м
|
4). 400 м
|
5). 500 м
|
1.17. Автоколонна длиной 200 м движется по мосту равномерно со скоростью 36 км/ч. За какое время колонна пройдет мост, если его длина 500 м?
| 1). 20 с
|
2). 30 с
|
3). 60 с
|
4). 70 с
|
5). 50 с
|
1.18. Если материальная точка первую половину пути двигалась равномерно со скоростью 4 м/с, а вторую - со скоростью 9 м/с, то средняя скорость точки на всём пути равна:
| 1). 5,5 м/с
|
2). 2,8 м/с
|
3). 6 м/с
|
4). 6,5 м/с
|
5). 1,4 м/с
|
1.19. Если материальная точка первую половину времени, затраченного на прохождение всего пути, двигалась со скоростью 4 м/с,
а вторую половину времени – со скоростью 9 м/с, то средняя скорость точки на всём пути равна:
| 1). 5,5 м/с
|
2). 2,8 м/с
|
3). 6 м/с
|
4). 6,5 м/с
|
5). 1,4 м/с
|
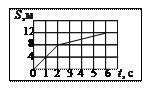 1.20. Средняя скорость материальной точки, зависимость пройденного пути которой от времени изображена на графике, за время 0 – 6 с равна: 1.20. Средняя скорость материальной точки, зависимость пройденного пути которой от времени изображена на графике, за время 0 – 6 с равна:
| 1). 3 м/с
|
2). 2 м/с
|
3). 6 м/с
|
4). 8 м/с
|
5). 9 м/с
|

1.21. По графику зависимости скорости тела от времени определить путь, пройденный телом за 6 с движения. Тело движется прямолинейно.
| 1). 48 м
|
2). 34 м
|
3). 42 м
|
4). 40 м
|
5). 36 м
|
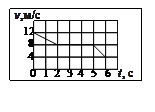
1.22. По графику зависимости скорости тела, от времени определить путь, пройденный телом за 6 с движения. Тело движется прямолинейно.
| 1). 48 м
|
2). 40 м
|
3). 24 м
|
4). 30 м
|
5). 50 м
|

1.23. По графику зависимости скорости тела от времени определить путь, пройденный телом за 6 с движения. Тело движется прямолинейно.
| 1). 58 м
|
2). 72 м
|
3). 60 м
|
4). 48 м
|
5). 50 м
|
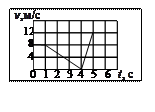
1.24. По графику зависимости скорости тела от времени определить путь, пройденный телом за 6 с движения. Тело движется прямолинейно.
| 1). 48 м
|
2). 40 м
|
3). 32 м
|
4). 30 м
|
5). 36 м
|
1.25. Проекция скорости тела при прямолинейном движении изменяется закону  . При этом путь, пройденный телом за 6 с, равен: . При этом путь, пройденный телом за 6 с, равен:
| 1). 8 м
|
2). 12 м
|
3). 15 м
|
4). 16 м
|
5). 20 м
|

1.26. По графику зависимости скорости тела от времени определить путь, пройденный телом за 12 с движения. Тело движется прямолинейно.
| 1). 72 м
|
2). 58 м
|
3). 60 м
|
4). 48 м
|
5). 50 м
|

1.27. По графику зависимости проекции скорости тела от времени определить путь, пройденный телом за 12 с движения. Тело движется прямолинейно.
| 1). 8 м
|
2). 20 м
|
3). 14 м
|
4). 22 м
|
5). 32 м
|
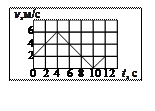
1.28. Точка движется вдоль оси х.
По графику зависимости проекции скорости от времени определить путь, пройденный точкой за интервал времени от 4 до 12 с.
| 1). 8 м
|
2). 12 м
|
3). 10 м
|
4). 6 м
|
5). 4 м
|
 1.29. Точка движется вдоль оси х.
По графику зависимости координаты от времени определить среднюю скорость точки в интервале времени от 1 до 6 с. 1.29. Точка движется вдоль оси х.
По графику зависимости координаты от времени определить среднюю скорость точки в интервале времени от 1 до 6 с.
| 1). 0,8 м/c
|
2). 1,6 м/c
|
3). 2,4 м/c
|
4). 3,2 м/c
|
5). 2,8 м/c
|
1.30.  Точка движется вдоль оси х.
По графику зависимости проекции скорости от времени определить путь, пройденный точкой за 12 с движения. Точка движется вдоль оси х.
По графику зависимости проекции скорости от времени определить путь, пройденный точкой за 12 с движения.
| 1). 24 м
|
2). 16 м
|
3). 20 м
|
4). 28 м
|
5). 30 м
|

1.31. По графику зависимости скорости тела от времени определить модуль ускорения тела в момент времени  . Тело движется прямолинейно. . Тело движется прямолинейно.

1.32. По графику зависимости скорости тела от времени определить модуль ускорения тела в момент времени  . Тело движется прямолинейно. . Тело движется прямолинейно.
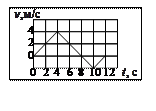
1.33. По графику зависимости проекции скорости тела от времени определить модуль ускорения тела в момент времени 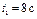 . Тело движется прямолинейно. . Тело движется прямолинейно.

1.34. По графику зависимости скорости тела от времени определить проекцию ускорения тела в момент времени  . Тело движется прямолинейно. . Тело движется прямолинейно.
1.35. Модуль ускорения материальной точки, двигающейся вдоль оси 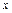 согласно уравнению согласно уравнению  (м), равен: (м), равен:

1.36. По графику зависимости скорости тела от времени определить ускорение тела в момент времени 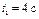 . Тело движется прямолинейно. . Тело движется прямолинейно.

1.37. Точка движется вдоль оси х
. По графику зависимости координаты от времени определить проекцию скорости движения точки на ось х
в момент времени 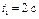 . .
1.38. Если тело, начавшее двигаться равноускоренно из состояния покоя, за первую секунду движения проходит путь S
,
то за третью секунду оно проходит путь:

1.39. Точка движется вдоль оси х.
По графику зависимости координаты от времени определить проекцию скорости движения точки на ось х
в момент времени  . .
1.40. Свободно падающее тело за последнюю секунду падения проходит путь 50 м. Каково полное время падения?
| 1). 4 с
|
2). 5 с
|
3). 5,5 с
|
4). 6 с
|
5). 6,5 с
|
1.41. На какую высоту поднимется тело, брошенное с Земли вертикально вверх со скоростью 30 м/с за 2 секунды движения?
| 1). 10 м
|
2). 20 м
|
3). 30 м
|
4). 40 м
|
5). 60 м
|
1.42. На какую максимальную высоту поднимется тело, брошенное с Земли вертикально вверх со скоростью 10 м/с?
| 1). 2 м
|
2). 4 м
|
3). 5 м
|
4). 10 м
|
5). 20 м
|
1.43. Тело бросают со скоростью 10 м/с под углом 15° к горизонту. Дальность полёта тела равна:
| 1). 2,5 м
|
2). 5 м
|
3). 7,5 м
|
4). 10 м
|
5). 15 м
|
1.44. Тело бросают, со скоростью 20 м/с под углом 30° к горизонту. Максимальная высота подъёма тела равна:
| 1). 15 м
|
2). 10 м
|
3). 7,5 м
|
4). 5 м
|
5). 2,5 м
|
1.45. Тело бросают со скоростью 15 м/с под углом 30° к горизонту. Время полёта до момента падения тела равно:
| 1). 1 с
|
2). 1,5 с
|
3). 2 с
|
4). 2,5 с
|
5). 3 с
|
1.46. Материальная точка при равномерном движении по окружности радиуса R
за время  совершила N
оборотов. Какое выражение определяет центростремительное ускорение? совершила N
оборотов. Какое выражение определяет центростремительное ускорение?
1.47. Материальная точка равномерно движется по окружности, совершая два оборота в секунду. Каков радиус окружности, если линейная скорость точки 3,14 м/с?
| 1). 1 м
|
2). 1,5 м
|
3). 2 м
|
4). 0,5 м
|
5). 0,25 м
|
1.48. Материальная точка движется по окружности с постоянной по величине скоростью. Линейную скорость точки увеличили в 2 раза,
а период обращения уменьшили в 2 раза. При этом центростремительное ускорение точки:
| 1). Увеличилось в 4 раза
|
2). Увеличилось в 2 раза
|
3).
Не изменилось
|
4). Уменьшилось в 2 раза
|
5). Уменьшилось в 4 раза
|
1.49. Минутная стрелка ручных часов вдвое длиннее секундной. Каково соотношение между линейными скоростями концов минутной ( ) и секундной ( ) и секундной (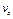 ) стрелок? ) стрелок?
1.50. Линейная скорость поверхности Земли, соответствующей  градусов северной широты, угловая скорость которой градусов северной широты, угловая скорость которой  , равна , равна
( – радиус Земли, Т –
период суточного обращения): – радиус Земли, Т –
период суточного обращения):
1.9. Задачи для самостоятельного решения
1.1. Из пункта А
со скоростью 60 км/ч выехал мотоциклист. Через 0,5 ч велел за ним выехала автомашина, скорость которой 80 км/ч. На каком расстоянии от пункта А
догонит автомашина мотоциклиста?
1.2. Навстречу друг другу идут пассажирский поезд со скоростью 90 км/ч и скорый поезд со скоростью 120 км/ч. Расстояние между поездами 70 км. На каком расстояний от скорого поезда должен находиться разъезд, чтобы поезда разошлись без остановки?
1.3. Две вагонетки катятся навстречу друг другу. Скорость одной вагонетки 0,3 м/с. Определить скорость второй вагонетки, если за 30 с они сблизились на 24 м.
1.4. Из точек А
и В
, находящихся на расстоянии 5 м, в одном направлении начали двигаться два шарика. Скорость одного шарика 2 м/с, другого 1,5 м/с. На каком расстоянии от точки А
произойдет столкновение?
1.5. Водитель легкового автомобиля начинает обгон трейлера при скорости 90 км/ч в тот момент времени, когда расстояние между машинами 20 м, и перестраивается в прежний ряд, когда расстояние между машинами стало 15 м. Определить время, за которое водитель автомобиля обогнал трейлер, движущийся со скоростью 72 км/ч. Длина легкового автомобиля 4 м,
трейлера -
16 м.
1.6. Пассажир поднимается по неподвижному эскалатору метрополитена за 3 мин, а по движущемуся вверх эскалатору за
2 мин. За какое время поднимется пассажир по эскалатору, движущемуся с той же скоростью вниз?
1.7. Эскалатор метро спускает идущего по нему человека за 1 мин. Если человек будет двигаться относительно эскалатора вдвое быстрее, то он спустится за 45 с. Сколько времени будет спускаться человек, стоящий на эскалаторе?
1.8. Два человека одновременно вступают на эскалатор с противоположных сторон и движутся навстречу друг другу с одинаковыми скоростями относительно эскалатора равными 2 м/с. На каком расстоянии от входа на эскалатор они встретятся? Длина эскалатора 100 м, его скорость 1,5 м/с.
1.9. При движении велосипедиста и пешехода в одну сторону за каждую минуту пешеход отстает от велосипедиста на 210 м,
а если, не изменяя по модулю скорости они движутся навстречу друг другу, то за каждые 2 минуты расстояние между ними уменьшается на 780 м. Определить скорость велосипедиста.
1.10. Колонна войск во время похода движется со скоростью 5 км/ч, растянувшись по дороге на 400 м. Командир, находящийся в хвосте колонны, посылает велосипедиста с поручением головному отряду. Велосипедист отправляется и едет со скоростью 25 км/ч и, на ходу выполнив поручение, сразу же возвращается обратно с той же скоростью. Через сколько после получения поручения он вернулся обратно?
1.11. В безветренную погоду человек опускается на парашюте с высоты 200 м с постоянной скоростью 4 м/с. Определить путь, пройденный парашютистом за время спуска, если поднявшийся ветер сносит его в горизонтальном направлении со скоростью 3 м/с.
1.12. С какой скоростью должен лететь самолет, чтобы за 2 ч пролететь точно на север путь, равный 300 км, если во время полёта дует северо-западный ветер под углом 30° к меридиану со
скоростью 27 км/м?
1.13. Вычислить среднюю скорость движения человека, если первую треть пути он шел со скоростью 0.7 м/с, а оставшуюся часть пути со скоростью 1,0 м/с.
1.14. Катер проходит расстояние между двумя пунктами на реке вниз по течению за 8 ч, обратно — за 12 ч. За сколько часов катер прошел бы то же расстояние в стоячей воде?
1.15. Мальчик проехал половину пути на велосипеде со скоростью
16 км/ч. Далее половину оставшегося времени он ехал со скоростью 12 км/ч, а затем до конца пути шел пешком со скоростью 5 км/ч. Определить (в км/ч) среднюю скорость движения мальчика на всем пути.
1.16. Велосипедист проехал первую треть пути по шоссейной дороге со скоростью 10 м/с, затем половину пути по проселочной дороге со скоростью 6 м/с и оставшуюся часть пути — по лесной тропинке со скоростью 2 м/с. Чему равна средняя путевая скорость велосипедиста?
1.17. Самолёт пролетел расстояние из города А
в город В
со скоростью 800 км/ч, а обратно – половину пути со скоростью 900 км/ч, вторую половину со скоростью 700 км/ч. Определить среднюю путевую скорость самолёта за все время полёта.
1.18. Мотоциклист едет из одного города в другой. Первые 2 ч пути он движется с постоянной скоростью 60 км/ч, а оставшиеся 160 км – со скоростью 80 км/ч. Определить среднюю путевую скорость мотоциклиста между городами.
1.19. Поезд первую половину пути шёл со скоростью, в 1,5 раза большей скорости на второй половине пути. Средняя путевая скорость поезда на всём пути была равна 43,2 км/ч. Какова скорость поезда на первой половине пути?
1.20. Самолёт летит из пункта А
в пункт В
и возвращается назад в пункт А.
Скорость самолёта в безветренную погоду равна 900 км/ч. Найти отношение средних скоростей всего перелёта для двух случаев, когда во время перелёта ветер дует: а) вдоль линии АВ;
б) перпендикулярно линии АВ.
Скорость ветра 30 км/ч.
1.21. Автомобиль двигается с ускорением 1,5 м/с2
и через 10 с после начала разгона продолжает движение с постоянной скоростью. Какое расстояние автомобиль пройдет за 30 с после начала разгона?
1.22. Автомобиль двигается равномерно, проходя за каждые 5 с расстояние 60 м. Какой путь пройдет автомобиль до остановки, если будет тормозиться с ускорением 2 м/с2
?
1.23. Тело, имеющее начальную скорость 20 м/с и ускорение 0,5 м/с2
, начинает двигаться из некоторой точки по прямолинейному пути. Через 20 сек. из этой же точки вслед за первым телом начинает двигаться другое тело с начальной скорость 5 м/с и ускорением
2 м/с2
. Через сколько времени второе тело догонит первое?
1.24. Водитель автобуса, едущего со скоростью 90 км/ч внезапно замечает впереди, на расстоянии 50 м, застрявший грузовик. Водитель тормозит с максимально возможным отрицательным ускорением – 5 м/с2
(более резкое торможение приведет
к скольжению колес и тормозной путь от этого только увеличиться). Определить среднюю скорость движения автобуса до столкновения с грузовиком.
1.25. Тело, двигаясь равноускоренно из состояния покоя, прошло 450 м за 6 с. На каком расстоянии от начального положения оно находилось через 4 с после начала движения?
1.26. Автомобиль начинает движение с ускорением 1 м/с2
. Проезжая мимо наблюдателя, он имеет скорость 10,5 м/с. На каком расстоянии от наблюдателя он находился секунду назад?
1.27. Автомобиль начинает движение с постоянным ускорением и за десятую секунду проходит 19 м. Определить ускорение автомобиля.
1.28. Тело, имея начальную скорость 4 м/с, прошло за шестую секунду движения 2,9 м. Найти ускорение тела.
1.29. Тело, двигаясь прямолинейно с постоянным ускорением -0,3 м/с2
, потеряло 3/4 своей начальной скорости 2 м/с. Какой путь прошло тело за время движения?
1.30. Автомобиль движется с постоянным ускорением и проходит путь равный 20 м за 4 с, а следующий участок пути равный 40 м за 5 с. Определить ускорение автомобиля.
1.31. С каким ускорением движется тело, если за восьмую секунду после начала движения оно прошло путь 30 м? Найти путь за 15-ую секунду.
1.32. Два велосипедиста едут навстречу друг другу. Один из них, имея начальную скорость 5,4 км/ч, спускается с горы, разгоняясь с ускорением 0,2 м/с2
; другой, имея начальную скорость 18 км/ч, поднимается в гору равнозамедленно с ускорением 0,3 м/с2
. Через какое время они встретятся, если расстояние между ними в начальный момент 195 м?
1.33. Два велосипедиста едут навстречу: один из них, имея скорость
7,2 км/ч, спускается с горы, разгоняясь с ускорением 0,3 м/с2
; другой, имея скорость 36 км/ч, поднимается в гору равнозамедленно
с ускорением 0,2 м/с2
. Каково было расстояние между велосипедистами в начальный момент времени, если они встретились через 0,5 мин от начала движения?
1.34. Два автомобиля выходят из одного пункта в одном направлении. Второй автомобиль выходит на 20 с позже первого. Оба движутся равноускоренно с одинаковым ускорением 0,4 м/с2
. Через сколько времени от начала движения первого автомобиля расстояние между ними окажется 240 м?
1.35. Два автомобиля вышли с остановки один после другого и шли с ускорением 0,4 м/с2
. Через 2 мин после выхода первого автомобиля расстояние между ними стало равным 1,9 км. С каким промежутком времени вышли автомобили?
1.36. Два автомобиля вышли с остановки через 1 мин один после другого и шли с ускорением 0,2 м/с2
. Через какой промежутком времени после выхода второго автомобиля расстояние между ними утроится?
1.37. От движущегося поезда отцепляется последний вагон. Поезд продолжает двигаться с той же скоростью. Как будут относиться пути, пройденные поездом и вагоном до момента остановки вагона? Считать, что вагон двигался равнозамедленно.
1.38. Расстояние между двумя станциями 3 км поезд метро проходит со средней скоростью 54 км/ч. При этом он разгоняется в течение 60 с, затем идет равномерно некоторое время, а затем движется равнозамедленно до полной остановки в течение времени 40 с. Определить наибольшую скорость поезда.
1.39. Точка из состояния покоя начинает двигаться вдоль прямой. Первые 5 с движение равноускоренное, затем равномерное, затем в течение 10 с равнозамедленное до остановки. Средняя скорость точки на всём пути оказалась равной 2м/с. Определить максимальное значение скорости точки, если за всё время движения она прошла путь, равный 30 м.
1.40. Троллейбус отошёл от остановки с ускорением 0,2 м/с2
. Достигнув скорости 36 км/ч, он в течение 2 мин двигался равномерно, затем, затормозив, равнозамедленно прошёл до следующей остановки путь равный 100 м. Определить среднюю путевую скорость троллейбуса на участке между остановками.
1.41. Тело, брошенное вертикально вверх с высоты равной 2 м над поверхностью земли, упало на землю через 2 с после броска. Пренебрегая сопротивлением воздуха, определить, на какую максимальную высоту относительно земли поднималось тело при своём движении.
1.42. Тело падает вертикально в высоты 19,6 м с нулевой начальной скоростью. За какое время тело пройдет последний 1 м своего пути. Сопротивление воздуха не учитывать.
1.43. Тело, падающее с некоторой высоты без начальной скорости, последние 196 м пути прошло за 4 с. С какой высоты падало тело? Сопротивлением воздуха пренебречь.
1.44. Тело, падающее с некоторой высоты без начальной скорости, за последнюю секунду движения прошло 1/4 часть своего пути. Определить высоту, с которой упало тело. Сопротивлением воздуха пренебречь.
1.45. Звук выстрела и пуля одновременно достигают высоты 680 м. Какова начальная скорость пути? Выстрел произведен вертикально вверх. Сопротивление воздуха движению пути не учитывать. Скорость воздуха принять равной 340 м/с.
1.46. Стальной шарик падает с высоты 1,5 м на стальную доску и отскакивает от неё с потерей 25% скорости. Определить время, которое проходит от начала движения шарика до его второго падения на доску.
1.47. С крыши дома оторвалась маленькая сосулька, которая за 0,2 с пролетела мимо окна высотой 1,5 м. С какой высоты относительно верхнего края окна упала сосулька? Сопротивлением воздуха пренебречь.
1.48. Тело, брошенное вертикально вверх, через промежуток времени, равный половине времени подъёма на максимальную высоту, находилось на высоте равной 9 м над точкой броска. На какую максимальную высоту поднималось тело при движении? Сопротивлением воздуха пренебречь.
1.49. Тело, брошенное вертикально вверх, на половине максимальной высоты подъёма имело скорость 10 м/с. Чему равна начальная скорость тела? Сопротивлением воздуха пренебречь.
1.50. Мяч брошен вертикально вверх из точки, находящийся на высоте равной 5 м. Определить время полёта мяча, если он пролетел до момента падения путь равный 15 м. Сопротивлением воздуха пренебречь.
1.51. С самолета, летящего горизонтально со скоростью 40 м/с, падает вниз тело. Какова скорость тела через 3 секунды после начала падения?
1.52. С холма в горизонтальном направлении брошено тело. Через 0,5 с после броска скорость тела по сравнению с начальной увеличилась в 1,5 раза. Определить начальную скорость тела. Сопротивлением воздуха пренебречь.
1.53. Тело брошено горизонтально. Через 5 с после броска угол между направлением скорости и ускорения стал равен 45°. Определить скорость тела в этот момент времени. Сопротивление воздуха не учитывать.
1.54. Какой горизонтальной скоростью обладал лыжник при прыжке с трамплина, находящегося на вершине горы, имеющей уклон 45°, если он приземлился на горе на расстоянии 29 м от вершины?
1.55. В мишень на расстоянии 50 м сделано два выстрела
в горизонтальном направлении при одинаковой наводке винтовки. Скорость первой пули 320 м/с, второй 350 м/с. Определить расстояние между пробоинами.
1.56. С вертолета, летящего на высоте 125 м со скоростью 90 км/ч, сбросили груз. На какой высоте его скорость будет направлена под углом 45° к горизонту?
1.57. Дальность полета тела, брошенного горизонтально со скоростью
4,9 м/с, равна высоте, с которой его бросают. Чему равна эта высота?
1.58. С берега высотой 5 м горизонтально бросают камень со скоростью
6,7 м/с. Определить направление скорости камня при достижении им воды.
1.59. Камень брошен горизонтально со скоростью 5 м/с. Определить радиус кривизны траектории камня через 1 с после начала движения, Сопротивлением воздуха пренебречь.
1.60. Камень брошен горизонтально со скоростью 4 м/с. Найти тангенциальное ускорение камня через 2 с после начала движения. Сопротивлением воздуха пренебречь.
1.61. Снаряд вылетел из ствола орудия под углом 60° к горизонту с начальной скоростью 660 м/с. Определить расстояние от орудия до цели, если снаряд достиг наивысшей точки полета через 45 с после вылета. Сопротивление воздуха не учитывать.
1.62. С башни высотой 20 м брошен камень с начальной скоростью 12 м/с, направленной под углом 60° к горизонту. Пренебрегая сопротивлением воздуха, определить дальность полёта камня по горизонтальному направлению.
1.63. С башни высотой 15 м брошен камень с начальной скоростью
20 м/с, направленной под углом 30° к горизонту. Пренебрегая сопротивлением воздуха, определить время полёта камня до земли.
1.64. Под каким углом к горизонту нужно бросить тело, чтобы дальность полета была в 2 раза больше максимальной высоты?
1.65. Определить максимальную высоту полёта тела, брошенного под углом к горизонту, если время полёта равно 6 с. Известно, что максимальная скорость полета тела была на 30% больше минимальной.
1.66. Определить дальность полёта тела, брошенного под углом к горизонту, если время полета равно 5 с. Известно, что максимальная скорость полёта тела была в 2 раза больше минимальной.
1.67. Два тела брошены с земли под углами 30° и 45° к горизонту из одной точки. Каково отношение сообщённых им начальных скоростей, если тела упали на землю в одной точке?
1.68. Под углом 60° к горизонту брошено тело с начальной скоростью
20 м/с. Через какое время модуль угла между скоростью тела
и горизонтальной плоскостью равен 45°?
1.69. Начальная скорость камня, брошенного под углом к горизонту, равна 10 м/с. На какую максимальную высоту над начальным уровнем поднимался камень, если спустя 0,5 с после начала движения скорость камня была равна 7 м/с? Сопротивлением воздуха пренебречь.
1.70. Камень, брошенный под углом к горизонту, упал на землю со скоростью 9,8 м/с. Чему равна дальность полёта камня, если его максимальная скорость во время движения вдвое больше минимальной скорости?
1.71. Под каким углом к горизонту необходимо бросить камень
с обрывистого берега реки, чтобы он упал в воду возможно дальше от берега? Высота обрыва 20 м, начальная скорость камня 14 м/с.
1.72. Камень, брошенный под углом к горизонту, упал на землю
со скоростью 19,6 м/с. Чему равна максимальная высота полёта камня, если его максимальная скорость во время движения втрое больше минимальной скорости?
1.73. Камень бросили вверх с начальной скоростью 16 м/с под углом 30е
. к ' горизонту. Пренебрегая сопротивлением воздуха, определить, с какой высоты был брошен камень, если его скорость
в момент падения на поверхность земли была в два раза больше скорости в высшей точке траектории.
1.74. Мяч бросили с некоторой высоты над поверхностью земли вверх под углом 60° к горизонту с начальной скоростью 20 м/с.
За время полета вертикальная составляющая его скорости
по величине увеличилась на 30%. Пренебрегая сопротивлением воздуха, определить, с какой высоты был брошен мяч.
1.75. Тело брошено с поверхности земли под углом 60° к горизонту с начальной скоростью 20 м/с. Найти модуль перемещения от начальной точки бросания тела до ближайшей точки, в которой нормальное ускорение тела равно 8 м/с2
.
1.76. Тело брошено с начальной скоростью 15 м/с под углом 60°
к горизонту. Найти радиус кривизны траектории в точке наивысшего подъёма тела над поверхностью земли. Сопротивлением воздуха пренебречь.
1.77. Снаряд вылетает из орудия под углом 45° к горизонту
с начальной скоростью 300 м/с. Для момента времени, равного 20 с после начала движения найти радиус кривизны траектории.
1.78. Из миномёта ведут обстрел объекта, расположенного на склоне горы. Угол наклона горы 30°, угол стрельбы 60° по отношению к горизонту. На каком расстоянии от миномета будут падать мины, если их начальная скорость равно 100 м/с?
1.79. Снаряд вылетает со скоростью 200 м/с из пушки, стоящей у основания горы, составляющей угол 15° с горизонтом, под углом 45° к поверхности горы. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории в точке максимального подъёма над поверхностью склона.
1.80. Под каким углом к горизонту надо бросить шарик, чтобы радиус кривизны траектории в начальный момент времени был
в 8 раз больше, чем в вершине?
1.81. Определить с какой частотой в об/мин вращается шкив диаметром 160 мм, если скорость точек на ободе шкива 6 м/с.
1.82. Длина минутной стрелки башенных часов Московского университета равна 4,5 м. С какой линейной скоростью перемещается конец стрелки?
1.83. Вычислить путь, который проехал за 30 с велосипедист, двигавшийся с угловой скоростью 0.1 рад/с по окружности радиуса 100 м.
1.84.  Цилиндрический каток радиуса 10 см помещён между двумя параллельными рейками. Рейки движутся в одну сторону Цилиндрический каток радиуса 10 см помещён между двумя параллельными рейками. Рейки движутся в одну сторону
со скоростями  и и  . Какова угловая скорость вращения катка, если проскальзывание отсутствует? . Какова угловая скорость вращения катка, если проскальзывание отсутствует?
1.85. Определить ускорение, которыми обладают точки земной поверхности на широте Санкт-Петербурга (60° с.ш.) за счет суточного вращения Земли.
1.86. Диск равномерно вращается относительно оси, проходящей через его центр и ему перпендикулярной. Линейная скорость точек края диска равна 3 м/с. У точек, расположенных на 10 см ближе к оси, скорость 2 м/с. Какова частота вращения диска?
1.87. Найти радиус вращающегося колеса, если известно, что линейная скорость точек обода колеса в 2,5 раза больше линейной скорости точки, лежащей на 5 см ближе к оси колеса.
1.88. Диск равномерно вращается вокруг своей оси так, что точки, расположенные на 30 см от оси, за 20 с проходят путь, равный 4 м. Сколько оборотов за это время сделает диск?
1.89. Диск равномерно вращается вокруг своей оси так, что точки, расположенные на 40 см от оси, за 30 с проходят путь, равный 5 м. Чему равен период обращения диска?
1.90. Материальная точка движется равномерно с частотой 0,2 с-1
по окружности радиусом 50 см. Найти путь, пройденный точкой за 20 с.
1.91. Материальная точка, движущаяся равномерно по окружности, совершает один оборот за 2 с. Найти радиус окружности, если за 5 мин точка прошла путь, равный 100 м.
1.92. Две точки равномерно движутся по окружности. Первая точка, двигаясь по часовой стрелке, делает один оборот за 5 с, вторая точка, двигаясь против часовой стрелки, делает один оборот за 2 с. Найти время между двумя последовательными встречами точек.
1.93. На легкий шкив радиусом 10 см намотана нить, к концу которой прикреплен груз. Груз начинает опускаться с ускорением 2 см/с2
. Чему будет равна угловая скорость шкива, когда груз опустится
на 100 см?
1.94. Два тонких диска вращаются на общей оси. Расстояние между дисками 30 см, скорость вращения 2000 об/мин. Пуля, летящая параллельно оси вращения на расстоянии 12 см от неё, пробивает оба диска. Пробоины в дисках смещены относительно друг друга
на 3 см, считая по дуге окружности. Определить скорость пули.
1.95. 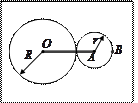 Кривошип ОА
, вращаясь с угловой скоростью 2,5 рад/с, приводит в движение малое колесо радиуса 5 см, катящееся по неподвижному колесу радиуса 15 см. Найти линейную скорость точки В. Кривошип ОА
, вращаясь с угловой скоростью 2,5 рад/с, приводит в движение малое колесо радиуса 5 см, катящееся по неподвижному колесу радиуса 15 см. Найти линейную скорость точки В.
1.96. Тонкий обруч радиусом 1 м равномерно катится без проскальзывания по горизонтальной поверхности. Определить расстояние между точками обруча, для которых модуль скорости
в  раз больше скорости центра обруча. Все скорости взяты относительно земли. раз больше скорости центра обруча. Все скорости взяты относительно земли.
1.97. Путь пройденный материальной точкой, движущейся равномерно по окружности, составил 15 м за 10 с. Определить модуль центростремительного ускорения точки, если радиус окружности равен 15 см.
1.98. Точка движется по окружности с постоянной скоростью 20 м/с. Вектор скорости изменяет направление на угол, равный 15° за время, равное 3 с. Чему равно нормальное ускорение точки?
1.99.  Нить, намотанную на катушку, тянут со скоростью 0,5 м/с. С какой скоростью движется центр катушки? Проскальзывания нет, внутренний радиус катушки равен 0,1 м, внешний – 0,2 м. Нить, намотанную на катушку, тянут со скоростью 0,5 м/с. С какой скоростью движется центр катушки? Проскальзывания нет, внутренний радиус катушки равен 0,1 м, внешний – 0,2 м.
1.100.  Нить, намотанную на катушку, тянут Нить, намотанную на катушку, тянут
со скоростью 0,5 м/с. С какой скоростью движется центр катушки? Проскальзывания нет, внутренний радиус катушки равен 0,1 м,
внешний – 0,2 м.
1.10. Распределение задач по вариантам
Для организации самостоятельной работы можно использовать приведенный ниже план распределения задач по вариантам.
| № варианта
|
№ задач
|
| 1
|
1.1
|
1.11
|
1.21
|
1.31
|
1.41
|
1.51
|
1.61
|
1.71
|
1.81
|
1.91
|
| 2
|
1.2
|
1.12
|
1.22
|
1.32
|
1.42
|
1.52
|
1.62
|
1.72
|
1.82
|
1.92
|
| 3
|
1.3
|
1.13
|
1.23
|
1.33
|
1.43
|
1.53
|
1.63
|
1.73
|
1.83
|
1.93
|
| 4
|
1.4
|
1.14
|
1.24
|
1.34
|
1.44
|
1.54
|
1.64
|
1.74
|
1.84
|
1.94
|
| 5
|
1.5
|
1.15
|
1.25
|
1.35
|
1.45
|
1.55
|
1.65
|
1.75
|
1.85
|
1.95
|
| 6
|
1.6
|
1.16
|
1.26
|
1.36
|
1.46
|
1.56
|
1.66
|
1.76
|
1.86
|
1.96
|
| 7
|
1.7
|
1.17
|
1.27
|
1.37
|
1.47
|
1.57
|
1.67
|
1.77
|
1.87
|
1.97
|
| 8
|
1.8
|
1.18
|
1.28
|
1.38
|
1.48
|
1.58
|
1.68
|
1.78
|
1.88
|
1.98
|
| 9
|
1.9
|
1.19
|
1.29
|
1.39
|
1.49
|
1.59
|
1.69
|
1.79
|
1.89
|
1.99
|
| 10
|
1.10
|
1.20
|
1.30
|
1.40
|
1.50
|
1.60
|
1.70
|
1.80
|
1.90
|
1.100
|
СОДЕРЖАНИЕ
1.1. Основные вопросы
3
1.2. Поступательное движение и его характеристики
3
1.3. Равномерное и равноускоренное движения
7
1.4. Равномерное движение по окружности
10
1.5. Методический аспект решения задач по кинематике
12
1.6. Контрольные вопросы
13
1.7. Примеры решения задач
15
1.8. Задания с выбором ответа для самостоятельной
работы
20
1.9. Задачи для самостоятельного решения
28
1.10. Распределение задач по вариантам
38
Пензенский государственный педагогический университет
имени В. Г. Белинского
ИЗБРАННЫЕ ВОПРОСЫ КИНЕМАТИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
И ТВЕРДОГО ТЕЛА
Авторы-составители: Антон Александрович Марко
Редактор –
Оригинал-макет – А. А. Марко
Корректор –
План университета 118
Подписано к печати 26.08.2010
Бумага писчая белая. Усл.-печ. л. 2,3. Уч.-изд. л. 2,5
Печать офсетная. Тираж 100 экз.
Заказ № 118/10 . Цена С. 118
Редакционно-издательский отдел Пензенского государственного
педагогического университета имени В. Г. Белинского:
440026, г. Пенза, ул. Лермонтова, 37. Корпус 5. Комн. 466.
Оригинал-макет изготовлен на кафедре теоретической физики и общетехнических дисциплин ПГПУ имени В. Г. Белинского
Типография ПГПУ имени В. Г. Белинского
|