| Министерство образования и науки РФ
Уральский государственный университет им. А.М.Горького
А.Г. Гейн, Н.А. Юнерман
ПОДГОТОКА К ЕДИНОМУ
ГОСУДАРСТВЕННОМУ ЭКЗАМЕНУ (ЕГЭ)
ПО ИНФОРМАТИКЕ
Методические рекомендации для учащихся
Екатеринбург, 2008
Введение
Предлагаемые методические рекомендации имеют своей целью оказать помощь учащимся в их подготовке к сдаче ЕГЭ по информатике. Весь представленный материал разбит на четыре раздела:
– общие методические указания по подготовке ЕГЭ по информатике;
– разбор части 1 демонстрационного варианта ЕГЭ 2008;
– примерные тренировочные варианты ЕГЭ;
– список литературы, которую полезно использовать при подготовки к ЕГЭ.
I.
Общие рекомендации
О Едином государственном экзамене (ЕГЭ) имеется достаточно много информации в различной учебно-методической литературе и Интернете. Поэтому мы не видим необходимости еще раз повторять истины, которые стали уже прописными. Но, во-первых, экзамен по любой дисциплине имеет свои особенности, и о них имеет смысл сказать конкретно; во-вторых, некоторые существенные, на наш взгляд, моменты все-таки редко находят свое отражение в указанных источниках информации. О таких особенностях и моментах и говорится в этом разделе.
Хотя наше пособие открывается этими рекомендациями, мы бы посоветовали разобрать сначала демонстрационный вариант ЕГЭ. Это можно сделать, получив такую версию с сайта Федерального института педагогических измерений (ФИПИ) по адресу www.fipi.ru, или обратившись к разделу II нашего пособия. После этого многие наши рекомендации будут восприняты с более точным пониманием. Впрочем, некоторые из них носят абсолютно универсальный характер и могут быть применены не только к экзамену по информатике.
Во время выполнения заданий ЕГЭ важно обращать внимание на следующие моменты:
– при выборе ответа необходимо обратить внимание на единицы измерения, в которых дан ответ, а при несовпадении своего ответа с предложенными попробовать преобразовать его к другому виду;
– если есть время и вы видите разные пути получения ответа, то хорошо их проделать и убедиться в одинаковости ответов;
– просмотреть все задания и начинать выполнение с того, которое кажется наиболее доступным (к этому надо подготовиться с помощью разбора демоверсии);
– при выполнении заданий части 1 выбрать правильный ответ часто помогает прямая подстановка предложенных вариантов в условие задания;
– в заданиях, где требуется определить, для чего предназначен предъявленный алгоритм, полезно выполнить прокрутку данного алгоритма на небольших исходных данных (например, массивах и строках небольших размеров);
– не делайте выкладки в уме.
Если, выполняя задание С2, вы колеблетесь, записать алгоритм на русском языке или языке программирования, то лучше писать на языке программирования. При этом мы советуем писать не фрагмент доработки, а программу целиком – она достаточно короткая и при такой записи у экспертов не возникает никаких вопросов относительно места, куда требуется вставить исправленный фрагмент или как заменить существующий.
Только на первый взгляд кажется, что оформление — дело простое.
1) Если ученик никогда до этого не работал с бланком ЕГЭ, то ему на проставление ответа (часть 1) или вписывание ответа (часть 2) требуется больше времени, чем ученику, уже работавшему с таким бланком. Главная причина замедления — боязнь испортить бланк. И его действительно нельзя портить — бланк не заменяется. А это время, которого на самом деле не так много.
2) Допускается исправление ошибочных ответов. Но и это осваивать во время экзамена уже поздно.
3) Надо избегать появления каких бы то ни было дефектов на бланке № 1. Бланк сканируется и обрабатываются автоматически! Апелляция возможна, но крайне затруднительна.
4) При вписывании ответов (часть 2) нужно придерживаться указанных образцов символов. Без привычки это тоже трудно. Каждый символ (например, запятая) — в отдельной клеточке, причем в отведенном для него месте клеточки (не должна стоять запятая в середине клетки, поскольку тогда распознающей системой она будет восприниматься как другой символ).
5) При описании решений части С не должно быть ничего лишнего. Отвечайте строго на поставленные вопросы.
II.
Разбор демонстрационного варианта ЕГЭ-2008
В этом разделе пособия представлен демонстрационный вариант ЕГЭ-2008. Для каждого представленного в нем задания
‑ приводится правильный ответ;
‑ обсуждаются наиболее эффективные пути выполнения задания;
‑ рассматриваются типичные трудности, возникающие при выполнении задания.
Условия заданий воспроизведены нами дословно. Также сохранена форма предъявления заданий. Кроме того, мы воспроизвели стандартную преамбулу об обозначениях и приоритетах логических операций, которая сопровождает каждый вариант ЕГЭ.
1. Обозначения для логических связок (операций):
a) отрицание
(инверсия, логическое НЕ) обозначается Ø
(например, Ø А);
b) конъюнкция
(логическое умножение, логическое И) обозначается /\
(например, А /\ В) либо & (например, А & В);
c) дизъюнкция
(логическое сложение, логическое ИЛИ) обозначается \/
(например, А \/ В) либо | (например, А | В);
d) следование
(импликация) обозначается ‑> (например, А ‑> В);
e) символ 1 используется для обозначения истины (истинного высказывания); символ 0 ‑ для обозначения лжи (ложного высказывания).
2. Два логических выражения, содержащих переменные, называются равносильными
(эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А ‑> В и (Ø А) \/ В равносильны, а А \/ В и А /\ В ‑ нет (значения выражений разные, например, при А=1, В=0).
3. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), эквивалентность (равносильность). Таким образом, Ø А /\ В \/ С/\ в совпадает с ((Ø А)/\ В) \/ (С/\ D). Возможна запись А /\ В /\ С вместо (А /\ В) /\ С. То же относится и к дизъюнкции: возможна запись А \/ В \/ С вместо (А \/ В) \/ С.
Часть 1
В кодировке Unicode на каждый символ отводится два байта. Определите информационный объем слова из двадцати четырех символов в этой кодировке.
| 1)
|
384 бита
|
2)
|
192 бита
|
3)
|
256 бит
|
4)
|
48 бит
|
Ответ: 1.
Обсуждение
. Прежде всего нужно обратить внимание на то, что все результаты даны в битах, а в условии кодировка оговорена в байтах. Если количество информации будет выражено в байтах, то получится число 48 и ошибочно может быть выбран ответ 4. С другой стороны, если же не учесть, что каждый символ кодируется двумя байтами, и сыграет роль обычно формирующийся стереотип, что каждый символ кодируется 8 битами, то получится число 192 и будет выбран ответ 2. Выбор числа 256 наименее вероятен, ибо оно возникает как результат возведения числа 2 в восьмую степень, т.е. это просто количество символов, которое можно закодировать однобайтовыми последовательностями из 0 и 1. Конечно, свою лепту в неправильный выбор ответа вносят арифметические ошибки.
Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?
Ответ: 3.
Обсуждение
. Это задание на самом деле не связано напрямую с информатикой, а относится к разделу математики, традиционно называемому комбинаторикой. Учащиеся, знакомые с комбинаторикой хотя бы на начальном уровне, сразу должны определить, что n
лампочек дают 3n
различных комбинаций своих состояний. Поскольку выполняется двойное неравенство 32
= 9 < 18 < 27 = 33
, дух лампочек недостаточно, а трех вполне хватает. Конечно, учащиеся могут рассуждать, непосредственно выписывая комбинации лапочек. Для одной лампочки на табло таких комбинаций по условию 3, для двух лампочек их получится 9, для трех – уже 27, из чего делается вывод о том, какой из предложенных вариантов ответа правильный. К неправильным ответам может привести слабое знание комбинаторных схем. Например, ответ 6 получается, если 18 разделить на 3 (вот пример неверного рассуждения: необходимое количество лампочек, обозначенное через х
, удовлетворяет уравнению 3х
= 18).
Для передачи секретного сообщения используется код, состоящий из десятичных цифр. При этом все цифры кодируются одним и тем же (минимально возможным) количеством бит. Определите информационный объем сообщения длиной в 150 символов.
| 1)
|
600 бит
|
2)
|
750 бит
|
3)
|
1200 бит
|
4)
|
60 байт
|
Ответ: 1.
Обсуждение
. Это задание по своей сути получено «скрещиванием» заданий А1 и А2: сначала надо найти длину кодирующей последовательности для одного символа (задача типа А2), а затем – информационный объем всего сообщения (задача типа А1). Поскольку 23
= 8 < 10 < 24
= 16, получаем, что цифры кодируются четырехбитовыми последовательностями. Умножая 4 на 150, получаем 600, что и определяет выбор ответа.
Сколько единиц в двоичной записи десятичного числа 194,5?
Ответ: 4.
Обсуждение
. Самый быстрый способ перевода числа 194 в двоичную систему заключается, на наш взгляд, в переводе этого числа алгоритмом деления в шестнадцатеричную или восьмеричную систему, а затем в расписывании его в двоичную. Поскольку 194 = С216
, то 194 = 110000102
. В свою очередь 0,5 = 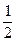 = 0,12
. Следовательно, 194,5 = 11000010,12
, откуда и получается требуемый ответ. Конечно, этот путь решения предполагает хорошее владение алгоритмом быстрого перевода чисел из шестнадцатеричной (восьмеричной) системы в двоичную. = 0,12
. Следовательно, 194,5 = 11000010,12
, откуда и получается требуемый ответ. Конечно, этот путь решения предполагает хорошее владение алгоритмом быстрого перевода чисел из шестнадцатеричной (восьмеричной) системы в двоичную.
Если хорошо помнить степени числа 2, то перевод в двоичную систему можно осуществлятьразложением числа в сумму степеней двойки. Конечно, такой путь решения тоже приемлем.
Вычислите сумму чисел x
и y
, при x
= A616
, y
= 758
.
Результат представьте в двоичной системе счисления.
| 1)
|
110110112
|
2)
|
111100012
|
3)
|
111000112
|
4)
|
100100112
|
Ответ: 3.
Обсуждение
. Здесь, как и в задании А4, оптимальный путь решения состоит в переводе каждого из чисел в двоичную систему счисления с последующим выполнением сложения. Поскольку A616
= 101001102
и 758
= 1111012
, то их сумма равна 111000112
. Как показывает практика, многие школьники предпочитают сначала перевести каждое число в десятичную систему счисления, затем найти сумму и результат перевести в двоичную систему. Такой многоходовый путь дает гораздо больше поводов допустить ошибку в вычислениях, чем тот способ, который предложен выше.
Определите значение переменной m
после выполнения фрагмента алгоритма.
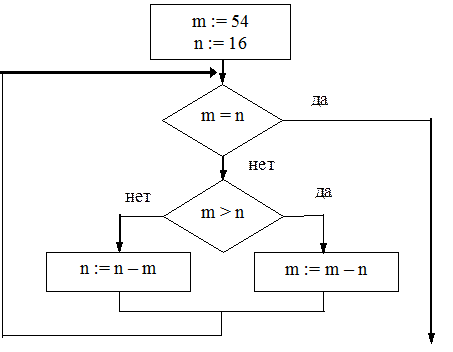
Примечание: знаком := обозначена операция присваивания.
Ответ: 2.
Обсуждение
. Этой блок-схемой представлен алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел. Этот алгоритм обязательно изучается в базовом курсе школьной информатики, поэтому его нетрудно распознать и получить ответ, не исполняя алгоритм по шагам. Конечно, такое распознавание весьма существенно экономит время выполнения задания, хотя и чревато ошибкой в том случае, если на самом деле алгоритм окажется лишь похожим на уже известный.
Если же алгоритм исполняется его по шагам, то типичными ошибками является либо выполнение тела цикла на один раз меньше, либо наоборот – на один раз больше.
Определите значение целочисленных переменных a
и b
после выполнения фрагмента программы:
| Бейсик
|
Паскаль
|
Алгоритмический
|
| a = 3 + 8 * 4
b = (a \ 10) + 14
a = (b MOD 10) + 2
'\ и MOD – операции, вычисляющие результат деления нацело первого аргумента на второй и остаток от деления соответственно
|
a:= 3 + 8*4;
b:= (a div 10) + 14;
a:= (b mod 10) + 2;
{div и mod – операции, вычисляющие результат деления нацело первого аргумента на второй и остаток от деления соответственно}
|
a:= 3 + 8*4
b:= div(a,10) + 14
a:= mod(b, 10) + 2
|div и mod – функции, вычисляющие результат деления нацело первого аргумента на второй и остаток от деления соответственно|
|
| 1)
|
a = 0, b = 18
|
| 2)
|
a = 11, b = 19
|
| 3)
|
a = 10, b = 18
|
| 4)
|
a = 9, b = 17
|
Ответ: 4.
Обсуждение
. При исполнении этого линейного алгоритма не требуется ничего, кроме внимательности. Ошибки, которые обычно здесь встречаются, носят либо арифметический характер, либо связаны с тем, что перепутано действие операций div и mod.
Значения двух массивов A[1..100] и B[1..100] задаются с помощью следующего фрагмента программы:
| Бейсик
|
Паскаль
|
Алгоритмический
|
| FOR n=1 TO 100
A(n)=(n-80)*(n-80)
NEXT n
FOR n=1 TO 100
B(101‑n)=A(n)
NEXT n
|
for n:=1 to 100 do
A[n]:= (n-80)*(n-80);
for n:=1 to 100 do
B[101‑n]:=A[n];
|
нц
для
n от
1 до
100
A[n]=(n-80)*(n-80)
кц
нц
для
n от
1 до
100
B[101‑n]=A[n]
кц
|
Какой элемент массива B будет наибольшим?
| 1)
|
B[1]
|
2)
|
B[21]
|
3)
|
B[80]
|
4)
|
B[100]
|
Ответ: 4.
Обсуждение
. Принципиальным моментом в решении этой задачи является то, что учащемуся не нужно исполнять этот алгоритм – немыслимо вычислить 100 значений для заполнения массива А, а затем переписать эти значения в виде массива В. Рассмотрев этот алгоритм, нужно понять, что в первом цикле вычисляется набор значений квадратичной функции, а во втором цикле полученные значения выписываются в обратном порядке. Следовательно, само максимальное значение элементов массива А и массива В будет одним и тем же, но стоять они будут на симметричных (относительно середины массива) местах. Далее выполнение этого задания может идти двумя путями.
1) Найти наибольшее значение квадратичной функции на отрезке [1; 100]. Поскольку функция равна (х
– 80)2
, т.е. ее график представляет собой параболу, ветви которой направлены вверх, то наибольшее значение достигается на концах отрезка. Ясно, что для данной функции таким концевым значением аргумента является 1. Поэтому в массиве В наибольший элемент будет B[100].
2) Поскольку какой-то из предъявленных четырех вариантов ответа обязательно правильный, достаточно вычислить только четыре элемента B[1], B[21], B[80] и B[100], после чего выбрать из них наибольший. Имеем: B[1] = А[100] = 400, B[21] = А[80] = 0, B[80] = А[21] = 3481 и B[100] = А[1] = =6241. Поэтому в массиве В наибольший элемент будет B[100].
Для какого из указанных значений числа X истинно высказывание
((X < 5) –> (X < 3)) /\ ((X < 2) –> (X < 1))
Ответ: 2.
Обсуждение
. Возможный путь решения этой задачи состоит в нахождении множества всех значений переменной Х, при которых данная логическая функция истинна. По нашему мнению, этот путь требует значительного времени и, что не менее важно, чреват промежуточными ошибками. Более эффективным, на наш взгляд, является путь, состоящий в вычислении для каждого предложенного значения Х соответствующего значения логической функции. Вот как это выглядит:
((1 < 5) –> (1 < 3)) /\ ((1 < 2) –> (1 < 1)) = (И –> И) /\ (И –> Л) = И /\ Л = Л;
((2 < 5) –> (2 < 3)) /\ ((2 < 2) –> (2 < 1)) = (И –> И) /\ (Л –> Л) = И /\ И = И;
((3 < 5) –> (3 < 3)) /\ ((3 < 2) –> (3 < 1)) = (И –> Л) /\ (Л –> Л) = Л /\ И = Л;
((4 < 5) –> (4 < 3)) /\ ((4 < 2) –> (4 < 1)) = (И –> Л) /\ (Л –> Л) = Л /\ И = Л.
Следовательно, верным является второй ответ.
Отметим, что два последних вычисления можно было не проводить, поскольку известно, что правильный ответ ровно один. Однако, для этого надо быть уверенным, что в ходе вычислений не была допущена ошибка. Можно сказать, что два последних вычисления осуществляют функцию косвенного контроля правильности полученного ответа – ведь если где-нибудь еще раз получилось значение Истина, то, значит, надо провести перепроверку.
Укажите, какое логическое выражение равносильно выражению
¬(A \/ ¬ B \/ C)
| 1)
|
¬A \/ B \/ ¬C
|
2)
|
A /\ ¬B /\ C
|
3)
|
¬A \/ ¬B \/ ¬C
|
4)
|
¬A /\ B /\ ¬C
|
Ответ: 4.
Обсуждение
. Стандартный путь решения таких задач – составление таблицы истинности для каждого из выражений и проверка на совпадение. Несмотря на кажущуюся трудоемкость, многие учащиеся выполняют это задание именно этим способом (спасает обычно то, что расхождение в таблицах истинности наблюдается не позже третьей строки, а верный вариант ответа редко бывает четвертым, как в данном случае). Но конкретно в этом задании проще всего воспользоваться законом де Моргана и правилом двойного отрицания.
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X
|
Y
|
Z
|
F
|
| 1
|
1
|
1
|
1
|
| 1
|
1
|
0
|
1
|
| 1
|
0
|
1
|
1
|
Какое выражение соответствует F?
| 1)
|
X \/ ¬Y \/ Z
|
| 2)
|
X /\ Y /\ Z
|
| 3)
|
X /\ Y /\ ¬Z
|
| 4)
|
¬X \/ Y \/ ¬Z
|
Ответ: 1.
Обсуждение
. Стандартный путь решения таких задач – составление таблицы истинности для каждого из предложенных вариантов функции F при тех значениях переменных, которые присутствуют в таблице. Ясно, что если при заполнении таблицы на каком-то наборе переменных значение не совпало со значением функции F, то дальше можно не продолжать. В частности, поэтому можно избрать несколько иной путь: для одного набора переменных вычислить значения всех тех функций, которые указаны в качестве вариантов ответа – часть из них почти наверняка можно будет тут же отбросить. потом также протестировать оставшиеся на следующем наборе и т.д., пока не останется одна функция.
Грунтовая дорога проходит последовательно через населенные пункты А, B, С и D. При этом длина дороги между А и В равна 80 км, между В и С – 50 км, и между С и в – 10 км.
Между А и С построили новое асфальтовое шоссе длиной 40 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге – 20 км/час, по шоссе ‑ 40 км/час?
| 1)
|
1 час
|
2)
|
1,5 часа
|
3)
|
3,5 часа
|
4)
|
4 часа
|
Ответ: 3.
Обсуждение
. По замыслу составителей ЕГЭ для выполнения этого задания учащиеся должны нарисовать нагруженный граф, у которого на ребрах проставлено время движения по данному ребру, и затем найти кратчайший путь на графе. Правда, пункт в здесь оказывается совсем не причем, а из А в В есть ровно два варианта, которыми можно добраться.
Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов ГБАВ и записать результат шестнадцатеричным кодом, то получится:
| 1)
|
D2
|
2)
|
132
|
3)
|
3102
|
4)
|
DBAC
|
Ответ: 1.
Обсуждение
. Официальное решение предполагает, что учащиеся перекодируют последовательность букв в двоичную последовательность и получившееся двоичное число переведут в шестнадцатеричный код. Однако легко понять, что в получающейся двоичной последовательности будет всего лишь 8 символов. Следовательно, в шестнадцатеричном коде может присутствовать лишь два символа. После этого выбор правильного варианта ответа становится очевидным.
В формировании цепочки из четырех бусин используются некоторые правила:
В конце цепочки стоит одна из бусин Р, N, Т, O. На первом – одна из бусин P, R, T, O, которой нет на третьем месте. На третьем месте – одна из бусин O, P, T, не стоящая в цепочке последней. Какая из перечисленных цепочек могла быть создана с учетом этих правил?
| 1)
|
PORT
|
2)
|
TTTO
|
3)
|
TTOO
|
4)
|
OOPO
|
Ответ: 4.
Обсуждение
. Составителями ЕГЭ это задание по кодификатору отнесено к теме «Формальное исполнение алгоритма, записанного на естественном языке». Фактически же никакого алгоритма, т.е. последовательности действий, приводящей к заданному результату, здесь нет. С некоторой натяжкой это задание можно было бы отнести к логическому программированию, но надо заметить, что таковое в стандартном школьном курсе информатики не изучается. На самом деле здесь просто требуется проверить, какая из предъявленных последовательностей удовлетворяет всем условиям, сформулированным в задании. Первому правилу удовлетворяют все цепочки, т.е. оно ничего не отвергает. Второе правило фактически дает одно содержательное ограничение – буквы, стоящие на первом и третьем местах обязательно различны. Это исключает второй вариант ответа. Наконец, третье правило означает, что не может в конце оказаться двух одинаковых букв, что отвергает ответ 3, и буквы R на третьем месте, что отвергает вариант 1.
Составители явно рассчитывают на сформированный стереотип проверять условия в том порядке, в каком они предъявлены. Именно поэтому первое правило ничего не отвергает, второе отвергает только один вариант, а самое строгое правило помещено последним. Зная эти приемчики составителей, мы советуем выполнять проверку правил, начиная с последнего – это сэкономит время.
Другой вариант выполнения этого задания состоит в проверке каждой цепочки на то, удовлетворяет ли она сформулированным условиям. Но и в этом случае отчетливо видно, что никакого исполнения какого бы то ни было алгоритма не осуществлялось.
Для групповых операций с файлами используются маски имен файлов
. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы:
Символ «?» (вопросительный знак) означает ровно один произвольный символ.
Символ «*» (звездочка) означает любую последовательность символов произвольной длины, в том числе «*» может задавать и пустую последовательность.
Определите, какое из указанных имен файлов удовлетворяет маске:
?a???*
| 1)
|
dad1
|
| 2)
|
dad22
|
| 3)
|
3daddy
|
| 4)
|
add444
|
Ответ: 2.
Обсуждение
. Основные ошибки, допускаемые учащимися состоят в том, что они предполагают возможность пустой последовательности символов вместо знака ? и, наоборот, считают, что вместо знака * обязательно должен стоять хоть какой-нибудь символ.
Из правил соревнования по тяжелой атлетике:
Тяжелая атлетика это прямое соревнование, когда каждый атлет имеет три попытки в рывке и три попытки в толчке. Самый тяжелый вес поднятой штанги в каждом упражнении суммируется в общем зачете. Если спортсмен потерпел неудачу во всех трех попытках в рывке, он может продолжить соревнование в толчке, но уже не сможет занять какое-либо место по сумме 2-х упражнений.
Если два спортсмена заканчивают состязание с одинаковым итоговым результатом, высшее место присуждается спортсмену с меньшим весом. Если же вес спортсменов одинаков, преимущество отдается тому, кто первым поднял победный вес.
Таблица результатов соревнований по тяжелой атлетике:
| Фамилия, И.О.
|
Вес спортсмена
|
Взято в рывке
|
Рывок с попытки
|
Взято в толчке
|
Толчок с попытки
|
| Айвазян Г.С.
|
77,1
|
150,0
|
3
|
200,0
|
2
|
| Викторов М.П.
|
79,1
|
147,5
|
1
|
202,5
|
1
|
| Гордезиани Б.Ш.
|
78,2
|
147,5
|
2
|
200,0
|
1
|
| Михальчук М.С.
|
78,2
|
147,5
|
2
|
202,5
|
3
|
| Пай С.В.
|
79,5
|
150,0
|
1
|
200,0
|
1
|
| Шапсугов М.Х.
|
77,1
|
147,5
|
1
|
200,0
|
1
|
Кто победил в общем зачете (сумме двух упражнений)?
| 1)
|
Айвазян Г.С.
|
| 2)
|
Викторов М.П.
|
| 3)
|
Михальчук М.С.
|
| 4)
|
Пай С.В.
|
Ответ: 1.
Обсуждение
. Составителями ЕГЭ предполагалось, что учащиеся должны составить по словесному описанию условий селективную формулу и с ее помощью получить ответ. Этот путь позволяет избежать ошибок, которые могут возникать из-за трудностей удерживать в поле зрения сразу несколько условий, причем связанных операциями конъюнкции или дизъюнкции. Нередко ими учитывается значение только одного операнда.
Для хранения растрового изображения размером 32´32 пикселя отвели 512 байтов памяти. Каково максимально возможное число цветов в палитре изображения?
Ответ: 3.
Обсуждение
. Это достаточно стандартная задача. Основные ошибки возникают из-за невнимательного отношения к единицам измерения, а также из-за не вполне отработанных навыков действий со степенями числа 2.
Дан фрагмент электронной таблицы:
| А
|
В
|
С
|
| 1
|
10
|
20
|
=A1+B$1
|
| 2
|
30
|
40
|
Чему станет равным значение ячейки С2, если в нее скопировать формулу из ячейки С1?
Знак $ обозначает абсолютную адресацию.
Ответ: 2.
Обсуждение
. Ответ 70 получается, если не учтен знак абсолютной адресации. Остальные ответы совсем малоправдоподобны.
Дан фрагмент электронной таблицы:
| |
A
|
B
|
C
|
D
|
| 1
|
3
|
4
|
| 2
|
=C1–B1
|
=B1–A2*2
|
=C1/2
|
=B1+B2
|
После выполнения вычислений была построена диаграмма по значениям диапазона ячеек A2:D2. Укажите получившуюся диаграмму.
Ответ: 4.
Обсуждение
. К сожалению, нередко возникают ошибки, связанные с определением порядка действий (возможно, кто-то воспринимает электронную таблицу как обычный калькулятор). Конечно, вносят свою лепту и ошибки невнимательности.
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
| вверх
|
вниз
|
влево
|
вправо
|
| При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
|
| сверху свободно
|
снизу свободно
|
слева свободно
|
справа свободно
|
Цикл
ПОКА < условие
> команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?
НАЧАЛО
ПОКА < справа свободно
> вправо
ПОКА < сверху свободно
> вверх
ПОКА < слева свободно
> влево
ПОКА < снизу свободно
> вниз
КОНЕЦ
Ответ: 4.
Обсуждение
. При выполнении этого задания важно заметить, что контур обхода всегда представляет собой прямоугольник и учесть направление обхода. При этом рисовать сам контур крайне вредно – он будет мешать проверке на допустимость следующей клетке. Разумеется, существенную роль играет культура организации перебора вариантов.
Результаты выполнения этого задания на реальном ЕГЭ колеблются в разных вариантах от 16% до 27%. Это намного ниже того, что прогнозировалось изначально разработчиками варианта. Причина низкого выполнения этого задания кроется, на наш взгляд, не в том, что учащиеся не умеют выполнять подобные задания (тем более, что аналогичное задание было предъявлено в демоверсии), а в том, что требовалось до двадцати раз проделать довольно трудоемкую процедуру (требующую на свое исполнение от 20 до 30 секунд и очень большого внимания). Кроме того, каждый раз процедура выполнялась на одном и том же чертеже, где было уже зафиксировано и предыдущее ее исполнение, что, несомненно, сказывалось отрицательно. В условиях дефицита времени, выделяемого на выполнение заданий групп А и В, это неизбежно влекло ошибки. Отметим, что для этого задания количество учащихся, отказавшихся от выбора ответа, наибольшее среди всех заданий группы А. Мы предполагаем, что реально учащиеся на каком-то шаге отказывались от полного выполнения этого задания и пытались частично угадать ответ. Легко подсчитать, что вероятность угадывания правильного ответа как раз и составляет 25%. По-видимому, это поведение надо признать оптимальной стратегией при выполнении данного задания на реальном ЕГЭ.
III.
Примерные варианты ЕГЭ для самостоятельной подготовки
Сравнение опубликованной демоверсии ЕГЭ по информатике 2009 года[1]
с демоверсиями предшествующих лет показывает, что в нем имеется, пожалуй, одно принципиальное отличие: два задания из части А перенесены в часть В. Ниже приведены два варианта комплектов заданий, составленных в соответствии с демоверсией 2009 года, учитывающих указанное отличие.
Каждый вариант содержит три части.
Часть 1 включает восемнадцать заданий с выбором ответа. К каждому заданию дается четыре ответа, из которых только один правильный.
Часть 2 состоит из десяти заданий с кратким ответом (к этим заданиям вы должны самостоятельно сформулировать и записать ответ в той форме, которая оговорена в задании).
Часть 3 состоит из четырех заданий. Для выполнения заданий этой части вам необходимо написать развернутый ответ в произвольной форме.
В своей подготовке к ЕГЭ мы советуем использовать предложенные нами варианты следующим образом.
Один из вариантов мы предлагаем прорешать без ограничения времени на выполнение каждого из заданий. Для каждого задания полученный ответ необходимо тут же сверить с контрольным вариантом ответа (они помещен в конце этого раздела). Более того, там же для заданий части 3 приведены образцы оформления решений. Полезно сравнить свои решения заданий части 1 с теми рекомендациями, которые даны в аналогичных заданиях, разобранной выше демоверсии 2008 года. Такое сравнение вовсе не означает, что необходимо дословно следовать этим рекомендациям, но всегда полезно проанализировать найденный путь решения с целью его оптимизации.[2]
Со вторым вариантом прорешивание проводится фронтально (как это происходит на самом ЕГЭ), а не отдельными заданиями. Для каждого задания фиксируется время, затраченное на его выполнение. Проверка ответов производится после того, как закончена работа со всем вариантом в целом. Выполнив такую работу и проанализировав ее результаты, вы сможете определить оптимальную конкретно для вас стратегию выполнения заданий ЕГЭ.
Мы рекомендуем также при выполнении заданий каждого из вариантов использовать копию бланков, которые используются на ЕГЭ.
Вариант 1
Часть 1
При выполнении заданий этой части в бланке ответов № 1 под номером выполняемого вами задания (А1 – А20) поставьте знак
«
´ » в клеточку, номер которой соответствует номеру выбранного вами ответа.
А1
. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 8-битном коде КОИ-8, в 16-битную кодировку Unicode. При этом информационное сообщение увеличилось на 240 бит. Какова длина сообщения в символах?
1) 15 2) 240 3) 60 4) 30
А2
. В велокроссе участвуют 459 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством, после того как промежуточный финиш прошли 160 велосипедистов?
1) 160 бит 2) 160 байт 3) 180 байт 4) 459 байт
А3
. Дано А = 2478
, B = A916
. Какое из чисел C, записанных в двоичной системе, отвечает условию A < C < B ?
1) 101010002
2) 101010102
3) 101010112
4) 101011002
А4
. Чему равна сумма чисел 348
и 4616
?
1) 1028
2) 1428
3) 17A16
4) 10100102
А5
. Определите значение целочисленных переменных a
, b
и c
после выполнения фрагмента программы:
| Бейсик
|
Паскаль
|
Алгоритмический
|
| a=50
b=17
c=(b*a)\b
a=(a\b)*b
b=c–a
' \ — стандартная операция, вычисляющая результат деления нацело первого аргумента на второй
|
a:=50;
b:=17;
c:=(b*a) div b;
a:=(a div b)*b;
b:=c–a;
{div — стандартная операция, вычисляющая результат деления нацело первого аргумента на второй}
|
a:=50
b:=17
c:=div(b*a, b)
a:=div(a, b)*b
b:=c–a
| div — стандартная функция, вычисляющая результат деления нацело первого аргумента на второй|
|
1) a
= 34, b
= 16, c
= 50
2) a
= 50, b
= 0, c
= 50
3) a
= 34, b
= 0, c
= 50
4) a
= 50, b
= – 16, c
= 34
А6
. Дан фрагмент программы, обрабатывающей массив A из n
элементов:
| Бейсик
|
Паскаль
|
Алгоритмический
|
| J = 1
FOR I = 1 TO n
IF A(I) < A(J) THEN J = I
NEXT I
s = A(J)
|
j:=1;
for i:=1 to n do
begin
if A[i]<A[j] then
j:=i
end
s:=A[j]
|
j:=1
нц для i от 1 до n
если A[i]<A[j] то
j:=i
все
кц
s:=A[j]
|
Чему будет равно значение переменной s
после выполнения данного алгоритма?
1) Минимальному элементу в массиве A
2) Индексу минимального элемента в массиве A (первому из них, если минимальных элементов несколько)
3) Индексу минимального элемента в массиве A (последнему из них, если минимальных элементов несколько)
4) Количеству элементов, равных минимальному в массиве A
А7
. Для какого из приведенных значений числа X истинно высказывание
((X > 3) \/ (X = 1) \/ (X = 2)) –> (X > 4) ?
1) 1 2) 2 3) 3 4) 4
А8
. Укажите, какое логическое выражение равносильно выражению
¬ (A /\ B /\ ¬C)
1) ¬A \/ ¬B \/ C
2) A \/ B \/ ¬C
3) ¬A /\ ¬B /\ C
4) A /\ B /\ ¬C
А9
. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X
|
Y
|
Z
|
F
|
| 1
|
0
|
0
|
0
|
| 0
|
0
|
0
|
0
|
| 1
|
1
|
0
|
1
|
Какое выражение соответствует F?
1) ¬X /\ ¬Y /\ Z 2) X /\ Y /\ ¬Z 3) ¬X \/ ¬Y \/ Z 4) X \/ ¬Y \/ ¬Z
А10
. Между четырьмя крупными аэропортами, обозначенными кодами ARK, LAO, ORH и TYU, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между этими аэропортами:
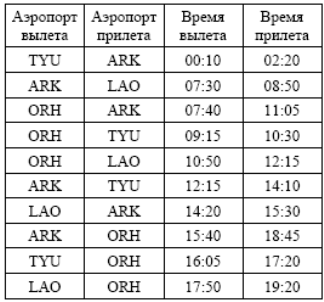
Путешественник находится в аэропорту ARK в полночь (0:00). Определите самое раннее время, когда он может оказаться в аэропорту ORH.
1) 07:40 2) 17:20 3) 18:45 4) 19:20
А11
. Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит, для некоторых – из трех). Эти коды представлены в таблице:
| m
|
n
|
o
|
p
|
r
|
| 000
|
11
|
01
|
001
|
10
|
Определите, какой набор букв закодирован двоичной строкой 01100110001001.
1) orpmro 2) ororpp 3) orprpp 4) orormro
А12
. Дешифровщику необходимо восстановить поврежденный фрагмент сообщения, состоящий из 4-х символов. Имеется достоверная информация, что использовано не более пяти букв (M, O, P, T, S). Причем на втором месте стоит один из символов M, T, O, S. На первом – одна из букв P, R, T, O, которой нет на третьем месте. На третьем месте – одна из букв O, R, T, S, не стоящая в слове на втором месте. На четвертом месте – одна из букв P, R, T, M, которой не было на первом месте. Появилась дополнительная информация, что возможен один из четырех вариантов. Какой?
1) OTMS 2) PMTP 3) PMTT 4) PSMT
А13
. Для групповых операций с файлами используются маски имен файлов
. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы: Символ «?» (вопросительный знак) означает ровно один произвольный символ. Символ «*» (звездочка) означает любую последовательность символов произвольной длины, в том числе «*» может задавать и пустую последовательность. Определите, какое из указанных имен файлов удовлетворяет маске:
b?ar*.?xt
1) blar.txt 2) bar.ext 3) baara.xt 4) blar.xt
А14
. Результаты тестирования представлены в таблице:

Сколько записей в ней удовлетворяют условию
«Пол=’м’ ИЛИ (Пол=’ж’ И Математика<40)»?
1) 5 2) 2 3)3 4) 4
А15
. Для кодирования цвета фона страницы Интернет используется атрибут bgcolor="ХХХХХХ", где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной RGB-модели. Какой цвет будет у страницы, заданной тэгом <body bgcolor="00FF00">?
1) белый 2) зеленый 3) красный 4) синий
А16
. Дан фрагмент электронной таблицы:
| А
|
В
|
| 1
|
0,5
|
1,5
|
| 2
|
9,5
|
=A1+A2/5
|
Чему станет равным значение ячейки B2, если значение ячейки A1 увеличить на 4, а значение ячейки A2 уменьшить на 2?
1) 3,5 2) 2 3) 8 4) 6
А17
. На диаграмме показаны объемы выпуска продукции трех видов: А, Б и В за каждый из месяцев первого квартала.
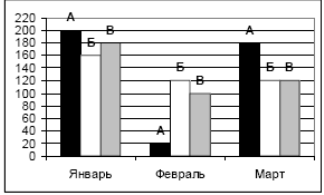
Какая из диаграмм правильно отражает соотношение объемов выпуска этих видов продукции за весь квартал?

А18
. Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды:
Вперед n
, где n
– целое число, вызывающая передвижение Черепашки на n
шагов в направлении движения
Направо m
, где m
– целое число, вызывающая изменение направления движения на m
градусов по часовой стрелке.
Запись Повтори 5 [Команда1 Команда2]
означает, что последовательность команд
в скобках повторится 5 раз.
Черепашке был дан для исполнения следующий алгоритм:
Повтори 5 [ Вперед 10 Направо 10]
Какая фигура появится на экране?
1) правильный пятиугольник
2) правильный треугольник
3) квадрат
4) незамкнутая ломаная линия
Часть 2
Ответом к заданиям этой части (В1 – В8) является набор символов, которые следует записать в бланк ответов
№
1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ пишите в отдельной клеточке в соответствии с приведенными образцами.
В1
. Одна ячейка памяти троичной ЭВМ (компьютера, основанного на троичной системе счисления) может принимать одно из трех возможных состояний. Для хранения некоторой величины отвели 5 ячеек памяти. Сколько различных значений может принимать эта величина?
В2
. Определите значение переменной c
после выполнения фрагмента алгоритма:
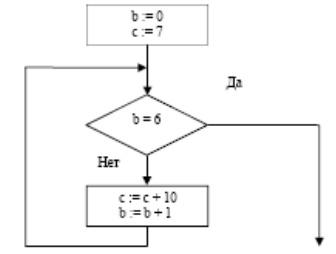
Примечание: знаком
:= обозначена операция присваивания.
В3
. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 1.
В4
. Сколько существует натуральных чисел X, для которых истинно высказывание
(X < 10) /\ ((X<5) –> (X<3)) ?
В5
. У исполнителя Квадратор две команды, которым присвоены номера:
1. возведи в квадрат,
2. прибавь 1.
Первая из них возводит число на экране в квадрат, вторая – увеличивает его на 1. Запишите порядок команд в программе получения из 1 числа 25, содержащей не более 4 команд, указывая лишь номера команд. (Например, программа 12122
– это программа:
возведи в квадрат,
прибавь 1,
возведи в квадрат,
прибавь 1,
прибавь 1,
которая преобразует число 1 в 6.)
В6
. Классный руководитель пожаловался директору, что у него в классе появилась компания из 3-х учеников, один из которых всегда говорит правду, другой всегда лжет, а третий говорит через раз то ложь, то правду. Директор знает, что их зовут Коля, Саша и Миша, но не знает, кто из них правдив, а кто – нет. Встретив однажды всех троих в коридоре, директор задал Коле два вопроса: "Ты всегда говоришь правду?" и "Саша всегда говорит правду?". На оба вопроса Коля ответил: "Нет". Директор понял, кто из них кто. Расположите первые буквы имен мальчиков в порядке: "говорит всегда правду", "всегда лжет", "говорит правду через раз". (Пример: если бы имена мальчиков были Рома, Толя и Вася, ответ мог бы быть: РТВ)
В7
. Скорость передачи данных через ADSL-соединение равна 128000 бит/c. Передача файла через это соединение заняла 2 минуты. Определите размер файла в килобайтах.
В8
. Строки (цепочки символов из букв русского алфавита) создаются по следующему правилу.
Первая строка состоит из одного символа – буквы «А». Каждая из последующих цепочек создается следующим действием:
в очередную строку дважды записывается предыдущая строка (цепочка за цепочкой, подряд), а в конец приписывается еще один символ, чей порядковый номер в алфавите соответствует номеру строки (на i
-м шаге дописывается «i
»-я буква алфавита).
Вот первые 4 строки, созданные по этому правилу:
(1) А
(2) ААБ
(3) ААБААБВ
(4) ААБААБВААБААБВГ
…
Начальная часть русского алфавита (для справки):
А Б В Г Д Е Ё Ж З И Й К …
Сколько раз в общей сложности встречаются в восьмой строке гласные буквы (А, Е, Ё, И, …
)?
В9
. Во время следствия были обнаружены четыре обрывка бумаги и криминалисты установили, что на них записаны фрагменты одного IP-адреса, которые условно обозначили буквами А, Б, В и Г. Необходимо восстановить IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.

В10
. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции “ИЛИ” в запросе используется символ |, а для логической операции “И” – &.
| 1
|
волейбол | баскетбол
|
| 2
|
волейбол & баскетбол
|
| 3
|
волейбол
|
| 4
|
волейбол | баскетбол | правила
|
Часть 3
| Для записи ответов к заданиям этой части (С1 – С4) используйте бланк ответов
№
2. Запишите сначала номер задания (С1 и т.д.), а затем полное решение.
[3]
Ответы записывайте четко и разборчиво.
|
| С1
.
|
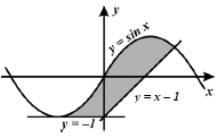
|
Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (x, y
– действительные числа) и определяет принадлежность точки заштрихованной области, включая ее границы. Программист торопился и написал программу неправильно.
|
| Программа на Паскале
|
Программа на Бейсике
|
Программа на СИ
|
| var x,y: real;
begin
readln(x,y);
if y>= –1 then
if y<=sin(x) then
if y>=x – 1 then
write('принадлежит')
else
write('не принадлежит')
end.
|
INPUT x, y
IF y>= –1 THEN
IF y<=SIN(x) THEN
IF y>=x – 1 THEN
PRINT "принадлежит"
ELSE
PRINT "не принадлежит"
ENDIF
ENDIF
ENDIF
END
|
void main(void)
{ float x,y;
scanf("%f%f",&x,&y);
if (y>= –1)
if (y<=sin(x))
if (y>=x – 1)
printf("принадлежит");
else
printf("не принадлежит");
}
|
Последовательно выполните следующее:
1) Приведите пример таких чисел x
, y
, при которых программа работает неправильно.
2) Укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы).
С2
. Опишите на русском языке или одном из языков программирования алгоритм вычисления минимальной разности двух последовательных значений элементов (из последующего вычитается предыдущий) в заданном целочисленном массиве из 30 элементов.
С3
. Два игрока играют в следующую игру. На координатной плоскости стоит фишка. Игроки ходят по очереди. В начале игры фишка находится в точке с координатами (1, 0). Ход состоит в том, что игрок перемещает фишку из точки с координатами (x, y) в одну из трех точек: или в точку с координатами (x+3, y), или в точку с координатами (x, y+3), или в точку с координатами (x, y+4). Выигрывает игрок, после хода которого расстояние от фишки до точки с координатами (0,0) не меньше 10 единиц. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
С4
. На вход программе подаются сведения о номерах школ учащихся, участвовавших в олимпиаде. В первой строке сообщается количество учащихся N, каждая из следующих N строк имеет формат: <Фамилия> <Инициалы> <номер школы>, где <Фамилия> – строка, состоящая не более чем из 20 символов, <Инициалы> – строка, состоящая из 4-х символов (буква, точка, буква, точка), <номер школы> – не более чем двузначный номер. <Фамилия> и <Инициалы>, а также <Инициалы> и <номер школы> разделены одним пробелом. Пример входной строки:
Иванов П.С. 57
Требуется написать как можно более эффективную программу, которая будет выводить на экран в порядке возрастания номера тех школ, ученики которых были на олимпиаде.
Вариант 2
Часть 1
При выполнении заданий этой части в бланке ответов № 1 под номером выполняемого вами задания (А1 – А20) поставьте знак
«
´ » в клеточку, номер которой соответствует номеру выбранного вами ответа.
А1
. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке длиной в 20 символов, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на
1) 320 бит 2) 20 бит 3) 160 байт 4) 20 байт
А2
. В велокроссе участвуют 56 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством, после того как все спортсмены прошли промежуточный финиш?
1) 42 байт 2) 56 байт 3) 56 бит 4) 280 бит
А3
. Чему равна разность чисел 1018
и 1001112
?
1) 1A16
2) 548
3) 428
4) E16
А4
. Вычислите сумму чисел x
и y
при x
= B216
, y
= 458
. Результат представьте в двоичной системе счисления.
1) 10100112
2) 110101112
3) 110111112
4) 101101112
А5
. Определите значение переменной c
после выполнения следующего фрагмента программы.
| Бейсик
|
Паскаль
|
Алгоритмический
|
| a = 6
b = 4
c = a + b
d = a * b / (a – b)
c = c – 2 * в
|
a:=6;
b:=4;
c:=a+b;
d:=a*b/(a–b);
c:=c–2*d;
|
a:=6
b:=4
c:=a+b
d:=a*b/(a–b)
c:=c–2*d
|
1) c = –2 2) c = 24 3) c = –14 4) c = –24
А6
. Дан фрагмент программы, обрабатывающей двумерный массив A размера n
´n
.
| Бейсик
|
Паскаль
|
Алгоритмический
|
| FOR i = 1 TO n
c = A(i,i)
A(i,i) = A(i,n – i + 1)
A(i,n – i + 1) = c
NEXT i
|
for i:=1 to n do
begin
c:=A[i,i];
A[i,i]:=A[i,n–i+1];
A[i,n–i+1]:=c
end
|
нц для i от 1 до n
c:=A[i,i]
A[i,i]:=A[i,n–i+1]
A[i,n–i+1]:=c
кц
|
Представим массив в виде квадратной таблицы, в которой для элемента
массива A[i,j] величина i
является номером строки, а величина j
– номером столбца, в котором расположен элемент. Тогда данный алгоритм меняет местами
1) два столбца в таблице
2) две строки в таблице
3) элементы двух диагоналей таблицы
4) элементы диагонали и строки таблицы
А7
. Для какого слова истинно высказывание
¬ (Последняя буква слова гласная –> Вторая буква слова гласная)
1) ГОРЕ
2) ПРИВЕТ
3) КРЕСЛО
4) ЗАКОН
A8
. Укажите, какое логическое выражение равносильно выражению
A \/ ¬ (B /\ ¬C)
1) ¬A \/ ¬B \/ ¬C
2) A /\ ¬B /\ ¬C
3) A \/ ¬ B \/ C
4) A \/ ¬B \/ ¬C
А9
. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X
|
Y
|
Z
|
F
|
| 1
|
0
|
0
|
0
|
| 0
|
0
|
0
|
1
|
| 1
|
0
|
1
|
1
|
Какое выражение соответствует F?
1) ¬X \/ Y \/ Z 2) X /\ Y /\ ¬Z 3) ¬X /\ ¬Y /\ Z 4) X \/ ¬Y \/ ¬Z
А10
. Между четырьмя крупными аэропортами, обозначенными кодами EDO, LIT, NSY и ZUI, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между этими аэропортами:
 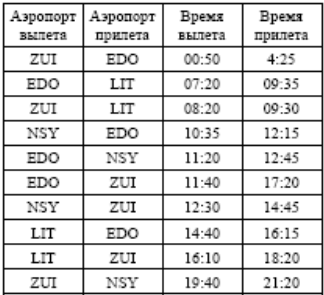
Путешественник находится в аэропорту EDO в полночь (0:00). Определите самое раннее время, когда он может оказаться в аэропорту ZUI.
1) 4:25 2) 14:45 3) 17:20 4) 18:20
А11
. Для кодирования букв А, Б, В, Г решили использовать трехразрядные последовательные двоичные числа (от 100 до 111, соответственно). Если таким способом закодировать последовательность символов ВГАБ и записать результат шестнадцатеричным кодом, то получится
1) В7А 2) 317 3) 15D 4) DE3
А12
. Четверо учеников, предполагающих сдавать переводной экзамен по геометрии, записали свои пожелания на очередность: Илья не хочет идти вторым или третьим, Андрей не хочет брать билет первым или третьим, Павел готов идти третьим или четвертым, Марина предложила зайти второй или первой. Предложено четыре варианта очереди. Какой из вариантов устроит всех? (Обозначения: И – Илья, А – Андрей, П – Павел, М – Марина)
1) И М А П 2) И М П А 3) М А И П 4) И А М П
А13
. Для групповых операций с файлами используются маски имен файлов
. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы: Символ «?» (вопросительный знак) означает ровно один произвольный символ. Символ «*» (звездочка) означает любую последовательность символов произвольной длины, в том числе «*» может задавать и пустую последовательность. Определите, какое из указанных имен файлов удовлетворяет маске:
?b*bek.htm*
1) ababek.html 2) babek.html 3) babek.htm 4) aabbek.html
А14
. На городской олимпиаде по программированию предлагались задачи трех типов: А, В и С. По итогам олимпиады была составлена таблица, в колонках которой указано, сколько задач каждого типа решил участник. Вот начало таблицы:
| Фамилия
|
А
|
В
|
С
|
| Иванов
|
3
|
2
|
1
|
За правильное решение задачи типа А участнику начислялся 1 балл, за решение задачи типа В – 2 балла и за решение задачи типа С – 3 балла. Следует отобрать участников, набравших больше 10 баллов и решивших хотя бы одну задачу типа С. Для этого достаточно найти в таблице записи, удовлетворяющие условию:
1) (А + В + С = 10) И (С = 1).
2) (А + 2В + 3С > 10) И (С > 1).
3) (А + 2В + 3С > 10) И (С > 0).
4) (А + 2В + 3С > 10) ИЛИ (С > 1).
А15
. Для кодирования цвета фона страницы Интернет используется атрибут bgcolor="ХХХХХХ", где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной RGB-модели следующим образом:
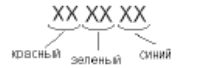
Какой цвет будет у страницы, заданной тэгом
<body bgcolor="00DDDD">?
1) белый 2) голубой 3) красный 4) черный
А16
. В электронной таблице значение формулы =СРЗНАЧ(С1:С3) равно 4. Значение формулы =СРЗНАЧ(С4:С5) равно 6. Чему будет равно значение формулы =СУММ(С1:С5)?
1) 5 2) 20 3) 24 4) 10
А17
. На диаграмме показаны объемы выпуска продукции трех видов: А, Б и В за каждый из месяцев первого квартала.

Какая из диаграмм правильно отражает соотношение объемов выпуска этих видов продукции за весь квартал?
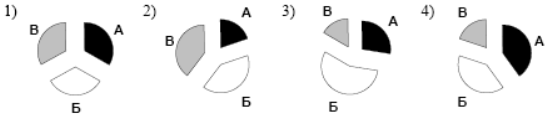
А18
. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
| сверху свободно
|
снизу свободно
|
слева свободно
|
справа свободно
|
Цикл
ПОКА < условие
> команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится и программа прервется.
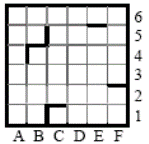
Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ уцелеет и остановится в той же клетке, с которой он начал движение?
| НАЧАЛО
ПОКА < сверху свободно
> вправо
ПОКА < справа свободно
> вниз
ПОКА < снизу свободно
> влево
ПОКА < слева свободно
> вверх
КОНЕЦ
|
|
1) 1 2) 2 3)3 4) 4
Часть 2
Ответом к заданиям этой части (В1 – В8) является набор символов, которые следует записать в бланк ответов
№
1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ пишите в отдельной клеточке в соответствии с приведенными образцами.
В1
. Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность важна). Какое количество различных сигналов может передать корабль при помощи линейки из трёх сигнальных флагов, если на корабле имеются флаги четырёх различных видов (флагов каждого вида неограниченное количество)?
В2
. Определите значение переменной c
после выполнения фрагмента алгоритма:
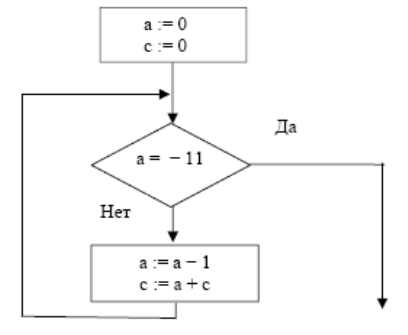
Примечание: знаком
:= обозначена операция присваивания.
В3
. Укажите через запятую в порядке возрастания все натуральные числа в десятичной системе счисления, не превосходящие 25, запись которых в восьмеричной системе счисления оканчивается на 7.
В4
. Сколько существует натуральных чисел X, для которых истинно высказывание
((X < 5) \/ (X > 10)) –> (X<3)) ?
В5
. Исполнитель Робот действует на клетчатой доске, между соседними клетками которой могут стоять стены. Робот передвигается по клеткам доски и может выполнять команды 1 (вверх), 2 (вниз), 3 (влево), 4 (вправо), переходя на соседнюю клетку в направлении, указанном в скобках. Если в этом направлении между клетками стоит стена, то Робот разрушается. Робот успешно выполнил программу
3314214
Какую последовательность из трех команд должен выполнить Робот, чтобы вернуться на ту клетку, где он был перед началом выполнения программы, и не разрушиться, вне зависимости от того, какие стены стоят на поле?
В6
. Классный руководитель пожаловался директору, что у него в классе появилась компания из 3-х учеников, один из которых всегда говорит правду, другой всегда лжет, а третий говорит через раз то ложь, то правду. Директор знает, что их зовут Коля, Саша и Миша, но не знает, кто из них правдив, а кто – нет. Однажды все трое прогуляли урок астрономии. Директор знает, что никогда раньше никто из них не прогуливал астрономию. Он вызвал всех троих в кабинет и поговорил с мальчиками. Коля сказал: "Мы и на прошлой неделе тоже прогуляли астрономию. Я всегда говорю правду". Саша сказал: "Я никогда не смешиваю ложь и правду, либо всегда лгу, либо говорю правду. Мы больше не будем прогуливать. То, что Коля сказал в начале, – неправда". Миша сказал: "Мы раньше не прогуливали астрономию. Я всегда лгу". Директор понял, кто из них кто. Расположите первые буквы имен мальчиков в порядке: "говорит всегда правду", "всегда лжет", "говорит правду через раз". (Пример: если бы имена мальчиков были Рома, Толя и Вася, ответ мог бы быть: РТВ)
В7
. Скорость передачи данных через ADSL-соединение равна 64000 бит/c. Через данное соединение передают файл размером 125 килобайт. Определите время передачи файла в секундах.
В8
. Строки (цепочки символов латинских букв) создаются по следующему правилу.
Первая строка состоит из одного символа – латинской буквы «А». Каждая из последующих цепочек создается такими действиями: в очередную строку вначале записывается буква, чей порядковый номер в алфавите соответствует номеру строки (на i-м шаге пишется «i
»-я буква алфавита), к ней справа дважды подряд приписывается предыдущая строка.
Вот первые 4 строки, созданные по этому правилу:
(1) A
(2) BAA
(3) CBAABAA
(4) DCBAABAACBAABAA
Латинский алфавит (для справки):
A B C в E F G H I J K L M N O P Q R S T U V W X Y Z
Сколько раз встречается символ «В» в первых восьми строках (суммарно)?
В9
. На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного IP-адреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г. Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.

В10
. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции “ИЛИ” в запросе используется символ |, а для логической операции “И” – &.
| 1
|
разведение & содержание & щеглы & канарейки
|
| 2
|
щеглы
|
| 3
|
канарейки | щеглы
|
| 4
|
содержание & щеглы & канарейки
|
Часть 3
| Для записи ответов к заданиям этой части (С1 – С4) используйте бланк ответов
№
2. Запишите сначала номер задания (С1 и т.д.), а затем полное решение.
[4]
Ответы записывайте четко и разборчиво.
|
| С1
.
|
|
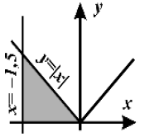
Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (x, y
– действительные числа) и определяет принадлежность точки заштрихованной области, включая ее границы. Программист торопился и написал программу неправильно.
|
| Программа на Паскале
|
Программа на Бейсике
|
Программа на СИ
|
| var x,y: real;
begin
readln(x,y);
if y<=abs(x) then
if x>= –1.5 then
if y>=0 then
write('принадлежит')
else
write('не принадлежит')
end.
|
INPUT x, y
IF y<=ABS(x) THEN
IF x>= –1.5 THEN
IF y>=0 THEN
PRINT "принадлежит"
ELSE
PRINT "не принадлежит"
ENDIF
ENDIF
ENDIF
END
|
void main(void)
{ float x,y;
scanf("%f%f",&x,&y);
if (y<=fabs(x))
if (x>= –1.5)
if (y>=0)
printf("принадлежит");
else
printf("не принадлежит");
}
|
Последовательно выполните следующее:
1) Приведите пример таких чисел x
, y
, при которых программа работает неправильно.
2) Укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы).
С2
. Опишите на русском языке или одном из языков программирования алгоритм подсчета произведения положительных элементов в заданном целочисленном массиве из 30 элементов, проверяя, что в нем есть хотя бы один положительный элемент.
С3
. Два игрока играют в следующую игру. На координатной плоскости стоит фишка. Игроки ходят по очереди. В начале игры фишка находится в точке с координатами (0, –4). Ход состоит в том, что игрок перемещает фишку из точки с координатами (x, y) в одну из трех точек: или в точку с координатами (x+4, y), или в точку с координатами (x, y+4), или в точку с координатами (x+4, y+4). Выигрывает игрок, после хода которого расстояние от фишки до точки с координатами (0,0) больше 12 единиц. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
С4
. На вход программе подается последовательность символов, среди которых встречаются и цифры. Ввод символов заканчивается точкой (в программе на языке Бейсик символы можно вводить по одному в строке, пока не будет введена точка). Требуется написать как можно более эффективную программу (укажите используемую версию языка программирования, например, Borland Pascal 7.0), которая составит из тех цифр, которые встречаются во входных данных, максимальное число. При составлении итогового числа каждая цифра может быть использована только один раз. Если во входных данных цифры не встречаются, то следует вывести “–1”. Например, пусть на вход подаются следующие символы:
14ф73п439
.
В данном случае программа должна вывести
97431
Ответы.
Часть 1
| Задание
|
Вариант
|
Задание
|
Вариант
|
| № 1
|
№ 2
|
№ 1
|
№ 2
|
| А1
|
4
|
4
|
А10
|
2
|
3
|
| А2
|
2
|
4
|
А11
|
2
|
4
|
| А3
|
1
|
1
|
А12
|
3
|
2
|
| А4
|
4
|
4
|
А13
|
3
|
1
|
| А5
|
1
|
3
|
А14
|
4
|
3
|
| А6
|
1
|
3
|
А15
|
2
|
2
|
| А7
|
3
|
3
|
А16
|
4
|
3
|
| А8
|
1
|
3
|
А17
|
2
|
4
|
| А9
|
2
|
1
|
А18
|
4
|
1
|
Часть 2
| Задание
|
Вариант
|
| № 1
|
№ 2
|
| В1
|
243
|
64
|
| В2
|
67
|
–66
|
| В3
|
2,11,22
|
7,15,23
|
| В4
|
7
|
8
|
| В5
|
1212
|
324
|
| В6
|
СМК
|
СКМ
|
| В7
|
1875
|
16
|
| В8
|
134
|
127
|
| В9
|
БАГВ
|
ВГБА
|
| В10
|
4132
|
1423
|
Часть 3.
Вариант 1
С1
. Элементы ответа:
1) Пример: x = –4, y = –0,5
В качестве примера может быть указана любая пара (x, y), для которой истинно условие:
y<–1 или y>sin x или (y>=–1 и y<=sin x и x< –π/2)
2) Хотя в формулировке задания приведены два пункта, на самом деле в задаче требовалось выполнить три
действия – указать пример входных данных, при которых программа работает неверно, и исправить две ошибки:
а) неправильное использование условного оператора, в результате чего при невыполнении первого или второго условия программа не выдавала ничего (отсутствуют случаи ELSE).
б) приведенным трем ограничениям удовлетворяют также те точки плоскости, у которых (y >= –1 и y <= sin x и x < –π/2).
Ниже мы приводим полный текст программы на Паскале, в которой фрагмент доработки выделен жирным шрифтом.
program ex_c1;
var x,y: real;
begin
readln(x,y);
if (y >= –1) and (y <= sin(x)) and (y >= x – 1) and (x >= –3.14/2)
then
write('принадлежит')
else write('не принадлежит')
end.
Могут быть и другие способы доработки.
Решение для варианта 2 полностью аналогично варианту 1.
С2
. Приведем алгоритм решения задачи на русском языке.
Введем целочисленную переменную Diff с первоначальным значением, равным разности второго и первого элементов, в которую будем заносить разности значений элементов. Введем также переменную MinDiff для записи результата вычислений. Установим первоначальное значение MinDiff равным Diff. В цикле от третьего элемента до конца массива вычисляем разность текущего элемента и предыдущего и заносим его в переменную Diff. Далее сравниваем значения Diff и MinDiff. В случае, если текущая разность меньше, заносим значение текущей разности в переменную MinDiff. По окончании цикла выводим значение переменной MinDiff.
Ниже приведена программа на Паскале, реализующая описанный алгоритм, использующий однократный проход по массиву. При этом количество элементов в массиве описано в разделе констант, что позволяет легко модифицировать данную программу для решения данной задачи для массива любой длины.
program ex_c2;
const N = 30;
var a:array[1..N] of integer;
Diff, MinDiff, i: integer;
begin
Diff := a[2] – a[1];
MinDiff := Diff;
for i := 3 to N do
begin
Diff := a[i] – a[i –1];
if MinDiff > Diff then MinDiff := Diff
end;
writeln(MinDiff);
end.
Решение для варианта 2 в целом аналогично варианту 1. Особенностью второго варианта является необходимость предусмотреть в алгоритме проверку присутствия в массиве положительного элемента, и в случае отсутствия таковых требуется выдать соответствующее сообщение.
С3
. Вариант 1.
Выигрывает второй игрок.[5]
Приведем два способа решения
1 способ. Построение неполного дерева игры.
При таком способе рассматриваются все возможные варианты позиций, которые могут получиться после выполнения очередного хода. Позиции при этом играют роль вершин графа, а возможность перехода от одной позиции к другой обозначается ребром, соединяющим эти позиции. Можно изображать получающееся дерево стандартным образом, а можно оформить его в виде таблицы, где в каждой ячейке записаны координаты фишки на каждом этапе игры. При этом некоторые ветви могут не рассматриваться, если они уже были рассмотрены ранее (тогда-то и получается неполное дерево игры), но надо точно обосновывать, что отсечение ветвей не приводит к потере нерассмотренных вариантов.
Приведем неполное дерево вариантов для данной игры.
| 1 ход
|
2 ход
|
3 ход
|
4 ход
|
| Стартовая позиция
|
I-й игрок (все варианты хода)
|
II-й игрок (выигрышный ход)
|
I-й игрок (все варианты хода)
|
II-й игрок (выигрышный ход, один из вариантов)
|
| 1, 0
|
1, 4
|
4, 4
|
4, 8
|
4, 12
|
| 4, 7
|
4 ,11
|
| 7, 4
|
10 ,4
|
| 1, 3
|
4, 3
|
4, 7
|
4 ,11
|
| 4, 6
|
4 ,10
|
| 7 ,3
|
10 ,3
|
| 4, 0
|
4, 4
или 4, 3
|
Уже рассмотрено
|
Таблица содержит все возможные
варианты ходов первого игрока. Из неё видно, что при любом ходе первого игрока у второго имеется ход, приводящий к победе.
Этот вывод должен быть обязательно
сформулирован. Без него решение считается неполным.
2 способ. Построение таблицы выигрышных и проигрышных позиций.
Скажем сначала несколько слов об этом способе, поскольку он практически отсутствует в учебной литературе
Совокупность всех незаключительных позиций игры разбивается на два множества: множество выигрышных позиций и множество проигрышных позиций. Обозначим множество выигрышных позиций буквой V
, а множество проигрышных позиций буквой Р
. Чем характеризуются эти множества? Это можно описать совершенно формально. Позиция х
является выигрышной (т.е. х
ÎV
), если существует
ход (т.е. ребро графа), ведущий из х
в заключительную позицию или позицию из множества Р
. В свою очередь, позиция х
является проигрышной (т.е. х
ÎР
), если любой ход из этой позиции ведет в позицию из множества V
. Это позволяет расставить знаки + и – по следующему правилу: знаком – отмечаются все заключительные и проигрышные позиции, а знаком + отмечаются все выигрышные. Фактически это некий алгоритм: сначала знак – выставляется для всех заключительных позиций, затем выставляется знак + для каждой позиции, в которой есть ход, ведущий в позицию, помеченную знаком –, затем выставляется знак – для каждой позиции, у которой все ходы ведут в позиции, помеченные знаком +, и т.д.
Вот как выглядит заполненная таблица:
| 13
|
‑
|
‑
|
‑
|
‑
|
| 12
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
‑
|
| 11
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
‑
|
| 10
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
‑
|
| 9
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
‑
|
| 8
|
+
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
| 7
|
‑
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
‑
|
‑
|
| 6
|
‑
|
‑
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
‑
|
‑
|
| 5
|
‑
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
‑
|
| 4
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
+
|
+
|
+
|
‑
|
| 3
|
+
|
+
|
‑
|
‑
|
+
|
+
|
+
|
‑
|
‑
|
+
|
+
|
+
|
‑
|
| 2
|
+
|
+
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
‑
|
+
|
+
|
+
|
‑
|
| 1
|
+
|
+
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
| 0
|
‑
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
‑
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
Поскольку исходная позиция отмечена знаком –, первый игрок проигрывает. Стратегия второго игрока состоит в том, чтобы на каждый ход первого игрока отвечать ходом в позицию, отмеченную знаком –.
Вариант 2. Выигрывает первый игрок. Для этого своим первым ходом он должен поставить фишку в точке с координатами (4,–4). Для доказательства того, что после этого хода он выигрывает, приведем неполное дерево вариантов игры, оформленное в виде таблицы, где в каждой ячейке координаты фишки на каждом этапе игры.
| 1 ход
|
2 ход
|
3 ход
|
4 ход
|
5 ход
|
| Позиция после первого хода
|
II-й игрок (все варианты хода)
|
I-й игрок (выигрышный ход)
|
II-й игрок (все варианты хода)
|
I-й игрок (выигрышный ход, один из вариантов)
|
| 4, –4
|
8, –4
|
12, –4
|
Выигрыш первого игрока
|
| 8, 0
|
12, 4
|
Выигрыш первого игрока
|
| 4, 0
|
4, 4
|
8, 4
|
12, 8
|
| 4, 8
|
8, 12
|
| 8, 8
|
12, 12
|
Таблица содержит все возможные
варианты ходов второго игрока. Из неё видно, что при любом ответе второго игрока у первого имеется ход, приводящий к победе.
А вот решение той же задачи с помощью таблицы выигрышных и проигрышных позиций:
| 13
|
‑
|
‑
|
‑
|
‑
|
| 12
|
+
|
‑
|
‑
|
‑
|
‑
|
| 11
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
‑
|
| 10
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
‑
|
| 9
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
–
|
‑
|
‑
|
‑
|
‑
|
| 8
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
‑
|
| 7
|
‑
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
| 6
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
| 5
|
‑
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
| 4
|
+
|
‑
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
+
|
–
|
‑
|
| 3
|
+
|
+
|
‑
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
+
|
–
|
‑
|
| 2
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
–
|
‑
|
| 1
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
–
|
‑
|
| 0
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
‑
|
| ‑1
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
‑
|
+
|
+
|
+
|
+
|
+
|
‑
|
| ‑2
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
+
|
+
|
+
|
+
|
+
|
‑
|
| ‑3
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
‑
|
+
|
+
|
+
|
+
|
+
|
‑
|
| ‑4
|
+
|
+
|
+
|
+
|
‑
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
–
|
| 0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
Поскольку исходная позиция отмечена знаком +, первый игрок выигрывает. Его стратегия состоит в том, чтобы на каждый ход второго игрока отвечать ходом в позицию, отмеченную знаком –.
С4
. Вариант 1.
Программа читает входные данные, не запоминая их все, а сразу подсчитывая в массиве, хранящем 99 целых чисел согласно номерам школ, количество участников олимпиады из каждой школы или метку, что ученики этой школы присутствовали. Затем распечатываются индексы ненулевых элементов этого массива.
Пример правильной и эффективной программы:
program ex_c4_1;
var nc:array[1..99] of integer;
p:1..99;
c:char;
i, k, N, max: integer;
begin
readln(N);
for i:=1 to 99 do nc[i]:=0;
for i:=1 to N do
begin
repeat read(c) until c =’ ’; {считана фамилия}
repeat read(c) until c =’ ’; {считаны инициалы}
readln(p);
nc[p] := nc[p]+1;
end;
for i:=1 to 99 do
if nc[i]>0 then writeln(i);
readln
end.
Вариант 2.
Программа читает все входные символы до точки один раз, помечая в массиве, состоящем из 10 элементов, какие цифры встретились во входных данных. Сами цифры при этом не запоминаются. За дополнительный проход этого массива печатаются те цифры, которые оказались помеченными, в противном случае выводится –1.
Пример правильной и эффективной программы на языке Паскаль:
program ex_c4_2;
var a: array[0..9] of boolean;
c: char;
i, k: integer;
begin
for i:= 0 to 9 do a[i]:=false;
read(c);
while c<>'.' do
begin
if c in ['0'..'9'] then
begin
k:=ord(c)-ord('0');
a[k]:=true
end;
read(c);
end;
k:=0;
for i:= 9 to 0 do
if a[i] then begin k := k+1; write(i) end;
if k=0 then write(–1);
writeln
end.
IV.
Литература
1. Гейн А.Г. Информатика и информационные технологии: учеб. для 8 кл. общеобразоват. учреждений / А.Г. Гейн, А.И. Сенокосов, Н.А. Юнерман. – М.: Просвещение, 2008. – 175 с.
2. Гейн А.Г. Информатика и информационные технологии: учеб. для 9 кл. общеобразоват. учреждений / А.Г. Гейн, А.И. Сенокосов.– М.: Просвещение, 2006. – 301 с.
3. Гейн А.Г. Информатика и ИКТ: учеб. для 10 кл. общеобразоват. учреждений / А.Г. Гейн, А.Б. Ливчак, А.И. Сенокосов, Н.А. Юнерман – М.: Просвещение, 2008. – 301 с.
4. Гейн А.Г. Информатика и ИКТ: учеб. для 11 кл. общеобразоват. учреждений / А.Г. Гейн, А.И. Сенокосов. – М.: Просвещение, 2009. – 337 с.
5. Гусева И.Ю. ЕГЭ. Информатика. Раздаточный материал тренировочных тестов. / И.Ю. Гусева. – СПб.: Тригон, 2008. – 120 с.
6. ЕГЭ 2008. Информатика. Федеральный банк экзаменационных материалов / Авт.-сост. П.Я.Якушкин, С.С. Крылов. – М.: Эксмо, 2008. – 128 с.
7. Единый государственный экзамен 2008. Информатика. Учебно-тренировочные материалы для подготовки учащихся / Авт.-сост. С.С. Крылов, В.Р. Лещинер, П.Я.Якушкин. – ФИПИ – М.: Интеллект-Центр, 2007. – 120 с.
8. Молодцов В.А. Информатика: тесты, задания, лучшие методики / В.А. Молодцов, Н.Б. Рыжикова. – Ростов на Дону: Феникс, 2008. – 217 с.
9. Русаков С.В. Тестовые задания по базовому курсу информатики / С.В. Русаков, Л.В. Шеставкова. – М.: Чистые пруды, 2006. – 32 с.
[1]
Ознакомиться с демоверсией ЕГЭ-2009 можно на сайте ФИПИ: www.fipi.ru
[2]
Такую работу можно выполнить, используя и демонстрационный вариант ЕГЭ-2009. Тогда оба предложенных нами варианта можно прорешать во втором режиме.
[3]
Мы дословно воспроизвели инструкцию к выполнению заданий этой части. На самом деле задания можно выполнять и записывать их решение в любом порядке, но для каждого из заданий нельзя разрывать запись его решения.
[4]
Задания можно выполнять и записывать их решение в любом порядке, но нельзя разрывать запись решения.
[5]
При определении расстояния от начала координат до текущей точки с координатами (х
, у
) надо пользоваться формулой 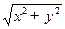 . .
|